Controle vetorial para velocidade de um motor de indução trifásico utilizando estimador filtro de Kalman

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

CENTRO DE TECNOLOGIA

PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA

ELÉTRICA

CONTROLE VETORIAL PARA VELOCIDADE DE UM MOTOR

DE INDUÇÃO TRIFÁSICO UTILIZANDO ESTIMADOR

FILTRO DE KALMAN

FLÁVIO GONÇALVES DANTAS

ii

Seção de Informação e Referência

Catalogação da Publicação na Fonte. UFRN / Biblioteca Central Zila Mamede

Dantas, Flávio Gonçalves

Controle vetorial para velocidade de um motor de indução trifásico utilizando estimador filtro de Kalman / Flávio Gonçalves Dantas. – Natal, RN, 2011.

56 f.; il.

Orientador: Andres Ortiz Salazar.

Dissertação (Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Tecnologia. Programa de Pós-Graduação em Engenharia Elétrica.

1. Controle vetorial – Dissertação. 2. Motor de indução trifásico – Dissertação. 3. Estimador – Dissertação. 4. Filtro de Kalman – Dissertação. 5. Controle de velocidade sensorless – Dissertação. I. Salazar, Andres Ortiz. II. Universidade Federal do Rio Grande do Norte. III. Título.

iii

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE TECNOLOGIA

PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA

CONTROLE VETORIAL PARA VELOCIDADE DE UM

MOTOR DE INDUÇÃO TRIFÁSICO UTILIZANDO

ESTIMADOR FILTRO DE KALMAN

FLÁVIO GONÇALVES DANTAS

Orientador: Prof. Dr. Sc. Andres Ortiz Salazar – UFRN – CT – DCA.

Natal, RN – Brasil Agosto / 2011

Dissertação submetida ao corpo docente da Coordenação do Programa de Pós-Graduação em Engenharia Elétrica da UFRN (Área de concentração: Automação e Sistemas) como parte integrante dos requisitos para obtenção do título de Mestre em

iv

FLÁVIO GONÇALVES DANTAS

CONTROLE VETORIAL PARA VELOCIDADE DE UM

MOTOR DE INDUÇÃO TRIFÁSICO UTILIZANDO

ESTIMADOR FILTRO DE KALMAN

Dissertação submetida ao corpo docente da Coordenação do Programa de

Pós-Graduação em Engenharia Elétrica da Universidade Federal do Rio Grande do

Norte como parte integrante dos requisitos necessários para a obtenção do título de

Mestre em Engenharia Elétrica.

Aprovado por:

___________________________________________________________ Prof. Andres Ortiz Salazar, D.Sc.(UFRN) - Orientador

___________________________________________________________ Prof. Jose Andres Santisteban Larrea, D.Sc.(UFF-RJ) - Examinador Externo

___________________________________________________________ Prof.André Laurindo Maitelli, D.Sc.(UFRN)

v

________________________________________

Agradecimentos

________________________________________

Ao Deus Pai Criador, entrego os meus mais jubilosos louvores de gratidão! A Ele

dou graças por mais essa grande conquista.

Ao Mestre dos mestres, Filho de Deus, Senhor e Salvador, Jesus Cristo.

Ao Consolador de todas as horas, Espírito Santo.

À minha querida e amada esposa, Sara Liziany, por todo seu amor e dedicação.

Aos meus pais Fernandes e Severina, meus irmãos Flademir e Fernanda, meus

sogros Francisco Júnior e Maria das Dores, meu cunhado Joás Letelier, e aos meus

demais familiares, por sempre acreditarem que seria possível alcançar esse ideal.

Ao Professor Andres Ortiz Salazar, por sua orientação, confiança e paciência.

Aos Professores Rasiah Ladchumananandasivam e Marcos Silva, pelo incentivo e

apoio, além do Superintendente de Infraestrutura da UFRN, Gustavo Rosado, pela

compreensão e apoio.

Aos meus estimados amigos e irmãos em Cristo, em especial a Emanuel Jônatas,

Emerson Natã, Isaque Leonardo e Fábio Barbosa, além de todos aqueles que se

lembram de mim em suas orações.

E aos companheiros da pós-graduação que pesquisam no LAMP e no LECA pela

vi

Aos meus amados pais, Fernandes e Severina, e meus irmãos;

À minha adorável esposa, Sara Liziany.

“Porque Deus amou o mundo de tal maneira que deu seu Filho unigênito, para que

vii

________________________________________

Sumário

________________________________________

Sumário Vii

Lista de Figuras e Tabelas ix

Lista de Símbolos xi

Resumo xiii

Capítulo 1 - Introdução 1

1.1. Estimação de Velocidade 2

1.2. Objetivos da Dissertação 2

1.3. Organização da Dissertação 3

Capítulo 2 - Modelagem do Motor de Indução Trifásico 4

2.1. Introdução 4

2.2. Equações do Motor de Indução Trifásico 6

2.3. Transformação

αβ

2.4. Transformação

d

−

q

2.5. Modelo Vetorial do Motor Orientado pelo Fluxo do Rotor 16

2.6. Conclusões 18

Capítulo 3 - Filtro de Kalman (KF) 20

3.1. Introdução 20

3.2. Definição Matemática do Filtro de Kalman (KF) 21

viii

3.4. Discretização do Estimador Filtro de Kalman (KF) 24

3.5. Conclusões 26

Capítulo 4 - Filtro de Kalman Estendido (EKF) 27

4.1. Introdução 27

4.2. Estimador Filtro de Kalman Estendido (EKF) 28

4.3. Conclusões 32

Capítulo 5 - Estimação de Grandezas do Motor de Indução Trifásico

Utilizando o Algoritmo Filtro de Kalman Estendido 34

5.1. Introdução 34

5.2. Discretização do Modelo do Motor 34

5.3. Conclusões 39

Capítulo 6 - Resultados Obtidos ₄₀

6.1. Introdução 40

6.2. Parâmetros do Motor 40

6.3. Inicialização das Matrizes do EKF 41

6.4. Projeto Proposto para Simulação 42

6.5. Resultados da Simulação 46

6.6. Conclusões 50

Capítulo 7 - Conclusões Finais ₅₁

7.1. Trabalhos Futuros 52

ix

________________________________________

Lista de Figuras e Tabelas

________________________________________

Figura Pág.

2.1 Esquema elétrico do motor de indução trifásico 6

2.2a Máquina trifásica simétrica 9

2.2b Máquina equivalente de duas fases simétricas 9

2.3 Seção transversal do motor de indução com enrolamentos bifásicos

9

2.4 Representação vetorial de uma grandeza elétrica do motor 10

2.5 Referência estacionária, transformação de eixos a-b-c para αβ 13

2.6

Transformação da referência estacionária αβ para referência

de rotação síncrona d−q

15

2.7 As correntes do motor nos diferentes referenciais abordados 16

3.1 O ciclo contínuo do Filtro de Kalman discreto 25

3.2

Um quadro completo da operação do Filtro de Kalman,

combinando o diagrama de alto-nível com as equações de

(3.13) à (3.17)

26

4.1 Um quadro completo da operação do EKF, combinando o diagrama de alto-nível com as equações de (4.21) a (4.25)

32

5.1 Estrutura do Sistema de Controle do EKF 38

6.1 Projeto utilizado para simulação 43

x

6.3 Estrutura interna do bloco “Controle de Pulsos” 44

6.4

Comparação da velocidade pelo Sistema de Controle Escalar

(Referência) com a velocidade do Controle Vetorial EKF

(Velocidade Estimada) com aumento de carga

47

6.5

Comparação das correntes de campo e quadratura do Controle

Escalar (Referência) com as correntes de campo e quadratura

do Controle Vetorial EKF (Estimada) sem aumento de carga

48

6.6

Comparação do torque do Sistema de Controle Escalar

(Referência) com o torque do Controle Vetorial EKF (Estimada)

sem aumento de carga

49

6.7

Comparação da velocidade do Sistema de Controle Escalar

(Referência) com a velocidade do Controle Vetorial EKF

(Velocidade Estimada) com aumento de carga

49

Tabela Pág.

xi

________________________________________

Lista de Símbolos

________________________________________

Símbolo Descrição

δ Defasagem angular entre o enrolamento da fase “a” do _{estator e a fase “a” do rotor} φ Defasagem angular no referencial genérico

αβ Coordenadas Bifásicas

d−q _{Eixos direto e quadratura}

s

i e i_{r Corrente do estator e do rotor}

s

V e V_{r Tensão do estator e do rotor}

s

R e R_{r Resistências de estator e de rotor por fase}

s

λ e λ_{r Fluxo de enlace do estator e rotor}

θ

ω _{Velocidade angular do referencial genérico}

mec

ω e ωˆ_{mec Velocidade angular do rotor medida e estimada}

mr

ω Velocidade angular referente à corrente de magnetização do rotor

LH Indutância de mútua entre enrolamentos de estator e rotor

Ls e Lr Indutâncias próprias do estator e do roto por fase

Te Torque Eletromagnético

Kd Coeficiente de atrito dinâmico

np Número de pares de pólos

J Momento de inércia do rotor

ml Carga constante imposta ao motor

σ Fator de dispersão

Ts Constante de tempo do estator

Tr Constante de tempo do rotor

KF Filtro de Kalman

xii

( )

v k e w k( ) _{Ruídos do processo e da medida}

( )

x k e z k( ) _{Vetores de medida e estado atuais}

( )

x kɶ _{e z k}ɶ_{( ) Vetores de medida e estado aproximados}

ˆ( )

x k _{Estimativa de estado anterior}

ˆ( 1)

x k+ _{Estimativa de estado atual}

( )

y k e y kˆ( ) _{Valores das saídas reais e estimadas}

( )

u k e u kˆ( ) _{Valores das entradas de controle reais e estimados}

A, B e C Matrizes de relações do Filtro de Kalman

Ad, Bd e Cd Matrizes de relação A e B discretizadas

R Matriz de ruídos de medição

Q Matriz de ruídos de estados

P Matriz de covariância

K Matriz ganho de Kalman

T Intervalo de amostragem

( )

x k

e e ez k( ) Erro de processo e de medida

( )

ˆ_{x k}

e e eˆz k( ) Erro estimado de processo e de medida

s

i e ir Vetor de correntes do estator e do rotor

s

V e Vr Vetor de corrente de estator e do rotor

s

λ e λr Vetor de fluxo do estator e do rotor

dt d

Operador de derivação de uma função ou variável

∫

sen x e cos x Funções seno e cosseno de um ângulo x genérico

xiii

________________________________________

Resumo

________________________________________

Dissertação de Mestrado

Programa de Pós-Graduação em Engenharia Elétrica

Universidade Federal do Rio Grande do Norte

Controle Vetorial Para Velocidade De Um Motor de Indução

Trifásico Utilizando Estimador Filtro de Kalman

Autor: Eng. Flávio Gonçalves Dantas

Orientador: D. Sc. Andres Ortiz Salazar

Esta dissertação apresenta o desenvolvimento de uma simulação

computacional com a finalidade de demonstrar o funcionamento do controle vetorial

para velocidade de um motor de indução trifásico utilizando método de estimação

pelo Filtro de Kalman Estendido, bem como os procedimentos necessários para sua

implementação prática. A motivação maior que influenciou a pesquisa está na

utilização de um sistema de controle inovador que não necessita de sensores no

eixo da máquina (técnica sensorless), proporcionando desta forma uma considerável

redução nos custos de acionamentos e manutenção, aumento da confiabilidade, da

robustez e da imunidade a ruídos em relação ao controle de motores convencionais

com sensores.

xiv

________________________________________

Abstract

________________________________________

Master Thesis on Electrical Engineering

Post-Graduate Program of Electrical Engineering

Federal University of Rio Grande of Norte

Speed Vector Control of Triphasic Induction Motor Estimator Using

Kalman Filter

Author: Eng. Flávio Gonçalves Dantas

Research Supervisor: D. Sc. Andres Ortiz Salazar

This paper describes the study, computer simulation and feasibility of

implementation of vector control speed of an induction motor using for this purpose

the Extended Kalman Filter as an estimator of rotor flux. The motivation for such

work is the use of a control system that requires no sensors on the machine shaft,

thus providing a considerable cost reduction of drives and their maintenance,

increased reliability, robustness and noise immunity as compared to control systems

with conventional sensors.

Keywords: vector control, triphasic induction motor, estimator, Kalman filter,

1

_______________________________________

Capítulo 1

_______________________________________

Introdução

Na atualidade diversas pesquisas são realizadas na área de controle para

velocidade de motores de indução trifásico com a finalidade de se obter um

desempenho mais próximo possível do comportamento do motor de corrente

contínua, mantendo as grandes vantagens do motor de indução como a

robustez, construção simples, necessidade de pouca manutenção e

possibilidade de fornecer um motor totalmente fechado (motor de gaiola),

permitindo assim suprir uma maior demanda de aplicações, como em lugares

mais profundos ou submetidos à alta poluição.

Em aplicações onde se faz necessário um alto desempenho dinâmico,

respostas rápidas e alta precisão de regulação de velocidade, o motor elétrico

deve fornecer essencialmente um controle preciso de torque para uma faixa

extensa de condições de operação. Para tais aplicações os acionamentos com

corrente contínua sempre representaram uma solução ideal, pois a

proporcionalidade da corrente de armadura, do fluxo e do torque num motor de

corrente contínua proporcionam um meio direto para o seu controle. Contudo, a

busca por avanços tecnológicos significativos tem diminuído esta hegemonia e,

gradativamente, estão aparecendo opções de novas alternativas, como o uso de

acionamentos em corrente alternada do tipo controle vetorial (Weg, 2004).

Em razão do controle vetorial nas máquinas de corrente alternada, as

2

desta forma as características de resposta transitória são similares às das

máquinas de corrente contínua de excitação independente. O sistema poderá

se adaptar a qualquer variação de carga e/ou variação do valor de referência

tão rápido quanto à máquina de corrente contínua (Gonzalez, 2004).

Para a aplicação do controle vetorial é de suma importância conhecer a

posição exata das componentes dos eixos d−q, ou seja, a posição correta do

fluxo do rotor (se este for utilizado como referência). Assim, se faz necessário

ter o conhecimento de algum parâmetro que auxilie a encontrar o ângulo do

fluxo do rotor ou a posição dele, obrigando desta forma a medir ou estimar a

velocidade do rotor, e, com o cálculo da velocidade do escorregamento,

determinar a velocidade do fluxo do rotor.

1.1. Estimação da Velocidade

No setor industrial é essencial a redução de custos em sistemas de

acionamentos. Isto pode ser obtido substituindo sensores mecânicos por

técnicas de estimação de velocidade. Esse processo de estimação sem o

auxílio de sensores é denominado técnica “sensorless”. Uma possível

alternativa para determinação da velocidade rotórica do motor é a utilização do

Filtro de Kalman.

1.2. Objetivos da Dissertação

A meta principal deste trabalho é analisar a possibilidade de

implementação de um sistema para controle da velocidade de um motor de

indução trifásico sem a utilização de sensores no eixo da máquina (sensorless)

pelo uso do algoritmo estimador Filtro de Kalman (na sua forma “estendida”, que

será abordada no capítulo 4), o que proporcionaria uma economia nos custos

de acionamentos e manutenção, além do aumento da confiabilidade e robustez

no controle da velocidade.

Para tal objetivo, foi projetado e simulado na plataforma computacional

“Simulink” do Software Matlab um sistema para controle da velocidade rotórica

3

acionamentos, bem como o algoritmo estimador Filtro de Kalman Estendido

(EKF) inserido no bloco “Embedded Function” do Simulink destinado para

programação.

1.3. Organização da Dissertação

No Capítulo 2 são apresentadas as equações que determinam o

comportamento das grandezas eletromecânicas do motor de indução trifásico,

bem como as transformações necessárias para implementação do modelo do

motor no Flitro de Kalman e para o controle vetorial da máquina.

O Capítulo 3 apresenta uma introdução do Filtro de Kalman, aborda seus

conceitos matemáticos bem como seu princípio de funcionamento e introduz os

conhecimentos que serão aplicados no estimador Filtro de Kalman.

No Capítulo 4 é abordada a variação estendida do Filtro de Kalman que

será aplicada ao modelo vetorial do motor de indução .

No Capítulo 5 são demonstradas as equações discretizadas e o algoritmo

do Filtro de Kalman Estendido que será usado para o controle sem sensor da

velocidade do motor e em seguida é apresentado o desenvolvimento de uma

simulação através da ferramenta Simulink/Matlab.

Já no capítulo 6 comprovam-se através de simulações os resultados do

funcionamento do controle da velocidade através do algoritmo estimador Filtro

de Kalman Estendido.

No Capítulo 7 são expostas as conclusões oriundas dos trabalhos

4

_______________________________________

Capítulo 2

_______________________________________

Modelagem do Motor de Indução Trifásico

2.1. Introdução

A facilidade de controle de fluxo e conjugado através das correntes de

campo e de armadura e o menor custo de implantação dos acionamentos de

corrente contínua, fizeram do motor de corrente contínua o mais utilizado nas

aplicações onde se exige rapidez de resposta e operação com alto

desempenho, sobretudo em baixas velocidades (Stopa, 1997).

Por outro lado, as desvantagens inerentes à existência de comutadores e

escovas no motor de corrente contínua, com manutenção excessiva,

não-aplicabilidade a ambientes corrosivos e explosivos, capacidade limitada de

comutação em altas velocidades e limitações a tensões e/ou sobrecargas

elevadas, levaram à procura de soluções que empregassem motores de

corrente alternada.

As máquinas de corrente alternada, entre elas os motores de indução

trifásico, são amplamente utilizados nas mais variadas aplicações em

instalações industriais e comerciais. Eles são adequados para o uso em cargas

que exigem velocidades constantes ou variáveis, ou ainda, com as que exigem

reversões e variadas velocidades.

Existem muitos tipos disponíveis, os quais cobrem uma larga faixa de

5

tipos de fontes de alimentações com diferentes combinações e valores de

número de fases, freqüências e tensões (De Almeida, 2001).

Os principais obstáculos à aplicação da máquina de indução em

acionamentos onde se empregavam máquinas de corrente contínua eram

associados ao limitado desempenho dinâmico das técnicas de controle até

então existentes. O fato das correntes de excitação e de carga na máquina de

indução circularem no mesmo enrolamento e não em enrolamentos separados,

como na máquina de corrente contínua, dificultava o controle. O

desenvolvimento das técnicas de controle vetorial mostrou ser possível o

controle da velocidade nos motores de corrente alternada com desempenho

competitivo com o motor de corrente contínua, despertando a atenção para o

uso de motores de corrente alternada em acionamentos controlados. As

vantagens do controle vetorial são (Weg, 2004):

•

•

•

•

O motor de indução com o rotor em gaiola de esquilo, em particular, por

ser uma das máquinas de corrente alternada mais barata e robusta, disponível

em várias as faixas de potência, é uma alternativa bastante interessante.

Os avanços na área de eletrônica de potência, com o barateamento dos

semicondutores de potência e também na área de processamento digital de

sinais, com o surgimento de processadores com velocidades cada vez maiores

e a custos decrescentes, tornaram os motores de corrente alternada uma opção

aos de corrente contínua em acionamentos com velocidades controladas.

Entre as principais vantagens dos motores de indução trifásicos,

podemos citar: menor custo, manutenção mais simples e menos freqüente,

menor relação peso/potência, potências maiores, mais simples de proteger em

ambientes com risco de explosão, além de potências limites superiores ao de

6

2.2. Equações do Motor de Indução Trifásico

Para a modelagem matemática de um motor de indução trifásico é

necessário conhecer sua estrutura física e o comportamento dinâmico das

grandezas internas como a corrente e tensão, os enlaces dos fluxos, o torque

eletromagnético além da velocidade e posicionamento do eixo do motor. Ainda

devem ser consideradas as seguintes informações (Krishnan, 2001):

•

•

•

O motor de indução escolhido para o desenvolvimento deste trabalho foi

do tipo “rotor em gaiola”, conforme as razões explicadas anteriormente. Este

tipo de motor apresenta curto-circuito nos terminais do rotor, o que torna a

tensão nos terminais do rotor nula, ou seja, Vr =0.

O modelo para este tipo de motor possui bobinas trifásicas no rotor e no

estator, conforme representado na figura 2.1, onde δ é a defasagem angular

entre o enrolamento da fase “a” do estator e a fase “a” do rotor, e θ é a

defasagem angular no referencial genérico, e V é a tensão entre os terminais da

bobina, referida “s” para estator e “r” para rotor, assim como sua respectiva fase

(“a”, “b” ou “c”).

7

Admitindo-se um referencial trifásico genérico “θ”, o comportamento

dinâmico da máquina, expresso em função das variáveis de estado velocidade,

fluxo do rotor e correntes do estator, é apresentado nas equações a seguir

(Maschio, 2006):

V_s R i_{s s} d _s K_{m s} dtλ ωθ λ

= + + (2.1)

0 r r r 2 m r

d

R i K

dtλ ω λ

= + + (2.2)

λ_s =L i_{s s}+L i_{H r} (2.3)

λr =L iH s +L ir r (2.4)

Te = −npλsTK im s =npλrTK im r (2.5)

d _mec 1(T_e K_{D mec} m_l)

dtω = J − ω − (2.6)

Com:

ω_ele =ω_θ −n_pω_mec (2.7)

0 1 1

1

1 0 1

3

1 1 0

m

K

−

 

 

= _ − _

₋ 

 

(2.8)

Onde:

Rs = Resistência do estator;

Rr = Resistência do rotor;

Vs = Tensão no estator;

Vr = Tensão no rotor;

is = Corrente do estator;

ir = Corrente do rotor;

λs= Fluxo de enlace do estator;

λ_r= Fluxo de enlace do rotor;

8

ωmec= Velocidade angular do rotor;

np = Número de par de pólos do motor;

LH = Indutância mútua entre enrolamentos de estator e rotor;

Ls = Indutância própria do estator;

Lr = Indutância própria do rotor;

Te = Torque eletromagnético;

J = Momento de inércia do motor;

Kd = Coeficiente de atrito dinâmico;

ml = Carga constante imposta ao motor;

As equações do motor podem ser descritas em diferentes referenciais.

Os casos mais adotados são:

•

•

•

No processo de estimação de velocidade são necessárias medições de

tensões e correntes no estator da máquina, por esse motivo o referencial mais

adequado será o estacionário.

2.3. Transformação

αβ

Modelar um motor de indução trifásico de corrente alternada é

consideravelmente complexo, em razão das três fases do circuito rotórico

mover-se em relação às três fases do circuito estatórico.

O fato do comportamento dinâmico do motor apresentar equações

diferenciais com indutâncias mútuas variando no tempo dificulta ainda mais sua

modelagem. Porém, um motor de três fases pode ser representado por uma

máquina equivalente de duas fases, como mostrado na figura 2.2. Essa

9

(a) (b)

Figura 2.2 – (a) Máquina trifásica simétrica; (b) Máquina equivalente de duas

fases simétricas.

Fisicamente a transformação αβ0 transforma o motor trifásico simétrico

em uma máquina simétrica bifásica, representado na figura 2.3, com mesma

potência mecânica, torque, velocidade e número de pólos (Barbi, 1985). Esse

tipo de abordagem no motor é também designado de “Transformação de

Clarke”.

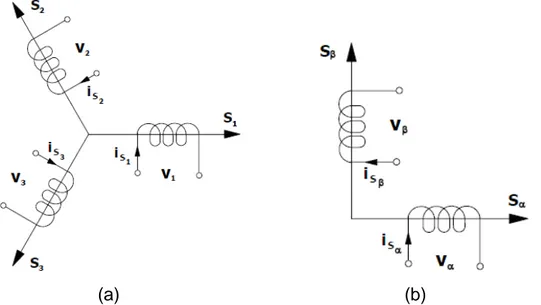
Figura 2.3 - Seção transversal do motor de indução com enrolamentos

bifásicos.

As grandezas que descrevem o modelo do motor passam a ter

representação como entidades complexas, sendo o eixo Real a projeção em α

10

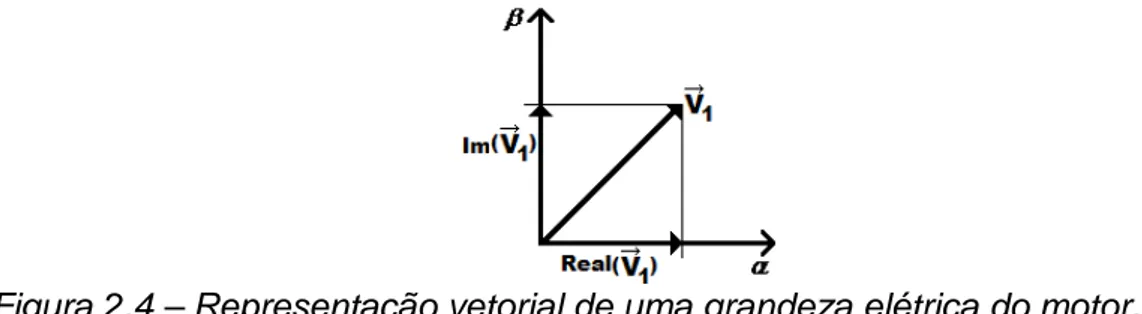
Figura 2.4 – Representação vetorial de uma grandeza elétrica do motor.

As equações das grandezas do motor representadas no plano complexo,

considerando que a fase “a” coincida com o eixo real do plano, são

apresentadas a seguir:

2 2

( )

3 a b c

V V_α jV_β V αV α V →

= + = + + (2.9)

2 2

( )

3 a b c

i i_α ji_β i αi α i →

= + = + + (2.10)

2 2

( )

3 a b c

j

α β

λ λ λ λ αλ α λ

→

= + = + + (2.11)

Com:

j2 /3 e π

α = (2.12) 2 j4 /3

e π

α = (2.13) correspondentes à direção espacial geométrica nas fases “b” e “c”, equivalente

aos operadores de deslocamento espacial de 120º e 240º, respectivamente.

Aplicando a transformada αβ0 nas equações (2.1) a (2.6) para o

referencial estacionário (ω_θ =0), ou referencial fluxo do estator, obtém-se:

s s s s

d V R i

dtλ

= + (2.14)

0 R i_{r r} d _r jn_{p mec r} dtλ ω λ

= + − (2.15)

λ_s =L i_{s s}+L i_{H r} (2.16)

λ_r =L i_{H s} +L i_{r r} (2.17)

3

( )

( )

Im Im

2 2

e p s s p r r

11

d _mec 1(T_e K_{D mec} m_l)

dtω = J − ω − (2.19)

O modelo do motor de indução no domínio contínuo pode ainda ser

escrito na forma de equações de estado, que será necessário para a

implementação do Filtro de Kalman, segmentando em parte real e imaginária

em função das variáveis corrente do estator e fluxo do rotor, obtendo-se:

1 1 1 _{H H}

s s s r r r

s s r s r r s r

L L

d

i V i

dt α L α T T α L L T α L L β

σ _{λ ω λ}

σ σ σ σ σ

 ₋ 

= − +  + −

  (2.20)

1 1 1 _{H H}

s s s r r r

s s r s r r s r

L L

d

i V i

dt β L β T T β L L T β L L α

σ _{λ ω λ}

σ σ σ σ σ

 ₋ 

= − +  + −

  (2.21)

1 H

r r s r r

r r

L d

i

dtλα = −T λα + T α+ω λβ (2.22)

1 H

r r s r r

r r

L d

i

dtλβ = −T λβ + T β−ω λα (2.23)

3 ( )

2

e H p r s r s

r

T L n i i

L λα β λβ α

= − (2.24)

Com: 2 1 H s r L L L

σ = − 

 é o fator de dispersão; (2.25)

s s s L T R

= é a constante de tempo do estator; (2.26)

r r r L T R

= é a constante de tempo do rotor; (2.27)

Representando as equações acima através de vetores e matrizes,

obtém-se o resultado a obtém-seguir (Kubota, 1993):

d x Ax Bu

dt = + (2.28)

12

Onde:

x=isα isβ λrα λrβT (2.30)

u=_V_sα V_sβ_T (2.31)

y=_i_sα i_sβ_T (2.32)

1 2 3

1 3 2

4 5 4 5 0 0 0 0 mec mec p mec p mec

a a a

a a a

A

a a n

a n a

ω ω ω ω −    _{− −}    =_{ − − }   −     (2.33) 1/ 0 0 1/ 0 0 0 0 s s L L B σ σ       =       (2.34)

1 0 0 0

0 1 0 0 C=_ _

  (2.35)

Sendo os coeficientes da matriz A definidos por:

1 1 1 s r a T T σ σ σ  ₋  = + 

  (2.36)

2

H s r r

L a

L L Tσ

= (2.37)

3 H p s r L a n

L Lσ

= (2.38)

4 H r L a T

= (2.39)

5

1

r

a T

= (2.40)

2.4. Transformação

d

−

q

Se para o processo de estimação da velocidade é ideal o referencial

estacionário (orientado pelo fluxo do estator) em coordenadas αβ , por outro

lado no controle vetorial é necessária a orientação pelo fluxo do rotor em

13

torque e fluxo, transforma-se o modelo da máquina de indução em um modelo

similar ao das máquinas de corrente contínua, cujo controle é bem mais simples

e eficaz, tanto para altas como para baixas rotações. O controle vetorial é

executado através das componentes d−q das correntes de campo e

quadratura, oriundas da transformação trifásica para bifásica αβ estacionária e

em seguida para coordenadas d−q, designada de “Transformação d−q”. A

seguir é apresentado o método para obtenção dessas correntes em

coordenadas d−q.

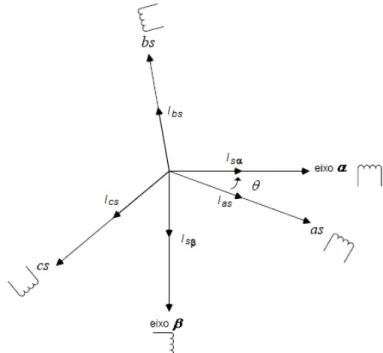
Considere uma máquina de indução de três fases simétricas, com os

eixos as-bs-cs estacionário, defasados de um ângulo de 2π_{/3, como mostrado}

na figura 2.5.

O objetivo é transformar as variáveis as-bs-cs da estrutura de referência

estacionária das três fases em variáveis αβ da estrutura de referência

estacionária de duas fases e então, transformá-la na estrutura d−q de

referência de rotação síncrona e vice-versa. Fisicamente, será a transformação

da máquina bifásica com enrolamentos estatóricos fixos e enrolamentos

rotóricos girantes em enrolamentos estatóricos fixos e rotóricos

pseudo-estacionários (Barbi, 1985). Essa abordagem da máquina é também

denominada de “Transformação de Park”.

14

Supondo que os eixos αβ sejam orientados pelo ângulo θ_{, como}

mostrado na figura 2.5, as correntes i_sα e i_sβ podem ser expressas em

componentes as-bs-cs e representadas na forma de matriz por:

(

)

(

)

(

)

(

)

cos 1

cos 120º 120º 1

cos 120º 120º 1

as s

bs s

cs s

i sen i

i sen i

sen i i α β θ θ θ θ θ θ            _{= − −}             _{+ +}

      (2.41)

A relação inversa correspondente é dada por:

(

)

(

)

(

)

(

)

0

cos cos 120º cos 120º 2

120º 120º

3

0.5 0.5 0.5

s as

s bs

cs s

i i

i sen sen sen i

i i

α

β

θ θ θ

θ θ θ

   _{− +}     ₌  _{− +}              _{ } _{ }   (2.42)

is0 é adicionado como componente de seqüência zero, que talvez esteja

presente ou não. A tensão e o fluxo podem ser transformados por equações

semelhantes.

É conveniente fixar θ_{=0, de modo que o eixo} α _{esteja alinhado com o}

eixo as. Ignorando a componente de seqüência zero, a relação de

transformação pode ser simplificada como:

as s

i =i_α (2.43)

1 3

2 2

bs s s

i = − i_α − i_β (2.44)

1 3

2 2

cs s s

i = − i_α+ i_β (2.45)

e inversamente:

2 1 1

3 3 3

s as bs cs as

i_α = i − i − i =i (2.46)

1 1

3 3

s bs cs

15

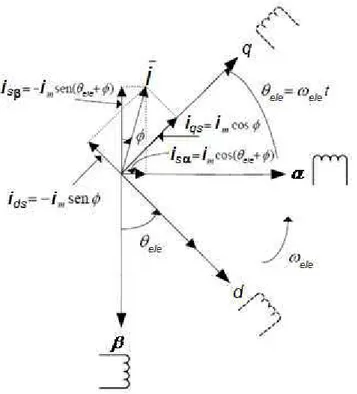
A figura 2.6 mostra os eixos d−q em rotação síncrona, que giram com

velocidade síncrona ω_ele com relação aos eixos αβ e o ângulo θ_ele =ω_elet. As

duas fases do enrolamento αβ são transformadas em um enrolamento

hipotético projetados nos eixos d−q. As correntes nos eixos αβ podem ser

transformadas para uma estrutura de eixos d−q, como mostrado a seguir:

Figura 2.6 – Transformação da referência estacionária αβ para

referência de rotação síncrona d−q.

Com base no diagrama acima, aplica-se a “Transformação de Park”:

cos

qs s ele s ele

i =i_α θ −i sen_β θ (2.48)

i_ds =i sen_sα θ_ele+i_sβcosθ_ele (2.49)

E a relação inversa, que também é conhecida como “Transformação

Inversa de Park”, é obtida por:

i_sα =i_qscosθ_ele−i sen_ds θ_ele (2.50)

cos

s qs ele ds ele

16

2.5. Modelo Vetorial do Motor Orientado pelo Fluxo do Rotor

Após as transformações αβ durante a modelagem do motor de indução

de corrente alternada foi estabelecida uma relação entre o torque

eletromagnético e as grandezas fluxo do rotor e corrente do estator, conforme

exposta na equação T_e=(3 / 2L L n_r) _{H p}[λ_{rα β}i_s −λ_{rβ α}i_s ]. No entanto, para obter um

controle de velocidade idêntico ao do motor de corrente contínua, é necessário

o desacoplamento entre o torque e o fluxo do rotor, sendo este último o

referencial para o referido controle. É possível esta orientação estimando a

magnitude e a posição exata desse fluxo do rotor girante baseado no modelo

vetorial do motor, método pelo qual executa o Filtro de Kalman (KF).

Representando as correntes do motor nos diferentes referenciais

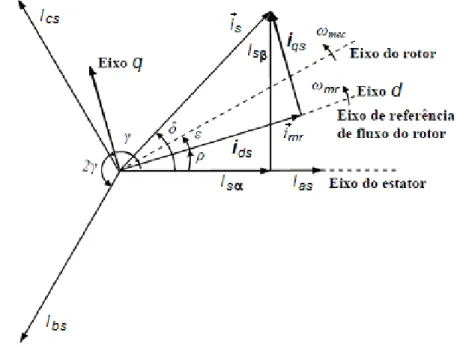
abordados e no mesmo diagrama vetorial, obtém-se o esquema da figura 2.7:

Figura 2.7 – As correntes do motor nos diferentes referenciais abordados

Onde:

mec

ω é a velocidade mecânica do rotor;

mr

ω é a velocidade do campo girante do rotor;

mr

i é a corrente de magnetização que está relacionada com a

17 r mr H i L λ

= (2.52)

Entretanto, se λ_r =L i_{H s}+L i_{r r}, então a nova equação para i_mr será:

r

mr s r

H

L

i i i

L

= + (2.53)

Observando o diagrama vetorial, tem-se que:

s sd sq

i =i + ji (2.54)

De maneira análoga, aplica-se também:

r rd rq

i = +i ji (2.55)

Substituindo (2.54) e (2.55) em (2.53), obtem-se:

( ) r ( )

mr sd sq rd rq mrd mrq

H

L

i i ji i ji i ji

L

= + + + = + (2.56)

Adotando o referencial solidário com fluxo do rotor, orientado por ω_mr,

considera-se que i_mr possui apenas parte real, pode-se obter então:

r

mrd sd rd

H

L

i i i

L

= + (2.57)

r 0

mrq sq rq

H

L

i i i

L

= + = (2.58)

Com intuito de encontrar as componentes d−q da corrente rotórica em

18

H ( )

rd mrd sd

r

L

i i i

L

= − (2.59)

H rq sq r L i i L

= − (2.60)

E finalmente, o modelo vetorial contínuo do motor de indução orientado pelo

fluxo do rotor, segmentado em parte real e imaginária, é mostrado a seguir:

mr 1 (mr sd)

r

d

i i i

dt =T − (2.61)

_mr sq _{p mec}

r mr

i n T i

ω = + ω (2.62)

T_e =K i i_{m mr sq} (2.63)

Onde:

3(1 ) 2

m s

K = −σ L (2.64)

Como se observa na equação (2.63), o torque eletromagnético Te é

determinado em função da corrente de magnetização i_mr (que depende da

corrente ids) e da componente em quadratura da corrente do estator isq,

consequentemente promovendo o desacoplamento entre os vetores fluxo e

torque, o que permitirá o controle vetorial independente de um em relação ao

outro, aproximando-se de um sistema de controle para máquina de corrente

contínua.

2.6. Conclusões

Neste capítulo foi apresentado o modelo vetorial contínuo do motor de

indução na forma de equações de estado em coordenadas αβ de referencial

estacionário, explicitado nas equações (2.28) a (2.40) e que serão utilizados na

implementação do estimador Filtro de Kalman Estendido. Também foi abordada

19

campo ids, que é a responsável pela produção de fluxo, e quadratura iqs, que é

a responsável pela produção de torque, ambas no referencial síncrono (fluxo do

20

_______________________________________

Capítulo 3

_______________________________________

Filtro de Kalman (KF)

3.1. Introdução

Conforme explicado anteriormente, será aplicado um algoritmo estimador

de velocidade denominado “Filtro de Kalman Estendido (EKF)”, que é um

método derivado do “Filtro de Kalman (KF)” convencional. Portanto, para se

compreender o funcionamento do EKF será imprescindível dominar a

metodologia utilizada pelo KF. A seguir será abordada a teoria que envolve as

características do estimador Filtro de Kalman.

O Filtro de Kalman é um conjunto de equações matemáticas que fornece

uma solução recursiva para o problema de estimação de estados para um

processo. A principal vantagem do método recursivo é sua eficiência

computacional em comparação com métodos clássicos, como os mínimos

quadrados, por exemplo. Outra característica importante é que no método

clássico, todas as medidas devem ser conhecidas de antemão para a

estimação, enquanto que o Filtro de Kalman atualiza os cálculos a cada nova

medida que é fornecida pelo sistema de observação. O filtro é muito importante

em vários aspectos como: estimação de estados passados, presentes e futuros,

mesmo quando a natureza do sistema modelado não seja conhecida. O objetivo

deste capítulo é fornecer uma conceituação teórica para a utilização do Filtro de

21

3.2. Definição Matemática do Filtro de Kalman (KF)

O Filtro de Kalman é utilizado em um problema geral da tentativa do

cálculo do estado n

x∈ℜ de um controle discreto de processo que é governado

por uma equação diferencial estocástica linear (Welch, 2004):

x k( )= Ax k( − +1) Bu k( − +1) w k( −1) (3.1)

e com uma medida m

z∈ℜ dada por:

z k( )=Hx k( )+v k( ) (3.2)

As variáveis aleatórias w e v representam ruídos do processo e da

medida (respectivamente). É assumido que os mesmos são independentes um

do outro, são do tipo branco, e com distribuições de probabilidade normais:

p w( )∼N(0, )Q _(3.3)

p v( )∼N(0, )R _(3.4)

Na prática, as matrizes de covariância do ruído Q e a covariância do

ruído R, podem mudar a cada passo de tempo ou medida, porém aqui são

assumidas como constantes.

A matriz Anxn na equação diferencial (3.1) relaciona os estados no

instante k-1 com o estado do passo k, na ausência de uma função ativadora ou

ruído de processo. A matriz Bnxl relaciona a entrada de controle u∈ℜlao estado

x. A matriz Hnxm na equação da medida (3.2) relaciona o estado com a medida

z. Como as matrizes R e Q, a matriz H também pode mudar a cada passo de

22

3.3. Estimador Filtro de Kalman (KF)

Definindo ˆ( ) n

x k −∈ℜ (notação “super menos”) como sendo o estimador

de estado a priori no passo k, determinando o conhecimento do processo antes

do passo k, e ˆ( ) n

x k ∈ℜ como sendo o estimador de estado a posteriori no

passo k, após a medida z k( ). Então se podem definir os erros dos estimadores

a priori e a posteriori como:

e k( )− ≡x k( )−x kˆ( )− (3.5)

e k( )≡x k( )−x kˆ( ) (3.6)

A covariância do erro no estimador a priori é dada por:

P k( )− =E e k e k[ ( )− ( ) ]−T (3.7)

e a covariância do erro no estimador a posteriori como:

( ) [ ( ) ( ) ]T

P k =E e k e k (3.8)

Ao derivar as equações para o Filtro de Kalman, tem-se como meta

encontrar uma equação que calcule uma estimativa de estado a posteriori x kˆ( ),

como uma combinação linear do estimador a priori x kˆ( )− e uma diferença

ponderada entre a medida atual z k( ) e uma predição de medida Hx kˆ( )−, como

mostrado na equação (3.9):

x kˆ( )=x kˆ( )−+K z k[ ( )−Hx kˆ( ) ]− (3.9)

A diferença [ ( )z k −Hx kˆ( ) ]− em (3.9) é chamada de inovação medida ou

residual. O resíduo reflete a discrepância entre a predição da medida Hx kˆ( )− e a

23

A matriz Knxm em (3.9) é escolhida para ser o ganho ou fator de mistura

que minimiza a covariância do erro a posteriori (3.8). Essa minimização pode

ser realizada primeiramente substituindo (3.9) na definição do erro e k( ), e em

seguida em (3.8), executando as expectativas indicadas, levando a derivada da

substituição do resultado com relação a K, colocando o resultado igual a zero e

resolvendo então para K.

Uma forma para K que resulta na minimização de (3.8) é dada por:

1

( ) ( ) T[ ( ) T ]

K k =P k −H HP k −H +R − ou ( ) ( ) ( )

T T

P k H K k

HP k H R −

−

=

+ (3.10)

Observando (3.10), pode-se notar que se a covariância do erro na

medida R k( ) se aproxima de zero, o ganho K atua sobre o resíduo mais

intensamente, especificamente:

1 ( ) 0

lim ( )

R k K k H

−

→ = (3.11)

Por outro lado, quando a covariância do erro do estimador a priori P k( )−

aproxima-se de zero, o ganho K atua menos intensamente no resíduo,

especificamente:

( ) 0

lim ( ) 0

P k

K k

−_→ = (3.12)

Outro modo de pensar sobre a atuação de K é que quando a covariância

do erro de medida R se aproxima de zero, a medida atual z k( ) _{é cada vez mais}

confiável, enquanto a predição da medida Hx kˆ( )− é cada vez menos confiável.

Por outro lado, quando a covariância do erro do estimador a priori P k( )− se

aproxima de zero, a medida atual z k( ) é cada vez menos confiável, enquanto a

24

3.4. Discretização do Estimador Filtro de Kalman (KF)

O Filtro de Kalman faz as estimativas de um processo usando uma forma

de controle de realimentação: o filtro estima o estado do processo em algum

momento e então obtém a realimentação na forma de medidas (ruidosas).

Como tal, as equações para o Filtro de Kalman se dividem em dois grupos:

equações de atualização de tempo e equações de atualização de medida. As

equações de atualização de tempo são responsáveis para projetar adiante o

estado atual, e o estimador da covariância do erro para obter um estimador a

priori para o próximo instante. As equações de atualização de medida são

responsáveis pela realimentação, isto é, por incorporar uma medida nova na

estimativa a priori para obter um estimador melhorado a posteriori.

As equações de atualização de tempo também podem ser vistas como

equações de predição, enquanto as equações de atualização de medida podem

ser vistas como equações de correção. Realmente o algoritmo final de

estimação se assemelha a um algoritmo de predição-correção para resolver

problemas numéricos como mostrado na figura 3.1. As atualizações de tempo

projetam o estimador de estado atual à frente no tempo. A atualização de

medida ajusta o estimador projetado, por uma medida atual naquele momento.

As equações específicas para as atualizações de tempo e medida são

apresentadas abaixo:

x kˆ( )− = Ax kˆ( − +1) Bu k( −1) (3.13)

( ) ( 1) T

P k − = AP k− A +Q (3.14)

Novamente nota-se que as equações de atualização de tempo (3.13) e

(3.14) projetam o estimador de estado e a covariância do erro de estado do

passo de tempo k-1 para o passo k.

1 ( ) ( ) T[ ( ) T ]

K k =P k −H HP k −H +R − (3.15)

ˆ( ) ˆ( ) ( )[ ( ) ˆ( ) ]

x k =x k −+K k z k −Hx k − (3.16)

( ) [ ( ) ] ( )

25

Figura 3.1 - O ciclo contínuo do Filtro de Kalman discreto.

A primeira tarefa durante a atualização de medida é calcular o ganho de

Kalman, K k( ). Note que a equação dada em (3.15) é igual a (3.10). O próximo

passo é medir de fato o processo para obter z k( ), e então gerar um estimador

de estado a posteriori incorporando a medida como em (3.16). Novamente

(3.16) simplesmente é (3.9) repetida aqui. O passo final é obter um estimador

da covariância de erro a posteriori calculado por (3.19).

Depois de cada par de atualizações de tempo e de medida, o processo é

repetido com o estimador a posteriori anterior usado para projetar ou predizer o

novo estimador a priori. Esta natureza recursiva é uma das características muito

atraentes do Filtro de Kalman e torna a implementação prática muito mais

viável. O Filtro de Kalman recursivamente condiciona a estimativa atual em

todas as medidas passadas.

A figura 3.2 oferece um quadro completo da operação do filtro,

combinando o diagrama de alto-nível da figura 3.1 com as equações (3.13),

26

Figura 3.2 – Um quadro completo da operação do Filtro de Kalman,

combinando o diagrama de alto-nível com as equações de (3.13) à (3.17).

3.5. Conclusões

Os conhecimentos adquiridos neste capítulo auxiliarão na compreensão

da versão estendida do Filtro de Kalman, pois o princípio de funcionamento do

Filtro de Kalman Estendido (EKF) é semelhante à versão convencional

abordada neste capítulo, divergindo apenas nas aproximações executadas pela

27

_______________________________________

Capítulo 4

_______________________________________

Filtro de Kalman Estendido (EKF)

4.1. Introdução

Como descrito no capítulo anterior, o Filtro de Kalman é utilizado em um

problema geral da tentativa do cálculo do estado n

x∈ℜ de um controle discreto

de processo que é governado por uma equação diferencial estocástica linear.

Mas, e se o processo a ser estimado e/ou o relacionamento das medidas do

processo for não-linear? Algumas das aplicações mais interessantes e bem

sucedidas da filtragem de Kalman tem sido nessas situações. O Filtro de

Kalman que lineariza determinado modelo de processo, sobre a covariância e o

modelo corrente, é conhecido como “Filtro de Kalman Estendido” ou “EKF”.

O Filtro de Kalman Estendido é basicamente, um observador estocástico

de ordem completa apropriado para estimação ótima recursiva de estado de

sistemas dinâmicos não-lineares (em tempo real), usando sinais que são

corrompidos por ruídos.

De certa forma, relacionado com as Séries de Taylor, é possível

linearizar a estimação em torno da estimativa atual, usando derivadas parciais

do processo e funções medidas para computarem estimativas (mesmo diante

de relacionamentos não-lineares). Assumindo que o processo tem um vetor de

estado n

x∈ℜ , mas agora é governado por uma equação diferencial estocástica

28

x k( )= f x k[ ( −1), (u k−1), (w k−1)] (4.1)

E com uma medida m

z∈ℜ dada por:

z k( )=h x k v k[ ( ), ( )] (4.2)

As variáveis aleatórias w k( ) _e v k( ) _{novamente representam o ruído do}

processo e da medida (respectivamente), como em (3.3) e (3.4). Neste caso, a

função não-linear da equação (4.1) relaciona o estado no instante k-1 com o

estado no instante k. Isso inclui como parâmetros algumas direções de funções

( 1)

u k− e o ruído do processo w k( ) médio nulo. A função não-linear h da

equação (4.2), relaciona o estado x k( ) com a medida z k( ).

Na prática, não se conhecem os valores individuais dos ruídos w k( )e

( )

v k para cada passo. No entanto, podem-se aproximar os vetores de estado e

medidas sem eles, como:

x kɶ( )= f x k[ (ˆ −1), (u k−1), 0] _(4.3)

E:

( ) [ ( ), 0]

z kɶ =h x kɶ _(4.4)

Onde x kˆ( ) é qualquer estimativa a posteriori do estado (vindo do passo

no instante k).

É importante notar que uma falha fundamental do EKF, é que a

distribuição (ou densidade no caso contínuo) das várias variáveis aleatórias,

não é normal depois de submeterem-se as respectivas transformações

não-lineares.

4.2. Estimador Filtro de Kalman Estendido (EKF)

Para estimar um processo com relacionamento de medidas e equações

29

( 1)

ˆ

( ) ( ) [ ( 1) ( 1)] _{W k}

x k ≈x kɶ +A x k− −x k− +W _{− (4.5)}

( )

( ) ( ) [ ( ) ( )] _{V k}

z k ≈z kɶ +H x k −x kɶ +V _(4.6)

Onde:

( )

x k e z k( ) são os vetores de medida e estado atuais;

( )

x kɶ _{e z k}ɶ_{( ) são vetores de medida e estado aproximados de (4.3)}

e (4.4);

ˆ( )

x k é uma estimativa a posteriori do estado no passo k;

As variáveis aleatórias w k( )e v k( )representam os ruídos das

mediadas e do processo como em (3.3) e (3.4);

A é a matriz Jacobiana das derivadas parciais de f referente a x,

calculado como:

[ ] [ , ]

[ ]

ˆ

[ ( 1), ( 1), 0]

i i j

j

f

A x k u k

x

δ δ

= − − (4.7)

W é a matriz Jacobiana das derivadas parciais de f referente a w,

calculada como:

[ ] [ , ]

[ ]

ˆ

[ ( 1), ( 1), 0]

i i j

j

f

W x k u k

w

δ δ

= − − (4.8)

H é a matriz Jacobiana das derivadas parciais de h referente à x,

calculada como:

[ ] [ , ]

[ ]

[ ( ), 0] i

i j

j

h

H x k

x

δ δ

= ɶ _(4.9)

V é a matriz Jacobiana das derivadas parciais de h referente à v,

calculada como:

[ , ] [ ] [ ]

[ ( ), 0] i

i j

j

h

V x k

v

δ δ

= ɶ _(4.10)

Para simplificar a notação, não foi usado subscrito do passo no tempo k

com as matrizes Jacobianas A, W, H e V mesmo sendo elas diferentes em cada

passo de tempo.

Agora definindo uma nova notação para a predição do erro:

30

E a medida residual:

eɶz k( ) ≡z k( )−z kɶ( ) (4.12)

Relembrando que na prática, não se tem acesso a x k( ) em (4.11), ele é o

vetor de estado atual, por exemplo, a grandeza a ser estimada. Por outro lado,

tem-se acesso a z k( ) em (4.12), que é a medida atual usada para estimar x k( ).

Usando (4.11) e (4.12), as equações do processo de erro tornam-se:

eɶx k( ) ≈A x k[ ( − −1) x kˆ( − +1)] ε( )k (4.13)

eɶz k( ) ≈Heɶx k( )+η( )k (4.14)

Onde ε( )k e η( )k representam novas variáveis aleatórias, tendo matrizes

de covariância WQWT e VRVT, com Q e R como em (3.3) e (3.4),

respectivamente.

Note que as equações (4.13) e (4.14) são lineares, e são muito parecidas

com as equações de medida e diferença (3.1) e (3.2) do Filtro de Kalman

Discreto. Isso motiva a usar a medida atual residual e kɶz( ) em (4.13) e um

segundo Filtro de Kalman (hipotético) para estimar a predição do erro e kɶ_x( )

dado por (4.13). Esta estimativa, chamada de e kˆ( ), poderia ser usada junto com

(4.11) para obter uma estimativa do estado a posteriori para um processo

não-linear como:

x kˆ( )=x kɶ( )+e kˆ( ) _(4.15)

As variáveis aleatórias de (4.13) e (4.14) tem aproximadamente as

seguintes probabilidades de distribuição:

[ ( )] [0, ( ( ) ( ) )]

T

x k x k x k

p eɶ ∼N E eɶ eɶ _(4.16)

p[ ( )]ε k ∼N[0,WQ k W( ) T] (4.17)

[ ( )] [0, ( ) T]

31

Dado estas aproximações, a equação do Filtro de Kalman para estimar

ˆ( )

e k é:

e kˆ( )=K k e( )ɶz k( ) (4.19)

Substituindo (4.19) em (4.15) e usando (4.12), vê-se que não há

necessidade do segundo Filtro de Kalman (hipotético):

x kˆ( )=x kɶ( )+K k e( )ɶ_{z k( )} =x kɶ( )+K k z k( )[ ( )−z kɶ( )] _(4.20)

A equação (4.20) pode agora ser usada na atualização de medidas do

Filtro de Kalman Estendido, com x kɶ( ) _{e z k}ɶ_{( ) vindo de (4.3) e (4.4), e o ganho}

de Kalman vindo de (3.15), com a substituição apropriada para a covariância do

erro medida.

O conjunto de equações de atualização de tempo e de medida do EKF é

mostrado seguir:

x kˆ( )−= f x k[ (ˆ −1), (u k−1), 0] (4.21)

P k( )− = A k P k( ) ( −1) ( )A k T +W k Q k( ) ( −1)W k( )T (4.22)

As equações de atualização de tempo (4.21) e (4.22) projetam os

estados e a covariância estimada do tempo k-1 para o tempo k. Novamente, f

em (4.21) vem de (4.3), já A(k) e W(k) são as Jacobianas no passo k, enquanto

Q(k) é a covariância do ruído (3.3) no passo k.

1

( ) ( ) ( ) [T ( ) ( ) ( )T ( ) ( ) ( ) ]T

K k =P k −H k H k P k −H k +V k R k V k − (4.23)

x kˆ( )=x kˆ( )−+K k z k( )[ ( )−H x k( ( ) , 0)]ˆ − (4.24)

P k( )= −[I K k H k P k( ) ( )] ( )− (4.25)

As equações de atualização de medidas (4.23), (4.24) e (4.25) corrigem a