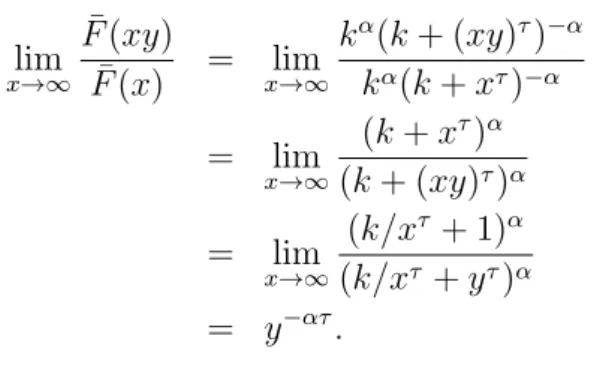Universidade Federal do Rio Grande do Norte
Centro de Ciˆencias Exatas e da Terra
P´os-Gradua¸c˜ao em Matem´atica Aplicada e Estat´ıstica
Wenia Valdevino F´
elix
Probabilidades Assint´
oticas da Cauda de Somas
Ponderadas de Vari´
aveis Aleat´
orias Dependentes
com Varia¸
c˜
ao Dominada
Wenia Valdevino F´elix
Probabilidades Assint´
oticas da Cauda de Somas
Ponderadas de Vari´
aveis Aleat´
orias Dependentes
com Varia¸
c˜
ao Dominada
Trabalho apresentado ao Programa de P´os-Gradua¸c˜ao em Matem´atica Apli-cada e Estat´ıstica da Universidade Fe-deral do Rio Grande do Norte, em cum-primento com as exigˆencias legais para a obten¸c˜ao do t´ıtulo de Mestre.
´
Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica.
Orientadora: Prof
a. Dr
a. D´ebora Borges Ferreira
UFRN / Biblioteca Central Zila Mamede. Catalogação da Publicação na Fonte
Félix, Wenia Valdevino.
Probabilidades assintóticas da cauda de somas ponderadas de variáveis aleatórias dependentes com variação dominada / Wenia Valdevino Félix – Natal, RN, 2015.
87 f.: il.
Orientadora: Profª. Drª. Débora Borges Ferreira.
Dissertação (Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Pós-Graduação em Matemática Aplicada e Estatística.
1. Probabilidade – Dissertação. 2. Cauda pesada – Dissertação. 3. Cauda de variação dominada – Dissertação. 4. Comportamento assintótico – Dissertação. 5. Somas aleatórias ponderadas – Dissertação. I. Ferreira, Débora Borges. II. Universidade Federal do Rio Grande do Norte. III. Título.
Dedicat´
oria
Agradecimentos
Agrade¸co em primeiro lugar a Deus, pela sua gra¸ca e miseric´ordia derramada sobre a minha vida, pois sem Ele nada posso fazer. Todas as dificuldades que passei, poder chegar aqui ´e a prova viva do amor de Deus para comigo.
Agrade¸co aos meus pais Elizabeth Ribeiro e Jo˜ao F´elix pelo carinho, dedica¸c˜ao, amor, paciˆencia, aten¸c˜ao que sempre tiveram comigo, pela educa¸c˜ao que me proporci-onaram e de me darem a oportunidade e o incentivo nos estudos em todas as etapas que j´a conclui e mais esta que estou `a concluir.
Agrade¸co a minha excelente orientadora, professora Dra. D´ebora Borges, por toda
dedica¸c˜ao e paciˆencia que teve comigo durante todo o mestrado, por ter me aceitado como orientanda e pela confian¸ca que teve em mim.
Agrade¸co aos irm˜aos da igreja Miss˜ao Evang´elica em Igap´o, a qual fa¸co parte, em especial ao Pastor Gonzaga e sua fam´ılia que muito me incentivou e me ajudou durante toda a minha gradua¸c˜ao, ao casal M´arcia e Paulo Morais que me presentiaram com o meu primeiro computador e tantas outros aux´ılios que me deram me aconselhando e orando por mim. A aben¸coada irm˜a Marlene, a qual me ensinou muitas li¸c˜oes de sabedoria que sempre vou levar guardadas no meu cora¸c˜ao.
Agrade¸co aos meus amigos do mestrado Eduardo, July, M´arcia, F´abio, Renato, Rumenick, Paulo, Daniel, Antˆonio, Anna Rafaella e Allyson, e aos amigos da gradua¸c˜ao que sempre estiveram por perto dando aquela for¸ca nos momentos de dif´ıceis, Isabel, Sara, Dami˜ao, Danillo, Micarlla, Geilson, Romildo.
Agrade¸co a todos os professores com quem tive aula em especial aos professo-res Juan Rojas, Viviane Simioli, Andr´e Gustavo, D´ebora Borges, Nir Cohen, Dione Valen¸ca. Aos professores da UFCG, Joelson e Itailma.
Agrade¸co ao meu namorado, amigo, professor, companheiro nos momentos feli-zes e de aperreio que n˜ao foram poucos, conselheiro, grande incentivador e por toda paciˆencia que teve comigo, Romildo lima.
Agrade¸co aos funcion´arios do CCET-UFRN sempre presentes, em especial, a Alderir, N´ızia, Severino, Rafael, Paulo e a minha amiga Liandra que me acompanhou desde a gradua¸c˜ao.
“Porque o Senhor d´a a sabedoria e da sua boca vem a inteligˆencia e o entendimento.”
Resumo
Neste trabalho estudamos o comportamento assint´otico das probabilidades da cauda das somas aleat´orias ponderadas de vari´aveis aleat´orias com certa estrutura de dependˆencia e de varia¸c˜ao dominada, baseados no artigo de Hai-zhong Yang, com t´ıtulo “Asymptotic Tail Probability of Randomly Weighted Sums of Dependent Random Va-riables with Dominated Variation”. Para tanto, apresentamos resultados essenciais sobre a classe de distribui¸c˜oes de cauda pesada que cont´em as seguintes subclasses: de cauda subexponencial, longa, varia¸c˜ao regular,varia¸c˜ao regular estendida e varia¸c˜ao dominada, dentre outras. Nosso objetivo ´e proporcionar todo um embasamento te´orico para esclarecer ao m´aximo a demonstra¸c˜ao do Teorema de Yang. Para isto, apresenta-mos a demonstra¸c˜ao de trˆes lemas principais e de alguns resultados que s˜ao utilizados na demonstra¸c˜ao desses lemas.
Abstract
In this work we study the asymptotic behavior of tail probability of random weighted sums of random variables with a certain dependence structure and dominated variation, based on the Hai-zhong Yang article, with title “Asymptotic Tail Probability of Randomly Weighted Sums of Dependent Random Variables with Dominated Vari-ation”.We present key results about the distributions of heavy tail class that contains the following subclasses: subexponential tail, long, regular variation, extended regular variation and variation dominated, among others. Our goal is provide an entire theo-retical foundation to detail proof of Yang’s Theorem. For this we demonstration three main lemmas and some results that are used in the demonstration of those lemmas.
Lista de nota¸
c˜
oes
1. v.a. : vari´avel aleat´oria;
2. i.i.d. : independentes e identicamente distribu´ıdas;
3. ¯F: cauda da distribui¸c˜ao F tal que ¯F(x) = 1−F(x) para todo x∈R; 4. S: subclasse subexponencial;
5. L: subclasse de cauda longa ;
6. D: subclasse de cauda de varia¸c˜ao dominada;
7. R: subclasse de cauda de varia¸c˜ao regular;
8. VRE: subclasse de cauda de varia¸c˜ao regular estendida;
9. a(x)&b(x) ⇒lim inf
x→∞ a(x)
b(x) ≥1;
10. a(x).b(x) ⇒lim sup
x→∞ a(x)
b(x) ≤1;
11. a(x)∼b(x) ⇒ lim
x→∞ a(x)
b(x) = 1;
12. X =d K: X segue uma distribui¸c˜aoK;
13. F ∗G: convolu¸c˜ao da distribui¸c˜ao F com aG;
14. JF+: ´ındice superior de Matuszewska;
15. JF−: ´ındice inferior de Matuszewska;
16. a∧b representa o m´ınimo entre os dois valores a eb;
17. a∨b representa o m´aximo entre os dois valores a e b;
18. o(h): dizemos que f(h)=o(h) se, e somente se, lim
h→0
f(h)
h = 0;
19. O(g(x)): dizemos quef(x) =O(g(x)) se, e somente se lim sup
x→∞
f(x)
g(x)
<∞.
21. X− =−{X∧0}: dizemos que X− ´e a parte negativa da vari´avel X.
22. µ: medida de Lebesgue.
Sum´
ario
Introdu¸c˜ao 2
1 Conceitos Preliminares 5
1.1 Distribui¸c˜oes de Cauda Pesada. . . 5
1.2 Subclasses de Distribui¸c˜oes de Cauda Pesada . . . 7
1.2.1 Subexponencial . . . 7
1.2.2 Cauda Longa . . . 10
1.2.3 Varia¸c˜ao Dominada . . . 10
1.2.4 Varia¸c˜ao Regular . . . 13
1.2.5 Varia¸c˜ao Regular Estendida . . . 15
1.3 Aplica¸c˜oes . . . 16
1.3.1 Modelo de Ru´ına . . . 16
1.3.2 Teoria de Filas . . . 20
1.3.3 Aloca¸c˜ao de capitais . . . 21
2 Resultados Preliminares e Lemas Principais 23 2.1 Resultados Preliminares 1 . . . 24
2.2 Resultados Preliminares 2 . . . 39
2.3 Lemas principais . . . 48
2.4 Teorema de Yang . . . 53
2.5 Considera¸c˜oes finais . . . 62
A Distribui¸c˜oes de Probabilidade e as Rela¸c˜oes entre as subclasses 66
A.1 Distribui¸c˜oes de Probabilidade . . . 66
A.2 Rela¸c˜oes entre as Subclasses de Distribui¸c˜oes . . . 73
Introdu¸
c˜
ao
Modelos matem´aticos que envolvem vari´aveis aleat´orias pertencentes `a classe de cauda pesada est˜ao presentes em diversas ´areas da ciˆencia. Por exemplo, em Ciˆencias Atuariais nos modelos de seguros e resseguros que envolvem grandes desastres naturais ou grandes perdas conjuntas, em Economia nas cota¸c˜oes da bolsa de valores de merca-dos muito oscilantes, em estumerca-dos de insurgˆencias e movimentos terroristas em Teoria Militar, dentre v´arios outros.
As vari´aveis aleat´orias que pertencem `a classe de cauda pesada s˜ao caracterizadas principalmente pelo decaimento das suas caudas (`a direita ou `a esquerda) que s˜ao bem mais lentos do que um decaimento exponencial. Neste trabalho nos referimos `as caudas somente `a direita, pois apresentamos v´arios exemplos e resultados que envolvem apenas vari´aveis aleat´orias n˜ao-negativas. Este detalhe ´e bastante relevante, porque o comportamento das caudas `a direita e `a esquerda n˜ao s˜ao sempre o mesmo.
Existem muitas fun¸c˜oes de distribui¸c˜ao que pertencem `a classe de cauda pesada como a t-Student, loggama, lognormal,α−est´aveis truncadas, Cauchy padr˜ao, Weibull com taxa de falha decrescente, Pareto, Burr entre outras. Apresentamos gr´aficos de algumas dessas distribui¸c˜oes, para observar o comportamento de suas caudas.
As principais subclasses de distribui¸c˜oes de cauda pesada s˜ao: subexponencial, cauda longa, cauda de varia¸c˜ao regular, cauda de varia¸c˜ao regular estendida e cauda de varia¸c˜ao dominada. Dentre todas as cinco subclasses, duas em especial s˜ao bastante utilizadas ao longo deste trabalho, as quais s˜ao as subclasses de cauda longa e cauda de varia¸c˜ao dominada. Baseamos nosso trabalho no artigo de Hai-zhong Yang que tem por t´ıtulo ”Asymptotic Tail Probability of Randomly Weighted Sums of Dependent Random Variables with Dominated Variation”.
Seja a sequˆencia de vari´aveis aleat´orias a valores reais {Xn;n ≥ 1} com fun¸c˜ao
de distribui¸c˜ao F. Seja a sequˆencia {θn;n ≥ 1} que chamamos de pesos aleat´orios,
essa sequˆencia ´e n˜ao-negativa e independente da sequˆencia{Xn;n ≥1}, e considere a
Sn = n
X
i=1
θiXi, (1)
onde {Xn;n ≥1} pertence `a subclasse de interse¸c˜ao de cauda longa e de varia¸c˜ao
do-minada, e satisfaz mais algumas condi¸c˜oes que est˜ao presentes do Teorema de Yang. O nosso principal objetivo ´e esclarecer a demonstra¸c˜ao do Teorema de Yang que investiga o comportamento assint´otico das caudas de somas ponderadas de vari´aveis aleat´orias em (1) que pertencem `a interse¸c˜ao das subclasses de cauda longa e de varia¸c˜ao domi-nada, ou seja, investigamos as hip´oteses para garantir a seguinte convergˆencia
P(Sn > x)∼ n
X
i=1
P(θiXi > x) ∀n= 1,2, ... e x→ ∞, (2)
para isto , precisamos provar v´arios resultados como os lemas principais que s˜ao enun-ciados no artigo do Hai-zhong Yang [22].
Uma motiva¸c˜ao para este resultado apresentamos na Se¸c˜ao 2.4, onde trazemos um exemplo na teoria da ru´ına. Neste exemplo queremos obter uma estimativa para a probabilidade de ru´ına a tempo finito, diante disso o resultado assint´otico (2) nos permite a facilita¸c˜ao dos c´alculos, pois encontrar a distribui¸c˜ao conjunta da cauda da probabilidades das somas ponderadas ´e muito mais complexo do que encontrar a da probabilidade conjunta do produto de v.a.’sθi e Xi.
As somas ponderadas aleat´orias tˆem um papel muito relevante em v´arios proble-mas te´oricos e aplicados. Mais adiante na Se¸c˜ao1.3, apresentamos exemplos envolvendo essas somas. Na teoria da ru´ına elas s˜ao utilizadas com frequˆencia na modelagem de super´avit de uma empresa de seguros. Atualmente existe uma ampla literatura envol-vendo essas somas ponderadas como tamb´em o comportamento assint´otico das caudas delas, por exemplo, Cline e Samorodnitsky [5], Tang e Tsitsiashvili [17] e [18], Cheng [4], Tang e Yuan [19], Geluk e De Vries [9], Zang et al [23] e Yang [22] dentre outras.
No Cap´ıtulo 2, apresentamos mais algumas defini¸c˜oes relevantes como os ´ındices de Matuszewska que utilizamos bastante nos enunciados de v´arios lemas, proposi¸c˜oes e teoremas ao longo do trabalho. Demonstramos v´arios resultados na Se¸c˜ao 2.1 e na Se¸c˜ao2.2que nos proporcionam embasamento te´orico para as demonstra¸c˜oes dos Lemas Principais que se encontram na Se¸c˜ao 2.3. Finalmente, na Se¸c˜ao 2.4 esclarecemos a demonstra¸c˜ao do resultado mais esperado deste trabalho, o Teorema de Yang, j´a citado anteriormente.
Cap´ıtulo 1
Conceitos Preliminares
Neste cap´ıtulo estudamos a classe de cauda pesada e algumas subclasses impor-tantes. Inicialmente apresentamos v´arias defini¸c˜oes que s˜ao utilizadas ao longo deste trabalho e alguns exemplos que nos mostram o comportamento da cauda de probabi-lidade de fun¸c˜oes de distribui¸c˜ao que pertence tanto a classe de cauda pesada quanto exemplos que pertencem a cada uma das cinco subclasses abordadas que s˜ao a su-bexponencial, cauda longa, varia¸c˜ao dominada, varia¸c˜ao regular e varia¸c˜ao regular es-tendida. Em seguida trazemos trˆes aplica¸c˜oes envolvendo vari´aveis aleat´orias de cauda pesada como tamb´em modelos e exemplos que utilizam as somas ponderadas aleat´orias. Quando nos referirmos a cauda da distribui¸c˜aoF usamos a seguinte nota¸c˜ao ¯F, tal que
¯
F = 1−F.
1.1
Distribui¸
c˜
oes de Cauda Pesada
Defini¸c˜ao 1.1. Uma fun¸c˜ao de distribui¸c˜ao F ´e dita de cauda pesada (`a direita) se para todoε >0,
lim sup
x→∞
¯
F(x)
e−εx =∞. (1.1)
Defini¸c˜ao 1.2. Uma fun¸c˜ao de distribui¸c˜ao F ´e dita de cauda leve se existir ε > 0, tal que
lim sup
x→∞
¯
F(x)
e−εx <∞. (1.2)
Defini¸c˜ao 1.3. Dizemos que X tem distribui¸c˜ao de cauda pesada (`a direita) se,
MX(θ) = E[eθX] =∞, ∀θ > 0. (1.3)
As Defini¸c˜oes 1.1 e 1.3 s˜ao equivalentes, ver o resultado que garante esta equi-valˆencia em Santana [16]. Existem muitas fun¸c˜oes de distribui¸c˜ao que pertencem `a classe de caudas pesadas como: a t-Student, loggama, lognormal,α−est´avel truncada, Cauchy Padr˜ao, Weibull com taxa de falha decrescente, Pareto, Burr, Benktander ti-pos I e II, entre outras. As fun¸c˜oes de distribui¸c˜ao de cauda leve s˜ao: a exponencial, a geom´etrica de parˆametros 0 ≤ p ≤ 1, Poisson de parˆametro λ > 0, normal entre outras.
Por que caudas pesadas?
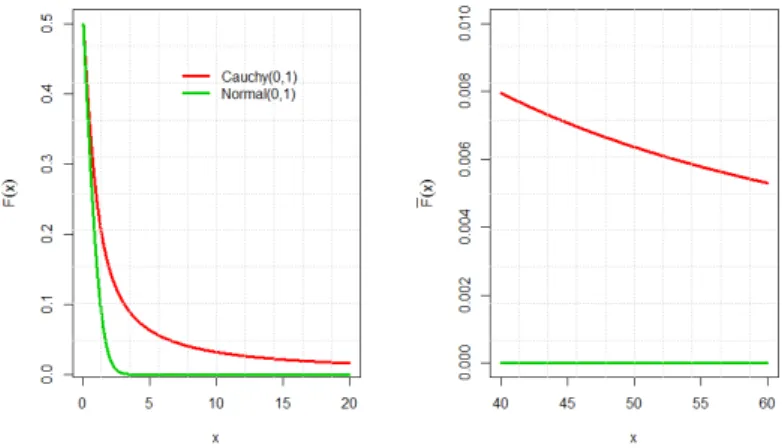
A Defini¸c˜ao 1.3, apresentada anteriormente, nos mostra a principal caracter´ıstica desta classe que ´e a de n˜ao apresentar fun¸c˜ao geradora de momentos. O decaimento da cauda de uma fun¸c˜ao de distribui¸c˜ao de uma vari´avel aleat´oria assim ´e mais lento do que o decaimento exponencial, o que nos leva a crer que nas suas caudas podemos obter mais informa¸c˜oes. ´E sabido que nas v´arias ´areas da probabilidade, em muitos problemas pr´aticos, as vari´aveis que melhor se ajustam aos modelos s˜ao as de cauda pesada. Existem v´arias situa¸c˜oes pr´aticas em que as evidˆencias estat´ısticas mostram que quantidades reais podem ser modeladas como uma vari´avel aleat´oria de cauda pesada. Por exemplo: renda de uma fam´ılia arbitr´aria, tamanhos de arquivos, tama-nhos de reivindica¸c˜oes entre outras. Nos exemplos que apresentamos a seguir, fazemos um comparativo com duas fun¸c˜oes de distribui¸c˜ao de cauda leve para visualizamos o comportamento do gr´afico das caudas dessas fun¸c˜oes de distribui¸c˜ao.
Exemplo 1.1. A distribui¸c˜ao Pareto pertence `a classe de distribui¸c˜ao de cauda pesada. Vamos comparar esta distribui¸c˜ao com a distribui¸c˜ao exponencial ambas com m´edia igual a 1 e observar o decaimento da cauda de cada uma na Figura1.1.
Figura 1.1: Gr´afico da distribui¸c˜ao Pareto x exponencial
Figura 1.2: Gr´afico da distribui¸c˜ao Cauchy x normal
1.2
Subclasses de Distribui¸
c˜
oes de Cauda Pesada
Nesta se¸c˜ao apresentamos as defini¸c˜oes das principais subclasses de distribui¸c˜oes que vamos abordar ao longo do nosso trabalho e alguns exemplos de fun¸c˜oes de distri-bui¸c˜ao de probabilidade que pertencem a cada subclasse, juntamente com o comporta-mento das suas caudas que ilustramos atrav´es de gr´aficos. Existem outras subclasses de distribui¸c˜oes de caudas pesadas, mas aqui s´o definimos as que nos interessa. Temos aqui o cuidado de para cada defini¸c˜ao das subclasses explicitar em que artigo esta-mos nos baseando, porque em diversos trabalhos que pesquisaesta-mos cada um aborda a defini¸c˜ao destas subclasses com algumas diferen¸cas aparentes.
1.2.1
Subexponencial
Defini¸c˜ao 1.4. SejamX1 e X2 vari´aveis aleat´orias i.i.d’s. Seja F¯2∗ = ¯F ∗F¯, ou seja, a convolu¸c˜ao de F¯ consigo mesma, onde F¯2∗(x) = P(X
F ∈ S se:
lim
x→∞
¯
F2∗(x)
¯
F(x) = 2. (1.4)
A subclasse S ´e denominada subexponencial. Esta defini¸c˜ao ´e baseada no artigo de Pitman ver [13].
Segundo Santana [16] uma motiva¸c˜ao para a subclasse subexponencial ´e baseada em modelos de reserva de capital de risco de uma empresa seguradora. Neste contexto ´e bastante relevante estabelecer uma rela¸c˜ao entre os valores individuais das indeniza¸c˜oes pagas e a quantia total paga ao final do per´ıodo de tempo considerado, desta forma surge o interesse em assumir hip´oteses sob as quais o valor da maior indeniza¸c˜ao de-termina o valor total das indeniza¸c˜oes pagas. Assim podemos interpretar as vari´aveis aleat´orias i.i.d’s X1, X2, ..., Xn com distribui¸c˜ao F como as respectivas indeniza¸c˜oes
pagas em cada per´ıodo de tempo n (por exemplo em anos).
Considere a soma parcial Sn=X1+X2+...+Xn que representa a quantia total
de indeniza¸c˜oes pagas e Mn = max{X1, X2, ..., Xn} representando o maior valor pago
dos n per´ıodos considerados. Ent˜ao nosso objetivo ´e encontrar fun¸c˜oes de distribui¸c˜ao
F de modo que as caudas das somas Sn e do m´aximo Mn sejam assintoticamente da
mesma ordem, isto ´e, P(Sn > x) ∼ P(Mn > x), o que indicaria a forte influˆencia da
maior indeniza¸c˜ao paga sobre o total de indeniza¸c˜oes. Note que,
P(Sn > x) = P n
X
i=1
Xi > x
!
= ¯Fn∗(x)∼P(Mn> x)∼nF¯(x).
Mais informa¸c˜oes sobre a subclasse subexponencial podem ser encontradas em Pitman [13], Embrechts [6], Cline e Samorodnitsky [5], Kl¨uppelberg [11] entre outros.
Exemplo 1.3. Considere a vari´avel aleat´oria X =d W eibull(1, τ) com taxa de falha λ
decrescente e com fun¸c˜ao de distribui¸c˜ao F(x) = 1−e−xτ
tal que 0 < τ < 1 e a sua fun¸c˜ao densidade de probabilidade ´ef(x) =τ xτ−1e−xτ
. Provemos que F ∈ S, para isto utilizamos a seguinte proposi¸c˜ao:
Proposi¸c˜ao 1.1. Seja F(x) uma fun¸c˜ao de distribui¸c˜ao de probabilidade e f(x) a sua fun¸c˜ao de densidade comλ(x) = f¯(x)
F(x), a taxa de falha deF, tal queλ(x)´e decrescente
parax≥x0, para algum x0 e 0≤ lim
Z ∞
0
exλ(x)f(x)dx <∞.
Ou seja, a fun¸c˜ao exλ(x)f(x) ´e integr´avel. Omitiremos a demonstra¸c˜ao que pode ser vista em Asmussen [1].
Calculando esta taxa de falha para a fun¸c˜ao distribui¸c˜ao do exemplo acima temos,
λ(x) = f¯(x)
F(x) =
τ xτ−1e−xτ
e−xτ =τ x
τ−1. (1.5)
Note queλ(x)satisfaz as hip´oteses da Proposi¸c˜ao1.1, usando (1.5)ef(x) =τ xτ−1e−xτ obtemos
Z ∞
0
exλ(x)f(x)dx =
Z ∞
0
exτ xτ−1τ xτ−1e−xτdx
=
Z ∞
0
τ xτ−1eτ xτ−xτdx
= e
xτ(τ−1)
τ −1
∞
0
= 1
1−τ < ∞.
Portanto, F ∈ S.
Figura 1.3: Figura da cauda da distribui¸c˜ao Weibull
1.2.2
Cauda Longa
Defini¸c˜ao 1.5. Seja X uma vari´avel aleat´oria com fun¸c˜ao de distribui¸c˜ao F.Dizemos queF ´e de cauda longa e denotamos por F ∈ L se:
lim
x→∞
¯
F(x+y) ¯
F(x) = 1, ∀ y∈R. (1.6)
Esta defini¸c˜ao ´e baseada no artigo de Yang ver [22].
Exemplo 1.4. O exemplo que apresentamos anteriormente da distribui¸c˜ao Weibull com taxa de falha decrescente tamb´em ´e um exemplo de distribui¸c˜ao de cauda longa, pois vemos na Se¸c˜ao A.2 do Apˆendice A que se uma distribui¸c˜ao pertence `a subclasse subexponencial, ent˜ao ela tamb´em pertence `a subclasse de cauda longa.
1.2.3
Varia¸
c˜
ao Dominada
Defini¸c˜ao 1.6. Seja X uma vari´avel aleat´oria com fun¸c˜ao de distribui¸c˜ao F.Dizemos queF ´e de varia¸c˜ao dominada e denotamos por F ∈ D se:
lim sup
x→∞
¯
F(xy) ¯
F(x) <∞ para todo y∈R. (1.7)
Baseada no artigo de Yang [22].
lim inf
x→∞
¯
F(xy) ¯
F(x) >0 para algum y >1. (1.8)
Baseada no artigo do Cline e Samorodnitsky [5].
Defini¸c˜ao 1.8. Seja X uma vari´avel aleat´oria com fun¸c˜ao de distribui¸c˜ao F.Dizemos queF ´e de varia¸c˜ao dominada e denotamos por F ∈ D se:
lim sup
x→∞
¯
F(xy) ¯
F(x) <∞ para algum 0< y < 1. (1.9)
Baseada no artigo do Geluk e Tang [8].
Apresentamos todas essas defini¸c˜oes de cauda de varia¸c˜ao dominada, pois utili-zamos esses artigos citados acima ao longo deste trabalho. Todas as defini¸c˜oes acima s˜ao equivalentes como vemos na Proposi¸c˜ao A.1do Apˆendice A.
Exemplo 1.5. Seja X =d Pareto tal que F¯(x) = (x0/x)α para x ≥ x0. E f´acil ver´ que esta distribui¸c˜ao pertence `a subclasse de varia¸c˜ao dominada, ou seja,
lim sup
x→∞
¯
F(xy) ¯
F(x) =y
−α <
∞ para algum 0< y <1.
Vejamos na Figura 1.4 seu gr´afico.
Figura 1.4: Gr´afico da distribui¸c˜ao Pareto
s˜ao: a Burr, a Weibull com taxa de falha decrescente, a Pareto e a fun¸c˜ao de dis-tribui¸c˜ao que est´a presente no Exemplo A.2 no Apˆendice A. Vejamos agora como de fato a distribui¸c˜ao Burr com parˆametrosα, k eτ estritamente positivos a Weibull com
τ = 12 e a Pareto com parˆametrosx0 = 1 pertencem a L ∩ D.
1) Burr
1.a) F ∈ L,de fato
lim
x→∞
¯
F(x+y) ¯
F(x) = xlim→∞
kα(k+ (x+y)τ)−α
kα(k+xτ)−α
= lim
x→∞
(k+xτ)α
(k+ (x+y)τ)α
= lim
x→∞
k+xτ
k+ (x+y)τ
α
=
lim
x→∞
k+xτ
k+ (x+y)τ
α
, pela regra do L’hospital
=
lim
x→∞
τ xτ−1
τ(x+y)τ−1
α
=
lim
x→∞
xτ−1
xτ−1(1 + y
x)τ−1
α = " lim x→∞ 1 (1 + yx)τ−1
#α
= 1.
1.b) F ∈ D,de fato
lim sup
x→∞
¯
F(xy) ¯
F(x) = lim supx→∞
kα(k+ (xy)τ)−α
kα(k+xτ)−α
= lim sup
x→∞
(k+xτ)α
(k+ (xy)τ)α
= lim sup
x→∞
(k/xτ+ 1)α
(k/xτ+yτ)α
= y−ατ < ∞.
2) Weibull
2.b) Vamos verificar que a Weibull com parˆametro τ = 12 pertence `a subclasse D,
utilizando a Defini¸c˜ao 1.8,
lim sup
x→∞
¯
F(xy) ¯
F(x) = lim supx→∞
e−(xy)1/2
e−x1/2
= lim sup
x→∞
e−(x1/2·y1/2)+x1/2
= lim sup
x→∞ e
x1/2·(1−y1/2)
< ∞,
pois 0 < y <1, isto implica que 1−y1/2 <0.
3) Pareto
3.a) Do Exemplo 1.5 j´a sabemos que a distribui¸c˜ao Pareto pertence `a subclasseD.
3.b) Vamos verificar que a Pareto com parˆametrox0 = 1 e α= 2 pertence `a subclasse L,
lim
x→∞
¯
F(x+y) ¯
F(x) = xlim→∞
1/(x+y)2
1/x2
= lim
x→∞ x2
(x+y)2
= lim
x→∞
x2
(x2+ 2xy+y2), pela regra do L’hospital
= lim
x→∞
2x
(2x+ 2y), pela regra do L’hospital = 1.
1.2.4
Varia¸
c˜
ao Regular
Defini¸c˜ao 1.9. Dizemos que a cauda da fun¸c˜ao F ∈ D ∩ L´e de varia¸c˜ao regular se:
lim
x→∞
¯
F(yx) ¯
F(x) =y
−α para algum α≥0, ∀y ≥1. (1.10)
Denotamos a classe das distribui¸c˜oes com essa propriedade de R. Esta defini¸c˜ao ´e baseada no artigo de Tang e Tsitsiashvili, ver [17].
Exemplo 1.6. Seja X =d Burr(α, k, τ) tal que α, k, τ > 0 e a sua cauda ´e dada por:
¯
lim
x→∞
¯
F(xy) ¯
F(x) = xlim→∞
kα(k+ (xy)τ)−α
kα(k+xτ)−α
= lim
x→∞
(k+xτ)α
(k+ (xy)τ)α
= lim
x→∞
(k/xτ + 1)α
(k/xτ +yτ)α
= y−ατ.
Assim, se chamarmos θ =ατ ≥0, obtemos que:
lim
x→∞
¯
F(xy) ¯
F(x) =y
−θ ∀ y≥1 para algum θ≥0.
Vejamos na Figura 1.5 o gr´afico da fun¸c˜ao de distribui¸c˜ao Burr, para isto, escolhemos alguns valores para os parˆametros τ, α e k.
Figura 1.5: Gr´afico da cauda da distribui¸c˜ao Burr
Defini¸c˜ao 1.10. Seja X uma vari´avel aleat´oria com fun¸c˜ao de distribui¸c˜ao F, dizemos que a sua cauda ´e de varia¸c˜ao r´apida se,
lim
x→∞
¯
F(xy) ¯
F(x) = 0, para todo y >1. (1.11)
Observa¸c˜ao 1.1. Outra nota¸c˜ao encontrada para a cauda de varia¸c˜ao regular ´eR−α,
onde se F¯ ∈ R−α, dizemos que a fun¸c˜ao relacionada com a cauda `a direita da
casos particulares importantes nesta subclasse. O primeiro ´e estabelecido para α = 0, ou seja, R0 e representa a subclasse das caudas das distribui¸c˜oes de varia¸c˜ao lenta. O segundo caso ´e estabelecido para α = ∞, ou seja, R−∞ e representa a subclasse das
caudas de distribui¸c˜oes de varia¸c˜ao r´apida. As defini¸c˜oes destas duas subclasses se encontram a seguir.
1.2.5
Varia¸
c˜
ao Regular Estendida
Defini¸c˜ao 1.11. Dizemos que F ∈ D ∩ L ´e subclasse de varia¸c˜ao regular estendida denotada por VRE(−α,−β) se existir algum 0< α≤β <∞ tal que:
y−β ≤lim inf
x→∞
¯
F(xy) ¯
F(x) ≤lim supx→∞
¯
F(xy) ¯
F(x) ≤y
−α para todo y
≥1. (1.12)
Esta defini¸c˜ao ´e baseada no artigo de Yang ver [22].
Exemplo 1.7. Seja X =d Cauchy(α, β) com α = 0 e β = 1 cuja densidade de proba-bilidade ´e dada por f(x) = [π(1 +x2)]−1I
(−∞,∞). Note que a Cauchy padr˜ao pertence `a subclasseVRE, pois basta verificar que ela pertence `a subclasse R j´a que R ⊂ VRE.
A cauda da distribui¸c˜ao Cauchy padr˜ao ´e dada por F¯(x) = 1 2 −
1
π arctan(x) tal que
−∞< x < ∞. Assim:
lim
x→∞
¯
F(xy) ¯
F(x) = limx→∞
1 2 −
1
π arctan(xy)
1 2 −
1
πarctan(x)
= 1 para θ= 0 e ∀y≥1.
Vejamos a Figura1.5 que representa o gr´afico da cauda da distribui¸c˜ao Cauchy padr˜ao com os parˆametros α = 0 e β = 1.
Figura 1.6: Inclus˜ao das Subclasses
1.3
Aplica¸
c˜
oes
Nesta se¸c˜ao apresentamos trˆes aplica¸c˜oes, a primeira em modelo de ru´ına, a se-gunda em teoria de filas e a terceira em aloca¸c˜ao de capitais. Essas aplica¸c˜oes nos mostram situa¸c˜oes em que as vari´aveis aleat´orias pertencentes `a classe de cauda pesada est˜ao envolvidas como tamb´em as somas ponderadas aleat´orias. Atualmente existe uma ampla literatura envolvendo as somas ponderadas aleat´orias especialmente em seguros, finan¸cas e gest˜ao de riscos. Dentre v´arios autores que investigam o comportamento das somas ponderadas citamos Cline e Samorodnitsky [5], Tang e Tsitsiashvili [18] e [17], Cheng [4], Tang e Yuan [19], Yang [22] dentre outros.
1.3.1
Modelo de Ru´ına
Modelo I
O modelo de risco cl´assico ´e um processo de Poisson composto, desenvolvido por Lundberg-Cram´er no in´ıcio do s´eculo XX, usado para descrever a trajet´oria do super´avit de uma seguradora at´e um dado instante. Esse modelo, a tempo cont´ınuo, considera apenas o capital inicial, o recebimento de prˆemios (importˆancia paga pelos segurados pela contrata¸c˜ao do seguro) a uma taxa de entrada constante ao longo do tempo, e as indeniza¸c˜oes pagas aos segurados no momento em que os sinistros ocorrem. A reserva ou lucro da seguradora at´e um dado instantet, comt ≥0,´e dada pela seguinte express˜ao:
R(t) = x+ct−
N(t)
X
i=1
Bi, (1.13)
onde:
• R(t) ´e o super´avit no instante t.
• x≥0 ´e o capital inicial da seguradora;
• c > 0 ´e a taxa fixa de prˆemios por unidade de tempo;
• {N(t)}t≥0 ´e um processo de Poisson com taxa de chegada λ >0 que expressa o
n´umero de indeniza¸c˜oes a serem pagas em um intervalo de tempo (0;t];
• B1, B2, ... s˜ao vari´aveis aleat´orias i.i.d., independentes de {N(t)}, e Bn denota o
valor do n-´esimo pedido de indeniza¸c˜ao.
Na Figura 1.7 apresentamos o gr´afico de uma trajet´oria de R(t).
Modelo II
Apresentamos agora a aplica¸c˜ao de uma empresa seguradora que utiliza as so-mas ponderadas proposta no artigo de Tang e Tsitsiashvili e que ´e abordada mais detalhadamente no trabalho de Santana [16].
Figura 1.7: Figura ilustrativa do super´avit de uma seguradora ao longo do tempo.
R0 =x, tal que x≥0
Rn =ξn·Rn−1+ (Wn−Zn), n= 1,2, ...
(1.14)
Denotamos as vari´aveis aleat´orias do seguinte modo:
• {Zn}n≥1 representa a quantia total das indeniza¸c˜oes pagas no per´ıodo (n−1, n);
• {Wn}n≥1 representa a quantia total dos prˆemios recebidos (n−1, n);
• {ξn}n≥1coeficiente de infla¸c˜ao, que representa o retorno do investimento realizado
no per´ıodo (n−1, n);
• {Zn, Wn}n≥1 s˜ao i.i.d. aos pares e s˜ao mutuamente independentes da sequˆencia {ξn}n≥1;
• {Rn}n≥1 representa o valor do capital da empresa no final de cada per´ıodon.
Assuma queP(ξn>0) = 1,para todo n≥1.
Ψ(x, n) =P
min
0≤m≤nRm <0|R0 =x
e Ψ(x) =P
min
m≥0Rm <0|R0 =x
.
Supondo uma estrutura de dependˆencia arbitr´aria para a sequˆencia {ξn}n≥1. Denote
Xn = Zn−Wn, vari´aveis aleat´orias i.i.d.’s. Desenvolvendo a equa¸c˜ao recursiva (1.14)
obtemos:
R0 =x
Rn=R0
n
Y
i=1
ξi− n X k=1 Xk n Y
i=k+1
ξi, n = 1,2...
Considere Yn = ξn−1 o fator de desconto no per´ıodo (n −1, n). Denote por
∼ Rn os
valores descontados deRn, e s˜ao dados por
∼ R0=x
∼
Rn=x− n X k=1 Xk k Y i=1
ξi, para n ≥1.
(1.15)
A probabilidade de ru´ına em quest˜ao neste problema ´e
Ψ(x, n) = P
min
0≤m≤n
∼ Rn<0|
∼ R0=x
, para n ≥1. (1.16)
Desenvolvendo a express˜ao (1.16), obtemos:
Ψ(x, n) = P max
1≤m≤n m X k=1 Xk k Y i=1
Yi > x
! ∼P m X k=1 Xk k Y i=1
Yi > x
!
.
Considerando θk = k
Y
i=1
Yi com 1≤k ≤n a probabilidade da ru´ına se reduz a:
Ψ(x, n) = P
m
X
k=1
Xkθk > x
!
A partir disto, o trabalho de Santana [16] utiliza resultados que permitem a obten¸c˜ao de aproxima¸c˜oes para Ψ(x, n) quando x → ∞ para os casos onde F ∈ S e
{ξn}n≥1 ´e limitada de alguma forma.
1.3.2
Teoria de Filas
Filas de espera em geral s˜ao encontradas nos lugares em que precisamos de servi¸cos prestados como em supermercados, hospitais ou lojas de conveniˆencia , ocasio-nando perda de tempo para os seus usu´arios e outros preju´ızos. Segundo Fraga [7], ”A Teoria de Filas ´e um ramo da ciˆencia que estuda o processo formador de filas a partir da modelagem anal´ıtica de processos em sistemas que resultam em espera”. Tem o objetivo de propor uma melhoria significativa para o atendimento dos clientes a fim de minimizar o tempo de espera nas filas. Abaixo vemos um exemplo bem simples de uma situa¸c˜ao em que a vari´avel de cauda pesada ´e utilizada para modelar uma fila com um ´
unico servidor. Neste processo assumimos que o crit´erio de atendimento ´e por ordem de chegada. Considere que
• As chegadas de clientes s˜ao de acordo com um processo de Poisson {Nt}t>0 com
taxa λ >0;
• {Ei}´e uma sequˆencia i.i.d. e representa o tempo entre ai-´esima e a (i+ 1)-´esima
chegada do cliente;
• {Bi} ´e uma sequˆencia i.i.d. e representa o tempo de atendimento do i-´esimo
cliente;
• {Xn} ´e uma sequˆencia i.i.d. expressa por Xn = n
X
i=1
Bi − n
X
i=1
Ei representa o
tempo de espera para ser atendido;
• {Wn} ´e o total de espera at´e a chegada do n-´esimo cliente.
Neste caso, a vari´avel aleat´oria em quest˜ao que assumimos ser de cauda pesada ´eXn,
pois quanto mais tempo o cliente espera para ser atendido, consequentemente torna-se maior a fila, e o que se espera ´e que possamos otimizar o m´aximo para que os clientes estejam satisfeitos.
Considere um cliente que necessita de assistˆencia t´ecnica den m´aquinas: Mn1, ...., Mnn
em s´erie, onde a m´aquinaMnj tem um tempo de servi¸co Wnj que ´e exponencialmente
distribu´ıdo com m´edia βj, 1≤j ≤ n, e onde os tempos de servi¸co {Wn1, ..., Wnn} s˜ao
independentes. Ent˜ao a soma dos{Wn1, ..., Wnn}representa o tempo total de servi¸co ao
cliente. Tome {Xnj},1≤j ≤n, n≥1,vari´aveis aleat´orias identicamente distribu´ıdas,
que s˜ao matrizes triangulares, onde X11 > 0 quase certamente e Xnj ´e independente
das {Wn1, ..., Wnn}.
InterpretandoXnj como a produ¸c˜ao da m´aquinaMnj por unidade de tempo de servi¸co,
a soma
Sn=
X
n≥1;1≤j≤n
WnjXnj
representa a produ¸c˜ao total para o cliente usando asn m´aquinas.
1.3.3
Aloca¸
c˜
ao de capitais
Sejam as vari´aveis aleat´orias a valores reais X1, X2, ...Xn independentes e
per-tencentes `a subclasse subexponencial, chamamos de vari´aveis aleat´orias prim´arias, e
θ1, θ2, ..., θn vari´aveis aleat´orias n˜ao-negativas que chamamos de pesos e s˜ao
indepen-dentes das vari´aveis aleat´orias prim´arias. A soma ponderadas de forma aleat´oria ´e dada a seguir:
Sn = n
X
i=1
θiXi. (1.18)
Agora, sejam as vari´aveis aleat´orias Z1, Z2, ..., Zn com a seguinte representa¸c˜ao
es-toc´astica,
Zi =θiXi, i= 1,2, ..., n, (1.19)
tal queZi representa o produto das vari´aveis aleat´orias prim´arias e os pesos aleat´orios
descritos acima.
Neste exemplo os pesos aleat´orios θ1, θ2, ..., θn s˜ao arbitrariamente dependentes
entre si, mas n˜ao necessariamente limitados.
Considere um investidor que investe em n linhas de neg´ocios. Cada linha i gera um potencial vari´avel com a perda l´ıquida Zi na forma de perda de lucro. Essas
em ambientes macroeconˆomicos semelhantes. Na representa¸c˜ao estoc´astica (1.19) em que, as vari´aveis aleat´orias X1, X2, ..., Xn s˜ao independentes com as suas respectivas
fun¸c˜oes de distribui¸c˜aoF1, F2, ..., Fn, enquanto os pesos aleat´oriosθ1, θ2, ..., θn s˜ao
n˜ao-negativos, n˜ao-degenerados no zero, e arbitrariamente dependentes uns dos outros, mas independentes das vari´aveis aleat´orias prim´arias, ent˜ao a soma aleat´oria ponderada em (1.18) representa a perda total.
Para alguns investidores regulamentados, tais como bancos ou companhias de seguros, uma reserva de capital de risco serve como uma almofada para protegˆe-los de grandes perdas. Nosso interesse ´e na aloca¸c˜ao do capital de risco para as linhas individuais.
Assumimos que cada vari´avel aleat´oria em (1.18) tem m´edia finita. De acordo com o princ´ıpio de Euler, mais informa¸c˜oes sobre isto ver Tasche [20], o montante de capital alocado na linhai ´e,
E[θiXi|Sn > x] =
E[θiXiI(Sn>x)]
P(Sn> x)
, i= 1, ..., n,
tal que x´e o valor de risco (VaR) de Sn, isto ´e,
x=V aRq[Sn] = inf{y ∈R:P(Sn≤y)≥q}, 0< q <1.
Cap´ıtulo 2
Resultados Preliminares e Lemas
Principais
Neste cap´ıtulo apresentamos resultados relevantes, a serem utilizados nas demons-tra¸c˜oes dos lemas principais, os quais proporcionam o embasamento te´orico necess´ario para esclarecer a demonstra¸c˜ao do Teorema de Yang. Este est´a presente no artigo base deste trabalho que tem por t´ıtulo “Asymptotic Tail Probability of Randomly Weighted Sums of Dependent Random Variables with Dominated Variation”.
Defini¸c˜ao 2.1. Seja X uma vari´avel aleat´oria e F a sua fun¸c˜ao de distribui¸c˜ao. De-finimosF¯∗ e F¯∗ respectivamente por:
¯
F∗(y) = lim inf
x→∞
¯
F(xy) ¯
F(x) , ∀y >0 e (2.1) ¯
F∗(z) = lim sup
x→∞
¯
F(xz) ¯
F(x) , ∀z >0. (2.2)
Defini¸c˜ao 2.2. Seja uma vari´avel aleat´oria X a valores reais com fun¸c˜ao de distri-bui¸c˜aoF. Para todo y >0dizemos queJF+´e o ´ındice superior de Matuszewska definido por:
JF+ =− lim
y→∞
log ¯F∗(y)
log(y) . (2.3)
Defini¸c˜ao 2.3. Seja uma vari´avel aleat´oria Y a valores reais com a fun¸c˜ao de distri-bui¸c˜aoG. Para todoz >0dizemos queJG−´e o ´ındice inferior de Matuszewska definido por:
JG− =− lim
z→∞
log ¯G∗(z)
Mais informa¸c˜oes sobre os ´ındices de Matuszewska ver Bingham [3]. Segundo Wang e Tang [21], os ´ındices de Matuszewska quando finitos exercem um papel semelhante ao ´ındice α das fun¸c˜oes de varia¸c˜ao regular. Se ¯F ∈ R−α, temos que JF− = JF+ = y−α, e
seF ∈ VRE(−α,−β), ent˜ao α ≤JF−≤JF+≤β.
A proposi¸c˜ao a seguir nos mostra que existe uma rela¸c˜ao muito relevante entre o ´ındice superior de Matuszewska e a subclasse de varia¸c˜ao dominada que ´e utilizada em alguns resultados ao longo do texto. Omitiremos a prova deste fato, mas a demons-tra¸c˜ao pode ser encontrada em Bingham [3].
Proposi¸c˜ao 2.1. Seja X uma vari´avel aleat´oria com fun¸c˜ao de distribui¸c˜ao F, temos queF ∈ D se, e somente se, o ´ındice superior de Matuszewska ´e finito.
2.1
Resultados Preliminares 1
At´e aqui apresentamos resultados que envolvem a fun¸c˜ao de distribui¸c˜ao de uma vari´avel aleat´oria. A partir de agora trazemos defini¸c˜oes e resultados concernentes `a distribui¸c˜ao do produto de vari´aveis aleat´orias, pois estes resultados ser˜ao de extrema relevˆancia para a demonstra¸c˜ao do Teorema de Yang.
Proposi¸c˜ao 2.2. Seja F uma fun¸c˜ao positiva, se JF+ <∞, ent˜ao para todo α > JF+, existem constantes positivas M, N, tais que:
F(y)
F(x) ≤M
y
x
α
(y≥x≥N). (2.5)
Ver demonstra¸c˜ao em Bingham [3].
Defini¸c˜ao 2.4. Dizemos que F pertence `a subclasse de fun¸c˜ao de varia¸c˜ao O-regular denotada por OR, se para todoλ ≥1
0<F¯∗(λ)≤F¯∗(λ)<∞. (2.6)
Mais informa¸c˜ao sobre essa subclasse ver Bingham [3].
A partir de agora considere X e Y vari´aveis aleat´orias independentes, onde X
assume valores emRcom fun¸c˜ao distribui¸c˜aoF eY estritamente positiva com a fun¸c˜ao de distribui¸c˜ao G. Escrevamos Z =XY e denotemos por H a fun¸c˜ao distribui¸c˜ao de
¯
H(x) =
Z ∞
0
¯
F(x/y)G(dy). (2.7)
Teorema 2.1. Sejam as vari´aveis aleat´orias X, Y e Z com as respectivas fun¸c˜oes de distribui¸c˜ao F, G e H.
i) Para F e G pertencentes `a subclasse de varia¸c˜ao O-R temos que
(JF−∧JG−)≤JH− ≤JH+ ≤(JF+∨JG+); (2.8)
ii) Se F ∈ D, ent˜ao H ∈ D;
iii) Se F ∈ D e G¯(t) = o( ¯H(bt)) para algum b >0, ent˜ao para cada λ >1,
¯
F∗(λ)≤H¯∗(λ)≤H¯∗(λ)≤F¯∗(λ); (2.9)
iv) Se F ∈ D e E(YJF++ǫ)<∞ para algum ǫ >0, ent˜ao (2.9)´e v´alida e
0<E( ¯F∗(Y−1))≤lim inf
x→∞
¯
H(x) ¯
F(x) ≤lim supx→∞
¯
H(x) ¯
F(x) ≤E( ¯F
∗(Y−1))<
∞. (2.10)
Lema 2.2. Sejam as fun¸c˜oes de distribui¸c˜ao F, G e H como definidas anteriormente, ent˜ao para cada λ >1,
a) H¯∗(λ)≥F¯∗(λ)∧G¯∗(λ).
b) H¯∗(λ)≤F¯∗(λ)∨G¯∗(λ) + 1
2F¯∗(λ)∧G¯∗(λ).
A demonstra¸c˜ao deste lema se encontra em Cline e Samorodnitsky [5].
Demonstra¸c˜ao do Teorema 2.1.
(i) Por defini¸c˜ao sabemos queJH−= lim
λ→∞
−log ¯H∗(λ)
logλ , pelo item (b) do Lema2.2, temos
que para quaisquerF e Ge para cada λ >1
¯
H∗(λ)≤( ¯F∗(λ)∨G¯∗(λ)) + 1/2( ¯F∗(λ)∧G¯∗(λ)).
log ¯H∗(λ)
log (λ) ≤
log[( ¯F∗(λ)∨G¯∗(λ)) + 1/2( ¯F∗(λ)∧G¯∗(λ))]
log(λ)
≤ log[(3/2)·(F∗(λ)∨G∗(λ))]
log(λ)
= log(3/2) log(λ) +
log[(F∗(λ)∨G∗(λ))]
log(λ) .
Aplicando o limite quandoλ → ∞
lim
λ→∞
−log ¯H∗(λ)
log (λ) ≥ λlim→∞
−log(3/2)
log(λ) + limλ→∞
−log( ¯F∗(λ)∨G¯∗(λ))
log(λ)
= lim
λ→∞
−log( ¯F∗(λ)∨G¯∗(λ))
log(λ) . (2.11)
Para obter a primeira desigualdade consideramos dois casos.
Caso (1): SeJF− ≤JG− e ambos s˜ao finitos, ent˜ao por defini¸c˜ao temos
lim
λ→∞−
log ¯F∗(λ)
logλ ≤λlim→∞−
log ¯G∗(λ)
logλ .
Isto implica que
lim
λ→∞
−log ¯F∗(λ) + log ¯G∗(λ)
logλ ≤0.
Assim
lim
λ→∞log
¯
G∗(λ)
¯
F∗(λ)
≤0.
Desta forma, paraλ suficientemente grande temos G¯¯∗(λ)
F∗(λ) ≤1, obtendo assim ¯G∗(λ)∨
¯
JH− = lim
λ→∞
−log ¯H∗(λ)
log(λ)
≥ lim
λ→∞
−log( ¯F∗(λ)∨G¯∗(λ))
log(λ)
≥ lim
λ→∞
−log ¯F∗(λ)
log(λ) = JF−.
Caso (2): SeJG− ≤JF− e ambos s˜ao finitos ent˜ao por defini¸c˜ao
lim
λ→∞−
log ¯G∗(λ)
logλ ≤λlim→∞−
log ¯F∗(λ)
logλ .
Isto implica que
lim
λ→∞
−log ¯G∗(λ) + log ¯F∗(λ)
logλ ≤0.
Assim
lim
λ→∞log
¯
F∗(λ)
¯
G∗(λ)
≤0.
Desta forma para λ suficientemente grande temos F¯¯∗(λ)
G∗(λ) ≤1, obtendo assim ¯F∗(λ)∨
¯
G∗(λ) = ¯G∗(λ). Unindo este resultado a (2.11) temos
JH− = lim
λ→∞
−log ¯H∗(λ)
log(λ)
≥ lim
λ→∞
−log( ¯F∗(λ)∨G¯∗(λ))
log(λ)
≥ lim
λ→∞
−log ¯G∗(λ)
log(λ) = JG−.
Dos casos (1) e (2) temos que,
JH−≥
JF−, se JF− ≤JG− J−
G, se JG− ≤JF−
Note que para toda fun¸c˜ao de distribui¸c˜aoH temos queJH−≤JH+.Para obter a ´ultima desigualdade basta utilizar o item (a) do Lema 2.2 e proceder de modo an´alogo `a demonstra¸c˜ao anterior.
(ii) Pela Proposi¸c˜ao2.1, para ver que H ∈ D basta que JH+ <∞. Primeiro provemos que JH+ ≤ JF+ no caso em queJF+ ´e finito, e consideremos JF+ < α, para algum α > 0. Note que se F ∈ D, ent˜ao F pertence `a subclasse de varia¸c˜ao O-R. Pelo Teorema da Representa¸c˜ao de fun¸c˜oes de varia¸c˜ao O-regular em Bingham [3] que esta enunciado no Apˆendice B, temos que
−log ¯F(t) =ηF(t) +
Z t
0
ςF(u)
u du, (2.12)
ondeηF ´e limitada eςF ≤α. Desde que ¯F seja mon´otona e limitada, podemos escolher
ςF eηF sendo n˜ao-negativas. Agora sejam as fun¸c˜oesρF(t) e ¯H0(t) dadas da seguinte
forma:
ρF(t) =
Z t
0
ςF(u)
u du e H¯0(t) =
Z ∞
0
e−ρF(t/y)G(dy).
Note que,
log ¯H(t) = log H¯¯(t)
H0(t)
+ log ¯H0(t)
= log H¯¯(t)
H0(t)
+
Z t
0
u·H¯′ 0(u)
u·H¯0
du.
Isto implica que,
−log ¯H(t) =−log H¯¯(t)
H0(t)
+
Z t
0
−u·H¯′ 0(u)
u·H¯0(u)
du.
Considere ηH(t) = −log
¯
H(t) ¯
H0(t)
e ςH(t) = −
tH¯0′(t)
¯
H0(t)
, ambas s˜ao limitadas e ςH(t) ∈
[0, α],∀t≥0. Ent˜ao
−log ¯H(t) =ηH(t) +
Z t
0
ςH(u)
u du.
Provamos agora que
ςH(t) =
1 ¯
H0(t)
Z ∞
0
ςF(t)e−ρF(t/y)G(dy)∈[0, α].
Apˆendice B proveniente da Teoria da Medida, assim
ςH(t) = −
tH¯′ 0(t)
¯
H0(t)
=− ¯t
H0(t) ·
Z ∞
0
e−ρF(t/y)G(dy)
′
= − ¯t
H0(t)·
Z ∞
0
(e−ρF(t/y))′G(dy)
= − ¯t
H0(t)·
Z ∞
0
(−ρF(t/y))′ ·e−ρF(t/y)G(dy)
= ¯t
H0(t) ·
Z ∞
0
(1/y)· ςF(t/y) (t/y) e
−ρF(t/y)G(dy)
= ¯1
H0(t) ·
Z ∞
0
ςF(t/y)·e−ρF(t/y)G(dy)
.
E mais,
ςH(t) =
1 ¯
H0(t)·
Z ∞
0
ςF(t/y)·e−ρF(t/y)G(dy)
≤ ¯1
H0(t)·
Z ∞
0
α·e−ρF(t/y)G(dy)
= α·
R∞
0 e−
ρF(t/y)G(dy)
R∞
0 e−ρF(t/y)G(dy)
= α.
Sendo assim temos que H satisfaz a representa¸c˜ao para OR para JH+ ≤ α. Uma vez que α pode ser escolhido `a vontade em (JF+,∞). Conclu´ımos que JH+ ≤ JF+ <∞, isto ´e, H ∈ D.
(iii) Se F ∈ D, pelo item anterior j´a sabemos que H ∈ D. Por hip´otese, temos que ¯
G(t) = o( ¯H(bt)), para algum b > 0. Provemos que ¯H∗(λ)≤ F¯∗(λ), para isto fixemos λ > 0 e escolha um t0 > 0 suficientemente grande tal que ¯F(λt) ≤ (1 +ε) ¯F∗(λ) ¯F(t)
para t≥t0 e para qualquer ε >0.Escolha agora t1 > t0 tal que ¯G(t/t0)≤εH¯(t) para
t≥t1. Em seguida, para tal t,
¯
H(λt) =
Z ∞
0
¯
F(λt/y)G(dy)
=
Z t/t0
0
¯
F(λt/y)G(dy) +
Z ∞
t/t0
¯
F(λt/y)G(dy)
≤
Z t/t0
0
¯
F(λt/y)G(dy) +
Z ∞
t/t0
continuando com o mesmo racioc´ınio
Z t/t0
0
¯
F(λt/y)G(dy) +
Z ∞
t/t0
G(dy) =
Z t/t0
0
¯
F(λt/y)G(dy) + 1−G(t/t0)
=
Z t/t0
0
¯
F(λt/y)G(dy) + ¯G(t/t0)
≤ (1 +ε) ¯F∗(λ)
Z t/t0
0
¯
F(t/y)G(dy) +εH¯(t)
≤ (1 +ε) ¯F∗(λ)
Z ∞
0
¯
F(t/y)G(dy) +εH¯(t)
= (1 +ε) ¯F∗(λ) ¯H(t) +εH¯(t) = [(1 +ε) ¯F∗(λ) +ε] ¯H(t).
Fazendoε→0 e depois aplicando o limite superior em ambos os lados obtemos,
lim sup
t→∞
¯
H(λt) ¯
H(t) ≤F¯
∗(λ) ⇒ H¯∗(λ)≤F¯∗(λ).
Temos tamb´em, para todoλ >0,que ¯H∗(λ)≥F¯∗(λ).
(iv) Por hip´otese F ∈ D e E(YJF++ε)<∞para algum ε >0.Sejap∈(J+
F, JF++ε). As
seguintes afirma¸c˜oes abaixo s˜ao verdadeiras:
a) lim
t→∞t
pG¯(t) = 0
b) lim
t→∞t
pF¯(t) =∞.
De fato, para mostrar o item a) basta usar a desigualdade de Markov da seguinte forma,
P(Y > t)≤ E(Y
(JF++ε))
t(JF++ε) ⇒t
pP(Y > t)≤tpE(Y(J
+ F+ε))
t(JF++ε) =
E(Y(JF++ε))
t(JF++ε)−p .
Aplicando o limite comt → ∞, obtemos lim
t→∞t
pG¯(t) = 0.
Para mostrar o item b) basta usarmos o item b) do Lema 2.7, provamos na Se¸c˜ao 2.3, que afirma que se F ∈ D, ent˜ao para todo p > JF+ temos que t−p = o( ¯F(t)), logo
tpF¯(t)→ ∞,ou seja, lim t→∞t
pF¯(t) =
∞.
¯
G(t) =o[ ¯F(bt)], ∀ b >0, (2.13)
pois
¯
G(t) ¯
F(bt) =
tpbpG¯(t)
tpbpF¯(bt) =
¯
G(t) ¯
F(bt).
Usando este resultado, conseguimos mostrar que ¯G(t) =o[ ¯H(bt)],∀b >0. De fato,
0≤ lim
t→∞
¯
G(t) ¯
H(bt) = limt→∞
¯
G(t)
R∞
0 F¯(bt/y)G(dy)
= lim
t→∞
¯
G(t)/F¯(bt)
R∞
0 F¯(bt/y)/F¯(bt)G(dy) ≤ lim
t→∞
¯
G(t) ¯
F(bt) · 1
1−G(1), com G(1)6= 1 = 0,
caso G(1) = 1 ter´ıamos que JG+ e JG− seriam nulos , o que n˜ao ´e interessante para este resultado. Ou ter´ıamos que a fun¸c˜ao de distribui¸c˜ao G seria de cauda leve o que seria um absurdo, portantoG(1) 6= 1.
Segue assim do item (iii) deste mesmo teorema que (2.9) ´e satisfeita. Provamos a partir daqui a express˜ao (2.10). Usando a Defini¸c˜ao A.9 do Apˆendice A obtemos que
E( ¯F∗(1/Y)) =E
lim inf
x→∞
¯
F(xy) ¯
F(x)
>0.
Agora vamos obter a pr´oxima desigualdade. Temos do Lema de Fatou
E( ¯F∗(Y−1)) =
Z ∞
0
¯
F∗(1/y)G(dy)
= Z ∞ 0 lim inf t→∞ ¯
F(t/y) ¯
F(t) G(dy)
≤ lim inf
t→∞
Z ∞
0
¯
F(t/y) ¯
F(t) G(dy)
= lim inf
t→∞
¯
H(t) ¯
Sabemos que o limite inferior ´e sempre menor ou igual que o limite superior, sendo assim ´e imediato que,
lim inf
t→∞
¯
H(t) ¯
F(t) ≤lim supt→∞
¯
H(t) ¯
F(t).
Para obter a desigualdade seguinte tomamost ≥t0,
¯
H(t) =
Z ∞
0
¯
F(t/y)G(dy) =
Z 1
0
¯
F(t/y)G(dy) +
+
Z t/t0
1
¯
F(t/y)G(dy) +
Z ∞
t/t0
¯
F(t/y)G(dy)
≤
Z 1
0
¯
F(t/y)G(dy) +
Z t/t0
1
¯
F(t/y)G(dy) + ¯G(t/t0).
Isto implica que
¯
H(t) ¯
F(t) ≤
Z 1
0
¯
F(t/y) ¯
F(t) G(dy) +
+
Z t/t0
1
¯
F(t/y) ¯
F(t) G(dy) + ¯
G(t/t0)
¯
F(t) .
Na equa¸c˜ao (2.13) se tomarmosb=t0 obtemos ¯G(t/t0) = o( ¯F(t)). Utilizando este fato,
aplicando o limite superior comt→ ∞juntamenente com o Lema de Fatou temos que
lim sup
t→∞
¯
H(t) ¯
F(t) ≤ lim supt→∞
Z 1
0
¯
F(t/y) ¯
F(t) G(dy) +
+ lim sup
t→∞
Z t/t0
1
¯
F(t/y) ¯
F(t) G(dy) + lim supt→∞
¯
G(t/t0)
¯
F(t)
≤ Z 1 0 lim sup t→∞ ¯
F(t/y) ¯
F(t) G(dy) +
+
Z t/t0
1
lim sup
t→∞
¯
F(t/y) ¯
F(t) G(dy).
lim sup
t→∞
¯
H(t) ¯
F(t) ≤
Z 1
0
¯
F∗(t/y)G(dy) +
Z t/t0
1
¯
F∗(t/y)G(dy)
≤
Z t/t0
0
¯
F∗(t/y)G(dy)
≤
Z ∞
0
¯
F∗(t/y)G(dy)
= E[ ¯F∗(1/Y)]<∞.
Finalmente para encontrar a ´ultima desigualdade, utilizaremos a Desigualdade (3.2) em Cline e Samorodnitsky [5]. Assim, para qualquerε′
∈(0, ε), existe C <∞ e t0 tal
que
¯
F(t/y) ¯
F(t) ≤
(
CyJ− F−ε
′
se y ≤1, t≥t0
CyJF++ε′ se 1< y≤t/t
0, t≥t0.
Assim para t > t0 temos ¯F∗(t/y) ≤ C{y(J + F+ε
′
) ∨ y(J− F+ε
′
)}. Deste modo, temos
E[ ¯F∗(Y−1)]<∞. Com efeito,
E[ ¯F∗(1/Y)] =
Z ∞
0
¯
F∗(t/y)G(dy)
≤
Z ∞
0
C· {y(JF++ε ′
)
∨y(JF−−ε ′
)
}G(dy)
= C·
Z ∞
0
y(JF++ε ′
)G(dy)
= C·E[Y(JF++ε ′
)]<∞.
Concluindo assim a nossa demonstra¸c˜ao.
Lema 2.3. Considere o produto Z = XY. Se F ∈ L e G¯(x) = o( ¯F(cx)) para algum
0< c <∞, ent˜ao H ∈ L.
Demonstra¸c˜ao. Vamos considerar dois casos, o primeiro em que a v.a. Y ´e limitada e o outro em que ela n˜ao ´e limitada.
Caso (1): Y ´e limitada.
e P(0< Y¯ ≤a)
G(a) ≤ε.
Provamos primeiro que ¯G(a) > 0. De fato, suponhamos por contradi¸c˜ao que ¯
G(a) = 0 desta forma ter´ıamos que P(Y > an) = 0 com 0 < an= 1/n <1 e para todo
n∈N, ent˜ao
lim
n→∞P(Y > an) = 0⇒P(Y >0) = 0⇒Y = 0,
o que ´e um absurdo, a v.a. Y ´e estritamente positiva. Vamos verificar tamb´em que
P(0< Y ≤a) ¯
G(a) ≤ε,
P(0< Y ≤a))
P(Y > a) =
P(Y ≤a)
P(Y > a) =
P(Y ≤a) ¯
G(a) .
Aplicando o limite quandoa→0, j´a que ¯G(a)>0,obtemos
lim
a→0
P(0< Y ≤a) ¯
G(a) = lima→0
P(Y ≤a)
P(Y > a) = 0.
Vamos agora verificar algumas desigualdades que ser˜ao utilizadas ao longo desta de-monstra¸c˜ao.
(1.a) Note que, para 0< a < 1 suficientemente pequeno, x >0 e t > a temos
x+ 1
t−a ≤ x
t +
1
a.
De fato, sabemos que t2−a2x−2at≥0 partindo disto temos
tax+ta≤tax+t2−a2x−at
Assim,
x+ 1
t−a ≤
xa+t ta
x+ 1
t−a ≤ x
t +
1
a.
Aplicando ¯F obtemos
¯
F
x+ 1
t−a
≥F¯
x t +
1
a
, (2.14)
(1.b) Mostramos que Z M a ¯ F x t + 1 a
G(dt)∼
Z M
0
¯
F x t
G(dt)−
Z a
0
¯
Fx t
G(dt). (2.15)
ComoF ∈ L, temos por defini¸c˜ao que
lim
x→∞
¯
F(x/t+ 1/a) ¯
F(x/t) = 1,
isto implica que∀ε >0,∃M > 0 com x > M tal que
(1−ε)·F¯(x/t)≤F¯(x/t+ 1/a)≤(1 +ε)·F¯(x/t).
Aplicando a integral nas desigualdades acima conclu´ımos
(1−ε)·
Z M
a
¯
F(x/t)G(dt) ≤
Z M
a
¯
F(x/t+ 1/a)G(dt)
≤ (1 +ε)·
Z M
a
¯
F(x/t)G(dt).
Portanto temos
Z M
a
¯
F(x/t+ 1/a)G(dt) ∼
Z M
a
¯
F(x/t)G(dt)
=
Z M
0
¯
F x t
G(dt)
−
Z a
0
¯
Fx t
G(dt).
(1.c) Provemos que
Z M
0
¯
F(x/t)G(dt)−
Z a
0
¯
F(x/t)G(dt)≥H¯(x)·
"
1−
Ra
0 F¯(x/t)G(dt)
RM
a F¯(x/t)G(dt)
#
. (2.16)
Com efeito,
¯
H(x) =
Z ∞
0
¯
F(x/t)G(dt)≥
Z M
a
¯
F(x/t)G(dt),
isto implica que
¯
H(x)
RM
a F¯(x/t)G(dt)
⇒ −H¯(x)·
Ra
0 F¯(x/t)G(dt)
RM
a F¯(x/t)G(dt)
≤ −
Z a
0
¯
F(x/t)G(dt)
⇒ H¯(x)− H¯(x)·
Ra
0 F¯(x/t)G(dt)
RM
a F¯(x/t)G(dt)
≤H¯(x)−
Z a
0
¯
F(x/t)G(dt)
⇒ H¯(x)·
"
1−
Ra
0 F¯(x/t)G(dt)
RM
a F¯(x/t)G(dt)
#
≤H¯(x)−
Z a
0
¯
F(x/t)G(dt).
Assim,
¯
H(x)·
"
1−
Ra
0 F¯(x/t)G(dt)
RM
a F¯(x/t)G(dt)
#
≤ H¯(x)−
Z a
0
¯
F(x/t)G(dt)
=
Z ∞
0
¯
F(x/t)G(dt)−
Z a
0
¯
F(x/t)G(dt)
=
Z M
0
¯
F(x/t)G(dt) +
Z ∞
M
¯
F(x/t)G(dt)
−
Z a
0
¯
F(x/t)G(dt)
≤
Z M
0
¯
F(x/t)G(dt)−
Z a
0
¯
F(x/t)G(dt)
+
Z ∞
M
G(dt)
≤
Z M
0
¯
F(x/t)G(dt)−
Z a
0
¯
F(x/t)G(dt)
+ G(∞)−G(M)
≤
Z M
0
¯
F(x/t)G(dt)−
Z a
0
¯
F(x/t)G(dt).
Como quer´ıamos demonstrar.
(1.d) Provamos que
1−
Ra
0 F¯(x/t)G(dt)
RM
a F¯(x/t)G(dt)
≥1− F¯(x/a¯)·P(0< Y ≤a)
Parat < a, isto implica que ¯F(x/t)<F¯(x/a), assim
Z a
0
¯
F(x/t)G(dt) ≤
Z a
0
¯
F(x/a)G(dt)
≤ F¯(x/a)[G(a)−G(0)] = F¯(x/a)[P(0< Y ≤a)].
Logo
−
Z a
0
¯
F(x/t)G(dt)≥ −F¯(x/a)·P(0< Y ≤a). (2.18)
Parat > a, isto implica que ¯F(x/t)>F¯(x/a), ent˜ao
Z M
a
¯
F(x/t)G(dt) ≥
Z M
a
¯
F(x/a)G(dt)
= F¯(x/a)
Z M
a
G(dt)
= F¯(x/a)(1−G(a)) = F¯(x/a) ¯G(a).
Temos assim que
1
RM
a F¯(x/t)G(dt)
≤ ¯ 1
F(x/a) ¯G(a). (2.19)
Unindo as express˜oes (2.18) e (2.19) obtemos
1−
Ra
0 F¯(x/t)G(dt)
RM
a F¯(x/t)G(dt)
≥ 1−
Ra
0 F¯(x/a)G(dt)
¯
F(x/a)·G¯(a)
≥ 1− F¯(x/a¯)·P(0< Y ≤a)
F(x/a)·G¯(a) .
Agora sabendo queF ∈ L, parax >0 e utilizando todos os itens acima vamos mostrar que
¯
Desta forma
¯
H(x+ 1) =
Z ∞
0
¯
F
x+ 1
y
G(dy)
= Z ∞ a ¯ F
x+ 1
t−a
G(dt)
≥ Z M a ¯ F
x+ 1
t−a
G(dt) de (2.14)
≥ Z M a ¯ F x t + 1 a
G(dt) de (2.15)
∼
Z M
0
¯
F x t
G(dt)−
Z a
0
¯
F x t
G(dt) de (2.16)
≥ H¯(x)·
"
1−
Ra
0 F¯(x/t)G(dt)
RM
a F¯(x/t)G(dt)
#
de (2.17)
≥ H¯(x)·
1− F¯(x/a¯)P(0< Y ≤a)
F(x/a) ¯G(a)
= H¯(x)·
1− P(0< Y¯ ≤a)
G(a)
≥ (1−ε)·H¯(x).
Conclu´ımos que lim
x→∞
¯
H(x+ 1) ¯
H(x) ≥1, e como limx→∞
¯
H(x+ 1) ¯
H(x) ≤1, pois ¯H(x+ 1)≤H¯(x), ent˜ao H ∈ L.
Caso(2): Y ´e ilimitada.
Dizemos que Y ´e ilimitada quando ¯G(x) > 0 para todo x ∈ R. Segundo [5] no item (iii) do Teorema 2.2 afirma que: se F ∈ D e ¯G(x) = o( ¯H(bx)),∀b > 0, ent˜ao H ∈ L.
Ent˜ao basta provar que ¯G(x) =o( ¯H(bx)),∀b >0. Note que
1 ¯
H(bx) ≤
1
R∞
b/cF¯(bx/t)G(dt)
,
de fato,
¯
H(bx) =
Z ∞
0
¯
F(bx/t)G(dt)
=
Z b/c
0
¯
F(bx/t)G(dt) +
Z ∞
b/c
¯
F(bx/t)G(dt)
≥
Z ∞
b/c
¯