AS DIFERENTES ESTRATÉGIAS DE RESOLUÇÃO DAS EQUAÇÕES ALGÉBRICAS ATÉ O TERCEIRO GRAU

(1)

UNIVERSIDADE FEDERAL DO CEAR ´A CENTRO DE CI ˆENCIAS

DEPARTAMENTO DE MATEM ´ATICA

PROGRAMA DE P ÓS-GRADUAÇ ÃO EM MATEM ÁTICA EM REDE NACIONAL

FABIANO LUIZ DA SILVA

AS DIFERENTES ESTRAT ÉGIAS DE RESOLUÇ ÃO DAS EQUAÇ ÕES ALG ÉBRICAS AT É O TERCEIRO GRAU

(2)

AS DIFERENTES ESTRAT ÉGIAS DE RESOLUÇ ÃO DAS EQUAÇ ÕES ALG ÉBRICAS AT É O TERCEIRO GRAU

Dissertação de Mestrado apresentada ao Programa de P ós-Graduação em Ma-temática em Rede Nacional, do Departa-mento de Matemática da Universidade Fe-deral do Ceará, como requisito parcial para a obtenção do T´ıtulo de Mestre em Ma-temática. Área de concentração: Ensino de Matemática.

Orientador: Prof. Ms. Mario de Assis Oli-veira

(3)

Dados Internacionais de Catalogação na Publicação Universidade Federal do Ceará

Biblioteca do Curso de Matemática

S58d Silva, Fabiano Luiz da

As diferentes estratégias de resolução das equações algébricas até o terceiro grau / Fabiano Luiz da Silva. – 2015.

69 f. : il. color., enc.; 31 cm

Dissertação (mestrado) – Universidade Federal do Ceará, Centro de Ciências, Departamento de Matemática, Programa de Pós-Graduação em Matemática em Rede Nacional, Juazeiro do Norte, 2015. Área de Concentração: Ensino de Matemática.

Orientação: Prof. Ms. Mario de Assis Oliveira

(4)

(5)

(6)

(7)

Ao Senhor Deus, criador do universo, que por intermédio de Jesus Cristo, capacitou-me para a realização desse trabalho.

`

A Fl´avia, Evellyn, Emilly e Ewerton pela paciˆencia que tiveram durante minha jornada.

`

A minha fam´ılia, em particular aos meus pais, José e Quitéria, pelo apoio e incentivo. Ao meu orientador, Professor Mestre Mario de Assis Oliveira por ricas sugest ões.

`

A CAPES, que contribuiu com o apoio financeiro necess´ario no decorrer do curso. Aos meus colegas de curso por todos os momentos dif´ıceis que enfrentamos e vence-mos juntos e tamb´em todos os momentos de alegria que compartilhavence-mos. Em especial aos colegas Israel, Jairo e Lucas pelos momentos que passamos juntos estudando.

Aos professores com quem convivi ao longo da graduação, p ós-graduação e Mes-trado: Evandro Carlos, Zélalber Gondim, Mario de Assis, Francisco Braga, Pedro, Paulo César, Junior Moreira, Silvana, enfim a todos que direta ou indiretamente contribu´ıram nesta carreira acadêmica.

A todos os meus professores do PROFMAT que me ajudaram a crescer profissio-nalmente durante todo o curso.

(8)

prema beleza – uma beleza fria e austera, como a da escultura.

(9)

O objetivo desse trabalho é apresentar explanaç ões e estratégias de resolução das equaç ões algébricas do primeiro, segundo e terceiro graus, uma vez que o ensino relativo à resoluç ões dessas equaç ões tem se restringido praticamente a apresentação da f órmula resolutiva e as relaç ões entre seus coeficientes e suas ra´ızes. Desta maneira procuramos demonstrar e até mesmo justificar todas as formas apresentadas para se resolver equaç ões até o terceiro grau através de métodos puramente algébricos ou geométricos, como também, exemplificar todos os métodos que foram exibidos no intuito de satisfazer as expectativas dos leitores, por isso, o texto foi produzido em uma linguagem simples, acess´ıvel à professores e alunos. Nesse contexto, espera-se que essa proposta de trabalho estimule os professores de Matemática do Ensino Básico a realizarem essa abordagem diferenciada das equaç ões algébricas em questão, pois acredita-se que com essa abordagem ocorram reflexos positivos no processo de ensino e aprendizagem das equaç ões e da Matemática.

(10)

The aim of this paper is to present explanations and solving strategies of algebraic equations of the first, second and third degrees, since the relative teaching on the re-solutions of these equations has been restricted practically the presentation of solving formula and the relationships between its coefficients and its roots . In this way we try to demonstrate and even justify all forms presented to solve equations to the third degree by purely algebraic or geometric methods, but also exemplify all methods that were displayed in order to meet the expectations of readers, so the text was produced in simple language, accessible to teachers and students. In this context, it is expected that this work proposal stimulate the mathematics teachers of Basic Education to perform this differentiated approach to algebraic equations in question, since it is believed that with this approach occur positive reflexes in the teaching and learning of equations and of mathematics.

(11)

Figura 1 – Solução geométrica da equação do 1o_{grau . . . .} ₁₈

Figura 2 – Solução geométrica da equação 4x=12 . . . 19

Figura 3 – M´etodo geom´etrico de completar quadrados . . . 33

Figura 4 – M´etodo geom´etrico alternativo de completar quadrados . . . 34

Figura 5 – Construção dos gráficos de f(x) e g(x) e seus pontos de intersecção . 36 Figura 6 – Gráfico do método de Leslie . . . 36

Figura 7 – Gr´afico do m´etodo de Leslie (x2 −3x+4=0) . . . 37

Figura 8 – M´etodo de Descartes (x2 ₌_bx₊_c2 _e _x2₌_c2 −bx) . . . 38

Figura 9 – Solução geométrica da equaçãox2 ₌₃_x₊_{4 . . . .} ₃₉

Figura 10 – Solução geométrica da equaçãox2 ₌₁₆₋₆_x_{. . . .} ₄₁

Figura 11 – M´etodo de Descartes (x2 ₌_bx₋_c2_{) . . . .} ₄₂

Figura 12 – M´etodo de Descartes (x2 ₌_bx₋_c2_{) . . . .} ₄₃

Figura 13 – Solução geométrica da equaçãox2 ₌₅_x₋_{4 . . . .} ₄₄

Figura 14 – M´etodo de Nelson Tunala (c>0) . . . 45

Figura 15 – M´etodo de Nelson Tunala (c<0) . . . 46

(12)

(13)

1 INTRODUC¸ ˜AO . . . . 14

2 A EQUAC¸ ˜AO DO PRIMEIRO GRAU . . . . 15

2.1 Relatos hist ´oricos . . . 15

2.2 Método da falsa posição . . . 16

2.3 M´etodo alg´ebrico . . . 16

2.4 M´etodo geom´etrico . . . 18

3 A EQUAC¸ ˜AO DO SEGUNDO GRAU . . . . 21

3.1 Contexto hist ´orico . . . 21

3.2 Tipos de equac¸˜ao do segundo grau . . . 23

3.3 Métodos de resolução de equaç ões do segundo grau completas . . . 25

3.4 M´etodo alg´ebrico de Sridhara . . . 25

3.5 Método de resolução convencional . . . 26

3.6 M´etodo da semi-soma e do produto . . . 27

3.7 M´etodo da soma e da diferenc¸a de quadrados . . . 28

3.8 M´etodo alternativo . . . 29

3.9 M´etodo de Vi`ete . . . 31

3.10 M´etodo geom´etrico de completar quadrados . . . 32

3.11 M´etodo geom´etrico alternativo de completar quadrados . . . 34

3.12 Método gráfico de um sistema de equaç ões . . . 35

3.13 M´etodo de Leslie . . . 36

3.14 M´etodo de Descartes . . . 38

3.15 M´etodo geom´etrico de Nelson Tunala . . . 45

4 A EQUAC¸ ˜AO DO TERCEIRO GRAU . . . . 49

4.1 Uma breve hist ória das equaç ões do terceiro grau . . . 49

4.2 A f ´ormula de Cardano . . . 52

4.3 Soluc¸˜ao de Cardano paray3+py=q (p,q>0) . . . 53

4.4 Soluc¸˜ao de Cardano paray3 ₌_py₊_q ₍_p_,_q_>_{0) . . . .} ₅₅

4.5 Solução da equação y3₊_py₊_q₌_{0, com}_p_,_q ∈ R . . . 56

4.6 Critério para classificação das ra´ızes da c úbica . . . 58

4.7 A solução algébrica de Viète . . . 60

4.8 A solução trigonométrica de Viète . . . 61

4.9 Uma solução das equaç ões do 3o_grau _{. . . .} ₆₃

(14)

AP ÊNDICE A – RELAÇ ÕES ENTRE OS COEFICIENTES E AS RAÍZES DA EQUAÇ ÃO DO SEGUNDO GRAU . . . . 68

AP ˆENDICE B – 3

q

2+ √5+ 3

q

(15)

Apesar dos avanços tecnol ógicos que n ós vivenciamos hoje, é raro ouvirmos fa-lar de novas descobertas matemáticas, principalmente no campo da matemática pura. Contudo, é poss´ıvel utilizarmos resultados importantes que contribu´ıram para o de-senvolvimento da Álgebra.

A resolução de equaç ões é um dos temas estudados no ensino básico. Resolver uma equação equivale a encontrar as suas ra´ızes, isto é, encontrar um valorcpara a função

f(x) tal que f(c)=0. Essa busca de ra´ızes normalmente é tratada de forma anal´ıtica, ou seja, são usados métodos algébricos de forma a encontrar à solução exata das equaç ões isso não quer dizer que essa seja a única maneira de resolvê-las.

Esse trabalho est´a organizado da seguinte forma:

No cap´ıtulo 2, iniciaremos nosso estudo sobre Equaç ões Algébricas fazendo menção as equaç ões mais simples – as equaç ões do primeiro grau – cuja resolução é conhecida desde a antiguidade. Visando dar um maior significado a expressão ax+b = 0 será mostrado algumas técnicas de resolução dessas equaç ões, de forma elementar, para que o professor do ensino básico, que venha a ler este trabalho, tenha argumentos para explicar a seus alunos, por exemplo, que cada pessoa já tem adquirido dentro de si uma perspectiva acerca do assunto e que essas divergências devem contribuir para o amadurecimento dos conhecimentos matemáticos de cada indiv´ıduo.

No cap´ıtulo 3, falaremos sobre as equaç ões do segundo grau mostrando, também, as diferentes formas que foram encontradas ao longo da hist ória para resolvê-las e enfatizando, é claro, as diferentes civilizaç ões e os vários matemáticos que contribu´ıram de alguma forma para a sua formalização e o seu desenvolvimento. Apresentamos problemas antigos cuja resolução recaem na equação do 2o_{grau, f órmulas algébricas e} f órmulas geométricas de completar quadrados, bem como outros métodos de resolução da equação quadrática.

(16)

Estudaremos agora alguns métodos de resolução das equaç ões do primeiro grau, mas, antes iremos definir quando uma sentença aberta representa de fato tal equação. Definição 2.1. Toda equação, na inc ógnitax, que puder ser escrita na formaax+b=0, sendoaebn úmeros reais, comadiferente de zero, representa uma equação do primeiro grau.

2.1 Relatos hist ´oricos

Acredita-se que o surgimento da Matemática bem como o seu desenvolvimento, a princ´ıpio, tenha acontecido de maneira espontânea para suprir algumas necessidades do dia a dia das pessoas. A criação de novos conceitos matemáticos, como a criação de n úmeros, por exemplo, não foi tão simples e rápida como se imagina, o homem teve problemas até mesmo para realizar pequenas contagens, sem se falar das diferentes simbologias adotadas ao longo dos tempos por cada civilização.

As primeiras descobertas no campo da Matemática conhecidas atualmente são re-gistros feitos em blocos de barro sumérios1_{, que estima-se terem sido produzidos por} volta de quatro mil anos a.C., sendo que as primeiras operaç ões que foram realizadas com n úmeros foram encontradas em blocos similares aos citados e datados de 2200 anos a.C., possivelmente, dentre os documentos matemáticos mais antigos que foram descobertos até hoje os mais famosos sejam oPapiro de Ahmes2_{(ou de}_Rhind3_{) e o}_Papiro

de Moscou4_.

Alguns dos problemas expostos neles consistiam em resolver exerc´ıcios numéricos envolvendo um valor desconhecido, mostrando assim que naquela época estudiosos já se dedicavam à resolução de equaç ões lineares com uma quantia desconhecida, atualmente chamada de variável ou inc ógnita – palavra originária do latim incognitu, que quer dizer coisa desconhecida.

Apesar dos eg´ıpcios não usarem os s´ımbolos algébricos que conhecemos e utiliza-mos eles também conseguiam resolver equaç ões, porém, os procedimentos utilizados se tornavam complicados e cansativos, comparados aos que usamos hoje. Os gregos, por sua vez, davam um tratamento diferente dos eg´ıpcios e resolviam equaç ões com métodos geométricos, mas, apesar dos esforços destas civilizaç ões foram os árabes que

1 _{Sumérios: povos que habitavam a região da baixa Mesopotâmia (Asia), local onde atualmente está}

localizado o Iraque e ´areas pr ´oximas.

2 _{Papiro de Ahmes – papiro eg´ıpcio de cerca de 1600 anos a.C., contendo 85 problemas de Aritm´etica}

e Geometria – descoberto em 1858.

3 _{Alexander Henry Rhind – advogado e antiqu´ario – comprou o papiro de Ahmes, no final do s´ec.}

XIX, ap ós sua morte o papiro foi comprado pelo Museu Britânico onde está exposto até hoje.

(17)

conseguiram ter um avanço mais significativo na resolução destas equaç ões. Para se ter uma ideia, quando representavam um valor desconhecido em uma equação, eles o chamavam de ”coisa”que em árabe, era pronunciada como xay. Com o decorrer dos anos, essa pronuncia foi sofrendo alteraç ões, devido as traduç ões dos textos, até se tornarx, que é como, geralmente, a conhecemos hoje.

2.2 Método da falsa posição

Para resolver equaç ões com um valor desconhecido os eg´ıpcios adotavam um método de resolução muito engenhoso e complicado para encontrar a resposta correta, método esse que mais tarde os europeus deram o nome de ”regra da falsa posição”.

O método consistia na escolha de um n úmero arbitrário para o valor desconhecido, a partir da´ı fazia-se o cálculo. Em seguida, comparava-se o resultado desta operação com o que deveria ser encontrado. Para finalizar, se o valor obtido fosse diferente do esperado calculava-se um fator de correção para obter o valor correto de modo a satisfazer a expressão original.

Vejamos um exemplo.

Exemplo 2.1. Qual é o n úmero que somado a sua terça parte resulta em 24?

Solução:Pela regra da falsa posição, fazia-se uma hip ótese (estimativa) inicial a respeito do n úmero e verificava-se o que acontecia.

Vamos imaginar, em nosso caso, que tal n úmero fosse 9. Ora, 9 somado com sua terça parte dá 9+3 = 12, exatamente a metade dos 24 que deveria dar. Portanto, o n úmero procurado é o dobro de 9, ou seja, 18.

Se tivéssemos escolhido o n úmero 15, por exemplo. Ter´ıamos 15 somado com sua terça parte 5 resultando em 20, que nesse caso é 24

20 vezes menor que o resultado esperado, logo, o n úmero procurado é encontrado usando-se o fator de correção 15·24

20, a partir da´ı, efetua-se as operac¸ ˜oes indicadas e encontra-se 18.

2.3 M´etodo alg´ebrico

A solução algébrica de uma equação do 1o_{grau baseia-se em dois axiomas devido} a Euclides.5

• Princ´ıpio aditivo da igualdade ou de Euclides: Podemos somar um n ´umero real a ambos os membros de uma igualdade que ela n˜ao se altera.

Em s´ımbolos: dadosa,becn ´umeros reais, tem-se

a=b=_⇒a+c=b+c

5 _{Euclides de Alexandria viveu por volta do s´ec. III a.C., ´epoca em que produziu} _{Os Elementos} _–

(18)

• Princ´ıpio multiplicativo da igualdade: Podemos multiplicar ambos os membros de uma igualdade por um n úmero real não nulo que ela não se altera.

Simbolicamente, dadosa,becn ´umeros reais, comc ,_{0, tem-se} a=b=_⇒a_·c=b_·c

Esses axiomas são a chave para encontrar a solução de equaç ões do primeiro grau. Para resolver a equaçãoax+b = 0, ou seja, encontrar o n úmero que substituirá a variávelxde maneira que essa sentença seja verdadeira, devemos somar o oposto deb

nos dois lados da igualdade e assim obter

ax+b+(−b)=0+(−b),

que implica

ax=₋b

Em seguida, multiplicando a express˜ao obtida pelo inverso do n ´umeroa, chega-se a

1

a ·ax=

1

a ·(−b)

que implica finalmente em

x= −b

a .

Exemplo 2.2. Resolva a equação 6x+10=28, ondex é um n úmero racional.

Solução: Aplicando o princ´ıpio aditivo, vamos adicionar (−10) aos dois membros da equação

6x+10=28 da´ı,

6x+10+(−10)=28+(−10)

em seguida isolar o termo que cont´em a inc ´ognitaxno 1o_membro. 6x+10−10=28−10

6x=18

Aplicando, agora, o princ´ıpio multiplicativo, vamos multiplicar os dois membros da equac¸˜ao por 1

6,

6x· ₁

6

=18· ₁

6

que resulta finalmente em

x=3 descobrindo assim o valor num´erico dex.

(19)

2.4 M´etodo geom´etrico

Se uma equação algébrica do 1o_{grau tem uma raiz positiva, ela poderá ser escrita} como ax = b, com aeb positivos. Geometricamente, o segmento de medida x forma uma proporção com os três segmentos de comprimento a, b e 1, ou seja, a : b = 1 : x

(de fato, essa última igualdade leva aax=b), de modo quexpode ser constru´ıdo com régua e compasso de forma simples, mostrada na Figura 1, onde a abertura do ângulo em O é qualquer (0o < O< 180o), OA =a, OB =b ,AC = 1 e o pontoD é marcado de modo queCDseja paralelo aAB. Então,BD=x, é a solução.

Figura 1 – Solução geométrica da equação do 1ograu

Fonte: O autor

De fato, por semelhança de triângulos ou equivalentemente pelo Teorema de Tales6 (AB//CD, construção), temos

OA

OB =

OC

OD ⇐⇒

a b =

a+1

b+x,

donde resulta que

a_·(b+x)=b_·(a+1),

que implica

ax=b.

Exemplo 2.3. Resolver a equação 4x=12, usando régua e compasso. Solução:

i) Utilizando uma r´egua construa uma semirreta de origemO, a qual chamaremos der.

(20)

ii) A partir deO, construa outra semirreta (s) distinta da anterior de tal forma que a abertura (ˆangulo) formada entre elas esteja entre 0o_{e 180}o_.

iii) Sobrermarque o pontoAque dista 4cmdeO. iv) Sobresmarque o pontoBque dista 12cmdeO.

v) Sobrer, novamente, marque o pontoC, tal queAC=1cm, comAentreOeC. vi) Finalmente marque sobreso pontoD, tal queCDseja paralelo aAB.

Figura 2 – Solução geométrica da equação 4x=12

Fonte: O autor

O segmento de comprimentoBD é a solução procurada e mede 3cm.

Na maioria dos casos, os alunos são ensinados a resolver esse tipo de equaç ões por métodos formais e podem não entender o procedimento que estão utilizando, boa parte deles são ensinados a utilizar o método da transposição onde aplicam mecanicamente o fato – muda de lado, inverte a operação, ficando, muitas vezes, sem compreender o porquê desta ”regra”.

A resolução de uma equação do 1ograu está ligada diretamente com noç ões básicas de outros conte údos como razão, proporção e regra de três simples, os alunos que aprendem a resolvê-la terão maior facilidade em compreender outros conte údos que estão relacionados com este, consequentemente, terão maior facilidade em prosseguir com seus estudos.

(21)

(22)

Falaremos um pouco sobre a hist ória das equaç ões do segundo grau destacando algumas civilizaç ões, como os babil ônios e os gregos, que utilizavam técnicas para resolver alguns tipos de equaç ões. Serão apresentados, também, diferentes métodos (algébricos e não algébricos) para a obtenção de ra´ızes, como por exemplo, o método que foi criado pelo matemático hindu Sridhara – primeiro matemático a estabelecer uma f órmula resolutiva (solução por radicais) para tais equaç ões.

3.1 Contexto hist ´orico

O primeiro registro de equaç ões do segundo grau que se tem not´ıcia até hoje foi encontrado em uma tábua de argila, produzido pelos povos da Babil ônia há aproxima-damente, 1700 anos a.C., onde sua resolução era dada na forma de palavras, ou seja, eles não usavam uma f órmula para determinar sua solução.

Considerando que os babil ônios utilizavam um sistema de numeração sexagesimal (base 60) e que o alfabeto ainda não era conhecido, os problemas envolvendo equaç ões eram resolvidos usando uma notação diferente da utilizada hoje.

Vejamos.

Exemplo 3.1. Encontrar o lado do quadrado sabendo que sua ´area menos a medida do lado ´e igual a 14,30 (base 60).

Solução: Usando a notação em base decimal e nomeando x como sendo o lado do quadrado, podemos escrever:

x2₋x=870

([14,30]60=14·601₊₃₀_·₆₀0 ₌₁₄_·₆₀₊₃₀₌₈₄₀₊₃₀₌_{[870]10). A solução apresentada, de} acordo com os babil ônios, seria assim: ”Tome a metade de 1 (coeficiente dex) que é 0,5 e multiplique por ela mesma (0,5·0,5=0,25). Some isto a 870 (termo independente) e encontramos 870,25 que é o quadrado de 29,5. Agora some 0,5 a 29,5 e o resultado é 30, o lado do quadrado procurado”. Esse procedimento é utilizado até hoje e o conhecemos como método de completar quadrados.

Outro problema bastante conhecido em Matem´atica consiste em encontrar dois n ´umeros, digamosxey, dada sua somase seu produtop. Da´ı, podemos escrever:

      

x+y=s x_·y=p

Isolandoyna 1a_{equac¸˜ao, encontramos}

(23)

substituindo o valor encontrado na 2a_{equac¸˜ao, tem-se}

x_·y=p=_⇒x_·(s₋x)=p=_⇒x2₋sx+p=0

Para solucionar esse tipo de equação precisavam encontrar dois n úmeros positivos cuja soma ése o produto ép, então, usavam a seguinte regra:

Eleve ao quadrado a metade da soma, subtraia o produto do valor encontrado e extraia a raiz quadrada dessa diferença. Em seguida, some ao resultado a metade da soma. Isso dará o maior dos n úmeros procurados. Subtraia-o da metade da soma para obter o outro n úmero.

Por não utilizarem n úmeros negativos1_{os babil ônios dividiam as equaç ões em três} tipos:

x2₊_sx₌_p_, _x2 ₌_sx₊_p _e _x2₊_p₌_sx_.

Os gregos (500 a 200 anos a.C.), por sua vez, fizeram avanços na resolução desse tipo de equaç ões com estudos ligados à Geometria, eles resolviam alguns tipos de equaç ões do segundo grau apenas com régua e compasso, representando n úmeros como quantidades geométricas, como áreas e comprimentos.

Dos matemáticos gregos que se destacaram na hist ória e que produziram traba-lhos importantes para o desenvolvimento de equaç ões do segundo grau podemos citar Euclides que desenvolveu técnicas de resolução de equaç ões do segundo grau e Diophanto2 _{por introduzir alguns s´ımbolos criando outra representação para essas} equaç ões em uma época onde a solução ainda era apresentada em forma de discurso, dentre outros.

Os hindus também realizaram trabalhos nessa área. Utilizando o método de com-pletar quadrados e métodos puramente algébricos, desenvolveram a f órmula que co-nhecemos hoje como f órmula de resolução das equaç ões quadráticas ou f órmula de Bhaskara, que recebeu esse nome não por ter sido criada por ele, mas, por ter sido pu-blicada em uma de suas obras, na realidade esse feito deve-se a outro indiano, Sridhar Acharya (870 - 930 d.C.) ou Sridhara que é como o conhecemos.

”O hábito de dar o nome de Bhaskara para a f órmula de resolução da equação do segundo grau se estabeleceu no Brasil por volta de 1960. Esse costume, aparentemente s ó brasileiro (não se encontra o nome de Bhaskara para essa f órmula na literatura internacional) não é adequado ... embora não se deva negar a importância e a riqueza da obra de Bhaskara não é correto atribuir a ele a conhecida f órmula de resolução da equação do 2o_{grau.”(ZAGO et al, 1996, p.54).}

1 _{A primeira referência hist órica a n úmeros negativos ocorre num livro chinês cuja a forma mais antiga}

data da Dinastia Han (202 a.C. - 220).

2 _{Diophanto de Alexandria, foi um importante matemático grego do século II e é considerado por}

(24)

Os árabes, por sua vez, deram uma grande contribuição para o avanço no estudo de várias áreas da Matemática e também para o estudo dessas equaç ões traduzindo para sua l´ıngua, o árabe, manuscritos hindus e gregos como por exemplo ”Os Elementos”de Euclides que trata-se de uma coleção de 13 livros escritos pelo pr óprio Euclides por volta de 300 anos a.C., trazendo consigo uma série de definiç ões, postulados, proposiç ões e demonstraç ões abordando várias áreas de conhecimento como a Geometria Euclidiana e a Teoria dos N úmeros. É o segundo livro mais publicado em todo o mundo chegando a uma marca de aproximadamente mil ediç ões, perde somente para a B´ıblia.

Os chineses não ficaram para trás e também desenvolveram trabalhos à procura da solução das equaç ões do segundo grau, a estratégia criada por eles intitulada como método fan-fan, publicado por Zhu Shijie (conhecido também por Chu Shih-Chieh) em 1303, apresentado em sua obra ”Ssu-yuan y ú-chien”que significa ”precioso espelho dos quatro elementos”, baseia-se em aproximaç ões sucessivas de ra´ızes.

No continente europeu, a partir do século XV, muitos matemáticos expuseram trabalhos relacionados à resolução das equaç ões quadráticas, dentre eles, podemos citar o francês François Viète (1540 - 1603) que utilizou s´ımbolos para representar equaç ões, onde até então, não se usava uma f órmula para obter as ra´ızes dessas equaç ões. A representação criada por ele era a seguinte:

BinA´area+CinA+D´e igual a 0.

Mais tarde, outro matemático também de nacionalidade francesa, de nome René Descartes (1596 - 1650), criou uma maneira mais prática para representar os s´ımbolos adotados por Viète, a partir desse fato, acabamos utilizando até hoje a representação

ax2+bx+c =0 que recebemos dos europeus e a soluc¸˜ao fornecida pelos hindus.

3.2 Tipos de equac¸˜ao do segundo grau

Definição 3.1. Chama-se equação do segundo grau, na inc ógnitax, toda equação que puder ser escrita na formaax2₊_bx₊_c₌_{0, sendo}_a_,_b_,_c_∈_R_com_a_,_0.

Observe que se tivéssemosa=0, ter´ıamos uma equação do primeiro grau da forma

bx+c =0, que poderia ser resolvida com um dos métodos apresentados no cap´ıtulo 2. Classificamos, então, as equaç ões do segundo grau em completas ou incompletas. A equação ax2 ₊_bx₊_c ₌ _{0 será dita completa quando}_b _e_c _{forem diferentes de zero.} Quando essa equação apresentar seus coeficientes, b = 0 ouc = 0 ou ainda, quando ambosb=c =0, diremos que ela está em sua forma incompleta.

Quando a equação tiver a formaax2 ₌ _{0 apresentará sempre ra´ızes nulas, uma vez} que, se o produto de dois n úmeros é igual a zero (a·x2 = 0), então: a = 0, x2 = 0 ou

(25)

Se as equaç ões são da formaax2₊_c ₌ _{0 devemos isolar a inc ógnita para encontrar} suas ra´ızes, da´ı:

ax2+c=0=_⇒ ax2=₋c =_⇒x2 =₋c

a =⇒x=±

r

−c

a,

esse tipo de equação possuirá duas ra´ızes reais se ₋c

a for um n ´umero positivo, nesse

caso, suas ra´ızes ser˜ao:

x′ _{= +} r

−c

a e x”=−

r

−c

a.

e n˜ao ter´a raiz real caso−c

a seja um n ´umero negativo.

Porém, se as equaç ões tiverem a forma ax2₊_bx ₌ _{0 basta colocar a inc ógnita em} evidência, que teremos

x·(ax+b)=0

para o produto ser igual a zero, basta que um dos fatores o seja, assim:

x=0 ou ax+b=0 Da´ı, chegamos a

x=0 ou x=₋b

a

que são as ra´ızes da equação.

Exemplo 3.2. Resolver as equac¸ ˜oes do segundo grau incompletas. a)2x2₊₈_x₌₀

b)3x2₋₁₂₌₀ c)7x2₌₀ Soluc¸˜ao:

a)2x2₊₈_x₌₀ _⇐⇒ _x_·₍₂_x₊₈₎₌₀ _⇐⇒ _x₌_{0 ou 2}_x₊₈₌₀ _⇐⇒ _x₌_{0 ou} _x₌₋_4.

b) 3x2 −12 = 0 ⇐⇒ 3x2 = 12 ⇐⇒ x2 = 12

3 ⇐⇒ x

2 ₌ ₄

⇐⇒ x = _±√4 ⇐⇒

x=_±2.

c)7x2₌₀

⇐⇒ x2 ₌₀

⇐⇒ x=0.

(26)

3.3 Métodos de resolução de equaç ões do segundo grau completas

Existem vários métodos para se encontrar as ra´ızes de uma equação do segundo grau. Entretanto, mostraremos apenas aqueles, que por sua simplicidade e elegância, podem ser demonstrados por meio de manipulaç ões algébricas, através de construç ões geométricas utilizando somente régua e compasso ou usando métodos gráficos ou ainda, por meio de técnicas de aproximação de ra´ızes. Sendo assim, desejamos que o leitor conheça as relaç ões existentes entre a Álgebra e a Geometria na resolução das equaç ões do segundo grau.

3.4 M´etodo alg´ebrico de Sridhara

A maneira encontrada por Sridhara para resolver as equaç ões do segundo grau é encontrar dois n úmeros x e y cuja soma seja s e cujo produto é p. Usando s´ımbolos, podemos escrever:       

x+y=s x·y=p

Fazendox= s

2+a e y=

s

2 −a coma>0, temos:

x·y=

_s

2+a

·

_s

2−a

= s

2

4 −a

2 ₌_p

que implica

a2 = s 2

4 −p=⇒a=

r

s2

−4p

4 . Logo, conclu´ımos que os valores dexeys˜ao:

x= s 2 +

r

s2−4p

4 e y=

s

2 −

r

s2−4p

4 Note que sea<0, os valores dexeys˜ao permutados.

Os matemáticos dessa época já sabiam que essas equaç ões poderiam apresentar no máximo 2 ra´ızes.

Sridhara ao enunciar a regra que originou a f órmula atual para a resolução de equaç ões do segundo grau batizou sua descoberta como ”f órmula geral para resolução da equação polinomial do segundo grau”.

Exemplo 3.3. Determinar as dimens ões de um terreno retangular de área 160m2_sabendo que seu per´ımetro é 56m.

Solução do problema:Sejaxo comprimento do terreno eya sua largura e lembrando que o per´ımetro de um pol´ıgono é dado pela soma de seus lados, podemos escrever:

      

2x+2y=56

x_·y=160 ou

      

x+y=28

(27)

Aplicando o m´etodo descrito acima, observamos que: s=28 ep=160, da´ı

x= s 2 +

r

s2

−4p

4 =

28 2 +

r

282₋₄_·₁₆₀

4 =14+

r

784−640

4 =14+

√

36=14+6=20 e

y= s 2 −

r

s2

−4p

4 =

28 2 −

r

282−4·160

4 =14−

r

784−640

4 =14−

√

36=14−6=8

3.5 Método de resolução convencional

Outro matemático indiano que também exp ôs uma técnica para encontrar as ra´ızes desse tipo de equaç ões foi Bhaskara 3_{que utilizou o método de completar quadrados} usado pelos babil ônios.

Dada a equac¸˜aoax2₊_bx₊_c₌_{0. Se a multiplicarmos por 4}_a_{, teremos:} 4a2x2+4abx+4ac=0

Observe que s ó teremos um trin ômio quadrado perfeito se adicionarmos um termo igual ab2_{aos dois lados da equação. Então:}

4a2x2+4abx+4ac+b2=b2

Reorganizando, temos:

4a2x2+4abx+b2 =b2₋4ac

Ou seja,

(2ax+b)2=b2−4ac

Portanto,

2ax+b =_±√b2₋₄_ac Da´ı,

2ax=₋b± √b2₋₄_ac e isolando a inc ´ognita temos:

x= −b±

√

b2₋₄_ac

2a ,

que é a f órmula resolutiva de equaç ões do segundo grau.

Podemos fazer várias manipulaç ões diferentes, da aplicada por Bhaskara, com a equação do segundo grau e encontrar uma dedução alternativa para a f órmula resolu-tiva da equação do segundo grau.

Exemplo 3.4. Vamos encontrar a solução da equaçãox2−5x+6=0. Solução:

x= −b±

√

b2₋₄_ac

2a =

−(−5)± p(−5)2₋₄_·₁_·₆

2·1 =

5±1

2 da´ı x=2 oux=3.

(28)

3.6 M´etodo da semi-soma e do produto

Dada a equação do segundo grauax2₊_bx₊_c ₌ _{0, com}_a_,_b_,_c _∈ _R_e_a_, _{0 podemos} usar uma manipulação diferente da que foi utilizada anteriormente e encontrar outra expressão para determinar as ra´ızes dessa equação.

Dividindo tudo pora, temos:

x2+b

ax+ c a =0

e fazendo

s=₋ b

2a e p= c a

uma vez que

s=₋ b

2a =⇒2s=− b

a =⇒ −2s= b a.

podemos escrevˆe-la da seguinte maneira

x2₋2sx+p=0

Como a solução da equação do segundo grau pode ser encontrada através da f órmula

x= −b±

√

b2₋₄_ac 2a

temos:

x= −(−2s)±

p

(₋2s)2₋₄_·₁_·_p 2·1

x= 2s±

p

4s2₋₄_·_p 2

x= 2s±

p

4(s2_{− ·}_p₎ 2

x= 2s±2

p

s2_{− ·}_p 2 finalmente chegamos a

x=s± q

s2₋_p

Mostrando, assim, outro modo de se resolver uma equação do segundo grau. Exemplo 3.5. Resolver a equação 2x2₋₇_x₊₃₌_{0, usando este método.}

Solução:Dividindo a equação por 2 encontramos

x2₋7 2x+

3

2 =0 ou x

2₋₂_· 7

(29)

fazendos= 7 4,p=

3

2 e aplicando esses valores na f ´ormula que foi deduzida, temos:

x= 7 4± r ₇ 4 2 − 3

2 =⇒x= 7 4 ± r 49 16 − 3

2 =⇒x= 7 4 ±

r

49−24

16 =⇒x= 7 4 ±

5 4. Portanto as ra´ızes s˜ao:

x′ ₌_{3 e} _x_”₌ 1

2. 3.7 M´etodo da soma e da diferenc¸a de quadrados

Dada a equac¸˜ao do segundo grau ax2₊_bx₊_c ₌ _{0, com} _a_,_b_,_c

∈ R ea , 0, vamos

encontrar uma expressão que determine suas ra´ızes, digamosx′_e_x_{” em função de seus}

coeficientes. Sabemos que

(x′+x”)2 =(x′)2+2x′x”+(x”)2 e

(x′−x”)2 =(x′)2−2x′x”+(x”)2

Subtraindo membro a membro a primeira identidade da segunda, obtemos: (x′+x”)2₋(x′₋x”)2 =4x′x”=_⇒(x′+x”)2₋4x′x”=(x′₋x”)2

Fazendox′₊_x_”₌_s_,_x′₋_x_”₌_d_e_x′_·_x_”₌_p_{, podemos formar o seguinte sistema de}

equac¸ ˜oes do primeiro grau

      

x′₋_x_”₌_d x′₊_x_”₌_s

Somando as duas equac¸ ˜oes temos:

2x′ =d+s=_⇒x′ = d+s 2

substituindo o valor encontrado em qualquer uma das equac¸ ˜oes acima, obtemos

x”= s−d 2 Comox′₊_x_”₌₋b

a ex

′_·_x_”₌ c

a, fato que est´a provado no Apˆendice A, temos:

(x′+x”)2−4x′x”=(x′−x”)2 =_⇒ ₋b

a

!2

−4c

a =d

2 ₌

⇒d=_±

r

b2₋₄_ac

a2

portanto

x′ ₌ −b+

√

b2₋₄_ac

2a e x”=

−b− √b2₋₄_ac

(30)

Exemplo 3.6. Encontrar a solução da equação 3x2

−30x+72=0.

Solução:Aplicando a f órmula encontrada, temos: a=3,b=₋30 ec=72. Da´ı,

x′ ₌ −b+

√

b2₋₄_ac

2a =

−(₋30)+ p(₋30)2₋₄_·₃_·₇₂

2_·3 =

30+ √36

6 =6

x”= −b−

√

b2₋₄_ac

2a =

−(−30)− p(−30)2₋₄_·₃_·₇₂

2·3 =

30₋ √36

6 =4

3.8 M´etodo alternativo

Quando resolvemos uma equação do segundo grau pelo método convencional encontramos a expressão b2 ₋ ₄_ac _{que comumente é chamada de discriminante da} equação e representada pela letra do alfabeto grego ∆ (delta). De acordo com esse discriminante, temos três casos a considerar:

1ocaso: Quando temosb2

−4ac>0 a equac¸˜ao apresenta duas ra´ızes reais e diferentes, assim representadas:

x′ ₌ −b+

√

∆

2a ex”=

−b₋ √∆

2a

2ocaso: Quando temosb2

−4ac=0 a equac¸˜ao tem duas ra´ızes reais e iguais.

x′ ₌_x_”₌₋ b

2a

3o_caso: _Quando_b2₋₄_ac_<_{0 o valor da expressão} √_∆_{não existe em}_R_{, não existindo,} portanto, ra´ızes reais. As ra´ızes da equação sãon úmeros complexos4_.

Dada express˜ao∆ = b2−4ac.

Podemos reescrevˆe-la da seguinte maneirab2

−∆ = 4ace fatorando obtemos

b_± √∆_·b_∓ √∆=2a_·2c,

dividindo tudo por 2a·b∓ √∆, encontramos

b_± √∆ 2a =

2c b_∓ √∆

finalmente multiplicando essa ´ultima express˜ao por (-1), temos:

−b∓ √∆

2a =

2c

−b± √∆.

4 _{Os n úmeros complexos foram introduzidos na ´}_{Algebra durante o século XVI por alguns matemáticos}

(31)

Note que o lado esquerdo dela é a f órmula resolvente da equaçãoax2₊_bx₊_c ₌ _0, da´ı

x= 2c

−b± √∆

é a solução da equaçãoax2₊_bx₊_c ₌_{0, com}_a_,_b_,_c_∈_R_e_a_,_b_e_c_{diferentes de zero.} Se não tivéssemos o conhecimento da f órmula resolutiva da equação do segundo grau, poder´ıamos encontrar a f órmula acima através do método algébrico de completar quadrados.

Demonstração:Multiplicando a equaçãoax2₊_bx₊_c ₌_{0 por 4}_c_{, temos:} 4acx2+4cbx+4c2 =0.

Adicionando e subtraindob2_x2_{ao primeiro membro dessa equac¸˜ao chegamos a} 4acx2+4cbx+4c2+b2x2−b2x2 =0.

Reagrupando os termos dessa equac¸˜ao podemos escrever 4acx2−b2x2+4cbx+4c2+b2x2 =0.

Colocando o fator−x2 _{em evidência nos dois primeiros termos e fatorando os três} últimos, encontramos

−x2(b2−4ac)+(bx+2c)2 =0.

logo,

x2(b2−4ac)=(bx+2c)2.

extraindo a raiz quadrada em ambos os lados, temos

±x√b2₋₄_ac₌_bx₊₂_c

ou

±x√b2₋₄_ac₋_bx ₌₂_c₌_⇒_x_±√_b2₋₄_ac₋_b₌₂_c

Assim conclu´ımos que a solução será:

x= 2c

−b± √b2₋₄_ac

Exemplo 3.7. Resolver a equação 3x2+7x+4=0 aplicando a f órmula encontrada. Solução:Comoa=3,b=7 ec =4, temos que:

∆ =b2₋₄_ac₌₇2₋₄_·₃_·₄₌₄₉₋₄₈₌₁ da´ı,

x= 2c

−b± √∆

= 2·4

−7± √1

= 8

−7_±1

portanto as ra´ızes s˜ao: x′ ₌₋4

3 e x”=−1.

(32)

3.9 M´etodo de Vi`ete

Viète5 _{encontrou uma maneira diferente para resolver a equação do segundo grau}

ax2 ₊_bx₊_c ₌ _{0, com} _a_,_b_,_c _∈ _R _e _a _, _{0. O modo baseia-se em relacionar a equação} em questão com uma equação do tipo ay2₊_p ₌ _{0, onde}_p _{é um n úmero que depende} dea,becde modo que qualquer solução dessa equação determinará uma solução da equaçãoax2+bx+c=0.

Podemos observar que a equaçãoay2₊_p₌_{0 admite duas soluç ões:}

y′ ₌ r

−p

a e y”=−

r

−p

a, se − p a ≥0.

Escrevendox= y+m, ondeyemsão inc ógnitas auxiliares. A equaçãoax2+bx+c=0 pode ser escrita como

a(y+m)2+b(y+m)+c =0 e, desenvolvendo, encontra-se

a(y2+2my+m2)+b(y+m)+c=0

ay2+2amy+am2+by+bm+c=0.

Reescrevendo essa igualdade como uma equação na inc ógnitay, obtemos

ay2+(2am+b)y+am2+bm+c=0.

Podemos transformar essa equação numa equação do 2o_{grau incompleta, anulando} o coeficiente de y, para isso, basta escolherm=₋ b

2a obtendo assim a equac¸˜ao

ay2+a − b

2a

!2

+b − b

2a

!

+c=0.

Agora aplicando um dos métodos que foi mostrado na seção 3.2 temos

ay2+a b

2

4a2

!

+b ₋ b

2a

!

+c=0

ay2+ b 2

4a − b2

2a +c=0 ay2+ 4ac−b

2

4a =0 ay2= b

2

−4ac

4a y2= b

2₋₄_ac

4a2

(33)

y=_±

r

b2

−4ac

4a2

y=_±

√

b2₋₄_ac 2a

Lembrando que m = ₋ b

2a e que x = y + m temos que as soluç ões da equação ax2₊_bx₊_c ₌_{0 são dadas por:}

x= y+m=₋ b 2a±

√

b2₋₄_ac 2a

que é a f órmula resolutiva de uma equação do segundo grau. Exemplo 3.8. Vamos encontrar as ra´ızes da equaçãox2

−7x+12=0.

Soluc¸˜ao:

Se estamos querendo saber quais são as ra´ızes dessa equação usando o método de Viéte devemos fazerx= y+me substituir na equação dada. Ou seja:

(y+m)2−7(y+m)+12=0 Desenvolvendo teremos:

y2+2my+m2−7y−7m+12=0

y2+(2m−7)y+m2−7m+12=0 Fazendom= 7

2, para anular o coeficiente de y, temos que:

y2+ 49 4 −

49

2 +12=0=⇒ y 2

− 1

4 =0=⇒ y=± 1 2 Comox= y+m, vem que:

x= 7 2 ±

1 2 Portanto as ra´ızes s˜aox′ ₌_{4 e}_x_”₌_3.

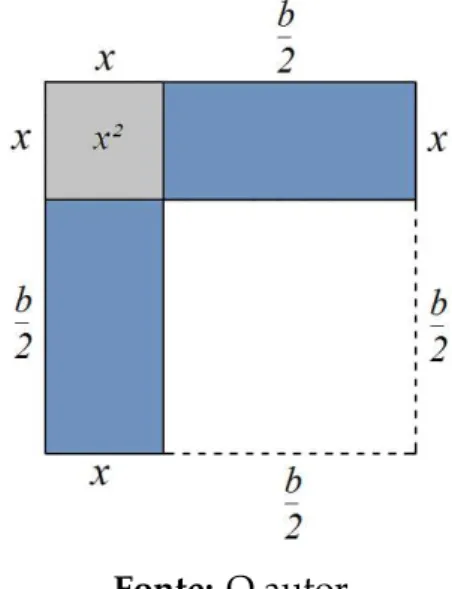
3.10 M´etodo geom´etrico de completar quadrados

Considere a equac¸˜ao:

x2₊_bx₌_c_{, onde}_c_>₀

(34)

Figura 3 – M´etodo geom´etrico de completar quadrados

Fonte: O autor

Observe que naFigura 3o retângulo de dimens õesbexestá representado como 4 retângulos menores de dimens ões b

4 exe que a ´area hachurada ´e igual ac.

Como podemos observar, ao completarmos o quadrado maior estaremos formando quatro quadrados menores de lados b

4 e com ´area medindo

b

4

!2

cada um. Sendo assim, a ´area dos quatro quadrados menores ´e dada por:

4 b 4

!2

=4· b

2

16 =

b2 4 =

b

2

!2

Portanto, a ´area total do quadrado externo ser´a igual ac+ b 2

!2

e a medida de seu lado será a raiz quadrada dessa área, que é igual a:

± s

c+ b 2

!2

Como

2· b

4 +x

| {z }

lado do quadrado externo

= _±

s

c+ b 2

(35)

O valor procurado (x) ´e o lado do quadrado externo subtra´ıdo de duas vezes o lado do quadrado menor, ou seja:

x=_±

s

c+ b 2

!2

−2· b

4 =⇒x=−

b

2±

s

c+ b 2

!2

Exemplo 3.9. Aplicando o método descrito acima encontre as ra´ızes da equação do segundo graux2₊₂_x₌_3.

Soluc¸˜ao :

x=₋b 2 ±

s

c+ b 2

!2

=₋2

2±

r

3+

₂

2

=₋1_± √4=₋1_±2

As ra´ızes procuradas são, portanto, 1 e −3. Embora não faça sentido falar num quadrado de lado−3, pois, não há comprimentos negativos.

3.11 M´etodo geom´etrico alternativo de completar quadrados

Considere novamente a equac¸˜ao:

x2₊_bx₌_c_{, onde}_c_>₀

O método alternativo consiste em dividir o retângulo de dimens õesb exem dois retângulos menores de dimens ões b

2 exe n˜ao mais em quatro, como foi visto anterior-mente. Veja aFigura 4abaixo.

Figura 4 – M´etodo geom´etrico alternativo de completar quadrados

(36)

Como a ´area hachurada representada naFigura 4 ´e igual ac. Se completarmos o quadrado maior, estaremos formando um quadrado menor de lado b

2, cuja ´area ser´a igual a b

2

!2

. Logo, a ´area total do quadrado maior ´e igual ac+ b 2

!2 .

Como podemos encontrar essa ´area fazendo x+ b 2

!2

, teremos:

x+ b 2

!2

=c+ b

2

!2

=_⇒ x+ b

2 =±

s

c+ b 2

!2

=_⇒x=₋b

2 ±

s

c+ b 2

!2

,

que é a solução da equação do segundo graux2₊_bx ₌_c_{, onde}_c_>_0.

3.12 Método gráfico de um sistema de equaç ões

Dada a equac¸˜aoax2₊_bx₊_c₌_{0, com}_a_,_b_,_c

∈R,a,0 ec ,0. Temos que: x(ax+b)=₋c=_⇒ax+b=₋c

x.

Fazendo f(x) = ax+be g(x) = ₋c

x podemos construir os gráficos das funç ões f(x)

e g(x) no mesmo plano e verificar se existem pontos de intersecção entre os gráficos, se houver, esses pontos de intersecção representam a solução da referida equação do segundo grau, caso contrário a equação não possuirá solução.

Exemplo 3.10. Vamos resolver a equaçãox2₊₂_x₋₁₅₌_{0, usando o método gráfico.} Solução:Para isso, faremos o seguinte:

x2+2x=15⇐⇒x(x+2)=15⇐⇒x+2= 15

x

Sendo f(x) = x+2 e g(x) = 15

x , basta agora construir os gráficos das funç ões f(x)

e g(x) no mesmo plano e teremos a solução da equação x2 ₊₂_x₋₁₅ ₌ _{0, onde}_x′ ₌ ₃

e x” = ₋5 são as ra´ızes da equação. Vejamos abaixo a visualização geométrica na Figura 5, que pode ser feita utilizando um software de matemática dinâmica como o GeoGebra6.

6 _{GeoGebra é um aplicativo de matemática que combina conceitos de geometria, álgebra e cálculo. Ele}

(37)

Figura 5 – Construção dos gráficos de f(x) e g(x) e seus pontos de intersecção

Fonte: O autor

3.13 M´etodo de Leslie

No s´eculo XVIII o inglˆes Sir John Leslie (1766 - 1832), em sua obra Elements of Geometry, apresentou o seguinte procedimento:

Dada uma equação quadrática na forma x2

− bx + c = 0, sobre um sistema de coordenadas cartesianas, marcam-se os pontos A(0,1) e B(b,c). Constr ói-se o c´ırculo de diâmetro AB. As abscissas dos pontos em que esse c´ırculo cortar o eixo x (eixo horizontal), se cortar, são as ra´ızes da equação quadrática dada.

Figura 6 – Gr´afico do m´etodo de Leslie

(38)

Com efeito, a equação da circunferência constru´ıda é dada por:

x₋ b

2

!2 +

y₋ c+1

2

= b

2

!2 +

_c₊₁

2 −1

2

e quando y=0, tem-sex2₋_bx₊_c₌_{0 ou}_x₌ b 2 ±

s

b

2

!2

−c. Exemplo 3.11. Resolver a equac¸˜aox2

−3x+4=0, usando esse método. Solução:Para isso, precisaremos de régua e compasso.

i) com a r´egua e o compasso em m˜aos trace um sistema de coordenadas cartesianas; ii) marquemos os pontosA(0,1) eB(3,4);

iii) construiremos, agora, o c´ırculo de diâmetroAB. Façamos o seguinte: – meça a distância deAatéBe marque um ponto (C) em sua metade;

– com o compasso centralizado nesse novo ponto e abertura igual a metade da distˆancia deAat´eB, desenhe o c´ırculo.

Figura 7 – Gr´afico do m´etodo de Leslie (x2

−3x+4=0)

Fonte: O autor

(39)

3.14 M´etodo de Descartes

No ano de 1637, René Descartes (1596 - 1650) desenvolveu um método geométrico para encontrar a solução positiva de equaç ões do segundo grau representadas nas formas:

x2 ₌_bx₊_c2_, _x2 ₌_c2₋_bx _e _x2₌_bx₋_c2 sempre combecpositivos.

• Vamos encontrar a solução da equaçãox2 ₌_bx₊_c2_.

O método desenvolvido por ele para resolver esse tipo de equação consiste em traçar um segmentoLM de comprimentoce em Ltraça-se uma perpendicularLN de comprimento b

2. Com centro emN constr ói-se um c´ırculo de raioLNe traça-se a reta passando por MeNque corta o c´ırculo no pontoOe no pontoP(Pestá entreMeN). Conforme indica aFigura 8. O segmentoOMé a solução positiva da equação.

Figura 8 – M´etodo de Descartes (x2 ₌_bx₊_c2 _e _x2 ₌_c2

−bx)

Fonte: Revista do Professor de Matem´atica, n.43, p.24

De fato, no triângulo retânguloMLN, retângulo emL, da figura acima, temos que: (NM)2 =(LN)2+(LM)2

ComoLN = b

2,LM = ce sabendo queLN =ON (s˜ao raios do c´ırculo). SeOM= x, temos que: NM=OM−ON=x− b

2. Logo,

(NM)2 =(LN)2+(LM)2

x− b

2

!2

= b

2

!2 +c2

que implicar´a emx2 ₌_bx₊_c2 _ou _x₌ b 2±

s

b

2

!2

+c2_{, onde a raiz positiva ´e dada por:}

x= b 2 +

s

b

2

(40)

Hoje, sabe-se que a outra raiz ´e₋PM.

Com efeito, como NM = NP+PM, se considerarmos o triângulo retângulo MLN, retângulo emLe nomearmosPM=x, teremos:

(NM)2 =(LN)2+(LM)2

x+ b 2

!2

= b

2

!2 +c2

x+ b 2 =±

s

b

2

!2 +c2

x=₋b 2±

s

b

2

!2 +c2

da´ı,−PM= b 2±

s

b

2

!2

+c2_{e a outra raiz ser´a}_x₌ b 2−

s

b

2

!2

+c2_{, entretanto, essa raiz} n˜ao foi considerada por Descartes na ´epoca por ser negativa.

Exemplo 3.12. Resolver a equaçãox2 ₌₃_x₊_{4, usando esse método.}

Solução:Vamos resolver geometricamente. Precisaremos de régua e compasso. i) com a régua e o compasso em mãos trace um segmentoLM=2;

ii) emLtrace uma perpendicularLNde comprimento 1,5;

iii) com o compasso centralizado emNconstrua um c´ırculo de raio 1,5;

iv) trace agora uma reta passando porMeN, essa reta cortar´a o c´ırculo em dois pontos:

OeP(comPentreMeN);

v) com a régua meça os segmentos OM ePM. As ra´ızes serão OM = 4 e −PM = ₋1. Conforme indica a figura abaixo.

Figura 9 – Solução geométrica da equaçãox2 ₌₃_x₊₄

(41)

• Vamos resolver a equac¸˜ao da formax2 ₌_c2

−bx.

O método desenvolvido por ele para resolver esse tipo de equação é o mesmo utilizado para encontrar a solução da equaçãox2 ₌_bx₊_c2_{. Nesse caso, continuaremos} usando aFigura 8. O segmentoPMé a solução positiva da equação.

De fato, no triângulo retânguloMLN, retângulo emL, temos: (NM)2 =(LN)2+(LM)2

ComoLN = b

2, LM= c e sabendo queLN = NP(s˜ao raios do c´ırculo). SePM = x, temos que: NM=NP+PM=x+ b

2. Logo,

(NM)2 =(LN)2+(LM)2

x+ b 2

!2

= b

2

!2 +c2

que implicar´a emx2 ₌_c2₋_bx _ou _x₌₋b 2 ±

s

b

2

!2

+c2_{, onde}_x₌₋b 2 +

s

b

2

!2

+c2 _é a raiz positiva da equação dada.

A outra raiz ´e−OM.

Com efeito, comoNM=OM−ONeON= b

2, se considerarmos o triˆangulo retˆangulo

MLN, retˆangulo emLe nomearmosOM=x, teremos: (NM)2 =(LN)2+(LM)2

x₋ b

2

!2

= b

2

!2 +c2

x− b

2 =±

s

b

2

!2 +c2

x= b 2±

s

b

2

!2 +c2

da´ı,₋OM=₋b 2 ±

s

b

2

!2

+c2_{e a outra raiz ser´a}_x₌₋b 2−

s

b

2

!2 +c2_.

Exemplo 3.13. Resolver a equac¸˜aox2 ₌₁₆

−6x, usando esse m´etodo.

Solução:Vamos resolver geometricamente. Precisaremos de régua e compasso. i) com a régua e o compasso em mãos trace um segmentoLM=4;

ii) emLtrace uma perpendicularLNde comprimento 3;

iii) com o compasso centralizado emNconstrua um c´ırculo de raio 3;

(42)

OeP(comPentreMeN);

v) com a régua meça os segmentos OM ePM. As ra´ızes serão ₋OM = ₋8 e PM = 2. Conforme indica a figura abaixo.

Figura 10 – Solução geométrica da equaçãox2 ₌₁₆₋₆_x

Fonte: O autor

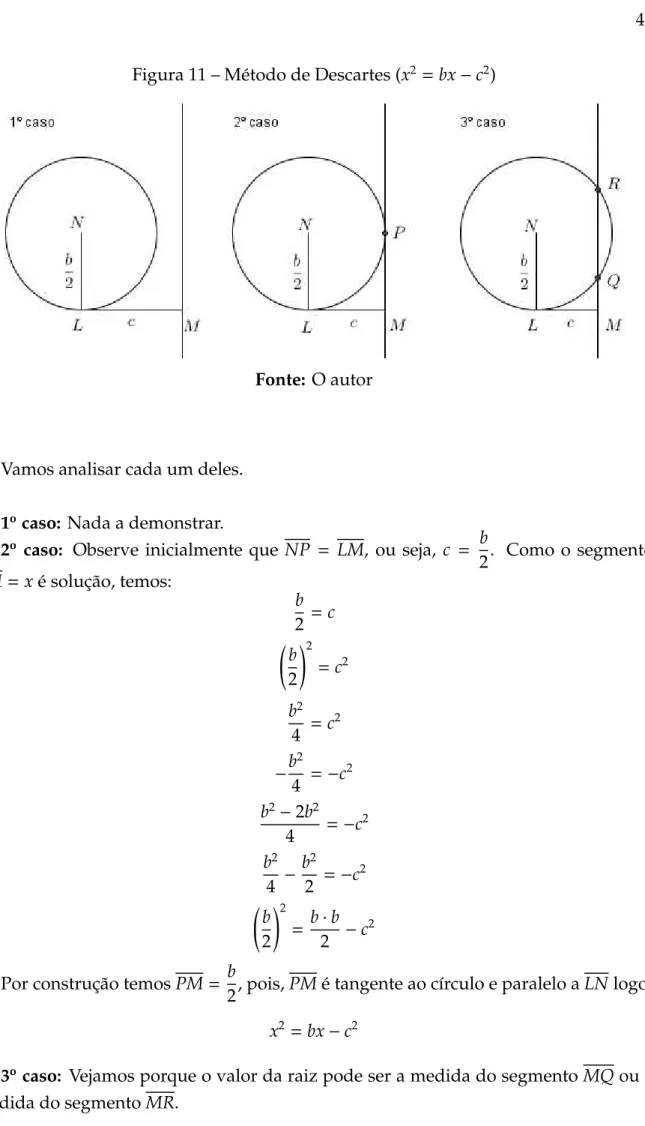
• Vamos resolver agora a equac¸˜aox2 ₌_bx₋_c2_.

A estratégia desenvolvida por ele para resolver esse tipo de equação seria a seguinte: constru´ımos um segmentoLMde medidac, emLtraçamos uma perpendicularLNde medida b

2 e em M traçamos uma reta paralela a LN. Com centro em N e raio LN constr ói-se um c´ırculo. Se houver intersecção desse c´ırculo com a reta paralela aLNa distância de cada ponto de intersecção ao pontoMrepresenta uma solução da equação

x2 ₌_bx

−c2_.

Pode ocorrer trˆes casos, como indica a figura abaixo.

1o_caso: _{a equação}_x2 ₌_bx₋_c2 _{não possui raiz real.}

(43)

Figura 11 – M´etodo de Descartes (x2₌_bx

−c2₎

Fonte: O autor

Vamos analisar cada um deles.

1o_caso: _{Nada a demonstrar.}

2o _caso: _{Observe inicialmente que} _NP ₌ _LM_{, ou seja,} _c ₌ b

2. Como o segmento

PM=x é solução, temos:

b

2 =c

b

2

!2 =c2

b2 4 =c

2

−b

2

4 =−c 2

b2₋₂_b2 4 =−c

2

b2 4 −

b2 2 =−c

2

b

2

!2

= b·b 2 −c

2

Por construc¸˜ao temosPM= b

2, pois,PM ´e tangente ao c´ırculo e paralelo aLNlogo,

x2 =bx−c2

3o_caso: _{Vejamos porque o valor da raiz pode ser a medida do segmento}_MQ_{ou a}

(44)

i) Vamos analisar o segmentoMRprimeiro.

Marcaremos sobre o segmentoMRo pontoZtalqueNZ seja paralelo aLM. Dessa forma, teremosNZ=LM=ceLN=MZ= b

2.

Figura 12 – M´etodo de Descartes (x2₌_bx

−c2₎

Fonte: O autor

Observando a figura acima, temos: NR= b

2 (raio) eZR=MR−MZ.

Se considerarmos MR = x, como o triângulo RZN é retângulo em Z, usando o Teorema de Pitágoras, temos:

(NR)2 =(NZ)2+(ZR)2 (NR)2=(NZ)2+(MR−MZ)2

b

2

!2

=c2+ x− b

2

!2

x− b

2

!2

= b

2

!2

−c2

que implicar´a emx2 ₌_bx₋_c2 _ou _x₌ b 2 ±

s

b

2

!2

−c2_.

ii) Para a outra raiz serMQ, observemos o seguinte:

QZ=MZ₋MQ.

Vamos usar novamente o Teorema de Pitágoras, dessa vez no triângulo NZQ, retângulo em Z. Observe que NQ = b

2 (raio). Se considerarmos agora MQ = x, teremos: