Uso de correntropia na generalização de funções cicloestacionárias e aplicações para a extração de características de sinais modulados

(1)

UNIVERSIDADE_FEDERALDO RIO GRANDE DO NORTE

DECOMPUTAÇÃO

Uso de Correntropia na Generalização de

Funções Cicloestacionárias e Aplicações para a

Extração de Características de Sinais

Modulados

Aluisio Igor Rêgo Fontes

Orientador: Prof. Dr. Luiz Felipe de Queiroz Silveira Co-orientador: Prof. Dr. Allan de Medeiros Martins

Tese de doutorado apresentada ao

Pro-grama de Pós-Graduação em Engenharia Elétrica e de Computação da UFRN como parte dos requisitos para a obtenção do grau de Doutor em Ciências.

(2)

Fontes, Aluisio Igor Rêgo

Uso de correntropia na generalização de funções cicloestacionárias e aplica-ções para a extração de características de sinais modulados. / Aluisio Igor Rêgo Fontes - Natal, RN, 2014

98 f: il.

Orientador: Dr. Luiz Felipe de Queiroz Silveira Co-orientador: Dr. Allan de Medeiros Martins

Tese (Doutorado) - Universidade Federal do Rio Grande do Norte. Centro de Tecnologia. Programa de Pós-Graduação em Engenharia Elétrica e Computação.

1. Correntropia 2. Cicloestacionariedade

3. Função de Correntropia Cíclica 4. Função de Densidade Espectral de Corren-tropia Cíclica

5. Extração de Características de Sinais. I. Silveira, Luiz Felipe de Queiroz. II. Martins, Allan de Medeiros III. Universidade Federal do Rio Grande do Norte. IV. Título.

(3)

(4)

(5)

(6)

À Deus, por sempre iluminar meu caminho.

À minha família pelo apoio, incentivo, paciência, força, amor e carinho. Em especial meus pais: Maria de Fátima Rêgo Fontes e Aluisio Fontes de Queiroz e minha irmã Fabíola Rêgo Fontes.

À minha namorada, Bruna Angelina Barreto Costa Lobo , pelo amor, paciência e por sua dedicação em minha vida acadêmica, me dando todo o apoio nos momentos difíceis. Ao professor Luiz Felipe de Queiroz Silveira, que sempre acreditou no meu potencial e se não fosse por sua enorme dedicação e orientação não teríamos concluído.

Ao professor Allan de Medeiros Martins, pela orientação, confiança, atenção, tempo de-dicado e todo o apoio para a realização deste trabalho.

Aos professores do Departamento de Engenharia de Computação e Automação.

Aos meus amigos Arthur, Avelino, Danilo, Eduardo, Fabrício, Lucas e Paolo por todo apoio, amizade e momentos de descontração indispensáveis.

(7)

A extração de informações de sinais aleatórios é um problema frequente e relevante em muitas aplicações de processamento digital de sinais. Nos últimos anos, diferentes métodos têm sido utilizados para a parametrização de sinais ou obtenção de descritores eficientes de suas características. Quando os sinais aleatórios possuem propriedades es-tatísticas cicloestacionárias, as funções de autocorrelação cíclica (CAF) e de densidade espectral cíclica (SCD) podem ser utilizadas na obtenção de informações cicloestacioná-rias de segunda ordem. Entretanto, em sinais contaminados com ruído não-gaussiano, apenas informações cicloestacionárias de segunda ordem podem não gerar bons descrito-res para aplicações em aprendizagem de máquinas e, neste caso, a análise cicloestacioná-ria deve ocorrer sobre informações estatísticas de ordem superior. Este trabalho propõe uma nova ferramenta matemática para a análise cicloestacionária de ordem superior ba-seada na função de correntropia. Especificamente, a teoria de análise cicloestacionária é revisitada sob um enfoque de teoria da informação, e as funções de correntropia cíclica (CCF) e densidade espectral de correntropia cíclica (CCSD) são definidas. É compro-vado analiticamente que a CCF contém informações de momentos cicloestacionários de segunda ordem e de ordem superior, sendo uma generalização da CAF. O desempenho dessas novas funções, na extração de características cicloestacionárias de ordem superior, é analisado em um cenário de comunicação sem fio com ruído não-gaussiano.

Palavras-chave: Correntropia, Cicloestacionariedade, Função de Correntropia

(8)

Information extraction is a frequent and relevant problem in digital signal processing. In the past few years, different methods have been utilized for the parameterization of signals and the achievement of efficient descriptors. When the signals possess statistical cyclostationary properties, the Cyclic Autocorrelation Function (CAF) and the Spectral Cyclic Density (SCD) can be used to extract second-order cyclostationary information. However, second-order cyclostationary information is poor in nongaussian signals, as the cyclostationary analysis in this case should comprise higher-order statistical information. This paper proposes a new mathematical tool for the higher-order cyclostationary analysis based on the correntropy function. Specifically, the cyclostationary analysis is revisited focusing on the information theory, while the Cyclic Correntropy Function (CCF) and Cyclic Correntropy Spectral Density (CCSD) are also defined. Besides, it is analytically proven that the CCF contains information regarding second- and higher-order cyclostatio-nary moments, being a generalization of the CAF. The performance of the aforementioned new functions in the extraction of higher-order cyclostationary characteristics is analyzed in a wireless communication system where nongaussian noise exists.

Keywords: Correntropy, Cyclostationary, Cyclic Correntropy Function, Cyclic

(9)

Sumário i

Lista de Figuras iv

Lista de Tabelas vi

Lista de Símbolos vii

1 Introdução 1

1.1 Motivação e Relevância . . . 1

1.2 Objetivo . . . 4

1.3 Organização do Trabalho . . . 4

2 Correntropia para Processos Aleatórios 6 2.1 Introdução à Correntropia . . . 6

2.2 Definições e propriedades . . . 7

2.2.1 Propriedades . . . 11

2.3 Influência do tamanho do kernel . . . 12

2.3.1 Domínio do tempo e da frequência . . . 12

2.3.2 Ruído impulsivo . . . 16

2.4 Síntese . . . 18

3 Processos Cicloestacionários 19 3.1 Introdução à Análise de Sinais Cicloestacionários . . . 19

3.2 Função de Autocorrelação Cíclica (CAF) . . . 20

(10)

3.4 Cicloestacionariedade de Ordem Superior (HOCS) . . . 24

3.5 Síntese . . . 26

4 Correntropia Cíclica 27 4.1 Introdução . . . 27

4.2 Função de Correntropia Cíclica (CCF) . . . 28

4.3 Função Densidade Espectral de correntropia Cíclica (CCSD) . . . 32

4.4 Síntese . . . 35

5 CCSD Aplicada a Análise de Sinais Cicloestacionários 36 5.1 Algoritmo Cyclic Periodogram Detection (CPD) . . . 37

5.2 Sensoriamento Espectral . . . 39

5.3 Assinaturas Cicloestacionárias para Modulações Digitais . . . 46

5.3.1 Modulações 16-QAM, QPSK, ASK e BPSK . . . 47

5.3.2 Modulações BFSK, MSK e AM . . . 52

5.4 Análise da Escalabilidade Paralela da CCSD . . . 56

5.5 Síntese . . . 61

6 Conclusões 63 6.1 Principais Contribuições . . . 64

6.2 Perspectivas para Trabalhos Futuros . . . 65

Referências bibliográficas 66

A Dedução Matemática da Generalização da CCF 72

(11)

D Publicações 81

(12)

2.1 correntropia como a integral no espaço gaussiano ao longo da retaxt1=xt2 [Liu et al. 2006] . . . 10 2.2 Sinal cosseno e autocorrelação do cosseno. . . 13 2.3 correntropia centralizada para diferentes tamanho dekernel. . . 13

2.4 Densidade espectral de potência de um cosseno com frequência de 10Hz. 14 2.5 Transformada de Fourier da autocorrentropia centralizada para diferentes

tamanho dekernel. . . 15

2.6 PDF do ruído impulsivo e o cosseno com outliers . . . 16 2.7 Cálculo da correntropia e correlação, no domínio do tempo e frequência,

para um cosseno comoutlier. . . 17

3.1 Visão tridimensional da SCD para a modulação AM . . . 22 3.2 Perfil alfa para modulação AM . . . 23

4.1 Cálculo da CCSD para um cosseno com uma frequência fundamental . . 34

5.1 Função densidade de probabilidade do ruído da impulsivo . . . 37 5.2 Passo 1.x[n],n=0,1,2,3, ...,N₋1,l=0,1,2,3, ...,L₋1 [Farias et al. 2011] 38

5.3 |SCD| e perfil-alfa para as modulações AM, MSK e BPSK com ruído não-gaussiano. . . 41 5.4 |SCD| e perfil-alfa para as modulações BFSK, QPKS e 16-QAM com

ruído não-gaussiano. . . 42 5.5 |CCSD| e perfil-alfa para as modulações AM, MSK e BPSK com ruído

não-gaussiano. . . 43

(13)

5.7 |CCSD| e SCD para a hipótese H1. . . 45

5.8 |CCSD| e perfil-alfa para as modulações 16-QAM paraσigual a 1, 0.1 e 0.01. . . 48

5.15 Diagrama de blocos com o pseudocódigo do algoritmo paralelo proposto para cálculo da CCSD. . . 57

5.16 Speeduppara diversos valores de tamanho de blocos (N) e quantidade de blocos (L), variando-se a quantidade de processadores p=1,2, ...,64. . . 59

5.17 Eficiência paralela para diversas configurações de tamanhos de blocosN e quantidade de blocosL, fixando-se o número de processadores em 64. . 60

5.18 Perfil alfa da CCSD utilizandoσigual a 0,1. . . 62

C.1 Onda quadrada. . . 77

C.2 Onda triangular. . . 78

C.3 Forma de onda senoidal com duas frequências 10 Hz e 20 Hz . . . 79

(14)

5.1 Parâmetros de simulação computacional dos sinais analisados . . . 37 5.2 Tempo de simulação para diferentes tamanhos de L e N com quantidade

de processadores variando de 1 a 64. . . 59

(15)

AMC Classificação Automática de Modulação

AM DSB-SC Modulação em Amplitude com Faixa Lateral Dupla e Portadora Suprimida

AM SSB-SC Modulação em Amplitude com Faixa Lateral Única e Portadora Suprimida

API Interface de Programação de Aplicativos AWGN Ruído Aditivo Gaussiano Branco

BFSK Modulação por Chaveamento de Frequência Binária BPSK Modulação por Chaveamento de Fase Binária CAF Função de Autocorrelação Cíclica

CPD Cyclic Periodogram Detection

FSK Modulação por Chaveamento em Frequência HMM Modelo Oculto de Markov

MSK Modulação por Chaveamento Mínimo

OFDM Multiplexação por Divisão de Frequência Ortogonal

OpenMP Multiprocessamento Aberto

PCA Análise de Componentes Principais QAM Modulação de Amplitude em Quadratura

QPSK Modulação por Chaveamento de Fase Quaternária SCD Função Densidade Espectral Cíclica

SNR Relação Sinal-Ruído

SVM Máquina de Vetor de Suporte

(16)

CTCMF Cyclic Temporal Cross-Moment Functions TCMF Temporal Cross-Moment Function

CSCMF Cyclic Spectral Cross-Moment

ATSC Advanced Television System Committee NTSC National Television System Committee FPGA Field Programmable Gate Array FAM FFT Accumulation Method

SSCA Strip Spectral Correlation Algorithm WLAN Rede sem Fio Local

GSM Sistema Global para Comunicações Móveis LTE Evolução de Longo Prazo

GCC GNU Compiler Collection

(17)

Introdução

Neste capítulo são apresentadas as linhas gerais deste trabalho, ressaltando-se a re-levância do problema estudado, os objetivos desejados e a organização proposta para o documento.

1.1 Motivação e Relevância

Nos últimos anos, foram desenvolvidos diferentes métodos para a parametrização de sinais aleatórios ou obtenção de descritores desses sinais. Os métodos para extração de características de sinais podem ser utilizados em tarefas de classificação, estimação ou predição, comuns em vários problemas de aprendizagem de máquina. Em geral, esses métodos possuem um padrão de funcionamento composto por duas etapas: aquisição de dados e extração de características.

A sintonia da etapa de extração de características ideais é fundamental em um sis-tema robusto. Essa etapa vem recebendo notáveis contribuições de técnicas avançadas de processamento digital de sinais, tais como: entropia, densidade espectral de potência, wa-velets, cumulantes, correntropia e cicloestacionariedade. Particularmente, as ferramentas matemáticas como correntropia e cicloestacionariedade destacam-se como extratores de características de sinais aleatórios.

(18)

por dispositivos físicos, possuem características estatísticos que variam periodicamente com o tempo. Tais sinais podem ser modelados como processos cicloestacionários ou po-licicloestacionários, se os seus parâmetros estatísticos variam no tempo, respectivamente, com um ou múltiplos períodos [Gardner et al. 1994].

Métodos estatísticos clássicos de processamento de sinais tratam os sinais cicloestaci-onários como se eles fossem estacicicloestaci-onários. Entretanto, frequentemente pode-se conseguir ganhos de desempenho em sistemas de processamento que reconhecem e exploram peri-odicidades não evidentes [Gardner et al. 1994]. Nos últimos anos, métodos que exploram as cicloestacionariedades de sinais têm sido utilizados em várias aplicações, tais como Te-lecomunicações [Cho & Narieda 2015, Jang 2014], Sistemas Biológicos [Newton 1982, Donohue et al. 1994], Meteorologia [Zeng et al. 1996, Hasselmann & Barnett 1981], Climatologia [Bloomfield et al. 1994], Oceanografia [Gini & Greco 2002, Dragan & Yavorskii 1982], Eletromagnetismo [Mykhajlyshyn & others 1996] e Máquinas Rotativas [Randall et al. 2002, Konig & Bohme 1994]. Neste contexto, as técnicas de processa-mento de sinais policicloestacionários podem explorar cicloestacionariedade de segunda ordem (SOCS), obtidas a partir de transformações quadráticas, ou cicloestacionariedade de alta ordem (HOCS) [Gardner et al. 1994], obtidas com transformações não lineares de ordem N. Em geral, a cicloestacionariedade presente no sinal de interesse pode ser

explorada para melhorar a confiabilidade da informação extraída a partir de um conjunto de medições do sinal [Gardner et al. 1994].

A técnica SOCS vêm sendo amplamente empregada em comunicações na concepção de sistemas de rádio cognitivo, especificamente em aplicações de sensoriamento espectral e classificação automática de modulações [Lei et al. 2011, Jang 2014, Satija et al. 2014a].

(19)

in-formação para diferenciá-las, por exemplo, das modulações M-PSK (para M>4) e QAM, e das modulações ASK e BPSK [Gardner et al. 1994]. Neste caso, a análise de ciclo-estacionariedades de ordem superior tende a melhorar o desempenho dos métodos de processamento de sinais empregados.

Por outro lado, os métodos HOCS empregam transformações não lineares de alta ordem cuja complexidade aumenta quando a ordem do momento estatístico analisado, podendo ser inviável em algumas aplicações. Isto posto, este trabalho propõe um novo método de análise cicloestacionária de ordem superior baseado em uma ferramenta de transformação não-linear, denominada correntropia.

(20)

1.2 Objetivo

Neste trabalho, a análise de sinais cicloestacionários é revisitada sob um enfoque de teoria da informação, sendo definidas novas ferramentas analíticas, denominadas fun-ção de correntropia cíclica (CCF) e funfun-ção densidade espectral de correntropia Cíclica (CCSD). É comprovado analiticamente que a CCF contém informações de momentos cicloestacionários de segunda ordem e de ordem superior, sendo uma generalização da clássica função de autocorrelação cíclica (CAF). O desempenho dessas novas funções, na extração de características cicloestacionárias de ordem superior, é analisado em um cenário de comunicação sem fio com ruído não-gaussiano. Além disso, são apresentadas novas assinaturas cicloestacionárias de ordem superior extraídas por meio da CCSD para as modulações BPSK, BFSK, MSK, OOK, 16-QAM, 4-PSK e AM.

1.3 Organização do Trabalho

Este texto é organizado em seis capítulos e dois apêndices.

No Capítulo 2 a correntropia para processos aleatórios é definida em conjunto com suas propriedades. Apresenta-se também a influência do tamanho dokernel, no seu

de-sempenho.

No Capítulo 3 são apresentadas as principais propriedades da teoria de cicloestaciona-riedade para processos aleatórios no domínio do tempo e da frequência e são definidas as principais funções da análise cicloestacionária: a função de autocorrelação cíclica (CAF) e a função densidade espectral cíclica (SCD).

No Capítulo 4 a teoria de cicloestacionariedade é revisitada sob um enfoque de Teoria da Informação, culminando com as definições das principais funções da análise cicloes-tacionária com correntropia.

(21)

correntropia. Os experimentos têm a finalidade de avaliar e analisar o desempenho dos dois extratores de características.

(22)

Correntropia para Processos Aleatórios

2.1 Introdução à Correntropia

A extração de informações de uma fonte de dados é um problema frequente e relevante em muitas aplicações de processamento de sinais. Nesse contexto, medidas estatísticas de similaridade, como a correlação, podem ser utilizadas com sucesso para a obtenção de informações e caracterização de dados. No entanto, para processos aleatórios não-gaussianos, a estatística de segunda ordem na forma de correlação pode ser ineficaz, pois não há garantia que a média dos sinal seja igual a zero.

Houve várias tentativas para solucionar o processamento de sinais não lineares e não gaussianos para treinamento de máquina, identificação de sistemas e extração de características de sinais aleatórios. Por exemplo, os trabalhos de Wiener e Hammers-tein foram os primeiros métodos propostos para a identificação de sistemas não lineares [Ljung 1998]. Nestes trabalhos, a não linearidade é solucionada através de uma Equação de Wiener-Hopf [Ljung 1998]. Outros trabalhos incluem séries de Volterra [Corduneanu & Sandberg 2000].

A fim de solucionar esse problema, o grupo de pesquisa do Laboratório de Compu-tação em NeuroEngenharia (CNEL) localizado no Estados Unidos, utilizou a entropia de Rényi e informação mútua para processar sinais não gaussianos, o qual foi

(23)

ITL não conseguiam trabalhar com informações temporais do processo aleatório, ou seja, quando o tempo é importante na variável aleatória. Para incorporar a estrutura temporal e a análise estatísticas de ordem superior, uma nova medida foi proposta por Santamaria em [Santamaria et al. 2006], denominada correntropia.

A correntropia é uma generalização da medida de correlação entre sinais aleatórios. Essa medida consegue extrair tanto informações estatísticas de segunda ordem, quanto de ordens superiores do sinal analisado. Embora, por definição, a correntropia seja se-melhante à Correlação, estudos recentes têm mostrado que ela funciona melhor do que a correlação ao lidar com sistemas não-lineares ou não-gaussianos, sem qualquer aumento significativo no custo computacional [Liu et al. 2007].

Nos últimos anos, a correntropia tem sido aplicada com sucesso na solução de diversos problemas de engenharia, tais como classificação automática de modulações [Fontes et al. 2015], sistema de classificação de vozes patológicas [Fontes et al. 2014], análises de componentes principais [He et al. 2011], identificação de sistemas não lineares [Leandro L.S. Linhares et al. 2015], reconhecimento de face e filtros adaptativos [Jeong & Principe 2006].

Neste capítulo serão apresentadas as principais propriedades da correntropia para pro-cessos aleatórios no domínio do tempo e da frequência. Também será abordado a influên-cia (kernel) da correntropia em seu desempenho.

2.2 Definições e propriedades

A correntropia para um processo estocástico ergódico e estacionário,_{xt,t∈T}com

T sendo um conjunto de índices ext ∈Rdé definida como [Santamaria et al. 2006]

Vx(xt1,xt2) =Ext₁xt₂[Gσ(xt1,xt2)] =

Z Z

(24)

em queE[.]representa o operador matemático do valor esperado sobre o processo estocás-ticoxt,Gσé uma função simétrica definida positiva ep(xt₁,xt₂)é a função de densidade de

probabilidade (PDF) conjunta. As funções simétricas definidas positivas mais utilizadas nas áreas de aprendizagem de máquinas, máquinaa de vetor de suporte e aproximação de funções são sigmoide, gaussiana e polinomial [Xu & Principe 2008]. Neste trabalho,Gσ

é umkernelgaussiano, definido por

Gσ(xt1,xt2) =

1

√

2πσexp

−(xt1−xt2)

2

2σ2

, (2.2)

em queσé denominada de tamanho ou largura dokernel. Quando o tamanho dokernel

tende a 0, o kernel gaussiano torna-se uma função deltaδ(xt₁,xt₂)e a Equação (2.1) passa

a ser

lim

σ→0Vx(xt1,xt2) =

Z

xt₁ Z

xt₂

δ(xt1,xt2)pxt₁,xt₂(xt1,xt2)dxt1xt2

=

Z ∞

xt₁=−∞

pxt₁,xt₂(xt1,xt1)dxt1 (2.3)

Na prática, a PDF conjunta da Equação (2.1) é desconhecida e apenas um número fi-nito de dados(xi,yi)N_i₌₁estão disponíveis. Neste caso, uma estimativa dessa PDF conjunta

pode ser obtida aplicando-se o método de Parzen, por [Liu et al. 2007]:

pz(z) =

1

N

∑

i=1

Gσ(z,zi) (2.4)

em queze zi são vetores formados pelos eventos aleatóriosxt1 ext2, isto éz= [xt1,xt2]t. Sext₁ ext₂ são variáveis aleatórias independentes com distribuições marginais de

proba-bilidade estimada por Parzen, logo pxt₁(xt1)e pxt₂(xt2)são definidas como

pxt₁,xt₂(xt1,xt2) = 1

N

∑

i=1

(25)

Dessa forma, quando a largura do kernel tende a zero e utilizando a propriedade de Parzen da Equação (2.4) e integrando ao longo da retaxt₁ =xt₂, a correntropia definida

pela Equação (2.1) pode ser calculada por

lim

σ→0Vx,x(xt1,xt2) ≈

Z ∞

−∞pxt1,xt2(xt1,xt2)|xt1=xt2=udu

≈ Z ∞ −∞ 1 N N

∑

i=1

G(xt1,xt1i)G(y,xt2i)|xt1=xt₂=udu (2.6)

= Z ∞ −∞ 1 N N

∑

i=1

G(u,xt1i)G(u,xt2i)du

= 1

N

∑

i=1

Z ∞

−∞G(u,xt1i)G(u,xt2i)du (2.7)

= 1

N

∑

i=1

G√₂_σ(xt1_i,xt2_i)

É importante ressaltar que na Equação (2.8) foi aplicada a propriedade da convolução de gaussianas. Tal propriedade diz que, a convolução de duas gaussianas resulta em outra gaussiana.

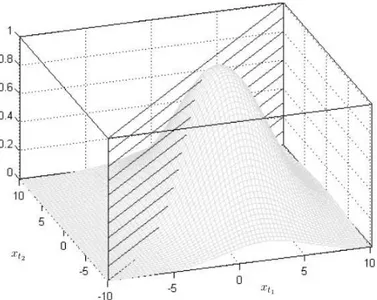
Observa-se que a integral da estimativa de Parzen com kernel Gaussiano é exatamente a estimativa da correntropia com largura dekernelde√2σ. A Figura 2.1 ilustra como a correntropia fornece a PDF na retaxt1 =xt2

Assim, utilizando a dedução da Equação (2.6), a correntropia definida pela Equação (2.1) pode ser reescrita como

V(τ) = 1

N

N−1

∑

n=0

G√₂_σ(xn,xn+τ) (2.8)

para todoτ, em que o processo aleatório de entrada deve ser estritamente estacionário para todos os momentos estatísticos de ordem par. Ou seja, todos os momentos estatísticos de ordem par devem ser invariante ao deslocamento do tempo quando umkernelgaussiano

(26)

Figura 2.1: correntropia como a integral no espaço gaussiano ao longo da retaxt1 =xt2 [Liu et al. 2006]

É importante ressaltar que para processos aleatórios que não sejam estritamente es-tacionários para todos os momentos estatísticos, a correntropia não terá sua eficiência máxima. Entretanto, através do ajuste do tamanho dokernelé possível obter bons

resul-tados, e no pior caso ficará igual à correlação convencional.

Além disso, a correntropia não possui garantia de média zero, mesmo quando os dados de entrada estão centralizados, por causa das transformações não lineares produzidas pelo

kernel. Dessa forma, para garantir média zero, foi proposto um estimador de correntropia

centralizado definido por: [Liu et al. 2007]

U(τ) = 1

N

N−1

∑

n=0

G√₂_σ(xn,xn+τ)−

1

N2

N−1

∑

n=0

N−1

∑

τ=0

G√₂_σ(xn,xn+τ). (2.9)

em quem _N12∑Nn=−01∑τN=−01G√2σ(xn,xn+τ)é a média da correntropia.

(27)

Vx(xt₁,xt₂) =

1

√

2πσ ∞

∑

k=0

(₋1)k

2k_σ2k_k_!E[(xt1−xt2)

2k_]_. _(2.10)

Nesse caso, a correntropia contém informação de infinitos momentos estatísticos de ordem par da variável aleatória (xt1−xt2). Verifica-se que outra funções resultarão em expansões diferentes, entretanto todas as funçõeskernelmencionadas anteriormente são

não-lineares e, portanto, incluem informações estatísticas de ordem superior sobre o pro-cesso aleatório de entrada [Xu & Principe 2008].

Dessa forma, observa-se na Equação (2.10) que os momentos estatísticos de ordem elevada são controlados pelo tamanho do kernel (σ), que é um parâmetro livre e deve ser selecionado adequadamente para o dado de entrada. Na literatura há várias aborda-gens para determinar o tamanho adequado do kernel, tais como a regra de Silverman [Silverman 1986], validação cruzada baseada no erro médio quadrático [Bowman 1984] e método adaptativo utilizando Curtose [Zhao et al. 2012]. Entretanto, todos esses métodos são estimativas de valores sub-ótimos do tamanho do kernel.

Similar à função de densidade espectral de potência convencional para processos alea-tórios estacionário no sentido amplo, a transformada de Fourier da função de correntropia centralizada para processo estritamente estacionários é denominada de densidade espec-tral de correntropia (CSCD) e definida como

Pσ(ω) =

Z ∞

−∞U(τ)e

−jωτ_d_τ_, _(2.11)

em queω é a frequência em radianos por segundos. Do mesmo modo, a transformada

inversa de Fourier aplicada aPσ(ω)resulta a correntropia centralizadaU(τ).

2.2.1 Propriedades

(28)

estacioná-rio em tempo discreto [Principe 2010]:

1. Para qualquerkernelsimétrico,V(τ)é uma função simétrica:V(τ)=V(₋τ).

2. V(τ)assume o valor máximo na origem. Por exemplo:V(τ)_≤V(0)_∀τ. 3. Devido ao uso dokernelgaussiano,V(τ)_≥0 eV(0) =1/√2πσ.

4. DadoV(τ)paraτ=0, ...,P₋1, é possível definir uma matriz de dimensãoPxP:

V =            

V(0) . . . V(P₋1)

. . .

V(P₋1) . . . V(0)

            (2.12)

2.3 Influência do tamanho do kernel

A correntropia possui um parâmetro livre denominado de tamanho dokernel(σ) que

influencia diretamente no seu desempenho. A influência desse parâmetro sobre a corren-tropia será analisada a seguir por meio de experimentos computacionais. Todos os testes foram realizados com um sinal cosseno de frequência 10 Hz e frequência de amostragem de 500 Hz.

2.3.1 Domínio do tempo e da frequência

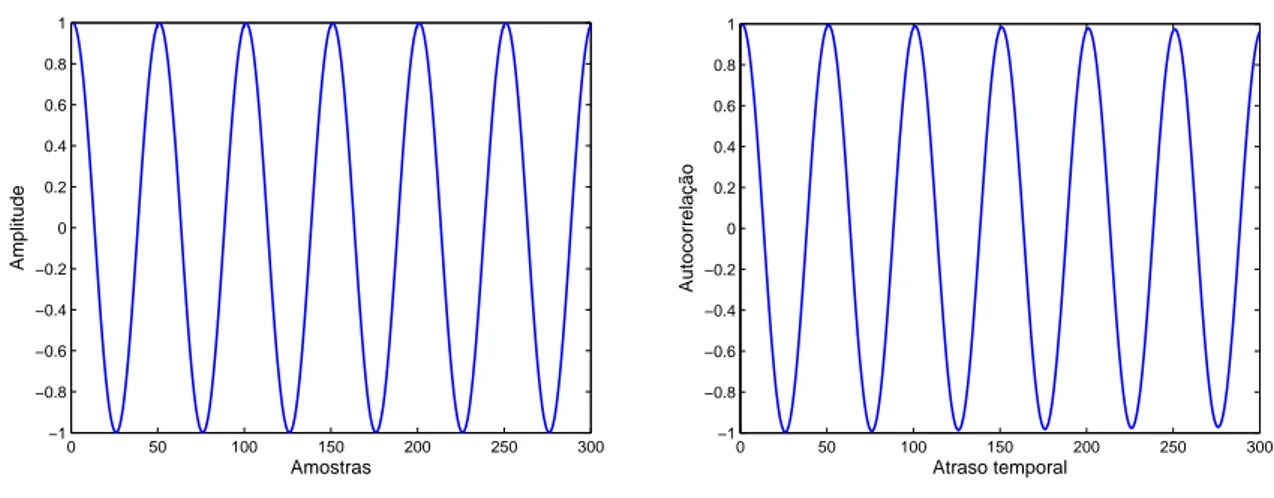
A função de autocorrentropia centralizada foi avaliada no domínio do tempo e da frequência com quatro diferentes tamanhos de kernel 0.04, 0.4, 1 e 10. Inicialmente, o sinal no domínio do tempo com sua função de autocorrelação foi ilustrado na Figura C.4. O valor da correntropia para diferentes tamanhos dekernelé ilustrado na Figura 2.3.

Observa-se que o aumento dokernelfaz com que a correntropia tenda à Correlação, ou

seja, para valores deσsuficientemente grande, os momentos de segunda ordem dominam

(29)

0 50 100 150 200 250 300 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Amplitude Amostras

(a) Forma de onda do cosseno com Frequência de 10Hz

0 50 100 150 200 250 300 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Autocorrelação Atraso temporal

(b) Autocorrelação do cosseno

Figura 2.2: Sinal cosseno e autocorrelação do cosseno.

correntropia tende a valores positivos e sua forma de onda se torna diferente da correlação. É importante ressaltar que independente do tamanho dokernela correntropia é periódica.

0 50 100 150 200 250 −1 −0.5 0 0.5 1 Correntropia Atraso temporal

(a)σ= 0.04

0 50 100 150 200 250 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Correntropia Atraso temporal

(b)σ= 0.4

(c)σ= 1

(d)σ= 10

(30)

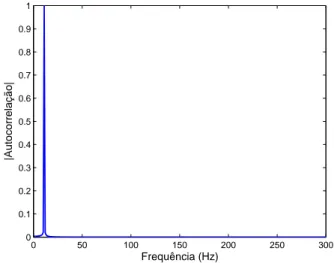
O segundo experimento realizou a mesma análise anterior no domínio da frequência. Inicialmente, foi computada a transformada de Fourier da autocorrelação, cujo resultado está ilustrado na Figura 2.4. Em seguida, a transformada de Fourier é aplicada na corren-tropia para diferentes tamanhos dekernele ilustrada na Figura 2.5.

0 50 100 150 200 250 300

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

|Autocorrelação|

Frequência (Hz)

Figura 2.4: Densidade espectral de potência de um cosseno com frequência de 10Hz.

Dessa forma, é possível concluir que tanto no domínio da frequência quanto no domí-nio do tempo a influência do tamanho dokernelobedece às mesmas propriedades. Além

disso, observa-se a partir da Figura 2.5 (d), comσ=10, que a densidade espectral de cor-rentropia possui as mesmas características da densidade espectral de potência ilustrada na Figura 2.4, ou seja o tamanho do kernel pondera os momentos estatísticos da correntropia. É importante ressaltar que, as frequências que surgem no cálculo da correntropia é devido a transformação não linear do kernel. No apêndice C é detalhado o cálculo da

(31)

0 20 40 60 80 100 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 |Autocorrentropia| Frequência (Hz)

(a)σ= 0,04

0 20 40 60 80 100

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 |Autocorrentropia| Frequência (Hz)

(b)σ= 0,4

0 20 40 60 80 100

(c)σ= 1

0 20 40 60 80 100

(d)σ= 10

(32)

2.3.2 Ruído impulsivo

O tamanho dokernelfunciona como umzoomque controla a janela de observação na

qual a similaridade é avaliada. A possibilidade de ajustar o tamanho do kernel fornece um mecanismo eficiente que permite eliminar os valores que são muito diferentes do conjunto de dados.

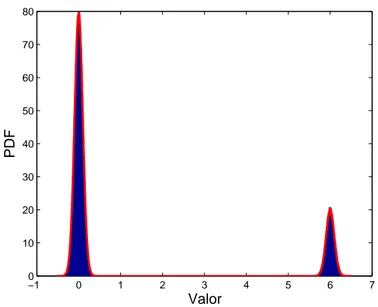
Com o objetivo de facilitar a compreensão desses conceitos, foi realizado um experi-mento computacional que compara o cálculo da correntropia e da correlação de um sinal em um ambiente com ruído impulsivo (outliers). Os outliers foram representados por um sinal não-gaussiano com distribuição de probabilidade bimodal ilustrada na Figura 2.6, cuja sua função de densidade de probabilidade é dada por:

P(i) =0.9N(0,0.01) +0.1N(4,0.01) (2.13)

−1 0 1 2 3 4 5 6 7 0

10 20 30 40 50 60 70 80

PDF

Valor

(a) Função de densidade de probabilidade do ruído da Equação (2.13)

0 50 100 150 200 250 300

−2 0 2 4 6 8

Tempo

Valor

(b) Cosseno com outliers

Figura 2.6: PDF do ruído impulsivo e o cosseno com outliers

Observa-se na Figura 2.7 que a autocorrelação é muito sensível ao ruído impulsivo, modificando completamente a forma de onda no tempo e o seu espectro de frequências.

(33)

o quanto a correlação é prejudicada com o ruído impulsivo.

Por outro lado, através do ajuste do tamanho dokernel, praticamente não houve

altera-ções na resposta da correntropia para o cosseno com ruído impulsivo. Quando realiza-se uma comparação entre as Figuras 2.5 (b) e 2.7 (d) para o mesmo tamanho de kernel,

observa-se que ooutliernão influência o cálculo da correntropia.

0 50 100 150 200 250 300 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Autocorrelação Atraso temporal

(a) Autocorrelação do cosseno com outlier

0 50 100 150 200 250 300 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 |Autocorrelação| Frequência (Hz)

(b) Densidade espectral de potência para o cosseno com outlier

0 50 100 150 200 250

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Correntropia Atraso temporal

(c) Autocorrentropia do cosseno com outlier eσ= 0,4

0 20 40 60 80 100

(d) Densidade espectral de correntropia para o cosseno com outlier eσ= 0,4

(34)

2.4 Síntese

Ao longo desse capítulo foi possível definir e demonstrar as propriedades da correntro-pia. Foi exemplificado, por simulação computacional, a importância do ajuste do tamanho

dokernelpara a correntropia. Além disso, ficou evidenciado que a correntropia consegue

extrair informações de infinitos momentos estatísticos de um processo aleatório.

O efeito do ruído impulsivo é amenizado pelo uso do kernel gaussiano no cálculo da correntropia. A diferença ao quadrado entre o sinal original e o outlier é realizado no

expoente de uma exponencial negativa, em que seu valor máximo é 1/√2πσ.

(35)

Processos Cicloestacionários

3.1 Introdução à Análise de Sinais Cicloestacionários

Por meio da análise de cicloestacionariedades procura-se identificar e caracterizar, nos sinais aleatórios, momentos estatísticos que variam periodicamente com o tempo. Neste sentido, um sinal com função de autocorrelação periódica apresentará comportamento pe-riódico de segunda ordem. Logo, pode-se extrair informações sobre esse comportamento analiando suas cicloestacionariedades.

As características cicloestacionárias podem ser encontradas em sinais reais ou ar-tificiais presentes em várias áreas, tais como telecomunicações [Jang 2014], sistemas biológicos [Newton 1982], meteorologia [Hasselmann & Barnett 1981], climatologia [Bloomfield et al. 1994], oceanografia [Dragan & Yavorskii 1982] e máquinas rotativas [Konig & Bohme 1994]. Em telecomunicações, especialmente no contexto de rádio cog-nitivo, a cicloestacionariedade é frequentemente aplicada em dois tipos de problemas: sensoriamento espectral e classificação de sinais modulados.

(36)

3.2 Função de Autocorrelação Cíclica (CAF)

Um processo aleatório, x(t), é denominado de cicloestacionário de segunda ordem

em sentido amplo se a sua média, E[x(t)], e sua função de autocorrelação, Rx(t,τ) =

E[x(t)x(t+τ)], forem periódicas com um certo períodoT0[Gardner et al. 2006]. Mesmo

se estas duas condições não forem verdadeiras para o sinal completo, pequenos segmentos do sinal podem ter a média e a correlação periódicos com o tempo [Gardner et al. 2006]. Matematicamente, a cicloestacionariedade de segunda ordem é descrita por

E[x(t+T0)] = E[x(t)] (3.1)

E[x(t+To)x(t+T0+τ)] = E[x(t)x(x+τ)],

em queE[.]é o operador valor esperado.

Uma vez que a função de autocorrelação de processos cicloestacionários de segunda ordem é periódica, ela pode ser descrita pela série de Fourier [Gardner et al. 2006] como

Rx(t,τ) =

∑

α

Rα_x(τ)ej2παt, (3.2)

em que α, chamado genericamente de frequência cíclica, denota todos os múltiplos da

frequência fundamental da autocorrelação, ou sejaα=n/T0, comn∈Z. Nessa série, os

coeficientesRα_X(τ)definem a Função de Autocorrelação Cíclica (CAF), expressa por:

Rα_x(τ) =

Z T0/2

−T0/2

Rx(t,τ)e−j2παtdt. (3.3)

(37)

[Gardner & Spooner 1992]:

Rα_x(τ) = lim

T→∞

1

T

Z T/2

−T/2x(t)x(t+τ)e

−j2παt_dt_. _(3.4)

Percebe-se através da Equação (3.3) que a CAF permite verificar se um processo apre-senta cicloestacionariedade, o que ocorre quando a funçãoRα_x(τ)é não-nula para algum valor de α ₆=0. Além disso, é importante destacar que para α =0 a CAF reduz-se à função de autocorrelação convencional do sinal.

3.3 Função Densidade Espectral Cíclica (SCD)

A transformada de Fourier da função de autocorrelação é denominada de densidade espectral de potência [Gubner 2006]. Essa relação, descrita no teorema de Wiener-Khinchin, também pode ser utilizada na CAF para obter a função densidade espectral cíclica (SCD),Sα_x(f), definida pela seguinte equação

Sα_x(f) =

Z ∞

−∞R α

x(τ)e−j2πfτdτ. (3.5)

Percebe-se que a função SCD representada pela Equação (3.5) possui as propriedades de simetria e é conhecida por espectro cíclico [Gubner 2006].

S−_xα(f) =Sα_x(f) (3.6)

Sα_x(₋f) =Sα_x(f)

(38)

S_x0(f) =

Z ∞

−∞R

0

x(τ)e−j2πfτdτ. (3.7)

A SCD para um sinal de frequência f0 e frequência cíclica α é apenas a correlação

dos dois valores do sinal no domínio da frequência separadas em frequência por α e centralizada na frequência f0.

Para ilustrar algumas propriedades da cicloestacionariedade de segunda ordem, a SCD foi computada para modulação AM com uma frequência fc=1024 Hz e ilustrada na

Fi-gura 3.1. Paraα=0 a SCD apresenta a densidade espectral de potência da onda senoidal, com dois impulsos em_±fc. Os outros dois picos correspondem à correlação do sinal após

o deslocamento em frequência de 2fc.

(39)

3.3.1 Perfil Alfa

A função SCD pode ser de difícil análise computacional, sendo interessante em algu-mas aplicações a redução de sua dimensionalidade [Fehske et al. 2005]. Neste trabalho, foi utilizado o método da projeção dos valores máximos da SCD sobre um plano ortogonal a f, para valores deα>0, matematicamente representado por

I(α) =max

f |S α

x(f)|. (3.8)

em que o símbolo_|._|é o valor absoluto do sinal. Ao longo do texto,I(α)será denominado

perfil alfado sinal aleatório.

Por meio da Equação (3.8) é possível reduzir a complexidade da representação da SCD, preservando os impulsos característicos. A Figura 3.2 ilustra o perfil alfa da SCD de um sinal com modulação AM.

1000 2000 3000 4000 5000 6000

0 0.2 0.4 0.6 0.8 1

Frequência cíclica

Perfil alpha

Figura 3.2: Perfil alfa para modulação AM

(40)

3.4 Cicloestacionariedade de Ordem Superior (HOCS)

A cicloestacionariedade de ordem superior utiliza momentos estatísticos de alta ordem para extrair informações do sinal analisado. Devido a essa característica, a HOCS é uma generalização da cicloestacionariedade de segunda ordem. Uma generalização natural e intuitiva é chamado delag product e pode ser expressa como:

L(t,τ)n=

n

∏

i=1

x(t+τi), (3.9)

em que o vetorτé composto de atrasos individuaisτj (j=1, ...,n).

A extração da HOCS de um sinalx(t)pode ser obtida a partir da análise da periodici-dade dolag productdefinida na Equação (3.9), denominada deCyclic Temporal Moment

Function(CTMF) e definida por meio da expressão [Renard et al. 2010]:

Rα_x(τ)n=

Lx(t,τ)ne−j2παt

, (3.10)

em que_h._i=limT→∞₂1_T R₋TT(.)dt. CasoLx(t,τ)nnão seja identicamente nula para algum

valor de α₆=0, assume-se que as N séries temporais apresentam cicloestacionariedade conjunta de N-ésima ordem. Além disso, pode-se definir a funçãocyclic spectral cross

-moment (CSCMF) de ordemncomo sendo a transformada de Fourier n-dimensional da

função CTMF de ordem N, sendo definida como:

Sα_x(f)n=

Z

RNR α

x(τ)ne−j2πfτdτ, (3.11)

em que f = [f1, ...,fn]T.

Em particular, o trabalho de [Gubner 2006] demonstra que a CTMF de um sinal pode ser visualizada como cumulantes de ordem ndo sinal. Dessa forma, utilizando as

(41)

temporal de cumulantes (TCF) é definido como:

Kx(t,τ)n=

∑

{P}

(₋1)p−1₍_p₋_1)!_∏p

j=1Rx(t,τj)nj

, (3.12)

em que_{P_}é o conjunto de índices(1,2, ...,n)eRx(t,τj)njé a CTMF. A função temporal

de cumulantes cíclicos CTCF são os coeficientes da série de Fourier da TCF e pode ser expressa como:

K_xα(τ)n=

∑

{P_}

(₋1)p−1₍_p₋_1)!_∑β_∏βj j=1R

βj x (τj)nj

, (3.13)

em que _{β_} é o vetor de frequência cíclicas definido pelo somatório deα (∑p_j₌₁=α) e

Rβxj(τj)nj é a CTMF do j-ésimo elemento de ordemnjda partição P na frequência cíclica βj.

(42)

3.5 Síntese

Foram apresentadas funções para a análise das características periódicas de um deter-minado processo aleatório. Observa-se que, em alguns processos aleatórios, a cicloesta-cionariedade de segunda ordem não consegue extrair informações relevantes, principal-mente quando o ruído é não gaussiano. Dessa forma, uma solução para esse problema é a análise de cicloestacionariedade de ordem superior.

(43)

Correntropia Cíclica

4.1 Introdução

A análise cicloestacionária de segunda ordem [Gardner & Spooner 1992] apresenta limitações quando aplicada à caracterização de sinais contaminados com ruído impulsivo ou de natureza não-gaussiana. Além disso, descritores obtidos a partir de cicloestaci-onariedades de segunda ordem são ineficazes na caracterização de alguns sinais, como modulações digitais de ordem elevada, sinais biológicos e sinais originados por vibrações mecânicas [Gardner & Spooner 1992]. Neste caso, a análise de cicloestacionariedades de ordem superior tende a melhorar o desempenho dos métodos de classificação empregados. A correntropia é capaz de extrair infinitos momentos estatísticos, sendo ainda robusta a ruídos não-gaussianos. Dessa forma, neste capítulo, a teoria de processos cicloestaci-onários é revisitada sob um enfoque de teoria da informação. O objetivo é investigar os benefícios que podem ser conseguidos com a substituição da medida de correlação, utili-zada nas funções clássicas de análise de cicloestacionariedades, pela correntropia. Espe-cificamente, duas novas funções são definidas, a função de correntropia cíclica (CCF) e a densidade espectral de correntropia cíclica (CCSD).

(44)

4.2 Função de Correntropia Cíclica (CCF)

Conforme visto no Capítulo 3, os processos são definidos como cicloestacionários de segunda ordem se estes possuem média e autocorrelação periódicas no tempo. Sabendo que a função de autocorrentropia de um processo pode possuir infinitos momentos es-tatísticos (ver o Capítulo 2), é possível concluir que um processo com pelo menos um momento estatístico de ordem par periódico possui a função de correntropia periódica.

Considera-se neste trabalho que os processos que têm função de correntropia periódica são cicloestacionários de segunda ordem ou de ordem superior.

Supondo que a função de correntropiaVx(t,τ)de um processox(t)é periódica,

pode-se reprepode-sentarVx(t,τ)(Equação 2.8) por uma série de Fourier, tal que

Vx(t,τ) =

∑

α

V_xα(τ)ej2παt, (4.1)

com os coeficientes de Fourier,

V_xα(τ) = 1

T0

Z T0/2

−T₀/2Vx(t,τ)e

−j2παt_dt_, _(4.2)

definindo a função de correntropia cíclica (CCF), em que α=n/T0 abrange todos os

múltiplos da frequência fundamental 1/T0.

Assumindo queV_xα(τ) é policicloergódico na correntropia [Gardner 1986], ou seja, apresenta mais do que uma frequência cíclica fundamental, é possível reescrever a Equa-ção (4.2) como segue

V_xα(τ) =

(Gσ(x(t),x(t+τ))e−j2παt, (4.3)

em queGσ(x(t),x(t+τ))é um kernel Gaussiano expresso pela Equação (2.2), e o símbolo

(45)

h._i= lim

T_→∞

1 2T

Z T

−T

(.)dt. (4.4)

A CCF permite identificar a presença de características cicloestacionárias da corren-tropia nos processos, o que ocorre quando a funçãoV_xα(τ)é não-nula para qualquer valor de α₆=0. Em particular, quando α=0, a CCF é equivalente à função de correntropia convencional.

Pode-se observar algumas propriedades interessantes ao se aplicar uma expansão em série de Taylor à funçãoV_xα(τ)da Equação (4.2). O resultado dessa expansão encontra-se a seguir e a dedução matemática detalhada está no Apêndice B.

V_xα(τ) = 1

T0

Z T0/2

−T0/2 1

√

2πσ ∞

∑

n=0

(₋1)n

2n_n_!_σ2nE

(x(t)₋x(t+τ))2+2σ2₋2jσ22παt) n

dt.

(4.5) Esta é uma expressão interessante porque fornece muitas informações sobre a CCF. Observa-se que para umkernelgaussiano, a soma de todos os momentos estatísticos

apa-recem na CCF, mantendo as informações estatísticas de segunda ordem fornecida pela CAF e os momentos estatísticos de ordem superior da variável aleatória, os quais são ponderados por 1/σ2n_{. Em muitas aplicações, os momentos estatísticos de ordem}

su-perior podem facilitar a extração de características do sinal analisado. A Equação 4.5 é meramente interpretativa, não sendo recomendado a computação da CCF através dela.

Assumindo a propriedade supracidade em queV_xα(τ) é policicloergódico na corren-tropia [Gardner 1986], a Equação 4.5 pode ser simplificada para

V_xα(τ) = √1

2πσ

* _∞

∑

n=0

(₋1)n

2n_n_!_σ2n

(x(t)₋x(t+τ))2+2σ2₋2jσ22παt) n+

. (4.6)

(46)

V_xα(τ) =_√1 2πσ

*

−βt,α+

β2_t_,_α

2 −

β_t3_,_α

6 +

−β2₄xσ2(2t))−

β2t,αx2(t+τ)

4σ2 +

β2t,αx(t)x(t+τ)

2σ2 +

x(t)x(t+τ)

σ2 +

−βt,αx(t_σ)x₂(t+τ)+βt,αx

2₍_t₊_τ₎

2σ2 −

x2(t) 2σ2 −

x2(t+τ)

2σ2 +

βt,αx2(t)

2σ2 +

+βt,αx3(t)x(t+τ))

2σ4 +

βt,αx(t)x3(t+τ)

2σ4 −

3βt,αx2(t)x2(t+τ)

4σ4 −

βt,αx4(t+τ)

8σ4 −

+βt,αx4(t)

8σ4 +

3x2(t)x(t+τ)2

4σ4 −

x3(t)x(t+τ)

2σ4 −

x(t)x3(t+τ)

2σ4 + x4(t)

8σ4 + x4(t+τ)

8σ4 +

−5x4(t₁₆)x_σ2(6t+τ)+

5x3(t)x3(t+τ)

12σ6 −

5x2(t)x4(t+τ)

16σ6 +

x5(t)x(t+τ)

8σ6 +

−₄₈x6(σt)6−

x6(t+τ)

48σ6 +

x(t)x5(t+τ)

8σ6 +...

+

em queβt,α =−j2παt.

Agrupando os termos que possuemσ2no denominador e nomeando os termos comσ

com potência maior do que 2 no denominador deξα_σ(t,τ), obtêm-se a seguinte Equação

V_xα(τ) =√1

2πσ

* _∞

∑

n=0

(₋1)nβnt,α n! +

nβn−1

t,α

2σ2n!(x(t)−x(t+τ))

2

+ξα_σ(t,τ) +

, (4.7)

em que

_∑

∞

n=0

nβnt,−α1

2σ2n!(x(t)−x(t+τ))

2_{representa os termos ponderados por 1}_/_σ2_.

Dado que

∞

∑

n=0

(₋1)nβ n t,α

n! é a expansão de Taylor para função exponencial com

coefici-ente negativo, a Equação (4.7) pode ser reescrita como

V_xα(τ) =

D

eβt,α

E

√

2πσ +

1 2√2πσ3

D

(x(t)₋x(t+τ))2eβt,αE₊_√1

2πσhξ α

σ(t,τ)i. (4.8)

(47)

V_xα(τ) = D

eβt,αE √

2πσ +

1 2√2πσ3

D

x2(t)eβt,α₊_x2₍_t₊_τ₎_eβt,α₋2_x₍_t₎_x₍_t₊_τ₎_eβt,αE₊_√1

2πσhξ α σ(t,τ)i,

(4.9) em queDx(t)x(t+τ)eβt,αEé a Função de Autocorrelação Cíclica (CAF) de um processo

policicloergódicox(t), denotada porRα_x(τ)[Gardner et al. 1994]. Substituindo o valor de

βt,α, reagrupando os termos e assumindo que no infinitox(t+τ) =x(t), obtêm-se:

V_xα(τ) = √1

2πσ

e−j2παt₋R

α x(τ) σ2 +

x2(t)e−j2παt

σ2 +hξ

α σ(t,τ)i

!

. (4.10)

A Equação (4.10) demonstra que independente do processo estocástico utilizado sem-pre haverá uma senoide deslocando a resposta, essa propriedade é devido ao termo

e−j2παt

e, o termoRα_x(τ)evidencia a presença dos momentos estatísticos de segunda ordem. Além disso, todos os termos são ponderados pelo tamanho dokernel, assumindo um papel muito

importante para ponderar os efeitos dos momentos estatísticos de segunda e alta ordem. De fato, para um tamanho de kernel suficientemente grande, a tradicional estatística de segunda ordem é preservado e o termo_hξα_σ(t,τ)_itende a zero. No Apêndice A encontra-se de forma detalhada a dedução da CCF demonstrando a influência do tamanho dokernel.

Dessa forma, a funçãoV_xα(τ)contempla as informações cicloestacionárias obtidas por meio da CAF, podendo ser considerada neste sentido, uma generalização da mesma. Ao contrário de Rα_x(τ), que evidencia apenas as cicloestacionariedades de segunda ordem

(48)

4.3 Função Densidade Espectral de correntropia Cíclica

(CCSD)

A transformada de Fourier da autocorrentropia é denominada Densidade Espectral de correntropia [Xu & Principe 2008]. Essa relação pode ser utilizada na CCAF para obter a Função de Densidade Espectral de correntropia Cíclica (CCSD),C_xα(f), definida pela

Equação

C_xα(f) =

Z ∞

−∞V α

x (τ)e−j2πfτdτ (4.11)

Análogo à SCD, a CCSD também possui as seguintes propriedades de simetria:

C_x−α(f) =C_xα(f) (4.12)

Cα_x(₋f) =C_xα(f)

Além disso, quandoα=0 a CCSD representa a densidade espectral de correntropia. A CCSD permite extrair características cicloestacionárias de segunda ordem ou de or-dem superior de processos aleatórios, generalizando a função SCD calculada a partir da autocorrelação. O uso dessa função pode ser interessante em aplicações de rádio cogni-tivo, tanto em problemas de sensoriamento espectral quanto na classificação automática de sinais modulados quando utiliza-se modulações de alta ordem, ou em outras aplicações que envolvem sinais com cicloestacionariedades de ordem superior.

(49)

computacio-nais com um sinal cosseno ilustrado na Figura 4.1.

Observa-se na Figura 4.1 resultados distintos para os dois diferentes tamanhos de

Kernel. Quando okernelé grande, os momentos estatísticos de alta ordem são ponderados

e a CCSD tende a clássica SCD de segunda ordem com o pico principal na posição duas vezes a frequência da senoide. Por outro lado, quando o tamanho dokerneldiminui os

(50)

0 0.002 0.004 0.006 0.008 0.01 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Tempo (s)

(a) Cosseno com frequência 1024 Hz e taxa de amostra-gem de 16.384 Hz

(b) |CCSD| com tamanho do kernel igual a 10.

1000 2000 3000 4000 5000 6000 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Frequência cíclica Perfil alpha

(c) Perfil alfa da CCSD com tamanho do ker-nel igual a 10.

(d) |CCSD| com tamanho do kernel igual a 0.1.

1000 2000 3000 4000 5000 6000 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Frequência cíclica Perfil alpha

(e) Perfil alfa da CCSD com tamanho do kernel igual a 0.1.

(51)

4.4 Síntese

Métodos tradicionais de análise de cicloestacionariedade de ordem superior são ge-ralmente complexos e inviáveis para a maioria das aplicações de tempo real. Como al-ternativa aos métodos clássicos de análise de cicloestacionariedades de ordem superior, o presente capítulo define uma nova ferramenta matemática para a análise de cicloestaciona-riedade de ordem superior baseada na função de correntropia, denominada de Função de correntropia Cíclica. Foi demonstrado matematicamente que a CCF contém informações de infinitos momentos estatísticos, sendo uma generalização da Função de Autocorrela-ção Cíclica. Além disso, foi demonstrado que o parâmetro livre σtem um papel muito

(52)

CCSD Aplicada a Análise de Sinais

Cicloestacionários

Neste capítulo serão apresentadas as assinaturas cicloestacionárias das modulações AM, BFSK, MSK, BPSK, QPSK e 16-QAM, utilizando-se os métodos SCD e CCSD. O objetivo é analisar a função densidade espectral de correntropia cíclica, relacionando-a ao desempenho da clássica função de densidade espectral cíclica na obtenção de des-critores de sinais cicloestacionários. Serão apresentadas as etapas do algoritmoCyclic

Periodogram Detectionresponsável pela implementação dos métodos SCD e CCSD

re-alizados neste trabalho. Além disso, serão analisados os detalhes da versão paralelizada da CCSD desenvolvida no contexto desta Tese. Resumidamente serão quatro experimen-tos, divididos da seguinte forma: sensoriamento espectral com ruído impulsivo, extração de característica com ruído gaussiano e não-gaussiano, assinaturas cicloestacionárias de sinais modulados e análise da escalabilidade paralela da CCSD.

Os sinais utilizados na análise de desempenho da CCSD foram criados com os parâ-metros de simulação apresentados na Tabela 5.1 com filtro de formatação de pulso do tipo raiz quadrada do cosseno elevado, com fator de rolamento (roll₋o f f)r=0.5. Todos os

(53)

distri-buição de probabilidade bimodal para representar um ruído impulsivo caracterizado pela Equação 5.1 e PDF ilustrada na Figura 5.1.

P(i) =0.8N(0,0.01) +0.2N(6,0.01) (5.1)

−1 0 1 2 3 4 5 6 7

0 10 20 30 40 50 60 70 80

PDF

Valor

Figura 5.1: Função densidade de probabilidade do ruído da impulsivo

Parâmetros Valores

Frequência de amostragem 16384 Hz Frequência Intermediária 1024 Hz

Taxa de símbolo 1024 Baud

Tabela 5.1: Parâmetros de simulação computacional dos sinais analisados

5.1 Algoritmo Cyclic Periodogram Detection (CPD)

(54)

cicloestacionárias dos experimentos realizados pode ser descrito por meio dos seguintes passos:

Passo 1. O sinal de entrada,x[n], é segmentado emLblocos de N amostras, como

ilus-trado na Figura 5.2.

Passo 2. Calcula-se a média da correntropia para cada bloco,l=0,1,2, ...,L₋1.

Ml=

N−1

∑

τn=0

N−1

∑

n=0

G(xl[n],xl[n+τn]) (5.2)

Passo 3. Calcula-se a correntropia centralizada para cada bloco de tamanhoNcomα[n] =

n

N,n=0,1,2, ...,N−1,l=0,1,2, ...,L−1.

Vαn

l [τn] = N−1

∑

n=0

[G(xl[n],xl[n+τn])−Ml]e−j2παnn (5.3)

Passo 4. Calcula-se o valor médio deCαn

l [τ]sobre osLblocos:

Vαn_[_τ

n] =

1

L

L−1

∑

l=0

Vαn

l [τn] (5.4)

Passo 5. Calcula-se o módulo da transformada discreta de Fourier sobreτn.

|Cαn_[_k_]_|₌_|1

N

N−1

∑

τn=0

Vαn_[_τ

n]e−j

2π

Nkτn_| (5.5)

(55)

O cálculo da SCD também foi baseada no algoritmo CPD por meio dos seguintes passos:

Passo 1. Dado o sinalxl[n], ondel=0,1, . . . ,L−1 identifica os blocos en=0,1, . . . ,N−

1 identifica as amostras nos blocos, calcula-se o a transformada discreta de Fourier de cada um dosLblocos, ou seja,

Xl[k] =

N−1

∑

n=0

xl[n]e−j

2π

Nkn,_k=0,1, . . . ,_N−1; (5.6)

Passo 2. Calcula-se a seguinte expressão parak=0,1, . . . ,N₋1 el=0,1, . . . ,L₋1:

T_lα[k] = 1

NXl

h

k+α

2 i

X_l∗

h

k₋α

2 i

; (5.7)

Passo 3. Calcula-se o valor médio deT_lα[k]sobre todos osLblocos:

Sαn_[_k_{] =} 1

L

L−1

∑

l=0

T_lα[k],k=0,1, . . . ,N₋1; (5.8)

5.2 Sensoriamento Espectral

Em geral os sinais de sistemas de comunicação exibem alguma periodicidade em seus parâmetros estatísticos, decorrentes, dentre outras ações, da presença de sinais que pos-suem periodicidade, tais como aqueles encontrados em processos de modulação, amos-tragem ou codificação por sequência de espalhamento espectral. Visando realizar uma comparação entre os métodos SCD e CCSD no sensoriamento espectral, foram criados duas hipótesesH0eH1expressas como

H0 : y[n] =s[n] +η[n] (5.9)

(56)

em quey(n)indica o sinal sensoriado,η(n)representa um ruído impulsivo caracterizado pela Equação (5.1) es(n)é o sinal transmitido pelo usuário utilizando uma das seguintes modulações: AM, MSK, BPSK, BFSK, QPSK e 16-QAM.

Os métodos SCD e CCSD são aplicados aos sinais, e o resultado classificado como

H0 ouH1. O objetivo é identificar periodicidade no sinaly[n], demonstrando a presença

de usuário primário. Inicialmente, o método SCD é avaliado para as modulações AM, MSK e BPSK e os resultados estão ilustrados na Figura 5.3. Através do perfil alfa de cada modulação é possível concluir que o método SCD não conseguiu identificar nenhuma característica que demonstrasse a presença de um sinal modulado no canal, evidenciando a ineficácia do método baseado na SCD para este cenário de sensoriamento, uma vez que a hipóteseH0contém um sinal transmitido por um usuário.

A Figura 5.4 ilustra o método SCD para as modulações BFSK, QPSK e 16QAM com relação sinal/ruído (SNR) fixa em 0,18 dB. Da mesma forma das modulações anteriores, o método SCD falhou na identificação do usuário primário no canal, exceto para a modu-lação BFSK, em que a SCD conseguiu extrair um pico na frequência 2000 Hz detectando a presença de um usuário primário durante o sensoriamento do canal.

Portanto, o método de sensoriamento baseado na função SCD foi ineficiente neste ce-nário de comunicação, caracterizado pelo ruído não-gaussiano, falhando em quase todos os testes de sensoriamento sob a hipótese H0, com exceção do sensoriamento do sinal

com modulação BFSK.

(57)

(a) |SCD| da modulação AM

1000 2000 3000 4000 5000 6000 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Frequência cíclica Perfil α

(b) Perfil alfa da modulação AM

(c) |SCD| da modulação MSK

(d) Perfil alfa da modulação MSK

(e) |SCD| da modulação BPSK

(f) Perfil alfa da modulação BPSK

(58)

(a) |SCD| da modulação BFSK

(b) Perfil alfa da modulação BFSK

(c) |SCD| da modulação QPSK

(d) Perfil alfa da modulação QPSK

(e) |SCD| da modulação 16QAM

(f) Perfil alfa da modulação 16QAM

(59)

(a) |CCSD| da modulação AM

(b) Perfil alfa da modulação AM

(c) |CCSD| da modulação MSK

(d) Perfil alfa da modulação MSK

(e) |CCSD| da modulação BPSK

(f) Perfil alfa da modulação BPSK

(60)

(a) |CCSD| da modulação BFSK

(b) Perfil alfa da modulação BFSK

(c) |CCSD| da modulação QPSK

(d) Perfil alfa da modulação QPSK

(e) |CCSD| da modulação 16QAM

(f) Perfil alfa da modulação 16QAM

(61)

A hipóteseH1 representa a presença de somente ruído no canal sensoriado e,

conse-quentemente, ocorre quando o canal encontra-se desocupado. Sendo assim, o falso alarme acontece quando um canal está desocupado, mas é detectado alguma característica na as-sinatura cicloestacionária, como o pico do sinal por exemplo. Dessa forma, os métodos SCD e CCSD foram analisados para hipóteseH1 e ilustrados na Figura 5.7. Observa-se

que ambos os métodos conseguiram um bom resultado ao não registrar um falso alarme.

(a) |SCD| para um canal com apenas ruído impulsivo

1000 2000 3000 4000 5000 6000 0

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Perfil

α

(b) Perfil alfa da |SCD| para um canal com apenas ruído impulsivo

(c) |CCSD| para um canal com apenas ruído impulsivo

1000 2000 3000 4000 5000 6000 0

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Perfil

α

(d) Perfil alfa da |CCSD| para um canal com apenas ruído impulsivo

(62)

5.3 Assinaturas Cicloestacionárias para Modulações

Di-gitais

Os modernos sistemas de comunicação sem fio empregam, frequentemente, técni-cas adaptativas de modulação para proporcionar uma alta taxa de transmissão enquanto asseguram Qualidade de Serviço (QoS). Para que as técnicas de modulação adaptativas funcionem no cenário de rádio cognitivo é necessário que o receptor identifique o tipo de modulação empregada pelo transmissor, procedimento denominado classificação automá-tica de modulação (AMC).

As arquiteturas de AMC são divididas em duas etapas: pré-processamento e clas-sificação. A primeira etapa consiste na extração de características do sinal analisado. Nos últimos anos, a extração de características cicloestacionárias para realizar o AMC tem sido proposta em vários trabalhos [Satija et al. 2014b, Ramkumar 2009, Zhou &

Man 2013, Phukan & Kumar Bora 2014]. O objetivo dessa seção é disponibilizar e analisar as assinaturas cicloestacionárias das modulações 16-QAM, QPSK, ASK, BPSK, BFSK, MSK e AM a partir do cálculo da função CCSD.

(63)

5.3.1 Modulações 16-QAM, QPSK, ASK e BPSK

É conhecido que alguns tipos de modulações digitais apresentam as mesmas caracte-rísticas cicloestacionárias de segunda ordem. A fim de solucionar esse problema, a fun-ção CCSD foi avaliada sobre essas modulações com três diferentes tamanhos dekernel.

Observa-se nas Figuras 5.8, 5.9, 5.10 e 5.11 que a CCSD para os tamanhos dekernel0,1

e 0,01 possuem assinaturas cicloestacionárias diferentes. Essa característica é devido aos infinitos momentos estatísticos que a CCSD consegue extrair do sinal analisado, fazendo com que o momento de segunda ordem seja complementada pelas informações contidas nos momentos de alta ordem.

Por outro lado, para um tamanho de kernel a partir de 1, as assinaturas

cicloesta-cionárias começam a ficar idênticas, não sendo possível diferenciá-las por uma simples inspeção. Isso acontece devido ao tamanho do kernel, que tem um papel importante na

ponderação dos efeitos dos momentos estatísticos. Para um tamanho dekernela partir de

(64)

(a) |CCSD| da modulação 16-QAM comσ=1

(b) Perfil alfa da modulação 16-QAM comσ=1

(c) |CCSD| da modulação 16-QAM comσ=0,1

(d) Perfil alfa da modulação 16-QAM comσ=0,1

(e) |CCSD| da modulação 16-QAM comσ=0,01

(f) Perfil alfa da modulação 16-QAM comσ=0,01

(65)

(a) |CCSD| da modulação QPSK comσ=1

(b) Perfil alfa da modulação QPSK comσ=1

(c) |CCSD| da modulação QPSK comσ=0,1

(d) Perfil alfa da modulação QPSK comσ=0,1

(e) |CCSD| da modulação QPSK comσ=0,01

(f) Perfil alfa da modulação QPSK comσ=0,01

(66)

(a) |CCSD| da modulação ASK comσ=1

(b) Perfil alfa da modulação ASK comσ=1

(c) |CCSD| da modulação ASK comσ=0,1

(d) Perfil alfa da modulação ASK comσ=0,1

(e) |CCSD| da modulação ASK comσ=0,01

(f) Perfil alfa da modulação ASK comσ=0,01

(67)

(a) |CCSD| da modulação BPSK comσ=1

(b) Perfil alfa da modulação BPSK comσ=1

(c) |CCSD| da modulação BPSK comσ=0,1

(d) Perfil alfa da modulação BPSK comσ=0,1

(e) |CCSD| da modulação BPSK comσ=0,01

(f) Perfil alfa da modulação BPSK comσ=0,01

(68)

5.3.2 Modulações BFSK, MSK e AM

Com o objetivo de aprofundar o estudo da CCSD na extração de características de modulações digitais, as modulações BSPK, MSK e AM também foram analisadas. Espe-cificamente, foram obtidas por meio da função CCSD, assinaturas cicloestacionárias para essas modulações, considerando diferentes tamanhos dekernel.

Nas Figuras 5.12 e 5.13 é possível observar que, independentemente do tamanho do

kernel, todas as assinaturas cicloestacionárias são diferentes entre se. Ou seja, mesmo

(69)

(a) |CCSD| da modulação BFSK comσ=1

(b) Perfil alfa da modulação BFSK comσ=1

(c) |CCSD| da modulação BFSK comσ=0,1

(d) Perfil alfa da modulação BFSK comσ=0,1

(e) |CCSD| da modulação BFSK comσ=0,01

(f) Perfil alfa da modulação BFSK comσ=0,01