UNIVERSIDADE FEDERAL DO TOCANTINS
CÂMPUS UNIVERSITÁRIO DE PALMAS
PROGRAMA DE MESTRADO PROFISSIONAL EM MATEMÁTICA
EM REDE NACIONAL Ű PROFMAT
JOSÉ GOMES TAVEIRA NETO
A IMPORTÂNCIA DO ESTUDO DO CÁLCULO
DIFERENCIAL NA EDUCAÇÃO BÁSICA
JOSÉ GOMES TAVEIRA NETO
A IMPORTÂNCIA DO ESTUDO DO CÁLCULO
DIFERENCIAL NA EDUCAÇÃO BÁSICA
Dissertação apresentado ao programa de Mestrado ProĄssional em Matemática em Rede Nacional - PROFMAT da Universidade Federal do Tocantins como requisito parcial para a obtenção do título de Mestre - Área de Concentração: Matemática.
Orientadora: Profa. Dra.HELLENA CHRIS-TINA FERNANDES APOLINÁRIO.
Dados Inoernacionais de Caoalogação na Publicação (CIP) Sisoema de Bibliooecas da Universidade Federal do Tocanoins
N469i Neto, José Gomes Taveira.
A IJPORTÃNCIA DO ESTUDO DO CÁLCULO DIFERENCIAl NA EDUCAÇÃO BÁSICA. / José Gomes Taveira Neto. – Palmas, TO, 2016.
48 f.
Dissertação (Jestrado Profissional) - Universidade Federal do Tocantins – Câmpus Universitário de Palmas - Curso de Pós-Graduação (Jestrado) Profissional em Jatemática, 2016.
Orientadora : Hellena Christina Fernandes Apolinário
1. Cálculo Diferencial. 2. Límite. 3. Derivada. 4. Educação Básica. I. Título CDD 510
TODOS OS DIREITOS RESERVADOS – A reprodução total ou parcial, de qualquer forma ou por qualquer meio deste documento é autorizado desde que citada a fonte. A violação dos direitos do autor (Lei nº 9.610/98) é crime estabelecido pelo artigo 184 do Código Penal.
AGRADECIMENTOS
A Deus, a quem credito tudo que sou e que faço a ele toda honra e toda glória. A minha mãe, que me deu além da vida, o entendimento que a educação muda e pode mudar não só a nossa realidade mas o nosso caráter e nossa forma de encarar a vida. A minha esposa, que Ąelmente me incentivou e me auxiliou em todos os momentos dessa árdua caminhada e sempre acreditou em mim, mesmo nos momentos que até eu mesmo não mais acreditava.
A igreja Metodista de Palmas pelas orações, em especial ao meu guia espiritual Pastor Everson Medeiros Dias.
A minha orientadora Dra.Hellena Christina Fernandes Apolinário, que tornou pos-sível a execução desse trabalho através da sua rica contribuição tanto acadêmica como humana sempre me incentivando e Ćexibilizando seus horários.
RESUMO
Este trabalho tem como objetivo expor a importância da introdução ao estudo do cálculo diferencial, através de situações problemas vivenciadas na prática docente, desde o ensino fundamental até o ensino médio. Inicialmente expomos como surgiu historicamente o cálculo diferencial, logo em seguida apresentamos noções básicas de cálculo direcionadas para estudantes do ensino médio, abordando tanto o aspecto geométrico como o algébrico. Algumas atividades foram trabalhadas em sala de aula por alunos tanto de ensino médio quanto de ensino fundamental em que a noção tanto de limite como de derivada já se faz presente em conteúdos abordados nesses ciclos ressaltando a importância desse estudo na educação básica. Por Ąm, é ressaltada aplicações de cálculo diferencial,por meio de exercícios propostos, em algumas disciplinas do ensino básico, entre elas a química,física e biologia e até mesmo no exame nacional do ensino médio ENEM.
ABSTRACT
This work aims to expose the importance of the introduction to the study of differential calculus through problem situations experienced in teaching practice, from elementary school through high school . Initially we set out as historically appeared differential cal-culus, then immediately present basics of calculation directed to high school students, addressing both the geometric aspect as the algebraic. Some activities were worked in the classroom for students in high school and elementary school in the sense both limit as derived already present on content covered in these cycles emphasizing the importance of this study in basic education. Finally, it is emphasized differential calculus applications through the exercises, in some disciplines of basic education, including chemistry, physics and biology and even in the national high school exam ENEM.
LISTA DE ILUSTRAÇÕES
Figura 1 Ű Quadrado Inscrito . . . 16
Figura 2 Ű Octógono Inscrito . . . 16
Figura 3 Ű Hexadecágono Inscrito . . . 16
Figura 4 Ű Paradóxo de Zenão . . . 17
Figura 5 Ű Área abaixo de uma curva I . . . 18
Figura 6 Ű Área abaixo de uma curva II . . . 18
Figura 7 Ű Método da tangente de Newton . . . 19
Figura 8 Ű Limite de uma função . . . 20
Figura 9 Ű Limite Lateral . . . 22
Figura 10 Ű Limite Inexistente I . . . 22
Figura 11 Ű Limite Inexistente II . . . 23
Figura 12 Ű Derivada de uma função . . . 23
Figura 13 Ű Atividade em sala de aula 1 . . . 28
Figura 14 Ű Atividade em sala de aula 2 . . . 29
Figura 15 Ű Atividade em sala de aula 3 . . . 30
Figura 16 Ű GráĄco item b . . . 32
Figura 17 Ű GráĄco item c . . . 33
Figura 18 Ű GráĄco atividade 2 . . . 34
Figura 19 Ű Taça gerada pela rotação de uma parábola . . . 35
Figura 20 Ű Tabela ENEM . . . 36
LISTA DE TABELAS
LISTA DE ABREVIATURAS E SIGLAS
SBM Sociedade Brasileira de Matemática UFT Universidade Federal do Tocantins ENEM Exame Nacional do Ensino Médio
PCNEM Parâmetros Curriculares Nacional do Ensino Médio U.A Unidade de Área
LISTA DE SÍMBOLOS
R Conjunto dos números reais
√︁ Somatório
fŠ(x) Derivada da função de uma variável 𝑓(𝑥) com relação à variável 𝑥
AΔ Área do triângulo Δ𝑦 Variação no eixo y
SUMÁRIO
1 INTRODUÇÃO . . . 14
2 UMA BREVE HISTÓRIA DO SURGIMENTO DO CÁLCULO DIFERENCIAL E NOÇÕES BÁSICAS DE CÁLCULO DIFE-RENCIAL . . . 16
2.1 O cálculo de Leibniz e Newton . . . 17
2.2 O método de Leibniz . . . 18
2.3 O método de Newton . . . 19
2.4 Noções básicas de cálculo . . . 20
2.5 Existência do limite de uma função . . . 21
2.6 Casos em que não existe o limite de uma função . . . 22
2.7 Noções e derivadas . . . 23
3 O ESTUDO DO CÁLCULO NA EDUCAÇÃO BÁSICA . . . 25
3.1 Desafios e barreiras. . . 25
3.2 Noções de cálculo no ensino fundamental . . . 26
3.2.1 Como justificar igualdades do tipo 1/3 = 0,3333.. ou1 = 0,9999... ?. . . 26
3.2.2 Uma forma diferente de calcular áreas de figuras planas . . . 27
3.2.3 O estudo do cálculo no ensino médio: A derivada como taxa de variação 31 3.2.4 Cálculo diferencial e ENEM, é possível? . . . 34
4 APLICAÇÕES DO CÁLCULO DIFERENCIAL EM OUTRAS DISCIPLINAS DA EDUCAÇÃO BÁSICA . . . 38
4.1 Aplicações do cálculo nas ciências biológicas . . . 38
4.2 Aplicações do cálculo nas ciências Físicas . . . 39
4.3 Aplicações do cálculo nas ciências Químicas . . . 40
5 CONCLUSÃO . . . 42
REFERÊNCIAS . . . 43
14
1 INTRODUÇÃO
O cálculo diferencial é uma das ferramentas mais completas e dinâmica que existe no estudo da matemática e possui aplicações em diversas áreas. O ensino da matemática na educação básica deve servir como alicerce em todos âmbitos de tal forma que assegure um entendimento dessa disciplina tanto na sua forma abstrata como na sua essência que nada mais é que usá-la como ferramenta na resolução de problemas. Baseado nessa premícia e na minha prática docente, que vai desde o ensino básico ao ensino superior, sempre questionei porque o "desprezo"ao cálculo diferencial no ensino básico, e qual o reĆexo disso no ensino superior.
Nesse sentido Junior (2014) coloca que:
Não propomos inserir Cálculo Diferencial e Integral no Ensino Médio em sua completude e sim ambientar os estudantes a interagirem de modo dinâmico com ideias que tem o intuito de desenvolver aptidões para uma melhor compreensão dos conceitos abordados no estudo dos limites, derivadas e integral. Propomos um estudo livre de formalizações e muito mais prático, algo que fuja das técni-cas e priorize a reĆexão dos conceitos por parte dos alunos, familiarizando-os com novas simbologias e que desperte a curiosidade nas inúmeras aplicaçõees dessa disciplina (JUNIOR, 2014, p. 02).
Brito (2013), apresenta o cálculo diferencial como ferramenta interdisciplinar para o ensino médio que dever ser usado principalmente na resolução de exercícios de compe-tências interdisciplinares.
Pascoal (2014) entende que:
Como o Cálculo Diferencial e Integral já fez parte do currículo escolar, caso fosse inserido no projeto pedagógico das escolas, novamente, e trabalhado efe-tivamente em sala de aula, poderia tornar a prática pedagógica do ensino da matemática mais proveitosa(PASCOAL, 2014, p. 14).
O nosso objetivo é ressaltar a importância da introdução dos conceitos básicos de cálculo diferencial desde o ensino fundamental até o ensino médio de uma forma con-textualizada e aproveitando os próprios conteúdos do ensino básico para aprofundar os conhecimentos dos alunos através dos conhecimentos iniciais de cálculo diferencial.
No capítulo 1 apresentamos um breve resgate histórico do cálculo que traz um pouco de como foi o seu surgimento e quais os principais nomes que contribuíram tanto para sua origem, quanto para seu desenvolvimento.
15
ensino fundamental ao ensino médio e que está presente até mesmo no Exame Nacional do Ensino Médio (ENEM).
O capítulo 3 é destinado a propostas de trabalhos interdisciplinares do cálculo em outras disciplinas do curriculo básico regular, como a física, quimíca e biologia.
16
2 UMA BREVE HISTÓRIA DO
SURGI-MENTO DO CÁLCULO DIFERENCIAL
E NOÇÕES BÁSICAS DE CÁLCULO
DI-FERENCIAL
Não é de hoje que a ideia do inĄnito sempre atrai e fascina os matemáticos, na Grécia antiga surgiram os primeiros conceitos ĄlosóĄcos, que mais tarde serviriam de base para estudos preciosos na área das ciências exatas, em especial, a matemática. Como sempre ocorre nessa ciência, problemas práticos começaram a instigar estudiosos a, além de formulá-los, também produzir uma resposta capaz de convencer todos que se deparavam com tais questionamentos.
Atribui-se a Arquimedes a primasia, mesmo que inconsciente, do uso de um dos conceitos mais importantes do cálculo diferencial, o conceito de limite, motivado por um problema da quadratura do círculo, que segundo Roque e Carvalho (2012) Şfazer a quadratura de uma área limitada por uma curva plana signiĄca construir um quadrado cuja área seja igual à da ĄguraŤ.
A idéia de Arquimedes era aproximar a área do círculo a área de poligonos incri-tos, a começar pelo quadrado (Ąg. 1), e na medida que duplica-se os lados desse polígono transformando-o em um octógono (Ąg.2), em um hexadecágono (Ąg.3) e assim sucessi-vamente, a área do polígono duplicado se aproxima cada vez mais da área do círculo, portanto, quanto mais se aumenta o número de lados do polígono, mais perto da área do círculo Ącará, o que hoje entendemos, que a área de um círculo é o limite das áreas dos polígonos regulares a ele inscritos, quando o número de lados n, tende a inĄnito.
Figura 1 Ű Quadrado Inscrito Figura 2 Ű Octógono Inscrito
Figura 3 Ű Hexadecágono Ins-crito
de-17
ram uma grande contribuição para o surgimento do estudo dos limites, dentre muitos, o paradoxo de Zenão de Eléia no Século IV a.C, ilustra de uma forma muito simples que somas inĄnitas podem convergir para valores Ąnitos, algo inaceitável para época. Nesse paradoxo, Zenão tenta mostrar como seria impossível um corredor que parte do ponto A chegar no ponto B percorrendo sempre a metade do caminho restante (Ąg.4). Hoje sabe-mos, de uma forma muito clara, que Zenão se deparou com o limite da soma dos inĄnitos termos de uma PG de razão igual a 1/2.
Segundo Eléia (1976) ŞO que se move deve sempre alcançar o ponto médio antes do ponto ĄnalŤ
Figura 4 Ű Paradóxo de Zenão
Quase dois mil anos depois o problema da quadratura seria, mais uma vez, uma porta de entrada para o surgimento do cálculo diferencial através de Pierre de Fermat e René Descartes que estavam interessados em obter a quadratura de curvas, que diferen-temente das obtidas por Arquimedes, eram curvas que vai ao inĄnito o que é o caso por exemplo da parábola.
Assim como Arquimedes, Fermat aproximou a área sob uma curva como sendo a soma de uma inĄnidades de polígonos, dessa vez retângulos cujas bases formavam uma progressão geométrica decrescente (Fig.5) e que pouco tempo depois associados a proble-mas de encontrar tangentes a curvas e áreas sob curvas, viriam inĆuenciar fortemente os estudos de Newton e Leibniz denominados os inventores do cálculo diferencial.
2.1
O cálculo de Leibniz e Newton
cri-18
adas por ele e usadas até hoje, como é o caso da palavra função, designando a ŞfunçãoŤ que uma reta desempenha em uma curva, como por exemplo, a de ser tangente a curva.
2.2
O método de Leibniz
Leibniz mostrou que o problema da quadratura de curvas poderia ser solucionado através de somas inĄnitesimais de áreas retangulares. Tomando-se uma curva qualquer (Ągura 5), a área abaixo da curva (quadratura da curva) pode ser calculada, de forma aproximada, somando-se as áreas de retângulos com bases congruentes.
Figura 5 Ű Área abaixo de uma curva I
Dessa forma, Leibniz notou que quanto maior a quantidade de retângulos (Ągura 6), melhor seria a aproximação da quadratura da curva. Leibniz também foi um dos primeiros a observar que encontrar retas tangentes a curvas seria a operação inversa de determinar sua quadratura, o que hoje entendemos como os processos de derivação e integração respectivamente.
19
2.3
O método de Newton
Diferentemente de Leibniz, o cálculo desenvolvido por Newton tinha como base a física. Newton enxergava uma curva como sendo um movimento contínuo de um ponto no tempo, método chamado por ele de Ćuxões e Ćuentes. Nesse sentido Roque e Carvalho (2012) destaca que:
A taxa de variação de uma quantidade com o tempo era chamada de Ćuxão. Se v,x,y e z são quantidades Ćuentes, seus Ćuxões eram designados respecti-vamente por v,x, y, e z. O problema fundamental do cálculo seria então: dada a relação entre quantidades Ćuentes, encontrar a relação entre seus Ćuxões, e vice e versa(ROQUE; CARVALHO, 2012, p. 288).
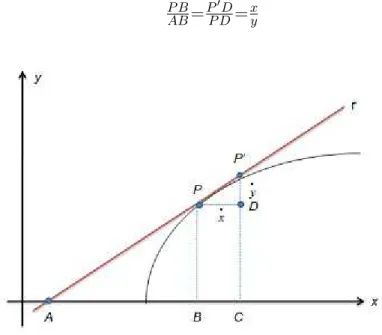
A partir do movimento de uma partícula de um ponto P para um ponto PŠ, Newton considerou os Ćuentes como sendo os aumentos das abscissas e ordenadas gerados pelo deslocamento da partícula e os Ćuxões e como sendo os comprimentos dos segmentos PD e PŠD, respectivamente (Ągura 7).
𝑃 𝐵 𝐴𝐵=𝑃
′ 𝐷 𝑃 𝐷=𝑥𝑦
Figura 7 Ű Método da tangente de Newton
Sendo o deslocamento da partícula P para PŠ muito pequeno, os triângulos ABP e PDPŠ são semelhantes e a razão de semelhança desses triângulos, para um P cada vez mais próximo de PŠ, se aproximava cada vez mais do coeĄciente angular de uma reta r tangente a curva, ou seja:
20
2.4
Noções básicas de cálculo
Segundo Lima (2004)
Diz-se que um número real L é limite de f(x) quando x tende para a e escreve-se limx⊃a𝑓(𝑥) =𝐿, quando para todo𝜖 >0 dado arbitrariamente, pode-se obter umÓ >0 tal que se tem♣𝑓(𝑥)⊗𝐿)♣< 𝜖sempre que x∈𝑋e 0<|x - a|<ÓŤ(LIMA,
2004, p. 13).
Para entendermos melhor a deĄnição dada acima considere o gráĄco da função
𝑓(𝑥) = 2𝑥⊗4 (Ągura 8), vamos analisar o que acontece com a imagem dessa função quando x se aproxima de um valor arbitrário, por exemplo 𝑥= 2.
Figura 8 Ű Limite de uma função
Tabela 1 Ű Valores de x tendendo a 2 pela direita e pela esquerda
(a)
x f(x) 1,91 - 0,18 1,93 - 0,14 1,95 - 0,1 1,97 - 0,06 1,99 - 0,02
(b)
x f(x) 2,09 0,18 2,07 0,14 2,05 0,1 2,03 0,06 2,01 0,02
21
2.5
Existência do limite de uma função
Dizemos que o limite de uma função f(x) quando x tende a certo valor a existe e é igual a determinado número L se:
lim𝑥⊃𝑎⊗𝑓(𝑥) = lim𝑥⊃𝑎+=𝑓(𝑥)lim𝑥⊃𝑎𝑓(𝑥) =𝐿.
em que: lim𝑥⊃𝑎⊗𝑓(𝑥) = lim𝑥⊃𝑎+𝑓(𝑥) são os limites laterais a esquerda e a direita da
função f(x).
Exemplo: Observe o comportamento da função𝑓(𝑥) =𝑥2-7x+10 quando os valores
de x se aproximam pela esquerda do 5 (Tabela 2 (a)) e quando os valores de x se aproximam pela direita do 5 (Tabela 2 (b)).
Tabela 2 Ű Função Quadrática
(a)
x f(x) 5,30 0,99 5,20 0,64 5,10 0,31 5,05 0,15 5,02 0,06
(b)
x f(x) 4,80 0,56 4,90 0,29 4,95 0,14 4,98 0,06 4,99 0,03
Podemos observar que a medida que se aproxima de x = 5 a partir da esquerda e da direita, f(x) sempre tende a 0, então os dois limites laterais existem e são iguais, o que nos permite concluir que:
22
GraĄcamente temos:
Figura 9 Ű Limite Lateral
2.6
Casos em que não existe o limite de uma função
Em geral, as funções que crescem ou decrescem indeĄnidamente não possuem li-mites, assim como funções que possuem limites laterais diferentes, também não possuem um limite. Vejamos alguns exemplos de funções que não possuem limites em𝑥= 0
Exemplo 1:𝑓(𝑥) =𝑐𝑜𝑠(1/𝑥), note que o gráĄco oscila sem tender para um limite.
Figura 10 Ű Limite Inexistente I
23
Figura 11 Ű Limite Inexistente II
2.7
Noções e derivadas
O conceito de derivada está relacionado a taxa de variação de uma função, segundo Lima (2004), A derivada de uma função f no ponto 𝑎 é o limite
𝑓′(
𝑎) = lim𝑥⊃𝑎
𝑓(𝑥)⊗𝑓(𝑎)
𝑥⊗𝑎 =limℎ⊃0
𝑓(𝑎+ℎ)⊗𝑓(𝑎)
ℎ
se esse limite existir, neste caso dizemos que f é derivável no ponto a. Representação gráĄca:
Figura 12 Ű Derivada de uma função
Ainda sobre o conceito de derivada Kelley (2013), destaca que:
24
Regras operacionais: (Demonstrações:Ver Apêndice A)
a) Regra da potência: A derivada do termo 𝑎𝑥𝑛 (em relação a x), onde 𝑎 e 𝑛 são números reais, é (𝑎𝑛)𝑥𝑛⊗1.
b) Regra do produto: Se uma função derivável ℎ(𝑥) é dada pelo produto de outras
duas funções também deriváveis𝑓(𝑥) e𝑔(𝑥), comℎ(𝑥) =𝑓(𝑥).𝑔(𝑥), então a derivada hŠ(x)
será da forma:
ℎ′(
𝑥) =𝑓′(
𝑥)𝑔(𝑥) +𝑓(𝑥)𝑔′(
𝑥)
c) Regra do quociente: Se uma função derivável ℎ(𝑥) é dada pelo quociente de
outras duas funções também deriváveis 𝑓(𝑥) e 𝑔(𝑥), isto é ℎ(𝑥) =𝑓(𝑥)/𝑔(𝑥), então a
derivadaℎ′(
𝑥) será da forma:
ℎ′(
𝑥) = 𝑔(𝑥)𝑓
′
(𝑥)⊗𝑓(𝑥)𝑔′(𝑥)
[𝑔(𝑥)]2 .
d)Regra da cadeia: A derivada de uma função compostaℎ(𝑥) =𝑓(𝑔(𝑥)), onde𝑓(𝑥)
e𝑔(𝑥) são funções diferenciáveis é dada por
ℎ′(
𝑥) =𝑓′(
𝑔(𝑥)).𝑔′(
25
3 O ESTUDO DO CÁLCULO NA
EDUCA-ÇÃO BÁSICA
3.1
Desafios e barreiras
Ao longo da história do ensino da matémática no Brasil noções de cálculo diferencial se fez presente em alguns períodos como disciplina obrigatória do currículo da educação básica, mas com o movimento da matemática moderna nas décadas de 70 e 80 esses conceitos foram excluídos do programa da educação básica entendendo-se que trata-se de conteúdos direcionados apenas para alunos de ensino superior. Segundo Avila (1991)
O Cálculo vem desempenhando um papel de grande relevância em todo o desen-volvimento cientíĄco-tecnológico. Portanto, descartá-lo no ensino é grave, por-que deixa de lado uma componente signiĄcativa e certamente a mais relevante da Matemática para a formação do aluno num contexto de ensino moderno e atual(AVILA, 1991, p. 02).
Segundo os Parâmetros Curriculares Nacionais do Ensino Médio, PCNEM (2002) o ensino da matemática na educação basica, prevê que:
Cabe à Matemática do Ensino Médio apresentar ao aluno o conhecimento de novas informações e instrumentos necessários para que seja possível a ele continuar aprendendo. Saber aprender é a condição básica para prosseguir aperfeiçoando-se ao longo da vida. Sem dúvida, cabe a todas as áreas do Ensino Médio auxiliar no desenvolvimento da autonomia e da capacidade de pesquisa, para que cada aluno possa conĄar em seu próprio conhecimento (PCNEM, 2002, p. 41).
Com a grande gama de conteúdos previstos para o ensino da matemática no ensino básico os professores se deparam com um calendário que não contempla na totalidade esses conteúdos, ou que obriga-o a expor de forma desarticulada e com pouco signiĄcado prático os referidos temas. Os poucos livros didáticos de matemática da educação básica que trazem noções de cálculo diferencial, preferem deixar esses tópicos como algo facultativo, que só deve ser lecionado se o calendário for Ćexivel, outro fator que pondera contra a inserção desse conteúdo em algum momento desse ciclo. Nesse sentido Avila (1991) destaca
É gratiĄcante constatar que alguns autores já estão incluindo a derivada em seus livros para o ensino médio, de maneira sensata, breve e equilibrada: mas, infelizmente, ainda na terceira série, já no Ąnal do curso, quando pouco se pode aproveitar desse estudo (AVILA, 1991, p. 37).
26
que prestam o exame ? As disciplinas aĄns também podem ser favorecidas com o estudo das noções de cálculo na educação básica?
Esses questionamentos foram, ao longo da minha prática docente, tornado-se cada vez mais frequentes e algumas motivações vindas de situações de sala de aula são expostas a seguir como forma de justiĄcar tais questionamentos e claro reaĄrmar a importância do estudo do cálculo diferencial na educação básica.
3.2
Noções de cálculo no ensino fundamental
A matemática do ensino fundamental constitui a base do estudo de toda matemá-tica da educação básica, é nesse ciclo que aprende-se o cálculo algébrico e os principais elementos de geometria. As noções de cálculo nesse ciclo deve ser consequência de situa-ções vivenciadas na prática docente, que leve ao próprio aluno romper com algumas ideias vindas dos ciclos iniciais, na expectativa de serem, de alguma forma, melhor contextuali-zadas nos ciclos vindouros.
Inúmeras situações, tanto na álgebra quanto na geometria, remetem a conceitos intimamente relacionados ao cálculo, por exemplo o conceito de limites e até mesmo de derivadas na sua forma mais comum, como taxa de variação. Dentro dessas experiên-cias, vivenciadas na prática de sala de aula, listo algumas delas que podem servir como ferramenta para a introdução do estudo do cálculo no ensino fundamental.
3.2.1
Como justificar igualdades do tipo
1
/
3 = 0
,
3333
..
ou
1 = 0
,
9999
...
?
Essa situação é muito corriqueira e estimulante no ensino fundamental, geralmente ela aparece aos alunos do sétimo ano, e representa a primeira barreira a ser derrubada para entendimento do conceito de quantidades inĄnitesimais e é claro de um leve entendimento de limites. Na primeira delas temos um fração ordinária irredutível igual a uma fração decimal, já na segunda situação temos um número inteiro igual a uma fração decimal. As expressões que aparecem no segundo membro dessas igualdades são rotuladas de ŞDizimas PeriódicasŤ, que devem ser interpretadas de forma correta para que as igualdades façam sentido. Vejamos como isso é possivel:
Uma fração decimal é uma fração ordinária cujo denominador é uma potência de 10, por exemplo, 5/10,13/100,35/1000. As frações ordinárias podem ser escritas na forma de fração decimal, isso pode ser feito de uma forma simples, basta apenas encontrar frações equivalentes com denominadores sendo potências de 10, como podemos observar nos exemplos abaixo:
a) 7 4 = 175100 b) 9
27
c)45 200 =
235 1000
O problema se encontra em, como encontrar um fração decimal que represente alguns tipos de frações ordinárias do tipo 1/3, 7/9, 3/11 , ou seja, as dízimas periódicas.
Vejamos o caso da fração 1/3:
Podemos escrever 1 como sendo 1,0 ou 1,00 ou 1,000... quantos zeros quisermos e logo em seguida efetuar a divisão por 3. Observe:
a) 1,0 = 3.0,3 + 0,1 b) 1,00 = 3.0,33 + 0,01
c) 1,000 = 3.0,333 + 0,001
Note que a fração ordinária 1/3 pode ser escrita da forma 3/10 (fração decimal)
com um erro de 0,1, da mesma forma também pode ser escrita na forma 33/100 com um erro de 0,01 e assim sucessivamente de tal forma que a fração 1/3 pode ser escrita da forma de fração decimal, 3/10, 33/100, 333/1000, com período 3 repetido n vezes, sendo
o erro cometido uma fração cujo numerador é 1 e o denominador é 1.10𝑛.
Nesse momento da análise o conceito de limite surge de forma sutil e jamais deve ser desprezado pois o aluno deve ser induzido a concluir que quanto maior o valor de n, menor será o erro cometido ou seja melhor será a proximação para a fração ordinária em questão, portanto o erro pode ser tão pequeno quanto se queira.
É importante aĄrmar ao aluno que as frações decimais da forma:
3/10 3/100 3/1000... etc
representam valores aproximados para a fração ordinária 1/3 por isso as reticências no Ąnal do símbolo 0,333.... para indicar que temos uma sequencia inĄnita de frações decimais que representam a fração 1/3. De forma análoga obtemos a outra igualdade citada, 1 = 0,9999..., entende-se que a sequência inĄnita de frações decimais:
0,90,990,9990,9999...𝑒𝑡𝑐
são valores aproximados para o número 1.
3.2.2
Uma forma diferente de calcular áreas de figuras planas
28
A ideia de calcular a área de Ąguras planas é uma das mais utilizadas no cálculo por meio do processo de integração, que por sua vez também nos remete ao processo de somas inĄnitesimais. Ao introduzir essa técnica do cálculo de áreas de Ąguras planas no ensino fundamental, a mesma pode ser estendida para o cálculo da área sob o gráĄco de funções já no ensino médio. Observe as seguintes situações proposta em uma sala de ensino fundamental para alunos do oitavo ano:
Atividade 1: Aproximando a área de um triângulo através de áreas de retângulos. Calcule a área do triângulo da Ągura abaixo:
Figura 13 Ű Atividade em sala de aula 1
Nesses tipos de exercícos o aluno é orientado a usar a fórmula do cálculo da área do triângulo, procedimento feito de uma forma simples:
Área do triângulo =𝐵𝑎𝑠𝑒.𝐴𝑙𝑡𝑢𝑟𝑎
2 = 6.62 = 18𝑢.𝑎
Nesse momento foi feito a seguinte pergunta aos alunos: como encontrar esse valor, ou algo bem próximo a ele, sem usar a fórmula da área ? Esse questionamento vem seguido de uma sugestão bem peculiar para o momento: ŞVamos aproximar a área desse triângulo a áreas de retângulosŤ.
29
primeira subdivisão o segmento de reta com extremos nos pontos (0,0) e (1,0), portanto uma aproximação da área seria feita da forma:
Á𝑟𝑒𝑎1 = 1𝑥0 = 0.𝑢.𝑎
Á𝑟𝑒𝑎2 = 1𝑥1 = 1.𝑢.𝑎
Á𝑟𝑒𝑎3 = 1𝑥2 = 2.𝑢.𝑎
Á𝑟𝑒𝑎4 = 1𝑥3 = 3.𝑢.𝑎
Á𝑟𝑒𝑎5 = 1𝑥4 = 4.𝑢.𝑎
Á𝑟𝑒𝑎6 = 1𝑥5 = 5.𝑢.𝑎
Figura 14 Ű Atividade em sala de aula 2
O aluno percebe de uma forma clara que uma aproximação para a área do triângulo (𝐴Δ) seria a soma de todas as áreas:
(𝐴Δ) = 6 ∑︁
𝑖=1
𝐴𝑖= 0 + 1 + 2 + 3 + 4 + 5 = 15𝑢.𝑎
Em um terceiro momento a seguinte pergunta é feita: Como aproximar cada vez mais da área do triângulo ? A resposta é esperada e imediata: Inserindo-se mais retângulos ŞdentroŤ do triângulo.
30
0,5 u.c, obtendo assim uma medida mais reĄnada, ou seja, mais próxima do valor real:
(𝐴Δ) = 12 ∑︁
𝑖=1
𝐴𝑖= 0 + 0,25 + 0,5 + 0,75 + 1,0 +...+ 2,5 + 2,75 = 16,5𝑢.𝑎
O valor encontrado aproximou-se mais do valor real da área do triângulo. Nesse momento leva-se ao aluno concluir que quanto maior for a quantidade de retângulos, mais próximo da área do triângulo chegamos, ou seja, sendo n a quantidade de retângulos inseridos no interior do triângulo, na medida que n cresce (n tendendo ao inĄnito) a área se aproxima cada vez mais do valor real da área do triângulo, mais uma vez surge o conceito intuitivo de limites, dessa vez aplicado a geometia plana.
Figura 15 Ű Atividade em sala de aula 3
Essa situação exempliĄcada pode ser estendida para alunos do ensino médio que já conseguem visualizar que o valor da base do retângulo é dada por 6/n em que n é o número de subdivisões que servem de base para os retângulos. A altura dos retângulos fomam uma PA crescente de razão r = 6/n, de tal forma que:
ℎ1 = 1.0
31
ℎ5 = 4.6𝑛
ℎ6 = 5.𝑛6 . . . ℎ𝑛= (𝑛⊗1)6
𝑛 .
A conclusão é imediata, pois a área do retângulo é encontrada pelo produto da sua base pela sua altura, portanto temos:
Área = 6
𝑛(h1 + h2 + h3 + h4 + h5 + h6 +...+ hn).
(h1 + h2 + h3 + h4 + h5 + h6 +...+ hn) representa a soma dos termos de uma P.A, logo:
Área = 6 𝑛
(ℎ1+ℎ𝑛)𝑛 2 =𝑛6
(0+(𝑛⊗1)(6/𝑛)𝑛
2 =3(6 - 𝑛6) = 18 - 6𝑛
Essa expressão permite calcular a área do triângulo em função da quantidade de subdivisões que se deseja construir, de tal forma que, como foi observado anteriormente, quanto maior o número de retângulos maior a aproximação do valor real da área procu-rada, logo fazendo n suĄcientemente grande, ou seja, n tendendo a inĄnito temos:
lim𝑛⊃∞(18 - 6𝑛) = 18u.a
Essa prática docente, com os alunos do ensino fundamental, retratam um ganho a médio prazo pois esses conceitos básicos podem e devem ser explorados de forma mais aprofundada no ensino médio, onde o aluno já tem maturidade o suĄciente para lidar com questões que requer o uso de limites de somas inĄnitesimais.
3.2.3
O estudo do cálculo no ensino médio: A derivada como taxa de
vari-ação
Nesse estágio da vida acadêmica o aluno tem outros anseios em relação a matemá-tica, o fazer sentido ou seja a aplicabilidade viabiliza o melhor entender da disciplina, já que a parte introdutória do cálculo algébrico(abstração) foi feita no ensino fundamental, o que torna esse ciclo um ambiente propício para introdução do cálculo diferencial mais especiĄcamente as aplicações dos conceitos de limites e derivadas, na forma de resolução de problemas.
32
Atividade 1:
Considere a função𝑓(𝑥) =𝑥2⊗2𝑥
a) Determine a taxa média de variação de f(x) em função de x, para x∈[4,5].
b) Construa o gráĄco da função𝑓(𝑥) =𝑥2⊗2𝑥e deterrmine os pontos A e B desse
gráĄco, que tem abscissas 4 e 5, respectivamente.
c) No gráĄco do item anterior, desenhe e reta que passa por A e B.
d) Que relação existe entre a taxa média de variação obtida no item a e o coeĄciente angular da reta desenhada no item c ?
Resolução:
a) Nesse item os alunos devem aplicar o conceito de taxa de variação média já estudado no estudo de funções.
Δ𝑦
Δ𝑥=
𝑓(5)⊗𝑓(4)
5⊗4 =
15⊗8 1 = 7
b) Através do software Geogebra obtemos os gráĄcos pedidos nos itens b) e c)
33
Figura 17 Ű GráĄco item c
c) Nesse item a sala comprovou que o coeĄciente angular da reta e a taxa média de variação representam a mesma coisa.
Atividade 2: Considere a função aĄm 𝑓(𝑥) = 6𝑥+ 2
a) Faça o gráĄco da função
b) Determine a taxa média de variação de f(x) em função de x, para𝑥∈[2,8]. c) Determine a taxa média de variação de f(x) em função de x, para𝑥∈[50,150].
d) Que relação existe entre a taxa média de variação obtida nos itens a,b e c e o coeĄciente angular da reta desenhada no item a ?
Resolução: a)
b) A taxa de variação será dada por
Δ𝑦
Δ𝑥 =
𝑓(2)⊗𝑓(8) 8⊗2 =
50⊗14 6 = 6 c) De forma análoga temos:
Δ𝑦
Δ𝑥 =
𝑓(50)⊗𝑓(150)
150⊗50 =
34
Figura 18 Ű GráĄco atividade 2
d) São todos iguais
3.2.4
Cálculo diferencial e ENEM, é possível?
Alguns tópicos cobrados no ENEM estão intimamente relacionados com o cálculo diferencial, o que nos leva a mais uma vez a destacar a importância desse estudo no ensino básico. Segue alguns exercícios que foram cobrados no ENEM, e sugestões de resolução, por meio de cálculo diferencial e por meio de conteúdos lecionados no ensino médio.
EXEMPLO 1: A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a Ągura. A função real que expressa a parábola, no plano cartesiano da Ągura, é dada pela lei f(x) = 2
3 𝑥2 Ű 6x + C, onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na Ągura, representa o vértice da parábola, localizado sobre o eixo x. Nessas condições, calcule a altura do líquido contido na taça, em centímetros.
RESOLUÇÃO:
Se o ponto V está localizado sobre o eixo x f(x) = 3
35
Figura 19 Ű Taça gerada pela rotação de uma parábola
Δ = (⊗6)2
⊗4(32)𝐶= 0 =⇒ 𝐶= 6
Derivando a função f(x), temos: 𝑓′(
𝑥) = 3𝑥⊗6, observe que o ponto onde essa derivada é nula corresponde a abscissa do vértice da parábola e que a ordenada do vértice é nula, portanto 3x Ű 6 = 0 , logo x = 2. Note que f(2) = 0 então: (3
2)22 Ű 6.2 +C = 0, portanto C = 6.
EXEMPLO 2: Um estudante está pesquisando o desenvolvimento de certo tipo de bactéria. Para essa pesquisa, ele utiliza uma estufa para armazenar as bactérias. A temperatura no interior dessa estufa, em graus Celsius, é dada pela expressão 𝑇(ℎ) = ⊗ℎ2+ 22ℎ⊗85, em que h representa as horas do dia. Sabe-se que o número de bactérias
é o maior possível quando a estufa atinge sua temperatura máxima e, nesse momento, ele deve retirá-las da estufa. A tabela associa intervalos de temperatura, em graus Celsius com as classiĄcações: muito baixa, baixa, média, alta e muito alta. Quando o estudante obtém o maior número possível de bactérias, de acordo com a tabela dada, qual será a classiĄcação da temperatura no interior da estufa?
RESOLUÇÃO:
Com o auxílio do software Geogebra vamos traçar o gráĄco dessa função:
A função𝑇(ℎ) =⊗ℎ2+22ℎ⊗85, por comparação, tem valor de a = -1 que é menor
que zero e por isso a função tem um ponto de máximo. Para determinar qual é esse ponto de máximo, podemos calcular por meio de fórmulas o vértice da parábola:
𝑋𝑣=⊗𝑏
2𝑎;𝑌 𝑣= ⊗Δ
36
Figura 20 Ű Tabela ENEM
Figura 21 Ű Função Quadrática
Na função da questão, y é a temperatura e x é a hora. Como queremos saber a temperatura máxima, só precisamos calcular Yv:
𝑌 𝑣=⊗222⊗4.1.(⊗85) 4(⊗1) = 36
37
Vamos agora resolver o mesmo exercício usando derivadas: Esse é um problema de ponto crítico máximo (Ver apêndice A).
Fazendo a derivada primeira da função𝑇(ℎ) =⊗ℎ2+ 22ℎ⊗85, igual a 0, temos:
𝑇′(
ℎ) =⊗2ℎ+ 22 = 0 ℎ= 11
Vamos agora, fazer a derivada segunda da função e observar o valor obtido: Se𝑇′′(
ℎ) >0, o ponto crítico é um ponto de mínimo
Se𝑇′′(
ℎ) <0, o ponto crítico é um ponto de máximo
𝑇′′
(ℎ) =⊗2.
Como -2 é menor do que 0; logo o ponto crítico é um ponto de máximo. Sabendo que h = 11 é o valor que resulta no maior valor de T (ponto máximo), substituo h = 11 na função para obter T, temos:
𝑇(ℎ) =⊗11 + 22.11⊗85 =⊗121 + 242⊗85 = 36𝐶
38
4 APLICAÇÕES DO CÁLCULO
DIFEREN-CIAL EM OUTRAS DISCIPLINAS DA
EDUCAÇÃO BÁSICA
Nesse capítulo mostraremos algumas aplicações do cálculo em outras disciplinas da educação básica, através da resolução de exercícos, destacando ainda mais a importância do contato com essa ferramenta também muita usada na física, química, biologia dentre outras áreas na qual o seu domínio facilita a resolução de situações-problemas nas mais diversas áreas.
4.1
Aplicações do cálculo nas ciências biológicas
ATIVIDADE 01: Uma cultura de bactérias começa com 800 bactérias, e o cresci-mento de sua população é modelada peça função:𝑃(𝑡) = 800.𝑒0,05𝑡 Em que P é o número
de bactérias e t é o tempo em minutos. Com base nessas informações determine:
a) A fórmula para a taxa de variação da população de bactérias em função de t. b) Arredondando para o número inteiro mais próximo, qual é a taxa de variação da população de bactérias quando t = 12 minutos?
Solução:
a)Precisamos derivar a população exempliĄcada para encontrar sua taxa de varia-ção. Portanto, pela regra da cadeia:
𝑃′
(𝑡) = 800.𝑒0,05𝑡.(0,05) = 40.𝑒0,05𝑡
b) Quando t = 12 minutos temos:
𝑃′
(12) = 40.𝑒0,05(12)= 73𝑏𝑎𝑐𝑡é𝑟𝑖𝑎𝑠 𝑚𝑖𝑛𝑢𝑡𝑜𝑠
ATIVIDADE 02: Os pinípedes são uma sub-ordem dos mamíferos aquáticos, tais como focas e morsas, cujos pés evoluem para nadadeiras. A relação comprimento/peso durante o crescimento fetal é dada por𝑃(𝑡) = 6.10⊗5
.[𝐶(𝑡)]2,74 onde C é o comprimento
(em, cm) e P é o peso (em Kg).
39
b) se o peso de uma foca é de 0,5Kg e varia à razão de 0,4Kg/mês, qual a taxa de variação de seu comprimento ?
Solução:
a)𝑃(𝑡) = 6.10⊗5
.[𝐶(𝑡)]2,74, pela regra da cadeia temos: 𝑃′(
𝑡) = (2,74)6.10⊗5
.[𝐶(𝑡)]1,74.𝐶′(
𝑡)
b)A taxa de variação do comprimento é dada por CŠ(t), pelo item (a) temos:
𝐶′
(𝑡) = 𝑃
′(
𝑡)
(2,74)6.10⊗5.[𝐶(𝑡)]1,74
Do enuciado temos que𝑃′(
𝑡) = 0,4 quando𝑃(𝑡) = 0,5 e que esta última informação
permite determinar C(t) pois
[𝐶(𝑡)]1,74= 𝑃(𝑡) 6.10⊗5
portanto:
[𝐶(𝑡)]1,74= 0,5
6.10⊗5 = 8333,33⇒ 𝐶= 26,97
Logo, o comprimento varia à taxa de:
𝐶′(
𝑡) = 0,5
(2,74)6.10⊗5.[26,74]1,74 = 7,876𝑐𝑚/𝑚ê𝑠
.
4.2
Aplicações do cálculo nas ciências Físicas
ATIVIDADE 01: Um móvel desloca-se sobre um segmento de reta obedecendo à equação horária 𝑠=𝑠𝑒𝑛(𝑡) (Unidades do SI). Determine:
a) Sua velocidade instante t = Þ / 4 segundos
b) Sua aceleração no instante t = Þ /6 segundos.
Solução:
Derivando-se a função s(t) = sent, obtém-se:
𝑠′
(𝑡) =𝑣(𝑡) =𝑐𝑜𝑠𝑡⇒𝑣(Þ
4) =𝑐𝑜𝑠(
Þ
4)⇒𝑣(
Þ
4) =
√
2 2 𝑚/𝑠 Derivando a velocidade em função do tempo tem-se:
𝑣′(
𝑡) =𝑎(𝑡) =⊗𝑠𝑒𝑛𝑡⇒𝑎(Þ
6) =⊗𝑠𝑒𝑛(
Þ
6)⇒𝑎(
Þ
6) =
⊗1
40
Concluimos então que sua velocidade e sua aceleração são, respectivamente:
√
2 2 ,
⊗1
2 .
ATIVIDADE 02: A posição de um corpo é dada pela expressão𝑠(𝑡) = 2𝑡3⊗3𝑡2+ 8.
Determine a aceleração e a velocidade do corpo nos instantes t = 0,t = 3 e t = 5? Solução:
Derivando-se a função s(t), obtém-se:
𝑠′(
𝑡) =𝑣(𝑡) = 6𝑡2⊗3𝑡
Derivando-se agora v(t), temos:
𝑣′
(𝑡) =𝑎(𝑡) = 12𝑡⊗3
Temos que: v(0) = 0, v(3) = 36, v(5) = 120, a(0) = 6, a(3) = 30 e a(5) = 54.
4.3
Aplicações do cálculo nas ciências Químicas
ATIVIDADE 01:O Prêmio Nobel de Química de 1999 foi outorgado ao químico egípcio-estadunidense, Ahmed H. Zewail, por seus estudos dos estados de transição de re-ações químicas por meio da espectroscopia em femtosegundos. Dessa maneira, a Academia Real Sueca de Ciências considera o investigador, pioneiro de reações químicas na escala de tempo em que elas efetivamente ocorrem Supondo que na reação genérica, 2A + 3BC, a concentração do reagente A relaciona-se com o tempo de acordo com a seguinte equação: [𝐴] = 3𝑡2⊗24𝑡, determine a velocidade (em mol/L.s) de formação de C no instante t=5s.
Solução:
Derivando-se [A] temos:
𝑑′
[𝐴] = 6𝑡⊗24 Logo a concentração de [A] em t = 5s será;
[𝐴] = 6(5)⊗24⇒[𝐴] = 6
Como a de C é metade, temos C = 3 mol/L .s
ATIVIDADE 02: Suponha que uma proteína de massa m se decomponha em ami-noácidos segundo a fórmula 𝑚(𝑡) = 25
41
Determine a taxa média de variação da massa no intervalo de tempo [0,1
4]. Qual a taxa de variação instantânea para t = 1h?
Solução:
A taxa média de variação da massa no intervalo de tempo [0,1 4] é: Δ𝑚
Δ𝑡 =
𝑀(14)⊗𝑀(0)
1 4⊗0
42
5 CONCLUSÃO
Nesse trabalho falamos um pouco sobre o surgimento do cálculo diferencial e abor-damos algumas noções básicas de cálculo. Também tentamos ressaltar a importância do estudo de noções de cálculo na educação básica, através de situações problemas vivenci-adas em sala de aula na minha prática docente.
Algumas limitações também foram destacadas na inserção desse conteúdo na edu-cação básica que é o caso da existência de poucos livros didáticos que abordam noções de cálculo diferencial direcionado ao ensino básico, bem como um calendário pouco Ćexível que obriga os docentes a tratar essas noções com pouca relevância.
Foi elaborado uma situação prática com alunos do 9o ano do ensino fundamental e da 1a série do ensino médio em que os conceitos de somas inĄnitesimais eram abordados de uma forma simples e sutil sendo ressaltado a importância do estudo de limites.
Foram surgeridos alguns exercícios que envolvem cálculo diferencial em outras dis-ciplinas, como a física a biologia e a química o que motiva ainda mais a prática desse estudo para alunos da educação básica.
Também constatamos que essas noções podem proporcionar aos alunos um melhor entendimento de determinados conteúdos que remetem a esses conhecimentos básicos de cálculo, tanto no ensino fundamental quanto no médio proporcionando assim um melhor entendimento das disciplinas aĄns que usam essa ferramenta, como é o caso da física, química e biologia.
A importância desse estudo na educação básica também foi enfatizada através de exercícios que constam no Exame Nacional do Ensino Médio (ENEM), que podem ser solucionados com noções de cálculo diferencial, o que vem a ressaltar o ganho que os alunos que tem contato com esses conteúdos podem ter quando se submetem ao exame.
43
REFERÊNCIAS
AVILA, G. O ensino de cálculo no 2 grau. Revista do Professor de Matemática, Sociedade Brasileira de Matemática, n. 18, p. 2, 1991.
BRITO, J. C. S. O Cálculo Diferencial e Integral como ferramenta interdisci-plinar no Ensino Médio: 2013. 02 f. Dissertação (Mestrado ProĄssional em Matemática-PROFMAT) Ů Universidade Federal do Piauí, Teresina-PI, 2013. ELéIA, Z. de.OS PRÉ-SOCRÁTICOS. 2. ed. São Paulo: Editora Abril, 1976.
JUNIOR, O. d. S.Cálculo no Ensino Médio:Números Reais: 2014. 02 f. Dissertação (Mestrado ProĄssional em Matemática-PROFMAT) Ů Universidade Federal do Rio de Janeiro, Rio de Janeiro-RJ, 2014.
KELLEY, W. M.O Guia Completo para Quem Não É C.D.F. – Cálculo. 2. ed. Rio de janeiro: Alta Books, 2013.
LEITHOLD, L. O Cálculo com Geometria Analítica. Tradução Ciro de Carvalho Patarra. 3. ed. São Paulo: Harbra, 1994. v. 2.
LIMA, E. L.Análise Real. 8. ed. Rio de Janeiro: SBM, 2004.
PASCOAL, J. U. M.Um Breve Estudo Sobre a utilização do Cálculo Diferencial e Integral na Educação Básica de Jaguaruana-CE: 2014.14 f. Dissertação (Mestrado ProĄssional em Matemática-PROFMAT) Ů Universidade Federal Rural do Semi-Árido, Mossoró-RN, 2014.
PCNEM. Parâmetros Curriculares Nacionais Ensino Médio. Ministério da Educação e Cultura, Brasília, DF, 2002. Disponível em:<http://portal.mec.gov.br/seb/ arquivos/pdf/blegais.pdf>. Acesso em: 10 ago. 2013.
45
APÊNDICE A – TEOREMAS E
DEMONSTRAÇÕES
Nesta secção todas as demonstrações podem ser encontradas em Leithold (1994).
Regras Operacionais de Derivação
Teorema 1: Se c for uma constante e se f(x) = c para todo x, então f’(x) = 0.
Prova:
𝑓′(
𝑥) = lim
∆𝑥⊃0
𝑓(𝑥+ Δ𝑥)⊗𝑓(𝑥)
Δ𝑥
𝑓′
(𝑥) = lim
∆𝑥⊃0
𝑐⊗𝑐
Δ𝑥
𝑓′
(𝑥) = lim ∆𝑥⊃00 = 0
A derivada de uma constante é zero.
Teorema 2: Se n for um inteiro positivo e se 𝑓(𝑥) =𝑥𝑛, então 𝑓′(
𝑥) =𝑛𝑥𝑛⊗1
.
Prova:
𝑓′(
𝑥) = lim
∆𝑥⊃0
𝑓(𝑥+ Δ𝑥)⊗𝑓(𝑥)
Δ𝑥 𝑓′
(𝑥) = lim
∆𝑥⊃0
𝑓(𝑥+ Δ𝑥)𝑛⊗𝑥𝑛
Δ𝑥
Aplicando o teorema binomial a (𝑥+ Δ𝑥)𝑛 teremos:
𝑓′
(𝑥) = lim
∆𝑥⊃0
[𝑥𝑛+𝑛𝑥𝑛⊗1Δ
𝑥+𝑛(𝑛2!⊗1)𝑥𝑛⊗2Δ(
𝑥2) +...+𝑛𝑥(Δ𝑥)𝑛⊗1+ (Δ
𝑥)𝑛]⊗𝑥𝑛
Δ𝑥
𝑓′
(𝑥) = lim
∆𝑥⊃0
𝑛𝑥𝑛⊗1Δ
𝑥+𝑛(𝑛2!⊗1)𝑥𝑛⊗2Δ(
𝑥2) +...+𝑛𝑥(Δ𝑥)𝑛⊗1+ (Δ
𝑥)𝑛
Δ𝑥
Dividindo o numerador e o denominador por Δ𝑥, obtemos:
𝑓′
(𝑥) = lim
∆𝑥⊃0𝑛𝑥
𝑛⊗1
+𝑛(𝑛⊗1) 2! 𝑥𝑛
⊗2
Δ𝑥+...+𝑛𝑥(Δ𝑥)𝑛⊗2
46
.
Todos os termos, exceto o primeiro, têm Δ𝑥 como fator assim sendo todos os termos, exceto o primeiro, tendem a zero quando Δ𝑥 tende a zero. Assim:
𝑓′(
𝑥) =𝑛𝑥𝑛⊗1
Teorema 3: Se f for uma função, c uma constante e g a função definida por g(x) = c.f(X) então, se f’(x) existir, g’(X) = c.f’(X)
Prova:
𝑔′(
𝑥) = lim
∆𝑥⊃0
𝑔(𝑥+ Δ𝑥)⊗𝑔(𝑥)
Δ𝑥
𝑔′(
𝑥) = lim
∆𝑥⊃0
𝑐𝑓(𝑥+ Δ𝑥)⊗𝑐𝑓(𝑥)
Δ𝑥
𝑔′(
𝑥) = lim
∆𝑥⊃0𝑐[
𝑔(𝑥+ Δ𝑥)⊗𝑔(𝑥)
Δ𝑥 ]
𝑔′(
𝑥) =𝑐.[ lim
∆𝑥⊃0
𝑔(𝑥+ Δ𝑥)⊗𝑔(𝑥)
Δ𝑥 ]
𝑔′(
𝑥) =𝑐.𝑓′(
𝑥)
A derivada de uma constante vezes uma função é a constante vezes a derivada da função, se essa derivada existir.
Teorema 4:Se f e g forem funções e h a função definida por h(x) = f(x)g(x) entao se existirem f’(x) e g’(x), h’(x) = f(x)g’(x) + g(x)f’(x)
Prova:
ℎ′(
𝑥) = lim
∆𝑥⊃0
ℎ(𝑥+ Δ𝑥)⊗ℎ(𝑥)
Δ𝑥
ℎ′(
𝑥) = lim
∆𝑥⊃0
𝑓(𝑥+ Δ𝑥).𝑔(𝑥+ Δ𝑥)⊗𝑓(𝑥).𝑔(𝑥)
Δ𝑥
Se𝑓(𝑥+ Δ𝑥).𝑔(𝑥) for somado e subtraido ao numerador, então:
ℎ′(
𝑥) = lim
∆𝑥⊃0
𝑓(𝑥+ Δ𝑥).𝑔(𝑥+ Δ𝑥)⊗𝑓(𝑥+ Δ𝑥).𝑔(𝑥) +𝑓(𝑥+ Δ𝑥).𝑔(𝑥)⊗𝑓(𝑥).𝑔(𝑥)
47
ℎ′
(𝑥) = lim
∆𝑥⊃0[𝑓(𝑥+ Δ𝑥).
𝑔(𝑥+ Δ𝑥)⊗𝑔(𝑥)
Δ𝑥 +𝑔(𝑥).
𝑓(𝑥+ Δ𝑥)⊗𝑓(𝑥)
Δ𝑥 ]
ℎ′
(𝑥) = lim
∆𝑥⊃0[𝑓(𝑥+ Δ𝑥).
𝑔(𝑥+ Δ𝑥)⊗𝑔(𝑥)
Δ𝑥 ] + lim∆𝑥⊃0[𝑔(𝑥).
𝑓(𝑥+ Δ𝑥)⊗𝑓(𝑥)
Δ𝑥 ]
Sabemos que:
lim
∆𝑥⊃0[𝑓(𝑥+ Δ𝑥).
𝑔(𝑥+ Δ𝑥)⊗𝑔(𝑥)
Δ𝑥 ] =𝑔
′
(𝑥)
lim ∆𝑥⊃0[𝑔(𝑥).
𝑓(𝑥+ Δ𝑥)⊗𝑓(𝑥)
Δ𝑥 ] =𝑓
′
(𝑥)
Dando assim:
ℎ′(
𝑥) =𝑓(𝑥)𝑔′(
𝑥) +𝑔(𝑥)𝑓′(
𝑥)
Teorema 5: Se f e g forem funções e se h for a função definida por h(x)= 𝑓(𝑥)𝑔(𝑥)
onde 𝑔(𝑥)̸= 0, então se f’(x) e g’(x) existirem, ℎ′(
𝑥) = 𝑔(𝑥)𝑓
′
(𝑥)⊗𝑓(𝑥)𝑔′(𝑥)
[𝑔(𝑥)]2 . Prova:
ℎ′
(𝑥) = lim
∆𝑥⊃0
ℎ(𝑥+ Δ𝑥)⊗ℎ(𝑥) Δ𝑥
ℎ′
(𝑥) = lim ∆𝑥⊃0
𝑓(𝑥+∆𝑥) 𝑔(𝑥+∆𝑥)⊗ 𝑓(𝑥) 𝑔(𝑥) Δ𝑥 ℎ′
(𝑥) = lim ∆𝑥⊃0
𝑓(𝑥+ Δ𝑥).𝑔(𝑥)⊗𝑓(𝑥).(𝑔(𝑥+ Δ𝑥)
Δ𝑥.𝑔(𝑥).𝑔(𝑥+ Δ𝑥)
Se somarmos e subtrairmos f(x).g(x) ao denominador, então:
ℎ′
(𝑥) = lim
∆𝑥⊃0
𝑓(𝑥+ Δ𝑥).𝑔(𝑥)⊗𝑓(𝑥).𝑔(𝑥)⊗𝑔(𝑥+ Δ𝑥) +𝑓(𝑥).𝑔(𝑥) Δ𝑥.𝑔(𝑥).𝑔(𝑥+ Δ𝑥)
ℎ′
(𝑥) = lim ∆𝑥⊃0[
𝑔(𝑥).𝑓(𝑥+ Δ𝑥)⊗𝑓(𝑥)
Δ𝑥 ]⊗[𝑓(𝑥).
𝑔(𝑥+ Δ𝑥)⊗𝑔(𝑥)
Δ𝑥 ]
ℎ′
(𝑥) = lim
∆𝑥⊃0
[𝑓(𝑥+ Δ𝑥).𝑔(𝑥+∆𝑥)∆𝑥⊗𝑔(𝑥)] + lim∆𝑥⊃0[𝑔(𝑥).
𝑓(𝑥+∆𝑥)⊗𝑓(𝑥)
∆𝑥 ]
48
Sendo:
ℎ′(
𝑥) = lim∆𝑥⊃0𝑔(𝑥+ Δ𝑥) =𝑔(𝑥)
ℎ′(
𝑥) = lim∆𝑥⊃0𝑔(𝑥) =𝑔(𝑥)
ℎ′(
𝑥) = lim∆𝑥⊃0𝑓(𝑥) =𝑓(𝑥)
Temos que:
ℎ′(
𝑥) = 𝑔(𝑥)𝑓
′
(𝑥)⊗𝑓(𝑥)𝑔′(𝑥)
[𝑔(𝑥)]2 .