Caracterização estatística de processos sísmicos via Distribuição Generalizada de Pareto. Estudo de caso: João Câmara-RN

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIÊNCIAS EXTAS E DA TERRA-CCET

PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA APLICADA E ESTATÍSTICA - PPGMAE

DISSERTAÇÃO DE MESTRADO

CARACTERIZAÇÃO ESTATÍSTICA DE EXTREMOS DE

PROCESSOS SÍSMICOS VIA DISTRIBUIÇÃO GENERALIZADA

DE PARETO. ESTUDO DE CASO: JOÃO CÂMARA – RN.

Autor: Raimundo Nonato Castro da Silva

Orientador: Prof. Dr. Paulo Sérgio Lucio

Co-orientador: Prof. Dr. Aderson Farias do Nascimento

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIÊNCIAS EXTAS E DA TERRA-CCET

PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA APLICADA E ESTATÍSTICA - PPGMAE

DISSERTAÇÃO DE MESTRADO

CARACTERIZAÇÃO ESTATÍSTICA DE EXTREMOS DE

PROCESSOS SÍSMICOS VIA DISTRIBUIÇÃO GENERALIZADA

DE PARETO. ESTUDO DE CASO: JOÃO CÂMARA – RN.

Autor: Raimundo Nonato Castro da Silva

Dissertação de mestrado apresentada em 5 de dezembro de 2008, para a obtenção do título de Mestre em Matemática Aplicada e Estatística pelo Programa de Pós-Graduação em Matemática Aplicada e Estatística (PPGMAE) da Universidade Federal do Rio Grande do Norte (UFRN).

Comissão Examinadora:

Prof. Dr. Paulo Sérgio Lucio (Orientador)

Prof. Dr. Aderson Farias do Nascimento (Co-orientador) Prof. Dr. Walter Eugênio de Medeiros

Profa. Dra. Sílvia Maria de Freitas

AGRADECIMENTOS

Agradeço a todos que contribuíram, direta ou indiretamente, para a realização deste trabalho.

Ao meu orientador, Prof. Paulo Sérgio Lucio, pela sua paciência e atenção.

À minha família, especialmente, meus pais.

A todos os meus amigos, especialmente, Francisco Marcio Barboza e Daniel Matos de Carvalho pelas discussões matemáticas e estatísticas e pelas dicas no R.

SUMÁRIO

1– Introdução... 6

2 – A Filosofia da Teoria de Valores Extremos... 9

2.1 – A Distribuição Generalizada de Valores Extremos (GEV)...9

2.2 – Inferência sobre os Parâmetros da GEV...13

2.2.1 – Estimação dos quantis extremos da GEV...19

2.3 – A Distribuição Generalizada de Pareto (GPD)...19

2.3.1 - Seleção de um Limiar...24

2.4 – Inferência sobre os Parâmetros da GPD...25

2.5 - Relação entre a Distribuição q-Exponencial e a GPD...26

3 – Alguns Métodos de Estimação dos Parâmetros da GPD...29

3.1 - Máxima Verossimilhança (MLE)...29

3.2 - Máxima Verossimilhança Penalizada (MPLE)...30

3.3 - Momentos (MOM)...30

3.4 - Pickands (PICKANDS)…………...………...31

3.5 - Momentos Ponderado por Probabilidades: (PWMB e PWMU)...31

3.6- Divergência Média da Densidade (MDPD)…...…...32

3.7 - Mediana (MED)...32

3.8 - Melhor Qualidade do Ajuste (MGF)……….……...33

3.9 – Máxima Entropia (POME)...33

3.9.1 - Especificação das Restrições...35

3.9.2 - Construção da Função de Entropia...35

3.9.3 - Relação entre os Parâmetros da GPD e as Restrições...36

4 – Diagnóstico de Adequação do Modelo...40

4.1 – Teste de Adequação do Modelo...41

5 – Estudo de Caso: João Câmara – RN...43

5.1 – Caracterização do Município e o Sismo Histórico...43

5.2 – Análise dos Dados...46

5.3 - Reconstrução de Extremos via Simulação de Monte Carlo...51

6 – Considerações Finais...55

Referencias Bibliográficas………...……...………..…57

RESUMO

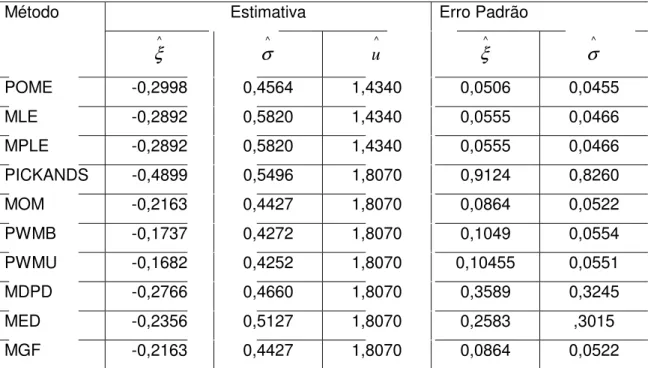
O objetivo desse trabalho é fazer uma breve discussão dos métodos de estimação dos parâmetros da distribuição generalizada de Pareto (GPD). Sendo abordadas as seguintes técnicas: máxima verossimilhança (MLE), máxima verossimilhança penalizada (MPLE), métodos dos momentos (moments), Pickands (Pickands), momentos ponderados pela probabilidade: viesado e não-viesado (PWMB, PWMU), divergência média da densidade (MDPD), melhor qualidade do ajuste (MGF), mediana (MED) e o método da máxima entropia (POME), técnica que neste trabalho receberá uma maior atenção. A título de ilustração foram feitos ajustes para a distribuição generalizada de Pareto, para uma seqüência de sismos intraplacas, ocorridos no município de João Câmara, NE Brasil que foi monitorado continuamente durante dois anos (1987 e 1988). Verificou-se que o MLE e o POME foram os métodos mais eficientes, dando basicamente os mesmos erros médios quadráticos. Com base no limiar de 1,5º foi estimado o risco sísmico para o município, sendo estimado o nível de retorno para os sismos de intensidade 1,5º, 2,0º, 2,5º, 3,0º e para o sismo mais intenso já registrado no município, ocorrido em novembro de 1986 que teve a magnitude de 5,2º.

Palavras-Chave: Eventos Extremos, Simulação Estocástica, Máxima Entropia, Risco

ABSTRACT

The work is to make a brief discussion of methods to estimate the parameters of the Generalized Pareto distribution (GPD). Being addressed the following techniques: Moments (moments), Maximum Likelihood (MLE), Biased Probability Weighted Moments (PWMB), Unbiased Probability Weighted Moments (PWMU), Mean Power Density Divergence (MDPD), Median (MED), Pickands (PICKANDS), Maximum Penalized Likelihood (MPLE), Maximum Goodness-of-fit (MGF) and the Maximum Entropy (POME) technique, the focus of this manuscript. By way of illustration adjustments were made for the Generalized Pareto distribution, for a sequence of earthquakes intraplacas which occurred in the city of João Câmara in the northeastern region of Brazil, which was monitored continuously for two years (1987 and 1988). It was found that the MLE and POME were the most efficient methods, giving them basically mean squared errors. Based on the threshold of 1.5 degrees was estimated the seismic risk for the city, and estimated the level of return to earthquakes of intensity 1.5°, 2.0°, 2.5°, 3.0° and the most intense earthquake never registered in the city, which occurred in November 1986 with magnitude of about 5.2º.

Key-words: Extreme Events, Stochastic Simulation, Maximum Entropy, Seismic

CAPÍTULO 1: INTRODUÇÃO

De forma geral, a previsão probabilística da ocorrência de eventos extremos é de vital importância para o planejamento das atividades sujeitas a seus efeitos adversos, e uma das formas de modelar esses eventos, é utilizar a teoria de valores extremos (TEV) proposta por Fisher e Tippett (1928). Onde segundo essa teoria, existem três tipos de distribuições assintóticas de valores extremos, a do tipo I conhecida como Gumbel, a do tipo II conhecida com Fréchet e a do tipo III conhecida com Weibull. Outra forma para esse tipo de modelagem é utilizar um importante teorema limite conhecido como distribuições acima de um limiar ( Peaks-over-Threshold - POT), conhecido como teorema de Gnedenko-Pickands-Balkema-Haan

(1941). De uma forma geral, o POT, refere-se à distribuição dos eventos condicionados por valores acima de um limiar pré-fixado. Esse teorema garante que sob certas condições (domínio de atração do máximo), que o limite dessa distribuição é a distribuição generalizada de Pareto (GPD), observa-se então que a idéia é estimar a cauda da distribuição, tanto na TEV como no POT.

Os sismos1 _{podem ser considerados como um exemplo de eventos extremos,}

uma vez que não é um fenômeno que ocorre normalmente, sua presença quando ocorre, aparece nas caudas da distribuição, dessa forma, tanto a TEV como o POT, podem ser utilizados para modelar esses tipos de evento.

Se a modelagem do sismo for através dos máximos observados em períodos de tempo, a abordagem deve ser feita através da TEV, mas Coles (2001) diz que na prática surge um problema em particular ao se escolher essa teoria. Escolhida a distribuição o grau de incerteza não poderá ser medido, uma vez, que se aceita o modelo, dessa forma não podendo ser medido o grau de incerteza, mesmo que esse possa ser significativo. Portanto, Jenkinson (1955) unificou os três tipos de distribuições assintóticas, numa única família conhecida como a distribuição de valores extremos Generalizadas (GEV), onde a mesma se baseia nos máximos de um bloco.

Os abalos sísmicos1 _{quando ocorrem, podem causar grandes impactos na}

sociedade. No município de João Câmara, situado no estado do Rio Grande do Norte, por exemplo, em novembro de 1986 ocorreu um sismo que atingiu a magnitude de 5,22

graus na escala de Ricther3_{, sendo um dos maiores já registrado no Brasil.}

Sismos de intensidades moderadas, como o ocorrido em João Câmara, podem causar danos nas estruturas de casas e prédios, queda nas redes de transmissão de energia elétrica e a vibração de estruturas e equipamentos. A importância dos efeitos deste fenômeno geofísico está, portanto, intimamente ligado ao desenvolvimento da tecnologia dos materiais e da engenharia estrutural. Segundo Pisarenko et al. (2008), os sismos passaram a ser um grande problema á medida que as construções tornaram-se mais altas e os tsunamis começaram a ocorrer.

Este manuscrito foi desenvolvido com o objetivo principal de apresentar a metodologia para se ajustar a distribuição generalizada de Pareto aos dados sísmicos do município de João Câmara, sendo feita também uma reconstrução das séries de sismos via simulações de monte Carlo, para obter a probabilidade de ocorrência diária de sismos acima de 1,5º na escala Ricther e estimar o período de retorno para os sismos de intensidade 1,5º, 2,5º, 3,0º e o sismo histórico de 5,2º na escala Ricther.

O texto encontra-se estruturado em seis capítulos. No presente capítulo é feita a justificativa do trabalho e delineado o seu objetivo, segue-se no capítulo 2 - A filosofia da teoria de valores extremos, onde foi feita uma revisão de literatura sobre a distribuição de extremos generalizadas (GEV), a distribuição generalizada de Pareto (GPD) bem como a seleção de um limiar e por fim a relação entre a distribuição q-exponencial e a GPD.

No capítulo 3 – Métodos de estimação dos parâmetros da distribuição generalizada de Pareto, mostramos vários métodos de estimação dos parâmetro da GPD dando um maior destaque ao método da máxima entropia (POME).

1

Um sismo, também chamado de terremoto, é um fenômeno de vibração brusca e passageira da superfície da Terra, resultante de movimentos subterrâneos de placas rochosas, de atividade vulcânica, ou por deslocamentos (migração) de gases no interior da Terra, principalmente metano. O movimento é causado pela liberação rápida de grandes quantidades de energia sob a forma de ondas sísmicas.

2

Na faixa de 5,0-5,9 um sismo é considerado moderado, podendo causar danos maiores em edifícios mal concebidos em zonas restritas. Provocam danos ligeiros nos edifícios bem construídos, sua freqüência é da ordem de 800 por ano

3

No capítulo 4 – Diagnóstico de adequação do modelo, são mostradas técnicas para verificar e testar o ajuste do modelo.

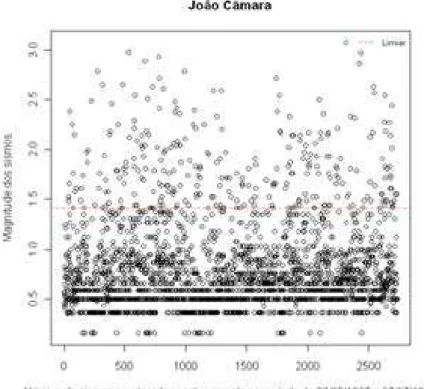
No capítulo 5 – Estudo de caso: João Câmara-RN, apresentamos os principais resultados obtidos pelo ajuste da GPD aos sismos observados de forma continua no município durante o período de 23/05/1987 a 07/07/1988.

No capítulo 6 – Considerações finais, apresentam-se os aspectos que se mostraram mais significativos no decorrer do estudo no que se refere aos resultados obtidos, bem como se incluem algumas sugestões sobre o que poderá ser a continuação iniciada com esse trabalho.

CAPÍTULO 2: A FILOSOFIA DA TEORIA DE VALORES EXTREMOS

A teoria de valores extremos tem como objetivo o estudo estatístico de fenômenos de risco elevado com impactos catastróficos, que surgem em diversos ramos das Ciências tais como a Meteorologia e a Climatologia. Valores extremos podem ser considerados aqueles eventos raros que ocorrem nas caudas das distribuições (fenômenos caudais), isto é, distantes do aglomerado ou da aglomeração (média e mediana) do amontoado da distribuição. Não há, todavia, uma definição que possa ser considerada universal de eventos extremos! Em muitas instâncias, eventos extremos podem ser definidos como aqueles eventos que excedem em magnitude a algum limiar ou patamar ou podem ser definidos como o máximo (ou mínimo) de uma variável aleatória em determinado período.

2.1 A distribuição Generalizada de Valores Extremos (GEV)

Seja X uma variável aleatória, assumindo valores nos reais. A freqüência relativa com que estes valores ocorrem define a distribuição de freqüência ou distribuição de probabilidade de X e é especificada pela função de distribuição acumulada dada por:

(

X x

)

P x

F_x( )= ≤ , F_x(x) é uma função não-decrescente de x, e 0≤F_x(x)≤1 para todo o x.

Em geral, estamos interessados em variáveis aleatórias continuas, para o qual

(

X=x

)

=0

P para todo x, isto é, as probabilidades pontuais são nulas. Neste caso, Fx(.)

é uma função continua e tem uma função inversa x(.), a função quantil de X. Dado

qualquer valor zp, 0<z_p<1, x(zp) é o único valor que satisfaz:

p p

x xz z

F( ( ))=

Para uma probabilidade p, x(p) é o quantil da probabilidade não excedente p, isto é, o valor tal que a probabilidade de X não exceder x(p) é p. O objetivo da análise de freqüência é estimar corretamente os quantis da distribuição de uma variável aleatória.

A abordagem clássica da teoria de valores extremos consiste em caracterizar as caudas (superior ou inferior) da distribuição de F_x a partir da distribuição do

máximo. Assim, definimos Mn=max

(

X1,...,Xn

)

como o máximo de um conjunto de n

variáveis aleatórias independentes e identicamente distribuídas. Para obter-se a distribuição do mínimo usa-se a relação:

(

X,...,Xn

)

max

(

X,...,Xn

)

Na teoria a função de distribuição exata do máximo pode ser obtida para todos os valores de n, da seguinte forma:

(

)

(

)

(

)

[

( )

]

n

x i

n

i n n

M PM x PX x X x PX x F X

F

n= ≤ = ≤ ≤ =∏ ≤ =

=1

1 ,..., ,

para x∈ℜ e n∈N. Todavia, este resultado não é útil na prática, visto que não conhecemos a função de distribuição de F_x. Segundo Coles (2001), uma

possibilidade é utilizar técnicas estatísticas para estimar F_x para dados observados, e

substituir esta estimativa na equação acima. Infelizmente, pequenas discrepâncias na

estimativa de F_x podem conduzir a substancias discrepâncias em

[

F_x

( )

X

]

n.

Uma alternativa é aceitar que F_x seja desconhecida, e olhar para as famílias

aproximadas dos modelos de

[

( )

]

n x X

F , que pode ser estimado com base somente em

dados extremos. Isto é similar a prática usual de aproximar a distribuição da média amostral pela distribuição normal, como justificado pelo teorema central do limite (TCL). Além disso, podemos pensar que o comportamento assintótico de M_n pode

estar relacionado com a cauda de F_x próximo do limite superior do suporte da

distribuição de X, pois os valores do máximo são aqueles que se localizam perto desse limite. Dessa maneira, denotamos por:

( )

{

: 1

}

sup ∈ℜ <

= x F x

xF_X x , o limite superior do suporte da distribuição de Fx.

Observamos que, para todo

x F x x< ,

(

≤

)

=

[

( )

]

n,→0

x

n x PF X

M

P , n→∞,

e, no caso de <∞

x

F

x , temos para x

F

x x> que:

(

M_n≤x

)

=P

[

F_x

( )

X

]

n=1

P ,

logo, à medida que n cresce a distribuição de M_n é degenerada4 sendo, portanto, um

resultado que não fornece muita informação.

Esta dificuldade pode ser sanada considerando-se uma seqüência de constantes

σ

_n >0 e

µ

_n tais que:

n n n n

M M

σ

µ

− =

*

convirja para uma função não-degenerada, para n→∞. O teorema seguinte fornece o

resultado de convergência em distribuição para o máximo centrado e normalizado.

4

Teorema (Fisher – Tippett, 1928): seja

( )

Xn uma seqüência de variáveis

aleatórias independentes e identicamente distribuídas. Se existirem seqüência de constantes normalizadoras

σ

n >0 e

µ

n e uma distribuição não-degenerada H tal que:

H M d n n n ⎯→ ⎯ −

σ

µ

,

onde ⎯⎯→d _{representa convergência em distribuição, então H é do tipo de uma das}

três funções de distribuição: i -Tipo I de Gumbel:

(

)

ℜ ∈  ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ − − −

= x x

x

HI( ) exp exp ,

σ

µ

_;

ii -Tipo II de Fréchet:

,

0

)

(

x

=

H

II se x≤0

(

)

⎪ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ − − = −ξ

σ

µ

x x

HIi( ) exp , se x>0;

iii -Tipo III de Weibull:

(

)

⎪ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ − − − = ξ

σ

µ

x x

HIII( ) exp , se x≤0

H

_III

(

x

)

=

1

,

se x>0.

A prova do teorema de Fisher-Tippett não será apresentada aqui, no entanto, uma demonstração rigorosa desse resultado é apresentada por Gnedenko (1943).

Ainda sob o ponto de vista da modelagem as três distribuições de valores extremos

H

_I

(

x

),

H

_II

(

x

)

e

H

_III

(

x

)

sejam bem diferentes, do ponto de vista

matemático estão bastante relacionadas. Pode-se mostrar que se X>0, então:

) ( ~ ) ( ~ ) ln( ) (

~ H x X H x X 1 H x

X II I III

−

− ⇔

⇔ ξ _.

⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − = − ξ σ µ ξ 1 1 exp )

(x x

H .

Definida no conjunto

(

)

 ⎬ ⎫ ⎩ ⎨ ⎧ > − + 0 1 : σ µ ξ x

x , sendo que os parâmetros satisfazem,

0 , > ∞ < < ∞

−

µ

σ

e −∞<

ξ

<∞, o modelo é tri-paramérico, sendo um parâmetro de localização, um de escala e um de forma, onde o parâmetro

ξ

é quem determina a

forma da distribuição, quando:

ξ

>0 tem-se a distribuição de Fréchet,

ξ

<0 obtem-se a de Weibull. Sendo que o limite de F(x) quando

ξ

→0, a distribuição assume a seguinte forma:

⎥

⎦

⎤

⎢

⎣

⎡



⎬

⎫

⎩

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−

−

−

=

σ

µ

x

x

H

(

)

exp

exp

,

−

∞

<

x

<

∞

,

que representa a função de distribuição da Gumbell, com parâmetros de localização e escala µ e σ, respectivamente, sendo σ>0.

Dessa forma, em vez de se ter que escolher uma família inicialmente, para depois estimar os parâmetros, a inferência se faz diretamente sobre o parâmetro de forma

ξ

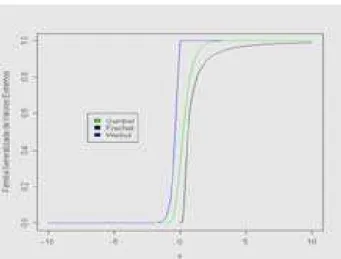
. A Figura 1, onde no apêndice B mostramos a rotina no R para gerar a

mesma, apresenta os gráficos da função de distribuição para

ξ

=−1,5 (Weibull),

ξ

tendendo a zero (Gumbel) e

ξ

=1,5 (Fréchet), com

µ

=0 e

σ

=0,4761.

Para se encontrar a função densidade de probabilidade (f.d.p.) da função generalizada de valores extremos (GEV), deriva-se a função de distribuição da GEV em relação à x, obtendo-se:

⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡  ⎬ ⎫ ⎩ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − + = − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛+ − ξ ξ ξ σ µ ξ σ µ ξ σ 1 1 1 exp 1 1 )

(x x x

h , onde ξ σ µ− < < ∞

− x , para

ξ

<0, que corresponde a densidade da Weibull e

∞ < < − x

ξ

σ

µ

_{, para}

0

>

ξ

, gerando-se a densidade da Fréchet, por fim quando o

limite para

ξ

tendendo a zero, tem-se:

 ⎬ ⎫ ⎩ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − =

σ

µ

σ

µ

σ

x x x

h( ) 1 exp exp exp , definida em

−

∞

<

x

<

∞

Figura 1: Ilustração das três funções de distribuições acumuladas da família de valores extremos generalizados (GEV).

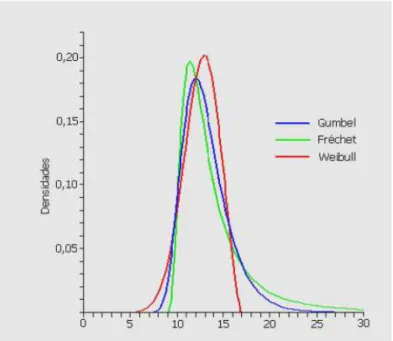
A Figura 2 apresenta os gráficos da função densidade de probabilidade da GEV para

ξ

=−0,4 (Weibull),

ξ

tendendo a zero (Gumbel) e

ξ

=0,4 (Fréchet), com

12

=

µ

e

σ

=2, onde observa-se que o parâmetro

ξ

é quem determina a natureza das caudas da distribuição.

Fazendo-se uso de uma linguagem mais informal, o caso

ξ

>0 é o caso das

“caudas pesada” no qual ξ

1 ~ ) ( 1

−

−H x x ,

ξ

<0 é o caso das “caudas leves”, em que a distribuição tem um ponto final finito (o menor valor de x para o qual H(x) =1) em que

µ

σ

µ

− =

x . Se

ξ

=0, as caudas da distribuição estão entre leves e pesadas, na qual

) (

1−H x decresce exponencialmente para grandes valores de x. Isto mostra que em aplicações as três famílias são bastante diferentes nos extremos.

Quanto às aplicações, a distribuição GEV tem sido utilizada em vários estudos, por exemplo, Hosking e Wallis (1997) utilizou a GEV para análise de freqüências de vazões, por outro lado, Bautista (2002) utilizou a GEV para analisar as velocidades máximas do vento.

2.2 Inferência sobre os Parâmetros da GEV

que as condições de regularidades sejam satisfeitas, ou seja, a função de verossimilhança seja monótona crescente.

Figura 2: Ilustração das funções densidade de probabilidades das três formas da família de valores extremos generalizados (GEV).

Smith (1985) observou que dependendo da estimativa do parâmetro de forma pelo método da máxima verossimilhança, essas condições nem sempre são observadas, uma vez que:

• Se

ξ

>−0,5, os estimadores de máxima verossimilhança são regulares, tendo

suas propriedades assintóticas habituais;

• Se, −1<

ξ

<−0,5 o estimador de máxima verossimilhança é geralmente encontrado, porém as condições de regularidades não são observadas;

• Se,

ξ

<−1não é possível obter os estimadores de máxima verossimilhança.

Hosking et al (1985b), ao utilizar simulações computacionais para estimar os parâmetros da GEV pelo método da máxima verossimilhança através do processo interativo de Newton-Raphson, observaram que poderia existir problemas de convergência, pelo fato das condições de regularidades não serem atendidas. Sendo que esse caso é muito raro, pois só ocorre quando

ξ

<−0,5, que de acordo com Coles (2001), corresponde ao caso onde a cauda superior é muito curta. Hosking et. al. (1985b) também mostraram que ao se trabalhar com dados reais o valor de

) 5 , 0 ; 5 , 0 (− ∈

computacionais por Brabson e Patutikof (2000), onde concluíram que o valor de ) 5 , 0 ; 5 , 0 (− ∈

ξ

, portanto a eficiência das estimativas de máxima verossimilhança dos

parâmetros na prática, não apresenta maiores problemas.

Todavia, além do estimador de máxima verossimilhança, outros métodos têm sido utilizados para estimar os parâmetros da GEV, podemos citar de acordo Hosking et. al. (1985b), por exemplo: método dos momentos, probabilidades ponderadas, método dos momentos L, onde os mesmos mostraram-se mais eficientes que o método da máxima verossimilhança, no que tange ao viés e as variâncias amostrais, em amostras cujos tamanhos variam entre 15 e 100. Porém, conforme Smith (2001), nenhum dos métodos citados permite a generalização como faz o método da máxima verossimilhança, portanto desenvolveremos agora esse método.

Considerando que X1,...,X_n são uma série de realizações aleatórias

independentes, identicamente distribuídas e ordenadas, com função densidade de

probabilidade da GEV, a função de verossimilhança

( )

(

)

_∏

(

)

= = = n i i x h L L 1 ; ,

,

σ

ξ

θ

µ

θ

é

dada por:

( )

(

)

_∏

∑

= = − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − ⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + = = n i n i i ξ i ξ ξ n σ μ x ξ σ μ x ξ σ ξ σ μ L θ L 1 1 1 1 1 exp 1 1 , , ,

que para ξ<0, assume valores diferentes de zero, se todos os valores de _xi

(

i

=

1

,

2

,...,

n

)

forem menores do que

ξ

σ

µ

− , ou seja, se − > xn

ξ

σ

µ

, sendo xn o maior

valor da série de observações, e para ξ >0, se todos os valores de _xi

(

i

=

1

,

2

,...,

n

)

forem maiores que

ξ

σ

µ

− , ou seja, − < x₁

ξ

σ

µ

o menor valor da série de

observações. Caso contrário

L

( )

θ

=

0

.

∑

= − ⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − = n i i ξ i σ μ x ξ σ μ x ξ ξ ξ σ 1 1 1 1 ln 1 ln ,

para − > x_n

ξ

σ

µ

e ξ <0 ou − <x₁

ξ

σ

µ

se ξ >0. Caso contrário o l

(

μ,σ,ξ

)

não

existe! Os estimadores de máxima verossimilhança de μ,

σ

e ξ são obtidos

maximizando o logaritmo da função verossimilhança l

(

μ

,

σ

,

ξ

)

em relação a cada

parâmetro e a raiz obtida, a sua solução. Assim:

(

, ,

)

0

0= ∂ ∂ = ξ σ μ l

μ μ μ ; ∂

(

, ,

)

0=0

∂ = ξ σ μ l

σ σ σ ; ∂

(

, ,

)

0=0

∂ = ξ σ μ l

ξ ξ ξ

ou, seja: 0 1 1 1 ^ 1 ^ ^ ^ = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − +

∑

= − n i ξ i

σ

w

ξ

σ

0 1 1 1 1 ^ ^ ^ 2 ^ ^ = ⎪ ⎪  ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + −

∑

= − n i i ξ i i w w ξ μ x σ σ n

( )

0

ln 1 1 1 ^ ^ ^ ^ ^ ^ 2 1 ^ = ⎪ ⎪  ⎪⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋

∑

= − n i i i i i i ξ i w σ μ x w σ ξ μ x w ξ

w , sendo

⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ − + = _^ ^ 1 σ μ x ξ

wi i .

Como este sistema de equações não possui solução analítica, utilizaram-se procedimentos iterativos para obter as estimativas dos parâmetros de máxima verossimilhança usando a matriz de informação de Fisher, M . A fórmula interativa é,

para j≥0, θ(j )=θ( )j +M_⎝⎜⎛θ⎟_⎠⎞ grad l

( )

θj

−

+ ^

1

1 _onde

(

)

ξ

σ

μ

θ

= , , com:

( )

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂ − ∂ ∂ − = − ξ l σ l μ l θ l

grad , , e

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ξ l E μ ξ l E σ ξ l E μ ξ l E μ l E σ μ l E σ ξ l E σ μ l E σ l E θ M 2 2 2 2 2 2 2 2 2 2 2 2 ^ ,

onde os elementos de M podem ser expressos em termos da função gama:

( )

r _e x _xr 1dx

como:

(

)

[

ξ p

]

ξ σ

n

σ

l

E _⎟⎟= − − +

⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂

− ₂ 1 2Γ 2

2 2 2

(

)

[

p ξ

]

ξ σ n μ σ l

E _⎟⎟= − −

⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂

− Γ 2

2 2

(

)

{

}

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ξ p q ξ ξ γ ξ σ n ξ σ l

E ₂ 1 1 Γ 2

2 p σ n μ l E 2 2 2 = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ξ p q σξ n ξ μ l E 2 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − ξ p ξ q ξ γ π ξ n ξ l E ₂ 2 2 2

2 _{1 2}

1

2

6 ,

sendo p=

₍

1−ξ

_{) (}

2Γ1−2ξ

)

,

(

) (

) (

)

 ⎬ ⎫ ⎩ ⎨ ⎧ − − − − = ξ ξ ξ ψ ξ

q Γ 2 1 1 e γ=0.5772157 a

constante de Eüler.

No procedimento iterativo, fixa-se um valor inicial arbitrário ξ₀ para ξ, e

sugerem-se como valores iniciais μ₀ e σ0 para μ e σ, valores tais que E

( )

X =X e

( )

X s

Var ₌ 2_{, sendo X a média e}

s

2 a variância da série de observações (amostrais).

Considerando-se a função densidade de probabilidade, obtém-se:

( )

= +

[

Γ

(

1−ξ

)

−1

]

ξ σ μ

X

E , se ξ<1,

e

( )

[

(

ξ

)

(

ξ

)

]

ξ σ

X

Var = Γ1−2 −Γ2 1−

2 2 , se 2 1 < ξ ,

sendo as seguintes expressões para os valores iniciais:

(

ξ

)

(

ξ

)

ξ s σ 0 2 0 2 0 0 1 Γ 2 1

Γ − − −

=

(

)

_[

₍

₎

_]

(

ξ

)

(

ξ

)

Jenkinson (1955) sugeriu que se devia usar a matriz informação de Fisher para amostras completas, entretanto para amostras censuradas estas esperanças não existem no sentido usual, e foi observado num número de estudos simulados, que a

convergência para θ é consideravelmente mais rápida, usando a matriz ⎟ ⎠ ⎞ ⎜ ⎝ ⎛^ θ

V ao

invés da matriz ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ^ θ

M . Assim é usual aproximar a matriz ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ^ θ

M por esta nova

matriz ⎟ ⎠ ⎞ ⎜ ⎝ ⎛^ θ

V , descrita por:

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ξ l μ ξ l σ ξ l μ ξ l μ l σ μ l σ ξ l σ μ l σ l θ V 2 2 2 2 2 2 2 2 2 2 2 2 ^ .

Com esta nova matriz, o cálculo iterativo de θ, envolve rapidez computacional e

converge para

grad

l

<

10

−3 em menos de 5 iterações.

Para o caso particular da distribuição generalizada de valores extremos com

0

→

ξ , temos a distribuição Gumbel, o logaritmo da função verossimilhança é dado

por:

(

)

∑

=  ⎬ ⎫ ⎩ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − = n i i i σ μ x σ μ x σ σ μ l 1 exp ln

, , e os estimadores de máxima

verossimilhança de μ e σ são obtidos pela solução de:

(

,

)

0

0= ∂ ∂ = σ μ l

μ μ μ ; _∂

(

,

)

0=0

∂

=

σ μ

l

σ σ σ ,

ou seja 0 exp 1 1 ^ ^ ^ = ⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ − − −

∑

= n σ μ x σ n i i _, 0 exp 1 1 ^ ^ ^ ^ ^ ^ ^ = ⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ − ⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ − − ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ − − ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ − −

∑

= n σ μ x σ μ x σ μ x σ n i i i i _.

Mais uma vez, este sistema não possui solução analítica e deve-se usar o mesmo método iterativo descrito a cima para a obtenção da solução numérica, tomando como valores iniciais μ₀ e σ0 para μ e σ a soluções obtidas através do

( )

X

μ γσ

E

=

+

,

( )

6 2 2

σ π

X

Var = ,

com γ=0.5772157 a constante de Eüler, logo s x

s

π γ

x

μ₀= − 6 ≅ −0.45005 , s s

π

σ0= 6 ≅0.77970 ,

que correspondem aos limites quando ξ₀

→

0

.

2.2.1 Estimação dos Quantis Extremos da GEV

Após terem sido estimados os parâmetros da GEV, será possível obter a estimação de quantis (z_p) as probabilidades (p), pois os mesmos dependem desses

parâmetros, para isso basta inverter a função de distribuição de valores extremos, onde os quantis são dados da seguinte forma:

(

)

{

}

[

ξ

]

ξ

σ

µ

− − − − −

= p

z_p 1 log1 , se

ξ

≠0

(

)

{

p

}

z_p =

µ

−

σ

log −log1− , se

ξ

=0,

onde: F

( )

zp =1− p. Sendo que zp, corresponde ao nível de retorno associado ao

período de retorno

p 1

.

Coles (2001), define yp =−log

(

1−p

)

, e na expressão dos quantis, tem-se:

[

ξ

]

ξ

σ

µ

− − −

= p

p y

z 1 , se

ξ

≠0

p

p y

z =

µ

−

σ

log , se

ξ

=0.

Isso permite gerar um gráfico em escala logarítmica, onde no eixo das abscissas representa-se yp e no das ordenadas zpou equivalentemente, o gráfico pode ser

gerado com logyp contra zp, onde o mesmo relaciona a freqüência de eventos

extremos, conforme o sinal do parâmetro de forma.

2.3 A Distribuição Generalizada de Pareto (GPD)

Suponha X₁,....,X_n variáveis aleatórias independentes e identicamente

distribuídas, tendo função de distribuição

F

_X. Seja

x F

x o limite superior da distribuição

de

F

_X. Chamamos de um limiar alto um valor no suporte de X perto de

Denominamos “excedentes” aqueles valores X_i tais que X_i >u. Denotamos por N_u

o número de excedentes do limiar u. Isto é,

∑

= >

=

n

i

u X

u _i

N 1

) (

1 , onde: 1(Xi>u) =1 se Xi >u,

1(X_i>u) = 0 caso contrário.

Os excessos (pontos excedentes) além do limiar u, denotados por Y1,....,Ynu são

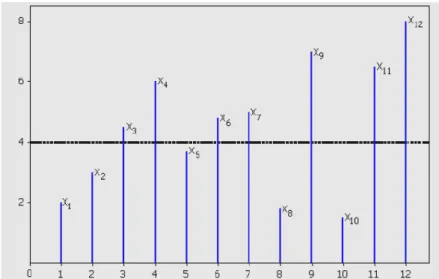
os valores X_i −u≥0. A Figura 3 mostra as observações

X

₁

,....,

X

₁₂ e os excessos além do limiar u=4.

Esta abordagem se diferencia da abordagem clássica, pois a teoria clássica se baseia na análise do valor do máximo (ou mínimo) em uma época. Como será visto na definição que se segue, essa abordagem permite a análise de todos os dados disponíveis que excedem um limiar, porém esse limiar deverá garantir a distribuição assintótica de valores extremos, sem as quais não será possível fazer as inferências.

Definição: Dado um limiar u, a distribuição dos valores de x acima de u é dada

por:

{

}

(

)

( )

, 0

1 1

| >

− + − = > +

> y

u F

y u F u

X y u X

P , (1)

que representa a probabilidade do valor de x ultrapassa u por no máximo um montante

y, onde y=x-u.

Seja F uma distribuição generalizada de valor extremo, tal que:

( )

⎪  ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − = − σ μ x ξ x F ξ 1 exp 1

para qualquer μ,σ>0 e ξ∈ℜ. Então a

probabilidade condicional, quando X >u, sabendo-se que

( )

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − ≈ − σ μ x ξ x F

nln 1 ξ

1

, e que para valores elevados de

x

se deve fazer uma

expansão à Taylor de forma que

ln

F

( )

x

≈

−

{

1

−

F

( )

x

}

, substituindo e re-arranjando

para

u

, tem-se

( )

_⎥

⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ≈ − − σ μ u ξ n u

F 1 1 ξ

1

1

e de uma forma similar para y >0,

(

)

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − + ≈ + − − σ μ y u ξ n y u

F 1 1 ξ

1

1

.

Desta forma, tem-se:

{

}

(

)

( )

⎟

_⎠

⎞

⎜

⎝

⎛

+ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − + = − + − = > + > − − − ~ 1 1 1 1 1 1 1 1 1 1 | σ y ξ σ μ u ξ n σ μ y u ξ n u F y u F u X y u X P ξ ξ ξ ,

com σ~ =σ+ξ

(

u−μ

)

.

Assim, a função distribuição de

(

X

−

μ

)

, condicionada a X >u, é aproximadamente:

( )

⎟

⎠

⎞

⎜

⎝

⎛

+ − = − ~ 1 1 1 σ y ξ y H ξ , definida em  ⎬ ⎫ ⎩ ⎨ ⎧ > ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +

>0 1 0

: ~ σ y ξ e y

y , onde σ=σ+ξ

(

u−μ

)

~

.

Coles (2001) afirma que a família de distribuições definida acima é chamada família generalizada de Pareto. A função distribuição condicional é aproximadamente a distribuição generalizada de Pareto (GPD), que representa as três distribuições em

uma só forma, sob a γ-parametrização: _W(x;γ)=₁−

(

₁+_γx

)

−1γ. Assim como as

Haan). As distribuições generalizadas de Pareto são da forma Exponencial (γ=0),

Pareto tipo II (γ>0) e Pareto comum ou Beta (γ<0).

Os parâmetros da distribuição generalizada de Pareto para excessos que ultrapassam limiares (Peaks-over-Threshold - POT) são determinados por aqueles

associados às distribuições generalizadas de valores extremos (GEV). No limite de

( )

x

F

quando ξ→0 tem-se a distribuição acumulada de Gumbel:

( )

_⎥

⎦ ⎤ ⎢

⎣ ⎡

⎟ ⎠ ⎞ ⎜

⎝

⎛ −

− − =

σ μ

x x

F exp exp , e a função distribuição de

(

X

−

μ

)

, condicional com

u

X > , é aproximadamente:

( )

⎟

⎠ ⎞ ⎜ ⎝ ⎛

− − =

σ

y y

H 1 exp , com y>0.

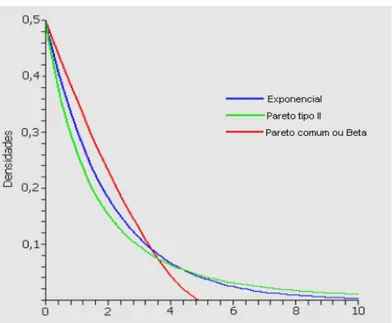
A Figura 4, onde a rotina para mostrar a ilustração encontra-se no apêndice B,, apresenta os gráficos da função de distribuição da GPD para

ξ

=−0,4 (Pareto comum ou Beta),

ξ

tendendo a zero (exponencial) e

ξ

=0,4 (Pareto tipo II), todas com

2

=

σ

, observa-se que assim como na GEV o parâmetro

ξ

é quem determina as caudas da distribuição.

Por fim, as distribuições GPD e GEV estão relacionadas da seguinte maneira:

(

(

)

)

ln

1

)

(

x

H

x

G

=

+

,

ln

(

H

(

x

)

)

>

−

1

.

Figura 4: Ilustração da função densidade de probabilidade das três formas da distribuição generalizada de Pareto (GPD).

Figura 5: Densidades da GPD e GEV. (a) Pareto comum (Beta) e Weibull, ambas com

0,2

2.3.1 Seleção do Limiar

Na escolha do limiar u nos deparamos com alguns problemas, pois um valor

para u muito “alto” implicará em um número pequeno de observações na cauda,

podendo resultar numa maior variabilidade dos estimadores. Porém, um limiar que não seja suficientemente alto não satisfaz as suposições teóricas e pode resultar em estimativas distorcidas, portanto uma idéia é monitorar os valores extremos como será descrito.

Para a determinação do limiar recorre-se à análise gráfica da linearidade de _nu

observações que excedem os vários limiares

u

determinados na própria amostra. Assim, o gráfico de vida média residual, usado para a determinação visual de u é

construído da seguinte forma:

₍

₎

 ⎬ ⎫ ⎩ ⎨ ⎧ < ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ −

∑

= x u u x n u n i i u u max 1 : 1

, , em que x1,x2,...,xnu

consistem nas observações que excedem

u

e xmax é o valor mais elevado das

observações.

Na prática dois métodos são avaliados para esse propósito: uma técnica exploratória e a outra é avaliar a estabilidade dos parâmetros estimados, baseado no ajuste de uma gama de limiares de acordo com o gráfico descrito acima.

Conforme Coles (2001), o primeiro método é baseado na média da distribuição da GPD. Se Y seguir uma distribuição generalizada de Pareto com parâmetros de escala e forma,

σ

,

ξ

, respectivamente, então:

ξ

σ

− = 1 ) (y

E , desde que

ξ

<1, uma vez que se

ξ

≥1a esperança será infinita; e

( )

ξ σ Y Var 2 1 2 −

= , com

2 1

<

ξ .

Seja _u0 o limiar mais baixo de uma série X1,X2,...,Xn arbitrária, então

( )

(

)

ξ σ u X u X E Y E u − = > − = 1 | 0 0

0 com ξ <1, em que σu0 é o parâmetro de escala

correspondente aos excessos do limiar _u0. Mas se a distribuição de Pareto é válida

para os excessos de _u0, também é igualmente válido para os excessos de limiares

u

u> 0, sujeitos a apropriada variação no parâmetro escala para

σ

u. Então, para:

u

u> 0,

(

)

ξ u ξ σ ξ σ u X u X

E u u

− + = − = > − 1 1

| 0 .

Segundo Coles (2001), a GPD é um modelo razoável para os excessos acima do limiar _u0, assim como para um limiar mais elevado u. Os parâmetros de forma das

limiar u >_u0 é σu=σu₀+ξ

(

u−u0

)

, que varia com u a menos que ξ =0. Esta

dificuldade pode ser remediada pela re-parametrização do parâmetro de escala como:

u

ξ σ

σ = u−

* _e

(

)

ξ

x

σu = 1− , com

x

a média dos excessos para de cada limiar

u

, e ξ

determinado da média e do desvio padrão dos excessos de cada limiar

u

, e

conseqüentemente as estimativas de ambos σ* e ξ serão constantes acima de _u0,

se u0 é um limiar valido para os excessos que seguem uma GPD. Assim, são

representados os gráficos de σ*e ξ versus

u

, juntamente com os intervalos de

confiança que são obtidos pela matriz variância e covariância V para ξ e para σ*

pelo método Delta, usando:

( )

σ _σ V σ

Var * *T _∇ *

∇

≈ , com

[

u

]

ξ σ σ σ σ

u T

− =

⎥ ⎦ ⎤ ⎢

⎣ ⎡

∂ ∂ ∂ ∂ =

∇ , 1,

* *

* .

2.4 Inferência sobre os Parâmetros da GPD

A estimação dos parâmetros da GPD pode ser feitos por vários métodos, entre eles, tem-se o da máxima verossimilhança, Davison (1984), Hosking e Wallis (1987), método dos momentos, método da máxima entropia (POME) e o método dos momentos ponderados, Singh e Guo (1995), onde a eficiência de cada método depende da situação estudada, estes métodos serão detalhados no capítulo 3, sendo dada nesse capítulo somente uma abordagem baseada numa importante propriedade da GPD.

Lin (2001) mostra que uma importante propriedade da distribuição generalizada de Pareto, ocorre quando

ξ

>−1, onde a média de excessos, ao longo de um limiar,

u, é uma função linear de u:

(

)

ξ

ξ

σ

+

−

=

>

−

1

/

X

u

u

u

X

E

, portanto o gráfico da linearidade da média de

excessos, poderá ser utilizado como um indicador da adequação do modelo da GPD. Essa propriedade permite estimar os parâmetros de forma e escala da distribuição generalizada de Pareto, da seguinte forma:

( )

(

)

{ }

∑

∑

= > = +

−

=

_n i u x n i i n í

u

X

u

e

1 1

1

, no que diz respeito ao limiar u, onde o + garante que apenas

os valores positivos de

(

Xi −u

)

serão contados. Ou seja, a MEA é a soma dos

excessos durante o limiar u, dividido pelo numero de pontos dos dados que excede ao

limiar u. Dessa forma a média de excessos da amostra é o estimador empírico da

média de excessos de um limiar (MEL), portanto,

ξ

e

σ

da GPD, podem ser

determinado pela inclinação e o intercepto da MEA utilizando as seguintes equações:

Inclinação=

ξ

ξ

+ − 1 e Intercepto=

ξ

σ

+ 1 .

2.5 Relação entre a Distribuição q-Exponencial e a GPD

Shalizi (2007), ao estudar o estimador de máxima verossimilhança da distribuição q-Exponencial, também conhecida como distribuição de T-salis, essa distribuição é definida através do complementar da função de distribuição, sendo mais conhecida como a função de sobrevivência, onde a mesma possui a seguinte forma:

(

)

q

q k k x q x X

P ⎟−

⎠ ⎞ ⎜ ⎝ ⎛ − − = ≥ 1 1 , 1 1 ) ( .

Essa reparametrização ajuda a simplificar a estimação dos parâmetros e fazer uma ligação com a distribuição de Pareto, para encontrar o estimador de máxima verossimilhança para a distribuição q-exponencial, portanto é mais fácil utilizar a reparametrização e no final retornar ao sistema inicial, caso seja desejado.

Shalizi (2007), define a nova reparametrização, da seguinte forma

q − − = 1 1

θ

e

k *

θ

σ

= , para recuperar os parâmetros iniciais basta fazer:

θ

1 1+ =

q e

θ

σ

=

k , logo

a função de sobrevivência, em relação aos novos parâmetros, é:

θ σ θ

σ

− ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + =

≥x x

X

P_, ( ) 1 , para se encontrar a função densidade de probabilidade,

1

, ( ) 1

− − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

+ =

θ

σ θ

σ

σ

θ

x

x

P , onde a mesma possui uma distribuição de Pareto com

parâmetro de forma

α

e ponto de corte y₀.

se P(y)=0, quando y< y0,

1

0 ) (

− − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

∝

α

y y y

P .

Assim X tem uma distribuição q-exponencial e

σ

x

+

1 , tem uma distribuição de

Pareto com ponto de corte igual a 1 e parâmetro de forma

θ

, resultando em uma distribuição de Pareto do tipo II, sendo sua forma padrão:

(

)

α

σ θ

σ

µ

−

⎟ ⎠ ⎞ ⎜

⎝

⎛ −

+

= x

x P_, ( ) 1

que é uma distribuição q-Exponencial quando

µ

=0 e

σ

=

θ

.

Neste capítulo foi vista a filosofia da teoria de valores extremos, através de uma revisão de literatura da GEV, bem como sobre as inferências a respeito dos seus parâmetros, dando maior ênfase ao estimador de máxima verossimilhança, uma vez, que de acordo com a revisão de literatura feita é o que tem mostrado melhor desempenho para estimar os parâmetros da GEV, em seguida foi feita uma revisão de literatura também para a GPD e mostrando a importante relação entre GEV e GPD, bem como a seleção do seu limiar e para encerrar foi vista uma relação importante entre a distribuição q-exponencial e a GPD, sendo gerada a partir de uma reparametrização na Pareto tipo II, esse artifício facilita bastante para encontrar o estimador de máxima veossimilhança da GPD quando o parâmetro de forma for positivo.

Dessa forma, têm-se duas maneiras de se modelar o máximo de uma seqüência de variáveis aleatórias independentes e identicamente distribuídas:

1. Máximo em Bloco, onde se seleciona o máximo de cada período, porém nessa abordagem corre-se o risco de deixarmos alguns máximos de fora, dessa forma comprometendo as estimativas bem como previsões/predições;

2. Observações acima de um limiar u, nesse tipo de modelagem busca-se

na escolha do mesmo, para não violar a convergência assintótica e nem ficar com poucas observações acima do limiar selecionado.

CAPÍTULO 3: ALGUNS MÉTODOS DE ESTIMAÇÃO DOS PARÂMETROS DA DISTRIBUIÇÃO GENERALIZADA DE PARETO (GPD)

Vários métodos de estimação dos parâmetros da GPD já foram propostos, sendo que nos últimos anos o método da máxima entropia (POME) tem sido bastante utilizado por vários autores, em geral Sing e Guo (1995), Oztekin (2004), onde o POME sempre que comparado com outros métodos, obteve menor erro quadrático médio. Por essa razão nas próximas secções, serão mostrados todos os métodos utilizados no presente estudo, sendo que o da máxima entropia será desenvolvido de forma integral.

3.1 Método da Máxima Verossimilhança (MLE)

Para se encontrar o estimador de máxima verossimilhança, precisamos encontrar o log da função de verossimilhança, que de acordo com Oztekim (2004) é:

(

)

∑

= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + − = n i i

i n x

x L 1 1 1 ln ) , , , ( µ σ ξ ξ ξ σ µ σ

ξ , onde os xi são valores observados na

amostra e n o tamanho da amostra, o método se baseia na maximização dos parâmetros da equação acima.

Para a maximização, Rheinboldt (1998), utilizou o método direto ou de Newton-Rapson, para isso ele resolveu as equação parciais em relação a cada parâmetro desconhecido, onde as derivadas parciais em relação ao parâmetro de forma são dadas a seguir:

( ) ( ) ( ) ( ) ( ₍ ) ₎ . 0 1 1 , 0 1 1 1 ln 1 2 1 2 1 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − − − = ∂ ∂ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = ∂ ∂

∑

∑

∑

= = = ξ σ µ ξ σ µ ξ ξ σ ξ ξ σ µ ξ σ µ ξ ξ σ µ ξ ξ n i i i n i i i n i i x x n L x x x L

Sendo que Singh e Guo (1995) mostraram que o log da função de verossimilhança é viesado em relação ao parâmetro de localização µ, dessa forma não

é possível encontrar o estimador de máxima verossimilhança para o parâmetro de localização. Para tanto será escolhido o menor valor da amostra para estimar o parâmetro de localização.

3.2 Método da Máxima Verossimilhança Penalizada (MPLE)

Apesar do método da máxima verossimilhança ser um dos mais eficientes, ele apresenta sérios problemas em relação às especificidades dos modelos de sismos, uma vez que a severidade apresenta eventos extremos. Assim, existe um maior interesse na cauda da distribuição subjacente, sendo que o método da máxima verossimilhança pondera cada valor da distribuição igualmente, por outro lado esse efeito da ponderação igualitária é resolvido por intermédio do método da máxima verossimilhança penalizada.

Coles e Dixon (1999), sugerem para o estimador de máxima verossimilhança penalizada usar a seguinte a função:

f(x)=1se xi ≤0

=

⎟ ⎟ ⎠ ⎞ ⎜

⎜ ⎝ ⎛

⎥ ⎦ ⎤ ⎢

⎣ ⎡

− − −

λ

α 1

1 1 exp

i x

, se 0≤xi ≤1

= 0 se xi ≥1,

onde

α

e

λ

, são as constantes penalizadas. Coles e Dixon (1999) sugerem ainda que

α

=

λ

=1.

3.3 Método dos Momentos (MOM)

As características das distribuições de probabilidades podem ser sumarizadas pelos momentos populacionais. O momento de primeira ordem, em relação à origem dos X, representa a média populacional

( )

µ , e o momento central de ordem r=2 é, por

definição, a variância

_{( )}

_σ2 de _X. As quantidades que podem ser deduzidas do

momento central de ordem 2 são o desvio-padrão

( )

σ e o coeficiente de variação

(CV). Para r>2, é usual descrever as características da função de distribuição através

das razões adimensionais µ_r e 2 2

r

−

µ , das quais se destacam os coeficientes de

assimetria (C_s) e de curtose (k), dados por:

2 3 2 3

−

=µ µ

s

C e 2

2 4

−

=µ µ

k .

Os momentos amostrais são estimados por quantidades similares, calculadas a partir dos dados de uma amostra de tamanho n. Por exemplo, o estimador natural de

origem, n x n i i ∑

= =1

-x , os momentos amostrais (m) de ordem (r) superior são estimadores viesados dos momentos populacionais de mesma ordem, entretanto podem ser corrigidos para produzir estimadores sem viés, por exemplo, para variância e assimetria, respectivamente:

(

)(

)

3 3 2 2 2 2 1 , 1 s m n n n C m n n S s − − = − =

Portanto, de acordo com Hosking e Wallis (1987) os estimadores da distribuição generalizada de Pareto pelo método dos momentos (MOM), são:

(

)

[

(

)(

)

]

(

)(

)

(

ξ

)

ξ ξ ξ σ ξ σ µ 3 1 1 1 2 , 2 1 2 1 , 1 2 2 2 + − − = + + = + + = − s C S x

onde 2

,S x

−

e C_s, são a media a variância e a assimetria, respectivamente

3.4 Método de Pickands (Pickands)

Os métodos de estimação do parâmetro de forma da distribuição generalizada de Pareto têm encontrados alguns problemas no que tange ao viés e a variância, com o intuito de amenizar esses problemas, Pickands (1975) propôs um estimador baseado em estatísticas robustas para o parâmetro de forma da GPD como pode ser visto a seguir:

Seja X_1,n,...,X_n,n, estatísticas de ordem para uma amostra independente de

tamanho n e função de distribuição da GPD. O estimador de Pickands é:

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = + − + − + − + − n k n n k n n k n n k n X X X X , 1 4 , 1 2 , 1 2 , 1 log 2 log 1

ξ , para

4 ,...,

1 n

k=

onde Dekkers e Haan (1989), verificaram a consistência e a normalidade assintótica do estimador.

3.5 Método do Momento Ponderado pelas Probabilidades: viesado e não-viesado (PWMB, PWMU)

Para o PWMB, PWMU aproximados, Dupuis e Tsao (1998), propõem a utilização de estimadores híbridos, uma vez que o mesmo evita o fato de não possuir pontos viáveis.

3.6 Divergência Média da Densidade (MDPD)

A estimação do parâmetro da distribuição generalizada de Pareto pelo MDPD foi proposta por Júarez e Schucany (2004), onde os mesmos recomendam para o parâmetro de forma da distribuição generalizada de Pareto (GPD) o valor de 0,1, nesse mesmo trabalho são recomendados valores pequenos para o parâmetro de

forma. Para um α>0 o estimador para a GPD é o valor _⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ^ ^ , α α σ

ξ , que minimizam a

equação abaixo:

(

)

α ξ α α α α ξ σ α ξα α σ σ ξ ) 1 ( 1 1 1 1 1 1 1 1 1 ) , ( − = − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − +

=

∑

i

n i X n H , sobre

(

)

{ }



⎬

⎫

⎩

⎨

⎧

+

<

<

<

<

−∞

<

>

Θ

∈

≤ ≤

α

α

ξ

ξ

σ

ξ

σ

σ

ξ

,

:

0

,

max

,

0

,

,

0

1

1 i n

X

i

e

A restrição

{ }

ξ

<

σ

≤ ≤i n Xi 1

max , deve-se à dependência do suporte dos parâmetros. A

restrição

α

α

ξ

<1+ é necessária para as condições de regularidades da integral da GPD.

3.7 Método da Mediana (MED)

Welsh e Peng (2001), no artigo “Robust Estimation of the Generalized Pareto Distribution”, utiliza o mesmo princípio que He e Fung (1999), quando eles propuseram

o método da mediana para a distribuição de Weibull com dois parâmetros, sendo os mesmos da seguinte forma:

) ( 1

2 − Mediana Xi = _ξ

ξ

σ

,

onde X_i, são os valores observados da variável aleatória.

(

)

(

)

( )

₂

1

1 1 log , 1 0

2

=

∫

⎪ ⎪ ⎬ ⎫ ⎪⎩

⎪ ⎨ ⎧

> − + − − <

< ξ

ξ ξ ξ

ξ

z y y

y

dy

.

3.8 Método da Melhor Qualidade do Ajuste (MGF)

Para o estimador MGF, Luceño (2005), propõem o seguinte algoritmo para estimar os parâmetros de forma e escala,

ξ

e

σ

da distribuição generalizada de

Pareto. São os seguintes passos no delineamento do pseudo-algoritmo:

(1) Calcule

∑

⎥

⎦

⎤

⎢

⎣

⎡

−

−

−

=

)

,...,

max(

1

ln

1

1

1 ~

n i

x

x

x

n

ξ

e

2 1

2

2 1

− =

∑

− =

x n x

z

n

i i

;

(2) se 0,75 ~

<

ξ

e Z<0,2, calcule os MLEs padronizados para

ξ

e

σ

;

(3) caso contrário estime

ξ

usando a equação do

ξ

~ e max( ₁,..., ₂) ~

~

x x

ξ

σ

= .

Segundo Luceño (2005), a justificativa para esse procedimento é que quando

ξ

é grande, a amplitude da GPD é

ξ

σ

≤ ≤ x

0 e o método da máxima verossimilhança

falha. Portanto para

ξ

uma alternativa é utilizar _~ max( ₁,..., ) ~

n x x

=

ξ

σ

_.

3.9 Método da Máxima Entropia (POME)