DEPARTAMENTO DE ENGENHARIA MEC ˆANICA
PROGRAMA DE P ´OS-GRADUAC¸ ˜AO EM ENGENHARIA MEC ˆANICA
SIMULAC¸ ˜AO DAS TEMPERATURAS DI ´ARIAS NA CIDADE DE NATAL-RN
DORGIVAL ALBERTINO DA SILVA J ´UNIOR
SIMULAC¸ ˜AO DAS TEMPERATURAS DI ´ARIAS NA CIDADE DE NATAL-RN
Disserta¸c˜ao de Mestrado apresentada ao Programa de P´os-Gradua¸c˜ao em Engenharia Mecˆanica da Universi-dade Federal do Rio Grande do Norte como requisito parcial para a obten¸c˜ao do t´ıtulo de Mestre em Engenharia Mecˆanica.
Orientador: Prof. Dr. Jos´e Ubiragi de Lima Mendes
SIMULAC¸ ˜AO DAS TEMPERATURAS DI ´ARIAS NA CIDADE DE NATAL-RN
Disserta¸c˜ao apresentada e aprovada em de de , pela banca examinadora composta pelos seguintes membros:
Prof. Dr. Jos´e Ubiragi de Lima Mendes Orientador
Prof. Dr. Carlos Magno de Lima Examinador Interno
Prof. Dr. Roberto Silva de Souza Examinador Externo
E ao meu anjo da guarda
`
A Deus, que me concede paz e felicidade. `
A minha fam´ılia, que me d´a suporte.
Aos meus bons amigos, que me orientam nas minhas escolhas.
Aos meus professores, que me ajudaram na minha forma¸c˜ao acadˆemica, pela amizade e apoio.
A recupera¸c˜ao de informa¸c˜oes ´e de extrema importˆancia em todas as ´areas do conhecimento. Em rela¸c˜ao as temperaturas da cidade de Natal, elas foram simuladas e analisadas. Desta forma, foi poss´ıvel recuperar, com certa precis˜ao, as tempera-turas de dias em que elas n˜ao foram coletadas. Para isso, construiu-se um software que indica o valor da temperatura em cada instante na cidade. O programa foi desenvolvido em linguagem Delphi com a utiliza¸c˜ao de fun¸c˜oes interpoladas poli-nomiais de terceiro grau. As equa¸c˜oes foram obtidas no Excel cujos dados foram coletados no Instituto Nacional de Pesquisas Espaciais(INPE). Essas fun¸c˜oes foram modificadas a partir de um fator de corre¸c˜ao de modo a fornecerem os valores de tem-peraturas entre aqueles que n˜ao foram coletados. De posse desse programa pode-se construir tabelas e gr´aficos para analisar as temperaturas em determinados per´ıodos de tempo. A mesma an´alise foi feita desenvolvendo matematicamente as fun¸c˜oes que descrevem as temperaturas. Com os dados fornecidos por esse software foi poss´ıvel afirmar quais s˜ao os hor´arios de maiores e menores temperaturas na cidade, assim como os meses que possuem os ´ındices com as maiores e menores temperaturas.
Information retrieval is of paramount importance in all areas of knowledge. Regarding the temperatures of Natal, they were simulated and analyzed. Thus, it was possible to recover, with some accuracy, the temperatures of days they were not collected. For this we constructed a software that displays the temperature value at each moment in the city. The program was developed in Delphi using interpo-lated polynomial function of third degree. The equations were obtained in Excel and data were collected at the Instituto Nacional de Pesquisas Espaciais (INPE). These functions were changed from a correction factor in order to provide values to temperatures between those who were not collected. Armed with this program you can build tables and charts to analyze the temperatures for certain periods of time. The same analysis was done by developing mathematical functions that describes the temperatures. With the data provided by this software is possible to say which are the hours of highest and lowest temperatures in the city, as the months have indexes with the highest and lowest temperatures.
Introdu¸c˜ao 2
Objetivos 5
1 Revis˜ao Bibliogr´afica 6
1.1 Recupera¸c˜ao de Informa¸c˜ao . . . 7
1.2 M´etodos Estat´ısticos . . . 8
1.3 Interpola¸c˜ao . . . 10
1.4 M´etodo de Resolu¸c˜ao de Sistemas Lineares . . . 14
2 Metodologia 20 2.1 Obten¸c˜ao dos dados . . . 21
2.2 An´alise dos dados . . . 23
2.3 Equa¸c˜oes pelo Excel . . . 26
2.4 Fator de Corre¸c˜ao . . . 33
2.5 Equa¸c˜oes pelo M´etodo Num´erico . . . 36
3 Resultados e Discuss˜oes 42
4 Conclus˜oes 82
Bibliografia 84
1 Evolu¸c˜ao da esperan¸ca de vida ao nascer. . . 3
2.1 Site do INPE . . . 21
2.2 Dados do INPE . . . 22
2.3 Sistema de Busca de Temperaturas . . . 26
2.4 Gr´afico das temperaturas as 5 horas . . . 27
2.5 Gr´afico das temperaturas as 8 horas . . . 28
2.6 Gr´afico das temperaturas as 11 horas . . . 29
2.7 Gr´aficos das temperatura as 14 horas . . . 30
2.8 Gr´afico das temperaturas as 17 horas . . . 31
2.9 Fator de corre¸c˜ao . . . 33
2.10 Fluxograma do m´etodo num´erico . . . 36
3.1 Dia 6 de Janeiro . . . 44
3.2 Dia 5 de Novembro . . . 46
3.3 Dia 15 de Junho . . . 48
3.4 Dia 15 de Julho . . . 50
3.5 Dia 10 de Janeiro . . . 52
3.6 Dia 20 de Dezembro . . . 54
3.7 Gr´afico de trˆes dias do mˆes de Janeiro . . . 56
3.8 Gr´afico de trˆes dias do mˆes de Fevereiro . . . 58
3.9 Gr´afico de trˆes dias do mˆes de Mar¸co . . . 60
3.10 Gr´afico de trˆes dias do mˆes de Abril . . . 62
3.11 Gr´afico de trˆes dias do mˆes de Maio . . . 64
3.12 Gr´afico de trˆes dias do mˆes de Junho . . . 66
3.13 Gr´afico de trˆes dias do mˆes de Julho . . . 68
3.14 Gr´afico de trˆes dias do mˆes de Agosto . . . 70
3.15 Gr´afico de trˆes dias do mˆes de Setembro . . . 72
3.16 Gr´afico de trˆes dias do mˆes de Outubro . . . 74
3.17 Gr´afico de trˆes dias do mˆes de Novembro . . . 76
3.18 Gr´afico de trˆes dias do mˆes de Dezembro . . . 78
3.19 Dia 16 de Janeiro . . . 80
3.20 Dia 7 de Fevereiro . . . 81
1.1 Pontos de um sistema . . . 12
2.1 5 horas de Janeiro . . . 23
2.2 Constantes . . . 35
2.3 Pontos de um sistema . . . 37
3.1 Dia 6 de Janeiro . . . 45
3.2 Dia 5 de Novembro . . . 47
3.3 Dia 15 de Junho . . . 49
3.4 Dia 15 de Julho . . . 51
3.5 Dia 10 de Janeiro . . . 53
3.6 Dia 20 de Dezembro . . . 55
3.7 Dados de Janeiro . . . 57
3.8 Temperaturas extremas de Janeiro . . . 57
3.9 Horas em que as temperaturas foram acima da m´edia . . . 57
3.10 Dados de Fevereiro . . . 59
3.11 Temperaturas extremas de Fevereiro . . . 59
3.12 Horas em que as temperaturas foram acima da m´edia . . . 59
3.13 Dados de Mar¸co . . . 61
3.14 Temperaturas extremas de Mar¸co . . . 61
3.15 Horas em que as temperaturas foram acima da m´edia . . . 61
3.16 Dados de Abril . . . 63
3.17 Temperaturas extremas de Abril . . . 63
3.18 Horas em que as temperaturas foram acima da m´edia . . . 63
3.19 Dados de Maio . . . 65
3.20 Temperaturas extremas de Maio . . . 65
3.21 Horas em que as temperaturas foram acima da m´edia . . . 65
3.22 Dados de Junho . . . 67
3.23 Temperaturas extremas de Junho . . . 67
3.24 Horas em que as temperaturas foram acima da m´edia . . . 67
3.25 Dados de Julho . . . 69
3.26 Temperaturas extremas de Julho . . . 69
3.27 Horas em que as temperaturas foram acima da m´edia . . . 69
3.28 Dados de Agosto . . . 71
3.30 Horas em que as temperaturas foram acima da m´edia . . . 71
3.31 Dados de Setembro . . . 73
3.32 Temperaturas extremas de Setembro . . . 73
3.33 Horas em que as temperaturas foram acima da m´edia . . . 73
3.34 Dados de Outubro . . . 75
3.35 Temperaturas extremas de Outubro . . . 75
3.36 Horas em que as temperaturas foram acima da m´edia . . . 75
3.37 Dados de Novembro . . . 77
3.38 Temperaturas extremas de Novembro . . . 77
3.39 Horas em que as temperaturas foram acima da m´edia . . . 77
3.40 Dados de Dezembro . . . 79
3.41 Temperaturas extremas de Dezembro . . . 79
O processo de recupera¸c˜ao de dados j´a ´e bastante usado no caso de arquivos de computadores, onde ´e poss´ıvel recuperar arquivos em discos r´ıgidos que n˜ao funcionam mais.
No caso de dados coletados em experimentos ou aparelhos, n˜ao ´e poss´ıvel recu-perar exatamente as informa¸c˜oes perdidas. No entanto, um processo de simula¸c˜ao pode ser utilizado para se aproximar dos valores perdidos.
A simula¸c˜ao pode ser feita para recuperar valores de v´arios sistemas, tais como crescimento populacional, prolifera¸c˜ao de doen¸cas, taxa de mortalidade, crescimento urbano, decaimento radioativo, dentre outros.
Numa pesquisa anual, por exemplo, se em determinado ano a pesquisa n˜ao for feita, ´e poss´ıvel obter os valores aproximados daquele ano utilizando os valores dos anos anteriores e posteriores.
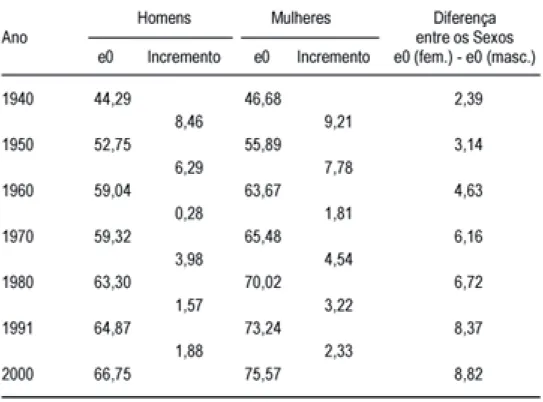
Em um processo muito simplificado, ´e poss´ıvel simular os valores para o ano de 1990, na fig. 1, apenas com os outros dados da tabela. Produzindo, dessa forma, uma tabela sobre a evolu¸c˜ao da esperan¸ca de vida ao nascer, por sexo, no Estado de S˜ao Paulo, com um intervalo de dez anos.
Figura 1: Evolu¸c˜ao da esperan¸ca de vida ao nascer.
A simula¸c˜ao de valores de temperaturas ´e um processo bem mais complexo, devido ao clima ser um sistema ca´otico. A dificuldade de se recuperar valores de temperaturas reside no fato de a quantidade de dados a serem analisados ser enorme, j´a que a temperatura varia a cada instante.
A proposta dessa disserta¸c˜ao ´e recuperar os valores das temperaturas utilizando apenas 11,5% dos dados dispon´ıveis em uma tabela que contˆem as temperaturas em fun¸c˜ao das horas.
a brisa constante torna a temperatura agrad´avel.
A medida das temperaturas faz-se necess´ario tamb´em para avaliar o risco que a popula¸c˜ao tem de contrair cˆancer de pele. Na cidade de Natal, esse risco ´e alto, j´a que as temperaturas na capital s˜ao elevadas.
A previs˜ao do Instituto Nacional do Cˆancer[5] mostra que o Rio Grande do Norte ter´a 2.930 casos de cˆancer de pele em 2010. O Instituto afirma que a m´edia anual era de 2,5 mil novos casos. Segundo o Instituto Nacional de Pesquisas Espaciais[6], a capital tem ´ındices alt´ıssimos do cˆancer.
Diante desse contexto, surge a necessidade de estudos experimentais e te´oricos capazes de analisar as temperaturas ambientais na cidade de Natal.
Finalmente, o presente trabalho foi dividido em 4 cap´ıtulos para uma melhor descri¸c˜ao do tema apresentado.
O primeiro cap´ıtulo ´e uma revis˜ao bibliogr´afica sobre os temas relacionados com o trabalho. Nesse cap´ıtulo est´a a fundamenta¸c˜ao te´orica, onde o modelo matem´atico de interpola¸c˜ao utilizado no programa ser´a apresentado nessa se¸c˜ao. Mas tamb´em ser´a apresentado o m´etodo utilizado para resolu¸c˜ao dos sistemas lineares.
J´a o segundo cap´ıtulo ´e reservado para a metodologia empregada nessa dis-serta¸c˜ao. Mostrando como foi o processo de coleta dos dados, e obten¸c˜ao das equa¸c˜oes que descrevem as temperaturas.
Gerais
Este trabalho objetiva simular e recuperar os valores das temperaturas da cidade de Natal durante um ano a partir de fun¸c˜oes interpoladas e modificadas por um fator de corre¸c˜ao.
Espec´ıficos
• Encontrar o grau do polinˆomio que descreva satisfatoriamente os pontos dese-jados.
• Construir tabelas de dados em intervalos regulares.
• Utilizar fun¸c˜oes interpoladas pelo Excel para retornar os valores de tempera-turas.
• Desenvolver matematicamente essas fun¸c˜oes e comparar seus resultados com os fornecidos pelo Excel.
• Modificar, experimentalmente, as equa¸c˜oes, de forma que elas possam fornecer dados mais pr´oximos dos reais.
• Verificar a validade do m´etodo, utilizando varia¸c˜oes temporais aleat´orias, e comparando os resultados simulados com os reais.
• Visualizar, por padr˜oes gr´aficos, o comportamento das temperaturas durante um ano nessa cidade.
Revis˜
ao Bibliogr´
afica
O setor de inform´atica lida com uma ´area conhecida como recupera¸c˜ao de in-forma¸c˜ao, que consiste em armazenar documentos e recuperar as informa¸c˜oes con-tidas neles.
Esse setor busca as informa¸c˜oes dentro de documentos, seja feita em banco de da-dos interligada-dos, seja na pr´opria internet. O tipo de arquivo pode ser tanto arquivos de texto, de sons, de imagens, quanto de dados.
O termo recupera¸c˜ao de informa¸c˜ao na inform´atica faz alus˜ao `a chamada de arquivos j´a existentes e completos. No caso dessa disserta¸c˜ao, o termo recupera¸c˜ao faz referˆencia `a simula¸c˜ao de dados que foram perdidos, ou n˜ao coletados.
Dessa forma, as simula¸c˜oes feitas nessa disserta¸c˜ao contribuem para a pera¸c˜ao de informa¸c˜ao em rela¸c˜ao `a coleta de dados. Com isso, ´e poss´ıvel recu-perar, com uma certa precis˜ao, dados que foram perdidos ou n˜ao coletados em uma observa¸c˜ao ou em um experimento.
Meireles et al. [8] utilizaram o termo recupera¸c˜ao como a representa¸c˜ao e o acesso a informa¸c˜ao j´a existente. Sendo portanto utilizado para modificar a forma com que os dados geogr´aficos s˜ao tratados e apresentados ao usu´ario, no caso por mapas tem´aticos.
Nos feriados, a bolsa de valores de S˜ao Paulo - Bovespa - n˜ao abre para o preg˜ao. No entanto, ´e poss´ıvel simular como teria sido o comportamento das a¸c˜oes naquele dia baseando-se em dias anteriores.
No caso da bolsa de valores, esse procedimento ´e conhecido como an´alise de curto prazo, ou an´alise gr´afica. Ao contr´ario da an´alise fundamentalista, a an´alise gr´afica faz simula¸c˜oes apenas baseadas nos valores anteriores das a¸c˜oes.
A natureza da recupera¸c˜ao de informa¸c˜ao exige representa¸c˜ao secund´aria em rela¸c˜ao ao fator social, levando pesquisadores a encontrar mecanismos mais eficientes de interpreta¸c˜ao dos registros armazenados. [7]
1.2
M´
etodos Estat´ısticos
A estat´ıstica tem participado nas atividades profissionais da atualidade, j´a que os n´umeros traduzem objetivamente as quest˜oes do cotidiano, proporcionando veri-fica¸c˜oes baseadas em fatos e dados.
A popula¸c˜ao ´e a cole¸c˜ao de todas as observa¸c˜oes potenciais sobre um determinado fenˆomeno. J´a a amostra ´e o conjunto de dados efetivamente observados ou extra´ıdos de uma popula¸c˜ao.[2]
´
E a partir de uma amostra que origina-se o estudo para fazer inferˆencias sobre a popula¸c˜ao.
M´edia Aritm´etica
A m´edia aritm´etica de um conjunto de dados ´e definida como a divis˜ao entre o somat´orio de todos os valores pela sua quantidade.
xa=
Pn
i=1xi
n (1.1)
M´edia Geom´etrica
A m´edia geom´etrica ´e o resultado da ra´ız en´esima do produto de todos os valores dados.
xa= ( n
Y
i=1
xi)n1 (1.2)
Mediana ´
E o valor que se encontra na posi¸c˜ao m´edia da s´erie ordenada de dados. [1] Se a quantidade de dados for par, ´e a medida dos dois valores de posi¸c˜ao m´edia da s´erie ordenada.
´
E o valor de mais alta frequˆencia de aparecimento numa s´erie dada.[1]
Em geral, a moda ´e utilizada quando os dados est˜ao em uma escala nominal. No entanto, existem conjuntos que n˜ao apresentam moda, e outros que s˜ao bi ou multimodal.
Medidas de Dispers˜ao
As medidas de dispers˜ao indicam se os valores est˜ao relativamente pr´oximos um dos outros, ou separados em torno de uma medida de posi¸c˜ao: a m´edia.[11] A Variˆancia e o Desvio Padr˜ao s˜ao medidas de dispers˜ao.
Variˆancia
A variˆancia para a amostra ´e aproximadamente a m´edia aritm´etica dos quadrados dos desvios de todos os valores dividido pela m´edia aritm´etica da popula¸c˜ao.
σa=
Pn
i=1(xi−x)2
n−1 (1.3)
Para a popula¸c˜ao
σp =
Pn
i=1(xi−x)2
n (1.4)
Desvio Padr˜ao
O desvio padr˜ao ´e a raiz quadrada da variˆancia. Para a amostra
σa= (
Pn
i=1(xi−x)2
n−1 )
1
2 (1.5)
Para a popula¸c˜ao
σp = (
Pn
i=1(xi−x)2
n )
1
1.3
Interpola¸c˜
ao
Ajuste de Curvas
Os valores das temperaturas s˜ao dependentes do dia e da hora, neste caso pode-se tra¸car um diagrama de dispers˜ao. No entanto, ´e muito dif´ıcil encontrar matematicamente uma curva que passe exatamente por esses pontos. Na verdade, torna-se prefer´ıvel encontrar uma curva que melhor se ajuste aos pontos fornecidos. Isso ocorre porque o procedimento de coleta de dados possuiu um erro que ´e inerente a qualquer experimento. Apenas pelo fato de ocorrer a medi¸c˜ao, os dados medidos j´a s˜ao modificados. ´E imposs´ıvel verificar as condi¸c˜oes de um sistema sem modific´a-lo.
O problema de ajuste de curvas consiste em m+ 1 fun¸c˜oes - onde m ´e o grau do polinˆomio que se deseja obter - g0(x), g1(x), . . . , gm(x), cont´ınuas no intervalo
[a, b], encontrar m+ 1 coeficientes β0,β1, . . . , βm de modo que:
f(x) = β0g0(x) +β1g1(x) +. . .+βmgm(x) (1.7) Ajuste Polinomial
O ajuste polinomial ocorre quando os pontos apresentados no diagrama n˜ao podem ser descritos por uma fun¸c˜ao linear. Nestes casos a fun¸c˜ao 1.7 ´e composta utilizando as seguintes fun¸c˜oes [9]
g0(x) = 1
g1(x) =x
g2(x) =x2 g3(x) =x3
...
gm(x) =xm
f(x) =β0+β1x+β2x2+. . .+βmxm. (1.9) Dessa forma,f(x) torna-se um polinˆomio de graum. Para se encontrar os valores deβ basta resolver o sistema abaixo:
n P
xi Px2i . . .
P xm i P xi P
x2i P
x3i . . . P
xmi +1
P x2 i P x3 i P x4
i . . .
P
xmi +2
... ... ... . .. ...
P
xm i
P
xmi +1 P
xmi +2 . . . P
x2m i × β0 β1 β2 ... βm = P yi P
yixi
P
yix2
i ...
P
yixmi
No caso particular de um polinˆomio de terceiro grau, esse sistema fica represen-tado por n P
xi P
x2 i P x3 i P
xi Px2i
P x3 i P x4 i P
x2i P
x3i P
x4i P
x5i
P x3 i P x4 i P x5 i P x6 i × β0 β1 β2 β3 = P yi P
yixi
P
yix2i
P
yix3
i
e a equa¸c˜ao desejada ´e
Interpola¸c˜ao Polinomial de Terceiro Grau Utilizando o M´etodo dos M´ınimos Quadrados
A tab. 1.1 mostra um conjunto de pontos coletados de um sistema qualquer:
Tabela 1.1: Pontos de um sistema
y x
y1 x1
y2 x2
y3 x3 y4 x4 y5 x5
y6 x6
y7 x7 y8 x8 y9 x9
Seja f(xi) a fun¸c˜ao resultante da intepola¸c˜ao. No caso de um polinˆomio de terceiro grau, f(x) = β0+β1x+β2x2+β
3x3.
O objetivo ´e fazer com que o desvio, di = yi − f(xi), seja m´ınimo. Pelo m´etodo dos m´ınimos quadrados:
D(β0, β1, β2, β3) = n
X
i=1
d2i = n
X
i=1
[yi−β0 −β1xi−β2x2i −β3x3i]2 (1.11) Derivando parcialmente essa fun¸c˜ao e igualando-a a zero para determinar o seu valor m´ınimo: ∂D ∂β0 = 2 n X i=1
[yi−nβ0−β1xi−β2x2i −β3x
3
i] = 0 (1.12)
∂D ∂β1 = 2 n X i=1
∂D ∂β2 = 2
n
X
i=1
[yi−β0−β1xi−β2x2i −β3x
3
i]x
2
i = 0 (1.14)
∂D ∂β3 = 2 n X i=1
[yi−β0−β1xi−β2x2i −β3x3i]x3i = 0 (1.15) Rearrumando os termos que podem zerar a equa¸c˜ao, e fazendo Pn
i=1 = P
:
nβ0+β1 X
xi+β2 X
x2i +β3 X
x3i =Xyi (1.16)
β0Xxi+β1 X
x2i +β2Xx3i +β3Xx4i =Xxiyi (1.17)
β0 X
x2i +β1 X
x3i +β2 X
x4i +β3 X
x5i =Xx2iyi (1.18)
β0Xx3i +β1Xx4i +β2Xx5i +β3Xxi6 =Xx3iyi (1.19) Fazendo um sistema matricial:
n P xi P
x2i P
x3i
P
xi Px2i
P x3 i P x4 i P
x2i P
x3i P
x4i P
x5i
P
x3i P
x4i P
x5i P
x6i
× β0 β1 β2 β3 = P yi P
yixi
P
yix2i
P
yix3i
1.4
M´
etodo de Resolu¸c˜
ao de Sistemas Lineares
Os m´etodos num´ericos para resolver sistemas lineares dividem-se em dois tipos: M´etodos Exatos, e M´etodos Iterativos.
• M´etodos Exatos S˜ao aqueles que permitiriam obter, se n˜ao fossem os erros de arredondamento, a solu¸c˜ao exata de um sistema com um n´umero finito de c´alculos.
• M´etodos IterativosS˜ao os que fornecem a solu¸c˜ao de um sistema de equa¸c˜oes, com uma certa precis˜ao, atrav´es de um processo infinito convergente.
Um dos m´etodos exatos ´e o de decomposi¸c˜ao LU, o qual pode ser utilizado para resolver um sistema matricial. Seu teorema ´e mostrado abaixo.[4]
Teorema 1.1 (Teorema LU) Seja A= (aij) uma matriz quadrada de ordem n, e
Ak o menor principal, constitu´ıdo das k primeiras linhas e k primeiras colunas de A.
Assumimos quedet(Ak)6= 0 parak= 1,2, . . . , n−1. Ent˜ao existe uma ´unica matriz triangular inferior L = (lij), com l11 = l22 = . . . = lnn = 1, e uma ´unica matriz
triangular superior U = (uij) tal que LU =A. Al´em diss, det(A) =u11u22. . . unn. Esse m´etodo consiste em transformar uma matriz [A], em um produto de duas matrizes, uma triangular inferior, [L], e a outra triangular superior, [U], e resolver dois sistemas envolvendo essas novas matrizes.
[A][X] = [B] (1.20)
[A] = [L][U] (1.21)
[L][Y] = [B] (1.23)
[U][X] = [Y] (1.24)
Os elementos das matrizes envolvidas no processo podem ser explicitados como abaixo:
a11 a12 . . . a1n a21 a22 . . . a1n ... ... ... ...
an1 an2 . . . ann
=
1 0 . . . 0
l11 1 . . . 0 ... ... ... ...
ln1 ln2 . . . 1 ×
u11 u12 . . . u1n
0 u22 . . . u1n ... ... ... ... 0 0 . . . unn
• Resolvendo para a primeira linha de U:
u11 =a11, u12=a12 , u13 =a13 , ... , u1j =a1j (1.25) com j = 1,2, ..., n.
• Resolvendo para a primeira coluna de L:
a21 =l21u11, a31=l31u11 , a41=l41u11 , ... , ai1 =li1u11
li1 =
ai1
u11 (1.26)
com i= 2,3, ..., n.
• Resolvendo para a segunda linha de U:
a21=l21u11, a22=l21u12+u22 , a23 =l21u13+u23
• Resolvendo para a segunda coluna de L:
a12 =u12 , a22=l21u12+u22 , a32=l31u12+l32u22
li2 =
ai2−li1u12
u22 (1.28)
com i= 1,2, ..., n.
Se o processo continuar, ´e poss´ıvel obter todos os elementos das matrizes trian-gulares inferiores e superiores, segundo as express˜oes:
lij =
aij −
Pj−1
k=1likukj
ujj
, i > j (1.29)
uij =aij − i−1
X
k=1
A solu¸c˜ao de um sistema triangular inferior ´e feita por substitui¸c˜ao direta, ou seja, determina-se o valor da primeira inc´ognita e substitui esse valor na equa¸c˜ao seguinte, at´e a en´esima equa¸c˜ao.
Defini¸c˜ao 1 Uma matriz triangular inferior ´e uma matriz quadrada C = (cij) tal
quecij = 0 para i < j.
l11y1 = b1
l21y1 + l22y2 = b2
l31y1 + l32y2 + l33y3 = b3
... ... ... . .. ...
ln1y1 + ln2y2 + . . . + lnnyn = bn
onde aii6= 0; i = 1, 2, . . . , n. A resolu¸c˜ao do sistema ´e feita como se segue:
y1 =
b1
l11 (1.31)
y2 =
b2−l21y1 l22
(1.32)
y3 = b3−l31y1−l32y2
l33 (1.33)
Se o processo continuar, pode-se estabelecer para todos os termos:
yi =
bi−Pi−1
j=1lijyj
lii
(1.34)
Sistema de Ordem n Triangular Superior
A solu¸c˜ao de um sistema triangular superior ´e obtida por retrosubstitui¸c˜ao, ou seja, determina-se o valor da en´esima inc´ognita e substitui-se esse valor na pen´ultima equa¸c˜ao, para determinar o valor de xn−1 e continuar o processo at´e a primeira inc´ognita.
Defini¸c˜ao 2 Uma matriz triangular superior ´e uma matriz quadrada C = (cij) tal
quecij = 0 para i > j.
u11x1 + u12x2 + u13x3 + . . . + u1nxn = y1 u22x2 + u23x3 + . . . + u2nxn = y2
. .. ... ... ...
u(n−2)x(n−2) + u(n−2)x(n−1) + u(n−2)xn = y(n−2)
u(n−1)x(n−1) + u(n−1)xn = y(n−1)
unnxn = yn
onde aii6= 0; i = 1, 2, . . . , n. A resolu¸c˜ao do sistema ´e feita a seguir:
xn=
yn
unn (1.35)
x(n−1) =
y(n−1)−u(n−1)nxn
u(n−1)(n−1)
(1.36)
x(n−2) = y(n−2)−u(n−2)(n−1)x(n−1)−u(n−2)xn
u(n−2)(n−2)
x(n−i) =
y(n−i)−
P
u(n−i)(n−j)x(n−j)
u(n−i)(n−i)
(1.38)
Por indu¸c˜ao matem´atica:
xi =
yi−Pn
j=i+1uijxj
uii (1.39)
Metodologia
O Instituto Nacional de Pesquisas Espaciais(INPE) divulga, no seu site, vari´aveis clim´aticas que podem ser apresentadas em arquivos do Excel em um determinado mˆes. A figura 2.1 mostra quais os parˆametros que o INPE disponibiliza.
A figura 2.1 mostra como esses dados s˜ao fornecidos `a popula¸c˜ao.
A partir dos dados coletados do INPE, foram selecionados dez dias de cada mˆes, seguindo a progress˜ao aritm´etica de trˆes dias. Em cada um desses dias, foi obtido o valor da temperatura em fun¸c˜ao da hora, para um determinado dia.
Por exemplo, `as 5 horas do dia 3 de Janeiro, verificou-se que a temperatura era de 27,6467oC; `as 5 horas do dia 6 de Janeiro, o valor da temperatura era 27,6637oC
e assim por diante at´e o dia 27.
Com isso, obteve-se uma amostra de 11.5% dos dados. Os dados foram dispostos em uma tabela como a que segue abaixo:
Tabela 2.1: 5 horas de Janeiro
Ano Dia Minuto Temperatura
2009 3 300 27,6467
2009 6 300 27,6637
2009 9 300 27,1717
2009 12 300 26,1033
2009 15 300 26,703
2009 17 300 26,5675
2009 21 300 26,432
2009 24 300 26,60885
Esse procedimento foi repetido para as 8 horas, 11 horas, 14 horas e 17 horas, levando em considera¸c˜ao que as maiores temperaturas ocorrem nesse per´ıodo, assim como a exposi¸c˜ao `a radia¸c˜ao ultra-violeta.
A escolha da interpola¸c˜ao polinomial foi feita devido ao fato de as temperaturas variarem muito. Um ajuste de curva linear n˜ao descreveria bem as temperaturas que ocorrem em um mˆes, porque n˜ao apresentam inflex˜oes.
Os gr´aficos descritos por uma fun¸c˜ao quadr´atica s˜ao os mais utilizados, justa-mente pelo fato de eles possuirem inflex˜oes capazes de passarem por pontos que seriam inacess´ıveis a uma fun¸c˜ao afim.
Os erros s˜ao inerente a qualquer experimento, a qualquer coleta de dados. Al´em do mais, algumas as temperaturas podem sofrer altera¸c˜oes bruscas durante a coleta de dados. O que gera grandes desvios na resposta.
Dessa forma, para definir uma fun¸c˜ao anal´ıtica que descreva o sistema proposto n˜ao se deve optar por uma forma polinomial interpoladora dos pontos fornecidos, mas sim uma curva que melhor se ajuste a estes pontos, levando em considera¸c˜ao a existˆencia de erros que, geralmente, n˜ao s˜ao previs´ıveis.
Embora n˜ao seja necess´ario for¸car uma fun¸c˜ao que apresente como resposta os valores exatos das temperaturas, justamente por apresentarem erros devido a coleta dos dados, e a mudan¸cas clim´aticas n˜ao dependentes apenas da temperatura, ´e razo´avel supor que a fun¸c˜ao obtida se aproxime ao m´aximo desses pontos e que descreva muito bem os pontos adjacentes.
desenvolvidos dois m´etodos:
• O primeiro consiste em plotar no Excel os dados das tabelas previamente coletados, e fazer com que seja mostrada a fun¸c˜ao polinomial que melhor se ajusta a esses pontos. Essa fun¸c˜ao foi ent˜ao modificada por um fator de corre¸c˜ao que torna a fun¸c˜ao capaz de descrever os valores de temperaturas entre aqueles que n˜ao foram coletados. A partir desses dados foi feito um programa, em Delphi - com uma interface mais amig´avel em rela¸c˜ao ao usu´ario -, tendo o objetivo de indicar o valor da temperatura simulada em fun¸c˜ao do tempo para o ano de 2009.
• O segundo m´etodo consiste em determinar essas fun¸c˜oes matematicamente, com o objetivo de utiliz´a-las para analisar as temperaturas, utilizando-se tamb´em o fator de corre¸c˜ao. Com isso ´e poss´ıvel simular os valores das temperaturas em fun¸c˜ao do tempo, assim como encontrar a m´edia, variˆancia, desvio padr˜ao, valores m´ınimos e m´aximos das temperaturas, e os hor´arios em que essas tem-peraturas encontram-se acima da m´edia. Esse procedimento foi feito tamb´em pelo autor dessa disserta¸c˜ao, mas agora utilizando a linguagem Fortran.
Essa mesma metodologia pode ser aplicada a qualquer ano, mas tamb´em para qualquer tipo de experimento.
2.3
Equa¸c˜
oes pelo Excel
Ap´os a coleta de dados, foram construidos cinco gr´aficos no Excel, um para cada hora. Esses gr´aficos tinham como vari´aveis independentes os dias do mˆes de Janeiro, e as dependentes as temperaturas em cada um desses dias. O objetivo da constru¸c˜ao desses gr´aficos ´e que pode-se obter as fun¸c˜oes interpoladas a partir deles.
Uma vez obtidas essas equa¸c˜oes, elas foram introduzidas no programa Sistema de Busca de Temperaturas para serem acessadas quando o usu´ario fornecer os valores da vari´avel dependente.
horas. Com isso, foi poss´ıvel obter uma fun¸c˜ao que descrevesse o comportamento da temperatura, nessa hora, durante o mˆes de Janeiro:
Figura 2.4: Gr´afico das temperaturas as 5 horas A equa¸c˜ao que descreve esse gr´afico ´e:
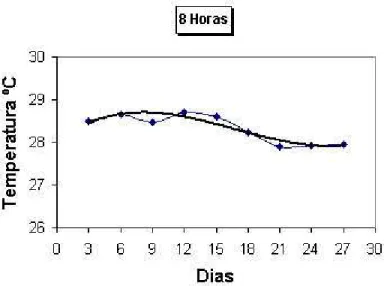
Da mesma forma foi feito para as 8 horas:
Figura 2.5: Gr´afico das temperaturas as 8 horas Equa¸c˜ao do gr´afico:
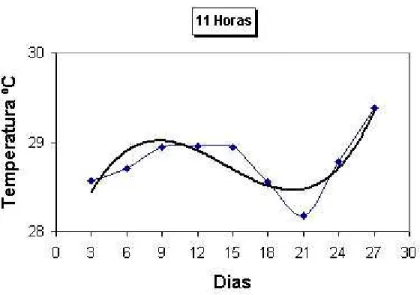
Figura 2.6: Gr´afico das temperaturas as 11 horas
Equa¸c˜ao do gr´afico:
Para as 14 horas:
Figura 2.7: Gr´aficos das temperatura as 14 horas
Equa¸c˜ao do gr´afico:
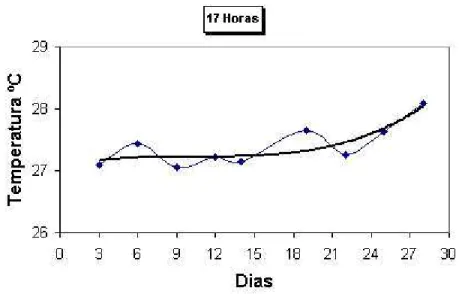
Figura 2.8: Gr´afico das temperaturas as 17 horas Equa¸c˜ao do gr´afico:
Todo esse procedimento foi feito para o mˆes de Janeiro, no entanto, para des-crever durante todo o ano de 2009 foi necess´ario repetir o mesmo processo para os outros meses.
Com o objetivo de melhorar a precis˜ao do programa, a partir do mesmo proce-dimento descrito acima, foram encontradas fun¸c˜oes interpoladas polinomialmente de sexto grau. No entanto, o resultado foi inesperado. Essas fun¸c˜oes descreviam muito bem - melhor at´e do que as fun¸c˜oes de terceiro grau encontradas anteriormente - os valores das temperaturas para dias menores do que cinco. Contudo, os resultados diferiam muito dos reais para dias maiores do que vinte, chegando a apresentar valores como 225oC para o dia 21 de Janeiro `as 14 horas.
Esse problema ´e conhecido na computa¸c˜ao num´erica como Runge’s phenomenon. Esse problema aparece geralmente quando ´e utilizado uma fun¸c˜ao polinomial de alto grau. Runge descobriu esse problema quando estava analisando o comportamento das fun¸c˜oes em rela¸c˜ao aos erros usando a interpola¸c˜ao polinomial para descrever certas fun¸c˜oes.[10]
As equa¸c˜oes foram coletadas dos gr´aficos e implementadas na linguagem do programa. No entanto, n˜ao ´e poss´ıvel descrever as temperaturas diferentes das coletadas. Para solucionar esse problema, foi necess´ario supor que as temperaturas di´arias se comportem semelhantes a uma distribui¸c˜ao normal.
Para construir um programa que se adequasse a todos os pontos dessa dis-tribui¸c˜ao, foi necess´ario ligar esses pontos por fun¸c˜oes. Sendo assim, cada uma dessas fun¸c˜oes foram modificadas devido a adi¸c˜ao experimental de um fator de corre¸c˜ao, de forma que os resultados fossem os mais pr´oximos dos reais.
O fator de corre¸c˜ao ´e uma fun¸c˜ao afim, com um coeficiente angular que foi determinado experimentalmente.
A figura abaixo mostra a tendˆencia de dire¸c˜ao das temperaturas expressas pelo fator de corre¸c˜ao:
Essa determina¸c˜ao consistiu na introdu¸c˜ao de valores para o coeficiente angular desse fator. A cada valor introduzido na f´ormula, o programa era reescrito para todos os meses, e recompilado.
Com o programa funcionando, era ent˜ao introduzidos a hora, o dia e o mˆes. Ap´os o processamento, o programa retornava um valor de temperatura, o qual era comparado com a temperatura real apresentada na tabela do INPE.
Um exemplo dessa modifica¸c˜ao ´e dada abaixo:
y= 4E−05x3+ 0,0038x2−0,1858x+ 28,332 (2.6) equa¸c˜ao obtida no Excel.
A equa¸c˜ao posta na linguagem do Delphi ´e
T r:= 0.00004power(t,3) + 0.0038power(t,2)−0.1858t+ 28.332 +corr; (2.7) cujo fator de corre¸c˜ao possui o seguinte valor:
corr := 0.4∗(StrtoF loat(edthora.T ext)−5); (2.8) A equa¸c˜ao (2.7) mostra como funciona esse fator de corre¸c˜ao. A hora inserida pelo usu´ario ser´a diminuida de 5 horas e multiplicada por 0.4.
Se a hora informada for menor do que 5, o valor do fator de corre¸c˜ao torna-se negativo, diminuindo da temperatura apresentada pelas equa¸c˜oes `as 5 horas.
O valor da temperatura torna-se satisfat´orio, pois ´e de se esperar que as temper-aturas `as 4 horas da manh˜a sejam menores do que as das 5 horas, assim como as das 6 horas sejam maiores do que as das 5 horas.
´
E conveniente observar que a contribui¸c˜ao m´axima desse fator de corre¸c˜ao ´e de 0.6 graus Celsius `as 6 horas e 30 minutos. Ou seja, foi proposto que as temperaturas `as 6 horas e 30 minutos s˜ao maiores do que as das 5 horas em 0.6 graus Celsius.
Mas tamb´em, a influˆencia desse fator desaparece quando ´e informada a hora igual `aquelas coletadas. Nesse exemplo, se o usu´ario digitar 5 horas, a temperatura apresentada ser´a exatamente igual `a fornecida pela fun¸c˜ao.
temperaturas devem diminuir ao longo do tempo. Das 12 horas e 30 minutos at´e `as 15 e 30 minutos o coeficiente foi -0.2. Finalmente, das 15 horas e 30 minutos at´e `as 17 horas, o coeficiente foi de -0.1.
Esse processo ´e resumido abaixo:
f(t) = α(t−β) (2.9)
Tabela 2.2: Constantes
Hora α β
2.5
Equa¸c˜
oes pelo M´
etodo Num´
erico
O fluxograma abaixo mostra o procedimento feito para o desenvolvimento com-putacional implementado na linguagem Fortran.
tempo tem a forma:
f(x) = β0+β1x+β2x2+β3x3 (2.10) Para encontrar essas fun¸c˜oes, ´e necess´ario resolver o sistema matricial abaixo:
n P
xi Px2i
P
x3i
P
xi
P
x2i P
x3i P
x4i
P x2 i P x3 i P x4 i P x5 i P
x3i P
x4i P
x5i P
x6i
× β0 β1 β2 β3 = P yi P
yixi
P
yix2i
P
yix3i
Onde os pontos (x,y) foram dispostos em uma tabela:
Tabela 2.3: Pontos de um sistema
y x
y1 x1
y2 x2
y3 x3 y4 x4 y5 x5
y6 x6
y7 x7 y8 x8 y9 x9
Denominei [E], como sendo a matriz dos somat´orios de x. A matriz [F] ´e a dos somat´orios de xy. E por ´ultimo, a matrix [X] ´e a matriz dos coeficientes da equa¸c˜ao.
[E][X] = [F] (2.11)
A matriz [D] ´e a que possui os dados da tabela. Ent˜ao para construir a matriz [E], a seguinte subrotina foi utilizada:
! SUBROTINA MATRIZ SOMATORIOX SUBROUTINE SOMATORIOX(W,P) ! E, D IMPLICIT NONE
INTEGER I, J, K
REAL, DIMENSION(9,2) :: P REAL, DIMENSION(4,4) :: W
DO I = 1, 4 DO J = 1, 4 W(I,J) = 0 ENDDO ENDDO
I=1
DO J=1, 4 DO I=1, 4 DO K=1, 9
W(I,J) = P(K,1)**(I+J-2) + W(I,J) ENDDO
ENDDO ENDDO W(1,1) = 9 END
! SUBROTINA MATRIZ SOMATORIOY SUBROUTINE SOMATORIOY(W,P) ! F, D IMPLICIT NONE
INTEGER I, K
REAL, DIMENSION(9,2) :: P REAL, DIMENSION(4,1) :: W
DO I = 1, 4 W(I,1) = 0 ENDDO
DO I=1, 4 DO K=1, 9
W(I,1) = P(K,2)*(P(K,1)**(I-1)) + W(I,1) ENDDO
ENDDO END
Nesse ponto, foi necess´ario decompor a matriz [E], em duas outras: uma trian-gular inferior [L] e a outra triantrian-gular superior [U], de forma que [E] = [L][U]. Pelas equa¸c˜oes (1.30) e (1.29), pode-se desenvolver um c´odigo para encontrar a matriz triangular superior [U] e triangular inferior [L].
lij =
aij −Pjk−=11 likukj
ujj
, i > j
uij =aij − i−1
X
k=1
likukj, i≤j O seguinte c´odigo foi desenvolvido:
! SUBROTINA LU
SUBROUTINE LU(W,P,Q)! E,L,U IMPLICIT NONE
INTEGER I,J,N,K,G
REAL,DIMENSION(4,4) :: W,P,Q,Z N=4
Z(1,1) = 0
DO G=1, N
! MATRIZ SUPERIOR I=G
DO J=1, N DO K=1, I-1
Z(I,J) = Z(I,J) + P(I,K)*Q(K,J) ENDDO
Q(I,J) = W(I,J) - Z(I,J) Z(I,J) = 0
! MATRIZ INFERIOR I=G
J=G
DO I=1, N DO K=1, J-1
Z(I,J) = Z(I,J) + P(I,K)*Q(K,J) ENDDO
P(I,J) = (W(I,J) - Z(I,J))/(Q(J,J)) Z(I,J) = 0
ENDDO
J=G ENDDO RETURN END
O subprograma acima calcula as matrizes [U] e [L] da seguinte forma: primeiro calcula todos os elementos da primeira linha de [U], ou seja [U]1j, depois, com esse
resultado, calcula os elementos da primeira coluna da matriz [L], que s˜ao [L]i1. Logo
Resultados e Discuss˜
oes
Nesse ponto ´e necess´ario verificar a validade do programa proposto. Para isso, ´e necess´ario escolher aleatoriamente alguns dias para comparar as temperaturas simuladas com as reais, e poder verificar a sua eficiˆencia.
Como pode-se observar nos gr´aficos seguintes, houve uma concordˆancia entre o m´etodo utilizando as fun¸c˜oes interpoladas pelo Excel, e o m´etodo usando as fun¸c˜oes feitas matematicamente. Por essa raz˜ao, o erro em rela¸c˜ao `as temperaturas reais foi calculado tomando apenas as temperaturas simuladas numericamente e as reais.
Embora seja poss´ıvel simular as temperaturas de todos os dias do ano, a apre-senta¸c˜ao dos resultados ficou compreendida entre os dias 3 e 27, os quais foram os dias em que se iniciaram e nos quais se encerraram a coleta de dados, respectiva-mente.
Essa verifica¸c˜ao ocorre devido a necessidade de constatar e validar o m´etodo utilizado comparando os resultados aos dados reais.
Em um primeiro momento, os gr´aficos com as temperaturas simuladas pelas equa¸c˜oes interpoladas pelo Excel s˜ao plotadas no gr´afico, juntamente com as tem-peraturas simuladas pelo m´etodo num´erico implementado em linguagem Fortran. No mesmo gr´afico encontram-se as temperaturas reais. Logo abaixo, encontra-se uma pequena explica¸c˜ao do comportamento dessas temperaturas.
Dia 6 de Janeiro
Figura 3.1: Dia 6 de Janeiro
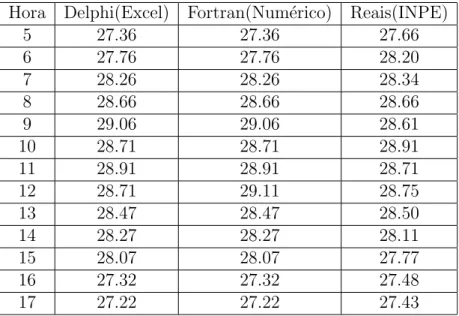
A tabela 3.1 mostra os dados apresentados pelo m´etodo utilizando o excel, pelo m´etodo num´erico, e pelas temperaturas reais.
Tabela 3.1: Dia 6 de Janeiro
Hora Delphi(Excel) Fortran(Num´erico) Reais(INPE)
5 27.36 27.36 27.66
6 27.76 27.76 28.20
7 28.26 28.26 28.34
8 28.66 28.66 28.66
9 29.06 29.06 28.61
10 28.71 28.71 28.91
11 28.91 28.91 28.71
12 28.71 29.11 28.75
13 28.47 28.47 28.50
14 28.27 28.27 28.11
15 28.07 28.07 27.77
16 27.32 27.32 27.48
17 27.22 27.22 27.43
O erro foi calculado em rela¸c˜ao `as temperaturas apresentadas pelo Fortran e pelo INPE, segundo a f´ormula:
ε=
P
Tnumerico−PTreais
P
Tnumerico
×100
ε= 367.18−367.1428
Dia 5 de Novembro
Figura 3.2: Dia 5 de Novembro
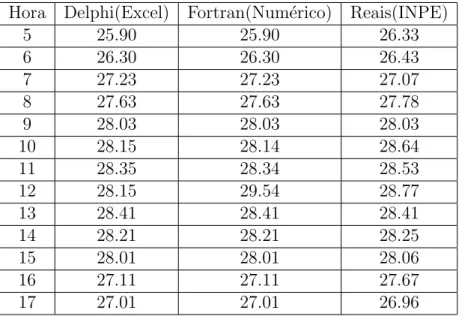
A tabela 3.2 mostra os dados apresentados pelo m´etodo utilizando o excel, pelo m´etodo num´erico, e pelas temperaturas reais.
Tabela 3.2: Dia 5 de Novembro
Hora Delphi(Excel) Fortran(Num´erico) Reais(INPE)
5 25.90 25.90 26.33
6 26.30 26.30 26.43
7 27.23 27.23 27.07
8 27.63 27.63 27.78
9 28.03 28.03 28.03
10 28.15 28.14 28.64
11 28.35 28.34 28.53
12 28.15 29.54 28.77
13 28.41 28.41 28.41
14 28.21 28.21 28.25
15 28.01 28.01 28.06
16 27.11 27.11 27.67
17 27.01 27.01 26.96
O erro foi calculado em rela¸c˜ao `as temperaturas apresentadas pelo Fortran e pelo INPE, segundo a f´ormula:
ε=
P
Tnumerico−PTreais
P
Tnumerico
×100
ε= 358.86−360.93
Dia 15 de Junho
Figura 3.3: Dia 15 de Junho
No mˆes de Junho, ocorreram varia¸c˜oes bruscas nas temperaturas, aproximando-se de um sistema ca´otico, onde a previs˜ao(simula¸c˜ao) dos resultados torna-aproximando-se impre-cisa.
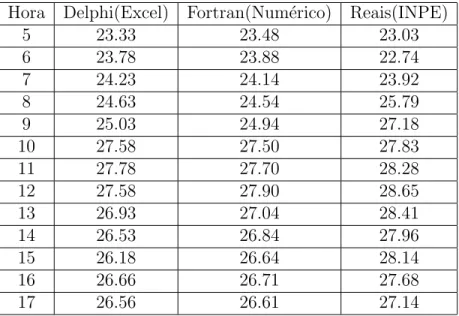
A tabela 3.3 mostra os dados apresentados pelo m´etodo utilizando o excel, pelo m´etodo num´erico, e pelas temperaturas reais.
Tabela 3.3: Dia 15 de Junho
Hora Delphi(Excel) Fortran(Num´erico) Reais(INPE)
5 23.33 23.48 23.03
6 23.78 23.88 22.74
7 24.23 24.14 23.92
8 24.63 24.54 25.79
9 25.03 24.94 27.18
10 27.58 27.50 27.83
11 27.78 27.70 28.28
12 27.58 27.90 28.65
13 26.93 27.04 28.41
14 26.53 26.84 27.96
15 26.18 26.64 28.14
16 26.66 26.71 27.68
17 26.56 26.61 27.14
O erro foi calculado em rela¸c˜ao `as temperaturas apresentadas pelo Fortran e pelo INPE, segundo a f´ormula:
ε=
P
Tnumerico−PTreais
P
Tnumerico
×100
ε= 337.92−346.74
Dia 15 de Julho
Figura 3.4: Dia 15 de Julho
A tabela 3.4 mostra os dados apresentados pelo m´etodo utilizando o excel, pelo m´etodo num´erico, e pelas temperaturas reais.
Tabela 3.4: Dia 15 de Julho
Hora Delphi(Excel) Fortran(Num´erico) Reais(INPE)
5 21.64 21.87 22.06
6 22.04 22.27 22.36
7 23.07 22.95 24.10
8 23.47 23.35 24.51
9 23.87 23.75 25.88
10 25.13 24.96 25.23
11 25.33 25.15 27.29
12 25.13 25.36 27.35
13 26.57 26.47 27.73
14 26.37 26.27 26.85
15 26.17 26.07 27.00
16 25.60 25.41 26.31
17 25.50 25.31 26.46
O erro foi calculado em rela¸c˜ao `as temperaturas apresentadas pelo Fortran e pelo INPE, segundo a f´ormula:
ε=
P
Tnumerico−PTreais
P
Tnumerico
×100
ε= 319.18−333.15
Dia 10 de Janeiro
Figura 3.5: Dia 10 de Janeiro
A tabela 3.5 mostra os dados apresentados pelo m´etodo utilizando o excel, pelo m´etodo num´erico, e pelas temperaturas reais.
Tabela 3.5: Dia 10 de Janeiro
Hora Delphi(Excel) Fortran(Num´erico) Reais(INPE)
5 26.90 26.88 27.67
6 27.29 27.28 28.01
7 28.29 28.27 28.52
8 28.69 28.67 28.76
9 29.04 29.07 28.87
10 28.87 28.80 29.03
11 29.03 29.00 28.91
12 28.87 29.20 28.93
13 28.12 28.21 28.31
14 28.00 28.01 27.98
15 27.80 27.81 27.32
16 27.37 27.33 27.25
17 27.27 27.23 27.06
O erro foi calculado em rela¸c˜ao `as temperaturas apresentadas pelo Fortran e pelo INPE, segundo a f´ormula:
ε=
P
Tnumerico−PTreais
P
Tnumerico
×100
ε= 365.76−366.6223
Dia 20 de Dezembro
Figura 3.6: Dia 20 de Dezembro
A tabela 3.6 mostra os dados apresentados pelo m´etodo utilizando o excel, pelo m´etodo num´erico, e pelas temperaturas reais.
Tabela 3.6: Dia 20 de Dezembro
Hora Delphi(Excel) Fortran(Num´erico) Reais(INPE)
5 25.44 25.50 26.56
6 25.84 25.90 26.78
7 26.89 26.70 27.41
8 27.29 27.18 27.93
9 27.69 27.58 28.22
10 27.84 28.16 28.90
11 28.04 28.36 29.19
12 27.84 28.56 28.74
13 28.82 28.80 28.66
14 28.62 28.60 28.67
15 28.42 28.40 28.25
16 27.49 27.41 27.91
17 27.39 27.31 27.51
O erro foi calculado em rela¸c˜ao `as temperaturas apresentadas pelo Fortran e pelo INPE, segundo a f´ormula:
ε=
P
Tnumerico−PTreais
P
Tnumerico
×100
ε= 358.46−364.73
Simula¸c˜oes das temperaturas em trˆes dias de cada mˆes
Figura 3.7: Gr´afico de trˆes dias do mˆes de Janeiro
Temperatura m´edia de Janeiro 27.94
Variˆancia 0.0009844
Desvio padr˜ao 0.0313757174
Tabela 3.8: Temperaturas extremas de Janeiro Temperatura Hora Dia Maior temperatura no mˆes 29.547 12 27 Menor temperatura no mˆes 26.434 5 19
Tabela 3.9: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 2
7 14
8 21
9 25
10 25
11 25
12 25
13 12
14 10
15 6
16 2
Figura 3.8: Gr´afico de trˆes dias do mˆes de Fevereiro
Temperatura m´edia de Fevereiro 27.98
Variˆancia 0.0007444
Desvio padr˜ao 0.02728
Tabela 3.11: Temperaturas extremas de Fevereiro Temperatura Hora Dia Maior temperatura no mˆes 29.503 13 14 Menor temperatura no mˆes 23.371 5 27
Tabela 3.12: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 6
8 12
9 16
10 25
11 25
12 25
13 20
14 20
15 19
16 19
Figura 3.9: Gr´afico de trˆes dias do mˆes de Mar¸co
Temperatura m´edia de Mar¸co 27.68
Variˆancia 0.089905
Desvio padr˜ao 0.29984
Tabela 3.14: Temperaturas extremas de Mar¸co Temperatura Hora Dia Maior temperatura no mˆes 30.036306 12 27 Menor temperatura no mˆes 23.93 7 3
Tabela 3.15: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 2
8 7
9 11
10 25
11 25
12 25
13 23
14 22
15 22
16 17
Figura 3.10: Gr´afico de trˆes dias do mˆes de Abril
Temperatura m´edia de Abril 27.40
Variˆancia 0094785
Desvio padr˜ao 0.30787
Tabela 3.17: Temperaturas extremas de Abril Temperatura Hora Dia Maior temperatura no mˆes 29.564 12 18 Menor temperatura no mˆes 24.401 5 24
Tabela 3.18: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 0
8 4
9 11
10 23
11 23
12 23
13 23
14 22
15 22
16 21
Figura 3.11: Gr´afico de trˆes dias do mˆes de Maio
Temperatura m´edia de Maio 26.74
Variˆancia 0.34792
Desvio padr˜ao 0.58985
Tabela 3.20: Temperaturas extremas de Maio Temperatura Hora Dia Maior temperatura no mˆes 29.987 12 14 Menor temperatura no mˆes 23.014 5 27
Tabela 3.21: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 11
8 13
9 16
10 18
11 18
12 19
13 16
14 16
15 15
16 14
Figura 3.12: Gr´afico de trˆes dias do mˆes de Junho
Temperatura m´edia de Junho 26.06 Variˆancia 0.018000 Desvio padr˜ao 0.13416
Tabela 3.23: Temperaturas extremas de Junho Temperatura Hora Dia Maior temperatura no mˆes 28.523 13 22 Menor temperatura no mˆes 23.026 5 22
Tabela 3.24: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 0
8 0
9 0
10 25
11 25
12 25
13 22
14 20
15 18
16 25
Figura 3.13: Gr´afico de trˆes dias do mˆes de Julho
Temperatura m´edia de Julho 25.04
Variˆancia 0.21145
Desvio padr˜ao 0.45983
Tabela 3.26: Temperaturas extremas de Julho Temperatura Hora Dia Maior temperatura no mˆes 28.225 12 27 Menor temperatura no mˆes 21.321 5 11
Tabela 3.27: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 1
6 1
7 1
8 2
9 3
10 19
11 25
12 25
13 25
14 25
15 25
16 25
Figura 3.14: Gr´afico de trˆes dias do mˆes de Agosto
No dia 5 de Agosto, as temperaturas tiveram um aumento de quase 2,5 graus Celsius das 9 horas `as 10 horas.
Temperatura m´edia de Agosto 25.77
Variˆancia 00091463
Desvio padr˜ao 0.095636
Tabela 3.29: Temperaturas extremas de Agosto Temperatura Hora Dia Maior temperatura no mˆes 28.382 13 3 Menor temperatura no mˆes 22.449 5 27
Tabela 3.30: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 5
8 9
9 11
10 20
11 25
12 25
13 25
14 22
15 19
16 17
Figura 3.15: Gr´afico de trˆes dias do mˆes de Setembro
Temperatura m´edia de Setembro 26.283
Variˆancia 0.02310
Desvio padr˜ao 0.14936
Tabela 3.32: Temperaturas extremas de Setembro Temperatura Hora Dia Maior temperatura no mˆes 28.524 12 3 Menor temperatura no mˆes 24.144 10 27
Tabela 3.33: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 7
8 11
9 14
10 13
11 15
12 17
13 25
14 25
15 19
16 10
Figura 3.16: Gr´afico de trˆes dias do mˆes de Outubro
Temperatura m´edia de Outubro 27.08
Variˆancia 0.018321
Desvio padr˜ao 0.13502
Tabela 3.35: Temperaturas extremas de Outubro Temperatura Hora Dia Maior temperatura no mˆes 28.309 12 21 Menor temperatura no mˆes 22.364 5 3
Tabela 3.36: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 0
8 14
9 20
10 25
11 25
12 25
13 25
14 25
15 25
16 0
Figura 3.17: Gr´afico de trˆes dias do mˆes de Novembro
Temperatura m´edia de Novembro 27.48
Variˆancia 0.016749
Desvio padr˜ao 0.12942
Tabela 3.38: Temperaturas extremas de Novembro Temperatura Hora Dia Maior temperatura no mˆes 28.849 12 3 Menor temperatura no mˆes 25.573 5 22
Tabela 3.39: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 1
8 8
9 25
10 22
11 22
12 23
13 25
14 25
15 25
16 0
Figura 3.18: Gr´afico de trˆes dias do mˆes de Dezembro
Temperatura m´edia de Dezembro 27.57
Variˆancia 0.00012757
Desvio padr˜ao 0.011295
Tabela 3.41: Temperaturas extremas de Dezembro Temperatura Hora Dia Maior temperatura no mˆes 28.800 13 19 Menor temperatura no mˆes 25.369 5 16
Tabela 3.42: Horas em que as temperaturas foram acima da m´edia Horas Quantidade de dias acima da m´edia
5 0
6 0
7 0
8 1
9 21
10 24
11 25
12 25
13 25
14 25
15 25
16 3
Temperaturas simuladas de dias em que n˜ao foram coletados os dados reais
No dia 16 de Janeiro, as temperaturas simuladas desse dia apresentaram os valores conforme a figura abaixo:
Conclus˜
oes
A partir dos gr´aficos do cap´ıtulo anterior, pode-se obter as seguintes con-clus˜oes:
• O fator de corre¸c˜ao utilizado nesse trabalho foi o respons´avel por descrever as temperaturas entre aquelas que foram coletadas.
• A determina¸c˜ao do coeficiente angular do fator de corre¸c˜ao foi feita de forma heur´ıstica, ou seja, sem comprova¸c˜ao matem´atica, apenas comparando os re-sultados simulados com os reais. No entanto, os valores para os coeficientes angulares apresentaram-se satisfat´orios.
• Os resultados apresentados pelo m´etodo de simula¸c˜ao feito no Excel, foram bastantes semelhantes com aqueles feitos numericamente.
• Com apenas 11.5% dos dados, foi poss´ıvel recompor 100% das temperaturas reais com uma incerteza menor do que 5%.
• A temperatura simulada m´axima anual foi de 30.04 graus Celsius, a qual ocor-reu no mˆes de Mar¸co, `as 12 horas do dia 27. J´a a temperatura m´ınima simulada foi de 21.32 graus Celsius, a qual ocorreu no mˆes de Julho, `as 5 horas do dia 11.
• Nos dias 16 de Janeiro e 7 de Fevereiro n˜ao foram coletados os dados das temperaturas reais. No entanto, a simula¸c˜ao apresentou resultados conforme as figuras do cap´ıtulo anterior.
• N˜ao foi poss´ıvel construir um programa com uma fun¸c˜ao de sexto grau, devido ao Runge’s phenomenon. Por isso, foi conveniente escolher uma fun¸c˜ao de terceiro grau, pois j´a apresenta pontos de inflex˜ao suficientes para descrever satisfat´oriamente as temperaturas.
[1] Cavanha Filho, A. O. - Estat´ıstica B´asica.
[2] Diniz, A. - Estat´ıstica B´asica Geoprocessamento UFMG, 2000.
[3] Ferneda, E. -Redes neurais e sua aplica¸c˜ao em sistemas de recupera¸c˜ao de informa¸c˜ao. Perspectivas em Ciˆencia da informa¸c˜ao, 2008.
[4] Franco, N. M. B. - C´alculo Num´erico Editora Pearson. [5] Instituto Nacional de Cˆancer - www.inca.gov.br
[6] Instituto Nacional de Pesquisas Espaciais, Centro Regional do Nordeste -www.crn2.inpe.br
[7] Martins, R. P. - Informa¸c˜ao e conhecimento: uma abordagem dos sis-temas de recupera¸c˜ao de informa¸c˜oes a partir das intera¸c˜oes sociais. Perspectivas em Ciˆencia da informa¸c˜ao, 2008.
[8] Meireles, M. R. G., Almeida, P. E. M., Resende Silva, A. C. M. -Recupera¸c˜ao de informa¸c˜ao no ambiente acadˆemico: georreferenciamento dos da-dos da-dos estudantes do Instituto de Educa¸c˜ao Continuada da PUC Minas. Perspectivas em Ciˆencia da informa¸c˜ao, 2009.
[9] Pedrosa, D. P. F. - Ajuste de Curvas. Notas de Aulas.
[10] Runges Phenomenon - /en.wikipedia.org/wiki/Runge’s-phenomenon acessada em Janeiro de 2010.
[11] Shiguti, W. A., Shiguti, V. S. C. -Estat´ıstica, Bras´ılia, 2006.