Utilizando estimadores entrópicos generalizados na estimação de modelos de apreçamento de ativos

FUNDAÇÃO GETULIO VARGAS

ESCOLA de PÓS-GRADUAÇÃO em ECONOMIA

Diego Gusmão Brandão

Utilizando Estimadores Entrópicos

Generalizados na Estimação de

Modelos de Apreçamento de Ativos

Diego Gusmão Brandão

Utilizando Estimadores Entrópicos

Generalizados na Estimação de

Modelos de Apreçamento de Ativos

Dissertação para obtenção do grau de mes-tre apresentada à Escola de Pós-Grauação em Economia

Área de concentração: Finanças Orientador: Caio Ibsen Almeida

Ficha catalográfica elaborada pela Biblioteca Mario Henrique Simonsen/FGV

Brandão, Diego Gusmão

Utilizando estimadores entrópicos generalizados na estimação de modelos de apreçamento de ativos / Diego Gusmão Brandão. – 2014.

27 f.

Dissertação (mestrado) - Fundação Getulio Vargas, Escola de Pós-Graduação em Economia.

Orientador: Caio Ibsen Almeida. Inclui bibliografia.

1. Avaliação de ativos (Modelo CCAPM). 2. Processo estocástico. 3. Risco (Economia). 4. Calamidades públicas – Aspectos econômicos. I. Almeida, Caio Ibsen Rodrigues de. II. Fundação Getulio Vargas. Escola de Pós-Graduação em Economia. III. Título.

Resumo

Este trabalho analisa as propriedades de uma nova medida de má especificação de modelos de apreçamento, que está relacionada com o tamanho do ajuste multiplicativo necessário para que o modelo seja corretamente especificado. A partir disso, caracterizamos o parâmetro que minimiza a medida a partir de um programa dual, de solução mais simples. Os estimadores naturais para esse parâmetro pertencem à classe de Generalized Empirical Likelihood. Derivamos as proprieda-des assintóticas proprieda-deste estimador sob a hipótese de má especificação. A metodologia é empregada para estudar como se comportam em amostras finitas as estimativas de aversão relativa ao risco em uma economia de desastres quando os estimadores estão associados a nossa medida de má especificação. Nas simulações vemos que em média a aversão ao risco é superestimada, mesmo quando ocorre um número significativo de desastres.

Sumário

1 Introdução 1

2 Modelos de Apreçamento 3

2.1 Modelos de Apreçamento de Ativos . . . 4 2.2 Determinação de θ . . . 7

2.3 Decomposição do Fator Estocástico de Desconto. . . 8

3 Distâncias multiplicativas 9

3.1 Determinação de θ . . . 10

3.2 Estimação . . . 12

4 Aplicação Para Economia de Desastres 15

4.1 A Economia . . . 15 4.2 Simulações e Resultados . . . 16

5 Conclusão 19

Capítulo 1

Introdução

Os modelos de apreçamento capturam certas características da realidade para explicar como os preços dos ativos estão relacionados a seus pagamentos futuros. Entretanto, modelos são aproximações do mundo real e em geral são incapazes de precificar ativos sem erro, isto é, eles estão potencialmente mal especificados. Este artigo propõe uma medida de má especificação para modelos de apreçamento que permite ordenar o desempenho de diferentes parametrizações do fator estocástico de desconto.

Os fatores estocásticos de desconto associam preço e payoff através da equação de Euler (Co-chrane, 2005; Duffie, 2001), mas modelos incorretamente especificados são incapazes de satisfazê-la precisamente. Porém, existem inúmeras formas de distorcer a medida de probabilidade real para apreçar sem erros os ativos. Nossa abordagem consiste em mensurar essas distorções e determinar o grau de má especificação a partir do menor ajuste necessário para que o modelo seja corretamente especificado.

Podemos interpretar as distorções da medida de probabilidade como um ajuste multiplicativo não paramétrico sobre o fator estocástico de desconto. Vamos estabelecer uma família de medidas, determinadas a partir de funções de Cressie-Read (Cressie e Read, 1984) que levarão em conta os diversos momentos populacionais para calcular o tamanho desse ajuste. Esta família específica de funções permite caracterizar os problemas de otimização desenvolvidos neste artigo de forma simples a partir de sua formulação dual (veja, por exemplo, Borwein e Lewis, 1991; Kitamura, 2000; Kitamura, 2006; Newey e Smith, 2004).

Nosso trabalho tem origem em Hansen e Jagannathan (1997), que estabelecem como medida de má especificação a distância, associada a norma do L2, entre a variável de apreçamento

do modelo e o conjunto de todos os fatores estocásticos de desconto. Como resultado, payoffs com maior variabilidade possuem menor peso na determinação do grau de má especificação. Almeida e Garcia (2012) generalizam a distância de Hansen e Jagannathan levando em conta de que forma diferentes momentos amostrais podem ser utilizados na avaliação de modelos. O emprego de diversos momentos populacionais na mensuração do grau de má especificação se torna interessante quando os payoffs da economia são não gaussianos. Neste caso, é possível se beneficiar das diversas informações contidas na distribuição dos ativos, sem se limitar ao segundo momento populacional.

2

a minimizar seu grau de má especificação. Isto pode ser útil se reconhecemos que um modelo está potencialmente mal especificado e temos interesse em empregá-lo para precificar ativos. Os parâmetros ótimos serão estimados a partir das versões amostrais da nossa metodologia e os estimadores se encontram na classe de Generalized Emprirical Likelihood (Newey e Smith, 2004; Smith, 1997; Qin e Lawless, 1994; Kitamura e Stutzer, 1997). No nosso artigo, provamos as pro-priedades de consistência e normalidade assintótica dos estimadores para modelos incorretamente especificados.

Capítulo 2

Modelos de Apreçamento

Neste capítulo será introduzido o arcabouço de Hansen e Jagannathan (HJ, 1997), caracterizando-se a estrutura de mercado e o ambiente em que a economia opera. Também vamos definir formalmente os conceitos de fator estocástico de desconto e de modelo de apreçamento de ativos utilizados ao longo do texto. Por fim, descreverei algumas medidas de má especificação de modelos de apreçamento presentes na literatura de Finanças.

Suponha uma economia com mercado de ativos cujas transações ocorrem no período t e os

payoffs são recebidos emt+1. O espaço de payoffs é um subconjunto doL2, o espaço das variáveis

aleatórias de segundo momento finito e mensuráveis em relação ao conjunto informacional det+1.

Mais especificamente, vamos supor que qualquer payoff pode ser escrito como a combinação linear de K ativos base, que serão representados pelo vetor x. Neste caso, o conjunto P de payoffs é

representado por:

P ={x·c|c∈❘K}

Vamos supor que a matriz ❊xx′é não singular. Com isso, podemos garantir que todo elemento p _∈P pode ser escrito unicamente como p = ¯c_·x para algum vetor ¯c _∈❘K_{. Sob ausência de}

arbitragem, o preço de qualquer payoff em P é determinado pelo vetor q de preços dos ativos

base. A função de apreçamentoπ(·)em P pode ser escrita como

π(p) =π(c_·x)_≡c_·q

ondec_∈❘K _{é o único portfólio que replica o payoff p.}

Uma variável aleatória m∈L2 tal que

π(p) =❊[m_·p] (2.1)

é chamada de fator estocástico de desconto. O teorema da representação de Riesz garante a existência de pelo menos um fator estocástico de desconto. Sob ausência de arbitragem, e devido à forma específica do conjunto de payoffs, para que uma variável m ∈ L2 satisfaça à equação

4

q=❊[m·x] (2.2)

Para a aplicação empírica, vamos seguir HJ (1997) e supor que esta equação é válida ao longo do tempo, isto é, existe uma sequência{(mt, xt, qt)} que satisfaz a equação 2.2 para todot.

2.1 Modelos de Apreçamento de Ativos

Os modelos de apreçamento tentam entender de que forma os preços dos ativos estão relacionados com os seus payoffs. Associados a esses modelos estão uma equação de apreçamento e um fator estocástico de desconto , que resume todas as informações relevantes para o nosso trabalho. Vamos restringir os modelos de apreçamento à classe paramétrica e representá-los a partir do seu fator estocástico de desconto y(θ), onde θ∈Θé um vetor de parâmetros.

O modelo de Consumption Capital Asset Pricing Model (CCAPM), por exemplo, é descrito pela variável

y(θ) =βG−α (2.3)

onde G é o crescimento do consumo, β é a taxa de impaciência e α corresponde à aversão

relativa ao risco. Na notação anterior, esses parâmetros são representados por θ = (α, β). A

forma funcional y(_·) em 2.3 é apenas uma das dimensões relevantes do fator estocástico de

desconto. A equação de apreçamento leva em conta de que forma as distribuições dos payoffs e de y(θ) estão relacionadas. A função y(θ) = βG−α _{pode corresponder, como veremos adiante,}

ao CCAPM ou a um modelo de desastres, por exemplo, dependendo de como especificamos a distribuição deG.

Os modelos econômicos são aproximações da realidade e pode-se esperar que suas equações de apreçamento não sejam satisfeitas na prática. O CCAPM dificilmente deve ser capaz de apreçar um grande número de ativos com apenas dois parâmetros de escolha. Queremos ser capazes de lidar com modelos mal especificados, cujos fatores estocásticos de desconto geram erros de apreçamento. Esse erros de apreçamento podem surgir, por exemplo, quando restringimos o número de fatores de risco em um modelo, ou quando nos limitamos a formas funcionais simples para o fator estocástico de desconto, como funções afins.

Dizemos que um modelo é mal especificado se não existe parâmetro θ∈Θtal que

q =❊[y(θ)_·x]

Se um modelo não é capaz de precificar corretamente os ativos, gostaríamos de ter uma medida sobre o grau de má especificação para cada θ _∈ Θ. Desta forma, podemos determinar

5

Uma medida natural de má especificação no caso especial em queK= 1é o valor absoluto do

erro de apreçamento do ativo base. Em uma economia com diversos ativos, entretanto, não é clara a forma de mapear todos os erros de apreçamento em uma única medida de má especificação. Hansen e Jagannthan (1997) propõem medir o grau de má especificação de um modelo a partir da distância, induzida pela norma doL2, entrey(θ)e o conjunto de todos os fatores estocásticos

de desconto, que será denotado porM. Para isso, definemδHJ(θ) como o valor:

δHJ(θ) = min

m∈M ky(θ)−mk (2.4)

Está claro que um modelo corretamente especificado satisfaz y(θ) ∈ M para algum θ ∈ Θ

e, neste caso, o valor de δHJ(θ) é igual a zero. Se o parâmetro θ for tal que y(θ) ∈ M/ , a

equação de apreçamento produzirá um vetor de erros diferente de zero. HJ (1997) mostram que a medida δHJ(θ) pode ser calculada a partir dos erros de apreçamento, e que a relação entre

as duas medidas não depende do modelo escolhido. Para entendermos como isso ocorre, é útil tratar o problema 2.4a partir de sua formulação dual, dada por

δ_HJ2 (θ) = min

m∈L2 sup

λ∈❘K

❊(y(θ)₋m)2+ 2λ′_{❊[xm]−2λ}′_q

Mantendo-se λconstante, é fácil verificar que o fator estocástico de desconto que resolve o

problema dual é m = y(θ)₋λ′_{x. Após substituir o valor de m na equação 2.4, resta apenas}

resolver o problema

δ_HJ2 (θ) = max

λ∈❘K❊[y(θ)

2_{−(y(θ)−λ}′_x)2_−2λ′_{q] (2.5)}

ou seja, é possível reduzir o problema original, cuja solução se encontra noL2, a encontrar um

vetorK-dimensional que resolve 2.5. Pela condição de primeira ordem, no ponto ótimo λ∗ _deve

valer

❊[x(y(θ)−λ∗′x)] =q

isto é, calcular a distância de Hansen e Jagannathan é equivalente a obter uma combinação linear dos ativos base da economia que corrige o fator estocástico de desconto de forma a tornar o modelo corretamente especificado. A partir deλ∗ _{podemos encontrar uma forma fechada para}

δHJ(θ).

δHJ(θ) =(❊xy(θ)−q)′(❊xx′)−1(❊xy(θ)−q)1/2 (2.6)

Pela equação acima, vemos que δHJ(θ) é encontrado aplicando-se uma forma quadrática

sobre os de erros de apreçamento. A matriz de peso associada é(❊xx′₎−1_{, isto é, o peso de cada}

6

associado. Quanto maior a variabilidade de determinado payoff, menor sua importância relativa para a avaliação deδHJ(θ).

A medida de má especificação proposta por Hansen e Jagannathan está intimamente ligada ao segundo momento dos payoffs que formam os ativos base da economia. Podemos nos perguntar quais as consequências de alterar essa noção de distância ao empregarmos diferentes momentos populacionais para penalizar erros de apreçamento. A partir desta premissa, Almeida e Garcia (AG, 2012) propõem avaliar a má especificação de modelos de forma robusta à escolha dos momentos dos payoffs.

A idéia de AG (2012) é utilizar a família de funções de Cressie-Read para determinar critérios de distância entre um modeloy(θ) e o conjunto_M. Uma função φ(_·) desta família é indexada

por um parâmetroγ e possui a forma

φ(π) = π

γ+1₋₁

γ(γ+ 1) (2.7)

Fixado o parâmetro γ, o grau de má especificação de um modelo y(θ)é medido por

δγ(θ) = min

m∈M❊[φ(1 +m−y(θ))] (2.8)

Pelo formato de 2.7, vemos queδγ(θ)leva em conta o momento populacional determinado por

γ para medir má especificação. Esta é uma generalização da distância de Hansen e Jagannathan,

que representa o caso especial em queγ = 1. A utilização de diferentes momentos para medir o

grau de especificação é útil, como argumentam AG (2012), quandoy(θ)depende não linearmente

dos ativos primitivos, ou quando esses ativos possuem payoffs não gaussianos. Nesses casos, diferentes momentos populacionais podem trazer informações relevantes sobre o grau de má especificação do modelo.

A escolha da classe de funções de Cressie-Read é útil por admitir uma formulação dual de simples solução. Da mesma forma que HJ (1997), a variável aleatória m ∈L2 que resolve 2.8

pode ser recuperada a partir de um vetor K-dimensional de multiplicadores de Lagrange. Para

isso, seja φ∗_{(·) o conjugado convexo deφ(·), definido por}

φ∗(b) = sup

m∈L2

m′b₋φ(1₋m₋y(θ))

Seguindo Borwein e Lewis (1991), pode-se mostrar que o programa dual a 2.8 é dado por

max

λ∈RKλ

′_q−❊[φ∗_(λ′_{x)] e, sob determinadas condições, obtém-se a equivalência entre o problema}

primal e o dual. Almeida e Garcia (2012) então derivam um modo relativamente simples de computarδγ(θ), a partir de

δγ(θ) = max λ∈❘Kλ

′_q

−❊

(

(γλ′_x)γ+1γ

γ+ 1 + (y(θ)−1)λ

′_x+ 1

γ(γ+ 1)

7

2.2 Determinação de

θ

Os modelos incorretamente especificados estão necessariamente associados a erros de apreça-mento, mas podem ser de interesse como aproximações para os fatores estocásticos de desconto. De que forma podemos parametrizar um modelo potencialmente mal especificado para apreçar um grupo de ativos? Uma possibilidade é fixar uma medida de má especificação e encontrar o parâmetro que a minimiza. Neste caso, estamos interessados emθ∗ _{tal que}

θ∗ =argmin

θ∈Θ

δ(θ)

Em modelos corretamente especificados, θ∗ _{é o elemento do espaço paramétrico que apreça}

corretamente os ativos e possui a propriedade de invariância com relação à escolha da medida. Se nenhum θ ∈Θ satisfaz a equação de apreçamento, então θ∗ será dependende da medida de

má especificação.

Em geral, não conhecemosθ∗_{e devemos estimar seu valor a partir dos dados disponíveis sobre}

ativos e sobre as variáveis que determinam o fator estocástico de desconto. Para isso, suponha a existência de uma série temporal de retornos {Rt}Tt=1, cujo preço é igual a 1 por definição,

e de uma série para as variáveis explicativas de {yt(θ)}Tt=1. Podemos estimar o parâmetro θ∗,

associado a uma determinada medida de má especificação, substituindo os termos populacionais por suas versões amostrais. Desta forma, o estimador_θˆ_{resolve o seguinte programa:}

ˆ

θ = argmin

θ∈Θ

max

λ∈❘K λ

′_✶ K− 1 T T X t=1

φ∗(λ′Rt)

Almeida e Garcia (2012) derivam as propriedades assintóticas de _θˆ _{levando em conta que}

os modelos são potencialmente mal especificados. O caso especial da distância de Hansen e Jagannathan merce destaque por estar conectado à classe de estimadores GMM. Para ver como isto acontece, basta escrever a versão amostral da equação 2.6. O estimador de θ∗ _{pode ser}

escrito como

ˆ

θ=argmin

θ∈Θ

  1 T T X t=1

yt(θ)Rt−✶K

!′ 1 T T X t=1

RtR′t

!−1

1 T

T

X

t=1

yt(θ)Rt−✶K

! 

isto é, o estimador_θˆ_{é equivalente ao GMM com matriz de peso W =}

1

T

PT

t=1RtRt′

−1

8

2.3 Decomposição do Fator Estocástico de Desconto

Gosh, Julliard e Taylor (GJT, 2013) decompõem o fator estocástico de desconto em dois com-ponentes para extrair informações sobre sua entropia. Esta metodologia é similar a utilizada neste trabalho e por este motivo incluimos nesta revisão. O obetivo do artigo de GJT (2013), entretanto, é distinto. Eles utilizam esta decomposição para derivar fronteiras entrópicas para o fator estocástico de desconto mais restritivas do que as fronteiras de média-variância encontradas em Hansen e Jagannathan (1991).

Suponha que um fator estocástico de descontoM pode ser decomposto em dois componentes

M =y(θ)π

onde y(θ) é um componente paramétrico e π é potencialmente não observável. Como M é um

fator estocástico de desconto, para um excesso de retorno Re _{deve valer a equação de Euler}

❊[πy(θ)Re] = 0

A idéia de GJT (2013) é incorporar o componente não observável πna medida real e utilizar

entropia para determiná-lo. Se a variável aleatória π for positiva e absolutamente contínua com

relação a medida da economia, então podemos utilizarπ/❊[π]como derivada de Radon-Nikodym

e escrever

❊π_[y(θ)Re_{] = 0}

.

onde ❊π_{[·]representa a expectativa com relação à medida transformada porπ/❊[π]. GJT (2013)}

utilizam uma noção de distância entre medidas como critério para determinar a variável π∗_,

solução do problema

π∗ = argmin

π ❊

h

π

❊[π]

ln_❊π_[π]i s.a. ❊π[m(θ)Rt] = 0

Capítulo 3

Distâncias multiplicativas

Neste capítulo descreveremos uma medida alternativa para o grau de má especificação de um modelo, que leva em conta o menor ajuste multiplicativo necessário para torná-lo corretamente especificado. Esta medida se relaciona com o artigo de Almeida e Garcia (2012), que utiliza ajustes aditivos para determinar o tamanho da má especificação.

Um ajuste multiplicativo sobre um modelo y(θ) é uma variável aleatória positiva π tal que

❊[π] = 1e

❊[πy(θ)x] =q

Pela equação acima, vemos que o modelo está bem especificado quando π = 1 é um ajuste

multiplicativo para y(θ). Como em GJT (2013), se pudermos garantir que o ajuste é

absolu-tamente contínuo em relação à medida real da economia, π pode ser interpretado como uma

derivada de Radon-Nikodym. Neste caso, um ajuste multiplicativo irá determinar uma nova medida de probabilidade que satisfaz

❊π_{[y(θ)x] =q}

Seguindo AG (2012), vamos utilizar a família de funções de Cressie-Read para medir o tama-nho dos ajustes. Como visto, uma função pertencente a essa família é indexada por um número realγ e possui o seguinte formato

φ(π) = π

γ+1₋₁

γ(γ+ 1)

Para os pontos γ = ₋1 e γ = 0, vamos definir φ(π) = ₋ln(π) e φ(π) = πln(π),

respecti-vamente. Pode-se mostrar que no nosso problema esses são os limites da função φ(_·) quandoγ

tende a -1 e 0.

Vamos definir o tamanho de um ajuste multiplicativo por ❊[φ(π)]. Esta medida está

relaci-onada ao momento deπ determinado pelo parâmetro γ. Note que φ(_·) é uma função convexa

quando restrita a números positivos. Pela desigualdade de Jensen, a função aplicada a um ajuste

10

❊[φ(π)]≥φ(❊[π]) = 0

Para um modeloy(θ), definiremos sua medida de má especificaçãoδ(θ)como o menor ajuste

multiplicativo necessário para que o modelo aprece os ativos corretamente, isto é

δ(θ) = min

π≥0 ❊[φ(π)]

s.a. ❊[πy(θ)x] =q (3.1)

❊[π] = 1

Podemos interpretarδ(θ)como a menor divergência entre a medida real da economia e a

me-dida ajustada para satisfazer a equação de Euler. Se o modelo estiver corretamente especificado, então o ajuste π = 1 será factível e a distância de y(θ) será igual a zero no valor verdadeiro

de θ. Caso isso não ocorra, a distância será estritamente positiva e levará em conta o momento

populacional definido porγ na função φ(_·).

3.1 Determinação de

θ

Como vimos no capítulo anterior, para um modeloy(θ), estamos interessados no parâmetroθ∗que

minimiza determinada noção de má especificação. Vamos estudar de que forma as propriedades de θ∗ _{se modificam ao utilizarmos a família de distâncias definidas por 3.1. O parâmetro θ}∗ _é

tal que

θ∗ _{= argmin}

θ∈Θ

δ(θ) (3.2)

Se queremos utilizar y(θ) para apreçar ativos, θ∗ _{é uma escolha natural para parametrizar}

o modelo. Em modelos corretamente especificados, θ∗ _{é o parâmetro que apreça corretamente}

os ativos e é invariante à escolha da distância. No caso de má especificação, θ∗ _{dependerá da}

medida associada a φ(_·).

Vamos caracterizar o parâmetroθ∗ _{a partir das condições de primeira ordem de seu problema}

de otimização. Para isso, escreva

θ∗ = argmin

θ∈Θ, π≥0 ❊

πγ+1−1 γ(γ+ 1)

s.a. ❊[πy(θ)x] =q (3.3)

❊[π] = 1

Defina π∗ _{como a solução para π do problema acima e assuma que π}∗_{>0 eθ}∗_{∈int(Θ). A}

11

L(θ, π, α, µ) =❊[φ(π)]−α′❊[π(y(θ)x−q)] +µ(1−❊[π])

No ponto ótimo(θ∗_{, π}∗_{, α}∗_{, µ}∗_{) deve valer:}

[π] : (π

∗₎γ

γ −α

∗′_(y(θ∗_)x

−q)₋µ∗ = 0 (3.4)

[θ] : α∗′❊

π∗x∂y ∂θ (θ

∗₎

= 0 (3.5)

[α] : ❊[π∗(y(θ∗)x−q)] = 0 (3.6) [µ] : ❊[π∗] = 1 (3.7)

Resolvendo a equação 3.4paraπ∗_{, encontramos}

π∗= γα∗′(y(θ∗x₋q) +γµ∗1_γ

Como ❊[π∗_{] = 1, deve valer1 =❊[π}∗_{] = (γµ}∗₎1γ❊

h

γ_γµα∗∗ ′

(y(θ∗_{x−q) + 1}i 1

γ

e finalmente

π∗=

γ_γµα∗∗

′

(y(θ∗_{)x−q) + 1}

1/γ

❊

"

γα∗

γµ∗

′

(y(θ∗_{)x−q) + 1}

1/γ# (3.8)

Vamos seguir Newey e Smith (2004) e mostrar que (θ∗_,π∗_{) pode ser recuperados pela CPO}

do seguinte problema:

¯

θ=argmin

θ∈Θ

sup

λ∈Λ(θ)−

❊

"

(γλ′_{(y(θ)x−q) + 1)}γ+1γ γ+ 1

#

(3.9)

onde Λ(θ) =_{λ_∈❘K : 1 +γλ′_{(y(θ)x−q))≥0}. Seja θ¯e ¯λ∈Λ(¯θ) soluções de 3.9 e suponha}

que eles sejam pontos interiores. Então, pelas condições de primira ordem, as seguintes equações devem ser satisfeitas

❊

γλ¯′ _y(¯θ)x−q

+ 11/γ¯

λ′_x∂y

∂θ(¯θ)

= 0

❊h γλ¯′ y(¯θ)x−q

+ 11/γ

y(¯θ)x−qi

= 0

Comparando as equações acima com as equações3.5e 3.6, juntamente com o valor deπ∗ _em

3.8, podemos perceber que _λ¯₌ α∗

γµ∗ e θ¯=θ

∗ _{são soluções da condição de primeira ordem. Logo,}

12

3.2 Estimação

Nesta seção vamos propor um estimador paraθ∗ _{e derivar suas propriedades assintóticas levando}

em conta que o modelo correspondente está potencialmente mal especificado. A idéia deste estimador é substituir os momentos populacionais em 3.9pelos seus correspondentes amostrais. O conjunto de dados sobre payoffs será descrito pela série temporal de retornos {Rt}Tt=1,

onde Rt é um vetor K-dimensional. Como visto anteriormente, esses payoffs têm preço igual

a 1 em qualquer período de tempo. Para a seção estatística, vamos representar um modelo de apreçamento de ativos por y(θ,zt), onde y(·,·) é a forma funcional do candidato a fator

estocástico de desconto, invariante no tempo, θ ∈ Θ parametriza a função e zt representa as

variáveis explicativas do modelo. O vetorzt pode conter variáveis como payoffs, retornos ou, por

exemplo, o crescimento do consumo, como no caso do CCAPM.

Para uma determinada medida de má especificação, associada a um parâmetro γ, vamos

estudar o estimador para θ∗ _{dado por}

ˆ

θ=argmin

θ∈Θ

max

λ∈Λ(θ) −

1 T

T

X

t=1

(γλ′_(y(θ,z

t)Rt−✶K) + 1)

γ+1

γ

γ+ 1 (3.10)

Este estimador pertence a classe de Generalized Empirical Likelihood (GEL) descrita por Smith (1997). Para determinados valores deγ,θˆé equivalente a outros estimadores conhecidos na

literatura, como Exponential Tilting (γ = 0)de Kitamura e Stutzer (1997), Empirical Likelihood (γ =₋1), como em Qin e Lawless (1994) e Continuous Updating Estimator (γ = 1)de Hansen,

Heaton e Yaron (1996).

Neste trabalho, vamos derivar as propriedades assintóticas de_θˆ_{para modelos potencialmente}

mal especificados, seguindo Almeida e Garcia (2012). Newey e Smith (2004) derivaram consis-tência e normalidade assintótica do estimador supondo a exisconsis-tência de um único parâmetro que satisfaz a equação de Euler. No nosso arcabouço, isto equivale a supor que o fator estocástico de desconto associado a um modelo apreça corretamente os ativos para um únicoθ. Vamos relaxar

esta hipótese e exigir apenas que θ∗ _{definido em3.2 é único. Esta metodologia abrange o caso}

em que o modelo está bem especificado, já que nesta situação o valor deθque minimiza a função

de distância é o mesmo que apreça corretamente os ativos.

Para o que segue, defina B(a,r) como a bola de centro ae raior, e a funçãof(θ,λ,z) por:

f(θ,λ,z) = (γλ

′_{(y(θ, z)R−✶) + 1)}γ+1γ γ+ 1

Seja Q(θ,λ) =−❊[f(θ,λ,z)] e os seguintes multiplicadores de Lagrange:

λ(θ) =max_λ∈Λ(θ)Q(θ,λ)

ˆ

λT(θ) =maxλ∈Λ(θ)

1 T

T

X

t=1

13

Por fim, defina λ∗ _{= λ(θ}∗_{). As hipóteses abaixo nos dão condições necessárias para que θˆ}

seja um estimador consistente.

Hipótese 1. Suponha que

1. zt é um processo iid

2. θ∈Θ, um conjunto compacto p-dimensional

3. ∃ um único (θ∗,λ∗)∈int(Θ×Λ(θ∗)) solução do problema (1)

4. Para r suficientemente pequeno, ❊[sup_θ¯∈B(θ,r)f(¯θ,λ,z)]<∞ para todo θ∈Θ

5. ❊[fλλ(θ,λ,z)] é uma matriz não singular para todoθ∈Θ

6. θj →θ∈Θ⇒y(θj,z)→y(θ,z) para quase todoz

Vamos utilizar a estratégia de Almeida e Garcia (2012) para provar consistência. A idéia é adaptar a demonstração da consistência do exponential tilting estimator de Kitamura e Stutzer (1997) para os estimadores de toda a família de Cressie-Read e para a possibilidade de má especificação.

Teorema 1. Sob a Hipótese 1,_θˆ_{em 3.10 converge em probabilidade paraθ}∗

Demonstração. Seja λ(θ) a solução demaxλ∈Λ(θ)−❊[f(θ,λ,z)]. A função λ(θ) é contínua pela

hipótese (5), que garante que o Jacobiano da condição de primeira ordem é não singular. Pela

continuidade dey(θ)eλ(θ), deve valerlimδ↓0supθ∈B(¯θ,δ)f(θ,λ(θ),z) =f(¯θ,λ(¯θ),z). Pela hipótese

(4), podemos utilizar o teorema da convergência dominada para mostrar que

lim

δ↓0❊

"

sup

θ∈B(¯θ,δ)

f(θ,λ(θ),z)

#

=Q(¯θ,λ(¯θ))< Q(θ∗,λ(θ∗)) ∀θ¯6=θ∗

Para um dadoδ >0, vamos cobrir o conjunto compactoΘ₋B(θ∗_{,δ) por H bolas B(θ}

j,δj),

onde cadaδj é pequeno o suficiente para que

❊

"

sup

θ∈B(θj,δj)

f(θ,λ(θ))

#

< Q(θ∗,λ(θ∗))

Defina o número positivohj por

2hj =Q(θ∗,λ(θ∗))−❊

"

sup

θ∈B(θj,δj)

f(θ,λ(θ))

#

Pela lei dos grandes números, podemos garantir que para um determinado ε > 0 existe Tj

suficientemente grande tal que paraT > Tj

P 1 T T X t=1 sup

θ∈B(θj,δj)

f(θ,λˆT(θ),z)> Q(θ∗,λ(θ∗))−hj

!

14

ComoΘ₋B(θ∗_{,δ)⊆ ∪}H

j=1B(θj,δj), paraT > maxjTj e h=minjhj deve valer

P sup

θ∈Θ−B(θ∗_,δ)

1 T

T

X

t=1

f(θ,ˆλT(θ),z)> Q(θ∗,λ(θ∗))−h

!

< ε

2 (3.11)

Pode-se mostrar, conforme AG (2012), que sob a hipótese 1, ˆ_λT(θ∗_{) satisfaz as condições de}

consistência de extremum estimators (ver Newey e Mcfadden (1994)) e converge em probabilidade paraλ(θ∗_{). Pela lei dos grandes números, para T suficientemente grande deve valer}

P 1 T

T

X

t=1

f(θ∗,ˆλT(θ∗),z)−Q(θ∗,λ(θ∗))<−

h 2

!

< ε

2 (3.12)

Pelas equações 3.11e 3.12, podemos concluir que

lim

T→∞P _θ∈Θ−sup_B(θ∗_,δ)

1 T

T

X

t=1

f(θ,λˆT(θ),z)−

1 T

T

X

t=1

f(θ∗,λ(θ∗),z)>₋h 2

!

= 0

MasP(ˆθ /_∈B(θ∗_,δ))≤Psup

θ∈Θ−B(θ∗_{,δ) T}1

PT

t=1f(θ,ˆλT(θ),z)−T1

PT

t=1f(θ∗,λ(θ∗),z)>0

_p

→

0. Como δ é arbritário, prova-se a consistência.

Para encontrar a distribuição assintótica de _θˆ_{, basta utilizar as condições de primeira ordem}

e obter a expansão de Taylor em torno de (θ∗,λ∗). Para facilitar notação, defina Φ = (θ,λ), G(Φ) = _∂∂_ΦT1 PT

t=1f(θ,λ,zt), Hn(Φ) = ∂

2

∂Φ2_T1

PT

t=1f(θ,λ,zt) e H(Φ) = ∂

2

∂Φ2❊[f(θ, λ, z)]. Pela

condição de primeira ordem, deve valer:

0 =G( ˆΦ) =G(Φ∗) +H( ¯Φ)( ˆΦ₋Φ∗)

onde _Φ¯ _{está entre Φ}ˆ _{e Φ}∗_{. Seguindo AG (2012), precisamos das seguintes hipóteses adicionais}

para obter a distribuição assintótica de (ˆθ,ˆλ)

Hipótese 2. Suponha que

1. V ar√T G(φ∗_)→p _S

Φ >0

2. H(Φ∗) é não singular

3. ❊hk_∂θ∂λ∂2 f(θ,λ,z)k2bi_{<∞ ∀λ∈❘}K

4. ∂

∂λf(θ,λ,z) é duas vezes continuamente diferenciável em θ∗, para qualquer λ e para quase

todo z

Se as hipóteses 1 e 2 são atendidas, AG (2012) demonstram que

√

TΦˆ₋Φ∗_{→ N}d (0,VΦ)

Capítulo 4

Aplicação Para Economia de Desastres

Neste capítulo, vamos utilizar nossa metodologia para estimar o coeficiente de aversão ao risco em uma economia simulada de desastres. Este tipo de economia é especialmente interessante já que os retornos são não gaussianos, um dos casos em que nosso método é de potencial interesse. O exercício será realizado com o uso de um modelo corretamente especificado, implicando que todos os estimadores devem convergir para o mesmo ponto, conforme discutido neste trabalho. O enfoque entretanto, será em amostras pequenas, um das motivações de se utilizar um modelo de desastre para explicar o alto equity premium histórico americano. O objetivo será comparar o desempenho dos estimadores quando modificamos a forma de medir ajustes multiplicativos.

4.1 A Economia

Vamos seguir o modelo de Barro (2006), juntamente com a estrutura de jumps desenvolvida em Backus, Chernov e Martin (2011). Seja uma economia de agente representativo como em Lucas (1978), com uma árvore e produção estocástica exógena. O produto da árvore será denotado por

At, que será igual a ct, o consumo, em equilíbrio. A utilidade do agente representativo é dada

por

❊

( _∞ X

t=1

βtu(ct)

)

onde u(c) = c1−α/(1−α) e α ≥ 0 é o coeficiente de aversão ao risco. Suponha um ativo

transacionado emtcujos dividendos Dt+1 são recebidos apenas em t+ 1. Podemos encontrar o

preço deste ativo pela condição de otimalidade do agente

Pt=❊

"

β

ct+1

ct

−α

Dt+1

#

Vamos considerar dois tipos de ativos. O primeiro paga como dividendo o produto do período, ou seja, Dt+1 =At+1, e o segundo é um ativo livre de risco que paga uma unidade no período

16

R_tf₊₁, respectivamente, e podem ser escritos como

Rt+1 = At+1

Pt

Rf_t+1= 1 P_tf₊₁

O fator estocástico de desconto é dado por

y(θ) =β

ct+1

ct

−α

A economia de desastres será caracterizada pela dinâmica do crescimento do produto, que possui a seguinte estrutura

lnAt+1 =lnAt+wt+1+zt+1

onde (wt+1, zt+1) são independentes entre si e através do tempo. O primeiro componente tem

distribuição normal w _{∼ N}(µ, σ2_{). O segundo componente, associado aos jumps, possui como}

elemento central a variável aleatória j, cujas realizações são números inteiros positivos com

probabilidade e−ω_ωj_{/j!. O parâmetro ω mede a intensidade de jumps e representa a média e}

variância de j. Condicional a um determinadoj, a variávelzt+1 possui distribuição normal

zt+1 ∼ N(jb, js2) para j= 0,1,2,...

4.2 Simulações e Resultados

Seguindo Martin (2013), nos perguntamos como se comportam as estimativas deαse a economia

de desastres for uma descrição perfeita da realidade. A premissa deste tipo de modelo é que uma pequena possibilidade de ocorrer um desastre pode gerar um grande equity premium. Os dados disponíveis sobre o consumo americano cobrem um período de um pouco mais de um século. É possível que nos últimos cem anos a economia americana tenha tido uma quantidade menor de desastres do que sua distribuição populacional implicaria devido à pequena probabilidade deste evento ocorrer.

O excesso de retorno nesta economia depende positivamente tanto do grau de aversão ao risco do consumidor representativo, quanto do risco presente na equity, relacionado diretamente com o risco de consumo. Se a realização de desastres é menor do que a esperada, podemos presumir que o estimador de α superestime a aversão ao risco verdadeira.

Vamos estudar como se comportam alguns componentes da classe de estimadores que desen-volvemos no artigo. Para isso, vou realizar um exercício similar a Martin (2013), que estimou

(β, α)em economias simuladas de 100 anos por GMM. Como foram utilizados 2 ativos para

esti-mar o mesmo número de parâmetros, o estimador de GMM é o vetor ( ˆβ,α)ˆ que satisfaz as duas

equações de momento. É fácil ver que este mesmo vetor é o estimador de (β, α) para qualquer

uma das medidas discutidas neste artigo.

Por este motivo, modificaremos o exercício supondo que o verdadeiro valor deβ é conhecido.

17

associados à nossa medida de má especificação: exponential tilting (γ = 0), empirical likelihood (γ =−1), continuous updating estimator (γ = 1)e o caso em queγ = 2.

Simulei 1000 vezes uma economia de 100 anos para cada parametrização, que descreveremos agora. Para todas as simulações utilizamosβ =.97 e α = 4. Vamos seguir Martin (2013), que

adota as frequências empíricas reportadas por Barro (2006) para determinar os parâmetros de seu modelo. O valor deω é .017, implicando que o número esperado de desastres em 100 anos é

igual a 1.7, mesma frequência de desastres de Barro (2006). Seguindo as estatísticas encontradas no mesmo artigo, o tamanho médio da contração da economia e o seu desvio padrão são dados porb =₋.38 e s=.25. Por fim, a parte gaussiana do modelo é determinada pelos parâmetros µ=.025eσ =.02. O exercício será refeito para outras parametrizações do componente de jump,

que refletem diferentes severidades dos desastres sobre a economia.

Na tabela1apresentamos, para cada especificação de parâmetros, o valor médio da estimação

deαˆ em relação em relação às 1000 simulações.

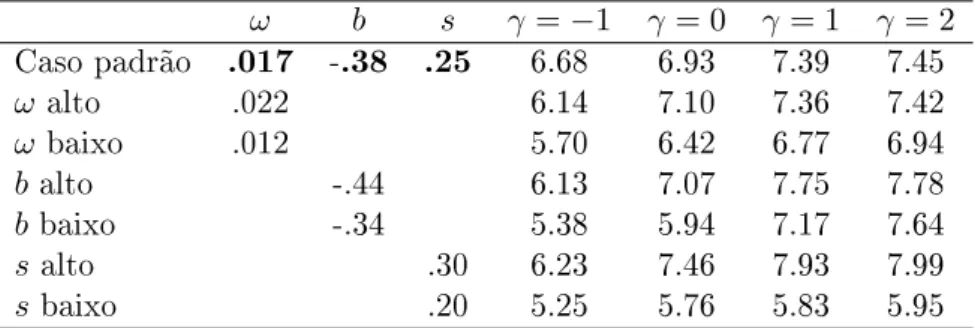
Tabela 4.1: Estimandoα

ω b s γ =₋1 γ = 0 γ = 1 γ = 2

Caso padrão .017 -.38 .25 6.68 6.93 7.39 7.45

ω alto .022 6.14 7.10 7.36 7.42

ω baixo .012 5.70 6.42 6.77 6.94

b alto -.44 6.13 7.07 7.75 7.78

b baixo -.34 5.38 5.94 7.17 7.64

salto .30 6.23 7.46 7.93 7.99

sbaixo .20 5.25 5.76 5.83 5.95

Podemos observar pela tabela acima que valores maiores de γ tendem a sobrevalorizar o

coeficiente de aversão ao riscoα em amostra finita (devemos lembrar que todos os estimadores

são consistentes). Isto nos leva a concluir, como em Martin (2013), que 100 anos não são suficientes, nem mesmo aproximadamente, para que os resultados assintóticos passem a valer em uma economia com jumps.

Como esperado, os resultados tendem a ser piores quando a economia se distancia do caso gaussiano, isto é, quando (ω,b,s) assumem seus valores mais altos. O problema é mitigado em

parte quando γ está perto de−1, 0, indicando que as medidas de má especificação possuem

desempenhos distintos em amostras pequenas.

É necessário ressaltar um problema computacional importante. O problema primal nos leva a procurar um vetor π tal que PT

t=1πt β(ct+1/ct)−αRt+1−✶

= 0. Como o modelo está

corretamente especificado, é possível atender à condição de Euler com probabilidade tendendo a 1. Em amostras pequenas, entretanto, o vetor π que atende a condição de momento pode

18

Na economia de desastres, esse problema é mais acentuado quando o evento de jump não está presente na amostra realizada. Neste caso, é fácil encontrar um vetorλtal que todos os valores

de λ′_(β(c

t+1/ct)−αRt+1−✶) sejam estritamente positivos. Com isso, a função que λminimiza

assume valores arbitrariamente baixos e o problema não possui solução. Por este motivo, a amostra simulada foi filtrada para cobrir apenas problemas de solução finita, e somente uma pequena parte dessa amostra tem zero desastres.

Intuitivamente, esperamos que se o número de desastres ocorridos na amostra for baixo, o estimador tenderá a superestimar o valor de α. Na tabela abaixo, apresentamos a média

do coeficiente de aversão ao risco estimado entre as simulações para diferentes valores de γ

condicional ao número de jumps. Devido ao pequeno número de amostras com nenhum desastre, este caso não foi incluído na tabela. Foram utilizados os parâmetros do caso padrão.

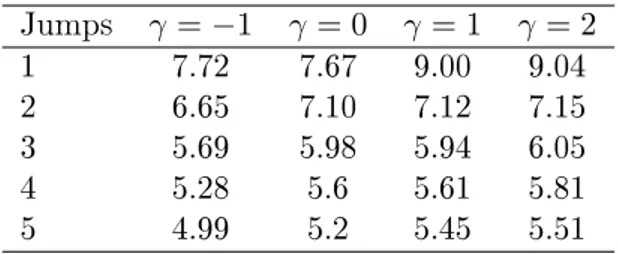
Tabela 4.2: Estimativas deα e número de jumps

Jumps γ =₋1 γ = 0 γ = 1 γ = 2

1 7.72 7.67 9.00 9.04

2 6.65 7.10 7.12 7.15

3 5.69 5.98 5.94 6.05

4 5.28 5.6 5.61 5.81

5 4.99 5.2 5.45 5.51

Pelos dados na tabela, podemos confirmar a intuição que a estimativa para α tende a ser

decrescente com relação ao número de desastres ocorridos. Com apenas um desastre em cem anos, isto é, com apenas um jump, a estimativa média para α varia de7,72 a9,04 nas amostras

simuladas, sendo crescente em relação a γ. No outro extremo, nas amostras com 5 jumps, o

estimador para o coeficiente de aversão ao risco varia menos em relação a escolha da medida, variando de4,99 a5,51.

Os resultados nos mostram que as medidas derivadas dos membros da família de Cressie-Read possuem desempenhos distintos em amostras pequenas. No caso da economia de desastres que simulamos, as probabilidades distorcidas associadas a resultados ruins foram ampliadas, reduzindo a aversão ao risco necessária para satisfazer a equação de Euler. Sob suspeita de desastres raros, a utilização de medidas associadas a γ baixos parece preferível se estivermos

Capítulo 5

Conclusão

Estudamos as propriedades de uma nova medida de má especificação, que leva em conta o tamanho do ajuste multiplicativo necessário para tornar um modelo corretamente especificado. Antes disso, revisamos as principais metodologias que se conectam ao nosso trabalho.

Para essas medidas, caracterizamos os parâmetros que as minimizam a partir de suas for-mulações duais. Os estimadores desse parâmetro pertencem à classe de Generalized Empirical Likelihood, e suas propriedades assintóticas foram obtidas supondo a possibilidade de má espe-cificação, como em Almeida e Garcia (2012).

Por fim, estudei o desempenho de alguns dos estimadores ligados à nossa metodologia para a aversão relativa ao risco em uma economia de desastres. Encontramos uma relação positiva entre a escolha doγ na família de Cressie Read e a estimativa média da aversão ao risco. Além

Referências Bibliográficas

[1] Almeida, C. e Garcia, R. (2012) Assessing misspecified asset pricing models with empirical likelihood estimators. Journal of Econometrics, Vol 170, Issue 2, 519-537

[2] Backus, D., Mikhail, C. e Martin, I. (2011) Disasters Implied by Equity Index Options (with David Backus and Mikhail Chernov), Journal of Finance, 66, 1969–2012

[3] Barro, R. (2006) Rare Disasters and Asset Markets in the Twentieth Century. The Quarterly Journal of Economics, 121, no. 3: 823-866

[4] Borwein J. e Lewis, A. (1991) Duality relationships for entrpy-like minimization problems SIAM Journal of Control and Optimization, 29, 2, 325-338

[5] Cochrane, J. (2005) Asset Pricing, Princeton University Press, Princeton, NJ

[6] Cressie, N. e Read, T (1984) Multinomial goodness of fit tests. Journal of the Royal Statistical Society Series B, 46, 440-464.

[7] Duffie, D (2001) Dynamic Asset Pricing Theory, 3➟ edição, Princeton University Press, Prin-ceton, NJ

[8] Hansen, L. e Jagannathan, R. (1991) Implications of security market market data for models of dynamic econonomies. Journal of Political Economy, 99, 2, 225-262.

[9] Hansen, L. e Jagannathan, R. (1997) Assessing specification errors in stochastic discount factors models. Journal of Finance, 52, 2, 557-589.

[10] Ghosh, A., Julliard, C. e Taylor, A. (2013) What is the Consumption-CAPM missing? An Information-Theoretic Framework for the Analysis of Asset Pricing Models. Working Paper, Carnegie Mellon University

[11] Kitamura, Y. (2000) Comparing misspecified dynamic econometric models using nonpara-metric likelihood. Working Paper, University of Pennsylvania.

[12] Kitamura, Y. (2006) Empirical likelihood methods in econometrics:theory and practice. Wor-king Paper, Yale University.

21

[14] Lucas, R. (1978) Asset prices in an exchange economy Econometrica, 46, 1429–1445.

[15] Luenberger, D. (1969) Optimization by vector space methods. John Wiley & Sons.

[16] Martin, I (2013) Consumption-Based Asset Pricing with Higher Cumulants. Review of Eco-nomic Studies, 80, 745–773

[17] Mehra, R. Prescott, E. (1985) The equity premium: a puzzle. Journal of Monetary Econo-mics, 15, 145-161.

[18] Newey, W. e McFadden, D. (1994) Large sample estimation and hypothesis testing. The Handbook of Econometrics, Volume IV, 2113-2247.

[19] Newey, W e Smith, R. (2004) Higher order properties of GMM and Generalized Empirical likelihood estimators. Econometrica, 72, 219-255.

[20] Qin, J e Lawless, J. (1994) Empirical Likelihood and General Estimating Equations. Annals of Statistics, 22, 300-325.