Fases e criticalidade no modelo ashkin - teller de três cores

(1)

0 2 4 6 8 10 0

2 4 6 8 10

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIˆENCIAS EXATAS E DA TERRA

DEPARTAMENTO DE F´ISICA T´EORICA E EXPERIMENTAL

FASES E CRITICALIDADE NO MODELO ASHKIN-TELLER DE TRˆES CORES

Francisco de Assis Pereira Piolho

Orientador: Prof. Dr. Francisco Alexandre da Costa Co-Orientador: Prof. Dr. Claudionor Gomes Bezerra

Tese apresentada ao Departamento de F´ısica Te´orica e Experimental da Universidade Federal do Rio Grande do Norte como requisito parcial para a obten¸c˜ao do grau de Doutor em F´ısica.

(2)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

CENTRO DE CIˆ

ENCIAS EXATAS E DA TERRA

PROGRAMA DE P ´

OS-GRADUAC

¸ ˜

AO EM F´ISICA

BANCA EXAMINADORA

Orientador:

Francisco Alexandre da Costa

Examinadores externos:

Edvaldo Nogueira Jr.

Idalmir de Souza Queiroz Jr.

Examinadores internos:

Claudionor Gomes Bezerra (Co-orientador)

Ananias Monteiro Mariz

Examinador suplente:

(3)

Conte´

udo

Dedicatoria iv

Agradecimentos v

Lista de abreviaturas vi

Lista de S´ımbolos vii

Prefácio à Versão Original viii

Introdu¸c˜ao 1

1 O Grupo de Renormaliza¸c˜ao na Rede Hier´arquica 13

1.1 Grupo de Renormaliza¸cão . . . 13 1.2 Estabilidade de Fases a partir dos Pontos Fixos . . . 17 1.3 Solu¸cão Exata na Rede Hierárquica. . . 19

2 O Modelo Ashkin-Teller de Duas Cores 23

2.1 Um Modelo para Ligas Quaternárias . . . 23 2.2 AT-2 Anisotrópico na Rede Hierárquica . . . 26

3 AT-2 em Rede Hier´arquica Aperi´odica 37

(4)

3.2 AT-2 Anisotrópico na Rede Hierárquica e Isotrópico no Acoplamento de

Dois Spins . . . 42

3.3 Reproduzindo Resultados . . . 44

3.3.1 Ising Puro Anisotr´opico . . . 44

3.3.2 AT-2 Isotr´opico nas Sub-Redes de Ising . . . 45

3.3.3 AT-2 Anisotr´opico nas Sub-Redes de Ising . . . 49

3.4 Conclus˜ao . . . 51

4 Ashkin-Teller de 3-cores na Rede Hier´arquica 53 4.1 C´alculo das Transmissividades . . . 54

4.1.1 Transmissividade para Spins Localizados Sobre uma Liga¸c˜ao com Pontas Soltas . . . 56

4.1.2 Transmissividade Para um Par de S´ıtios com s Liga¸c˜oes em S´erie . . 59

4.1.3 Transmissividade Para um Par de S´ıtios com r Liga¸cões em Paralelo 66 4.2 Isotropia nas Liga¸cões Ferromagnéticas e nos Acoplamentos de Quatro Spins com Intera¸cões de Troca Aperiódica . . . 70

4.3 Criticalidade no Modelo IAT-3 . . . 73

4.4 Pontos Fixos, Expoentes Cr´ıtidos e o Diagrama de Fases em IAT-3 . . . . 80

4.5 Conclus˜ao . . . 83

5 Conclus˜oes Finais 90 5.1 Perspectivas Futuras . . . 93

Apˆendice A 95 5.2 O Hamiltoniano de Potts . . . 95

5.3 A Matriz Substitui¸c˜ao . . . 96

5.4 Rela¸c˜oes de Recorrˆencia (RR) . . . 97

5.5 Matriz Hessiana e Estabilidade . . . 99

(5)

Apˆendice B 106

5.7 Introduction . . . 107

5.8 Physical model . . . 109

5.9 The isomorphism of the phase diagram . . . 111

5.10 The critical hipersurfaces . . . 112

5.10.1 Two decoupled Ising models . . . 112

5.10.2 Isotropic Ashkin-Teller model . . . 113

Apˆendice C 116 5.11 Introduction . . . 117

5.12 Physical model . . . 118

5.13 The phase diagram of the 3AT model . . . 120

5.14 Conclusions . . . 122

(6)

Dedicat´

oria

A quem posso ”eu”, filho do carbono, Dedicar tantas noites de pouco sono? Se não àqueles que me forjaram No colo ´ıntimo de suas entranhas. A quem? ...se não às mãos estranhas

(7)

Agradecimentos

Apresento, em particular, os meus agradecimentos ao colegas e amigos: Francisco Alexandre da Costa pela coragem de orientar uma alma gêmea; Claudionor Gomes Bezerra pelo belo trabalho de Co-Orienta¸cão important´ıssimo nesta fase final; Edvaldo Nogueira Jr. pela cr´ıtica consistente, zelosa e cuidadosa na condi¸cão de examinador externo; Ana-nias Monteiro Mariz pela postura ética, elegância acadêmica e o zelo responsável na cr´ıtica sutil; Idalmir Queiroz Jr. pelo companherismo de todos os momentos; João Medeiros de Araújo o amigo discretamente presente em todas as horas; Dory Hélio A. L. Anselmo que torceu e me salvou tantas vezes das armadilhas do mundo da informática; Paulo Fulco pelo insentivo integral; Roosevelt Fonseca Soares pela torcida silenciosa e a presen¸ca cons-tante nas horas dif´ıceis; e, em especial, ao meu ”irmão”Francisco Valdomiro de Morais que, além da presen¸ca constante, investiu nessa idéia ao me convidar, através de João Medeiros de Araújo, para integrar os quadros da F´ısica na UERN.

Finalmente,

(8)

Lista de abreviaturas

AT - Ashkin-Teller;

RSGR - Grupo de Renormaliza¸c˜ao no Espa¸co Real; AAT2 - Modelo Ashkin-Teller Anisotropico de 2 Cores; IAT2 - Modelo Ashkin-Teller Isotropico de 2 Cores; AAT-3 - Modelo Ashkin-Teller Anisotropico de 3 cores; IAT-3 - Modelo Ashkin-Teller Isotropico de 3 Cores; AT-N - Modelo Ashkin-Teller de N Cores;

AAT-N - Modelo Ashkin-Teller Anisotropico de N Cores; IAT-N - Modelo Ashkin-Teller Isotropico de N Cores;

(9)

Lista de S´ımbolos

Ji,j - Energias de acoplamento entre pares de spins

εi,j - Energia de conﬁgura¸c˜ao

Si,j - Variaveis aleatorias

T - Temperatura absoluta

M - Magnetiza¸c˜ao

(10)

Pref´

acio `

a Vers˜

ao Original

(11)

Resumo

O modelo Ashkin-Teller (AT) usual consiste na superposi¸cão de dois modelos de Ising acoplados por um termo de intera¸cão de quatro spins. Em duas dimensões o modelo AT apresenta uma linha de pontos fixos com expoentes cr´ıticos variando continuamente, sobre a qual ele se torna solúvel através de um mapeamento no modelo Baxter. Motivado por esta riqueza de comportamento multicr´ıtico em duas dimensões, Grest e Widom intro-duziram e estudaram o modelo Ashkin-Teller de N cores (AT-N), nas versões anisotrópica (AAT-N) e isotrópica (IAT-N), através de vários métodos anal´ıticos e computacionais.

Neste trabalho apresentamos uma versão mais geral do modelo Ashkin-Teller de 3 cores (AT-3) onde é introduzido um acoplamento de 6 spins. Estudamos o modelo através da análise da estrutura de suas simetrias, seguido de análises de poss´ıveis diagramas de fases determinados por técnicas de grupo de renormaliza¸cão no espa¸co real. Esses diagramas são obtidos em temperatura finita na região onde predomina o comportamento ferromagnético. Com o aux´ılio do conceito de transmissividade obtemos as rela¸cões de recorrência em redes hierárquicas com liga¸cões periódicas e quasi-periódicas.

(12)

neste caso, como a aperiodicidade da rede afeta as flutua¸cões geométricas, causando mudan¸cas no comportamento cr´ıtico do modelo. Essas análises foram feitas utilizando defini¸cões apropriadas de transmissividade.

Em seguida passamos ao estudo do modelo Ashkin-Teller de 3 cores onde, além do acoplamento de 4 spins, introduzimos um acoplamento de 6 spins, que torna o modelo mais atraente do ponto de vista das simetrias que ele passa a apresentar. Calculamos rela¸cões de recorrências gerais para o modelo na versão anisotrópica (AAT-3), de onde podemos obter o caso particular do sistema isotrópico (IAT-3), em certas redes hierárquicas. A versão IAT-3 do modelo foi estudada detalhadamente na região onde predominam as intera¸cões ferromagnéticas. Determinamos os pontos fixos e respectivos expoentes cr´ıticos. Analisando as bacias de atra¸cão desses pontos fixos, conseguimos obter o diagrama de fases tri-dimensional (temperatura_×acoplamento de quatro spins _×acoplamento de seis spins). Identificamos pontos fixos do tipo Ising e de Potts de 4 e de 8 estados, além de ind´ıcios de um ponto fixo reminiscente do Potts de 6 estados e uma possibilidade de uma linha de Baxter. Identificamos também pontos fixos cr´ıticos instáveis que não pertencem a nenhuma classe de universalidade identificada com o modelo de Potts q estados.

(13)

Abstract

The usual Ashkin-Teller (AT) model is obtained as a superposition of two Ising models coupled through a four-spin interaction term. In two dimension the AT model displays a line of ﬁxed points along which the exponents vary continuously. On this line the model becomes soluble via a mapping onto the Baxter model. Such richness of multicritical be-havior led Grest and Widom to introduce the N-color Ashkin-Teller model (N-AT). Those authors made an extensive analysis of the model thus introduced both in the isotropic as well as in the anisotropic cases by several analytical and computational methods.

In the present work we deﬁne a more general version of the 3-color Ashkin-Teller model by introducing a 6-spin interaction term. We investigate the corresponding sym-metry structure presented by our model in conjunction with an analysis of possible phase diagrams obtained by real space renormalization group techniques. The phase diagram are obtained at ﬁnite temperature in the region where the ferromagnetic behavior is predom-inant. Through the use of the transmissivities concepts we obtain the recursion relations in some periodical as well as aperiodic hierarchical lattices.

(14)

out by the use of appropriated deﬁnitions of transmissivities.

Finally, we considered the modified 3-AT model with a 6-spin couplings. With the in-clusion of such term the model becomes more attractive from the symmetry point of view. For some hierarchical lattices we derived general recursion relations in the anisotropic ver-sion of the model (3-AAT), from which case we can obtain the corresponding equations for the isotropic version (3-IAT). The 3-IAT was studied extensively in the whole region where the ferromagnetic couplings are dominant. The fixed points and the respective crit-ical exponents were determined. By analyzing the attraction basins of such fixed points we were able to find the three-parameter phase diagram (temperature _× 4-spin coupling

×6-spin coupling). We could identify fixed points corresponding to the universality class of Ising and 4- and 8-state Potts model. We also obtained a fixed point which seems to be a sort of reminiscence of a 6-state Potts fixed point as well as a possible indication of the existence of a Baxter line. Some unstable fixed points which do not belong to any aforementioned q-state Potts universality class was also found.

(15)

Introdu¸c˜

ao

O grande desafio para os teóricos que estudam sistemas da natureza está na cria¸cão de modelos matemáticos que codifiquem, em linguagem corrente e universal, a fenomenologia das nossas observa¸cões através de parâmetros mensuráveis controlados. E tudo come¸ca na identifica¸cão desses parâmetros. Que grandezas podem representar, por exemplo, o estado de um sistema e suas diversas fases? Como se dá a transi¸cão de um estado desordenado de alta entropia para um estado ordenado de baixa entropia? A transi¸cão de um metal para um supercondutor? A transi¸cão Hélio 3 para Hélio 4 ou de um fluido para um superfluido? Será que existe uma teoria que unifique tudo isso?

A busca por explica¸cões e respostas para essas questões gerou, ao longo de décadas, es-pecula¸cões em torno de modelos fenomenológicos baseados nas teorias clássicas (Mecânica e Magnetismo), culminando, após o advento da Mecânica Quântica, nos sofisticados mo-delos de spins localizados.

(16)

Figura 1: a) Transi¸cão l´ıquido-gás; b) Transi¸cão ferro-antiferro.

outras ´areas do conhecimento.

No tocante ao estudo de fluidos, através de modelos magnéticos, a conexão é feita via gás de rede4_{. A busca, então, pelos modelos magnéticos, lembrando que estamos} na origem das primeiras iniciativas nesse campo, se tornavam cada vez mais instigantes, embora com uma Mecânica Estat´ıstica incipiente e sem a clareza de como juntar aspectos tão distintos de fenômenos aparentemente tão diferentes. O grande impulso ocorre quando em 1905 Langevin5 _{postula a existência de momentos magnéticos atômicos e ressalta a} importância do efeito cooperativo no ferromagnetismo.

Considerando o caso em que estes momentos se apresentavam com duas orienta¸cões opostamente privilegiadas, Lenz6 _{propôs em 1920 um modelo, em que a cada s´ıtio i é} associado uma variável σi, onde s´ıtios vizinhos interagem entre si, com uma energia

(17)

premis-e possui carátpremis-er cooppremis-erativo — muitos graus dpremis-e libpremis-erdadpremis-e corrpremis-elacionados — mantpremis-endo a ordem em face a agita¸cão térmica.

Esses fenômenos ocorrem de acordo com mudan¸cas nas condi¸cões externas ou na com-posi¸cão de um sistema em equil´ıbrio termodinâmico, e são caracterizados por uma variável chamada parâmetro de ordem, que se torna nula, completamente, na fase de maior en-tropia (desordenada). Mariz ressalta os vários tipos de desordem, destacando os casos da estrutura cristalina, que podem ser classificados como: substitucional, na qual alguns átomos da substância são substituidos por impurezas; intersticial, onde as impurezas são introduzidas nos interst´ıcios dos s´ıtios cristalinos; e estrutural, caracterizada por uma distribui¸cão aleatória dos átomos da substância. Quando a desordem, associada à substância, ocorre por meio de um rebaixamento rápido da temperatura, para aquém da temperatura cr´ıtica, chamamos temperada (”quenched”). Por outro lado, é dita reco-zida (”annealed”) se este resfriamento é feito de forma lenta, permitindo que o sistema se acomode aos estados de mais baixa energia livre. Assim, podemos ter sistemas rep-resentados por parâmetros de ordem escalares (ferromagnetos altamente anisotrópicos), vetoriais (ferromagnetos usuais), tensoriais (cristais l´ıquidos) ou até uma grandeza com-plexa (superfluidos).

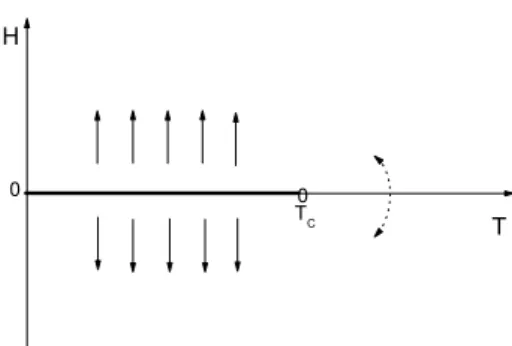
Do ponto de vista termodinâmico, as transi¸cões de fases ocorrem quando há uma sin-gularidade no potencial termodinâmico (energia livre) apropriado. E conforme exista ou não calor latente elas são denominadas de primeira ordem (descont´ınua) ou de segunda ordem (cont´ınua), respectivamente. Segundo a classifica¸cão de Fisher7_{, a transi¸cão de} primeira ordem ocorre quando o parâmetro de ordem apresenta uma descontinuidade no ponto de transi¸cão, enquanto a transi¸cão de segunda ordem ocorre quando o parâmetro de ordem vai a zero continuamente, ou seja, das proximidades até o ponto de transi¸cão. Vamos ilustrar considerando um sistema ferromagnético simples sujeito a um campo ex-terno H. No diagrama de fases, mostrado na Figura 2, existe uma linha 0 ₋TC sobre a qual a transi¸cão é de primeira ordem terminando em um ponto cr´ıtico (TC), onde a susceptibilidade diverge.

(18)

Figura 2: Diagrama de fases de um ferromagneto simples mostrando a linha de transi¸c˜ao de primeira ordem (0< T < TC) e a transi¸cˆao cont´ınua paraT > TC, emH = 0.

na Figura 3 que: a) Para T > TC a magnetiza¸cão varia continuamente; b) Para T =TC, M é uma curva cont´ınua com derivada infinita em H = 0, indicando uma transi¸cão de segunda ordem; c) ParaT < TC, M é descont´ınua em H = 0 e, portanto, a transi¸cão é de primeira ordem.

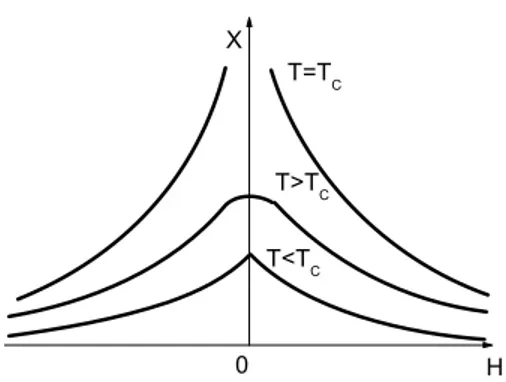
Sendo a derivada da magnetiza¸cão (M) em rela¸cão ao campo (H) definida como a susceptibilidade magnética (χ) do sistema, a Figura 4 mostra como ela reage à varia¸cão da temperatura nos limites do ponto cr´ıtico, suscitando a curiosidade dos estudiosos na busca de explica¸cões. Ver-se que: a) Para T > TC, χ é uma fun¸cão suave de H; b) Para

T < TC surge uma cúspide em H = 0 caracterizando uma transi¸cão de primeira ordem; e c) Para T =TC há uma divergência na susceptibilidade em H = 0, caracterizando uma transi¸cão de fase de segunda ordem. Essas transi¸cões que ocorrem a campo nulo (H = 0), são devido a simetria do ferromagneto ser invertida na presen¸ca do campo magnétido externo H.

(19)

Figura 3: No diagrama acima ver-se como o parâmetro de ordem, neste caso a magnetiza¸cão M, se comporta na presen¸ca de um campo externo H para três intervalos de temperaturas diferentes, em torno deH = 0: (a) entreT < TC, M é descont´ınua; (b) emTC, M é cont´ınua mas tem uma

derivada infinita e (c) paraT > TC, M é cont´ınua com derivada finita.

associadas a estados metaestáveis. Assim, a transi¸cão ocorre quando as fases distintas possuem a mesma energia livre. Na transi¸cão de segunda ordem não existe coexistência de fases. Sobre a linha 0₋TC, da Figura 2, coexistem as fases ferromagnética e antiferro-magnética. No ponto cr´ıtico (T =TC) não há coexistência, as fases se fundem. Enquanto que, para T > TC as fases ferromagnética e/ou antiferromagnética não coexistem, nem como estado estável nem como estado metaestável.

(20)

desorde-Figura 4: Dependência da susceptibilidade com o campo magnético externo nas proximidades de H= 0 para três temperaturas diferentes.

nada separada por duas linhas de segunda ordem de duas fases ordenadas - uma delas é uma fase ferromagnética e a outra é uma fase modulada; e os pontos cr´ıticos terminais12 quando duas linhas de primeira ordem se encontram com uma de segunda. Finalmente temos a existência de pontos de múltiplas fases no encontro de linhas de transi¸cão de segunda ordem.

´

E a partir dos pontos cr´ıticos que se vislumbra as fronteiras cr´ıticas como divisor de águas das diversas fases. Identificá-las e sobre elas estudar, a partir de argumentos de escala, o comportamento assintótico de parâmetros relevantes é identificar espoentes que geram classes de universalidades na classifica¸cão de sistemas f´ısicos, a elas, associados.

´

E sabido que um conjunto importante desss grandezas - obtido por diversos processos: anal´ıtico, num´erico e monte carlo - ´e de interesse f´ısico relevante:

• C_→ O calor espec´ıﬁco;

(21)

• χ_→ Fun¸c˜ao resposta - por exemplo, a susceptibilidade;

• ξ_→ O comprimento de correla¸cão - mede o alcance da fun¸cão de correla¸cão (Γ(r)), que diverge em transi¸cões cont´ınuas.

Todas elas apresentam um comportamento peculiar nas transi¸cões e geram, na criti-calidade (T = TC), um conjunto de expoentes (α, β, γ, ν, etc.), denominados expoentes cr´ıticos, que geram classes de universalidades caracter´ısticas de cada sistema. O inter-essante é que estes expoentes guardam rela¸cões entre s´ı de modo que um par deles é suficiente para encontrarmos os demais. Para identificar e caracterizar os principais ex-poentes cr´ıticos recorremos ao modelo do ferromagneto, nas proximidades de T = TC e

H = 0, tomando o parˆametro t =T ₋TC para averiguar o que ocorre com as grandezas nas proximidades de um ponto cr´ıtico quando nos aproximamos deste por cima (T > TC) ou por baixo (T < TC). Veriﬁca-se um comportamento da forma:

C _∼(₋t)−α′; t <0, H = 0, (1)

C _∼(t)−α; t >0, H = 0, (2)

M _∼(₋t)β; t <0, H = 0, (3)

χT ∼(−t)−γ

′

; t <0, H = 0, (4)

χT ∼(t)−γ; t >0, H = 0, (5)

ξ _∼(₋t)−ν′

; t <0, H = 0, (6)

(22)

M _∼(₋H)1/δ; t= 0, H = 0, (8) onde α, β, γ, ν e δ são, respectivamente, associados ao calor espec´ıfico (C), a magne-tiza¸cão (M) a campo nulo, a susceptibilidade (χ), ao comprimento de correla¸cão (ξ) e a magnetiza¸cão (M) com H = 0.

As propriedades de escala e hiperescala dos potenciais termodinâmicos, conjecturadas a partir da homogeneidade da energia livre no ponto cr´ıtico, mostraram que esses ex-poentes não são independentes entre si, pois apenas dois determinam todos os demais. Algumas dessas rela¸cões foram obtidas por meio de argumentos termodinâmicos e de Mecânica Estat´ıstica13_{, por Fisher}14_{, Josephson}15_{, Rushbrooke}16_{e Griffiths}17_{. As rela¸cões} são,

γ =ν(2₋η) (F isher), (9)

dν = 2₋α (Josephson), (10)

α+ 2β+γ = 2 (Rushbrooke), (11)

α+β(1 +δ) = 2 (Grif f iths). (12)

Estas rela¸cões têm sido sistematicamente verificadas por meio da análise de dados ex-perimentais e de cálculos exatos ou numéricos através de expansões em séries de altas temperaturas.

(23)

Tabela 1: Valores num´ericos de expoentes cr´ıticos para alguns Modelos e Sistemas1_.

Modelos e sistemas α β γ δ ν η

Campo M´edio 0(desc.) 1/2 1 3 1/2 0

Ising (d=2; exato) 0(log.) 1/8 7/4 15 1 1/4

Esf´er.(d= 3; exato) -1 1/2 2 5 1 0

Ising (d= 3; num´erico) 0.125 0.313 1.250 5 0.638 0.041 Heisenberg (d= 3; S = 1/2; num´erico) 0 0.345 1.375 5 0.702 0.043

Xenˆonio (d= 3; Fluido) <0.2 0.35 1.26 4.4 0.57

H´elio-4 (d= 3; Fluido) 0.36 1.24

CO2 (d= 3; Fluido) <0.1 0.35 1.26 4.2

Fe (Ferromagneto) <0.17 0.35 1.33 0.64 0.07

um número menor de equa¸cões a serem resolvidas. Mas, por isso mesmo, seus expoentes cr´ıticos (α = 0, β = 1/2, γ = 1) se mostraram pouco realistas, comparados com outros modelos e sistemas (ver tabela 1) estudados por métodos anal´ıticos (exatos), numéricos, etc. Dos expoentes apresentados na tabela pelo menos dois são obtidos diretamente, enquanto os demais são calculados de forma indireta através das rela¸cões de escala ap-resentadas em 9-12. Por outro lado as solu¸cões de campo médio se tornaram eficazes na constru¸cão de diagramas de fases, importantes para a análise de linhas de transi¸cões, e para determinar propriedades de criticalidade. Como nas regiões cr´ıticas as correla¸cões (ξ) são de longo alcance e envolvem um número muito grande de graus de liberdade, torna-se muito dif´ıcil a abordagem teórica dos problemas de transi¸cões de fases.

(24)

determi-narmos os demais a partir das rela¸cões de escala de 9 a 12. É importante frisar que no processo de renormaliza¸cão obtemos rela¸cões de recorrência dos parâmetros em estudo, e como estamos interessados nas propriedades cr´ıticas, toda tarefa se resume a identificar os atratores - pontos cr´ıticos estáveis para os quais o sistema flui como submetido a um potencial atrativo - que caracterizam as fases obtidas a partir de rela¸cões de recorrência calculadas usando a técnica do GR. Estes atratores definem bacias limitadas por fronteiras cr´ıticas de transi¸cão entre uma bacia e outra - constituindo uma cadeia de pontos que faz o papel das abas al¸cadas da bacia atratora - ou regiões de ”crossover”(superposi¸cão), por-tadoras de grande instabilidade, que apresentam ”topografia”própria no tocante a certos dom´ınios, ou seja, a existência dessas bacias determina regiões de competi¸cão, e é nelas que o dom´ınio de um atrator pode ser repentinamente substituido por outro, e a´ı dizemos que este desfruta de um dom´ınio apenas aparente, como mostra a Figura 5. Isto quer dizer que no mapeamento, ou constru¸cão do diagrama de fases, um determinado ponto é inicialmente atra´ıdo por um ponto fixo, até que outro predomina e o atrai para sua região de fronteiras ou bacia. O expoente que mede esta tendência numa região em que existem vários pontos fixos é chamado expoente cr´ıtico de crossover, que representa a razão entre dois logar´ıtimos dos autovalores da matriz hessiana obtida das rela¸cões de recorrência citadas anteriormente,

φ= ln|λ2 | lnλ1

. (13)

No numerador, o logaritmo do autovalor relevante (λ2) cujo autovetor aponta na dire¸c˜ao tangente a linha de fronteira, e, no denominador, o logar´ıtimo do autovalor relevante (λ1) cujo campo de escala ´e perpendicular a fronteira cr´ıtica.

No caso das redes com aperiodicidade, o expoente de crossover (φ), é identificado como o ”wandering exponent”22 _{de flutua¸cões geométricas (}_ω_{), cujos autovalores} _λ

(25)

Figura 5: As linhas de ﬂuxo mostram que o ponto P ´e inicialmente atra´ıdo pela bacia de P1 e

a partir de certo ponto todo ﬂuxo se volta paraP2. conhecermos Γ - ou a partir da rela¸c˜ao de Fisher.

Para os próximos cap´ıtulos vamos sistematizar o estudo de forma que: No cap´ıtulo um introduziremos a técnica do Grupo de Renormaliza¸cão para calcular expoentes cr´ıticos e mostrar sua eficácia para solu¸cões exatas em redes hierárquicas; a idéia de dizima¸cão preservando as propriedades de escala do sistema em estudo e falar de estabilidade como forma de distinguir a criticalidade de fases espec´ıficas.

No cap´ıtulo dois vamos revisitar o modelo AT-2 em uma rede hierárquica, a partir de um “cluster básico” - célula matriz que substitue liga¸cões - de ponte de Wheatstone e em rede diamante aperiódica, e identificar “hiperplanos” que, também, podem ocultar impressões digitais de fases cr´ıticas.

No cap´ıtulo três, usaremos um “cluster” básico para uma rede diamante simples com intera¸cões de troca aperiódica onde investigaremos o comportamento das flua¸cões geométricas para AT-2 e com alguns resultados estudados na literatura podem ser repro-duzidos.

(26)

de 3 cores em uma rede hierárquica tipo diamante. Quase nenhum trabalho utilizou este método, para um modelo assim, devido as dificuldades operacionais. Consideraremos um ”cluster”com r ”bra¸cos”(bond ou liga¸cões) em parelelo e parâmetro de rede b = s

(27)

Cap´ıtulo 1

O Grupo de Renormaliza¸

c˜

ao na

Rede Hier´

arquica

1.1 Grupo de Renormaliza¸

c˜

ao

Como já mencionamos na introdu¸cão, o campo molecular de Weiss3_{, mesmo sendo} inibidor de flutua¸cões e de graus de liberdade para a análise de fenômenos cr´ıticos, transformou-se em um paradigma para os modelos clássicos de alcance infinito. Em 1937 Landau25 _{propõe um modelo fenomenológico para a energia livre na região de transi¸cão,} que unifica as teorias clássicas de Van der Walls (1813), para fluidos; Weiss1907, para o ferromagnetismo e Ornstein-Zernicke (1914), para a fun¸cão de correla¸cão; que recebe o nome de teoria de campo médio. A idéia básica do método consiste em expandir a energia livre (_F) em uma série de potências do parâmetro de ordem (Φ), na vizinhan¸ca do ponto cr´ıtico, onde este assume valores pequenos. Ou seja, uma expansão do tipo,

F =a0+a1Φ +a2Φ2+a3Φ3+a4Φ4+... (1.1) onde os coeficientes ai podem depender da temperatura e os termos ´ımpares se anulam por argumentos de simetria, já que _F é uma fun¸cão par de Φ a campo (externo) nulo.

(28)

re-ferências26,27_{. A teoria mostra, por exemplo, que o calor espec´ıfico observado na solu¸cão do} modelo de Ising, em duas dimensões, apresenta anomalias emT =TC e expoentes cr´ıticos nulos, mas o comportamento do calor espec´ıfico é caracterizado por uma divergência, e não uma descontinuidade28_{, t´ıpica de transi¸cão de primeira ordem, como era de se esperar.} A teoria de Landau enxerga além de modo a permitir a descri¸cão correta da transi¸cão, mas não consegue inserir de forma adequada as flutua¸cões e, consequentemente, resulta em estimativas errôneas para os expoentes cr´ıticos.

Para resolver o problema Migdal e Kadanoff20 introduziram a idéia de eliminar graus de liberdade, eliminando as correla¸cões de curto alcance e, Wilson21_{, constroi a base} teórica e operacional do que se chamou Grupo de Renormaliza¸cão29,30_{. Trata-se de um} procedimento sistemático de redu¸cão de graus de liberdade, até um limite em que é poss´ıvel aplicar métodos aproximativos tradicionais. A idéia é substituir o sistema original de HamiltonianoHopor um sistema efetivo de HamiltonianoH1, preservando as propriedades termodinâmicas igualando os pesos de Boltzmann, ou as fun¸cões de parti¸cão.

Esta teoria baseia-se nas hipóteses de escala18,19,17 _{a partir da idéia de homogeneidade} da fun¸cão de correla¸cão (Γ(ξ)) e dos potenciais termodinâmicos. Os valores atingidos pelo comprimento de correla¸cão (ξ) fazem com que praticamente todas as escalas de comprimentos estejam presentes numa transi¸cão, predominando, na região cr´ıtica, àqueles de longo alcanse que dão origem às intera¸cões cooperativas necessárias para efetuar a transi¸cão e responsáveis pelo aparecimento de singularidades termodinâmicas como, por exemplo, a susceptibilidade mostrada na Figura 4. Entretanto, não devemos esquecer, como lembra Mariz no Cap´ıtulo I de sua tese31_{, que ”os efeitos f´ısicos provenientes dos} graus de liberdade microscópicos são convenientemente estudados, supondo que o sistema macroscópico encontra-se no limite termodinâmico, onde o número de part´ıculas (N) e o volume (V) divergem, mas a densidade (N/V) é finita”.

Há dois procedimentos básicos utilizados na aplica¸cão da técnica do Grupo de Renor-maliza¸cão:

(29)

primentos de onda. Se mostra eficaz no cálculo dos expoentes cr´ıticos de dimensões altas, mas falha para grandezas sens´ıveis à estrutura da rede como, por exemplo, Tc;

b) A Renormaliza¸cão do Espa¸co Real32_{, na versão Kadanoff usada no presente} trabalho, que consiste em dividir o sistema em blocos, como mostra a Figura 1.1 para uma rede quadrada de spins localizados e parâmetro de rede a. Em seguida efetuamos tra¸cos parciais sobre os n-2 spins de cada par de blocos, eliminando, assim, graus de liberdade internos entre os blocos. O parâmetro de redea1 do novo sistema estará é igual ao parâmetro anterior multiplicado por um fatorb >1 e estarão suprimidas as correla¸cões para a _≤ξ _≤ a1 =ba. O sucesso do método está, em grande parte, associado a escolha do tamanho e a simetria dos blocos a serem renormalizados. A renormaliza¸cão pode ser compreendida geometricamente, como uma dilata¸cão por um fator linear b, que reduz o número N de graus de liberdade paraN1 =N/bd, reescalonando as dimensões lineares de X para X1 = X/b e os momentos de Q para Q1 = bQ, sendo d a dimensão da rede. A renormaliza¸cão pode ser escrita como uma transforma¸cão Rb(_H) que se aplica em uma susseciva fam´ılia de s Hamiltonianos, cada um representando um novo sistema, tal que

H1 =Rb(H0) ; H2 =Rb(H1) ; ... ; Hs =Rb(Hs−1) (1.2)

com os comprimentos de correla¸c˜ao dados por:

ξ1 =ξ0/b ; ξ2 =ξ1/b ; ... ; ξs=ξs−1/b=ξ0/bs. (1.3)

Realizando o processo iterativo até que o comprimento de correla¸cão se torne da ordem do parâmetro de rede (ξs ∼a), obteremos um sistema que pode ser estudado por métodos que viabilize uma solu¸cão exata ou numérica.

No espa¸co de parˆametros do Hamiltoniano (_H = _H{K_}), com K = J

kBT, a trans-forma¸cão que leva Ki em Ki′ através da rela¸cão de recorrência.

K′

(30)

Figura 1.1: Esquema de Kadanoﬀ para redu¸c˜ao de graus de liberdade.

pode ser estudada analisando-se o ﬂuxo dos pontos sob a a¸c˜ao de Ri

b. Assim, os pon-tos de maior interesse nesse mapeamento s˜ao aqueles invariantes sob a transforma¸c˜ao, caracterizados por

{K∗_}=Rb{K∗}, (1.5)

cujos comprimentos de correla¸c˜ao associados obedecem a seguinte rela¸c˜ao

ξ∗ =ξ∗/b. (1.6)

Os pontos em que ξ∗ _{= 0, associados `as temperaturas} _T _{= 0 e} _T ₌ _∞_{, s˜ao chamados}

pontos fixos triviais (estáveis), caracter´ısticos de diferentes fases, enquanto àqueles de

(31)

fronteiras que separam as fases.

1.2 Estabilidade de Fases a partir dos Pontos Fixos

´

E importante que se compreenda o significado da estabilidade dos pontos fixos porque esta análise distingue a natureza e, consequentemente, a importância de cada ponto no diagrama das fases. Se na Equa¸cão 1.4 olharmos para um ponto fixo não trivial, ou seja,

K_i∗ =Rib(_{K∗_}) ; (i= 1,2, ..., s) (1.7) e, na vizinhan¸ca deste ponto, ﬁzermos uma an´alise linear expandindoRi_b(_{_K∗_}_{), obtemos}

a matriz Hessiana cujos autovalores (Λi) nos permite escrever, em coordenadas normais, express˜oes

△X_i′ = Λi_△Xi (1.8)

em cujo espa¸co de parâmetros correspondem a variáveis que determinam campos de escala (para um ferromagneto equivale aos campos t e H), e se anulam nos pontos fixos (Xi =

f(Ki)), onde podemos determinar fun¸c˜oes de estado (apˆendice A) que caracterizam o sistema.

Os autovalores (Λi) determinam a estabilidade dos pontos ﬁxos na dire¸c˜ao de cada campo de escala. Assim:

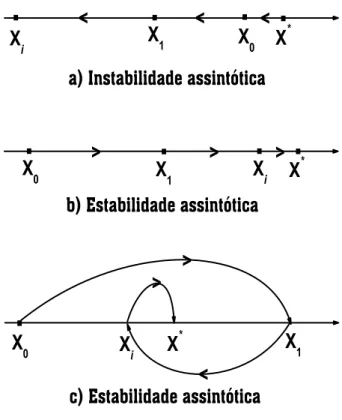
a) Se, em uma dada dire¸cão, o autovalor for maior do que um (Λi >1) significa que o fluxo do mapeamento é no sentido de se afastar do ponto fixo (_△X′

i >△Xi) e a intera¸c˜ao associada ao campo de escala ´e dita relevante (Figura 1.2a);

b) Se, em outra dire¸c˜ao, o autovalor for maior que zero e menor do que um (0 <

Λi < 1) significa que o fluxo do mapeamento é no sentido de se aproximar do ponto fixo (_△X′

(32)

Figura 1.2: Diagrama de ﬂuxo do mapeamento indicando, a partir dos autovalores, a estabili-dade do sistema. Temos: a) (Λi>1); b) (0<Λi<1) e c) (−1<Λi<0)

aproxima¸cão assintótica ocorre de forma alternada se₋1<Λi <0, como mostra a figura 1.2c;

c) Agora, se por outro lado, o autovalor ´e nulo (Λi = 0) temos, ent˜ao, _△X′

i =△Xi e a análise linear é insuficiente para estabelecer critérios de estabilidade do ponto cr´ıtico.

(33)

t′ = ΛTt (1.9)

e

ξ′ =ξ/b. (1.10)

As Equa¸c˜oes 1.9 e 1.10 combinadas com a Equa¸c˜ao 5 do Cap´ıtulo anterior, obtemos

νT = lnb/ln ΛT. (1.11)

Dessa forma, também obtemos os expoentes para o campo H e usando as rela¸cões de escala (Equa¸cões 10 a 13 do Cap´ıtulo anterior) teremos um conjunto completo de expoentes que definem uma classe de universalidade para o sistema em estudo.

Há de se ressaltar, ainda, que além dos métodos anal´ıticos outras técnicas aproxima-tivas têm sido desenvolvidas para o estudo de fenômenos cr´ıticos, principalmente as que envolvem tratamentos computacionais. Destacamos as Expansões em Séries33_{; as} sim-ula¸cões de Monte-Carlo34_{; os Métodos de Simula¸cão não Estocásticos como a dinâmica} molecular e dinâmicas determin´ısticas35 _{e técnicas mistas de GR com Monte-Carlo. A} busca dessas solu¸cões alternativas estão relacionadas com o que desejamos enxergar no problema abordado. Se estamos interessados na análise das fases, por exemplo, de um sistema que está imerso num campo de escala de temperatura, neste caso, o GR em re-des hierárquicas como técnica para dar visibilidade as suas diversas fases, se apresenta como uma excelente ferramenta e é com ela que vamos trabalhar para ter as primeiras informa¸cões gerais sobre o modelo que desejamos estudar e identificar fases novas.

1.3 Solu¸

c˜

ao Exata na Rede Hier´

arquica.

(34)

para redes quadradas que simula espa¸cos bi-dimensionais quando usamos um formato de grafo denominado diamante. No geral trata-se de grafos das mais diversas formas e tamanho, com várias liga¸cões representando as energias de troca (Jij) entre um dado par de spins numa rede idealizada para esse fim. As liga¸cões unem s´ıtios de spins localizados, que se renormaliza em um grafo com um par de spins extremos em uma liga¸cão com condi¸cões de contorno livre. Um exemplo é a rede diamante mostrada na Figura 1.3.

O primeiro passo é a obten¸cão de rela¸cões de recorrência por um processo chamado di-zima¸cão, que quer dizer suprimir liga¸cões (Ji) na rede idealizada - isso equivale a aumentar a correla¸cão e suprimir flutua¸cões, e reescrever as novas energias de acoplamento (J′

i) em fun¸cão das antigas (Ji) preservando aspectos f´ısicos relevantes, impondo a condi¸cão de invariância da fun¸cão de parti¸cão e da fun¸cão de correla¸cão, respectivamente, que de outra forma significa igualar os pesos de Boltzmann. Ou seja,

e−βH′ = T r

{i<σ<j}e

−βH _(1.12)

e

ξ′ = ξ

b ≈ ⎧ ⎪ ⎨ ⎪ ⎩

(₋t′₎−νT (₋t)−νT_.

⎫ ⎪ ⎬ ⎪ ⎭ (1.13)

Aqui νT é o expoente associado a divergência de ξ na dire¸cão do campo de escala t, que se transforma segundo

(35)

equa¸cão 1.11 nos fornece apenas um expoente cr´ıtico (ν) e precisamos de pelo menos dois para obter os demais a partir das equa¸cões 9-12 (Introdu¸cão). Em resumo, com as rela¸cões de recorrência obtidas de 1.12 escrevemos a matriz ressiana, calculamos seus autovalores e αT (expoente cr´ıtico associado ao calor espec´ıfico) fica bem determinado pela rela¸cão de Josephson.

Neste trabalho exploraremos as fases e as propriedades cr´ıticas do modelo Ashkin-Teller, com um olhar sobre algumas versões já estudadas na literatura, buscando descrever fases ainda desconhecidas, e, especificamente, estudar a criticalidade desse sistema numa rede tipo diamante simples como mostra a figura 1.3 considerando duas liga¸cões em série (s= 2) e duas em paralelo (r= 2).

(36)

Figura 1.3: O grafo da esquerda representa a célula geradriz da rede hierárquica com dimensão fractal df = lnsr/lns, sendo s o número de liga¸cões em série e r o número de liga¸cões em

(37)

Cap´ıtulo 2

O Modelo Ashkin-Teller de Duas

Cores

2.1 Um Modelo para Ligas Quatern´

arias

Este modelo, conhecido na literatura como modelo AT-2, foi proposto em 1943 por J. Ashkin e E. Teller38 para descrever a transi¸cão ordem-desordem em ligas quaternárias, onde cada s´ıtio de uma rede idealizada pode ser ocupado por um dos quatro tipos de átomos A, B, C ou D.

Sobre essa rede hipotética, onde s´ıtios podem conter átomos, as energias de acopla-mento (εij), entre s´ıtios primeiros vizinhos, dependem dos tipos de átomos que ocupam os s´ıtios como mostra a tabela 2.1. Se há atra¸cão entre átomos iguais (ε0 <0), os autores mostraram que o modelo satisfaz, na rede quadrada, a uma rela¸cão de dualidade (análoga a de Kammers e Wannier39 _{para o modelo de Ising), tinha uma temperatura cr´ıtica e,} portanto, uma linha de transi¸cão. Esta transi¸cão separava duas fases: a ordenada, onde era mais provável a forma¸cão de ”cluster”de átomos iguais; e a desordenada, onde todas as vizinhan¸cas eram equiprováveis quanto as energias de acoplamento.

(38)

,

Tabela 2.1: Energias de Acoplamento entre S´ıtios

εij s´ıtios vizinhos

ε0 AA, BB, CC, DD

ε1 AB, CD

ε2 AC, BD

ε3 AD, BC

associando-se a cada s´ıtio da rede duas (2) vari´aveis de ising (Tabela 2.2) de modo que ,

Tabela 2.2: Conex˜ao com o Magnetismo

Tipo de ´Atomo (σ, τ)

A (+,+)

B (+, -)

C (- ,+)

D (- , -)

deﬁnindo-se constantes de acoplamento apropriadas,

J0 =−

ε0+ε1+ε2+ε3

4 (2.1)

J1 =−

ε0+ε1−ε2−ε3 4

J2 =−

ε0−ε1+ε2−ε3 4

J4 =−

ε0−ε1−ε2+ε3 4

(39)

εij =−{J0+J1σiσj+J2τiτj +J4σiσjτiτj} (2.2) Redefinindo o zero da energia de modo que J0 = 0, o Hamiltoniano do sistema fica assim definido:

H = ₋

i,j

(J1σiσj+J2τiτj +J4σiτiσjτj) (2.3)

No magnetismo as fases são determinadas pelas magnetiza¸cões, que representam va-lores médios das variáveis de spins sobre configura¸cões com probabilidades diversas de ocorrer, diretamente associadas a presen¸ca ou não de um ou mais átomos naquela fase. A variedade de fases que este modelo pode apresentar significam concentra¸cões maiores ou menores de atomos presentes de uma ou de outra natureza.

Podemos, ainda, apresentar o Hamiltoniano na forma reduzida:

H

kBT

= ₋

i,j

(K1σiσj+K2τiτj +K4σiτiσjτj) (2.4)

onde

i,j representa a soma sobre os primeiros vizinhos, (σi, σj, τi, τj)=±1 eKl = _kJ_Bl_T. Além do fenômeno de adsor¸cão41 _{como uma de suas generalidades o modelo} corres-ponde a dois sistema de Ising acoplados pela intera¸cão de 4 spins de energia de trocaK4, e se relaciona com outros modelos de Mecânica Estat´ıstica, tais como: (i) O modelo de Ising para K1=K4=0 ou K1=K2=0 ou K2=K4=0; (ii) O modelo de Potts com quatro estados para K1=K2=K4 e (iii) O modelo Z(4) quando fazemos K1 = K2 = K4, tendo Potts como caso particular. Várias de suas propriedades f´ısicas são conhecidas em 2-d.

(40)

paramagnética e sobre a qual os expoentes cr´ıticos crescem continuamente. Essa versão foi, ainda, estudada por Christiano e Rosa Jr.44,45_{, e por Costa et all}46 _{que observaram} fases adicionais previstas por Ditzian et all47_{. Em duas e três dimensões foi estudado} por E. S. de Souza48_{, além das generaliza¸cões com a presen¸ca de dilui¸cão de liga¸cões}49 e de intera¸cões competitivas50,51_{, também, foram investigadas. Wiseman e Domany}52 estudaram através do método de Monte-Carlo34 _{para o caso isotrópico bidimensional, ou} seja, K1 =K2 =K4.

2.2 AT-2 Anisotr´

opico na Rede Hier´

arquica

A vers˜ao Askhin-Teller Anisotr´opica foi estudada por Wu e Lin53 ₍_K

1 = K2 = K4), usando rela¸cões de dualidade, investigaram a forma geral do diagrama de fases sem pro-por valores numéricos para as fronteiras cr´ıticas; Domany e Riedel54 _{com argumentos de} dualidade e grupo de renormaliza¸cão tipo Migdal-Kadanoff apresentaram um diagrama do modelo que mais tarde foi aprimorado por C. G. Bezerra em sua tese de mestrado55_, num espa¸co de dimensão fractal entre dois e três. Uma versão na árvore de Caley56 _foi, também, estudada na tese de Mestrado de J. M. de Araújo.

(41)

1

2

1

2

3

4 (a)

(b)

Figura 2.1: Grafo para gera¸cão de um ”cluster básico”tipo Ponte de Wheatstone (b) estudado por Bezerra para obter propriedades cr´ıticas do modelo AT₋2 anisotrópico, renormalizando-o para um par de s´ıtios com uma liga¸cão simples (a).

Cada etapa da constru¸cão dessa rede é chamada de gera¸cão de ordem n. A rede resul-tante ao fim do processo recebe o nome de rede hierárquica. Para obter as rela¸cões de recorrência (5.50 a 5.52) ele usou o conceito de transmissividade (4.2), e construiu um di-agrama de fase que está mostrado na Figura 2.2. Nele esconde-se um isomorfismo de fases simétricas em rela¸cão aos eixos duais, mas não revela detalhes importantes sobre planos de multifases ou hipersuperf´ıcies de pontos cr´ıticos que reproduzam versões particulares de AT-2, como percebemos mais tarde através dos novos recursos gráficos computacionais. Nós reestudamos essa versão, como fonte de subs´ıdio para nosso trabalho e encontramos uma solu¸cão geral (5.56) para a equa¸cão de pontos fixos (5.57), obtida das rela¸cões de recorrência (RR), onde idetificamos os pontos fixos cr´ıticos das bacias atratoras das fases

(42)

·

· F

s

F

t

F

I

P

Potts

I

1

I

2

I

3

I

4

I

5

I

6

I

7

I

8

I

9

t

D

1 t

D

3 t

D

2

Figura 2.2: Diagrama de fases do modelo AT-2 anisotrópico com os pontos fixos não triviais, os atratores das fases ferromagnética (F), paramagnética (P)e Intermediárias: (I), (σ) e (τ). As linhas pontilhadas indicam as fronteiras cr´ıticas entre as respectivas fases.

A novidade aqu´ı é que não se tinha percebido que estes pontos estão sobre essas superf´ıcies planas isomorfas (Sc), perpendiculares a linha que contém o ponto de Potts e unindo as fases F (ferromagnética) e P (pararamagnética). Na Figura 2.5 vemos uma dessas superf´ıcies, cujas equa¸cões paramétricas são:

tD₁ =x (2.5)

tD₂ = 1₋x₋y tD

(43)

chamadas transmissividades duais (5.53 a 5.55) , que tamb´em pode ser escrita na forma

f(x, y) = 0 (2.6)

onde x e y s˜ao vari´aveis reais entre zero e um, inclusive.

(44)

Figura 2.3: O gráfico mostra a superf´ıcie isomorfa (S1) que contém os atratores das fases σ,τ

e I; os pontos ﬁxos n˜ao triviais I1,I4,I7 e Potts; e as fronteiras cr´ıticas dos modelos IAT e dois

(45)

Figura 2.4: Curva de autovalores da linha sobre o plano isomorfoSc (parac= 1) com solu¸c˜oes

paraKi =Kj, revelando trˆes autovalores relevantes no ponto de Potts.

Podemos ver na Figura 2.3 que: a) os pontos I1, I4 e I7, identificados como pontos de Ising na Figura 2.4, são pontos de fronteiras cr´ıticas com dois autovalores relevantes e um irrelevante, portanto, instável em duas dire¸cões e pode ser identificado como um ponto de sela na Figura 2.5; b) o ponto fixo de Potts, com três autovalores relevantes, é completamente instável nas dire¸cões dos campos de escala, no espa¸co de parâmetros, pode ser um ponto de multiplas fases identificado no topo da Figura 2.5.

(46)

Figura 2.5: Hipersuperf´ıcie hK1=K2

hKi =f(x, y) (2.7)

e equivalem, respectivamente, às solu¸cões paramétricas sobre S1 para Ki = 0 e Ki =Kj. Essas solu¸cões implicam em tomarmos: (tD

(47)

Figura 2.6: Proje¸c˜ao dos zeros das hipersuperf´ıcieshK sobre um plano perpendicular aos planos

Sc que cont´em a linha de Potts.

As hipersuperf´ıcies contém as fases descritas por cada modelo em particular e são a novidade nesta nova compreensão do modelo AAT (Apêndice C). Vejamos, por exemplos, o caso de isotropia estabelecida pela igualdade das energias de acoplamento entre termos distintos de dois spins no hamiltoniano estudado. A hipersuperf´ıcie mostrada na figura 2.2, cujos zeros definem pontos cr´ıticos não trivias que se encontram sobre o plano isomorfo

S1 e definem, no espa¸co de parâmetros, o diagrama de fases do modelo isotrópico ou Z(4), já estudados por Mariz-Tsallis-Fulco58 _{e Mariz-Souza}48_{, quando fazemos} _K

1 = K2. A equa¸c˜ao que gera 2.2, tem a forma:

hKi=Kj =

A

(48)

Onde,

A=x4+x4y4+ 2y3x4+x3₋3y2x3+ 2x3y4+yx3+ 3x3y3+ 3yx2

−9x2y2 ₋3x2₋3x2y3+y3x+x+ 3xy2₋xy₋3y2+y+y4+y3 (2.9)

B =x3y3+x3₋yx3 +y2x3+x2y3+x2₋yx2+x2y2₋y3x₋x

+xy₋xy2+y3+ 1₋y+y2 (2.10)

Por outro lado se olharmos os planos isomorfos (Sc) sobre um plano que passa pela origem do espa¸co dual, contendo a linha de potts e o eixo F-I, em duas dimens˜oes, veremos como se alinham os pontos ﬁxos, projetados neste plano, sobre os Sc (2.2).

Neste diagrama se confirma que o ponto de Potts é um ponto de múltiplas fases com três autovalores relevantes (2.2), sobre o qual se dá a transi¸cão Ferro-Para (F-P). As regiões hachuriadas, mostradas na figura, idetificam as fases Ising (Fσ,τ e I) sobre o plano isomorfo S1 unidas, também, pelo ponto fixo de Potts. Os pontos fixos cr´ıticos de Ising (I2, I3, I5, I6, I8, I9), se alinham sobre outros dois planos isomorfos (S√2−1 eS2√2−1) paralelos aS1 passando, respectivamente, pelos pontos (I2, I5, I8) e (I3, I6, I9), mostrados na mesma figura. As linhas I2 −P, I3 −P, I5,8 −P e I6,9 −P podem ser obtidas por métodos numéricos.

Na figura 2.2a podemos mostrar como evoluem os autovalores sobre o plano S1, no espa¸co das variáveis (x e y) que parametrizam esta superf´ıcie sobre o espa¸co dual, sem restringir-se a quaisquer dom´ınios, se não a todo espa¸co de fase. Alguma restri¸cão de dom´ınio que se dá aos limites é imposta pelo próprio espa¸co dual (dom´ınio ferro-magnético). Lembre-se que os t’s duais são variáveis definidas como tD

(49)

A inversão dos parâmetros (giro horário de 90 graus no plano xy), em relaão a figura a, é somente uma questão de visibilidade. Já em c fizemos duas inversões: uma de 90 graus anti-horária no plano xy e outra de 180 graus sobre a dire¸cão vertical que representa os expoentes de crossover.Embora não haja muito clareza sobre que propriedades gerais podem ser enchegardas nos gráficos mostrados, uma idéia é importante: o fato de se ver como evoluem entre s´ı gerando ponto a ponto uma série de expoentes cr´ıticos t´ıpicamente universais.

(50)

Figura 2.7: A superf´ıcie Auto-dual S1 apresenta, sobre o plano (x,y): a) Trˆes auto-valores

(51)

Cap´ıtulo 3

AT-2 em Rede Hier´

arquica

Aperi´

odica

3.1 Aperiodicidade em AT-2

(52)

crescimento da rede, a partir de um ”cluster básico”, de modo que letras são substituidas por um conjunto de outras letras representantes das novas liga¸cões. Entre o passo n e o passo n + 1 na sua forma mais geral, podemos criar regras de substitui¸cão de vários tipo com cluster’s os mais diversos. Neste trabalho vamos usar um formato mais geral na forma apresentada na figura 3.3.3. Ou seja, as letras representativas das energias de troca entre spins para denotar energias iguais ou diferentes, em cada passo, serão substituidas pela regra: An1Bn2

(53)

3.1.1 Rela¸

c˜

oes de Recorrˆ

encia na Troca A por AB.

Partindo do Hamiltoniano (2.4), igualando os pesos de Boltzmann (1.12) ou as fun¸cões de parti¸cões e realizando a soma sobre os spins intermediários do grafo da figura 3.1.2a paras = 2, obteremos as rela¸cões de recorrência, para o primeiro passo de crescimento da rede, substituindo a liga¸cão A do grafo com duas pontas soltas por quatro liga¸cões sendo duas do tipo A e duas do tipo B. Usando o fato que

x₋y

x+y = tanh

1

2ln(x/y) (3.1)

e definindo ti = tanhKi, as expressões de renormaliza¸cão para r conexões sobre o grafo tipo diamante mostrado na figura 3.3.3, tornam-se:

t′_1A = tanh1 2ln[

( ˆa1+ ˆa2)( ˆd1+ ˆd2) ( ˆb1+ ˆb2)( ˆc1+ ˆc2)

]r/2 (3.2)

( ˆa1+ ˆa2)( ˆc1+ ˆc2) ( ˆb1+ ˆb2)( ˆd1+ ˆd2)

]r/2 (3.3)

( ˆa1+ ˆa2)( ˆb1+ ˆb2) ( ˆc1+ ˆc2)( ˆd1+ ˆd2)

]r/2 (3.4)

sendo,

ˆ

(54)

ˆ

a2 = (t1A+t1B)(t2A+t2B)(t4A+t4B) (3.6)

ˆ

b1 = (1−t1At1B)(1−t2At2B)(1 +t4At4B) (3.7)

ˆ

b2 = (t1A−t1B)(t2A−t2B)(t4A+t4B) (3.8)

ˆ

c1 = (1−t1At1B)(1 +t2At2B)(1−t4At4B) (3.9)

ˆ

c2 = (t1A−t1B)(t2A+t2B)(t4A−t4B) (3.10)

ˆ

d1 = (1 +t1At1B)(1−t2At2B)(1−t4At4B) (3.11)

ˆ

d2 = (t1A+t1B)(t2A−t2B)(t4A−t4B) (3.12)

3.1.2 Rela¸

c˜

oes de Recorrˆ

encia na Troca B por AA.

(55)

(3.3.3b - s=2), repetimos as mesmas opera¸cões anteriores para eliminar os spins dos s´ıtios intermediários. Obtemos as rela¸cões de recorrência análogas as já obtidas, evidentemente com um grau de dificuldade maior porque, agora, o tra¸co será efetuado sobre dois dia-mantes como mostra a figura 3.1.2 para o caso de um ”cluster básico”diamante simples com r liga¸cões em paralelo. Efetuando a soma dos pesos de Boltzman sobre os spins intermediários do diamante da direita e igualado ao mesmo cálculo feito sobre o diamante da esquerda, obtemos:

Figura 3.1: O gráfico mostra como se efetua a troca de liga¸cões (A e B) entre o passo n e o pass n+ 1 num grafo diamante simples com r liga¸cões em série.

t′

1B = tanh 1 2ln(

ad bc)

r/2 _(3.13)

t′_2B = tanh1 2ln(

ac bd)

r/2 _(3.14)

t′_4B = tanh1 2ln(

ab cd)

r/2 _(3.15)

sendo

(56)

b = (1₋t2_1A)(1₋t2_2A)(1 +t2_4A) (3.17)

c = (1₋t2_1A)(1 +t2_2A)(1₋t2_4A) (3.18)

d = (1 +t2

1A)(1−t22A)(1−t24A) (3.19) Este último conjunto de equa¸cões poderiam ser obtidas a partir dos resultados encon-trados nas equa¸cões 3.2 a 3.4 fazendo, naquelas equa¸cões: tiA=tiB.

3.2 AT-2

Anisotr´

opico

na

Rede

Hier´

arquica

e

Isotr´

opico no Acoplamento de Dois Spins

Com este subt´ıtulo estamos dizendo que um modelo assim teria as energias de acoplamento ferromagnéticas distintas entre s´ı para liga¸cões do tipo A e B distintos. Isto equivale a tornar, nas equa¸cões de 3.2 a 3.4 e 3.13 a 3.15: t1A=t2A e t1B =t2B. Por outro lado é fácil perceber que os ai, bi, ci edi, nestas equa¸cões, são polinômios de termos idênticos (ti) que podem ser rearranjados de modo que:

t′_1A = 2t1At1B(1 +t4A)(1 +t4B) (1 +t2

1At21B)(1 +t4At4B) + (t1A2 +t21B)(t4A+t4B)

(3.20)

(57)

t′_1B = 2t 2

1A(1 +t4A)2 (t2

1A+t4A)2+ (1 +t21At4A)2

(3.22)

t′4B =

t2

1A(1 +t4A)2+ (1 +t21At4A)2

t2

1A(1 +t4A)2+ (t21A+t4A)2

(3.23)

onde,

f = (1 +t 4

1A)(1 +t4At4B) + (t21A+t21B)(t4A+t4B) 2t1A[t1A(1 +t4At4B) +t1B(t4A+t4B)]

(3.24)

g = a1+a2

b1+b2

(3.25)

a1 = (1−t1At1B)(t4At4B−t1At1B) (3.26)

a2 = (t1A−t1B)(t1At4B−t1Bt4A) (3.27)

b1 = (1−t1At1B)(1−t4At4Bt1At1B) (3.28)

(58)

E, assim, poderemos construir um conjunto de situa¸cões que reproduzam resultados sobre todos os modelos que possam ser derivados de AAT numa rede hierárquica diamante simples. Mais tarde veremos que se tornará trivial generalizar essas expressões para s liga¸cões em série e r liga¸cões em paralelo. Podemos demonstrar analiticamente para os casos mais simples e calcular com aux´ılio do maple para os casos mais complicados, que as transmissividades estão relacionadas pelo produto enre s´ı ou entre as duais. Nas próximas se¸cões vamos reproduzir alguns resultados conhecidos e ver outros novos.

3.3 Reproduzindo Resultados

3.3.1 Ising Puro Anisotr´

opico

Em primeiro lugar é necessário esclarecer essa nomenclatura: ”Ising Puro Anisotrópico”. Queremos dizer com isso que o Hamiltoniano AAT só tem um termo de troca enquanto os outros dois são nulos, mas as sub-redes existem e interagem entre s´ı. Isto significa que todos os parâmetros de acoplamento são nulos exceto para um par de spins (σiσj,τiτj) de subredes diferentes de forma que: tiA =tA =tiB = tB, ambos diferentes de zero. Assim teremos um par de rela¸cões de recorrência escritas na forma da transmissividade térmica (ti = tanhki), obtidas diretamente de 3.2 a 3.4 e 3.13 a 3.15 resultando em:

t′_A = 2tAtB 1 +t2

At2B

(3.30)

t′B = 2t2

A 1 +t4

A

(3.31)

(59)

Essas expressões podem, ainda, ser escritas na forma de duais inversas (xi = exp 2ki), para os dois modelos. Após alguns passos, no algebrismos da mudan¸ca de variáveis, obtemos:

x′_A = (xAxB+ 1

xA+xB

)2 (3.32)

x′B = (

x2 A+ 1 2xA

)2 (3.33)

São resultados que já estão disponibilizados numa ampla literatura e servem para checar as nossas equa¸cões. A energia livre pode ser expressa como uma série infinita das duais inversas e isso, também já foi feito (Apêndice A), mas, para ilustrar, temos:

f(xA, xB) = inf n=0

(2m)−n[1 3ln(x

(n) A +x

(n) B ) +

1 6ln(2x

(n)

A )] (3.34)

ondexA, B(n)é a n-ézima intera¸cão nas rela¸cões de recorrência. O expoente cr´ıtico associ-ado ao calor espec´ıfico, também pode ser diretamente obtido tanto da energia livre quanto dos autovalores da matriz hessiana calculada a partir da lineariza¸cão das RR. Sendo assim podemos escrever:

α = 2₋1.3862.../ln Λ (3.35)

onde Λ ´e o autovalor relevante associado.

3.3.2 AT-2 Isotr´

opico nas Sub-Redes de Ising

(60)

de recorrˆencia, 3.2 a 3.4 e 3.13 a 3.15, que tomar: tiA =tiB =ti e t1 =t2, para obter:

t′₂ = tanh1 2ln

(t2

2+ 1)2(t24+ 1) + 8t22t4 (1₋t2

2)2(t24+ 1)

(3.36)

t′₄ = tanh1 2ln

[(t2

2+ 1)2(t24+ 1) + 8t22t4](t24+ 1) (1 +t2

2)2(1−t24)2

. (3.37)

Este modelo foi estudado por F.A. da Costa/Oliveira e Salinas46 _{na ´arvore de Cayle} explorando propriedades de assimetria na fase Baxter. Se reescrevermos estas equa¸c˜oes para t2 =x et4 =y, com um pouco de algebrimos, teremos

x′ = 2x

2₍_y2 _{+ 1 + 2}_y₎

x4_y2₊_x4₊_y2_{+ 1 + 4}_x2_y (3.38)

y′ = 2y(x

4_y_{+ 2}_x2_y2_{+ 2}_x2_{+ 2}_x2_y₊_y₎

x4_y4₊_x4_{+ 4}_x2_y3_{+ 4}_x2_y_{+ 2}_x2_{+ 2}_x2_y4₊_y4_{+ 1} (3.39)

que para x′ ₌_y′ ₌_x∗ ₌_y∗ ₌_y _{resulta no hiperplano,}

h = y₋ 2y(y

4₋₂_y3_{+ 4}_y2₋₄_y_{+ 1)}

y4₋₂_y3_{+ 4}_y2₋₂_y_{+ 1} (3.40) cuja solu¸cão parah= 0 resulta em dois pontos fixos cr´ıticos trivias (0 e 1) e um ponto fixo cr´ıtico não trivial, exatamente, emy_∗=x_∗=.3611030806.... Para analizar a estabilidade desse ponto fazemos a lineariza¸cão de 3.38 e 3.39 e a matriz hessiana pode ser escrita como:

J =

⎛

⎜ a11 a12 ⎞

(61)

onde,

a11=

∂x′

∂x

= −4x(y

2_{+ 1 + 2}_y₎₍_x4_y2₊_x4₋_y2₋₁₎

(x4_y2₊_x4₊_y2_{+ 1 + 4}_x2_y₎2 (3.42)

a12=

∂x′

∂y

= −4x

2₍₋₂_x2_y2₊_x4_y2₋_x4₊_y2₋_{1 + 2}_x2₎

(x4_y2₊_x4₊_y2_{+ 1 + 4}_x2_y₎2 (3.43)

a21 =

∂y′

∂x

= −8xy(−y

6₊_y4₊_y2₊_x4₋_x4_y2₋_x4_y4₊_y6_x4₋₁₎

(x4_y4 ₊_x4_{+ 4}_x2_y3_{+ 4}_x2_y_{+ 2}_x2_{+ 2}_x2_y4 ₊_y4_{+ 1)}2 (3.44)

a22=

∂y′ ∂y = X Y (3.45) onde,

X = ₋4(y5₋6x4y₋5x2y2+ 5x2y4₋x2₋2x4₋10x4y2₋4x2y₋y+ 10x4y4+ 4x6y5₋4x6y+ 6x4y5+ 4x2y5+ 2y6x4+y6x2₋x6+ 5x6y4+

x6y6₋5x6y2₋yx8+x8y5) (3.46)

Y = (x4y4+x4+ 4x2y3+ 4x2y+ 2x2+ 2x2y4+y4+ 1)2 (3.47)

Os autovalores da matriz hessiana (3.41), em torno do ponto fixo não trivial, são dados por:

λ_±= 1

2[(a11+a22)±

√

(62)

com

Δ = (a11−a22)2+ 4a12a21 (3.49) A solu¸cão de simetria não trivial, conduz a dois autovalores relevantes: λ1 = 1.852601595 e λ2 = 1.277793838, que define um ponto onde o sistema é estremamente instável para temperatura finita e caracteriza uma região de fronteira ou um ”saddle-point”. É importante observar que na dire¸cão do autovalor maior o sistema tem um comportamento parecido com o modelo de ising na mesma rede hierarquica com uma regra de substitui¸cão de três letras59_{, pois este apresenta um autovalor} _λ

1 = 1.854101... que margeia o anterior naquela dire¸cão. Significa que o nosso sistema com esse grau de instabilidade, em torno desse ponto fixo cr´ıtico não trivial, pode sofrer mudan¸cas na criticalidade e dar origem a uma nova classe de universalidade. Essa sens´ıbilidade é ali-mentada pelas fluta¸cões geométricas da aperiodicidade. Essas fluta¸cões tem um caráter relevante ou não para a criticalidade e quem identifica isso é o expoente de cruzamento (φ) definido por Luck22_{. Obtido por argumentos eur´ısticos, o expoente tem a forma:}

φ_≡1 +dνμ(̟−1) (3.50)

onde d é a dimensão fractal eνu (1.11) é o expoente cr´ıtico de correla¸cão do caso uniforme e ω é o ”wandering”expoente de flutua¸cões geométricas dado por:

̟ = ln|λ2 | lnλ1

(3.51)

(63)

φ = 0 não podemos prever o que ocorrerá (caso marginal). Esse é o critério e deve ser usado com as restri¸cões contidas no apêndice referido.

Com o uso da rela¸cão de hiperescala, dνu = 2−αu, que deve valer para todo d ≤ 4, e da limita¸cão termodinâmica α _≤ 1 para transi¸cões cont´ınuas, podemos reenunciar a condi¸cão de relevância fazendo em 3.50 φ= 0 e obter:

̟ > ωc =

1₋αu 2₋αu

(3.52)

onde foi introduzido um “valor cr´ıtico” (ou limiar) do expoente de flutua¸cão,ωc, a partir do qual a aperiodicidade afeta de maneira relevante o sistema. Diferente da forma como se encontra no apêndice D, colocamos uma barra sobre̟ para resgatar o conceito inicial de expoente de crossover 13. Assim, podemos mostrar, a partir de evidências, que para valores de ̟ > ωc = 0.555... as flutua¸cões geométricas geram viola¸cões na criticalidade do sistema.

3.3.3 AT-2 Anisotr´

opico nas Sub-Redes de Ising

Podemos refazer nossos c´alculos considerando as energias de acoplamento iguais entre s´ı mas diferentes nas duas sub-redes, representadas pelas letras A e B. Isto equivale a tomar, nas equa¸c˜oes de 3.2 a 3.4 e 3.13 a 3.15, t1A = t2A = t4A e t1B = t2B = t4B, para encontrar:

a) Para as rela¸c˜oes de recorrˆencia,

x′ = 2xy

(64)

Tabela 3.1: Expoentes Cr´ıticos para a Solu¸c˜ao do Ponto Fixo y_∗= 0,36110308... expoentes valor

νμ 1.12416...

αμ -0.24832...

y′ = x

3₍₋₂_x₋₂_x3₊_x5₊_x7_{+ 8}₋₁₆_x2_{+ 8}_x4₎

2 + 2x2₋₂_x4₋₂_x6₊_x8₊_x10_{+ 8}_x3₋₁₆_x5_{+ 8}_x7 (3.54) b) Os mesmos pontos ﬁxos cr´ıticos do caso uniforme: (0,1,0.3611030806); mas com criticalidade diferente pois os autovalores s˜ao respectivamente: λ1 = 1.266331881 e λ2 =

−0.3400310827.

Isto resulta num expoente de crossover ̟ = 0.829... > ωc = 0.555.... Luck.

(65)

3.4 Conclus˜

ao

(66)

(67)

Cap´ıtulo 4

Ashkin-Teller de 3-cores na Rede

Hier´

arquica

O modelo AT-2 apresenta uma linha de pontos fixos com expoentes cr´ıticos variando continuamente, sobre a qual o modelo é solúvel através de um mapeamento no modelo Baxter. Esta riqueza de comportamento multicr´ıtico estimularam Grest e Widom a estu-darem o modelo Ashkin-Teller de N cores (AT-N) através de vários métodos anal´ıticos e computacionais. Uma dessas abordagens , devido a Migdal e Kadanoff, nos permite obter ”certos resultados”ora com uma aproxima¸cão sistemática para redes reais, ora como re-sultados exatos em rede hierárquica. Pretendemos explorar as propriedades cr´ıticos e o diagrama de fases para o modelo IAT-3 (definiremos mais tarde) numa rede quadrada via rede hierárquica. Vamos come¸car com um hamiltoniano bem geral para obter rela¸cões de recorrências as mais gerais poss´ıveis em uma rede hierárquica com intera¸cões de troca aperiódicas crescida a partir do ”cluster”da figura (4.1.2). Na forma reduzida a nossa “fun¸cão energia” será expresso assim,

−_κH

BT =

i,j

(K1σiσj +K2θiθj +K3τiτj +K4σiθiσjθj+K5θiτiθjτj+K6σiτiσjτj) +

i,j

(K7σiθiτiσjθjτj) (4.1)

onde

(68)

de troca reduzida entre s´ıtios primeiros vizinhos. Através do grupo de renormaliza¸cão no espa¸co real, vamos estudar as simetrias deste modelo, em temperatura finita na região onde predomina o comportamento ferromagnético (

iKi ≥0), com o aux´ılio do conceito de transmissividade para calcular as rela¸c˜oes de recorrˆencia.

4.1 C´

alculo das Transmissividades

Em primeiro lugar vamos retomar o conceito de transmissividade definida por Alcaraz-Tsallis24 a partir de um par de spins (i,j) localizados, sobre dois s´ıtios quaisquer de uma rede. Denotando como mostra a equa¸cão a seguir, ela é uma média térmica apropriada da correla¸cão entre os spins desses dois s´ıtios, podendo, portanto ser escrita na forma,

tij =< σiσj >=

i,jσiσje−εij/κBT

i,je−εij/κBT

= Nij

Dij

. (4.2)

Define-se, ainda, a transmissividade dual para o mesmo par de spins, numa dada comfigura¸cão, como o peso de Boltzman associado a uma certa configurã¸cão escolhida convenientemente com o propósito de obter regras simples que permitam calcular trans-missividades em série e em paralelo como veremos mais adiante. Assim sendo, escrevemos,

tD_ij = e−εij/κBT _(4.3)

(69)

Tabela 4.1: Energias Degeneradas das Configura¸cões na Equa¸cão 4.1

Item Conﬁgura¸c˜oes ₋εij/κBT Deg.

a σi =−σj; θi =θj; τi =τj −K1+K2+K3 −K4+K5−K6−K7 8 b σi =σj; θi =−θj; τi =τj K1−K2+K3−K4−K5+K6−K7 8 c σi =σj; θi =θj; τi =−τj K1+K2−K3+K4−K5−K6−K7 8 d σi =−σj; θi =−θj; τi =τj −K1−K2+K3+K4−K5−K6+K7 8 e σi =σj; θi =−θj; τi =−τj K1−K2−K3−K4+K5−K6+K7 8 f σi =−σj; θi =θj; τi =−τj −K1+K2−K3−K4−K5 +K6+K7 8 g σi =−σj; θi =−θj; τi =−τj −K1−K2−K3+K4+K5+K6−K7 8 h σi =σj; θi =θj; τi =τj K1+K2+K3+K4+K5 +K6+K7 8

O que se vê na tabela 4.1 é obtido a partir do hamiltoniano 4.1. Escolhemos as configura¸cões de spins e contamos as suas respectivas energias degeneradas para obter a contribui¸cão de cada configura¸cão no cálculo das transmissividades, seja entre um par de s´ıtios primeiros vizinhos ou não. Entre dois s´ıtios no topo de uma rede hierárquica qualquer, já vimos que, entre o passo n e o passon+1 de crescimento da rede, existem uma infinidade de caminhos conectados por liga¸cões ora em série, ora em paralelo. Isso nos leva a come¸car o problema pelo lado mais simples até obtermos as rela¸cões de recorrência finais, representativas do conjunto das correla¸cões, que nos conduza ao diagrama de fases do modelo investigado. Vamos, portanto, come¸car nossa tarefa com o propósito de obter as rela¸cões de recorrência para uma rede diamante simples e estendê-lo, na se¸cão 4.1.3, para o caso mais geral de um ”cluster”aperiódico com r liga¸cões em paralelo, como mostrado na figura 4.1, e a partir dessas rela¸cões estudarmos os casos mais simples de interesse no momento.

(70)

Figura 4.1: Cluster para o passo 1 no crescimento de uma rede com r liga¸coes em paralelo e parˆametro de redeb= 2.

4.1.1 Transmissividade para Spins Localizados Sobre uma

Liga¸

c˜

ao com Pontas Soltas

Neste passo escreveremos as transmissividades definidas pela equa¸cão 4.2 a partir das energias das configura¸cões da tabela 4.1 e calculamos as médias térmicas para cada intera¸cão entre spins de s´ıtios distintos, assim:

t1 = < σiσj > = f1(tDi )