Simulações de Monte Carlo para os modelos Ising e Blume-Capel em redes complexa

DEPARTAMENTO DE FÍSICA TEÓRICA E EXPERIMENTAL PROGRAMA DE PÓS

-

S

IMULAÇÕES DE

M

ONTE

CARLO PARA OS

M

ODELOS

I

SING E

B

LUME-CAPEL EM

R

EDES

COMPLEXA

F

RANCISCO

BIAGIONE DE

LIMA

JÚNIOR

NATAL-RN

S

IMULAÇÕES DE

M

ONTE

CARLO PARA OS

M

ODELOS

I

SING E

B

LUME-CAPEL EM

R

EDES

COMPLEXA

Dissertação de Mestrado apresentada ao Programa de Pós-Graduação em Física do Departamento de Física Teórica e Expe-rimental da Universidade Federal do Rio Grande do Norte como requisito parcial para a obtenção do grau demestreem Física.

Orientador: Professor Adriano de Oliveira Sousa

NATAL-RN

ao meu irmão Bruno Alves de Lima.

Gostaria de agradecer a minha noiva Tiely Virginio da Hora, a minha mãe Ma-ria Conceição Alves de Lima, a meu irmão Bruno Alves de Lima que estiveram comigo, sempre apoiando-me, motivando-me e dando conselhos.

Gostaria de agradecer ao Programa de Pós Graduação em Física, da Universidade Federal do Rio Grande do Norte por aceitar-me como aluno.

Gostaria de agradecer ao Professor Adriano de Oliveira Sousa por ter aceitado ser meu orientador, sempre dando-me conselhos e ter sido paciente comigo.

Gostaria de agradecer a todos os Professores da Universidade Federal do Rio Grande do Norte que contribuem para a formação dos alunos.

Gostaria de agradecer aos Professores Ananias Monteiro Mariz e Francisco We-lington de Sousa Lima por ter aceitado o convite de participar da banca examinadora e pelos valiosos comentários sobre o trabalho.

Gostaria de agradecer a Deus por permitir a minha existência.

Neste trabalho estudamos o modelo de Ising ferromagnetico com spin-1/2 e o mo-delo Blume-Capel com spin-1,∆ > 0em rede mundo pequeno, usando simulação

com-putacional através do algoritmo de Metropolis. Calculamos grandezas macroscópicas do sistema, tais como a energia interna, a magnetização, o calor específico, a susceptibilidade magnética e o cumulante de Binder. Encontramos para o modelo de Ising o mesmo resul-tado obtido pelos Coreanos H. Hong, Beom Jun Kim e M. Y. Choi [6] e um comportamento crítico similar o modelo Blume-Capel.

Palavras chave: Metropolis, Redes Complexa, Sistemas magnéticos.

We studied the Ising model ferromagnetic as spin-1/2 and the Blume-Capel mo-del as spin-1, ∆ > 0 on small world network, using computer simulation through the

Metropolis algorithm. We calculated macroscopic quantities of the system, such as inter-nal energy, magnetization, specific heat, magnetic susceptibility and Binder cumulant. We found for the Ising model the same result obtained by Koreans H. Hong, Beom Jun Kim and M. Y. Choi [6] and critical behavior similar Blume-Capel model.

Key words: Complex Networks, Magnetic system, Metropolis.

2.1 Representação gráfica de uma cidade formada pelos cidadãosA,B,C,D,EeF. . 4

2.2 Coeficiente de agrupamento local para o sítioide uma rede. . . 9

2.3 Ilustração da rede aleatória de Erdös-Rényi (ER). . . 11 2.4 Histograma da distribuição de conectividade com 1000 amostras para N = 10000

sítios e diferentes valores de probabilidadepna rede aleatória de Erdös-Rényi. . . 13

2.5 Ilustração da rede de mundo pequeno de Watts e Strogatz (WS). . . 14 2.6 Histograma da distribuição de conectividade com 1000 amostras para N = 10000

sítios e diferentes valores de probabilidadepna rede de pequeno mundo de Watts

e Strogatz comm= 3. . . 16 2.7 Ilustração da Rede de Barabasi-Albert param0= 3em= 2. . . 17

2.8 Histograma da distribuição de conectividade com 1000 amostras para N = 10000 sítios em= 3na rede Barabasi e Albert. . . 19

2.9 Coeficiente de agrupamento versus o número de sítios para diferentes valores de

mna rede Barabasi e Albert. . . 20

3.1 Gráfico (a) da energia interna e (b) da magnetização para diferentes valores de passos de Monte Carlo em uma rede quadrada comL= 50. . . 25 3.2 Gráfico da energia interna para uma rede quadrada com diferentes tamanhos de

rede. . . 26

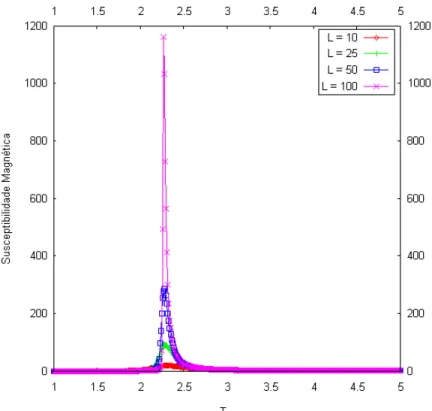
rede. . . 27 3.5 Gráfico da susceptibilidade magnética para uma rede quadrada com diferentes

tamanhos de rede.. . . 27 3.6 Gráfico do cumulante de Binder versus temperatura (a) em rede quadrada e (b) em

rede cúbica para diferentes tamanhosL. . . 29

3.7 Gráfico da variação do cumulante de Binder versus tamanho da redeLna

tempe-ratura crítica (a) em rede quadrada e (b) em rede cúbica. . . 30 3.8 Gráfico da da magnetização versus tamanho da redeLna temperatura crítica (a)

em rede quadrada e (b) em rede cúbica. . . 31 3.9 Gráfico da susceptibilidade magnética versus tamanho da redeLna temperatura

crítica (a) em rede quadrada e (b) em rede cúbica. . . 32 3.10 Ilustração da rede de mundo pequeno estudada por Andrzej Pe¸kalski. . . 34 3.11 Gráfico (a) da variação do cumulante de Binder versusN e (b) da variação do calor

específico versusN para o modelo de Ising em rede de mundo pequeno comp= 1. 35 3.12 Gráfico (a) da variação do calor específico versusT (b) da magnetizaçãom(T)N1/4

versusT (c) do cumulante de Binder versusT e (d) da susceptibilidade magnética

χ(T)N−1/2versusT para o modelo de Ising em rede de mundo pequeno comp= 1. 36

3.13 Gráficos do Cumulante de Binder versus a temperatura para o modelo de Ising em rede mundo pequeno (a) parap= 0.3e (b) parap= 0.6. . . 37 3.14 Gráfico da temperatura crítica versus a probabilidade de adicionar ligaçõesp. . . . 38

3.15 Gráficos da variação do Cumulante de Binder(com∆T = 0.08)versus o número

de sítios para o modelo de Ising em Rede de Mundo Pequeno (a) parap= 0.3e (b)

parap= 0.6. . . 40

3.16 Gráficos da magnetização na temperatura críticaTcversus o número de sítios para

o modelo de Ising em Rede de Mundo Pequeno (a) parap= 0.3e (b) parap= 0.6.. 41 3.17 Gráficos da Susceptibilidade magnética na temperatura críticaTc versus o número

de sítios para o modelo de Ising em Rede de Mundo Pequeno (a) parap= 0.3e (b) parap= 0.6. . . 42

4.2 Gráfico do Cumulante de Binder versus a temperatura para o modelo de Blume-Capel com∆ = 0.0em rede quadrada. . . 44

4.3 Gráfico do Cumulante de Binder versus a temperatura para o modelo de Blume-Capel com∆ = 0.5em rede quadrada. . . 45

4.4 Gráfico do Cumulante de Binder versus a temperatura para o modelo de Blume-Capel com∆ = 1.0em rede quadrada. . . 45 4.5 Gráficos da variação do Cumulante de Binder(com∆T = 0.08)versus o tamanho

da redeLpara o modelo de Blume-Capel em rede quadrada (a) para∆ = 0.0e (b)

para∆ = 1.0. . . 47

4.6 Gráficos da magnetização na temperatura críticaT_c versus o tamanho da redeL

para o modelo de Blume-Capel em rede quadrada (a) para ∆ = 0.0 e (b) para ∆ = 1.0. . . 48 4.7 Gráficos da Susceptibilidade magnética na temperatura críticaTcversus o tamanho

da redeLpara o modelo de Blume-Capel em rede quadrada (a) para∆ = 0.0e (b)

para∆ = 1.0. . . 49

4.8 Gráficos do Cumulante de Binder versus a temperatura para o modelo de Blume-Capel com diferentes valores de∆em Rede de Mundo Pequeno comp= 1. . . 51

4.9 Diagrama de fases do modelo Blume-Capel em rede mundo pequeno comp= 1. . 52 4.10 Gráficos da variação do Cumulante de Binder versus o número de sítios para o

modelo de Blume-Capel com diferentes valores de∆em Rede de Mundo Pequeno comp= 1. . . 53

4.11 Gráficos da magnetização na temperatura críticaT_cversus o número de sítios para

o modelo de Blume-Capel com diferentes valores de ∆em Rede de Mundo

Pe-queno comp= 1. . . 54 4.12 Gráficos da Susceptibilidade magnética na temperatura críticaTc versus o número

de sítios para o modelo de Blume-Capel com diferentes valores de∆em Rede de Mundo Pequeno comp= 1. . . 55

3.1 Tabela do resultado encontrado para os expoentes críticos e os resultados espera-dos na literatura. . . 33 3.2 Tabela do resultado encontrado para os expoentes críticos em rede mundo pequeno. 39

4.1 Tabela do resultado encontrado para os expoentes críticos em rede quadrada. . . . 46 4.2 Tabela do resultado encontrado para os expoentes críticos em rede mundo pequeno. 52

1 Introdução 1

2 Redes Complexas 3

2.1 O que é uma Rede Complexa? . . . 3

2.2 Teoria de Grafos . . . 4

2.3 Distribuição de Conectividade . . . 6

2.4 Coeficiente de Agrupamento . . . 9

2.5 Menor Caminho Médio . . . 10

2.6 Rede aleatória de Erdös-Rényi . . . 11

2.7 Rede de Watts-Strogatz . . . 14

2.8 Rede de Barabasi-Albert . . . 16

3 Modelo Ising 21 3.1 Em uma Rede de Mundo Pequeno . . . 33

4 Modelo Blume-Capel 43 4.1 Em uma Rede de Mundo Pequeno . . . 50

5 Conclusões e Perspectivas 56

Apêndices 62

A Algoritmo de Metropolis 62

Apêndices 65

B Expoentes Críticos 65

INTRODUÇÃO

Os modelos de sistemas magnéticos tentam descrever propriedades reais dos ma-teriais, como por exemplo, o paramagnetismo, o ferromagnetismo e o antiferromagne-tismo. As redes complexas tentam descrever os tipos de relações ou conexões entre os elementos de um sistema real como por exemplo, a rede de citações, as redes sociais, as redes ecológicas, a rede de internet, a WWW entre outras.

Neste trabalho estudamos o modelo de Ising [1] e o modelo Blume-Capel [2, 3] em rede mundo pequeno [4]. Reproduzimos os estudos feitos por Pe¸kalski [5] e pelos Co-reanos H. Hong, Beom Jun Kim and M. Y. Choi [6] para o modelo de Ising em rede mundo pequeno e fizemos o mesmo estudo para o modelo Blume-Capel nessa rede. Utilizamos o algoritmo de Metropolis [7] para calcular algumas grandezas macroscópicas dos sistemas (a energia interna, a magnetização, o calor específico, a susceptibilidade magnética e o cumulante de Binder).

No capítulo 2 estudamos um pouco sobre redes complexas, algumas grandezas que caracterizam uma rede complexa, o formalismo matemático para descrever uma rede complexa e algumas redes bastante estudadas recentemente como, por exemplo, a rede aleatória de Erdös-Rényi [8, 9], a rede mundo pequeno de Watts-Strogatz [4] e a rede sem escala de Barabasi-Albert [10].

No capítulo 3 e 4 estudamos o modelo de Ising e Blume-Capel, respectivamente, em uma rede mundo pequeno. Calculando através do algoritmo de Metropolis [7] (que pode ser visto no apêndice A) algumas grandezas macroscópicas, o cumulante de Binder

e os expoentes críticos.

REDES COMPLEXAS

Nos últimos anos, um dos problemas que tem despertado bastante interesse por muitos pesquisadores, são os estudos envolvendo sistemas reais descritos por redes com-plexas. Podemos citar: a Internet [11], a World Wide Web (WWW) [12], as redes ecológicas [13], as redes na linguística [14], entre outras [10, 15]. Diversos modelos teóricos foram construídos com o intuito de estudar esses sistemas.

Entre os modelos de redes mais estudados estão a rede aleatória de Erdös-Rényi [8, 9], a rede mundo pequeno de Watts-Strogatz [4] e a rede sem escala de Barabasi-Albert [10].

2.1

O que é uma Rede Complexa?

Uma rede complexa é uma estrutura formada por elementos de um determinado sistema real como, por exemplo, computadores, células, palavras, pessoas, páginas na web. O qual cada elemento do sistema está ligado com outros elementos idênticos através de alguma propriedade entre eles, como por exemplo: conexões entre computadores via cabos ou wireless , ligações químicas entre moléculas, links entre páginas na web.

A topologia de uma rede complexa pode ser caracterizada pela medida de três grandezas fundamentais: função de distribuição de conectividade, coeficiente de agrupamentoe menor caminho médio.

lismo matemático dado pela Teoria dos grafos que veremos a seguir.

2.2

Teoria de Grafos

Um grafo, representado pelo símboloG, é uma estrutura formada por dois

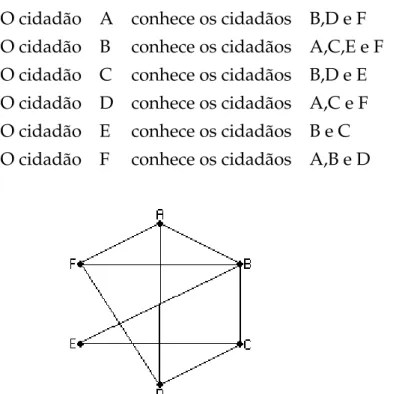
con-juntos básicos: o conjunto dos vértices e o conjunto das arestas. Por exemplo, suponha que uma certa cidade seja formada por6cidadãosA,B,C,D,E eF, os quais

O cidadão A conhece os cidadãos B,D e F O cidadão B conhece os cidadãos A,C,E e F O cidadão C conhece os cidadãos B,D e E O cidadão D conhece os cidadãos A,C e F O cidadão E conhece os cidadãos B e C O cidadão F conhece os cidadãos A,B e D

Figura 2.1: Representação gráfica de uma cidade formada pelos cidadãosA,B,C,D,EeF.

Podemos escrever para o exemplo acima o conjunto dos vérticesV(G)como

V(G) =_{A;B;C;D;E;F_} (2.2.1)

que é formado pelos elementos do grafo (os cidadãos). Podemos escrever o conjunto das arestasA(G)como

A(G) = _{(A, B); (A, D); (A, F); (B, C); (B, E); (B, F); (C, D); (C, E); (D, F)_} (2.2.2)

Uma outra maneira de representar um grafo é através utilização damatriz de adja-cênciaou damatriz de incidência, onde a matriz de adjacência é definida como

xij = (

1 se ij _∈A(G)

0 se ij /_∈A(G) (2.2.3)

enquanto a matriz de incidência é definida como

xij = (

1 se a arestaj é incidente ao vértice i

0 caso contrário. (2.2.4)

para o exemplo de nossa cidade (figura 2.1) podemos escrever a matriz de adjacência da seguinte forma

A B C D E F A 0 1 0 1 0 1

B 1 0 1 0 1 1

C 0 1 0 1 1 0

D 1 0 1 0 0 1

E 0 1 1 0 0 0

F 1 1 0 1 0 0

e a matriz de incidência

AB AD AF BC BE BF CD CE DF A 1 1 1 0 0 0 0 0 0

B 1 0 0 1 1 1 0 0 0

C 0 0 0 1 0 0 1 1 0

D 0 1 0 0 0 0 1 0 1

E 0 0 0 0 1 0 0 1 0

F 0 0 1 0 0 1 0 0 1

O grau de um vérticei(vamos denotar pelo símbolo ki) é dado pela quantidade

kA = 3

kB = 4

kC = 3

kD = 3

kE = 2

kF = 3

SejaEo número de arestas do grafo comNvértices, a soma de todos os graus dos

vértices é sempre o dobro deE, ou seja

2E =

N X

i=1

ki (2.2.5)

para o nosso exemplo o número de elementos do conjunto das arestasA(G)éE = 9, e a

somakA+kB+kC +kD +kE+kF = 18.

2.3

Distribuição de Conectividade

A função distribuição de conectividade é uma das grandezas que caracterizam uma rede complexa. O qual podemos extrair diversas informações através do seu trata-mento estatístico.

Seja P(k, s, N)a probabilidade de um sítio sterk vizinhos em uma rede comN

sítios. A probabilidade de um sítio escolhido aleatoriamente terkvizinhos é dada por

P(k, N) = 1

N

N X

s=1

P(k, s, N) (2.3.1)

ondeP(k, N)é a função distribuição de conectividade que iremos escrever comoP(k).

Se desejarmos saber qual o valor médio de conectividade_hk_ida rede comNsítios,

basta conhecer a função distribuição de conectividade e calcular utilizando a seguinte expressão

hk_i=

N−1

X

k=1

kP(k) (2.3.2)

Podemos também calcular os outros momentos dado por

hkn_i=

N−1

X

k=1

knP(k). (2.3.3)

As redes complexas podem ter distribuições de conectividade P(k) conhecidas, por exemplo, a distribuição Gaussiana, a distribuição Binomial, a distribuição de Poisson, distribuições que obedecem uma lei de potência entre outras. A partir das quais podemos classificar-las comohomogêneaouheterogêneacalculando o grau de heterogeneidadeκque

é definido como

κ= hk

2_i

hk_i. (2.3.4)

Dizemos que uma rede é homogênea quando existe poucas flutuações para o va-lor médio dek, ou seja, para κ _{∼ h}k_i. Caso contrário, para κ _{≫ h}k_i a rede é dita

hete-rogênea. Um exemplo de uma rede heterogênea é uma rede descrita pela distribuição de conectividade que obedece uma lei de potência

P(k) = Ak−γ, (2.3.5)

ondeAé a constante de normalização.

Suponha uma rede muito grande com N sítios (N _{→ ∞}). Sejam o menor grau

da rede ekm o maior grau da rede (km → ∞). Podemos aproximark por uma variável

contínua e normalizar nossa distribuição

lim

km→∞

Z km

m

P(k)dk = 1 (2.3.6)

A lim

km→∞

Z km

m

k−γdk =A lim

km→∞ k1−γ

m

1₋γ −A m1−γ

1₋γ (2.3.7)

encontrando

A= (γ₋1)mγ−1 (2.3.8)

Calculando o primeiro momento temos

hk_i= lim

km→∞

Z km

m

kP(k)dk (2.3.9)

hk_i= (γ₋1)mγ−1 lim

km→∞

Z km

m

k−γ+1dk (2.3.10)

hk_i= (γ₋1)mγ−1 lim

km→∞ k2−γ

m

2₋γ + γ₋1

γ₋2m (2.3.11)

encontrando um valor finito

hk_i= γ−1

γ₋2m (2.3.12)

paraγ >2. Agora calculando o segundo momento temos

hk2_i= lim

km→∞

Z km

m

k2P(k)dk (2.3.13)

hk2_i= (γ₋1)mγ−1 lim

km→∞

Z km

m

k−γ+2dk (2.3.14)

hk2_i= (γ₋1)mγ−1 lim

km→∞ k3−γ

m

3₋γ + γ₋1

γ₋3m

2 _(2.3.15)

que diverge quando

2< γ _≤3 (2.3.16)

então o grau de heterogeneidade dessa rede também diverge

κ_{→ ∞} (2.3.17)

logo, nessas condições, o valor médio deknão é uma escala característica da rede. É daí

2.4

Coeficiente de Agrupamento

Se o sítio ide uma rede possui conectividade ki, o número máximo de pares de

ligações possíveis entre os vizinhos dele será dada

C₂ki = ki! 2!(ki−2)!

(2.4.1)

pela combinação deki tomada2.

Definindoyi como o número de pares de ligações existentes entre os vizinhos do

sítio i. A razão entre yi e o número máximo de pares de ligações possíveis dado pela

equação (2.4.1) será

ci =

2yi

ki(ki−1)

(2.4.2)

o coeficiente de agrupamento do sítioique representa quanto os vizinhos do sítioiestão

conectados entre si, esse é conhecido como coeficiente de agrupamento local. Note que se todos os vizinhos do sítioi estiverem conectados entre si, o coeficiente de agrupamento

do sítioi assumirá seu valor máximo ci = 1. O outro extremo é para ci = 0 que ocorre

quando não existe ligações entre os vizinhos do sítioi.

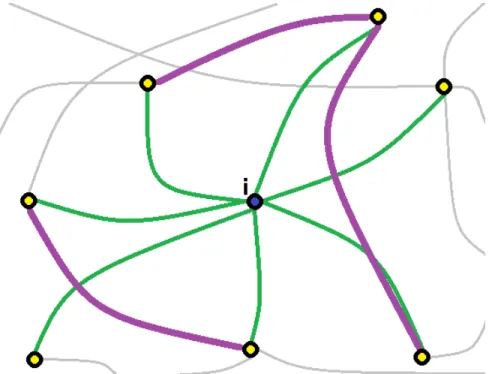
Como exemplo, podemos calcular o coeficiente de agrupamento local de um sítio

i(veja a figura 2.1) que apresenta conectividadeki = 7. Seus vizinhos apresentam3pares

de ligações, ou sejayi = 3. Logo o coeficiente de agrupamento para o sítioide acordo com

a equação (2.4.2) seráci = 1/7.

Se somarmos todos os coeficientes de agrupamentos locais de uma rede e dividi-mos pelo número total de sítios teredividi-mos ocoeficiente de agrupamento globaldado por

C= 1

N

N X

i=1

ci (2.4.3)

que representa o quanto os sítios da rede estão conectados entre si.

2.5

Menor Caminho Médio

O caminho entre dois sítios i e j em uma rede é caracterizado pela medida da

distância entre eles. Essa distância é definida como o número de arestas existentes entre os sítiosiejda rede.

Sejalij a menor distância entre os sítiosiej. O menor caminho médio da rede será

a razão entre a soma de todos os pares de menor distância entre os sítios com o número de pares possíveis. Logo

hl_i= 1

N(N ₋1)

N X i=1 N X j=1

lij. (2.5.1)

O exemplo mais simples do cálculo dessa grandeza é num grafo completo, onde todos os sítios estão conectados entre si. Para qualquer valor deiej, a menor distância

entre os sítios sempre serálij = 1. Logo o menor caminho médio nesse grafo seráhli= 1.

Em sua experiência, se o remetente conhecesse o destinatário, entregaria a carta pessoalmente. Caso contrário, entregaria para um amigo que tivesse em seu círculo de amizades maior número de amigos. E obteve como resultado quehl_i = 6, ou seja, seria necessário apenas6pessoas entre o remetente e o destinatário para a carta chegar no seu

destino. O resultado dessa experiência ficou conhecido comoseis graus de separação.

2.6

Rede aleatória de Erdös-Rényi

Em 1959 Paul Erdös e Alfréd Rényi escreveram um algoritmo para construir um grafo aleatório [8] e [9] com o objetivo de estudar aspectos estatísticos.

Nesse modelo iniciamos comNsítios sem ligações e com uma dada probabilidade p conectamos pares de sítios escolhidos aleatoriamente na rede até obtermos o número total de ligaçõesE.

p = 0.0000 p = 0.5000 p = 1.0000

Figura 2.3: Ilustração da rede aleatória de Erdös-Rényi (ER).

Na figura acima podemos observar que quando p = 0não exite nenhum par de

sítios conectados. Porém, quandop= 1provavelmente todos os sítios estarão conectados.

Logo, o número de ligações E existentes na rede será aproximadamente o número de ligações possíveis multiplicado pela probabilidadep, ou seja

E ∼= N(N−1)

2 p (2.6.1)

a partir do qual podemos obter o número médio de ligações na rede, dividindo a soma das conexões de todos os sítios pela quantidade de sítios

hk_i= 2E

para uma rede comN muito grande, podemos fazer a seguinte aproximação

hk_{i ∼}=N p. (2.6.3)

Como cada ligação é adicionada aleatoriamente e independe da ligação adicio-nada no passo anterior, a probabilidade de um sítio terkvizinhos é igual a probabilidade

dele estar conectado ak sítios com probabilidadepe desconectado aos N ₋1₋k sítios

restantes com probabilidade1₋p. Logo, a função distribuição de conectividade para a rede de Erdös-Rényi é dada pela distribuição binomial

P(k) =C_kN−1pk(1₋p)N−1−k= (N −1)!

k!(N ₋1₋k)!p

k₍₁

−p)N−1−k (2.6.4)

P(k) = 1

k!(N −1)(N −2)(N −3)· · ·(N −k)p

k₍₁

−p)N−1−k (2.6.5)

que pode ser reescrita

P(k) = 1

k!

k X

i=0

(₋1)k−iaiNipk(1−p)N−1−k (2.6.6)

ondeai é uma constante real positiva para qualquer valor deieak= 1.

Utilizando a equação (2.6.3) na equação (2.6.6) acima temos

P(k) = hki

k

k!

1₋ hki

N

N−1−k k X

i=0

(₋1)k−iaiN−(k−i) (2.6.7)

a qual podemos aproximar para a distribuição de Poisson

P(k) = hki

k

k! e

−hki _(2.6.8)

para uma rede com muitos sítios(N _{→ ∞}).

A figura 2.4 mostra o resultado obtido através da simulação numérica feita na rede de Erdös-Rényi para obter a distribuição de conectividade. Note que aumentando o valor de probabilidade de conexãopo valor máximo da distribuição de conectividade

Figura 2.4:Histograma da distribuição de conectividade com 1000 amostras para N = 10000 sítios e diferentes valores de probabilidadepna rede aleatória de Erdös-Rényi.

aumenta, ou seja, uma maior região de sítios na rede terão maiores conexões. Que é es-perado intuitivamente, pois o limite em que a probabilidade de conexãoptende para seu

valor máximo emp= 1, os sítios da rede tedem estarem totalmente conectados entre si.

Para um sítioidessa rede, a probabilidade de dois de seus vizinhos estarem conec-tados entre si é dada pela probabilidade de conexãop. Logo, o coeficiente de agrupamento

local e global para essa rede é

C =p. (2.6.9)

Se utilizarmos o valor médio de conexão _hk_i e elevarmos pelo menor caminho

médio_hl_iteremos uma boa aproximação para o número total de sítios da rede aleatória,

logo podemos dizer que

hl_i= log(N)

o menor caminho médio depende do logaritmo do número de sítios da rede. Podemos utilizar a equação 2.6.3 na equação 2.6.10 para obtermos

hl_i= log(N)

log(N p) =

log(N)

log(N) +log(p). (2.6.11)

Note que, quando a probabilidade de conexão for muito próximo p _≈ 1, temos

que o menor caminho médio será próxima do menor valor possivel que é _hl_i = 1 para

qualquer tamanho N dessa rede. Somente quando p _≪ 1, teremos o menor caminho médio_hl_{i ≫}1com alto valor.

2.7

Rede de Watts-Strogatz

Em 1998 Duncan J. Watts e Steven Strogatz [4] desenvolveram um algoritmo ba-seado na rede de Erdös e Rényi com o intuito de estudar redes sociais. A rede estudada por eles tem a geometria de um anel circular e é formada por um número fixoN de sí-tios o qual cada sítio estará conectado a 2m vizinhos mais próximos geometricamente.

Formando um número fixo de ligações na rede, dado por

E =mN. (2.7.1)

Com uma dada probabilidade de redirecionamento p, mudaremos

aproximada-mentepmN ligações aleatoriamente na rede.

p = 0.0000 p = 0.1875 p = 1.0000

Figura 2.5: Ilustração da rede de mundo pequeno de Watts e Strogatz (WS).

Podemos observar o processo de construção dessa rede pela figura 2.5. Note que para p = 0 nenhuma ligação foi mudada. Mas, com o aumento da probabilidade de

Vários cálculos analíticos foram feitos com o objetivo de conhecer as propriedades de uma rede de mundo pequeno como, por exemplo, o realizado por Barrat e Weigt [17]. Em seu trabalho, eles calcularam a distribuição de conectividade

Pp(k) =

min(k−m,m)

X

n=0

C_kn(1₋p)npm−n (pm)

k−m−n

(k₋m₋n)!e

−pm_{, k}

≥m (2.7.2)

o coeficiente de agrupamento

C(p) = 3m(m−1)

2m(2m₋1)(1−p)

3 _(2.7.3)

e o menor caminho médio

l(N,0) = N(N + 2k−2) 4k(N₋1) ∼

N

4k (2.7.4)

quandop= 0e

l(N, p)_∼p−1dF k(N p

1

d) (2.7.5)

quandop >0, onde

Fk(N p

1

d) =

(

N p1d/4k se N p

1

d ≪1

ln(N p1d) se N p

1

d ≫1

. (2.7.6)

A figura 2.6 mostra o resultado obtido através da simulação numérica feita na rede de Watts-Strogatz para obter a distribuição de conectividade. Podemos observar que para qualquer valor de probabilidade de redirecionamentop, a conectividade média é sempre a mesma_hk_i= 6.

Quando essa probabilidade tende para seu menor valor em p _≈ 0, a função

dis-tribuição de conectividade tende para uma função delta, ou seja, todos estão conectados exatamente com6vizinhos mais próximos que é a configuração inicial da rede. O

contrá-rio ocorre parap > 0, com o aumento dessa probabilidade ocorre um aumento da região

Figura 2.6:Histograma da distribuição de conectividade com 1000 amostras para N = 10000 sítios e diferentes valores de probabilidadepna rede de pequeno mundo de Watts e Strogatz comm= 3.

2.8

Rede de Barabasi-Albert

Pesquisas com redes reais como a rede de Internet, as redes sociais, a World Wide Web, entre outras mostraram que elas são descritas por distribuições de conectividade que obedecem uma lei de potência [10] dada pela equação 2.3.5, apresentando um valor típico para o expoenteγentre

2< γ _≤3 (2.8.1)

t = 0 t = 1 t = 2

t = 3 t = 4 t = 5

Figura 2.7: Ilustração da Rede de Barabasi-Albert param0 = 3em= 2.

Na figura 2.7 podemos observar o processo de construção dessa rede. Inicial-mente, começamos com um número pequenom0 de sítios. E a cada passot, um novo sítio

é adicionado a rede ligando-se am _≤ m0 sítios da rede. A probabilidade Q(ki) de um

novo sítio conectar-se a um sítioida rede é dada por

Y

(ki) =

ki P

jkj

. (2.8.2)

onde o somatório emj é de todos os sítios já pertencentes a rede.

Depois de um tempot, teremosN =t+m0sítios eE =mt+m0ligações na rede. A

probabilidadeQ

(ki)muda no tempotigualmente comki. Se assumirmos a conectividade

kicomo uma variável contínua, podemos escrever a seguinte equação

∂ki

∂t =m

Y

∂ki

∂t =m ki P

jkj

(2.8.4)

onde a soma de todas as conectividades da rede é igual ao dobro do número de ligações

X

j

kj = 2(mt+m0) (2.8.5)

onde podemos considerar para uma rede com muitos sítiosN _≫1, a equação acima pode ser aproximada para2mt, pois o termo2m0 ≪2mt. Assim, podemos reescrever a equação

2.8.4 da seguinte forma

∂ki

∂t = ki

2t. (2.8.6)

No tempo inicial t0 a conectividade do sítio i é ki(t0) = m. Logo, resolvendo a

equação 2.8.6 temos

ki =m

t t0

12

. (2.8.7)

Usando a equação 2.8.7 podemos escrever a probabilidade de terki(t)menor que

kcomo

P(ki(t)< k) =P

t0 <

m2_t

k2

(2.8.8)

P(ki(t)< k) = 1−

m2_t

k2 P(t0) (2.8.9)

onde a probabilidade de termos t0 para um novo sítio adicionado a rede assume uma

distribuição de probabilidade constante dada por

P(t0) =

1

m0+t

(2.8.10)

logo

P(ki(t)< k) = 1−

m2_t

k2_(m 0+t)

Podemos obter a distribuição de conectividade P(k)derivando a equação 2.8.11

em relação ak[10, 18]

P(k) = ∂P(ki(t)< k)

∂k (2.8.12)

pois a probabilidade de termos ki(t) < k, é igual calcular a área abaixo de P(k) até k.

Podemos fazer essa operação porque a função distribuição de conectividade é uma quan-tidade admensional, logo não teriamos problemas com análise dimensional. Temos como resultado

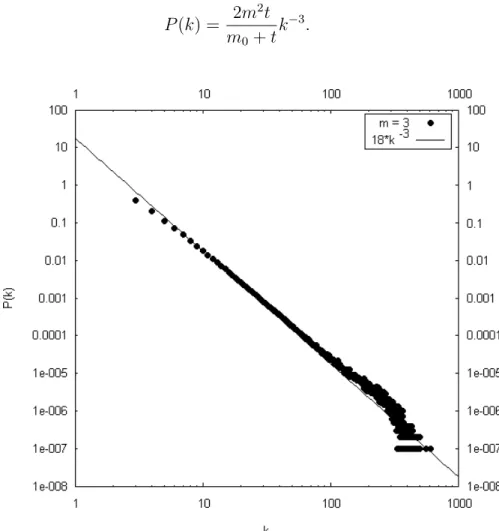
P(k) = 2m

2_t

m0+t

k−3. (2.8.13)

Figura 2.8:Histograma da distribuição de conectividade com 1000 amostras para N = 10000 sítios em= 3na rede Barabasi e Albert.

Para uma rede com muitos sítios (N _{→ ∞})temos que t _{→ ∞} e a equação 2.8.13

pode ser escrita como

Note que a equação 2.8.14 satisfaz as equações 2.3.5 e 2.3.8 paraγ = 3. Indicando

que a rede de Barabasi e Albert é uma rede livre de escala.

Na figura 2.8 podemos observar o resultado da simulação numérica e compara-la com a equação 2.8.14.

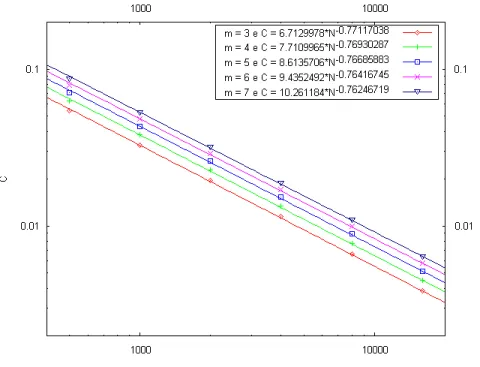
O coeficiente de agrupamento para a rede de Barabasi e Albert também segue uma lei de potência [10], dada por

C =N−0.75 (2.8.15)

apresentando baixo coeficiente de agrupamento para uma rede com muitos sítios.

Figura 2.9: Coeficiente de agrupamento versus o número de sítios para diferentes valores dem

na rede Barabasi e Albert.

Na figura 2.9 podemos observar o resultado obtido para o coeficiente de agrupa-mento para diferentes valores dem(número de ligações de um novo sítio). Esse resultado

é muito semelhante com a equação 2.8.15. Note também que a medida que aumentamos

N o número de sítios da rede, o coeficiente de agrupamento diminui. Isso significa que

MODELO ISING

O Modelo de Ising foi proposto em 1920 por Wilhelm Lenz e estudada em 1925 por Ernest Ising [1] para um rede linear com campo magnético externo nulo e spin 1/2

(a história detalhada do surgimento desse modelo é discutido em 1967 por Stephen G. Brush [19]). Ele partiu inicialmente de um hamiltoniano simples considerando apenas as interações dos momentos magnéticos entres os vizinhos mais próximos dada por

−Jsi(si+1+si−1), (3.0.1)

ondeJ representa a energia de interação entre os spins, si, si−1 e si+1 representa os

mo-mentos magnéticos do sítioi,i₋1ei+ 1respectivamente.

Ele calculou analiticamente expressões algébricas para as grandezas macroscópi-cas do sistema, como por exemplo a energia interna e a magnetização. Para (J > 0) e

campo magnético externo nulo, esperava-se encontrar um estado ferromagnético em uma região de temperaturas abaixo da temperatura crítica de transição. Porém, não encontrou transição de fases e magnetização expontânea. Aparentemente sua proposta de trabalho não poderia explicar esse fenômeno de grande interesse no meio científico.

Em 1936 Peierls [20] mostrou que o modelo de Ising para redes regulares com dimensões maiores que(d > 1), apresentam uma temperatura crítica de transição maior

que o valor nulo e que para o caso unidimensional essa transição acontece na temperatura nula(Tc = 0).

Resolver o modelo de Ising na física estatística, consiste em soma todas as pos-síveis configurações (que é definida como função de partição), e fazer a conexão com a termodinâmica através dos parâmetros macroscópicos do sistema.

Para um sistema descrita pela estatística de Boltzmann a função de partição em termos da temperaturaT, campo externoH0, número de partículasN do sistema é dada

por

Z(T, H0, N) =

X

e−kB TH (3.0.2)

onde e−kB TH é o peso estatístico de Boltzmann, _H é o hamiltoniano do sistema e _kB é a

constante de Boltzmann. O qual podemos fazer a conexão com a termodinâmica através da energia livre de Helmholtz por partícula dada por

a(T, H0) = lim

N→∞−

1

N β ln(Z(T, H0, N)) (3.0.3)

ondeβ = _kB1_T. A partir do qual podemos obter as grandezas macroscópicas, como por

exemplo a energia interna

u(T, s) = a+T s, (3.0.4)

magnetização

m(T, H0) =−

∂a ∂H0 T , (3.0.5)

o calor específico

c(T, H0) = −T

∂2_a

∂T2

H0

, (3.0.6)

e a susceptibilidade magnética

χ(T, H0) =−

∂2_a

∂H2 0

T

Para o modelo de Ising o hamiltoniano é dado pela seguinte expressão

H =₋JX

(i,j)

sisj (3.0.8)

onde nessa soma consideramos apenas as interações dos spinssi esj mais próximos, os

quais podem assumir os valores _±1. Para J > 0, se todos os spins estiverem com os

mesmos valores de spins (si = 1ousi =−1para qualqueri), o sistema terá menor energia

para o estado ferromagnético. Enquanto que para J < 0, se todos os spins estiverem

alternadamente com esses valores (si = 1esi+1 =−1), o sistema terá menor energia para

o estado antiferromagnético.

A função distribuição de Boltzmann leva em consideração tanto a energia como a temperaturaT do sistema. ParaJ > 0, se a energia tiver seu menor valor possível a

bai-xas temperaturas, a probabilidade de sistema estar no estado ferromagnético é maior. Ao passo que aumentamos a temperatura do sistema, essa probabilidade diminui. Fazendo com que o sistema saia da fase ferromagnética para a fase desordenada. É intuitivo ima-ginar um valor de temperatura que separa a mundança dessas fases, ou seja, ocorre uma transição de fases numa dada temperaturaTc que é conhecida como temperatura crítica.

Muitos sistemas físicos conhecidos apresentam transição de fases de primeira or-dem ou transição de fases de segunda oror-dem (conhecido também como transição de fases contínua). A transição de fases de primeira ordem ocorre quando as primeiras deriva-das da energia livre de Gibbs sofrem variações finitas. Enquanto na transição de fases de segunda ordem ocorre quando as primeiras derivadas são contínuas porém as segundas derivadas da energia livre de Gibbs divergem ou são descontínuas [21].

Podemos adicionar a esse modelo outros termos de interações ao sistema, como por exemplo um campo magnético externoH0. Assim, o hamiltoniano seria dado por

H =₋JX

(i,j)

sisj+H0

N X

i=1

Em 1944 Lars Onsager [22] resolveu analiticamente o modelo de Ising na ausencia de campo em rede quadrada. E calculou a magnetização a campo externo nulo, dada pela expressão

m(T, H0 = 0) =

1₋sinh−4

2J kBT

18

(3.0.10)

e a temperatura crítica

kBTc

J =

2

ln(1 +√2) ∼= 2.269185315. (3.0.11)

Em 1953 Nicholas Metropolis [7] e colaboradores construíram um algoritmo ba-seado no método de Monte Carlo (veja o Apêndice A). Desde então muitos pesquisadores têm usado esse método para estudar modelos de sistema magnéticos por esse método computacional, pois os resultados obtidos usando esta técnica, se aproximam muito dos resultados analíticos, como por exemplo, para o modelo de Ising em uma rede quadrada. Para um sistema com muitas partículas, necessitaremos um número grande de passos de Monte Carlo (veja o Apêndice A) que é proporcional ao tempo computacional que será utilizado.

Na figura 3.1 temos o resultado da energia interna e da magnetização para di-ferentes valores de passos de Monte Carlo em uma rede quadrada com L = 50. Para

T = 1.000, podemos observar que depois de aproximadamente 12000 passos de Monte

Carlo o sistema começa apresentar poucas flutuações para a energia interna e para mag-netização convergindo para um valor. Porém, não ocorre o mesmo para uma temperatura

T = 2.269 próxima da temperatura crítica Tc (conhecido como região crítica).

Apresen-tando flutuações mesmo com o aumento de número de passos de Monte Carlo.

Assim, ao usar o algoritmo de Metropolis, podemos utilizar10_×L_×Lpassos de

Monte Carlo para calcular as grandezas macroscópica do sistema, os quais os resultados obtidos pela primeira metade de passos de Monte Carlo iremos descartar, já que o sistema precisa apresentar poucas flutuações. Para o nosso exemplo da figura 3.1, o número de passos de Monte Carlo que poderíamos utilizar é10_×50_×50 = 25000onde os primeiros 12500passos de Monte Carlo não iremos utilizar para calcular as grandezas.

susceptibili-(a)

(b)

dade magnética.

Figura 3.2:Gráfico da energia interna para uma rede quadrada com diferentes tamanhos de rede.

Figura 3.4:Gráfico do calor específico para uma rede quadrada com diferentes tamanhos de rede.

Na figura 3.2 temos o resultado encontrado da energia interna para o modelo de Ising em rede quadrada. Podemos observar que para baixos valores de temperatura, as configurações mais prováveis são aquelas que apresentam o menor valor de energia interna. Ao passo que ao aumentarmos a temperatura, observamos que a energia do sistema aumenta.

Na figura 3.3 temos o resultado encontrado da magnetização para o modelo de Ising em rede quadrada. Podemos observar magnetização espontânea (fase ferromag-nética) para temperaturas com valores abaixo de uma certa temperatura de transição, e ocorre mudança da fase ordenada para a fase desordenada para temperaturas com valo-res acima dessa temperatura de transição.

Nas figuras 3.4 e 3.5 temos os resultados encontrados do calor específico e da susceptibilidade magnética para o modelo de Ising em rede quadrada. Podemos observar que ambos apresentam uma descontinuidade na temperatura de transição, ou seja, as segundas derivadas da energia livre Helmholtz em relações a temperatura e ao campo magnético externo apresenta descontinuidade. Logo, podemos dizer que o modelo de Ising em rede quadrada com campo magnético nulo eJ >0, apresenta transição de fases

de segunda ordem.

Embora exista muitas flutuações para as grandezas macroscópicas na região crí-tica (para temperaturas próximas da temperatura crícrí-tica), elas apresentam um comporta-mento bem estabelecido, descrita pelos expoentes críticos (veja o Apêndice B).

Podemos calcular o valor médio da n-ésima potência da distância entre a mag-netização em relação ao valor médio da magmag-netização que é definido como o n-ésimo momento da magnetização_h(∆M)n_i.

Em 1981 Binder [23] calculou o quarto momento da magnetização dado por

h(∆M)4_{i ≡}U4 = 1− h

M4_i

hM2_i2 (3.0.12)

onde_hM4_{i representa o valor médio da quarta potência da magnetização e hM}2_i

repre-senta o valor médio da segunda potência da magnetização.

(a) (b)

Figura 3.6: Gráfico do cumulante de Binder versus temperatura (a) em rede quadrada e (b) em rede cúbica para diferentes tamanhosL.

A figura 3.6 é o resultado obtido para o modelo de Ising em rede quadrada e cúbica onde foram utilizadas1000amostras e um intervalo de temperatura∆T = 0.001.

A temperatura crítica encontrada nessa simulação em rede quadrada foi de apro-ximadamenteTc = 2.269±0.0002que estar de acordo com a equação 3.0.11 nas três casas

decimais. E o resultado encontrado em rede cúbica para temperatura crítica foi de aproxi-madamenteTc = 4.510±0.0006que estar próximo do resultado estudado por Heuer [24]

onde encontrouTc = 4.5115.

Podemos agora, encontrar os expoentes críticos das grandezas macroscópicas uti-lizando o algoritmo de Metropolis para calcular essas grandezas na temperatura crítica.

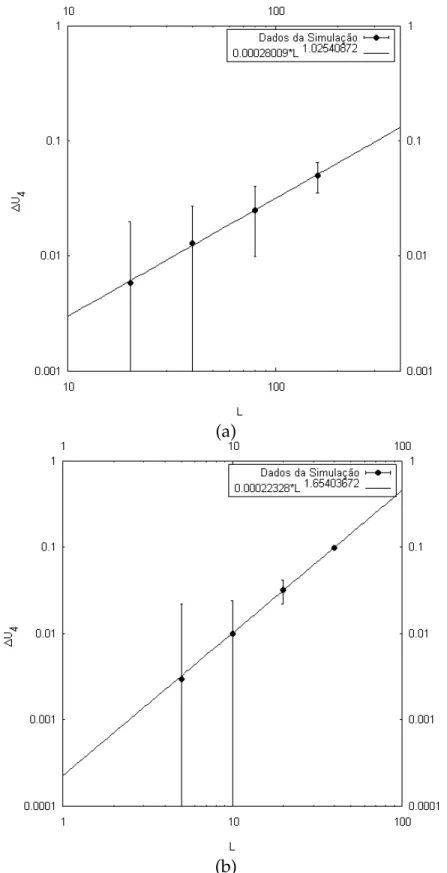
Nas figuras 3.7, 3.8 e 3.9 podemos observar que o comportamento da variação do cumulante de Binder, da magnetização e da susceptibilidade magnética na temperatura crítica obedecem leis de escalas dada pelos expoentes ν, β e γ respectivamente (veja o Apêndice B). Assim, temos a variação do cumulante de Binder

∆U4 ∼L

1

(a)

(b)

Figura 3.7:Gráfico da variação do cumulante de Binder versus tamanho da redeLna temperatura

(a)

(b)

Figura 3.8: Gráfico da da magnetização versus tamanho da redeLna temperatura crítica (a) em

(a)

(b)

Figura 3.9: Gráfico da susceptibilidade magnética versus tamanho da rede L na temperatura

a magnetização

m(Tc,0)∼L− β

ν, (3.0.14)

e a susceptibilidade magnética

χ(Tc,0)∼L γ

ν. (3.0.15)

Podemos obter esses expoentes críticos, analisando as figuras 3.7, 3.8 e 3.9 . Para o modelo de Ising em rede quadrada, os resultados obtidos foram1/ν = 1.02540872, β/ν = 0.12420128 e γ/ν = 1.71219804. Para o modelo de Ising em rede cúbica, os resultados

obtidos foram1/ν = 1.65403672,β/ν = 0.94831001eγ/ν= 2.00645829.

Exato [22] Expansão em série [36] Simulação Simulação

2D 3D 2D 3D

ν 1 5/8 0.98 0.60

β 1/8 5/16 0.12 0.57

γ 7/4 5/4 1.67 1.21

Tabela 3.1: Tabela do resultado encontrado para os expoentes críticos e os resultados esperados na literatura.

Na tabela 3.1 podemos observar que os resultados obtidos pela simulação numé-rica são satisfatório se comparados com os valores da literatura. A partir do qual podemos obter os demais expoentes crítico utilizando as relações entre eles dadas pelas leis de es-calas.

3.1

Em uma Rede de Mundo Pequeno

Diferente de Watts e Strogatz onde o número de sítios e de ligações é fixo para qualquer valor dep(probabilidade de redirecionamento). A rede estudada por Pe¸kalski

apresenta diferentes números de ligações quando mudamos a probabilidadepde adicio-nar ligações extras.

p = 0.0000 p = 0.5000 p = 1.0000

Figura 3.10: Ilustração da rede de mundo pequeno estudada por Andrzej Pe¸kalski.

Podemos observar o processo de construção dessa rede observando a figura 3.10. Inicialmente a rede começa comN sítios ligados somente com os vizinhos mais próximos,

ou seja,p = 0. Com o aumento da probabilidade (p > 0) serão adicionados no máximo a metade da quantidade total de sítiosN, ou seja,E =N/2ligações. Onde a conectividade

de cada sítio pode aumentar somente uma vez.

Note que para p = 0 ep = 1 todos os sítios têm a mesma conectividade, porém

para0< p <1alguns sítios terão mais ligações do que outros.

Utilizando o algoritmo de Metropolis para estudar o Modelo de Ising nessa rede para o caso em quep = 1(mesmo estudo feito por Hong e colaboradores [6]).

Calcula-mos as grandezas macroscópicas em redes com2000 até16000sítios e utilizamos 10_×N

passos de Monte Carlo, dos quais descartamos a metade e a outra metade utilizamos para calcular as grandezas. Nessa simulação foram utilizados1000amostras e um intervalo de

temperatura∆T = 0.01.

Nas figuras 3.11 e 3.12 podemos observar que as grandezas calculadas pela simu-lação obedecem bem aos resultados obtidos por Hong e colaboradores [6] para os expo-entes críticos (ν = 2,α = 0,β = 1/2eγ = 1), pois o cruzamento das curvas das grandezas para esses expoentes ocorrem na temperatura crítica encontrada (que foi de aproximada-menteT = 1.82) que é igual ao resultado obtido por Hong e colaboradores. O expoente

νencontrado nessa simulação foi de aproximadamente ν = 2.05(figura 3.11(a))ν = 1.71

(a)

(b)

Figura 3.11: Gráfico (a) da variação do cumulante de Binder versusN e (b) da variação do calor

(a) (b)

(c) (d)

Figura 3.12: Gráfico (a) da variação do calor específico versusT (b) da magnetizaçãom(T)N1/4

versus T (c) do cumulante de Binder versus T e (d) da susceptibilidade magnética χ(T)N−1/2

versusT para o modelo de Ising em rede de mundo pequeno comp= 1.

Fazendo o mesmo procedimento para o caso em que 0 < p < 1. Calculamos o

cumulante de Binder para redes entre 4000 e 16000 sítios para encontrar a temperatura

(a)

(b)

Figura 3.14: Gráfico da temperatura crítica versus a probabilidade de adicionar ligaçõesp.

Podemos observar o ponto de cruzamento das curvas na figura 3.13 parap= 0.3e

p= 0.6(o mesmo procedimento foram feitos para os outros valores dep). E estimar o valor

aproximado da temperatura crítica com erro de aproximadamente∆T_±0.0005. Na figura

3.14 podemos observar que a relação entre a temperatura críticaTc e a probabilidade de

adicionar ligações extraspé dada por

Tc = 1.8054285p0.38044262 (3.1.1)

uma lei de potência.

Do ponto de vista matemático uma lei de potência é uma função simples de tra-balhar, pois ao escrever uma curva como uma lei de potência, o expoente pode ser obtido facilmente gerando gráficos das curvas em escalas logaritmas e estimando o coeficiente angular dessa reta, ou seja, dada uma expressão do tipo

y(x) =axα, (3.1.2)

na escala logaritma teríamos

ondeαseria o coeficiente angular dessa reta.

Em fenômenos críticos, as relações de escalas na região crítica, indica que o com-portamento das grandezas macroscópicas encontradas não depende do tamanho do sis-tema. Como na física estatística, a validade do comportamento dessas grandezas ocorre no limite termodinâmico, ou seja, o limite o qual o tamanho do sistema vai a infinito. En-tão, podemos inferir que os resultados obtidos para L finito em nossas simulação (que

obedecem a relações de escalas), também são válidos para o limite termodinâmico.

Uma vez conhecendo os valores das temperaturas crítica, utilizamos o algoritmo de Metropolis para calcular as grandezas macroscópicas nestas temperaturas e seus com-portamentos descritas pelos expoentesν,β eγ.

Podemos observar esse comportamento nas figuras 3.15, 3.16 e 3.17 para a varia-ção do cumulante de Binder, a magnetizavaria-ção e a susceptibilidade magnética dado pelos expoentes ν, β e γ respectivamente. E calcular esses expoentes utilizando as equações

3.0.13, 3.0.14 e 3.0.15.

Expoentes críticos

p ν β γ

0.1 1.95 0.56 1.18 0.2 1.69 0.60 1.14 0.3 2.07 0.83 1.31 0.4 2.33 1.20 1.42 0.5 2.07 0.92 1.08 0.6 2.37 1.51 0.95 0.7 1.88 0.84 1.08 0.8 2.10 0.73 1.19 0.9 2.06 1.07 1.04

Tabela 3.2: Tabela do resultado encontrado para os expoentes críticos em rede mundo pequeno.

A tabela 3.2 mostra os expoentes críticos obitdos por nossas simulações para di-ferentes valores de probabilidade de adicionar ligações extrasp. Esses resultados são di-ferentes dos encontrados para p = 1 que foramν = 2, β = 1/2e γ = 1. Posteriormente

iremos refazer essas simulações, pois acreditamos que os resultados deveriam ser iguais para aos obtidos para p = 1, já que esse sistema é uma cadeia linear sob o mesmo

(a)

(b)

Figura 3.15: Gráficos da variação do Cumulante de Binder(com∆T = 0.08)versus o número de

(a)

(b)

Figura 3.16:Gráficos da magnetização na temperatura críticaTcversus o número de sítios para o

(a)

(b)

Figura 3.17: Gráficos da Susceptibilidade magnética na temperatura críticaTc versus o número

MODELO BLUME-CAPEL

O modelo Blume-Capel foi elaborado em 1966 por Blume [2] e Capel [3] em traba-lhos independentes. O qual o Hamiltoniano para esse modelo em uma rede comN spins

é dado por

H =₋JX

(i,j)

sisj + ∆ N X

i=1

s2_i (4.0.1)

ondeJ é o termo de interação de troca entre os spins e∆ é o termo de anisotropia. Se

considerarmos as interações dos spins com um campo magnético externoH0 ao sistema,

teremos

H =₋JX

(i,j)

sisj+ ∆ N X

i=1

s2_i +H0

N X

i=1

si. (4.0.2)

Diversos trabalhos para o modelo Blume-Capel foram feitas tanto para redes re-gulares (como, por exemplo, o trabalho de Paul D. Beale [34] o qual construiu o diagrama de fase (figura 4.1) e encontrou o ponto tricrítico para esse modelo em rede regular bidi-mensional) como também para redes complexas (como, por exemplo, o trabalho de F.P. Fernandes [33]).

Figura 4.1:Diagrama de fase do modelo Blume-Capel para rede bidimensional ([34] página 1717).

No diagrama de fase da figura 4.1 observamos que para ∆ < ∆t o sistema

apre-senta transição de fases de segunda ordem, e para∆ > ∆t e∆ ≤ 2o sistema apresenta

transição de fases de primeira ordem (onde∆t = 1.9655±0.005eTt = 0.610±0.0010é o

ponto tricrítico no diagrama de fase [34]).

Escolhemos três pontos da tabela I da referência [34] página 1719 para reprodu-zirmos (∆ = 0.0, ∆ = 0.5e∆ = 1.0) e simularmos através do algoritmo de Metropolis o

modelo Blume-Capel em rede quadrada.

Figura 4.3:Gráfico do Cumulante de Binder versus a temperatura para o modelo de Blume-Capel com∆ = 0.5em rede quadrada.

Nas figuras 4.2, 4.3 e 4.4 calculamos o cumulante de Binder e encontramos as seguintes temperaturas de transisões:T = 1.6936para∆ = 0.0,T = 1.5661para∆ = 0.5e

T = 1.3976para∆ = 1.0. Que são muitos parecidos com as temperaturas encontradas por Beale [34] (T = 1.695,T = 1.567eT = 1.398respectivamente).

Com os resultados valores obtidos anteriormente para as temperaturas de transi-ção calculamos a variatransi-ção do cumulante de Binder em torno dessas temperaturas (figura 4.5), a magnetização (figura 4.6) e a susceptibilidade magnética (figura 4.7) nessas tempe-raturas. Os quais podemos estimar os expoentes críticosν, γ eβ utilizando as equações

3.0.13, 3.0.14 e 3.0.15 para os resultados encontrados nesses gráficos.

Expoentes críticos

∆ ν β γ

0.0 0.94 0.09 1.52 0.5 1.00 0.07 1.57 1.0 0.97 0.10 1.63

Tabela 4.1: Tabela do resultado encontrado para os expoentes críticos em rede quadrada.

Na tabela 4.1 podemos observar que os expoentes críticos encontrados são prati-camente os mesmos para os valores de∆que escolhemos, indicando um mesmo

(a)

(b)

Figura 4.5:Gráficos da variação do Cumulante de Binder(com∆T = 0.08)versus o tamanho da

(a)

(b)

Figura 4.6:Gráficos da magnetização na temperatura críticaTc versus o tamanho da redeLpara

(a)

(b)

Figura 4.7: Gráficos da Susceptibilidade magnética na temperatura críticaTc versus o tamanho

4.1

Em uma Rede de Mundo Pequeno

No capítulo 3 na seção 4.1 calculamos o modelo de Ising em rede mundo pe-queno e vimos que o modelo de Ising nessa rede possui transição de fase tanto para o caso quandop = 1quanto o caso quando 0 < p < 1. Nessa seção calculamos o cumulante de

Binder e as grandezas macroscópicas do sistema apenas para o caso em quep= 1.

Em todas as simulações, utilizamos o algoritmo de Metropolis com1000amostras,

um intervalo de temperatura∆T = 0.001e10_×N passos de Monte Carlo o qual metade

foram descartadas e a outra metade utilizadas para calcular as grandezas macroscópicas. Utilizando os mesmos procedimentos do capítulo 3, calculamos o cumulante de Binder versus a temperatura para encontrar a temperatura de transição com erro de apro-ximadamente ∆T _±0.0004 para os diferentes valores de∆(0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9e1.0). E a partir do qual, calculamos as grandezas macroscópicas do sistema

na temperatura crítica com o objetivo de calcular os expoentes críticos.

Na figura 4.8, podemos observar o ponto de cruzamento das curvas do cumulante de Binder e estimar o valor aproximado da temperatura crítica para∆ = 0.0(a),∆ = 0.3

(b),∆ = 0.6(c) e∆ = 1.0(d) (também calculamos para os outros valores de∆). A partir

do qual construimos o diagrama de fases da figura 4.9.

Com os resultados obtidos para a temperatura crítica utilizamos o algoritmo de Metropolis para calcular as grandezas macroscópicas na temperatura crítica e obter o com-portamento crítico. Podemos observar os comcom-portamentos, da variação do cumulante de Binder em torno da temperatura de transição (figura 4.10), da magnetização (figura 4.11) e da susceptibilidade magnética (figura4.12) na região crítica descritas pelos expoentesν, β eγ respectivamente. Os quais foram estimados utilizando as equações 3.0.13, 3.0.14 e

3.0.15 para construirmos a tabela 4.2.

Os resultados encontrados para os expoentes críticos da tabela 4.2 parecem indicar que o modelo Blume-Capel em rede mundo pequeno, assim como o modelo de Ising em rede mundo pequeno estudada por Hong e colaboradores [6] estão na mesma classe de universalidade que o modelo de Ising em rede unidimensional (com os expoentesν = 2,

(a) (b)

(c) (d)

Figura 4.9: Diagrama de fases do modelo Blume-Capel em rede mundo pequeno comp= 1.

Na figura 4.9 podemos observar o diagrama de fases do modelo Blume-Capel em rede mundo pequeno comp = 1, onde a linha composta pelos pontos (∆, T)representa

uma linha de transição de fases de segunda ordem. Expoentes críticos

∆ ν β γ

0.0 1.85 0.77 1.04 0.1 2.07 0.97 1.16 0.2 1.94 0.94 1.07 0.3 2.03 0.90 1.14 0.4 1.88 0.88 1.06 0.5 1.83 0.81 1.04 0.6 1.81 0.88 1.03 0.7 1.71 0.76 0.95 0.8 2.04 0.98 1.12 0.9 1.96 0.86 1.10 1.0 1.91 0.81 1.08

(a) (b)

(c) (d)

(a) (b)

(c) (d)

Figura 4.11:Gráficos da magnetização na temperatura críticaT_cversus o número de sítios para o

(a) (b)

(c) (d)

Figura 4.12: Gráficos da Susceptibilidade magnética na temperatura críticaTc versus o número

de sítios para o modelo de Blume-Capel com diferentes valores de∆em Rede de Mundo Pequeno

CONCLUSÕES E PERSPECTIVAS

Neste trabalho estudamos o modelo de Ising e Blume-Capel em uma rede de mundo pequeno utilizando o algoritmo de Metropolis. Observamos que ambos os mo-delos apresentam transição de fases e como consequência um comportamento descrito pelos expoentes críticos.

Tivemos, praticamente, os mesmos resultados encontrados por Hong e colabora-dores [6] para os expoentes críticos do modelo de Ising em rede mundo pequeno quando

p = 1. Já para o caso em que0 < p < 1obtivemos aproximações para o expoenteν _≈ 2

eγ _≈ 1 para qualquer p que são os mesmos valores para p = 1. Porém o expoente

re-lacionado ao parâmetro de ordem do sistemaβ, apresentou valores não muito próximos

do valor parap = 1 de forma que não posso afirmar que esse modelo apresenta mesmo

comportamento crítico para qualquer valorp.

Na figura 3.9 podemos observar que a relação entre a temperatura crítica e a pro-babilidade de adicionar ligações pode ser descrita por uma lei de potência dada pela se-guinte aproximação

Tc = 1.8054285p0.38044262. (5.0.1)

Os expoentes críticos que estimamos para o modelo Blume-Capel em uma rede de mundo pequeno quandop= 1podem ser visto na tabela 4.2. E foram aproximadamente

ν _≈ 2, β _≈ 0.8e γ _≈ 1 para qualquer valor de∆. Esperarvamos encontrar os mesmos

expoentes críticos que encontramos para o modelo de Ising nessa rede, porém os expoen-tes críticos encontrado para o modelo Blume-Capel direfe apenas no valor deβ do valor

encontrado para o modelo de Ising em rede mundo pequeno.

Pretendemos continuar os estudos do modelo Blume-Capel em rede mundo pe-queno refazer o caso em que p = 1 e fazer também para o caso em que 0 < p < 1.

[1] E. Ising.Beitrag zur Theorie des Ferromagnetismus. Zeitschrift für Physik 31 (1925) 253.

[2] M. Blume.Theory of the First-Order Magnetic Phase Change inU O+₂. Physics Re-view 141 (1966) 517.

[3] H. W. Capel. Physica (Amsterdam) 32 966 (1966)

[4] D. J. Watts, S. H. Strogatz.Collective dynamics of “small-world” networks. Nature 393 (1998) 440.

[5] A. Pekalski. Ising model on a small world network. Physical Review E 64 (2001) 057104.

[6] H. Hong, B. J. Kim, M. Y. Choi. Comment on “Ising model on a small world network”. Physical Review E 66 (2002) 018101.

[7] N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller.Equation of State Calculations by Fast Computing Machines. The Journal of Chemical Physics 21 (1953) 1087.

[8] P. Erdös, A. Rényi.On Random Graphs. I. Publicationes Mathematicae 6 (1959) 290. [9] P. Erdös, A. Rényi.The Evolution of Random Graphs. Magyar Tud. Akad. Mat.

Ku-tató Int. Közl. 5 (1960) 17.

[10] R. Albert, A.-L. Barabási.Statistical Mechanics of Complex Networks. Reviews of Modern Physics 74 (2002) 47.

[11] M. Faloutsos, P. Faloutsos, C. Faloutsos.On power-law relationships of the internet topology. Comput. Commun. Rev. 29 (1999) 251.

[12] R. Albert, H. Jeong, A.-L. Barabási.Internet: Diameter of the World-Wide Web. Na-ture 401 (1999) 130.

[13] R. V. Solé, J. M. Montoya.Complexity and fagility in ecological networks. Proc. R. Soc. Lond. 268 (2001) 2039.

[14] R. Ferrer i Cancho, R. V. SoléThe small world of human language. Santa Fe Institute (2001).

[15] S. Boccaletti, V. Latora, Y. Moreno, M. Chavez, D.-U. Hwang. Complex networks: Structure and dynamics. Physics Reports 424 (2006) 175.

[16] S. MilgramThe Small World Problem. Psychology Today 2 (1967) 6067.

[17] A. Barrat, M. Weigt.On the properties of small-world network models. The Euro-pean Physical Journal B 13 (2000) 547.

[18] A.-L. Barabási, R. Albert, H. Jeong. Mean-field Theory for Scale-free Random Networks. Physica A 272 (1999) 173.

[19] S. G. Brush.History of the Lenz-Ising Model. Reviews of Modern Physics 39 (1967) 883.

[20] R. E. Peierls. On Ising’s Model of Ferromagnetism. Proceedings of the Cambridge Philosophical Society 32 (1936b) 477.

[21] H. E. Stanley. Introduction to phase transitions and critical phenomena. Oxford (1971).

[22] L. Onsager.Crystal Statistics. I. A Two - Dimensional Model with an Order - Di-sorder Transition. Physical Review 65 (1944) 117.

[24] H.-O. Heuer.Critical Crossover Phenomena in Disordered Ising Systems. Journal of Physics A 26 (1993) L333.

[25] A. Aleksiejuk. Microscopic Model for the Logarithmic Size Effect on the Curie Point in Barabási-Albert Networks. International Journal of Modern Physics C 13 (2002) 1415.

[26] A. Aleksiejuk, J. A. Holyst, D. Stauffer.Ferromagnetic Phase Transition in Barabási-Albert Networks. Physica A 310 (2002) 260.

[27] F. P. Fernandes, F. W. S. Lima.Persistence in the Zero-Temperature Dynamics of the q-states Potts Model on Undirected-Directed Barabasi-Albert Network and Erdös-Rénye Random Graphs. International Journal of Modern Physics C 19 (2008) 1777.

[28] G. Bianconi.Mean Field Solution of the Ising Model on a Barabási-Albert Network Physics Letters A 303 (2002) 166.

[29] K. Suchecki, J. A. Hołyst.Ising model on two connected Barabasi-Albert networks. Physical Review E 74 (2006) 011122.

[30] A. L. Ferreira, J. F. F. Mendes, M. Ostilli.First- and second-order phase transitions in Ising models on small-world networks: Simulations and comparison with an effective field theory. Physical Review E 82 (2010) 011141.

[31] C. P. Herrero. Antiferromagnetic Ising model in small-world networks. Physical Review E 77 (2008) 041102.

[32] D. Jeong, H. Hong, B. J. Kim, M. Y. Choi.Phase transition in the Ising model on a small-world network with distance-dependent interactions. 68 (2003) 027101.

[33] F.P. Fernandes, F.W.S. Lima, J.A. Plascak.Blume–Capel model on directed and un-directed small-world Voronoi–Delaunay random lattices. Computer Physics Com-munications 181 (2010) 1218.

[34] P. D. Beale.Finite-size scaling study of the two-dimensional Blume-Capel model. Physical Review B 33 (1986) 1717.

[36] M. E. Fisher.The theory of equilibrium critical phenomena. Reports on Progress in Physics 30 (1967) 615.

[37] A. Fronczak, P. Fronczak, J. A. Holyst.Averange Path Length in Random Networks. Physical Review E 70 (2004) 0561101.

[38] A.-L. Barabási, R. Albert.Emergence of Scaling in Random Networks. Science 286 (1999) 509.

[39] B. Bollobás, O. Riordan.The Diameter of a Scale-free Random Graph. Combinato-rica 24 (2004) 5.

[40] F. G. B. Moreira.Trancisções de Fase e Fenômenos Críticos. Recife: UFPE, 2009. [41] G. Alves.Contribuições ao Estudo das Redes Complexas: Modelo de Qualidade.

2000. Dissertação (Mestrado) - Departamento de Física Teórica e Experimental, Uni-versidade Federal do Rio Grande do Norte, Natal.

[42] M. E. J. Newman, S. H. Strogatz, D. J. Watts.Random graphs with arbitrary degree distributions and their applications. Physics Review E 64 (2001) 026118.

ALGORITMO DE METROPOLIS

O algoritmo de Metropolis [7] foi introduzido por Nicholas Metropolis e colabo-radores com o intuito de calcular numericamente grandezas físicas macroscópicas a partir de sistemas físicos microscópicos que entram em estado de equilíbrio com o tempo.

Esse algoritmo é baseado no método de Monte Carlo e utiliza conhecimentos de física estatística, o qual é muito conhecido para o ensemble canônico (T,V,N) seguindo a função de distribuição de Boltzmann, podendo calcular a média das grandezas físicas macroscópicas numa amostra simulada. E foi generalizado para outros ensembles em 1970 por W. K. Hastings [35].

O objetivo do algoritmo é levar o sistema para uma configuração mais provável. Contudo, seria necessário conhecer todas as possíveis configurações desse sistema. As-sim, numericamente, o algoritmo de Metropolis utiliza passo a passo a razão entre duas possíveis configurações para determinar a configuração mais provável.

Dada uma configuraçãomoun, a probabilidade do sistema estar na configuração mouné

P(m) =e−EmkT (A.0.1)

P(n) = e−EnkT (A.0.2)

respectivamente.

Logo a razão entre as configuraçãonemé dada por

W = P(n)

P(m) =

e−En_kT e−Em_kT =e

−En−Em

kT =e−

∆E

kT (A.0.3)

Agora podemos escrever o algoritmo de Metropolis para um modelo de sistemas magnéticos seguindo os seguintes passos:

1. Gerar uma amostra aleatória de spin na rede.

2. Escolher um spin da rede, alterar sua orientação e calcular a diferença de energia

∆E entre a configuração atualme a nova configuraçãon.

3. Se ∆E < 0, aceitar a nova configuraçãon, ou seja,Em = Em+ ∆E, e voltar para o

passo2. Caso contrário, não aceitar a nova configuraçãone ir para o próximo passo.

4. Sortear um número aleatóriorentre[0,1]e calcularW dado pela equação (A.0.3). Se r _≤ W, aceitar a nova configuração n e voltar para o passo2. Caso contrário, não

aceita a nova configuraçãone ir para o passo2.

Depois de um passo de Monte Carlo, que corresponde a visitar todos os sítios de uma rede, o sistema estará numa dada configuraçãot. Podendo calcular algumas médias

importantes para essa configuraçãot, como a magnetização e a energia interna

m(t) = 1

N

N X

i=1

mi (A.0.4)

E(t) = 1

N

N X

i=1

Ei (A.0.5)

Iremos calcular essas grandezas ppassos de Monte Carlo e assim podemos obter as grandezas macroscópicas da amostra simulada. Que são a magnetização

M _{≡ h}m(t)_i= 1

p

p X

t=1

m(t), (A.0.6)

a energia interna

E _{≡ h}E(t)_i= 1

p

p X

t=1

o calor específico

cH ≡

N kT2(hE

2_(t)

i −(_hE(t)_i)2), (A.0.8)

a susceptibilidade magnética

χH ≡

N kT(hm

2_(t)

i −(_hm(t)_i)2), (A.0.9)

e o cumulante de Binder [23]

U4 ≡ h(∆m(t))4i= 1− h

m4_(t)i

EXPOENTES CRÍTICOS

Num sistema que apresenta transição de fase as funções respostas como a sus-ceptibilidade magnética e o calor específico divergem na região crítica. Além disso, o parâmetro de ordem como, por exemplo, a magnetização para um sistema magnético, anula-se nessa região. O comportamento dessas grandezas segue uma relações de escalas na região crítica descrita pelos expoentes críticos.

Seja a temperatura reduzida adimensional

t= (T −Tc)

Tc

(B.0.1)

ondeTc é temperatura crítica. O parâmetro tmede a distância de uma dada temperatura

em relação a temperatura crítica de transição, ou seja, o quanto sua grandeza estar pró-xima da região crítica (quandot_→ 0). O mesmo podemos dizer para o campo magnético

reduzido adimensional

h= (H−Hc)

Hc

. (B.0.2)

Podemos fazer uma expansão de uma grandeza termodinâmica em função da variáveltdado por

F(t) =Atx(1 +Bty +Ctz+...), (B.0.3)