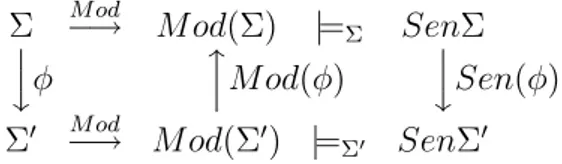A Linguagem de Especificação algébrica CASL e o Tipo de Dados Intervalos

(1)

Katiane Ribeiro Lopes

TRABALHO SUBMETIDO AO COLEGIADO DA P ÓS-GRADUAÇ ÃO EM SISTEMAS E COMPUTAÇ ÃO COMO REQUISISTO PARCIAL PARA A OBTENÇ ÃO DO TÍTULO DE

MESTRE EM SISTEMAS E COMPUTAC¸ ˜AO

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

ORIENTADOR: PROF. DR. REGIVAN HUGO NUNES SANTIAGO

NATAL, BRASIL ABRIL,2004

c

(2)

(3)

A disserta¸cão entitulada “A Linguagem de Especifica¸cão Algébrica CASL e o Tipo de Dados Intervalos” de autoria de Katiane Ribeiro Lopes foi submetida ao programa de Pós-Gradua¸cão em Sistemas e Computa¸cão como requisito parcial para a obten¸cão do grau de Mestre em Sistemas e Computa¸cão sendo avaliada e aprovada pela banca examinadora abaixo:

Data: Abril,2004

Orientador:

Prof. Dr. Regivan Hugo Nunes Santiago

Examinadores:

Prof. Dr. Marc´ılia Andrade Campos

Prof. Dr. Anamaria Martins Moreira

(4)

Data: Abril,2004

Autor: Katiane Ribeiro Lopes

Titulo: A Linguagem de Especifica¸cão Algébrica CASL e o Tipo de Dados Intervalos

Depto: Departamento de Informática e Matemática Aplicada Grau: M.Sc. Convoca¸cão: Abril Ano: 2004

Assinatura do Autor

(5)

e exatos possível, porém a imprecisão dos dados de entrada desse tipo de computação pode estar associada às medidas obtidas por equipamentos que fornecem dados truncados ou arredondados, fazendo com que os cálculos com esses dados produzam resultados imprecisos. Os erros mais comuns durante a computação científica são: erros de truncamentos, que surgem em dados infinitos e que muitas vezes são “truncados", ou interrompidos; erros de arredondamento que são responsáveis pela imprecisão de cálculos em seqüências finitas de operações aritméticas. Diante desse tipo de problema Moore, na década de 60, introduziu a matemática intervalar, onde foi definido um tipo de dado que permitiu trabalhar dados contínuos, possibilitando, inclusive prever o tamanho máximo do erro.

A matemática intervalar é uma saída para essa questão, já que permite um controle e análise de erros de maneira automática. Porém, as propriedades algébricas dos intervalos não são as mesmas dos números reais, apesar dos números reais serem vistos como intervalos degenerados, e as propriedades algébricas dos intervalos degenerados serem exatamente as dos números reais. Partindo disso, e pensando nas técnicas de especificação algébrica, precisa-se de uma linguagem capaz de implementar uma noção auxiliar de equivalência introduzida por Santiago [6] que ``simule" as propriedades algébricas dos números reais nos intervalos.

A linguagem de especificação CASL, Common Algebraic Specification Language, [1] é uma linguagem de especificação algébrica para a descrição de requisitos funcionais e projetos modulares de software, que vem sendo desenvolvida pelo CoFI, The Common Framework Initiative [2] a partir do ano de 1996. O desenvolvimento de CASL se encontra em andamento e representa um esforço conjunto de grandes expoentes da área de especificações algébricas no sentido de criar um padrão para a área.

A dissertação proposta apresenta uma especificação em CASL do tipo intervalo, munido da aritmética de Moore, afim de que ele venha a estender os sistemas que

manipulem dados contínuos, sendo possível não só o controle e a análise dos erros de aproximação, como também a verificação algébrica de propriedades do tipo de sistema aqui mencionado. A especificação de intervalos apresentada aqui foi feita apartir das especificações dos números racionais proposta por Mossakowaski em 2001 [3] e introduz a noção de igualdade local proposta por Santiago [6, 5, 4].

Palavra-chave: matemática intevalar, CASL, igualdade local

Referências:

[1] CASL, Common Algebraic Specification Language, www.brics.dk/Projects/CoFI, 2001.

(6)

Arithmetic and Validated Numerics – SCAN 2000, International Conference on Interval Methods in Science and Engeneering, Karlsruhe – Germany, 2000.

(7)

Sum´ario iv

Lista de Tabelas vi

Lista de Figuras vii

Agradecimentos viii

1 Introdu¸c˜ao 1

2 Matem´atica Intervalar 4

2.1 Defini¸c˜oes B´asicas . . . 4

2.2 Matrizes e vetores Intervalares . . . 16

2.3 Rela¸c˜oes de Ordem sobre Intervalos . . . 26

2.4 Considera¸c˜oes Finais . . . 27

3 CASL 29 3.1 Introdu¸c˜ao . . . 29

3.2 CASL . . . 31

3.3 Especifica¸c˜oes B´asicas . . . 32

3.3.1 Aspectos Pragm´aticos . . . 33

3.3.2 Conceitos Semˆanticos . . . 37

3.3.3 Constructos da Linguagem . . . 42

3.3.4 Exemplo de uma Especifica¸c˜ao B´asica . . . 49

3.4 Especifica¸c˜oes Estruturadas . . . 51

3.4.4 Exemplo . . . 63

(8)

3.5.3 Constructo da Linguagem . . . 67

3.5.4 Exemplo . . . 70

3.6 Especifica¸c˜oes de Bibliotecas . . . 70

4 Igualdade Local Intervalar e CASL 75 4.1 Igualdade e Existˆencia . . . 76

4.2 Uma L´ogica para Elementos Parciais . . . 77

4.2.1 Identidade e Existˆencia . . . 82

4.2.2 Reflexividade e Existˆencia . . . 83

4.3 Ω-conjuntos . . . 87

4.4 CASL e a Igualdade de Scott . . . 91

4.4.1 Igualdade Local e Intervalos . . . 91

4.5 Aplicando a no¸c˜ao de Igualdade Local em Intervalos . . . 99

5 Congruência e Indicernibilidade 102 5.1 Congruências e Princ´ıpios da Substitui¸cão de Iguais por Iguais para a Igual-dade Local . . . 106

5.2 Considera¸c˜oes finais . . . 116

6 Conclus˜oes e trabalhos futuros 117 6.1 Conclus˜ao . . . 117

6.2 Trabalhos Futuros . . . 118

A Especiﬁca¸c˜ao CASL dos Intervalos de Moore 120

Bibliograﬁa 126

(9)

2.1 Opera¸cão de multiplica¸cão . . . 10 2.2 Opera¸cão de Divisão . . . 10

(10)

3.1 Diagrama da Sobrecarga . . . 36

3.2 Diagrama da Sobrecarga . . . 38

3.3 Assinatura Senten¸cas e Classe de Modelos . . . 39

3.4 Assinatura e Conjunto de Senten¸cas . . . 39

3.5 Diagrama de Institui¸c˜ao . . . 40

3.6 Diagrama do Morfismo . . . 52

3.7 Diagrama Comutativo . . . 65

(11)

• A Deus por toda a capacidade para realizar esse trabalho.

• A meus pais e irmãos que mesmo de tão longe me deram o apoio necessário para cumprir essa etapa tão importante e d´ıficil.

• Ao meu orientador Prof. Regivan pela confian¸ca, aprendizado e paciˆencia.

• A minha colega de mestrado Samara pela amizade e for¸ca nas horas que precisei.

• Ao Prof. Benjam´ın pela colabora¸c˜ao e contribui¸c˜ao.

• A D. Wilma e fam´ılia pelo acolhimento em sua casa.

• E à todos que conheci no DIMAp que contribuiram para que esse tempo longe de casa fosse uma época de conquista e de amizades que serão para sempre carregadas.

Katiane Ribeiro Lopes

(12)

Introdu¸

c˜

ao

Na computa¸cão cient´ıfica é necessário que os dados sejam o mais precisos e exatos poss´ıvel, porém a imprecisão dos dados de entrada desse tipo de computa¸cão pode estar associada às medidas obtidas por equipamentos que fornecem dados truncados ou arredondados, fazendo com que os cálculos com esses dados produzam resultados imprecisos. Os erros mais comuns durante a computa¸cão cient´ıfica são: erros de truncamentos, que surgem em dados infinitos e que muitas vezes são “truncados”, ou interrompidos; erros de arredondamento que são responsáveis pela imprecisão de cálculos em seqüências finitas de opera¸cões aritméticas.

O controle desses erros pode ser monitorado por um meta-algoritmo, que geralmente é dispendioso. Com o objetivo de eliminar os meta-algoritmos, no final dos anos 50, Moore e Sunaga propuseram a Matemática Intervalar. Com isso, o intervalo [a,b], contém o número a ser computado bem como o erro cometido por essa representa¸cão que será no máximo b−_{2 .}a Como os resultados dos cálculos serão sempre um intervalo [a,b], contendo a resposta ideal, então se terá o controle dos erros durante o processo computacional.

A computa¸cão cient´ıfica, do ponto de vista de implementa¸cão já está bastante avan¸cada. Entretanto, quando se leva em considera¸cão o processo de desenvolvimento de software para

(13)

esse tipo de sistemas em algum ponto do processo de especifica¸c˜ao 1_{, tem-se que pensar na}

questão dos erros de aproxima¸cão e como controlá-los durante as opera¸cões do sistema. A matemática intervalar é uma sa´ıda para essa questão, já que permite um controle e análise de erros de maneira automática. Porém, as propriedades algébricas dos intervalos não são as mesmas dos números reais, apesar dos números reais serem vistos como intervalos de-generados, e as propriedades algébricas dos intervalos degenerados serem exatamente as dos números reais. Partindo disso, e pensando nas técnicas de especifica¸cão algébrica, precisa-se de uma linguagem capaz de implementar uma no¸cão auxiliar de equivalência introduzida por Santiago [12] que “simule”as propriedades algébricas dos números reais nos intervalos.

A linguagem de especifica¸cão CASL, Common Algebraic Specification Language, [9] é uma linguagem de especifica¸cão algébrica para a descri¸cão de requisitos funcionais e projetos modulares de software, que vem sendo desenvolvida pelo CoFI, The Common Framework Initiative[3] a partir do ano de 1996. O desenvolvimento de CASL se encontra em andamento e representa um esfor¸co conjunto de grandes expoentes da área de especifica¸cões algébricas no sentido de criar um padrão para a área.

Essa disserta¸cão introduz princ´ıpios da congruência e da indicernibilidade para a igual-dade local [12] de maneira que a mesma possa ser descrita numa biblioteca CASL e assim possa-se escrever especifica¸cões CASL utilizando intervalos de extremos racionais. Com isso pretense fornecer um ambiente munido da aritmética de Moore, para que se possa de-screver algebricamente sistemas que manipulem dados cont´ınuos, sendo poss´ıvel não só o controle e a análise dos erros de aproxima¸cão, através da utiliza¸cão de intervalos, como também a verifica¸cão de propriedades do tipo de sistema aqui mencionado. A especifica¸cão de intervalos apresentada no apêndice A foi feita a partir das especifica¸cões dos números

1

(14)

racionais proposta por Mossakowski em 2001 [4] e introduz a no¸cão de igualdade local de-senvolvida no cap´ıtulo 4 e proposta por Santiago em [12, 14, 13] além dos princ´ıpios de congruência e substitui¸cão de iguais por iguais desenvolvidos no Cap´ıtulo 5.

Para ser auto-contido, esse documento introduz nos primeiros dois cap´ıtulos a matemática intervalar e a linguagem CASL. As contribui¸cões dessa disserta¸cão encontram-se a partir do Cap´ıtulo 4.

O cap´ıtulo 2 é portanto uma breve introdu¸cão a aritmética de Moore e sua extensão para a versão matricial. O cap´ıtulo 3 é uma tentativa de reescrita de ”Uma Introdu¸cão a linguagem CASL”escrita por Mosses em [9], e visa introduzir o leitor na linguagem CASL, bem como tornar o texto auto-contido.

(15)

Matem´

atica Intervalar

Esse cap´ıtulo introduz a matemática intervalar, que é utilizada na computa¸cão cient´ıfica como uma ferramenta para o tratamento de erros existentes em algumas computa¸cões. Esta surgiu nos anos 60, como alternativa para os meta-algoritmos que eram usados para controle e análise de erros. Moore e Sunaga [7, 17] desenvolveram paralelamente uma aritmética para intervalos utilizando a estrutura dos números reais. Porém, existem leis que são satisfeitas pelos números reais, que não são válidas para todos os intervalos. Esse cap´ıtulo foi baseado em [15, 5, 16].

2.1 Deﬁni¸

c˜

oes B´

asicas

Deﬁni¸c˜ao 2.1.1 (Intervalo de reais e I ).

Seja o conjunto dos n´umeros reais e x1 , x2 ∈ , tal quex1 ≤ x2. Ent˜ao, o conjunto

{x_∈ :x1 ≤x≤x2}´e umintervalo de extremos reaisou simplesmente umintervalo, e

ser´a denotado porX = [x1, x2]. Os elementos do conjunto dos intervalos ser˜ao denotados por

letras latinas mai´usculas, e denota-se por I o conjunto de todos os intervalos de reais, i.e., I = {[x1, x2]/x1, x2∈ , x1 ≤x2}.Os intervalos da forma [x, x] s˜ao chamados degenerados,

(16)

Exemplos 2.1.1.

[1,3],[2,2],[₋5,₋2], e[₋2,2] são alguns exemplos de intervalos. Sendo que [2,2] corre-sponde ao próprio número real 2.

Considerando cada intervalo da reta como um conjunto, a no¸cão de igualdade entre dois intervalosé dada pela no¸cão de igualdade entre conjuntos; ou seja:

A = B⇔ ∀x∈A,∀x∈B,x∈A⇔x∈B1_{. Assim:}

Deﬁni¸c˜ao 2.1.2 (Igualdade entre Intervalos).

Sejam A = [a1, a2] e B = [b1, b2] dois intervalos em I . Diz-se que A = B se, e somente

se a1 =b1 ea2 =b2.

Logo, dois intervalos s˜ao considerados iguais se eles forem iguais enquanto conjuntos.

Defini¸cão 2.1.3 (Opera¸cões aritméticas em I ).

Sejam A, B _∈I , dois intervalos reais. As opera¸cões de soma, subtra¸cão, multiplica¸cão e divisão em I são definidas por A _∗ B = _{a_∗b:a_∈A_∧b_∈B_} onde _{∗ ∈ {}+,₋,_×, /_}

é uma das quatro opera¸cões aritméticas. Para a opera¸cão de divisão, 0 _∈/ B. Se α é uma opera¸cão unária e X ∈ I , então αX é definida por αX = α(X) = {α(x)/x∈X} ⊆

[min{α(x)/x ∈X}, max{α(x)/x∈X}].

Deﬁni¸c˜ao 2.1.4 (Soma Intervalar).

Sejam ent˜ao A, B_∈ I dois intervalos reais, com A = [a1, a2] e B = [b1, b2]. Ent˜ao A +

B = [(a1+b1),(a2+b2)].

1

(17)

Exemplos 2.1.2.

Sejam A = [5,10] e B = [3,6]. Tem-se:

A + B = [5,10] + [3,6] = [(5 + 3),(10 + 6)] = [8,16]

Teorema 2.1.1. (Propriedades da Soma) Santos [15]

Sejam A, B, C _∈ I intervalos de extremos racionais. Ent˜ao, valem as seguintes pro-priedades:

1. Fechamento: Se A, B ∈ I ent˜ao A + B∈ I ;

2. Associatividade: A + (B + C) = (A + B) + C;

3. Comutatividade: A + B = B + A;

4. Elemento Neutro: ∃! 0 = [0;0]∈ I tal que A + 0 = 0 + A = A.

Deﬁni¸c˜ao 2.1.5 (Pseudo Inverso Aditivo). Santos [15]

Seja A ∈I um intervalo de reais, com A =[a1, a2]. Ent˜ao -A = [−a2,−a1].

Exemplos 2.1.3.

Seja A = [5,6]. Ent˜ao -A = ₋[5,6] = [₋6,₋5].

Pode-se observar que o conjunto I n˜ao possui inverso aditivo, i.e., nem sempre ´e poss´ıvel achar um intervalo “-A”tal que A + (-A) = 0. Por exemplo, tomando A = [5,10], tem-se: A + (- A) = [5,10] + (-[5,10]) = [5,10] + [-10,-5] = [-5,5]= [0,0], mas 0_∈[-5,5], como mostra o teorema abaixo.

(18)

Seja A um intervalo de extremos reais. Ent˜ao, 0_∈(A -A).

Demonstra¸c˜ao: Dado A = [a1, a2], como A∈I , segue quea1 ≤a2. Mas A - A = [a1, a2]

- [a1, a2] = [a1, a2] + [−a2,−a1] = [a1−a2, a2−a1]. Comoa1 ≤a2, segue quea1−a2 ≤0 e

a2−a1 ≥0, ou seja 0 ∈ A - A.

Defini¸cão 2.1.6 (Subtra¸cão Intervalar).

Sejam A, B _∈I dois intervalos reais, com A = [a1, a2] e B = [b1, b2]. Ent˜ao A - B = A

+ (-B) = [a1, a2] + [−b2,−b1] = [(a1−b2) , (a2−b1)].

Exemplos 2.1.4.

Sejam A = [4,5] e B = [6,7]. Ent˜ao,

A - B = [4,5]₋[6,7] = [4,5] + (₋[6,7]) = [4,5] + [₋7,₋6] = [4₋7,5₋6] = [₋3,₋1]

Defini¸cão 2.1.7 (Multiplica¸cão Intervalar).

Sejam A, B ∈ I dois intervalos reais, com A = [a1, a2] e B = [b1, b2]. Ent˜ao, A · B =

[min _{a1.b1, a1.b2, a2.b1, a2.b2}, max {a1.b1, a1.b2, a2.b1, a2.b2}].

Exemplos 2.1.5.

Sejam A = [−4,6] e B = [−5,7]. Ent˜ao,

A · B = [−4,6]·[−5,7] = [min{(−4).(−5),(−4).7,6.(−5),6.7}, max{(−4).(−5),(−4).7,6.(−5),6.7}] = [min{20,−28,−30,42}, max_{20,₋28,₋30,42_}] = [₋30,42].

(19)

Sejam A, B, C_∈ I intervalos de reais. Ent˜ao, valem as seguintes propriedades:

1. Fechamento: Se A, B ∈ I , ent˜ao A . B ∈I ;

2. Associatividade: A . (B . C) = (A . B) . C;

3. Comutatividade: A . B = B . A;

4. Elemento Neutro: _∃! 1 = [1;1] _∈I tal que A.1 = 1.A =A

5. Sub-distributividade: A.(B + C) ⊆(A . B) + (A .C).

Deﬁni¸c˜ao 2.1.8 (Pseudo Inverso Multiplicativo). Santos [15]

Seja A ∈I um intervalo real, com A = [a1, a2] e 0 ∈/ A.

Ent˜ao A−1

= 1_A = _a1₂,_a1₁. Exemplos 2.1.6.

a) Seja A =[4,5]. Ent˜ao A−1

= 1_A = _[41_,_5] = 1₅,1₄

b) Seja A = [−5,−4]. Ent˜ao A−1 _{= 1}

A = [−51,−4] =

−1₄,−1₅

Observa-se mais uma vez que o conjunto I não possui inverso multiplicativo, i.e., nem sempre é poss´ıvel achar A _× (A−1_{) = 1 . Por exemplo, se A = [5,6], então o inverso}

multiplicativo ´e:

A . (A−1

) = [5,6] .([5,6]−1

) = [5,6] / [5,6] =5₆,6₅ = [1,1] = 1.

Mas 1 _∈5₆,6₅, como mostra o teorema abaixo.

(20)

Seja A um intervalo, tal que0 _∈/ A. Ent˜ao, 1_∈ A/A.

Demonstra¸c˜ao: Dado A = [a1, a2], como A ∈I segue que a1 ≤ a2. Mas A/A = [a1, a2]

/ [a1, a2] = [a1, a2] . [1/a2,1/a1] = [a1/a2, a2/a1]. Comoa1 ≤a2 segue quea1/a2 ≤1 ea2/a1

≥ 1, logo, 1∈ A/A.

Defini¸cão 2.1.9 (Divisão Intervalar).

Sejam A, B _∈I dois intervalos reais, com A = [a1, a2] e B = [b1, b2] e 0 ∈/ B. Ent˜ao, _BA

= A . B−1 ₌ _mina1

b2, a 1

b1, a 2

b2, a 2

b1

, maxa1

b2, a 1

b1, a 2

b2, a 2

b1

com 0_∈/ [b1, b2].

Exemplos 2.1.7.

Sejam A = [6,7] e B =[8,9]. Ent˜ao,

A / B = [6,7]/[8,9] = [min_{6/9,6/8,7/9,7/8_}, max_{6/9,6/8,7/9,7/8_}] =6₉,7₈. Teorema 2.1.5.

Se A, B ∈I e A· B = 0, ent˜ao A = 0 ou B = 0.

Demonstra¸c˜ao: Sejam A = [a1, a2] e B = [b1, b2]. Como, por hip´otese, A .B = 0, segue que

A . B = [min_{a1.b1,a1.b2,a2.b1,a2.b2}, max{a1.b1,a1.b2,a2.b1,a2.b2}] = [0,0]⇔min{a1.b1,a1.b2,

a2.b1,a2.b2} = 0 e max{a1.b1,a1.b2,a2.b1,a2.b2}= 0. Logo, pode-se concluir que A = [0,0] ou

b = [0,0].

Analisando os sinais dos extremos dos intervalos, pode-se implementar de maneira mais otimizada, as opera¸cões de multiplica¸cão e divisão sobre os intervalos, veja as tabelas 2.1 e 2.2 respectivamente.

(21)

Dados os intervalos A = [a1, a2] e B = [b1, b2], tem-se:

Ordem Intervalos Multiplica¸c˜ao

1 a1 ≥0 e b1 ≥0 ⇒ A.B=[a1.b1, a2.b2]

2 a1≥0 eb1 <0≤b2 ⇒ A.B=[a2.b1, a2.b2]

3 a1 ≥0 e b1 <0 ⇒ A.B=[a2.b1, a1.b2]

4 a1 <0≤a2 eb1 ≥0 ⇒ A.B=[a1.b2, a2.b2]

5 a1 <0≤a2 eb1≤0≤b2 ⇒ A.B=[min{a1.b2, a2.b2},max{a1.b2, a2.b2}]

6 a1 <0≤a2 eb2<0 ⇒ A.B=[a2.b2, a1.b2]

7 a2 <0 e b1 ≥0 ⇒ A.B=[a1.b2, a2.b2]

8 a2 <0 eb1 <0≤b2 ⇒ A.B=[a1.b2, a1.b1]

9 a2 <0 e b2 <0 ⇒ A.B=[a2.b2, a1.b1]

Tabela 2.1: Opera¸c˜ao de multiplica¸c˜ao

Dados os intervalos A = [a1, a2] e B = [b1, b2], tem-se:

Ordem Intervalos Divis˜ao

1 a1 >0 eb1> 0 ⇒ A/B=[a1/b2, a2/b1]

2 a1 >0 e 0∈[b1, b2] ⇒ A/B= N˜ao definida

3 a1 >0 eb2< 0 ⇒ A/B=[a2/b2, a1/b1]

4 a1< 0< a2 eb1 >0 ⇒ A/B=[a1/b1, a2/b1]

5 a1 <0< a2 e 0∈[b1, b2] ⇒ A/B=N˜ao definida

6 a1< 0< a2 eb2 <0 ⇒ A/B=[a2/b2, a1/b2]

7 a2 <0 eb1> 0 ⇒ A/B=[a1/b1, a2/b2]

8 a2 <0 e 0∈[b1, b2] ⇒ A/B=[a1/b2, a1/b1]

9 a2 <0 eb2< 0 ⇒ A/B=[a2/b1, a1/b2]

(22)

Teorema 2.1.6. (Inclus˜ao monotˆonica) Santos [8]

Sejam A, B, C, D ∈ I intervalos de extremos reais, tais que A ⊆ C e B ⊆ D. Ent˜ao, valem as seguintes propriedades:

1. A + B ⊆C + D;

2. -A ⊆-C;

3. A - B _⊆C - D;

4. A . B _⊆C . D;

5. 1/A⊆ 1/C, sempre que 0∈/ A e 0 ∈/ C;

6. A/B ⊆C/D, sempre que 0 ∈/ B e 0∈/ D.

Teorema 2.1.7. (Propriedades da inclus˜ao) Santos [15]

Sejam A, B, C_∈ I intervalos reais. Ent˜ao, valem as seguintes propriedades:

1. A + B = A + C_⇒ B = C;

2. B - A = C - A _⇒ B = C;

3. A + B ⊆A + C ⇒ B ⊆C

4. A . [0,0] = [0,0] . A = [0,0];

5. _∀α, β _∈ vale que (α.β) . A = α. (β .A);

6. _∀α, β _∈ vale que (α+β) . A _⊆(α . A) + (β .A);

(23)

Defini¸cão 2.1.10 (Intervalo Simétrico).

Um intervalo A ∈ I é um intervalo simétrico se - A = A. Isto ocorre quando os extremos são equidistantes em rela¸cão a zero.

Exemplos 2.1.8.

[₋5,5],[0,0],[₋π, π]s˜ao exemplos de intervalos sim´etricos.

Teorema 2.1.8. Santos [15]

Todo intervalo sim´etrico ´e da forma [-a,a], com a_≥0.

Corol´ario 2.1.1. Santos [15]

Se A∈I é um intervalo simétrico, então A = |A|. [-1,1].

Teorema 2.1.9. (Propriedades dos Intervalos Sim´etricos) Santos [15]

Sejam A, X, Y_∈I intervalos de reais, com X e Y sim´etricos. Ent˜ao, valem as seguintes propriedades:

1. A + X = A - X;

2. A . X = _|A_|. X;

3. A . X = |A|. X . [-1,1];

4. A . (X _±Y) = (A . X) _±(A . Y).

A seguir, serão definidas as opera¸cões de interseçcão, união e união convexa de intervalos.

(24)

Sejam A = [a1,a2] e B = [b1,b2] dois intervalos. A intersec¸c˜ao dos intervalos A e B

´e dada pelo intervalo A _∩ B = [max_{a1,b1},min{a2,b2}]. Caso max {a1,b1} > min {a2,b2}

então A _∩B = _∅, que não é um intervalo.

Exemplos 2.1.9.

[3,6]_∩[4,9] = [max_{3,4_}, min_{6,9_}] = [4,6]; [4,9]∩[−2,12] = [max{4,−2}, min{9,12}] = [4,9]; [−2,1]∩[1,5] = [max{−2,1}, min{1,5}] = [1,1]; [−3,4]∩[3,8] = [max{−3,3}, min{4,8}] = [3,4] [2,3]∩[4,5] = ∅

Teorema 2.1.10. (Propriedades)

Sejam A, B, C, D _∈ I . Se A_⊆C e B_⊆D, então A_∩B _⊆ C_∩D. Ou seja, a interseçcão entre intervalos é uma opera¸cão monotônica.

Exemplos 2.1.10.

Sejam A = [4,6], B = [₋2,5], C =[3,9] e D = [₋2,7].

Assim, se A_⊆CeB _⊆D, ent˜ao, A_∩B = [4,5], C_∩D= [3,7] e [4,5]_⊆[3,7].

Defini¸cão 2.1.12 (União de dois Intervalos).

Sejam A = [a1;a2] e B = [b1;b2] dois intervalos tais que A ∩ B = ∅ . A uni˜ao dos

(25)

Exemplos 2.1.11.

[3,6]_∪[4,9] = [min_{3,4_}, max_{6,9_}] = [3,9];

[4,9]∪[−2,12] = [min{4,−2}, max{9,12}] = [−2,12]; [−2,1]∪[1,5] = [min{−2,1}, max{1,5}] = [−2,5]; [−3,2]∪[3,8] = [min{−3,3}, max{2,8}] = [−3,8]

Defini¸cão 2.1.13 (União convexa de dois Intervalos).

Sejam A = [a1,a2] e B = [b1,b2] dois intervalos quaisquer. Auni˜ao convexados intervalos

A e B ´e dada pelo intervalo A ⋒ _B_{= [min}{_a₁_{, b}₁}_,max{_a₂_{, b}₂}_].

Obs: Note que nessa união, a interseçcão entre os dois intervalos pode ser vazia, man-tendo o fato que a união de dois intervalos é o intervalo que possui o menor diâmetro e que contém os intervalos operados.

Exemplos 2.1.12.

[3,6]⋒[4,9] = [min{3,4}, max{6,9}] = [3,9];

[4,9]⋒[−2,12] = [min{4,−2}, max{9,12}] = [−2,12];

[₋2,1]⋒[1,5] = [min{−2,1}, max{1,5}] = [−2,5];

[−3,2]⋒_[3_,_{8] = [}_min{−₃_,₃}_{, max}{₂_,₈}_{] = [}−₃_,_8]

Existem fun¸cões que mapeiam intervalos em números reais, i.e. são fun¸cões da forma f : I _→ . A seguir algumas dessas fun¸cões são introduzidas:

(26)

A amplitude de um intervalo A = [a1,a2] ´e definida por:

w(A) =a2−a1.

A amplitude serve como uma medida de qualidade do intervalo enquanto representa¸cão dos números reais que ele contém, i.e. quanto maior a amplitude, pior será a qualidade do intervalo.

Deﬁni¸c˜ao 2.1.15 (Valor Absoluto).

O valor absoluto de um intervalo A = [a1,a2] ´e definido por:

|A_| = max(_|a1|,|a2|).

Defini¸cão 2.1.16 (Ponto Médio).

O ponto m´edio de um intervalo A = [a1,a2] ´e definido por:

m(A) = (a1+a2)/2,

Defini¸cão 2.1.17 (Distância entre intervalos).

A distância entre dois intervalo A = [a1,a2] e B = [b1,b2] é dado pela fun¸cão d: I( ) ×

I( ) _→ :

d(A, B) =max(_|a1−b1|,|a2−b2|).

(27)

2.2 Matrizes e vetores Intervalares

Deﬁni¸c˜ao 2.2.1 (Matriz Intervalar).

Denota-se uma matriz intervalar por A = (Aij)m×n com ordemm(linhas) porn(colunas),

onde cada elemento (Aij) ´e um intervalo.

Assim, A =

[a, b] [c, d] [e, f] [g.h]

´e uma matriz intervalar com duas linhas e duas colunas.

Deﬁni¸c˜ao 2.2.2 (Vetor Intervalar).

Supondo A = (Aij) uma matriz intervalar de ordem m_× n, se m =1, então a matriz A é chamada matriz linha ou vetor linha e, se n = 1, então A é chamada matriz coluna ou vetor coluna. Por exemplo:

1. A = ([a,b] [c,d] [e,f]) ´e uma matriz ou vetor linha 1 _×3 .

2. A = ⎛ ⎜ ⎜ ⎝

[a, b] [c, d] [e, f]

⎞ ⎟ ⎟

⎠´e uma matriz ou vetor coluna 3 ×1 .

Considera-se, por conven¸c˜ao, um vetor intervalar como uma matriz coluna.

Deﬁni¸c˜ao 2.2.3 (Igualdade entre matrizes intervalares).

Sejam as matrizes intervalares: A = (Aij)m×n e B = (Bij)r×s. Diz-se que A = B se, e

somente se, m = r, n = s e Aij = Bij, para todos os ´ındices 1 ≤i≤ n e 1≤j ≤ m.

Exemplos 2.2.1. As matrizes intervalares A=

[1,3] [0,1] [1, e] [3,3]

e B =

[√1,√9] [₋1,1]2

exp[0,1] [3,3]

(28)

Deﬁni¸c˜ao 2.2.4 (Matriz intervalar nula).

Uma matriz intervalar A = (Aij)m×n ´e considerada nula se todos os seus elementos s˜ao

nulos, ou seja, se Aij = [0,0], _∀i,j. Representa-se a matriz nula por 0.

Exemplos 2.2.2. A matriz intervalar A=

[0,0] [0,0] [0,0] [0,0]

´e nula de ordem 2 _× 2.

Deﬁni¸c˜ao 2.2.5 (Matriz Intervalar Identidade).

Uma matriz intervalar I = (Iij)m×n ´e considerada identidade, se todos os elementos da

diagonal principal s˜ao intervalos identidade e os demais elementos s˜ao intervalos nulos, ou seja, se Iij = [1,1] para i = j eIij = [0,0] para i= j.

Exemplos 2.2.3. A matriz intervalar I =

[1,1] [0,0] [0,0] [1,1]

´e identidade de ordem 2 _×2.

Apresenta-se a seguir, as principais opera¸cões com matrizes intervalares, como a soma, a diferen¸ca, o produto por um intervalo, a multiplica¸cão entre matrizes intervalar, a interseçcão e a união, além da rela¸cão de inclusão.

Deﬁni¸c˜ao 2.2.6 (Soma de Matrizes Intervalares).

Sejam A = (Aij) e B = (Bij) duas matrizes intervalares de mesma ordem. A matriz soma das matrizes A e B, ´e definida como sendo a matriz S = A + B, com os elementosSij =Aij

+ Bij,∀i,j.

Exemplos 2.2.4. Dado as matrizes

A=

[2,3] [1,3] [2,2] [3,3]

e B =

[−3,3] [−1,3] [−2,1] [−2,−2]

tem-se: S = A + B =

[2,3] + [₋3,3] [1,3] + [₋1,3] [2,2] + [₋2,1] [3,3] + [₋2,₋2]

=

[₋1,6] [0,6] [0,3] [1,1]

(29)

Defini¸cão 2.2.7 (Subtra¸cão de Matrizes Intervalares).

Sejam A = (Aij) e B = (Bij) duas matrizes intervalares de mesma ordem. A diferen¸ca entre A e B, ´e definida por D = A - B, com os elementos Dij = Aij + (- Bij), ∀i,j.

A=

[2,3] [1,3] [2,2] [3,3]

e B =

[−3,3] [−1,3] [₋2,1] [₋2,₋2]

tem-se: S = A - B =

[2,3]−[−3,3] [1,3]−[−1,3] [2,2]−[−2,1] [3,3]−[−2,−2]

=

[−1,6] [−2,4] [1,4] [5,5]

.

Deﬁni¸c˜ao 2.2.8 (Produto de um Intervalo por uma Matriz).

Seja A = (Aij) uma matriz intervalar de ordem m × n e I um intervalo. O produto do

intervalo I pela matriz A ´e a matriz intervalar P = (Pij), onde cada elemento ´e dado porPij

= I . Aij ,_∀ij.

Exemplos 2.2.6. Dado a matriz

A=

[2,3] [1,3] [2,2] [3,3]

e o intervalo I = [-1,2] tem-se:

P =I.A= [₋1,2].

[2,3] [1,3] [2,2] [3,3]

=

[₋1,2].[2,3] [₋1,2].[1,3] [₋1,2].[2,2] [₋1,2].[3,3]

=

[₋3,6] [₋3,6] [₋2,4] [₋3,6]

.

(30)

Sejam A = (Aij)m×pe B = (Bij)p×n. A multiplica¸c˜ao de A por B ´e uma matriz intervalar

M = (Mij)m×_n= A . B, cujos os elementos s˜ao dados por (M_ij) = Σ

p

k=1 Aik×Bkj.

A=

[2,3] [1,3] [2,2] [3,3]

e B =

[₋3,3] [₋1,3] [₋2,1] [₋2,₋2]

tem-se: M = A . B =

[2,3].[₋3,3] + [1,3].[₋2,1] [2,3].[₋1,3] + [1,3].[₋2,₋2] [2,2].[₋3,3] + [3,3].[₋2,1] [2,2].[₋1,3] + [3,3].[₋2,₋2]

=

[₋9,9] + [₋6,3] [₋3,9] + [₋6,₋2] [−6,6] + [−6,3] [−2,6] + [−6,−6]

=

[₋15,12] [₋9,7] [12,9] [−8,0]

.

Defini¸cão 2.2.10 (Interseçcão de Matrizes Intervalares).

Sejam A = (Aij) e B = (Bij) duas matrizes intervalaresde mesma ordem. A intersec¸c˜ao

de A com B ´e a matriz intervalar Γ = A _∩ B, onde cada Γij = Aij ∩ Bij, ∀i,j. Caso n˜ao

exista interseçcão entre dois elementos intervalares correspondentes, ou seja Aij _∩ Bij = _∅ para algum i,j, então não existirá a interseçcão entre A e B. Dessa maneira, assim como a interseçcão entre intervalos é parcial, então a interseçcão entre matrizes intervalares também será parcial.

A=

[1,3] [0,3] [1,2] [3,3]

e B=

[₋3,2] [4,6] [₋2,0] [2,2]

tem-se: Γ= A _∩ B =

[1,3]∩[−3,2] [0,3]∩[4,6] [1,2]_∩[₋2,0] [3,3]_∩[2,2]

=

[1,2] ∅

∅ ∅

=∅,

(31)

Defini¸cão 2.2.11 (União de Matrizes Intervalares).

Sejam A = (Aij) e B = (Bij) duas matrizes intervalaresde mesma ordem. A união de A com B é a matriz intervalar U = A ∪B, onde cadaUij = Aij ∪ Bij,∀i,j. Caso não exista união entre dois elementos intervalares correspondentes, ou seja Aij ∪Bij = ∅, então não existirá a união entre A e B. Assim, semelhante a interseçcão intervalar, a união de matrizes é também uma opera¸cão parcial.

Exemplos 2.2.9. 1. Dado as matrizes

A=

[1,3] [0,3] [₋2,2] [₋1,2]

eB =

[₋3,2] [2,6] [1,2] [3,3]

tem-se: U =A∪B=

[1,3]∪[−3,2] [0,3]∪[2,6] [₋2,2]_∪[1,2] [₋1,2]_∪[3,3]

=

[−3,3] [0,6] [₋2,2] [₋1,3]

.

2. Dado as matrizes

A=

[1,3] [0,3] [₋2,0] [₋1,2]

e B =

[−1,0] [4,6] [1,2] [2,3]

tem-se: U =A∪B=

[1,3]∪[−1,0] [0,3]∪[2,6] [−2,0]∪[1,2] [−1,2]∪[2,3]

=

∅ [0,6]

∅ [−1,3]

= _∅,

onde ∅, como no caso anterior, indica parcialidade.

Defini¸cão 2.2.12 (Inclusão de Matrizes Intervalares).

Sejam A = (Aij) e B = (Bij) duas matrizes intervalares de mesma ordem. A matriz

(32)

A=

[1,3] [4,6] [1,1] [₋6,0]

e B=

[1,4] [2,6] [₋2,2] [₋6,0]

tem-se que [1,3]⊆[1,4] , [4,6]⊆[2,6], [1,1]⊆[−2,2] e [−6,0]⊆[−6,0]. Logo, B ´e uma inclus˜ao para a matriz A , ou seja A _⊆B.

Teorema 2.2.1. (Propriedades das Matrizes Intervalares)

Sejam A, B e C, matrizes intervalaresde mesma ordem. Então, são válidas as seguintes propriedades:

1. A + (B + C) = (A + B) + C _→ Associatividade

2. A + 0 = 0 + A = A → Elemento neutro da adi¸c˜ao: matriz nula

3. A + B = B + A _→ Comutatividade

4. A . I = I . A = A _→ Elemento neutro da multiplica¸c˜ao: matriz identidade

5. (A + B) . C ⊆A.C + B.C → Sub-distributividade.

Demonstra¸c˜ao: Considerando as matrizes A = (Aij) e B = (Bij) e C =(Cij) trˆes matrizes intervalares da mesma ordem, tem-se:

1) _⇒ A + (B + C)_⇒ Aij + (Bij +Cij) =Aij+Xij. Como

Xij =Bij +Cij, ent˜aoAij+Xij =Aij+Bij+Cij. Logo, A + (B + C) = A + B + C.

⇐ (A + B) + C _⇒ (Aij +Bij) +Cij Yij +Cij. ComoYij =Aij+Bij, Ent˜ao

(33)

Portanto, A + (B + C) = (A + B) + C, c.q.d.

2) _⇒ A + 0_⇒ Aij + 0 = Aij. Logo, A + 0 = A.

⇐ 0 + A_⇒ 0 + Aij = Aij. Logo, 0 + A = A. Portanto, A + 0 = 0 + A, c.q.d.

3) _⇒ A + B_⇒ Aij+Bij = Bij+Aij. Logo, A + B = B + A

⇐ B + A_⇒ Bij +Aij = Aij +Bij. Logo, B + A = A + B. Portanto, A + B = B + A, c.q.d.

4) ⇒ A.I⇒pk=1Aik ×Ikj = Aij. Logo, A.I = A

⇐ I.A⇒pk=1Iik ×Akj = Aij. Logo, I.A = A.

Portanto, A.I = I.A = A, c.q.d.

5) ⇒ (A + B).C⇒(A + B).C = S . C, onde S = A+B e cada

Sij=Aij+Bij. S.C =

p

k=1Sik×

Ckj=Pij e considerando que A,B,C e S sejam da mesma ordem e

quadrada, ou seja, número de linhas igual ao número de colunas, então P terá a mesma ordem de S e C.

⇐ A.C + B.C_⇒ p_k=1Aik×Ckj +

p

k=1Bik×Ckj = Xij + Yij.

(34)

Exemplos 2.2.11. Sejam as matrizes

A

[1,1] [0,1] [1,1] [₋1,1]

,B

[₋1,2] [3,4] [2,2] [₋6,₋4]

e C

[0,3] [1,4] [₋1,8] [3,15]

Calcular:

A.B

[₋1,2] + [0,2] [3,4] + [₋6,0] [−1,2] + [−2,2] [3,4] + [−6,6]

=

[₋1,4] [₋3,4] [−3,4] [−3,10]

B.C

[₋3,6] + [₋4,32] [₋4,8] + [9,60] [0,6] + [₋48,6] [2,8] + [₋90,₋12]

=

[₋7,38] [5,68] [₋48,12] [₋88,₋4]

(A.B).C

[₋3,12] + [₋24,32] [₋4,16] + [₋45,60] [9,12] + [₋24,80] [₋12,16] + [₋45,150]

=

[₋27,44] [₋49,76] [₋33,92] [₋57,166]

A.(B.C)

[₋7,38] + [₋48,12] [5,68] + [₋88,₋4] [₋7,38] + [₋48,48] [5,68] + [₋88,88]

=

[₋55,50] [₋83,76] [₋55,86] [₋83,156]

Logo, A.(B.C) = (A.B).C.

As próximas defini¸cões, referem-se a algumas transferências de dados entre matrizes reais e matrizes intervalares. As matrizes reais são transformadas naturalmente em matrizes intervalares pontuais, bastando para isto considerar cada elemento da matriz real como sendo um intervalo pontual (degenerado) da matriz intervalar correspondente. Por outro lado, a transferência de dados de matrizes intervalares para matrizes reais pode ser realizada de diferentes formas, como pode ser visto a seguir.

Defini¸cão 2.2.13 (Matriz diâmetro).

Seja A = (Aij) uma matriz intervalar. A matriz diˆametro de A, ´e a matriz onde

(35)

Exemplos 2.2.12.

diam

[1,2] [0,2] [₋2,3] [₋2,1]

= 1 2 5 3 .

Defini¸cão 2.2.14 (Matriz ponto médio).

Seja A = (Aij) uma matriz intervalar. A matriz ponto médio de A é a matriz onde cada elemento corresponde ao ponto médio do respectivo intervalo da matriz intervalar, ou seja med(A) = (med(Aij)).

Exemplos 2.2.13.

med

[1,3] [0,2] [₋1,3] [2,4]

= 2 1 1 3 .

Defini¸cão 2.2.15 (Matriz módulo).

Seja A = (Aij) uma matriz intervalar. A matriz módulo de A é a matriz onde cada elemento corresponde ao módulo do respectivo intervalo da matriz intervalar, ou seja |A|= (_|Aij|).

Exemplos 2.2.14.

[1,3] [0,4] [2,6] [−1,2]

= 3 4 6 2 .

Defini¸cão 2.2.16 (Ínfimo da matriz intervalar).

Seja A = (Aij) uma matriz intervalar. O´ınfimo de A é a matriz cujos elementos são os

extremos inferiores dos intervalos correspondentes dessa matriz, ou seja inf(A) = (inf(Aij)).

Exemplos 2.2.15.

inf

[1,3] [0,5] [₋2,2] [₋1,1]

=

1 0

−2 ₋1

(36)

Deﬁni¸c˜ao 2.2.17 (Supremo da matriz intervalar).

Seja A = (Aij) uma matriz intervalar. O supremo de A, ´e a matriz cujos elementos s˜ao os extremos superiores dos intervalos correspondentes dessa matriz, ou seja sup(A) = (sup(Aij)).

Exemplos 2.2.16.

sup

[1,3] [0,5] [₋2,2] [₋1,1]

= 3 5 2 1 .

Defini¸cão 2.2.18 (Matriz Distância).

Sejam A e B duas matrizes intervalaresde mesma ordem. A matriz distância _D entre A e B é a matriz real cujos elementos correspondem a distância entre os respectivos intervalos das matrizes A e B, ou seja _D(A,B) = (d(Aij, Bij)),_∀i,j.

Exemplos 2.2.17. Sejam

A=

[2,2] [0,1] [2,2] [₋1,1]

e B =

[₋2,3] [2,3] [3,3] [₋5,₋3]

,

ent˜ao D(A,B)

d([2,2],[₋2,3]) d([0,1],[2,3])

d([2,2],[3,3]) d([₋1,1],[₋5,₋3]) = 4 2 1 4 .

(37)

2.3 Rela¸

c˜

oes de Ordem sobre Intervalos

Além das opera¸cões intervalares mostradas, destacam-se, ainda, as seguintes rela¸cões de ordem sobre o conjunto dos intervalos:

Defini¸cão 2.3.1 (Rela¸cão de pré-ordem).

Sejam X = [a,b] e Y = [c,d] dois intervalos.

X<Y se, e somente se b< c (2.1)

Em outras palavras X < Y se todo o conte´udo de X estiver estritamente a esquerda de Y.

Defini¸cão 2.3.2 (Rela¸cão de ordem de inclusão).

Sejam X = [a,b] e Y = [c,d] dois intervalos de reais.

X⊆Y se, e somente se, c≤ a≤b ≤d (2.2) Deﬁni¸c˜ao 2.3.3 (Ordem de Kulisch-Miranker).

X≤Y se, e somente se, a≤ c e b ≤d (2.3) Defini¸cão 2.3.4 (Ordem de Informa¸cão).

X_⊑Y se, e somente se, a_≤c _≤d _≤b (2.4)

(38)

Defini¸cão 2.3.5 (Rela¸cão de Aproxima¸cão).

X≪Y se, e somente se, a<c ≤d <b (2.5)

(lˆe-se [a,b] aproxima [c,d]).

2.4 Considera¸

c˜

oes Finais

Essas duas últimas rela¸cões sobre os intervalos foram introduzidas por Scott e utilizadas por Acióly em [5]. Elas formalizam a no¸cão de “um intervalo enquanto informa¸cão ou aproxima¸cão de um outro intervalo ou de um número real”. No cap´ıtulo 4 será apresentada a proposta de Santiago [13] para uma rela¸cão de equivalência que se baseia nessa formaliza¸cão. Ela é mais fraca que a no¸cão usual de equivalência (i.e. uma rela¸cão que é reflexiva, simétrica e transitiva). Naquele cap´ıtulo será proposta a versão booleana para a igualdade de Santiago, a qual[3] será constru´ıda a partir da igualdade simples de Scott — uma das no¸cões primitivas de identidade da linguagem CASL. Essa rela¸cão permitirá que as propriedades algébricas de corpo, tornem-se operacionais em intervalos, fazendo com que do ponto de vista algébrico se possa raciocinar com intervalos como se fossem números reais. Assim será poss´ıvel enxergar um intervalo como uma espécie de número real difuso que carrega uma estimativa de erro.

Note que propriedades alg´ebricas como a distributividade da multiplica¸c˜ao pela soma

A.(B+C) =A.B+A.C,

(39)

atingir o propósito deste trabalho, ou seja tornar poss´ıvel a defini¸cão equacional de sistemas cont´ınuos, através de intervalos e raciocinar equacionalmente2_{sobre eles. O próximo cap´ıtulo}

apresentará alguns detalhes da linguagem de especifica¸cão CASL, que será utilizada para descrever a biblioteca intervalar munida da igualdade local proposta por Santiago.

2

(40)

CASL

3.1 Introdu¸

c˜

ao

A abordagem algébrica para especifica¸cão desoftware originou-se em meados dos anos 1970. Desde então, dúzias de linguagens de especifica¸cão algébrica tem sido desenvolvidas - todas elas suportam a idéia básica do uso de axiomas para especificar álgebras1 _{mas diferem na}

escolha do projeto a respeito da sintaxe e semântica. A falta de uma estrutura comum para esse tipo especifica¸cões i.e., um padrão para essa abordagem tem desencorajado, de certa forma, a aceita¸cão do método algébrico por parte da indústria, impedindo a sua difusão, e limitando a aplicabilidade das respectivas ferramentas.

O grupo COFI: “Common Framework Initiative” para especifica¸cões e desenvolvimento algébrico, reúne grandes expoentes da área de especifica¸cões algébricas no sentido de criar esse padrão para a área. A visão do COFI, como o próprio nome diz, é fornecer essa estru-tura comum2 _{através de um esfor¸co colaborativo para especifica¸cão algébrica e}

desenvolvi-mento, que seja atrativo tanto para pesquisadores quanto para uso industrial. Dessa forma, ele propõe uma linguagem de especifica¸cão uniforme, cuja sintaxe seja de uso amigável e

1

em outras palavras um software ´e visto como uma ´algebra. 2

A Common Framework.

(41)

semântica clara. Além disso, essa estrutura de especifica¸cão pretende resumir frameworks anteriores, agregando o que eles tenham de positivo. Por fim, propõe-se que o ambiente seja livre, mas protegido.

O escopo do COFI abrange:

• a especifica¸c˜ao de requisitos funcionais;

• o desenvolvimento formal e verifica¸c˜ao de software;

• a rela¸cão de especifica¸cões para requisitos informais e implementa¸cão de código;

• prototipagem e provas autom´aticas de teorema;

• bibliotecas, re-uso e evolu¸c˜ao;

• ferramentas de interoperabilidade.

A linguagem de especifica¸cão desenvolvida pelo COFI é chamada CASL:Common Alge-braic Specification Language. As suas principais caracter´ısticas são:

• uma sele¸c˜ao cr´ıtica de construtores conhecidos;

• expressividade, simplicidade e praticidade;

• orienta¸c˜ao para especifica¸c˜ao de requisitos, e projeto, de pacotes de software conven-cional;

• restri¸c˜oes para sub-linguagens;

(42)

O projeto CASL come¸cou em setembro de 1995. Uma versão inicial foi proposta em maio 1997 e experimentalmente aprovada por IFIP WG1.3. Com exce¸cão de poucos detalhes, o projeto foi finalizado em abril de 1998, com um “draft” completo da linguagem incluindo a sintaxe concreta. Por fim a versão CASL 1.0 foi liberada em outubro de 1998.

Esse cap´ıtulo foi fortemente baseado no artigo [9] e seu principal objetivo é tornar a disserta¸cão auto-contida e servir de referencia inicial para a linguagem CASL. A autora fez algumas altera¸cões no texto original incluindo alguns diagramas e acrescentando algumas interpreta¸cões do texto original.

3.2 CASL

A linguagem CASL é dividida em 4 partes independentes (ortogonais) e que podem ser entendidas e usadas separadamente, cada parte contempla um aspecto do processo de es-pecifica¸cão como eses-pecifica¸cão em módulos básicos, reusabilidade, descri¸cão das unidades que serão implementadas separadamente e as suas liga¸cões, agrupamento de especifica¸cões em bibliotecas, etc.

• Especifica¸cões Básicas: são as unidades básicas (o ponto partida) da especifica¸cão. Nelas estão contidas as declara¸cões, defini¸cões e os axiomas.

(43)

• Especifica¸cões Arquiteturais: descrevem as unidades que serão implementadas sep-aradamente, indicando como elas podem serligadaspara dar o resultado desejado. São compostas de: implementa¸cões inteiras e composi¸cões.

• Especifica¸cões de Bibliotecas: são formadas pelo agrupamento de especifica¸cões es-truturadas, visões, especifica¸cões arquiteturais e especifica¸cões de unidades. Caracterizam-se por bibliotecas locais ou distribu´ıdas.

Como as partes acima são ortogonais, i.e independentes, pode-se restringir qualquer uma das partes afim de se obter sub-linguagens. Um exemplo de defini¸cão dessas sub-linguagens é feito pelo grupo de sistemas reativos (veja [2]).

Al´em disso, o projeto de CASL integra v´arios aspectos diferentes; a saber:

• aspectos pragm´aticos: metodologia, ferramentas e est´etica;

• conceitos semânticos: formal (institui¸cão e ambiente), informal (expansões e escopo);

• constructos da linguagem: sintaxe abstrata (estrutura e anota¸c˜oes); sintaxe concreta (formato de entrada e formato display).

No que segue ser´a descrito cada componente ortogonal da linguagem com os respectivos aspectos

3.3 Especiﬁca¸

c˜

oes B´

asicas

(44)

No que segue considera-se vários aspectos pragmáticos que afetam o projeto CASL, com rela¸cão as especifica¸cões básicas. Em seguida a se¸cão 3.3.2 apresenta os conceitos principais em que se baseia a semântica dessas especifica¸cões básicas. Finalmente, a subse¸cão 3.3.3 fornece exemplos que ilustram os constructos da linguagem CASL para que o leitor tenha idéia de como usá-los nas especifica¸cões básicas.

3.3.1 Aspectos Pragm´

aticos

Fun¸cões Totais e Parciais: CASL suporta especifica¸cões parciais e totais. A parcialidade é uma particularidade, e uma maneira simples e natural para tratar erros (tais como divisões por zero, etc). A propaga¸cão desses erros torna-se impl´ıcita, de maneira que sempre que o argumento de uma opera¸cão estiver indefinido então o resultado também será indefinido. CASL possui as no¸cões de igualdade forte e existencial que relacionam a parcialidade com o conceito de identidade3

e que será útil para implementar a igualdade local de Santiago descrita nos cap´ıtulos 4 e 5. CASL também inclui a no¸cão de supersorts e subsorts, que permitem a especifica¸cão do tratamento de exce¸cão quando for relevante. Totalidade é uma importante propriedade, e CASL permite que ela seja declarada juntamente com os tipos de fun¸cões, em vez de deixá-la para os axiomas. O dom´ınio de uma fun¸cão parcial f: A _→? B, pode ser explicitado pela introdu¸cão do dom´ınio de f como um subsort B de A, “B < A”, e declarando que f é total em B 4_.

Na presen¸ca da parcialidade, equa¸cões podem exigir ou não definibilidade, e.g. a equa¸cão 3

Isso ser´a melhor descrito no cap´ıtulo 4. 4

(45)

x+(y+z) = (x+y)+z que exprime a associatividade da soma nos naturais exige que os termos x+(y+z) e (x+y)+z estejam definidos para todo x,y e z, enquanto que x_◦(y_◦z)_≡(x_◦y)_◦z não exigem a definibilidade dos termos para todo x,y e z. Dessa forma, CASL assume dois sentidos para a igualdade e introduz dois tipos de rela¸cões de igualdade; a saber: as equa¸cões “existenciais” que exigem a definibilidade (vide. o primeiro exemplo), e as equa¸cões ditas “fortes”que não exigem a definibilidade (vide o segundo exemplo)5_{. Em}

geral, é apropriado utilizar equa¸cões existenciais em expressões que envolvam condi¸cão de existência dos termos, já que não se pode concluir propriedades a partir da indefini¸cão; e.g. não tem sentido dizer que 1/0 tenha qualquer propriedade. Por outro lado equa¸cões fortes são adequadas em defini¸cões indutivas de fun¸cões. Dessa forma CASL permite ambos os tipos de equa¸cões.

Na verdade, como será visto no cap´ıtulo 4, existe uma rela¸cão impl´ıcita entre as no¸cões de identidade e definibilidade. Portantoasser¸cões de definibilidade podem, também, ser expressas diretamente pois CASL permite a declara¸cão expl´ıcita da definibilidade de termos através da expressão “def T”, onde T é um termo. De fato a definibilidade de um termo pode ser reescrita em termos da igualdade existencial através da seguinte equivalência: x=x

↔ def x, demonstrando a rela¸cão impl´ıcita descrita anteriormente. A igualdade existencial é equivalente à conjun¸cão da igualdade forte com as declara¸cões de definibilidade de seus termos; a saber: x = e =y⇔ x = y ∧ def x ∧ def y, já a igualdade forte é equivalente à conjun¸cão de dois condicionais envolvendo somente a igualdade existencial: x = y ↔[def x

→ x = e = y] ∧[def y → x = e= y], ou equivalentemente x = y↔ [def x∨def y → x = e = y].

5

(46)

Lógica e Predicados: CASL é baseada na lógica de primeira ordem bi-valorada clássica6_,

com a interpreta¸cão usual dos conectivos. Ela suporta predicados declarados pelo usuário, o que produz algumas vantagens sobre as fun¸cões totais booleanas que eram usadas na maioria das linguagens anteriores. Quando um argumento de um predicado é indefinido, a aplica¸cão do predicado não é válida. CASL fornece os quantificadores universal e existencial padrões, além dos conectivos lógicos. A motiva¸cão para isto é a expressividade: restri¸cões à equa¸cões condicionais às vezes requerem que especifica¸cões completas sejam realizadas. Por exemplo: é um exerc´ıcio direto especificar quando uma string é uma permuta¸cão de outra usando quan-tificadores, a nega¸cão fornece a propriedade complementar, mas é completamente desajeitada para ser especificada utilizando equa¸cões condicionais (positivas).

Classes de Modelos: Muitas das estruturas de especifica¸cão algébrica anteriores per-mitiam somente um tipo de classe de modelos associada às especifica¸cões. O “default”em CASL é tomar todos os modelos de uma especifica¸cão, o que também é chamado semântica livre (loose semantics); mas é também poss´ıvel especificar a restri¸cão desses modelos para a classe dos modelos gerados, i.e. somente valores express´ıveis são inclu´ıdos, e as propriedade podem ser provadas por indu¸cão, ou ainda para a classe dos modelos iniciais (livremente gerados), certamente os modelos iniciais podem não existir quando a disjun¸cão, a nega¸cão, etc. são usadas.

Sobrecarga: Em uma especifica¸cão CASL o mesmo s´ımbolo pode ser declarado com vários perfis, i.e. com a lista de argumentos e sorts resultantes. Por exemplo, ‘+’ pode ser declarado como uma opera¸cão sobre inteiros, reais, e strings. Quando um s´ımbolo de sobrecarga é usado, o perfil desejado é determinado pelo contexto. A remo¸cão de ambiguidade

pode ser usada de maneira expl´ıcita quando necess´ario, pela especifica¸c˜ao do perfil, ou do 6

(47)

(2_⏐,2) _−→ 4 ⏐ ⏐ ⏐ × −→+ inj ⏐ ⏐ ⏐ ⏐ inj ×_⏐ −→+ ⏐ ⏐ ⏐ (2,2) _−→ 4

Figura 3.1: Diagrama da Sobrecarga

sort resultante em uma aplica¸c˜ao.

Subsorts: É apropriado declarar um sort como um subsort de outro. Por exemplo, tanto os inteiros positivos quanto os inteiros ´ımpares positivos são melhores descritos como subsorts do sort dos números naturais, no qual é ele próprio um subsort dos inteiros. Em contraste com a maioria das abordagens anteriores, CASL interpreta subsorts como mergulho entre “carriers”₋ e não necessariamente como a inclusão. Isto permite, por exemplo, que valores de modelos do tipo inteiro sejam representados diferentemente dos valores do tipo real. CASL ainda permite modelos onde subsorts são subconjuntos.

As imersões dos subsort comutam com as fun¸cões de sobrecarga (veja figura 3.1), por isso os valores são independentes de qualquer perfil usado, ou seja: “2+2=4”, indiferentemente se a opera¸cão ‘+’ é aquela declarada para os números naturais ou para os números inteiros. Ou seja o diagrama 3.1 comuta.

(48)

s˜ao permitidas em CASL.

Construtores e Seletores de Tipos de Dados: Especifica¸cões de ‘tipos de da-dos’ com opera¸cões de construtores e (possivelmente também) seletores são frequentemente necessárias: elas correspondem à união disjunta de tipos registro e tipos enumerados nas linguagens de programa¸cão. CASL fornece constructos especiais para a declara¸cão dos tipos de dados, afim de abreviar as declara¸cões tediosas e axiomas de seletores e construtores. Tipo de dados podem ser “loose”, “generated”ou “free”.

3.3.2 Conceitos Semˆ

anticos

Como ´e de se esperar, CASL por ser uma linguagem que descreve teorias de 1a _{ordem possui}

uma semântica associada. Os conceitos semânticos essenciais para especifica¸cões básicas são bem conhecidos: assinaturas (declara¸cão de s´ımbolos), modelos (interpreta¸cão dos s´ımbolos), e senten¸cas (declara¸cão das propriedades do sistema), além de uma rela¸cão de satisfa¸cão entre modelos e conjuntos de senten¸cas. Definindo isto, juntamente com algumas estruturas categóricas, tal que a tradu¸cão dos s´ımbolos preservem a rela¸cão de satisfa¸cão, obtém-se o que se chama por institui¸cão para especifica¸cões básicas. (c.f. figura 3.5).

(49)

× −−−→+

Inj

⏐ ⏐

Inj

⏐ ⏐

× −−−→+

Figura 3.2: Diagrama da Sobrecarga

Assinaturas: Uma assinatura = (S,TF,PF,P,_≤) para uma especifica¸cão CASL con-siste de um conjunto de sorts S; conjuntos disjuntos TF e PF de s´ımbolos de opera¸cões totais e parciais respectivamente (para cada perfil de argumento e sort resultante); um conjunto de s´ımbolos de predicados P (para cada perfil de argumento) e uma ordem parcial ≤ sobre S que expressará quando um sort será subsort de outro, indicando a existência das imersões entre os sorts da assinatura. O mesmo s´ımbolo pode ser sobrecarregado com mais de um perfil e não há condi¸cões na rela¸cão entre sobrecarga e subsorts. São permitidas sobrecarga “ad-hoc”e “sobrecarga de subsort”.

Modelos: Um modelo M_∈Mod() fornece um conjunto (carrier) não vazio para cada sort em S, uma fun¸cão parcial para cada s´ımbolo de opera¸cão em PF _∪TF (para cada um dos perfis), uma rela¸cão para cada s´ımbolo de predicado em P (para cada um dos perfis), e uma imersão para cada par de sort relacionados por “≤”. A interpreta¸cão de um s´ımbolo de opera¸cão em TF tem que ser uma fun¸cão total. Além disso, as imersões e as sobrecargas têm que ser compat´ıveis: ou seja, as imersões devem comutar com as opera¸cões de sobrecarga (c.f. exemplo da figura 3.2). A classe de todos os modelos de uma assinatura é dada por Mod() — veja a figura 3.3.

(50)

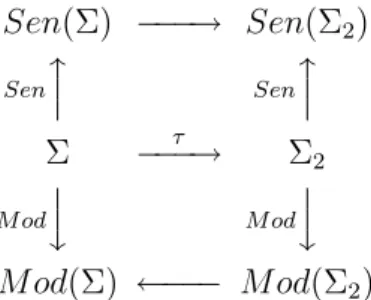
Sen(Σ) _−−−→ Sen(Σ2) Sen ⏐ ⏐ Sen ⏐ ⏐ Σ −−−→τ Σ2

M od ⏐ ⏐ M od ⏐ ⏐

M od(Σ) _←−−− M od(Σ2)

Figura 3.3: Assinatura Senten¸cas e Classe de Modelos Σ _−−−→τ Σ2

⏐ ⏐ ⏐ ⏐

Sen(Σ) −−−→ Sen(Σ2)

Figura 3.4: Assinatura e Conjunto de Senten¸cas

qualificados7

. Os termos nas fórmulas atômicas são formados pela aplica¸cão de opera¸cões completamente qualificadas8_{, variáveis, termos explicitamente tipados (interpretados como}

imersões de subsorts) ou “casts”(interpretados como proje¸cões sobre subsorts). O conjunto de todas as senten¸cas de uma especifica¸cão básica é denotado por Sen(). Veja figura 3.4.

Satisfa¸cão: Denotada por M |= Φ, a satisfa¸cão de uma senten¸ca de primeira ordem Φ em um modelo M é como o usual; i.e considerando os quantificadores e conectivos lógicos, ela envolve a validade de fórmulas abertas, e os valores de termos, relativo às atribui¸cões dos valores às variáveis. O valor do termo pode ser indefinido quando ele envolver a aplica¸cão de um s´ımbolo de opera¸cão parcial (ou um cast). Quando o valor de qualquer termo de argumento é indefinido, a aplica¸cão de um predicado sobre esse termo nunca é válido, e a aplica¸cão de uma opera¸cão sobre esse termo é sempre indefinida (como usual em álgebra parcial). A definibilidade de termos também afeta a validade de fórmulas atômicas: uma

7

i.e. s´ımbolos de predicados da formaPw ondew∈S∗. 8

(51)

Σ_⏐ _−→M od M od(Σ) _|=Σ SenΣ

⏐

φ ⏐_⏐M od(φ) ⏐⏐Sen(φ) Σ′ M od

−→ M od(Σ′₎

|=Σ′ SenΣ′ Figura 3.5: Diagrama de Institui¸c˜ao

equa¸cão existencial é válida quando ambos termos são definidos e iguais, já no caso de uma equa¸cão forte, ela será válida quando ambos os termos forem definidas e iguais ou simplesmente estiverem indefinidos9_.

Restri¸cão de Gera¸cão de Sort: (S’,F’)_⊆(S,F), onde F = TF _∪ PF: Uma restri¸cão de gera¸cão de sort é tratada como um tipo adicional de senten¸ca. Ela é satisfeita em um modelo quando os conjuntos que interpretam os sorts em S’ são gerados por fun¸cões em F’ (possivelmente a partir de sorts em S _\S’ ).

Institu¸cão: A institu¸cão para especifica¸cões básicas em CASL é dada equipando-se a assinatura com morfismos, e os modelos com homomorfismos. Um morfismo de assinaturaσ

de em′

preserva a sobrecarga, os mergulhos e a totalidade dos s´ımbolos das opera¸c˜oes.

Um homomorfismoh:M1 →M2; ondeM1, M2 ∈Mod(

)preserva os valores das opera¸c˜oes (incluindo a definibilidade) e a validade dos predicados. Um morfismo de assinatura σ de

em ′

determina uma tradu¸c˜ao de senten¸cas de Sen() para Sen(′

), e um funtor redutor Mod(σ) :Mod(′

)_→Mod(). As tradu¸c˜oes preservam a satisfa¸c˜ao:

M′

|=σ(Φ) sss Mod(σ)(M′

)_|= Φ (3.1)

como visto na figura 3.5.

Fun¸cões Semânticas: Enquanto que as aplica¸cões de predicados e opera¸cões nas fórmulas 9

(52)

atômicas e nos termos dainstitui¸cão CASL são completamente qualificadas pelo seus perfis, as especifica¸cões básicas na linguagem CASL permitem que os perfis sejam omitidos desde que eles estejam evidentes no contexto. Em geral, pode-se ter muitos caminhos, e possivel-mente nenhum, para expandir uma fórmula atômica da linguagem CASL (pela inser¸cão de perfis) para se obter uma fórmula atômica bem tipada e completamente qualificada para constru¸cão de uma senten¸ca na institui¸cão subjacente10_{. A fórmula atômica é considerada}

bem formada quando ela se expande para uma única fórmula na institui¸cão (a menos da co-mutatividade das imersões com a sobrecarga das opera¸cões); os axiomas de uma especifica¸cão básica bem formada determinam um conjunto de senten¸cas da institui¸cão CASL.

De fato a institui¸cão CASL com subsorts descrita acima pode ser reduzida para uma institui¸cão CASL heterogênea ordinária, pela substitui¸cão da pré-ordem “_≤” por um mer-gulho expl´ıcito; i.e. = (S,TF,PF,P,_≤) reduz-se para ′

= (S,TF _∪ Emb,PF _∪ Proj,P _∪ Memb) ondeEmb =_{embs,s′|s≤s

′

}é um conjunto de s´ımbolos de opera¸cões totais que rep-resentarão megulhos de subsorts, e os conjuntos Proj (de proje¸cões sobre subsorts) e Memb (predicados de pertinência para subsort) são definidos similarmente.

Dessa forma, a semântica de uma especifica¸cão básica bem formada em CASL é dada por uma assinatura junto com a classe daqueles modelos M_∈ Mod() que satisfazem todas as senten¸cas determinadas pela especifica¸cão; ou seja o par , M od().

10

Ou seja, o que se quer e transportar senten¸cas ϕ da linguagem CASL para senten¸cas Φ∈Sen₍_{) na}

(53)

3.3.3 Constructos da Linguagem

Esta subse¸cão fornece exemplos que ilustram os constructos da linguagem CASL para o uso em especifica¸cões básicas, são eles : declara¸cões e defini¸cões (tipos, opera¸cões, pred-icados e tipo de dados), restri¸cão de gera¸cão de sorts e axiomas (envolvendo declara¸cão, quantifica¸cão, conectivos, fórmulas atômicas e termos).

Note que CASL permite que declara¸cões sejam disseminadas com defini¸cões e axiomas. A visibilidade é linear, i.e s´ımbolos tem que ser declarados antes que sejam usados (exceto dentro da declara¸cões de tipo de dados, onde não há visibilidade linear para que sejam permitidos tipos de dados mutuamente recursivos).

Tipos: V´arios sorts podem ser declarados de uma vez, possivelmente como subsorts de algum outro sort:

sort Elem

sorts Zero,Pos <Nat

Os valores de um subsort podem também ser definidos através de uma fórmula, por exemplo:

sort Odd =_{n :Nat • odd(n)}

Isto corresponde a declarar Odd < Nat e declarar que o valor n em Nat é a imersão de alguns valores de Odd se e somente se a fórmula odd (n) for válida.

(54)

ops zero:Zero;

suc :Nat _→Pos; pre :Nat _→?Pos;

+ :Nat_×Nat _→Nat,

assoc,comm,unit 0;

onde assoc, comm e unit0 são atributos indicando que a opera¸cão é associativa, comu-tativa e possui elemento neutro “0”. Note que isso é apenas uma abrevia¸cão dos axiomas:

∀m,n,k : Nat

•m + (n + k) = (m + n) + k

•m + n = n + m

•m + 0 = 0 + m

•m + 0 = m

A chamada nota¸cão mixfix é permitida. Essa nota¸cão é assim denominada pelo fato de generalizar as nota¸cões infixa, pós-fixa e prefixa, permitindo a mistura arbitrária das por¸cões dos argumentos e identificadores. Os “place-holders”11 _{são escritos como pares de}

“underscores”12_{. Exemplos:}

• − −+− −

• − − − −+

O primeiro caso significa que um termo envolvendo a soma será da forma “a+b” e no segundo que os termos serão da forma ab+. Todos os s´ımbolos deverão ser inclu´ıdos no

11

Local para colocar um argumento da opera¸c˜ao. 12

(55)

formato ISOLATIN-1, mas as anota¸c˜oes13 _{podem causar um efeito de formata¸c˜ao diferente}

-e.g. como o aparecimento de s´ımbolos matem´aticos “_→” em vez do par de caracteres “->”.

Em casos simples, as opera¸cões podem também ser definidas no mesmo instante em que elas são declaradas em vez de definidas através dos axiomas:

ops 1 :Nat =suc (0);

dbl(n :Nat) :Nat = n+n

Predicados: A declara¸cão de predicados assemelha-se a declara¸cão das opera¸cões, mas não há sort resultante, pois é pressuposto que o sort resultante será a álgebra booleana

{V,F_}14_.

preds odd :Nat;

≤ :Nat _×Nat

As declara¸cões de predicados também podem ser definidas no mesmo tempo que elas são declaradas, através do conectivo “_⇔ ” :

preds even(n :Nat)⇔ ¬odd(n);

≤ (m,n:Nat)⇔ m <n ∨m =n

No que segue dá-se exemplos de duas especifica¸cões básica em CASL contendo a sua defini¸cão e sua semântica:

(1) Especifica¸c˜ao com um ´unico sort

spec Elem

13

Informa¸cões que não afetam a semântica da especifica¸cão e são utilizadas como aux´ılio para as ferramentas que processarão a especifica¸cão (analisadores ou provadores automáticos de teoremas).

14

(56)

sort Elem end

Essa especifica¸cão bem simples é definida como sendo o par, ψ, onde: = (S,PF,TF,P), S = {Elem}, P F =T F =P = ψ = ∅, e cujo significado é: , M od(), de maneira que Mod() = Set (i.e os modelos da especifica¸cão é a categoria de todos os conjuntos).

(2) Especifica¸cão com um sort mais um predicado binário homogêneo

spec ORDER

sort Elem

pred _≤ :Elem_×Elem end

Essa especifica¸c˜ao tamb´em declara apenas a assinatura ={S2, P F2, T F2, P2}ondeS2

= _{Elem_}, P F2 = T F2 = ∅,P2 ={≤} e Mod(

2) ´e a classe de todos os conjuntos munidos

de uma rela¸c˜ao bin´aria.

Tipo de Dados: Uma declara¸cão de tipo de dados é vista como uma gramática livre de contexto, i.e. uma variante de BNF. Ela declara os s´ımbolos na esquerda de “::=”como os sorts, e para cada alternativa na direita declara um construtor possivelmente com alguns seletores. Quando os tipos de dados são declarados como “livres”, nos modelos associados os construtores de termos distintos, do mesmo sort, são interpretados como valores distintos, e cada sort declarado é livremente gerado por seus construtores. Assim os modelos de um tipo livre são os modelos iniciais da categoria Mod(). Exemplo:

(57)

free type Pair ::=pair(left,right :Elem)

Tomando Pair como exemplo, essa declara¸c˜ao estabelece quepair :Elem_×Elem_→P air

é um construtor e lef t, right : P air _→ Elem são destrutores. Assim para uma declara¸cão da forma free type S:= ci(si:Si ,. . ., sn:Sn) tem-se que S é um sort constru´ıdo livremente,

ci ´e um construtor e si, . . . , sn s˜ao seletores da forma: ci : Si ×Sn → S; si : S → Si e

sn :S → Sn.

Quando há mais do que uma alternativa em uma declara¸cão de tipo de dados, os seletores são geralmente parciais, e nesse caso tem que ser declarados como tais pela inser¸cão de ’ ?’. Exemplo:

free type List[Elem] ::= nil |cons(ﬁrst :?Elem;rest :?List[Elem])

significando que List[Elem] ´e um sort livremente gerado, nil _∈ List[Elem], cons :

Elem_×List[Elem] _→ List[Elem], f irst : List[Elem] _→? Elem e rest : List[Elem] _→?

List[Elem].

Os seletores parciais podem ser evitados pelo uso de imers˜ao de subsorts como constru-tores:

free types List[Elem] ::=nil _|sort Nelist

Nelist ::=cons(ﬁrst :Elem;rest :List[Elem])

Significando queList[Elem] =nil_∪N elist, eN elist´e constru´ıdo livremente.

A última declara¸cão acima ilustra a não viabilidade linear dentro de uma lista de declara¸cões de tipo de dados: NeList é usado antes de ter sido declarado.

(58)

declarados como tipos “gerados”, i.e. os sorts s˜ao obrigados a serem gerados pelos seus construtores (e subsorts imersos):

generated type Num ::=0 |1 | 0(Num)| 1(Num) generated types Nat ::=0 |sort Pos

Pos ::=suc(pre :Nat)

Onde no segundo caso N at ´e obrigado a ser gerado a partir de 0 e pelo mergulho do subsort P os(que ´e gerado pelo construtor suc).

Mais geralmente, qualquer grupo de declara¸cões de assinaturas pode estar sujeito à uma obrigatoriedade de gera¸cão dos sorts, por exemplo:

generated { sorts Pos <Nat ops 0 :Nat; suc :Nat _→Pos}

Axiomas: As vari´aveis usadas nos axiomas podem de antem˜ao ser declaradas global-mente:

vars m,n :Nat;p :Pos

axioms n <m _→...;suc(n) =p _→...;...

Onde vars declara as vari´aveis m, n : N at e p : P os como globais para toda a especi-fica¸c˜ao, numa biblioteca.

As variáveis podem também ser declaradaslocalmentenuma lista “itemizada”de fórmulas:

vars x,y,z :Elem

&#65279;A Linguagem de Especificação algébrica CASL e o Tipo de Dados Intervalos

Katiane Ribeiro Lopes

Introdu¸

c˜

ao

Matem´

atica Intervalar

2.1

Deﬁni¸

c˜

oes B´

asicas

2.2

Matrizes e vetores Intervalares

2.3

Rela¸

c˜

oes de Ordem sobre Intervalos

2.4

Considera¸

c˜

oes Finais

CASL

3.1

Introdu¸

c˜

ao

3.2

CASL

3.3

Especiﬁca¸

c˜

oes B´

asicas

3.3.1

Aspectos Pragm´

aticos

3.3.2

Conceitos Semˆ

anticos

3.3.3

Constructos da Linguagem

A Linguagem de Especificação algébrica CASL e o Tipo de Dados Intervalos