Aquisi~ao de Dados Usando Logo
e a Porta de Jogos do PC
C. E. Aguiar e F. Laudares
Instituto deFsia,UniversidadeFederaldoRio deJaneiro
Cx.P.68528,Riode Janeiro, 21945-970,RJ
Reebidoem10deAbrilde2001. Aeitoem3deJaneiro2002.
Desrevemos um sistema de aquisi~ao de dados baseado na porta de jogos do IBM-PC om
plataformaWindows. Os programas deaquisi~ao e analise s~ao totalmenteesritos nalinguagem
Logo. O sistemae utilizado paramedir operodo de ump^endulo omofun~aodaamplitudede
osila~ao.
AdataaquisitionsystemusingthegameportofanIBM-PCrunningWindowsisdesribed.The
programsfordataaquisitionandanalysisareall writteninLogo. Thesystemisusedtomeasure
theperiodofapendulumasfuntionoftheosillationamplitude.
I Introdu~ao
Oomputadoreumotimoinstrumentodelaboratorio.
Ele presta-semuito bem a experi^enias que envolvem
medidas de tempo, aquisi~ao de dados em grandes
quantidades, e tratamento de dados em tempo real
[1℄. Apesardetodasestasaraterstiasfavoraveis,os
omputadores t^em sidopouousadosnos laboratorios
didatios. E quando isto oorre,e quase sempre om
oauxliode\kits"pre-fabriados-paotesdeiruitos
eletr^onioseprogramasproduzidosporempresas
espe-ializadas,vendidosapreosrelativamentealtos,eque
muitas vezes operam omo verdadeiras aixas-pretas.
Em geral e difil usar estes paotes para realizar
ex-perimentosdiferentesdaquelesparaosquaiselesforam
projetados, o que limita a sua utilidade didatia [2℄.
Esta falta de exibilidade tem origem, em parte, nos
programas de aquisi~ao e tratamento de dados
onti-dosnoskits,queraramente podem sermodiadosou
mesmoompreendidospor professoreseestudantes.
Neste trabalho desrevemos omo montar um
sis-tema de aquisi~ao de dados simples, de baixo usto,
utilizavelem laboratoriosdidatiosdaesolamedia,e
que daaalunos eprofessores ontrole ompletosobre
o seuuso. Osistema estabaseadona substitui~ao do
\joystik",emgeralusadoparaontrolarjogosno
om-putador,porsensoresquepodemserutilizadosemuma
grandevariedadedeexperi^enias. Aideiadeusara
in-terfaedejogosparaaquisi~aodedadosn~aoenova.
En-tretanto, propostasanteriores[3,4,5℄ utilizavam
om-MSX, ou programas de aquisi~ao esritos em
lingua-genspouo usadashoje, omo Pasale Basi(que
de-ramorigem ao Delphi e VisualBasi, muito populares
mas pouo apropriados ao ensino medio). Uma
im-plementa~ao reente desta ideia pode ser enontrada
narefer^enia [6℄, omprogramasde aquisi~aoesritos
emC eQBasi. Noque sesegue desreveremos omo
montar umsistema deaquisi~ao de dadosa partirda
porta de jogos de um IBM-PC om plataforma
Win-dows (95/98/ME), usando programas totalmente
es-ritosemLogo. Estaeuma linguagemsimples,
desen-volvidaparausodidatio,equefrequentementee
ensi-nadanaesolafundamentalemedia. Comistotodosos
aspetosdo sistema que desrevemospodem ser
om-preendidosemodiadosporestudanteseprofessores,
proporionando-lhesumagrandeexibilidadeno
plane-jamentoeexeu~aodeexperimentos. Avers~aodoLogo
queutilizamoseoSuperLogo,produzidopeloNuleode
InformatiaApliadaaEdua~ao(NIED)daUniamp
[7℄. Esta vers~ao tem os omandos em portugu^es, e e
distribudagratuitamente viaInternet. Uma proposta
semelhante adeste trabalho,usandooMSWLogo (em
ingl^es)[8℄,podeserenontradanarefer^enia[9℄.
Omotivoprinipalparaseusaraportadejogosem
umlaboratoriodidatioeaseguranaefailidadeom
que podemos onetar sensores a esta interfae. Um
joystik e essenialmente um onjunto de resist^enias
variaveis ujos valoress~ao lidos a ada momento pelo
omputador. Substituindo o joystik por um
dade luminosa, por exemplo) podemos monitoraresta
grandeza,registrarasuaevolu~aotemporalem
interva-losmuitopequenos,emanipularquantidadesdedados
quediilmente seriamalanaveisemumlaboratorio
didatioonvenional.
Esteartigoestaorganizadodaseguintemaneira.Na
se~ao II disutimos o funionamento do joystik e da
portade jogos [10, 11℄. Uma forma simples de medir
tempose apresentada na se~ao III. Na se~ao IV
des-revemossuintamente algunssensoresquepodem ser
onetados a porta de jogos. Na se~ao V mostramos
um experimento realizado omo sistema. Alguns
o-mentariosgeraiseonlus~oesest~aonase~aoVI.
II A porta de jogos
II.1 O joystik
OtipomaisomumdejoystikparaIBM-PCs~aoos
joystiksanalogios. Estesjoystikst^emdois bot~oes e
doispoteni^ometrosujasresist^eniasv~aode0a100k
(emalgunsasosate150k). Omovimento
esquerda-direita do joystik (eixoX) muda aresist^enia deum
dospoteni^ometros,eomovimentofrente-tras(eixoY)
muda aresist^enia dooutro. Emgeral asresist^enias
s~aonulas quandoojoystik estatodoparaaesquerda
eparaafrente. Umesquemadojoystikestamostrado
na Fig. 1. Os dois bot~oes est~ao representados pelas
havesA e B,e X eY s~ao ospoteni^ometrosja
men-ionados. A tens~ao de 5 V e o aterramento n~ao s~ao
forneidospelojoystik,maspelaportadejogosaqual
eleeonetado.
Figura1.Esquemadeumjoystik
II.2 A porta de jogos
Aportadejogos doIBM-PCeuma interfaepara
doisjoystiksanalogios,emboraexistaaonex~aopara
apenas um deles. O uso simult^aneo de dois joystiks
soepossvelomumaboespeialemformade`Y'.O
joystikeonetadoapartetraseiradoomputadorvia
Figura2. Osoqueteondeeonetadoojoystik.
Aportadejogosn~aofazparteda\plaam~ae". Em
geral ela e implementada em uma plaa propria ou,
maisfrequentemente,oloadanaplaadesom. Neste
ultimoasooonetortemdoisdosseus15pinos
dedi-adosaportaMIDI(musial instrumentsdigital
inter-fae). Os outros pinos d~ao aesso aos quatro bot~oes
e quatro poteni^ometros (dois eixos X e dois Y)
or-respondentes aosdois joystiks,aum potenial de+5
Volts, e a um terra. Estaporta e muito segura, mas
devemostomaruidadoomurto-iruitosentreo
po-tenialde5Veoterra.
Afun~aodospinosdaportadejogospodeservista
na tabela 1. Cadaum dosjoystiks(quehamamos1
e2)temdoisbot~oes(AeB)edoispoteni^ometros(X
eY). AssimA1eobot~aoA dojoystik1, X2eo
po-teni^ometroXdojoystik2,et. Muitosjoystiksd~ao
aesso aos 4 bot~oes. Nestes asos A1 eB1 referem-se
aosbot~oesprinipais,eA2eB2aosseundarios.
PINO FUNC ~
AO
1 +5Volts
2 Bot~aoA1
3 Poteni^ometroX1
4 Terra
5 Terra
6 Poteni^ometroY1
7 Bot~aoB1
8 +5Volts(ousemuso)
9 +5Volts
10 Bot~aoA2
11 Poteni^ometroX2
12 Terra(ouportamidi)
13 Poteni^ometroY2
14 Bot~aoB2
15 +5Volts(ouportamidi)
Tabela 1. Pinosdainterfaedejogos
II.3 Como a porta de jogos trabalha
AFig. 3mostraosiruitosligadosaadaumdos
15 pinos da portade jogos. Os iruitos onetamos
bot~oesepoteni^ometrosdosjoystiksa8linhasb0...b7.
Estaslinhasalimentam8bits(1byte),numerados
en-o estado dos bot~oes de forma bastante direta. Como
vemosnaFig.3,quandoumbot~aoepressionadoo
po-tenial na linha de sadatorna-se0 V, oque oloa o
bit orrespondentenovalor0. Quandoobot~aoesolto
opotenialdalinhasobepara5Veovalordobitpassa
aser1.
Figura3. Esquemadaportadejogos.
Osbitsde0a3,orrespondentesas linhas b0...b3,
s~ao usados para determinar a resist^enia dos
po-teni^ometros. Esta determina~ao e mais ompliada
que no aso dos bot~oes, e e feita om o auxlio de
umiruitointegrado,oNE558,ompostobasiamente
por4\multivibradoresmonoestaveis" [12℄. O iruito
mantem os bits 0...3 om valor zero ate que se
es-revaalgonoendereodaporta. Nesteinstanteiruito
desarrega os apaitoresligados ao poteni^ometros e
oloaosbits0...3noestado1. Cadaapaitoromea
ent~aoaser arregadoatravesdoseu poteni^ometro, e
o bit orrespondente e mantido no valor 1 ate que a
tens~aonoapaitoratinjaerade3,3V(2/3dovalor
maximo 5 V). A partir da o iruito oloa o bit de
volta no estado 0. O tempo T durante o qual o bit
permaneenoestado1dependedaresist^eniaRdo
po-teni^ometrosegundoaformula
T(s)=24;2+11R (k)
Enontrando este tempoobtemos aresist^enia do
po-teni^ometro. A medida de tempo pode ser feita om
umprogramasimplesdeontagem[5,9℄. Talprograma
devesermuitorapido, eportanton~ao pode seresrito
emumalinguageminterpretadaomoLogo. Poristoo
SuperLogotemumomando espeial paradeterminar
o tempoT, que seradisutido mais afrente. Observe
que omR =100kgastamosaproximadamente 1ms
em uma medida de resist^enia. Note tambem que se
n~ao houvernada onetado a uma determinadalinha
(R = 1) o bit orrespondente pode ar
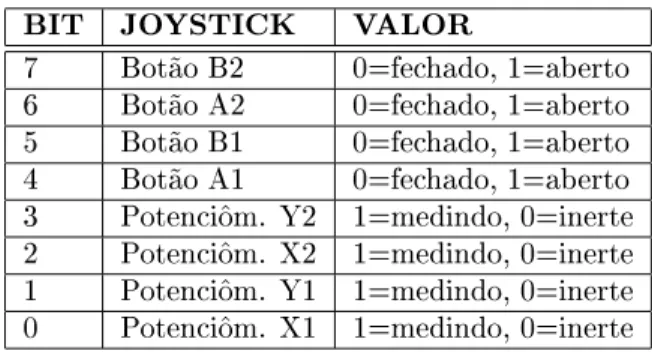
indenida-A tabela 2 resume omo o estado dos joystiks e
mapeado nobyte daporta. A numera~ao dosbits, de
0a7,orrespondeasigni^aniadeles nobyte (os de
menorndie est~ao\adireita"dosdemaiorndie).
BIT JOYSTICK VALOR
7 Bot~aoB2 0=fehado,1=aberto
6 Bot~aoA2 0=fehado,1=aberto
5 Bot~aoB1 0=fehado,1=aberto
4 Bot~aoA1 0=fehado,1=aberto
3 Poteni^om. Y2 1=medindo,0=inerte
2 Poteni^om. X2 1=medindo,0=inerte
1 Poteni^om. Y1 1=medindo,0=inerte
0 Poteni^om. X1 1=medindo,0=inerte
Tabela2. Bits daportadejogos.
II.4 Lendo a porta de jogos
Muitas vers~oes do Logo t^em omandos que l^eem
a porta de jogos. No SuperLogo isto e feito om
portaentradab 513, onde 513e oendereo da porta
dejogos(512 tambemserve). Setivermosumjoystik
onetadoaportaeexeutarmosainstru~ao
mostre portaentradab 513
obteremos o byte da porta, ou melhor, a sua
repre-senta~ao deimal (um numero deimal entre 0 e255).
Paraobteroestadodeadaumadas8linhasdaporta
(o valor de ada bit) devemos onverter este numero
paraarepresenta~aobinaria. Amaneiramaiseiente
defazer isto e usaraopera~aologiaE, denida por:
0E0=0,0E1=0,1E0=0,1E1=1. Existeno
Su-perLogouma opera~ao, bite,que toma dois numeros
inteirosomoargumentoeaplia aopera~aoE aada
parde bits de mesma signi^ania (mesma \posi~ao"
no byte). Por exemplo, apliando bite aos numeros
binarios 1100 e 1010 obtemos 1000. Como oLogo so
usaarepresenta~aodeimal, estaopera~aoerealizada
omainstru~ao
mostre bite 12 10
ja que12
de
= 1100
bin e 10
de
= 1010
bin
. A resposta
queoLogoapresentae8,pois8
de =1000
bin .
Ent~ao, se quisermos saber qual e o N-esimo bit
(N =0;1;2:::) de umnumero X,basta fazer obite
de 2 N
om X. Todos os bits de 2 N
valem 0, om
exe~aodo N-esimobit quevale 1. Portanto, seoN
esimobitdeX for0oresultadodaopera~aosera0. Se
oN-esimobitfor1oresultado sera2 N
. Porexemplo,
para saber se o bot~ao A1 (que orresponde ao bit 4)
estaapertadooun~ao,tomamosobitede2 4
=16om
mostre (bite 16 portaentradab 513)/16
Se o bot~ao estiver apertado o resultado sera 0, e se
ele estiverlivre oresultado sera1. Parasaberovalor
deadaumdos8bitsdaporta,bastaapliaro
proedi-mentoaimaparaN=0;1;2;3:::7,oqueorresponde
ausar1;2;4;8:::128embite. Istopodeserfeitoom
ainstru~ao
mostre mapeie[(bite ? portaentradab 513)/?℄
[128 64 32 16 8 4 2 1℄
que produz uma lista om o valor dos oito bits da
porta.
Com estes proedimentos podemos usar os bot~oes
dojoystikpara ontrolarprogramasLogo. E oquee
maisimportante,podemosmonitorarsensoresexternos.
Porexemplo,fotodiodosefototransistoress~ao
ompo-nentes eletr^onios que onduzemorrente dependendo
dainid^eniadeluz(vejaase~aoIV).Substituindoum
bot~aodojoystikporalgumdestes fotosensores,
pode-mosusaroomputadorparamonitorarseosensoresta
sendoiluminadooun~ao.
II.5 Medindo resist^eniasom aporta de
jogos
Como ja omentamos, a resist^enia de um
po-teni^ometro do joystike obtida medindo-se o tempo
queobitorrespondentepermaneeomvalor1. Este
tempo e tipiamente menor que alguns milisegundos.
Fazer um programa em Logo para medi-lo n~ao e
e-iente, pois tal programaseria muito lento. Para
re-alizar esta medida o SuperLogo tem uma fun~ao
es-peial, portajoystik :M. Esta fornee o tempo que
umbitdaportadejogos,espeiadopelavariavelM,
permaneenoestado1. OsvaloresM=1,2,4,8
orres-pondemaosbits0,1,2,3,ouseja,aospoteni^ometros
X1,Y1,X2,Y2. Porexemplo,paramediraresist^enia
deX1exeutamosainstru~ao
mostre portajoystik 1
Devemos ter algum uidado ao tentar medir os
po-teni^ometros X2 e Y2. Como eles quase nuna est~ao
ligados a porta (pois o segundo joystik raramente e
usado) a resist^enia que e enontrada e innita, e o
tempo a sermedido tambem. Neste aso o omando
portajoystik fornee o valor -1, mas pode levar
muitotempo(atealgunsminutos,dependendodo
om-putador)parafazer isto.
Otempoforneidoporportajoystikn~aoestaem
unidades predeterminadas. Mas, omo ja vimos, este
tempovarialinearmente omaresist^enia, oquee
su-iente para muitas aplia~oes. De qualquer forma,
usando resist^enias onheidas e possvel alibrar a
sadadeportajoystik. Comesteomandopodemos
masLogo. E,prinipalmente,podemosmonitorara
re-sist^eniadesensoresexternosomofotoresistorese
ter-mistores (resistoresdependentes deluzetemperatura,
vejaase~aoIV)oloadosnolugardospoteni^ometros.
III A medida de tempo
Agoraque jasabemosler aporta dejogos, oproximo
passo e registrar a evolu~ao temporal dos sinais que
ela reebe. Para isto preisamos aprender a medir o
instante em que o sinal foi lido. No SuperLogo isto
podeserfeitoomoomandotempomili,quefornee
o tempo em milisegundos deorrido desde que o
sis-tema operaional(Windows)foi iniiado. Exeutando
ainstru~ao
mostre tempomili
obtemos a quantos milisegundos o Windows esta
operando.
E importante saber que otempo forneido
por tempomili n~ao e atualizado a ada milisegundo,
mas em intervalos uja magnitude depende do
om-putadoredaongura~aodosistema. Resolu~oes
tem-porais tpias de tempomili est~ao na faixa de 3 a15
ms.
Quandolemosapenasoestadodosbot~oes,epossvel
obter uma resolu~ao temporal melhordo quea itada
aima. Quer o bot~ao esteja aberto ou fehado, uma
medidadoseuestadolevasempreomesmotempopara
ser realizada. Como este tempo e bem menor que a
resolu~aotemporaldetempomili,podemosusara
on-tagemdemedidas omorelogio. Ointervalodetempo
entre duas medidas suessivasealulado dividindo o
tempo total de aquisi~ao, que pode ser medido om
tempomili, pelo numero de medidas realizadas. Este
proedimento n~ao pode ser utilizadose lemosum
po-teni^ometro(viaportajoystik)pois,omojavimos,
neste aso adura~ao da medida depende do valor da
resist^enia.
IV Conetando sensores a porta
de jogos
Nolugardosbot~oesepoteni^ometrosdojoystik,
pode-mosonetaraportadejogosomponenteseletr^onios
de resist^enia variavel e usa-los omo sensores. Nesta
se~ao disutiremos rapidamente alguns desses
ompo-nentes: otermistor NTC,o fotoresistor,ofotodiodo e
ofototransistor[12,13℄.
IV.1 Termistores
O termistor e um omponente eletr^onio uja
re-sist^enia varia onsideravelmente om a temperatura.
tem-om o aumento da temperatura. Um termistor NTC
efeito de material semiondutor, eetipiamente
uti-lizadonafaixadetemperaturasentre-50 Æ
Ce150 Æ
C.
Arela~aoentre aresist^eniaeatemperatura
abso-lutadeumNTC(urvaaraterstiaR =T)ealtamente
n~ao-linear,epodeseraproximadaporR=exp(=T).
Medindoaresist^eniaparaduastemperaturas
diferen-tes podemos obter as onstantes e e onstruir
uma urvade alibra~aorazoavelmentepreisa. A
re-sist^eniadeumNTCegeralmenteespeiadaa25 Æ
C,
e na maioria dos asos esta entre 100 e 100 k.
Tipiamente, a sensibilidade a 25 Æ
C e da ordem de
-4%/ Æ
C.
IV.2 Fotoresistores
Ofotoresistor,tambemhamadodeelula
fotoon-dutora, fotoelula, ou LDR (light dependent resistor)
possui uma resist^enia quedepende da quantidade de
luz queele reebe. Noesuroosfotoresistorest^em
re-sist^eniaelevada,tipiamentenafaixadeM. Quando
s~ao expostos a luz, a resist^enia diminui por ordens
de magnitude. Sua desvantagem omo sensor esta na
lentid~ao de resposta, que hega adeimosde segundo
- umafotoelulapoden~aoperebero\pisa-pisa" de
60Hzdeumal^ampadauoresente.
IV.3 Fotodiodos
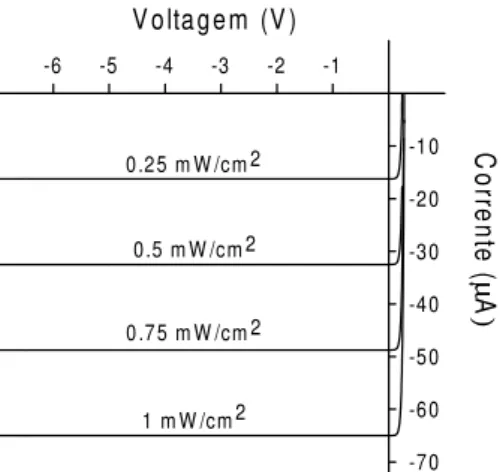
O fotodiodo e um diodo semiondutor em que a
jun~aoestaexpostaaluz. Aorrentereversadeum
fo-todiodo aumentalinearmente omainid^enia deluz,
omo pode servistonas urvasaraterstiasI=V da
Fig. 4. Noesuroaorrentereversaemuitopequena,
geralmentedaordemdenA.Observequeasurvas
a-raterstiaspassampeloquartoquadrante(VI<0),
demodoqueofotodiodopodeproduzirenergiaeletria
-as elulassolaress~aoumtipodefotodiodo.
-6
-5
-4
-3
-2
-1
V o lta g e m (V )
-70
-60
-50
-40
-30
-20
-10
1 m W /cm 2
0 .75 m W /cm 2
0.5 m W /cm 2
0.25 m W /cm 2
Co
rr
e
n
te
(
µ
A
)
Figura4. CurvasaraterstiasI=V deumfotodiodo,para
diferentesintensidadesluminosas. Osvaloresmostradoss~ao
apenasrepresentativos;dependendodotipo,fotodiodost^em
sensibilidades diferentes. Noteque ofotodiodoopera om
Osfotodiodoss~ao uteis omo sensoresde radia~ao
visveleinfravermelha. Arespostaespetral
(sensibili-dadea diferentes omprimentos de onda) de um
foto-diododesilioatingeomaximoem torno900nm,no
infravermelho. Alguns fotodiodos t^em oberturas que
ltramaluzvisvelouaradia~aoinfravermelha.
As orrentes obtidasom um fotodiodo s~ao
geral-mentebaixas,menoresque100Aparaumainid^enia
luminosade 1 mW/m 2
. Comisto n~ao podemosusar
umfotodiododiretamentenolugardeumbot~aodo
joy-stik. ComovemosnaFig.3,omobot~aoapertado
pas-sampeloiruitoerade5mA(naverdade4mAja
s~aointerpretados omo \bot~ao apertado" pela porta).
Para obter orrentes desta magnitude temos que
am-pliarosinaldofotodiodo,ligando-oaumtransistor
omoestamostradonaFig.5.
+
tra n sisto r
fo to d io d o
Figura5. Ciruitoparaampliaraorrentedeum
fotodi-odo.
IV.4 Fototransistores
Os fototransistores s~ao transistores om a jun~ao
oletor-base exposta a luz. Fototransistores s~ao bem
maissensveisquefotodiodos,gerandoorrentesda
or-dem demAquandoiluminadosa1mW/m 2
. Um
fo-totransistorom\ganho"suientementealtopodeser
usado diretamente no lugar de um bot~ao do joystik.
CasoontrarioumiruitosemelhanteaodaFig.5(um
fotodarlington) pode ser usado para ampliar a
or-rente.
V Aplia~ao: Perodo do p^
endu-lo a grandes osila~oes
V.1 A montagem do experimento
Oobjetivodaexperi^eniaemediroperododeum
p^endulo omo fun~ao da amplitude de osila~ao. O
aparatoutilizadoestamostradonaFig.6. Omovimento
dop^enduloemonitoradoapartirdasinterrup~oesque
lâmpada
fotosensor
para a porta
de jogos
Figura6. Esquemadoarranjo experimental.
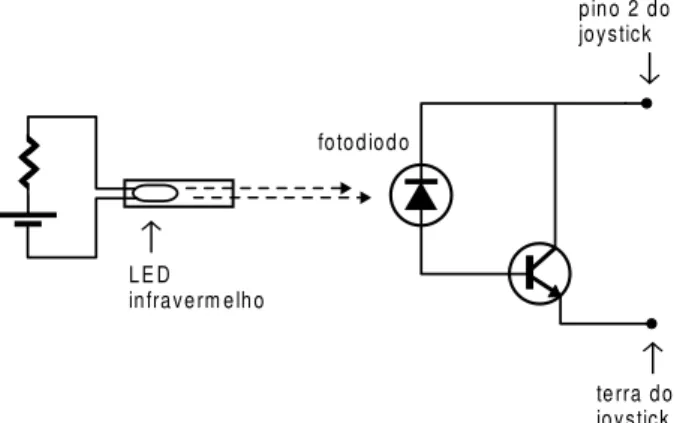
Usamos omo detetor o onjunto
fotodiodo-transistor disutido na se~ao IV.3, iluminado por um
LED infravermelhoobtido em um ontrole remoto de
TV. O fotodiodo foi tirado de um mouse sem uso, e
aamplia~aofoi feitaporumtransistorNPNde uso
generio(BC548C).AFig. 7mostra osistema usado.
O transistorestaligado a porta de jogos via ospinos
2 e4 do onetor, que orrespondem ao bot~ao A1 do
joystike ao terra(vejaa se~aoII.2). Assim,quando
o fotodiodo estiver no esuro, ou reebendo uma
ilu-mina~ao insuiente, otransistorseomportaraomo
umahaveaberta. Seofotodiodoreeberumsinal
lu-minosomaisforteotransistorpermitiraapassagemde
uma orrente alta entre o pino 2e oterra, simulando
o apertar do bot~ao do joystik. Portanto, quando o
p^endulopassaentreoLEDeofotodiodo,deixandoeste
ultimo na sombra, obit 4 daporta vale 1. Quando a
luzatingeofotodiodoobit4passaavaler0.
L E D
in fra ve rm e lh o
fo to d io d o
te rra d o
jo ystick
p in o 2 d o
jo ystick
↑
↑
↓
Figura7. Diagramadosistemadedete~ao. A\l^ampada"e
tem p o
0
1
→ ←
∆
t
→
←
p e río d o
Figura8.Sinalnodetetorgeradopelaosila~aodop^endulo.
Ao osilar, o p^endulo gera ent~ao um sinal omo o
mostrado na Fig.8. Registrando este sinal podemos
obter o perodo da osila~ao, e o tempo t durante
o qual o p^endulo esteve em frente ao fotosensor. A
veloidadedop^endulonestepontoedadapor
V
0 =
D
t ;
emqueDeodi^ametrodoobjetoosilanteou,mais
exa-tamente,adist^aniaqueesteobjetoperorreenquanto
aportareebe\1"omosinal. Estadist^aniapodeser
medidaindependentemente,oquepermitealularV
0 .
Comoofotosensorestaemfrenteaposi~aodeequilbrio
dop^endulo,V
0
eaveloidademaximadaosila~ao. A
veloidadeangularorrespondentee
0 =
V
0
R =
D=R
t ;
em que R e a dist^ania do feixe luminoso ao ponto
de xa~ao do p^endulo. Na nossa montagem D =
3;30:1 m e R = 48;80:5 m. Conheendo
0
podemosalularo^angulomaximodeosila~ao,
max ,
dadopor
os
max =1
R
G
2g
2
0
onde R
G
eoraiode gira~aodop^enduloeg ea
aele-ra~aodagravidade.
V.2 O programa de aquisi~ao
O programa de aquisi~ao que utilizamos
(aquisiao) esta listado abaixo. O par^ametro de
entrada tmax determina a dura~ao da aquisi~ao de
dadosemmilisegundos. Oprogramal^eontinuamente
o tempo e oestado do bot~ao A1, queorrespondeao
pinodainterfaedejogosligadoaofotosensor. Aada
leituraosresultadoss~aooloadosnasvariaveistea1,
que em seguida s~ao esritas em um arquivo hamado
dados.txt. O valor de a1 e 0 quando o sensor esta
iluminadoe16quandoele estanoesuro.
aprenda aquisiao :tmax
abraparaesrever "dados.txt
mudeesrita "dados.txt
atribua "t0 tempomili
atribua "t tempomili-:t0
atribua "a1 (bite 16 portaentradab 513)
(esreva :t :a1)
℄
mudeesrita [℄
fehearq "dados.txt
esreva [*** fim da aquisi~ao ***℄
fim
Paraobteroperodoeamplitudedeadaosila~ao
do p^endulo devemosanalisarosdadosontidosno
ar-quivo geradopelo programade aquisi~ao. Istoefeito
pelo programa analise, mostrado no Ap^endie, que
alula o perodo e a veloidade angular a ada
pas-sagemdop^endulopela posi~aodeequilbrio.
V.3 Resultados experimentais
Mostramos a seguir os resultados de um
experi-mento em que o movimento do p^endulo foi
aompa-nhadodurante4minutos. AFig.9mostraaveloidade
angular maxima
0
omo fun~ao do tempo. O
amor-teimento da osila~ao ausado pelas foras de atrito
e bem visvel. O perodo das osila~oes omo fun~ao
do tempo esta apresentado na Fig.10. A diminui~ao
doperodoreeteasuadepend^enianaamplitudeque,
omovimos,egradativamentereduzidapelosatritos.A
estabiliza~aodoperodoqueoorreaposalgum tempo
orresponde a entrada do p^endulo no \regime de
pe-quenasosila~oes".
0
5 0
1 0 0
1 5 0
2 0 0
2 5 0
te m p o (s)
0 .1
1
1 0
vel
o
ci
dade m
á
xi
m
a
(
ra
d/
s)
Figura 9. A veloidade angular maximaomo fun~ao do
tempo.
0
5 0
1 0 0
1 5 0
2 0 0
2 5 0
te m p o (s)
1 .3 8
1 .4 0
1 .4 2
1 .4 4
1 .4 6
1 .4 8
1 .5 0
per
íodo (
s
)
Figura10. Operodoomofun~aodotempo.
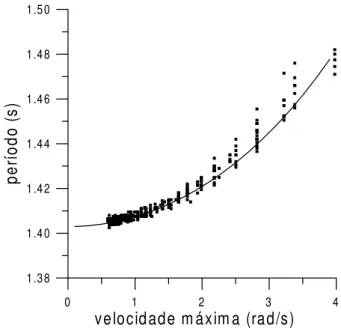
AFig.11mostraomooperododependeda
veloi-dade angular maxima. As osila~oes de maior
ampli-tude t^em
0
4rad/s, o que orrespondea
max
50 Æ
. Paraestasamplitudes operodoeerade0,08s
maiorqueparaaspequenasosila~oes,umaumentoda
ordemde5%.
0
1
2
3
4
velocidade m áxim a (rad/s)
1 .3 8
1 .4 0
1 .4 2
1 .4 4
1 .4 6
1 .4 8
1 .5 0
per
íodo (
s
)
Figura11. O perodo omofun~ao daveloidade angular
maxima. Aurvaontnuaeoresultadodoalulodesrito
nase~aoV.4.
Paraaspequenasosila~oessabemosqueoperodo
edadopor
T =2 s
R
G
g :
O p^endulo que utilizamos tem um raio de gira~ao
R =48;80;2m. Usandog =978,8m/s 2
aelera~aogravitaionalnoRio deJaneiro (segundo o
ObservatorioNaional)obtemos T =1;4030;003s.
AFig. 11mostraqueestealuloestaembomaordo
omoresultadoexperimentalabaixasveloidades
(pe-quenasamplitudes).
V.4 Perododo p^enduloagrandes
ampli-tudes
A Fig.11 mostra algo que diilmente e medido
em um laboratorio didatio onvenional: a varia~ao
do perodo de um p^endulo om a amplitude da
os-ila~ao. Comparar esta medida om a previs~ao da
me^aniaNewtonianaeinstrutivo. Umalulosimples
do perodo de grandes osila~oes pode ser realizado
resolvendo numeriamente a equa~ao de movimento
do p^endulo. Isto e feito no programa Logo listado a
seguir, pendulo,que alula operodo(em segundos)
omofun~aodaveloidadeangularmaxima,dadapelo
par^ametro de entrada omega0 (em rad/s). No
pro-grama a variavel x e o omprimento do arodesrito
pelo p^endulo a partir do ponto de equilbrio, e v e a
s~aoaveloidadeeaelera~aoorrespondentes. Oefeito
dasforasdeatritosobreoperodofoiignoradoporser
muito pequeno no nosso aso, mas pode ser inludo
failmente noprogramaseforneessario.
aprenda pendulo :omega0
atribua "dt 0.0001 ;salto de tempo (s)
atribua "g 978.8 ;ael. grav. (m/s2)
atribua "rg 48.8 ;raio de gira~ao (m)
atribua "t 0 ;instante iniial
atribua "x 0 ;posi~ao iniial
atribua "v :omega0*:rg ;velo. iniial
faaenquanto [passo℄ [:x > 0℄
atribua "periodo 2*(:t-:x/:v)
esreva (lista :omega0 :periodo)
fim
aprenda passo
atribua "a -:g*(senrad :x/:rg)
atribua "v :v + :a*:dt ;nova veloidade
atribua "x :x + :v*:dt ;nova posi~ao
atribua "t :t + :dt ;novo tempo
fim
A urva que esta na Fig.11 foi obtida om o
pro-gramaaima. Oaluloreproduzbastantebemo
om-portamento dos dados experimentais. Observe que o
alulodoperodonoprogramapenduloutilizaapenas
oneitosques~aofamiliaresnoensinomedio
(essenial-mente x =vte v =at, veja arotina passo).
Esteeumbomexemplodeomoosomputadores
po-dem failitar a modelagem matematia de fen^omenos
fsios,tornando-aaessvelaalunosquen~aoonheem
VI Comentarios nais
Neste trabalho nos disutimos a utiliza~ao da porta
de jogos de um PC/Windows omo interfae para
aquisi~ao de dados. O sistema apresentado tem as
seguintesaraterstias:
Podesermontadosemfazermodia~oesno
om-putador.
Utiliza omo sensores omponentes eletr^onios
simplesefaeisdeenontrar.
Efaildeompreendereimplementar.
Eversatil, podendo serusadoemmuitos
experi-mentosdiferentes.
Ebastante rapido, pelo menospara osobjetivos
deumlaboratoriodidatio,alanandoresolu~oes
temporaisdaordemdemilisegundos.
Tem usto proximo de zero se o omputador ja
estiverdisponvel.
Osprogramasdeaquisi~aoeanalisededados
po-demsertodosesritosemLogo.
Osistemapodeserusadoemlaboratoriosdidatios
do ensino medio, em ondi~oes tais que tanto alunos
quanto professores s~ao apazes de ompreender e
on-trolartodasasetapasdoproessodeaquisi~aoeanalise
dos dados. Isto sedeven~ao apenas asimpliidade da
interfae,masprinipalmenteaofatodequeos
progra-masdeaquisi~aoeanalises~aointeiramenteesritosem
umalinguagemaessvelomoLogo.
Aaquisi~aodedadospelaportadejogosn~ao
repre-senta,obviamente,auniaformadeutiliza~aodo
om-putador em um laboratorio didatio. Alem dos kits
omeriaisjamenionados(algunsateusamaportade
jogos),inumerasoutraspropostasexistem,om
diferen-tesgrausdesostia~aoeusto. Paraalgunsexemplos,
vejaasrefer^enias[2,14,15,16,17,18℄. Qualquer que
seja a proposta, paree laro que ao introduzir
om-putadores no laboratorio didatio passamos a ser
a-pazes deobservaruma variedademaiordefen^omenos,
e a analisa-los om mais failidade. Se somarmos a
isto o potenial que oomputador tem enquanto
ins-trumentode modelagem matematia,vemosque estas
maquinaspodemterumimpatomuitopositivono
en-sino defsia,possibilitandouma liga~aoentre
experi-mento e teoriaqueraramente e alanadaom outros
meios.
Agradeemos o apoio dado pelo Laboratorio
Ap^endie
Neste ap^endie mostramos o programa analise, que
utilizamosparaanalisarosdadosobtidosnaexperi^enia
omop^endulo(se~aoV).Osdadoss~aolidosnoarquivo
dados.txt,geradopelo programaaquisi~ao(verse~ao
V.2). O programa de analise alula o instante t em
que oorre uma passagemdo p^endulo pela posi~ao de
equilbrio,eoperodoT eveloidadeangular
0 nesta
passagem. Para isto o programaloaliza os instantes
em que o sinal na porta deu os \saltos" mostrados
na Fig.8, oloa esses tempos em uma lista (saltos),
e a partir desta lista alula os valores de t, T e
0
(variaveis t, periodo e omega). Uma tabela om os
resultados e esrita no arquivo tpo.dat. A variavel
fatorusadaparaalular
0
orrespondeaD=R(ver
se~aoV.1). Todosos temposs~ao onvertidospara
se-gundos.
aprenda analise
atribua "fator 3.3/48.8 ; valor de D/R
esreva [*** aguarde ***℄
;
; >>> Cria lista om tempos de salto
atribua "saltos [℄
abraparaler "dados.txt
mudeleitura "dados.txt
atribua "dado leialista
atribua "t0 primeiro :dado
atribua "x0 ultimo :dado
atribua "xi :x0
ateque [efimarq℄ ~
[
atribua "dado leialista
atribua "t1 primeiro :dado
atribua "x1 ultimo :dado
teste :x1=:x0
sefalso ~
[
atribua "saltos juntenofim :t1 :saltos
atribua "t0 :t1
atribua "x0 :x1
℄
℄
atribua "xf :x1
mudeleitura [℄
fehearq "dados.txt
;
; >>> Primeiro salto deve ser 0->16
se (:xi=16) [atribua "saltos sp :saltos℄
; >>>
Ultimo salto deve ser 16->0
se (:xf=16) [atribua "saltos su :saltos℄
;
; >>> Calula tempo, perodo e omega
abraparaesrever "tpo.dat
mudeesrita "tpo.dat
para [i 1 :nsaltos-6 2℄ ~
[
atribua "t1 elemento :i :saltos
atribua "t2 elemento :i+1 :saltos
atribua "t3 elemento :i+2 :saltos
atribua "t4 elemento :i+3 :saltos
atribua "t5 elemento :i+4 :saltos
atribua "t6 elemento :i+5 :saltos
atribua "periodo (:t5+:t6-:t1-:t2)/2000
atribua "omega :fator/(:t4-:t3)*1000
atribua "t (:t3+:t4)/2000
(esreva :t :periodo :omega)
℄
mudeesrita [℄
fehearq "tpo.dat
esreva [*** fim da analise ***℄
fim
Referenes
[1℄ J.C. Alves, Uma Proposta Pedagogia para Uso do
ComputadoremAmbientesdeEnsinoExperimentalde
Fsia,TesedeDoutorado,COPPE-UFRJ,2000
[2℄ M.A. Cavalante e C.R.C. Tavolaro, Projete Vo^e
Mesmo Experimentos Assistidos por Computador:
Construindo Sensores e Analisando Dados, Revista
BrasileradeEnsinodeFsia22(2000)421
[3℄ M.L.deJongeJ.W.Layman,UsingtheApple IIasa
laboratory instrument, The Physis Teaher 22 (May
1984)291
[4℄ W.M. Gonalvez, A.F. Heinrih e J.C. Sartorelli,
Aquisi~ao de dadosom aporta de jogos de
omputa-doresApple,RevistadeEnsinodeFsia13(1991)63
[5℄ J. Fuller, Siene Experimenters' Kit, http://
www.southwest.om.au/~jfuller/sikit.zip
[6℄ R.Haag,Utilizando a Plaa de Som doMiroPC no
Laboratorio Didatio de Fsia, Revista Brasileira de
EnsinodeFsia23(2001)176
[7℄ Nuleo de Informatia Apliada a Edua~ao
(Nied/Uniamp),SuperLogo3.0,
http://www.nied.uniamp.br
[8℄ G.Mills,MSWLogo,
http://www.softronix.om/logo.html
[9℄ J.Fuller,GamesPortInput,
http://www.southwest.om.au/~jfuller/logo tut/games.htm
[10℄ T. Engdal, Joystiks and other game ontrollers,
http://www.hut./Mis/Eletronis/ dos/joystik/
[11℄ R.ZelenovskyeA.Mendona,PC:umguiapratiode
hardware einterfaeamento,EditoraMZ,1999
[12℄ G.J. Deboo e C.N. Burrous, Integrated Ciruits and
SemiondutorDevies,MGraw-Hill,1977
[13℄ S.M. Sze, Physis of Semiondutor Devies, Wiley,
1969
[14℄ R.D.Peters,Experimentalomputationalphysisusing
[15℄ P.J. Collings e T.B. Greensdale, Using the omputer
asa laboratory instrument,ThePhysisTeaher(Feb
1989)76
[16℄ R.V. Ribas, A.F. Souza e N. Santos, Um sistema de
aquisi~ao de dados de baixo usto para o laboratorio
didatio, Revista Brasileira de Ensino de Fsia 20
(1998)293
[17℄ D.Fagundes, J. Sartori, T. Catunda e L.A.O. Nunes,
Usando a porta paralela do miro PC, Revista
BrasileiradeEnsinodeFsia17(1995)196
[18℄ D.F. Souza, J. Sartori, M.J.V. Bell e L.A.O. Nunes,
Aquisi~aodedadoseaplia~oessimplesusandoaporta
paralelado miroPC,RevistaBrasileiradeEnsinode