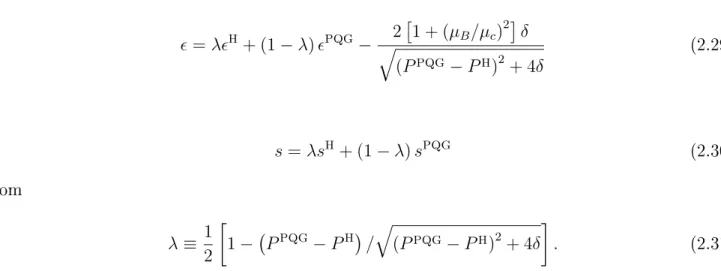Sobre a evolução hidrodinâmica da matéria nuclear criada em colisões de íons pesados...

Instituto de Físia

Sobre a evolução hidrodinâmia da matéria nulear riada

em olisões de íons pesados relativístios - um estudo om

ondições iniiais utuantes

Rone Peterson Galvão de Andrade

Orientador: Prof. Yogiro Hama

Tese de doutorado apresentada ao

Instituto de Físia para a obtenção

do título de Doutor em Ciênias.

BanaExaminadora:

Prof. Dr. Yogiro Hama(USP)

Prof. Dr. Alexandre Alaron do Passo Suaide (USP)

Prof. Dr. Fernando Silveira Navarra (USP)

Prof. a

Dra. Sandra dos SantosPadula (IFT/UNESP)

Prof. Dr. Eduardo SouzaFraga (UFRJ)

À minha esposa, Thays Correia e Silva Andrade, pelo amor dediado a mim todos os dias; pela

ompreensão, paiênia, ompanheirismo e inentivo onstantes; por reonheer o valor do meu

trabalhoe por não me deixar esmoreer diantedas diuldades.

Ao professor Yogiro Hama, meu orientador, por me ensinar que devemos areditar em nossas

própriasidéias, busandosempre aperfeição emnossostrabalhos; pormeensinar omotrilharos

aminhos daFísia.

Aoprofessor Takeshi Kodamauja generosidadesempre iluminouo meu aminho.

À professora SandraPadula pelorespeito earinho om que sempreme tratou.

Aos professores João Zaneti, Luís Carlos de Menezes e Manoel Robilotta ujos ensinamentos

ontribuíramde maneira inestimávelpara minhaformação.

Aos professores Otávio Soolowski Jr. e Bernardo Tavares eao doutorando Gabriel Deniol pela

inestimávelajuda om asquestões ténias doprograma SPheRIO.

Ao doutor Fernando Gardim por ter me ajudado a testar o programa hidrodinâmio em duas

dimensões.

Aoprofessor Jorge Noronha pelas valiosassugestõese disussões queaprimoraram este trabalho.

Aosolaboradores, professores Wei-Liang Qian,Frederique Grassi eJun Takahashi.

À equipede suportee manutençãodarede de omputadores dodepartamentode Físia

Matemá-tia - professor Jorge de Lyra, Sybele Guedes e João Borges ujo trabalho foi essenial para a

realização desta tese.

Aosfunionáriosda seretaria dodepartamento de Físia Matemátia quesempre meatenderam

À minhamãe,Josinauva DuarteGalvão,aomeupai, GumerindoAlvesde Andrade,eàsminhas

irmãs Cleonie, Elaine e Isabel.

À minha faleida avó, Jovina Barreto, ujo amor dediado a mimdurante toda aminha infânia

e juventude foiessenial para minha formação.

Ao meu primo João Augusto dos Santos Andrade pela nossa amizade e pelo arinho om que

sempre metratou.

À minha sogra, Mariana de Jesus Correia e Silva, e ao meu sogro, Nilson Correia e Silva, pela

nossa amizadee peloapoioque sempremederam.

Aomeu amigo Edvaldo Cabral pelanossa longa amizade.

À minha amiga Patríia Rebello Teles pelo exemplo de dediação e perseverança, que tanto me

inspirouem momentos difíeis.

Aos meus amigos João de Oliveira Jr., Claudeníio dos Reis Ferreira e Cesar Eugênio Miltons

pelos anos extraordináriosque passamos emCuritiba.

Ao meu amigo Mário Coneição de Oliveira pelos exelentes momentos que ompartilhamos

du-rantetodoo períodode graduação e mestrado.

Aos meus padrinhos de asamento, Edna e Mário, pela nossa amizade e pelo apoio que sempre

mederam.

Aomeu amigo Edgar Zanellaporter me ajudado om osistema operaionalLinux.

Aomeu amigo Wilson Roberto quetodos osdias mereebeu om alegria; pelas nossas onversas

sobre Santose Corinthians que sempreforammuito agradáveis.

AosamigosdoInstitutode Físiaomosquaistiveoprazerdeonviverdurantetodos estesanos:

Silas Carvalho, Marelos Peres, Pedro Tavares, Helder Casa Grande, Sandro Miheletti, Laura

Paului, Maria Isabel Veras, Eder Annibale, José Edmar, Gabriel Weber, Fernanda Pinheiro,

Danillo Liarte, Cedrik Mello, Juliano Neves, Jorgivan Dias, Matthias Moeferdt, David Fogaça,

Débora Andrade, Roberto Maluf, Paula Jaramillo, Marela Gontijo, Sergio Giardino, Walney

Fernandes, Masayuki Hase, Henrique Guidi, Luas Costa, Átilla Leães, Maion Faria, William

À Universidade de São Paulo e ao Instituto de Físia que foram minha morada nesses últimos

doze anos.

Nestetrabalhousamosummodelohidrodinâmioomondiçõesiniiaisutuanteseventoaevento

para estudar alguns observáveis em olisões de íons pesados relativístios. Mostramos que a

introdução de utuações, araterizadas por tubos longitudinais de alta densidade de energia,

tornaoálulodosobserváveismais próximodos dados,emomparaçãoàabordagemtradiional,

na qual as ondições iniiais são parametrizadas através de funções suaves e simétrias. No aso

da distribuição de partíulas em função do momento transversal, observamos um aumento do

número de partíulas na região onde

pt

&

2

.

0

GeV, omo onsequênia da expansão rápida dos tubosdealtadensidadedeenergia,prinipalmenteostubospróximosàsuperfíiedamatéria,que

hamamosdetubosperiférios. Noasode

v

2

emfunçãodomomentotransversal,observamosuma redução douxo elíptionamesmaregião,devidoàexpansãoisotrópiados tubosperiférios. No

aso de

v

2

emfunção da pseudo-rapidez,observamos,om o uso das ondiçõesiniiais utuantes, uma urva om um perl triangular muito próximo dos dados. No aso dafunção de orrelação

de duas partíulas, observamos que os tubos periférios dão origem às hamadas estruturas de

Ridge. Estas estruturas representam orrelações de longo alane, nadireção longitudinal, entre

as partíulas trigger e as partíulas assoiadas. Obtivemos uma função de orrelação om três

Ridges, respetivamente, nas posições:

∆

φ

= 0

,

∆

φ

∼

2

e

∆

φ

∼ −

2

. Mostramos, também, que o modeloreproduz ohamadoefeitoin-plane/out-of-plane,queestárelaionado omadependênia

dafunçãodeorrelaçãodeduaspartíulasemrelaçãoaoânguloazimutaldomomentodapartíula

trigger. Demodogeral,observamosque,omoajusteorretodosparâmetrosdomodelo,omopor

exemplo,adistribuiçãode densidadedeenergiainiialmédiaeatemperaturade desaoplamento,

In this work we apply a hydrodynami model with utuating initial onditions in a event by

event basis to study some observables in relativisti heavy ion ollisions. We show that the

introdution of utuations, haraterized by longitudinal high energy density tubes, turn the

omputationof theobservableslosertodata,inomparisontothe traditionalapproah,inwhih

the initialonditionsare parametrizedbyusing smoothand symmetrialfuntions. In thease of

the transverse momentum distribution,we observe anenhanement of the numberof partilesin

the regionwhere

pt

&

2

.

0

GeV, as a onsequene of the fast expansion of the high energy density tubes, mainly the tubes that are lose to the surfae of the matter, alled peripheral tubes. In

the ase of

v

2

as a funtion of the transverse momentum, we observe a redution of the ellipti ow at the same region, due to the isotropi expansion of the peripheral tubes. In the ase of

v

2

as a funtion of the pseudorapidity, we observe, by using the utuating initial onditions,

a urve with a triangular shape very lose to data. In the ase of the two partile orrelation

funtion,weobserved thattheperipheraltubesgiverise totheRidgestrutures. Thesestrutures

representa longrange orrelation,inthe longitudinal diretion,between the triggerpartilesand

theassoiatedpartiles. WegotatwopartileorrelationfuntionwiththreeRidges,respetively,

atthepositions:

∆

φ

= 0

,

∆

φ

∼

2

e

∆

φ

∼ −

2

. Inaddition,weshowthatthemodelreproduesthe in-plane/out-of-planeeet,whihisrelatedwiththetwopartileorrelationfuntiondependene

onthe azimuthalangleofthemomentumofthe triggerpartile. Generally,weobserved that,with

the properadjustmentof the parameters of the model,as, forexample, the averageinitialenergy

density and the freeze-outtemperature, allobservables disussed inthis thesis show areasonable

1 Introdução 8

2 Modelo hidrodinâmio 12

2.1 Equações de movimento . . . 12

2.2 Equação de estado . . . 13

2.3 Condiçõesiniiais . . . 19

2.4 Meanismode desaoplamento . . . 22

3 Métodos numérios 26 3.1 MétodoSPH. . . 26

3.1.1 Sistemade oordenadas hiperbólio emolisõesde íons pesados . . . 32

3.2 Desaoplamento noformalismo SPH . . . 34

3.3 ProgramaNexSPheRIO . . . 35

3.4 Modelo bidimensionalom uxo de Bjorken . . . 37

4 Alguns observáveis 43 4.1 Fluxo elíptio . . . 43

4.2 Correlação de duas partíulas . . . 47

5 Resultados 53 5.1 Janelasde entralidade . . . 53

5.2 Ajusteda distribuiçãode momentotransversal e pseudo-rapidez . . . 55

5.3 Fluxo elíptioe suas utuações . . . 60

5.4 Cálulosde orrelaçãode duas partíulas - efeitoRidge . . . 61

5.4.1 Colisõesentrais . . . 62

5.4.1.1 Resultados doNexSPheRIO . . . 62

5.4.1.2 Modelo de um tubo . . . 64

5.4.1.3 Variaçãodos parâmetros . . . 69

5.4.2 Colisõesperiférias - efeitoin-plane/out-of-plane . . . 74

5.4.2.1 Resultados doNexSPheRIO . . . 74

5.4.2.2 Modelo de um tubo . . . 76

5.4.3 Umaproposta para próton-próton . . . 81

5.5 Efeitodas ondiçõesiniiaisutuantes eventoaeventonadistribuiçãode momento

transversal eno uxo elíptio . . . 83

6 Conlusão 86

A Conservação da entropia 90

B Gás de bósons 92

C Limite ultra-relativístio 93

D Formulação variaional 96

E Equações de movimento no método SPH 98

Introdução

Colisões de íons pesados relativístios possibilitam o estudo do omportamento da matéria sob

ondiçõesextremasde pressãoe temperatura. Nestas olisões, umaquantidadegrandede energia

édepositadanumapequenaregiãodoespaço-tempo,atravésdatransformaçãode energiainétia

emenergia interna,dando origema formasde matériaom altíssimasdensidades de energia. Por

exemplo, nas olisões realizadas no RHIC 1

, os núleos podem alançar uma energia da ordem

de 100GeV por nuleon. Assim, numa olisão de dois núleos de ouro, a energia no entro de

massadosistemaseriadaordemde 2x197x100GeV=39.4TeV.Supondoquemetadedesta energia

seja depositada numa região om o volume da ordem do volume do átomo de ouro, teríamos

uma densidade de energia de aproximadamente

11

GeV/fm

3

, ou seja, duas ordens de grandeza

maior que a densidade de energia da matéria nulear ordinária. Outro exemplo é o LHC 2

, que

iniiou suas operações no segundo semestre do ano passado. Nesta máquina, os núleos podem

alançarumaenergiade3TeVpornuleon,oquelevariaaumadensidadedeenergiatrêsordensde

grandeza maiorquea densidade de energiadamatérianulearordinária. Naturalmente, oestudo

do proesso de produção de partíulas nestas olisões é de grande interesse, pois pode revelar as

propriedadesdesta matéria.

Infelizmente, ainda não existe um formalismo que reproduza integralmente o fenmeno de

produção de partíulas nestas olisões. Usualmente, divide-se o proesso de olisão em várias

etapas e se tenta entender, separadamente, ada uma delas om a teoria ou om o modelo mais

adequado. Assim, podemos desrever o proesso de olisão de dois íons pesados relativístios da

seguinteforma: iniialmenteosnúleosinidentessemovemom veloidadepróximaàveloidade

da luz. Devido a esta veloidade, eles sofrem uma intensa ontração de Lorentz. Em olisões

omoasquesãofeitasnoRHICadimensãolongitudinaldos núleoséreduzidaporum fator

γ

da ordemde 100. Portanto,adanúleo inidentepode seronsiderado omoum disoom pequena

espessura. Durante aolisão entre osonstituintes de ada núleo inidente, uma matériade alta

densidade de energia é riada nas vizinhanças do entro de massa do sistema. Os fragmentos

que não interagiram seguem sua trajetória original, levando onsigo parte da energia iniial do

1

RelativistiHeavy-Ion Collider (noBrookhavenNationalLaboratory).

2

sistema. Devidoaoproessoomplexodeinteraçãoentreaspartíulasnestamatériareémriada,

densaequente, esperamosqueum estadodeequilíbriotérmioloalsejaalançadorapidamente 3

.

Então, osistemaseexpandede aordoomasequaçõesdahidrodinâmiarelativístia. Durantea

expansão,atemperaturaderese eolivreaminhomédioentre aspartíulas aumenta. Quandoo

livre aminhomédio é suientemente grande,da ordem das dimensões do sistema,as partíulas

esapamdouido,mantendoseusmomentosinalterados. Finalmente,aspartíulasderessonânia

sofremdeaimentoseoonjuntoompostopelaspartíulasdiretasepelasoriundasdedeaimantos

alançaos detetores guardando uma memóriados estados iniiais damatéria.

Usualmente,oálulodasprimeirasinterações,quedãoorigemàmatériainiial,éfeitoatravés

de algumgeradorde eventos, assoiadoaalgummodelomirosópiodainteraçãonestasolisões.

Em nosso aso usamos o gerador de eventos Nexus [1℄, baseado no modelo de Gribov-Regge [2℄

para olisõeshadrnias. Este programapode forneerasondiçõesiniiais paraahidrodinâmia

numa hiper-superfíiede tempoprópriodouido,para qualquer par de núleosinidentes.

Deve-seenfatizarqueoobjetivodestetrabalhonão éoestudodos modelosmirosópios,masoestudo

das onsequênias, para os observáveis, da distribuiçãode matériaobtida om estes modelos.

Para aetapa de expansãohidrodinâmiausamos aaproximação de uido ideal,a qualtem se

mostradosuienteparadesreverumasériede araterístiasdosdados. Comoébemonheido,

um dos ingredientes dos modelos hidrodinâmiosé equação de estado da matéria, que relaiona

as grandezas termodinâmiasloalmente. Usamos uma equação de estado om uma transição de

fase de primeiraordem entre a fase de plasma de quarks e gluons e afase hadrnia. Em ambas

asfases,ouidoéonsideradoomoumamisturade gasesideaisemequilíbriotérmioequímio.

Inluímos, também, uma parametrização de um ponto rítio sobre a urvade transição de fase,

o queria uma regiãode rossover naregião de pequenopotenialquímio barinio.

Na etapa de desaoplamento,naqual aspartíulas esapam douido, existe uma grande

di-uldadeparaseriar,duranteaexpansãodosistema,umatransição entreosestadostermalizados

eestadosforadoequilíbrio. Estatransição éimportante, poisaspartíulasqueesapamdouido

ertamente o fazem em regiões rarefeitas onde a hipótese de equilíbrio térmio não é razoável.

Atualmente, existem modelos que usam uma abordagem mista na qual a hidrodinâmia usual é

aoplada à equação de Boltzmann [3℄. Entretanto,este tipo de abordagemestá fora daproposta

deste trabalho. Nesta tese usamos a presrição de Cooper-Frye [4℄ para o desaoplamento. Nesta

presrição, aspartíulas são emitidasrepentinamentequando atravessam umahiper-superfíiede

temperaturaonstante.

Aideiadeonsideraramatériariadanaolisãoemequilíbriotérmioe,portanto,deusar

mé-todosestatístiosparaestudaraproduçãodepartíulasemolisõeshadrniassedeveaotrabalho

pioneirode EnrioFermi[5℄. Seumodelopreviaorretamentearelaçãoentreamultipliidade 4

ea

3

A hipótese de equilíbrio térmio é difíil de ser justiada a priori, uma vez que o número de partíulas

observadasnosexperimentosémuitopequeno(daordemdemilhares). Nestatese,nãoprouraremosjustiartal

hipótesea partirdeprimeiros prinípios. No entanto, esperamosque ela sejajustiada a posteriori, atravésdo

estudoexperimental eteóriodosobserváveis.

energiainidente, oque signiouum grandeavançopara a époa. No entanto, omodelo falhava

na previsão da abundânia relativa entre os káons e os píons. Isso oorria porque as partíulas

eram emitidas de uma matéria em repouso e exessivamente quente. Devido à altatemperatura,

as abundânias relativas eram determinadas, basiamente, pelos pesos estatístios de ada

espé-ie. Assim, eleenontrou afração 4/3 para a razãoentre o número de káons eo número de píons

(quatro tipos de káons e três de píons). Contrariamente, os dados mostravam, e ainda mostram,

queaquantidadedepíons émuitosuperioràquantidadedekáons. Alémdisso,seu modeloprevia

uma distribuição angular de partíulas isotrópia, o que, também, é uma ontradição, uma vez

que, nos experimentos, observa-se uma distribuição alongadanadireção longitudinal.

Aproveitandoa ideiainovadorade Fermia respeito doequilíbrio térmioemolisões

hadrni-as, Landau propsque o problema daabundânia relativae oproblema da distribuição angular

poderiaser resolvidosea matériasofresse uma expansãohidrodinâmiaantes daemissão de

par-tíulas[6, 7℄. Deste modo, atemperaturamais baixairiafavoreera produçãode partíulas mais

leves, ospíons,aomesmotempoqueaexpansãodouidoalongariaadistribuiçãode partíulasna

direçãolongitudinal. Apesardasuasimpliidade,omodelodeLandauaindaéabase dosmodelos

hidrodinâmiosatuais. Desde asua invenção, muitos aperfeiçoamentosforam feitos,omo

disu-timos aima, nas ondições iniiais, na equação de estado e nomeanismo de desaoplamento, o

que se deve ao giganteso avanço dos omputadores e das ténias omputaionais nos últimos

sessenta anos.

Neste trabalhovamosnos onentrar nos efeitos, emalguns observáveis, das ondiçõesiniiais

utuantes obtidasomogeradordeeventos Nexus. Emborasejaomum ousode parametrizações

suaves e simétriaspara adistribuição de matériainiial, érazoável esperar que amatériariada

numa olisão seja bastante irregular,uma vez que osnúleos são formados por um número nito

de partíulas. Mostraremos que asondições iniiaisobtidas om ogerador de eventos Nexus, de

fato, são bastante irregulares, em partiular, são araterizadas portubos longitudinais om alta

densidade de energia, também onheidos omo tubos de uxo, os quais levam a efeitos muito

interessantes na função de orrelação de duas partíulas. Notavelmente, eles dão origem, nesta

função, a uma estrutura alongada na direção longitudinal, também onheida omo Ridge. O

estudo da função de orrelação de duas partíulas, no ontexto das ondições iniiais utuantes

evento a evento, éo tema prinipaldesta tese.

Pararesolverasequaçõesdahidrodinâmiarelativístia,om ondiçõesiniiaistãoirregulares

e sem simetria, um método numério espeial foi utilizado. Este método, hamado métodoSPH

[8, 9℄, é a base do programa omputaional SPheRIO 5

[10, 11℄, desenvolvido pelo nosso grupo

de pesquisa. Chamamos de NexSPheRIO a junção dos programas Nexus e SPheRIO. Com este

programa híbrido é possível alular, para qualquer par de núleos inidentes, a distribuição de

partíulasproduzidas, nãosevalendodenenhumasimetriapré-estabeleida. Resultadosanteriores

obtidos om oprograma NexSPheRIO podem ser vistosem[11, 12, 13, 14, 15℄.

A seguir, apresentamos omo esta tese está dividida.

No apítulo 2 mostramos os aspetos básios do modelo hidrodinâmio: as equações de

mo-vimento da hidrodinâmia relativístia, a equação de estado da matéria, as ondições iniiais e

o meanismo de desaoplamento. No apítulo 3 disutimos o método SPH, para modelos

tridi-mensionais e bidimensionais. No álulo bidimensional o uxo longitudinal é do tipo invariante

de boost. No apítulo 4 apresentamos os oneitos básios do parâmetro de uxo elíptio

v

2

e da função de orrelaçãode duas partíulas, quesão os objetosde estudo destetrabalho. No apítulo

Modelo hidrodinâmio

2.1 Equações de movimento

Se onsiderarmosa matéria formada naolisão omo um uido ideal, as equações de movimento

são dadas por [16, 17℄:

∂ν

T

µν

= 0

(2.1)

e

∂ν

(

niu

ν

) = 0 (

para

i

= 1

,

2

, ..., N

)

(2.2)

emque

T

µν

_{= (}

_ǫ

₊

_p

₎

_u

µ

_u

ν

−

pg

µν

(2.3)

é o tensor de energia-momento. Na relação 2.3

g

µν

é a métria 1

. As quantidades

u

ν

,

ǫ

,

p

,

ni

são, respetivamente, a quadri-veloidade do uido, a densidade de energia, a pressão e a

i-ésima densidade de arga 2

. Observe que no referenial loal, onde

(

u

ν

_{) = (1}

_,

₀

_,

₀

_,

₀₎

,

(

T

µν

_{) =}

diag

(

ǫ, p, p, p

)

. A equação2.1 representa a onservação daenergiae domomento ea equação 2.2 a onservação dai-ésima arga. Por questão de simpliidade onsideraremos o número barinio

omo aúnia arga onservada, assim

∂ν

(

nBu

ν

) = 0

(2.4)

emque

nB

é a densidade barinia.

As equações2.1e2.4formam um onjuntode 5equaçõesom 6inógnitas. Para feharmoso

sistemadeequaçõesvamosaresentaraequaçãodeestadodamatéria. Esta relaionaloalmente

as quantidades termodinâmias do uido - um exemplo seria a pressão omo uma função da

1

Usaremosaonvenção

(

g

µν

_{) =}

diag

(1

,

−

1

,

−

1

,

−

1)

. 2

densidade de energiae dadensidade barinia,

p

=

p

(

ǫ, nB

)

. Disutiremosisso naseção 2.2. Noasodeumuidoideal,umapropriedadeimportanteéaonservaçãodaentropia. Portanto,

devemos enontrar que

∂ν

(

su

ν

) = 0

(2.5)

emque

s

é adensidade de entropia (veja o apêndieA).

2.2 Equação de estado

Nesta seção desreveremos a equação de estado que usamos para a fase de plasma de quarks

e gluons (PQG) e para a fase hadrnia (H). Vamos disutir, também, o proedimento para a

riação de uma transição de fase. Iniiaremos om uma transição de primeira ordem e mais

adiante disutiremos a parametrização de um ponto rítio sobre a linha de transição, o que dá

origem auma região de rossover no diagramade fases.

Em nosso modelo supomos que ada fase é omposta por uma mistura de gases ideais em

equilíbrio térmioe químio 3

. Então, para ada uma temosque

p

(

T, µB

) =

X

i

pi

(

T, µi

)

(2.6)

om

µi

=

BiµB,

(2.7)

emque

p

(

T, µB

)

e

µB

são a pressão total e o potenialquímio barinioda mistura. As quanti-dades

pi

(

T, µi

)

,

µi

e

Bi

são, respetivamente, a pressão, o potenial químio e a arga barinia dai-ésima omponente damistura.

No ontexto do Ensemble GrandeCannio, sabemos que

pi

(

T, µi

) =

θigi

(2

π

)

3

β

ˆ

ln

1 +

θie

β

(

µ

i

−

ε

i

(

~

k

))

d

³

~k,

(2.8)

om

εi

=

q

k

2

₊

_m

2

i

,

(2.9)

em que denimos

ℏ

==1,

kB

=1,

θi

=

±

1

(+ para férmions e - para bósons),

β

=

1

T

(é o inverso datemperatura),

mi

a massa dai-ésima espéie e

gi

o i-ésimofatorde degeneresênia.

As demais quantidades termodinâmiassão dadas, naturalmente, por:

3

ni

=

∂pi

(

T, µi

)

∂µi

T

,

(2.10)

ǫi

=

₋

∂

(

βpi

(

T, µi

))

∂β

λ

i

,

(2.11)

e

si

=

β

(

pi

+

ǫi

₋

µini

)

.

(2.12)

Na relação2.11

λi

=

e

βµ

i

é afugaidade.

Pormeio das relações 2.6, 2.7e 2.10 denimos adensidade bariniada misturaomo:

nB

(

T, µB

)

_≡

∂p

(

T, µB

)

∂µB

=

X

i

∂pi

(

T, µi

)

∂µB

=

X

i

Bi

∂pi

(

T, µi

)

∂µi

=

X

i

Bini.

(2.13)

Integrando 2.8porpartes enontramos que:

pi

(

T, µi

) =

gi

6

π

2

ˆ

∞

0

k

4

p

k

2

₊

_m

2

i

1

e

β

√

k

2

+

m

2

i

−

µ

i

+

θi

dk.

(2.14)

Substituindo 2.14 e2.7 narelação 2.6enontramos que:

p

(

T, µB

) =

X

i

{

férmions

}

gi

6

π

2

ˆ

∞

0

k

4

p

k

2

₊

_m

2

i

1

e

β

√

k

2

₊

_m

2

i

−

B

i

µ

B

+ 1

dk

+

X

i

{

bósons

}

gi

6

π

2

ˆ

∞

0

k

4

p

k

2

₊

_m

2

i

1

e

β

√

k

2

+

m

2

i

−

1

dk.

(2.15)

Na relação 2.15 esrevemos separadamente a ontribuição dos férmions e dos bósons (note que

Bi

= 0

para osbósons).

Para a fase hadrnia,temos que:

p

H

(

T, µB

) =

X

i

{

férmions

}

gi

6

π

2

ˆ

∞

0

k

4

p

k

2

₊

_m

2

i

1

e

β

√

k

2

+

m

2

i

−

B

i

µ

B

+ 1

dk

+

X

i

{

bósons

}

gi

2

π

2

m

2

i

T

2

∞

X

j

=0

K

2

m

_T

i

(

j

+ 1)

(

j

+ 1)

2

.

(2.16)

Na relação2.16 aontribuiçãodos bósons pode ser integradaanalitiamente(veja o apêndieB).

Para a fase de plasmade quarkse gluons, temos que:

p

PQG

(

T, µB

) =

X

i

{

u

,

u

,

d

,

d

,

s

,

s

}

gi

6

π

2

ˆ

∞

0

k

4

p

k

2

₊

_m

2

i

1

e

β

√

k

2

+

m

2

i

−

B

i

µ

B

+ 1

+

gg

6

π

2

ˆ

∞

0

k

3

1

e

βk

₋

₁

dk

− B

.

(2.17)

Na relação 2.17 estamos onsiderando apenas os quarks u, d e s e os gluons.

B

é a pressão do

váuo nomodelode saolas(MITBag Model). Nestemodelo, apressãodogás dequarksegluons

é ontrabalaneada pelapressão dováuo 4

[20, 21℄.

Considerando

mu

=

md

= 0

,oqueéumaboaaproximaçãonohamadolimiteultra-relativístio, podemosreesrever 2.17 omo (veja apêndieC):

p

PQG

(

T, µB

) =

µ

4

B

162

π

2

+

T

2

_µ

2

B

9

+

37

90

π

2

_T

4

+

X

i

{

s

,

s

}

gi

6

π

2

ˆ

∞

0

k

4

p

k

2

₊

_m

2

i

1

e

β

√

k

2

+

m

2

i

−

B

i

µ

B

+ 1

dk

_{− B}

.

(2.18)

Na região de oexistênia das fases devemos ter que:

p

H

(

T, µB

) =

p

PQG

(

T, µB

)

.

(2.19)

Aequação2.19 deneumaurvaquedivideoplano

(

µB, T

)

emduas regiões,omoémostrado na Figura 2.1. A região do diagramaonde

p

H

(

T, µB

)

> p

PQG

(

T, µB

)

é a fase hadrnia 5

e a região

onde

p

H

(

T, µB

)

< p

PQG

(

T, µB

)

é afase de plasma de quarks e gluons.

0

0.5

1

1.5

2

µ

0

0.04

0.08

0.12

0.16

0.2

T (GeV)

(GeV)

B

PQG

H

Figura2.1: diagramade fasesno plano

(

µB, T

)

.

Na seção 2.1 menionamos que a equação de estado deveria ser aresentada ao onjunto de

equações2.1 e 2.4de modoaeliminaruma inógnitaexedente. De fato,para ambas asfases, as

relações:

4

Usamos

B

= 380

MeV/fm

3

.

nB

=

nB

(

T, µB

) =

X

i

Bini

(

T, BiµB

)

(2.20)

e

ǫ

=

ǫ

(

T, µB

) =

X

i

ǫi

(

T, BiµB

)

(2.21)

podem ser invertidas obtendo-se:

T

=

T

(

ǫ, nB

)

(2.22)

e

µB

=

µB

(

ǫ, nB

)

.

(2.23)

Então, a pressão total pode ser dada omo uma função da densidade de energia e da densidade

barinia,

p

=

p

(

ǫ, nB

)

, o quefehao sistemade equações.

Para obtermos as equações invertidas 2.22 e 2.23 sobre a urva de transição de fase, um

proedimentoadiionaléneessário. Observequenodiagrama2.1ambasasfasesestãoemontato

atravésdaurvadetransição2.19. Entretanto,mapeandooplano

(

T, µB

)

noplano

(

ǫ, nB

)

,através das relações 2.20 e 2.21, enontramos que a fase de plasma não está mais em ontato om a fase

hadrnia existindo entre elas uma região não mapeada. Esta é hamada de fase mista. Então,

para enontrarmoso ponto

(

T, µB

)

, sobre aurvade transição,assoiando aum ponto

(

ǫ, nB

)

na fase mista,fazemos oseguinte mapeamento:

s

=

s

PQG

(

T, µB

)

₋

s

H

(

T, µB

)

n

PQG

B

(

T, µB

)

−

n

H

B

(

T, µB

)

nB

₋

n

H

B

(

T, µB

)

+

s

H

(

T, µB

)

.

(2.24)

Na Figura2.2 mostramos o diagramade fases noplano

(

nB, s

)

.

0

0.4

0.8

1.2

1.6

2

n (fm )

0

4

8

12

s (fm )

-3

B

-3

PQG

Mista

H

40

50

60

70

80

90

100

110

120

130

140

150

155

160

T (MeV)

Até o momento, onstruímos uma equação de estado para a matéria formada na olisão om

umatransiçãode primeiraordementre afasede plasmade quarksegluonseafasehadrnia. No

entanto,estudos de QCD narede [22, 23℄ indiama existêniade um ponto rítiosobre a urva

de transição. Assim, na região de pequeno número barinioa transição seria do tipo rossover

(veja Figura2.3).

0

0.5

1

1.5

2

µ

0

0.04

0.08

0.12

0.16

0.2

T (GeV)

(GeV)

B

PQG

H

µ

_c

Figura 2.3: diagrama de fases no plano

(

µB, T

)

om ponto rítio.

µc

é o potenial químio bariniorítio.

Com a nalidade de estudar os efeitos da presença de um ponto rítio sobre a linha de

transição, introduzimos aseguinte parametrização daequação de estado[12,13℄:

P

₋

P

PQG

P

₋

P

H

=

δ

(

µB

)

(2.25)

emque

δ

(

µB

) =

δ

0

exp

−

(

µB/µc

)

2

.

(2.26)

Na relação 2.26

δ

0

é uma onstante e

µc

é o potenial químio barinio rítio. É importante enfatizar que esta é apenas uma parametrização fenomenológia que para o nosso objetivo de

estudar aexpansão hidrodinâmia douido ésatisfatória.

Resolvendo a equação 2.25 e usandoas relações termodinâmias2.11, 2.12 e 2.13,temos que:

P

=

λP

H

+ (1

₋

λ

)

P

PQG

+

q

2

δ

(

P

PQG

−

P

H

)

2

+ 4

δ

,

(2.27)

nB

=

λn

H

+ (1

₋

λ

)

n

PQG

−

2 (

µB/µ

2

c

)

δ

q

(

P

PQG

−

P

H

)

2

+ 4

δ

ǫ

=

λǫ

H

+ (1

₋

λ

)

ǫ

PQG

−

2

1 + (

µB/µc

)

2

δ

q

(

P

PQG

−

P

H

)

2

+ 4

δ

(2.29)

e

s

=

λs

H

+ (1

₋

λ

)

s

PQG

(2.30)

om

λ

_≡

1

2

1

₋

P

PQG

−

P

H

/

q

(

P

PQG

−

P

H

)

2

+ 4

δ

.

(2.31)

NaFigura2.4mostramosadensidadedeenergia(relação2.29),adensidadedeentropia(relação

2.30) e a pressão (relação 2.27), dadas em função da temperatura, para três valores de potenial

químio barinio. As linhas traejadas orrespondem à equação de estado sem ponto rítio

(

δ

0

= 0

)easlinhasontínuasàequaçãodeestadoompontorítio(

δ

0

6

= 0

). Comoesperado,para uma equação de estado om transição de primeira ordem as quantidades extensivas apresentam

umadesontinuidadenatemperaturade transição. Com aintroduçãodopontorítioatransição

de fase se torna ontínua e lisa na região de pequeno número barinio(

µB

.

0

.

2

GeV). Observe que onforme o potenial químio barinio aumenta, ou de forma equivalente onforme

δ

→

0

, reupera-se a transição de primeiraordem.

Na Figura2.5 mostramos a razão

s/ǫ

e a pressão, dadas em função da densidade de energia, paratrês valoresde potenialquímiobarinio. Introduzindo-seopontorítioobservamosduas

mudanças -na regiãode pequeno potenialquímiobarinio(

µB

.

0

.

2

GeV).A primeiraéquea razão

s/ǫ

sofreumaumento,oque impliaemum aumentodadensidadede partíulasdouido

6

.

A segundaéque ogradientede pressãonafasemistadeixade ser nulo, indiandoqueaexpansão

douido oorresempre de forma aelerada.

Nesta tese usamos a equação de estado om ponto rítio. Um estudo dos efeitos do ponto

rítio sobre osobserváveis é feitoem [12, 13℄.

Figura2.5: urvasde

s

ǫ

(

ǫ

)

e

p

(

ǫ

)

obtidaspormeiodaequaçãodeestadoom pontorítio(linhas ontínuas) e sem ponto rítio(linhas traejadas) [12, 13℄.

2.3 Condições iniiais

As ondições iniiais para as equações da hidrodinâmia 2.1e 2.2 são dadas pelotensor

energia-momento no referenial loal

(

T

µν

_{) =}

diag

(

ǫ, p, p, p

)

, pelaquadri-veloidade do uido

u

µ

e pelas

densidades de argas onservadas

ni

(por exemplo, arga elétria, número barinio, estranheza et.), todas essas grandezas aluladas no tempo iniial

τ

=

√

t

2

₋

_z

2

, que é o tempo,

suposta-mente, neessário para que a matériaalaneum estado de equilíbriotérmio loal 7

.

Na abordagem hidrodinâmia tradiional as ondições iniiais são funções simétrias e lisas,

parametrizadas de forma onveniente, o que orresponderia a uma média do estado iniial das

quantidades hidrodinâmias que araterizam a matéria térmia formada na olisão. Portanto,

nesta abordagem, o álulo de um observável deve ser entendido omo um valormédio assoiado

6

Noasodeumuidoidealonstituídodepíons,podemosonsiderarque

ρ

≈

αs

,emque

ρ

édensidadedepíons

e

α

éumaonstante[7℄. Lembre-seque,emolisõesdeíonspesados,ospíonssãoagrandemaioriadaspartíulas

observadas. Seamassadospíons fordesprezível,

α

= 45

ζ

(3)

/

2

π

4

≈

0

.

278

[11℄. 7

auma erta lassede eventos 8

-esolhidos, porexemplo, de aordoom oparâmetro de impato.

Assim,não selevaemonta,noálulohidrodinâmio,osefeitos dasutuaçõesquepossamsurgir

nas ondições iniiais de ada evento. Este método, que hamaremos de álulo om ondições

iniiais médias,pode ser representado daseguinte forma[11℄:

h

CI

_{i ≡}

N

ev

X

j

=1

wj

(

CI

)

_j

_{→ hOi}

,

(2.32)

emque

Nev

éonúmerode eventos,

wj

éalgum peso,

(

CI

)

j

éaondição iniialdoj-ésimoevento 9

e

O

é alguma grandeza observável. A seta india que partindode

h

CI

i

, resolvemos as equações hidrodinâmias, alulamos a distribuição de partíulas nais (disutiremos isso na seção 2.4) e,

nalmente, obtemos osobserváveis.

Uma vez que as dimensões do sistema riado na olisão são muito pequenas - ou de maneira

equivalente, onsiderando a natureza granular dos núleos inidentes - é razoável esperar que

asondiçõesiniiais

(

CI

)

j

sofram utuações onsideráveis de evento para evento, mesmoquando xamososparâmetrosdaolisãoomo,porexemplo,aenergiainidenteeoparâmetrodeimpato.

É possível até que estas utuações não sejam ompletamente aleatórias mas apresentem uma

estrutura bem denida. Sendo assim, uma maneira alternativa e mais próxima do proedimento

experimental éalularoobservável

O

aada olisãoe,posteriormente, tomaroseu valormédio.

Desta maneira podemos estudar os efeitos das utuações nos observáveis. Este método, que

hamaremos de álulo evento a evento, pode ser representado daseguinteforma[11℄:

N

ev

X

j

=1

wj

(

CI

_{→ O}

)

_j

=

_hOi

,

(2.33)

em que

(

CI

→ O

)

j

é o valor do observável

O

alulado no j-ésimo evento. Note que, agora, podemosalular adispersão doobservável, ou seja,

σ

2

_O

=

N

ev

X

j

=1

wj

(

CI

_{→ O}

)

_j

_{− hOi}

2

.

(2.34)

Para obtermos asondiçõesiniiais

(

CI

)

j

,evento a evento, éneessário adotaralgum modelo mirosópioque dê ontadas interaçõesomplexasentre as partíulasque onstituema matéria

nulear formada na olisão. Um destes modelos é o Nexus[1℄. Este gerador de eventos pode

forneerotensorenergia-momento

T

µν

,asdensidadesde orrentebarinia

j

µ

B

,de estranheza

j

µ

S

e de arga

j

µ

Q

,emadapontodoespaço,notempopróprio

τ

=

√

t

²

−

z

²

∼

1fm,paraqualquer par

de núleos inidentes 10

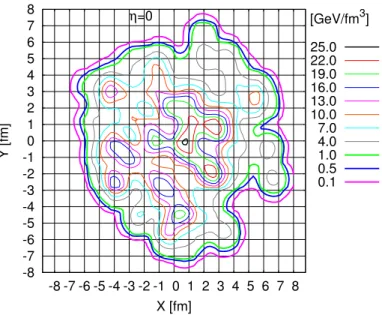
. Na Figura 2.6 mostramos a distribuição de densidade de energia iniial,

8

Nestetextoumeventosigniaumaolisãoentredoisnúleos.

9

Aondiçãoiniial

(

CI

)

j

,assoiadaaoj-ésimoevento,representaoestadoiniialdasgrandezashidrodinâmias, taisomo: densidadedeenergia,densidadebarinia,veloidadedouidoet.

10

Em nosso modelo usamos, em ada evento, adensidade de energia

ǫ

, adensidade barinia

n

B

e a quadri-veloidade

u

ν

forneidaspelo programaNexus. Atravésda equação deestado da matériaalulamos apressão,

p

=

p

(

ǫ, n

B

)

, e, assim, onstruímos o tensor energia-momento térmio

T

µν

_{= (}

_ǫ

₊

_p

₎

_u

µ

_u

ν

₋

_pg

µν

para uma olisãoentralAu+Au om energiainidentede 200AGeV,alulada om ogerador de

eventos Nexus [1℄. No gráo à esquerda mostramos a distribuição no plano transversal

ηs

= 0

11

e no gráo à direita a distribuição no plano longitudinal

y

= 0

. Na Figura 2.7 mostramos a distribuição de veloidadeiniial para o mesmoevento.

1

4

7

10

13

16

19

22

25

28

−8

−4

0

2

4

6

8

−8

−6

−4

−2

0

2

4

6

8

1

4

4

4

7

7

7

7

10

10

13

13

13

13

16

16

16

16

19

22

X [fm]

Y [fm]

[GeV/fm

3

]

η

s

=

0

1

4

7

10

13

16

19

22

25

28

−8

−4

0

2

4

6

8

−6

−4

−2

0

2

4

6

1

4

7

7

10

10

13

13

16

16

19

19

22

25

X [fm]

η

s

[GeV/fm

3

]

y = 0

Figura 2.6: distribuição de densidade de energia iniial, para uma olisão entral Au+Au om

energiainidentede200AGeV,aluladaomogeradordeeventosNexus[1℄. Nográoàesquerda

mostramosadistribuiçãonoplanotransversal

ηs

= 0

enográoàdireitaadistribuiçãonoplano longitudinal

y

= 0

.

Figura2.7: distribuiçãodedensidadedeenergiaeveloidadeiniialparaomesmoeventomostrado

naFigura 2.6.

Vemos nestes gráos que a distribuição de densidade de energia iniial, alulada om o

programa Nexus, éaraterizadapelapresença de estruturas em formade tuboslongitudinais de

alta densidade de energia, hamados de tubos de uxo. A quantidade de tubos bem omo suas

propriedades-oraio, aenergiaeaposiçãonoplanotransversal-variamaleatoriamentede evento

barinia

j

µ

B

=

n

B

u

µ

noinstante iniial

τ

= 1

fm. 11

Avariável

η

s

=

1

2

ln

t

+

z

t

−

z

para evento. Portanto,a utuaçãogerada om oprograma Nexus não é ompletamentealeatória

mas surge emforma de tubos longitudinais.

Ostubosde uxo(ou strings)representam umaparametrizaçãodoshamadossoft partons,os

quais não podem ser tratadosde modo perturbativo. O objetivo desta parametrização é estimar

a ontribuição destespartons para a distribuiçãode densidade de energia iniialdo sistema[1℄.

A m de ilustrar adisussão sobre ondiçõesiniiais médias,mostramos na Figura2.8a

den-sidade de energia iniial média, no plano transversal

ηs

= 0

(esquerda) e no plano longitudinal

y

= 0

(direita),para olisõesAu+Au om energiainidentede 200AGeV.Nesta média

onsidera-mosdezmileventosomparâmetrodeimpatoentre 5.9e7.6fm. Observequeaestrutura tubular

desaparee, aose alulara média.

0.05

1.55

3.05

4.55

6.05

7.55

9.05

10.55

12.05

−8

−4

0

2

4

6

8

−8

−6

−4

−2

0

2

4

6

8

0.05

1.55

3.05

4.55

6.05

7.55

9.05

10.55

X [fm]

Y [fm]

[GeV/fm

3

]

η

s

=

0

0.05

1.55

3.05

4.55

6.05

7.55

9.05

10.55

12.05

−8

−4

0

2

4

6

8

−6

−4

−2

0

2

4

6

0.05

0.05

1.55

1.55

1.55

3.05

4.55

6.05

7.55

9.05

10.55

X [fm]

η

s

[GeV/fm

3

]

y = 0

Figura2.8: densidade de energia iniialmédia, noplano transversal

ηs

= 0

(esquerda) e noplano longitudinal

y

= 0

(direita),paraolisõesAu+Auomenergiainidentede200AGeV.Nestamédia onsideramos dez mileventos om parâmetro de impato entre 5.9e 7.6fm.

Oobjetivoprinipaldestatese éexplorarasonsequênias,para osobserváveis, das estruturas

tubulares que araterizam as ondições iniiais do gerador de eventos Nexus. Mostraremos que

os efeitos destas utuações sempre vão no sentido de aproximar os resultados dos dados. Em

partiular, mostraremos que os tubos longitudinais estão intimamente relaionados om o efeito

RidgeobservadonaorrelaçãodeduaspartíulasparaolisõesAu+Aua200AGeVepróton-próton

a 7.0TeV.

2.4 Meanismo de desaoplamento

Omeanismode desaoplamentomais omum emmodeloshidrodinâmiosé dadopelapresrição

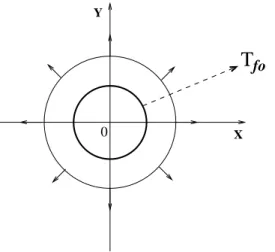
si-Figura2.9podemosveruma ilustraçãodestasituação. Observeque asisotermassão

irunferên-ias entradas naorigem.

0

X

Y

T

_fo

Figura2.9: expansãoradialde um uidonoplano

(

x, y

)

. Asisotermassão irunferênias entra-das na origem.

Conforme osistema expande ese tornamais frio,o livreaminhomédio

l

, entre as partíulas que formam ouido, aumenta. Quando

l

setorna suientemente grande, osistema, queera um uido,transforma-seemum onjunto departíulas livres. Chamamoseste proessode

desaopla-mento. Para se obter a distribuição de momento das partíulas livres (ou partíulas emitidas do

uido),as seguintes aproximações são amplamenteempregadas (presrição de Cooper-Frye [4℄):

1. Dene-se uma temperatura de desaoplamento

Tf o

, de modo que o livre aminho médio, nesta temperatura, sejada mesmaordem de grandeza das dimensõesdo sistema

12

.

2. Considera-se que uma partíulado uido se torna livrequando elaatravessa a isoterma de

temperatura

Tf o

em direçãoà regiãode baixatemperatura.

A isotermade temperatura

Tf o

é obtida,para ada instantede tempo, através daondição:

T

(

t, x, y

) =

Tf o,

(2.35)

emqueafunção

T

(

t, x, y

)

éobtidapormeiodasoluçãodasequaçõesdahidrodinâmiarelativístia (vejaseção2.1). Arelação2.35deneumasuperfíiede temperaturaonstante

Σ

. Umailustração

desta superfíie, para o aso disutido aima, enontra-se na Figura 2.10. Note que dentro da

superfíie as partíulas têm omportamento hidrodinâmio e depois de atravessá-la tornam-se,

repentinamente, livres.

12

NomodelohidrodinâmiodeLandau, paraolisõespróton-próton,atemperaturade desaoplamentofoi

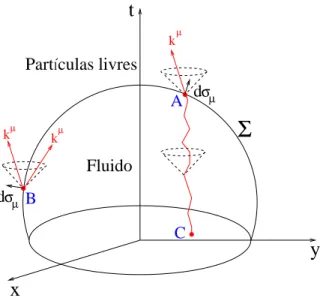
Nossoobjetivoagoraéalularonúmerototaldepartíulasemitidas. Paraissodevemosontar

onúmerodepartíulasqueatravessaaisoterma

Tf o

,emdireçãoàregiãodebaixatemperatura,em todos os instantes de tempo. Esta ontagem pode ser feitaalulando-se ouxo, na superfíie

Σ

,

daslinhasde universodas partíulasdouido(Figura2.10). Paraisso, devemosfazerasseguintes

observações:

d

σ

_µ

d

σ

_µ

k

k

µ

k

µ

µ

Fluido

l

Part culas livres

Σ

x

y

t

B

A

C

Figura 2.10: superfíie de temperatura onstante

Σ

. A linha ontínua, entre os pontos A e C, representaalinhadeuniverso deuma partíuladouido. Apósapartíulaatravessarasuperfíie

Σ

,seu momentonão émais alterado.

1. Se o vetor normal à superfíie

dσµ

for do tipo tempo (Figura 2.10, ponto A), o uxo de linhas de universo oinideom o númerode partíulas emitidas. Note que,neste ponto,as

partíulas estão sempresaindo do uido,isto é,

k

µ

_dσµ

_>

₀

.

2. Se o vetor normal à superfíie

dσµ

for do tipo espaço (Figura 2.10, ponto B), o uxo de linhasde universo nãooinide, neessariamente,om onúmerode partíulasemitidas. Isso

oorre porque algumaspartíulas podem estarretornando parao uido 13

,ou seja,podemos

ter

k

µ

_dσµ

_<

₀

_.

Para fazermos os álulos, vamos onsiderar uma situação mais geral na qual a expansão oorre

emtrês dimensões. Assim,

Σ

éuma hiper-superfíienoespaço-tempo, obtida pelaondição:

T

(

t, x, y, z

) =

Tf o.

(2.36)

Uma vez que emada ponto dahiper-superfíie

Σ

existe equilíbriotérmio loal, a densidade

de partíulas num ponto arbitráriode

Σ

édada por:

13

n

=

ˆ

f

(

T

(

~x

)

, µ

(

~x

)

, k

ν

_uν

₍

_~x

₎₎

_d

3

_~k

(2.37)

emque

f

(

T

(

~x

)

, µ

(

~x

)

, k

ν

uν

(

~x

)) =

g

(2

π

)

3

1

exp [(

k

ν

_uν

₍

_~x

₎

₋

_µ

₍

_~x

₎₎

_/T

₍

_~x

_)]

_∓

₁

.

(2.38)

Narelação2.38

uν

(

~x

)

éaquadri-veloidadedouido,

~x

= (

t, x, y, z

)

éumpontonahiper-superfíie

Σ

e

g

é o fator de degeneresênia da partíulaem onsideração. O sinal positivo está assoiado

aos férmions e onegativo aos bósons.

A partir de 2.37 podemos esrever que:

dn

=

f

(

T

(

~x

)

, µ

(

~x

)

, k

ν

_uν

₍

_~x

₎₎

_d

3

_~k.

(2.39)

Denimos a densidade de orrente de partíulas

j

µ

de modoque:

dj

µ

=

k

µ

E

dn.

(2.40)

Narelação2.40

E

=

k

0

éaenergiadapartíula. Substituindo2.39em2.40edepoisintegrando,

temos:

j

µ

=

ˆ

f

(

T

(

~x

)

, µ

(

~x

)

, k

ν

uν

(

~x

))

k

µ

E

d

3

_~k.

(2.41)

Com isso, onúmero de partíulas emitidas é dadopor

N

=

ˆ

Σ

j

µ

dσµ,

(2.42)

ouseja,

N

=

ˆ

ˆ

Σ

f

(

T

(

~x

)

, µ

(

~x

)

, k

ν

_uν

₍

_~x

₎₎

k

µ

E

dσµd

3

_~k.

(2.43)

Finalmente, através da relação 2.43, esrevemos a distribuição de momento das partíulas

emitidasda seguinte forma:

E

dN

d

3

~k

=

g

(2

π

)

3

ˆ

Σ

k

µ

_dσµ

exp [(

k

ν

_uν

₍

_~x

₎

₋

_µ

₍

_~x

₎₎

_/T

₍

_~x

_)]

_∓

₁

.

(2.44)

A relação 2.44 é onheida omo fórmula de Cooper-Frye[4℄. Na seção 3.3, disutiremos, no

Métodos numérios

3.1 Método SPH

O Método SPH 1

é a ferramenta básia que usamos para resolver as equações de movimento do

uido. Suaformulaçãoéfeitaemtermos doprinípiovariaional. Assim, iniiamosom a

formu-lação lagrangianada hidrodinâmiarelativístia[10, 24℄. Tal formulaçãoé dada pelaação

I

=

₋

ˆ

ǫ

(

nB, s

)

√

₋

gd

4

x

(3.1)

e pelas equaçõesde vínulo:

(

nBu

ν

)

_;

_ν

=

_√

1

−

g

∂ν

√

−

gnBu

ν

= 0

,

(3.2)

(

su

ν

)

_;

_ν

=

_√

1

−

g

∂ν

√

−

gsu

ν

= 0

(3.3)

e

u

ν

_uν

_{= 1}

_.

(3.4)

Naequação3.1,

ǫ

éadensidadede energiadouido,noreferenialpróprio,

x

= (

x

0

_{, x}

1

_{, x}

2

_{, x}

3

₎

éa

oordenada generalizada,

g

é odeterminante damétria

(

gµν

)

e

√

−

g

é o determinantedamatriz

jaobiana. As equações 3.2e3.3representam, omosabemos, aonservação donúmero barinio

e daentropia. A equação3.4 éa ondição de normalizaçãodaquadri-veloidade douido.

Neste formalismovamos onsiderar somenteas métriasom a seguinte forma:

(

gµν

) =

g

00

0

0

₋

g

!

,

(3.5)

emque

−

g é aparte espaialdo tensor (umamatriz 3x3).

1

Naturalmente, a i-ésima omponenteda veloidade é dadapor:

v

i

=

u

i

u

0

,

(3.6)

emque

u

0

₌

_γ

éo fatorde Lorentz generalizado.

Usando as relações 3.4, 3.5e 3.6enontramos que:

γ

=

q

1

g

00

−

[

~v

]

T

g

~v

.

(3.7)

A notação

[

~v

]

T

india quedevemos transpor ovetor

~v

.

Aapliaçãodoprinípiovariaionalàação3.1-sobosvínulosdadospelasequações3.2,3.3e

3.4-levaàsequaçõesdahidrodinâmiarelativístiaparaumsistemadeoordenadas generalizado

[24℄. No aso emque

(

gµν

) =

diag

(1

,

−

1

,

−

1

,

−

1)

obtemos aequação 2.1(veja oapêndie D). Uma vez que denimos oformalismo lagrangianodahidrodinâmiarelativístia,vamos agora

introduzir os oneitos do métodoSPH. A idéia básia deste método éparametrizar a densidade

das grandezas extensivas,que estão assoiadas aalguma arga onservada, daseguinte forma 2

:

a

∗

₍

_{~x, τ}

_{) =}

X

j

αj

W

(

~x

₋

~xj

(

τ

) ;

h

)

(3.8)

em que

a

∗

₍

_{~x, τ}

₎

é a densidade daarga

A

, vista de um referenial xo, e

τ

=

x

0

é o tempo. A

quantidade

αj

é umaonstantee

W

(

~x

−

~xj

(

τ

) ;

h

)

é umafunção positivaqueemnossaversão do métodotem as seguintes propriedades:

W

(

~x

₋

~xj

(

τ

) ;

h

) =

W

(

~xj

(

τ

)

₋

~x

;

h

)

,

(3.9)

ˆ

W

(

~x

₋

~xj

(

τ

) ;

h

)

d

3

~x

= 1

(3.10)

e

lim

h

7→

0

W

(

~x

−

~xj

(

τ

) ;

h

) =

δ

3

₍

_~x

−

~xj

(

τ

))

.

(3.11)

O parâmetro

h

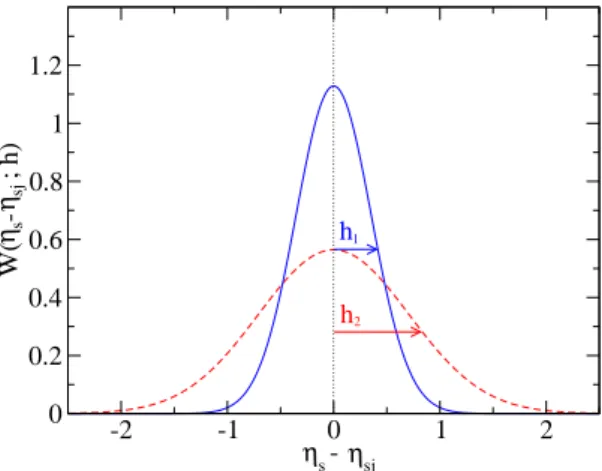
é a largura dafunção. Na Figura 3.1mostramos dois exemplos dafunção

W

. A oordenadanesteasopartiular éarapidezespaial

ηs

,queestáassoiadaàdireçãolongitudinal. As urvassão funções gaussianas.

Devemos observar que devido ao uso da propriedade 3.10, para a normalização de

W

, a den-sidade

a

∗

não é,neessariamente, uma densidade volumétria. Assim, vamos deniraquantidade

˜

a

∗

de modoque:

˜

a

∗

₌

_√

a

∗

−

g

=

d

_A

√

−

gd

3

_~x

.

(3.12)

Narelação3.12estamosimpondo,impliitamente,queadimensãode

αj

éadimensãodaargaem onsideração. Notequeoelementode volume

d

3

_~x

deveser orrigidopelomódulododeterminante

jaobiano para que

˜

a

∗

seja uma densidade volumétria 3

.

-2

-1

0

1

2

0

0.2

0.4

0.6

0.8

1

1.2

W( - ; h)

h

h

1

2

η

η

s

sj

s

η

η

-

_sj

Figura 3.1: exemplos da função

W

. A oordenada neste aso partiular é a rapidez espaial

ηs

, que está assoiada à direção longitudinal. As urvas são funções gaussianas. Quanto menor é o

valor de

h

, mais detalhada éa desrição daevolução hidrodinâmia.

Naturalmente, a transformação dadensidade de argaé dada por:

˜

a

∗

₍

_{~x, τ}

_{) =}

_γa,

(3.14)

emque

a

éadensidadedaarga

A

noreferenialloal. Usando arelação3.12podemosreesrever 3.14 omo:

a

∗

₍

_{~x, τ}

_{) =}

√

₋

_gγa,

(3.15)

o queoneta, diretamente, adensidade própria om aparametrização (ou interpolação) 3.8.

Am deganharalgumaintuiçãoarespeitodométodoSPH,vamosalularaquantidadetotal

de

A

através daparametrização 3.8. Então,

A

total

=

ˆ

a

∗

(

~x, τ

)

d

3

~x

=

ˆ

γa

√

₋

gd

3

~x

=

X

j

αj

ˆ

W

(

~x

₋

~xj

(

τ

) ;

h

)

d

3

~x

=

X

i

αi.

(3.16)

3

Demaneiraompatível,poderíamosdenirque:

ˆ

W

(

~x

−

~x

j

(

τ

) ;

h

)

√

−

gd

3

~x

= 1

,

(3.13)

oquetornariaaquantidade

a

∗

uma densidadevolumétria. Entretanto, emálulosusandoométodoSPHnãoé

Na relação3.16 a laro que troamoso uido ontínuopor um onjunto de partíulas e ada

uma delas arrega uma porção

αj

da quantidade extensiva

A

. Chamamos essas partíulas de partíulasSPH.Deve-seenfatizarquenestemétodoasoordenadasnãoestãoxasnumretiulado,

mas se movemjuntamente om o uido.

A propriedade fundamental da parametrização 3.8 é assegurar a onservação loalde

A

, não

importando omo as partíulas SPH se movemno espaço-tempo. Para ver isso, devemos derivar

a densidade

a

∗

emrelação aotempo

τ

. Assim,

∂

∂τ

a

∗

₍

_{~x, τ}

_{) =}

₋

X

j

αj

d ~

xj

dτ

· ∇

W

(

~x

−

~xj

(

τ

) ;

h

) =

−∇ ·

X

j

αj

d ~

xj

dτ

W

(

~x

−

~xj

(

τ

) ;

h

)

.

(3.17)

Considerando quea veloidadedo uido noponto

(

~x, τ

)

, nestaparametrização, é dada por

~v

(

~x, τ

) =

1

a

∗

₍

_{~x, τ}

₎

X

j

αj

d ~

xj

dτ

W

(

~x

−

~xj

(

τ

) ;

h

) =

~

Ja

(

~x, τ

)

a

∗

₍

_{~x, τ}

₎

,

(3.18)

emque

Ja

~

(

~x, τ

)

é adensidade de orrente, a equação 3.17 pode ser reesrita daseguinte forma:

∂

∂τ

a

∗

₍

_{~x, τ}

_{) =}

_{−∇ ·}

₍

_a

∗

₍

_{~x, τ}

₎

_~v

₍

_{~x, τ}

₎₎

_.

(3.19)

Substituindo a relação 3.15 em 3.19 enontramos, nalmente, a equação de ontinuidade da

arga 4

A

, ouseja,

∂ν

√

₋

gau

ν

= 0

.

(3.20)

Este resultado sugere asseguintes parametrizações:

n

∗

B

(

~x, τ

) =

X

j

βj

W

(

~x

₋

~xj

(

τ

) ;

h

)

(3.21)

e

s

∗

₍

_{~x, τ}

_{) =}

X

j

νj

W

(

~x

₋

~xj

(

τ

) ;

h

)

,

(3.22)

emque

βj

e

νj

sãoasporçõesde númerobarinioedeentropia,arregadaspelaj-ésimapartíula SPH. Deste modo, garantimos que as equações de onservação 3.2 e 3.3 sejam satisfeitas por

onstrução. Isso émuito onveniente poisparametrizando a ação 3.1emtermos das oordenadas

das partíulas SPH podemos apliar o proedimento variaional a esta ação sem nos preoupar

om as equações de vínulos.

Antes, porém, um omentário sobre a parametrização 3.22 deve ser feito. Em uidos ideais,

omomostramos noapêndie A,aentropia seonservaloalmentedurante aevolução

hidrodinâ-4

Devemosassegurar,emnossomodelo,aondição:

√