Distribuição espacial das espécies arbóreas da floresta equatorial de terra-firme.

DISTRIBUIÇÃO ESPACIAL DAS ESPÉCIES ARBÓREAS DA FLORESTA EQUATORIAL DE TERRA-FIRME.

F e r n a n d o C r i s t o v á m d a S i l v a J a r d i m (*)

RESUMO

Analiòa a diAt/Ubui.ção espacial dat> còpícieA aibóicaò com

 ΌΑΡ

maioi ou igual a 10

θ)\ em uma faloKCòta equatorial

de

tenxa- fainme, propondo um novo Índice,

de

diòpeAòão

 ΊΌ

 = 

onde

 W

c o Índice

de

diòppjiòao,

F i é α

Seqüência, abòoluta

e A B I

e

 α

abundância,

nelativa daò

e-spec-ceó,

concluindo que. exiàtem

 39

e&pecieí, com di&tfiibuição agregada, en

tne

 αλ

quail, catão a& maü> abuvidayiteA,

92

eòpecieò com di^tftibuicao oJieojtõhÁA

e 108

eò-pecieA com diitiibuição negulcüi, o que. contfioxia algun& autoieó que afainmam ich. muito ia

na a oconAmcÃjx deòòc ultimo tipo de diòtiibuição cm ^loieòtaò natwiaió.

INTRODUÇÃO

A g r a n d e h e t e r o g e n e i d a d e f l o r í s t i c a d e f l o r e s t a s t r o p i c a i s ú m i d a s o u e q u a t o r i a i s , c o m o a a m a z ô n i c a , c o n s t i t u i um d o s f a t o r e s l i m i t a n t e s ã a p l i c a ç ã o d a s v ã r i a s t é c n i c a s d e e s t u d o s f i t o s s o c i o l o g i c o s d e s e n v o l v i d a s e m o u t r o s t i p o s d e f l o r e s t a s . Em f l o r e s t a s t r o -p i c a i s , s e g u n d o G r e i g - S m i t h ( 1 9 6 7 ) , -p a r a o b t e r c e r c a d e 1 0 ¾ d e c o e f i c i e n t e d e v a r i a ç ã o d a d e n s i d a d e d e e s p é c i e s m a i s a b u n d a n t e s s e r i a m n e c e s s á r i o s p e l o m e n o s 1 0 h e c t a r e s d e a m o s t r a s , o q u e u l t r a p a s s a r i a o s l i m i t e s d e u m a v e g e t a ç ã o u n i f o r m e . P o r é m , e m e s t u d o s f í -t o s s o c i o l õ g i c o s c o m o b j e -t i v o d e ' m a n e j o f l o r e s -t a l , L a m p r e c h -t ( 1 g 6 4 ) a f i r m a q u e o -t a m a n h o da a m o s t r a n ã o d e v e s e r i n f e r i o r a 1 h e c t a r e p a r a p o d e r s e r r e p r e s e n t a t i v o .

D e q u a l q u e r f o r m a , p a r a e s t u d a r a d i s t r i b u i ç ã o e s p a c i a l d a s e s p é c i e s , B r o w e r 6 Z a r d i s t i n g u e m d o i s t i p o s p r i n c i p a i s d e m é t o d o s : o m é t o d o d o s q u a d r a d o s , q u e e n v o l v e p a r c e l a s a m o s t r a i s e o m é t o d o d a s d i s t â n c i a s q u e e n v o l v e d i s t â n c i a s e n t r e p l a n t a s o u d i ^ t â n c i a s e n t r e p l a n t a s e p o n t o s a o a c a s o . N o m é t o d o d o s q u a d r a d o s , c o n t a - s e o n ú m e r o d e i n d i v í d u o s em p a r c e l a s d i s t r i b u í d a s a o a c a s o o u s i s t e m a t i c a m e n t e a r r a n j a d a s , c o m o e m J a r _ d i m ε   H o s o k a w a  ( 1 9 8 6 ,  1 9 8 7 ) .  Q u a n d o  e s s e n ú m e r o é e x p r e s s o p o r u n i d a d e d e á r e a é d e n o -m i n a d o a b u n d â n c i a . I n i c i a l -m e n t e e s s e s r e s u l t a d o s f o r a -m e x p r e s s o s n a f o r -m a d e p a r c e l a s o u q u a d r a d o s o c u p a d o s p e l a e s p é c i e , o q u e a t u a l m e n t e r e p r e s e n t a o c o n c e i t o d e f r e q ü ê n -c i a , q u e , s e g u n d o G r e i g - S m i t h ( 1 9 5 2 ) , é p r o p o r -c i o n a l a a b u n d â n -c i a , p o r é m n ã o s e g u e uma r e l a ç ã o l i n e a r , o q u e f o i c o m p r o v a d o p o r J a r d i m ( s . d . ) , q u e e n c o n t r o u u m a r e l a ç ã o geome_ t r i c a e n t r e a a b u n d â n c i a r e l a t i v a e a f r e q ü ê n c i a a b s o l u t a d a s e s p é c i e s , e x p r e s s a p e l a

( * ) I n s t i t u t o N a c i o n a l d e P e s q u i s a s d a A m a z ô n i a - I N P A , M a n a u s - A M .

e q u a ç γ o Υ  =  a X ,  o n d e Y é a  a b u n d β n c i a  r e l a t i v a , X é a  f r e q ٧ ê n c i a  a b s o l u t a , a =  3 , 1 ^785 e 

b =  1 , 1 2 2 9 2 . 

M u i t o s  a u t o r e s ,  s e g u n d o  R o b i n s o n  ( 1 9 5 ^ ) ,  t e n t a r a m  a j u s t a r a  d i s t r i b u i ç γ o  d a s  e s p é  c i e s γ  d i s t r i b u i ç γ o  d e  P o i s s o n ,  c o n f o r m e  s u g e r i u  B l a c k m a n  ( 1 9 3 5 ) .  p o r é m ,  n a  m a i o r i a  d o s  c a s o s ,  e n c o n t r a r a m  d i f e r e n ç a s  s i g n i f i c a t i v a s  e n t r e  a s  d u a s  d i s t r i b u i ç υ e s ,  p r i n c i p a l m e n ­ t e ,  s e g u n d o  G r e i g ­ S m i t h  ( 1 9 5 2 ) ,  d e v i d o γ  d i s t r i b u i ç γ o  n γ o  a l e a t σ r i a  d e  m u i t a s  e s p é c i e s ,  o  q u e  e v i d e n c i a ,  p e l o  m e n o s ,  d o i s  t i p o s  d e  d i s t r i b u i ç γ o .  E n t r e t a n t o  B r o w e r 6  Z a r ( l 9 8 M  c a r a c t e r i z a m  t r ê s  t i p o s b á s i c o s d e d i s t r i b u i ç ã o : u n i f o r m e o u r e g u l a r , c a s u a l o u a l e a t ó -r i a e a g -r e g a d a o u c o n t a g i o s a . P a -r a c a -r a c t e -r i z á - l a s , s e g u n d o H o p k i n s  ( 1 9 5 Ό ,  n o r m a l m e n ­ t e  s e  c o m p a r a a a b u n d â n c i a o b s e r v a d a c o m a a b u n d â n c i a e s t i m a d a p e l a d i s t r i b u i ç ã o d e P o i s s o n , a t r a v é s d o " q u í - q u a d r a d o " o u d o t e s t e " t " .

N a A m a z ô n i a , V i l l a n u e v a ( 1 9 8 ? ) e C a r v a l h o ( 1 9 8 2 , 1983) u s a r a m o s m é t o d o s d e M a c G u i n e s s ( 1 9 3 * 0 , F r a c k e r & B r i s c h i e ( ) 9 ^ ) , H a z e n ( 1 9 6 6 ) e o f n d i c e n ã o - a l e a t o r i z a d o d e P a y a n d e h ( 1 9 7 0 ) p a r a a f i r m a r s e u m a e s p é c i e t e m d i s t r i b u i ç ã o a g r e g a d a o u c o m t e n d ê n c i a a a g r e g a ç ã o . P o r o u t r o l a d o , S i l v a & L o p e s ( 1 9 8 2 ) , u t i l i z a n d o o m é t o d o d a s d i s t â n c i a s d e s e n v o l v i d o p o r P i e l o u ( 1 9 5 9 ) , e n c o n t r a r a m d i s t r i b u i ç õ e s f o r t e m e n t e a g r e g a d a s p a r a n o v e d a s o n z e e s p é c i e s e s t u d a d a s , e m e s m o p a r a o t o t a l d a s e s p é c i e s , a d i s t r i b u i ç ã o f o i , d e u m a m a n e i r a g e r a l , a g r e g a d a . P o r n ã o e n c o n t r a r n e n h u m a e s p é c i e c o m d i s t r i b u i ç ã o r e g u l a r r a t i f i c o u a r a r i d a d e d e s s a d i s t r i b u i ç ã o e m f l o r e s t a s n a t u r a i s . E n t r e t a n t o , c o m o j á d e m o n s t r o u J a r d i m ( s . d . ) , s e f o r e m p l o t a d o s e m u m s i s t e m a c a r t e s i a n o a a b u n

d a n c i a  ( Υ ) ,  e m f u n ç ã o d a f r e q ü ê n c i a  ( Χ ) ,  o s  p o n t o s  d e t e r m i n a d o s  d i s t r i b u e m ­ s e  d e  t a l  f o r  ma  q u e  n a o  u l t r a p a s s a m o  l i m i t e  e s t a b e l e c i d o  p e l a  c u r v a  d e d i s t r i b u i ç ã o r e g u l a r o n d e c a d a p o n t o r e p r e s e n t a a m í n i m a a b u n d â n c i a p a r a d e t e r m i n a d a f r e q ü ê n c i a o u a m á x i m a d i s p e r s ã o . A p a r t i r d e s s a c u r v a e x i s t e um g r a d i e n t e d e d i s t r i b u i ç ã o a t é a m á x i m a a g r e g a ç ã o , e v i d e n _ c i a n d o q u e , e m f l o r e s t a s e q u a t o r i a i s c o m o a a m a z ô n i c a , e x i s t e m o s t r ê s t i p o s d e d i s t r i -b u i ç ã o m e n c i o n a d o s a n t e r í o . n e n t e e q u e , a -b u n d â n c i a e f r e q ü ê n c i a , i s o l a d a m e n t e , n a o p o d e m c a r a c t e r i z a r o p a d r ã o d e d i s t r i b u i ç ã o d a s e s p é c i e s . A s s i m s e n d o , a q u i s e p r e t e n d e i d e n t i f i c a r o t i p o d e d i s t r i b u i ç ã o d a s e s p é c i e s a r b ó r e a s d e u m a f l o r e s t a e q u a t o r i a l d e t e r -r a - f i -r m e , a t -r a v é s d e um í n d i c e d e d i s p e -r s ã o q u e -r e l a c i o n a n a m e s m a e x p -r e s s ã o a a b u n d â n _ c i a r e l a t i v a e a f r e q ü ê n c i a d a s e s p é c i e s .

MATERIAIS Ε MÉTODOS

A á r e a d e e s t u d o , o s i s t e m a d e a m o s t r a g e m e a s m e d i ç õ e s s a o a q u e l a s a p r e s e n t a d a s n a a n á l i s e e s t r u t u r a l f e i t a p o r J a r d i m £ H o s o k a w a ( 1 9 8 6 , 1987) p a r a o n í v e l I I I d e a b o r d a g e m , q u e c o b r i u o p o v o a m e n t o d e á r v o r e s c o m D A P m a i o r o u i g u a l a 2 0 c m , e m u m a f l o r e ^ t a e q u a t o r i a l d e t e r r a - f i r m e . D e s s e s r e s u l t a d o s , a q u ? f o r a m c o n s i d e r a d o s a p e n a s a a b u n d â n c i a e a f r e q ü ê n c i a , q u e t a m b é m f o r a m u t i l i z a d a s p o r J a r d i m ( s . d . ) p a r a a v a l i a r a r e

A B % 

0 . 1  0 . 2  0 . 3  0 . 4  0 . 5  0 6  0 . 7  0 ­ 8  0 . 9  1 . 0 

Pig.  1 .  R e l a ç γ o  e n t r e  a b u n d β n c i a  r e l a t i v a e  f r e q ٧ ê n c i a  a b s o l u t a  d a  e s p é c i e ,  e s t i m a d a  p o r 

d i f e r e n t e s  m o d e l o s m a t e m á t i c o s em J a r d i m ( s . d . ) .

A p a r t i r d a e q u a ç ã o g e r a d o r a a p r e s e n t a d a p o r J a r d i m ( s . d . ) f o i e s t a b e l e c i d o um í n t e r v a l o d e c o n f i a n ç a , c o m 95¾ d e p r o b a b i l i d a d e , p a r a a a b u n d â n c i a r e l a t i v a e s t i m a d a , C J J j o s v a l o r e s m é d i o s r e p r e s e n t a m a e x p e c t a t i v a m é d í a d e a b u n d â n c i a r e l a t i v a p a r a u m a d a d a

f r e q ü ê n c i a .

P a r a c a r a c t e r i z a r o t i p o d e d i s t r i b u i ç ã o e s p a c i a l d e c a d a e s p é c i e , e x p r e s s a n d o a v a r i a ç ã o c o n j u n t a d a a b u n d â n c i a r e l a t i v a ( A B % ) e f r e q ü ê n c i a a b s o l u t a ( F r ) , a q u i s e p r o

-A B ^

p õ e o í n d i c e d e d i s p e r s ã o ( l D ) , r e p r e s e n t a n d o p e l a e q u a ç ã o I D = F r , o n d e I D é o í n d j _ c e d e d i s p e r s ã o , F r e A B ¾ s ã o r e s p e c t i v a m e n t e f r e q ü ê n c i a a b s o l u t a e a b u n d â n c i a r e l a t i v a d a s e s p é c i e s , c o n f o r m e d e f i n i d a s em J a r d i m & H o s o k a w a ( 1 9 8 6 , 1 9 8 7 ) .

r e s p e c t i  v γ m e n t e . 

APRESENTAÇÃO Ε DISCUSSÃO DOS RESULTADOS

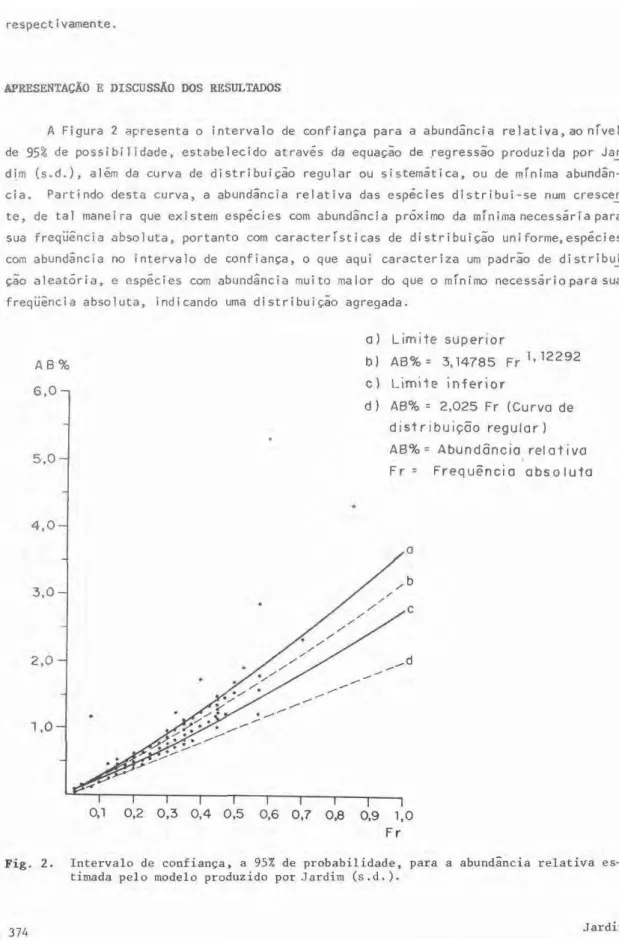
A  F i g u r a 2  a p r e s e n t a o  i n t e r v a l o  d e  c o n f i a n ç a  p a r a a  a b u n d β n c i a  r e l a t i v a ,  a o  n í v e l  d e  9 5 Ύ àe  p o s s i b i l i d a d e ,  e s t a b e l e c i d o  a t r a v é s  d a  e q u a ç γ o  d e  r e g r e s s γ o  p r o d u z i d a  p o r Ja_r  d i m  ( s . d . ) ,  a l é m  d a  c u r v a  d e  d i s t r i b u i ç γ o  r e g u l a r  o u s i s t e m á t i c a , o u d e m í n i m a a b u n d â n -c i a . P a r t i n d o d e s t a -c u r v a , a a b u n d â n -c i a r e l a t i v a d a s e s p é -c i e s d l s t r i b u i - s e n u m -c r e s -c e j i t e , d e t a l m a n e i r a q u e e x i s t e m e s p é c i e s c o m a b u n d â n c i a p r ó x i m o d a m í n i m a n e c e s s á r i a p a r a s u a f r e q ü ê n c i a a b s o l u t a , p o r t a n t o c o m c a r a c t e r í s t i c a s d e d i s t r i b u i ç ã o u n i f o r m e , e s p é c i e s c o m a b u n d â n c i a n o i n t e r v a l o d e c o n f i a n ç a , o q u e a q u i c a r a c t e r i z a um p a d r ã o d e d i s t r i b u i ^ ç ã o a l e a t ó r i a , e e s p é c i e s c o m a b u n d â n c i a m u i t o m a i o r d o q u e o m í n i m o n e c e s s á r i o p a r a s u a f r e q ü ê n c i a a b s o l u t a , i n d i c a n d o u m a d i s t r i b u i ç ã o a g r e g a d a .

A Β  % 

6 , 0Π 

5 , 0 ­

4 , 0 ­

3 , 0 ­

2 , 0 ­

1,0 

α )  L i m i t e  s u p e r i o r  b )  A B % =  3 , 1 4 7 8 5 Fr

 1 , 12 2 92 

c )  L i m i t e  i n f e r i o r 

d )  A B % =  2 , 0 2 5  F r  ( C u r v a  d e  d i s t r i b u i ç ã o r e g u l a r ) A B % = A b u n d â n c i a r e l a t i v a F r = F r e q ü ê n c i a a b s o l u t a

1 Γ _{ι ι ι ι τ  1 1} 

0 , 1  0 , 2  0 , 3  0 , 4  0 , 5  0 , 6  0 , 7  0 , 8  0 , 9  1 , 0  F r 

A  p a r t i r  d o s  v a l o r e s  d o s  l i m i t e s  s u p e r i o r e  I n f e r i o r  d o  i n t e r v a l o  d e  c o n f i a n ç a  d a  F i g u r a 2  f o i  c o n s t r u í d o o  i n t e r v a l o  d e  c o n f i a n ç a  p a r a o  í n d i c e  d e  d i s p e r s γ o  n o r m a l ( I D N )  a p r e s e n t a d o  n a  F i g u r a 3»  q u e  t a m b é m  a p r e s e n t a a  c u r v a  d o  í n d i c e  d e m á x i m a d i s p e r s ã o , ob

t i d o c o m o s v a l o r e s d a c u r v a d e m í n i m a a b u n d â n c i a . C o m o s e p o d e o b s e r v a r , d a m e s m a f o r

ma como na F i g u r a 2, p a r t i n d o d a c u r v a d e m á x i m a d i s p e r s ã o , o í n d i c e d e d i s p e r s ã o d a s e s

p ê c i e s ( I D E ) d i s t r i b u i - s e d e t a l m a n e i r a q u e e x i s t e m e s p é c i e s c o m I D E e n t r e o I D m á x i m o e o i n t e r v a l o d e c o n f i a n ç a d o Í D N , e v i d e n c i a n d o u m a d i s t r i b u i ç ã o r e g u l a r o u s ? s t errai t ic a ,

e s p é c i e s c o m I D E d e n t r o d o i n t e r v a l o d e c o n f i a n ç a , s e n d o - l h e s a q u i a t r i b u í d o o c a r á t e r a l e a t ó r i o d e d i s t r i b u i ç ã o e e s p é c i e s c o m I D E a b a i x o d o i n t e r v a l o d e c o n f i a n ç a , i n d i c a n -d o q u e e s s a s e s p é c i e s t e m u m a -d i s t r i b u i ç ã o a g r e g a -d a . T a m b é m p o -d e s e r o b s e r v a -d o n a F i g ^ j r a 3 q u e o í n d i c e d e d i s p e r s ã o ( I D ) v a r i a n o i n t e r v a l o 0 < I D < 1, p o d e n d o a l c a n ç a r o v a l o r m á x i m o q u a n d o a f r e q ü ê n c i a a b s o l u t a ( F r ) f o r m á x i m a , e t e n d e n d o p a r a o m á x i m o q u a n -d o a a b u n -d â n c i a r e l a t i v a t e n -d e p a r a o m í n i m o , n e s t e c a s o n a o a l c a n ç a n -d o o v a l o r m á x i m o .

a) Curva do ID máximo

b) Limite superior do IDN

c ) Limite inferior do IDN

Fr = Freqüência a b s o l u t a

I D = Fr

A 8 %

( í n d i c e de dispersão)

A B % = Abundância relativa

Fig.

3 .

Ί  I 1 Ί  I I I I Γ  0 , 1  0 , 2  0 , 3  0 , 4  0 , 5  0 , 6  0 , 7  0 , 8  0 , 9 1,0 

Fr 

I n t e r v a l o  d e c o n f i a n ç a p a r a o í n d i c e d e d i s p e r s ã o n o r m a l ( I D N ) e c u r v a d o í n d i c e d e m á x i m a d i s p e r s ã o .

0 Q u a d r o I a p r e s e n t a o t i p o d e d i s t r i b u i ç ã o d e c a d a u m a d a s 239 e s p é c i e s c o m D A P m a i o r o u i g u a l a 20 c m e n c o n t r a d a s p o r J a r d i m δ   H o s o k a w a ( 1 9 8 6 , 1987) em  u m a  f l o r e s t a  e q u a t o r i a l  d e  t e r r a ­ f i r m e ,  o b t i d o  p e l a c o m p a r a ç ã o d o í n d i c e d e d i s p e r s ã o d a e s p é c i e ( I D E )

embora com uma  f r e q ٧ ê n c i a  m u i t o  a l t a ( 0 , 9 5 )  a p r e s e n t a uma  a b u n d β n c i a  r e l a t i v a  m a i s da 

d u a s  v e z e s  m a i o r  q u e a  e s p e r a d a  p o r uma  d i s t r i b u i ç γ o  a l e a t σ r i a ;  ρ ί γ o z i n h o ( M i c r a n d r o p s i a 

s c l e r o x y l o n j com o menor  í n d i c e de  d i s p e r s γ o (0,066)  d e v i d o a uma  a b u n d β n c i a  t r ê s  v e z e s 

m a i o r que a  e s p e r a d a  p e l a  d i s t r i b u i ç γ o  a l e a t σ r i a ; e  a s  p a l m e i r a s , com  I D E de 0 , 0 Ί 9 ,  c u ­

j o s  ٥ n i c o s  r e p r e s e n t a n t e s com DAP  m a i o r ou  i g u a l a 20 cm  s a o  b a c a b a ( O e n o c a r p u s b a c a b a ) ,

p a t a u γ ( G e i s s e n i a b a t a u a ) e  b u r i t i ( M a u r i t i a f l e x u o s a ) , que  s a b i d a m e n t e  s σ  o c o r r e m  n a s 

b a i x a d a s  d o s  c u r s o s d'agua,  d a í  s u a  a l t a  a g r e g a ç γ o . 

C o m p a r a n d o ­ s e  o s  r e s u l t a d o s  a q u i  a p r e s e n t a d o s com  o s  r e s u l t a d o s de  V i l l a n u e v a 

( 1 9 8 l ) ,  v e r i f i c a ­ s e também  q u e  a q u i , de uma  m a n e i r a  g e r a l ,  a s  e s p é c i e s  m a i s  a b u n d a n t e s 

a p r e s e n t a r a m uma  d i s t r i b u i ç γ o  a g r e g a d a , o  q u e  r e f o r ç a a  c o n s i s t ê n c i a do  í n d i c e de  d i s p e £ 

s γ o  p r o p o s t o .  E n t r e t a n t o ,  e m b o r a  S i l v a 6  L o p e s (1982)  t e n h a m também  e n c o n t r a d o  e s s a  p r e 

d o m i n γ n c i a de  a g r e g a ç γ o  p a r a  a s  e s p é c i e s  m a i s  a b u n d a n t e s e mesmo  p a r a o  t o t a l  d a s  e s p é ­

c i e s ,  n a o  e n c o n t r a r a m nenhuma  e s p é c i e com  d i s t r i b u i ç γ o  u n i f o r m e  o u  r e g u 1  a r , a f i m n a n d o  s e r 

m u i t o  r a r a  s u a  o c o r r ê n c i a em  f l o r e s t a s  n a t u r a i s , o  q u e  a q u i  s e  d e i r o n s t r a  n a o  s e r  r e a l , 

uma  v e z  q u e  m a i s de ^5%  d a s  e s p é c i e s  a p r e s e n t o u  e s s a  d i s t r i b u i ç γ o . 

CONCLUSÕES Ε RECOMENDAÇÕES

A  u t i l i z a ç γ o da  a b u n d β n c i a  r e l a t i v a (AB%) e  d a  f r e q ٧ ê n c i a  a b s o l u t a  ( F r ) em um mo­

d e l o  g r o m e t r i c o  p a r a  e x p r e s s a r o  g r a u de  d i s p e r s γ o  d a s  e s p é c i e s é  a l t a m e n t e d e s e j á v e l ,

uma v e z q u e a v a r i a ç ã o c o n j u n t a d a s mesmas e q u e i n d i c a o p a d r ã o de d i s t r i b u i ç ã o d a s e s

r — A B ^

p e c i e s . A s s i m s e n d o , o í n d i c e de d i s p e r s ã o I D - F r 1

p r o p o s t o é b a s t a n t e c o n s i s t e n t e ,

q u a n d o c o m p a r a d o com o u t r o s m é t o d o s e m p r e g a d o s na A m a z ô n i a . P a r t i n d o de um v a l o r máx_i_

m o , o b t i d o p e l a máxima f r e q ü ê n c i a p a i a d e t e r m i n a d a a b u n d â n c i a , o u de o u t r a f o r m a , p e l a

m í n i m a a b u n d â n c i a p a r a d e t e r m i n a d a f r e q ü ê n c i a , q u e r e p r e s e n t a a máxima d i s p e r s a o o u d i s ^

t r i b u i ç a o r e g u l a r ou s i s temãt i ca , e l e d e c r e s ce com o a u m e n t o da a b u n d a η  c i a  r e i a t i  v a ,  p a s s a n ­

do  p o r unia d i s t r i b u i ç a o a l e a t ó r i a , a q u i r e p r e s e n t a d a p e l o i n t e r va l o d e c o n f i a n ç a com ~ib% de

p r o b a b i 1 i d a d e de a b u n d â n c i a ne I e o c o r r e r , a té uma d i 51 r i bu i ç a o a g r e g a d a , o n d e a a b u n d â n c i a é

i to ma i o r que 3 e s p e r a d a p a r a de t e r m i n a d a f r e q ü θ n c i a . D e s s a f o r m a , o índ i c e d e d i s p e r s ã o

de c a d a e s p é c i e ( I D E ) e v i d e n c i o u q u e e x i s t e m o s t r ê s t i p o s p r i n c i p a i s de d i s t r i b u i ç ã o ,

uma v e z q u e 39 e s p é c i e s têm d i s t r i b u i ç ã o a g r e g a d a , 92 e s p é c i e s s a o a l e a t o r i a m e n t e d i s

-t r i b u í d a s , e IO8 e s p é c i e s -têm um p a d r ã o de d i s -t r i b u i ç ã o r e g u l a r o u s i s -t e m á -t i c o .

ReccKTienda-se a u t i l i z a ç ã o do m é t o d o em o u t r a s r e g i õ e s da A m a z ô n i a e a u t i l i z a ç ã o

υ

1

qj ο .

1/1 

«3 ro Φ — — φ Ό Φ ro

1­ L­ ~ σ  V. I­ L.  L L L  "O L_ L_ Ό  L_ L_  L. L. "D l_  L> " Ο  ί— Ό  L. "D 

ID  Π 3 (Ώ Ό Φ 1ΐ ) ro ro ro <D Γ 0 13 Φ Ό Φ ro Ό  <D Φ

TO 

CD  CO Φ Ό ro . —  .— Ο Ι ' — ' —

— ·—  . —  D ) ·— — C7>  * J —  —  * J σ ι . —  c n — σ ι — c n

3  3 QJ 3 3 3  3 3 3  <D 3 3 Q3 Φ  3  3 Φ 03 3  3  OJ 3 OJ 3 OJ

σ ι σ ι »— c n ο ι σ ι c n C7> C7)  L O) OI L Q) Dl  σ ι CÜ ι ­ c n σ ι Cn  Ι ­ σ ι u

α > QJ U 3 QJ 0 ) 03

α ) α » o> c n 0 ) ai c n — oi ο ί — σ ι _<u <u cn  Ο c n OJ σ >

ι_  ι— ra ι_ ν_ »_  l_ V. 1­ (D L_ 1_  ( D flj L.  L.  I D CO L­ ί ­ I D  1­ co ι ­ <Ό 

— ­3­ ­3­ ­3· ­3­ 3­ —  ­3­­3­ — c o o c n CM — CO 

ο 

L A ­3·  c n c n

α:. > C N ν ο  ΟΑ c n c n CM c n tsi  vO ( A N Ν  —  P A  vŁ>  P A  L A c n C M  ΟΛ  r­­.  C A  C A  O O 

­ τ j  j ­  j ­ L A ­3"  L A  ­3­­3­  L A ­3­  L A  L A  L A  L A  L A  L A  \0 L A  M D  V O  V O 

Ο  o o CD ο ο .O O O  O Ό  CD CD O O  O O O  CD  Ο  CD  0 0  CD Ο 

. 3· ­3­ ­3"  ­ J "  , 5· —  ­3­ ­3­ — c n  ­ χ  ­3·  ­3­ c n r­~ c n r­» h * Γ — Γ­ ­ r­^ ­3­

>£) M D  — ­ CO CO CO  vDCOvO  —  C O sQ ­Τ  —  C O  _{3­ c n ­ τ} c n L A  L A  C A  _{C A ­ 3 ­}

­3  ­ 3 ­ ­ 3 ­ ­ 3 ­ L A ­3" ­3"  L A  L A ­3"  L A  L A  L A  L A  L A  \ Ł > 

r>. 00 

ο  ο ο ο ο ο O CD O  O  C D CD O O O  CD Ο  Ο  O  0  Ο  O CD  0 0 

c n ( Τ \ 0 Ν Ν Ν c n c n CD — —  vŁ>  vŁ>

\Q

M ) 

ο Ο  Γ ».  C A  C A  Ρ Α  O  Γ Α O  1—  C A 0 ­— r­^  C A  r­~  • —  L O  . —  xO CM  CM Ο  0 — 

J  ­ Ύ ­ ­3"  J " ­3"  ­ 3 ­ ­ 3 ­ ­ 3 ·  ­3­  ­ 3  ­ J ­  L A 3 3  ­3­  L A  L A  L A  L A  N O  r ­ ~ c o

ο ο Ο  Ο  Ο  Ο  O O CD  O O O O O O  O O O  O  C D Ο  0 0  0 0 

Ο  Ο  Ο  L A LTN  L A  O  L A O  O  L A O  L A CD  L A  Ο   L A Ο L A  CD L A  L A Ο  O  L A 

C3  D  U M ^ N f s  o t— σ 1/1 O Ν   Ι Λ Ι ­ ν  L A CM Ο  C M  Ο  L A  L A CM 

C M  CM — .  O I —  < N  C M —  — — ·— —  —  CD  CD Ο  CD Ο 

Ο  o  o α  o o  o o o  O O O O CD  C D  O O O  Ο  Ο  Ο  Ο  Ο  Ο 

­3"  L A  L A  L A  ­3­  L A r­~  L A ­3­  L A  ­ 3  L A Γ ­L A  CM  CM c n c n 0 

­— — ­3" ­3" ­3"  — ­3" —  r~­ ­3· — Ο  f"^ ­3­ N O Μ ₀  C A  Γ —  r­­ O  O  L A 

L A  L A  C A ­ 3 " ­3" ­3"  L A ­3"  L A  C A  ­ 3  L A  Ρ Α  Γ Α ­ 3 ­ Γ Α   C A  C M  Γ Α  CM  * " " • —  •— 0 

ο O O  C l O O  O O CD  O O O O O O  O O O  O  CD  CD  0 0  0 0 

M D  L A  L A  L A  L A  L A  L A Ο  Ο  Ο  Ο  Ο 

­ 3 ­ ­ 3 ­ ­ 3 ­ ­ 3 ­ ^ 3 ­ 3 ­

L A  L A  L A 

O O O  ­ 3 ­ ­ 3 ­ ­ 3 ­

L A  L A  L A  L A  L A  L A  Ο  Ο  Ο   L A  L A  L A 

­ 3 ­ ­ 3 ­ ­ 3 "  C A  C A  C A 

­ 3  ­ 3  C A  C A  Ο  Ο   L A  L A  C A Γ  A  C M  C M 

O O O O O O  O O O O O O  O O O O 

Ο  Ο 

Ο  Ο 

L A 

CM CM 

\ 0 3 Μ 

IS  " ­ O ­3­ O —  C M 

0 0 0 0 

r­~ ­3· ο  ο  — ­3­ ­3­

C A Ο  ι—  C M 

O O O  LACO Ο  Γ Ο ο

Ο  CM  C M  O O O 

Ν Ο  C O Ν Ο

V O CO ­3" 

Ι Λ  _{—  cs}  0 

_·»

·. « κ 

Ο —  a C A  O  O  O O O O  o o o o

XJ  •0  υ

<^

ji c n L A O  C M  L A  C A  —  M D ­3­ c n ί_  c ·— •Μ  O  r s C A  M D r ­ ­  C A c n \Ł> CO  C A O 

<D  _.—­ L Ü  L Ü 4> _{Ε c »} — C M  CM O — —  O — CM  C A 

OJ  Ν 

OJ  . 0 m

u  flj O 

c o c n „ r. « ­ »  „ „ _ „

,—,

υ D_  • 3 L CO  θ 0 0 O  O O O O  O  O O O O 

ί ­ 3  C L  O­O  1)  ε o L A — r­~ O  C A CM c n  C A  CO O A O CM  M D 

sz 

α ) Ο  OJ  0J O­ ί α 3 L A  L A  C A  —  ­3­  L A CM  O O  ­3­ c o  C A c n

• M  _·— Φ jŁ lO 

Q JS δ ι c O 1— *— *— C­J

CM O •— ·—  C A  _O —  C M  C M 

CO 

r: CO  L.  υ D­ Q JS _{>­ φ —}

*• —* "D  3  w  OJ r ^

PD _{C cγ  ­— C rg} 0 0 0 0  p 0 0 C D  O O O O  0  0 0 α  0 0 

CJ *J 0  _{ro >} (0 3  C A  L A « CO  0 ­3­L A  L A c n c o c n C A  _R— L A  C A ­3­  C A ­ 3 ­

(0 4­ _{c u} L. 

ro l. α  _{u c n 0}  L A O _{do ­3"}  C M  C M r­^ C M 3 Ι Λ Ν  Γ ­ — 

η

6

< —

>.

c 3  _{u υ o.—}  C M rS — ­— — —  — 0 •  P A  CM CD —  C M  C M CM 

σ ι υ QJ — _Ε Ι Λ  vO 

c in c 0  0)  _υ  Ε  3  ­ ­ 0 

c CL 3  m  u  L .  0  CJ  g 0 0 "  0  O O 0  0  O O O O  O  α  O O O O O 

(/1  3  _u ν ­ C 3  L A Γ*— O ÉS α r~­ ­3­ c n L A CO  C A  C A 1— 1  L A  C M — CM CO  C M 

ϋ Ι Λ  _{φ ·} U £1  _{ro α υ} .— CA xO  L A CM •— O v£> •— O  C ­ ( S (Ν  N C D ₀  C M ­3­ CM  M D — 

C · — —  Q .  3  ­ C  "O 0 —  C M c n 1  — 0 1  C A O O •— — C A  C M O —  C M  C M — 

L N  _ro Ν  _ro

Φ C L  u 0 CM 

— Ü _Β *J Μ 4­i  _{— u} Ρ

c 4­1 Q _>. L. FFJ L. «J .— Δ _{υ  0 0 0} O  o 0 0 0  Cl  CD O CD CD O  O  O O CD CD O  3  Q _{υ ro cn Ν}

OJ 

ro QJ 73  _φ  ­3­ ­3­ ­3­L A VO CM  M D  C A c n O CO ­3­ O C D O A  L A  • — —  C M O  Ο α ϊ _{X C} Ν

OJ 

L. 

(β ς m  C  C N  C A — CO C A  —  C M .—­ c n _­ ­ o> Ν O 

C A  _O CO — \o ­3­

>

0­

Ł 

_ J CO —  s :  —J < 0  < O — O CM  O O O — CM o o o — C A  _{O  O O} CM  C M O 

υ L­ Φ  Ο .—,^­, ,—..—. .—. .—.

3  Φ I  I  L­ Φ  * * ­Κ  ­Κ 

Φ  Í3 _α ­ c m 1 Φ  ο υ ' ' ' '  ^ — ' ­W " ^ '  '—­* — '  ——^ 

XJ Φ  Φ  —  χ : 

_φ

ι _

χ : c Ι Λ Ι Λ

0J 1/1  ( Λ  0  QJ — • —  Ο  Φ  1/1 1/1 1/1  Ι Λ  1/1 Ι/ ) Ι Λ Ι Λ α> Ι Λ 03 ι Λ

ΐ ­ I  I  1_ _{ε ο ο ω} I  L .  0) QJ 0J QJ GJ QJ 0) 0) · ­ 0) — 03

Ο­ Φ  3  •Τ Ι  L.  u ν ­ Φ Χ 3  .— .—  • —  ­ —  ­ — ·—  — υ — υ . —

ι C χ : ­ C 1) Ο ) I  Φ  >—  • — 1 ­ I  Ο ο υ ο υ υ ο υ · <ΰ  υ i ω Ο φ 'D <J _c '­ι­ > Φ  _{•—\  3}  . ­ (D ι d ) 1

0) < QJ ι α ) · α> · α> ι ο ' 0 ) Q .

>03 α . 103

Χ !  ί ­ 3  φ 1 1  X I  Φ 

.

Φ  t f Ο.  X I ν —  ο . α α CD. ο . e x α C L  Ι Λ  Q .  Ι Λ  C L  1 D _{α . c} 4­J 

ro Φ 13 _•σ 1— ι — Φ  3 <3  3  Ι Λ   Ι Λ  Ι Λ  Ι Λ Ι Λ Ι Λ ι Λ

Ι Λ α> Ι Λ 03 Ι Λ

3  ι — 0  (Λ _{σ ι}

c n ro 3  3 

.

1_  Ο 3 ~ 1  0J 0J 0 ) Q) QJ QJ QJ _{α >} 03 03

υ - ά 3 CO _c C ι  — Φ  3  _{α > QJ 3 υ} Φ  ­3­ Γ * . 

3  s í CQ 0

_{— — —}

Ε  ε  α ­ Ι ­ c o η C J  C A ­3* c n ­3" ­3" νŁ > c n M D  C M  ­3"  C M  C A 

cont i nuaçao

( Q u a d r o I ) .

N o m e V u l g a r E s p é c i e A B %

I

F r I D N I D E T i p o

N o m e V u l g a r

O B S E S T I N F S U P D i s t r i b u i ç ã o

6 l  e s p é c i e s (») 

com um  i n d i v í d u o em toda a amostragem 

0 , 0 5 1 0,050 0 , 0 2 5  0 , 8 1 6 0,844  0 , 8 2 9 

a Í e a t ó r i a

(AB|) é a abundância r e l a t i v a , observada (OBS) e estimada ( E S T ) ;

(Fr) é a f r e q ü ê n c i a a b s o l u t a o b s e r v a d a ;

— — AB% ~

(ID) é ρ í n d i c e de d i s p e r s ã o , c a l c u l a d o pela e x p r e s s ã o ID = Fr ° , se for u t i l i z a d a AB% OBS é chamado í n d i c e de d i s p e r s ã o da

e s p é c i e ( I D E ) , caso seja AB% EST é então chamado í n d i c e de d i s p e r s ã o normal ( I D N ) , onde ABIEST = 3,14785 x F r l > 2 2 9 2 . | D N

INF. e IDN SUP. são o s l i m i t e s de c o n f i a n ç a para o IDN para 9 5 1 de p r o b a b i l i d a d e .

(··') o número r e p r e s e n t a o c ó d i g o d e s s a s e s p é c i e s em Jardim & Hosokawa ( 1 9 8 6 / 8 7 ) ;

SUMMARY

An anatyòiò ο& the òpatial dibtfú.butx.on o& tk.ee òpeeleò in an equatofUal faoAeòt

on tehxa-^ihme waò made with neganA to new cLLbpeAòi-on index

IV

 =  F t '

whesie

TV

 .υς

the

diapeAAion Index,

FA ÍÁ

fae.que.ncy and AB% ,a> the Aetative abandonee., concluding that

thehe. ate

 39

òpeeleò with

  a g g r e g a t e

cLLòtAtbutton, 92 òpecÁeò with random dÁAtAihution and

70S

òpecteò ani^oAm

OA

AegataA diòtAibutton opposing to many AeòeaAcheAÁwh-ich have

ai^i/vm that the loot one ietdon

  o c c a / i

in natwie.

Referências bibliográficas

Blackman, G. E . - 1935. A study of the distribution of species in grassland associa-tions. A n n . Bot., 49:749.

Brover, J. E. & Z a r , J. H. - 1984. Field & Laboratory methods for general ecology..2 ed. Dubuque, Iowa, W m . C. Brown Publishers. 334p.

Carvalho, J. 0. P. de - 1982. Análise estrutural da regeneração natural em floresta tro

picai densa na região do Tapajós n o Estado d o Pará. Curitiba. Tese de Mestrado.UFPr.

63p.

_ 1983. Abundância, freqüência e grau de agregação do pau-rosa (Aniba duckei Kos~

termans) na floresta Nacional do Tapajós. (EMBRAPA/CPATU). Boletim de P e s q u i s a ,( 5 3 ) : 1-18.

Fracker, S. & Brischle, H. - 1944. Measuring the local distribution of shrubs. Ecology,

25:283-303.

Greig-Smith, P. - 1 9 5 2 . The u s e of random and contiguous quadrats in the study of the structure of plant communities. A n n . Bot., 16(62):293-316.

Greig-Smith, P.j A u s t i n , M. P.; W h i t m o r e , T. C. - 1 9 6 7 . The application of quantitative methods to vegetation survey. I. Association-analysis and principal component ordina tion of rain forest. J. Ecol., 55(2):483-503.

Hazen, W. E . - 1966. Analysis of spatial pattern in epiphytes. Ecology, 47(4):634-635.

Hopkins, B. - 1 9 5 4 . A new method for determining the type of distribution of plant in-dividuals. A n n . Bot., 18(70):213-227.

Jardim, F. C. da S. ( s . d . ) . A relação entre abundância e freqüência na floresta equato rial de terra-firme. Acta Amazônica [no p r e l o ] .

Jardim, F. C. da S. & Hosokawa, R. T. - 1986/1987. Estrutura da floresta equatorial úmi da d a Estação Experimental de Silvicultura Tropical do INPA. Acta Amazônica,16/17(n? único):411-508.

Lamprecht, H. - 1 9 6 4 . Ensayo sobre la estructura floristica de la parte sur-oriental dei Bosque Universitário El Caimital, Estado Barinas. Rev. F o r . V e n . , 7 ( 1 0 1 1 ) : 7 7 -119.

Mac Guiness, W. G. - 1 9 3 4 . The relationships between frequency index and abundance as applied to plant populations in a semi-arid region. Ecology, 15:263-382.

Payandeh, B. - 1970. Comparison of method for assessing spatial distribution of trees.

Pielou, Ε. C. - 1959. The use Df point to plant distances in study of pattern of plant populations. J. E c o l ., 47(3):607-613.

Robinson, P. - 1954. The distribution of plant populations. A n n . Bot., 18(69):35-45.

Silva, J. Ν. M. & L o p e s , J. do C. A. - 1982. Distribuição espacial de arvores na Flo-resta Hacional do Tapajós. (EMBRAPA/CPATU). Circular Técnica, 26:1-4.

Villanueva, A. G. - 1981. Avaliação estrutural e quantitativa de uma floresta tropical

úmida em Iquitos-Peru. Curitiba. Tese de Mestrado. U F P t . 144p.