Modelo de tempo de falha acelerado com fração de cura : uma abordagem unificada

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIˆENCIAS EXATAS E DA TERRA

PROGRAMA DE P ÓS-GRADUA ¸C ÃO EM MATEM ÁTICA APLICADA E ESTATÍSTICA

MODELO DE TEMPO DE FALHA ACELERADO COM FRA ¸C ˜AO DE CURA

UMA ABORDAGEM UNIFICADA

Alysson L´ıvio Vasconcelos Guedes

(2)

MODELO DE TEMPO DE FALHA ACELERADO COM

FRA ¸

C ˜

AO DE CURA

UMA ABORDAGEM UNIFICADA

Alysson L´ıvio Vasconcelos Guedes

´

Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica

Orientadora: Profa_{. Dr}a_{. Dione Maria Valen¸ca}

Disserta¸c˜ao apresentada ao Corpo Docente do

Programa de Pós-Gradua¸cão em Matemática

Aplicada e Estat´ıstica - CCET - UFRN, como

requisito parcial para obten¸c˜ao do t´ıtulo de

Mestre em Matem´atica Aplicada e Estat´ıstica.

Natal, outubro de 2011

(3)

Fazei, pois, descer de vosso santo c´eu a sabedoria, e envia-a do trono de vossa gl´oria, para que, junto de mim, tome parte em meus trabalhos.

Sabedoria 9-10

(4)

Catalogação da Publicação na Fonte. UFRN / SISBI / Biblioteca Setorial Centro de Ciências Exatas e da Terra – CCET.

Guedes, Alysson Lívio Vasconcelos.

Modelo de tempo de falha acelerado com fração de cura: uma abordagem unificada / Alysson Lívio Vasconcelos Guedes. - Natal, 2011.

52 f. il.:

Orientador(a): Profa. Dra. Dione Maria Valença.

Dissertação (Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Programa de Pós-Graduação em Matemática Aplicada e Estatística.

1. Análise de sobrevivência – Dissertação. 2. Programa computacional R – Dissertação. 2. Fração de cura – Dissertação. 3. Câncer de mama – Dissertação. I. Valença, Dione Maria. II. Título.

(5)

Agradecimentos

Agrade¸co a Deus pai e a Santa Maria por todas as bˆen¸c˜aos que recebi em toda a

minha vida.

Agrade¸co a toda paciˆencia e aten¸c˜ao da minha orientadora Dione Maria Valen¸ca

que com um cora¸c˜ao de m˜ae soube orientar este trabalho. `

A minha amada mãe, à minha madrinha Socorro e aos meus irmãos por serem fonte

de amor e apoio em toda minha vida. Agrade¸co especialmente ao meu pai, que como

exemplo de homem de caráter, deu sua vida à doar-se pela fam´ılia e ao próximo.

Aos meus amigos e companheiros de mestrado Juliane Caroline, Kelly Christina,

Kaline Nascimento, Tatiane Farache, Jeane Lima, Cl´audia Macedo, Daniel Matos e

todos os demais pela amizade e pelo acolhimento. `

A Nara Ang´elica e a toda fam´ılia Mesquita por serem como uma fam´ılia pra mim

nessa etapa final do trabalho.

Aos meus amigos de toda a vida Gedvan Dias, Luciana Vital, Thiago Gouveia,

Nadja Cristina, Marcus Vin´ıcius, Nailson Cunha e aos irm˜aos Curvelo. `

A todos os professores e servidores do PPGMAE. `

A Capes pelo apoio financeiro.

(6)

Resumo

Neste trabalho apresentamos um estudo sobre o modelo de tempo de falha acelerado

gama generalizado com fra¸c˜ao de cura sob uma abordagem unificada. O modelo se

propõe a estimar simultaneamente o efeito de covariáveis na acelera¸cão/desacelera¸cão

do tempo até a ocorrência de um evento e na fra¸cão de cura. O método é implementado

nosoftware estat´ıstico livre R. Por fim o modelo é aplicado a dados reais referente ao tempo até o retorno da doen¸ca em pacientes diagnosticados com câncer de mama.

Palavras-chave: Análise de sobrevivência , Fra¸cão de cura, Câncer de mama

(7)

Abstract

In this work we study the accelerated failure-time generalized Gamma regression

models with a unified approach. The models attempt to estimate simultaneously the

effects of covariates on the acceleration/deceleration of the timing of a given event and

the surviving fraction. The method is implemented in the free statistical software R.

Finally the model is applied to a real dataset referring to the time until the return of

the disease in patients diagnosed with breast cancer.

Keywords: Survival analysis , cure fraction, breast cancer

(8)

Sum´

ario

1 Introdu¸c˜ao 1

1.1 Objetivos . . . 2

1.2 Descri¸c˜ao dos cap´ıtulos . . . 3

2 Análise de Sobrevivência 4 2.1 Conceitos fundamentais de Análise de Sobrevivência . . . 4

2.1.1 Fun¸c˜ao de sobrevivˆencia . . . 5

2.1.2 Fun¸c˜ao taxa de falha ou fun¸c˜ao risco . . . 5

2.1.3 Censura . . . 5

2.1.4 Representa¸c˜ao dos dados de sobrevivˆencia . . . 6

2.2 Modelos de Tempo de Falha Acelerado . . . 8

3 Modelos de Sobrevivência com Fra¸cão de Cura 9 3.1 Modelo de Mistura Padrão . . . 10

3.2 Modelo de tempo de promo¸c˜ao . . . 11

3.3 Modelo Unificado . . . 12

3.4 Alguns casos particulares do modelo unificado . . . 14

3.4.1 Modelo de Mistura Padr˜ao . . . 15

3.4.2 Modelo de Tempo de Promo¸c˜ao . . . 16

3.4.3 Fun¸c˜ao de Verossimilhan¸ca . . . 16

3.4.4 Verossimilhan¸ca Marginal . . . 19

3.5 Incluindo Covari´aveis na Fra¸c˜ao de Cura . . . 20

3.5.1 Fun¸c˜ao de Verossimilhan¸ca . . . 21

(9)

4 Modelos de tempo de falha acelerado com fra¸c˜ao de Cura: Uma

abor-dagem unificada 22

4.1 Regress˜ao log-gama generalizada . . . 22

4.2 MTFA incluindo covari´aveis na fra¸c˜ao de cura . . . 24

4.3 Casos Particulares do MTFA com fra¸c˜ao de cura unificado . . . 26

4.3.1 MTFA l.g.g. com modelo de mistura padr˜ao . . . 26

4.3.2 MTFA l.g.g com Modelo de Tempo de Promo¸c˜ao . . . 27

4.4 Estimando os parˆametros . . . 28

5 Reprodu¸cão de resultados e Aplica¸cão 30 5.1 Reprodu¸cão de resultados . . . 30

5.1.1 MTFA l.g.g. com modelo de mistura padr˜ao . . . 30

5.1.2 MTFA l.g.g. com modelo de tempo de promo¸c˜ao . . . 31

5.2 Aplica¸c˜ao . . . 32

5.3 Descri¸c˜ao das covari´aveis . . . 33

5.4 Ajuste de modelos sem fra¸c˜ao de cura . . . 34

5.5 Ajuste dos MTFA l.g.g. padr˜ao com fra¸c˜ao de cura . . . 37

6 Considera¸cões finais 39 A Comandos no R 41 A.1 Regressão Log-gama Generalizada com covariáveis . . . 41

A.2 MTFA l.g.g com Modelo de Mistura Padr˜ao . . . 44

A.3 MTFA l.g.g com Modelo de Tempo de Promo¸c˜ao . . . 45

B Demonstra¸cões 48 B.1 Fun¸cão de sobrevivência populacional . . . 48

B.2 Casos particulares do Modelo Unificado . . . 49

B.2.1 Modelo de Mistura Padr˜ao . . . 49

B.2.2 Modelo de Tempo de Promo¸c˜ao . . . 49

(10)

Cap´ıtulo 1

Introdu¸

c˜

ao

Em modelos de sobrevivˆencia, estamos interessados em estudar o tempo at´e a

ocor-rˆencia de um evento de interesse comumente chamado ”tempo at´e a falha” ou ”tempo

de vida”. Porém, em algumas situa¸cões, uma propor¸cão da popula¸cão pode ser

con-siderada ”curada”, ou seja, alguns indiv´ıduos n˜ao est˜ao mais sujeitos ao evento de

in-teresse. Os modelos que tratam desta abordagem s˜ao chamados de modelos de fra¸c˜ao

de cura. Um grande número de observa¸cões censuradas à direita em um per´ıodo de

acompanhamento suficiente, pode ser um indicativo da presen¸ca de indiv´ıduos curados

na popula¸c˜ao. Por exemplo, em estudos sobre a recidiva de determinados tipos de

câncer, muitos pesquisadores consideram que um paciente estará curado se não houver

reincidência da doen¸ca num per´ıodo de 5 a 10 anos após aplica¸cão de tratamentos,

sendo este tempo determinado pela experiˆencia do pesquisador.

Modelos de sobrevivˆencia com fra¸c˜ao de cura tem sido extensivamente discutidos

na literatura estat´ıstica por v´arios autores. Uma abordagem dada inicialmente por

Boag (1949) e Berkson e Gage (1952) , considera uma mistura de distribui¸c˜oes. Neste

modelo, conhecido como modelo de mistura padrão, é assumido que uma fra¸cão π da popula¸cão está curada, e a restante 1−π, não curada. O livro de Maller e Zhou (1996) apresenta diversas referências sobre trabalhos que abordam modelos de mistura.

Alternativamente, Yakovlev et al. (1993) prop˜oem uma nova classe de mistura

en-volvendo uma estrutura de riscos competitivos, que foi estendida por Chen et al. (1999),

(11)

1.1 Objetivos 2

o qual nos referimos como modelo de tempo de promo¸cão. Uma abordagem unificada, que inclui o modelo de mistura padrão e o modelo de tempo de promo¸cão como dois

casos especiais, ´e discutido em Rodrigues et al. (2009). Neste contexto, a distribui¸c˜ao

assumida para a vari´avel latente, representando o n´umero de causas que competem para

a ocorrˆencia do evento, determina uma classe de modelos. As distribui¸c˜oes Bernoulli e

Poisson representam respectivamente os modelos de mistura e de tempo de promo¸c˜ao.

Yamaguchi (1992) prop˜oe uma extens˜ao dos modelos de tempo de falha acelerado

log-Gama generalizada com fra¸c˜ao de cura inserido na forma de modelo de mistura,

considerando também a fra¸cão de cura como fun¸cão das covariáveis. Em uma

abor-dagem semelhante, Ortega et al. (2009) propõe uma extensão para modelos de regressão

Gama Generalizada incluindo fra¸c˜ao de cura em um modelo de tempo de promo¸c˜ao,

al´em de apresentar resultados sobre influˆencia local e res´ıduos para este modelo.

1.1 Objetivos

Neste trabalho, partindo da abordagem unificada dada em Rodrigues et al. (2009)

estudamos as extens˜oes dos modelo de regress˜ao Log-Gama Generalizada dadas por

Yamaguchi (1992) e Ortega et al. (2009), propondo ent˜ao uma ´otica unificada para

essas extens˜oes. Em seguida apresentamos de forma diferenciada o ajuste destes

mo-delos atrav´es do software estat´ıstico R (R Development Core Team 2011). Aplicamos

esta abordagem em um conjunto de dados reais obtidos de Macedo e Valen¸ca (2009),

contendo informa¸c˜oes a respeito de 355 pacientes com cˆancer de mama atendidas no

Hospital Prof. Dr. Luiz Antˆonio, Natal RN, no per´ıodo de 1991 `a 1995, para estudar

o efeito de covari´aveis no tempo em que as pacientes permanecem livres do retorno da

doen¸ca bem como seus efeitos sobre a fra¸c˜ao de cura, ap´os terem sido submetidas ao

(12)

1.2 Descri¸c˜ao dos cap´ıtulos 3

1.2 Descri¸

c˜

ao dos cap´ıtulos

No Cap´ıtulo seguinte mostramos uma breve introdu¸cão à análise de sobrevivência

e seus principais conceitos. No Capitulo 3 abordamos os modelos cl´assicos de fra¸c˜ao

de cura e o modelo unificado proposto por Rodrigues et al. (2009). No quarto

cap´ı-tulo abordamos os modelos propostos por Yamaguchi (1992) e por Ortega et al. (2009)

que estendem o modelo de tempo de falha acelerado log-gama generalizado associando

covariáveis tanto ao tempo de vida quanto à fra¸cão de curados. Através dessa ótica

discutimos um modelo unificado para os modelos de tempo de falha acelerado com

fra¸c˜ao de cura. No Capitulo 5 ajustamos os modelos a dados reais atrav´es do software

estat´ıstico R, reproduzindo inicialmente as aplica¸c˜oes dadas por Yamaguchi (1992) e

Rodrigues et al. (2009). Guardamos os comandos usados no R para o Apˆendice A e

al-gumas demonstra¸cões para o Apêndice B. Reservamos para Capitulo 6 as considera¸cões

(13)

Cap´ıtulo 2

An´

alise de Sobrevivˆ

encia

Neste cap´ıtulo fazemos uma breve introdu¸c˜ao aos principais conceitos de an´alise

de sobrevivˆencia e ao Modelos de Tempo de Falha Acelerado.

2.1 Conceitos fundamentais de An´

alise de

Sobre-vivˆ

encia

A análise de sobrevivência tem um papel importante em várias áreas de

conhe-cimento como engenharia e ciências biológicas. Sua variável de interesse é o tempo

até a ocorrência de um certo evento, também chamado de tempo de vida ou tempo

at´e a falha podendo ser, por exemplo, o tempo de dura¸c˜ao de um certo componente

eletrônico, o tempo até a morte de um paciente, ou ainda, o tempo até o retorno de

uma doen¸ca (recidiva) em um paciente.

A variável aleatória T corresponde ao tempo até a ocorrência de um determinado evento de interesse de alguma popula¸cão. ParaT devemos definir: o tempo de in´ıcio, como a data de in´ıcio do estudo por exemplo; a escala de medida, que é em geral o

tempo do estudo, podendo ser outra medida como quilometragem de um carro; e um

evento de interesse, como a morte do paciente.

(14)

2.1 Conceitos fundamentais de An´alise de Sobrevivˆencia 5

2.1.1 Fun¸

c˜

ao de sobrevivˆ

encia

SejaT uma variável aleatória cont´ınua, não negativa com fun¸cão densidade de pro-babilidadef(t) e fun¸cão distribui¸cão acumuladaF(t). Definimos a fun¸cão sobrevivência deT como:

S(t) =P(T > t) =

Z t

0

f(u)du= 1−F(t) t >0. (2.1) Note que S(t) é uma fun¸cão monótona decrescente com S(0) = 1 e

S(∞) = limt_→∞S(t) = 0.

2.1.2 Fun¸

c˜

ao taxa de falha ou fun¸

c˜

ao risco

A fun¸cão risco corresponde à taxa de falha instantânea no momento t.

h(t) = lim

∆t→0

P(t ≤T < t+ ∆t|T ≥t)

∆t

= lim

∆t→0

1 ∆t

P(t≤T < t+ ∆t)

P(T ≥t) = lim

∆t→0

1 ∆t

F(t+ ∆t)−F(t)

S(t)

= 1

S(t)∆limt→0

F(t+ ∆t)−F(t)

∆t

= 1

S(t)F

′₍_t_{) =} f(t)

S(t).

(2.2)

Da defini¸c˜ao dada na equa¸c˜ao (2.1) temos ainda que:

f(t) =−dS(t)

dt . (2.3)

2.1.3 Censura

Uma ocorrência frequente em dados de sobrevivência é a presen¸ca de censura, que é

caracterizada pela observa¸c˜ao apenas parcial da resposta. Isto se refere a situa¸c˜oes em

(15)

a observa¸c˜ao n˜ao pode ser mais acompanhada ou devido ao final do experimento. Isto

significa que toda informa¸c˜ao referente `a resposta se resume ao conhecimento de que

o tempo de falha ´e superior `aquele observado. Sem a presen¸ca de censura, as

técni-cas estat´ıstitécni-cas clássitécni-cas, como análise de regressão e planejamento de experimentos,

poderiam ser utilizadas na an´alise deste tipo de dados, provavelmente usando uma

transforma¸c˜ao para a resposta.

Tipos de censura

O tipo de censura mais comum é a censura à direita. É dito à direita pois o tempo

até a ocorrência do evento de interesse é superior ao tempo registrado. Desprezar essa

informa¸c˜ao faria com que o risco de ocorrˆencia do evento de interesse fosse

superesti-mado, pois o tempo até a falha é desconhecido, mas o evento de interesse não ocorreu

até o último momento observado. Os três mais conhecidos mecanismos de censura à

direita s˜ao:

• Censura do Tipo I: O estudo será terminado após um per´ıodo pré-estabelecido

de tempo. As observa¸c˜oes para os quais o evento de interesse n˜ao foi observado

at´e este tempo s˜ao ditas censuradas;

• Censura do Tipo II: O estudo ser´a terminado ap´os ter ocorrido o evento de

interesse para um número pré-estabelecido de observa¸cões;

• Censura Aleat´oria: Ocorre se a observa¸c˜ao for retirada no decorrer do estudo

sem ter ocorrido o evento de interesse ou se o evento de interesse ocorrer por uma

raz˜ao diferente da estudada.

2.1.4 Representa¸

c˜

ao dos dados de sobrevivˆ

encia

Considere uma variável aleatória positiva T representando o tempo até a falha e

(16)

T∗ =min(T, C) e al´em disso definimos uma indicadora de forma

δ=







1 se T ≤C

0 se T > C

A representa¸cão dos dados para o i-ésimo individuo, sendo i = 1, . . . , n, é o par (t∗

i, δi), sendo t∗i o valor observado de T∗ para o individuoi e δi vari´avel indicadora de

censura definida acima.

Considere, como ocorre na pr´atica, a sobrevivˆencia dos pacientes portadores de

alguma doen¸ca associada a informa¸c˜oes (caracter´ısticas) como o tipo de tratamento

usado, idade, etc. Para tratar da dependˆencia dos tempos de sobrevivˆencia com estas

informa¸c˜oes auxiliares associamos a cada indiv´ıduo um vetor de medidas (vari´aveis

discretas ou cont´ınuas), chamado geralmente de vetor de covari´aveis, e denotado por

x= (1, x1, . . . , xp)′.

Assim os dados de sobrevivˆencia s˜ao da forma:

t δ x1 · · · xp

t1 δ1 x11 · · · x1p

... ... ... ... ...

tn δn xn1 · · · xnp

Uma maneira de determinar o relacionamento entre o tempo de sobrevivˆencia e as

covariáveis é através de um modelo de regressão. Uma classe importante de modelos

de regressão para tratar de dados de sobrevivência é a classe dos Modelos de Tempo

(17)

2.2 Modelos de Tempo de Falha Acelerado 8

2.2 Modelos de Tempo de Falha Acelerado

Considere os modelos de posi¸c˜ao e escala caracterizados pelo fato que Y = logT

possui um distribui¸cão com parâmetro de posi¸cão µe de escala σ. Desta forma temos

Y =µ+σǫ, (2.4)

sendo−∞< µ <∞ eσ > 0.

Considerando a presen¸ca de p covari´aveis, assumimos que µ = µ(x) = x′β sendo

x = (1, x1, . . . , xp)′ um vetor de covari´aveis e β = (β0, β1, . . . , βp)′ um vetor de

parâ-metros desconhecidos. Sejam g(·) e G(·) as fun¸cões densidade de probabilidade e de sobrevivência de ǫ respectivamente, então a fun¸cão densidade de probabilidade de Y

para um dado vetor de covari´aveis xser´a dada por

f(y;x,β, σ) = 1

σg

y−x′β σ

− ∞< y <∞, (2.5) e a de sobrevivˆencia por

S(y;x,β, σ) =G

y−x′β σ

− ∞< y <∞, (2.6) Desta forma o modelo 2.4 é um modelo log-linear paraT com res´ıduoǫ. Chamamos este modelo de Modelo de Tempo de Falha Acelerado devido ao fato que as covariáveis têm a fun¸cão de acelerar ou desacelerar o tempo de ocorrência do evento

(18)

Cap´ıtulo 3

Modelos de Sobrevivˆ

encia com

Fra¸

c˜

ao de Cura

Os modelos clássicos de Análise de Sobrevivência pressupõem que quando o tempo

vai para o infinito a probabilidade de sobrevivˆencia ´e igual a zero (limt_→∞S(t) = 0).

Quando a probabilidade de sobrevivˆencia no infinito ´e diferente de zero (limt→∞S(t) =π)

interpretamos esta quantidadeπ > 0 como uma fra¸cão de curados (Miller et al. 1981). Não podemos observar o conjunto de dados no infinito, porém para alguns casos a

existência de uma fra¸cão de cura parece ser bem razoável. Por exemplo tome o tempo

até que um casal recém casado se divorciar ou o tempo até a conclusão de curso de

um estudante. Esses eventos podem nunca acontecer. Ou seja, existe uma parcela da

popula¸c˜ao que chamamos de “imune ao evento”. Entendemos por imunes os indiv´ıduos

que não estão sujeitos à ocorrência do evento de interesse. Em algumas situa¸cões, como

pacientes de cˆancer, podemos usar a terminologia curados.

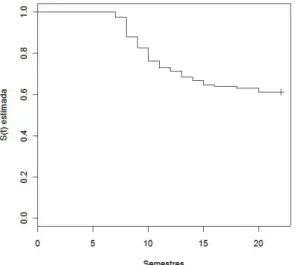
Observando a calda direita do gráfico da fun¸cão de sobrevivência estimada

(Esti-mador de Kaplan-Meier) podemos ter um indicativo da presen¸ca de imunes. Uma calda

bem acima de zero sugere uma fra¸c˜ao de curados como ilustrado pela Figura 3.1.

Um fator que pode nos levar a considerar a presen¸ca de imunes em um conjunto de

dados é a alta presen¸ca de censura à direta ao fim do estudo. Porém um estudo com

tempo de acompanhamento relativamente curto pode nos levar a uma falsa conclus˜ao

da existˆencia de imunes, pois o evento de interesse ainda pode ocorrer para muitas

(19)

3.1 Modelo de Mistura Padr˜ao 10

Figura 3.1: Fun¸cão de Sobrevivência estimada para os dados de tempo até a conclusão do curso de gradua¸cão em Estat´ıstica da UFRN - 1997 a 2004. Amostra com n = 414 alunos.

serva¸c˜oes. Desta forma, Maller e Zhou (1996) sugerem um tempo de acompanhamento

suficientemente grande, citando como exemplo, um problema real de uma esp´ecie de

tartaruga em que é dif´ıcil a identifica¸cão do sexo. Essa identifica¸cão pode ser feita

ape-nas por cirurgia ou no momento em que uma tartaruga coloca ovos, sendo declarado

desta forma fêmea. Portanto para identificar a propor¸cão de fêmeas em uma amostra

dessas tartarugas o estudo deve durar pelo menos at´e a maturidade da esp´ecie.

3.1 Modelo de Mistura Padr˜

ao

Em uma abordagem dada inicialmente por Boag (1949) e Berkson e Gage (1952) ´e

proposto um modelo param´etrico que consiste em uma mistura de distribui¸c˜oes. Uma

representa a fun¸c˜ao de sobrevivˆencia dos indiv´ıduos suscet´ıveis ao evento de interesse,

que ir˜ao falhar, e a outra uma fun¸c˜ao degenerada que permite tempos de vida infinitos

para os imunes. Nos referimos a esse modelo comomodelo de mistura padrão. Assuma que um indiv´ıduo i está associado à uma variável aleatória M sendo:

M =







1 se o indiv´ıduo suscet´ıvel ao evento

(20)

3.2 Modelo de tempo de promo¸c˜ao 11

e tamb´em

P(M =m) =







π se m= 0 1−π se m= 1

Veja que todos os indiv´ıduos comM = 0 tem T =∞. Portanto:

P(T > t|M = 0) = 1

P(T > t|M = 1) =S∗(t)

Portanto para todo t≥0 a verdadeira fun¸cão de sobrevivência para a popula¸cão é dada por:

Sp(t) = P(T > t) = P(T > t, Mi = 0) +P(ti > t, Mi = 1)

= P(T > t|Mi = 0)P(Mi = 0) +P(T > t|Mi = 1)P(Mi = 1)

= π+ (1−π)S∗₍_t₎

(3.1)

3.2 Modelo de tempo de promo¸

c˜

ao

Um modelo alternativo ´e proposto por Yakovlev et al. (1993) e Chen et al. (1999)

referido por Rodrigues et al. (2008) como modelo de tempo de promo¸c˜ao. Este modelo

consiste em pressupor a existˆencia de v´arias causas que competem entre si para causar

no indiv´ıduo o evento de interesse.

Sejam Z1, Z2, ..., ZM variáveis aleatórias latentes que representam os tempos até a

ocorrência de um evento de interesse, sendoM uma variável aleatória não observável que representa o número de causas que competem para produzir o evento de interesse.

SeM = 0 definimos Z0 tal que P(Z0 =∞) = 1 e neste caso dizemos que o indiv´ıduo

não é suscet´ıvel ao evento de interesse. O tempo de sobrevivência observável é definido

como T = min{Z0, Z1, ..., ZM}. Assumindo M como uma vari´avel aleat´oria com

(21)

3.3 Modelo Unificado 12

distribu´ıdas com fun¸cão de distribui¸cão F(·) e sobrevivência S(·) = 1−F(·). Temos que a fun¸cão de sobrevivência populacional é dada por:

Sp(t) = e−θF(t). (3.2)

A fra¸c˜ao de cura correspondente ao modelo 3.2 ´e dada por:

lim

t_→∞Sp(t) =e −θ_.

3.3 Modelo Unificado

Abordamos agora o modelo de fra¸c˜ao de cura unificado proposto por Rodrigues

et al. (2009) que representa uma extens˜ao dos modelos de longa dura¸c˜ao proposto por

Chen et al. (1999).

Como antes, seja M, uma variável aleatória representando o número de causas ou riscos da ocorrência de um particular evento de interesse com distribui¸cão denotada por

p(m) =P(M =m), m= 0,1,2, ...

Considere que, dado M =m, Zj,j = 1, ...m, são variáveis aleatórias independentes

e identicamente distribu´ıdas, representando o tempo de ocorrˆencia do evento de

inte-resse devido à j-ésima causa ou risco, com fun¸cão de sobrevivência S(·) = 1−F(·) e fun¸cão de densidade de probabilidadef(·) independentes de M.

O tempo até ocorrência do evento de interesse para um indiv´ıduo da popula¸cão é

dado por T = min{Z0, ..., ZM}, sendo que P(Z0 = ∞) = 1. Esta suposi¸c˜ao admite

a possibilidade de uma propor¸cão p(0) da popula¸cão não apresentar a ocorrência do evento de interesse. As variáveis aleatórias Zj e M são variáveis latentes, ou seja, não

observáveis, enquanto T é uma variável observável. Sejaa =am uma sequência de números reais. Se

(22)

3.3 Modelo Unificado 13

converge para s ∈ [0,1], então definimos Aa(s) como a fun¸cão geradora da sequência

am (Feller 2008).

A fun¸cão de sobrevivência populacional deT definido porSp(t) = P(T > t) é dada

abaixo (sua demonstra¸c˜ao encontra-se no Apˆendice B.1).

Sp(t) = Ap(S(t)) = ∞

X

m=0

p(m)(S(t))m_, _(3.4)

sendoAp(·) a fun¸cão geradora da sequência p=p(m). Note queSp é imprópria, ou

seja, o limt_→∞Sp(t) = p(0) = P(M = 0) > 0 corresponde `a propor¸c˜ao de indiv´ıduos

imunes ou curados, ou seja, a fra¸c˜ao de cura.

Podemos ent˜ao apresentar a fun¸c˜ao Sp(t) dada em (3.4) como uma mistura de

dis-tribui¸c˜oes

semelhante ao Modelo de Mistura Padr˜ao apresentado na Se¸c˜ao 3.1.

Defina S∗₍_t_{) =} _P₍_{T > t}_|_{M >} _{0), ´e f´acil ver que esta pode ser representada por}

S∗₍_t_{) =} P∞

m=1p∗(m)[S(t)]m, sendo p∗(m) = p(m)

1−p(0) a fun¸c˜ao de sobrevivˆencia

condi-cional de T dada a ocorrência do evento de interesse, temos então que o modelo de fra¸cão de cura unificado proposto por Rodrigues et al. (2009) pode ser representado

por

Sp(t) =p(0) + (1−p(0))S∗(t) (3.5)

Note também que S∗₍_t_{) é uma fun¸cão de sobrevivência própria pois}

limt_→∞S∗(t) = 0.

A fun¸cão de densidade para a popula¸cão é obtida pelo negativo da derivada de

(3.4), ou seja,

fp(t) =−

∂Sp(t)

∂t =−S

′ p(t) =

∞

X

m=0

f(t)p(m)m(S(t))m−1. (3.6) Decorre de (3.5) que a fun¸cão densidade condicional à ocorrência do evento de

(23)

3.4 Alguns casos particulares do modelo unificado 14

f∗(t) = −∂S∗(t)

∂t =−S

∗′₍_t₎_. _(3.7)

A fun¸cão risco incondicional à ocorrência do evento de interesse, denotado porhp(t)

´e dada por

hp(t) =

fp(t)

Sp(t)

, (3.8)

e a condicional `a ocorrˆencia do evento de interesse por

h∗(t) = f∗(t)

S∗₍_t₎. (3.9)

3.4 Alguns casos particulares do modelo unificado

Sabemos que M é uma variável aleatória discreta representando o número de pos-s´ıveis causas que podem levar um indiv´ıduo ao evento de interesse. Nesta se¸cão

apre-sentamos algumas fun¸c˜oes geradoras (retiradas de Feller 2008) das probabilidades

as-sociadas a importantes distribui¸c˜oes de probabilidade que podemos usar para definir

M.

• SE M ∼ Bernoulli(1−θ), p(m) = (1−θ)m_θ1−m_{, sendo 0} _{< θ <} _{1 e} _m _{= 0}_, ₁

ent˜ao

Ap(s) = θ+ (1−θ)s.

• Se M ∼ Binomia(θ), p(m) = _mn

θm₍₁₋ _θ₎n−m_{, sendo 0} _{< θ <} _1, _n _≥ _{1 e}

m = 0,1,2, . . . ent˜ao

Ap(s) = (1−θ+θs)n.

• Se M ∼Poisson(θ),p(m) = e−θ_θm

m! , sendoθ > 0 e m= 0,1,2, . . . ent˜ao

Ap(s) =e−θ(1−s).

(24)

ent˜ao

Ap(s) =

θ

1−(1−θ)s.

• Se M ∼BinomiaNegativa(η, θ),p(m) = Γ(η_Γ(η−−11+m)_)m!

ηθ 1+ηθ

m

(1 +ηθ)−

1

η, sendoθ >

0, η > −1

θ e m = 0,1,2, . . . nesta vers˜ao mais geral da distribui¸c˜ao binomial

negativa (Piegorsch 1990; Saha e Paul 2005) temos

Ap(s) = (1 +ηθ(1−s))−

1

η.

Devemos por´em observar com mais cuidado dois desses casos particulares, pois estes

se apresentam como os resultados das Se¸c˜oes 3.1 e 3.2.

3.4.1 Modelo de Mistura Padr˜

ao

Considere que M possui uma distribui¸c˜ao Bernoulli(1 − θ). Desta forma

p(m) = Pθ(M = m) = (1 − θ)mθ1−m, m = 0, 1. Logo existe apenas uma causa

que pode levar um indiv´ıduo ao evento de interesse, portanto, T = min{Z0, Z1} com

P(Z0 = ∞) = 1 e P(Z1 > z) = S(z). Sendo p(0) = Pθ(M = 0) = θ a fra¸c˜ao de

cura correspondente. Os resultados obtidos est˜ao relacionados ao modelo de mistura

padrão visto na Se¸cão 3.1. As respectivas fun¸cões de sobrevivência, densidade e risco

populacionais e condicionais à ocorrência do avento de interesse são dadas por:

Fun¸cões de Fun¸cão Populacional de T Fun¸cão condicional

`a ocorrˆencia do evento de interesse

Sobrevivˆencia Sp(t) = θ+ (1−θ)S∗(t) S∗(t) =S(t)

Densidade fp(t) = (1−θ)f∗(t) f∗(t) =f(t)

Risco hp(t) =f(t)

1−θ

θ+ (1−θ)S(t) h

∗₍_t_{) =} f(t)

(25)

3.4.2 Modelo de Tempo de Promo¸

c˜

ao

Considerando que o n´umero de poss´ıveis causas que podem levar um indiv´ıduo ao

evento de interesse seja M ∼ Poisson(θ). Neste caso temos p(m) = Pθ(M = m) = e−θ_θm

m! , m = 0,1,2, . . . com T = min{Z0, Z1, . . . , ZM}, P(Z0 =∞) = 1 e P(Z1 > z) =

S(z). A fra¸c˜ao de cura neste caso ´e dada por p(0) = Pθ(M = 0) = e−θ. Os resultados

obtidos est˜ao relacionados com o modelo de tempo de promo¸c˜ao visto em 3.2. As

respectivas fun¸cões de sobrevivência, densidade e risco populacionais e condicionais à

ocorrˆencia do evento de interesse s˜ao dadas por:

Fun¸cões de Fun¸cão Populacional de T Fun¸cão condicional

`a ocorrˆencia do evento de interesse

Sobrevivˆencia Sp(t) =e−θ(1−S(t)) S∗(t) =

exp{−θ(1−S(t))} −exp{−θ}

1−exp{−θ}

Densidade fp(t) =θf(t)e−θ(1−S(t)) f∗(t) =

exp{−θ(1−S(t))}

1−exp{−θ} θf(t)

Risco hp(t) = θf(t) h∗(t) =

exp{−θ(1−S(t))}

exp{−θ(1−S(t))} −exp{−θ}hp(t)

3.4.3 Fun¸

c˜

ao de Verossimilhan¸

ca

Suponha uma amostra com n indiv´ıduos e para cada indiv´ıduo i, i= 1, . . . , n, s˜ao associados as seguintes vari´aveis:

• Mi: Variável aleatória não observável discreta com fun¸cão de probabilidade

Pθ(Mi =mi) =pθ(mi), sendo θ um vetor de parˆametros desconhecidos;

• Zij: Variáveis i.i.d. não observáveis representando o tempo até a ocorrência do

evento de interesse devido àj-ésima causa ou risco, j = 1, ..., Mi, com fun¸cão

dis-tribui¸cãoF(·;ψ), fun¸cão de sobrevivênciaS(·;ψ) = 1−F(·;ψ) e fun¸cão densidade

(26)

• Ti: tempo de falha observado, dado por Ti = min{Ti∗, Ci}, com

T∗

i = min{Zi0, Zi1, . . . , ZiMi} e Ci o tempo de censura para o individuo i; • δi: indicador de falha, sendo δi =







1 , se T∗ i ≤Ci

0 , se T∗ i > Ci

;

O conjunto dos dados completos ´e representado porDc = (n,T,δ,M), sendo T =

(T1, T2, . . . , Tn)′, δ = (δ1, δ2, . . . , δn)′, M = (M1, M2, . . . , Mn)′ e o conjunto de dados

observados por D = (n,T,δ). A fun¸cão de verossimilhan¸ca relativa à distribui¸cão conjunta dos vetoresT,δ e Mpode ser representada por:

L(ψ, θ;Dc) = Q_i=1n f(ti, δi, mi)

= Qn

i=1f(ti, δi|mi)pθ(mi).

(3.10)

Sejam fT e g as fun¸c˜oes densidade de probabilidade de Ti∗ e Ci respectivamente, e

ST e Gsuas fun¸cões de sobrevivência. Então:

ST(t|mi) = P(Ti ≥t|Mi =mi)

= P(min{Z0, Z1, . . . , Zmi} ≥t)

= P(Z0 ≥t, Z1 ≥t, . . . , Zmi ≥t)

= P(Z0 ≥t)P(Z1 ≥t), . . . , P(Zmi ≥t)

= 1·S(t;ψ)·S(t;ψ)· · ·S(t;ψ) = S(t;ψ)mi.

(3.11)

Por (3.6) temos

fT(t|mi) =

∂Sp(t|mi)

∂t

= mif(t;ψ)S(t;ψ)mi−1.

(3.12)

A express˜ao f(ti, δi|Mi =mi) pode ser particionada em dois casos disjuntos. Para

δi = 0 e para δi = 1. Desta forma, e utilizando (3.11) e (3.12), temos:

(27)

f(ti, δi|mi) = lim ∆t→0

P(ti ≤Ti < ti+ ∆t, δ = 0|Mi =mi)

∆ti

= lim

∆ti→0

P(ti ≤Ci < ti+ ∆t, Ti∗ > Ci|Mi =mi)

∆t

∼

= lim

∆ti→0

P(ti ≤Ci < ti+ ∆t, Ti∗ > t|Mi =mi)

∆t

= lim

∆t→0

P(ti ≤Ci < ti+ ∆ti|Mi =mi)

∆t

P(Ti > t|Mi =mi)

= g(ti|mi)ST(ti|mi)

= S(ti;ψ)mig(ti|mi)

(3.13)

e paraδ = 1

f(ti, δi|mi) = lim ∆t→0

P(ti ≤Ti < ti+ ∆t, δ= 1|Mi =mi)

∆t

= lim

∆t→0

P(ti ≤Ti∗ < ti+ ∆t, Ti∗ ≤Ci|Mi =mi)

∆t

∼

= lim

∆t→0

P(ti ≤Ti∗ < ti+ ∆t, Ci ≥t|Mi =mi)

∆t

= lim

∆t→0

P(ti ≤Ti∗ < ti+ ∆t|Mi =mi)

∆t

P(Ci ≥t|Mi =mi)

= fT(ti|mi)G(ti|mi)

= G(ti|mi)mif(ti;ψ)S(ti;ψ)mi−1.

(3.14)

Portanto, de (3.13) e (3.14), a distribui¸c˜ao de (ti, δi) dadoMi =mi, i= 1, . . . , n ´e

f(ti, δi|mi) =







S(ti;ψ)mig(ti|mi) seδ = 0

G(ti|mi)mif(ti;ψ)S(ti;ψ)mi−1 seδ = 1

(3.15)

(28)

f(ti, δi|mi) = [S(ti;ψ)mig(ti|mi)]1−δi

G(ti|mi)mif(ti;ψ)S(ti;ψ)mi−1

δi

(3.16)

Substituindo (3.16) em (3.10) temos que a fun¸c˜ao de verossimilhan¸ca para os dados

completos, sob a suposi¸cão de censura não informativa para os parâmetros de interesse

e usando um certo abuso de linguagem para abandonar o s´ımbolo “proporcional” ´e:

L(ψ, θ;Dc) = n

Y

i=1

[S(ti;ψ)mi]1−δi

mif(ti;ψ)S(ti;ψ)mi−1

δi

pθ(mi) (3.17)

3.4.4 Verossimilhan¸

ca Marginal

Para obter a verossimilhan¸ca marginal fazemos o somat´orio da distribui¸c˜ao conjunta

de (Ti,δi, Mi) nas vari´aveis n˜ao observadas mi.

f(ti, δi) = ∞

X

mi=0

f(ti, δi, mi)

=

∞

X

mi=0

f(ti, δi|mi)pθ(mi)

(3.18)

Portanto a verossimilhan¸ca marginal para o conjunto de dados observados

D= (n,T,δ) ´e dada por:

L(ψ, θ;D) =

n

Y

i=1 ∞

X

mi=0

[S(ti;ψ)mi]1− δi

mif(ti;ψ)S(ti;ψ)mi−1

δi

pθ(mi). (3.19)

Abordando agora o modelo de sobrevivˆencia de longa dura¸c˜ao consideramos (3.19)

nos seguintes casos:

(29)

3.5 Incluindo Covari´aveis na Fra¸c˜ao de Cura 20

L(ψ, θ;D) =

n Y i=1 ∞ X m=0

[pθ(mi)S(ti;ψ)mi]

=

n

Y

i=1

Sp(ti;φ),

(3.20)

sendo φ= (ψ, θ). Recorrendo `a (3.4) na ´ultima passagem.

• δ = 1

L(φ;D) =

n Y i=1 ∞ X m=0

f(ti;ψ)pθ(mi)miS(ti;ψ)mi−1

=

n

Y

i=1

fp(ti;φ),

(3.21)

recorrendo `a (3.6) na ´ultima passagem. Desta forma, sintetizando (3.20) e (3.21)

em uma ´unica equa¸c˜ao

L(φ;D) =

n

Y

i=1

[Sp(ti;φ)]1−δi[fp(ti;φ),]δi (3.22)

3.5 Incluindo Covari´

aveis na Fra¸

c˜

ao de Cura

Descrevemos na Se¸c˜ao 2.2 os modelos de tempo falha acelerado que associam

co-variáveis ao tempo de vida através do parâmetro de posi¸cão µ = x′β. Em modelos de sobrevivência com fra¸cão de cura, as covariáveis podem ser inclu´ıdas através do

parˆametroθ =θ(x′γ) sendoγ = (γ0, γ1, . . . , γp) um vetor de coeficientes de regress˜ao.

Nos modelos de Mistura e de Promo¸cão (vistos nas se¸cões 3.1 e 3.2) essa associa¸cão

entre covariáveis e fra¸cão de cura está relacionada com à fun¸cão de liga¸cão canônica

considerada em Modelos Lineares Generalizados (Nelder e Wedderburn 1972). Portanto

associamos covari´aveis ao Modelo de Mistura considerando a liga¸c˜ao log´ıstica:

θ(x′γ) = e x′γ

(30)

3.5 Incluindo Covari´aveis na Fra¸c˜ao de Cura 21

θ(x′γ) = ex′γ_.

Aqui desejamos descrever no contexto do modelo unificado, a inclus˜ao de

covariá-veis no parâmetro θ. Considere que θ =θ(x′_γ_{) é uma fun¸cão das covariáveis. Assim,}

seja M uma variável aleatória discreta representando o número de causas que podem levar um indiv´ıduo a ocorrência do evento de interesse com fun¸cão de probabilidade

p(m) = Pθ(M = m), m = 0,1,2, ... . Dado M = m sejam Zj, j = 1, ...m,

vari-´aveis aleat´orias independentes e identicamente distribu´ıdas, representando o tempo

de ocorrência do evento de interesse devido à j-ésima causa ou risco, com fun¸cão de

sobrevivência S(·;ψ) = 1−F(·;ψ) e fun¸cão de densidade de probabilidade f(·;ψ) in-dependentes de M. Esta inclusão de covariáveis na fra¸cão de cura é apresentada em Rodrigues et al. (2008) usando como exemplo para a densidade de Z a distribui¸cão Weibull para o Modelo de Mistura e para o Modelo de Promo¸cão.

3.5.1 Fun¸

c˜

ao de Verossimilhan¸

ca

Sejam x= (xi1, xi2, . . . , xip)′ vetor de covari´aveis relacionado a cada indiv´ıduo em

uma amostra de tamanhon. Sejaγ = (γ1, γ2, . . . , γp) coeficientes de regress˜ao

associa-dos à fra¸cão de curaassocia-dos através de θ(x′_γ_{) pela fun¸cão de probabilidade da variável}

aleatória M, pγ(m) = Pθ(x′γ)(M = m), m = 0,1,2, ... então de forma muito seme-lhante a se¸cão 3.4.3 obtemos a fun¸cão de verossimilhan¸ca para os dados completos

Dc = (n,x,T,δ,M):

L(φ;Dc) = n

Y

i=1

[S(ti;ψ)mi]1− δi_m

if(ti;ψ)S(ti;ψ)mi−1

δi

pγ(mi), (3.23) sendoφ = (ψ, γ) e a verossimilhan¸ca marginal para os dados observadosD= (n,x,T,δ) dada por:

L(φ;D) =

n

Y

i=1

[Sp(ti;φ)]1− δi

[fp(ti;φ)] δi

(31)

Cap´ıtulo 4

Modelos de tempo de falha

acelerado com fra¸

c˜

ao de Cura: Uma

abordagem unificada

Vimos no Cap´ıtulo anterior modelos que fazem uso de covari´aveis apenas na fra¸c˜ao

de cura. Usando o Modelo de Mistura Padr˜ao Yamaguchi (1992) estende o MTFA

log-gama generalizado para a avaliar simultaneamente o efeito de covari´aveis tanto

na acelera¸cão/desacelera¸cão do tempo de falha quanto seus efeitos na fra¸cão de cura.

De forma similar Ortega et al. (2009) utiliza o MTFA log-gama generalizado usando

o Modelo de Tempo de Promo¸c˜ao. Neste Cap´ıtulo propomos uma vis˜ao unificada

para estes modelos e observamos essas duas abordagens como casos particulares de um

modelo geral. Por fim implementamos esses casos no software R.

4.1 Regress˜

ao log-gama generalizada

A partir da distribui¸c˜ao gama generalizada introduzida por Stacy (1962) e

repara-metrizada por Prentice (1974), Farewell e Prentice (1977) e Lawless (1980) apresentam

o modelo de regress˜ao log-gama generalizado estendido (l.g.g.). O modelo l.g.g.

esten-dido ´e de grande importˆancia pois possui como casos particulares alguns dos modelos

paramétricos mais usados na análise de sobrevivência como os modelos weilbull e

log-normal.

(32)

4.1 Regress˜ao log-gama generalizada 23

Considere um vetor de covariáveis x, de ordem p×1, associado com o tempo de vida T para cada indiv´ıduo. Modelos de tempo de falha acelerado são modelos de regressão que se caracterizam pelo fato da variável Y = log(T) ter uma distribui¸cão com parâmetro de posi¸cão µ(x) =β′_x_{, e um parâmetro de escala} _σ _{constante. Pode}

ser representada por:

Y = log(T) = βx′ +σǫ, (4.1)

sendo σ > 0 e β=(β1,· · ·, βp)T parˆametros desconhecidos e ǫ um erro aleat´orio cuja

distribui¸c˜ao n˜ao depende dex.

A fam´ılia estendida log-gama generalizada (l.g.g.) paraY ´e obtida quando assumi-mos queǫ tem densidade

fǫ(ǫ) =







|q_| Γ(q−2

)(q− 2₎(q−2

)_exp_{_q−1_ǫ₋_q−2_exp(_qǫ₎_} _{se q} ₆_{= 0} 1

√

2π exp(− ǫ−2

2 ) se q= 0,

(4.2)

e fun¸c˜ao de sobrevivˆencia

Sǫ(ǫ) =

        

Q[q−2_{, q}−2_e{qǫ_}_] _se _{q <}₀

1−Q[q−2_{, q}−2_e{qǫ_}_] _se _{q >}₀

1−Φ(ǫ) seq = 0,

(4.3)

sendo −∞< q <∞ e Q(k, a) a fun¸c˜ao integral gama incompleta

Q(k, a) =

Z ∞

a

tk₋1

Γ(k)e

−t

dt. (4.4)

Obtemos como casos particulares do modelo l.g.g. estendido o modelo Weibull para

(33)

4.2 MTFA incluindo covari´aveis na fra¸c˜ao de cura 24

4.2 MTFA incluindo covari´

aveis na fra¸

c˜

ao de cura

A inclusão de fra¸cão de cura com covariáveis ao MTFA permite uma análise

si-multânea da influência das covariáveis na acelera¸cão/desacelera¸cão do tempo de falha

e seus efeitos na fra¸c˜ao de curados.

Suponha para uma amostra denindiv´ıduos o vetor de covari´aveisxi = (xi1, xi2, . . . , xip)′.

Seja Mi o n´umero de causas ou riscos da ocorrˆencia do evento de interesse para cada

indiv´ıduo com fun¸cão de probabilidade pγ(mi) = Pθ(x′γ)(Mi = mi), mi = 0,1,2, ..., sendo γ = (γ0, γ1, . . . , γp)′ vetor de parâmetros desconhecidos associados à fra¸cão de

cura. Dado Mi = mi, sejam Zij, j = 1, ...mi, vari´aveis aleat´orias independentes e

identicamente distribu´ıdas, com fun¸c˜ao densidade de probabilidade e de sobrevivˆencia

independentes de M representando o tempo até a ocorrência do evento de interesse para oi-ésimo indiv´ıduo. Considere tambémT∗

i = min{Zi0, Zi1, . . . , ZiMi}o tempo at´e

a ocorrˆencia do evento de interesse para o indiv´ıduoi.

Tomando a variável aleatóriaWij = log(Zij) como pertencente à fam´ılia de modelos

de posi¸c˜ao e escala temos

Wij =x′iβ+σǫi,

sendoβ = (β0, β1, . . . , βp)′ vetor de parˆametros desconhecidos associados ao tempo

de falha e ǫ uma variável aleatória com fun¸cão densidade de probabilidade g(·;ξ) e fun¸cão de sobrevivênciaG(·;ξ), sendo ξ um vetor de parâmetros desconhecidos.

Então a fun¸cão densidade de probabilidade deWij para um dado vetor de covariáveis

xi ser´a dada por

f(wij;xi,β, σ, ξ) =

1

σg

wij −x′iβ

σ ;ξ

, (4.5)

e fun¸c˜ao de sobrevivˆencia dada por

S(wij;xi,β, σ, ξ) = G

wij −x′iβ

σ ;ξ

(34)

4.2 MTFA incluindo covari´aveis na fra¸c˜ao de cura 25

Considere agora Ti = min{Ti∗, Ci} e Yi = log(Ti) respectivamente o tempo at´e a

ocorrˆencia do evento de interesse observado e seu logaritmo, sendo T∗

i o tempo at´e a

ocorrˆencia do evento de interesse e Ci o tempo de censura, para o i-´esimo indiv´ıduo.

Portanto Yi = min{logT∗,logC} e logT∗ = min{log(Zi0),log(Zi1), . . . ,log(ZiMi)}

en-tão obtemos de forma semelhante à equa¸cão 3.4 a fun¸cão de sobrevivência populacional

dada por

P(logT_i∗ > vi) =Sp(vi;φ) = ∞

X

mi=0

pγ(mi)[S(vi;xi,β, σ, ξ)]

mi_, _(4.7)

sendo vi = log(ti) e φ = (β,γ, σ, ξ). Tamb´em de forma semelhante ao modelo

unificado (equa¸c˜ao 3.5) apresentamos o MTFA com Fra¸c˜ao de Cura Unificado dado por:

Sp(vi;φ) = pγ(0) + (1−pγ(0))S∗(vi;φ), (4.8) sendo pγ(0) a fra¸c˜ao de cura dependente de γ, e

S∗(vi;φ) = ∞

X

mi=1

[p∗γ(mi)S(vi;x,β, σ, ξ)]

mi_, _sendo _p∗

γ(mi) =

pγ(mi) 1−pγ(0)

,

a fun¸cão de sobrevivência dependente à ocorrência do evento de interesse. A fun¸cão de

densidade populacional ser´a

fp(vi;φ) = −Sp′(vi;φ) (4.9)

De forma similar aos resultados obtidos na se¸c˜ao 3.4.3 temos que a fun¸c˜ao de

verossimilhan¸ca para os dados completosDc = (n,x,Y,δ,M), sendoY = (y1, . . . , yn)

o vetor do logaritmo dos tempos observados e δ = (δ1, . . . , δn) o vetor dos indicadores

de censura, ser´a

L(φ;Dc) = n

Y

i=1

[S(yi;φ)mi]1−δi

mif(yi;φ)S(yi;φ)mi−1

δi

(35)

4.3 Casos Particulares do MTFA com fra¸c˜ao de cura unificado 26

e a verossimilhan¸ca marginal para os dados observadosD= (n,x,Y,δ) ser´a

L(φ;D) =

n

Y

i=1

[Sp(yi;φ)]1−δi[fp(yi;φ)]δi. (4.11)

4.3 Casos Particulares do MTFA com fra¸

c˜

ao de cura

unificado

Vimos na se¸cão 3.4 alguns casos particulares para o númeroM de poss´ıveis causas que podem levar um indiv´ıduo ao evento de interesse para o modelo unificado (equa¸cão

3.5). Apresentamos nesta se¸c˜ao alguns casos particulares para diferentes distribui¸c˜oes

de Mi e assumimos o modelo de regress˜ao log-gama generalizado para log (Zij),

i= 1, . . . , n ej = 1, . . . , Mi.

4.3.1 MTFA l.g.g. com modelo de mistura padr˜

ao

Partindo do MTFA com fra¸c˜ao de cura unificado apresentado na equa¸c˜ao 4.8,

atribu´ımos para a variável aleatóriaM uma distribui¸cão Bernoulli(1−θ). Desta forma as fun¸cões de densidade e de sobrevivências populacionais são semelhantes às

apresen-tadas na se¸cão 3.4.1. A partir das equa¸cões 4.11, 4.5 e 4.6 apresentamos fun¸cão de

verossimilhan¸ca

L(φ;D) =

n

Y

i=1

θ(x′iγ) + (1−θ(x′iγ))G

yi−x′iβ

σ ;ξ

1−δi

(1−θ(x′iγ))

1

σg

yi−x′iβ

σ ;ξ

δi

,

(4.12)

sendoφ= (β,γ, σ, ξ),yi = log(t∗i) o logaritmo do tempo observado, δi o indicador se o

tempo é de falha ou de censura,γ = (γ0, γ1, . . . , γp)′ o vetor de covariáveis de regressão

associados à fra¸cão de cura, β = (β0, β1, . . . , βp)′ o vetor de covariáveis de regressão

associados ao tempo de falha eθ(x′_iγ) = x′_iγ

1+x′_iγ.

(36)

Apre-4.3 Casos Particulares do MTFA com fra¸c˜ao de cura unificado 27

sentamos ent˜ao a fun¸c˜ao de log-verossimilhan¸ca para o MTFA l.g.g. com modelo de

mistura:

l(β,γ, σ, q;D) = Pn

i=1[(1−δi) log[(1−θ(x′iγ))Sǫ(ǫi;q,β, σ)−logσ) +θ(x′iγ)]

+δi[log(1−θ(x′iγ)) + logfǫ(ǫi;q,β, σ)−logσ]],

(4.13)

sendo ǫi = (log(ti)−x′iβ)/σ. Desta forma conseguimos apresentar o mesmo resultado

mostrado por Yamaguchi (1992).

4.3.2 MTFA l.g.g com Modelo de Tempo de Promo¸

c˜

ao

Partindo novamente do MTFA com fra¸c˜ao de cura unificado apresentado na equa¸c˜ao

4.8, atribu´ımos agora para a variável aleatória M uma distribui¸cão Poisson(θ). Desta forma as fun¸cões de densidade e de sobrevivências populacionais são semelhantes às

apresentadas na se¸cão 3.4.2. A partir das equa¸cões 4.11, 4.5 e 4.6 apresentamos fun¸cão

de verossimilhan¸ca

L(φ;D) = Qn

i=1





 "

e−θ(x

′

iγ)

1−G

yi−x′

iβ σ ;ξ

#1−δi

×

"

θ(x′ iγ)σ1f

_y

i−x′_iβ

σ ;ξ

e−θ(x

′

iγ)

1−G

yi−x′

iβ σ ;ξ

#δi





= Qn

i=1

("

e−θ(x

′

iγ)

1−G

yi−x′

iβ σ ;ξ

#

h

θ(x′ iγ)1σf

_y

i−x′_iβ

σ ;ξ

iδi

)

.

(4.14)

As fun¸cõesgeGcorrespondem respectivamente às fun¸cões de densidade e de sobre-vivência do modelo de regressão log-gama generalizado. Apresentamos então a fun¸cão

(37)

4.4 Estimando os parˆametros 28

l(β,γ, σ, q;D) = Pn

i=1[−θ(x′iγ)(1−Sǫ(ǫi;q,β, σ))

+δi(log(θ(x′iγ))−log(σ) + log(fǫ(ǫi;q,β, σ)))],

= P

i∈C{log(θ(x′iγ))−log(σ) + log(fǫ(ǫi;q,β, σ))}

−θ(x′

iγ)(1−Sǫ(ǫi;q,β, σ))

(4.15)

sendo a nota¸c˜ao i ∈ C correspondente aos itens censurados e ǫi = (log(ti)−x′iβ)/σ.

Desta forma conseguimos apresentar o mesmo resultado mostrado por Ortega et al.

(2009).

4.4 Estimando os parˆ

ametros

Para obter as estimativas de verossimilhan¸ca dos coeficientes β, γ e σ, Yamaguchi (1992) utiliza o m´etodo de Newton-Raphson em um procedimento de 2 etapas

apresen-tado em Lawless (1982) para o MTFA l.g.g. fazendo uma adapta¸c˜ao para a inclus˜ao de

covari´aveis na fra¸c˜ao de cura. Ortega et al. (2009) utiliza-se da sub-rotinaMAXBFGS

dispon´ıvel no software Ox (ver, por exemplo, Doornik 2001) utilizando tamb´em do

pro-cedimento de 2 etapas.

Este procedimento consiste em fixarmos diferentes valores paraqno intervalo [−3,3] e encontramos as estimativas de m´axima verossimilhan¸ca β˜(q), γ˜(q) e ˜σ(q) determi-nado a fun¸c˜ao de verossimilhan¸ca maximizada Lmax(q), o maior valor de Lmax(q) nos

retornará ˆq. As estimativas de máxima verossimilhan¸ca de β, γ e σ são respectiva-mente os valores de βˆ = β˜(ˆq), γˆ = ˜γ(ˆq) e ˆσ = ˜σ(ˆq). Os valores de q são escolhidos no intervalo [−3,3] pois a fun¸cão densidade da distribui¸cão l.g.g. pouco se diferencia para valores distantes deq= 0. O método em duas etapas é recomendado na literatura pois evita problemas de convergência para a estima¸cão dos parâmetros (ver detalhes

em Valen¸ca 1994).

Neste trabalhos propomos a estima¸cão dos parâmetros através da sub-rotinaoptim

(38)

4.4 Estimando os parˆametros 29

da fun¸c˜ao de verossimilhan¸ca marginalizada (equa¸c˜ao 4.11). Inicialmente tentamos a

estima¸cão simultânea dos parâmetros β, γ, σ e q, porém não obtivemos convergência nos resultados. Constru´ımos então um algoritmo utilizando-se do método em 2 etapas

obtendo resultados muito semelhantes aos obtidos por Yamaguchi (1992) e Ortega et al.

(39)

Cap´ıtulo 5

Reprodu¸

c˜

ao de resultados e

Aplica¸

c˜

ao

Neste Cap´ıtulo reproduzimos os resultados obtidos por Yamaguchi (1992) e Ortega

et al. (2009) em seus respectivos trabalhos usando nosso algor´ıtimo apresentado no

Apˆendice A. Em seguida estudamos um conjunto de dados reais obtidos de Macedo e

Valen¸ca (2009), contendo informa¸c˜oes a respeito de 355 pacientes com cˆancer de mama

atendidas no Hospital Prof. Dr. Luiz Antˆonio, Natal RN, no per´ıodo de 1991 `a 1995.

5.1 Reprodu¸

c˜

ao de resultados

Para confirmar a eficiˆencia do nosso algor´ıtimo, reproduzimos alguns resultados

relevantes para o nosso estudo.

5.1.1 MTFA l.g.g. com modelo de mistura padr˜

ao

Em seu artigo Yamaguchi (1992) estuda a mobilidade inter-firmas de trabalhadores

no Japão, observando o tempo até separa¸cão do empregado em diferentes empresas.

Desta forma um trabalhador que se aposenta em um empresa corresponde a um

indiv´ı-duo “imune”. As covariáveis envolvidas são o tamanho da empresa, medido pelo número

de funcion´arios ou se a empresa ´e governamental, e o tipo de empregado, classificados

como colarinho azul para trabalhos que requerem m˜ao-de-obra f´ısica e colarinho branco

(40)

5.1 Reprodu¸c˜ao de resultados 31

para os que n˜ao s˜ao considerados trabalhos manuais.

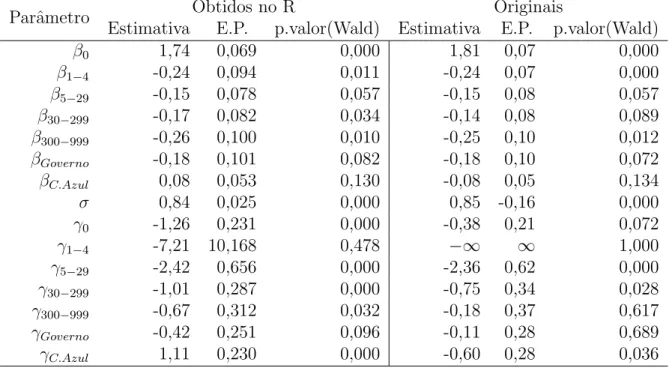
Tabela 5.1: Estimativa dos parˆametros para o MTFA l.g.g. com modelo de mistura padr˜ao - 1975 Social Stratification and Mobility Survey in Japan

Parˆametro Obtidos no R Originais

Estimativa E.P. p.valor(Wald) Estimativa E.P. p.valor(Wald)

β0 1,74 0,069 0,000 1,81 0,07 0,000

β1−4 -0,24 0,094 0,011 -0,24 0,07 0,000

β5−29 -0,15 0,078 0,057 -0,15 0,08 0,057

β30−299 -0,17 0,082 0,034 -0,14 0,08 0,089

β300−999 -0,26 0,100 0,010 -0,25 0,10 0,012

βGoverno -0,18 0,101 0,082 -0,18 0,10 0,072

βC.Azul 0,08 0,053 0,130 -0,08 0,05 0,134

σ 0,84 0,025 0,000 0,85 -0,16 0,000

γ0 -1,26 0,231 0,000 -0,38 0,21 0,072

γ1−4 -7,21 10,168 0,478 −∞ ∞ 1,000

γ5−29 -2,42 0,656 0,000 -2,36 0,62 0,000

γ30−299 -1,01 0,287 0,000 -0,75 0,34 0,028

γ300−999 -0,67 0,312 0,032 -0,18 0,37 0,617

γGoverno -0,42 0,251 0,096 -0,11 0,28 0,689

γC.Azul 1,11 0,230 0,000 -0,60 0,28 0,036

Na Tabela 5.1 vemos a semelhan¸ca entre os resultados obtidos por Yamaguchi e os

obtidos pelo nosso algor´ıtimo. Podemos ver por´em uma dificuldade de convergˆencia

quanto aos coeficientes que assintoticamente v˜ao para −∞ e para∞.

5.1.2 MTFA l.g.g. com modelo de tempo de promo¸

c˜

ao

Ortega et al. (2009) apresenta uma aplica¸c˜ao para dados de pacientes com cˆancer

de pele ,obtido de Ibrahim et al. (2001), para o MTFA l.g.g. com modelo de tempo

de promo¸c˜ao. Sendo as covari´aveis x1: Tratamento; x2: Idade em anos; x3: Tipo de

(41)

5.2 Aplica¸c˜ao 32

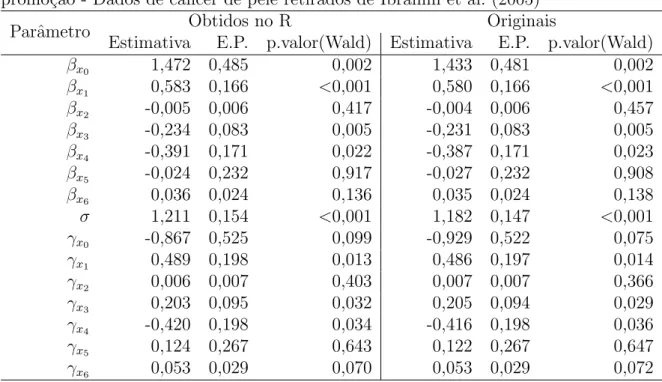
Tabela 5.2: Estimativas dos parâmetros para o MTFA l.g.g. com modelo de tempo de promo¸cão - Dados de câncer de pele retirados de Ibrahim et al. (2005)

Parˆametro Obtidos no R Originais

Estimativa E.P. p.valor(Wald) Estimativa E.P. p.valor(Wald)

βx0 1,472 0,485 0,002 1,433 0,481 0,002

βx1 0,583 0,166 <0,001 0,580 0,166 <0,001

βx2 -0,005 0,006 0,417 -0,004 0,006 0,457

βx3 -0,234 0,083 0,005 -0,231 0,083 0,005

βx4 -0,391 0,171 0,022 -0,387 0,171 0,023

βx5 -0,024 0,232 0,917 -0,027 0,232 0,908

βx6 0,036 0,024 0,136 0,035 0,024 0,138

σ 1,211 0,154 <0,001 1,182 0,147 <0,001

γx0 -0,867 0,525 0,099 -0,929 0,522 0,075

γx1 0,489 0,198 0,013 0,486 0,197 0,014

γx2 0,006 0,007 0,403 0,007 0,007 0,366

γx3 0,203 0,095 0,032 0,205 0,094 0,029

γx4 -0,420 0,198 0,034 -0,416 0,198 0,036

γx5 0,124 0,267 0,643 0,122 0,267 0,647

γx6 0,053 0,029 0,070 0,053 0,029 0,072

Observamos novamente na Tabela 5.2 uma grande semelhan¸ca entre os coeficientes

j´a publicados e os coeficientes por obtidos n´os. Devido ao fato de conseguirmos

re-produzir razoavelmente os resultados anteriores tivemos confian¸ca para aplicar nosso

algor´ıtimo em um conjunto de dados reais.

5.2 Aplica¸

c˜

ao

Consideramos um conjunto de dados proveniente de 355 pacientes diagnosticados

com cˆancer de mama no Hospital Prof. Dr. Luiz Antˆonio Unidade I da Liga Contra

o Câncer (Natal/RN). Estas informa¸cões foram obtidas em caráter retrospectivo ao

per´ıodo de 1991 `a 1995. No estudo realizado por Macedo e Valen¸ca (2009) ´e utilizado

o modelo de regress˜ao de Cox, (Cox 1972), para observar o efeito de covari´aveis no

tempo em que as pacientes permanecem livres do retorno da doen¸ca (recidiva). No

mesmo estudo pode-se observar evidências da existência de fra¸cão de cura devido à alta

(42)

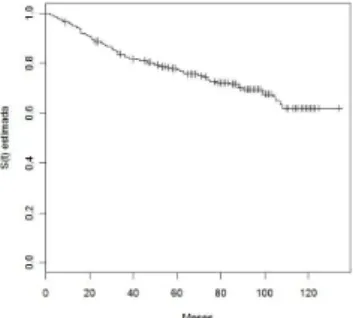
5.3 Descri¸c˜ao das covari´aveis 33

de Kaplan e Meier (1958) na Figura (5.1). Este fato nos levou `a aplica¸c˜ao do Modelo

de Tempo de Falha Acelerado Log-Gama Generalizado com Fra¸c˜ao de Cura. Todos os

resultados foram obtidos atrav´es dos software estat´ıstico R, os comandos encontram-se

no Apˆendice A.

Figura 5.1: Estimativas de Kaplan-Meier para o tempo até a recidiva de pacientes com câncer de mama- Natal/RN 1991 à 1995

5.3 Descri¸

c˜

ao das covari´

aveis

Descrevemos agora as covari´aveis significantes ao nosso estudo, por´em Macedo

e Valen¸ca (2009) fizeram uma an´alise sobre um conjunto maior de covari´aveis

rela-cionadas ao câncer de mama, além da sua devida contextualiza¸cão na área médica.

PLC Propor¸cão de linfonodos axilares comprometidos com metástase, categorizada em três grupos: 0%; entre 0% e 50% e acima de 50%. Com as variáveis indicadoras

PLC.1 e PLC.2.

Tabela 5.3: O fator PLC

PLC2 Vari´aveis indicadoras_PLC2.1 _PLC2.2

0% 0 0

entre 0% e 50% 1 0

acima de 50% 0 1

(43)

5.4 Ajuste de modelos sem fra¸c˜ao de cura 34

TNC Tipo de tratamento n˜ao-cir´urgico ao qual a paciente foi submetida. Catego-rizada em dois grupos: tratamentos com hormonoterapia e tratamentos sem

hor-monoterapia. Com a vari´avel indicadora TNC.1.

Tabela 5.4: O fator TNC

TNC Vari´avel indicadora_TNC.1

Com hormonoterapia 0

Sem hormonoterapia 1

A Figura 5.3 ilustra as fun¸c˜oes de sobrevivˆencia estimada para os 2 grupos.

Figura 5.2: Estimativas de Kaplan-Meier para o tempo até a recidiva de pacientes com câncer de mama para a covariável PLC. Natal/RN 1991 à 1995

Figura 5.3: Estimativas de Kaplan-Meier para o tempo até a recidiva de pacientes com câncer de mama para a covariável PLC. Natal/RN 1991 à 1995

5.4 Ajuste de modelos sem fra¸

c˜

ao de cura

Ajustamos essas covari´aveis para o modelo de regress˜ao de Cox. Pelos resultados

da tabela (5.5) vemos que as pacientes com propor¸c˜ao de linfonodos comprometidos

(44)

se comparadas com as pacientes com propor¸c˜ao de linfonodos comprometidos igual a

zero. As pacientes que se submeteram aos tratamentos sem hormˆonios tˆem um risco de

recidiva da doen¸ca aproximadamente 3,5 vezes maior quando comparadas com aquelas

que se submeteram aos tratamentos com hormˆonios, indicando que a hormonioterapia

´e o elemento diferenciador que contribui no aumento do tempo livre de recidiva.

Tabela 5.5: Resultados do ajuste do modelo de regressão de Cox para o tempo até a recidiva de pacientes com câncer de mama. Natal/RN 1991 à 1995

Parˆametro Estimativa exp(Estimativa) E.P. p-valor

βP LC.1 0,486 1,630 0,244 0,047

βP LC.2 1,927 6,870 0,274 <0,001

βT N C.1 1,270 3,560 0,283 <0,001

Complementamos essa an´alise com o ajuste da regress˜ao log-gama generalizada.

Figura 5.4: Contorno da verossimilhan¸ca maximizada Lmax(q) para a regress˜ao

log-gama generalizada, dados de pacientes com cˆancer de mama - Natal/RN 1991 `a 1995

A figura 5.4 ilustra os diferentes valores para a fun¸c˜ao de log-verossimilhan¸ca em

rela¸cão ao parâmetroq, conforme descrito na se¸cão 4.4.

A partir deste ajuste desejamos escolher um modelo mais simples. O teste da raz˜ao

de verossimilhan¸ca, utilizado para selecionar os submodelos da log-gama generalizada

(45)

Tabela 5.6: Resultados do ajuste do modelo de regressão log-gama generalizada para o tempo até a recidiva de pacientes com câncer de mama. Natal/RN 1991 à 1995

Parˆametro Estimativa E.P. p.valor(Wald)

β0 5,798 0,202 <0,001

βP LC.1 -0,415 0,219 0,058

βP LC.2 -1,855 0,282 <0,001

βT N C.1 -1,212 0,288 <0,001

σ 1,197 0,099 <0,001

i adequa¸cão do modelo de regressão Weibull: T RV = 3.1516 (p-valor = 0.0759) ii adequa¸cão do modelo de regressão log-normal:T RV = 1.1872 (p-valor = 0.2759).

Este resultado indica o modelo log-normal como adequado para o conjunto de dados.

Faremos ent˜ao interpreta¸c˜oes por esse modelo.

Tabela 5.7: Resultados do ajuste do modelo de regressão log-normal para o tempo até a recidiva de pacientes com câncer de mama. Natal/RN 1991 à 1995

Parˆametro Estimativa exp{Estimativa} E.P. p.valor(Wald)

β0 5,705 300,366 0,202 <0,001

βP LC.1 -0,412 0,662 0,221 0,0629

βP LC.2 -1,882 0,152 0,299 <0,001

βT N C.1 -1,267 0,282 0,313 <0,001

σ 1,410 – 0,080 <0,001

Com base nos valores obtidos na Tabela 5.7 podemos inferir que o tempo mediano

at´e a recidiva das pacientes com uma propor¸c˜ao de linfonodos axilares

comprometi-dos com metástase acima de 50% é aproximadamente 85% menor em compara¸cão aos

pacientes sem linfonodos axilares comprometidos. As pacientes que se submeteram

aos tratamentos sem hormonioterapia tˆem um tempo mediano de recidiva da doen¸ca

aproximadamente 72% maior quando comparadas com aquelas que se submeteram aos

tratamentos com hormonioterapia. Esses resultados refor¸cam os obtidos pelo modelo

(46)

5.5 Ajuste dos MTFA l.g.g. padr˜ao com fra¸c˜ao de cura 37

5.5 Ajuste dos MTFA l.g.g. padr˜

ao com fra¸

c˜

ao de

cura

As Figuras 5.5 e 5.6 mostram o contorno da verossimilhan¸ca maximizada para os

diferentes valores estimados de Lmax(q) para o MTFA l.g.g. padr˜ao com modelo de

mistura padr˜ao e com modelo de tempo de promo¸c˜ao respectivamente. A estimativas

de m´axima verossimilhan¸ca dos coeficientesβˆ, γˆ e ˆσ obtidas pelo software estat´ıstico R para os dois modelos s˜ao apresentados na Tabela (5.8).

Figura 5.5: Contorno da verossimi-lhan¸ca maximizada Lmax(q) para o

MTFA l.g.g. padrão com modelo mis-tura padrão, dados de pacientes com câncer de mama. Natal/RN 1991 à 1995

Figura 5.6: Contorno da verossimi-lhan¸ca maximizada Lmax(q) para o

MTFA l.g.g. padrão com modelo tempo de promo¸cão, dados de pacientes com câncer de mama. Natal/RN 1991 à 1995

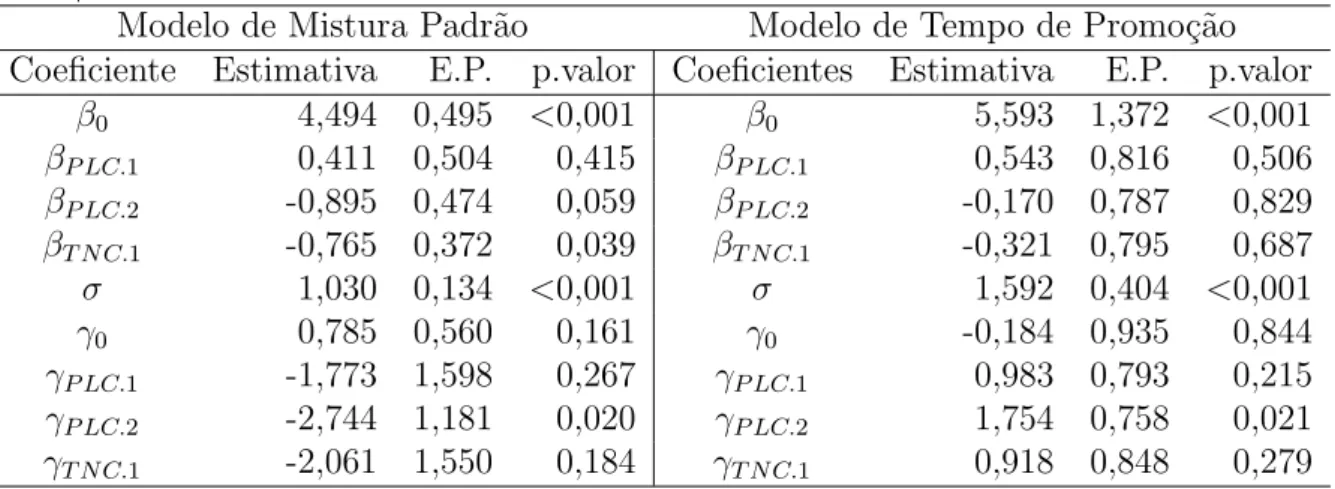
Pelos resultados apresentados na Tabela 5.8 para o MTFA l.g.g. padr˜ao com

mo-delo de mistura padrão vemos que os parâmetros do vetor β associados à acelera-¸cão/desacelera¸cão do tempo até a ocorrência do evento de interesse do MTFA l.g.g.

padr˜ao com modelo de mistura padr˜ao apresentados na Tabela 5.8 apresentam

resulta-dos semelhantes ao apresentaresulta-dos na se¸cão 5.4. Para os parâmetrosγ apenas a variável PLC.2 é significante, ou seja, existe diferen¸ca significativa para a fra¸cão de curadas nas

(47)

com-5.5 Ajuste dos MTFA l.g.g. padr˜ao com fra¸c˜ao de cura 38

para¸c˜ao com as pacientes que apresentam 0%. O fato deγP LC.2 ser negativo indica que

a propor¸cão de curadas é menor em compara¸cão com as pacientes que apresentam 0%.

N˜ao existe diferen¸ca significativa na fra¸c˜ao de curadas entre as pacientes com 0% e as

pacientes com PLC entre 0% e 50%.

Tabela 5.8: Resultados do ajuste para MTFA l.g.g. padrão com modelo de mistura padrão e modelo de tempo de promo¸cão - Dados de pacientes com câncer de mama. Natal/RN 1991 à 1995

Modelo de Mistura Padr˜ao Modelo de Tempo de Promo¸c˜ao Coeficiente Estimativa E.P. p.valor Coeficientes Estimativa E.P. p.valor

β0 4,494 0,495 <0,001 β0 5,593 1,372 <0,001

βP LC.1 0,411 0,504 0,415 βP LC.1 0,543 0,816 0,506

βP LC.2 -0,895 0,474 0,059 βP LC.2 -0,170 0,787 0,829

βT N C.1 -0,765 0,372 0,039 βT N C.1 -0,321 0,795 0,687

σ 1,030 0,134 <0,001 σ 1,592 0,404 <0,001

γ0 0,785 0,560 0,161 γ0 -0,184 0,935 0,844

γP LC.1 -1,773 1,598 0,267 γP LC.1 0,983 0,793 0,215

γP LC.2 -2,744 1,181 0,020 γP LC.2 1,754 0,758 0,021

γT N C.1 -2,061 1,550 0,184 γT N C.1 0,918 0,848 0,279

Os demais resultados parecem ser conflitantes com os resultados das se¸c˜oes

ante-riores. A variável PLC não apresenta significância na fra¸cão de curados em nenhum

dos 2 modelos, o que parece contrariar a Figura 5.2. O MTFA l.g.g. padr˜ao com

modelo tempo de promo¸cão não apresenta significância em nenhuma das covariáveis

no vetor β o que também contraria os resultados anteriores. Acreditamos que estas incoerências podem ser devidas à inclusão do parâmetro γ0 nos modelos e não devido

`a algum erro no algoritmo apresentado, pois reproduzimos de forma muito similar os

resultados de Yamaguchi (1992) e Ortega et al. (2009) com seus respectivos bancos de

(48)

Cap´ıtulo 6

Considera¸

c˜

oes finais

Nesta disserta¸cão estudamos os modelos de sobrevivência com fra¸cão de cura, dando

ˆenfase a uma abordagem unificada destes modelos. Al´em disso, discutimos os modelos

de tempo de falha acelerados com fra¸c˜ao de cura, que permitem a observa¸c˜ao do efeito

de covariáveis tanto na acelera¸cão/desacelera¸cão do tempo até a ocorrência do evento

de interesse como também na fra¸cão de cura, e sugerimos uma ótica unificada sobre

esses modelos.

Particularizamos este modelo, que chamamos de Modelo de Tempo Falha Acelerado

com Fra¸c˜ao Cura Unificado, para os casos em que ele corresponde ao MTFA log-gama

generalizada padr˜ao com modelo de mistura padr˜ao e MTFA log-gama generalizada

padrão com modelo de tempo de promo¸cão, e aplicamos à um conjunto de dados reais

de pacientes com cˆancer de mama.

Os resultados foram obtidos atrav´es de um algor´ıtimo no software estat´ıstico R. Que

se mostrou eficaz para reproduzir resultados j´a existentes na literatura, mas que por´em

apresentou resultados pouco coerentes quando aplicados ao nosso conjunto de dados.

Acreditamos que essas incoerências são devido à algum problema de convergência ou

devido à inclusão do parâmetro γ0 no modelo.

(49)

40

Para trabalhos futuros propomos um estudo sobre os res´ıduos do Modelo de Tempo

Falha Acelerado com Fra¸c˜ao Cura Unificado, a constru¸c˜ao de um algor´ıtimo no software

R mais flex´ıvel a respeito da inclusão ou retirada de covariáveis e também que seja

(50)

Apˆ

endice A

Comandos no R

O método aqui utilizado faz uso da fun¸cão “optim” do pacote base do software R para maximizar a fun¸cão de verossimilhan¸ca. Podemos utilizar o mesmo método

para encontrar outros estimadores de m´axima verossimilhan¸ca. Primeiro definiremos

as principais fun¸cões para compor a fun¸cão de verossimilhan¸ca que será maximizada.

Usamos também a fun¸cão“Rgamma”do pacote“zipfR”(Evert e Baroni (2008)) que corresponde à fun¸cão integral gama incompleta (equa¸cão 4.4).