UNIVERSIDADE FEDERAL DE MINAS GERAIS
INSTITUTO DE CIÊNCIAS EXATAS
DEPARTAMENTO DE MATEMÁTICA
Dissertação de Mestrado
SOBRE PROCESSOS DE AGLOMERAÇÃO
DISTRIBUÍDA
Silvério Lúcio de Moura
Orientador:
Bernardo Nunes Borges de Lima
Resumo
No algoritmo de aglomeração distribuída introduzido por Coffman, Courtois, Gilbert e Piret [5], cada vértice de ℤ recebe inicialmente uma quantidade de um recurso, em seguida a cada iteração o vér-tice transfere todo seu recurso para o vérvér-tice vizinho que nesta etapa detém o máximo de recurso dentre todos os vizinhos. Prova-se neste trabalho que, Prova-se a distribuição inicial dos recursos é in-variante sob as translações no reticulado, o fluxo em cada vértice para após finitas etapas e que também nunca tais recursos esca-pam para o infinito, no sentido de que, para um dado vértice, a esperança da quantidade final de recurso é menor que a esperança da quantidade inicial.
Palavras-chave: distribuição de recursos, aglomeração distribuída, fluxo de recursos, grafos em ℤ , florestas, árvores, árvores com terminal único.
Abstract
In a distributed clustering algorithm introduced by Coffman, Cour-tois, Gilbert and Piret [5], each vertex ofℤ receives an initial amount of resource, at each iteration, transfers all of its resource to the neighboring vertex which currently holds the maximum amount of resource. It proves in this work that for a initial distribution of resources invariant under lattice translations, the flow of resource at each vertex terminates after finitely many steps and that resour-ces nevertheless escape to infinity, in sense that the final amount of resource at a given vertex is strictly smaller in expectation than the initial amount.
Para
Agradecimentos
Conteúdo
1 Introdução 1
2 Fixação para um Processo de Aglomeração Distribuída 3
1 O modelo e a dinâmica do Processo . . . 3 2 Prova do Teorema Principal . . . 9
3 Fuga de Recursos em Processos de Aglomeração Distribuída 25
1 Definições e o enunciado do resultado principal . . . 25 2 Florestas emℤ invariantes por translação . . . 27 3 Prova do resultado principal . . . 30
4 Observações e Problemas abertos 37
Apêndice 39
Princípio do Transporte de Massa 39
Referências Bibliográficas 41
Lista de Figuras
1.1 Representação do conjunto 𝒢 , quando = 2 . . . 4
1.2 Situações possíveis de empates . . . 4
1.3 Fluxo dos recursos quando = 1 . . . 5
1.4 Distribuição inicial dos recursos na etapa 0. . . 5
1.5 Recursos na etapa 1 após transferências. . . 6
1.6 Recursos na etapa 2 após transferências . . . 6
1.7 Recursos na etapa 3, já fixados. . . 6
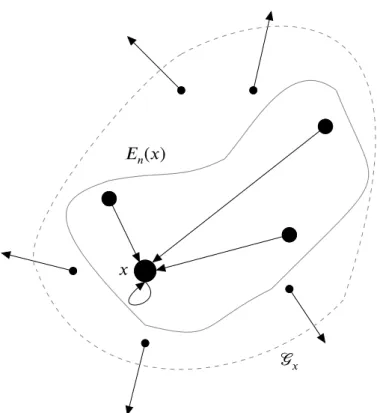
1.8 Representação de um exemplo do conjunto 𝑛( ), quando = 2 7 1.9 Diagrama esquemático para a notação usada. . . 9
2.1 Diagrama esquemático dos conjuntos 𝒢 e 𝑛( ). . . 10
2.2 Conjunto 𝒢 , o vértice , e uma possível configuração para = 2 14 2.3 Representação dos recursos nas etapas 𝑛 e 𝑛 + 1 quando = 2 16 2.4 Recursos nas etapas 𝑚e 𝑚 + 1 nos vértices vizinhos a . . . . 17
2.5 Representação dos recursos na etapa 𝑛 e do conjunto 𝑛( ). . . 19
2.6 Recursos na etapa 𝑛 + 1, 𝑛( ) e o possível vértice . . . 20
2.1 Representação de um grafo finito e um caminho em . . . 28
2.2 Terminal único partindo de um vértice . . . 28
2.3 Para = 3, tem-se três camadas da decomposiçãoℤ2× ℤ. . . . 30
3.1 Vértice pai e descendentes e . . . 32
3.2 Representação da aplicação 𝜙. . . 32
CAPÍTULO 1
Introdução
O objetivo desta dissertação é estudar em todos o seus detalhes os artigos
Fixation for Distributed Clustering Processes [10] escrito por Hilário, M. R., Louidor, O., Newman, C. M., Rolla, L. T., Sheffield S. e Sidoravicius, V., e
Escape of Resources in Distributed Clustering Processes [3] escrito por van der Berg, J., Hilário, M. R., Holroyd A. E.,.
O primeiro artigo [10] descreve e estuda um fluxo de recursos, distribuí-dos inicialmente de forma aleatória nos vértices de ℤ com ≥ 1, durante
uma série discreta de etapas onde vértices mais ricos em recursos atraem os recursos dos vértices vizinhos menos ricos. A dinâmica acima é um al-goritmo deaglomeração distribuída e foi introduzida por Coffman, Courtois, Gilbert e Piret, em 1991 em [5], onde são mencionados exemplos destes ti-pos de fenômenos em vários camti-pos da ciência, tais como Biologia e Ciência da Computação. Todo o Capítulo 2 desta dissertação será dedicado a esse artigo.
O interesse está focado no estudo dos seguintes fenômenos, considerando a propriedade de estabilidade desta dinâmica:
Questão 1. Cada vértice a menos de uma quantidade finita de vezes transfere seus recursos para o mesmo vértice fixado?
Questão 2. O fluxo em cada vértice termina após uma quantidade finita de etapas?
Questão 3. Se a resposta à questão anterior é afirmativa, o valor esperado do recurso final é igual ao valor esperado do recurso inicial?
Como mencionado no artigo [10], van den Berg e Meester em [4] conside-raram o modelo em ℤ2 com quantidade de recursos iniciais i.i.d.,
continu-amente distribuídos e responderam a Questão 1. A saber, eles mostraram que a probabilidade do evento “a menos de uma quantidade finita de etapas, o vértice transfere seu recurso para um mesmo vértice fixado”, é igual a
1. Eles também responderam a Questão 2 em qualquer dimensão e com re-cursos assumindo valores em ℕ, provando que a probabilidade do evento “a menos de uma quantidade finita de etapas o vértice transfere seu recurso para si próprio” é igual a 1.
O Capítulo 3 desta dissertação tem sua atenção voltada para o estudo do artigo [3], onde será respondida a Questão 3 negativamente para ≥ 2:
existe uma distribuição inicial não-negativa para a qual os recursos não escapam para o infinito. De fato o teorema principal a ser provado mostrará que nestas condições existe uma distribuição inicial tal que para um tempo muito grande a média da distribuição será menor que a distribuição inicial.
CAPÍTULO 2
Fixação para um Processo de
Aglomeração Distribuída
1 O modelo e a dinâmica do Processo
O propósito desta seção é discutir a dinâmica para o modelo de aglomeração distribuída a ser estudado, bem como desenvolver exemplos esclarecedores, para o melhor entendimento do artigo [10]. Aqui também serão estabelecidas as definições, convenções e notações a serem usadas em todo o trabalho deste capítulo. Ao final será enunciado o teorema principal cuja prova será totalmente desenvolvida na próxima seção.
Após uma distribuição inicial aleatória de recursos nos vértices do grafo
ℤ com ≥ 1, será estudado o processo de fluxo em etapas discretas dos
recursos nestes vértices. Assim inicialmente a cada vértice ∈ ℤ está assi-nalada aleatoriamente uma quantidade de recursos medida por um número real positivo com a seguinte notação, 0 ≤ 0( ) < ∞, distribuídos de acordo
com uma distribuição qualquer, invariante por translação.
Cada ponto ∈ ℤ é representado pelas coordenadas de números inteiros
= { 1, 2, … , } e a distancia 𝛿( , ) entre dois pontos , é definida pela
fórmula
𝛿( , ) = ∑=1| − | ,
e dois vértices são ditos adjacentes em ℤ se 𝛿( , ) = 1.
Deste modo será denotado por ∼ dois vértices adjacentes e escreve-se
≃ se = ou ∼ . Com essas definições e notações tem-se o conjunto
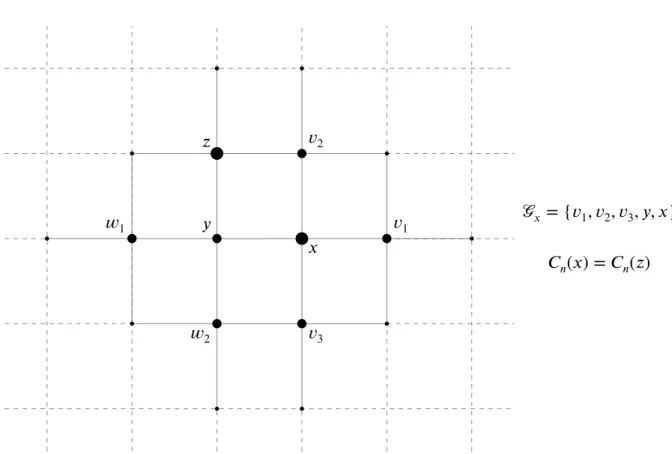
𝒢 = { ∶ ≃ } significando o conjunto de todos os vertices adjacentes a bem como o próprio . No caso particular de ℤ2 tem-se 𝒢 = {
1, 2, 3, 4, }
como pode-se ver na Figura 1.1. Define-se o vértice 𝑎𝑛( ) ∈ 𝒢 como o
vér-tice adjacente ao vérvér-tice ou o próprio que detém a maior quantidade de
1 2
3
4
Figura 1.1: Representação do conjunto 𝒢 , quando = 2
recursos na etapa 𝑛 = 0, 1, 2, …, formalmente,
𝑎𝑛( ) ={ argmax {, 𝑛( ), ∈ 𝒢 } , sese 𝑛( ) > 0 𝑛( ) = 0
onde 𝑛( ) é o recurso no vértice , na etapa𝑛.
Agora descreve-se a dinâmica do processo emℤ . Ela é definida indutiva-mente com se segue. Na etapa𝑛cada vértice detendo uma certa quantidade de recurso 𝑛( )transferirá seus recursos para o vértice 𝑎𝑛( ) ∈ 𝒢 que
pos-sui o recurso máximo. Todos os vértices serão atualizados simultaneamente desta forma, levando ao estado na etapa 𝑛 + 1, isto é a( 𝑛+1( ), ∈ ℤ ), onde
𝑛+1( ) = ∑ ∈ 𝑛( ) 𝑛
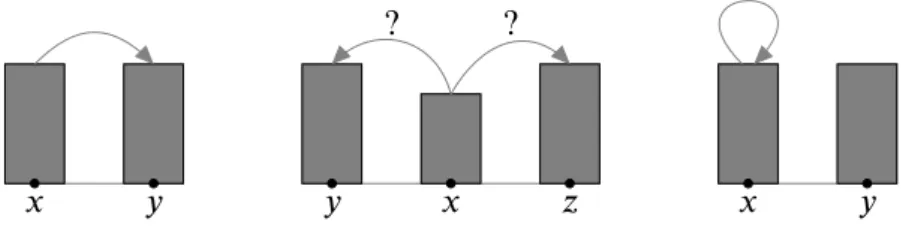
( ) é a soma dos recursos transferidos para na etapa 𝑛. Configura-se umempate quando mais de um vértice ∈ 𝒢 possui o mesmo
? ?
Figura 1.2: Situações possíveis de empates
recurso máximo e neste caso o vértice 𝑎𝑛( ) é escolhido aleatoriamente
Seção 1 O modelo e a dinâmica do Processo 5
duas possibilidades entre os vizinhos e o sorteio determinará quem será o
𝑎𝑛( ); e, finalmente, na terceira o vértice foi sorteado e envia recurso para
si mesmo,𝑎𝑛( ) = .
Com o intuito de melhor mostrar como funciona a dinâmica do processo um exemplo simples será útil, usando a idéia expressa em [5], representada na figura 1.3. Este exemplo representa a transferência de recursos em um subconjunto de ℤ, quando = 1, com 10 pontos consecutivos na reta, re-presentando os vértices neste caso. Os números são recursos e as setas mostram a direção da transferência. Observa-se que para = −1supõe-se
= 0 1 2 3 4 5 6 7 8 9
0( ) = 0, 65 →0, 80 →0, 90 ← 0, 85 ← 0, 70 ← 0, 15 0, 30 0, 25→0, 80 0, 65→ ?
1( ) = 0 0, 65 →2, 55 ← 0, 70 ← 0, 15 0 0, 30 0 1, 05 0
2( ) = 0 0 3, 90 ← 0, 15 0 0 0, 30 0 1, 05 0 3( ) = 0 0 4, 05 0 0 0 0, 30 0 1, 05 0
Figura 1.3: Fluxo dos recursos quando = 1
um valor do recurso menor do que 0, 80 do vértice = 1, por isso o valor do recurso em = 0, isto é, 0, 65 é transferido para = 1. Da mesma forma entende-se que no vértice = 10existe um recurso maior do que0, 80situado no vértice = 8 daí a transferência de = 9 para = 10.
Portanto, como pode-se ver os recursos movem-se de acordo com a dinâ-mica até a etapa𝑛 = 3, quando então permanecem estabilizados, mostrando sua fixação.
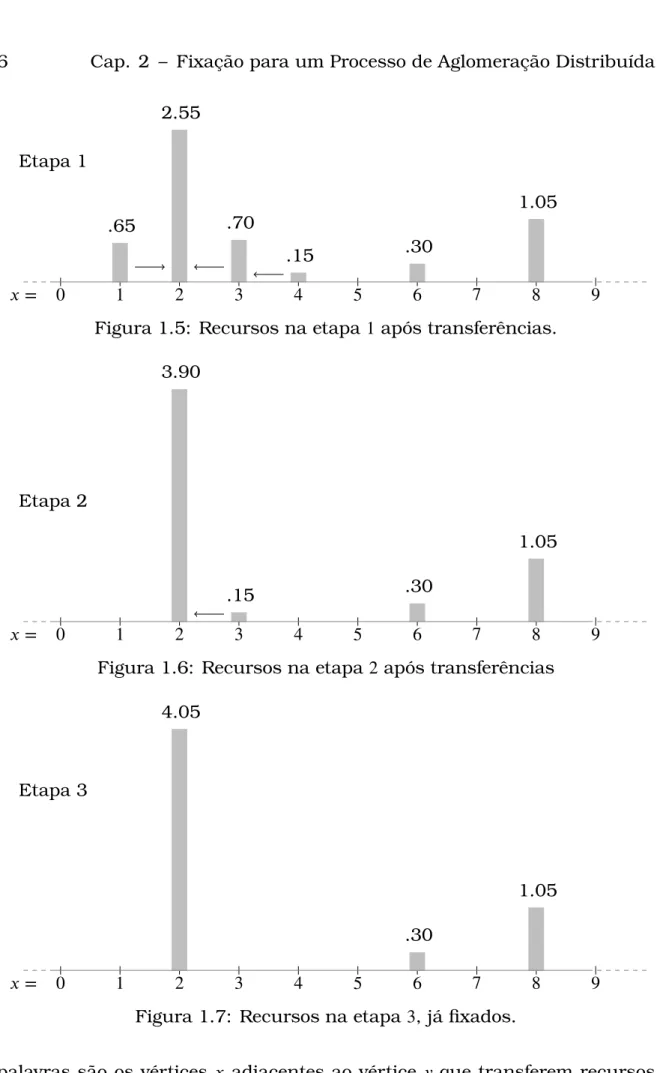
Note-se que após estas etapas todos os recursos que estavam distribuídos aleatoriamente nos vértices, na etapa0, concentram-se, agora, em somente três vértices. Nas figuras 1.4, 1.5, 1.6 e 1.7 a mesma dinâmica representada num gráfico. Define-se também o conjunto 𝑛( ) = { ∈ 𝒢 ∶ 𝑎𝑛( ) = }, em
0 1 2 3 4 5 6 7 8 9
.65 .80 .90 .85 .70
.15 .30 .25
.80 .65 Etapa 0
=
0 1 2 3 4 5 6 7 8 9
.65
2.55
.70
.15 .30
1.05 Etapa 1
=
Figura 1.5: Recursos na etapa 1 após transferências.
0 1 2 3 4 5 6 7 8 9
3.90
.15 .30
1.05 Etapa 2
=
Figura 1.6: Recursos na etapa 2 após transferências
0 1 2 3 4 5 6 7 8 9
4.05
.30
1.05 Etapa 3
=
Figura 1.7: Recursos na etapa 3, já fixados.
Seção 1 O modelo e a dinâmica do Processo 7
é importante observar que as áreas dos círculos nos vértices representam a quantidade de recursos designados para aqueles vértices.
> < ∨
∧
1 2
3
4
Figura 1.8: Representação de um exemplo do conjunto 𝑛( ), quando = 2
Também é necessário observar que a menos de possíveis empates e os respectivos desempates durante a dinâmica, somente a condição inicial é aleatória. Sejam a medida de probabilidade ℙ e o valor esperado 𝔼 para as quantidades de recursos iniciais e os possíveis empates.
Este modelo é um exemplo de uma estrutura proveniente de um estado inicial desordenado que se organiza a si mesmo durante o processo.
Respondendo à questão 2 mencionada no Capítulo 1, da forma mais geral possível e considerando qualquer dimensão, bem como qualquer invariância por translação na distribuição inicial, enuncia-se o teorema principal deste capítulo.
Teorema 1.1. Em ℤ , ∀ ≥ 1, para qualquer distribuição inicial de recursos
invariante por translação, quase certamente, o fluxo em cada vértice para após uma quantidade finita de etapas.
lemas enunciados na Seção 2 e suas combinações. Para alcançar este obje-tivo será usado oPrincípio de Transporte de Massa, cuja demonstração pode ser vista no Apêndice,
Agora introduz-se algumas notações adicionais que serão úteis nas for-mulações de tais lemas e suas respectivas demonstrações.
Para a cardinalidade de um conjunto será usada a notação|⋅|. Para cada
∈ ℤ e 𝑛 = 0, 1, …, somente um dos eventos descritos a seguir ocorrerá:
𝒜𝑛( ) = [ 𝑛( ) = 0] ,
ℬ𝑛( ) = [ 𝑛( ) > 0, 𝑛( ) = { }] ,
𝒞𝑛( ) = [ 𝑛( ) = { } para algum ≠ ] ,
𝒟𝑛( ) = [| 𝑛( )| > 1] ,
ℰ𝑛( ) = [ 𝑛( ) =∅] . Também para cada 𝑛 = 0, 1 …, define-se
′
𝑛( ) ∶= 𝑛(𝑎𝑛( )) ,
𝑛+1( ) ∶= 𝑎𝑛( 𝑛( )) com 0( ) = , 𝑛( ) ∶= { ∶ 𝑛( ) = }.
Com os seguintes significados: 𝑛( ) é a localização na etapa 𝑛 do recurso que inicialmente começou no vértice , e 𝑛( ) denota o conjunto de todos o vértices cujo recurso inicial está localizado no vértice = 𝑛( ) na etapa 𝑛,
observando-se que ′
𝑛( )≥ 𝑛( ).
Recordando que 𝑛( ) é o conjunto dos vértices na vizinhança de que transferem recursos para e 𝑎𝑛( ), é o vértice da vizinhança de que tem
o maior recurso, cabem algumas considerações a respeito das notações dos eventos descritos acima:
• 𝒜𝑛( ) = [ 𝑛( ) = 0]
O recurso no vértice é zero, não tem o que transferir e sendo coerente transfere ”nada” para si mesmo.
• ℬ𝑛( ) = [ 𝑛( ) > 0, 𝑛( ) = { }]
Neste caso o vértice possui o maior recurso dentre os vértices adja-centes a ele, pois 𝑎𝑛( ) = . Logo ele transfere o recurso para si mesmo.
Seção 2 Prova do Teorema Principal 9
Aqui o vértice que tem o maior recurso é algum adjacente a e dife-rente deste, 𝑎𝑛( ) = .
• 𝒟𝑛( ) = [| 𝑛( )| > 1]
Existem mais de um vértice com recurso maior do que os demais adja-centes. Um deles será sorteado para ser o 𝑎𝑛( ).
• ℰ𝑛( ) = [ 𝑛( ) =∅]
O vértice e adjacentes têm a mesma quantidade de recursos. Não existe o 𝑎𝑛( ).
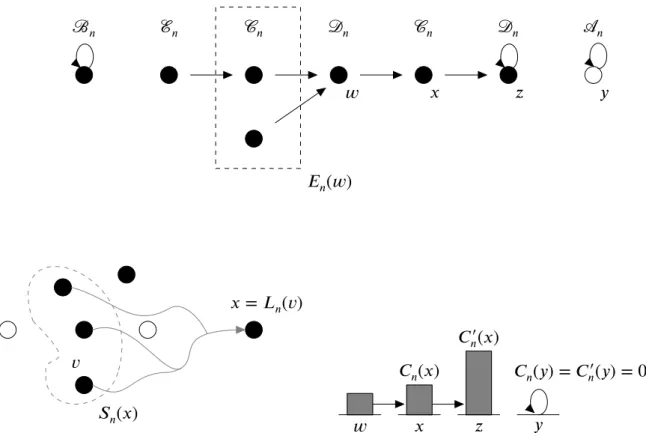
A Figura 1.9 exibe um diagrama que ajuda a entender as notações usadas no texto.
ℬ𝑛 ℰ𝑛 𝒞𝑛 𝒟𝑛 𝒞𝑛 𝒟𝑛 𝒜𝑛
𝑛( )
= 𝑛( )
𝑛( ) ′ 𝑛( )
𝑛( ) = 𝑛′( ) = 0 𝑛( )
Figura 1.9: Diagrama esquemático para a notação usada. Os círculos bran-cos representam vértices sem recurso
2 Prova do Teorema Principal
Nesta seção serão enunciados e demonstrados os lemas e um corolário que juntos levarão à demonstração do teorema principal enunciado na Seção 1.
Prova: Primeiramente,ℰ𝑛( ) = [ 𝑛( ) =∅] ocorre para no máximo um valor de 𝑛, após o qual sempre se tem 𝒜𝑛( ) = [ 𝑛( ) = 0]. Realmente por definição 𝑛( )é o conjunto dos elementos que enviam recursos para o vértice , sendo
vazio, os recursos em nesta etapa findaram, i. e., 𝑛( ) = 0, daí a ocorrência de𝒜𝑚( ),∀ 𝑚 > 𝑛. Portanto fica claro queℰ𝑛( )ocorre apenas para um valor de
, resultando ℙ [ℰ𝑛( ) i.v.] = 0 e a primeira parte do enunciado fica provada. Agora, como 𝒟𝑛( ) = [| 𝑛( )| > 1] segue que 𝒟𝑛( ) = [| 𝑛( )| − 1 > 0] e é o
evento que tem mais de um vértice que transfere recursos para . A Figura 2.1 é uma representação esquemática dos conjuntos𝒢 e 𝑛( ), onde as áreas dos círculos representam a quantidade de recursos em cada vértice. No caso
𝒢
𝑛( )
Figura 2.1: Diagrama esquemático dos conjuntos 𝒢 e 𝑛( )
acima tem-se que 𝑛( ) = { ∈ 𝒢 ∶ 𝑎𝑛( ) = } com 𝑎𝑛( ) = argmax{ 𝑛( ), ∈
Seção 2 Prova do Teorema Principal 11
Então o valor esperado da variável | 𝑛( )| será
𝔼 [| 𝑛( )|] = 𝔼 [|{ + ∈ 𝒢 ∶ 𝑎𝑛( + ) = }|]
= 𝔼
[∑𝟙[𝑎𝑛( + )= ]]
= ∑𝔼[𝟙[𝑎𝑛( + )= ]]
= ∑ℙ[𝑎𝑛( + ) = ]
De acordo com a invariância por translação pode-se escrever
(2.1) 𝔼 [| 𝑛( )|] = ∑ℙ[𝑎𝑛( ) = − ] .
Considerando a partição do espaço Ω = ⋃ {𝑎𝑛( ) = − } onde os eventos
[𝑎𝑛( ) = − ] são disjuntos tem-se que
(2.2) 1 = ℙ (Ω) = ℙ
[⋃𝑎𝑛( ) = − ]= ∑ℙ[𝑎𝑛( ) = − ] .
Por (2.1) e (2.2) segue que
𝔼 [| 𝑛( )|] = 1.
Definindo 𝑛( ) = | 𝑛( )| − 1, e calculando o valor esperado da variável 𝑛( )
resulta
𝔼 [ 𝑛( )] = 𝔼 [| 𝑛( )| − 1] = 𝔼 [| 𝑛( )|] − 1 = 0,
pois𝔼 [| 𝑛( )|] = 1 como demonstrado acima. Sabe-se ainda que: (2.3) 𝑛( ) = 𝑛( )+− 𝑛−( ) = 𝟙[ 𝑛( )]≥0− 𝟙[ 𝑛( )<0].
Onde, +
𝑛( ) = max( 𝑛( ), 0) e −𝑛( ) = − min{ 𝑛( ), 0} = − max{− 𝑛( ), 0}. O
valor esperado da expressão em (2.3) será
(2.4) 𝔼 [ 𝑛( )] = 𝔼 [ +
𝑛( )] − 𝔼 [ 𝑛−( )] = 𝔼 [ 𝑛( )] = ℙ [ 𝑛( )≥0] − ℙ [ 𝑛( ) < 0] .
Por outro lado,
𝑛( )+ = 1 ⋅ 𝟙[ 𝑛( )≥0]+ 0 ⋅ 𝟙[ 𝑛( )<0]
𝔼 [ 𝑛( )+] = 𝔼 𝟙[ 𝑛( )≥0] = ℙ [ 𝑛( )≥0], e como 𝑛( ) = | 𝑛( )| − 1 e 𝑛( ) ≥0 vem que
| 𝑛( )| − 1≥0 ⟹ | 𝑛( )|≥1.
Ainda tem-se a relação,
𝔼 [ −
𝑛( )] = 𝔼 [𝟙[ 𝑛( )<0]] = ℙ [ 𝑛( ) < 0].
Como 𝑛( ) = | 𝑛( )| − 1 e 𝑛( ) < 0 resulta que | 𝑛( )| < 1 acarretando
| 𝑛( )| = 0e consequentemente 𝑛( ) = −1.
É válida a seguinte relação
𝔼 [ +
𝑛( )] = 𝔼 [ 𝑛( ) ⋅ 𝟙[ 𝑛( )>0]]
≥𝔼 [1 ⋅ 𝟙
[ 𝑛( )]>0]
= ℙ [ 𝑛( ) > 0] .
(2.6)
e ainda considerando os resultados de (2.5) e (2.6) conclui-se a seguinte expressão
ℙ [ 𝑛( ) > 0]≤𝔼 [ +𝑛( )] = 𝔼 [ −𝑛( )] = ℙ [ 𝑛( ) = −1] .
Tem-se assim que comoℙ [ 𝑛( ) = −1] = ℙ [| 𝑛( )| = 0]eℙ [| 𝑛( )| = 0] = ℙ [ 𝑛( ) =∅] =
ℙ [ℰ𝑛( )] implica queℙ [ 𝑛( ) > 0]≤ℙ [ℰ𝑛( )].
Ou seja
(2.7) ∑∞
𝑛=1ℙ [ 𝑛( ) > 0]
≤
∞
∑𝑛=1ℙ [ℰ𝑛( )]≤1
Onde a desigualdade acima segue do fato de queℰ𝑛( )ocorre para no máximo
um valor de 𝑛. Como ∑
𝑛 ℙ [ 𝑛( ) > 0] < ∞ ou ∞
∑
𝑛=1ℙ [| 𝑛( )| > 1] = ∞
∑
𝑛=1ℙ [|𝒟𝑛( )|] < ∞, segue
pelo Lema de Borel-Cantelli queℙ [𝒟𝑛( ) i. v.] = 0, provando a segunda parte
do enunciado do lema. ∎
Observação. É importante notar que 𝑛+1( ) > 𝑛( ) somente pode ocorrer no evento 𝒟𝑛( ). Assim como a sequência ( 𝑛( ))𝑛∈ℕ é não-negativa e a partir de um determinado índice𝑛ela será não-crescente, quase certamente, temos que
lim
Seção 2 Prova do Teorema Principal 13
Lema 2.2. Em um vértice fixado, quase certamente, os empates não podem ocorrer infinitas vezes.
Prova: Para um par de vértices ≃ , seja o conjunto:
𝑛( , ) = {0 < 𝑛( ) = 𝑛( ) = max{ 𝑛( ), ≃ } para algum ≃ , ≠ }.
que denota o evento em que existe um empate no vértice , na etapa 𝑛, e é um dos candidatos para seus recursos, onde max{ 𝑛( ), ≃ } significa o
maior recurso nos vértices adjacentes a ou igual . Seja ℱ,𝑛 a 𝜎-álgebra gerada por
( 𝑚( ), 𝑚 ≤ 𝑛e ∈ ℤ ) e (𝑎𝑚( ), 𝑚 ≤ 𝑛 e ∈ ℤ ou 𝑚 = 𝑛 e ≠ )
que significam: os recursos no vértice em etapas anteriores a 𝑛 ou na própria etapa𝑛, e os vértices na vizinhança de ≠ que recebem os recursos
nas etapas anteriores a𝑛 ou na etapa𝑛 no vértice .
A𝜎-álgebraℱ ,𝑛contém todas as informações até a etapa𝑛, exceto por um
possível desempate no vértice na𝑛-ésima etapa. Seja 𝑛
\ = | 𝑛( )\{ }|a variável aleatória. Nota-se que 𝑛\ e 𝑛( , ) são
ℱ,𝑛-mensuráveis. No âmbito da 𝜎-álgebra ℱ ,𝑛 tem-se:
• Se 𝑛
\ = | 𝑛( )\{ }| = 0e também ocorre 𝑛( , )ou seja um empate,
en-tão, com probabilidade no mínimo 1
2, ocorrerá𝑎𝑛( )≠ . Esta afirmação
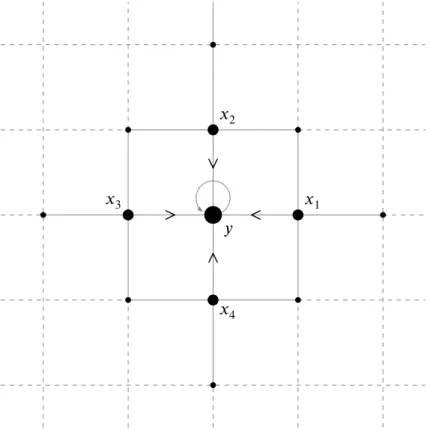
é válida em todo o espaço ℤ , mas para maior clareza no entendimento admite-se o raciocínio quando = 2, o que não invalida o processo em geral. Então para ℤ2 tem-se, tomando como referência a notação na
Figura 2.2, o conjunto 𝑛( ) = { 1, 2, 3, , } representa o conjunto dos
vértices que poderão transmitir recursos para o vértice , neste caso
𝑎𝑛( ) = . Então 𝑛
\ = | 𝑛( )\{ }| = |{ 1, 2, 3, }| = 4
Como 𝑛
\ = 0, todos os vértices na adjacência do vértice ,exceto o
tice , enviam recursos para outros vértices diferentes de , exceto o vér-tice . Havendo empate nos cinco vérvér-tices tem-se que ℙ ([𝑎𝑛( ) = ]) = 15 implicando que ℙ ([𝑎𝑛( )≠ ]) = 4
5. Se ocorre empate em quatro
vérti-ces resulta ℙ ([𝑎𝑛( )≠ ]) = 3
4, em três vértices ℙ ([𝑎𝑛( )≠ ]) = 2
final-1 2
3 1
2
𝒢 = { 1, 2, 3, , } 𝑛( ) = 𝑛( )
Figura 2.2: Conjunto 𝒢 , o vértice , e uma possível configuração para = 2
mente em dois vérticesℙ ([𝑎𝑛( )≠ ]) = 1
2 que é o menor valor dentro das
probabilidades nestes casos. Desse modo segue que ocorrerá o evento
ℰ𝑛( ) = [ 𝑛( ) =∅], assim 𝑛( ) = 0 para todo 𝑚 > 𝑛. Portanto o evento
𝑛( , ), que representa os empates, não pode ocorrer novamente.
• Se 𝑛
\ = | 𝑛( )\{ }| > 0e também ocorre 𝑛( , ), ou seja empate, então
com probabilidade no mínimo 1
2 + 1, ocorrerá 𝑎𝑛( ) = . Resultando
na ocorrência do evento 𝒟𝑛( ) = [ 𝑛( ) > 1]. Portanto a ocorrência de 𝑛( , ), empate, infinitas vezes implica também, quase certamente, a
ocorrência de 𝒟𝑛( ) infinitas vezes e pelo Lema 2.1,
ℙ ([𝒟𝑛( )infinitas vezes]) = 0
Finalizando a prova. ∎
Seção 2 Prova do Teorema Principal 15
ocorrerá, quase certamente: lim sup𝑛𝒜𝑛( ),lim sup𝑛ℬ𝑛( ) oulim sup𝑛𝒞𝑛( ), onde:
𝒜𝑛( ) = [ 𝑛( ) = 0]
ℬ𝑛( ) = [ 𝑛( ) > 0, 𝑛( ) = { }]
𝒞𝑛( ) = [ 𝑛( ) = { }, para algum ≠ ] .
Prova: Fixado ∈ ℤ , pelos Lemas 2.1 e 2.2 pode-se tomar𝑛0 ∈ ℕde modo
que𝒟𝑛( ) e ℰ𝑛( ) não ocorram e nem exista um empate em qualquer vértice
∈ 𝒢 , adjacente a , para todo 𝑛 ≥ 𝑛0.
Se 𝒜𝑛( ) ocorre para algum ∈ ℕ, também ocorrerá para todo 𝑚 > 𝑛.
Assim basta provar que se 𝒞𝑛( ) ocorre para algum 𝑛 ≥ 𝑛0, então 𝒞𝑛+1( )
também ocorrerá.
Agora se 𝒞𝑛( ) = [ 𝑛( ) = { }, para algum ≠ ] ocorre com 𝑛( ) = { } e
= 𝑎𝑛( ), tem-se
𝑛+1( )≥ 𝑛( ) > 𝑛( ) = 𝑛+1( )
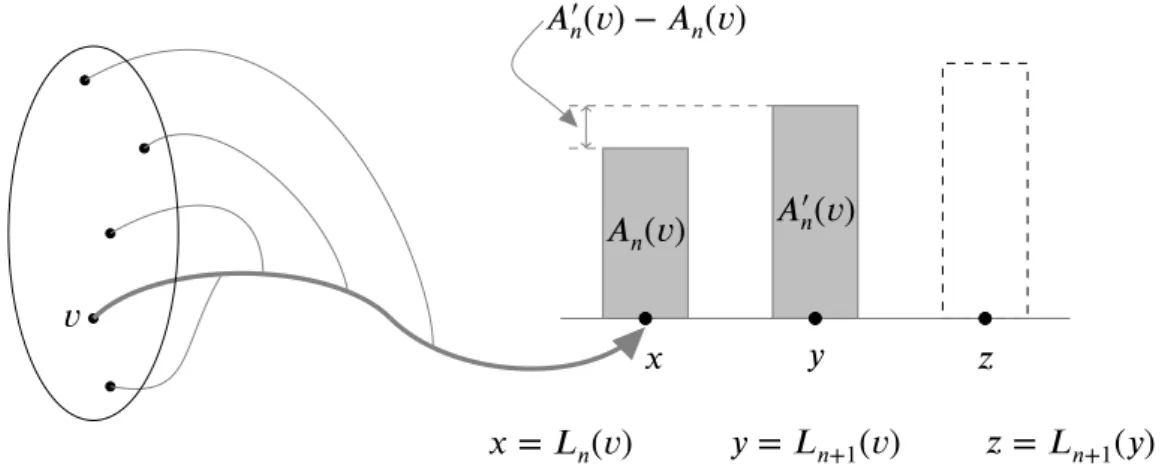
É necessário comentar a expressão acima com desigualdades e igualdades entre recursos na vizinhança de : a primeira desigualdade pode ser não-estrita, havendo a possibilidade da quantidade de recurso no vértice na etapa 𝑛 + 1 ser igual a quantidade transferida do vértice na etapa 𝑛, caso o recurso do vértice tenha sido transferido para um outro vértice na sua vizinhança tenha recurso maior. A segunda desigualdade é estrita pois a hipótese diz para𝑛≥𝑛0não ocorre empates, logo estes dois vértices vizinhos,
e , nunca terão recursos iguais, e finalmente, a igualdade final é fruto da transferência de recursos de acordo com a dinâmica do processo na etapa
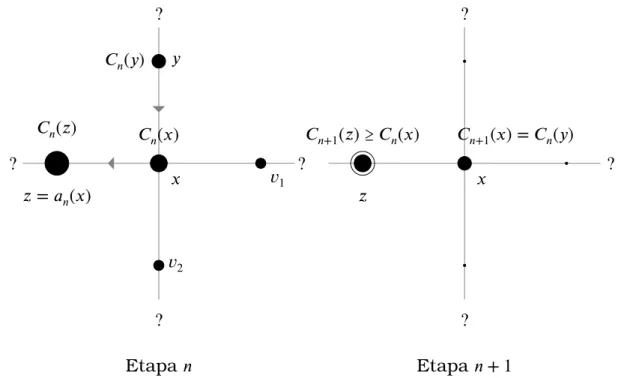
𝑛 + 1. A situação descrita é facilmente compreendida com a ajuda da Figura 2.3. Portanto 𝑎𝑛+1( ) ≠ , e desde que 𝒟𝑛( ) e ℰ𝑛( ) foram excluídos, deve-se
ter𝒞𝑛+1( ). Logo o evento 𝒞𝑛( )ocorre para todo 𝑚 > 𝑛. ∎ Pelo Lema 2.3 pode-se definir, de forma única, 𝒜-vértice, ℬ-vértice e
𝒞-vértice, conforme a ocorrência de lim sup
𝑛 𝒜𝑛( ), lim sup𝑛 ℬ𝑛( ) e lim sup𝑛 𝒞𝑛( ),
respectivamente.
Corolário 2.4. Para todo ∈ ℤ , lim𝑛 ( ′
𝑛( ) − 𝑛( )) = 0, quase certamente.
Prova: Para provar este corolário será seguida a estratégia esboçada a se-guir
Relembrando que ′
𝑛( ) ∶= 𝑛(𝑎𝑛( )) pode-se examinar as duas hipóteses
𝑛( )
= 𝑎𝑛( )
𝑛( )
?
𝑛( )
1 2 ? ? ? ? ? ?
Etapa 𝑛 Etapa 𝑛 + 1
𝑛+1( )≥ 𝑛( ) 𝑛+1( ) = 𝑛( )
Figura 2.3: Representação dos recursos nas etapas𝑛 e 𝑛 + 1 quando = 2
• Se é um𝒜-vértice, ou seja ocorrelim sup𝑛𝒜𝑛( ), onde𝒜𝑛( ) = [ 𝑛( ) = 0]
e neste caso𝑎𝑛( ) = , por definição segue que 𝑛′( ) = 𝑛(𝑎𝑛( )) = 𝑛( ) =
0, para todo𝑛suficientemente grande, logo ′
𝑛( ) − 𝑛( ) = 0, implicando
a convergência quase certamente.
• Se é umℬ-vértice, ou seja ocorrelim sup𝑛ℬ𝑛( ), ondeℬ𝑛( ) = [ 𝑛( ) > 0, 𝑛( ) = { }]
resulta ′
𝑛( ) = 𝑛(𝑎𝑛( )) = 𝑛( ), logo 𝑛′( ) − 𝑛( ) = 0, para todo𝑛
sufici-entemente grande, acarretando a convergência quase certamente.
Eliminadas as hipóteses acima resta analisar a terceira hipótese: se é um
𝒞-vértice.
Isto significa que para ocorre unicamente lim sup𝑛𝒞𝑛( ), onde 𝒞𝑛( ) =
[ 𝑛( ) = { }, para algum ≠ ] ou seja o vértice ∈ 𝑛( ) é o único vértice
que manda recurso para na etapa 𝑛.
Tome𝑛0 de modo que𝒞𝑛( ) ocorre para todo𝑛≥𝑛0.
Pelo Lema 2.1 pode-se assumir que𝒟𝑛( ) = [| 𝑛( )| > 1]não ocorrerá para
qualquer ∈ 𝒢 e 𝑛 ≥ 𝑛0, pois ℙ[𝒟𝑛( ) i. v.] = 0, em particular 𝑛+1( ) ≤ 𝑛( ),
pois transfere seu recurso para .
Afirmação: ′
𝑛+2 ( )≤ 𝑛( )para todo 𝑛≥𝑛0, onde 𝑛+2′ ( ) = 𝑛+2 (𝑎𝑛+2 ( )).
Desde que, adicionalmente, 𝑛+2 ( ) ≤ 𝑛+2′ ( ) e lim
ob-Seção 2 Prova do Teorema Principal 17
servação após a prova do Lema 2.1, tem-se então
𝑛+2 ( )≤ 𝑛+2′ ( )≤ 𝑛( ) ⟹ 𝑛+2 ( )≤ 𝑛( )
o que finalizará a prova. Logo basta mostrar a afirmação acima. Sejam𝑛0 fixado e 𝑛≥𝑛0. Com𝑚≥𝑛 define-se o conjunto
𝑚 = { ∼ ∶ 𝑚( ) > 𝑛( )} .
Pode-se descrever o conjunto 𝑚 da seguinte forma: são todos os vértices
4 3
1
2
𝑛( ) 𝑚( 3)
𝑚( 2)
𝑚( 1)
𝑚( 4)
Etapa𝑚
4 3
1
2
𝑚+1( 1)
𝑚+1( 2)
𝑛( )
𝑚+1( 3) 𝑚+1( 4)
Etapa 𝑚 + 1
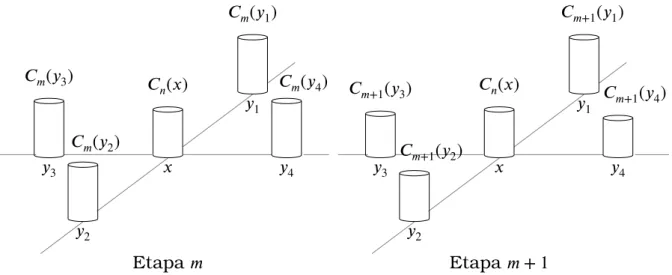
Figura 2.4: Para = 2, recursos nas etapas𝑚 e𝑚 + 1 nos vértices vizinhos a , referenciados ao vértice com recurso 𝑛( ) na etapa𝑛.
adjacentes ao vértice , tomado como referência, tais que na etapa 𝑚 a quantidade de recurso em é maior do que a quantidade de recurso em na etapa𝑛.
Como os recursos não crescem mais, na etapa 𝑚 + 1 os vértices mantém os seus recursos ou os transferem resultando que 𝑚+1 ⊆ 𝑚. A Figura 2.4
consiste, para = 2 e tomando sempre como referência o vértice e o seu respectivo recurso na etapa𝑛, da representação particular em que os recur-sos nos vértices adjacentes a ele são iguais na etapa 𝑚 e na etapa seguinte após a transferência de recursos foram alterados, mostrando que o novo conjunto de vértices adjacentes pode permanecer igual ou diminuir como é o caso representado.
Além do mais a ocorrência de 𝒞𝑛( ) implica que o vértice que recebe
re-curso de é diferente de , i. e.,𝑎𝑛( ) ≠ e como𝒟𝑛(𝑎𝑛( )) = [| 𝑛(𝑎𝑛( ))| > 1]
𝑛(𝑎𝑛( )) = { }. Assim 𝑛+1(𝑎𝑛( )) = 𝑛( )e portanto 𝑎𝑛( ) ∉ 𝑛+1
Se 𝑛+1 =∅ a prova está finalizada.
Se 𝑛+1 ≠∅ novamente encontra-se 𝑎𝑛+1( ) ∈ 𝑛+1\ 𝑛+2.
Prosseguindo desta maneira e como | 𝑛| < 2 encontramos 𝑛+ = ∅ para algum ∈ {1, … , 2 }o que conclui a prova da afirmação. ∎
Lema 2.5. Para cada ∈ ℕe ∈ ℤ fixados,
ℙ [0 < ′
𝑛( ) − 𝑛( ) < 𝛿, | 𝑛( )| ≤ ] →0, uniformemente em𝑛, quando 𝛿 →0.
Prova: Antes de iniciar a prova deste lema faz-se necessário discorrer sobre o significado do que se pretende provar.
O evento para o qual é calculada a probabilidade, isto é,
[0 < 𝑛′( ) − 𝑛( ) < 𝛿, | 𝑛( )|≤ ] ,
tem duas partes: a primeira diz que a quantidade de recurso no vértice que recebe recurso de na etapa 𝑛, i. e., ′
𝑛( ) = 𝑛(𝑎𝑛( )) difere muito pouco do
recurso no vértice também na etapa 𝑛, 𝑛( ), e ′
𝑛( ) > 𝑛( ). A segunda
parte afirma que a quantidade de vértices cujos recursos iniciais se juntam em , na etapa 𝑛, é limitado pr um valor ∈ ℕ.
Deseja-se provar que a probabilidade deste evento tende a zero, unifor-memente, quando a diferença dos recursos fica inferior a 𝛿 que, por sua vez, torna-se cada vez menor. Segue, agora, a prova.
Seja ∈ ℤ e considere 𝑛( 𝑛( )) como o conjunto dos vértices cujos
recursos iniciais, se juntarão ao recurso do vértice na etapa 𝑛. 𝑛( ) é o vértice, na etapa𝑛, em que está localizado o recurso que inicialmente estava no vértice . De acordo com as regras da dinâmica do processo, uma vez que duas ou mais fontes inicialmente distintas se juntam, elas não mais se separam.
Defina, agora, 𝑛( ) ∶= | 𝑛( 𝑛( ))|como o número de vértices no conjunto
𝑛( 𝑛( )) definido acima.
Para cada vértice fixado, o conjunto 𝑛( ) poderá ou não ser acrescen-tado de vértices com recursos iniciais em 𝑛+1( ) ao se passar para a etapa
𝑛+1, constituindo-se assim o conjunto 𝑛+1( 𝑛( )). resultando 𝑛+1( )≥ 𝑛( ).
Assim 𝑛( ) é não-decrescente em 𝑛.
Sejam 𝑛( ) = 𝑛( 𝑛( )) a quantidade total de recurso no vértice 𝑛( ),
na etapa 𝑛, e ′
Seção 2 Prova do Teorema Principal 19
𝑛+1( 𝑛( )) ≥ 𝑛( 𝑛( )) resulta que para cada vértice , o valor de
′
𝑛( ) − 𝑛( ) = 𝑛( 𝑛+1( )) − 𝑛( 𝑛( ))
é não-negativo, e como os recursos ao longo das etapas tendem a diminuir pode-se fazer a seguinte afirmação:
Afirmação: Para cada vértice fixo, a sequência ( ′
𝑛( ) − 𝑛( ))𝑛∈ℕ somente
pode decrescer nas etapas𝑛 tais que 𝑛( ) cresce, isto é, o tamanho do con-junto 𝑛( )aumenta.
Para provar esta afirmação, suponha que 𝑛( )não cresça, isto é, 𝑛( ) =
𝑛+1( ), quer dizer entre as etapas 𝑛e 𝑛 + 1 não há contribuição de nenhum
vértice ao conjunto 𝑛( ), assim 𝑛( ) = 𝑛+1( ), como pode ser observado na
figura 2.5. Então neste caso deseja-se mostrar que
𝑛( )
′ 𝑛( )
= 𝑛( ) = 𝑛+1( ) = 𝑛+1( ) ′
𝑛( ) − 𝑛( )
Figura 2.5: Representação dos recursos na etapa 𝑛 e do conjunto 𝑛( ).
(2.8) ′
𝑛+1( ) − 𝑛+1( )≥ ′𝑛( ) − 𝑛( ).
Na etapa𝑛 + 1 os recursos do vértice = 𝑛( )são transferidos para o vértice
= 𝑎𝑛( 𝑛( )) = 𝑛+1( ), e como não existe contribuição de um outro conjunto
para o vértice temos que 𝑛+1( ) = 𝑛( ), logo, demonstrar (2.8) é o mesmo
que mostrar que
′
𝑛+1( )≥ ′𝑛( ),
ou, equivalentemente, que
𝑛+1(𝑎𝑛+1( 𝑛+1( )))≥ 𝑛(𝑎𝑛( 𝑛( ))).
?
?
= 𝑛+1( ) = 𝑛+2( ) 𝑛+1( ) = 𝑛( )
′ 𝑛( )
′ 𝑛+1( )
= 𝑎𝑛+1( 𝑛+1( )) = 𝑎𝑛+1( ) ′
𝑛( ) = 𝑛+1(𝑎𝑛+1( 𝑛+1( )))
Figura 2.6: Recursos na etapa 𝑛 + 1, 𝑛( ) e o possível vértice .
vértice após a transferência para existe o sinal de interrogação indicando que não se sabe o que ocorre aí, e para efeito desta demonstração não há interesse neste fato. Vê-se que em agora existe o valor transferido de . Em
tem-se a ′
𝑛( ) transferido de e pode-se ter a contribuição de um outro
grupo de vértices constituindo o conjunto e além disto pode existir um outro vértice , vizinho de com recursos superiores aos de e que atrai os recursos de daquele.
Além disso também é vizinho de . Desta forma tem-se a as seguintes relações entre os recursos:
′
𝑛+1( ) = 𝑛+1(𝑎𝑛+1( ))≥ 𝑛 + 1( )≥ ′𝑛( ).
Resultando em
′
𝑛+1( )≥ ′𝑛( ),
e como sabe-se que 𝑛+1( ) = 𝑛( ), subtraindo em ambos os membros da
desigualdade acima implica que
′
Seção 2 Prova do Teorema Principal 21
Logo, se a diferença ′
𝑛( ) − 𝑛( ) diminui, então houve contribuição, o que
mostra a afirmação.
É, portanto, natural falar para
[ ′𝑛( ) − 𝑛( ); ∃𝑛tal que 𝑛( )≤ , ∈ ℕ, e ′𝑛( ) > 𝑛( )] ,
do seuínfimo, isto é
= inf𝑛 [ ′
𝑛( ) − 𝑛( ); 𝑛tal que 𝑛( )≤ , ∈ ℕ, e ′𝑛( ) > 𝑛( )]
que é uma variável aleatória estritamente positiva.
Calculando a probabilidade vem
ℙ [0 < ′
𝑛( ) − 𝑛( ) < 𝛿, 𝑛( ) ≤ ]≤ℙ
[[ ′𝑛( )>inf𝑛( )][
′
𝑛( ) − 𝑛( )] < 𝛿, 𝑛( ) ≤ ]
≤ℙ [ < 𝛿]→0, com 𝛿 →0.
Em particular, para fixado,
(2.9) ℙ [0 < ′
𝑛( ) − 𝑛( ) < 𝛿, 𝑛( ) ≤ ]→0, uniforme em 𝑛, com 𝛿 →0.
O limite em (2.9) será relacionado com o resultado desejado via um uso quantitativo do Princípio do Transporte de Massa. Omite-se𝛿, de agora em diante e denota-se o evento em (2.9) por 𝑛( )ou seja
𝑛( ) = [0 < ′𝑛( ) − 𝑛( ) < 𝛿, 𝑛( ) ≤ ] .
Para ∈ ℤ , denote por 𝑛( ) o evento 𝑛( )ocorrendo para algum ∈ 𝑛( ),
isto é, 𝑛( ) = ⋃∈ 𝑛( ) 𝑛( ). Se 𝑛( ) ocorre para algum , então ele ocorre
para todos eles porque os valores de 𝑛, ′
𝑛e 𝑛são constantes dentro de 𝑛( )
e iguais a 𝑛( ), ′
𝑛( ) e | 𝑛( )|, respectivamente. Para ∈ ℤ e escrevendo
𝑚( , ) = 𝟙[ 𝑛( )= , 𝑛( )] tem-se tomando o somatório em ,
∑ 𝑚( , ) = ∑ 𝟙[ 𝑛( )= , 𝑛( )]
= ∑ 𝟙[ 𝑛( )= ]⋅ 𝟙[ 𝑛( )] o segundo fator não depende de , logo,
Resultando ∑ 𝑚( , ) = 𝟙[ 𝑛( )]. A invariância da translação do processo dá
𝔼
[∑𝑚( , + )]= 𝔼[∑ 𝟙[ 𝑛( )= + , 𝑛( )]]
= ∑ 𝔼[𝟙[ 𝑛( )= + , 𝑛( )]]
= ∑ℙ[ 𝑛( ) = + , 𝑛( )]
= ∑ℙ[ 𝑛( − ) = , 𝑛( − )] , translação
Calculando no sentido inverso obtemos 𝔼 [∑ 𝑚( , + ) = 𝔼 ∑ 𝑚( − , )]. Significando o seguinte,
(2.10) 𝔼
[∑𝑚( , )]= 𝔼[∑𝑚( , )] ∀ .
Como foi demonstrado acima 𝟙 𝑛( ) = ∑ 𝑚( , ),e tomando a esperança
ℙ [ 𝑛( )] = 𝔼 [𝟙 𝑛( )] = 𝔼 [∑𝑚( , )]
= 𝔼
[∑𝑚( , )] por (2.10) = 𝔼
[∑ 𝟙[ 𝑛( ), 𝑛( )= ]] pela definição
= 𝔼
[∑ 𝟙[ 𝑛( ), ∈ 𝑛( )]]
= 𝔼 [𝟙[ 𝑛( )]] ∑ 𝟙[ ∈ 𝑛( )]
= ℙ [ 𝑛( )] ⋅ | 𝑛( )|≥ℙ [ 𝑛( )] , ∀ , .
Resulta
ℙ [ 𝑛( )] ≥ ℙ [ 𝑛( )] , ∀ , .
Agora, 𝑛( ) é exatamente o evento considerado na afirmação deste lema e como ℙ [ 𝑛( )] → 0, uniformemente em 𝑛, quando 𝛿 → 0, fica provado o
resultado. ∎
Utilizando os resultados obtidos nos lemas anteriores bem como no Co-rolário 2.4 passa-se à prova do teorema principal enunciado na Seção 1.
Seção 2 Prova do Teorema Principal 23
lim sup𝑛ℬ𝑛( )ou lim sup𝑛𝒞𝑛( ), ocorrerá, quase certamente..
Seℙ [lim sup𝑛[𝑎𝑛( )≠ ]] = 0, quando𝑛→∞, conclui-se que o evento[lim sup𝑛𝒞𝑛( )]
não ocorrerá, quase certamente, ocorrendo portanto𝒜𝑛( )ouℬ𝑛( ), o que dá
a fixação. Logo basta provar queℙ [lim sup𝑛[𝑎𝑛( )≠ ]] = 0
Tomando qualquer 𝛿 > 0, se 𝑎𝑛( )≠ tem-se os seguintes resultados:
(i) ′
𝑛( ) = 𝑛( ), caracterizando um empate em , ou
(ii) ′
𝑛( ) − 𝑛( )≥𝛿, ou
(iii) 0 < ′
𝑛( ) − 𝑛( ) < 𝛿
Levando-se em conta o que diz o Lema 2.2 e o Corolário 2.4 as probabilidades dos dois primeiros eventos tendem a0, quando 𝑛→∞.
Resta, portanto, considerar o último evento. E neste caso para qualquer escolha de ∈ ℕ, este evento pode ser dividido em dois casos, a saber: 1) | 𝑛( )| = 𝑛( )≤ , ou
2) | 𝑛( )| = 𝑛( ) > .
Pela equação (2.9) no Lema 2.5, a probabilidade de que ocorra o primeiro caso tende a 0, uniformemente a0, quando 𝛿 →0. Portanto, para concluir a
prova do teorema basta mostrar que lim
→+∞[ 𝑛( ) > ] = 0. Define-se a função de massa
𝑚( , ) = 𝟙[ 𝑛( )= ].
Assim, pode-se escrever
𝑛( ) = | 𝑛( )| = ∑ 𝟙[ 𝑛( )= ] = ∑ 𝑚( , ).
Tomando a esperança de ambos lados, resulta
𝔼 [ 𝑛( )] = 𝔼 [∑ 𝑚( , )] = 𝔼[∑ 𝑚( , )] = 𝔼[∑ 𝟙[ 𝑛( )= ]]= 𝔼 [1] = 1.
Onde na segunda igualdade foi utilizada o Princípio de Transporte de Massa. Logo, pela Desigualdade de Tchebychev, segue
Finalmente lim
CAPÍTULO 3
Fuga de Recursos em Processos de
Aglomeração Distribuída
1 Definições e o enunciado do resultado principal
Nesta seção, com o propósito de melhor esclarecer o contexto, as notações convenções e definições poderão ser repetidos ou apresentadas de forma di-ferente, e, é claro serão introduzidos novos. Assim, da mesma forma como definido no Capítulo 2, considera-se para ≥ 1, inteiro, o reticulado com
dimensão , i.e., o grafo com vértices emℤ e o conjunto de elos compreen-dendo todos os pares de vértices( , )(= ( , )) com| − | = 1, onde|⋅|denota a norma emℝ e tais vértices são ditos adjacentes. A notação ℤ será usada para o grafo como também para o conjunto de vértices e tal uso ficará claro no contexto.
A dinâmica do processo no modelo de ‘distribuição aglomerada’ introdu-zido por Coffman, Courtois, Gilbert e Piret [5] é o mesma descrita no ca-pítulo acima citado. Apenas fazendo um breve resumo: para cada vértice do reticuladoℤ será designado aleatoriamente um número não-negativo
0( ) ∈ [0, ∞) que será entendido como a quantidade de recurso inicial
depo-sitado no vértice na etapa0. A família ( 0( ); ∈ ℤ ) não será necessaria-mente assumida independente. Então a cada etapa do processo cada vértice transfere seu recurso para o vértice maisrico na sua vizinhança.
Recordando, a evolução é definida recursivamente, como anteriormente. Suponha que na etapa 𝑛 a quantidade de recurso em cada vértice seja denotada por 𝑛( )e seja o conjunto𝒢( ) = { ∈ ℤ ∶ | − |≤1}avizinhança
de , onde ele próprio está incluso e, ainda, o conjunto
𝑛( ) = { ∈ 𝒢( ) ∶ 𝑛( ) = max∈𝒢( ) 𝑛( )}.
Agora seja um vértice escolhido uniformemente ao acaso no conjunto
𝑛( ), independentemente para cada e toma-se
𝑎𝑛( ) = , se 𝑛( ) = 0,
, se 𝑛( ) > 0.
Observa-se que 𝑎𝑛( ) é o vértice para o qual os recursos localizados em
na etapa 𝑛 (se existir algum) serão transferidos durante a etapa 𝑛 + 1 na evolução do processo.
Tem-se também a seguinte notação para os recursos na etapa 𝑛 + 1 no vértice ,
𝑛+1( ) ∶= ∑ ∶𝑎𝑛( )=
𝑛( ).
Para um determinado vértice será usada a notação ∞( ) para repre-sentar 𝑛lim
→∞ 𝑛( ).
Se para, todo 𝑛 suficientemente grande, tem-se 𝑎𝑛( ) = e 𝑎𝑛( ) ≠ para
todos os vizinhos de , diz-se que o fluxo em termina após finitas eta-pas e neste caso o limite de 𝑛( ) é atingido após finitas iterações e será denominado quantidade final do recurso em .
Se para todo𝑛suficientemente grande𝑎𝑛+1( ) = 𝑎𝑛( )diz-se que , a menos
uma quantidade finita de etapas, transfere seu recurso para o mesmo vértice fixado.
Define-se ainda para um vértice , a variável aleatória 0( ) como o a quantidade de recurso inicial na etapa em , e a família ( 0( ); ∈ ℤ ) como
configuração inicial. De forma análoga tem-se que ( 𝑛( ); ∈ ℤ ) será a con-figuração na etapa 𝑛.
Considera-se que umempate ocorre no vértice quando a cardinalidade de 𝑛( )é estritamente maior do que um, e neste caso 𝑎𝑛( )é escolhido
uni-formemente ao acaso entre os vértices na vizinhança de que maximiza
𝑛( ).
É importante observar que fora os possíveis desempates toda a aleato-riedade está contida na configuração inicial, e logo que um vértice tenha recurso zero assim ele permanecerá. Além disso, os recursos transferidos de dois ou mais vértices para o mesmo vértice, estes serão somados no vér-tice que os recebe.
Seção 2 Florestas emℤ invariantes por translação 27
Teorema 1.1. Seja ≤2. Existe uma distribuição invariante por translação
para uma configuração inicial( 0( ); ∈ ℤ ) tal que para cada ∈ ℤ
(1.1) 𝔼 [ ∞( )] < 𝔼 [ 0( )]
O Teorema 1.1 será provado na Seção 3, para tal tarefa na Seção 2 será construída uma coleção aleatória de árvores (floresta) com terminal único, imersa emℤ , de uma forma invariante por translação e também será apre-sentada um breve discussão sobre florestas aleatórias em ℤ . Aos vértices desta floresta serão alocados quantidades de recursos de modo que durante a evolução do processo cada recurso segue o único caminho autoevitante para o infinito na floresta.
A conclusão do Teorema 1.1 é falsa para = 1. De fato, suponha que o evento, “os recursos iniciando na origem não param após uma quantidade finita de etapas” tem probabilidade positiva, então pela invariância da trans-lação existe, com probabilidade positiva, uma quantidade de vertices para os quais o recurso inicial não pararão após uma quantidade finita de etapas. Segue daí que, com probabilidade positiva, existem uma quantidade infinita de etapas nas quais o recurso entra ou deixa a origem, contradizendo a fixa-ção provada no Capítulo 2 deste trabalho. Observe que o mesmo argumento pode ser generalizado, por exemplo, para qualquer grafo da forma ℤ ×
onde é um grafo-vértice transitivo finito. (Para tais grafos a invariância por translação é substituída pela invariância por automorfismo)
2 Florestas em
ℤ
invariantes por translação
Nesta seção serão utilizados conceitos da Teoria dos Grafos, cuja referência é [6]. Um grafo é um par = ( , ) de conjuntos, onde ⊆ × . Os elementos do conjunto são chamados de vértices de e os elementos de são denominados oselos do grafo . Dado = ⟨ , ⟩ ∈ diz-se que , são vérticesvizinhosem , simplifica-se escrevendo = . Ograude um vértice é o número de elos que possuem tal vértice, e, ainda um grafo é conexo se para todo , ∈ , existe um caminho em ligando a , onde umcaminho
é um grafo não-vazio = ( , ) da forma
= { 0, 1, … , } = { 0 1, 1 2, … , −1 }
Para o grafo = ( , ) se ⊂ e ⊂ então = ( , )é denominado
subgrafo de .
Os vértices 0 e estão ligados por e são chamados de terminais, a Figura 2.1 mostra um exemplo com um grafo finito. Quando 0 = tem-se um ciclo ou circuito. Um caminho é denominado autoevitante se todos os seus vértices são distintos.
Figura 2.1: Representação de um grafo finito e um caminho em .
Seja = ( , )um grafo infinito, ou seja com os conjuntos da forma:
= {… , 0, 1, … , , …} = {… , 0 1, 1 2, … , −1 , …}
onde também todos os são distintos. Valem todas as definições dadas acima e no restante deste trabalho serão considerados grafos infinitos. Uma
∞
Seção 2 Florestas emℤ invariantes por translação 29
floresta de é um subgrafo de que não tem ciclos e uma árvore é uma floresta conexa. Um subgrafo gera se ele contém todos os vértices de . Uma floresta geradora em é um subgrafo de que é uma floresta e que gera , e a mesma afirmação vale para a árvore, que será denominada
árvore geradora. Os vértices de uma floresta que possuem somente um vizinho são chamadas defolhas. Um caminho autoevitante infinito iniciando em um dado vértice é denominado terminal, na Figura 2.2 pode-se ver um exemplo de terminal único partindo de um vértice ∈ ℤ2. O número de terminaisde uma árvore é o número de terminais distintos iniciando em um vértice. Uma árvore é denominadaterminal únicose ela tem um terminal. Foi escolhido um reticulado inteiro de dimensão como o grafo subjacente. Para esta escolha a literatura provê inúmeras construções de florestas geradoras aleatórias com distribuição invariante por translação, ver [1] e [13]
Neste trabalho será discutido uma construção baseada em uma árvore geradora mínima em duas dimensões, que se passa a descrever a seguir.
Sejam um conjunto de elos de um reticulado ℤ2 e a família
{ ; ∈ }
de variáveis aleatórias independentes distribuídas uniformemente no inter-valo[0, 1].
Para cada ciclo do reticulado será excluído o elo para o qual o valor de é o máximo no ciclo de elos. Após estas exclusões o grafo resultante será de-nominado defloresta geradora minimal que é, quase certamente, uma árvore de terminal único invariante e ergódica sob as translações no reticulado, ver [9].
Usando a floresta geradora minimal emℤ2pode-se construir uma floresta
aleatória emℤ com > 2onde a distribuição é invariante sob as translações do reticulado, no qual cada componente é um terminal único.
Para tal considere ℤ como ℤ2 × ℤ −2 e em cada ‘camada’ ℤ2× { }, onde
percorre ℤ −2 faz-se a imersão de uma cópia da árvore geradora minimal
. O subgrafo de ℤ resultante é uma floresta minimal geradora invariante por translação com terminais únicos como componentes. Na Figura 2.3 representam-se as camadas emℤ3 = ℤ×ℤ2. O acima descrito leva ao seguinte
lema.
Lema 2.1. Para cada ≥ 2, existe uma floresta aleatória invariante por
translação emℤ , na qual cada componente conexa é um terminal único, quase certamente.
Corolário 2.2. Para cada ≥2, existe uma floresta aleatória invariante por
Z
X
Y
ℤ2
ℤ2
ℤ2
0 1 2
Figura 2.3: Para = 3, tem-se três camadas da decomposiçãoℤ2× ℤ. certamente
(i) Toda componente conexa de é terminal único.
(ii) Todo elo deℤ2 no qual os extremos estão em , é um elo de .
Prova: Seja uma floresta geradora como no Lema 2.1 e define-se os se-guintes conjuntos:
( ) é conjunto de elos de e ( ) é o conjunto de vértices de . Seja ̃ a floresta com o conjunto de vértices definidos por
( ̃) = {2 ∶ ∈ ( )} ∪ { + ∶ ⟨ , ⟩ ∈ ( )}e o conjunto de elos
( ̃) = {⟨2 , + ⟩ ∶ ⟨ , ⟩ ∈ ( )}.
Pode-se dizer que os conjuntos acima fazem com que ̃ corresponda à floresta que é obtida quando é ampliado duas vezes.
Como se pode ver a construção com estes novos conjuntos fazem corres-ponder cada elo ⟨ , ⟩ de a dois elos ⟨2 , + ⟩e ⟨ + , 2 ⟩ em ̃.
Observe que ̃ é uma floresta aleatória que é invariante com respeito às translações de 2ℤ e que possui a propriedade de que todo par de vértices
, satisfazendo a relação | − | = 1está conectado por um elo em ̃.
Afim de se configurar a invariância com respeito à todas as translações de ℤ seja um elemento uniformemente aleatório do cubo {0, 1} ,
inde-pendente de ̃ e faça = ̃ + . ∎
3 Prova do resultado principal
Seção 3 Prova do resultado principal 31
Como pode-se ver pelo enunciado do Teorema 1.1 o objetivo é mostrar que existe uma distribuição tal que para um número suficientemente grande de etapas a esperança do recurso nesta etapa é menor que a esperança do re-curso inicial em cada vértice de ℤ . Assim será mostrado que existe uma configuração inicial ( 0( ); ∈ ℤ ) com distribuição invariante por transla-ção e que vale (1.1), no Teorema 1.1.
Entretanto, antes de prosseguir faz-se necessário introduzir alguns con-ceitos, definições e notações que ajudarão a provar os lemas e o próprio teorema.
Seja uma floresta aleatória em ℤ dada como no Corolário 2.2. (a) Para vértices e escreve-se ∼ se ⟨ , ⟩é um elo de .
(b) Define-se uma ordem parcial (aleatória) ≤ em ℤ . Diz-se ≤ se, e
so-mente se e são vértices de e pertence a um único caminho infinito autoevitante em iniciando em .
(c) Se ≤ diz-se que umancestral de e que é umdescendente de .
(d) Se ≤ e ∼ diz-se que é o pai de . É importante ressaltar que
cada vértice de possui um único pai. Ademais, para todo vértice de , exatamente um vértice em{ ∶ ∼ }é o pai de , e os outros são des-cendentes de . A Figura 3.1 mostra um vértice com dois desdes-cendentes, onde este vértice é o pai de .
(e) Define-se, agora, para cada vértice ∈ ℤ , a quantidade inicial de recurso no vértice :
(3.1) 0( ) = ∑∈ℤ 𝟙[ ≤ ], se ∈
0, se ∉ .
Observe que se ∈ , então 0( ) é o número de descendentes de . Como toda componente conexa de é um terminal único segue que este número é finito de acordo com as definições acima. Portanto, deve-se notar que como a distribuição de é invariante sob as translações de
ℤ , a família( 0( ); ∈ ℤ ) também será.
∞
Figura 3.1: Vértice pai e descendentes e .
eliminando-se todas suas folhas, i. e., vértices que têm somente um vizinho. Seja 0 = e para𝑛 = 1, 2, …define-se indutivamente 𝑛 = 𝜙( 𝑛−1).
Na Figura 3.2 pode-se ver a aplicação𝜙agindo.
A observação seguinte é justificável pelas definições anteriores, e o exame da situação representada na Figura 3.2.
∞ ∞
𝜙
𝑛 𝜙 ( 𝑛) = 𝑛+1
Seção 3 Prova do resultado principal 33
Observação 3.1. Sejam um vértice de , o pai de e𝑛 ∈ ℕ ∪ {0}. Então está em 𝑛+1 se, e somente se, está em 𝑛.
Lema 3.2. Para todo vértice em , existe um índice finito 𝑛0 (dependendo de ) tal que, para todo𝑛≥𝑛0, não pertence a 𝑛
Prova: Pela Observação (3.1), 𝑛0( ) é no máximo 1 mais o número de
des-cendentes de . E como visto anteriormente este número é finito. ∎
Lema 3.3. Suponha que, para todo , 0( )é dado por (3.1). Então para todo
𝑛 ∈ ℕ ∪ {0}
(3.2) 𝑛( ) > ∑∶ ∼ ,≤
𝑛( ), se ∈ 𝑛
= 0, se ∉ 𝑛.
Prova: A prova será por indução em𝑛.
Para𝑛 = 0, pela expressão (3.1) vê-se que com ∈ 0(= )pode-se escrever 0( ) = ∑
∈ℤ
𝟙[ ≤ ]
Por outro lado se ∈ 0 e ainda com ∼ , ≤ , i. e., é pai de sabe-se,
também por (3.1), que
0( ) = ∑ ∈ℤ 𝟙[
≤ ]
Tomando o somatório em ambos os lados da primeira expressão vem que,
∑
∶ ∼ ,
≤
0( ) = ∑ ∶ ∼ ,
≤
∑∈ℤ 𝟙[ ≤ ] = ∑
∈ℤ \{ }
𝟙[ ≤ ] = 0( ) − 1.
Logo,
0( ) > ∑ ∶ ∼ ,
≤
0( )
Se ∉ 0, então 0( ) = 0 por definição. Logo o resultado está provado para
𝑛 = 0.
flo-resta de acordo com o Corolário 2.2 e considerando ainda que dois vértices de 𝑛 são vizinhos em ℤ , eles estarão conectados por um elo de 𝑛.
Pelo descrito acima e a expressão (3.2), vê-se claramente que para cada vértice de 𝑛, tem-se que 𝑎𝑛( ) (recordando: é o vértice para o qual os
re-cursos, em , no tempo𝑛 são transferidos na etapa𝑛 + 1) é o pai de , isto é,
∼ 𝑎𝑛 e ≤𝑎𝑛( ).
Na expressão (3.2), verifica-se se um vértice ∉ 𝑛, fora de 𝑛, o valor de 𝑛( ) = 0, assim na etapa 𝑛 + 1 tem-se
𝑛+1( ) = 0 se ∉ 𝑛+1,
(3.3)
𝑛+1( ) = ∑ ∶ ∼ ,
≤
𝑛( ) se ∈ 𝑛+1.
(3.4)
Onde (3.4) vem da definição dada na Seção 1 deste capítulo. Agora aplicando (3.2) no vértice , na etapa𝑛, tem-se que
(3.5) 𝑛( ) > ∑
∶ ∼ ,
≤
𝑛( )
Tomando o somatório em ambos os lados da expressão acima obtem-se,
(3.6) ∑
∶ ∼ ,
≤
𝑛( ) > ∑ ∶ ∼ ,
≤
∑
∶ ∼ ,
≤
𝑛( )
E agora, aplicando (3.4), e a Observação (3.1), e ainda observando que para
∈ 𝑛\ 𝑛+1, também vale, desde que ambos os lados de (3.4) são iguais a zero,
segue que para ∈ 𝑛+1 obtemos,
(3.7) 𝑛+1( ) = ∑
∶ ∼ ,
≤
𝑛( ) > ∑ ∶ ∼ ,
≤
∑
∶ ∼ ,
≤
𝑛( ) = ∑ ∶ ∼ ,
≤
𝑛+1( ).
Vê-se que as equações (3.3) e (3.7) valendo para a etapa𝑛 + 1e reescritas abaixo
𝑛+1( )
> ∑∶ ∼ ,
≤
𝑛+1( ), se ∈ 𝑛+1
= 0. se ∉ 𝑛+1.
Seção 3 Prova do resultado principal 35
Prova do Teorema 1.1: Seja ∈ ℤ e a configuração inicial ( 0( ); ∈ ℤ ). Pelo Lema 3.3, 𝑛( ) = 0se ∉ 𝑛, e invocando o Lema 3.2, com um𝑛0tal que
𝑛≥𝑛0 implicando ∉ 𝑛, tem-se quase certamente, que 𝑛( ) = 0 para todo 𝑛
suficientemente grande. Assim 𝑛lim
→∞ 𝑛( ) = 0
, quase certamente.
𝔼 [ 0( )] = 𝔼 ∑ ∈ℤ 𝟙[
≤ ] = ∑
∈ℤ 𝔼 [𝟙[
≤ ]] = ∑
∈ℤ ℙ [
≤ ] .
Como as árvores geradoras minimais são invariantes por translação, pela definição de 0( )temos que ℙ [ 0( ) > 0] > 0.
E como a ℙ [ 0( ) > 0] > 0 acarreta
𝔼 [ 0( )] > 0
segue que
0 = 𝔼 [lim𝑛→∞ 𝑛( )] = 𝔼[ ∞( )] < 𝔼 [ 0( )]
𝔼 [lim𝑛→∞ 𝑛( )] < 𝔼[ 0( )] .
concluindo a prova do teorema. ∎
CAPÍTULO 4
Observações e Problemas abertos
Nos capítulos anteriores foram estudados os resultados obtidos nos artigos [10] e [3], onde foram analisadas o fluxo das distribuições em vértices, numa quantidade grande de etapas.
O propósito deste pequeno capítulo é destacar a importância de algumas observações relativa aos temas objeto dos capítulos anteriores. Nele serão tratadas observações que se aplicam a todo o trabalho, bem como a propo-sição de outras questões.
A primeira delas é relativa a mencionada obviedade de 𝔼 [ 0( )] > 0 para todo vértice . Acontece, entretanto, que este valor esperado é até mesmo
∞, como se vê nos cálculos a seguir
𝔼 [ 0( )] = ∑ ∈ℤ
ℙ [ ≤ ] = ∑
∈ℤ
ℙ [ + ≤ ]
= ∑∈ℤ ℙ [ ≤ − ] = ∑
∈ℤ
ℙ [ ≤ ] = ∞.
onde a segunda e quarta igualdades são resultado de substituições e a ter-ceira é válida devido à invariância por translação e a igualdade final segue do fato de que tem uma quantidade infinita de ancestrais, quase certamente. Como mencionado em [3] não é possível construir um exemplo no qual os recursos escapam para o infinito, exceto quando a quantidade de recurso inicial num dado vértice tem um valor esperado finito. É interessante per-guntar se tais exemplos existem.
Particularmente, na construção idealizada em [3], a configuração inicial foi escolhida de tal forma que, quase certamente, a dinâmica induzida acon-tece em uma floresta com componentes com terminal único, imersa emℤ , e em cada etapa os recursos são transferidos do vértice com recurso não-nulo para o seu respectivo vértice pai. Não fica claro se para toda configuração inicial com estas propriedades o valor esperado da quantidade de recurso
inicial em um vértice é infinita. Essas considerações são formuladas mais formalmente nas duas questões seguintes.
Questão 4. Suponha que ( 0( ), ∈ ℤ ) tenha uma distribuição invariante por translação e é positiva nos vértices de uma floresta com terminais úni-cos. Alem disso, suponha que durante a 𝑛-ésima etapa da evolução, todo vértice no qual 𝑛−1( ) > 0 transfere seu recurso para o seu vértice pai. É o caso em que 𝔼 [ 0( )] = ∞?
Questão 5. Existe uma distribuição invariante por translação para uma con-figuração inicial na qual 𝔼 [ ∞( )] < 𝔼 [ 0( )] < ∞?
APÊNDICE
Princípio do Transporte de Massa
Neste apêndice, que é um resumo do artigo [8], será discutido o importante
Princípio de Transporte de Massa. Informações mais detalhadas poderão ser encontradas no artigo citado.
Inicialmente algumas definições e ao final o Teorema do Princípio de Transporte de Massa.
Definição Seja = ( , ) um grafo infinito. Uma aplicação bijetiva ∶ →
tal que o elo ⟨ ( ), ( )⟩ ∈ se, e somente se, o elo ⟨ , ⟩ ∈ é chamado
automorfismo de grafospara . O grafo é dito transitivo se para qualquer
, ∈ existe um automorfismo de grafos tal que ( ) = .
Definição Sejam = ( , ) um grafo transitivo e Aut( ) o grupo de auto-morfismos de e um subgrupo fechado de Aut( ). Para ∈ defina
estabilizador de como o subgrupo Aut ( ) = {ℎ ∈ ∶ ℎ = }. Então é dito ser unimodular se para todo , ∈
|stab ( ) | = |stab ( ) |
O grupo é dito serunimodular se existe um subgrupo fechado unimodular de Aut( ) que age transitivamente em .
Definição Seja grupo enumerável e suponha que é um conjunto simé-tricos de geradores. Defina um grafo = ( , ) com o conjunto de vértices tal que o elo ⟨ , ⟩ é um elo se, e somente se, 𝑠 ∈ tal que = 𝑠. O grafo é chamado umgrafo de Cayley à direita de .
Considere uma variável aleatória como um automorfismo invariante tomando valores em um conjunto finito dos elos do grafo = ( , ); uma invariância de automorfismo significa que para qualquer conjunto de elos
{⟨ 1, 1⟩ , … , ⟨ , ⟩} e qualquer automorfismo de a distribuição de
( (⟨ 1, 1⟩ , … , ⟨ , ⟩)) ,
é o mesmo que
( (⟨ ( 1), ( 1)⟩ , … , ⟨ ( ), ( )⟩))
(Um exemplo básico de tal variável é quando é uma percolação de elos.) Seja 𝑚 ∶ × × →ℝuma função que é invariante sob a ação diagonal de
Aut( ), i. e. tal que para todo automorfismo e todos , ∈ , também todo
𝜔 ∈ tem-se𝑚( , , 𝜔) = 𝑚( , , 𝜔). Intuitivamente pensa-se em 𝑚( , , )
como a quantidade de massa transportada de para quando = 𝜔.
Teorema (Teorema do Princípio de Transporte de Massa). Se é um grafo transitivo e unimodular, então a quantidade de massa esperada transportada para fora de um vértice é igual a quantidade de massa transportada para o próprio vértice, i. e., para qualquer vértice
𝔼 ∑∈ 𝑚( , , ) = 𝔼 ∑∈ 𝑚( , , ).
A prova do teorema fica bem mais simples se for considerada restrita aos grafos de Cayley.
Prova: Se e são vértices, então eles também são membros de um sub-jacente grupo e existe um único elemento ℎ = −1 ∈ tal que = ℎ .
Assim
∑∈ 𝔼𝑚( , , ) = ∑ℎ∈ 𝔼𝑚( , ℎ , ) = ∑ℎ∈ 𝔼𝑚(ℎ−1 , , ℎ−1 ) = ∑ℎ∈ 𝔼𝑚(ℎ−1
, , ) = ∑∈ 𝔼𝑚( , , ).
Referências Bibliográficas
[1] Alexander, K. S.,Percolation and minimal spanning forests in infinite graphas. Ann. Probab., 19(1991), no. 4, 87-104.
[2] van den Berg, J., Ermakov, A., On a distributed clustering process of Coffman, Courtois, Gilbert and Piret. J. Appl. Probab. 35 (1998), no. 4, 919-924.
[3] van den Berg, J., Hilário, M. R., Holroyd, A. E., Escape of resources in distributed clustering processes. Elet. Comm. em Prob. 15, no. 40, (2010), 442-448.
[4] van den Berg, J., Meester, R. W. J. Stability properties in graphs. Ran-dom Structures Algotithms 2(1991), no 3, 335-341.
[5] Coffman, E., Courtois, P. J., Gilbert, E., Piret, P,A distributed clustering process, J. Appl. Probab. 28(1991), no. 4, 737-750.
[6] Diestel, Reinhard,Graph Theory, third edition, Springer-Verlag, 2005.
[7] Grimmett, G., Percolation, Springer-Verlag, New York, 1989, ISBN 3-540-996843-1.
[8] Häggström, O., Jonassom, J.,Uniqueness and non-uniqueness in perco-lation theory. Probability Surveys3 (2006), 289-344.
[9] Lyons, R., Peres, O., Schramm,Minimal spanning forests.Ann. Probab.,
34, (2006), no. 5, 1665-1692.
[10] Hilário, M. R., Louidor, O., Newman, C. M., Rolla, L. T., Sheffield, S., Si-doravicius, V.,Fixation for distributed clustering processes.Comm. Pure and Appl. Math. 63 (2009), no. 7, 926-934.
[11] James, B. R., Probabilidade: um curso em nível intermediário, Impa, Projeto Euclides, 1981.
[12] Shiryaev, A. N., Probability, second edition, Springer-Verlag, New York, 1996. ISBN 0-387-94549-0.
[13] Pemantle, R., Choosing a spanning tree for the integer lattice uniformly.