Determinação da taxa de juros implícita em esquemas genéricos de financiamento: comparação entre os algorítimos de Wild e de Newton-Raphson

•

•

_•

•

•

•

•

•

_•

•

•

_•

•

•

_•

•

ESCOLA DE PÓS-GRADUAÇÃO EM ECONOMIA DO INSTITUTO BRASILEIRO DE ECONOMIA

DA FUNDAÇÃO GETULIO VARGAS

DETERMINAÇÃO DA TAXA DEJUROS IMPLrCITA EM ESQUEMAS GEN~RICOS DE FINANCIAMENTO:

COMPARAÇÃO ENTRE OS ALGORrTMOS DE WI LD E DE NEWTON-RAPHSON

CLOVIS DE FARO

•

".

•

•

•

•

_•

.'

•

•

•

_•

•

_•

•

_•

•

_•

•

•

•

•

•

•

_•

•

•

_•

•

_•

•

_•

•

•

•

fNDICE

i - Introdução . . . • . Pág. 1

II - Conceituação do Problema . . . . Pág. 2

i 11 - O _{Método de Newton-Raphson . . . . Pág. 5}

111.1 - Implementação: o procedimento de Horner . . . . Pág. 6

111.2 - Exemplo . . . • . . . Pág. 9

IV - O Algorftmo de WlId . . . • . . . • . . . Pág. 12

V.l - Exemplo • . . . Pág. 13

V - Casos Particulares . . . • . . . • . . . Pág. 14

V.l - Esquemas com Prestações Constantes • . . . Pág. 15

V.2 - Esquemas com Pagamentos Variáveis em Progressão Aritmética ... . Pág. 16

V.3 - Esquemas com Prestações Variáveis em Progressão Geométrica ... Pág. 17

V.4 .- Esquemas com Parcelas i ntermed iárias . . . , Pág. 19

VI - Fórmulas Aproximadas de Karpin e de Evans ...•...•... Pág.21

Vl.l - Adaptação para Prestações em Progressão Geométrica . . . . . . .. Pág. 22

VI.2 - Exemplos ... . . . • . . . . . . . . • . . . . .. Pág. 23

VII -

Avaliação Empírica . . . " . . . Pág. 25

Vll.l - Caracterização dos Casos . . . • . . . " Pág. 26

VI1.2 - Resultados Numéricos ... , . . . , ... , . . . .. Pág.

26

VII.3 - Análise ... , ... , . . . • . . . Pág.30

VIII - Um Procedimento Híbrido ... , . . . Pág.48

Vii Li - Justificativa para o Emprego da Função Valor Futuro ... " Pág. 49

VIII.2 - Exemplo . . . , ... , ... , . . . Pág.52

IX - Conclusão . . . Pág.54

Referências ... , . . . " Pág. 55

Apêndice A - Esquemas com Reajustes Periódicos ã Taxas Constantes. . . .. Pág.57

Apêndice B - Resultados Auxiliares . . . " . . . ,.. Pág. 67

•

,.

•

•

_•

•

_•

.'

_•

•

_•

•

_•

•

_•

•

•

_•

•

_•

•

•

_•

•

•

•

•

•

_•

•

•

•

•

_~

••

•

•

•

•

•

_•

•

_•

•

I - INTRODUÇÃO

Um importante problema de interesse prático, é o de especificar o

va-lar numérico da taxa periódica de juros compostos que está sendo efetivamente cobrada em um

dado esquema de financiamento. Isto é, uma vez fornecidos os valores de uma seqüência de

pa-gamentos periódicos, usualmente denominados de prestações e que estão associados ao resgate

de determinada operação de empréstimo, a questão que se quer resolver é a de determinar a taxa

de juros que está impllcita na transação financeira em apreço. ( 1 )

Excetuando·se certos casos extremamente particulares, tais como os

de pagamento único· e os relativos a determinados esquemas especificas de prestações

decrescen-tes em progressão aritmética, a solução do problema não só não é trivial como só pode ser alcan·

çada de uma maneira aproximada. Além do mais, regra geral, o processo de cálculo é bastante

penoso, pois que requer o emprego de procedimentos iterativos que, na prática, só são realmente

passiveis de implementação med.iante o concurso de máquinas de calcular eletrônicas.

o

propósito básico do presente trabalho é o de efetuar um estudo

comparativo entre os desempenhos de dois procedimentos iterativos de caráter geral: o clássico

método de Newton-Raphson e o algoritmo recentemente desenvolvido por Wild. Subsidiaria·

mente, para o caso, de freqüentes ocorrências na prática, em que as prestações são constantes,

serão também cotejados os resultados derivados das aplicações das fórmulas aproximadas

respec-tivamente devidas a Evans e a Karpin; mostrando-se ainda como extensões dessas fórmulas se

comportam no caso em que os pagamentos variam segundo uma progressão geomética. Em

con-clusão, com fundamento na análise dos resultados numericamente obtidos, será sugerido um

procedimento, de cunho heurfstico, que procura mesclar os méritos dos diverSOS métodos

eXB-minados.

( 1 )

Convém re3saftaí que, no mais das vêzes, seja por ditas exIgências de reciprocidade ou por cobrança de taxas de

abertura de crédito, ou ainda devido ao fato de que às prestaçõe, se incorporem parcelas requeridas a titulo de

taxas de administração e seguros, a taxa implfcita é substancialmente superior àquela que, geralmente ~ob a

,2,

11- CONCEITUAÇAO DO PROBLEMA

Seja o esquema genérico de financiamento caracterizado através da

seguin-te seqüência, finita, ( 1 ) de números reais:

( 1 )

Em ( 1 ), C

>

O denota o valor do capital emprestado, e p, ;;;, O,

I

j

=

1,2, •. " n, representa a j-ésima prestação de resgate, que é suposta pagável j períodos após

a data do empréstimo, Prestações intermediárias podem ser nulas, exceto a última que deverá ser

positiva; isto é, sem que se acarrete perda de generalidade, ao menos p

'*

O.

n

Dado ( 1 ), o problema que se posiciona é o de determinar o valor

numé-rico da taxa de juros i, cujo período a que se refere coincide com o intervalo de tempo entre

paga-mentos consecutivos, que promove a equivalência financeira entre o capital emprestado e a sucessão

de prestações.

Ou

seja, formalmente, busca-se determinar o valor da taxa i, aqui considerada sob

forma unitária, que anula a chamada função valor atual, V ( i ):

n

V(i)= -C + l: PJ- (1+ifj,

j =

1

> -1 _{( 2 )}

A solução da equação poli nominal V ( i ) " O, restrita ao campo associado

a taxas de juros com significação econômica e que é definido por i

> -

1, solução esta que é

de-nominada de taxa de juros implícita na operação financeira em apreço, tem existência e unicidade

assegurados, pois que:

a) sendo um polinomio em i, a função valor atual é contínua no intervalo considerado;

( 1 )

O caso de número infinito de pagamentos é roais de interesse teórico do que prático. Para uma análise de cettos tipos

espec(ficos de seqüências infinitas, veja-se. por exemplo, de Faro (4, Cap_ 7).

•

•

•

•

•

•

_•

•

•

•

_•

•

•

•

•

•

•

_•

•

•

•

•

_•

•

•

_•

•

•

•

_•

•

•

•

_•

•

•

_•

•

•

,3.

b) para taxas negativas e próximas do limite de significação econômica (-100% por período) a

função valor atual assume valores positivos e infinitamente grandes, tendendo ao simétrico

do capital emprestado para taxas de juro suficientemente elevadas, visto que

1in: V(i) ~

+

00,

;-+00

e

1íc V(i)

~

-C

<

O;

;-+00

c) sob

as

condições anteriormente explicitadas,

a

função valor atual é estritamente decrescente

ao longo do intervalo definido por j

>

';"1, já que sua derivada primeira

é negativa.

n

V'

(i)'"

dV{i

)/c;i~

-

E jP

_j (l+i

f

j -i

j=l

Além do mais, observando-se que

V(O) =

n

-C + E p,

'J

j=l

( 3 )

e definindo-se como juros totais a diferença entre a soma de todas as prestações e o capital

empres-tado, segue-se que o sinal da taxa implícita coincide com o do total de juros (sendo que a taxa

im-plíeita será nula se a soma das prestações igualar o capital emprestado).

Conseqüentemente, observando-se ainda'quea função valor atual é estri.

_ 4 .

V" (i )

n

~ l:

j= 1

( 4 I

é positiva, segue-se que, denotando-se a taxa implícita por i~ o comportamento da função valor

atual pode ser sumarizado como esquematizado na Figura I (que corresponde ao caso onde os juros

totais são positivos).

I

I

I

I

I

I I

I

I I

I

I

I n

I i:

I . 1

I J~

-1

v

(i)

p.

-c

J

o

i

-c

_

....

---

-FIGURA I

Comportamento da Funçã'o Valor Atual

De um modo geral, excetuando-se os casos onde o número de prestações

não excede a quatro, quando é então possível o emprego de f6rmull!s algébricas exatas, ( 1 ) a

de-terminação do valor numérico da taxa impl(cita só pode ser efetuada de uma maneira aproximada.

Para tanto, é feito uso de processos ditos iterativos, 0$ quais produzem resultados cada vez mais

próximos do verdadeiro valor da taxa j* raiz da equação V ( i ) = O. Concentrando-se atenção ao

caso, que é o de ocorrência comum na prática, no qual o total de juros é positivo, ( 2) passemos

111

Expressões anal(ticas par. o cálculo das raIzes de polinômios do terceiro e quarto graus rio encontrados em, por

exemplo, (2, pags. 93-96).

( 2 )

Os procedimentos aqui considerados são também aplicáveis aos casos em que OS juros toteis rio negativos. Porém,

•

_•

•

•

•

_••

•

•

•

•

_•

•

_•

•

•

•

_•

•

•

•

_•

•

•

•

•

•

•

•

•

_•

•

_•

•

•

•

•

•

•

_•

•

•

_•

,5,

agora a um estudo comparativo entre dois de tais procedimentos.

111 - O M!:TODO DE NEWTON-RAPHSON

Um processo clássico para a determinação das raízes reais de uma certa

função, em um dado intervalo, é o chamado método iterativo de Newton-Raphson. Este

procedi-mento, que é considerado como dos mais eficientes, pois que apresenta convergência dita

quadráti-ca, é de aplicação garantida desde que a função em exame apresente determinadas propriedades; tais

como monotonicidade e ausência de mudança de concavidade no intervalo em apreço. ( 1 )

No caso de interesse, ( 2 ) fixando-se atenção ao intervalo [ 0, 00), o

mé-todo de Newton-Raphson

é

de implementação assegurada. Para tanto, denotando-se por i

1 o valor

numérico da primeira aproximação para o verdadeiro valor da taxa impl ícita i"; tome-se:

o )

i

l= - - - - -_V

I J)

v

( 5 )

A seguir, representando-se por i a aproximação obtida na k-ésima

ite-k

ração do processo, k = 1, 2, ' .. , o valor dei será obtido, recursivamente, via a relação:

k + 1

v

(i

k)

i 1:+ 1 = i,. ( 6 )

" VI \ i I. )

"

Geometricamente, como indicado na Figura 11, a primeira aproximação é

dada pela abcissa da intersecção com o eixo dos i da tangente

à

função valor atual no ponto de

I 1 I

Para uma análise destas propriedades veja-se Henrici I 13, pags. 77-86 ),

(2)

É curioso observar que, na literatura pertinente, a primeira sugestão concreta para o emprego do método de Newton~

.6.

coordenadas (O, V ( O ) ). Similarmente, a segunda aproximação será obtida determinando·se a ab·

cissa da intersecção com o eixo dos i da tangente ã função valor atual no ponto de coordenadas

0"

V

0,) );

e assim, sucessivamente.

E,

pois, fácil perceber que a busca da taxa implfcita será

limi-tada ao intervalo [O, i*

1 ,

obtendo-se uma sucessão de aproximações da forma:

v

(i)

O

i

FIGURA 111

Interpretação Geométrica do Método de Newton-Raphson

111.1 - Implementação: o procedimento de Horner

Do ponto de vista prático, um inconveniente associado a implementação

do algorftmo de Newton- Raphson é a necessidade de que tanto a função valor atual como a sua

derivada primeira tenham seus respectivos valores numérico,s repetidamente calculados para distintos

valores da taxa de juros. Entretanto, o esforço computacional exigido pode ser substancialmente

reduzido fazendo-se USO do chamado método de Horner para a avaliação de polinômios. ( , )

Fazendo-se x = (' + i) - ' , segue-se que a função valor atual e sua

deriva-( 1 )

•

•

•

•

•

_•

•

•

•

•

_•

•

_•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

_•

•

_•

•

.7 .

da primeira podefTl ser respectivamente escritas como os seguintes polinômios, de graus n e

n-l em x:

( 7)

e

( 8 )

Cencentremo·nos, 'inicialmente, no problema de determação do va lo r

numérico de P( x ) no ponto

x

correspondente a uma dada taxa i. Dividindo-se P( x) por

x -

x,

obteremos COfTlO qüociente um polinômio do grau n-l em x, com o resto sendo uma

constante não nula s~

x

não for uma raiz. Isto F ,"m perda de generalidade, podemos

escre-ver:

( 9 )

Ora, visto que, de ( 9

l.

P(

x )

= bO' segue-se que o valor numérico de

P( x ) no ponto

x

_{será conhecido deterr,linando-se bO' Igualando-se os coeficientes de mesma}

potência de x em (7) e ( 9 ), temos que:

p = b

n n

xb - 1"

J+

j=

n-1, n-2, _ _ _ , 1

( 10 )

Ou seja, de ( 10 :, partindo-se de bn = Pn' vemos que o valor de bO

.8.

Similarmente, dividindo·se P' ( x) por x - X, teremos:

( 11 )

com

( 12 )

j= n~l,

n-2, . . .

,1

Isto é, P' (

x )

= aI' com aI ' podendo ser determinado recursivamente,

via ( 12 ), por meio de n-l multiplicações e n-l adições. Entretanto, tal SÓ é verdade se,

pre-viamente, tivermos efetuado os n produtos jP., j = 1, ... , n.

1:,

pois, interessante que se

bus-J

que um procedimento alternativo para a determinação do valor numérico de P' (

x ).

decorre, de ( 9 ), que:

Definindo-se

n-1

H(x)= b1

+

Q2 x

+ . . - +

_{bn x}

P'

(x)= (x-x)

H' (x)

+

H(x)

( 13 )

( 14)

Ou seja, P' (

x )

= H (

x ).

Portanto, aplicando-se o método de Horner

para a avaliação numérica do polinômio H ( x ) no ponto

x,

vem que, tendo em vista ( 11 ),

P' (

x )

= aI' com:

-f

•

•

•

•

_•

•

•

•

•

•

•

•

•

_•

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

•

•

.,

•

_•

•

•

•

•

•

•

•

•

b = aJo - Xb

J. + 1

.i

j = n-1, n-2, . . ., 1

. 9.

( 15 )

Isto é, a avaliação numérica de P' ( x) é efetuada simultaneamente

com a de P( x) e aproveitando os resultados desta última.

111.1 - Exemplo

A t(tulo de ilu5tração, seja determinar a taxa de juros implfcita no

esquema de financiamento definido pela seguinte seqüência:

e

{ - =0, = 2 4, 8, 16}

Tendo em vista a relação (5 ), a primeira aproximação é igual a:

n

L

. V(O) j=l

, =---=~~--=

1 VXO) n

L jp .

j=l J Então, observando-se que

21

129 =0,162791

~1 -1 - 1 -1 -1

' u .

G fazendo-se uso de ( 6 ), segue-se que teremos a seguinte_ seqüência de aproximações:

v

(i 1 )

6,786322

i2~ 1

1

"

0,162791

+

"

0,281294

V'(i

₁

)

57,266955

V (i 2 )

1,501635

i - i

_r

₂

'" 0,281294

+

_'"

0,325062

V' (i 2)

34,309262

i

~

_{i3 -}

V (i 4)

_"

_0,325062

₊

0,124997

_0,329402

"

4

_{V' (i}

3

)

28,795143

V (i 4)

0,001057

i5~

i4 -

_"

0,329402

+

_"

0,329440

V' (i

₄

)

28,309770

Como V( i5 ) ~ 7 X

10

-8 , podemos afirmar que, com bastante

preci-são, a taxa implícita associada ao esquema de financiarr>ento considerado é de

32,9440%

por

pe-ríodo _

Alternativamente, fazendo-se x = (1 + i) - 1 e trabalhando -se com O

polinômio P ( x

l,

podemos apl icar o método de Birge-Vi~ta, tal como sumarizado no Quadro 1.

Para tanto, dado que i = O "'" x = 1, tornaremos como primeira aproximação:

n

_-c

p _{(1 )} 1:

Pj

xl

~

1 -

~

1 -

j

~

1

"

0,83720930

P' ( 1 )

n

1: Jp . j ~

1

J

No Quadro 1, onde P O -C, vemos que, apôs a quinta iteração:( 1 )

( 1 I

Observe-se que, fazendo-se i,'" (l-x,) / xl' a primeira aproximação obtida a partir de P ( x ) é sempre

supe-rior à determinada diretamente da função valor atuaL A comprovação formal dessa afirmativa aparece no apêndice

•

•

QUADRO I

•

•

Aplicação do Método de Birge-Vieta

•

•

Pj b· aj

•

J

•

5 16 16 16

•

4 8 21,39534884 34,79069768

•

3 4 21,91238507 51,03948080

2 2 20,34525262 63,07598073

•

1 1 18,03323475 70,84103257

•

°

·10 5,09759188

•

_•

x2 = 0,83720930 - 5,09759188/70,84103257 ~ 0,76525112

•

5 16 16 16

•

4 8 20,24401793 32,48803586

•

3 4 19,49175741 44,35326326

•

2 2 16,91608920 50,85747362

•

1 1 13,94505622 52,8637949 1

°

·10 0,67146990

•

_•

x3 = 0,76525112 - 0,67146990 /52,86379491 ~ 0,75254923

•

•

5 16 16 16

•

4 8 20,04078776 32,08157552

3 4 19,08167949 43,22464460

•

2 2 16,35990330 48,88857651

•

1 1 13,3 116327 1 50, 10269355

•

°

·1 0 0,01765901

•

x4 = 0,75254923 - 0,01765901 / 50, 10269355 ~ 0,75219678

•

•

5 16 16 16

•

4 8 20,035 14845 32,07029690

•

3 4 19,07037412 43,19354813

2 2 16,34467398 48,83472173

•

1 1 13,2944111 1 50,02773147

•

°

·10 0,00001321

•

•

x5 = 0,75219678 - 0,0000 132 1 / 50,02773 147 ~ 0,75219651

. 12 .

x

₅= 0,75219651 = i 5 " 0,329440

IV - O Algorítmo de Wild

Em um artigo recentemente publicado, Wild ( 17 I propos um procedi·

mento, de caráter heurístico, para a determinação da chamada taxa interna de retorno associada a

um dado projeto de investimento. ( 1 I Fixando-se atenção ao caso de interesse específico,

caracte-rizado pela seqüência ( 1 I, o algorítmo de Wild, que consiste de quatro distintos passos, produz a

seguinte sucessão de aproximações para a taxa implícita:

ai Definindo-se

n

E _{j P j} V' ( O ) j = 1

b_O= = ( 15 I

n

V(O) +

C

E p.

j = 1 J

e

K(i)= 1 + V(i) / C ( 16

I

tome-se como primeira aproximação ( 2 I

I 1 I

Para a conceituação deste problema mais geral, veja-se, por exemplo, de Faro (3, paga. 61-81 ). Wild apresenta um

programa para uso em cãlc~ladoras de bolso.

( 2 I

Como O I~it~r poderá facilmente verificar, i1 será o valor correto no caso I!artlcular onde somente Pn'" O. Deve-se

ainda notar que, se as prestações forem constantes a expressão de

i,

coincide com a do parimetro R.. que aparece

na chamada fórmula de Baily; veja·se de Fineui ( 9, pago 191 I.

•

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

•

•

•

•

com

,- =

1

l/b

_O

K (O) ~l

b) Para K ~ 2 e 3, faça

1

_k

=

(l +

c) Como aproximação final, tome:

13.

( 17 )

( 18 )

( 19 )

( 20 )

Deve-se frisar que, como mencionado, o procedimento é de cunho

heurís-tico, donde não ser possível garantir-se formalmente a qualidade da aproximação obtida.

Entretan-to, investigações empíricas, como corroboradas pelos casos aqui apresentados, dão margem a que

possamos confiar em seus resultados. ( 1 )

IV.l - Exemplo

Reconsidere,se o esquema de financiamento estudado no item 111.2.

Apli-cando-se o algorítmo de Wild, e tendo em vista a expressão que foi apresentada para a função valor

( 1 )

Esta inferência parece ser válida apenas para o caso particular aqui considerado (p j

>

O, todo

n.

Pois,

contra-riamente ao afirmado por Wild ( 17 ), o comportamento do algorítmo revelou-se bastante errático para certos

. 14.

atual, obteremos os resultados sumarizados no Quadro 11.

QUADRO 11

Aplicação do Algorítmo de Wild

k _ik V(ik)

1 0,31243912 0,49764943 2 0,32854153 0,02547133 3 0,32939231 0,00134489 4 0,32943977 0,00000149

IV - CASOS PARTICULARES

A implementação de qualquer dos dois procedimentos considerados

é

bas-tante trabalhosa, já que, para diferentes taxas de juros, demandam a repetida avaliação numérica da

função valor atual (e ainda, no caso do algorítmo de Newton-Raphson, de sua derivada primeira).

Para esquemas de financiamentos em que as prestações sejam arbitrariamente estipuladas, no sentido

de que não sigam uma bem definida lei de formação, tais avaliações deverão ser efetuadas

recursiva-mente, mediante a aplicação do método de Horner para a determinação do valor numérico de um

polinômio. Entretanto, ao menos para certos casos particulares de leis de formação de prestações, as

necessárias determinações numéricas podem ser mais eficientemente processadas; pois que, então, é

possível a explicitação de formas fechadas para a função valor atual, bem como para sua derivada

primeira.

~,lesta

seção, trataremos dos casos particulares mais comuns. ( 1 )

(1)

No Apêndice A, são ainda examinados dois outros casos que corresponder iam a esquemas com cláusulas de correção monetária periódica, pré-fixada a uma taxa constante.

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

.i

_.1

.1

_I

.i

_.1

_,

.1

.,

,

.,

•

1

_I

.1

•

•

•

•

_•

•

•

•

•

•

_•

•

•

•

•

_•

•

•

_•

•

_•

•

•

•

_•

•

•

•

•

•

•

•

•

_•

•

•

•

•

_•

•

_•

•

V.1 - Esquemas com Prestações Constantes

Para o caso em que P.

=

p, j

=

1, ... ,

n,

temos que:

J

v

(i ) =

-C

+

P

~

(1

+

1

f

j = p

I

j=l

n

(1 +i) -1

i (1+;) n

ou, lançando mão da notação clássica em Matemática Financeira

com

V(i)= -C

+ p

a

ilji

V(O)= -C

+

np

I

-c

. 15.

( 21 )

( 22 )

Derivando-se a função valor atual, e tendo em vista resultados apresenta·

dos em de Faro ( 4, pags. 142-4 ), vem que:

n .

1

n

V'(i)= -p E j(l+i)-J- = -

~

E

j=l

.1+1 j=i

com

ou

com

P

V'(i)=· -

(I a)

1 +p

nj

i

V'(O)= -

n(n

2

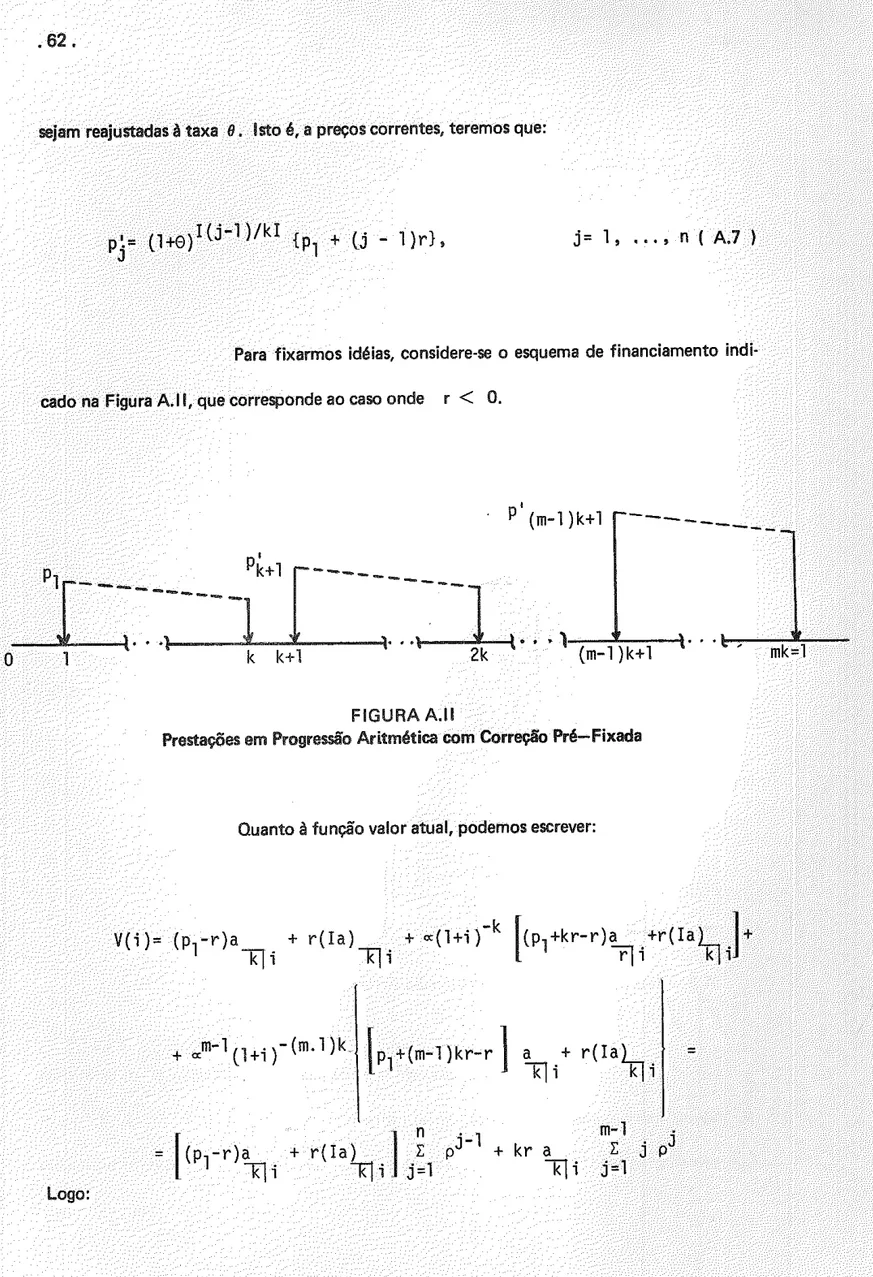
l)p

V.2 - Esquemas com Pagamentos Variáveis em Progressão Aritmétice

Seja o caso onde

j=l, ... , n, r

=1=

O

Então:

V(i)=-C +

.~

rPl + (j-l)r (l+ifj]

J =1

V(i)=-C+(pl-r)a + r ( I a ) ·

. nji

nji

V(O)= -C

+

_{n [2 P1}

+

(n-1)r

1 /

2

Quanto

à

derivada da função valor atual, tem-se:

( 23 )

( 24 )

( 25 )

( 26 )

( 27 )

•

•

_•

•

•

_•

•

•

•

•

•

•

•

•

•

,

•

•

•

_•

•

•

•

•

_•

•

•

•

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

•

•

_•

•

•

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

_•

•

•

•

•

, 17,

, P1-r n (1' )-j r

~

J,2(1+1' )-j

V (i) = - 1: j +1 t..

1+i j=i l+i j=l

Observando-se que, como mostrado no Apênd ice 8, para, v-= (1 + j) - 1

podemos escrever:

p -r

V'(i)= -

_1_

(I a)

1+;

!ili

+ r (l+i )-n [(l+;+n; )2)+1+;]-(1+; )(2+;)

(l

+; )

3

ou:

V'

(i)= -

-1-I(P1-

r ) (I a) - r(12 a)

1

1 +i 1.1

ri']

i

ri']

i

( 28 )

com

V'

(O)= - n (n + 1) [3P 1 + 2 r (n - 1)] / 6

( 29 )

V.3 - Esquemas com Prestações Variáveis em Progressão Geométrica

Se as prestações periódicas forem tais que

, -1

P

,=

P

qJ , j =

1, ' , , ,

n,

q >

O,

q

=1=

1

, 18.

ter-5e-á:

com

que:

n

V(i)= -C

+ l:

j = 1

H

pq

. n q

(l+i )-J= -C +...L l: ( _ _

q

j=1 1 +

Fazendo-se p = q / (1

+

i), decorre, então, que:

-C

+

np / q,

_se

_p

₌

₁

v

(i ) =

n

- C + pp (1 - p ) / q (1 - p),

_se

_p

+

₁

n

V(O)=-C

+ p(q - 1) / (q - I)

Por outro lado, tem-se:

n p n

V'(i)=-p

l: jqj-l(l+iyH _ _ _ l:

jpj

j=1 q(l+i) j=1

( 31 )

( 32 )

( 33 )

Logo, face ao resultado apresentado em de Faro ( 5, pág. 193), segue-se

V' (i )=

-np(n

+

1) /2(1

+

i)2 ,

pp { l-pn[l+n(1 - p)] }

q(1+i) (l_p)2

se p

= 1 ( 34 )

•

•

•

•

_•

•

_•

•

•

•

_•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

_•

•

•

_•

. 19.

com

V' (0)= -p {l_qn [l+n(l-q)J} / Cl-q)2 _{( 36 )}

V.4 - Esquemas com Parcelas Intermediárias

Um outro caso particular, que apresenta freqüente ocorrência na prática, é

aquele no qual, além das n prestações periódicas usuais, são também exigidos certos pagamentos

intermediários. Consideremos o caso, que

é

comum, onde Seja estabelecida a cobrança de m

par-celas intermediárias, constantes e iguais a P, venc!veis a cada k = n

I

m per(odos. ( 1 )

Sem perda de generalidade, representando-se por V 1 ( i) o valor atual, à

taxa i, das prestações periódicas regulamentares, e por V2 ( i) o valor atual, ã mesma taxa i,

das parcelas intermediárias, segue-se que, face à sua propriedade de aditividade, a função valor atual

associada ao esquema de financiamento considerado pode ser escrita como:

com

onde

( 1 )

V'(i)"- Viii) + V

₂

(i)

n

Vl(i)= l:

PJ-

(l+i)-j

j = 1

( 37 )

( 38 )

( 39 )

Via de. regra, k é um número inteiro. Entretanto, as fórmulas aqui derivadas permanecem válidas para valores

FUNDAÇÃO

Bit?i90teca Mario Henrique Sirnonsen

e

Trabanhando-se com a taxa i_{k ,} equivalente a

de tempo entre parcelas intermediárias consecutivas, isto é,

segue-se de ( 40 ) que:

ou

com

Quanto ã derivada primeira de V 2 ( ), tem-se:

m

E

9.= 1

k P m - - - E

l+i9.=l

( 40 )

e relativa ao intervalo

( 41 )

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

•

•

•

,

•

•

•

•

•

•

•

•

•

•

ou

com

k P

-1 + i

(I a)

m]i

k

V2(O)~

-

n

P

(m +

1)

I 2

VI - FÓRMULAS APROXIMADAS DE KARPIN E DE EVANS

.21 .

( 44 )

( 45 )

Devido a $ua importância prática, pois que, indubitavelmente, é o esquema

de financiamento mais Comumente adotado, grande dose de atenção tem sido devotada ao estudo da

determinação da taxa implícita para o caso de prestações constantes. Assim, na literatura técnica,

têm sido apresentadas diferentes fórmulas aproximadas. ( 1 ) Dentre estas, tanto pela facilidade de

suas respectivas aplicações como pela qualidade dos resultados obtidos, destacam-se as devidas a

Evans ( 11 ) e a Karpin ( 15 ).

Definindo-se

a~ (np-C) / C _{( 46 )}

e

b~

0,2 + --3--

411

n+T

+ 0,1 (l+a)

1/21

_{( 47 )}

( 1 )

a aproximação para o verdadeiro valor da taxa implícita, segundo Evans, será dada por:

( 48 )

De outro lado, de acordo com Karpin, sendo o parâmetro a como dado

por ( 46 ), a aproximação será igual a:

2a (3+a)

\ =

-2na + 3(n+ 1 )

( 49 )

V I. 1 - Adaptação para Prestações em Progressão Geométrica

Para o caso de pagamentos constantes, trabalhando-se com a notação

clás-sica em Matemática Financeira, onde v = (1 + i) -1, segue-se de ( 21.) que a taxa implícita i

deve ser tal que:

( 50 )

Nesta notação, tanto a fórmula de Evans como a de Karpin nos dão

solu-ções aproximadas para ( 50 ), sob a forma:

-

v

i = ( 51 )

V

( 1 )

Tanto quanto sabemos, a adaptação aqui sugerida se nos afigura Como original.

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

•

_•

•

•

•

•

•

_•

•

•

_•

•

_•

•

_•

•

•

•

•

•

•

_•

•

_•

•

•

•

•

_•

•

•

_•

.23.

Por outro lado, no caso de prestações em progressão geométrica de razão

q e primeiro pagamento igual a p, sabemos que, respectivamente de ( 31 ) e ( 32 ), a taxa

implícita deve ser agora tal que:

n

p

se

i= q - 1

( 52 )

q.

c=

+1

p(l-p )

n

I '

se

p= q

I

(1 +i)

-=/=

1

_{( 53 )}

1-p

Comparando·se ( 50 ) com ( 53 ), ocorre·nos, então, que, por

analo-gia, substituindo·se o valor do financiamento pelo produto qC, tanto a fórmula de Evans como a

de Karpin fornecerão valores aproximados para a expressão (1 - p) / p. Por sua vez, através da

relação p = q / (1 + i

lo

tais valores produzirão aproximações para o verdadeiro valor da taxa impl(·

cita.

Ainda mais, tal adaptação não só permanece válida para o caso expresso

por ( 52 ), como, então, obteremos a solução exata i = q - 1.

VI.2 - Exemplos

constantes e iguais a 40.

e

Considere-se o caso onde, para C = 1.000, são cobradas 36 prestações

Tlmdo em vista que

a=

36 X 40 - 1.000

b= 0,2

+

_-3-

4

-ir-.

_{0,1 (1 .0,4411121 00,396036}

segue-se que:

i

E" 0,021205

_com

e

i

_{k" 0,021217}

com

Ou seja, no caso em apreço, as fórmulas de Evans e de Karpin fornecem

aproximações razoáveis, respectivamente por falta e por excesso, do verdadeiro valor da taxa

implí-cita (que é ligeiramente superior a 2,121114%).

Suponha-se agora que, para o mesmo valor de C, sejam estabelecidas

-18 prestações crescentes em progressão geométrica de razão q

=

1,01, com pagamento inicial

e

( 1 )

Face à adaptação aludida no item anterior, teremos:

a=

48

X

30 - 1,01

X

1.000

1 ,01'X 1.000

" 0,425743

bo

0,2 •

+

-,i,.

0,1 (1<0,4257431 li2]

o

0,386417

Observe-se que tal especificação conduz a uma taxa implícita de, aproximadamente, 2,567664%.

•

•

•

•

•

•

•

•

•

_•

•

•

•

_•

•

_•

•

•

•

•

•

•

.

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

_•

•

•

•

•

•

•

_•

•

_•

•

•

_•

•

•

•

_•

•

•

•

•

•

_•

•

•

_•

•

_•

_,

.25.

Logo, a partir da fórmula de Evans, obtemos:

1 - PE

'" 0,015516

Por conseguinte:

i

E 1,01 (1+0,015516) - 1 '" 0,025671 com V(iE) ~ 0,108575

Por outro lado, trabalhando-se com a fórmula de Karpin, teremos:

- P

_--.-::k " 0,015526

₌

_{\ " 0,025682, V (\) " - 0,106101}

VII- AVALIAÇÃO EMPfRICA

Para que possamos ter uma idéia concreta dos desempenhos de cada um

dos procedimentos aqui considerados, é necessário que procedamos a uma investigação numérica de

um número razoavelmente grande de esquemas de financiamento. Com tal finalidade, e buscando

reduzir o esforço computacional exigido, iremos concentrar atenção aos casos usuais de prestações

seguindo leis definidas, com a possível inclusão de parcelas intermediárias, de tal maneira que

pode-remos fazer uso das fórmulas apresentadas na Seção V. Ainda mais, objetivando cobrir as situações

geralmente encontradiças na prática, onde as prestações costumam ter periodicidade mensal, a

análi-se análi-será limitada a taxas de juros no intervalo de O a 10"A. ao mês, com prazos de financiamento

.26.

VIU - Caracterização dos Casos

Fixando-se o valor do empréstimo em C; 100.000, foram examinados

144 distintos esquemas de financiamento, que aparecem grupados segundo cada um dos três tipos

particulares de lei de formação de prestações. Assim, no Quadro 111, são especificadas as

caracterís-ticas dos casos com pagamentos constantes; no Quadro IV, as relativas aos esquemas com prestações

que formam progressões aritméticas; e no Quadro V, as que se referem a desembolsos que variam

segu ndo progressões geométricas.

No Quadro 111, para cada caso, identificado por um rótulo específico, são

fornecidos:

a) Valor da prestação periódica e constante;

b) Prazo de financiamento (como medido em número de pagamentos);

c) Valor e número de parcelas intermediárias;

d) Sob forma percentual, valor correto (até a sexta casa decimal) da taxa implícita periódica.

Nos Quadros IV e V são estipulados os valores da prestação inicial e da

razão da particular progressão a que se refere, e as demais informações como no Quadro 111.

VII.2 - Resultados Numéricos

Para cada um dos casos considerados, foram efetuadas as quatro iterações

regulamentares do algorítmo de Wild, as primeiras quatro iterações do método de

Newton-Raph-son, como calculadas a partir da função valor atual, ( 1 ) e, onde aplicável, empregaram-se as

fór-mulas aproximadas de Evans e de Karpin. Para tanto, foi feito uso do programa para computador,

{ 1 I

Cabe aqui ressaltar que, na realidade, embora trabalhando-se somente Com a função valor atual, procedeu-se a uma

dupla aplicação do método de Newton-Raphsono Isto porque, buscando dar uma indicação quantitativa do fato de

que a iteração inicial obtida a partir de P{ x I é superior à determinada diretamente a partir da função VI i I,

achou-se por bem cotejar as seqüências de iterações associadas a esses dois distintos pontos de partida. O programa

constante do Apêndice C, considera como primeira iteração a determinação a partir de PI x I.

•

•

•

•

•

•

•

_•

•

•

•

,27 o

•

•

_•

QUADRO 111

•

•

Casos de Pagamentos Constantes

•

Parcelas Intermediárias

•

Caso Prestação Prazo Taxa Periódica ( %

I

Valor Número

•

•

CTOl 8.600 12 0,487953 CT02 8.000 12 5.000 2 0,875741

•

CT03 10.000 12 2,922854

•

CT04 10.470 12 10.000 2 5,965093

•

CT05 13.000 12 7,606170 CT06 12.000 12 20.000 2 9,892572

•

CT07 4.500 24 0,625075

•

CT08 4.000 24 6.000 4 1,451480 CT09 6.000 24 3,149127

•

CT10 5.410 24 10.000 4 4,500111

•

CT11 8.000 24 6,043558

•

CT12 7.000 24 15.000 4 7,485666 CT13 3.100 36 0,605707

•

CT14 2.930 36 5.000 3 1,004726

•

CT15 3.950 36 2,042321 CT16 3.800 36 10.000 6 4,024560

•

CT17 6.250 36 5,264247

•

CT18 8.400 36 5.000 12 9,544772 CT19 2.000 60 0,618341

•

CT20 1.100 60 15.000 5 1,086204

•

CT21 3.600 60 2,982811

•

CT22 5.200 60 3.500 10 5,475391 CT23 8.000 60 7,917276

•

CT24 9.500 60 10.000 5 9,935534

•

CT25 1.400 84 0,498513 CT26 140 84 10.000 14 1,000308

•

CT27 3.200 84 2,913200

•

CT28 3.150 84 6.000 28 4,967771 CT29 7.050 84 7,026508

•

CT30 8.270 84 15.000 7 9,007972

•

CT31 1.100 120 0,483020

•

CT32 1.150 120 8.000 10 1,452191 CT33 3.500 120 3,439509

•

CT34 4.000 120 10.000 20 5,444406

•

.28.

•

•

•

QUADRO IV

.,

Casos de Pagamentos em Progressão Aritmética

.:

.:

Caso Prestação Inicial Razão Prazo Parcelas Intermediárias Taxa Periódica ( % )

.:

\7alor f\Júmero

.:

PAOl 9.300 -80 12 0,972093

.!

PA02 8.000 -100 12 10.000 2 1,341146

.:

PA03 7.000 500 12 2,274607

.:

PA04 3.800 500 12 13.500 4 3,981408

PA05 13.000 -100 12 6,908329

•

PA06 11.050 -100 12 7.000 6 8,979004

.:

PA07 4.880 -40 24 0,495199

.:

PA08 4.070 -50 24 15.000 2 0,990373

PA09 4.760 50 24 2,001004

.:

PA10 4.040 50 24 13.500 4 3,998654

.!

PA11 7.090 100 24 6,002066

PA12 2.660 200 24 17.000 8 8,000104

. i

PA13 3.465 -25 36 0,497591

.:

PA14 3.000 -50 36 15;000 3 1,067844

PA15 2.758 100 36 2,499756

.:

PA16 3.820 50 36 8.800 6 4,639196

.:

PA17 6.578 60 36 6,500081

•

PA18 6.880 -100 36 10.000 12 8,493560

PA19 2.380 -16 60 0,497291

.:

PA20 2.060 -25 60 10.500 5 1,000232

•

PA21 2.550 50 60 2,988961

PA22 5.231 -50 60 6.000 10 4,999972

•

PA23 6.845 60 60 7,498332

•

PA24 8.750 -100 60 6.000 20 9,504070

PA25 689 20 84 0,499523

•

PA26 1.780 -20 84 3.000 28 1,506647

•

PA27 2.500 -20 84 2,997035

•

PA28 4.465 -30 84 8.000 14 4,999191

PA29 8.720 -50 84 8,096838

•

PA30 7.472 50 84 20.000 7 9,009946

•

PA31 500 10 120 0,394829

PA32 2.000 -15 120 2.000 10 1,010172

•

PA33 1.075 30 120 2,001383

•

PA34 2.315 50 120 3.500 20 4,001203

•

PA35 7.270 -50 120 6,500576

PA36 6.930 100 120 5.000 40 9,500116

•

PA37 500 5 180 0,547489

•

PA38 1.490 -5 180 5.000 15 1,494796

PA39 3.225 10 180 3,499861

4p

PA40 4.880 10 180 3.000 30 5,497008

•

PA41 7.565 -5 180 7,498304

PA42 8.140 180 3.000 60 8,999608

•

PA43 235 5 240 0,499054

•

PA44 1.074 -4 240 1.000 80 0,999969

•

PA45 2.496 -10 240 1,999324

PA46 2.920 15 240 3.000 40 3,771581

•

PA47 6.345 10 240 6,498870

•

PA48 8.560 -5 240 10.000 20 9,000929

•

QUADRO V

Casos de Pagamentos em Progressão Geométrica

Caso Prestação Inicial Razão Prazo Parcelas Intermediárias Taxa Periódica (%)

. Valor r'Jumero

30.

escrito em FORTRAN-IV, que está incluído no Apêndice C. Tal programa determina ainda, com

precisão até a sexta casa decimal da forma percentual, o valor da taxa impl ícita; para tanto, se ne·

cessá rio, são realizadas iterações adicionais do método de Newton-Raphson.

Com o objetivo de, para os distintos casos, tornar mais homogênea a

com-paração entre os desempenhos dos diferentes procedimentos considerados, os resultados derivados

do programa acima mencionado foram colocados sob forma de erros percentuais. Isto é, para cada

caso, e para cada particular iteração de cada um dos diversos algoritmos, foi calculado o valor da

relação:

ô = 100 (

'1 -

i* )

*

i

onde

f

é o valor da aproximação e i* é o "valor correto" da taxa implícita. ( 1 )

( 54 )

Os erros percentuais assim calculados foram agrupados de acordo com os

diferentes prazos de financiamento considerados, e aparecem tabulados nos Quadros VI a XIII.( 2 )

Nestes Quadros, trabalhando-se com os valores absolutos de ~, são também apresentados os

res-pectivos erros médios.

VII.3 - Análise

O simples exame dos resultados obtidos permite com que sejam feitas as

seguintes inferências:

a) como indicado pela análise dos erros médios, com exceção dos relativos às fórmulas

aproxi-( 1 )

Como as aprox imações podem ser por falta ou por excesso, observe-se Que 8 é irrestrito em sinal.

(2 )

Relativamente ao método de Newton-Raphson, note-se que, à cada caso, correspondem duas seqüências de valores.

A primeira diz respeito ao fato de ter sido tomado como iteração inicial a obtida a partir de V( i l. enquanto que a

segunda, cujos termos aparecem entre parêntesis, corresponde à iteração inicial a partir de P( x ). Erros inferiores 8

0,0001 por certo foram indicados pelo símbolo €.

s-e

•

•

•

•

•

•

•

•

•

•

_•

•

•

•

•

•

•

•

•

•

•

•

•

•

_•

•

_•

•

•

• •••••••••••••••••••••••••••••••••••••••••••••

QUADRO VI

ERROS PERCENTUAIS

1 - Prazo de 12 Períodos

e

=

0,0001

WI LD NEWTON - RAPHSON

Caso

( 1 )

( 2 )

( 3 ) ( 4 ) ( 1 )

( 2 )

( 3 ) ( 4 ) EVANS KARPIN

r

CTO! -0,4472 -0,0018 0,0000 0,0000 -2,2361 -0,0010 0,0000 0,0000 0,0000 -0,0006

(-1,7674) (-0,0006) ( " ) ( " )

CT02 -0,7916 -0,0063 -0,0001 0,0000 -4,0429 -0,0067 0,0000 0,0000

(-3,2296) (-0,0043) ( " ) ( " )

CT03 -2,6754 -0,0723 -0,0020 0,0000 -12,2740 -0,1931

>-e

0,0000

>-€

-0,0164

(-9,9654) (-0,1274) ( " ) (

"

)

CT04 -5,3215 -0,2886 . -0,0157

>-ê

-23,2318 -1,3521 -0,0047 0,0000

(-19,5476) (-0,9606) (-0,0024) ( " )

CT05 -6,9076 -0,4873 -0,0344 -0,0001 -27,3921 -2,2327 -0,0153 0,0000 0,0134 -0,0370

(-23,1478) (-1,6018) (-0,0078) ( " )

CT06 -.8,5855 -0,7571 -0,0669 -0,0001 -34,4813 -4,5314 -0,0817

>-€

(-29,9404) (-3,4392) (-0,0471) { " }

PAOl -0,9046 -0,0082 0,0000 0,0000 -4,3400 -0,0083 0,0000 0,0000

(-,3,4422) (-0,0052) ( " ) ( " )

PA02 -1,2196 -0,0149 -0,0001 0,0000 -6,1471 -0,0238 0,0000 0,0000

(-4,9508) (-0,0154) ( " ) ( " )

PA03 -1,8547 -0,0348 -0,0007 0,0000 -10,1705 -0,1095

>-€

0,0000

(-8,2967) (-0,0729) ( " ) ( " )

Continua ...

to)

· .. Continuação do Quadro VI

WILD NEWTON - RAPHSON

Caso

( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 1 ) ( 2 ) ( 3 ) ( 4 ) EVANS KARPIN

PA04 -2,9995 -0,0913 -0,0028 0,0000 -17,0746 -0,5302 -0,0005 0,0000

(-14,2432) (-0,3697) (-0,0003) ( " )

PA05 -6,3563 -0,4115 -0,0266

>-€

-25,2635 -1,7416 -0,0085 0,0000

(-21,1947) (-1,2307) (-0,0042) ( " )

PA06 -8,0532 -0,6615 -0,0544 -0,0001 -31,0711 -3,2798 -0,0378 0,0000

(-26,5235) (-2,4034) (-0,0203) ( " )

PGOl -0,4358 -0,0019. 0,0000 0,0000 -2,2399 -0,0010 0,0000 0,0000 0,0000 0,0008

(-1,7748) (-0,0006) ( " ) ( " )

PG02 -0,9768 -0,0096 -0,0001 0,0000 -4,5456 -0,0096 0,0000 0,0000

(-3,6246) (-0,0061) ( " ) ( " )

PG03 -2,2029 -0,0491 -0,0011 0,0000 -10,8110 -0,1315

>-€

0,0000

>-€

-0,0002

(-8,7819) (-0,0869) ( " ) ( " )

PG04 -4,2801 -0,1863 -0,0081 0,0000 -19,9653 -0,8517 -0,0016 0,0000

(-16,6431) (-0,5935) (-0,0008) ( " )

PG05 -6,4881 -0,4326 -0,0289 -0,0001 -27,7002 -2,3207 -0,0168 0,0000 0,0008 -0,0167

(-23,5560) (-1,6864) (-0,0089) ( " )

PG06 -8,0419 -0,6589 -0,0540 -0,0001 -32,1629 -3,6504 -0,0488

>-€

(-27,6283) (-2,7096) (-0,0269) (0,0000)

Méd;a 3,8079 0,2319 0,0164 € 16,3972 1,1653 0,0121

e

0,0024 0,0120

(13,7921) (0,8508) (0,0066) ( " )

•

•••••••••••••••••••••••••••••••••••••••••••••••

aUADROVII

ERROS PERCENTUAIS

2 - Prazo de 24 Per lodos

e = 0,0001

WI LO NEWTON - RAPHSON

Caso

( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 1 ) ( 2 ) ( 3 ) ( 4 ) EVANS KARPIN

CT07 -1,1978 -0,0146 -0,0002 0,0000 - 5,1965 -0,0144 0,0000 0,0000 -0,0013 -0,0019

(-4,6314) (- 0,0115) (" ) (

..

)

CT08 -2,6956 -0,0740 -0,0021 0,0000 -11,6728 -0,1667 -0,0001 0,0000

1-10,5257) 1- 0,1357) 10,0000) (

..

)

CT09 -6,0022 -0,3732 -0,0232 -0,0001 -22,3771 -1,2148 -0,0037 0,0000 -0,0214 - 0,0086

1-20,4321) (-1,0148) . (- 0,0026) (

..

)

CT10 -8,2273 - 0,7068 -0,0609 -0,0002 -30,1862 -3,0433 -0,0321 0,0000

(-27,9217) (-0,0237) (" )

CTll - 11 ,3573 - 1,3611 -0,1639 -0,0010 -36,5716 -5,4689 -0,1287 - 0,0001 -0,0476 0,1569

(- 34,0432) (-4,7590) (-0,0975) (>-e)

CT12 -13,3348 -1,8798 -0,2664 -0,0019 -42,7958 -8,8516 -0,4045 -0,0009

(-40,2464) (-7,8687) 1-0,3202) (0,0005)

PA07 -0,9784 -0,0095 0,0000 0,0000 - 4,0790 -0,0069 0,0000 0,0000

(- 3,6212) (-0,0055) (

..

) (

..

)

PA08 -1,9078 -0,0369 -0,0007 0,0000 -8,4590 -0,0627 0,0000 0,0000

(- 7,6216) (-0,0509) ( ") ( ")

PA09 -3,6914 -0,1399 - 0,0053 0,0000 - 15,4827 -0,3948 -0,0003 0,0000

1-14,0288) (-0,3244) (- 0,0002) (" )

Continua .. .

W

... Continuação do Quadro VII .J>.

WI LD NEWTON - RAPHSON

Caso

( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 1 ) ( 2 ) ( 3 ) ( 4 ) EVANS KARPIN

PAIO -6,9524 -0,5040 -0,0366 -0,0001 -28,0842 -2,4463 -0,0192 0,0000

(-25,9549) (-2,0954) (-0,0141) ( " )

PA11 -10,8503 -1,2516 -0,1452 -0,0010 -37,0401 -5,7143 -0,1437 -0,0001

(-34,5675) (-4,9989) (-0,1101) (>-e)

PA12 -13,1323 -1,8448 -0,2608 -0,0022 -45,4706 -10,7288 -0,6458 -0,0024

(-42,9833) (-9,6427) (-0,5229) (-0,0016)

PG07 -0,7966 -0,0066 -0,0002 0,0000 -3,8167 -0,0057 0,0000 0,0000 0,0095 0,0254

(-3,4065) (-0,0045) ( " ) ( " )

PGOS -1,9157 -0,0371 -0,0007 0,0000 -8,1974 -0,0570 0,0000 0,0000

(-7,3510) (-0,0458) ( " ) ( " )

PG09 -1,7720 -0,0318 -0,0005 0,0000 -8,4177 -0,0618 0,0000 0,0000 0,0035 0,0092

(-7,5690) (-0,0500) (

..

) ( " )

PG10 -9,5886 -0,9512 -0,0946 -0,0003 -30,2284 -3,0288 -0,0314 0,0000

(-27,9646) (-2,5995) (-0,0232) ( " )

PG11 -9,9856 -0,9447 -0,0889 0,0006 -23,5702 -1,3278 -0,0042 0,0000 13,0962 9,3721

1-19,5927) (-O,9179) (-0,0020) ( ")

PG12 -12,6548 -1,7732 -0,2510 -0,0034 -49,0333 -13,6795 -1,1753 -0,0090

(-46,7237) (-12,5034) (-0,9850) (-0,0063)

Média 6,5023 0,6634 0,0778 0,0006 22,8155 3,1263 0,1438 0,0007 2,1966 1,5951

(21,0659) (2,7578) (0,1168) (0,0005)

•

••••••••••••••••••••••••••••••••••••••••••••••

QUADRO VIII

ERROS PERCENTUAIS

3 - Prazo de 36 Períodos

€ ; 0,0001

WI LD NEWTON - RAPHSON

aso

( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 1 ) ( 2 ) ( 3 ) ( 4 ) EVANS KARPIN

T13 -1,7659 -0,0315 - 0,0005 0,0000 -7,2403 -0,0391 0,0000 0,0000 -0,0031 - 0,0017

1-6,7161) (-0,0337) ( " ) ( " )

T14 -2,8705 -0,0842 -0,0025 0,0000 - 11,8117 - 0,1732 0,0000 0,0000

(-11,0233) (-0,1 509) ( " ) _{I" )}

T15 -5,9269 - 0,3656 -0,3656

> - E

-21,4552 -1,07 16 ' -0,0027 0,0000 - 0,0284 0,0226

1-20,1747) (-0,9487) (-0,0021) 1 " )

Tl6 -11 ,1146 - 1,3117 - 0,1556 -0,0011 -36,5508 -5,4912 -0,1308 -0,0001

1- 34,8489) 1-5,0177) (- 0,1039) (

..

)

T17 -14,8806 -2,3795 - 0,3835 -0,0043 -42,9547 -8,9796 - 0,4198 - 0,0009 - 0,1110 0,4146

1- 41,1886) (- 8,2865) (-0,3580) (0,0007)

1'18 -25,1775 -6,8527 - 1,8823 - 0,0323 -59,3586 -23,7633 -4,1773 -0,1346

(-57,7184) (-22,5740) (-3,7799) (-0,1103)

13 -1,5105 -0,0231 -0,0004 0,0000 . -5,8610 -0,0207 0,0000 0,0000

(-5,4181) (-0,0177) (

..

) (

..

)

14 -3,2054 -0,1047 -0,0035 0,0000 -12,4988 -0,2052 -0,0001 0,0000

(-11,6735) (- 0,1791) (" ) (

..

)

A15 -6,2110 -0,4090 -0,0270 -0,0001 -26,5146 -2,0707 -0,0130 0,0000

(-25,1395) (-1,8651) (- 0,0106) (

..

)

Continua , . .

W

• o o Continuação do Quadro VIII

WI LD Caso

( 1 )

( 2)

( 3 ) ( 4 ) ( 1 j

PA16 -12,2704 -1,6200 -0,2154 -0,0020 -40,7238

(-39,0477)

PA17 -17,5466 -3,3618 -0,6512 -0,0108 -49,4435

(-47,7256)

PA18 -23,1472 -5,6747 -1,3988 -0,0134 -55,1082

(-53,3287)

PG14 -3,1891 -0,1039 -0,0034 0,0000 -12,6600

(-11,8251)

PG15 -7,5780 -0,6078 -0,0490 -0,0003 -27,9443

(-26,4827)

PG16 -15,0037 -2,3656 -0,3748 -0,0026 -40,5432

(-38,7039)

PG17 -20,3049 -4,6086 -1,0621 -0,0268 -56,3280

(-54,7469)

PG18 -28,2676 -8,0756 -2,2950 0,0236 -56,7916

(-54,8506)

Média 11,1876 2,1111 0,4738 0,0065 31,6595

(30,3475)

...

'.

. ... .

NEWTON - RAPHSON

( 2 )

( 3 )

-7,6812 -0,2922

(-7,0866) (-0,2491)

-13,8397 -1,1815

(-12,9509) (-I,0367l

-18,8679 -2,3929

(-17,7445) (-2,1210)

-0,2136 -0,0001

(-0,1864) (0,0000)

-2,4207 -0,0188

(-2,1786) (-0,0153)

-7,4383 -0,2642

(-6,8000) (-0,2211)

-20,6541 -3,0901

(-19,6086) (-2,7933)

-20,0302 -2,6234

(-18,7453) (-2,3009)

7,3883 0,8115

(6,9108) (0,7218)

( 4 )

-0,0004 (-0,OO03)

-0,0089 (-0,0068) -0,0397 (-0,0312) 0,0000

( " )

>-€

( " ) -0,0003 (-0,0002) -0,0725 (-0,0593) -0,0458 (-0,0353)

0,0169 (0,0136)

EVANS

0,0138

-0,0918

0,0414

KARPIN

0,0072

0,4019

0,1413

w

••••••••••••••••••••••••••••••••••

QUADRO IX

ERROS PERCENTUAIS

4 - Prazo de 60 Períodos

e = 0,0001

W I LD _{NEWTON - RAPHSON}

Caso

1

I

:2

j

_!

3

j

₁₄

J ( 1 ) ( 2 ) ( 3 ) ( 4 ) EVANS KARPIN

CT19 -3,0364 -0,0944 -0,0029 0,0000 -11,6268 -0,1653 0,0000 0,0000 -0,0097 0,0026

(-11,1411) (-0,1517) I " ) ( " I

CT20 -4,8773 -0,2467 -0,0125 0,0000 -19,9106 -0,8558 -0,0017 0,0000

(-19,2078) (-0,7970) (--'0,0014) ( " )

CT21 -14,2714 -2,2050 -0,3437 -0,0043 -40,9692 -7,8071 -0,3027 -0,0004 -0,1454 0,4223

(-39,9112) (-7,4251) (-0,2740) ( " )

CT22 -24,5953 -6,6273 -1,8083 -0,0422 -57,7257 -21,9732 -3,4989 -0,0924

(-56,7240) (-21,2788) (-3,2867) (-0,0816)

CT23 -33,3413 -12,1223 -4,4519 -0,1094 -67,2156 -34,3038 -9,8223 -0,8471 -0,1355 2,1518

(-66,3420) (-33,5151) (-9,3935) (-0,7753)

CT24 -38,8691 -16,2811 -6,8491 -0,0869 -72,7196 -42,9705 -16,4121 -2,5214

(-71,9596) (-42,1920) (15,8525) (-2,3543)

PAI9, -2,5937 -0,0684 -0,0018 0,0000 -9,1126 -0,0784 0,0000 0,0000

(-8,El999) (-0,0716) ( " ) ( " )

PA20 -5,1369 -0,2711 -0,0143 0,0000 -17,5126 -0,5736 0,0006 0,0000

(-16,8264) (-0,5298) (-0,0005) (

..

)

PA21 -12,6920 -1,7831 -0,2533 -0,0037 -42,7247 ~,9978 -0,4325 -0,0010

(-41,7271) (-8,6035) (-0,3958) (-O,OOOg)

Continua. , .

w

(%

.,. Continuação doOuadro IX

WI LD NEWTON - RAPHSON

Caso _{( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 1 ) ( 2 ) ( 3 ) . ( 4 )} EVANS KARPIN

PA22 -23,3254 -5,7901 -1,4476 -0,0182 -53,3909 -17,1481 -1,9067 -0,0242

(-52,2780) (-16,4831) (-1,7638) (-0,0207)

PA23 -31,0536 -10,7642 -3,7905 -0,1382 -66,9940 -34,3193 -10,0382 -0,9142

(-66,1564) (-33,5704) (-9,6257) (-0,8414)

PA24 -37,8963 -14,9400 -5,8674 -0,0614 -69,2562 -36,6901 -11,0427 -1,0340

(-68,3309) (-35,8052) (-10,5315) (-0,9410)

PA25 -2,2919 -0,0537 -0,0012 0,0000 -9,6096 -0,0976 0,0000 0,0000 0,0000 0,0000

(-9,2073) (-0,08511 ( " ) ( " )

PG20 -4,3693 -0,2006 -0,0107 -0,0017 -18,6610 -0,7054 -0,0025 -0,0015

(-17,9942) (-0,6566) (" ) (-0,0011)

PG21 -15,5042 -2,4250 -0,3792 -0,0001 -33,8897 -4,1601 -0,0642

>-€

-0,2935 4,6404

(-32,5482) (-3,8417) (-0,0547) (0,0000)

PG22 -21,3620 -5,1071 -1,2404 -0,0336 -56,9932 -21,4195 -3,3707 -0,0877

(-66,0443) (-20,7756) (-3,1768) (-0,0779)

PG23 -32,4338 -10,5961 -3,4351 0,0588 -59,6945 -23,0774 -3,6029 -0,0891 0,7485 3,6395

(-58,4377) (-22,1581) (-3,3244) (-0,0759)

PG24 -35,6930 -14,3264 -5,8359 -0,2373 -73,7349 -45,4979 -19,3394 -3,7882

(-73,0623) (-44,7567) (-18,8009) (-3,5840)

Média 19,0747 5,7724 1,9859 0,0442 43,4301 16,7131 4,4355 0,52222 0,2221 1,8094

(42,5888) (16,2610) (4,2492) (0,4864)

·

••••••••••••••••••••••••••••••••••.

-QUADRO X

ERROS PERCENTUAIS

5 - Prazo de 84 Períodos

€ = 0,0001

WI LD NEWTON - RAPHSON EVANS KARPIN

aso

( 1 I ( 2 I ( 3 ) ( 4 ) ( 1 )

( 2 ) ( 3 ) ( 4 )

CT25 -3,4428 -0,1220 -0,0044 0,0000

-12,8677 -0,2253 -0,0002 0,0000

-0,0130 0,0066

(-12,4877) !-0,2122) ( " ) ( " )

CT26 -6,4977 -0,4428 -0,0302 -0,0001

-23,9035 -1,4996 -0,0060 0,0000

(-23,31981 (-1,42831 {-0,0055\ ( " I

CT27 -19,2003 -4,0485 -0,8646 -0,0176

-49,2795 -13,7062 -1,1534 -0,0084

-0,2466 0,8710

(-48,5188) !-13,31171 1-1,0889) (-0,0075)

CT28 -30,0693 -9,9302 -3,3208 -0,0921

-63,9143 -29,7008 -7,0717 -0,4212

(-63,2556) (-29,1538) (-6,8228) (-0,3923)

CT29 -39,1743 -16,6800 -7,1553 -0,1604

-12,1680 -42,0899 -15,6640 -2,2806

0,0394 2,5844

(-71,6128) (-41,52741 (-15,26841 (-2,16Bl)

CT30 -45,2963 -21,8869 -10,5575

-0,0678 -77,5276 -51,4440 -24,5480

-5,8550

(-77,0633) (-50,9199) (-24,0798) 1-5,6369)

PA25 -2,6591 -0,0733 -0,0020 0,0000

-13,8220 -0,2821 -0,0002 0,0000

(-13,4494) (-0,2673) ( " ) ! " I

PA26 -10,8433 -1,2311 -0,1404 -0,0007

-30,0972 -2,9989 -0,0309 -0,0001

(-29,3532) (-2,8552) (-0,0279) (0,0000)

PA27 -18,0082 -3,6600 -0,7562 -0,0195

-51,7902 -16,1547 -1,7432 -0,0211

(-51,0834) (-15,7504) (-1,6588) (-0,0191)

... Continua

eM <.O