Invariantes do tipo Vassiliev de aplicações estáveis de 3-variedade em 'R POT. 4...

(1)

Invariantes do tipo Vassiliev de aplicações estáveis

de 3-variedade em R

4

(2)

(3)

Invariantes do tipo Vassiliev de aplicações estáveis de

3-variedade em R

4

Catiana Casonatto

Orientadora:

_{Profa. Dra. Roberta Godoi Wik Atique}

Co-orientadora:

_{Profa. Dra. María del Carmen Romero Fuster}

Tese apresentada ao Instituto de Ciências Matemáticas e de Computação - ICMC-USP, como parte dos requisitos para obtenção do título de Doutor em Ciências - Matemática.

VERSÃO REVISADA_.

USP

–

São Carlos

Agosto de 2011

SERVIÇO DE PÓS-GRADUAÇÃO DO ICMC-USP

Data de Depósito: 02/08/2011

(4)

com os dados fornecidos pelo(a) autor(a)

C341i

Casonatto, Catiana

Invariantes do tipo Vassiliev de aplicações estáveis de 3-variedade em R4 / Catiana Casonatto; orientadora Roberta Godoi Wik-Atique -- São Carlos, 2011.

114 p.

Tese (Doutorado - Programa de Pós-Graduação em Matemática) -- Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, 2011.

(5)

i

Ao meu amado Jean, companheiro de todas as horas.

(6)

(7)

Agradecimentos

`

A Deus, simplesmente por tudo.

Com muita gratidão, respeito e admira¸cão, agrade¸co às minhas orientadoras Roberta Godoi Wik Atique e Mar´ıa del Carmen Romero Fuster, pela significativa contribui¸cão em minha inici-a¸cão à pesquisa matemática, pelo exemplo de profissionalismo e pela amizade.

Aos meus pais, Carlos e Marilene, por todo amor e apoio incondicional. Pelo exemplo de perseveran¸ca, determina¸c˜ao e car´ater.

`

A minha irm˜a e amiga Susi´eli, ao meu querido cunhado Ariel e ao meu amado sobrinho afilhado Joaquim por estarem ao meu lado em todos os momentos e fazerem os meus dias mais felizes.

Ao meu noivo, meu grande amor e companheiro, por estar sempre ao meu lado, me dando o exemplo, a for¸ca e a coragem que necessito para n˜ao desistir da luta di´aria de me tornar uma profissional e uma pessoa melhor.

Aos professores do Instituto de Ciências Matemáticas e Computa¸cão (ICMC-USP) pelos valiosos ensinamentos, em especial, à Professora Maria Aparecida Soares Ruas.

Aos professores, funcion´arios e alunos do departamento de Topolog´ıa y Geometr´ıa da Uni-versidad de Valencia pela calorosa acolhida.

Ao amigo Raúl, pelas divertidas e produtivas discussões matemáticas.

Aos meus amigos que estiveram ao meu lado nesta caminhada, tornando tudo mais agradável e divertido: Nazira Harb, Marcio Fenille, Tha´ıs Monis, Kleyber Cunha, Tha´ıs Jordão, Éder Aragão, Mario Henrique, Luiz Hartmann, Romero Melo, Thiago Catalan, Flank Bezerra, Márcio Jorge.

Ao CNPq pelo apoio financeiro.

(8)

(9)

-resumo

Neste trabalho obtemos que o espa¸co dos invariantes locais do tipo Vassiliev de primeira ordem de aplica¸cões estáveis de 3-variedade fechada orientada em R4 _{é 4-dimensional. Damos}

uma interpreta¸cão geométrica para 2 dos 4 geradores deste espa¸co, a saber, IQ o número de

pontos quádruplos e I_C/P o número de pares de pontos do tipo crosscap/plano, da imagem de uma aplica¸cão estável. Ao reduzir o espa¸co das aplica¸cões para o das imersões estáveis, obtemos que o espa¸co dos invariantes locais de imersões estáveis é 3-dimensional. Os invariantes que obtemos são: IQ o número de pares de pontos quádruplos da imagem de uma imersão estável e

dois ´ındices de interse¸c˜aoI_ℓ+ e I_ℓ− introduzidos por V. Goryunov em [15].

Como in´ıcio de um estudo que almejamos realizar sobre a geometria de uma m-variedade emRm+1 _{com singularidades, obtemos os tipos de contatos gen´ericos da suspens˜ao do crosscap}

(´unica singularidade est´avel deR3 _emR4_{) com hiperplanos de} R4_.

(10)

(11)

-abstract

In this work we obtain that the space of first order local Vassiliev type invariants of stable maps of oriented 3-manifolds in R4 _{is 4-dimensional. We give a geometric interpretation for}

two of the four generators of this space, namely, IQ the number of quadruple points and IC/P

the number of pairs of points of crosscap/plane type, of the image of a stable map. In the case of stable immersions, we obtain that the space of local invariants of stable immersions is 3-dimensional. The invariants that we obtain are: IQ the number of pairs of quadruple points

of the image of a stable immersion and the positive and negative linking invariantsI_ℓ+ and I_ℓ−

introduced by V. Goryunov in [15].

As a beging of a study that we want to realise about the geometry of am-manifold inRm+1

with singularities, we obtain the generic contacts of the suspension of crosscap (the only stable singularity from R3 _toR4_{) with hyperplanes of}R4_.

(12)

(13)

-Conte´

udo

1 Classifica¸c˜ao de multigermes de R3 _em R4 _{e de coposto} ₁ ₅

1.1 Teoria cl´assica de Singularidades . . . 6

1.1.1 Rela¸c˜oes de equivalˆencias e espa¸cos tangentes . . . 7

1.1.2 M´etodo de classifica¸c˜ao . . . 9

1.1.3 Desdobramentos versais . . . 11

1.1.4 Opera¸cões de aumenta¸cão e concatena¸cão . . . 12

1.1.5 Suspens˜ao do crosscap . . . 14

1.2 Classifica¸c˜ao de bigermes . . . 14

1.3 Classifica¸c˜ao de trigermes . . . 26

1.4 Classifica¸c˜ao de quadrigermes, pentagermes e hexagermes . . . 32

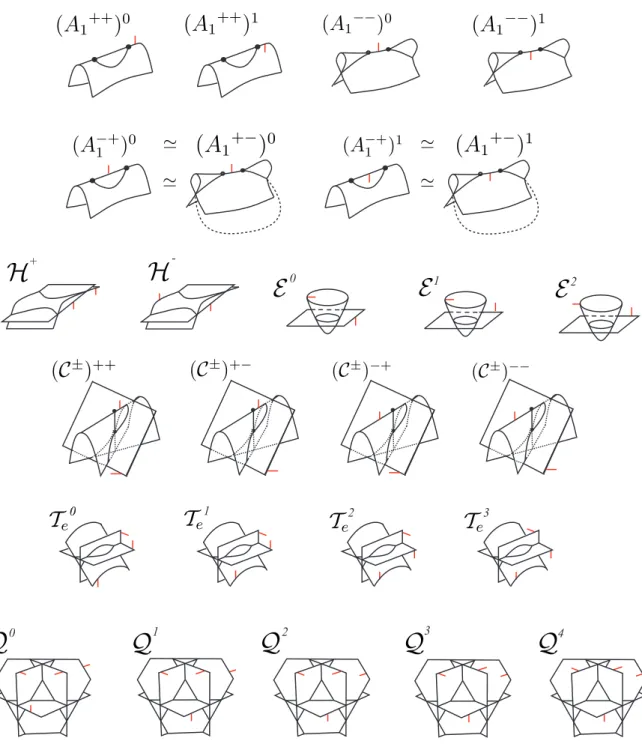
2 Conjuntos de bifurca¸cão dos germes de _Ae-codimensão2 40 2.1 Conjuntos de bifurca¸cão dos monogermes . . . 42

2.2 Conjuntos de bifurca¸c˜ao dos bigermes . . . 48

2.3 Conjuntos de bifurca¸c˜ao de trigermes . . . 58

2.4 Conjuntos de bifurca¸c˜ao dos quadrigermes, pentagermes e hexagermes . . . 65

3 Invariantes locais do tipo Vassiliev de primeira ordem 73

(14)

-3.1 M´etodo de Vassiliev . . . 73

3.2 Invariantes de aplica¸c˜oes est´aveis de 3-variedades em R4 _{. . . .} ₇₆

3.2.1 Coorienta¸c˜ao dos estratos de codimens˜ao 1 . . . 77

3.2.2 Parti¸c˜ao dos estratos de codimens˜ao 1 . . . 83

3.2.3 Condi¸c˜oes de compatibilidade e geradores . . . 85

3.2.4 Invariante não local de aplica¸cão estável . . . 98

3.3 Invariantes de imers˜oes est´aveis de 3-variedades em R4 _{. . . .} ₉₉

4 Fun¸c˜oes na suspens˜ao do crosscap 102 4.1 Transversalidade . . . 103

4.2 Geometria da suspens˜ao do crosscap . . . 103

Apêndice 112 Apêndice A: comandos dos programas Superf´ıcie I e Mathematica utilizados na visualiza¸cão dos estratos de codimensão 1 . . . 112

(15)

Introdu¸

c˜

ao

Na década de 60 J. Mather desenvolveu uma série de trabalhos que contribuiram para o avan¸co de classifica¸cões de singularidades. De particular relevância podemos citar sua clas-sifica¸cão de singularidades estáveis obtida em [22]. Tal clasclas-sifica¸cão foi realizada segundo a

A-equivalência, isto é, mudan¸cas de coordenadas na fonte e na meta. A partir de então se ini-ciou o estudo de singularidades menos frequentes (as singularidades não estáveis) e classifica¸cões foram sendo obtidas considerando-se pares espec´ıficos de dimensões, singularidades de codimen-são e coposto baixos, singularidades simples, entre outras. Algumas classifica¸cões conhecidas são:

(i) Singularidades simples de germes de fun¸c˜oes deRn _emR_{, por V. I. Arnol’d em [2];}

(ii) Singularidades simples de germes de aplica¸c˜oes deR2 _em R3_{, por D. Mond em [23];}

(iii) Singularidades simples de germes de aplica¸c˜oes de Kn emK2 (K =R_ou _K ₌C_{), por J.}

H. Rieger e M. A. S. Ruas em [31];

(iv) Singularidades simples de germes de aplica¸c˜oes de R3 _em R3_{, por W. L. Marar e F. Tari}

em [21];

(v) Singularidades simples de germes de aplica¸c˜oes de R3 _emR4_{, por K. Houston e Kirk em}

[19];

(vi) Singularidades simples de multigermes de aplica¸c˜oes de C2 _emC3_{, por R. G. Wik Atique}

em [36].

Os resultados sobre classifica¸cão de singularidades são aplicados em diversas situa¸cões in-teressantes. Um exemplo disto é a teoria dos invariantes do tipo Vassiliev. No in´ıcio da década de 90, Vassiliev em [34] desenvolveu um método para definir invariantes numéricos de nós, hoje conhecidos comoinvariantes do tipo Vassiliev de ordem finita. Ele obteve estes invariantes estu-dando cuidadosamente uma certa parti¸cão dosubconjunto discriminante Σ de C∞₍_S1_,_R3_{), isto}

´e, o subconjunto deC∞₍_S1_,_R3_{) consistindo das aplica¸c˜}_{oes n˜}_{ao est´}_{aveis. Desde ent˜}_{ao este m´etodo}

(16)

discriminante é particionado em vários estratos de codimensão 1 e 2. Já que estes invariantes são locais, esta parti¸cão é feita de acordo com o tipo local de singularidade que as aplica¸cões em Σ apresentam. É neste aspecto que a classifica¸cão de germes de aplica¸cões contribui para a obten¸cão de invariantes do tipo Vassiliev. O objetivo inicial é determinar o número de geradores do espa¸co dos invariantes de primeira ordem das aplica¸cões estáveis emM. Uma segunda etapa é obter interpreta¸cões geométrica para tais geradores ou para combina¸cões lineares deles. Os invariantes do tipo Vassiliev de primeira ordem já obtidos são de:

(i) Curvas planas imersas, por V. I. Arnol’d em [3];

(ii) Aplica¸c˜oes est´aveis de superf´ıcies em R3_{, por V. Goryunov em [15];}

(iii) Aplica¸c˜oes est´aveis de superf´ıcies em R2_{, por T. Ohmoto e F. Aicardi em [26];}

(iv) Aplica¸c˜oes est´aveis de 3-variedades em R2_{, por M. Yamamoto em [40];}

(v) Aplica¸c˜oes est´aveis de 3-variedades emR3_{, por R. Oset Sinha e M. C. Romero Fuster em}

[27].

Um dos objetivos deste trabalho é estudar os invariantes locais do tipo Vassiliev de primeira ordem de aplica¸cões estáveis de uma 3-variedade fechada orientada em R4_.

Assim, no Cap´ıtulo 1 obtemos a classifica¸c˜ao dos multigermes deR3 _em R4 _{sob a a¸c˜}_{ao do}

grupo _A com _Ae-codimensão no máximo 2. Para isso utilizamos o método descrito por R. G.

Wik Atique em [36] que nos permite reduzir aA-classifica¸cão de multigermes para a classifica¸cão de germes de fun¸cões definidos em R4 _{segundo o subgrupo} _VK _{do grupo de contato}_K_.

No Cap´ıtulo 2 determinamos os conjuntos de bifurca¸c˜ao dos multigermes de_Ae-codimens˜ao

2 e seus diagramas de adjacˆencias. Para cada germe f de Ae-codimens˜ao 2, seja fu,v uma

deforma¸cão_Ae-versal def, onde (u, v) são os parâmetros da fam´ılia. O conjunto dos parâmetros

para os quais o germefu,v é não estável,B(f), é denominadoconjunto de bifurca¸cão def . Para

(u, v)∈ B(f) identificamos osfu,v′sem nossa lista de germes deAe-codimens˜ao menor ou igual a

1, isto é, determinamos osdiagramas de adjacências def. Para obter os conjuntos de bifurca¸cão dos monogermes utilizamos o método descrito por J. Rieger em [29], o qual descrevemos a seguir de maneira sucinta. Seja

Dk(fu,v) ={(x1, x2,· · ·, xk)∈R3× · · · ×R3; fu,v(x1) =· · ·=fu,v(xk), xl6=xj sel6=j}

o espa¸co dos pontosk-múltiplos defu,v. Associamos afu,v germes de aplica¸cõesGcujas fun¸cões

coordenadas definem Dk(fu,v). Em [20], W. L. Marar e D. Mond obt´em estas fun¸c˜oes

coorde-nadas. O conjunto de bifurca¸c˜ao def consiste dos parˆametros (u, v) para os quais os germesG

são não submersivos. Para os multigermes procedemos de maneira análoga, só que neste caso cada fun¸cão coordenada deGé calculada diretamente da defini¸cão de Dk(fu,v).

(17)

3

aplica¸c˜oes est´aveis de uma 3-variedade orientada M emR4_{. Como comentado anteriormente, o}

conjunto discriminante deC∞(M,R4_{) ´e particionado em estratos de codimens˜ao 1 e 2, os quais}

correspondem aos germes obtidos na nossa classifica¸cão. Para cada estrato de codimensão 1 associamos uma coorienta¸cão que consiste em estabeler um critério que distingua quando um caminho transversal em C∞(M,R4_{) cruza-o de maneira positiva ou negativa. Considerando a}

orienta¸cão da 3-variedadeM obtemos uma parti¸cão dos estratos de codimensão 1. A importˆ an-cia de tal etapa é percebida durante o processo. Em seguida determinamos osistema coerente, isto é, um sistema de equa¸cões lineares que é obtido tomando caminhos fechados ao redor de cada estrato de codimensão 2. Ao resolver este sistema de equa¸cões obtemos que o espa¸co dos invariantes locais do tipo Vassiliev de primeira ordem de aplica¸cões estáveis de uma 3-variedade orientada em R4 _{é 4-dimensional. Para dois dos quatro geradores estabelecemos a seguinte}

in-terpreta¸cão geométrica: o número de pontos quádruplosIQ da imagem de uma aplica¸cão estável

e o n´umero de pares de pontos do tipo crosscap/plano IC/P de uma tal imagem.

Ainda no Cap´ıtulo 3, estudamos o caso de imersões estáveis e determinamos os invariantes locais para esta situa¸cão. Obtemos que o espa¸co dos invariantes locais do tipo Vassiliev de primeira ordem de imersões estáveis de uma 3-variedade orientada emR4 _{é 3-dimensional. Uma}

interpreta¸cão para cada gerador é: o número de pares de pontos quádruplos IQ da imagem de

uma imersão estável e dois ´ındices de interse¸cãoI_ℓ+ eI_ℓ− introduzidos por V. Goryunov em [15].

Provamos ainda que a caracter´ıstica de Euler da imagem das imersões estáveis é um invariante do tipo Vassiliev e a expressamos como combina¸cão linear dos outros três invariantes.

Os resultados obtidos no caso de imersões estáveis estão reunidos no artigo Topological invariants of stable immersions of oriented 3-manifolds in R4_{, veja [7].}

Para finalizar os estudos do Cap´ıtulo 3 obtemos como invariante não local do tipo Vassiliev o número de componentes conexas da curva de pontos triplos na imagem de uma aplica¸cão estável.

Como outra aplica¸cão da classifica¸cão de singularidades podemos citar o trabalho de J. W. Bruce e J. M. West [6], onde investigam a geometria do crosscap emR3 _{através do seu contato}

com planos deR3 _{na origem . Este estudo ´e feito por meio da fam´ılia de fun¸c˜}_{oes altura. Seja} _g

uma parametriza¸c˜ao do crosscap, ou seja, g ´e _A-equivalente a f(x, y) = (x, y2_{, xy}_{). A imagem}

def é chamada de crosscap padrão. Bruce e West observam que uma fun¸cão altura definida na imagem deg pode ser vista como uma fun¸cão definida no crosscap padrão. Então, eles mostram que genericamente os germes de fun¸cões altura definidos no crosscap tem XR-codimensão no

máximo 2, onde X é o crosscap padrão. Desta maneira, analisando as singularidades destes germes de fun¸cões, obtém informa¸cões sobre a geometria da curva de pontos duplos do crosscap e sobre o contato dele com planos.

Analogamente, no Cap´ıtulo 4, obtemos informa¸cões sobre a geometria da suspensão do crosscap (única singularidade estável de R3 _em R4_{, cuja parametriza¸c˜}_ao _g _é _A_{-equivalente a}

f(x, y, z) = (x, y, z2_{, yz}_{)) considerando seu contato com hiperplanos de}_R4 _{na origem .}

(18)

(19)

Cap´ıtulo 1

Classifica¸

c˜

ao de multigermes de

R

3

em

R

4

_{e de coposto}

1

Nosso objetivo neste cap´ıtulo ´e obter as formas normais dos multigermes simples de R3

em R4 _de _A_e_-codimens˜_{ao 1 e 2 e coposto 1. Tal classifica¸c˜ao ´e fundamental para o estudo que}

desenvolveremos no Cap´ıtulo 3 sobre os invariantes locais do tipo Vassiliev de uma 3-variedade fechada emR4_.

A lista dos multigermes est´aveis foi obtida por Mather em [22] e ´e a seguinte:

1. (x, y, z,0)

2. (x, y, z2_{, yz}₎

3.

(

(x, y, z,0)

(x, y,0, z)

4.

(

(x, y, z2, yz) (0, x, y, z)

5.

   

  

(x, y, z,0)

(x, y,0, z)

(x,0, y, z)

6.

            

(x, y, z,0)

(x, y,0, z)

(x,0, y, z) (0, x, y, z)

Em [19], K. Houston e N.P. Kirk obt´em uma classifica¸c˜ao para monogermes. Os de _Ae

(20)

M onogerme _Ae−codimens˜ao Nome

(x, y, z2_{, z}₍_z2_±_x2_±_yk₎₎_, _k_{= 1}_,₂ _k _A±±

k

(x, y, z3+xz, zk+3+yz), k= 1,2 k Rk

(x, y, z2, z(z4±x2±y2)) 2 A3

(x, y, z3_±_y2_{z, xz}₊_yz2₎ ₂ _S±

Na Se¸cão 1.1 apresentamos algumas defini¸cões básicas e resultados da teoria de singulari-dade que se fazem necessários para o bom entendimento de nosso trabalho. É também nesta se¸cão que descrevemos o método que utilizamos na obten¸cão dos multigermes de R3 _em R4

de _Ae-codimensão 1 e 2 e coposto 1. Nas demais se¸cões desenvolvemos tal método obtendo a

classifica¸c˜ao desejada.

1.1 Teoria cl´

assica de Singularidades

Seja S um subconjunto de Rn_{. Consideremos o conjunto de todas as aplica¸c˜}_{oes de classe}

C∞_f _:_U _→Rp_{, onde}_U _{´e uma vizinhan¸ca de}_S _emRn_._{Neste conjunto introduzimos a seguinte}

rela¸cão de equivalência: duas aplica¸cões f :U1 → Rp e g :U2 → Rp são equivalentes se existir

uma vizinhan¸ca U ⊂ U1 ∩U2 de S em Rn tal que f|U = g|U. As classes de equivalˆencia

s˜ao chamadas multigermes de f em S e denotadas por f : (Rn_{, S}₎ _→ ₍Rp_{, f}₍_S_{)). Quando} _S

consiste de um único elemento tais classes são também chamadas monogermes. Quando não houver a necessidade de especifica¸cão usaremos o termogerme para denominar um monogerme ou multigerme.

Consideremos S um conjunto finito, ou seja, S = _{s1, . . . , sr}. ´E suficiente estudarmos

multigermes onde f(S) = 0, uma vez que a classifica¸cão de multigermes com f(S) finito e não unitário se reduz a este caso. O germe de f em si será chamado de ramo e denotado

por f(i) _{: (}_Rn_{, s}

i) → (Rp,0). Quando necess´ario mencionarmos o n´umero de ramos de um

multigerme, o denominaremos porr-germe.

SejamEno anel local dos germes de fun¸c˜oes de classeC∞f : (Rn,0)→(R,0) eMn={f ∈

En; f(0) = 0} seu ideal maximal . O conjunto dos monogermesf : (Rn,0)→(Rp,0), denotado

porEn,p, é um En-módulo livre de posto p.O submódulo consistindo dos germes que satisfazem

f(0) = 0 ´e dado por _Mn· En,p. Assim, o conjunto dos multigermes f : (Rn, S) → (Rp,0) ´e

isomorfo `a _⊕r

1Mn·En,p, isto é, à soma direta de r cópias de Mn·En,p.

Um germef _{∈ E}n,p induz o homomorfismo de ´algebras

f∗ _: _E

p → En

(21)

1.1 Teoria cl´assica de Singularidades 7

A multiplicidade local de um germe de aplica¸c˜ao f _{∈ E}n,p´e

mf(0) = dimR_fE∗_Mn

p

Denotamos porJk(n, p) o espa¸co vetorial real das aplica¸c˜oesf :Rn_→Rp _{onde cada fun¸c˜}_ao

coordenada fi de f ´e um polinˆomio de grau menor ou igual a k nas coordenadas x1, . . . , xn e

com termo constante nulo. Os elementos de Jk(n, p) s˜ao chamadosk-jatos.

Sejamf ∈ En,p ek∈Z, k≥1. Ok-jato de f ema, denotado porjkf(a), ´e definido por

Df(a)(x) +

1 2!D

2_f

(a)(x, x) +· · ·+

1

k!D

k_f

(a)(x, . . . , x),

isto é,jkf(a) é a expansão em série de potências def(x+a)−f(a) em torno da origem, truncada no termo de grauk.

Um germe f _{∈ M}n· En,p ´e dito k− G-determinado (onde G ´e um grupo de Mather) se

qualquer g ∈ Mn·En,p tal que jkg(0) =jkf(0) ´eG-equivalente a f. Sef ´ek− G-determinado

para algumk diremos simplesmente que f ´e finitamente_G-determinado.

1.1.1 Rela¸c˜oes de equivalˆencias e espa¸cos tangentes

Introduzimos algumas rela¸c˜oes de equivalˆencias considerando os grupos de Mather A,R e

K e os subgrupos _V_R e _VK. Para ver detalhes de defini¸cões básicas e resultados destas e de outras rela¸cões de equivalências utilizadas na teoria de singularidades, veja [5, 10, 35] .

Seja R o grupo de germes de difeomorfismos ψ : (Rn_{, s}₎ _→ ₍Rn_{, s}_{) com a opera¸c˜ao de}

composi¸c˜ao. Este grupo age em _En,p da seguinte maneira: dois germes f, g : (Rn, s) → (Rp,0)

s˜ao_R-equivalentes se existir ψ_{∈ R}tal queg=f_◦ψ−1_{. Denominamos tal grupo de}_{grupo das}

mudan¸cas de coordenadas na fonte.

SejaA o grupo dos pares de germes de difeomorfismos (ψ, ϕ), onde ψ∈ R e ϕ: (Rp_,₀₎_→

(Rp_,_{0), com a opera¸c˜}_{ao de composi¸c˜ao em cada coordenada. Este grupo age em}_E_n,p_{da seguinte}

maneira: dois germes f, g : (Rn_{, s}₎ _→ ₍Rp_,_{0) s˜ao} _A_{-equivalentes} _{se existir (}_{ψ, ϕ}₎ _{∈ A} _{tal que}

ϕ◦g=f ◦ψ.

A _A-equivalˆencia de multigermes ´e definida como segue: dois r-germes f, g : (Rn_{, S}₎ _→

(Rp_,_{0) s˜}_ao _A_-_equivalentes _{se existirem (}_ψ(i)_{, ϕ}₎ _{∈ A}_,_i_{= 1}_{, . . . , r}_{, tais que}_ϕ_◦_g(i) ₌_f(i)_◦_ψ(i)_.

Isto significa que para cada ramo podemos escolher uma mudan¸ca de coordenadas na fonte, enquanto que na meta a mesma mudan¸ca de coordenadas deve ser aplicada para todos os ramos.

Consideremos (_V,0) um germe de uma subvariedade anal´ıtica em (Rp_,_{0) (para mais}

deta-lhes, veja [16]) e seja I o ideal em _Ep que define V, isto ´e, o ideal dos germes de fun¸c˜oes que

se anulam em V. Denotamos por _VR o subgrupo de R consistindo dos germes em R tais que

(22)

Definimos _K (grupo de contato) como sendo o grupo dos germes de difeomorfismos H : (Rp_×R_,₀₎_→₍Rp_×R_,_{0) dados por} _H₍_{x, t}_{) = (}_ψ₍_x₎_,_He₍_{x, t}_{)), onde} _ψ_{∈ R} _e_He₍_x,_{0) = 0. Este}

grupo age em_Ep da seguinte maneira: seh1, h2 ∈ Ep, então h1 eh2 sãoK-equivalentes se existir H _{∈ K} tal que H(x, h1(x)) = (ψ(x), h2(ψ(x))). Em outras palavras, H leva o gráfico de h1 no

gr´afico de h2. Denotamos por VK o subgrupo de K consistindo dos germes de difeomorfismos

H= (ψ,He) como acima, tais queψ_∈_VR. E por_VKk, o subgrupo de_V_Kconsistindo dosk-jatos de germes de difeomorfismos em_V_K.

Para mais detalhes da pr´oxima defini¸c˜ao, veja [35].

O espa¸co tangente aA-´orbita def : (Rn_{, S}₎_→₍Rp_,_{0) ´e dado por}

T_A·f =tf(_Mnθ(n)S) +ωf(Mpθ(p))⊆ Mnθ(f)

ondeθ(n) consiste dos germes em 0 de campos vetoriais emRn_,_θ₍_n₎_S_{´e a soma direta de}_r_-c´_opias

de θ(n) eθ(f) consiste dos germes em 0 de campos vetoriais ao longo de f. Neste casoθ(f) é a soma direta de θ(f(i)_{), onde} _f(i) _{é ramo de} _f_{, e pode ser identificado com a soma direta de} r-cópias deEn,p. O espa¸co tangente estendido é dado por

T_Ae·f =tf(θ(n)S) +ωf(θ(p))⊆θ(f)

e a_Ae-codimens˜ao def ´e dada por

dimR

θ(f)

TAe·f

= dimRNAef,

onde a dimensão é como espa¸co vetorial sobreR_e _N_A_e_f _{é chamado de espa¸co normal a} _f_.

O pr´oximo resultado nos fornece o espa¸co tangente ah_{∈ E}p segundo o grupoVR(veja [5]).

Lema 1.1 Seja h_{∈ E}p. Ent˜ao

TVR·h={ξ·h; ξ ∈ Mpθ(p)∩Derlog(V)}

e

T_V_Re·h={ξ·h; ξ ∈Derlog(V)}

onde Derlog(_V) =_{ξ _∈θ(p); ξ_·h˜ _∈I,_∀ ˜h_∈I_} e I _{⊆ E}p ´e um ideal que define V.

Usaremos o programa Macaulay [4] para calcular oDerlog(V) onde necess´ario.

O espa¸co tangente ah∈ Ep segundo o grupoVK´e

T_V_K·h=T_V_R·h+h∗(_M1)· Mp.

O espa¸co tangente estendido ´e

(23)

e a_V_Ke-codimens˜ao de h´e

dimR

θ(h)

TVKe·h

= dimRNVKe·h.

Observemos que se a origem ´e fixada por todos os elementos deDerlog(V), ent˜ao T_VR·h=

T_VRe·h. Logo, TVK·h=TVKe·h.

Seja_VRk o subgrupo de VRque consiste dos elementos de VR cujok-jato ´e a identidade.

O espa¸co tangente ah_{∈ E}p segundo o grupoVR1 ´e

T_VR1·h={ξ·h; ξ ∈ M2pθ(p)∩Derlog(V)}

e o espa¸co tangente segundo o grupoT_VK1·h ´e

T_VK1·h=TVR1·h+h∗(M1)· Mp.

1.1.2 M´etodo de classifica¸c˜ao

Determinar as A-classes de germes finitamente determinados em ⊕r

1En,p n˜ao ´e uma tarefa

fácil. Afortunadamente, no caso (n, n+ 1) podemos reduzir a _A-classifica¸cão de multigermes para a _V_K-classifica¸cão de monogermes de fun¸cões em _En+1. O resultado que nos permite tal

abordagem ´e devido a R. G. Wik Atique (veja [36]) e ´e o seguinte.

Teorema 1.2 Dados Se = _{s1, ..., sr−1} e S = Se∪ {sr} subconjuntos de Cn e fe: (Cn,Se) →

(Cn+1_,₀₎ _{um multigerme finitamente} _A_{-determinado, consideremos} _g,_e_g _{: (}Cn_{, S}₎ _→ ₍Cn+1_,₀₎

multigermes finitamente _A-determinados tais que g(i) =eg(i) =f(i) para i= 1, . . . , r₋1. Ent˜ao

g e g_e são _A-equivalentes se, e somente se, h e eh são _V_K-equivalentes onde h,eh _{∈ O}n+1 são

equa¸c˜oes reduzidas que definem as imagens de g(r) e eg(r), respectivamente, e V ´e a imagem de e

f.

Precisamos agora de uma rela¸cão entre as Ae-codimensões de f eg com a VKe-codimensão

de h . Neste sentido temos o seguinte resultado (veja [36]).

Teorema 1.3 Sejam Se = {s1, ..., sr−1} e S = Se∪ {sr} subconjuntos de Cn, f : (Cn,Se) →

(Cn+1_,₀₎ _{um multigerme finitamente} _A_{- determinado e} _g,_e_g _{: (}Cn_{, S}₎ _→ ₍Cn+1_,₀₎ _satisfazendo

g(i) ₌_f(i) _para _i_{= 1}_{, . . . , r}₋₁ _e _g(r) _{uma imers˜}_{ao. Se} _h _{∈ O}

n+1 ´e uma equa¸c˜ao reduzida que

define a imagem de g(r) e V é a imagem de f, então a Ae-codimensão de g é dada pela soma

das _Ae-codimens˜ao de f e a VKe-codimens˜ao de h.

O próximo resultado foi obtido por J. Mather em [22] e nos dá como determinar asG-órbitas emM, ondeGé um grupo de Lie eM uma variedade diferenciável.

(24)

(1) Para qualquer x_∈S, TxG·x⊇TxS;

(2) A dimens˜ao de TxG·x independe de x∈S;

(3) S ´e conexa.

EntãoS está contida numa única G-órbita.

O m´etodo da tranversal completa que descrevemos abaixo, juntamente com o Lema de Mather, nos permite obter as VKk_-´_{orbitas em}_Jk₍_n_{+ 1}_,_{1) da seguinte maneira:}

(i) Dado um determinado k-jato, aplicamos a transversal completa para obter as poss´ıveis ´

orbitas emJk+1(n+ 1,1) de (k+ 1)-jatos cujo k-jato ´e o considerado;

(ii) A fim de reduzir esta lista aplicamos o Lema de Mather ou realizamos mudan¸cas de coor-denadas apropriadas;

(iii) Para cada poss´ıvel (k+ 1)-jato verificamos a ordem de sua determina¸c˜ao como germe. Se for (k+ 1)-determinado obtemos o representante de uma _V_K-´orbita em _En+1. Caso

contr´ario, repetimos o procedimento descrito em (i).

´

E com o Teorema da Transversal Completa que produzimos uma lista de poss´ıveis (k+ 1)-jatos.

Teorema 1.5 (Teorema da Transversal Completa) Sejamσ_∈Jk₍_n₊₁_,₁₎_{, H}k+1 _⊂_Jk+1₍_n₊

1,1), o subespa¸co das aplica¸c˜oes polinomiais homogˆeneas de grau k+ 1, e T = hβ1, . . . , βri ⊂

Hk+1 _{subespa¸co tais que}

Mkn+1+1·En+1⊂TVK1·σ+T +Mk_n+2₊₁·En+1.

Ent˜ao para qualquer σ˜_∈Jk+1(n+ 1,1)com jkσ˜(0) =σ ´e _VKk₁+1-equivalente a

σ+

r X

i=1 αiβi,

onde αi∈R.

O subespa¸coT =hβ1, . . . , βri´e a transversal completa.

Por fim, um critério para a VK-determina¸cão finita. O resultado seguinte é análogo ao do grupo _K (veja [36]).

(25)

1.1.3 Desdobramentos versais

Umdesdobramento a m-parˆametros de umr-germef0 : (Rn, S)→(Rn+1,0) ´e um r-germe

F : (Rn_×Rm_{, S}_{× {}₀_}₎ _→ ₍Rn+1_×Rm_,₀₎

(x, u) 7→ (f(x, u), u)

tal quef(x,0) =f0(x). O germef(x, u), que denotaremos porfu(x), ´e chamado umadeforma¸c˜ao

de f0.

Consideremos o grupo de Mather A (os resultados seguintes s˜ao an´alogos para qualquer outro grupo de Mather). Dois desdobramentos F, G: (Rn_×Rm_{, S}_{× {}₀_}₎_→₍Rn+1_×Rm_,_{0) de}

f0s˜aoisomorfosse existirem germes de difeomorfismosφi: (Rn×Rm,{si}×{0})→(Rn×Rm,0),

i= 1, . . . , r, e ψ : (Rn+1_×Rm_,₀₎_→ ₍Rn+1_×Rm_,_{0) que s˜ao desdobramentos a} _m_-parˆ_ametros

dos germes da identidade em Rn _e Rn+1_{, respectivamente, e} _G(i) ₌_ψ_◦_F(i)_◦_φ−1

i , i= 1, . . . , r,

lembrando que G(i) e F(i) denotam o i-´esimo ramo deGe F.

Dado um germe h : (Rt_,₀₎ _→ ₍Rm_,_{0) e} _F _{um desdobramento de} _f₀_{, definimos o}

pull-back de F por h, denotado por h∗_F_{, como sendo o desdobramento a}_t_-parˆ_ametros _h∗_F₍_{x, v}_{) =}

(f(x, h(v)), v).

Dizemos que F e G s˜aoequivalentes se existir um difeomorfismo Φ : (Rm_,₀₎_→₍Rm_,_{0) tal}

queG´e isomorfo a Φ∗_F_{. Se}_G_{´e um desdobramento a}_t_-parˆ_{ametros de}_f

0(tn˜ao necessariamente

igual am), dizemos queG´e induzidopor F se existir um germeh: (Rt_,₀₎_→₍Rm_,_{0) tal que}_G

´e isomorfo ah∗(F).

Seja F(x, u) = (f(x, u), u) um desdobramento de f0. Dizemos que F ´e versal se todos os

desdobramentos def0 s˜ao induzidos por F.

Enunciemos agora o teorema fundamental da existˆencia de desdobramentos versais.

Teorema 1.7 Um desdobramento a m-parˆametros F(x, u) = (f(x, u), u) de f0 ´e Ae-versal se,

e somente se, aAe-codimens˜ao de f0 ´e finita e

T_Ae·f0+R{F˙1, . . . ,F˙m}=⊕r1En,n+1,

onde F˙i= _∂u∂f_i(x,0), para i= 1, . . . , m.

Observemos que se a Ae-codimens˜ao def0 ´ece g1,· · ·, gc ∈ ⊕r1En,n+1 formam uma R-base

do complementar deT_Ae·f0 em⊕r1En,n+1, ent˜ao

F(x, u) = (f0(x) +

c X

i=1

uigi(x), u)

(26)

1.1.4 Opera¸cões de aumenta¸cão e concatena¸cão

Todos os multigermes com mais de um ramo de_Ae-codimens˜ao 1 e coposto 1 de aplica¸c˜oes de

classeC∞ (ou anal´ıticas) (Kn, S)→(Kp,0), com n≥p−1, (n, p) nas boas dimens˜oes segundo Mather e K =C _ou _K ₌R_{, podem ser obtidos por opera¸c˜oes de} _aumenta¸c˜_ao _e _{concatena¸c˜}_ao_.

Para mais detalhes sobre o assunto veja o trabalho de T. Cooper, D. Mond e R. G. Wik-Atique [9].

Sejamf : (Rn_{, S}₎_→₍Rp_,_{0) um germe de}_A_e_-codimens˜_{ao 1 onde} _S_{´e um subconjunto finito}

de Rn _e

F : (Rn_×R_{, S}_{× {}₀_}₎ _→ ₍Rp_×R_,₀₎

(x, u) 7→ (fu(x), u)

.

um desdobramentoAe-versal de f. Definimos

A±_f : (Rn_×R_{, S}_{× {}₀_}₎ _→ ₍Rp_×R_,₀₎

(x, λ) _7→ (f_±_λ2(x), λ)

.

A A-classe de equivalˆencia de A±_f independe da escolha do desdobramento Ae-versal F de f.

ChamamosA+_f deaumenta¸c˜ao positiva de f eA−_f deaumenta¸c˜ao negativa de f. O germeA±_f tem

Ae-codimens˜ao 1 e um desdobramentoAe-versal deA±_f ´e dado porG(x, λ, µ) = (f_±λ2₊_µ(x), λ, µ).

Exemplo 1.8 Seja f±(x, z) = (x, z2, z3 ±x2z) o germe de R2 _em R3 _de _A_e_-codimens˜_ao ₁_.

Consideremos o seguinte desdobramento_Ae-versal de f±,

F±(x, z, u) = (x, z2, z3_±x2z+uz, u).

Então, as aumenta¸cões positiva e negativa def+ são dadas por A±_f+(x, z, u) = (x, z2, z3+x2z±

u2_{z, u}₎_{. Logo, obtemos os germes de} _R3 _em_R4

A±₁+: (x, y, z2, z(z2±x2+y2))

de _Ae-codimens˜ao 1. Se considerarmos a aumenta¸c˜ao negativa de f− obtemos o germe A−−1 ,

tamb´em de _Ae-codimens˜ao 1.

Há duas opera¸cões de concatena¸cão: mônica e binária. A opera¸cão deconcatena¸cão mônica

consiste em produzir a partir de um multigerme comr-ramos um novo multigerme com r+ 1-ramos, onde o ramo extra é uma dobra (no caso n _≥p) ou uma imersão (no caso n < p). Já a concatena¸cão binária consiste em combinar dois multigermes de codimensão 1 para obter um novo multigerme.

Daremos ênfase à opera¸cão de concatena¸cão mônica para a obten¸cão de multigermes deRn

emRn+1 _{e de} _A_e_-codimens˜_{ao 1.}

Sejaf : (Rn_{, S}₎_→₍Rn+1_,_{0) um multigerme de}_A_e_-codimens˜_{ao 1 e}_F₍_{x, u}_{) = (}_f_u₍_x₎_{, u}_{) um}

(27)

Cf : (Rn×R, S× {0})→(Rn+1×R,0) dado por

Cf : (

(x, u)7→(fu(x), u)

(x, u)_7→(x,0) .

A _A-classe de equivalˆencia deCf independe da escolha do desdobramento Ae-versal F de f. O

germeCf temAe-codimens˜ao 1.

Vejamos um exemplo desta opera¸c˜ao.

Exemplo 1.9 Seja f :

(

(y, z2, yz)

(y, y, z) o bigerme de

R2 _em R3 _de _A_e_-codimens˜_ao₁_.

Considere-mos o seguinte desdobramento _Ae-versal de f, F : (

(y, z2, yz, u)

(y+u, y, z, u) . A concatena¸c˜ao mˆonica

de f ´e dada por

Cf :    

  

(y, z2, yz, u)

(y+u, y, z, u)

(y, z, u,0)

.

Realizando mudan¸cas de coordenadas na fonte e na meta obtemos o trigerme de R3 _em R4 _de

Ae-codimens˜ao1

Tc :       

(x, y, z2, yz) (0, x, y, z)

(x, x+y, y, z)

.

Sejaf : (Rn_{, S}₎_→₍Rn+1_,_{0) um multigerme de}_A_e_-codimens˜_{ao 1 e}_f_u _{sua deforma¸c˜ao versal.}

A menos de homeomorfismo, existem duas (possivelmente equivalentes) escolhas para a imagem de fu: uma para u positivo e outra para u negativo. Denotamos tais imagens por D+(f) e

D−₍_f_{), respectivamente. Da mesma maneira denotamos por}_D+₍_A±

f) e D−(A±f) as imagens de

f_±_u2₊_λ paraλpositivo e negativo, respectivamente.

Os pr´oximos resultados foram obtidos por T. Cooper, D. Mond e R. G. Wik-Atique em [9].

Proposi¸c˜ao 1.10 Com a nota¸c˜ao acima

(i) D+₍_A+

f) ´e homotopicamente equivalente a D+(f);

(ii) D−(A+_f) ´e homotopicamente equivalente a S(D−(f));

(iii) D+(A−_f) ´e homotopicamente equivalente a S(D+(f));

(iv) D−₍_A−

f) ´e homotopicamente equivalente a D−(f);

(28)

Com respeito a opera¸cão de concatena¸cão mônica temos o seguinte.

Proposi¸cão 1.11 Seja f um multigerme de _Ae-codimensão1. A imagem de uma deforma¸cão

versal do multigerme Cf é homotopicamente equivalente à suspensão da imagem de uma

defor-ma¸c˜ao versal de f.

1.1.5 Suspens˜ao do crosscap

A superf´ıcie em R3 _{dada pela equa¸c˜ao} _W2 ₋_Y2_Z _{= 0, onde (}_{Y, Z, W}_{) representam as}

coordenadas em R3_{, ´e chamada de} _{guarda-chuva de Whitney}_{. Notemos que a ´}_{unica parte do}

guarda-chuva de Whitney que pertence a regi˜ao Z <0 ´e o eixoZ.

Y Z

W

Seja fe : (R2_,₀₎ _→ ₍R3_,_{0) o germe definido por} _fe₍_{y, z}_{) = (}_{y, z}2_{, yz}₎_. _{A imagem de} _fe_´e

o guarda-chuva de Whitney sem seu “cabo”, isto é, sem a semirreta Y = W = 0 e Z < 0. Definimos um crosscap como a imagem de qualquer germe g que éA-equivalente a fe. Oponto de crosscap é a imagem da origem de R2 _{pelo germe} _g_{. Chamamos o crosscap parametrizado}

por fede crosscap padrão. Whitney provou em [39] que tal singularidade é estável e que é a ´

unica singularidade local que aparece numa aplica¸c˜ao est´avel deR2 _em R3_.

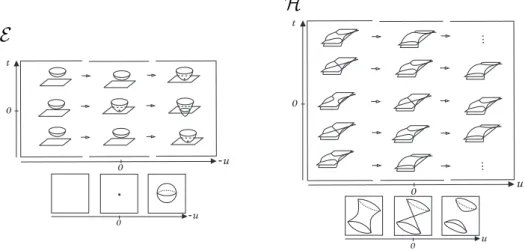
Consideramos agora a variedade V definida pela mesma equa¸c˜ao que o guarda-chuva de Whitney emR3_,_W2₋_Y2_Z _{= 0, mas agora em}R4 _{e com coordenadas (}_{X, Y, Z, W}_{). O desenho}

acima representaV em cada se¸c˜ao 3-dimensional (t, Y, Z, W),comt∈R_{fixo. Seja}_f _{: (}R3_,₀₎_→

(R4_,_{0) o germe de aplica¸c˜ao definido por} _f₍_{x, y, z}_{) = (}_x,_fe₍_{y, z}_{)) = (}_{x, y, z}2_{, yz}_{). Temos que a}

imagem de f ´e dada por _V menosY = W = 0 X _∈ R _e _{Y <}_{0. Definimos uma} _suspens˜_{ao do}

crosscap como sendo a imagem de qualquer germe h que ´eA-equivalente a f. A imagem de h

contém uma curva de pontos de crosscap. A suspensão do crosscap parametrizado por f será chamada desuspensão do crosscap padrão (ou simplesmente suspensão do crosscap).

1.2 Classifica¸

c˜

ao de bigermes

A partir deste momento denotaremos por (x, y, z) e (X, Y, Z, W) as coordenadas em R3 _e R4 _{respectivamente.}

(29)

1.2 Classifica¸c˜ao de bigermes 15

Lema 1.12 Seja f um bigerme de R3 _em R4_{, onde cada ramo ´e uma imers˜}_{ao. Ent˜}_ao _f _´e

A-equivalente a

(

(x, y, z,0)

(x, y, z, ϕ(x, y, z)) ,

onde ϕ(x, y, z) ´e chamada fun¸c˜ao de contato.

Proposi¸c˜ao 1.13 Sejam

f :

  

(x, y, z) f1

→(x, y, z,0) (x, y, z) f2

→(x, y, z, ϕ(x, y, z)) e

e

f :

  

(x, y, z) fe1

→(x, y, z,0)

(x, y, z) fe2

→(x, y, z,ϕ_e(x, y, z))

ent˜ao,

(i) f ´e A-equivalente afese, e somente se,ϕ ´eK-equivalente a ϕe.

(ii) Se f ´e finitamente_A-determinado, ent˜ao

T_Ae·f =     

E3 E3

TKe·ϕ TKe·ϕ     +

    

0 0

∆(E3 × E3)

    ,

onde ∆(_E3× E3)´e a diagonal em E3× E3.

Demonstra¸c˜ao: (i) Suponhamos ϕ_K-equivalente aϕe. Ent˜ao, existe um germe de difeomor-fismo

H : (R3_×R_,₍₀_,₀₎₎_→₍R3_×R_,₍₀_,₀₎₎

dado por H(x, y, z, t) = (h(x, y, z),He(x, y, z, t)) e satisfazendo

(a) h: (R3_,₀₎_→₍R3_,_{0) ´e um germe de difeomorfismo;}

(b) He(x, y, z,0) = 0;

(c) H(x, y, z, ϕ(x, y, z)) = (h(x, y, z),ϕe(h(x, y, z)).

´

E f´acil ver queH_◦fi=fei◦h,i= 1,2. Portanto,f ´eA-equivalente afe.

Reciprocamente, suponhamosf A-equivalente af .e Ent˜ao, existem germes de difeomorfismos

φi: (R3,0)→(R3,0), i= 1,2, e ψ: (R4,0)→(R4,0), ψ = (ψ1, ψ2, ψ3, ψ4) tais que

(1) ψ_◦f1=fe1◦φ1;

(30)

Definimos

H : (R3_×R_,₍₀_,₀₎₎ _→ ₍R3_×R_,₍₀_,₀₎₎

(x, y, z, t) 7→ (φ2(x, y, z), ψ4(x, y, z, t)) .

Segue de (1) queψ4(x, y, z,0) = 0 e comoψ´e um difeomorfismo, ∂ψ_∂t4(0)6= 0. Logo,H ∈ K. De

(2) temos que H(x, y, z, ϕ(x, y, z)) = (φ2(x, y, z),ϕe(φ2(x, y, z))) e portanto ϕ´e K-equivalente a

e

ϕ.

(ii) Primeiramente mostremos que

    

E3 E3

T_Ke·ϕ TKe·ϕe      +      0 0 0 0 0 0

∆(_E3 × E3)

   

⊆TAe·f.

Seja π : R4 _→ R3 _{a proje¸c˜}_{ao dada por} _π₍_{X, Y, Z, W}_{) = (}_{X, Y, Z}_{), consideremos o}

homo-morfismo induzido

π∗_: _E

3 → E4

g 7→ g◦π

e     

g1 eg1 g2 eg2 g3 eg3

0 0     ∈     

E3 E3

0 0

   

.Ent˜ao

    

g1 eg1 g2 eg2 g3 eg3

0 0

    = tf

  

g1−eg1 0 g2−eg2 0

g3−eg3 0

 

 + ωf

    

π∗₍_g_e

1) π∗(g2e)

π∗₍_g_e

3) 0     . Logo,     

E3 E3

0 0

   

⊆TAe·f.

SejaA=

     0 0 0 0 0 0 g 0    

com g∈TKe·ϕ. Notemos que A∈TAe·f. De fato, como g∈TKe·ϕ,

existem p, hi ∈ E3, i= 1,2,3,tais queg=h1·ϕx+h2·ϕy+h3·ϕz+p·ϕ. Assim, 

   

0 ₋h1

0 −h2

0 ₋h3

g 0

    =tf

  

0 −h1

0 ₋h2

0 ₋h3

  +ωf

  

0 0

π∗₍_g₎₋_W _·_π∗₍_p₎  

(31)

Agora, se considerarmos

     0 h1

0 h2

0 h3

0 g

    =tf

  

0 h1

0 h2

0 h3

  +ωf

  

0 0

W ·π∗(p)

 

∈TAe·f,

temos que      0 0 0 0 0 0 0 g    

∈TAe·f.

Por fim, seg_{∈ E}3, ent˜ao

     0 0 0 0 0 0 g g     =ωf

     0 0 0 0 0 0

π∗(g) π∗(g)

   

∈TAe·f,

isto ´e,      0 0 0 0 0 0

∆(E3 × E3)

   

⊆TAe·f.

Resta mostrarmos queT_Ae·f ⊆     

E3 E3

T_Keϕ TKeϕe      +      0 0 0 0 0 0

∆(_E3 × E3)

    . Seja     

h1 eh1 h2 eh2 h3 eh3 g _eg

   

∈TAe·f,comg, g, he i, ehi ∈ E3, i= 1,2,3. Ent˜ao, existema, b, c, ea,eb, ec∈

E3 e m, n, p, q∈ E4 tais que

    

h1 eh1 h2 eh2 h3 eh3 g eg

    =     

a ea

b eb

c ec

0 a_·ϕx+b·ϕy+c·ϕz     +     

m_◦f1 m◦f2 n_◦f1 n◦f2 p◦f1 p◦f2 q_◦f1 q◦f2

    .

Logo, g=q(x, y, z,0),_eg=a_·ϕx+b·ϕy+c·ϕz+q(x, y, z, ϕ(x, y, z)) e

e

g−g=a·ϕx+b·ϕy+c·ϕz+d·ϕ(x, y, z)∈TKe·ϕ,

(32)

Portanto     

h1 eh1 h2 eh2 h3 eh3 g _eg

    =     

h1 eh1 h2 eh2 h3 eh3

0 _eg₋g

    +      0 0 0 0 0 0 g g     ⊆     

E3 E3

T_Ke·ϕ TKe·ϕ      +      0 0 0 0 0 0

∆(_E3 × E3)

    . ✷

Corolário 1.14 Com as mesmas hipóteses de (ii) da Proposi¸cão 1.13, N Ae·f é isomorfo a

N Ke·ϕ.

Corolário 1.15 Sejam ϕ e f como na Proposi¸cão 1.13. Então, f é k− A-determinada se, e somente se, ϕé k_{− K}-determinado.

Para o pr´oximo resultado, veja a K-classifica¸c˜ao de germes em E3 em [2].

Corol´ario 1.16 Um bigerme de imers˜oes de(R3_{, S}₎_em₍R4_,₀₎_{e de}_A_e_-codimens˜_{ao no m´}_aximo

2 tem uma das seguintes formas normais:

Ae-codimens˜ao Nome (

(x, y, z,0)

(x, y,0, z) 0

(

(x, y, z,0)

(x, y, z, x2₊_y2₊_z2₎ 1 E

(

(x, y, z,0)

(x, y, z, x2₊_y2₋_z2₎ 1 H

(

(x, y, z,0)

(x, y, z, x2_±_y2₊_z3₎ 2 B

±

2

Observa¸cão 1.17 Os germes _E e_Hobtimos acima são aumenta¸cões de f :

(

(y, z,0)

(y, z, y2+z2) .

De fato, consideremos o seguinte desdobramento Ae-versal def,

F :

(

(µ, y, z,0)

(µ, y, z, µ+y2+z2) .

(33)

Classificaremos agora os bigermes onde um dos ramos é a suspensão do crosscap. Neste caso em particular, estamos interessados nos bigermes de Ae-codimensão até 3 (e não até 2),

pois esta classifica¸cão é necessária aos estudos que desenvolvemos no Cap´ıtulo 4.

Proposi¸c˜ao 1.18 Seja f : (R3_{, S}₎ _→ ₍R4_,₀₎ _{um bigerme de} _A_e₋_codimens˜_{ao no m´}_aximo ₃ _e

onde um dos seus ramos é a suspensão do crosscap. Então f tem uma das seguintes formas normais:

Ae−codimens˜ao Nome

(1)

(

(x, y, z2_{, yz}₎

(0, x, y, z) 0

(2)

(

(x, y, z2_{, yz}₎

(x, y_±xk_{, y, z}₎ k−1 k≥2 C

± ₍_k_{= 2)}

(3)

(

(x, y, z2_{, yz}₎

(x, x2_±_yk_{, y, z}₎ k k≥2

(4)

(

(x, y, z2_{, yz}₎

(x, y2_±_xk_{, y, z}₎ k k≥3

(5)

(

(x, y, z2_{, yz}₎

(x, xy+xk_{, y, z}₎ k k≥3

(6)

(

(x, y, z2_{, yz}₎

(x, y,_±x2_±_yk_{, z}₎ k k≥2

(7)

(

(x, y, z2_{, yz}₎

(x, y,_±y2_±_xk_{, z}₎ k k≥3

(8)

(

(x, y, z2_{, yz}₎

(x, y, xy_±xk_{, y, z}₎ k k≥3

(9)

(

(x, y, z2_{, yz}₎

(x, y, z, x2_±_z2₎ 3

Demonstra¸cão: Seja_V a imagem da suspensão do crosscap que é definida porW2₋Y2Z = 0. Então

(34)

Segue do Teorema 1.2 que as _A-classes de tais germes s˜ao dadas pelas _VK-classes em _E4.

Consideremos a a¸c˜ao de_V_K1 _em _J1₍₄_,₁₎_.

Sejah∈ E4 e j1h=aX+bY +cZ+dW ∈J1(4,1).Segue do Lema 1.1 que

T_VK1_·j1h=_M4hai+E4hbY −2cZ,2cW, bY +dW, bWi+E4

j1h+_M2₄. (1.1)

Determinemos as ´orbitas emJ1₍₄_,_{1) sob a a¸c˜}_{ao de}

VK1.

Suponhamos a6= 0 e consideremos S = {σ =aX +bY +cZ +dW ∈ J1(4,1);a > 0}. S

é um aberto de J1(4,1) e portanto é uma subvariedade. Além disso, S é claramente conexa e

TσS =J1(4,1) =TVK1·σ,∀σ ∈S. Logo, segue do Lema de Mather que S est´a contida numa

´

unica órbita, cujo representante é X. O caso a < 0 é análogo, com representante −X que é

VK1−equivalente a X.

Suponhamos agoraa= 0. Temos quej1h=bY +cZ+dW e por (1.1) que

T_VK1·j1h=E4hbY −2cZ,2cW, bY +dW, bWi+E4j1h+M24.

Consideremosb_·c₆= 0 eS=_{σ=bY+cZ+dW _∈M; b >0, c >0_}. Segue do Lema de Mather queSestá contida numa única órbita, cujo representante éY+Z. Considerando os outros casos obtemos órbitas com representantes±Y ±Z que são VK1_{-equivalentes a}_Y ₊_Z_.

Prosseguindo desta maneira obtemos as seguinte ´orbitas emJ1(4,1): X, Y +Z, Y, Z, W,0.

Para uma melhor compreensão dos próximos passos desta demonstra¸cão sugerimos que acompanhe o esquema da Figura 1.1.

(i) Seja h_{∈ E}4 cujo 1-jato ´e X. Ent˜ao

TVK1·j1h=M4+M24 e M24⊆ M4 TVK·j1h+M34.

Segue da Proposi¸cão 1.6 que j1_h _{é 1-}_VK−_{determinado. Logo,} _h _é

VK−equivalente a X e tem

VKe-codimens˜ao igual a 0. Pelo Teorema 1.2 obtemos o seguinte germe est´avel (

(x, y, z2, yz)

(0, x, y, z) .

(ii) Sejah_{∈ E}4 cujo (k−1)-jato ´eY +Z,k≥2. A k−transversal ´e calculada como segue.

T_V_K1·jk−1h = {ξ·jk−1h; ξ ∈ M24θ(4)∩Derlog(V)}+E4jk−1h

= M4hY −2Z, W, Yi+E4

jk+1h

= _M2₄_{\ E}4

X2, X3, . . ..

Ent˜ao Xk_{´e a} _k₋_transversal.

Segue do Teorema da Transversal Completa que osk₋jatos cujo (k₋1)₋jato ´e igual aY+Z

s˜ao_VKk₋_{equivalentes a}_Y ₊_Z₊_λXk_{, onde} _λ_∈_R_{. Em particular,}_jk_h_∼

VKk Y +Z+λX

k_.

(35)

1. 2 Cl ass ifi ca¸ c˜ao d e b iger me s 21

J1₍₄_,₁₎ _X _Y ₊_Z _Y

W 0

1-determinado

J2₍₄_,₁₎ _Y₊_Z_±_X2 _Y ₊_Z 2-determinado

Y +Z

Y +Z J3₍₄_,₁₎

J4₍₄_,₁₎

3-determinado

4-determinado 4-determinado 4-determinado 4-determinado 4-determinado 4-determinado 4-determinado

3-determinado 3-determinado 3-determinado 3-determinado 3-determinado 3-determinado

2-determinado 2-determinado 2-determinado

Y

Y +X2_±_Z2 _Y₊_X2 _Y₊_Z2 _Y₊_XZ _Z_±_X2_±_Y2 _Z_±_X2 _Z

±Y2 _Z₊_XY

W+X2_±_Z2

Y +Z+X3

Y +Z±X4

Y+X2

Y +X2

±Z3

Y +X2

±Z4

Y+Z2

Y+XZ

Y+Z2₊_X3

Y +Z2

±X4

Y+XZ+X3

Y+XZ+X4

Z±X2

Z±X2₊_Y3

Z±X2

±Y4

Z±Y2

Z±Y2₊_X3

Z±Y2

±X4

Z+XY

Z+XY±X4

Z+XY+X3

Z

(∗) (∗)

(∗∗)

(∗)

(_∗∗)Os germes cujo 1-jato é este, tem V Ke-codimensão maior que 3.

Os germes cujo2-jato é este, tem _{V K}e-codimensão maior que 3.

(_{∗ ∗ ∗})

(∗ ∗ ∗)

Das demais órbitas obtém-se germes deV Ke-codimensão maior que 3.

(36)

mudan¸ca de coordenada na fonte:

H: (R4_,₀₎ _→ ₍R4_,₀₎

(X, Y, Z, W) 7→ 1

k

√

ε·λX, Y, Z, W

.

ondeε= 1 seλ >0 eε=₋1 se λ <0. Como

TVKk·jkh=M4

D

Xk−1E+E4hY, Z, Wi+Mk4+1,

segue quejk_h_´e_k

-VK−determinado. EntãohéVK−equivalente aY+Z±Xke temVKe−codimensão

igual ak−1, k≥2. Pelo Teorema 1.2 obtemos o seguinte germe deAe−codimens˜aok−1,k≥2 : (

(x, y, z2_{, yz}₎

(x, y_±xk, y, z) .

(iii) Seja h_{∈ E}4 cujo 1-jato ´eY. Determinemos as VK2-´orbitas emJ2(4,1).

Temos queT_VK1_·_j1_h₌_E

4hY, Wi+M24. Segue do Teorema da Transversal Completa que

o 2-jato deh ´eVK2₋_{equivalente a}_Y ₊_aX2₊_bZ2₊_cXZ,_onde_{a, b, c}_∈_R_._Ent˜_ao,

T_V_K2_·j2h=_M4h2aX+cZi+E4

2bZ2+cXZ, Y, W+_E4

j2h+_M3₄.

Suponhamosa(4ab₋c2₎₆_{= 0 e consideremos}

S={σ=Y +aX2+bZ2+cXZ ∈J2(4,1); a >0,4ab−c2>0}.

´

E f´acil ver queS ´e uma subvariedade conexa de J2₍₄_,_{1). Notemos que} _T

σS ⊆TVK2·j2h,para

todo σ∈S. De fato, como

2aX2+cXZ, 2aXZ+cZ2, 2bZ2+cXZ _∈ T_VK2_·j2h,

TσS =X2, XZ, Z2 ∈ TVK2·j2h. Segue do Lema de Mather que S est´a contida numa ´unica

´

orbita, cujo representante éY +X2+Z2.Os casos a(4ab−c2) <0 e a < 0,4ab−c2 <0 são análogos, com representanteY +X2₊_Z2_.

Suponhamos agoraa₆= 0,(4ab₋c2_{) = 0. Realizando mudan¸cas de coordenadas que}

preser-vam V na fonte obtemos uma órbita cujo representante éY +X2. Analogamente, para a= 0 obtemos as seguintes órbitas: Y +XZ, Y +Z2, Y. Portanto, temos 5 órbitas em J2(4,1) cujos representantes possuem 1-jato igual a ₋Y: Y +X2_±_Z2_{, Y} ₊_X2_{, Y} ₊_Z2_{, Y} ₊_{XZ, Y}_.

(iii.1) Sejah∈ E4 cujo 2-jato ´e Y +X2±Z2.Temos que

T_VK2_·j2h=_M4hXi+E4

Z2, Y, W+_E4

j2h+_M3₄.

Logo,j2_h_{´e 2}_−V_K−_{determinado e portanto}_h_´e

(37)

o seguinte germe de _Ae−codimens˜ao 2 (

(x, y, z2, yz)

(x, x2±y2, y, z).

(iii.2) Sejah_{∈ E}4 cujok−1-jato ´eY +X2,k≥3. Ak-transversal ´e dada por

Zk_{. Logo,}

o k-jato deh´e VKk₋_{equivalente a} _Y ₊_X2₊_λZk_{, λ}_∈_R_.

Suponhamosλ6= 0. Realizando mudan¸cas de coordenadas que preservamV na fonte obte-mos quejkh ´e_V_K−equivalente a Y +X2_±Zk. Temos que

T_VKk·jkh=M4hXi+E4

D

Zk−1, Y, WE+Mk4+1.

Logo,jkhék_−V_K-determinado e portantohé_V_K−equivalente aY +X2_±Zk.Obtemos assim o germe de _Ae−codimensão k, k≥3:

(

(x, y, z2, yz)

(x, x2±yk, y, z).

Para os casos em que o 2-jato éY+Z2 ouY+XZ procedemos de maneira análoga a (iii.2) e obtemos os seguintes germes de_Ae-codimensãok, com k≥3, respectivamente:

(

(x, y, z2, yz)

(x, y2₊_xk_{, y, z}₎ e (

(x, y, z2, yz) (x, xy_±xk_{, y, z}₎_.

Os germes cujo 2-jato éY são de_V_Ke-codimensão maior que 4.

(iv) Seja h_{∈ E}4 cujo 1-jato éZ. Procedendo como em (iii) obtemos 5 órbitas emJ2(4,1): Z±X2±Y2, Z±X2, Z±Y2, Z+XY, Z. Com argumentos análogos aos anteriores conclu´ımos que se o 2-jato é

(a) Z_±X2_±_Y2_{, o germe obtido ´e o (6), para} _k_{= 1;}

(b) Z_±X2, o germe obtido ´e o (6), parak >1;

(c) Z±Y2, o germe obtido ´e o (7);

(d) Z+XY, o germe obtido ´e o (8);

(e) Z, os germes obtidos s˜ao de_V_K_e₋codimens˜ao maior que 4.

(v) Seja h ∈ E4 cujo 1-jato ´e W. Segue que TVK1·j1h = E4hWi+M24. Pelo Teorema da

Transversal Completa temos quej2h´e_V_K2₋equivalente aW+aX2+bY2+cZ2+dXY+eXZ+

f Y Z.Suponhamosa(4ab₋e2₎₆_{= 0 e consideremos}

(38)

Segue do Lema de Mather queSestá contida numa única órbita, cujo representante éW+X2_± Z2.Os demais casos são análogos, com representantes W +X2±Z2.

Se a(4ab−e2) = 0 obtemos germes de _VKe-codimens˜ao maior que 3.

Sejah∈ E4 cujo 2-jato ´e −W +X2±Z2. Temos que

T_V_K2_·j2h=_M4hXi+E4W, Y2, Z2, Y Z+M34.

Logo, j2h ´e 2 − VK−determinado. Portanto, h ´e _VK−equivalente a W +X2 ± Z2 e tem

VKe−codimens˜ao igual a 3. Desta maneira obtemos o germe de Ae−codimens˜ao 3: (

(x, y, z2, yz) (x, y, z, x2_±_z2₎_.

✷

Observa¸c˜ao 1.19 Os germes _C± _{obtimos acima s˜}_{ao aumenta¸c˜}_{oes de} _f _: (

(y, z2, yz)

(y, y, z) . De

fato, consideremos o seguinte desdobramentoAe-versal de f,

F :

(

(µ, y, z2, yz)

(µ, y+µ, y, z) .

Ent˜aoC+₌_A+

f eC−=A−f.

Consideremos agora os bigermes onde um dos ramos ´e o germe de Ae-codimens˜ao 1

A±±₃ : (x, y, z2, z(z2_±x2_±y2)).

Na prova do resultado seguinte obtemos oDerlog(V) paraV a imagem deA++₃ .Para os demais,

V eDerlog(_V) são os mesmos a menos de alguns sinais. Como as mudan¸cas de coordenadas na fonte e os espa¸cos tangentes envolvidos na demonstra¸cão do resultado independem destes sinais, a prova é válida paraA±±₃ .

Proposi¸c˜ao 1.20 Seja f : (R3_{, S}₎ _→ ₍R4_,₀₎ _{um bigerme de} _A_e_-codimens˜_ao ₂ _{onde um dos}

ramos ´eA±±₃ : (x, y, z2_{, z}₍_z2_±₍_x2_±_y2₎₎_{. Ent˜}_ao_f _{tem a seguinte forma normal}

(

(x, y, z2_{, z}₍_z2_±_x2_±_y2₎₎

(x,0, y, z) .

Demonstra¸c˜ao: Seja_V a imagem deA++₃ que ´e definida por

(39)

Ent˜ao

Derlog(V) = (Y,−X,0,0), (0, W, 0, 2X2Y Z+ 2Y3Z+ 2Y Z2), (XY, 3Z+Y2,−4Y Z, 0),

(0,0,2W, X4_{+ 2}_X2_Y2₊_Y4_{+ 4}_X2_Z_{+ 4}_Y2_Z_{+ 3}_Z2₎_,₍₃_Z₊_X2_{, XY,}₋₄_XZ,₀₎_,

(W,0,0,2X3Z+ 2XY2Z+ 2XZ2),(XW, Y W,₋4ZW,6Z3+ 6Y2Z2+ 6X2Z2),

(X, Y,2Z,3W)i.

Consideremos a a¸c˜ao de_V_K1 _em _J1₍₄_,₁₎_.

Sejah_{∈ E}4 e j1h=aX+bY +cZ+dW ∈J1(4,1). Segue que

T_VK1_·j1h=_E4haY −bX, bW, bZ, cW, aZ, aW, aX+bY + 2cZ+ 3dWi+E4

j1h+_M2₄.

Determinemos quais s˜ao as _VK1_-´_{orbitas em}_J1₍₄_,_1).

Seja S = _{σ = aX +bY +cZ +dW _∈ J1₍₄_,_1); _{a >} ₀_{, a}2 ₊_b2 ₆_{= 0}_}_. _{Segue do Lema de}

Mather que S está contida numa única órbita, cujo representante é X. Os demais casos são análogos, com representante X. Procedendo desta maneira obtemos as seguintes órbitas em

J1(4,1): X, Z, W,0.

(1) Sejah∈ E4 cujo 1-jato ´eX. Segue que

T_V_K1j1h=_E4hX, Y, Z, Wi+M24.

ClaramenteX é 1−VK-determinado. Logohé_VK−equivalente aX e temVKe−codimensão 1.

Pelos Teorema 1.2 e 1.3 obtemos o seguinte germe deAe-codimens˜ao 2: (

(x, y, z2_{, z}₍_z2_±_x2_±_y2₎₎

(0, x, y, z) ∼A

(

(x, y, z2_{, z}₍_z2_±_x2_±_y2₎₎

(x,0, y, z) .

Os germes cujo 1-jato éZ, W ou 0 são de _VKe-codimensão maior que 2.

✷