FUNDAÇÃO GETÚLIO VARGAS
ESCOLA DE PÓS-GRADUAÇÃO EM ECONOMIA
DISSERTAÇÃO DE MESTRADO
Comparação de metodologias para a construção da estrutura a termo de
taxas de juros (ETTJ) dos títulos públicos brasileiros.
______________________________ Pedro Calmanowitz Carvalho
Orientador: Caio Almeida
Comparação de metodologias para a construção da estrutura a termo de
taxas de juros (ETTJ) dos títulos públicos brasileiros.
Pedro Calmanowitz Carvalho
Dissertação apresentada à Banca Examinadora da Escola de Pós-Graduação em Economia da Fundação Getúlio Vargas como requisito parcial para a obtenção do grau de Mestre em Economia
Orientador: Caio Almeida
Agradecimentos ... 4
Resumo... 5
1. Introdução... 6
2. Metodologia ... 9
2.1. Modelo básico ... 9
2.2. McCulloch Spline (MS)... 10
2.2.1. Exemplo ... 12
2.3. Spline Pontos Fixos (SPF) ... 14
2.4. Svenson Lambda Fixo (SVLF) ... 17
2.5. Spline Exponencial da Merrill Lynch (SEML)... 20
2.6. Testes estatísticos ... 21
3. Resultados Empíricos ... 23
3.1. Base de dados... 23
3.2. Resultados ... 23
4. Conclusão ... 29
5. Bibliografia ... 31
6. Gráficos ... 33
Gráfico 1: Movimentos da ETTJ sob o modelo SVLF para um dia específico (Cross Section)... 33
Gráfico 2: Parâmetros do Svenson Lambda Fixo ao longo do tempo (curva prefixada)... 33
Gráfico 3: Parâmetros do Svenson Lambda Fixo ao longo do tempo (curva IPCA).. 34
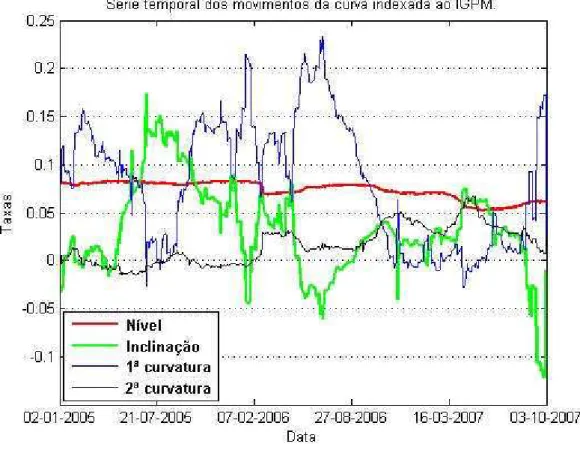
Gráfico 4: Parâmetros do Svenson Lambda Fixo ao longo do tempo (curva IGPM). 34 Gráfico 5: Curvas prefixadas – 27/jul/2007 ... 35
Gráfico 6: Curvas IPCA – 27/jul/2007... 35
Gráfico 7: Curvas IGPM – 27/jul/2007... 36
Gráfico 8: Curvas prefixadas – 10/jan/2007... 36
Gráfico 9: Curvas IPCA – 10/jan/2007 ... 37
Gráfico 10: Curvas IGPM – 10/jan/2007 ... 37
Gráfico 11: Série temporal dos erros gerados pelos modelos – LTN 07/2007... 38
Gráfico 12: Série temporal dos erros gerados pelos modelos – LTN 01/2009... 38
Gráfico 13: Série temporal dos erros gerados pelos modelos – NTNF 01/2010... 39
Gráfico 14: Série temporal dos erros gerados pelos modelos – NTNF 01/2014... 39
Gráfico 15: Série temporal dos erros gerados pelos modelos – NTNB 08/2008... 40
Gráfico 16: Série temporal dos erros gerados pelos modelos – NTNB 08/2024... 40
Gráfico 17: Série temporal dos erros gerados pelos modelos – NTNB 05/2045... 41
Gráfico 18: Série temporal dos erros gerados pelos modelos – NTNC 04/2008... 41
Gráfico 19: Série temporal dos erros gerados pelos modelos – NTNC 03/2011... 42
Agradecimentos
A todos os meus professores, os quais ajudaram em minha formação pessoal. Ao meu orientador, Caio, por ter me incentivado e ajudado em todas as fases desta dissertação.
À ANDIMA e sua equipe, pelos preciosos dados sobre títulos públicos no Brasil e pelas sugestões sobre a dissertação.
À minha família pelo apoio incondicional que sempre tive. Ao Bruno e o Axel pelas frutíferas discussões sobre o tema. À Mariana, minha inspiração.
Resumo
Este trabalho tem como objetivo construir estruturas a termo da taxa de juros de títulos públicos brasileiros através do uso de modelos estatísticos paramétricos. Estudou-se a capacidade de ajuste de modelos distintos do tipo “splines” e
“exponenciais” através de testes de apreçamento de diferentes títulos públicos (prefixados, e indexados à inflação), sob métricas que incluem análises dentro e fora da amostra utilizada no processo de estimação dos modelos. Identificamos que os modelos baseados em funções exponenciais se sobressaem nos testes e parecem ser os mais adequados para construção destas curvas de juros de títulos públicos brasileiros.
Vislumbramos os resultados deste estudo como um primeiro passo para a criação de uma importante ferramenta de auxílio à regulação dos mercados de títulos públicos brasileiros, pois a construção de curvas de juros adequadas possibilita uma marcação a mercado de cada título coerente com o preço dos demais, oferecendo melhora na capacidade de se estimar regiões de confiança para preços futuros destes títulos.
1.
Introdução
A estrutura a termo da taxa de juros (ETTJ) é uma curva ou função que associa uma taxa de juros única para cada maturidade, inclusive aquelas em que não há nenhum título vencendo na data, sendo importante para análise do mercado de títulos de renda fixa.
O principal objetivo deste trabalho será o de identificar uma metodologia única de construção da ETTJ que sirva para analisar os títulos públicos federais com maior relevância no mercado brasileiro. Espera-se que, com esta metodologia, entidades auto-reguladoras, bancos centrais e outras instituições do mercado financeiro possam ampliar a gama de parâmetros para avaliar, por exemplo, a volatilidade esperada de um título específico no mercado1 ou avaliar a inflação implícita contida nos preços negociados.
Quem primeiro estudou uma metodologia de construção da ETTJ foi McCulloch (1971, 1975), o qual tentou construir esta curva via função desconto. A vantagem desta modelagem inicial era a de que os parâmetros apareciam linearmente no modelo de estimação.
Outro grupo passou a tentar estimar a ETTJ por modelos estatísticos não-lineares, modelando diretamente a taxa de juros, e não mais a função desconto. Dentro desta categoria podemos citar os modelos exponenciais (Nelson e Siegel (1971), Svenson (1984), Bolder e Gusba (2002), e outros), os modelos polinomiais (Chambers e outros (1984), Almeida e outros (1998)) e até funções diferentes como as senóides presentes em Bolder e Stréliski (1999).
Esta classe de modelos de modelos estatísticos não lineares mostrou bastante útil para a análise e precificação de títulos de renda fixa, especialmente o modelo exponencial proposto por Nelson e Siegel (1971) e expandido por Svenson (1994), que passou a ganhar grande relevância na literatura internacional pois seus parâmetros podem ser entendidos como rotações dos movimentos da curva obtidos por Litterman e Scheinkman (1991) sendo também bons previsores da taxa de juros futura (ver Diebold e Li (2006)). Estes parâmetros podem ainda ser comparados com variáveis
macroeconômicas, fazendo com que este modelo seja útil na tomada de decisões sobre política monetária, sendo muito utilizado por bancos centrais do mundo todo, tal como mostrado no trabalho nº. 25 do BIS (2005). Para o caso brasileiro, Almeida e outros (2007) mostram que a previsão de taxas futuras na curva de DI também é boa para este modelo, ficando ainda melhor com a inclusão de um fator exponencial adicional2.
Como visto acima, existe uma enorme gama de metodologias para a construção da ETTJ. Estas metodologias já foram testadas e comparadas por diversos pesquisadores para dados dos EUA. Porém, pouca pesquisa foi realizada para dados de economias emergentes, aonde os problemas de falta de liquidez e alta volatilidade das taxas são mais agudos.
O objetivo deste trabalho foi o de testar os modelos mais relevantes da literatura internacional para a construção de curvas de títulos públicos brasileiros. Adotamos títulos prefixados como sempre foi feito, bem como títulos indexados à inflação, os quais já são relevantes para a economia brasileira há alguns anos.
O primeiro modelo testado foi o exponencial, baseado no trabalho de Svenson (1994). A segunda metodologia testada foi o modelo exponencial da função desconto, proposto pela Merrill Lynch e aplicado pelo banco central do Canadá. As outras duas metodologias são modificações do modelo proposto por McCulloch.
Para compará-las utilizou-se as métricas propostas por Bliss (1996). Estes testes além de darem importância ao erro dentro da amostra (“in-sample tests”), estimam
também os erros cometidos fora da amostra (“out-of-sample tests”).
Depois disto, foram feitos testes para saber se os erros são ou não ruídos brancos (“white noise”), mostrando possíveis problemas desta classe de modelos tais
como variáveis omitidas ou métodos de estimação pouco robustos para os parâmetros dos modelos.
Acreditamos que a construção destas curvas de títulos públicos e os testes dos diferentes modelos propostos possam ser um primeiro passo para a obtenção de melhores mecanismos de regulação do mercado interno de títulos públicos brasileiros. Por exemplo, uma vez conhecida a ETTJ a marcação a mercado de cada título será coerente com o preço dos demais. Além disso, testes de previsões de taxas e volatilidades de taxas futuras podem ser realizados, indicando regiões ou intervalos para aceitação de preços marcados por entidades financeiras participantes do mercado.
2.
Metodologia
2.1.
Modelo básico
A premissa básica para estimação de todas as curvas de juros que virão a seguir é a de que o preço de um título de renda fixa é igual ao fluxo de caixa futuro prometido pelo emissor, trazido a valor presente por uma função desconto3. Assim,
. t i, , k ) (T b F ) (T b F ... ) (T b F ) (T b F P t i, i j j i, t t j, i, t i, K i, t t Ki, i, i,2 t t i,2, i,1 t t i,1, t i, i ∀ + = = + + + + =
∑
= ε ε 1 (2.1.1)Em que Fi,j,té o j-ésimo pagamento (cupom e/ou amortização) do i-ésimo título na data t,
j i,
T é o prazo em que ocorre o pagamento j do i-ésimo título,
i
K é o numero de pagamentos do título i,
t i,
P é o preço do i-ésimo título na data t,
t i,
ε é o erro cometido pelo modelo para o título i na data t e
) (T
bt i,j é a função desconto da data t para a maturidadeT . i,j
Esta função desconto pode também ser escrita como função da taxa de juros
“zero cupom” ou ETTJ para a data t - rt(Ti,j). Neste caso,
(
)
Ti,jj i, t j i, t (T r 1 1 ) (T b ) +
= se r(Ti,j) for discreta ou (2.1.2)
j i, j i, t(T T
r -j i, t
(T
)
e
b
=
)* se r(Ti,j) for contínua. (2.1.3)
Um ponto importante a ser ressaltado sobre os modelos apresentados a seguir é que eles são sempre reestimados a cada data analisada e que os parâmetros da data anterior não influenciam em nada a estimação dos parâmetros na data atual. Com isso, e para diminuir a notação, não foi colocado o subescrito do tempo nas nomeclaturas matemáticas, ficando subentendido que estamos sempre avaliando o modelo na data t.
2.2.
McCulloch Spline (MS)
Este modelo, chamado nesta tese de “McCulloch Spline” (MS), fará uma interpolação da função desconto e não da taxa de juros ou do preço dos ativos diretamente, que normalmente são mais usados no mercado. Isto foi feito pois, modelando a função desconto, podemos chegar a equações lineares o que facilita a solução do sistema de preços e restrições. Esta metodologia foi proposta inicialmente por McCulloch (1971 e 1975).
Neste primeiro modelo o preço de cada título gerado pela curva será
igual àquele do mercado4, ou seja, o erroεi,t da equação (2.1.1) será zero para todo i e
todo t. Neste modelo, a função descontob(T)será modelada como sendo um conjunto
de M polinômios. Em termos matemáticos temos:
M 1,..., m
e T T T p/ T d T c T b a (T)
bm = m + m + m 2 + m 3 m-1 < ≤ m =
(2.2.1)
Aonde am, bm, cme dm são constantes para cada um dos M polinômios.
Assim, podemos reescrever o preço do título como sendo:
) T d T c T b (a k k F ... ) T d T c T b (a k F ) (T b k k F ... k ) (T b F P 3 j i, 2 j i, j i, M i, -1 M i, j i, 3 j i, 2 j i, j i, i,1 j i, j i, M M i, -1 M i, j i, i j i, 1 j i, i M M M M 1 1 1
1 + + + + + + + +
= = + + =
∑
∑
∑
∑
= = = = j j j j 1 1 (2.2.2)Em que ki,m −ki,m-1 é o número de pagamentos que está dentro do intervalo de
tempo entre Tm-1 e Tm.
Além disso, estes polinômios serão ligados de tal maneira que, nos pontos de junção ou nós o polinômio anterior será igual ao polinômio posterior e terá a primeira e a segunda derivadas iguais, ou seja,
T
d
T
c
T
b
a
T
d
T
c
T
b
a
m-1+
m-1 m-1+
m-1 m2-1+
m-1 m3-1=
m+
m m-1+
m m2-1+
m m3-1T
d
3
T
c
2
b
T
3d
T
c
2
b
m-1+
m-1 m-1+
m-1 m2-1=
m+
m m-1+
m m2-1 eM 1,..., m p/ T d 6 c 2 T 6d c
2 m-1 + m-1 m-1 = m + m m-1 =
Precisamos ainda de uma condição inicial e terminal para esta curva. A condição inicial mais usada é a de que a função desconto tenha valor 1 no tempo zero, ou seja, que 1 real hoje valha 1 real.
1 a (0) b1 = 1 =
A última condição é a de que a segunda derivada seja zero no ponto terminal da curva de desconto. Esta condição serve para que não haja oscilações muito grandes na parte final da curva.
0
T
6d
c
2
T
))
(T
(b
M M M 2 M M 2=
+
=
∂
∂
Para que isto ocorra, precisamos ter N-1 polinômios, sendo N o número de títulos usado para a construção da ETTJ.
Precisamos de N-1 polinômios, pois, com dois títulos, ou seja, quando N=2, temos 2 restrições de preços e 2 restrições devido à condição inicial e final da curva. Dado que, para cada polinômio precisamos estimar quatro parâmetros, temos o mesmo número de equações e de incógnitas. A partir daí, cada título adicionado gerará uma
nova restrição5. Adicionando mais um polinômio, este criará 3 novas restrições no nó
intermediário6 . Como cada polinômio a mais implicam mais 4 parâmetros, continuamos
tendo o mesmo número de equações e de incógnitas.
Podemos a partir daí reescrever este sistema de forma matricial. Chamando Q da matriz de parâmetros, o sistema pode ser definido como:
Q * A R =
Em que R é um vetor de tamanho 4*(N-1), A é uma matriz quadrada 4*(N-1) X 4*(N-1) e Q é um vetor 4*(N-1). A solução deste sistema será:
R * A Q= -1
Obs.: esta solução só existirá se o posto de A for cheio. Neste caso, isto implica
que não podemos utilizar títulos públicos que sejam combinações lineares de outros
neste método7.
2.2.1. Exemplo
Abaixo temos um exemplo de como este sistema matricial deve ser escrito, se tivermos 3 títulos, o que implica que temos dois polinômios com junção em T1. Além
disso, suponha que os títulos 1 e 2 vencem antes de T1. Assim, na primeira linha de A
temos a restrição de que a função desconto seja 1 no tempo 0, nas três linhas seguintes
5 Igualdade entre o preço e o fluxo de caixa trazido a valor presente
6 Igualdade com o polinômio anterior e igualdades na primeira e na segunda derivada
temos as restrições de que os preços sejam iguais aos seus fluxos de caixa descontados, nas linhas 5, 6 e 7 temos a restrição de que os dois polinômios devem passar pelo mesmo ponto em T1, terem a mesma derivada e a mesma segunda derivada respectivamente e na última linha temos a restrição de que a segunda derivada seja zero no ponto terminal.
=
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
= = = = = = = = = = = = = = = = 2 2 2 2 1 1 1 1 2 1 1 2 1 1 2 1 1 3 1 2 1 1 3 1 2 1 1 3 j 3, 3,2 3,1 j 3, 2 j 3, 3,2 3,1 j 3, j 3, 3,2 3,1 j 3, 3,2 3,1 j i, 3 j i, 3,1 1 j i, 2 j 3, 3,1 1 j 3, j 3, 3,1 1 j 3, 3,1 1 j 3, 3 j 2, 2,1 1 j 2, 2 j 2, 2,1 1 j 2, j 2, 2,1 1 j 2, 2,1 1 j 2, 3 j 1, 1,1 1 j 1, 2 j 1, 1,1 1 j 1, j 1, 1,1 1 j 1, 1,1 1 j 1, 3 2 1 d c b a d c b a * 6T 2 0 0 0 0 0 0 6T -2 -0 0 6T 2 0 0 3T -2T -1 -0 3T 2T 1 0 T -T -T -1 -T T T 1 T k k F T k k F T k k F k k F T k F T k F T k F k F 0 0 0 0 T k F T k F T k F k F 0 0 0 0 T k F T k F T k F k F 0 0 0 0 0 0 0 1 0 0 0 0 P P P 1 j j j j j j j j j j j j j j j jA partir daí, basta construir a função desconto usando a definição dada anteriormente: 1 3 1 2 1 1 1
1(T) a b T c T d T p/ 0 T T
b = + + + < ≤
2 1 3 2 2 2 2 2
2(T) a b T c T d T p/ T T T
b = + + + < ≤
E depois transformá-la em curva de juros pela fórmula abaixo:
2 T 1
T
T
0
p/
1
-b(T)
1
i(T)
<
≤
=
2.3.
Spline Pontos Fixos (SPF)
Este método é muito parecido com o anterior, mas com a diferença de que teremos agora um número maior de títulos do que de parâmetros livres, pois os nós
utilizados serão fixos8, não dependendo, portanto, do número de títulos utilizados na
análise. Neste caso, será utilizado um processo de minimização quadrática ponderada dos erros (WLS), para que se chegue à solução do sistema.
A vantagem deste e dos outros métodos apresentados a seguir sobre o
McCulloch Spline (MS) é o de poderem utilizar toda a informação disponível para a
construção da ETTJ9, além de se criar uma curva mais suave do que a anterior,
principalmente no caso de existirem títulos com taxas muito discrepantes. Ou seja, a partir deste, nenhum modelo acertará todos os preços existentes no mercado.
Utilizando a mesma notação que na metodologia anterior, a função desconto definida anteriormente para o MS em (2.2.1) se transformará em:
M ,..., 1 m p/ e T T T p/ ) T d T c T b (a *
αT)
exp( (T)
bm = − m + m + m 2 + m 3 m-1 < ≤ m =
(2.3.1)
Aonde α é uma constante que servirá para todos os intervalos.
Na equação (2.3.1) percebe-se que foi introduzida uma exponencial em relação à (2.2.1). Isto foi motivado pelo fato de que existe certa intuição econômica de que a função desconto tenha um formato exponencial, tal como mostrado em Vasicek e Fong (1982).
Além disso, com este formato de função desconto, podemos entender α como
sendo uma taxa de juros “zero cupom” (em tempo contínuo) média para o título de vencimento mais longo (taxa de longo prazo) e os polinômios modelariam desvios em relação a esta taxa em cada um dos intervalos selecionados.
Assim, as restrições do processo de minimização passam a ser:
8 Os intervalos usados nesta tese foram: Curva prefixada: 0,5; 1; 2 e 4,75 anos. Curva IPCA: 1, 4, 10, 21 anos. Curva IGPM: 1,3 e 12 anos.
Eles foram escolhidos de forma ad hoc, dentro de um intervalo razoável, pois fazendo pequenas variações nestes parâmetros de escala o erro quadrático médio cometido pelo modelo variava muito pouco.
( )
(
)
(
)
(
)
( )
(
)
(
)
(
)
( )
(
)
(
)
(
)
( )
(
)
(
)
(
)
(2.3.9) 1 T d T c b a ) (T b (2.3.8) 0 T 3d T c 2 b T ) (T b (2.3.7) 0 T 6d c 2 T ) (T b (2.3.6) 1 a (0) b (2.3.5) M 1,..., m p/ 6T T * 6α -T α d 2 T * 4α -T α c 2α -T α b α a ... ... 6T T * 6α -T α d 2 T * 4α -T α c 2α -T α b α a (2.3.4) M 1,..., m p/ αT -3T d αT -2T c αT -1 b α -a ... ... αT -3T d αT -2T c αT -1 b α -a (2.3.3) M 1,..., m p/ ... .... T d T c T b a T d T c T b a S.a. (2.3.2) ) ) (T b k k F ... k ) (T b F -(P W Min 3 M M 2 M M M M M M 2 M M M M M M M M M M 2 M M 2 1 1 . . . . . . 1 -m 2 1 -m 3 1 -m 2 m 1 -m 2 1 -m 2 m 1 -m 2 m 2 m 1 -m 2 1 -m 3 1 -m 2 1 -m 1 -m 2 1 -m 2 1 -m 1 -m 2 1 -m 2 1 -m . . . . . . 3 1 -m 2 1 -m m 2 1 -m 1 -m m 1 -m m m 3 1 -m 2 1 -m 1 -m 2 1 -m 1 -m 1 -m 1 -m 1 -m 1 -m 3 1 -m m 2 1 -m m 1 -m m m 3 1 -m 1 -m 2 1 -m 1 -m 1 -m 1 -m 1 -m N 1 2 j i, M M i, 1 -M i, j i, i 1 j i, 1 j i, i i = + + + = = + + = ∂ ∂ = + = ∂ ∂ = = = + + + + + = = + + + + + = + + + = = + + + = + + + = + + + + +∑
∑
∑
= = =i j j
Em que F é o j-ésimo pagamento (cupom e/ou amortização) do i-ésimo título, i,j
j i,
T é o prazo em que ocorre o pagamento j do i-ésimo título,
1 -m i, m i, k
k − é o número de pagamentos que está dentro do intervalo de tempo
entre Tm-1 e Tm,
i
P é o preço do i-ésimo título,
)
b(Ti,j é a função desconto para o prazo,
m
a , bm, cme dm são constantes para cada um dos M polinômios e
i
Este sistema de equações é similar ao MS. Na equação (2.3.2) é utilizado o inverso da duration como ponderador (Wi), para que os erros em termos de taxas sejam homoscedásticos. Sem esta ponderação, a variância do erro nas taxas longas seria bem menor do que na parte curta da ETTJ. As equações (2.3.3), (2.3.4) e (2.3.5) fazem com que, respectivamente, a função desconto, a primeira derivada e a segunda derivada sejam iguais em cada nó ou junção. A equação (2.3.6) força a função desconto a começar em 1 e as equações (2.3.7), (2.3.8) e (2.3.9) fazem com que a taxa de longo prazo na curva seja constante, pois força o modelo a não ter mais variações em relação à
αT)
exp(− (o polinômio tem valor um no nó terminal), acabando com o problema de
extrapolação da taxa para modelos que utilizam a metodologia de Splines na função desconto. Uma restrição importante deste modelo é a de que o número de polinômios (M) tem que ser menor do que o número de ativos (N), para o problema ficar bem definido.
Assim como no caso anterior, este problema também pode ser escrito da forma matricial mostrada abaixo:
C C C C Q QQ Q * ** * H H H
H =
S.a.
Min (P- A*Q)'W(P- A*Q)
Sendo:
A uma matriz de tamanho N por 4*M, que contém o somatório dos fluxos de
pagamentos dos títulos públicos, definido da mesma forma que na matriz do exemplo 2.2.1 nas linhas 2, 3 e 4.
P é um vetor coluna de tamanho N por 1 com os preços dos títulos públicos.
Q é um vetor coluna de tamanho 4*M por 1 que contém os parâmetros que
queremos estimar, com exceção do α.
H é uma matriz 3*(M-1)+4 por 4*M, a qual define, junto com C as restrições de igualdades da função, da primeira e segunda derivadas nos nós e tem a primeira linha e a última linha definindo as condições de contorno.
2 2 2 2 2 2 2 2 2 22
2 ****QQQQ CCCC H H H H = S.a.
Min Q2'ωQ2
Sendo
≡ WA A' WP A' -WA P' WP P'
ω ,
≡ Q
Q2 1 ,
≡ C
C2 1
e
≡ H 0 0 H2 ˆ ˆ 1
Em que P, A, Q, H e C são definidos como anteriormente e 0ˆ é uma matriz de zeros conformável para fazer com que a matriz H2esteja bem definida.
Esta minimização funcionará bem para um α fixo. Como não sabemos qual o α
ótimo, é feito um grid de alphas10 e então é escolhido aquele que minimiza a soma
ponderada dos erros dos preços ao quadrado, para cada data de análise.
2.4.
Svenson Lambda Fixo (SVLF)
O método utilizado por este trabalho é baseado no modelo proposto por Svenson (1994), o qual é uma extensão do modelo de Nelson e Siegel (1971).
Em seu trabalho, Nelson e Siegel (1971) definem a taxa forward pela seguinte
equação: τ -λ t t τ -λ t t
t
(
τ
)
=
β
1+
β
2e
t+
β
3λ
τ
e
tf
(2.4.1)Ou seja, a taxa forward é modelada como sendo um polinômio multiplicado por
um decaimento exponencial. A taxa zero correspondente seria então:
−
+
+
=
-λτt τ -λ t t τ -λ t t t t t t
e
τ
λ
e
-1
τ
λ
e
-1
τ
)
1 2 3(
β
β
β
r
(2.4.2)
Diebold e Li (2006) em seu trabalho utiliza o modelo de três fatores (com lambda fixo) para tentar estimar a taxa de juros futura e prova que esta estimação é melhor do que o passeio aleatório. Além disso, eles mostram que cada parâmetro desta equação tem uma interpretação geométrica11.
Assim, o λt controla a taxa de decaimento exponencial, ou seja, quanto menor
(maior) o parâmetro, mais lento (rápido) será o decaimento e melhor será a adequação da curva para a parte longa (curta) da ETTJ. Além disso, λt determina onde a carga de
t 3
β atinge seu máximo.
Os outros 3 parâmetros podem ser entendidos como sendo rotações dos fatores da análise de componentes principais feita por Litterman e Scheinkman (1991). Ou seja,
t 1
β , β2t e β3t teriam a interpretação respectivamente dos fatores de nível, inclinação e curvatura da ETTJ. Um exemplo do que seriam estes fatores está mostrado na figura 112. Outra maneira de interpretar estes fatores é considerá-los como modelando os termos de longo, curto e médios prazos, pois quando τ→∞ o único fator que sobra é
t 1
β , o que faz com que este fator governe as taxas de longo prazo. A carga de β2tque é igual a
(
1-e)
/λ τt τ
-λt começa em 1 e cai rapidamente para zero quando τ aumenta,
mostrando que este fator governa as taxas de curto prazo. Já a carga de β3t que é
(
)
-λτt τ
-λt /λ τ e t e
-1 − começa em zero, é crescente no início e depois tende para zero
quando τ→∞, fazendo com que este fator governe as taxas de médio prazo.
A diferença entre o modelo proposto por Nelson e Siegel (1971) e aquele proposto por Svenson (1994) é que em Svenson (1994) foi inserido um quarto fator para
modelar a taxa forward. Almeida e outros (2007) e Pooter (2007) mostraram que a
inserção de um quarto fator ajuda na modelagem e no poder preditivo deste modelo para
curvas de juros no Brasil e nos EUA respectivamente.
Assim, neste trabalho, o modelo estimado será:
τ
-λ
2t t 4
τ
-λ
t t 3
τ
-λ
t 2 t 1
t
(
τ
)
=
β
+
β
e
t+
β
λ
τ
e
t+
β
λ
τ
e
2tf
(2.4.3)Em termos de curva zero, a nova fórmula ficará:
11 Diebold e Li (2006)
−
+
−
+
+
=
-λ τ2t τ -λ t 4 τ λ -t τ -λ t 3 t τ -λ t 2 t 1 t 2t 2t t t t
e
τ
λ
e
-1
e
τ
λ
e
-1
τ
λ
e
-1
)
τ
(
β
β
β
β
r
(2.4.4)
Este quarto termo da equação pode ser entendido como uma curvatura a mais em
um modelo de fatores, pois como λt e λ2tdeverão ser diferentes, β3t e β4t terão seus
máximos em pontos diferentes, o que fará com que a ETTJ gerada por este modelo possa se adequar melhor a formatos diferentes da curva de juros.
Dado que já temos um modelo para a taxa de juros “zero cupom” (função (2.4.4)), podemos definir a função desconto como:
(
τ
)
p/
τ
1,...,
T
τ
b
τ t t=
+
=
)
(
1
1
)
(
r
(2.4.5)E, assim como em SPF, o problema de minimização passa a ser a equação
(2.4.6) para cada data de análise (t)13:
∑
∑
= = N 1 2 i 1 j i, t j i, i i)
k
)
(T
b
F
-(P
W
Min
i j (2.4.6)Um ponto de discussão importante sobre a utilização deste modelo é a de utilizar
t
λ e λ2tfixos em (2.4.4), tal como nos trabalhos de Diebold-Li (2006) ou Almeida e
outros (2007) ou tentar identificar um método para estimar os melhores λt e λ2t para
cada data analisada.
Nesta tese serão utilizados lambdas fixos. Com isso, a série temporal dos betas fará sentido, criando um bom modelo para estimação da curva para dias ou meses subseqüentes, mas diminuirá dois graus de liberdade no modelo e criará uma
dificuldade, que é a de impor quais são estes parâmetros14. Um exemplo desta série é
apresentada nos gráficos 2, 3 e 4, os quais contém as séries temporais dos parâmetros para as curvas prefixada, indexada ao IPCA e indexada ao IGPM respectivamente.
Em seu trabalho, Diebold-Li (2006) fixa λt como sendo 0,730815, o que implica
que o valor máximo da curvatura ocorre aos 30 meses ou 2,45 anos. Almeida e outros
(2007), fazendo a análise da curva de DI utilizam o λt como sendo 3,58 e λ2tsendo
7,16, o que implica que seus máximos estarão em 0,5 e 0,25 anos respectivamente. Abaixo segue a tabela com os valores usados para cada curva no modelo SVLF e em parênteses estão os valores em anos para os quais a curvatura 1 e a curvatura 2 atingem seus máximos:
Prefixados IPCA IGPM
λt 1,6 (1,12) 1,05 (1,71) 4,1 (0,44) λ2t 1,13 (1,59) 0,8 (2,24) 0,47 (3,82)
2.5.
Spline Exponencial da Merrill Lynch (SEML)
Este método, utilizado pelo banco central do Canadá16 utiliza uma soma de nove
exponenciais para modelar a função desconto, tal como mostrado na equação abaixo:
e
β
b(T)
9 -i T 1i α
∑
=
=
i(2.5.1)
Nesta tese modelarei a função desconto como sendo a soma de cinco exponenciais, pois temos poucos títulos em cada categoria. Além disso, escolhi a combinação de parâmetros que melhor se adaptava aos dados brasileiros. Com isso, a equação utilizada na tese foi:
e
β
e
β
e
β
e
β
e
β
b(T)
-9 T9 T -8 8 T -3 3 T -2 2 T
-1 α
+
α+
α+
α+
α=
(2.5.2)Como temos a função desconto, basta substituí-la na equação (2.5.3) para termos um problema de minimização bem definido, para cada data de análise t.
15 Diebold e Li (2006) em seu trabalho utilizam lambda como sendo 0.0609. Porém, a unidade de medida que eles utilizam é mês. Como nesta tese é utilizada base anual, o parâmetro usado por eles equivale a 0.7308 nesta nova base.
∑
∑
= =
N
1
2 i
1
j i, t j i, i
i
)
k
)
(T
b
F
-(P
W
Min
i j
(2.5.3)
Esta minimização é linear se α for fixo. Então o processo utilizado é criar um
grid de alphas e escolher aquele que minimiza (2.5.3). O α escolhido têm a interpretação de ser a taxa de juros contínua de longo prazo.
Em termos matriciais basta fazer o mesmo processo que no SPF e, assim como naquela metodologia, pode-se colocar restrições em relação à função desconto. Nesta tese, a única restrição sobre a função desconto foi a de que ela começasse em um, o que é o mesmo que restringir que a soma dos betas seja igual a 1.
2.6.
Testes estatísticos
O primeiro teste feito é o de comparar o erro dentro da amostra para cada uma das três metodologias17. Tal como visto em Bliss (1996), o erro dentro da amostra pode ser bastante viesado em favor de modelos altamente parametrizados e que fazem um
overfitting da ETTJ.
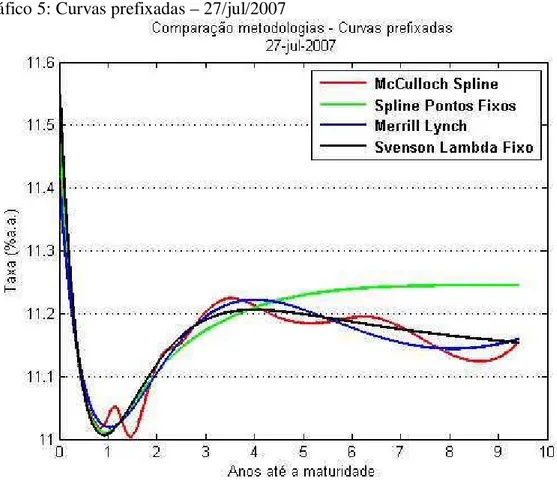
No nosso caso, o modelo MS terá sempre erro zero em relação aos preços, e nem por isso ele será melhor do que os outros, pois ele pode incorporar problemas, tais como erro de coleta de preços de fechamento ou diferenças nos preços devido à falta de liquidez de um determinado título. Este caso pode ser visto no gráfico 5, aonde a ETTJ vermelha apresenta uma oscilação grande na curva perto de um ano, a qual foi causada por um problema na precificação da LTN com vencimento em outubro de 2008 nesta data.
Após isto, o segundo teste consistirá em organizar os títulos por datas de vencimento e, após isto, escolher aleatoriamente ou todos os títulos pares ou todos os títulos ímpares, os quais serão considerados como “dentro da amostra”. Com estes, serão construídas as ETTJs por cada metodologia. Os títulos que não forem selecionados (“fora da amostra”) serão precificados pela curva construída com os primeiros18. Serão então coletados os erros dos preços dos títulos “fora da amostra”
ponderados pelo inverso da duration. Neste teste, o problema da alta parametrização diminui bastante, apesar de não desaparecer, já que dois títulos com vencimentos muito próximos podem conter problemas parecidos na sua precificação, tais como problemas de liquidez ou de diferenças tributárias.
A última bateria de testes feita será a de coletar os erros em termos de cotação19 e testar estes erros para saber se eles têm uma estrutura de autocorrelação20. Se os erros forem aleatórios, ou seja, ruído branco (“white noise”), não haverá autocorrelação dos
erros, nem heteroscedasticidade.
Os testes utilizados para estas hipóteses serão os de Ljung-Box-Pierce Q-teste e de Engle’s21 na série de erros. Além disso, será rodado um AR (1) GARCH (1,1) nos erros22, tal como mostrado na equação abaixo:
2 1 2 2
1 1 2 2
1
* *
*
− −
− + +
=
+ +
=
t t
t
t t t
C Y C
Y
ε α σ α σ
ε β
Sendo: Yt a série temporal (os erros das estimações de cada modelo) no tempo t,
C2 eC constantes,
2
t
σ a variância da série no tempo t,
εt o erro da série temporal no tempo t.
Na seção seguinte mostraremos os principais resultados de nossa análise.
19 Cotação é definida como sendo o preço de mercado dividido pelo valor nocional acumulado (VNA). Os erros são dados em termos de cotação para que os erros de títulos com nocionais diferentes possam ser comparados. Este caso é ainda pior quando estamos trabalhando com títulos indexados à inflação em que o nocional é atualizado diariamente.
20 Este teste será feito apenas com os modelos SPF, SVLF e SEML, já que o MS tem erro zero por definição.
21 O teste Ljung-Box-Pierce testa se há autocorrelação de ordem p na série. A hipótese nula é de que não há autocorrelação.
O teste de Engle’s testa se existem na série efeitos GARCH ou heteroscedasticidade. A hipótese nula é de que não há heteroscedasticidade na série.
3.
Resultados Empíricos
3.1.
Base de dados
Para esta tese foram usados os preços indicativos unitários e as taxas internas de retorno divulgadas pela ANDIMA dos títulos públicos federais para o fechamento de
cada dia útil23, desde janeiro de 2005 até 03 de outubro de 2007. Só foram considerados
os dados dos títulos prefixados (LTNs e NTNFs) e indexados à inflação (NTNBs e
NTNCs24)25.
Além disso, foi utilizada a taxa Selic26 e a expectativa de inflação futura para a
construção de um título fictício de um dia. Isto foi feito para que tivéssemos parâmetros para a parte curtíssima da curva, já que, dependendo da época e do indexador, o título mais curto tinha mais do que um ano e meio, dificultando a estimação da parte curta da curva de juros.
3.2.
Resultados
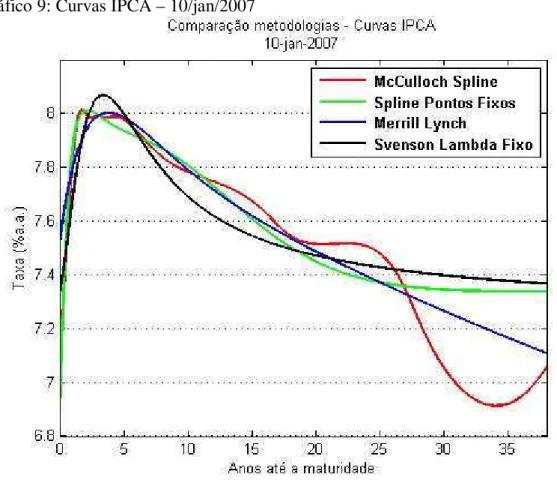
Nos gráficos de 5 a 10 são mostradas as ETTJs calculadas de acordo com as metodologias citadas anteriormente. Foram escolhidos os dias 10 de janeiro de 2007 e 27 de julho de 2007 por ser um dia normal de negociação e um dia de estresse de mercado (alta volatilidade) respectivamente. Como podemos perceber o MS é o modelo com maiores oscilações da curva, o que é uma característica indesejável para uma ETTJ.
O primeiro teste feito para avaliar as metodologias é calcular o erro quadrático médio dos títulos. Neste caso, os modelos mais parametrizados levam vantagens em relação aos outros. Porém, isto não quer dizer que estes modelos sejam melhores do que os outros, já que estes modelos incorporarão erros cometidos na precificação de determinado título devido à, por exemplo, falta de liquidez do papel. Na tabela abaixo
23 Dia útil é entendido aqui como aqueles que não são fins de semana ou feriados em São Paulo. 24 LTNs são títulos emitidos pelo Tesouro Nacional prefixados que não pagam cupons intermediários. NTNFs são títulos prefixados com cupons intermediários, NTNBs são títulos com cupom indexados ao IPCA e NTNCs títulos indexados ao IGPM.
25 Nos títulos indexados a inflação, a taxa utilizada é a taxa real de juros paga pelo título. Ou seja, estes títulos pagarão no futuro a taxa negociada mais a inflação do período.
vemos que o modelo MS não têm erros por ser muito parametrizado, o SEML com cinco parâmetros livres tem o segundo menor erro e os modelos SPF e SVLF com quatro parâmetros livres cada têm erros bastante parecidos.
Tabela com erros quadráticos médios:
Erros * MS SPF SEML SVLF
Títulos Prefixados 0,0000 0,0048 0,0007 0,0010 Títulos indexados ao IPCA 0,0000 0,0133 0,0154 0,0343 Títulos indexados ao IGPM 0,0000 0,0261 0,0258 0,0345
Tabela 1
* Soma dos erros quadráticos médios de todos os títulos governamentais para todos os dias entre 02/01/2005 e 03/10/2007, ponderado pelo inverso da duration.
Nas tabelas a seguir vemos os erros “fora da amostra”, calculado como descrito na seção 3.6. O que podemos perceber nas tabelas abaixo é que, na média, os modelos que têm os menores erros são os modelos exponenciais (tabelas 2, 3, 4 e 5). Isto pode ser visto na comparação modelo a modelo.
O SVLF, por esta metodologia, é sempre melhor do que os modelos derivados dos Splines de McCulloch (SPF e MS), pois em qualquer categoria de títulos e em
qualquer subperíodo de tempo ele sempre comete erros menores do que os dois27. Uma
das explicações para esta diferença reside no fato de que estes dois modelos tendem a gerar curvas com maiores oscilações que o SVLF, errando mais quando fazemos interpolações.
Na comparação de modelos baseados em exponenciais podemos perceber que eles, para este teste, se equivalem. Para títulos indexados ao IPCA, o SEML consegue erros menores do que o SVLF nos anos de 2006 e 2007, tendo resultados muito parecidos em 2005. Já para os títulos prefixados, o SVLF tem sistematicamente erros menores do que o SEML, não sendo possível, por este critério, dizer qual das duas metodologias é a melhor.
Tabelas com erros fora da amostra:
Erros "fora da amostra" * MS SPF SEML SVLF Títulos Prefixados 0,0021 0,003 0,0036 0,0010 Títulos indexados ao IPCA 0,2094 0,6298 0,0879 0,1016
Títulos indexados ao IGPM ** - - -
-Tabela 2
* Soma dos erros quadráticos médios de todos os títulos governamentais não incluídos na amostra utilizada para a construção das curvas, para todos os dias entre 02/01/2005 e 03/10/2007, ponderado pelo inverso da duration.
** Não existiam títulos suficientes para testes com esta classe de ativos.
Erros "fora da amostra" 2005 * MS SPF SEML SVLF Títulos Prefixados 0,0006 0,0023 0,0029 0,0006 Títulos indexados ao IPCA 0,1513 0,6025 0,0736 0,0723
Títulos indexados ao IGPM ** - - -
-Tabela 3
* Soma dos erros quadráticos médios de todos os títulos governamentais não incluídos na amostra utilizada para a construção das curvas, para todos os dias úteis de 2005, ponderado pelo inverso da duration.
** Não existiam títulos suficientes para testes com esta classe de ativos.
Erros "fora da amostra" 2006 * MS SPF SEML SVLF Títulos Prefixados 0,0012 0,0004 0,0005 0,0003 Títulos indexados ao IPCA 0,0359 0,0177 0,0121 0,0206
Títulos indexados ao IGPM ** - - -
-Tabela 4
* Soma dos erros quadráticos médios de todos os títulos governamentais não incluídos na amostra utilizada para a construção das curvas, para todos os dias úteis de 2006, ponderado pelo inverso da duration.
** Não existiam títulos suficientes para testes com esta classe de ativos.
Erros "fora da amostra" 2007 * MS SPF SEML SVLF Títulos Prefixados 0,0004 0,0003 0,0001 0,0001 Títulos indexados ao IPCA 0,0221 0,0096 0,0022 0,0087
Títulos indexados ao IGPM ** - - -
-Tabela 5
* Soma dos erros quadráticos médios de todos os títulos governamentais não incluídos na amostra utilizada para a construção das curvas, para todos os dias entre 02/jan/2007 e 03/out/2007, ponderado pelo inverso da duration.
** Não existiam títulos suficientes para testes com esta classe de ativos.
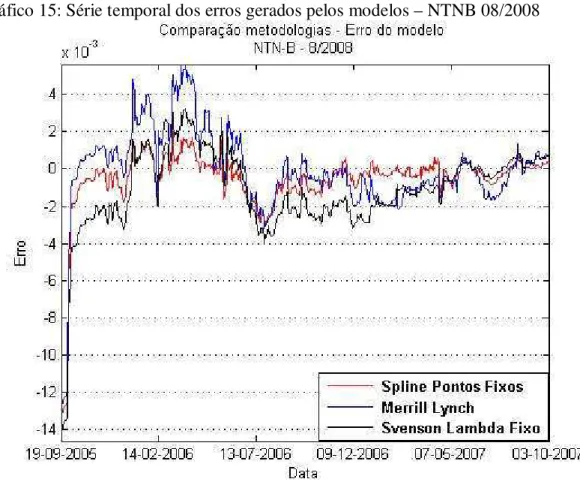
SVLF28. Foram analisados 10 títulos. Duas LTNs (uma curta e uma com prazo de maturidade um pouco maior), duas NTNFs (uma curta e uma longa), três NTNBs e três NTNCs (uma curta, uma média e uma longa). A série temporal de cada um dos títulos
está mostrada nos gráficos de 11 a 2029.
Nos 30 testes de Ljung-Box-Pierce (LBP), todos mostraram que havia alguma correlação serial entre os erros. Todos os testes de Engle (com exceção da NTNF com vencimento em 2014 no modelo SPF) mostraram que havia também heteroscedasticidade dos erros.
Agora, nas tabelas abaixo são mostrados os resultados da regressão da série temporal dos erros (Yt), segundo a seguinte equação:
2 1 2 2
1 1 2 2
1
* *
*
− −
− + +
=
+ +
=
t t
t
t t t
C Y C
Y
ε α σ α σ
ε β
SPF SEML SVLF
LTN jul/07 0,8402 0,9497 0,9602
LTN jan/09 0,3968 0,9158 0,8956
NTNF jan/10 0,8888 0,9365 0,9282 NTNF jan/14 -0,0024 * 0,9184 0,7808 NTNB ago/08 0,8803 0,8962 1,0000 **
NTNB ago/24 0,9814 0,9935 0,9677
NTNB ago/45 0,9737 0,9564 0,9949
NTNC abr/08 0,9616 1,0000 ** 0,9796 NTNC mar/11 0,9735 1,0000 ** 0,9927
NTNC jan/31 0,7809 0,8836 0,9911
* Foi testado um AR (2) para este caso, e os parâmetros encontrados foram beta1 = 0,6477 e beta2 = 0,2322, como o teste de Ljung-Box-Pierce foi positivo, isto implica que existe uma estrutura de autocorrelação neste caso também. ** O resultado da regressão não foi 1, mas foi muito próximo disto. Como não utilizei mais do que 4 casas decimais, o parâmetro que aparece é 1.
Vencimento
Título Modelos
Tabela 6 - Parâmetro β
28 O MS não foi incluído na análise pois, por definição, ele não comete erros em relação aos preços de mercado incluídos no modelo.
SPF SEML SVLF LTN jul/07 0,4510 0,4683 0,5249 LTN jan/09 0,6560 0,5645 0,6785 NTNF jan/10 0,5677 0,5855 0,4236 NTNF jan/14 0,9562 0,6268 0,7654 NTNB ago/08 0,0798 0,2769 0,1627 NTNB ago/24 0,6232 0,7661 0,5956 NTNB ago/45 0,6568 0,5787 0,5526 NTNC abr/08 0,4847 0,4126 0,4348 NTNC mar/11 0,7520 0,5507 0,7426 NTNC jan/31 0,3272 0,2365 0,7849
Tabela 7 - Parâmetro α1
Título Vencimento Modelos
SPF SEML SVLF
LTN jul/07 0,5490 0,5317 0,4645 LTN jan/09 0,2645 0,3736 0,2022 NTNF jan/10 0,3937 0,3637 0,5764 NTNF jan/14 0,0086 0,3732 0,1410 NTNB ago/08 0,9202 0,7231 0,8373 NTNB ago/24 0,3297 0,1468 0,4044 NTNB ago/45 0,3432 0,1828 0,4474 NTNC abr/08 0,5153 0,5874 0,5652 NTNC mar/11 0,0987 0,4493 0,1646 NTNC jan/31 0,6728 0,7635 0,1199
Tabela 8 - Parâmetro α2
Título Vencimento Modelos
Na tabela 6 vemos que os parâmetros Beta, do modelo AR(1) foram muito altos e em sua maioria próximos de 1, o que , junto com o resultado do teste LBP, mostra que há forte autocorrelação entre os erros. Na tabela 7 vemos que o parâmetro alpha1 também foi muito alto, mostrando que, junto com o teste de Engle, temos também heteroscedasticidade em todos os títulos e modelos analisados.
Um dos motivos para este padrão dos erros pode ser o problema de variáveis omitidas, já que o preço de um título é definido não só pelo fluxo de caixa trazido à valor presente como também por outros fatores tais como a liquidez do papel,
diferenças na tributação30 ou variáveis macroeconômicas.
4.
Conclusão
N
esta tese mostramos metodologias bastante parcimoniosas e simples deconstrução da ETTJ. Dentre estas metodologias, a que apresentou o menor erro quadrático médio foi a MS, pois esta metodologia não comete erros em relação aos preços de mercado.
Porém, este não é um bom parâmetro de comparação, já que modelos muito parametrizados levam vantagens em relação aos outros modelos, sem serem necessariamente melhores do que os outros. Isto é particularmente verdade no caso do MS, onde a parametrização é máxima. Neste caso, os pontos de junção ou nós são variáveis, tirando qualquer interpretação intertemporal de seus parâmetros. Além disso, como este modelo é obrigado a acertar todos os preços do mercado, quando um destes preços apresenta problemas de precificação, a curva ficará distorcida devido a
problemas neste título31.
Utilizando o conceito de erros “fora da amostra” (tal como definido em Bliss (1996)) os modelos que performaram melhor foram aqueles baseados em exponenciais, ou seja, o SEML e o SVLF. Estes são os modelos mais utilizados por Bancos Centrais ao redor do mundo.
Para escolher entre o SEML e o SVLF, penso que o SVLF é mais interessante pois seus parâmetros são rotações dos movimentos da ETTJ descobertos por Litterman e Scheinkman (1991) e têm bom poder preditivo para as taxas futuras, assim como mostrado em Diebold e Li (2006) e Pooter (2007) para dados americanos e Almeida e outros (2007) para dados brasileiros.
A última bateria de testes feita mostrou que esta classe de modelos testada, por ser muito simples e parcimoniosa incorre em problemas de autocorrelação e heteroscedasticidade dos erros. Este problema pode ser devido a variáveis omitidas, tais como diferenças de liquidez dos títulos, diferenças de tributação ou variáveis macroeconômicas. Este problema pode ser parcialmente resolvido se fizermos estimações dos parâmetros por técnicas de painel ou se incluirmos parte destas
31 Um exemplo deste caso pode ser visto no gráfico 5, aonde a LTN com vencimento em outubro de 2008, por ter pouca liquidez, não ajustou seu preço no fechamento, tendo preço (ou taxa) muito diferente dos demais títulos. Para poder acertar o preço deste título, a curva construída pelo método do MS foi obrigada a ter um curva a mais que os outros modelos no ponto perto de um ano de maturidade, o que,
variáveis, tal como feito por Ang e Piazzesi (2003) e Diebold, Rudebusch e Aruoba (2006) que incluem variáveis macroeconômicas no modelo.
Apesar dos problemas citados acima, esta classe de modelos é parcimoniosa, o que a torna bastante interessante para determinadas aplicações tais como estimações de curvas futuras, estimações das volatilidades intradiárias dos títulos de renda fixa (mesmo que estes não tenham tido negócios no período) ou estimação da inflação implícita nos negócios realizados no dia.
5.
Bibliografia
Almeida, C. I. R.; Duarte, A. M.; Fernandez, C. A. C. “Decomposing and
simulating the movements of term structure of interest rates in emerging eurobonds markets.” Journal of fixed income, 8, 1, pp. 21-31, 1998.
Almeida, C.I.R.; Gomes, R.; Leite, A.; Vicente, J. “Does Curvature Enhance
Forecasting?”, Julho 2007.
Ang A.; Piazzesi M. (2003) “A no-arbitrage vector autoregression of term
structure dinamics with macroeconomic and latent variables.” Journal of Monetary Economics, 50, pp. 745-787, 2003.
BIS Papers, “Zero-coupon yield curves: technical documentation”. BIS Papers,
Nº 25, October 2005.
Bliss, R. R. “Testing term structure estimation methods”. Federal Reserve Bank
of Atlanta, Working Paper 96-12a, November 1996.
Bolder, D.; Stréliski, D. “Yield curve modeling at the bank of Canada”.
Technical report number 84, Bank of Canada, 1999.
Bolder, D. J.; Gusba, S. “Exponentials, Polynomials, and Fourier series: more
yield curve modeling at the Bank of Canada”. Bank of Canada, Working Paper 29, 2002.
Chambers D. R.; Carleton W. T.; Waldman D. W. “A new approach to
estimation of the term structure of interest rates”. Journal of Financial and quantitative analysis, 19, 3 pp. 233-251, 1984.
Diebold, F. X.; Li, C. “Forecasting the term structure of government bond
yields”. Journal of Econometrics, 130, pp. 337 – 364, 2006.
Diebold, F. X.; Rudebusch, G. D.; Aruoba, S. B. “The macroeconomy and the
yield curve: A dynamic latent factor approach.” Journal of Econometrics, 131, pp. 309-338, 2006.
Litterman, R., Scheinkman, J.A. “Common Factors Affecting Bond Returns”.
Journal of Fixed Income, 1, 54-61, 1991.
McCulloch, J. H. “Measuring the Term Structure of Interest Rates”. The Journal
of Business, Vol. 44, Nº. 1, pp. 19-31, January 1971.
McCulloch, J. H. “The tax-adjusted yield curve”. Journal of finance, 30, pp.
Nelson, C., Siegel, A. “Parsimonious Modeling of Yield Curves”, Journal of
Business, 44, 19-31, 1971.
Svenson, L. E. O. “Estimating and interpreting forward interest rates: Sweden
1992-1994”. NBER Working Paper, 4871, September 1994.
Pooter, M. “Examining the Nelson-Siegel Class of Term Structure Models.”
Tinbergen Institute Working Paper, September 2007.
Vasicek, O. A., Fong, H. G. “Term structure modeling using exponential
6.
Gráficos
Gráfico 1: Movimentos da ETTJ sob o modelo SVLF para um dia específico (Cross Section).
Os fatores do modelo Svenson para os movimentos da ETTJ
0 0,2 0,4 0,6 0,8 1 1,2
0,00 1,00 2,00 3,00 4,00 5,00 6,00 7,00 8,00 9,00 10,00
Anos até a maturidade Deslocamento paralelo
Inclinação Curvatura 1 Curvatura 2
Gráfico 3: Parâmetros do Svenson Lambda Fixo ao longo do tempo (curva IPCA).
Gráfico 5: Curvas prefixadas – 27/jul/2007
Gráfico 7: Curvas IGPM – 27/jul/2007
Gráfico 9: Curvas IPCA – 10/jan/2007
Gráfico 11: Série temporal dos erros gerados pelos modelos – LTN 07/2007
Gráfico 13: Série temporal dos erros gerados pelos modelos – NTNF 01/2010
Gráfico 15: Série temporal dos erros gerados pelos modelos – NTNB 08/2008
Gráfico 17: Série temporal dos erros gerados pelos modelos – NTNB 05/2045
Gráfico 19: Série temporal dos erros gerados pelos modelos – NTNC 03/2011