Efeitos de Confinamento de Vórtice Magnético em Nanodiscos de Fe e Py

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIˆENCIAS EXATAS E DA TERRA

DEPARTAMENTO DE FÍSICA TE ÓRICA E EXPERIMENTAL PROGRAMA DE P ÓS-GRADUAÇ ÃO EM FÍSICA

Efeitos de Confinamento de V´

ortice

Magn´

etico em Nanodiscos de Fe e Py

Autor: Thiago Rafael de Silva Moura

Orientador: Prof. Dr. Artur da Silva Carri¸co

Co-orientadora: Prof(a). Dra. Ana L´ucia Dantas

Disserta¸cão apresentada à Universidade Federal do Rio Grande do Norte como requisito parcial à obten¸cão do grau de Mestre em F´ısica.

(2)

e Joana D’arc da Silva Moura_.

(3)

ii

A Deus_{, por tudo, pela inspira¸c˜ao e pela expira¸c˜ao.}

Ao Prof. Artur da Silva Carri¸co, por sua orienta¸c˜ao durante o per´ıodo de mestrado.

A Prof. Ana Lúcia Dantas, por sua co-orienta¸cão e importantes discussões sobre magnetismo.

A todos os professores do Departamento de F´ısica da UFRN que contribu´ıram para a minha forma¸c˜ao profissional e cidad˜a.

A todos os funcion´arios do Departamento de F´ısica da UFRN.

A todos os componentes do Grupo de Magnetismo e Materiais Magn´eticos.

A Tiago de Medeiros Vieira por todas as importantes discuss˜oes sobre F´ısica Funda-mental.

(4)

Apresentamos dois trabalhos teóricos baseados em simula¸cões numéricas. O primeiro estudo consiste na investiga¸cão das fases de equil´ıbrio e de nuclea¸cão de vórtice em na-noelementos de Ferro e Permaloy com bases circular e quadrada. O outro possui o objetivo de investigar a intera¸cão magnetostática em pares de nanodiscos de Ferro e de Permaloy e seu impacto na estrutura do vórtice.

(5)

Abstract

We report two theoretical works, based in numerical simulations. The first study consists in the investigation of equilibrium phases and vortex formation in Ferro and Permalloy circular and square nanoelements.The another have the aim to investigate the magneto-static interaction between pairs of nanodisks of Ferro and Permalloy and it‘s impact in the vortex structure.

(6)

Resumo iii

1 Introdu¸c˜ao 1

1.1 Motiva¸c˜ao Te´orica . . . 1

1.1.1 Equa¸c˜ao de Landau-Lifshitz . . . 2

1.1.2 Equa¸c˜ao de Landau-Lifshitz-Gilbert . . . 6

1.2 Motiva¸c˜ao Experimental . . . 11

2 Energia 13 2.1 Introdu¸c˜ao . . . 13

2.2 Constru¸c˜ao da Energia . . . 13

2.2.1 Energia de Troca . . . 14

2.2.2 Energia Anisotr´opica Uniaxial . . . 16

2.2.3 Energia Magnetost´atica . . . 18

2.2.4 Energia Zeeman . . . 18

2.2.5 Energia de Interface . . . 19

2.3 Discretiza¸c˜ao da Energia . . . 20

2.3.1 C´elula de Simula¸c˜ao . . . 20

2.3.2 Energia de Troca por C´elula . . . 23

2.3.3 Energia de Anisotropia Uniaxial por C´elula . . . 25

(7)

SUM ´ARIO vi

2.3.4 Energia Zeeman por c´elula . . . 26

2.3.5 Energia de Interface por c´elula . . . 26

2.3.6 Energia Magnetost´atica por c´elula . . . 26

2.3.7 Energia total por c´elula . . . 29

2.4 Campo M´edio Local Sobre C´elulas . . . 29

2.4.1 Campo Dipolar . . . 30

2.5 O M´etodo Auto Consistente . . . 32

3 Forma¸cão de Vórtices em Nanodiscos de Fe e Py 33 3.1 Introdu¸cão . . . 33

3.2 Efeitos de correla¸cão magnético e geométrico dos nano-elementos . . . 34

3.3 Modelo Te´orico . . . 36

3.4 Pr´ıncipais resultados . . . 38

3.5 Conclus˜ao . . . 42

4 Efeitos de forma¸cão de vórtice em pares de nanodiscos 43 4.1 Introdu¸cão . . . 43

4.2 Modelo Te´orico . . . 45

4.3 Forma¸c˜ao de v´ortice em nanodiscos colineares . . . 49

5 Conclus˜oes e Perspectivas 70 5.1 Retrospectiva e Perspectivas . . . 70

Referˆencias 72

(8)

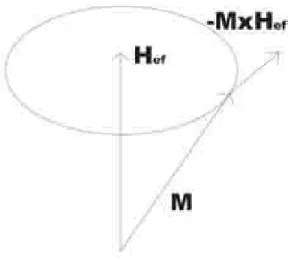
1.1 Esquematiza¸cão da rota¸cão da magnetiza¸cão em torno do campo magnético aplicado. . . 4 1.2 Esquematiza¸cão da rota¸cão da magnetiza¸cão em torno do campo magnético

aplicado com a a¸c˜ao de amortecimento. . . 4

2.1 Figura esquemática da representa¸cão do espa¸co dos momentos magnéticos. 16 2.2 Figura esquemática da representa¸cão da magnetita. Os ´ıonsF e3+_estão

dis-tribu´ıdos espacialmente sob as geometrias octaédrica e tetraédrica com mo-mentos de dipolo antiparalelos e os ´ıons F e2+_{octaédricamente distribu´ıdos}

e responsáveis pelo momento magnético da estrutura. . . 21 2.3 Figura esquemática da representa¸cão atômica, e do sistema magnético

estu-dado neste trabalho. O ´ındiceirepresenta a célula na qual se quer conhecer os campos que atuam sobre ela, j representa os vizinhos responsáveis pelo campo de troca sobre i, enquanto k representa os vizinhos dipolares da célula i. Retirada da Tese de Doutorado de G.O.G Rebou¸cas, 2010. . . 28

(9)

LISTA DE FIGURAS viii

2.4 Figura esquemática mostrando o perfil de cada termo do campo magnético local que atua em cada célula e devido a cada célula. O ´ındiceirepresenta a célula na qual se quer conhecer os campos que atuam sobre ela,j representa os vizinhos responsáveis pelo campo de troca sobrei, enquantokrepresenta os vizinhos dipolares da célula i.Retirada da Tese de Doutorado de G.O.G Rebou¸cas,2010. . . 31

3.1 Figura esquemática de um nanodisco com anisotropia uniaxial no plano (x,y) em um substrato antiferromagnético, (a) e (b) são poss´ıveis con-figura¸cões magnéticas para o nanodisco na ausência de campo e (c) é a configura¸cão magnética com o campo magnético de satura¸cão no plano (x,y). 36 3.2 Magnetiza¸cão de nanoelementos de Fe com 30nm de altura:(a)quadrado

com 48nm de dimensao lateral e (b)circular com 54nm de diâmetro. Ao lado da curva de remanência é apresentado a estrutura do núcleo do vórtice para os nanoelementos, a barra em cores é usada para mostrar a varia¸cão da componente z da magnetiza¸cão. . . 38 3.3 Estrutura magnética selecianada de alguns pontos da figura 3.1. A barra

em cores mostra a varia¸cão da componente z da magnetiza¸cão e as linha cont´ınuas, nos painéis (b),(c) e (e) separa as áreas com cargas opostas da componente z do campo local. . . 39 3.4 Estrutura magnética do núcleo do vórtice (a) sem o substrato

antiferro-magnético e (b) com o substrato antiferroantiferro-magnético para um nanoelemento de Py com 30nm de altura e 62nm de diâmetro. A barra colorida mostra a componente z da magnetiza¸cão e a linha cont´ınua representa Sz no núcleo

(10)

3.5 Estrutura magnética do núcleo do vórtice (a) sem o substrato antiferro-magnético e (b) com o substrato antiferroantiferro-magnético na interface e (c) na superficie para um nanoelemento de Fe com 30nm de altura e 62nm de diâmetro. A barra colorida mostra a componente z da magnetiza¸cão e a linha cont´ınua representa Sz no núcleo do vórtice em (a) x = 0nm, (b)

x=−2nme (c) x=−2nm. . . 41

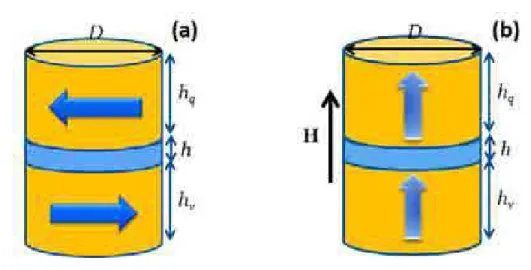
4.1 Figura esquemática de nanodiscos de mesmas altura e diâmetro, (a) no estado inicial sem a presen¸ca de campo magnético aplicado e (b) com campo de satura¸cão aplicado ao longo do eixoz, separados por um espassador não-magnético de espessura h. . . 45 4.2 Curva de remanência de dois nanodiscos de Fe com 81nm de diâmetro

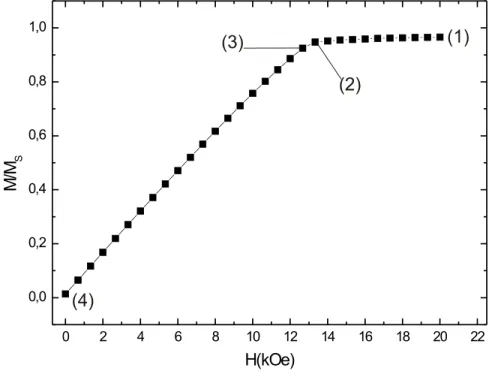
e 12nm de altura, a partir do estado saturado (H=20kOe) ao estado de remanência (H=0kOe), com 6nm de distância interdicos. . . 50 4.3 Estados magnéticos de dois nanodiscos de Fe com 81nm de diâmetro e

12nm de altura, a partir do estado saturado ao estado de remanência e 6nm de distância interdicos. Os estados magnéticos ao longo da curva de remanência da Fig.4.2 estão esquematicamente apresentados nos painéis acima, a partir do estado (1), saturado, com H = 20kOe, ao estado (4), remanente, com H = 0kOe. . . 51 4.4 Curva de remanência de dois nanodiscos de Py com 81nm de diâmetro

(11)

LISTA DE FIGURAS x

4.5 Estados magnéticos de dois nanodiscos de Py com 81nm de diâmetro e 12nm de altura, a partir do estado saturado ao estado de remanência e 9nm de distância interdicos. Os estados magnéticos ao longo da curva de remanência da Fig.4.4 estão esquematicamente apresentados nos painéis acima, a partir do estado (1), saturado, com H = 8kOe, ao estado (4), remanente, com H = 0kOe. . . 53 4.6 Evolu¸cão do diâmetro do núcleo do vórtice dependente da distância

in-terdiscos, para nanodiscos de Permaloy magnetostaticamente interagentes, com 81nm de diâmentro e 12nm de altura. . . 55 4.7 Evolu¸cão do diâmetro do núcleo do vórtice dependente da distância

inter-discos, para nanodiscos de Ferro magnetostaticamente interagentes, com 81nm de diâmentro e 12nm de altura. . . 57 4.11 Evolu¸cão do diâmetro do núcleo do vórtice dependente da distância

(12)

4.12 Evolu¸cão do diâmetro do núcleo do vórtice dependente da distância inter-discos, para nanodiscos de Ferro magnetostaticamente interagentes, com 81nm de diâmentro e 18nm de altura. . . 58 4.13 Evolu¸cão do diâmetro do núcleo do vórtice dependente da distância

inter-discos, para nanodiscos de Ferro magnetostaticamente interagentes, com 81nm de diâmentro e 21nm de altura. . . 59 4.14 Gráfico da mudan¸ca da quiralidade em rela¸cão ao aumento da distância

interdiscos para nanoelementos de Permaloy com 81nm de diâmentro e alturas de 12nm e 15nm. . . 60 4.15 Transi¸cão de fase magnética associada ao produto da quiralidade (Cr =

c1.c2) entre dois nanodiscos de Py com 81nm de diˆametro e 12nm de

al-tura. Os pontos retirados da curva de quiralidade, Fig. 4.14, onde ocorrem as transi¸cões magnéticas são: (X) com d = 7,19515nm de distância inter-discos, (Y) com d= 7,19518nm, (Z) comd= 38,61897nm e para o estado (W) com d= 38,618991nm. A coluna colorida representa a componente z

da magnetiza¸cão. . . 61 4.16 Transi¸cão de fase magnética associada ao produto da quiralidade (Cr =

al-tura. Os pontos retirados da curva de quiralidade, Fig. 4.14, onde ocorrem as transi¸cões magnéticas são: (K) com d = 2,12439nm de distância inter-discos, (L) comd= 2,12442nm, (N) comd = 14,36694nme para o estado (M) com d = 14,36695nm. A coluna colorida representa a componente z

da magnetiza¸cão. . . 62 4.17 Gráfico da mudan¸ca da quiralidade em rela¸cão ao aumento da distância

(13)

LISTA DE FIGURAS xii

4.18 Gráfico da mudan¸ca da quiralidade em rela¸cão ao aumento da distância interdiscos para nanoelementos de Ferro com 81nm de diâmentro e alturas de 12nm e 15nm. . . 64 4.19 Transi¸cão de fase magnética associada ao produto da quiralidade (Cr =

c1.c2) entre dois nanodiscos de Fe com 81nm de diˆametro e 12nm de altura.

Os pontos retirados da curva de quiralidade, Fig. 4.18, onde ocorrem as transi¸cões magnéticas são: (P) comd= 5,0355nmde distância interdiscos, (Q) com d = 5,03559nm, (R) com d = 29,43195nm e para o estado (S) com d = 29,43198nm. A coluna colorida representa a componente z da magnetiza¸cão. . . 65 4.20 Transi¸cão de fase magnética associada ao produto da quiralidade (Cr =

al-tura. Os pontos retirados da curva de quiralidade, Fig. 4.18, onde ocorrem as transi¸cões magnéticas são: (K) com d = 2,12439nm de distância inter-discos, (L) comd= 2,12442nm, (N) comd = 14,36694nme para o estado (M) com d = 14,36695nm. A coluna colorida representa a componente z

da magnetiza¸cão. . . 66 4.21 Gráfico da mudan¸ca da quiralidade em rela¸cão ao aumento da distância

interdiscos para nanoelementos de Ferro com 81nm de diâmetro e alturas de 18nm e 21nm. . . 67 4.22 Gráfico da mudan¸ca da polaridade em rela¸cão ao aumento da distância

interdiscos para nanoelementos de Ferro com 81nm de diâmetro e alturas de 12nm e 15nm. . . 68 4.23 Gráfico da mudan¸ca da polaridade em rela¸cão ao aumento da distância

(14)

4.24 Gráfico da mudan¸ca da polaridade em rela¸cão ao aumento da distância in-terdiscos para nanoelementos de Permaloy com 81nm de diâmetro e alturas de 12nm e 15nm. . . 69 4.25 Gráfico da mudan¸ca da polaridade em rela¸cão ao aumento da distância

(15)

Cap´ıtulo 1

Introdu¸c˜

ao

1.1 Motiva¸c˜

ao Te´

orica

A motiva¸cão primordial desse trabalho é inevitavelmente teórica, decorrente do estudo ainda simplório da equa¸cão de Landau-Lifshitz apresentada pelos autores -Landau e Lifshitz- no ano de 1935 e posteriormente pela abordagem Langrangeana admitida por Gilbert motivada pelo estudo do efeito de amortecimento anômalo provocado por cor-rentes de Foucault em filmes ferromagnéticos de Py, que resultou na conhecida equa¸cão de Lifshitz-Gilbert e possui correspondência direta com a equa¸cão de Landau-Lifshitz como será demonstrado na subse¸cão 1.1.2 deste cap´ıtulo. Outra motiva¸cão, ainda teórica, para o estudo que será apresentado neste trabalho é adivinda do interesse por estudar sistemas não lineares que apresentam extrema riqueza em termos de F´ısica Fun-damental e Aplicada. No caso do presente trabalho o foco se encontra em nanoestruturas magnéticas cil´ındricas e no estudo de como efeitos geométricos são determinantes na forma¸cão de alguns padrões magnéticos em nanoestruturas de baixa dimensionalidade de interesse, com diâmetro ou aresta menor que 100 nm.

(16)

1.1.1 Equa¸c˜

ao de Landau-Lifshitz

Classicamente a rela¸c˜ao entre o momento de dipolo magn´etico de uma part´ıcula de carga

q ´e

~

m =γ~L (1.1)

onde γ é o fator giromagnético, que é diretamente proporcional ao produto entre o fator de Landé g e inversamente proporcional a massam da part´ıcula de cargaq

γ = gq

2m (1.2)

Realizando o produto vetorial do momento de dipolo magn´etico elementar m~ com o campo magn´etico H~

~

m×H~ =γ~L×H~ (1.3)

é obtida a defini¸cão de torque proveniente de um dipolo magnético m~ sob a a¸cão de um campo magnético de magnitude |H~|. Seguindo com a constru¸cão, segue-se que pela Mecânica Clássica o torque é definido como a taxa de varia¸cão temporal do momento orbital

d~L

dt =γ~L×H~ (1.4)

multiplicando a eq.(1.4) pela eq.(1.2)

gq

2m d~L

dt =γ gq

2mL~ ×H~ (1.5)

fazendo uma pequena manipula¸cão algébrica e usando a defini¸cão da eq.(1.1)

d ~m

dt =γ ~m×H~ (1.6)

(17)

CAPÍTULO 1. INTRODUÇ ÃO 3

na maior parte da literatura atual sobre o assunto com sinal negativo, que também será empregado aqui com o objetivo de não fugir desse padrão adotado, segue-se que a equa¸cão anterior escrita sob essas circunstâncias é reescrita agora com sinal negativo

d ~m

dt =−γ ~m×H~ (1.7)

(18)

Figura 1.1: Esquematiza¸cão da rota¸cão da magnetiza¸cão em torno do campo magnético aplicado.

(19)

Para resolver este problema, Landau e Lifshitz propuseram de maneira engenhosa a ex-istência de uma a¸cão f´ısica, que aqui será representada pelo vetor ~h, que for¸cará o ali-nhamento do momentum de dipolo com o campo magnético; este novo termo surge na equa¸cão por razões puramente fenomenológicas e foi chamado de a¸cão de amortecimento, então adicionando a a¸cão de amortecimento a eq.(1.7)

d ~m

dt =−γ ~m×H~ +~h (1.8)

A a¸cão de amortecimento deve ser constru´ıda de maneira perpendicular ao momento de dipolo, caso contrário, o módulo de m~ não permanece constante, o que não é f´ısicamente aceitável, pois não é desejável derivar uma equa¸cão com o módulo do momento de dipolo magnético variante e admitir tal fato não é pertinente quando não existe qualquer com-prova¸cão da veracidade do mesmo, principalmente quando a ordem da energia magnética é de 10−3_eV _{enquanto a ordem da energia atômica é de 1}_eV_{. Um caminho para a}

con-stru¸cão dessa equa¸cão é partir de uma fundamenta¸cão puramente fenomenológica de que a a¸cão de amortecimento for¸ca o alinhamento do dipolo com o campo e por este motivo é fact´ıvel pelas razões já apresentadas construir a a¸cão de amortecimento como se segue

~h =m~ ×~c (1.9)

onde

~c=−αγ ~m×H~ (1.10)

e α é a constante de amortecimento. Integrando as constru¸cões das eq.s (1.9) e (1.10) a eq.(1.8) é encontrada a equa¸cão que descreve a precessão do momento de dipolo em torno do campo magnético com termo de amortecimento, ou seja, é encontrada a equa¸cão derivada por Landau e Lifshitz

d ~m

(20)

Para ultimar esta subse¸cão serão substitu´ıdos o termo de campo magnético H~ pelo a¸cão do campo magnético efetivo H~ef proveniente da superposi¸cão de todos os campos que

competem em um meio magnético acrescido do termo do campo magnético externo. Esses campos a menos do campo aplicado são derivados do Hamiltoniano total que descreve a competi¸cão energética existente num material magnético e substituiremos o momento de dipolo elementarm~ por seu efeito macroscópico e conjunto de muitos momentos de dipolo quando o limite termodinâmico é atingido, a magnetiza¸cão M~. Por hora o campo efetivo será expresso matematicamente sem explicitar quais são seus campos intr´ınsecos, deixando a deriva¸cão dos mesmos através do Hamiltoniano para o cap´ıtulo 2 deste documento. Escrevendo o campo magnético efetivo

~ Hef =

X

i

~

Hi (1.12)

consequêntemente a equa¸cão de Landau-Lifshitz é reescrita

d ~M

dt =−γ ~M ×H~ef − αγ Ms

~

M ×(M~ ×H~ef) (1.13)

1.1.2 Equa¸c˜

ao de Landau-Lifshitz-Gilbert

(21)

condu¸cão, etc. Com o objetivo de apresentar uma teoria com fundamenta¸cão largamente fenomenológica, Gilbert propôs uma abordagem Langrangeana para descrever o efeito de amortecimento anômalo apresentado nos filmes de permaloy. Sem obstar o entendimento para a deriva¸cão da equa¸cão de Gilbert, serão omitidos resultados que já foram derivados neste documento mas que podem ser reavaliados no artigo publicado em 2004 extra´ıdo da tese do próprio Gilbert [1]; o ponto de partida para construir a equa¸cão encontrada por Gilbert será dado através da eq.(1.7) mudado apenas o campo magnético pelo campo efetivo

d ~m

dt =−γ ~m×H~ef (1.14)

e seguindo a filosofia adotada por Gilbert, para apresentar o campo magn´etico efetivo

~ Hef =

∂U

∂ ~m (1.15)

em que U é a energia potencial relacionada ao trabalho realizado para rotacionar o momento de dipolo contra qualquer for¸ca presente, desde que seja poss´ıvel fazê-lo. Prosseguindo, considerando um conjunto discreto de momentosm~j, j=1,...,n; as equa¸cões

do movimento s˜ao

d ~mj

dt =−γ ~mj ×H~j (1.16)

e a equa¸c˜ao do campo efetivo agindo no j-´esimo momento

~ Hj =−

∂U(m~1, ..., ~mn)

∂ ~mj

(1.17) para a energia potencial generalizada U(m~1, ..., ~mn) que leva em conta intera¸c˜oes que

exercem qualquer a¸cão sobre os momentos individuais. Como estas equa¸cões são clássicas para o conjunto de momentos magnéticos individuais com m~j espacialmente localizado

em r~j, estas podem ser transformadas para equa¸c˜oes cl´assicas de campo ao introduzir o

campo cont´ınuo

~

(22)

onde ∆Vj ´e o volume em que o momento de dipolo ´e encontrado. Empregando a mudan¸ca

do campo cont´ınuo na equa¸c˜ao dinˆamica

~

mj =m~(r~j)∆Vj (1.19)

em

d(m~(r~j)∆Vj)

dt =−γ(m~(r~j)∆Vj)×H~j (1.20)

tomando o limite de ∆Vj →0, o conjunto discreto de momentos se torna o campo

magne-tizante e fun¸c˜oes do tipoF(m~1, ..., ~mn) se transformam em funcionais,F(m~(~r)) em termos

do campo cont´ınuom~(~r) e por consequˆencia as derivadas deU(m~1, ..., ~mn) eF(m~1, ..., ~mn)

se transformam em funcionais deriv´aveis

∂U(m~1, ..., ~mn)

∂ ~mj

(1.21)

e

dF ~M(~r)≡

Z _dF₍_M_~₍_~r₎₎

d ~M(~r) d ~M(~r)d~r (1.22) Segue-se, que esta nova filosofia leva a equa¸cão clássica de movimento para um campo magnético não amortecido

d ~M(~r, t)

dt =−γ ~M(~r, t)×H~ef (1.23)

e o campo efetivo

~

Hef =−

dU(M~(~r, t))

d ~M(~r, t) (1.24) agora U(M~(~r, t)) ´e a energia potencial associada ao campo magnetizante M~(~r, t).

(23)

por razões puramente fenomenológicas será constru´ıda uma for¸ca que se opõe a for¸ca macroscópica.

A for¸ca que se opõe a for¸ca macroscópica será chamada de for¸ca de amortecimento, quando o ganho de energia proporcionado pela for¸ca macroscópica é balanceado pelas perdas de energia provocadas pela for¸ca de amortecimento, essas duas for¸cas estão em equil´ıbrio e o estado estacionário é mantido.

A formula¸cão Langrangeana adotada é um funcional deM~(~r, t) eM~˙ (~r, t), sendo o primeiro termo do campo magnetizante e o segundo sendo sua derivada em rela¸cão ao tempo, sendo assim, o caso em que não existe amortecimento permite a seguinte formula¸cão Lagrangeana

d dt

∂L(M~(~r, t), ~M˙(~r, t))

∂ ~M˙(~r, t)

− ∂L(M~(~r, t), ~M˙(~r, t))

∂ ~M(~r, t) = 0 (1.25) em que

L(M~(~r, t), ~M˙(~r, t)) =T(M~(~r, t), ~M˙ (~r, t))−U(M~(~r, t)) (1.26)

para a energia cin´etica T e a energia potencial U do campo magnetizante.

Com o objetivo de converter esta equa¸cão para uma formula¸cão Langrangeana com termo de amortecimento, por constru¸cão é adicionada uma for¸ca dissipativa

∂Q(M~˙(~r, t))

∂ ~M˙(~r, t)

(1.27)

acrescentada a equa¸c˜ao de Langrange sem o amortecimento

d dt

∂L(M~(~r, t), ~M˙(~r, t))

∂ ~M˙(~r, t)

− ∂L(M~(~r, t), ~M˙ (~r, t))

∂ ~M(~r, t) +

∂Q(M~˙(~r, t))

∂ ~M˙(~r, t)

= 0 (1.28)

em que a for¸ca dissipativa é uma forma quadrática da derivada do campo magnetizente com parâmetro de amortecimento de ajuste isotrópicoα, como se segue

Q(M~˙ (~r, t)) = α 2

Z

~_˙

(24)

e o trabalho realizado pelo sistema contra a for¸ca dissipativa ´e

dW dt =α

Z

~_˙

M(~r, t)·M~˙ (~r, t)d~r (1.30)

substituindo a eq.(1.26) na eq.(1.28)

d dt

∂(T −U)

∂ ~M˙ (~r, t)

− ∂(T −U)

∂ ~M(~r, t) +

∂Q(M~˙(~r, t))

∂ ~M˙(~r, t)

= 0 (1.31)

d dt

∂T(M , ~~ M˙)

∂ ~M˙(~r, t)

− ∂T(M , ~~ M˙)

∂ ~M(~r, t) +

∂U(M~)

∂ ~M(~r, t)+

∂Q(M~˙ (~r, t))

∂ ~M˙ (~r, t)

= 0 (1.32)

d dt

∂T(M , ~~ M˙)

∂ ~M˙(~r, t)

− ∂T(M , ~~ M˙)

∂ ~M(~r, t) −

~

Hef(~r, t) +α ~M˙(~r, t) = 0 (1.33)

fazendo concluir que o termo de amortecimento afeta o efeito do campo efetivo, por isso, adicionando o termo de redu¸c˜ao do campo efetivo a eq.(1.14) e renomeando as constantes

γ para γG e α para αG

d ~m

dt =−γGm~ ×(H~ef −αGm~˙(~r, t)) (1.34)

chega-se a equa¸cão com base fenomenológica encontrada por Gilbert para a descri¸cão da dinâmica de precessão do momento de dipolo magnético em torno do campo efetivo. Para mostrar a equivalência dessas duas equa¸cões será reproduzido aqui fielmente a demonstra¸cão feita na referência [2], então sendo assim, tomando o produto vetorial do momento de dipolo m~ com a equa¸cão de Landau-Lifshitz, segue-se que

~

m× d ~m

dt =−γ ~m×(m~ ×H~ef)−αγ ~m×(m~ ×(m~ ×H~ef)) (1.35)

usando a rela¸c˜oes matem´aticas

~a·(~b×~c) =~b·(~c×~a) =~c·(~a×~b) (1.36)

e

(25)

fazendo |m~|=1, facilmente ´e mostrado que

~

m×(m~ ×(m~ ×H~ef)) = −m~ ×H~ef (1.38)

substituindo e multiplicando por α

α ~m× d ~m

dt =−γα ~m×(m~ ×H~ef) +α

2_{γ ~}_m_×_H_~

ef (1.39)

após algumas manipula¸cões algébricas se obtém

d ~m

dt =−γ(1 +α

2₎_m_~ _×_H_~

ef +α ~m×

d ~m

dt (1.40)

que comparada a equa¸c˜ao encontrada por Gilbert leva a seguinte rela¸c˜ao entre as con-stantes

γG =γ(1 +α2) (1.41)

e

αG =

α

γ(1 +α2₎ (1.42)

de forma que fica mostrada a equivalência entre a equa¸cão de Landau-Lifshitz e a equa¸cão obtida por Gilbert para afeitos de amortecimento anômalo.

1.2 Motiva¸c˜

ao Experimental

(26)

de nano-osciladores sincronizados que sob condi¸cões espec´ıficas ampliam o sinal emitido. Alguns resultados apresentados pelo NIST em que foram constru´ıdos nano-osciladores com 50 nanometros de diâmetro e dispostos topologicamente numa estrutura sandwich separadas por um espa¸cador nã-magnético de cobre (Cu), mostram que um único nano-oscilador desses possui frequência de microonda de 10 nanowatts enquanto um conjunto de 10 nano-osciladores sincronizados possuem uma frequência emitida de 1 microwatt re-sultante da oscila¸cão conjunta dos nano-osciladores, ou seja 1000 maior do que a de um ´

(27)

Cap´ıtulo 2

Energia

2.1 Introdu¸c˜

ao

Os termos que compreendem a energia total de um meio magnético t´ıpico que fora apenas comentado no cap´ıtulo anterior, categorizando cada uma das energias que configuram a competi¸cão energética, em outras palavras, serão apresentados os campos que compentem entre si para determinar parcialmente o estado magnético dos nanoelmentos que podem ser estudados e que possuem seus estados magnéticos também parcialmente determinados pela geometria do nanoelemento. Posteriormente será introduzido o conceito de célula de simula¸cão e serão discretizados a partir da energia total, a ser, a densidade de energia magnética por célula e os campos provenientes desse conceito de energia.

2.2 Constru¸c˜

ao da Energia

A energia efetiva é composta por um conjuto de energias que competem entre si; o estado magnético que possa ser obtido em uma nanoestrutura qualquer não pode ser previsto, já que o mesmo depende dos estados magnéticos acess´ıveis ao nanoelemento e qual desses estados ele acessou até o momento em que está sendo observado, mas a(s) energia(s)

(28)

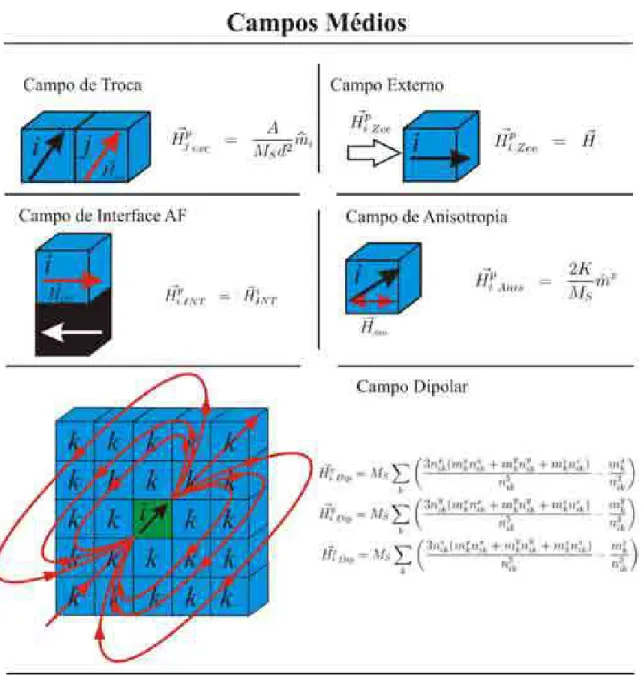
dominante(s) certamente será(ão) um fator decisivo para a proje¸cão neste novo estado magnético. A equa¸cão abaixo mostra algumas dessas energias que serão usadas para modelar os nanodiscos de Fe e Py.

E = − Je

X

i

X

k

~si·~sk−H.M~ SV

X

i

~si

− H~IN T.MSV

X

i

~si−

KV

2 X

i

(szi)

2

(2.1)

+ M

2

SV

2 X

i

X

k

~si.~sk

r3

ik

− 3(~si.~rik)(~sk.~rik)

r5

ik

Os termos que compõe esta equa¸cão são respectivamente: a energia de troca, a energia Zeeman, a energia de interface proveniente do sub-extrato antiferomagnético, a energia de anisotropia uniaxial e a energia dipolar ou magnetostática.

2.2.1 Energia de Troca

A energia de troca de acordo com a Mecânica Quântica não é explicada quando se con-sidera apenas a fun¸cão de onda de um elétron, mesmo que sejam tomados dois átomos separadamente, por exemplo. Cada átomo com um elétron desemparelhado e descrito pelas fun¸cões de Wannier - não trataremos desse assunto afundo-, que são fun¸cões con-stru´ıdas a partir da superposi¸cão das fun¸cões de onda dos dois elétrons individualmente, o que não é o suficiente para descrever a origem da intera¸cão de troca entre dois elétrons, para o leitor interessado em se aprofundar neste assunto, é deixada a referência [6] para a compreen¸cão desta constru¸cão feita por Wannier, que foi refutada e leva a aceitata¸cão não diger´ıvel do Hamiltoniano de Heisenberg que parece aceitável atualmente mas nem sempre foi assim como as próprias fun¸cões de Wannier.

(29)

CAP´ITULO 2. ENERGIA 15

A intera¸cão de troca pode ocorrer de duas maneiras: entre elétrons de átomos difer-entes chamada de intera¸cão interatômica, ou entre átomos localizados no mesmo átomo, intera¸cão intra-atômica.

Para a intera¸cão intra-atômica, enquanto o acoplamento anti-paralelo↑↓é favorecido pelo Princ´ıpio de Exclusão de Pauli, de contra partida é desfavorecido pela intera¸cão Coulom-biana, quando dois elétrons estão acoplados paralelamente ↑↑ quando favorecidos pelo Princ´ıpio de Exclusão eles devem estar em orbitais distintos o que minimiza a energia eletrostática, por outro lado, favorece o aumento de energia de um dos elétrons. Por ex-emplo, se algum desses elétrons está no estado fundamental, o outro pelas Regras de Rund, deve estar no primeiro estado excitado ou outro estado excitado, obedecendo o princ´ıpio de minimiza¸cão da energia, de maneira mais direta, o acoplamento ferromagnético é fa-vorecido nas intera¸cões intra-atômicas. A constru¸cão da fun¸cão de onda que descreve a intera¸cão de dois elétrons é feita através do produto das fun¸cões de onda ortogonais de elétrons individuais. A intera¸cão entre elétrons localizados em um conjunto de orbitais para o par de fun¸cões de onda Ψi(~r) e Ψj(~r) - sem muitos detalhes - levam a constru¸cão

dos valores esperados da energia Coulombiana e da energia de intera¸c˜ao de troca, escritas a baixo, respectivamente

< Vc(r~1, ~r2)>=

Z Z Ψ∗

i(r~1)Ψ∗i(r~2)V(r~1, ~r2)Ψi(r~1)Ψi(r~2)d3~r1d3~r2 (2.2)

Jij =

Z Z Ψ∗

i(r~1)Ψj(r~2)V(r~1, ~r2)Ψ∗j(r~1)Ψi(r~2)d3~r1d3~r2 (2.3)

e então como derivado por Heisenberg a partir da teoria de Heitler-London, o hamiltoniano para as intera¸cões interatômicas é escrito da forma a seguir

Eex = −P_iP_jJij~si·~sj (2.4)

e como visto acimaJij ´e a integral de energia de troca, que para a constru¸c˜ao do

(30)

Hamil-toniano de troca

Eex = −JP_iP_j~si·~sj (2.5)

2.2.2 Energia Anisotr´

opica Uniaxial

A energia anisotrópica possui multiformes manifesta¸cões, apenas para citar algumas, exis-tem: a anisotropia cúbica, anisotropia uniaxial, anisotropia magnetocristalina, anisotropia de forma, etc. A energia anisotrópica que compõe nossa energia total é a energia de anisotropia uniaxial. A energia anisotrópica uniaxial tem como caracter´ıstica a existência de um eixo espacial em que a magnetiza¸cão tende a se orientar naturalmente.

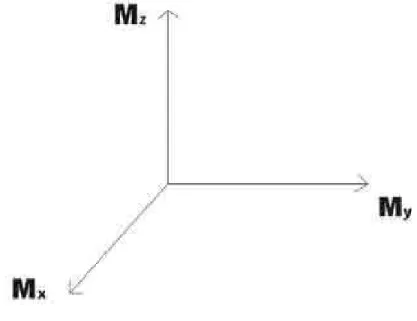
Para citar uma constru¸cão comumente encontrada na literatura, primeiramente imaginam-se as componentes da magnetiza¸cão Mx, My e Mz como componentes do vetor unitário

|Mˆ|=1, em que M~ = ˆM Ms, e pela figura 2.1.

(31)

As rela¸c˜oes entre θ, φ, Mx, MyeMz s˜ao

Mx =sen(θ)cos(φ) (2.6)

My =sen(θ)sen(φ) (2.7)

Mz =cos(θ) (2.8)

ˆ

M = ˆisen(θ)cos(φ) + ˆjsen(θ)sen(φ) + ˆkcos(θ) (2.9)

Escolhendo o eixoMz para ser o eixo de f´acil magnetiza¸c˜ao,Mx2+My2 = 1−Mz2 =sen2(θ)

para uma superf´ıcie anisotrópica energética situada ao longo da dire¸cão ˆM, Ea( ˆM).

Para a energia de troca a superfic´ıe energética é esfericamente distribu´ıda; quando o privilégio do controle da energia anisotrópica ao longo de um eixo espec´ıfico é promovida a quebra de simetria na superf´ıcie energética, por meio da qual a equa¸cão

∂Ea( ˆM)

∂Mˆ = 0 (2.10)

revela solu¸cões que representam os m´ınimos locais, pontos de sela ou máximos locais. Em que os m´ınimos locais identificam o eixo de fácil magnetiza¸cão.

Retomando a equa¸c˜ao M2

x +My2 = sen2(θ), e pela quebra de simetria da superf´ıcie

energética ao longo do eixo fácil, têm-se que a densidade de energia é invariante por rota¸cões ao redor do eixo fácil. E para evidenciar isso de maneira aceitável, basta expandir a fun¸cão M2

x +My2 = sen2(θ) em termos do cos(θ) para obter o termo geral da energia

anisotr´opica

Ea= k0+k1sen2(θ) +k2sen4(θ) +... (2.11)

onde as constantes k0, k1, k2, etc, s˜ao identificadas como constantes anisotr´opicas, com

(32)

possui apenas termos de ordem par, onde os termos de ordem ´ımpar possuem origem de comportamentos magnéticos particulares, tais como, polariza¸cão de troca, ou efeitos relativ´ısticos advindos de intera¸cões de Moriya-Dzialoshinskii.

Então, para ultimar a forma da densidade de energia anisotrópica uniaxial que comporá o Hamiltoniano total, a expansão será truncada com rela¸cão aos termos superiores a ordem quadrática emsen(θ), resultando em

Ea=k0+k1sen2(θ) (2.12)

no entantok0 ´e a medida da densidade de energia anisotr´opica realizada no zero absoluto,

podendo ser tomada como nula j´a que k1 ´e aconstante de anisotropia medida em uma

temperatura arbitrária T diferente de zero, ou seja, a forma final da equa¸cão é

Ea = k1sen2(θ) (2.13)

2.2.3 Energia Magnetost´

atica

A energia que descreve a intera¸cão entre dois momentos de dipolos elementares é propor-cional a sobreposi¸cão de dois fatores, o primeiro é proporpropor-cional ao produto de intera¸cão dos momentos e inversamente proporcional ao cubo da distância entre os dipolos, o se-gundo é diretamente proporcional ao produto quadrático entre o momentum e a distância que os separam com o fator de decaimento espacial proporcional ao inverso da quinta potência da distância que separam os dipolos.

Matematicamente, a energia dipolar por ´atomo

Ed= M2

SV

2

P

i

P

k

~ si.~sk

r3

ik −

3(~si.~rik)(~sk.~rik)

r5

ik

(2.14)

2.2.4 Energia Zeeman

(33)

magnético; essa energia é minimizada quando o campo magnético e o momentum estão alinhados paralelamente.

EZee = −H.M~ SV P_i~si (2.15)

2.2.5 Energia de Interface

A energia de interface apresentada nesta subse¸cão é produto da tentativa de modelagem do substato antiferromagnético, representado pelo campo de interface HIN T que interage

apenas com a primeira camada do nanoelemento em estudo. Pela escolha da forma de modelagem do substrato através de um campo fixo, significa que o substrato não sofre influência do campo externo aplicado e é representado por isso como uma célula única, ou seja o substrato não relaxa com qualquer tipo de ten¸cão exterior. Embora seja uma maneira ainda não fechada e até certo ponto pobre de modelar, o substrato modelado dessa maneira se mostra aceitável já que a camada que o campo representa pode ser constru´ıda experimentalmente. Escrevendo então a energia de interface como o produto do campo de interface e os momentos da primera camada do nanoelemento, segue-se que

(34)

2.3 Discretiza¸c˜

ao da Energia

2.3.1 C´

elula de Simula¸c˜

ao

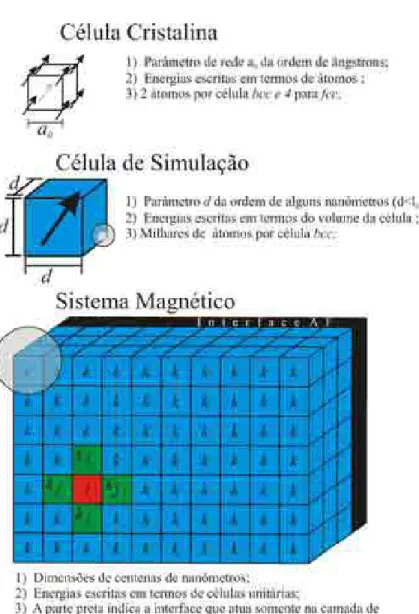
Antes de discretizar a energia total que descreve o comportamento das estruturas magnéticas que serão estudadas nos cap´ıtulos 3 e 4, será introduzido primeiro um conceito fundamental, que faz parte da filosofia adotada para a modelagem das nanoestruturas, este é o conceito de célula de simula¸cão. Para introduz´ı-lo, será usado o fato de que um material magnético pode ser dividido em unidades menores que possuem as caracter´ısticas fundamentais para a constru¸cão das ferramentas e do método desejado; estas unidades fundamenais são as redes de Bravais.

Como elemento magnético para introduzir o conceito de célula de simula¸cão, será utilizada a magnetita,F e2O4.

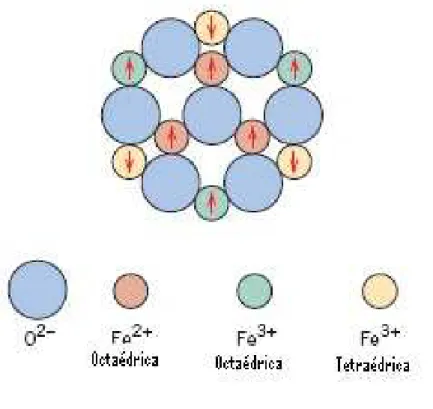
A magnetita está distribuida espacialmente em duas geometrias, uma ostaédrica e outra tetraédrica. De sua constitui¸cão fazem parte o ´ıons bivalente de Ferro, F e2+ _e

triva-lente, F e3+_{. Os ´ıons} _{F e}3+ _{est˜ao organizados em duas estruturas, uma octa´edrica e outra}

tetraédrica antiparalela a estrutura octaédrica e juntas configuram o momento magnético liqu´ıdo da rede nulo. Os ´ıons bivalentes do ferro estão geométricamente distribu´ıdos em um octógono, onde cada ´ıon F e2+ _{possui 4}_µ

B (magn´etons de Bohr) respons´aveis pelo

(35)

Figura 2.2: Figura esquemática da representa¸cão da magnetita. Os ´ıons F e3+ _estão

distribu´ıdos espacialmente sob as geometrias octaédrica e tetraédrica com momentos de dipolo antiparalelos e os ´ıons F e2+ _{octaédricamente distribu´ıdos e responsáveis pelo}

(36)

A magnetita ´e modelada por meio de uma estrutura cristalina c´ubica com 8F e2+ _´ıons

respons´aveis pelo magnetismo e possui parˆametro de rede a0 igual a 0,839nm, sendo

assim, fazendo uma an´alise para um nanoelemento de aresta d= 10nm, existem

N = 8(d a0)

3 _(2.17)

aproximadamente 13.545 ´ıons de F e2+_{. Este n´}_{umero implica dizer que ser˜ao precisos}

inicializar e achar a configura¸cão de equil´ıbrio de 4x13.545 = 54.182 magnetons de Bohr, que torna o cálculo computacional inviável. Neste contexto pode ser introduzido o conceito de célula de simula¸cão; em que para uma determinada célula de aresta l inferior ao comprimento de troca lex, que é o comprimento sob o qual os momentos magnéticos

não sofrem mudan¸cas significativas em rela¸cão a dire¸cão dos momentos magneticos nesta região, este é o comprimento de troca, que indica a região no material onde a energia de troca é dominante sobre a energia magnetostática. Escolher uma dimensão para a célula de simula¸cão em que l > lex significa perder caracter´ıticas fundamentais do material

magnético majorados pela energia de troca. O comprimento de troca é escrito em termos da rigidez de trocaA e da magnetiza¸cão de satura¸cãoMsdo material [7]

lex =

s 2A M2

s

(37)

2.3.2 Energia de Troca por C´

elula

Para a constru¸cão da energia de troca por célula de simula¸cão, primeiramente toma-se que a energia de troca do i-ésimo átomo com seus vizinhos, considerando a integral de troca isotrópicaJ

Ei

ex =−J

X

j

− →

Si ·

− →

Sj (2.19)

segue-se que somando todos os i-ésimos átomos vizinhos com todos os j-ésimos átomos vizinhos, a energia de troca total obtida é

X

i

Eexi =−J

X i X j − →

Si·−→Sj (2.20)

Eex =−J

X i X j − →

Si·

− →

Sj (2.21)

Quando os spins vizinhos fazem ângulos pequenos um com o outro, é razoavél considerar pela teoria de dom´ınios os spins como uma matriz composta por vetores clássicos, de maneira que podemos reescrever a equa¸cão anterior como se segue

He =−JS2

X

i,j

cos(φi,j) (2.22)

ent˜ao expressando o cos(φi,j) em termos dos vetores adjacentes paralelosubi eubj separados

pela distˆancia~rij

cos(φi,j) =ubi·ubj =α1iα1j +α2iα2j+α3iα3j (2.23)

onde α1, α2 e α3 são os co-senos diretores de um vetor unitário com rela¸cão aos eixos

x, y, e z, respectivamente. Desde que o ˆangulo entre os vetores unit´arios u_bi e ubj seja

pequeno, os co-senos diretores deu_bi podem ser expandidos por s´erie de Taylor em termos

do co-seno diretoru_bj. Para o primeiro termo da equa¸c˜ao 2.23:

α1iα1j =α1i

α1i+−→ri,j · ∇α1i+

1 2(

−

→_r

i,j· ∇α1i)2α1i+...

(38)

Então somando sobre todos os vizinhosj. Num cristal cúbico devido a sua alta simetria, a intera¸cão pode ocorrer em suas seis faces [6],[7] fatores como P_j−→ri,j · ∇α1i e termos

cruzados comoP_j1/2(−→ri,j · ∇α1i)2 como Pxi,jyi,j(∂2αi,j/∂xi,j∂yi,j) s˜ao zero por causa

da simetria. Sem mais delongas, como ´e o objetivo desse cap´ıtulo, pelo argumento de simetria do cristal c´ubico

X

j

x2i,j =

X

j

yi,j2 =

X

j

zi,j2 =

1 3

X

j

r2i,j (2.25)

´e obtido

X

j

cos(φi,j) =z+

1 6

X

j

r2i,jub· ∇2ub (2.26)

Levando em conta a identidade vetorial

∇2₍

b

u·u_b) = 2[(∇α1)2+ (∇α2)2+ (∇α3)2] + 2(bu· ∇2bu)

= 0

e considerando apenas o termo vari´avel da eq.(2.24) a energia de troca ´e reescrita

Eex =

JS2

6 X

j

ri,j2 [(∇α1)2+ (∇α2)2+ (∇α3)2] (2.27)

Para redes de Bravais, bcc e fcc a express˜ao P_jr2

i,j = 6a2, ondea ´e o parˆametro de rede.

Conduzindo a energia de troca de uma célula unitária com parâmetro de rede, a

Eex =JS2a2[(∇α1)2+ (∇α2)2+ (∇α3)2] (2.28)

Lembrando que a célula unitária cúbica bcc tem 2 átomos por célula unitária e a fcc 4. Dessa maneira, usando o conceito de célula de simula¸cão, para a fase final da discretiza¸cão da eneria de troca; pelo qual uma célula cúbica de lado d, constituida por um conjunto N de subcélulas com parâmetro de rede a e expresso através de N = (d

a)

3_{. Explicitando}

(39)

Eex =N JS2a2

X

mnk

dα1(m, n, k)

dx

2

+

dα2(m, n, k)

dx

2

+

dα3(m, n, k)

dx

2

+

dα1(m, n, k)

dy

2

+

dα2(m, n, k)

dy

2

+

dα3(m, n, k)

dy

2

+

dα1(m, n, k)

dz

2

+

dα2(m, n, k)

dz

2

+

dα3(m, n, k)

dz

2

e após uma pequena manipula¸cão algébrica da equa¸cão anterior, obtemos a densidade de energia de troca entre duas células unitárias

Eexc

d3 =

A d2

X

i,j

1−1µ_bi·bµj

(2.29)

onde A´e conhecida como rigidez de troca

A= 2JS

2

a (2.30)

e o vetor unitário µ_b está associado ao momento magnético da célula de simula¸cão que representa a dire¸cão média dos momentos na magnitude do comprimento de troca em que os mesmos podem ser considerados paralelos. E a soma da densidade de energia para as células de simula¸cão segue a mesma filosofia do Hamiltoniano de Heisenberg, onde a soma é empregada apenas para os primeiros vizinhos.

2.3.3 Energia de Anisotropia Uniaxial por C´

elula

Como derivada anteriormente por razões especificamente fenomenológicas, a energia anisotrópica uniaxial é escrita da seguinte maneira

Ea=KV sen2(θ) (2.31)

(40)

da c´elula de simula¸c˜ao V =d3_{, e obter a densidade de energia discretizada}

Ea

d3 =Ksen

2₍_θ₎ _(2.32)

2.3.4 Energia Zeeman por c´

elula

Através da filosofia da célula de simula¸cão, a energia Zeeman não é mais resultante da intera¸cão de um momento de dipolo atômico sob a a¸cão do campo magnético externo, mas sim é o produto da a¸cão do campo magnético empregado na célula de simula¸cão representante cont´ınuo de todos os momenta que a compõe, ou seja o torque é estudado de acordo com as rota¸cões da célula de simula¸cão. De sorte que basta escrever a densidade de energia Zeeman por célula

1

d3EZeeman =H.M~ S

X

i

ˆ

mi (2.33)

2.3.5 Energia de Interface por c´

elula

A a¸cão do campo de interface é empregada apenas na primeira camada z = 1 do ferro-magneto para modelar a intera¸cão provocada pelo antiferroferro-magneto, sua representa¸cão discretizada segue a mesma forma da energia Zeeman, onde é independente da célula de simula¸cão

Ez=1

IN T

d3 =−H~IN T.MS

X

i

ˆ

mi (2.34)

2.3.6 Energia Magnetost´

atica por c´

elula

Para discretizar a energia magnetost´atica, basta tomar a energia escrita por ´atomo, com escrita abaixo para relembrar a sua forma

Edip =

M2

SV2

2 X

i

X

k

~si.~sk

r3

ik

−3(~si.~rik)(~sk.~rik)

r5

ik

(41)

e reescrevê-la em fun¸cão da célula de simula¸cão por meio da substitui¸cão do vetor ~rik

que representa a distância entre dois momentos magnéticos i e k, por ~nd, e também reescrevendo o volume através da aresta do cubo de simula¸cão V = d3_{, segue-se que a}

energia de intera¸cão dipolar interatômica é escrita como a energia dipolar de intera¸cão intercélulas de simula¸cão.

Edip =

M2

Sd6

2d3

X

i

X

k

ˆ

µi.µˆk

n3

ik

−3(ˆµi.~nik)(ˆµk.~nik)

n5

ik

i representa a partir de agora a localiza¸cão das células unitárias na rede do sistema e admite todas as posi¸cões. E k seus vizinhos dipolares é todo o sistema. O termo 2 na fra¸cão corrige a somatória para evitar contagem dupla das energias do sistema. A figura 2.3 mostra a representa¸cão de uma célula cristalina, a célula de simula¸cão e o sistema magnético. Ou seja, a densidade de energia magnetostática por célula de simula¸cão é:

Edip

d3 =

M2

S

2 X

i

X

k

ˆ

µi.µˆk

n3

ik

− 3(ˆµi.~nik)(ˆµk.~nik)

n5

ik

(42)

(43)

2.3.7 Energia total por c´

elula

De mãos das dicretiza¸cões realizadas nas subse¸cões anteriores, a densidade de energia total a que estarão submetidas as nanoestruturas que serão estudadas no próximo cap´ıtulo é

ETV =

A d2 X j X k

(1−mˆj.mˆk)−MSH~IN T.

X

j

ˆ

mj−

MSH.~

X

j

ˆ

mj−K

X

j

(mx j)

2₊ _(2.35)

M2 S 2 X j X k ˆ

mj.mˆk

n3

jk

− 3( ˆmj.ˆnjk)( ˆmk.nˆjk)

n5

jk

!

o que leva a conclusão da se¸cão sobre a aboradagem escolhida para representa¸cão da energia.

2.4 Campo M´

edio Local Sobre C´

elulas

´

E satisfatório utilizar a defini¸cão de campo magnético efetivo como o divergente da den-sidade de energia total em fun¸cão do momento, de maneira geral

~ Hi

ef =−

1

MS

∂ET

∂mˆp_i (2.36)

Onde p indica a dire¸c˜ao x, y e z do campo local. Derivando o campo efetivo a partir da densidade de energia total

~

Hef =H~_{i exc}p +H~_{i Zee}p +H~_{i IN T}p +H~_{i Anis}p +H~_{i Dip}p (2.37)

~

Hef = _MA_S_d2

P

jmb p

j +H~ +H~IN Ti + 2 K MSmˆ

x₊_H~p

i Dip (2.38)

(44)

2.4.1 Campo Dipolar

O campo dipolar possui a caracter´ıstica de ser um campo de longo alcance, de maneira que cada célula de simula¸cão interage com todas as outras células que compõe a nanoestrutura. Então derivando as componentesx, yez do campo magnetostático, são respectivamente:

~ Hx

i Dip=MS

X

k

3nx

ik(mxknxik+m y kn

y

ik+mzknzik)

n5 ik −m x k n3 ik (2.39) ~

H_{i Dip}y =MS

X

k

3ny_ik(mx

knxik+m y kn

y

ik+mzknzik)

n5 ik − m y k n3 ik (2.40) (2.41) ~ Hz

i Dip =MS

X

k

3nz

ik(mxknxik+m y kn

y ik+m

z knzik)

n5 ik − m z k n3 ik (2.42)

(45)

(46)

2.5 O M´

etodo Auto Consistente

O cálculo numérico deste trabalho possui como objetivo apresentar as poss´ıveis estruturas de equil´ıbrio para nanodiscos e nanoelementos de base quadrada de mesma área deF e e

P y, com base nas energias que foram apresentadas nas subse¸c˜oes anteriores, associadas a equa¸c˜ao do torque escrita abaixo

d ~M

dt =−γ ~M ×H~ef (2.43)

sob a filosofia do Método Auto Consistente desenvolvido no GMM (Grupo de Magnetismo e Materiais Magnéticos). O Método Auto Consistente é apresentado de maneira simplifi-cada, mas não deixando de lado as principais caracter´ısticas de sua filosofia, através dos seguintes passos:

1. Inicialize o sistema com uma configura¸c˜ao magn´etica.

2. Calcule o campo efetivo local sobre cada c´elula.

3. Compare o valor calculado para a configura¸cão magnética obtida pela equa¸cão do torque em rela¸cão a uma tolerância.

4. Se o torque for menor ou iqual a tolerância, então, aceite a configura¸cão.

5. Se o torque for maior do que a tolerância, então, os momentos são alinhados com o campo efetivo local, então, retorne ao passo 2.

(47)

Cap´ıtulo 3

Forma¸c˜

ao de V´

ortices em

Nanodiscos de Fe e Py

3.1 Introdu¸c˜

ao

O rescente conceito de Spintronica, surgiu quando come¸cou a se levar em conta que a corrente elétrica não carrega apenas carga mas também spin por meio de seus consti-tuintes. Abrindo uma quantidade imensa de poss´ıveis aplica¸cões para a indústria de nanomagnetismo e nanoestruturas, possibilitando aos pesquisadores insteressados em na-noestruturas de baixa dimensionalidade, construir instrumentos nanoestruturados com propriedades magnéticas espec´ıficas para a solu¸cão de problemas espec´ıficos. Um tipo de nanoestrutura de interesse para aplica¸cões são as que apresentam forma¸cão de vórtices, se apresentam como grandes candidatos para a estrutura de oscila¸cão de nano-osciladores, por mostrarem oscila¸cões mais coerentes e com potência emitida maior quando compara-dos aos mocompara-dos de oscila¸cão uniformes e ainda mais não necessitam de aplica¸cão de campo magnético externo, o que reduz a complexidade das poss´ıveis aplica¸cões. [8] O vórtice não é apenas uma estrutura derivada teoricamente através de equa¸cões como a equa¸cão de

(48)

Thiele [9] ou produto resultante de simula¸cões numéricas. Sua observa¸cão experimental é o que viabiliza o estudo teórico e experimental dessas nanoestruturas e consequente-mente suas poss´ıveis aplica¸cões. Grandes grupos como o NIST apostam na possibilidade de aplica¸cões em telefones celulares, emissores de radar, chipes de computador [10]; e ainda no desenvolvimento de tecnologias para wireless [11], por exemplo, medidas foram feitas para um nano-oscilador desenhado pelo grupo de pesquisa do Army Research Lab-oratory em colabora¸cão com pesquisadores do NIST, mostrando que os nano-osciladores já atingem uma frequência emitida na ordem de terahertz, embora desmonstrem pouca eficiência. [12] Antes de iniciar o estudo da dinâmica de vórtice através de uma corrente polarizada em spin derivada por Slonckzewski, que não será apresentado no presente tra-balho, é imprecind´ıvel estudar e determinar as principais caracter´ıticas fenomenológicas dos pré-candidatos a nano-osciladores no estado de remanência. Neste trabalho serão apresentados dois desses pré-candidatos.

Apresentamos um estudo de forma¸cão de vórtice em nanodiscos e nanoelementos de base quadrada de Fe (Ferro) e Py (Permaloy). Para pequenas dimensões, os nanoelementos circulares apresentam o diâmetro do núcleo do vórtice menor do que os nanoelementos de base quadrada com mesma área. Para um intervalo de área variando entre 1900nm2

e 6700nm2_{, o tamanho do n´}_{ucleo do v´ortice para os nanoelementos com 30}_nm _{de altura}

variam de 32nma 36nmpara o Fe e entre 36nm e 48 para o Py.

3.2 Efeitos de correla¸c˜

ao magn´

etico e geom´

etrico dos

nano-elementos

(49)

CAPÍTULO 3. FORMAÇ ÃO DE V ÓRTICES EM NANODISCOS DE FE E PY 35

do nano-elemento e é este segundo que é visto como elemento central de estudo para o desenvolvimento de nano-osciladores.[13] O perfil magnético do núcleo do vórtice confi-nado em nanoestruturas é relevante para um grande número de fenômenos de interesse, e manipular o núcleo do vórtice é a chave para um conjunto de aplica¸cões fundamen-tadas. Entre elas temos: nano-osciladores emissores de microondas, quando excitado por uma corrente polarizada em spins; o estudo das oscila¸cões de vórtices quando há aparec-imento de vórtice por passagem de corrente em nano-contatos metálicos[14]; intera¸cão entre vórtices em nano-estruturas dispostas em camadas ou distribu´ıdos em uma matriz [15], etc. O tipo de confinamento leva a consideráveis mudan¸cas na forma e no tamanho do núcleo do vórtice [16]. Os efeitos dipolares são fortemente dependentes da forma por seu caráter de longo alcance, de maneira que os efeitos de confinamento provocados no núcleo do vórtice em nanodiscos são diferentes dos efeitos provocados por nano-estruturas de base quadrada. Ainda mais, o acoplamento de troca em nanoelementos ferromagnéticos para um subtrato antiferromagnético com alta anisotropia uniaxial, favorecerá na camada em contato com o plano de interface uma tendencia de forma¸cão de vórtice no nano-elemento como um todo [17], [18], [19]. Assim, para nanoelementos com altura baixa, a superf´ıcie polarizada deve conduzir a um perfil magnético dependente dela. Neste cap´ıtulo apre-sentaremos um estudo da estrutura de equil´ıbrio de nano-estruturas de Fe e Py com área superficial pequena (aresta = diâmetro<100nm) que nucleiam vórtice. Foi considerada a altura de 30nm e variada a área superficial do nano-elementos de 1936nm2 _{a 6724}_nm2_.

O Permaloy é um material composto por dois elementos, o Ferro e o N´ıquel, em nossas simlu¸cões estaremos usando a liga de Permaloy com as seguintes propor¸cões, 20% de Ferro e 80% de N´ıquel. A razão para se escolher nanoelementos planos é que se pode analizar dois aspectos de correla¸cão para a determina¸cão do comportamento magnético no estado de equil´ıbrio, o confinamento e a tendência da interface. Os nanoelementos com 30nm

(50)

remanência a partir da camada de interface até a camada livre na superf´ıcie. Apresen-tamos o impacto das dimensões laterais sobre todo o rearranjo dos spins para minimizar o campo dispersivo que é maior em nanoelementos circulares. Para nano-elementos com mesma área e altura o raio do núcleo do vórtice é menor para os nanodiscos do que para os nanoelementos de base quadrada. A diferên¸ca se torna insignificante para nano-elementos com dimessões bem superiores ao comprimento de troca. E o estado de vórtice do na-noelemento de Py é mais suscept´ıvel a polariza¸cão de interface do que os nana-noelementos de Fe.

3.3 Modelo Te´

orico

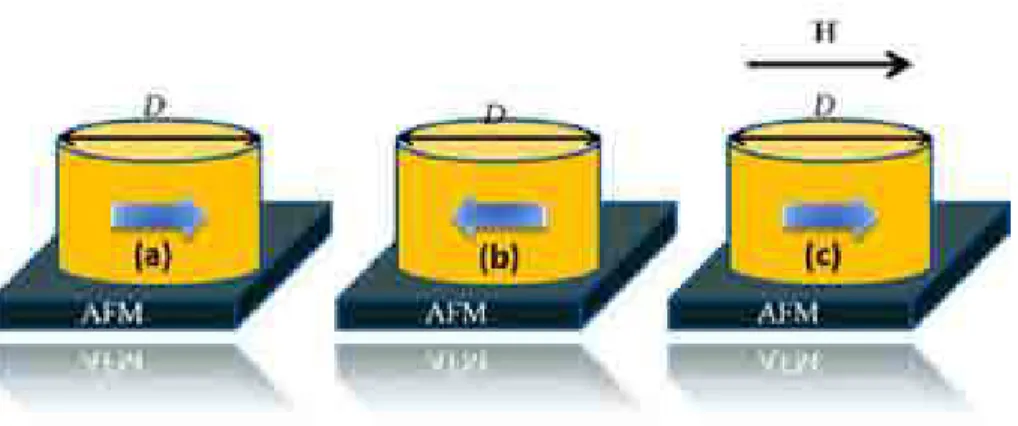
Figura 3.1: Figura esquemática de um nanodisco com anisotropia uniaxial no plano (x,y) em um substrato antiferromagnético, (a) e (b) são poss´ıveis configura¸cões magnéticas para o nanodisco na ausência de campo e (c) é a configura¸cão magnética com o campo magnético de satura¸cão no plano (x,y).

(51)

densidade de energia dada por

ETV =

A d2

X

j

X

k

X

j

ˆ

mj−

MSH.~

X

j

ˆ

mj−K

X

j

(mx j)

2₊ _(3.1)

M2

S

2 X

j

X

k

ˆ

mj.mˆk

n3

jk

n5

jk

!

onde o primeiro termo é a energia de troca com intera¸cão realizada entre os primeiros vizinhos e A é a rigidez de troca ferromagnética. O segundo termo é a energia de interface, modelada através da a¸cão do campo de interfaceHIN T para o material antiferromagnético

com a soma restrita a primeira camada de células do elemento ferromagnético. O terceiro é a energia Zeeman, o quarto a energia de anisotropia uniaxial e o quinto é a energia magnetostática. Ms é a magnetiza¸cão de satura¸cão, K é a constante de anisotropia

uniaxial que possui unidades de densidade de energia por volume, ˆmi ´e a dire¸c˜ao do

momento magnético da i-ésima célula enij é a distância entre as célulasiej em unidades

dos tamanhos da c´elulad.

Os parˆametros usados para a simula¸c˜ao foram: para o Ferro, usamosMs = 1.7×106A/m,

A = 2.5 ×10−11_J/m _e _K _{= 2}_.₅_× ₁₀−11_J/m_{, para o Permaloy foram usadas,} _M

s =

0.8×106_A/m_, _A_{= 1}_.₃_×₁₀−11_J/m_e_K _{= 0. O valor do campo m´edio aplicado foi usado}

para achar a configura¸cão de equil´ıbrio num conjunto de dire¸cões em todas as células ( ˆmi, i = 1, ..., N) que faz o torque ser inferior a 10−26J[19], [20]. Obtemos o padrão

(52)

3.4 Pr´ıncipais resultados

As diferen¸cas da estrutura magnética do núcleo do vórtice para nanoelementos de bases circular e quadrada de áreas iguais é resultado do reajustamento das densidades de cargas de magnetiza¸cão superf´ıcial e volumétrica próximos as áreas laterais. Como mostrado nas figuras 3.2 e 3.3, próximo as bordas dos nanoelementos quadrados, existem fortes mudan¸cas na componente perpendicular da magnetiza¸cão local. A nuclea¸cão de

esta-Figura 3.2: Magnetiza¸cão de nanoelementos de Fe com 30nm de altura:(a)quadrado com 48nm de dimensao lateral e (b)circular com 54nm de diâmetro. Ao lado da curva de remanência é apresentado a estrutura do núcleo do vórtice para os nanoelementos, a barra em cores é usada para mostrar a varia¸cão da componente z da magnetiza¸cão.

(53)

Figura 3.3: Estrutura magnética selecianada de alguns pontos da figura 3.1. A barra em cores mostra a varia¸cão da componente z da magnetiza¸cão e as linha cont´ınuas, nos painéis (b),(c) e (e) separa as áreas com cargas opostas da componente z do campo local.

estado de vórtice centralizado em remanência. O estado uniforme dos nanodiscos é estável partindo da satura¸cão com campo de 4kOe até aproximadamente 2kOe onde um vórtice é formado fora do centro. Deste ponto até o valor de campo externo nulo o vórtice se desloca em dire¸cão ao centro do nanoelemento. De maneira geral o impacto da energia dipolar é maior em nanodiscos de Py, fazendo o diâmetro do núcleo do vórtice variar mais do que nos outros nanoelementos analizados, como mostrado na tabela 3.1.

(54)

elemento sem a presen¸ca do campo de interface possui o núcleo de vórtice centrado e com 44nm de diâmetro, já o nanoelemento com campo de interface de 10kOepossui o núcleo do vórtice descentralizado, da camada inferior na interface até a camada superior. Para o Fe o campo dipolar é mais forte e consequêntemente o estado de vórtice é mais estável do que para o Py. As mudan¸cas promovidas pelo campo de interface de 10kOesão menores em rela¸cão ao nanoelemento sem o campo de interface. A camada superior continua com o núcleo do vórtice centralizado ao nanoelemento em quando que a camada acoplada ao substrato antiferromagnético tem o vórtice deslocado pelo campo de interface.

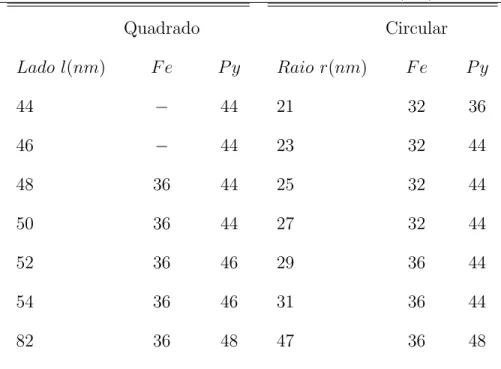
Tabela 3.1: Diâmetro do núcleo do vórtice (nm). Quadrado

Lado l(nm) F e P y

44 − 44

46 − 44

48 36 44

50 36 44

52 36 46

54 36 46

82 36 48

Circular

Raio r(nm) F e P y

21 32 36

23 32 44

25 32 44

27 32 44

29 36 44

31 36 44

(55)

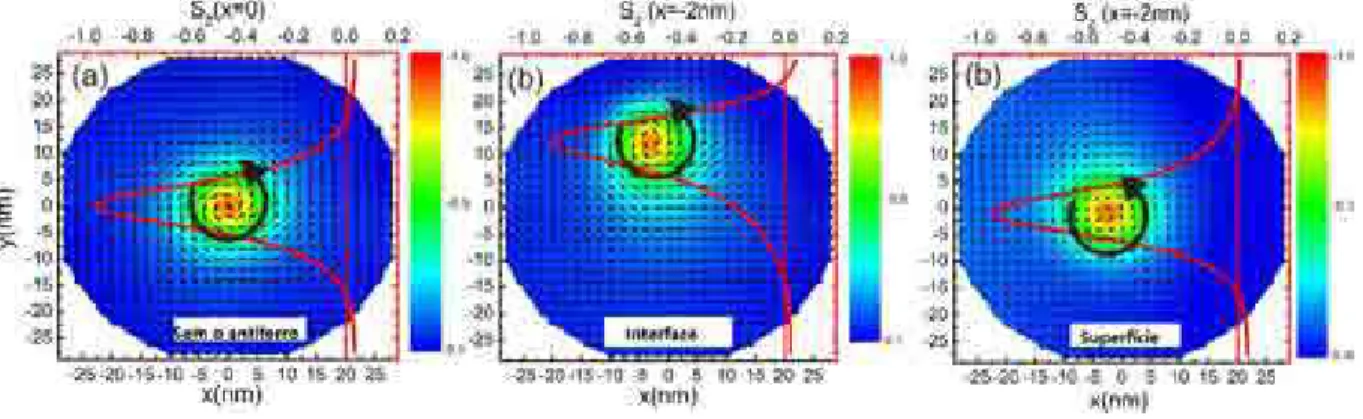
Figura 3.4: Estrutura magnética do núcleo do vórtice (a) sem o substrato antiferro-magnético e (b) com o substrato antiferroantiferro-magnético para um nanoelemento de Py com 30nm de altura e 62nm de diâmetro. A barra colorida mostra a componente z da mag-netiza¸cão e a linha cont´ınua representa Sz no núcleo do vórtice em (a) x = 0nm e (b)

x=−6nm na camada da superf´ıcie.

Figura 3.5: Estrutura magnética do núcleo do vórtice (a) sem o substrato antiferro-magnético e (b) com o substrato antiferroantiferro-magnético na interface e (c) na superficie para um nanoelemento de Fe com 30nm de altura e 62nm de diâmetro. A barra colorida mostra a componente z da magnetiza¸cão e a linha cont´ınua representa Sz no núcleo do vórtice

(56)

3.5 Conclus˜

ao

Partindo dos resultados obtidos das simula¸cões micromagnéticas, foram estudados os im-pactos do efeito de forma em nanoelementos de Fe e Py com geometria circular e quadrada e do campo de interface na estrutura do núcleo do vórtice. Dos quais foram observados, que a estrutura de vórtice assim como sua forma¸cão a partir do campo de satura¸cão até o estado de remanência são diferentes para as duas geometrias, fato relacionado pela maior atua¸cão do campo dispersivo nos nanodiscos do que nos elementos quadrados. Os nan-odiscos apresentaram de maneira geral o diâmetro do núcleo do vórtice menor do que os quadrados como mesma área superficial. Foram ainda comparados nanodiscos com 62nm

(57)

Cap´ıtulo 4

Efeitos de forma¸c˜

ao de v´

ortice em

pares de nanodiscos

4.1 Introdu¸c˜

ao

A observa¸cão direta de vórtice magnético em nanoelementos micrométricos e nanométricos apontam para um grande número de poss´ıveis aplica¸cões em dispositivos eletrônicos.[23],[26] Discos micrométricos que apresentam nuclea¸cão de vórtice no estado de remanência é um componente promissor para uso em meios de grava¸cão e armazena-mento de dados. Esta aplicabilidade é contemplada pela própria natureza do microele-mento, magneticamente apresenta dois estados degenerados associados a componente não uniforme da magnetiza¸cão, a polaridade do núcleo do vórtice, que pode apresentar polar-idades, p = +1 para “up”, ou p = −1 para “down”, e estes estam relacionados aos bits “1”e “0”respectivamente.[24],[28] De mesma maneira a observa¸cão direta de nuclea¸cão de vórtice em elementos nanométricos aponta para uma nova possibilidade de constru¸cão de nano-osciladores, para a constru¸cão de transmissores e receptores de microondas a serem aplicados em telefones celulares, comunica¸cão sem fio “wireless”, sistemas de radar, etc;

(58)

compat´ıveis e consequentemente integrados a sistemas semi-condutores.[21],[30],[31] Sin-croniza¸cão é a palavra que representa o limiar para a constru¸cão de meios de grava¸cão e armazenamento e também aplica¸cão em nano-osciladores. Nanoelementos não intera-gentes vem sendo estudados através de campo magnéticos aplicado e recentemente por meio de corrente de spins polarizados que provocam torque na estrutura do núcleo do vórtice, mostrando que é uma estrutura magnética controlável. A oscila¸cão do vórtice está relacionada com o modo girotrópico, este, é definido como o movimento translacional feito pelo núcleo do vórtice ao redor do centro do nanoelemento quando submetido a a¸cão de um campo magnético ou corrente polarizada em spins, desde que possuam magnitude suficiente para mover o núcleo do vórtice sem projetar o sistema global a um novo estado magnético não nucleado por vórtice.[26],[29],[32] A sincroniza¸cão do modo girotrópico de vários nanoelementos interagentes é a chave para a potencializa¸cão da emissão em microondas pelos nano-osciladores.[21],[22].

Elementos nanométricos mostram por meio de simula¸cão numérica e através de exper-imentos que a estrutura do núcleo do vórtice é consequência do tipo de confinamento geométrico, como mostrado através dos resultados do cap´ıtulo 3. Permanecendo na mesma linha de racioc´ınio, no entanto, não na mesma filosofia. A posi¸cão que os nanoelementos estão uns em rela¸cão aos outros é um parâmetro importante para o estudo dos estados magnéticos aos quais irão se induzir por meio da intera¸cão, ou seja, assim como nanoele-mentos interagentes colineares ao longo de eixo z apresentam comportamento diverso de um nanoelemento livre (não-interagente com outro nanoelemento), também apresentam diferen¸cas de comportamento de nanoelementos interagentes organizados em uma matriz por exemplo, como será mostrado no estudo ainda simplório deste cap´ıtulo.

(59)

quirali-CAPÍTULO 4. EFEITOS DE FORMAÇ ÃO DE V ÓRTICE EM PARES DE NANODISCOS 45

dade c, esta é consequência de rota¸cão conjunta dos momentos magnéticos do elemento, se a rota¸cão for sentido horário, c=−1, se for no sentido anti-horário, então, c= +1. Para dois discos colineares em rela¸cão ao eixo z, existem quatro estados magnéticos possiveis relacionados a polaridade p e a chiralidade c.[24],[27],[28] A intera¸cão magnetostática e o confinamento lateral influenciam os estados magnéticos dos nanoelementos interagentes tanto em remanência quanto influenciam suas propriedades dinâmicas.[36],[39],[40],[41] Dessa forma um estudo prévio para encontrar o estado remanente em discos interagentes de Fe e Py é pertinente e necessário antes de partir para o estudo das propriedades dinâmicas dos modos girotrópicos sincronizados através do mecanismo de Slonczewski[32], de corrente polarizada em spins.

4.2 Modelo Te´

orico

(60)

Assim como o corpo principal desse trabalho, o objetivo deste cap´ıtulo é apresentar resul-tados provenientes de simula¸cões numéricas. Neste cap´ıtulo o ambiente muda, no cap´ıtulo 3 o estudo foi concentrado no impacto do efeito de forma do nanoelemento em rela¸cão ao estado magnético com nuclea¸cão de vórtice, onde o termo geral de energia foi escrito da seguinte maneira

ETV =

A d2 X j X k

X

j

ˆ

mj−

MSH.~

X

j

ˆ

mj−K

X

j

(mx

j)2+ (4.1)

M2 S 2 X j X k ˆ

mj.mˆk

n3

jk

n5

jk

!

em que o primeiro termo é a energia de troca, o segundo e o terceiro são as energias Zeeman e de Anisotropia Uniaxial, o quarto é a intera¸cão de interface e o quinto é a intera¸cão magnetostática. Baseado na equa¸cão anterior é poss´ıvel construir o termo total de energia para dois nanoelementos interagentes magnetostáticamente. Como primeiro passo não existirá camada para representar a intera¸cão de interface, então, podemos fazer

~

HIN T = (0,0,0) resultando simplesmente na equa¸c˜ao

ET =

A d2 X j X k

(1−mˆj.mˆk)−

MSH.~

X

j

ˆ

mj −K

X

j

(mx j)

2₊ _(4.2)

M2 S 2 X j X k ˆ

mj.mˆk

n3

jk

− 3( ˆmj.nˆjk)( ˆmk.ˆnjk)

n5

jk

!

O próximo passo, será considerar dois nanoelementos interagentes, o q-ésimo nanoele-mento e o v-ésimo nanoelenanoele-mento, separados por uma distância ~rqv -que é a distância