Problemas elípticos com expoente crítico e potencial de Hardy

(1)

Universidade Federal de Minas Gerais Instituto de Ciˆencias Exatas Departamento de Matem´atica

Problemas el´ıpticos com expoente cr´ıtico e

potencial de Hardy

Daiane Campara Soares

(2)

(3)

Universidade Federal de Minas Gerais Instituto de Ciˆencias Exatas Departamento de Matem´atica

Problemas el´ıpticos com expoente cr´ıtico e

potencial de Hardy

Daiane Campara Soares

Dissertação apresentada ao Departamento de Matemática do Instituto de Ciências Exa-tas da Universidade Federal de Minas Gerais, como requisito parcial para a obtenção de t´ıtulo de Mestre em Matemática.

Orientador: Prof. Dr. Ronaldo B. Assunc¸˜ao

(4)

Problemas el´ıpticos com expoente cr´ıtico e potencial de Hardy

xiv + 74 páginas. Dissertação (Mestrado) — Universidade Federal de Minas Gerais, Instituto de Ciências Exatas, Departamento de Ma-temática

1. Operador laplaciano. 2. Potenciais de Hardy.

3. Expoente cr´ıtico de Sobolev. 4. Problemas de minimizac¸˜ao.

(5)

(6)

(7)

(8)

(9)

Agradecimentos

A Deus, por sempre estar ao meu lado e por cuidar de mim em todas as horas.

Aos meus pais, José Pedro e Leange, pela educação, por todo amor, por todo esforço para que eu conquistasse meus objetivos e pelo constante incentivo e apoio.

Aos meus irm˜aos, Deise, Denise e Daniel, bem como aos meus sobrinhos, Pedro Henrique, Julia, Gabriel, Nataly e Maria pelo encorajamento e incentivo.

Ao Prof. Ronaldo Brasileiro Assunção, pelos ensinamentos matemáticos e por ter me orien-tado com muita paciência, competência e imensa dedicação.

A Comissão Avaliadora, pela atenção dada ao trabalho e pelas sugest ões valiosas.

Ao professor Carri˜ao, pela sua disponibilidade em auxiliar sempre.

Ao meu namorado Guilherme, pelo seu apoio, amor, atenção, sua inesgotável paciência e disposição em me ajudar.

Aos amigos e professores da Universidade Federal de Santa Maria, em especial aos pro-fessores Maur´ıcio Fronza da Silva, João Batista Peneireiro, Márcio Miotto e Ta´ısa Miotto, pelas oportunidades, por sua enorme atenção e principalmente por acreditarem em meu trabalho e participarem do meu desenvolvimento, mesmo de longe, auxiliando-me sempre.

Aos amigos daqui de Belo Horizonte que em sua maioria conheci durante o mestrado, Flávia, Luciana, Willian, Silvia, Natália, Amanda, Charles, Carlos e José. Obrigada pela com-panhia nos estudos, pelas brincadeiras descontra´ıdas e especialmente pela amizade. Sucesso a todos!

Ao meu amigo Leonel, agradeço por toda compreensão, por todas as situaç ões que enfren-tamos, especialmente pela amizade e ajuda para que esse trabalho pudesse ser realizado.

Aos meus amigos do sul, que mesmo distantes, sempre estiveram presentes me incenti-vando, em especial Marcela, Rian, Carolina, Aline Armanini, Aline Alves, Aline Machado, Danilo, Leonardo e Itaianan.

(10)

Nesta dissertação estudamos resultados de existência e de não-existência de soluç ões para a seguinte classe de problemas el´ıpticos não-lineares:

          

−∆_u(x)₋λu(x)₋µu(x)

|x|2 =u(x)2 ∗₋₁

, x∈Ω_,

u(x)>0, x_∈Ω_,

u(x) =0, x∈∂Ω_,

(P)

em queΩ _⊂RN _{denota um conjunto aberto contendo a origem, limitado ou n˜ao, com}_N >_4.

A equação diferencial envolve o expoente 2∗ = 2N/(N−2), conhecido como expoente cr´ıtico de Sobolev e o termoµu(x)/_|x_|2_{, que é chamado potencial de Hardy.}

Procuramos soluç ões para o problema (P) no espaço de Sobolev H₀1(Ω) definido como o fecho de C∞₀ (Ω)em H1(Ω). Para obter resultados de existência de soluç ões demonstramos uma versão do Lema de Concentração-Compacidade de Lions.

Palavras-chave Operador laplaciano, potenciais de Hardy, expoente cr´ıtico de Sobolev,

proble-mas de minimizac¸˜ao.

Abstract

In this dissertation we study results of existence and non-existence for the following class of nonlinear elliptic problems:

          

−∆u(x)₋λu(x)₋µu(x)

|x_|2 =u(x)2 ∗₋₁

, x∈Ω,

u(x)>0, x∈Ω,

u(x) =0, x_∈∂Ω_,

(P)

whereΩ _⊂ RN _{denotes an open set containing the origin, bounded or not, with} _N > _{4. The}

equation involves the exponent 2∗ = 2N/(N₋2), known as critical exponent in the Sobolev inequality, and the termµu(x)/_|x|2_{, which is called Hardy potential.}

We look for solutions of the problem (P) in the Sobolev space H1

0(Ω) which is defined

as is the closure of C∞₀ (Ω) in H1(Ω). To obtain existence results we prove a version of the concentration-compactness lemma by Lions.

Key-words Laplacian operator, Hardy potentials, critical exponent of Sobolev, minimization

problems.

(11)

Nota¸c ˜oes

:= igualdade por definic¸˜ao

R+ _{conjunto dos n ´umeros reais positivos}

x= (x1, . . . ,xN) elemento deRN

|x|= ∑_iN₌₁x2_i1/2 norma do elementox ∈RN

B(x,ρ) bola aberta de raioρe centro emx∈RN

ωN ´area da bolaB(x,ρ)emRN

NωN ´area da superf´ıcie esf´erica∂B(x,ρ)emRN

p′ _≡ p

p−1 expoente conjugado de p

2∗ ≡ _N2N

−2 expoente cr´ıtico de Sobolev

∇u(x)_≡∂u(x) ∂x1 , . . . ,

∂u(x) ∂xN

gradiente da func¸˜aou

div(u1(x), . . . ,uN(x))

≡ ∂u_∂x1(x) 1

+_{· · ·}+∂uN(x)

∂xN divergente do campo(u1(x), . . . ,uN(x))

∆_u(x)_≡div∇u(x)= N

∑

i=1

∂2u(x) ∂x2

i

operador laplaciano

X∗ espac¸o dual do espac¸oX

C0₍Ω) espaço das funç ões reais cont´ınuas

Ck₍Ω) espaço das funç ões reaisk-vezes

continua-mente diferenci´aveis C∞

0 (Ω) espaço das funç ões infinitamente

diferen-ci´aveis e de suporte compacto emRN

Lp₍_Ω₎ _{espac¸o de Lebesgue}

kukLp ≡ Z

Ω|u(x)|

p_d_x1/p _{norma no espac¸o de Lebesgue}_Lp₍_RN₎

H1₍_Ω₎_{≡ {}_u_∈ _L2₍_Ω₎_:_∇_u₍_x₎_∈₍_L2₍_Ω₎₎N_} _{espac¸o de Hilbert}

ku_{k ≡} Z

Ω|∇u(x)|

2_d_x₊Z

Ω|u(x)|

2_d_x1/2 _{norma no espac¸o de Hilbert}_H1₍_Ω₎

H1

0(Ω) espac¸o de Hilbert com trac¸o nulo

un →uemX convergˆencia forte (na norma deX)

un ⇀uemX convergˆencia fraca emX

un →uq.t.p. emX convergˆencia em quase todo ponto deX H_0,1_G(Ω)_{≡ {}u∈ H₀1(Ω): u◦g=u∀g∈G} subespac¸o deH₀1(Ω)invariante porG V(Ω_,_G)_{≡ {}u∈ H_0,1_G(Ω):

Z

Ωu

2∗

(x)dx=1} v´ınculo no subespac¸oH_0,1_G(Ω)

Sµ_λ(Ω_,_G)_≡infu∈V(Ω,G)R(u) melhor constante das imers ˜oes de Sobolev

R(u)_≡ Z

Ω|∇u(x)|

2_d_x −λ

Z

Ωu

2₍_x₎_d_x −µ

Z

Ω u2₍_x₎

|x|2 dx

(12)

(13)

Sum´ario

Resumo . . . viii

Abstract. . . viii

Notac¸ ˜oes . . . ix

1 Introdu¸cão aos métodos variacionais 1 1.1 Formulação fraca de problemas el´ıpticos . . . 1

1.2 Problemas envolvendo o expoente cr´ıtico . . . 7

1.3 Problemas cr´ıticos envolvendo potenciais de Hardy . . . 11

1.4 Resultados principais . . . 13

2 Existência de solu¸c ões de energia m´ınima 17 2.1 Existência de solução em todo o espaço . . . 17

2.2 Não-existência de soluç ões em dom´ınios limitados . . . 22

2.3 Existência de solução em dom´ınios limitados . . . 32

3 Existência de solu¸c ões em dom´ınios não limitados 35 3.1 Lemas auxiliares. . . 35

3.2 Lema de concentrac¸˜ao-compacidade . . . 37

3.3 Existência de soluç ões em dom´ınios contidos em cilindros . . . 50

4 Existência de solu¸c ões em dom´ınios invariantes 55 4.1 Soluç ões invariantes . . . 55

4.2 O casod>₂ _{. . . .} ₅₅

4.3 O casod=1 . . . 58

A Resultados auxiliares 61 A.1 Espaços de Funç ões . . . 61

A.2 O grupo ortogonal . . . 62

A.3 Resultados de An´alise . . . 62

A.3.1 As notac¸ ˜oes de Landau . . . 62

A.3.2 Desigualdades . . . 63

A.3.3 Integrac¸˜ao em coordenadas polares . . . 63

(14)

A.4 Resultados de An´alise Funcional . . . 65

A.4.1 Teorema da Convergˆencia Dominada . . . 65

A.4.2 Teorema de imers˜ao de Rellich-Kondrachov . . . 65

A.4.3 Convergˆencia fraca em medida . . . 65

A.4.4 Lema de Br´ezis-Lieb . . . 66

A.4.5 O princ´ıpio variacional de Ekeland. . . 66

A.4.6 O teorema do passo da montanha . . . 66

A.5 Desigualdade de Hardy . . . 68

Bibliografia 71

´Indice Remissivo 72

(15)

-1-Introdu¸c˜ao aos m´etodos variacionais

1.1 Formula¸c˜ao fraca de problemas el´ıpticos

Esta dissertação tem como principal objetivo demonstrar resultados de existência e de não-existência de soluç ões para uma classe de equaç ões el´ıpticas não-lineares definidas em dom´ınios

Ω_⊂RN_{, limitados ou n˜ao, envolvendo o expoente cr´ıtico de Sobolev e o potencial de Hardy.}

Neste cap´ıtulo apresentamos alguns resultados básicos da teoria de minimização de funcionais, cujas referências básicas são o livro de Ambrosetti e Malchiodi [1] e o memorial de Jeanjean [9]. Assim, podemos indicar as maiores dificuldades para demonstrar os teoremas principais da dissertação que se baseiam no artigo de Ruiz e Willem [14].

Comec¸amos considerandoΩ _⊂ RN _{um dom´ınio limitado com fronteira}_∂Ω_{. Suponhamos}

que devemos resolver o seguinte problema de Dirichlet 

 

−∆_u(x) =_|u|p−2_u _x_∈_Ω_,

u(x) =0 x∈∂Ω_, (1.1)

em que ∆u(x) := ∑_iN₌₁∂2_u₍_x_)/_∂x2

i denota o operador laplaciano e p ∈ (1, 2∗], em que 2∗ := 2N/(N−2) é o expoente cr´ıtico de Sobolev. Se a funçãou: Ω _→ R_{for tal que}_u _∈ C2₍Ω)_∩ C0₍Ω)verifica o problema (1.1) pontualmente, dizemos que u é uma solução clássica do pro-blema de Dirichlet. Em geral, o propro-blema de garantir a existência de uma solução clássica para o problema (1.1) é bastante dif´ıcil. Uma forma de resolver as dificuldades encontradas é enfraquecer as condiç ões impostas sobre a funçãou. Por exemplo, podemos exigir que a pri-meira equação em (1.1) seja válida no sentido das distribuiç ões. Para prosseguir nessa linha de investigação suponhamos queu seja uma solução clássica. Dada uma função ϕ ∈ C∞

0 (Ω),

multiplicamos ambos os lados da equação diferencial em (1.1) por ϕe, integrando por partes, obtemos a equação

Z

Ω∇u· ∇ϕdx = Z

Ω|u|

p−2_uϕ_dx

∀ϕ_∈C∞

0(Ω). (1.2)

Dessa forma, uma solução clássica do problema de Dirichlet (1.1) verifica a equação (1.2). Agora podemos substituir a condição de fronteirau(x) = 0 para todox ∈ ∂Ω_{pela condição de que}

u∈ H₀1(Ω); dessa forma, temos o novo problema de determinar uma func¸˜aoutal que

   Z

Ω∇u· ∇ϕdx= Z

Ω|u|

p−2_uϕ_dx

∀ϕ∈ H₀1(Ω),

u∈ H₀1(Ω).

(1.3)

(16)

Observamos que se u _∈ H1

0(Ω), então pela densidade de C10(Ω) em H01(Ω), a equação (1.2)

vale para toda função ϕ ∈ H1₀(Ω). O problema (1.3) é conhecido como a formulação fraca do problema de Dirichlet (1.1) e suas soluç ões são denominadas soluç ões fracas. Seu é uma solução clássica e se u(x) = 0 para todo x ∈ ∂Ω_{, pontualmente, então} _u _∈ _H1

0(Ω); logo, a

funçãou é uma solução fraca do problema (1.3). Por outro lado, seu ∈ C2₍Ω) é uma solução fraca do problema (1.3), entãoué uma solução clássica do problema (1.1).

Podemos agora reconhecer que as soluç õesu 6= 0 do problema (1.3) são pontos cr´ıticos do funcional J: H1

0(Ω)→Rdefinido por

J(u):= 1 2

Z

Ω|∇u|

2_dx − 1_p

Z

Ω|u|

p_dx_. _(1.4)

De fato, usando resultados conhecidos do cálculo variacional em espaços de Banach, temos que o funcionalJ, denominado funcional de energia , é diferenciável e que o operadorJ′: H₀1(Ω)_→ (H₀1(Ω))∗ _{é dado por}

J′(u)ϕ= Z

Ω∇u· ∇ϕdx− Z

Ω|u|

p−2_u_ϕ_dx_. _(1.5)

Portanto, a obtenção de soluç ões clássicas para (1.1) será feita utilizando o seguinte método: primeiro demonstramos a existência de soluç ões fracas para o problema (1.3), utilizando o fun-cionalJ(u); e em seguida usamos resultados de regularidade, que garantem que as soluç ões fra-cas de fato possuem a diferenciabilidade requerida para que sejam também soluç ões clássifra-cas. Nesta dissertação tratamos apenas dos resultados de existência de soluç ões fracas; para a parte da regularidade das soluç ões fracas referimos aos trabalhos de Brézis [4, Caps. 8 e 9] e de Evans [7, Cap. 6].

Para ilustrar as principais dificuldades encontradas ao aplicar o programa descrito acima, conhecido como método direto do cálculo das variaç ões, distinguimos três casos bastante dis-tintos e dependentes do parâmetro p, que indica o crescimento da não-linearidade da equação diferencial. Na discussão que se segue, trabalhamos com o espaço H1

0(Ω)munido da norma

do gradiente, isto é, kuk = (R_Ω_|∇u|2_dx₎1/2_{. Pela desigualdade de Poincaré, essa norma é}

equivalente `a norma usual de H1

0(Ω). Lembramos também que a imersãoH01(Ω)֒→ Lp(Ω) é

cont´ınua sep ∈[1, 2∗]e ´e compacta se p∈[1, 2∗).

A seguir analisamos alguns resultados de existência e de não-existência de solução para o problema (1.3) dependendo da potência do termo não linear. Como um comentário geral, analisamos apenas os casos em quep∈[1, 2∗_]_{pois assim podemos garantir, pela continuidade}

da imers˜aoH1

0(Ω)֒→Lp(Ω), que o funcional de energiaJ est´a bem definido emH01(Ω).

CASO 1: p ∈ [1, 2). Como a imers˜ao H₀1(Ω) ֒→ Lp(Ω) ´e cont´ınua, existe uma constante C,

dependente apenas dep, tal que|u_|p6Ckukpara toda func¸˜aou∈ H₀1(Ω). Assim temos que

J(u) = 1 2kuk

2₋ 1 p|u|

p p > 1

2kuk

2₋Cp p kuk

(17)

1.1. Formulac¸˜ao fraca de problemas el´ıpticos 3

paraku_ksuficientemente grande. Parap<2 o termo quadrático é dominante e o funcionalJ é coercivo .

Al´em disso, temos que

−∞<m:= inf u∈H1

0(Ω)

J(u)<0.

De fato, argumentando por contradição, suponhamos que exista uma sequência(un)n_∈N ⊂

H₀1(Ω)tal que J(un) → −∞. Como o funcional J é coercivo, segue-se que existe R ∈ R+ tal quekunk6R. Como o espaçoH10(Ω)é reflexivo, existe uma subsequência, ainda denotada da

mesma forma, e existe uma func¸˜aou∈ H₀1(Ω), tais queun⇀ufracamente emH₀1(Ω).

Além disso, como o funcionalJ é fracamente semicont´ınuo inferiormente , isto é, para todo α _∈ R_{o conjunto} _{_u _∈ _H1

0(Ω): J(u) > α} é aberto, inferimos que J(u) 6 lim infn∈N J(un) = −∞_{, o que é uma contradição. Para verificar que} _m < 0 selecionamos uma função u ∈ H1

0(Ω)\{0}e testamos o funcionalJem func¸ ˜oes da formatu, comt∈ R+. Assim, temos

J(tu) = t

2

2kuk

2 − t

p

p |u| p p.

Comop<2, a contribuição da parcela negativa de J é dominante quandot →0 e isso implica quem<0.

Para garantir que o ´ınfimo m é atingido, isto é, para demonstrar que existe uma função u ∈ H₀1(Ω)tal que J(u) = m, argumentamos da seguinte forma: Seja(un)n∈N ⊂ H₀1(Ω)uma

sequência minimizante , isto é, uma sequência tal que J(un) _→ mquandon _→ ∞. Como J é coercivo, a sequência(un)n∈N é limitada no espaço reflexivo H₀1(Ω). Dessa forma, existe uma

subsequência, ainda denotada da mesma forma, e existe uma funçãou∈ H1₀(Ω)tal queu⇀u fracamente emH₀1(Ω). Pela compacidade da imersão H1₀(Ω) ֒→ Lp(Ω), novamente passando a uma subsequência obtemos a convergência forteun→uemLp(Ω). Portanto,

m6 _J(u)6_{lim inf}

n→∞ J(un) =m.

Como o m´ınimo do funcional J é atingido, conclu´ımos que o ponto de m´ınimo corresponde a uma solução fraca do problema (1.3).

CASO2: p=2. Nesse caso o problema ´e linear e se escreve na forma

  

−∆_u(x) =λu x ∈Ω_,

u(x) =0 x ∈∂Ω_, (1.7)

(18)

1.1 Proposi¸c˜ao. 1. O problema(1.7)possui uma sequˆencia de autovalores(λn)n_∈N ⊂R+tal que

0<λ1<λ2 6λ36· · ·6λn6λn+16· · · e lim

n→+∞λn= +∞.

Na desigualdade acima usamos a conven¸cão de que autovalores m últiplos são repetidos de acordo com suas multiplicidades. O primeiro autovalorλ1é simples, ou seja, tem multiplicidade igual a um e a correspondente autofun¸cão não muda de sinal no dom´ınioω⊂R_{. Além disso, o autovalor}

λ1 é o único autovalor com essa propriedade. É comum denotar a primeira autofun¸cão por φ1 e selecioná-la de modo queφ1(x)> 0para todo x ∈Ωe tal quekφ1kL2 = 1. Correspondendo aos demais autovaloresλk, as correspondentes autofun¸cões são denotadas porφne são tais que

Z

Ωφnφmdx =   

1 se n=m

0 se n₆=m.

2. Vale a igualdade

λ1 min

u∈H1 0(Ω) u(x)6≡0

Z

Ω|∇u|

2_dx

Z

Ω|u|

2_dx . (1.8)

3. Definindo Wn= n

u∈ H₀1(Ω): Z

Ω∇u· ∇φmdx=0, 1

6_m6_n₋₁o_{, valem as igualdades}

λn= min u∈Wn u(x)6≡0

Z

Ω|∇u|

2_d_x Z

Ω|u|

2_d_x

para todo n∈N_.

As relaç ões dos ´ıtens2e3são denominadas de caracterizaç ões variacionais dos autovalores. Observamos também que do item2obtemos a desigualdade

λ1 6 Z

Ω|∇u|

2_d_x Z

Ω|u|

2_d_x

para toda func¸˜aou∈ H1

0(Ω)tal queu6≡0, conhecida como desigualdade de Poincar´e.

CASO 3: p ∈ (2, 2∗). O funcional J n˜ao ´e mais limitado inferiormente nesse caso. De fato,

selecionando uma funçãou∈ H₀1(Ω)_\{0}e um n úmero realt ∈R+_{, temos que}

J(tu) = t

2

2 kuk

2₋ tp p |u|

p

p → −∞ (t→∞),

(19)

1.1. Formulac¸˜ao fraca de problemas el´ıpticos 5

Além disso, J também não é limitado superiormente. Por exemplo, considerando Ω = (0,π)_⊂R_e_p₌_{4 segue-se que o funcional}_J_: _H1

0(Ω)→Rtem a forma

J(u) = 1 2

Z π

0 |∇u| 2_d_x

− 1₄

Z π

0 |u| 4_d_x_.

Escolhendou0(x) =sen(kx)em quek∈N, c´alculos diretos mostram que J(tu0)→∞quando t → ∞_{. Consequentemente, n˜ao existe extremo global para o funcional} _J _{e o problema de}

determinar um ponto cr´ıtico ´e mais complexo.

Uma das abordagens frequentemente usadas é a de determinar outras caracterizaç ões va-riacionais para os pontos cr´ıticos. Para isso, selecionamos uma função v ∈ H₀1(Ω) tal que J(v)<0. Observando que J(0) =0 consideramos o conjuntoΓ_{de todos os caminhos unindo a}

origem à funçãov, isto é,

Γ:=_{γ: [0, 1]_→ H01(Ω);γ(0) =0,γ(1) =v}.

Tamb´em definimos o n ´umero

c:= inf

γ∈Γ_tmax_∈_[_0,1_]J(γ(t)),

comumente denominado valor de “minimax”. Agora mostramos que

c>max{J(0),J(v)_}=0. (1.9)

De fato, usando a desigualdade (1.6) obtemos que J(u) > _k_u_k2_{/4 para} _k_u_k _{suficientemente}

pequeno. Em particular, existeρ∈ R+_{tal que}_ρ_< _k_v_k_e _J₍_u₎> _ρ2_{/4 se}_k_u_k=ρ. Como todos os caminhos deΓ_{devem cruzar a esfera de raio}ρ, isso garante que vale a desigualdade (1.9).

Dizemos que um funcional que verifica a desigualdade (1.9) para alguma funçãov∈ H₀1(Ω) e para o n´ıvel de minimaxc definido acima tem a geometria do passo da montanha; o valor c é denominado n´ıvel do passo da montanha . Intuitivamente, procuramos um ponto cr´ıtico u ∈ H₀1(Ω)para o funcional J no n´ıvel do passo da montanha, mas esse ponto cr´ıtico nem sempre existe. Para mais detalhes, veja o TeoremaA.17no Apêndice.

Entretanto, uma consequência da geometria do funcionalJ é a existência de uma sequência (un)n∈N ⊂ H₀1(Ω)tal que J(un) → c ekJ′(un)k → 0 quando n → ∞. Uma sequência com essa propriedade é denominada sequência de Palais-Smale. Se uma sequência de Palais-Smale possui uma subsequência convergente, dizemos que verifica a condição de Palais-Smale no n´ıvelc.

Para garantir que existe uma sequência de Palais-Smale, um resultado frequentemente usado é o princ´ıpio variacional de Ekeland , enunciado no Apêndice (ProposiçãoA.4.5).

Para prosseguir na argumentação como no CASO1, devemos verificar que uma sequência de Palais-Smale é limitada. Pela definição do funcional J, a saber, J(u) = 1

2kuk

2₋ 1 p|u|

p p, e

usando o fato de queJ(un)_→cquandon_→∞, obtemos

kunk2− 2 p|un|

p

(20)

Al´em disso, o limitekJ′(un)_{k →}0 quandon _→∞_{pode ser reescrito na forma}

−∆_u_n_{− |}_u_n_|p−2_u

n→0 (H01(Ω))∗ (1.11)

Multiplicando ambos os lados da última expressão pela funçãoune integrando sobre o dom´ınio

Ωobtemos

_kunk2− |un|pp

6_ε_n_k_u_n_k _(1.12)

em que εn → 0 quando n → ∞. Agora usamos o fato de que p > 2 e as diferentes ho-mogeneidades nas express ões em (1.10) e (1.12) para concluir que a sequência das normas (_kunk)n∈N ⊂R+ é limitada.

Argumentando como no caso precedente, da limitação da sequência (un)n∈N ⊂ H₀1(Ω)

podemos supor que existe uma subsequência, sempre denotada da mesma forma, e que existe uma funçãou ∈ H₀1(Ω)tais queun⇀ ufracamente emH10(Ω)eun→ ufortemente emLq(Ω) para todoq∈[2, 2∗_).

A pr óxima etapa da argumentação é mostrar que vale o limite un → u fortemente em

H₀1(Ω). Comoun → ufortemente em Lp(Ω), sabemos pela desigualdade (1.12) quekunk2 →

|un|ppquandon→∞. Além disso, pela caracterização dada em (1.11), deduzimos que Z

Ω∇un· ∇u dx− Z

Ω|un| p−2_u

nu dx→0 (n→∞). (1.13)

Usando a convergˆencia forte em Lq₍_Ω₎_{para todo}_q_∈ _{(2, 2}∗_{), a convergˆencia fraca e a}

desi-gualdade de H ¨older, obtemos Z

Ω|un| p−2_u

nu dx→ Z

Ω|u| p_dx₌

|u_|pp (n→∞).

Por outro lado, da convergˆencia fraca, para a parcela envolvendo os gradientes temos que Z

Ω∇un· ∇u dx → Z

Ω|∇u|

2_dx₌

kuk2 (n→∞).

Portanto, combinando esses resultados obtemos que ku_k2 ₌ _|_u_|p_{p; e como j´a temos a}

con-vergênciakunk2 → |u|p, segue-se quep kunk2→ kuk2. Por fim, usando um resultado conhecido de Análise Funcional (veja [4, Theorem 3.32, pág. 78]), conclu´ımos que un → u fortemente

em H₀1(Ω). Al´em disso, pela continuidade de J e de J′, resulta que u ´e um ponto cr´ıtico do

funcional J no n´ıvelcdo passo da montanha. Finalmente, como c > 0 = J(0), segue-se que o ponto cr´ıtico u é diferente de zero e obtemos, assim, uma solução fraca não trivial para o problema (1.3).

Resumimos esses argumentos enunciando uma vers˜ao de um resultado conhecido na lite-ratura como teorema do passo da montanha .

1.2 Proposi¸c˜ao. Seja X um espa¸co de Banach e seja J: X → R _{um funcional continuamente}

(21)

1.2. Problemas envolvendo o expoente cr´ıtico 7

1. _kv_k>ρ;

2. para todo u∈ X tal quekuk=ρvale a desigualdademax{J(0),J(v)_}<c06 J(u). Ent˜ao o funcional J possui um valor cr´ıtico c>_c₀_{definido por}

c:= inf

γ∈Γtmax∈[0,1] J(γ(t)).

Para a demonstrac¸˜ao, referimos ao livro de Ambrosetti e Malchiodi [1, Theorem 8.1] ou de Willem [19, Theorem 1.15].

CASO4: p=2∗ =2N/(N₋2). Nesse caso o funcionalJainda possui a geometria do teorema do passo da montanha. Além disso, todas as sequências de Palais-Smale são limitadas; em particular, existe uma sequência(un)n∈N ⊂ H₀1(Ω)tal que J(un) → c, kJ′(un)k → 0 e un ⇀ u fracamente em H₀1(Ω)quando n → ∞_{. A diferença em relação ao} CASO 3 é que agora a convergência fracaun ⇀ u em H01(Ω) não implica a existência de uma subsequência, ainda

denotada da mesma forma, tal que un → u fortemente em Lp(Ω). Isso se deve ao fato de que a imersão H₀1(Ω) ֒→ Lp(Ω)não é compacta . Essa dificuldade não é simplesmente uma questão técnica. Veremos na pr óxima seção que, devido à identidade de Pohozaev, o funcional J não possui ponto cr´ıtico no n´ıvel do passo da montanha quando o dom´ınioΩ_{for estrelado.}

Consequentemente, o problema (1.1) não possui solução no caso p = 2∗ para esse tipo de dom´ınio.

Em resumo, vimos que no CASO1 a compacidade ´e garantida a priori pela escolha do tipo

de crescimento da não-linearidade, que é sublinear. No CASO 2, em que temos um problema linear de autovalor, a compacidade é garantida. No CASO3, em que a não-linearidade ainda é

subcr´ıtica, a compacidade é garantida, mas a dificuldade é que o funcional é indefinido, isto é, não é limitado superiormente nem inferiormente. No CASO4, temos um exemplo de problema sem compacidade, em que a não-linearidade tem crescimento cr´ıtico. Outras situaç ões em que a mesma dificuldade aparece são problemas definidos em dom´ınios não limitados. Esse último caso é o ponto de partida para uma grande linha de pesquisa que se iniciou com o trabalho pioneiro de Brézis e Nirenberg [5].

Na pr óxima seção descrevemos alguns tipos de problemas sem compacidade e as técnicas usadas para resolvê-los.

1.2 Problemas envolvendo o expoente cr´ıtico

Começamos esta seção enunciando um resultado devido a Pohozaev .

1.3 Proposi¸c˜ao. SejaΩ_⊂RN_{um conjunto aberto com fronteira}_∂Ω_∈_C1_{e limitado e denotemos por}

(22)

F(t):=R₀t f(s)ds. Se u∈C2(Ω)for uma solu¸c˜ao cl´assica do problema 

 

−∆_u(x) = f(u) x ∈Ω_,

u(x) =0 x _∈∂Ω_, (1.14)

ent˜ao

N₋2 2

Z

Ω|∇u|

2_dx −N

Z

ΩF(u) dx= − 1 2

Z

∂Ω _∂u

∂ν 2

ν(x)_·x dσ. (1.15)

A demonstração dessa proposição, conhecida como identidade de Pohozaev, pode ser en-contrada nos livros de Ambrosetti e Malchiodi [1, Theorem 8.30] ou de Badiale e Serra [2, The-orem 3.4.26] .

Como consequência da Proposição 1.3, vemos que a condição de crescimento para a não linearidade nos casos analisados na seção anterior não pode ser eliminada. De fato, para um conjunto estrelado em relação à origem, isto é, um conjunto tal que ν(x)_·x > 0 para todo x_∈∂Ω_{, vale a seguinte desigualdade.}

1.4 Corolário. Seja Ω _⊂ RN _{um dom´ınio estrelado em rela¸cão à origem e com fronteira} _∂Ω _∈ _C1_.

Então toda solu¸cão clássica do problema(1.14)verifica a desigualdade

N Z

ΩF(u)dx− N−2

2 Z

Ω f(u)u dx>0.

Usando o Corol´ario 1.4, suponhamos queu ∈ H1

0(Ω)seja uma solução não trivial do

pro-blema (1.1). Usando a teoria de regularidade (Consulte Brézis [4, Cap. 7 e 8]), podemos garan-tir que u ∈ C2₍Ω)eu é de fato uma solução clássica do problema. Dessa forma, aplicando a Proposição1.3no caso em que f(t) =_|t_|p−2_t_{, segue-se que}

_N p −

N−2 2

Z

Ω|u|

p_dx_>_0.

Portanto, seu(x) _6≡0, então devemos ter p < 2N/(N−2) =2∗ e esse expoente é cr´ıtico não apenas do ponto de vista das imers ões de Sobolev mas também do ponto de vista da existência de soluç ões não triviais do problema de Dirichlet (1.1).

O Corolário1.4implica que o problema (1.1) não possui solução positiva quandoΩ_⊂ RN

é um dom´ınio estrelado em relação à origem e p = 2∗. Em contraste com esse resultado de não-existência, Brézis e Nirenberg [5] obtiveram um resultado fundamental de existência de solução ao adicionar uma perturbação linear ao problema (1.1). Mais especificamente, seja o problema de valor de fronteira

        

−∆_u(x)₋λu(x) =u2∗−1(x) x∈ Ω_,

u(x)>0 x∈ Ω,

u∈ H₀1(Ω)

(23)

1.2. Problemas envolvendo o expoente cr´ıtico 9

em queN>_3,Ω_⊂RN _{é um conjunto aberto e limitado com fronteira}_∂Ω_{e o espaço} H1 0(Ω)é

equipado com a normakuk:= (R_Ω_|∇u|2_dx₎1/2_{. Adaptando as ideias desenvolvidas na sec¸˜ao}

anterior, as soluç ões fracas do problema (1.16) são pontos cr´ıticos do funcionalJλ: H₀1(Ω)→R

definido por

Jλ(u):= 1

2 Z

Ω|∇u|

2_dx₋λ

2 Z

Ω|u|

2_dx₋ 1

2∗ Z

Ω|u|

2∗_dx_.

Apresentamos agora alguns comentários sobre o intervalo de variação para o parâmetroλ da perturbação linear. Para isso, usamos a notação e a caracterização do primeiro autovalor λ1do operador laplacianoL[u]:= −∆u(x)em H10(Ω)dada por (1.8) na Proposição1.1. É fato

conhecido queλ1 > 0 e que λ1 é atingido, isto é, existe solução para o problema−∆u(x) =

λ1u(x). Se λ < λ1, então o funcional Jλ verifica a condição 1 da Proposição1.2. Além disso,

selecionando uma função não nulau_∈ H1

0(Ω)temos queJλ(tu)→ −∞quandot →∞, o que

garante que o funcionalJλverifica a condição 2 da Proposição1.2.

Por outro lado, usando novamente a Proposição 1.3, se Ωfor um dom´ınio estrelado em relação à origem, então o problema (1.16) não possui solução se λ6 _{0. Dessa forma, para}

ob-termos resultados de existência de soluç ões para o problema (1.16) devemos considerar valores positivos paraλ.

A falha na utilização da Proposição1.2mostra que a condição de Palais-Smale não é verifi-cada. Isso ocorre como consequência da imersãoH1

0(Ω)֒→L2 ∗

(Ω)não ser compacta. O principal resultado que discutimos nesta seção é devido a Brézis e Nirenberg [5].

1.5 Proposi¸cão. 1. Se N >₄_{, então o problema}₍_1.16₎_{tem uma solu¸cão para todo}_λ_∈ (0,λ1), em

queλ1´e o primeiro autovalor definido em(1.8).

2. Se N= 3, então existeλ0= λ0(Ω)comλ0 ∈[0,λ1)e tal que o problema(1.16)tem solu¸cão se, e somente se,λ∈ (λ0,λ1). Em particular, no caso em queΩé a bola unitária, temosλ0 = λ1/4 e o problema(1.16)tem solu¸cão se, e somente se,λ_∈ (λ1/4,λ1).

Para descrever o roteiro utilizado por Brézis e Nirenberg na demonstração da Proposição1.5

necessitamos de algumas notaç ões. A melhor constante das imers ões de Sobolev H₀1(Ω) ֒→ L2∗₍_Ω₎_{é denotada por}_S_{e é dada por}

S=S(Ω):=inf_{ku_k2: u_∈ H₀1(Ω),_|u_|2∗ =1}.

As funç ões que realizam a melhor constanteS(RN₎_{são os m últiplos de}

U(x):= c

(1+_|x|2₎(N−2)/2, c:= (N(N−2))

(N−2)/4 _(1.17)

que verifica a equac¸˜ao diferencial

(24)

De forma geral, as soluç ões dessa equação diferencial formam a fam´ılia de funç ões

Uε,y(x):=ε−(N−2)/2U((x−y)/ε) (1.18) em quey ∈ RN _e_ε _∈ R+_{. Notamos que essa fam´ılia de funç ões é obtida a partir da função}_U

através de translaç ões e dilataç ões. Além disso, temos queUε,y ∈ L2∗(RN),∇Uε,y ∈ L2(RN)e

kUε,yk2 =|Uε,y|2₂∗∗ = SN/2.

Pode-se mostrar queSindepende do dom´ınioΩ_{. De fato, para qualquer dom´ınio}Ω_,

esten-dendo uma func¸˜aou∈ H1₀(Ω)como sendo nula no complementar deΩ_{, podemos considerar}

H₀1(Ω)como um subconjunto deH₀1(RN_{). Assim,}_S₍Ω)6_S(RN_{). Por outro lado, se}₍_u_n₎_n_∈N ⊂

H1

0(RN)for uma sequˆencia minimizante paraS(RN), usando argumentos de densidade

pode-mos supor que (un)n∈N ⊂ C₀∞(RN). Efetuando as translac¸ ˜oes e homotetias dadas por (1.18),

podemos supor que 0∈ Ω_{e que a nova sequˆencia}(vn)n∈N dada porvn(x) = (un)εn,yn(x)´e tal

que(vn)n_∈N ⊂ C₀∞(Ω). Usando a invariância das normas envolvidas na definição de S pela

transformac¸˜ao indicada, segue-se queS(Ω) 6 _{lim infn}_→∞||vn||2 = S(RN)em que|vn|2∗ = 1.

Assim,S(Ω) =S(RN_).

Além disso, o ´ınfimo S s ó é atingido seΩ = RN_{. De fato, se} _S₍Ω)for atingido por uma função u ∈ H1

0(Ω) em que Ω RN, novamente estendendo u como sendo nula no

com-plementar deΩ_{, segue-se que essa função também realiza o ´ınfimo} _S(RN_{). Mas isso é uma}

contradição pois as únicas funç ões que realizam S(RN₎ _{são dadas pelas funç ões (}_1.17_{) que}

nunca se anulam.

Agora podemos descrever a estratégia para demonstrar a Proposição1.5. Brézis e Nirenberg demonstraram os seguintes fatos:

1. O funcional Jλverifica a condic¸˜ao de Palais-Smale para todo n´ıvelcdo passo da

monta-nha tal quec< SN/2/N.

2. Se cλ denota o n´ıvel cr´ıtico do passo da montanha, ent˜ao cλ < SN/2/N desde queλ ∈

(0,λ1)no caso em queN>4 e desde queλ∈(λ0,λ1)no caso em queN=3.

Para obter a condição de Palais-Smale no passo 1, Brézis e Nirenberg usaram o LemaA.15

de Br´ezis e Lieb. E para mostrar que o n´ıvel do passo da montanha cλ fica abaixo do valor

SN/2/N no passo 2, utilizaram func¸ ˜oes cortes apropriadas deUε,y. Mais especificamente,

su-pondo que 0 ∈ Ω_{, seja} ϕ _∈ C∞

0 (Ω)tal que ϕ(x) = 1 em uma bola centrada na origem e seja

uε(x):= ϕ(x)Uε,0(x). Fazendo estimativas assint ´oticas refinadas das normas deuεem diversos

espaços de funç ões, Brézis e Nirenberg obtiveram o passo 2. Para os detalhes da demonstração, citamos o artigo original de Brézis e Nirenberg [5] e os livros de Ambrosetti e Malchiodi [1, The-orem 11.6] e de Struwe [15, Cap. 3, Theorem 2.1]. Veja também a demonstração do Teorema2.2.

1.6 Observa¸cão. Usando a notação anterior, vemos que o n´ıvel do passo da montanhacλ é tal

quecλ 6maxt>0Jλ(tuε). E como

Jλ(tuε) = t

2

2 kuεk

2

−λ|uε|22

− t 2∗

2∗ |uε|

(25)

1.3. Problemas cr´ıticos envolvendo potenciais de Hardy 11

segue-se que maxt>0Jλ(tuε)ocorre no pontoτe valeJλ(τuε), dados por

τ= kuεk

2₋_λ_|_u

ε|2₂

|uε|22∗∗

!(N−2)/4

e Jλ(τuε) = 1

N

kuεk2−λ|uε|2₂

|uε|22∗

!N/2

.

Assim, usando a desigualdadekuεk2−λ|uε|22 <S|uε|22∗(veja [1, Lemma 11.12]), obtemos

cλ 6max

t>0 Jλ(tuε) = Jλ(τuε) =

1 N

kuεk2−λ|uε|2₂

|uε|2₂∗

!N/2 < S

N/2

N .

Dessa forma,cλ < SN/2/N, a desigualdade apresentada no passo 2, é equivalente à condição

Sλ <Sem queSλ :=inf{kuεk2−λ|uε|22: u∈ H01(Ω),|uε|2∗ =1}. Essa equivalˆencia ser´a usada

frequentemente nesta dissertac¸˜ao.

Prosseguindo no estudo dessa classe de problemas el´ıpticos, Ramos, Wang e Willem [13] consideraram o problema (1.16) no caso de dom´ınios não limitados e demonstraram um resul-tado de existência de solução para o problema (1.16). Para enunciá-lo, estabelecemos as seguin-tes notaç ões. Parad ∈ N_{tal que 1} 6 _d 6 _N₋_{1, escrevemos}RN ₌ RN−d_×Rd_,_x _{= (}_y_,_z₎ _∈ RN−d_×Rd_{. Para um dado conjunto} _A _⊂ Rd _denotamos _A_δ ₌ _{_y _∈ Rd_{: dist(}_y_,_A₎ _< _δ_}_e

b

A=RN−d_×_A_{. Al´em disso, para}_y_∈Rd_denotamosΩy₌ _{_z_∈_Rd_: ₍_y_,_z₎_∈_Ω_}_.

1.7 Proposi¸c˜ao. Seja N >₄_{e seja}Ω_⊂RN _{um conjunto satisfazendo as seguintes hip´oteses.}

1. Existem dois conjuntos abertos não vazios e não limitados F e G tais que F ⊂ G ⊂ Rd_{, F é um}

dom´ınio de Lipschitz eFb⊂Ω_⊂ _G.b

2. Para cadaδ >0existe M>0tal queΩt⊂ Fb_δpara todo|t|> M. Seλ∈(0,λ1(Ω)), então o problema(1.16)tem uma solu¸cão não nula.

1.3 Problemas cr´ıticos envolvendo potenciais de Hardy

Generalizando a classe de problemas considerados na sec¸˜ao anterior, Jannelli [8] considerou uma variante do problema (1.16), ainda em dom´ınios limitados, envolvendo o expoente cr´ıtico de Sobolev e com o potencial de Hardy. Mais precisamente, seja o problema

          

|x|2 =u(x)2 ∗₋₁

, x _∈Ω_,

u(x)>0, x ∈Ω,

u(x) =0, x ∈∂Ω_,

(1.19)

em queN>3,Ω_⊂RN _{´e um conjunto aberto, limitado e contendo a origem, 2}∗ ₌₂_N_/(_N₋₂₎

denota o expoente cr´ıtico de Sobolev, µ ∈ R _{e o termo} _µ_|_u_|_/_|_x_|2_{, denominado potencial de}

Hardy.

(26)

ku_k := (R_Ω_|∇u_|2_dx₎1/2_{. A equação diferencial do problema (}_1.19_{) é a equação de}

Euler-Lagrange associada ao funcional Jλ,µ: H10(Ω)→Rdefinido por

Jλ,µ:= 1

2 Z

Ω|∇u|

2_dx −λ₂

Z

Ω|u|

2_dx − 1₂

Z

Ω

|u|2 |x|2 dx−

1 2

Z

Ω|u|

2∗_dx_.

Como consequência da desigualdade de Hardy (A.7), devemos considerar o parâmetroµ menor do que a melhor constante da desigualdade de Hardy , isto é,µ< µ¯ := (N−2)2/4.

Assim como no caso do problema (1.16), podemos definir λ1(µ), o primeiro autovalor do

operador el´ıptico definido porL[u]:=₋∆u₋µ u

|x|2, e que pode ser caracterizado por

λ1(µ):= inf

u∈H1 0(Ω) u(x)6≡0

Z

Ω|∇u|

2_dx −µ

Z

Ω

|u|2 |x|2 dx Z

Ω|u|

2_dx . (1.20)

É poss´ıvel mostrar que λ1(µ) > 0 é função decrescente do parâmetro µ e, quando µ → µ¯,

segue-se que λ1(µ)tende a uma constante positiva. Al´em disso, o valor λ1(µ) ´e atingido se

Ω_⊂RN _{´e um dom´ınio limitado.}

Usando uma desigualdade do tipo de Pohozaev, ´e poss´ıvel mostrar que seΩ_{for um dom´ınio}

estrelado em relação à origem e seλ6_{0, então o problema (}_1.19_{) não tem solução. Portanto,}

as-sim como no caso do problema (1.16), devemos considerarλ∈(0,λ1(µ)). Com essas hip ´oteses,

Jannelli [8] demonstrou os seguintes resultados.

1.8 Proposi¸cão. Se µ 6 _µ_¯₋₁_{, então o problema}₍_1.19₎ _{tem pelo menos uma solu¸cão u} _∈ _H1

0(Ω) quandoλ∈(0,λ1(µ)).

1.9 Proposi¸cão. Seµ¯₋1<µ<µ, então o problema¯ (1.19)tem pelo menos uma solu¸cão u_∈ H1

0(Ω) quandoλ0(µ)< λ< λ1(µ), em que

λ0(µ):= min

ϕ∈H1 0(Ω)

ϕ6≡0 Z

Ω

|∇ϕ(x)_|2 |x|2γ dx

Z

Ω ϕ2(x)

|x|2γ dx

eγ := √µ¯ +√µ¯ −µ. Em particular, no caso em que Ω= B(0,R)é uma bola de raio R centrada na origem, então o problema(1.19)não tem solu¸cão seλ6λ0(µ).

Para demonstrar esses resultados, Jannelli usou a mesma estratégia usada por Brézis e Ni-renberg. Mais precisamente, considerou o problemaL[U] = U2∗−1_em _RN_{, que tem soluç ões} da forma

Uε(x):= Cε

(27)

1.4. Resultados principais 13

em queε_∈R+_,

σ:= pµ¯ ₋pµ¯₋µ e Cε :=

₄_εN₍_µ_¯₋_µ₎ N−2

√

¯

µ/2

. (1.22)

Para mais detalhes, consulte o artigo de Jannelli [8]. Veja também a Observação1.6e a demons-tração do Teorema2.2.

1.4 Resultados principais

Nesta seção apresentamos o objetivo principal da dissertação, que é demonstrar resultados de existência e de não-existência de soluç ões para uma classe de equaç ões el´ıpticas não-lineares envolvendo o expoente cr´ıtico de Sobolev e o potencial de Hardy. Mais especificamente, trata-mos do problema

          

|x|2 =u(x)2 ∗₋₁

x_∈ Ω_,

u(x)>0 x∈ Ω,

u(x) =0 x∈ ∂Ω_,

(1.23)

em queΩ_⊂RN_{denota um conjunto aberto contendo a origem, limitado ou n˜ao, com}_N>_{4 e}

2∗ =2N/(N−2)denota o expoente cr´ıtico na desigualdade de Sobolev.

O problema (1.23) que estudamos está relacionado com o problema (1.16) estudado por Brézis e Nirenberg fazendoµ= 0 e é o mesmo problema (1.19) estudado por Jannelli. Porém, consideramos outros tipos de dom´ınios, incluindo dom´ınios não limitados e tratamos outros intervalos para o parâmetro µ. A referência básica para este trabalho é o artigo de Ruiz e Willem [14].

Como nos casos j´a mencionados, trabalhamos no espac¸o de SobolevH1

0(Ω)definido como

o completamento deC₀∞(Ω)emH1(Ω), em que

H1(Ω) =nu∈ L2(Ω): ∂u ∂xi ∈ L

2₍_Ω_),_i₌_{1, . . . ,}_No_.

Consideramos tamb´em o funcionalI : H₀1(Ω)_→R_{definido por}

I(u) = 1 2 Z

Ω|∇u(x)|

2_dx₋ λ

2 Z

Ωu

2₍_x₎_dx₋ µ

2 Z

Ω u2₍_x₎

|x_|2 dx−

1 2∗

Z

Ωu

2∗₍_x₎_dx_.

Observamos que a integral Z

Ω u2(x)

|x_|2 dxest´a bem definida devido `a desigualdade de Hardy .

Soluç ões fracas do problema (1.23) são pontos cr´ıticos do funcionalI e verificam a equação I′(u)v=0 para todov_∈ H1

0(Ω), ou seja, Z

Ω∇u(x)∇v(x)dx−λ Z

Ωu(x)v(x)dx−µ Z

Ω

u(x)v(x)

|x|2 dx− Z

Ωu

(28)

para todov_∈ H1 0(Ω).

Como o funcionalI não é limitado inferiormente, procuramos soluç ões usando as mesmas estratégias utilizadas por Brézis e Nirenberg e também por Jannelli. Dessa forma, usamos a teoria de multiplicadores de Lagrange e definimos o problema

Sµ_λ(Ω)_≡inf Z

Ω|∇u(x)|

2_dx −µ

Z

Ω u2(x)

|x|2 dx−λ Z

Ωu

2₍_x₎_dx_: _u

∈V(Ω)

restrito ao v´ınculo

V(Ω) =

u∈ H01(Ω): Z

Ω|u(x)|

2∗

dx=1

.

Assim, nosso objetivo é demonstrar que o valorSµ_λ(Ω)é atingido. Como nos casos já descritos, também usamos a seguinte hip ótese:

µ6_µ₋₁= (N−2)

2

4 −1 e λ∈(0,λ1(µ)) (H)

em queλ1(µ)´e definido pela f ´ormula (1.20).

No cap´ıtulo 2estudamos inicialmente o caso Ω = RN _{e demonstramos um resultado de}

existência de solução (Teorema2.1). Em seguida consideramos dom´ınios limitadosΩ _⊂ RN

comµ < 0 e demonstramos um resultado de não-existência de solução no caso em queλ= 0 (Teorema 2.2). Prosseguindo, consideramosλ > 0 e mostramos que S_λµ(Ω) < Sµ₀(Ω); assim, usando a Observação1.6 segue-se que Sµ_λ(Ω) é atingido. Para isso consideramos as funç ões Uε, soluç ões radiais do problema (1.23) quandoλ= 0 e usamos funç ões corte ϕ∈ Co∞(Ω)que se anulam fora de uma vizinhança da origem. Dessa forma, as funç ões uε(x) := ϕ(x)Uε(x)

são usadas para construir sequências minimizantes paraSµ₀(Ω). A condição (H) é fundamen-tal para assegurarmos a desigualdadeSµ_λ(Ω) < Sµ₀(Ω). Contudo, as funç õesuε formam uma

sequência minimizante paraSµ₀(Ω)somente seµ > _{0. Assim, quando} _µ < 0 a demonstração apresentada por Jannelli [8] não é válida e devemos argumentar de outra forma. Para obtermos o resultado, demonstramos queSµ₀(Ω) = S(Teorema2.2) e também queSµ_λ(Ω)<Sµ₀(Ω) (Teo-rema2.4). Com esses dois resultados podemos finalmente demonstrar a existência de solução para o problema (1.23) (Teorema2.5).

No cap´ıtulo 3 consideramos dom´ınios n˜ao limitados Ω _⊂ RN _{e novamente usamos a}

hip ótese (H). O problema (1.23) comµ=0, isto é, o problema (1.16) em dom´ınios não limitados foi estudado por Lions [12] e por Ramos, Wang e Willem [13]. Demonstramos inicialmente um resultado de existência de solução no caso em queΩ_{está contido em, e tende assintoticamente}

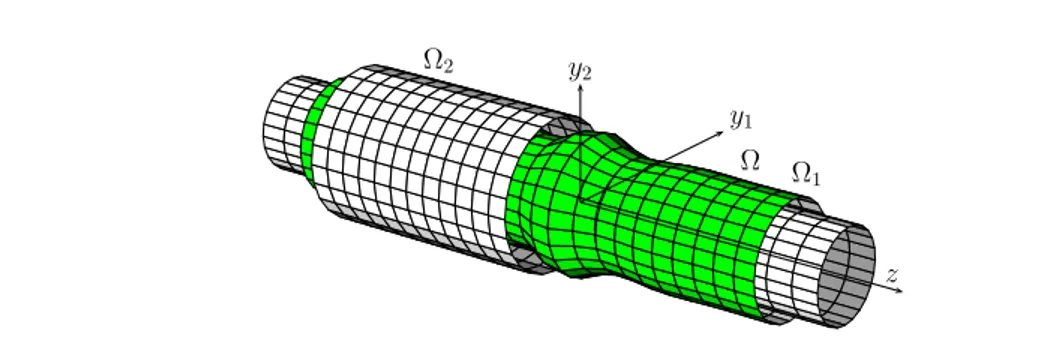
para, um cilindro (Teorema3.5). Em seguida consideramos dom´ınios da formaΩ = Ω₁_×R_d

em queΩ₁ _⊂ R_N

−d é um dom´ınio limitado comN> d >1. Demonstramos queµ>0 é uma condição necessária e suficiente para que o problema (1.23) tenha solução nesse tipo de dom´ıno caso em queΩ_{é um cilindro (Teorema}_3.6_{). Essa condição representa uma diferença qualitativa}

(29)

1.4. Resultados principais 15

No cap´ıtulo4lidamos com um tipo invariante de dom´ınio que inclui, como um caso parti-cular, dom´ınios do tipoΩ = Ω₁_×Rd_{. Nesse caso, estudamos a existência de soluç ões para o}

problema (1.23) da formau(y,z) =u(y,_|z_|)sey_∈ Ω₁,z _∈Rd_{. No caso em que}_d>_{2 obtemos}

um resultado de existência de solução (Teorema 4.2). No caso em que d = 1 obtemos uma condição suficiente para a existência de solução (Teorema4.4).

(30)

(31)

-2-Existˆencia de solu¸c ˜oes de energia m´ınima

2.1 Existˆencia de solu¸c˜ao em todo o espa¸co

Começamos esta seção estabelecendo algumas notaç ões que serão usadas no restante da dis-sertação. Denotamos porO(N) o grupo linear das transformaç ões isométricas em RN_{, isto}

´e,

O(N) =_{A∈ GLN: A−1 = AT}.

Esse conjunto também é conhecido como grupo ortogonal de matrizesN×N. Veja o ApêndiceA.2

para mais detalhes. Se G ´e um subgrupo de O(N), dizemos que Ω _{´e invariante por} _G _se

g(Ω) =Ω_{, para todo}_g_∈_G_{. Se}Ω_{´e invariante por um grupo}_G_{, definimos o espac¸o}

H0,1G(Ω):= n

u∈ H01(Ω): u◦g=u ∀g∈G o

.

Tamb´em definimos o valor

Sµ_λ(Ω_,_G):=inf Z

Ω|∇u(x)|

2_dx₋_µZ

Ω u2(x)

|x_|2 dx−λ Z

Ωu

2₍_x₎_dx_: _u_∈ _V₍_Ω_,_G₎

, (2.1)

que ´e positivo pela desigualdade de Hardy , em que o v´ınculoV(Ω)´e definido por

V(Ω_,_G):=

u∈ H_0,1_G(Ω): Z

Ω|u(x)|

2∗_dx₌₁

.

No que se segue, no caso especial em queG= _{1_}contém apenas a aplicação identidade, omitimos a referência ao grupoG. Além disso,S =S0₀(RN₎_{é a melhor constante das imers ões}

de Sobolev .

Pela teoria dos multiplicadores de Lagrange, sabemos que se o ´ınfimo Sµ_λ(Ω) é atingido, então existe uma solução fracau0do problema

−∆u₋λu₋µ u 2

|x|2 = S

µ λ(Ω)u2

∗₋₁

,

isto ´e, Z

Ω∇u0(x)∇v(x)dx−λ Z

Ωu0(x)v(x)−µ Z

Ω

u0(x)v(x)

|x|2 dx=S

µ λ(Ω)

Z

Ωu

2∗₋₁

0 (x)v(x)dx, (2.2)

para todov∈ H₀1(Ω).

(32)

Definindo w(x) = Sµ_λ(Ω)2∗−12u₀(x)temos quew é uma solução fraca do problema (1.23) . Para verificar a afirmativa, calculamos

Z

Ω∇w(x)∇v(x)dx−λ Z

Ωw(x)v(x)dx−µ Z

Ω

w(x)v(x)

|x|2 dx

= Z

Ω∇(S

µ λ(Ω)

1

2∗−2u₀(x))∇v(x)dx

−λ Z

ΩS

µ λ(Ω)

1

2∗−2u₀(x)v(x)dx−µ Z

Ω

Sµ_λ(Ω)2∗−12u₀(x)v(x)

|x|2 dx

= Sµ_λ(Ω)2∗−12 Z

Ω∇u0(x)∇v(x)dx−λ Z

Ωu0(x)v(x)dx−µ Z

Ω

u0(x)v(x) |x|2 dx

= Sµ_λ(Ω)2∗−12

Sµ_λ(Ω) Z

Ωu

2∗−1

0 (x)v(x)dx

= Sµ_λ(Ω)2∗−12+1 Z

Ωu

2∗₋₁

0 (x)v(x)dx, (2.3)

em que na pen última passagem utilizamos a equação (2.2). Comou0(x) =Sµλ(Ω)

−1

2∗−2w(x), temos então que o lado direito da equação (2.3) vale

Sµ_λ(Ω)2∗−12+1 Z

Ωu

2∗−1

0 (x)v(x)dx=S

µ λ(Ω)

1 2∗−2+1

Z

Ω

w(x) Sµ_λ(Ω)2∗−12

!2∗−1

v(x)dx

=Sµ_λ(Ω)2∗−12+1Sµ

λ(Ω)−

2∗−1 2∗−2

Z

Ωw

2∗−1₍_x₎_v₍_x₎_dx

= Z

Ωw

2∗−1₍_x₎_w₍_x₎_dx_.

Portanto,w(x) =u0(x)Sµ_λ(Ω) 1

2∗−2 é solução fraca do problema (1.23).

Como vimos no cap´ıtulo 1, Brézis e Nirenberg [5] e Jannelli [8] demonstraram que a desi-gualdade estritaSµ_λ(Ω) < Sµ₀(Ω) é uma condição suficiente para o ´ınfimoS_λµ(Ω)ser atingido quando o dom´ınio Ω _{é limitado. A ideia para verificar essa desigualdade é considerar uma}

sequˆencia minimizante(νε)⊂ H₀1(Ω)paraSµ₀(Ω)e mostrar que a express˜ao

Qλ(ε):=

Z

Ω|∇νε(x)|

2_dx −µ

Z

Ω νε2(x)

|x|2 dx−λ Z

Ων

2

ε(x)dx

Z

Ω|νε(x)|

2∗_dx 2

2∗

,

atinge valores abaixo deS₀µ(Ω). Para isso, é necessário um estudo em detalhes do ´ınfimoSµ₀(Ω) e de suas sequências minimizantes . Observamos que, pela invariância das integrais envolvidas na definição de Sµ₀(Ω)por homotetias, esse valor não depende do conjunto aberto Ω_{. Além}

disso, se definimos o espac¸o de SobolevD1,2₍RN₎_como

D1,2₍RN₎_:=

u_∈ L2∗(RN₎

_∂x∂u_i ∈ L2(RN), i=1, 2, . . . ,N