Um estudo na teoria do movimento brownianno com viscosidade variável

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIˆENCIAS EXATAS E DA TERRA

DEPARTAMENTO DE FÍSICA TE ÓRICA E EXPERIMENTAL PROGRAMA DE P ÓS-GRADUAÇ ÃO EM FÍSICA

UM ESTUDO NA TEORIA DO MOVIMENTO

BROWNIANNO COM VISCOSIDADE VARI ´

AVEL

AUTOR: JO ˜AO MARIA DA SILVA

ORIENTADOR: PROF. Dr. JOS´E ADEMIR SALES DE LIMA

Disserta¸cão de mestrado apresentada ao Departamento de F´ısica Teórica e Experimental da Universidade Federal do Rio Grande do Norte como requisito parcial à obten¸cão do t´ıtulo de MESTRE em

F´ISICA.

(2)

Sum´

ario

1 Quatro Abordagens para o Movimento Browniano 5

1.1 Introdu¸c˜ao . . . 5

1.2 Movimento Browniano e equa¸c˜ao de difus˜ao: O Tratamento de Einstein . . 6

1.3 O Tratamento de Langevin . . . 15

1.4 A Equa¸c˜ao de Fokker-Planck . . . 22

1.5 Caminhadas Aleat´orias: Tratamento de M. Kac . . . 27

1.6 A Equa¸c˜ao de Difus˜ao Generalizada . . . 31

2 Descri¸cão Lagrangiana para Sistemas com Amortecimento Variável 36 2.1 Introdu¸cão . . . 36

2.2 Lagrangiana Para Sistemas Dissipativos . . . 37

2.3 O q-Oscilador . . . 40

2.4 Um exemplo: Dinˆamica de Campos Escalares em Cosmologia . . . 46

3 Sistemas com Amortecimento Vari´avel: Formalismo de Langevin 49 3.1 Introdu¸c˜ao . . . 49

3.2 Equa¸c˜ao de Langevin com Viscosidade Dependente do Tempo . . . 50

3.3 Equa¸c˜ao de Langevin Com Ru´ıdo Colorido . . . 56

3.4 Ru´ıdo Colorido: O Caso Geral . . . 63

3.5 Part´ıcula Ligada por um Potencial Harmˆonico . . . 67

3.6 Difusão Anômala e Normal em Sistemas com Memória . . . 71

3.7 Conclus˜oes e Perspectivas . . . 75

A Um M´etodo de Integra¸c˜ao Mais Geral 77

B O q-Oscilador: Uma Solu¸c˜ao Formal 80

(3)

Lista de Figuras

1.1 As curvas mostram a evolu¸cão temporal da distribui¸cão de probabilidade η(x, t) no regime difusivo unidimensional. Para tempos próximos de zero a curva azul representa uma fun¸cão delta centrada em torno da origem x0 = 0. Com o passar do tempo esta curva evolui como uma distribui¸cão

gaussiana de largura vari´avel. . . 14 2.1 O balde de massaM est´a suspenso por um fio de comprimentol. O sistema

executa um movimento harmônico simples, mas tem sua amplitude variável devido às gotas de água da chuva caindo numa taxa constante. A massa M cresce obedecendo a rela¸cão M =meλt_{. . . 38}

2.2 Evolu¸cão do coeficiente de friçcãoγq(t) para diferentes valores do parâmetro

livre q. O gráfico à esquerda representa o comportamento paraq <1, e no outro, à direita, a evolu¸cão para q >1. . . 42 2.3 Comportamento caracter´ıstico da amplitude dos q-osciladores. Da

(4)

Nota¸

c˜

ao e Algumas Defini¸

c˜

oes

Constante de Boltzmann: kB

N´umero de Avogadro: Na

Coeficiente de difus˜ao: D

Coeficiente de difus˜ao generalizado: Dq(t)

Coeficiente de viscosidade: γ Constante universal do gases: R

Raio das part´ıculas em movimento browniano: rp

Constante de Hubble: H0

Fator de escala do universo: a(t)

Fun¸cão Gamma: Γ(n) = (n₋1)(n₋2)(n₋3)...(n₋m)Γ(n₋m) = (n₋1)! Fun¸cão de Bessel de primeira espécie: Jν(x) = Σ∞s=0

(−1)s

s!(n+s)!(

x

2) 2s+n

Fun¸c˜ao de Bessel de segunda esp´ecie: Yν(x) = cosνπJν(x)

−J

−ν(x)

sinνπ

Fun¸c˜ao de Bessel modificada de ordem zero: I0

Distribui¸c˜aoq-exponencial: eq(x) = [1 + (1−q)x]1/1

(5)

Agradecimentos

• Ao meu bom Deus criador de todas as coisas, por ter me concedido o dom do pensar.

• Ao Prof. Dr. José Ademir Sales de Lima, pela escolha do tema, pela orienta¸cão, pela dedica¸cão, pelo amigo que tem sido, e principalmente, pela confian¸ca depositada em mim. Meus sinceros agradecimentos pela sua extrema preocupa¸cão no encaminhamento deste trabalho e pela aten¸cão que tem me dedicado durante todo esse tempo.

• A minha m˜ae, ao meu pai, enfim, `a toda minha fam´ılia, por ter me` incentivado e me fornecido o suporte emocional e moral.

• Meus sinceros agradecimentos a todos os meus amigos do DFTE: à Rose Cl´ıvia pelos momentos de descontra¸cão e pela sua ajuda nos momentos dif´ıceis, isso fortaleceu nossa amizade. À José Roberto pelos momentos agradáveis com suas historinhas e piadas, à Pedro Carlos pelo amigo que tem se mostrado, à Edcarlos, João Vital, Jean Ricardo, Carlos Heitor, Marcelo Durval, Marcelo Bruno, Armando Araújo e Edalmir. À Fábio Sales pela sua extrema competência em representar os estudantes da pós-gradua¸cão. À Francisco Carlos pela amizade e pelas brincadeiras nas horas vagas. À Rubens, Ana Cristina, Robson, Neemias e outros mais que agora não me vem à mente. Aos antigos e atuais integrantes do P.E.T, por estarem sempre presente, principalmente nos finais de semana, enfim, à todos que, de uma forma ou de outra, contribu´ıram para a conclusão deste trabalho.

(6)

Resumo

Neste trabalho nós investigamos o comportamento estocástico de uma grande classe de sistemas com amortecimento variável descritos por uma lagrangiana dependente do tempo. Nossa abordagem estocástica é baseada no formalismo de Langevin descrevendo o comportamento de uma part´ıcula browniana clássica de massa m. Duas situa¸cões de interesse f´ısico são consideradas. Inicialmente, uma aplica¸cão do tratamento padrão de Langevin (ru´ıdo branco) para viscosidade variável é discutido em detalhe. Na segunda abordagem, um ponto de vista mais geral é adotado supondo uma dada expressão para o chamado ru´ıdo colorido. Em ambos os casos as equa¸cões diferenciais básicas são analiticamente resolvidas, e todas as quantidades fisicamente relevantes são explicitamente determinadas. Os resultados dependem de um parâmetro arbitrário (q) medindo como o comportamento dinâmico do sistema se afasta daquele apresentado pela part´ıcula browniana com viscosidade constante. Vários tipos de comportamentos estocásticos (subdifusivos and superdifusivos) são obtidos quando o parâmetro livre q varia continuamente. Contudo, no limite

(7)

Abstract

(8)

Introdu¸

c˜

ao

Os estudos experimentais e teóricos sobre teoria de flutua¸cões em f´ısica e áreas relacionadas têm feito avan¸car consideravelmente nossa compreensão sobre a natureza dos processos estocásticos. Em particular, a f´ısica estat´ıstica e a termodinâmica para processos fora de equil´ıbrio têm nos proporcionado uma visão cada vez mais elaborada do comportamento f´ısico de tais sistemas.

´

E bem conhecido que muitos fenômenos na natureza se conectam por quantidades que podem variar com o tempo de maneira bastante complexa e irregular, como por exemplo, a posi¸cão e a velocidade de uma part´ıcula executando movimento browniano. A origem desse fenômeno remonta ao ano de 1828 quando Robert Brown, botânico inglês, verificou que pequenos grãos de pólen imersos na superf´ıcie de um l´ıquido adquiriam uma espécie de movimento irregular.

(9)

época. Entretanto, à medida em que o século XIX chegava ao fim, se generalizava a aceita¸cão da realidade dos átomos e das moléculas, ainda que permanecessem alguns grupos de resistência. Mesmo de posse dessas e outras observa¸cões, não foi poss´ıvel estabelecer, na época, uma teoria satisfatória que tornasse claro a verdadeira essência do movimento browniano, e por isso, este fenômeno permaneceu por um longo tempo na fronteira da f´ısica como um grande mistério.

Somente no in´ıcio do século XX, com base na idéia de pressão osmótica e na sua rela¸cão com a teoria da difusão, Einstein consegue chegar a primeira dedu¸cão teórica das leis que governam o movimento browniano [1]. Sua subseqüente verifica¸cão experimental feita por Jean Perrin, contribu´ıram de forma significativa para o reconhecimento da realidade f´ısica da estrutura atômico molecular da matéria.

Numa série de experimentos cujos primeiros resultados foram publicados em 1908, Perrin conseguiu obter uma precisão até então inigualável na confirma¸cão de quase todas as previsões de Einstein. Nesses primeiros experimentos, Perrin testou uma fórmula para a distribui¸cão vertical de part´ıculas em suspensão sob a influência da gravidade. Desafiado pelos cr´ıticos da época, ele aplicou seus métodos na determina¸cão do número de Avogadro, obtendo resultados em excelente acordo com as previsões teóricas de Einstein.

Os estudos de Einstein sobre o movimento browniano constituem um dos pontos altos da longa tradi¸cão de pesquisa sobre a teoria cinética do calor1 e ainda das suas próprias contribui¸cões para esse campo. Tais trabalhos serviram também como ponto de partida para estabelecer os estudos dos fenômenos de flutua¸cões como um novo campo na área da f´ısica teórica, pois

1_{Grandes contribui¸c˜}_{oes para a teoria cin´etica do calor foram obtidas por Clausius, Maxwell, Boltzmann}

(10)

os m´etodos por ele criado abriram novos horizontes para a f´ısica estat´ıstica2 e para uma teoria geral dos processos estoc´asticos.

Atualmente, os processos estocásticos constituem uma ferramenta da F´ısica extremamente apropriada para se investigar sistemas de não equil´ıbrio nos mais diferentes dom´ınios, incluindo economia, biologia, f´ısica da matéria condensada, astrof´ısica e cosmologia [2-5]. Por exemplo, no campo das ciências econômicas, é poss´ıvel investigar um sistema que possue caracter´ısticas semelhantes a de um sistema randômico. Nesse caso, conceitos de f´ısica estat´ıstica, tais como dinâmica estocástica, correla¸cão de curto e longo alcance e auto-similaridade, permitem um entendimento do comportamento global do sistema [6]. Usualmente, tais sistemas estão entre os mais fascinantes e intrigantes sistemas complexos que podem ser investigados.

´

E neste contexto das teorias que descrevem os processos estocásticos que se insere o presente trabalho. Em poucas palavras, nosso objetivo básico é estender o tratamento de Langevin para uma classe de sistemas lagrangianos com amortecimento variável.

No cap´ıtulo I, faremos uma revisão detalhada da teoria padrão do movimento browniano apresentando quatro maneiras independentes de reproduzir os mesmos resultados. Primeiramente, discutiremos o tratamento de Einstein [1] que foi de fundamental importância para a consolida¸cão da teoria, e em seguida, o tratamento de Paul Langevin [7] obtido via uma equa¸cão diferencial estocástica. Posteriormente, apresentaremos o tratamento em termos da equa¸cão Fokker-Planck [9], e finalmente, a abordagem via caminhadas aleatórias proposta por M. Kac [8].

No cap´ıtulo II ´e feito uma revis˜ao da f´ısica envolvendo alguns sistemas

2_{Em seus trabalhos sobre mecˆanica estat´ıstica, Einstein chamou aten¸c˜}_{ao para o importante papel das}

(11)

com amortecimento variável. A teoria é desenvolvida através de uma

q-lagrangiana que generaliza a lagrangiana padr˜ao e incorpora de forma natural os efeitos de amortecimentos dependentes do tempo. Tais sistemas ser˜ao genericamente denominados de q-osciladores, sendo o oscilador amortecido com viscosidade constante um caso particular.

(12)

Cap´ıtulo 1

Quatro Abordagens para o

Movimento Browniano

1.1 Introdu¸

c˜

ao

O movimento irregular de pequenas part´ıculas imersas num banho térmico (ou num l´ıquido) e vis´ıveis com o aux´ılio de um microscópio, foi primeiramente observado pelo botânico Inglês Robert Brown em 1828. Ele notou que essas part´ıculas em suspensão adquiriam uma espécie de movimento errático que posteriormente ficaria popularmente conhecido pelo nome de Movimento Browniano (MB_{). Durante muito tempo, um}

(13)

estendida por muitos outros f´ısicos. Importantes contribui¸cões foram dadas por Langevin [10], Fokker [11], Planck [12], Burger [13], Fürther [14], Ornstein [15], Smoluchowski [16] e outros mais. Em virtude de um grande número de trabalhos terem se dedicado a generalizar e compreender tal problema, discutiremos neste cap´ıtulo, como é poss´ıvel abordar o movimento browniano de quatro maneiras distintas, a saber: o tratamento de Einstein, o de Paul Langevin, a abordagem via equa¸cão de Fokker-Planck, e finalmente, as caminhadas aleatórias de M. Kac.

O movimento browniano tem sido intensamente investigado do ponto de vista f´ısico e matemático, como um exemplo importante de processo estocástico e constitue uma ferramenta fundamental para o estudo de sistemas f´ısicos de não equil´ıbrio. Tais sistemas são encontrados em diferentes áreas da f´ısica, desde a n´ıvel microscópio, como verificado na difusão de part´ıculas num solvente até escalas de ordem astronômicas, tal como observado em sistemas estelares [17]. Um exemplo interessante desse ´

ultimo tipo é um Buraco Negro (BN) no centro de um sistema estelar denso. Quando sua massa é muito grande, o BN adquire um movimento que é semelhante ao de uma part´ıcula em suspensão num l´ıquido ou gás [18].

1.2 Movimento Browniano e equa¸

c˜

ao de difus˜

ao: O

Tratamento de Einstein

(14)

pequeno em compara¸c˜ao com os tempos de observa¸c˜ao, mas suficientemente longo para que os movimentos executados por diferentes part´ıculas no intervalo de tempo τ possam ser considerados eventos independentes.

Suponhamos que existamN part´ıculas em suspensão num l´ıquido. Num intervalo de tempo τ, as coordenadas x das part´ıculas variam de _△x = ρ, onde ρ pode assumir valores diferentes (positivo ou negativo) para cada part´ıcula. Uma determinada lei de distribui¸cão de probabilidades deve ser satisfeita pela variável ρ: o número de part´ıculas dN que sofrem um deslocamento entre x e x+ ρ no intervalo de tempo τ, pode ser expresso por uma equa¸cão da forma [1]

dN = N φ(ρ)dρ (1.1)

com a distribui¸cão φ(ρ) satisfazendo a condi¸cão de normaliza¸cão

Z +∞

−∞ φ(ρ)dρ = 1, (1.2)

onde φ(ρ) é uma fun¸cão par (φ(ρ) = φ(₋ρ)) e diferente de zero apenas para valores muito pequenos. Sejaη(x, t) o número de part´ıculas por unidade de comprimento e calculemos a distribui¸cão de part´ıculas no instante t+τ, a partir da distribui¸cão delas no instante t. Baseado na defini¸cão da fun¸cão

φ(ρ), o n´umero de part´ıculas que no instante t+τ se encontram entre x e

x+ρ, ´e dado por[1]:

η(x, t+τ)dx = dxZ ρ=+∞

ρ=−∞ η(x+ρ, t)φ(ρ)dρ. (1.3)

Comoτ é muito pequeno, podemos fazer uma expansão até segunda1 ordem no tempo

η(x, t+τ) =η(x, t) +τ∂η(x, t) ∂t +

τ2

2

∂η2(x, t)

∂t2 + ..., (1.4)

1_{Einstein considerou em seus resultados apenas a expansão em primeira ordem. Por razões que serão}

(15)

além do mais, como ρ também é pequeno, desenvolveremos η(x+ρ, t) em potências até segunda ordem em ρ

η(x+ρ, t) = η(x, t) +ρ∂η(x, t) ∂x +

ρ2

2!

∂2η(x, t)

∂x2 + .... (1.5)

Inserindo esses dois ´ultimos resultados na integral (1.3), obtemos

η+∂η

∂tτ+ τ2

2

∂2_η

∂t2 = η

Z +∞

−∞ φ(ρ)dρ+

∂η ∂x

Z +∞

−∞ ρφ(ρ)dρ+

∂2_η

∂x2

Z +∞

−∞

ρ2

2 φ(ρ)dρ+... (1.6) No lado direito dessa equa¸cão, o segundo, o quarto e sexto termos etc, são todos identicamente nulos uma vez que φ(ρ) = φ(₋ρ). Logo, considerando a equa¸cão (1.2) e desprezando termos de terceira ordem em diante, temos

τ

2

∂2η ∂t2 +

∂η ∂t = D

∂2η

∂x2, (1.7)

onde

D = 1

τ

Z +∞

−∞

ρ2

2 φ(ρ)dρ. (1.8)

A equa¸cão (1.7) representa uma espécie de difusão generalizada. A quantidade η(x, t) é a concentra¸cão de part´ıculas por unidade de comprimento em torno de x num instante arbitrário e a constante D é o coeficiente de difusão. No limite

τ

2

∂2η ∂t2 <<

∂η

∂t (1.9)

a equa¸c˜ao (1.7) se reduz para

∂η ∂t = D

∂2η

∂x2, (1.10)

(16)

do movimento browniano tal como analisado por Einstein. Como um exemplo ilustrativo desse tratamento, vamos obter a solu¸cão da equa¸cão (1.10) quando o processo difusivo satisfaz a seguinte condi¸cão inicial

η(x, t = 0) = N δ(x), (1.11)

onde N é o número total de part´ıculas e δ denota a fun¸cão de Dirac. De fato, a condi¸cão inicial acima implica que

Z +∞

−∞ η(x, t = 0)dx =

Z +∞

−∞ N δ(x)dx = N. (1.12)

A solu¸cão da equa¸cão (1.10) é mais facilmente obtida considerando o método de integral de Fourier. De acordo com esse método, a concentra¸cão pode ser definida como [19]

η(x, t) = √1 2π

Z +∞

−∞ ηk(t)e

ikx_dk, _(1.13)

onde os coeficientes da expans˜ao s˜ao determinados pela transformada inversa

ηk(t) = 1 √

2π

Z +∞

−∞ η(x

′_{, t}₎_e−ikx′

dx′. (1.14)

Calcularemos as derivadas temporal e espacial deη(x, t) e substituiremos os resultados na equa¸cão de difusão (1.10). Vemos de (1.13) que as derivadas são dadas por:

∂η ∂t =

1 √

2π

Z +∞

−∞

∂ηk

∂t e

ikx_dx, _(1.15)

∂2η ∂x2 = −

1 √

2π

Z +∞

−∞ k

2_η

k(t)eikxdk (1.16)

que substitu´ıdas em (1.10), resulta na seguinte express˜ao

1 √

2π

Z +∞

−∞

∂ηk

∂t e

ikx_dx₊ _√1 2π

Z +∞

−∞ Dk

2_η

(17)

ou equivalentemente, 1 √

2π

Z +∞

−∞ (

∂ηk

∂t +Dk

2_η

k)eikxdk = 0. (1.18)

Como a equa¸cão acima é válida para todo instante, seu integrando deve ser identicamente nulo, de forma que

∂ηk

∂t +Dk

2_η

k = 0, (1.19)

cuja solu¸c˜ao pode ser escrita imediatamente como:

ηk(t) = ηk0e−Dk

2_t

. (1.20)

Com este resultado, a defini¸c˜ao (1.13) toma a seguinte forma:

η(x, t) = √1 2π

Z +∞

−∞ ηk0(t)e −Dk2_t

eikxdk. (1.21)

Por outro lado, considerando que

η(x,0) = √1 2π

Z +∞

−∞ ηk0(t)e

ikx_dk, _(1.22)

temos para a transformada inversa

ηk0 = 1 √

2π

Z +∞

−∞ η(x

′_,₀₎_e−ikx′

dx′, (1.23)

e de (1.21), a concentra¸c˜ao de part´ıculas pode ser reescrita como

η(x, t) = 1 2π

Z +∞

−∞ η(x

′_,₀₎_dx′Z +∞

−∞ e

−Dk2_t

eik(x−x′)dk = 1

2π

Z +∞

−∞ η(x

′_,₀₎_dx′Z +∞

−∞ e

−Dk2_t

×

{cos[k(x₋x′)] +isin[k(x₋x′)]_}dk. (1.24)

Note que a segunda parcela na expressão acima é igual a zero, pois trata-se do produto de uma fun¸cão par por uma fun¸cão ´ımpar, com a equa¸cão se reduzindo para

η(x, t) = 1 2π

Z +∞

−∞ η(x

′_,₀₎_dx′Z +∞

−∞ e

−Dk2_t

(18)

A integra¸cão deste resultado é mais facilmente obtida considerando as seguintes mudan¸cas de variáveis: k = y, ρ = x ₋ x′ _e _α ₌ _Dt_{, com a} expressão (1.25) tomando a seguinte forma

η(x, t) = √ 1 4πDt

Z +∞

−∞ η(x

′_,₀₎_e−(x−x′)2

4Dt dx′. (1.26)

Para integrar essa expressão, devemos notar que de acordo com a condi¸cão (1.11), em t = 0 todas as part´ıculas estão centradas em torno da origem, ou seja, η(x′,0) = N δ(x′). Segue portanto, que a concentra¸cão pode ser escrita como

η(x, t) = √ N 4πDte

−x2

4Dt. (1.27)

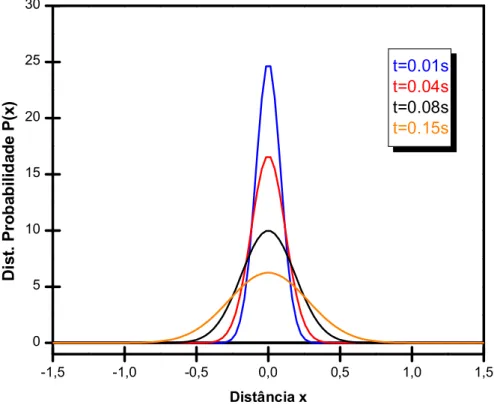
O resultado acima nos mostra que as part´ıculas se comportam como num processo gaussiano difusivo. A fun¸cão η(x, t) inicialmente representa uma delta centrada em torno da origem x = 0. No entanto, como veremos a seguir, à medida que o tempo passa ela evolui como uma distribui¸cão gaussiana de largura variável.

Uma vez calculado a fun¸cão η(x, t), é interessante determinar a distribui¸cão de probabilidade de que uma part´ıcula da amostra ocupe a posi¸cão entre x e x + ρ, quando em t = 0, iniciou seu movimento da posi¸cão x0 com velocidade inicial v0. O conhecimento de tal fun¸cão é de fundamental importância para se obter quantidades de interesse f´ısico, tais como o deslocamento quadrático médio e a variância na velocidade. A distribui¸cão de probabilidade pode ser obtida dividindo-se a concentra¸cão pelo número total de part´ıculas. Ou seja,

P(x, t) = η(x, t)

N =

1 √

4πDte

−x2

4Dt. (1.28)

Comparando essa equa¸c˜ao com a distribui¸c˜ao de probabilidades gaussiana

P(x) = √ 1 2πσ2e

−(x−<x>)2

2σ2 , (1.29)

(19)

Este resultado significa que na teoria do movimento browniano, as grandezas fisicamente relevantes estão diretamente relacionadas com os primeiros e os segundos momentos, que é uma propriedade geral da distribui¸cão gaussiana. Tais momentos podem ser calculados da rela¸cão:

< xn >= Z +∞

−∞ x

n_P₍_{x, t}₎_dx. _(1.30)

Utilizando a fun¸cão distribui¸cão (1.29), o valor de < x > e σ2 _{podem ser} obtidos diretamente por cálculos algébricos considerando a expressão geral. O primeiro momento é o deslocamento médio2,

< x >= Z +∞

−∞ x

1 √

4πDte

−x2

4Dtdx = 0. (1.31)

Seguindo a mesma prescri¸cão, o segundo momento da distribui¸cão é o deslocamento quadrático médio3 que pode ser escrito como (veja [19])

< x2 >= √ 2 4πDt

Z ∞

0 x

2_e−x2

4Dtdx = 2Dt (1.32)

que na teoria do MB é conhecida como rela¸cão de Einstein. O coeficiente de difusão D na equa¸cão (1.32) deve ser uma fun¸cão da temperatura e dos parâmetros geométricos da part´ıcula. Einstein mostrou que para part´ıculas esféricas de raio rp, o coeficiente D pode ser calculado a partir da mobilidade b e da temperatura do meio no qual a part´ıcula se encontra. O parâmetro b, denominado de mobilidade, pode ser obtido da fluidodinâmica, mais precisamente a partir da lei de Stokes [20]. A rela¸cão exata satisfeita por D é:

D = kBT b =

kBT

6πγrp (1.33)

onde γ representa o coeficiente de viscosidade do meio, rp é o raio das part´ıculas e b = 1/6πγrp. Com isso, o deslocamento quadrático médio das part´ıculas no MB fica perfeitamente determinado [21], a saber

2_{Pois o integrando ´e composto pelo produto de uma fun¸c˜}_{ao par por uma fun¸c˜}_{ao ´ımpar.}

3_{Para avaliar essa integral, basta fazer uso da seguinte rela¸c˜}_ao: R+∞ −∞ x

n_e−αx2_dx₌ 1

2 Γ(n+1

2 )

α(

n+1

(20)

< x2 >= RT 3πNaγrp

t. (1.34)

Na express˜ao acima utilizamos o fato de que a constante de Boltzman kB pode ser escrita como

kB =

R Na

, (1.35)

onde R é a constante universal dos gases e Na é o número de Avogadro. Portanto, vemos que a part´ıcula se comporta como um processo difusivo com < x2 > _∝ t. Toda essa formula¸cão unidimensional pode ser consistentemente extendido para três dimensões. Neste caso, não é dif´ıcil demonstrar que [20]

< r2 >= 6kBT bt =

RT πNaγrp

t, (1.36)

onde utilizamos o fato de que kB = R/Na.

As medidas experimentais do valor de < r2 > feitas por Jean Perrin em 1911, permitiram pela primeira vez se fazer uma estimativa do número de Avogadro4 [22], obtendo-se resultados bastante precisos para a época. Dessa forma, o movimento browniano tratado via descri¸cão de Einstein, passou a ser entendido como um método direto de se obter tal número, visto que os resultados estimados por outros autores não estavam de acordo com tais experiências.

Einstein posteriormente observou que seus resultados apresentavam inconsistência para escalas de tempos curtas em compara¸cão com os tempos caracter´ısticos do sistema. Uma maneira bastante fácil de perceber tais dificuldades é calculando a velocidade da part´ıcula diretamente da equa¸cão (1.36)

v =

v u u t

RT

2πNaγrp 1 √

t1/2. (1.37)

4_{Na ´epoca, Einstein j´a conhecia a constante universal dos gases}_R _{e a constante de Boltzmann} _k

B,

combinou uma rela¸c˜ao entre elas duas dada porkB=R/Na e dessa maneira foi poss´ıvel estimar o valor

(21)

Como pode ser visto na express˜ao acima, no limite t _−→ 0, a velocidade

v _{−→ ∞}, sendo esta a raiz da dificuldade.

Figura 1.1: As curvas mostram a evolu¸cão temporal da distribui¸cão de probabilidade η(x, t) no regime difusivo unidimensional. Para tempos próximos de zero a curva azul representa uma fun¸cão delta centrada em torno da origem x0 = 0. Com o passar do

tempo esta curva evolui como uma distribui¸c˜ao gaussiana de largura vari´avel.

(22)

permanecem v´alidos para um regime de tempo suficientemente longo em compara¸c˜ao a escala de tempo caracter´ıstica do sistema.

Para corrigir essas dificuldades, precisar´ıamos considerar o termo de derivada segunda com respeito ao tempo na equa¸cão de difusão (1.10). Em outras palavras, é importante considerar a solu¸cão anal´ıtica da equa¸cão (1.7), já que ela incorpora naturalmente o termo ∂η2/∂t2, sugerindo que para tempos curtos teremos uma descri¸cão ondulatória. Isso será feito com detalhe na se¸cão (1.6). Por enquanto, vamos proseguir examinando as diversas abordagens da teoria padrão do movimento browniano.

1.3 O Tratamento de Langevin

Poucos anos após o trabalho de Einstein, o f´ısico francês Paul Langevin [10], posteriormente seguido por Fürther [14], Ornstein [15] e outros mais, iniciaram uma série de estudos numa tentativa de abordar uma poss´ıvel generaliza¸cão daqueles resultados. Tal abordagem, comumente conhecida como tratamento de Langevin, será examinada com detalhe nesta se¸cão.

O tratamento de Langevin para o movimento browniano de uma part´ıcula livre, isto é, na ausência de um campo de for¸ca externo, é baseado na dinâmica de uma equa¸cão diferencial estocástica, mais popularmente conhecida como equa¸cão de Langevin [7]

dv

dt = −γv+ ξ(t), (1.38)

onde v denota a velocidade da part´ıcula. Nesta equa¸cão, a influência do meio sobre o movimento da part´ıcula é decomposta em duas partes. Em primeiro lugar, existe uma for¸ca que varia lentamente, F = ₋γv, representando uma friçcão dinâmica sobre o movimeto da part´ıcula, onde

(23)

de observa¸cão. Em outras palavras, ξ(t) é uma for¸ca flutuante que é uma caracter´ıstica básica de uma equa¸cão diferencial estocástica. Esta fun¸cão possui propriedades que Langevin definiu por duas condi¸cões

< ξ(t) >= 0, (1.39)

< ξ(t)ξ(t′) >= Γδ(t₋t′). (1.40)

De acordo com Ze’ldovich [23], essas propriedades caracterizam o chamado ru´ıdo branco (ver discuss˜ao nas p´aginas. 54 e 55).

A solu¸c˜ao anal´ıtica de (1.38) pode ser obtida pelo seguinte procedimento. Come¸camos por escrever a solu¸c˜ao da seguinte maneira (veja [7]):

v(t) = u(t)e−γt, (1.41)

onde u é uma fun¸cão de t a ser determinada. Calculando a derivada temporal da expressão acima e substituindo o resultado na equa¸cão original (1.38), vemos que ela satisfaz

du dt = e

γt_ξ₍_t₎_, _(1.42)

cuja solu¸c˜ao ´e trivialmente obtida:

u(t) =u0 +

Z t

0 e

γt′

ξ(t′)dt′, (1.43)

e substituindo em (1.41) temos que a solu¸cão geral da equa¸cão de Langevin é dada por [7]

v(t) = v0e−γt +e−γt

Z t

0 e

γt′

ξ(t′)dt′. (1.44)

Devemos agora usar as propriedades da fun¸cão ξ(t) para determinar a média e a variância na velocidade. Fazendo uso da propriedade (1.39) obtemos o valor médio da velocidade

(24)

Para determinar a dispers˜ao na velocidade, devemos primeiramente calcular a diferen¸ca v₋ < v >. Assim, obtemos

v₋ < v >= e−γtZ t

0 e

γt′

ξ(t′)dt′, (1.46)

que elevando ao quadrado segue a rela¸c˜ao

(v₋< v >)2 = e−2γtZ t

0

Z t

0 e

γ(t′

+t′′

)_ξ₍_t′₎_ξ₍_t′′₎_dt′′_dt′_, _(1.47)

a qual, tomando a m´edia, utilizando a propriedade (1.40) e afetuando a integra¸c˜ao pode ser escrita como

(_△v)2 = Γ

2γ(1−e

−2γt₎_. _(1.48)

onde (_△v)2 =< v2 > ₋ < v >2. Para determinar a constante Γ, lembremos que o regime estacionário é alcan¸cado para intervalos de tempos muito longos quando comparados com os tempos de flutua¸cão da fun¸cão ξ(t), de modo que < v > em (1.45) se anula, e segue também de (1.48) que

< v2 >= Γ

2γ. (1.49)

Por outro lado, o teorema da equiparti¸cão, impõe que a energia cinética média de uma part´ıcula em movimento corresponde a 1₂kBT para cada grau de liberdade, mais precisamente

1

2m < v

2 _>₌ 1

2kBT, (1.50)

onde kB é a constante de Boltzmann. Relacionando as duas últimas equa¸cões, obtemos a rela¸cão exata entre o coeficiente Γ e a temperatura do meio externo, a saber

Γ = 2γkBT

m . (1.51)

(25)

x = x0 +

Z t

0 v(t

′₎_dt′ _(1.52)

onde x0 é a posi¸cão da part´ıcula em t = 0. Considerando o valor de v(t) dado pela expressão (1.44), segue o resultado:

x = x0 +v0

Z t

0 e

−γt′

dt′+ Z t

0 e

−γt′Z t ′

0 ξ(t

′′₎_eγt′′

dt′dt′′, (1.53)

o qual, efetuando a integral em t’ e invertendo a ordem da ´ultima parcela, obtemos

x = x0 +v0 1

γ(1−e

−γt_{) +} 1

γ

Z t

0 ξ(t

′′₎₍₁₋_eγ(t′′

−t)₎_dt′′_. _(1.54)

Desta equa¸cão obtemos também o deslocamento médio

< x >= x0 +v0 1

γ(1−e

−γt₎_, _(1.55)

sendo o deslocamento quadr´atico m´edio obtido calculando-se primeira-mente a diferen¸ca

x₋< x >= 1

γ

Z t

0 ξ(t

′′₎₍₁₋_eγ(t′′

−t)₎_dt′′ _(1.56)

de onde obtemos

(x₋< x >)2 = 1

γ2

Z t

0

Z t

0 ξ(t

′₎_ξ₍_t′′₎₍₁₋_eγ(t′

−t)₎₍₁

−eγ(t′′−t))dt′dt′′. (1.57)

Tomando a m´edia na express˜ao acima, usando a propriedade (1.40) e efetuando as integrais, encontramos

(_△x)2 = Γ

γ2{t− 2

γ(1−e

−γt_{) +} 1

2γ(1−e

−2γt₎

}. (1.58)

Desta expressão, segue que no regime de tempos longos, o termo dominante é o primeiro, com a variância na posi¸cão se reduzindo para

(_△x)2 = Γ

(26)

e considerando o resultado (1.51) para o coeficiente Γ, temos que

(_△x)2 = 2kBT

mγ t, (1.60)

ou equivalentemente

(_△x)2 = 2Dt (1.61)

que é o resultado de Einstein e D é o coeficiente de difusão que pode ser dado por kBT /mγ ou pela equa¸cão (1.33).

Portanto, vemos que no regime de tempos longos em compara¸cão com os tempos próprios do sistema, a abordagem de Langevin é equivalente a descri¸cão de Einstein.

A partir de agora, é interessante determinar a distribui¸cão de probabilidade relativa à variável v, pois ela pode ser vista como uma outra maneira de calcular quantidades de interesse f´ısico conforme mostrado na se¸cão anterior. Como vimos, a velocidade de uma part´ıcula livre imersa num meio viscoso e sujeita a for¸ca estocástica ξ(t), varia de acordo com a equa¸cão de Langevin. A distribui¸cão de probabilidade é mais facilmente obtida discretizando o tempo em intervalos iguais, simplesmente escrevendo

t = nτ. Dessa maneira, a equa¸c˜ao (1.38), pode ser reescrita como (veja [7])

vn+1 −vn

τ = −γvn +cξn, (1.62)

onde c ´e uma constante a ser determinada. Tal equa¸c˜ao ainda poder ser reescrita na seguinte forma

vn+1 = αvn+cξn, (1.63)

onde estamos considerando o fato de que α = (1₋ γτ). A constante c é determinada a partir das médias temporais das fun¸cões ξ(t) e ξ(t′), e não é dif´ıcil verificar que seu valor é dado por c =

r

Γ

(27)

é obter uma expressão geral para a velocidade vn, entretanto, precisamos antes de mais nada, determinar alguns valores para vn+1, afim de obter uma expressão geral para vn. Alguns resultados são computados

v1 = √

Γτ ξ0; (1.64)

v2 = √

Γτ_{αξ0 +ξ1}; (1.65)

v3 = √

Γτ_{α2ξ0 +αξ1 +ξ2}; (1.66)

v4 = √

Γτ_{α3ξ0 + α2ξ1 + αξ2 + ξ3}; (1.67)

v5 = √

Γτ_{α4ξ0 + α3ξ1 +α2ξ2 +αξ4}. (1.68)

Considerando os resultados acima, n˜ao ´e dif´ıcil perceber que o termo geral pode ser escrito como [7]

vn = n−1

X

l=0

ωl, (1.69)

onde ωl ´e definido por

ωl = √

Γτ αlξn−1−l. (1.70)

Nestes resultados estamos simplesmente supondo que v0=0. Para se calcular a densidade de probabilidade da variável vn, no caso de n suficientemente grande, basta usar a expansão da fun¸cão caracter´ıstica5 em cumulantes até segunda ordem [7]

g(k) = eiak−b2k2 (1.71)

5_{Podemos interpretar a fun¸c˜}_{ao caracter´ıstica como sendo uma fun¸c˜}_{ao geradora dos momentos. A}

expans˜ao de uma fun¸c˜ao caracte´ıstica geral pode ser escrita como φ(k) =R

eikx_p(x)dx₌R

p(x)dx(1 + ikx−2!1k2x2−

1

3!k3x3+...) = 1 +ik < x >−

k2

2! < x2>+...+ (ik)n

n! < x

(28)

onde a e b, são respectivamente a média e a variância. No nosso caso, se a variável aleatória vn é definida pela expressão (1.69), então a fun¸cão caracter´ıstica relativa a tal variável é definida como sendo

gn(k) =< eikvn >= n−1

Y

l=0

< eikωl _>, _(1.72)

pois as variáveisωl são todas independentes. Supondo que a distribui¸cão de probabilidade da variável ξl seja uma gaussiana de média zero e variância 1, segue que a distribui¸cão da variável ωl também será uma gaussiana de média zero, no entanto, de variância b = α2lΓτ. Logo

< eikωl _>₌ _e−α2lΓτk

2

2 (1.73)

e de (1.72) segue que

gn(k) =e−Γτ

Pn−1

l=0α2

l_k2_/2

= e−bnk2/2_, _(1.74)

onde o termo bn ´e dado por

bn = −Γτ n−1

X

l=0

α2l = Γτ1−α

2n

1₋α2 . (1.75)

Como é bem conhecido, a distribui¸cão de probabilidade é obtida através da antitransformada de fourier da fun¸cão gn(k), mais precisamente

Pn(vn) = 1 2π

Z ∞

−∞gn(k)e

−ikvn_dk ₌ 1

2π

Z ∞

−∞e −bnk

2

2 (coskv_n−isinkv_n)dk.

(1.76) Nesta expressão, apenas o primeiro termo se mantém, pois o segundo se trata do produto de uma fun¸cão par por uma fun¸cão ´ımpar, com a equa¸cão se reduzindo para

Pn(vn) = 1 2π

Z ∞

−∞e −bnk

2

2 coskv

ndk = 1 √

2πbn

e−vn2/2bn. (1.77)

(29)

escrita como

Pn(vn) = 1

q

2πb(t)e

−vn2/2b(t), (1.78)

onde b(t) ´e o limite de bn, dado por

b(t) = Γ

2γ(1−e

−γt_{) =} kBT

m (1−e

−γt₎_. _(1.79)

Portanto, quando t_{→ ∞} observamos que b(t) _→ KT_m e a distribui¸cão da variável aleatótria vn segue uma maxwelliana dada por [17]

P(v) = ( m 2πkBT

)12 exp(− mv

2

2kBT

). (1.80)

1.4 A Equa¸

c˜

ao de Fokker-Planck

Como vimos na se¸cão 1.3, a equa¸cão de Langevin na forma (1.38) descreve o movimento de uma part´ıcula de massa m imersa em um fluido com coeficiente de viscosidade γ. Este mesmo sistema pode ser descrito através de uma equa¸cão de movimento que governa a evolu¸cão temporal de uma distribui¸cão de probabilidades. Tal equa¸cão é comumente conhecida como equa¸cão de Fokker-Planck e constitue o objeto de investiga¸cão desta se¸cão. A equa¸cão de Fokker-Planck é um tipo especial de equa¸cão mestra (veja [9], [24]), freqüentemente usada como uma boa aproxima¸cão para descrever processos markovianos mais gerais. Suas elegantes propriedades matemáticas servem de ferramentas indispensáveis para fazer aplica¸cões em diferentes situa¸cões f´ısicas, particularmente em sistemas não lineares.

Suponha uma equa¸c˜ao de Langevin da seguinte forma (veja [7])

dx

dt = f(x) +ξ(t), (1.81)

onde a variávelx denota a coordenada generalizada, que em princ´ıpio pode ser de velocidade ou de posi¸cão. A equa¸cão de Fokker-Planck para uma variável pode ser escrita na forma (como exemplo, veja [9])

∂η(x, t)

∂t = − ∂

∂x[f(x)η(x, t)] +

Γ 2

∂2η(x, t)

(30)

onde f(x) está relacionado com a natureza da for¸ca atuando na equa¸cão (1.81) e η(x, t) é a distribui¸cão de probabilidade de encontrar a part´ıcula no intervalo de coordenada x e x+dx. A equa¸cão (1.82) também pode ser reescrita como

∂η(x, t)

∂t +

∂S(x, t)

∂x = 0, (1.83)

que representa uma equa¸c˜ao de continuidade para a densidade de probabilidade η(x, t), enquanto a quantidade S(x, t) deve ser interpretada como sendo uma corrente de probabilidade definida por

S(x, t) =f(x)η(x, t)₋ Γ 2

∂η(x, t)

∂x . (1.84)

A integra¸c˜ao de (1.83) no intervalo que x assume valores [a, b] nos fornece

∂ ∂t

Z b

a η(x, t)dx = S(a, t)−S(b, t) (1.85)

e como

Z b

a η(x, t)dx = 1, (1.86)

segue que

S(a, t) =S(b, t). (1.87)

Portanto, a conserva¸cão da probabilidade total não deve ser uma conseqüência apenas da equa¸cão de Fokker-Planck mas também das condi¸cões de contorno.

Vamos determinar a solu¸cão da equa¸cão de Fokker-Planck na forma (1.83) para o caso estacionário, ou seja, para o caso em que η(x, t) não depende explicitamente do tempo. Assim, segue de (1.84)

f(x)η(x) = Γ 2

∂η(x)

∂x = 0, (1.88)

pois no regime estacionário o valor de s(x, t) não exerce nenhuma dependência com o tempo. A solu¸cão da equa¸cão acima pode ser escrita como

η(x) =AeΓ2 R

(31)

onde a constante A é obtida da condi¸cão de normaliza¸cão de η(x). Temos que

A =

Ã

m

2πkBT

!1/2

, (1.90)

com a densidade de probabilidade assumindo a forma

η(x) =

"

m

2πkBT

#1/2 exp Ã Γ 2 Z

f(x)dx

!

. (1.91)

Para o caso de uma for¸ca viscosa,f(x) = ₋γv, a solu¸c˜ao acima ser´a escrita como

η(v) =

Ã

m

2πkBT

!1/2

exp



−

mv2

2kBT



, (1.92)

que é a distribui¸cão de velocidades de Mawell. Outro exemplo interessante é observado quando a for¸ca atuante no sistema é do tipo elástica, ou seja,

f(x) =₋kx. Neste caso a solu¸c˜ao pode ser dada por [7]

η(x) =

Ã

k

2πkBT

!1/2

exp



−

kx2 2kBT



, (1.93)

que ´e tamb´em uma maxwelliana.

A solu¸cão geral válida para qualquer tempo é obtida resolvendo diretamente a equa¸cão (1.82). Para o caso de uma for¸ca viscosa ₋γv, a equa¸cão de Fokker-Planck (1.82) pode ser escrita como [9]

∂η(v, t)

∂t = γ ∂

∂v[vη(v, t)] +

γkBT

m

∂2η(v, t)

∂v2 , (1.94)

com solu¸c˜ao dada por [29]:

η(v, t) =





m

2πkBT(1−e−2γt)

  1/2 exp  −

m(v ₋v0e−γt)2 2kBT(1−e−2γt)



. (1.95)

Comparando a expressão acima com a distribui¸cão gaussiana (veja equa¸cão 1.29), vemos que o valor de < v > é dado por

(32)

e a variˆancia (_△v)2 como

(_△v)2 = m 2πkBT

(1₋e−2γt). (1.97)

Portanto, vemos que para intervalos de tempos suficientemente longos, esses resultados nos mostram que o sistema relaxa para o estado de equil´ıbrio e a distribui¸cão de probabilidades se reduz para uma maxwelliana. Vemos também que o movimento browniano de uma part´ıcula livre, pode ser descrito tanto do ponto de vista da equa¸cão de Langevin quanto da equa¸cão de Fokker-Planck, de forma que quando esses dois métodos são comparados, nos fornecem os mesmo resultados.

A partir de agora, o nosso objetivo é fazer uma poss´ıvel conexão com o problema da caminhada aleatória e a equa¸cão de Fokker-Planck. Como discutido na se¸cão anterior, um caminhante aleatório que se desloca ao longo de uma coordenada x obedece a uma distribui¸cão de probabilidade da forma

ηN(m) =

N!

(N+m₂ )!(N−₂m)!p

N+m

2 (1−p)

N−m

2 , (1.98)

obedecendo a seguinte rela¸c˜ao de recorrˆencia

ηN+1(m) = pηN(m −1) +qηN(m+ 1). (1.99)

A passagem para o cont´ınuo é feita levando a fun¸cão de variáveis discretas

ηN(m) numa fun¸cão de variáveis cont´ınuas η(x, t). Conforme já foi visto, é fácil mostrar que

ηN+1(m) =η(t+τ, x), (1.100)

ηN(m+ 1) = η(t, x+l), (1.101)

e

(33)

Substitu´ındo esses resultados na equa¸cão (1.99) e fazendo uma expansão em série de Taylor até termos de segunda ordem, obtemos

∂2η(x, t)

∂t2 + 2

τ

∂η(x, t)

∂t =

2l(q ₋p)

τ2

∂η(x, t)

∂x + l2

2τ2

∂2η(x, t)

∂x2 . (1.103)

A expressão acima representa uma equa¸cão de Fokker-Planck generalizada para a distribui¸cão de probabilidade η(x, t), pois contém uma derivada segunda da fun¸cão η com respeito ao tempo. Note que, considerando o mesmo tipo de aproxima¸cão (ver Eq.(1.9))

∂2η(x, t)

∂t2 << 2

τ

∂η(x, t)

∂t , (1.104)

ficamos com

∂η(x, t)

∂t = −

l(p₋q)

τ

∂η(x, t)

∂x + l2

4τ

∂2η(x, t)

∂x2 , (1.105)

ou equivalentemente (veja [7])

∂η(x, t)

∂t = −c

∂η(x, t)

∂x +

Γ 2

∂2η(x, t)

∂x2 , (1.106)

onde estamos utilizando o fato de que c = l(p_τ−q) e Γ = _2τl2. A solu¸c˜ao geral da equa¸c˜ao acima pode ser escrita como

η(x, t) =

  1 2πl2 τ t   1/2 exp   −

[x₋ l(p_τ−q)t]2 2l2

τ t





, (1.107)

onde podemos ver que a m´edia6 _{e a variˆancia podem ser dadas} respectivamente por

< x >= l(p−q)

τ t, (1.108)

(_△x)2 = l 2

τ t. (1.109)

Portanto, observamos que o problema da caminhada aleatória está intimamente relacionado a equa¸cão de Fokker-Planck, de forma que as grandezas de interesse f´ısico podem ser obtidas diretamente da fun¸cão distribui¸cão.

6_{Esse resultado nos mostra que para}_p₌_q_{= 1/2, o valor de}_{< x >}_{´e nulo como haver´ıamos de esperar.}

(34)

1.5 Caminhadas Aleat´

orias: Tratamento de M. Kac

O problema do caminhante aleatório, é dotado de um caráter bastante universal em f´ısica. No magnetismo, por exemplo, um átomo de spin 1/2 tem um momento magnético ~µ e de acordo com a mecânica quântica, o spin pode está “up” ou “down”, com respeito a uma dada dire¸cão. Se essas possibilidades são igualmente prováveis, então qual o momento magnético médio < ~µ > para uma amostra contendo N átomos? Um outro problema bastante familiar, corresponde a difusão de part´ıculas num meio intermolecular. Suponha que uma part´ıcula percorre uma distância média l entre duas colisões sucessivas com as moléculas do meio. Qual será a distância percorrida após N colisões?

O principal critério de solu¸cão para o problema da caminhada aleatória, na sua forma mais geral, é facilmente entendido considerando a versão mais simples do problema em uma dimensão tal como originalmente investigado por M. Kac [8]. Suponha que um caminhante aleatório partindo da origem e se deslocando em linha reta, realiza n1 passos de comprimento fixo l para a direita com probabilidade p ou realiza n2 passos para a esquerda com probabilidade q = 1 ₋ p, de modo que p + q = 1. Além do mais, estamos considerando que os passos são eventos mutuamente independente. O problema é determinar qual a probabilidade PN(m) de encontrar o caminhante na posi¸cão x = ml, onde ₋N _≤ m _≤ N, depois de ter dado N

passos. O n´umero total de passos ´e

N = n1 +n2, (1.110)

sendo m a grandeza que parametriza a distˆancia l´ıquida percorrida, isto ´e,

m = n1 −n2. (1.111)

(35)

a partir da origem ´e dada por

x = (n1 −n2)l = ml. (1.112)

Considerando que os passos são estatisticamente independentes, de probabilidades p e q, então a probabilidade de realizar n1 passos para a direita e n2 passos para a esquerda é independente da sequência de passos e pode ser escrita como (veja [27])

p.p.p...p_×q.q.q...q = pn1_qn2_. _(1.113)

Existem várias maneiras de arranjar os N passos de forma que n1 seja o número de passos para a direita e n2 seja o número de passos para a esquerda. Na verdade, descobrir o número de maneiras de arranjar os passos n1 e n2, é descobrir de quantas maneiras distintas podem ser arranjados n1 + n2 objetos, sendo que a permuta¸cão de qualquer um dos objetos (n1 + n2) é irrelevante. Tal fato significa que o número de probabilidades distintas é exatamente [25]

N!

n1!n2!

. (1.114)

A probabilidade totaluN(n1) de realizar n1 passos para a direita en2 para a esquerda num total de N passos, em qualquer ordem, ´e dada pelo produto [27]

uN(n1) =

N!

n1!(N −n1)!

pn1_qN−n1_, _(1.115)

pois todas as sequˆencias s˜ao independentes. Como vemos, o valor de

uN obedece a então chamada distribui¸cão binomial. Lembrando que a expansão binomial de (p+ q)N, onde p e q são dois números quaisquer, é dada por

(p+q)N = XN

n=0

N!

n1!(N −n1)!

pn1_qN−n1_, _(1.116)

segue que a distribui¸c˜ao uN(n1) ´e normalizada [19], ou seja, N

X

n1=0

uN(n1) = N

X

n=0

N!

n1!(N −n1)!

(36)

A partir de agora, vamos determinar a probabilidade PN(m) do caminhante se encontrar na posi¸c˜ao x = ml. Das equa¸c˜oes (1.110) e (1.111), temos que

n1 =

N +m

2 , n2 =

N ₋m

2 , (1.118)

e substituindo esses resultados em (1.115), segue que a distribui¸c˜ao,PN(m), ´e dada por

PN(m) =

N!

(N+m₂ )!(N−₂m)!p

N+m

2 q

N−m

2 , (1.119)

ou, equivalentemente,

PN(m) =

N!

(N+m₂ )!(N−₂m)!p

N+m

2 (1−p)

N−m

2 . (1.120)

Para fazer a conexão com fenômenos de difusão, temos que descrever o problema do caminhante aleatório por meio de uma equa¸cão diferencial envolvendo variáveis cont´ınuas. Supondo que τ seja o tempo necessário para realizar um passo, então PN(m) dado por (1.120) é a probabilidade da part´ıcula se encontrar na posi¸cão x = ml no tempo N τ. Somente uma part´ıcula que esteja emx = (m₋1)l oux = (m+1)l no tempot = (N₋1)τ

poderá atingir a posi¸cãox = ml. No passo seguinte, a probabilidadePN(m) obedece a rela¸cão de recorrência (veja [8] )

PN+1(m) =pPN(m−1) +qPN(m+ 1). (1.121)

(37)

fun¸cão cont´ınuaη(N τ, ml) = η(t, x). Reescrevendo a rela¸cão de recorrência (1.121) para η(t, x), temos

PN+1(m) =η((N + 1)τ, ml) =η(N τ +τ, ml) = η(t+ τ, x), (1.122)

PN(m+ 1) = η(N τ,(m+ 1)l) =η(N τ, ml+l) = η(t, x+l), (1.123)

PN(m−1) = η(N τ,(m −1)l) =η(N τ, ml−l) =η(t, x−l). (1.124)

Portanto, pode ser observado de (1.121) que a seguinte rela¸cão de recorrência para a nova fun¸cão cont´ınua η(N τ, ml) deve ser satisfeita

η(t+ τ, x) = pη(t, x₋l) +qη(t, x+l). (1.125)

Expandindo ambos os lados em s´erie de Taylor at´e termos de segunda ordem, temos

η+τ∂η ∂t+

1 2τ

2∂2η

∂t2 = p



η −l

∂η ∂x +

l2

2

∂2η ∂x2



+q 

η +l

∂η ∂x +

l2

2

∂2η ∂x2



, (1.126)

ou ainda

η +τ∂η ∂t +

1 2τ

2∂2η

∂t2 = (p+q)η +l(q −p)

∂η

∂x + (p+q) l2

2

∂2_η

∂x2. (1.127)

Considerando o fato de que a probabilidade total satisfaz p+q = 1, temos que

τ

2

∂2η ∂t2 +

∂η ∂t =

l

τ(q −p) ∂η ∂x +

l2

2τ ∂2η

∂x2, (1.128)

(38)

Algumas aproxima¸cões interessantes devem ser discutidas na equa¸cão (1.128). Primeiramente, verificamos que a conexão direta com o movimento browniano difusivo é estabelecida quando assumimos que p = q = 1/2. Neste caso, definindo

D = l 2

2τ (1.129)

a equa¸c˜ao (1.128) se reduz para

τ

2

∂2_η

∂t2 +

∂η ∂t = D

∂2_η

∂x2, (1.130)

que é precisamente a equa¸cão (1.7). Por se tratar de uma equa¸cão diferencial hiperbólica, o resultado acima representa uma difusão generalizada de part´ıculas. A equa¸cão de difusão usual que serviu de base para o tratamento de Einstein é novamente recuperada quando fazemos o mesmo tipo de aproxima¸cão (veja a equa¸cão (1.9))

τ

2

∂2η ∂t2 <<

∂η

∂t, (1.131)

com a equa¸c˜ao (1.130) se reduzindo a forma usual

∂η ∂t = D

∂2η

∂x2. (1.132)

Portanto, a conexão com o cont´ınuo fica perfeitamente estabelecida, de modo que todo o tratamento posterior, em particular, o cálculo dos valores médios das grandezas relevantes, permanece idêntico ao da se¸cão (1.2).

1.6 A Equa¸

c˜

ao de Difus˜

ao Generalizada

Como vimos nas se¸cões (1.2) e (1.5), se expandirmos até segunda ordem a fun¸cão η(x, t), obtemos uma equa¸cão generalizada para a difusão de part´ıculas, a qual é do tipo hiperbólica. Com uma aproxima¸cão conveniente (τ₂∂_∂t2η2 <<

∂η

(39)

utilizada para descrever transmissão de calor e difusão de part´ıculas, constitue na verdade, um modelo aproximado para uma descri¸cão menos rigorosa de tais fenômenos. Um argumento favorável a essa visão se baseia na idéia de que equa¸cões parabólicas do tipo (1.132) transmitem sinais com velocidades infinitas. Naturalmente, tal resultado é inconsistente já que a velocidade máxima com a qual uma perturba¸cão se propaga num determinado meio elástico, ou num fluido, deve ser da ordem da velocidade do som. Entretanto, (1.132) pode ser aplicada para regimes de tempo suficientemente longos quando comparados aos tempos caracter´ısticos do sistema.

Se considerarmos que em cada intervalo de tempo τ a part´ıcula se desloca aleatoriamente com uma velocidade c = _τl, vemos que a equa¸c˜ao (1.130) pode ser reescrita como

∂2η ∂t2 +

c2 D

∂η ∂t = c

2∂2η

∂x2, (1.133)

que representa uma equa¸cão de onda amortecida para a caminhada aleatória. Tal equa¸cão deve ser relevante do ponto vista conceitual, já que a introdu¸cão de uma derivada segunda com respeito ao tempo em η(x, t), pode ser útil para resolver algumas ambiguidades presentes na descri¸cão de Einstein. Conforme mencionado antes, essas dificuldades surgem naturalmente devido ao fato de que equa¸cões do tipo (1.132) apresentam inconsistências para pequenos intervalos de tempos. Entretanto, tais dificuldades podem ser corrigidas se ao invés de considerarmos a equa¸cão de difusão usual, que é do tipo parabólica, considerarmos a equa¸cão (1.130) que é uma equa¸cão do tipo hiperbólica.

Para estudar a influˆencia do termo ∂2η/∂t2 vamos considerar uma onda plana se deslocando num meio infinito. Em x = 0 ´e assumido que

(40)

(1.130), pode ser escrita como [28]

η(x, t) = eAxei(ωt−Bx), (1.134)

que nos fornece

A2 = _ω2 1

2c2[(1 + c 4

D2_ω2)1/2 + 1]

, (1.135)

onde c é a velocidade média das part´ıculas e ω é a freqüência de vibra¸cão da onda. A constante B é dada por

B2 = ω 2

2c2[(1 +

c4 D2_ω2)

1/2 _{+ 1]}_. _(1.136)

A velocidade de propaga¸c˜ao da onda pode ser escrita como

v2 = ω 2

B2 =

2c2

[(1 + _Dc24_ω2)1/2 + 1]

< c2. (1.137)

Para o caso em que ω << c2/D, ou equivalentemente,

∂2η ∂t2 <<

∂η

∂t, (1.138)

as rela¸c˜oes anteriores se reduzem a

A2 = B2 = ω

2D, (1.139)

v2 = 2ωD, (1.140)

(41)

A solu¸cão geral da equa¸cão (1.130) para as condi¸cões η(x,0) = δ(x) e (∂η/∂t)t=0 = 0 pode ser escrita como [28]

η(x, t) = e−t/τ

"

1

2δ(x+ct) + 1

2δ(x−ct)

#

+

1 2cτJ0[

(x2 ₋c2t2)1/2

cτ ] + t

2τ

J1[(x2 −c2t2)1/2/cτ]

(x2 ₋_c2_t2₎1/2 , (1.141)

que é válida para _| x _|≤ ct. Na expressão acima, J0 e J1 são fun¸cões de Bessel de primeira espécie.

Para o caso _| x _|> ct, nós recuperamos a solu¸cão de D’Alambert para uma onda plana amortecida se deslocando na dire¸cão x

η(x, t) = e−t/τ

"

1

2δ(x+ct) + 1

2δ(x−ct)

#

. (1.142)

A equa¸cão acima nos mostra que a velocidade de propaga¸cão da onda nunca excede a velocidade das part´ıculas. Como o produtocτ é da ordem do livre caminho médio λ, o argumento das fun¸cões J0 e J1 cresce rapidamente qundo _| x _| é muito menor que ct. Neste caso podemos usar a expansão assintótica para as fun¸cões de Bessel

Jν(x) ≈ 2

πxcos

"

x₋ π

2(p+ 1 2)

#

. (1.143)

Com isso, (1.141) fica escrita como

η(x, t) = e−t/τ

"

1

2δ(x+ ct) + 1

2δ(x−ct)

#

+

e−τty

2

4cτ

"

πt

2τ(1−y

2₎1/2

#−1/2 h

1 + (1₋y2)−1/2i (1.144)

(42)

No limite y << 1, ou equivalentemente x << ct (tempos longos), o segundo termo da solu¸c˜ao acima tende para

η(x, t) = 1

(2c2_{τ tπ}₎1/2e

−x2_/2c2_{τ t}

= 1

(4πDt)1/2e

−x2_/4Dt

(1.145)

onde reintroduzimos D pela equa¸cão (1.129). A fun¸cão acima representa exatamente a solu¸cão da equa¸cão de difusão usual, que serviu de base para a descri¸cão de Einstein, como pode ser verificado na se¸cão (1.2).

(43)

Cap´ıtulo 2

Descri¸

c˜

ao Lagrangiana para Sistemas

com Amortecimento Vari´

avel

2.1 Introdu¸

c˜

ao

O conhecimento adquirido na investiga¸cão de sistemas oscilatórios tem uma extensa literatura na f´ısica. Em particular, um considerável esfor¸co foi dedicado ao estudo do comportamento temporal de osciladores harmônicos (amortecido e for¸cado) no dom´ınio clássico, estat´ıstico e quântico [31-53]. O crescente interesse por tais sistemas vem da possibilidade de modelar uma grande variedade de fenômenos f´ısicos alterando ligeiramente sua estrutura vibracional básica. Estudos modernos nesse campo estão diretamente relacionados a modelos dissipativos para dinâmica de terremotos e avalanches em sistemas granulares [32], descri¸cão de ´ıons quânticos altamente resfriados [33], estudos não clássicos da luz [34], bem como o movimento de ´ıons e átomos em armadilhas iônicas e magneto-ópticas [35].

(44)

e velocidades na fun¸cão lagrangiana [37]. Na proposta de Bateman, os efeitos de amortecimentos são incorporados ao oscilador harmônico simples através de uma exponencial dependente do tempo que generaliza a descri¸cão lagrangiana padrão para sistemas conservativos. Embora apresente algumas ambiguidades conceituais na sua descri¸cão quântica [43]-[52], este modelo é considerado relevante tanto do ponto de vista teórico quanto conceitual, tendo recebido considerável aten¸cão na literatura.

Neste cap´ıtulo descreveremos um tratamento lagrangiano para sistemas dissipativos que generaliza a abordagem de Bateman, cujo comportamento estoc´astico ser´a discutido na parte original desse trabalho (ver cap. III).

2.2 Lagrangiana Para Sistemas Dissipativos

Iniciaremos esta se¸cão focalizando nossa aten¸cão no seguinte problema: vamos considerar um pêndulo descrevendo pequenas amplitudes de oscila¸cão cuja massa varia satisfazendo uma rela¸cão do tipo M = meλt. Tal sistema pode ser representado por um balde preso a um fio de comprimento

l descrevendo um movimento oscilatório simples. A varia¸cão de sua massa deve-se unicamente às gotas de água caindo numa taxa constante (ver figura 2.1).

Classicamente, tal sistema pode ser descrito pela lagrangiana [49]

L = 1 2(me

γt_{) ˙}_x2 ₋ 1 2(me

γt₎_ω2_x2_, _(2.1)

ou equivalentemente [50],

L = 1 2Mx˙

2 ₋ 1

2M ω

2_x2_. _(2.2)

A lagrangiana acima, descreve um oscilador harmônico simples de freqüência ω2 = g/l, entretanto a massa é variável M = meγt, onde m

(45)

Figura 2.1: O balde de massa M está suspenso por um fio de comprimento l. O sistema executa um movimento harmônico simples, mas tem sua amplitude variável devido às gotas de água da chuva caindo numa taxa constante. A massa M cresce obedecendo a rela¸cãoM =meλt_.

pode ser escrita como [50]

Mx¨+ ˙Mx˙ + ∂V

∂x = 0, (2.3)

que representa um sistema com massa variável. O momento canônico é definido da maneira usual [36]

pc =

∂L

∂x˙ = Mx,˙ (2.4)

que também é o momento cinético. Da mesma forma, a hamiltoniana é definida por [20, 36]

H = px˙ ₋L = 1 2Mx˙

2 ₊_V₍_x_{) =} p

2 c

2M +V(x) =E (2.5)

(46)

por meγt a lagrangiana se reduz para [49]

L(x,x, t˙ ) = eγt

"

1 2mx˙

2

− 1

2mω 2_x2

#

(2.6)

cuja equa¸c˜ao de movimento pode ser escrita como

¨

x = ₋γx˙ ₋ω2x = 0, (2.7)

que mostra explicitamente a presen¸ca da for¸ca de friçcão ₋γmx˙ e que também descreve o oscilador harmônico unidimensional. O momento canônico é definido da maneira usual

pc =

∂L ∂x˙ = e

γt_p

cin, (2.8)

da mesma forma a hamiltoniana ser´a escrita como

H = eγtE. (2.9)

Portanto, vemos que o momento canônico pc é diferente do momento cinético pcin, assim como a hamiltoniana é diferente da energia total do sistema. No entanto, tal energia pode ser obtida multiplicando (2.7) por

˙

x, que nos fornece

dE

dt = Fdx,˙ (2.10)

onde Fd = −γmx˙ é a for¸ca dissipativa. Assim, vemos que o lado direito da equa¸cão acima é a potência dissipada devido a for¸ca de friçcão, mostrando que (2.6) deve ser interpretada como a lagrangiana de um sistema dissipativo, cuja for¸ca viscosa é proporcional a velocidade.

(47)

2.3 O

q

-Oscilador

Uma classe mais geral de sistemas amortecidos que não podem ser descritos dentro da aproxima¸cão lagrangiana de Bateman é representado por osciladores sujeitos a uma friçcão dependente do tempo. Nesta se¸cão, vamos nos concentrar nesta categoria de comportamento oscilatório, para o qual foi recentemente proposta uma lagrangiana dependente do tempo descrita por um parâmetro cont´ınuo q tomando valores sobre os números reais. Assumiremos que o potencial tem pontos de retorno. Por simplicidade, consideraremos somente o caso unidimensional. Tal espécie de sistemas será genericamente chamados deq-osciladores. Para uma classe especial de potenciais, as equa¸cões de movimento resultantes são resolvidas considerando diferentes taxas de amortecimentos e regimes desta fam´ılia paramétrica de osciladores. Como veremos adiante, o oscilador harmônico simples é um atrator estável para esta classe de sistemas vibracionais. Isto significa dizer que uma larga classe de fenômenos transientes onde a energia é parcialmente dissipada, entram em um regime oscilatório simples depois de uma escala de tempo finita. O comportamento dinâmico dos

q-osciladores com amortecimento dependente do tempo, pode ser descrito pela seguinte lagrangiana [53]

Lq(x,x, t˙ ) = eq(γt)[ 1 2mx˙

2

−V(x)], (2.11)

onde γ é uma constante arbitrária com dimensão de inverso de tempo. A fun¸cão eq(γt) é chamada q-exponencial, a qual é definida por

eq(γt) = [1 + (1−q)γt]1/1−q, (2.12)

(48)

como também o q-análogo de muitas fun¸cões especiais também tem sido estudado, veja [55] e referências lá citadas. Naturalmente, uma visão mais rigorosa desta distribui¸cão está além do presente estudo. No nosso caso, vamos considerá somente a propriedade fundamental da q-exponencial que é definida como [56]

lim

q→1eq(y) =e

y_. _(2.13)

Portanto, quando q _→ 1 vemos que eq(γt) → eγt e a q-lagrangiana (2.11) se reduz a forma original de Bateman quando assumimos V(x) = m₂ω₀2x2

[38]. A fun¸c˜ao hamiltoniana correspondente ´e escrita como

Hq(x, p, t) = ˙x∂Lq

∂x˙ −Lq =

p2

2m

1

eq(γt)

+ V(x)eq(γt), (2.14)

que se reduz a hamiltoniana de Bateman

H = e−γt p

2

2m +e

γt_V₍_x₎ _(2.15)

no limite q _→ 1. A dependˆencia temporal expl´ıcita de (2.14) implica que

Hq(x, p, t) não é a energia do sistema, ou seja, ele é de fato não conservativo. A equa¸cão de movimento obtida da q-lagrangiana (2.11) pode ser dada por

mx¨+mγq(t) ˙x+

dV

dx = 0, (2.16)

onde

γq(t) =

γ

1 + (1₋q)γt. (2.17)

(49)

0 20 40 60 t (s)

0.00 0.05 0.10 0.15

γq

(t)

q = 0.5 q = 0.8 q = 0.95 q = 0.99 q = 1.0

0 20 40 60

t(s) −2.0

−1.0 0.0 1.0 2.0

γq

(t)

q = 1.1 q = 1.2 q = 1.5

Figura 2.2: Evolu¸cão do coeficiente de friçcão γq(t) para diferentes valores do parâmetro

livreq. O gráfico à esquerda representa o comportamento paraq <1, e no outro, à direita, a evolu¸cão para q >1.

amortecidas são um atrator estável para o q-oscilador com amortecimento variável. Isto é uma diferen¸ca fundamental entre o oscilador amortecido usual com constante γ e o q-oscilador discutido aqui. O comportamento de γq(t) para diferentes valores de q é mostrado na Fig. (2.2).

Para q < 1, o coeficiente γq(t) diminue continuamente com o tempo sendo a taxa de decrescimento mais rápida para menores valores de q. Porém, para q > 1, γq(t) inicialmente aumenta se aproximando de um valor infinito em t = [γ(q₋1)]−1_{, e então muda abruptamente seu sinal, se} aproximando de zero para grandes valores do tempo. Naturalmente, estas caracter´ısticas apontam um comportamento qualitativo bastante diferente para uma distribui¸cão natural de q-osciladores em duas subclasses. A primeira é um subconjunto bem comportado caracterizado por q < 1, enquanto a segunda (o caso anômalo) tem q maior que a unidade.

(50)

varia¸c˜ao da energia do sistema. A energia total ´e definida por

E = 1 2mx˙

2 ₊_V₍_x₎_. _(2.18)

Reescrevendo a express˜ao (2.14) em termos do par (x,x˙) obtemos

Hq = eq(γt)[1 2mx˙

2 ₊_V₍_x_{)] =} _e

q(γt)E, (2.19)

agora derivando (2.18) com respeito ao tempo e usando a equa¸cão de movimento (2.16) é fácil mostrar que a taxa de dissipa¸cão da energia pode ser escrita como

dE

dt = −mγq(t) ˙x

2 ₌

− mγx˙

2

1 + (1₋q)γt. (2.20)

Esta expressão mostra que a taxa de varia¸cão da energia vai efetivamente a zero para escalas de tempo muito maior que_|γ(1₋q)_|−1. Neste limite, para todas as proposta práticas, o q-oscilador se aproxima do regime oscilatório harmônico. No entanto, para q > 1 e tempo t > _|γ(q ₋ 1)_|−1 temos uma mudan¸ca de sinal nas expressões acima. Conseqüentemente, embora se aproximando do mesmo regime final depois desta escala de tempo, a segunda classe deq-osciladores se comporta na maior parte do tempo como um oscilador harmônico for¸cado sob a a¸cão de uma for¸ca dependente do tempo

Fext = |γq(t)|x.˙ (2.21)

Agora vamos considerar o mais interessante dos q-osciladores do ponto de vista f´ısico, aquele para o qual q é muito menor que a unidade. Para mostrar as solu¸cões anal´ıticas da equa¸cão (2.16), vamos considerar o potencial do oscilador harmônico, V(x) = 1₂mω₀2x2. Introduzindo um tempo auxiliar

T = 1 + (1₋q)γt, (2.22)

a equa¸c˜ao de moviment (2.16) toma a seguinte forma

d2x dT2 −

1 (q ₋1)

1

T dx dT +δ

2

(51)

onde

δq =

ω0

γ(1₋q). (2.24)

A solu¸cão geral da equa¸cão de movimento (2.23) é dada por [56]

x(T) =Tνζν(δqT) (2.25)

onde ζν denota combina¸c˜oes lineares das fun¸c˜oes de Bessel de ordem ν que depende do par ˆmetro q, da seguinte forma

ν = q

(q₋1). (2.26)

Agora, retornando a antiga variável t, a solu¸cão geral da equa¸cão de movimento (2.16) pode ser escrita como [53]

x(t) = [eq(γt)]−q/2{AJν(ω0t+δq) +BYν(ω0t+δq),} (2.27)

onde Jν e Yν são fun¸cões de Bessel de primeira e segunda espécie respectivamente, e A e B são constantes a serem determinadas de acordo com as condi¸cões iniciais. Para as condi¸cões iniciais arbitrárias x(0) = x0 e ˙x(0) = v0 as constantes A e B são

A = π

2δq[x0Yν−1(δq)−

v0

ω0

Yν(δq)] (2.28)

e

B = ₋π

2δq[x0Jν−1(δq)−

v0

ω0

Jν(δq)]. (2.29)

A Fig.(2.3) mostra os gr´aficos do q-oscilador para alguns valores do parˆametro q sobre o intervalo 0 < q <1.