Soluções cosmológicas e locais para uma eletrodinâmica modificada

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE PROGRAMA DE P ÓS-GRADUAÇ ÃO EM FÍSICA

DISSERTAC¸ ˜AO DE MESTRADO

Solu¸

c˜

oes Cosmol´

ogicas e locais para uma

Eletrodinˆ

amica modificada

Calistrato Soares da Cˆamara Neto

Submetida para obten¸c˜ao do grau de Mestre em F´ısica

(2)

SUM ´

ARIO

1

Introdu¸

c˜

ao

5

2

Eletromagnetismo de Maxwell

7

2.1 Equa¸c˜oes de Maxwell . . . 7

2.2 Formula¸c˜ao das Equa¸c˜oes de Maxwell na Relatividade Especial . . . 12

2.2.1 Covariˆancia da equa¸c˜ao da for¸ca de Lorentz . . . 17

2.3 O tensor momento-energia para o campo eletromagn´etico na Rela-tividade Especial. . . 17

3

Eletromagnetismo na Relatividade Geral

19

3.1 O Princ´ıpio da Equivalˆencia e as equa¸c˜oes de Einstein . . . 19

3.2 O Princ´ıpio da Covariˆancia Geral e o Princ´ıpio do Acoplamento Gra-vitacional M´ınimo . . . 22

3.3 Equa¸c˜oes de Maxwell na Relatividade Geral . . . 23

3.3.1 C´alculo Variacional para a Eletrodinˆamica de Maxwell na Re-latividade Geral . . . 25

3.4 O tensor momento-energia para o campo eletromagn´etico na Rela-tividade Geral . . . 26

4

Propostas Alternativas de Eletromagnetismo

28

4.1 Eletrodinˆamica N˜ao-Linear . . . 28

4.2 Lagrangeanas de Primeira Classe . . . 30

4.3 Lagrangeanas de Segunda Classe . . . 31

4.4 Lagrangeanas efetivas para uma teoria n˜ao-linear . . . 32

(3)

5

Aplica¸

c˜

oes `

a Cosmologia

34

5.1 Introdu¸cão. . . 34 5.2 Solu¸cão geral paraΛ = 0 e um campo magnético dependente do tempo 37 5.3 Solu¸cão Geral para Λ =constante₆= 0 e um campo magnético

depen-dente do tempo . . . 39 5.4 Solu¸c˜ao Geral para um campo magn´etico constante e Λ dependente

do tempo . . . 40 5.5 Um coment´ario sobre a solu¸c˜ao para Λ = 0 e um campo magn´

e-tico dependente do tempo a partir de corre¸cões quânticas para a eletrodinâmica clássica . . . 44

6

Aplica¸

c˜

oes ao Problema da Massa Puntual Carregada

50

6.1 Introdu¸cão. . . 50 6.2 Equa¸cões fundamentais. . . 50 6.3 Solu¸cão das Equa¸cões de Einstein-Maxwell . . . 53

7

Conclus˜

oes

75

A

Relatividade Especial

80

(4)

LISTA DE FIGURAS

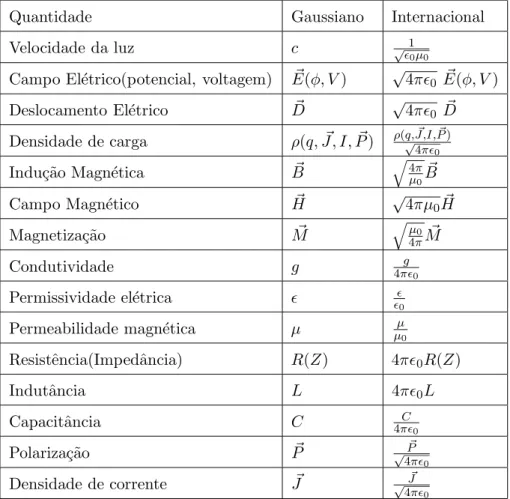
5.1 O painel superior mostra o fator de escala (linha s´olida) e o campo magn´etico

(linha tracejada), enquanto que o painel inferior mostra a densidade de energia

(linha s´olida) e a press˜ao (linha tracejada) para o modelo com

ω= 6,67_×10−31m2/N e Λ = 0. B0foi escolhido de tal forma que

q

2ω B0 = 0.2 eB0/Bcr= 0.5. . . 47

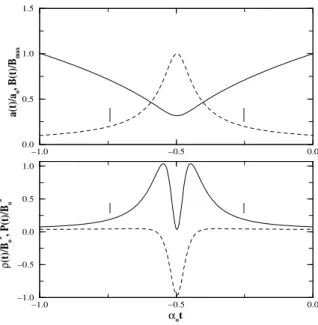
5.2 O painel superior mostra o fator de escala (linha s´olida) e o campo magn´etico

(linha tracejada), enquanto que o painel inferior mostra a densidade de energia

(linha s´olida) e a press˜ao (linha tracejada) para o modelo com

ω= 6,67_×10−31 m2/N e uma constante n˜ao-nula Λ. Os valores para Λ e B0

s˜ao tais que√λ/α0 = 2×10−4 e

q

2ω

B0 = 0.2. . . 48

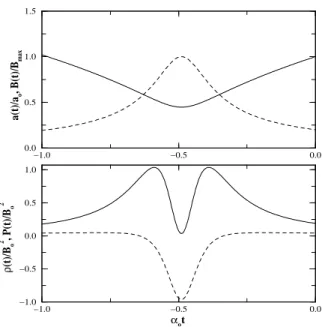
5.3 Como na Figura 5.2 mas para √λ/α0 = 5×10−5 e

q

2ω

B0 = 0.05. . . 48

5.4 O fator de escala (linha sólida) e o parâmetro cosmológico (linha tracejada)

para o modelo com campo magn´etico constante, ω = 6,67_×10−31 m2/N, Λ

dependente do tempo e K0 > 0 (

q

2ω

B0 = 1). No painel superior

√

λ0/α0 = 1

enquanto que no painel inferior √λ0/α0= 0.5. . . 49

5.5 Como na Figura 5.4 mas para K0 < 0 (

q

2ω

B0 = 0.1). No painel superior

√

λ0/α0= 1 enquanto que no painel inferior √λ0/α0 = 0.5. . . 49

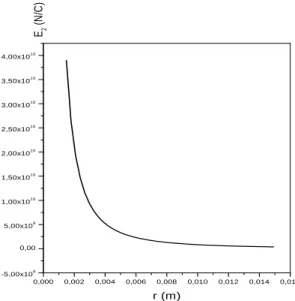
6.1 A figura mostra o campo el´etrico radial E2, rela¸c˜ao (6.41), para

ω= 1_×10−12 m2/N,α= 382 C.m/s e π

3 >Θ≥

π

6

. . . 66

ω= 1_×10−12 m2/N,α= 382 C.m/s e

−π3 >Θ≥ −

π

2

. . . 66

ω= 1_×10−12 m2/N,α= 382 C.m/s e hπ >Θ_≥ 5₆πi . . . 67

ω= 1_×10−12 m2/N,α=₋382 C.m/s e

0<Θ_≤ π₆

(5)

6.5 A figura mostra o campo el´etrico radial E2, rela¸c˜ao (6.41), para ω= 1_×10−12 _m2_/N_,_α₌₋₃₈₂ _C.m/s _e h₋2π

3 <Θ≤ −π2

i

. . . 68

ω= 1_×10−12 _m2_/N_,_α₌₋₃₈₂ _C.m/s _e h2π

3 <Θ≤ 5

π

6

i

. . . 68

ω= 1_×10−12 _m2_/N_,_α_{= 382} _C.m/s _e

−π3 >Θ≥ −

π

2

. . . 69

6.8 A figura mostra o campo el´etrico radial E3 , rela¸c˜ao (6.42), para

ω= 1_×10−12 _m2_/N_,_α_{= 382} _C.m/s _e π

3 >Θ≥

π

6

. . . 69

ω= 1_×10−12 m2/N,α= 382 C.m/s e

−π

3 >Θ≥ −π2

. . . 70

ω= 1_×10−12 m2/N,α=₋382 C.m/s e h₋2₃π <Θ_{≤ −}π₂i . . . 70

6.11 A figura mostra o campo el´etrico radial E3 , rela¸c˜ao (6.42), para

ω= 1_×10−12 _m2_/N_,_α₌₋₃₈₂ _C.m/s _e h2π

3 <Θ≤ 5

π

6

i

. . . 71

ω= 1_×10−12 _m2_/N_,_α₌₋₃₈₂ _C.m/s _e

0<Θ_≤ π₆

. . . 71

6.13 A figura mostra o gr´afico da componente g00, solu¸c˜ao (6.55), para

ω= 6,67_×10−11 m2/N e α= 1,6_×102 C.m/s . . . 72

6.14 A figura mostra o campo el´etrico radial E da solu¸c˜ao (6.58)

(li-nha sólida) e o campo elétrico clássico (linha tracejada), obtidos para

ω= 6,67_×10−11 _m2_/N _e _α_{= 160}_C.m/s _{. . . .} ₇₂

6.15 A figura mostra o campo el´etrico radial E da solu¸c˜ao (6.58)

(li-nha sólida) e o campo elétrico clássico (linha tracejada), obtidos para

ω= 6,67_×10−11 m2/N e α=₋160 C.m/s . . . 73

6.16 A figura mostra o campo el´etrico radial E da solu¸c˜ao (6.60) para

ω=₋6,67_×10−11 m2/N e α= 160C.m/s . . . 73

6.17 A figura mostra a componente g00 da m´etrica para a solu¸c˜ao de

Reissner-Nordström (linha sólida) e a rela¸cão (6.59) obtida numericamente

(6)

LISTA DE TABELAS

2.1 Equa¸cões de Maxwell, rela¸cões constitutivas e constantes eletromagnéticas nos

principais sistemas de unidade . . . 11

2.2 Principais grandezas eletromagn´eticas no SI e no Sistema Gaussiano . . . 12

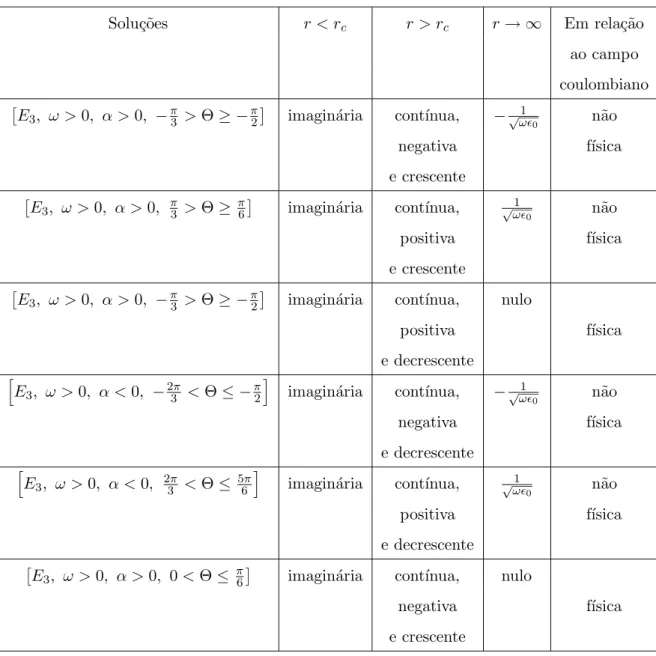
6.1 A tabela abaixo mostra o comportamento das solu¸c˜oesE1 parar > rc er > rc,

o comportamento assint´otico (r_{→ ∞}) e analisa a validade f´ısica dessas solu¸c˜oes

em rela¸c˜ao ao campo coulombiano. . . 59

6.2 A tabela seguinte mostra, de forma an´aloga a tabela anterior, o comportamento

para as solu¸c˜oes E2. . . 60

6.3 A tabela seguinte mostra, de forma an´aloga a tabela anterior, o comportamento

(7)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE Solu¸cões Cosmológicas e locais para uma Eletrodinâmica modificada

Submetida para obten¸c˜ao do grau de Mestre em F´ısica Novembro 2001

Calistrato Soares da Cˆamara Neto ABSTRACT

The present work investigates some consequences that arise from the use of a modified lagrangean for the eletromagnetic field in two different contexts: a spatially homogeneous and isotropic universe whose dynamics is driven by a magnetic field plus a cosmological parameter Λ, and the problem of a static and charged point mass (charged black hole). In the cosmological case, three different general solutions were derived. The first, with a null cosmological parameter Λ, generalizes a particular solution obtained by Novello et al [gr-qc/9806076]. The second one admits a constant Λ and the third one allows Λ to be a time-dependent parameter that sustains a constant magnetic field. The first two solutions are non-singular and exhibit inflationary periods. The third case studied shows an inflationary dynamics except for a short period of time. As for the problem of a charged point mass, the solutions of the Einstein-Maxwell equations are obtained and compared with the

stan-dard Reissner-Nordstr¨om solution. Contrary to what happens in the cosmological case, the

(8)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE Solu¸cões Cosmológicas e locais para uma Eletrodinâmica modificada

Submetida para obten¸c˜ao do grau de Mestre em F´ısica Novembro 2001

Calistrato Soares da Cˆamara Neto RESUMO

No presente trabalho são investigadas algumas conseqüências da utiliza¸cão de uma nova

la-grangeana para a eletrodinˆamica em dois contextos: um universo espacialmente homogˆeneo

e isotrópico com campo magnético mais um parâmetro cosmológico Λ e o problema da massa

puntual carregada e est´atica (buraco negro carregado). No caso cosmol´ogico, foram

obti-das três solu¸cões gerais: a primeira delas, para Λ = 0, generaliza uma solu¸cão particular

obtida por Novello et al [gr-qc/9806076], a segunda admite um parˆametro cosmol´ogico

con-stante e n˜ao-nulo e a terceira corresponde a um campo magn´etico constante sustentado por

um Λ dependente do tempo . As duas primeiras solu¸cões são não-singulares e possuem

per´ıodos inflacionários. A terceira solu¸cão apresenta uma dinâmica inflacionária exceto por um curto intervalo de tempo. No contexto do problema da massa puntual carregada, a

solu¸cão das equa¸cões de Einstein-Maxwell é obtida e comparada com a solu¸cão padrão de

(9)

AGRADECIMENTOS

A Deus, por ter me dado essa oportunidade.

A minha Fam´ılia, pela paciˆencia e colabora¸c˜ao durante todos os anos da minha vida.

Ao meu orientador, Prof. Dr. M´arcio Maia, pelos quatro anos de amizade .

Aos Professores Joel Cˆamara Carvalho e Jos´e Ademir Sales de Lima, pela importante

contribui¸c˜ao nesse trabalho.

Ao colega Jailson, pelos conselhos e pela colabora¸c˜ao importante nos momentos

deci-sivos.

Aos demais colegas e professores da Pós-Gradua¸cão pela amizade e pela contribui¸cão

para a minha forma¸c˜ao acadˆemica.

Ao DFTE e ao Programa de P´os-Gradua¸c˜ao em F´ısica da UFRN, pelo apoio importante

para a realiza¸c˜ao desse trabalho.

`

(10)

CAP´

ITULO 1

Introdu¸

c˜

ao

A Relatividade Geral tem tido grande ˆexito na sua tentativa de explicar a origem e a

evolu¸cão do universo. Várias das suas previsões teóricas foram confirmadas

observacional-mente ao longo do século XX. Por outro lado, a Teoria da Gravita¸cão de Newton é bastante

adequada para descrever a maioria dos fenˆomenos f´ısicos que ocorrem em nossa gal´axia.

Já a Eletrodinâmica Clássica de Maxwell é uma teoria formulada a partir da observa¸cão

macroscópica de fenômenos eletromagnéticos e sua aplica¸cão tecnológica atual é bastante

extensa. No dom´ınio atômico, contudo, essa teoria requer modifica¸cões. A Eletrodinâmica

Quˆantica ´e uma das propostas para se descrever esse dom´ınio da realidade.

Em uma descri¸c˜ao mais real´ıstica da origem do universo, assim como na an´alise dos

bu-racos negros, a estrutura de pequena escala deve ser considerada [1]-[2]. Nessa estrutura, o

acoplamento entre a gravita¸cão e as outras intera¸cões se modificam em rela¸cão a estrutura

de larga escala.

O presente trabalho analisa algumas eletrodinâmicas não clássicas e suas correla¸cões com

a gravita¸cão. Esse assunto tem sido extensivamente estudado ao longo das últimas décadas

[3]-[10]. Tratamos aqui, mais especificamente, da altera¸cão de solu¸cões cosmológicas no

con-texto dos modelos de Friedmann-Robertson-Walker (FRW) e de solu¸c˜oes para uma massa

puntual carregada, generalizando a solu¸cão de Reissner-Nordström [11]. A disserta¸cão está

organizada em cap´ıtulos como se segue.

No Cap´ıtulo 2 ´e feita uma introdu¸c˜ao ao Eletromagnetismo de Maxwell, apresentando

as principais equa¸cões na formula¸cão diferencial e na formula¸cão covariante no contexto da

Relatividade Especial. A referˆencia [12] foi a principal fonte utilizada.

No Cap´ıtulo 3 s˜ao apresentados os principais princ´ıpios e equa¸c˜oes da Relatividade Geral.

(11)

a partir do Princ´ıpio do Acoplamento M´ınimo.

O Cap´ıtulo 4 apresenta um resumo de algumas das propostas de eletromagnetismo n˜ao

clássico e suas principais conseqüências. Dentre as fontes utilizadas, a mais analisada para

esse cap´ıtulo foi a referˆencia [4].

O Cap´ıtulo 5 constitui uma aplica¸c˜ao `a Cosmologia do acoplamento escolhido para ser

analisado neste trabalho. Esse cap´ıtulo mostra como uma eletrodinˆamica n˜ao-linear altera

a solu¸cão cosmológica padrão para o universo de FRW. Ao final do cap´ıtulo é feita uma

compara¸cão entre a nossa solu¸cão e a solu¸cão da referência [1], obtida a partir de corre¸cões

quˆanticas.

O Cap´ıtulo 6 é uma aplica¸cão ao problema da massa puntual carregada. A solu¸cão padrão

de Reissner-Nordström é resgatada e uma nova solu¸cão é obtida para uma eletrodinâmica

não-linear. Essas duas solu¸cões são comparadas e algumas diferen¸cas são apresentadas e

discutidas.

O Cap´ıtulo 7 resume alguns resultados e dificuldades e apresenta propostas de

desenvolvi-mento desse trabalho.

O Sistema Internacional de Unidades (SI) ser´a utilizado ao longo de toda esta disserta¸c˜ao,

salvo men¸c˜ao expl´ıcita em contr´ario.

A assinatura da métrica utilizada é₋2. Os ´ındices gregos assumirão os valores 0, 1, 2 e 3

(12)

CAP´

ITULO 2

Eletromagnetismo de Maxwell

Como fundamenta¸cão teórica para essa disserta¸cão, apresentarei um resumo da parte principal

da teoria da Eletrodinâmica Clássica na Relatividade Especial, a qual será utilizada neste

trabalho.

As Equa¸c˜oes de Maxwell s˜ao apresentadas, tanto nas formas diferencial e covariante,

como a partir de cálculo variacional. Os aspectos e as conseqüências f´ısicas relevantes dessas

equa¸cões também são discutidos.

No final do cap´ıtulo, é apresentada a formula¸cão covariante da equa¸cão da for¸ca de Lorentz.

Uma explica¸c˜ao mais detalhada do assunto referente a esse cap´ıtulo ´e encontrada nas

referˆencias [11]-[13].

2.1 Equa¸c˜oes de Maxwell

A teoria eletromagn´etica cl´assica foi desenvolvida a partir de um extenso trabalho

experi-mental. Suas leis fundamentais s˜ao, portanto, de natureza emp´ırica. Por essa raz˜ao, elas

não podem ser provadas do ponto de vista teórico. Durante mais de dois séculos, foram

realizadas diversas experiˆencias que comprovaram macroscopicamente a sua validade. Essas

leis são expressas pelas quatro Equa¸cões de Maxwell, que são as equa¸cões fundamentais da

teoria eletromagn´etica.

No SI, as equa¸cões de Maxwell, para fontes no vácuo, são [12]

∇ •E~ = ρ

ǫ0

, (2.1)

∇ ×B~ = µ0J~+µ0ǫ0 ∂ ~E

∂t, (2.2)

∇ ×E~ + ∂ ~B

(13)

∇ •B~ = 0, (2.4) onde E~, B~, J~, µ0, ǫ0 e ρ são, respectivamente, o campo elétrico, a indu¸cão magnética, a

densidade de corrente, a permeabilidade magnética do vácuo, a permissividade elétrica do

v´acuo e a densidade de carga.

A primeira rela¸c˜ao expressa a Lei de Gauss para a eletricidade e pode ser obtida da Lei

de Coulomb para a a for¸ca el´etrica.

A dependência da for¸ca elétrica com o inverso do quadrado da distância foi mostrada

quantitativamente por Coulomb e Cavendish. Atrav´es das suas experiˆencias com a balan¸ca

de tor¸cão e esferas concêntricas, eles mostraram essa dependência com pequena precisão .

Experiˆencias mais precisas testam a validade da lei do inverso do quadrado da distˆancia

de duas formas:

(a) Supondo que a for¸ca varia com _r2+1δ, onde r é a distância entre duas cargas elétricas, e

estabelecendo um limite superior paraδ.

(b) Admitindo que o potencial eletrost´atico tem a forma do potencial de Yukawar−1_e−αr _e

estabelecendo um limite para αouα−1. Como α= mγc

¯

h ondemγ ´e a massa do f´oton, c

é a velocidade da luz no vácuo e ¯h é a constante de Planck dividida por 2π, o teste da

lei do inverso do quadrado da distˆancia pode ser realizado atrav´es do estabelecimento

de um limite superior para mγ.

Williams, Faller e Hill [12], realizando uma experiˆencia semelhante `a de Cavendish,

ob-tiveram o limiteδ _≤(2,7_±3,1)_×10−16.

Medidas do campo geomagn´etico da terra fornecem um limite para a massa do f´oton de

mγ≤4×10−51 kg ou α−1 ≥108 m.

Experiências mais precisas mostram que a Lei de Coulomb é válida para r _≥ 10−17 _m,

podendo a massa do f´oton ser considerada nula nesse caso.

A segunda equa¸cão é uma generaliza¸cão da Lei de Ampère. O termoµ0ǫ0∂ ~∂tE foi adicionado

por Maxwell à Lei de Ampère _{∇ ×}B~ =µ0J~. A introdu¸cão desse termo é considerada como

uma das maiores contribui¸cões dada por Maxwell à teoria eletromagnética.

A equa¸cão (2.3) expressa a Lei de Indu¸cão de Faraday e nos permite quantificar o fenômeno

da indu¸c˜ao eletromagn´etica.

(14)

Tomando-se o divergente da rela¸cão (2.2) e empregando a equa¸cão (2.1), obtém-se uma

equa¸c˜ao de continuidade relacionando a densidade de corrente e a densidade de carga

∂ρ

∂t +∇ •J~= 0. (2.5)

Outra importante conseqüência das equa¸cões de Maxwell é que a luz é uma onda

eletro-magn´etica e sua velocidade em um determinado meio pode ser medida atrav´es da

permissivi-dade elétrica ǫe da permeabilidade magnética µ desse meio. Para o vácuo essa velocidade é

c= 2,99792458_×108m/s, valor este que tem extrema importância nos fenômenos óticos e no estudo da Teoria da Relatividade. Ela também é uma das constantes fundamentais da F´ısica

e ´e utilizada para definir o metro no SI.

Outra rela¸c˜ao importante do Eletromagnetismo ´e a for¸ca de Lorentz que age sobre uma

part´ıcula carregada q movendo-se com velocidade ~v,

~

F =q(E~ +~v_×B~). (2.6)

As equa¸cões de Maxwell no vácuo são lineares nos campos E~ e B~. A dispersão cromática e a difra¸cão dos raios-X são exemplos de fenômenos f´ısicos em que essa linearidade é válida.

Diversas observa¸cões experimentais mostram que a linearidade é válida tanto para campos

macrosc´opicos como para campos criados em n´ıveis atˆomicos.

Existem também situa¸cões em que efeitos não-lineares ocorrem. Os materiais

ferro-magn´eticos e os cristais submetidos a intensos feixes de laser s˜ao alguns exemplos.

Em n´ıveis atômicos e subatômicos, a linearidade pode também não ser válida. Existe

uma não linearidade dos campos eletromagnéticos na Mecânica Quântica que surge devido

ao Princ´ıpio da Incerteza permitir a cria¸cão de um par elétron-pósitron por dois fótons e um

subseqüente desaparecimento do par com a emissão de dois outros fótons diferentes. Este

processo ´e conhecido como espalhamento de luz por luz.

Para um meio qualquer, as equa¸c˜oes de Maxwell s˜ao escritas para os campos macrosc´

o-picos, ou seja, n˜ao s˜ao considerados os campos produzidos por cada part´ıcula elementar que

constitui a distribui¸cão de carga e sim a média macroscópica dos campos por elas produzidas.

Essas equa¸c˜oes s˜ao

∇ •D~ = ρ, (2.7)

∇ ×H~ = J~+ ∂ ~D

(15)

∇ ×E~ + ∂ ~B

∂t = 0, (2.9)

∇ •B~ = 0, (2.10)

ondeD~ é o deslocamento elétrico eH~ é o campo magnético.

As rela¸cões constitutivas D~ = D~(E~), H~ = H~(B~) e J~ = J~(E~), para meios lineares e isotrópicos, são, no SI,

~

D = ǫ ~E, (2.11)

~

H = µ ~B, (2.12)

~

J = g ~E, (2.13)

ondeǫ, µ e g são, respectivamente, a permissividade elétrica, a permeabilidade magnética e

a condutividade elétrica do meio. A terceira rela¸cão constitutiva é conhecida como Lei de

Ohm.

´

E poss´ıvel também relacionar D~ e E~ com a polariza¸cão P~ e H~ e B~ com a magnetiza¸cão

~ M,

~

D = ǫ0E~ +P ,~ (2.14)

~

H = 1

µ0 ~

B₋M .~ (2.15)

Existem ainda situa¸c˜oes mais gerais em que (2.11), (2.12) e (2.13) s˜ao generalizadas pelas

rela¸c˜oes D~ =D~(E, ~~ B), H~ =H~(E, ~~ B) e J~=J~(E, ~~ B).

A Tabela 2.1 mostra as equa¸c˜oes de Maxwell nos sistemas de unidades mais comuns [12],

assim como os valores de ǫ0 e µ0. As rela¸c˜oes entre D~,E~ e P~ e entreH~, B~ e M~ tamb´em se

encontram nesta tabela.

A Tabela 2.2 mostra como converter as diversas grandezas eletromagn´eticas do Sistema

(16)

Tabela 2.1: Equa¸cões de Maxwell, rela¸cões constitutivas e constantes eletromagnéticas nos

principais sistemas de unidade

Sistema ǫ0 µ0 D~,H~ Equa¸c˜oes de

Max-well

Eletrost´atico 1 c−2 D~ =E~ + 4π ~P _{∇ •}D~ = 4πρ

∇×H~ = 4π ~_cJ+1_c∂ ~_∂tD

~

H=B~ ₋4π ~M _{∇ ×}E~ +1_c∂ ~_∂tB = 0

∇ •B~ = 0

Eletromagn´etico c−2 1 D~ = _c12E~+4π ~P ∇ •D~ = 4πρ

∇ ×H~ = 4π ~J+∂ ~_∂tD

~

H=B~ ₋4π ~M _{∇ ×}E~ +∂ ~_∂tB = 0

∇ •B~ = 0

Gaussiano 1 1 D~ =E~ + 4π ~P _{∇ •}D~ = 4πρ

∇×H~ = 4π ~_cJ+1_c∂ ~_∂tD

~

H=B~ ₋4π ~M _{∇ ×}E~ +1_c∂ ~_∂tB = 0

∇ •B~ = 0

Heaviside-Lorentz

1 1 D~ =E~ +π ~P _{∇ •}D~ =ρ

∇ ×H~ = J_c~ +1_c∂ ~_∂tD

~

H=B~ ₋π ~M _{∇ ×}E~ +1_c∂ ~_∂tB = 0

∇ •B~ = 0

MSKA ₄_πmc1072

4π

107 D~ =ǫ0E~ +P~ ∇ •D~ =ρ

∇ ×H~ =J~+∂ ~_∂tD

~

H= _µ1₀B~ ₋M~ _{∇ ×}E~ +∂ ~_∂tB = 0

(17)

Tabela 2.2: Principais grandezas eletromagn´eticas no SI e no Sistema Gaussiano

Quantidade Gaussiano Internacional

Velocidade da luz c √_ǫ1

0µ0

Campo El´etrico(potencial, voltagem) E~(φ, V) √4πǫ0 E~(φ, V)

Deslocamento El´etrico D~ √4πǫ0 D~

Densidade de carga ρ(q, ~J , I, ~P) ρ(q, ~√J ,I, ~P)

4πǫ0

Indu¸c˜ao Magn´etica B~ q4_µπ

0

~ B

Campo Magn´etico H~ √4πµ0H~

Magnetiza¸c˜ao M~ qµ0

4πM~

Condutividade g ₄_πǫg

0

Permissividade el´etrica ǫ ǫ

ǫ0

Permeabilidade magn´etica µ _µµ

0

Resistˆencia(Impedˆancia) R(Z) 4πǫ0R(Z)

Indutˆancia L 4πǫ0L

Capacitˆancia C C

4πǫ0

Polariza¸c˜ao P~ √P~

4πǫ0

Densidade de corrente J~ √J~

4πǫ0

2.2 Formula¸c˜ao das Equa¸c˜oes de Maxwell na Relatividade Especial

Em 1904, H. A. Lorentz encontrou um tipo de transforma¸c˜ao que deixava as Equa¸c˜oes de

Maxwell invariantes na sua forma. Apesar dessa descoberta, ele n˜ao conseguiu dar um

signifi-cado f´ısico para a mesma. Essa transforma¸cão é conhecida como transforma¸cão de Lorentz.

Poincaré e Lorentz demonstraram a invariância da forma das Equa¸cões de Maxwell sob as

transforma¸cões de Lorentz antes da formula¸cão da Relatividade Especial. A invariância da

forma, ou covariˆancia, dessas equa¸c˜oes, e da for¸ca de Lorentz, implica que as fontesρ e J~e

os campos E~ e B~ transformam-se de uma maneira bem definida sob as transforma¸c˜oes entre

referenciais inerciais.

(18)

covariante na Relatividade Restrita. Para a equa¸c˜ao da continuidade (2.5) podemos definir

um quadrivetor correnteJα_{= (}_{cρ, J}1_{, J}2_{, J}3_{), onde}_J1 ₌_J

x,J2 =Jy,J3=Jz. Dessa forma,

a equa¸c˜ao da continuidade ´e escrita na forma covariante como

∂αJα= 0 . (2.16)

A defini¸cão deJα como quadrivetor decorre do fato que a carga elétrica q é invariante sob

as transforma¸cões de Lorentz. Esta invariância é provada experimentalmente. Experiências

mostram que a carga do el´etron n˜ao depende significativamente da velocidade, pelo menos

para velocidades da ordem de 0,4c. Comodq´e invariante edq=ρd3_x _onde_d3_x_{´e o elemento}

infinitesimal de volume, ent˜aocρse transforma como a componentex0do quadrivetor posi¸c˜ao,

isto ´e, como a componente temporal da quadricorrente. De forma an´aloga,

~

J = (J1, J2, J3) se transforma como as componentes espaciais da quadricorrente.

Das equa¸c˜oes (2.3) e (2.4), obtemos as rela¸c˜oes abaixo para os campos E~ e B~ ~

E = ₋∂ ~A

∂t − ∇φ, (2.17)

~

B = _{∇ ×}A,~ (2.18)

ondeA~ é o potencial vetor eφé o potencial elétrico. Substituindo-se (2.17) e (2.18) em (2.2), obtemos

∇ × ∇ ×A~ =µ0J~+µ0ǫ0 ∂ ∂t −

∂ ~A ∂t − ∇φ

!

. (2.19)

Usando-se um pouco de ´algebra vetorial e o fato de que_{∇ × ∇ ×}A~ =_∇(_{∇ •}A~)_{− ∇}2A~, a equa¸c˜ao (2.19) pode ser escrita como

1

c2 ∂2A~

∂t2 − ∇

2_A_~₊_∇_{∇ •}_A_~₊_µ 0ǫ0

∂φ ∂t

=µ0J.~ (2.20)

As escolhas do potencial elétrico φe do potencial vetor A~ não são únicas. A partir destes

dois potenciais, podemos definir v´arios outros potenciais φ′ e A~′ que tamb´em satisfazem as

equa¸c˜oes (2.17) e (2.18) desde que

φ′ =φ+∂ψ

∂t, (2.21)

~

A′=A~_{− ∇}ψ . (2.22)

onde ψ é uma fun¸cão escalar arbtrária. A escolha da fun¸cão ψ é denominada condi¸cão de

gauge (ou condi¸cão de calibre) . A escolha mais usual é a condi¸cão de Lorentz, que é dada

pela rela¸c˜ao

µ0ǫ0 ∂φ

(19)

Usando-se a condi¸cão de Lorentz na rela¸cão (2.20), obtemos a equa¸cão de onda para o

potencial vetor,

1

c2 ∂2A~

∂t2 − ∇

2_A_~₌_µ

0J .~ (2.24)

Substituindo-se a rela¸c˜ao (2.17) em (2.1) e utilizando-se a condi¸c˜ao de Lorentz, obtemos

a equa¸c˜ao de onda para o potencial el´etrico,

1

c2 ∂2φ

∂t2 − ∇

2_φ₌ ρ ǫ0

. (2.25)

A equa¸cão de onda mais geral, rela¸cão (2.20), e a condi¸cão de Lorentz são escritas em

uma forma covariante se definirmos um quadripotencial Aα _{= (}φ

c, A1, A2, A3) onde A1 =Ax,

A2=Ay,A3=Az. Obtemos assim,

✷Aα₋_∂α₍_∂

βAβ) =µ0Jα, (2.26)

∂βAβ = 0, (2.27)

onde o operador✷´e definido no Apˆendice B. Substituindo (2.27) em (2.26), obtemos a forma

covariante das rela¸c˜oes (2.24) e (2.25),

✷Aα =µ0Jα. (2.28)

As componentes dos campos E~ eB~ também são obtidas através de um tensor de segunda

ordem e antissim´etrico: o tensor intensidade de campo eletromagn´eticoFαβ_{. Observando as}

rela¸c˜oes (2.17) e (2.18), definimos este tensor em termos do quadripotencial como

Fαβ =∂αAβ₋∂βAα. (2.29)

Na forma matricial, este tensor ´e escrito como

Fαβ =         

0 Ex

c

Ey

c

Ez

c

−Ex

c 0 Bz −By

−Ey

c −Bz 0 Bx

−Ez

c By −Bx 0

         . (2.30)

Com a utiliza¸cão da métrica de Minkowskiηαβ , rela¸cão (B.15), obtemos o tensor

inten-sidade de campo eletromagn´etico covariante na forma matricial

Fαβ =

        

0 ₋Ex

c − Ey c − Ez c Ex

c 0 Bz −By Ey

c −Bz 0 Bx Ez

c By −Bx 0

(20)

ou pode ser definido por

Fαβ =∂βAα−∂αAβ, (2.32)

onde o quadripotencial covarianteAαé obtido do contravarianteAαatravés da rela¸cão (B.16)

.

A forma covariante das rela¸c˜oes (2.21) e (2.22) ´e

¯

Aα=Aα+∂αΨ. (2.33)

A partir do tensor covarianteFαβ ´e poss´ıvel definir um tensor intensidade de campo

eletro-magn´etico dual F∗αβ_{. Antes disso, ´e necess´}_{ario definir o tensor de quarta ordem totalmente}

antissim´etrico ǫαβγδ_{, como}

ǫαβγδ = 

    

    

+1 paraα= 0,β = 1,γ = 2, δ= 3 e permuta¸c˜oes pares

−1 para permuta¸c˜oes ´ımpares

0 para quaisquer ´ındices iguais

. (2.34)

O tensor intensidade de campo eletromagn´etico dual F∗αβ _{´e definido na Relatividade}

Restrita pela rela¸c˜ao

F∗αβ =₋1 2ǫ

αβγδ_F

γδ . (2.35)

Na forma matricial,

F∗αβ = 

       

0 ₋Bx −By −Bz

Bx 0 E_cz −E_cy

By −E_cz 0 E_cx

Bz E_cy −E_cx 0



       

. (2.36)

As equa¸c˜oes (2.1) e (2.2) assumem uma forma covariante em termos deFαβ e de Jα atrav´es

da rela¸c˜ao

∂βFαβ =µ0Jα. (2.37)

A forma covariante das outras duas Equa¸c˜oes de Maxwell, (2.3) e (2.4), ´e obtida em termos

deF∗αβ _e_F

αβ atrav´es da equa¸c˜ao

∂βF∗αβ = 0, (2.38)

ou, alternativamente,

∂αFβγ+∂βFγα+∂γFαβ = 0. (2.39)

Para o caso das Equa¸c˜oes de Maxwell macrosc´opicas (ver Tabela 2.1), define-se mais um

tensorGαβ_{. Este tensor ´e obtido do tensor} _Fαβ_{, substituindo-se as componentes de} E~

(21)

de c ~D e as componentes de B~ pelas de H~. A forma covariante das Equa¸cões de Maxwell macroscópicas são dadas, então, pelas rela¸cões

∂βGαβ = Jα, (2.40)

∂βF∗αβ = 0. (2.41)

Uma outra forma de se obter as Equa¸c˜oes de Maxwell na Relatividade Especial ´e

uti-lizando-se a densidade lagrangeana _LR para o campo eletromagn´etico. Para obten¸c˜ao dessa

densidade lagrangeana são utilizados três critérios [8] : linearidade, invariância de gauge e

de Lorentz. O primeiro critério exige que as equa¸cões da eletrodinâmica envolvam derivadas

primeiras dos campos elétrico e magnético. O segundo e o terceiro critério exigem que as

equa¸c˜oes de campo sejam invariantes sob a escolha do calibre e as transforma¸c˜oes de Lorentz.

Portanto, a densidade lagrangeana deve ser uma combina¸c˜ao linear dos invariantes de Lorentz.

Para a Relatividade Especial, os invariantes de Lorentz F eF∗ _s˜_ao

F =FαβFαβ. (2.42)

e

F∗ =Fαβ∗ Fαβ. (2.43)

Exigindo-se a conserva¸cão de paridade como critério adicional,_LRé dada pela rela¸cão

LR=−

1 4µ0

F ₋JγAγ, (2.44)

onde o ´ındice R se refere a Relatividade Restrita.

No entanto, sabemos que

FαβFαβ =gαµgβνFαβFµν. (2.45)

As equa¸cões de Euler para a densidade lagrangeana do campo eletromagnético são

∂ ∂xβ

"

∂_LR

∂(∂βAα)

#

−∂_∂ALR

α

= 0 . (2.46)

Usando-se a densidade lagrangeana (2.44) na rela¸c˜ao anterior e a defini¸c˜ao deFαβ_{, dada}

por (2.29), obtemos

∂_LR

∂Aα

=Jα (2.47)

e

∂_LR

∂(∂βAα)

= 1

µ0

gαµgβνFµν =

1

µ0

Fαβ. (2.48)

Substituindo as rela¸cões (2.47) e (2.48) na rela¸cão (2.46), obtemos as equa¸cões de Maxwell

(22)

2.2.1 Covariˆancia da equa¸c˜ao da for¸ca de Lorentz

O quadrivetor for¸caf que atua em uma determinada part´ıcula ´e definido como

fα = d(mU

α₎

dτ = ~ U_•f~

c , U0f1

c , U0f2

c , U0f3

c

!

=qFβαUβ, (2.49)

ondeU~ = (U1, U2, U3) eU0s˜ao as componentes espaciais e a componente temporal da

quadri-velocidade Uα. A quadrivelocidade covariante Uβ é obtida através da rela¸cão (B.16) .

A grandezam´e a massa do corpo medida em um referencial em que o corpo est´a em repouso

(massa de repouso) e f~= (f1, f2, f3) ´e a for¸ca tridimensional que age no corpo.

A for¸ca de Lorentz (2.6) que age sobre uma part´ıcula de cargaqtamb´em pode ser expressa

pela rela¸c˜ao

~ F = d~p

dt =q(E~ +~v×B~), (2.50)

onde~p=m ~U = (p1, p2, p3) ´e a parte espacial do quadrivetor momento. Diferenciando ~p em

rela¸cão ao tempo próprio τ e usando a rela¸cão (2.49), temos que a componente espacial do

quadrivetor for¸ca ´e

d~p dτ =

q

c(U0E~ +c ~U×B~). (2.51)

A parte temporal ´e dada por

dp0 dτ =

q

cU~ •E.~ (2.52)

A covariância das equa¸cões (2.51) e (2.52), bem como das equa¸cões de Maxwell, é exigida

pela teoria da Relatividade Restrita e representa a covariˆancia da equa¸c˜ao da for¸ca de Lorentz.

2.3 O tensor momento-energia para o campo eletromagn´etico na Relativi-dade Especial

No contexto da Relatividade Restrita, podemos definir um tensor que possui entre as suas

componentes as densidades de energia e de momento do campo eletromagn´etico. Esse tensor

é chamado tensor momento-energia Tµν e, para o vácuo, é definido pela rela¸cão

Tµν =−4

∂_LR

∂F F

α µFαν +

_∂

LR

∂F∗F∗− LR

ηµν. (2.53)

Utilizando-se a densidade lagrangeana (2.44) na rela¸c˜ao (2.53), encontramos o tensor

(23)

Tµν =

₁

µ0

FµαFαν +

₁

4

FαβFαβηµν

(2.54)

e as suas componentes

T00 =

1

2 ǫ0E

2₊B2 µ0

!

, (2.55)

(T01, T02, T03) = −

1

c(E~ ×B~), (2.56)

T11 =

1 µ0 " 1 2 _E2

c2 −B 2

!

− E

2

x

c2 −B 2

y −Bz2

!#

, (2.57)

T22 =

1 µ0 " 1 2 _E2

c2 −B 2

!

− E

2

y

c2 −B 2

x−Bz2

!#

, (2.58)

T33 = 1 µ0

"

₁

2

_E2

c2 −B 2

!

− E

2

z

c2 −B 2

x−By2

!#

, (2.59)

Tmn = −

₁

µ0

EmEn

c2 +BmBn

, (2.60)

ondem₆=n.

Tij =Tji . (2.61)

As rela¸c˜oes (2.55) e (2.56) expressam, respectivamente, as densidades de energia e

mo-mento do campo eletromagnético. A grandeza (E~ _×B~) também é conhecida como vetor de

Poynting .

Subindo-se os ´ındices do tensor momento-energia (2.54) com o aux´ılio do tensor m´etrico

contravariante ηαβ e diferenciando-o em rela¸cão a xβ, obtemos através das equa¸cões de

Maxwell para o v´acuo

∂βTαβ = 0. (2.62)

As rela¸c˜oes (2.62) e (2.61) expressam, respectivamente, a conserva¸c˜ao da

(24)

CAP´

ITULO 3

Eletromagnetismo na Relatividade Geral

3.1 O Princ´ıpio da Equivalˆencia e as equa¸c˜oes de Einstein

A formula¸cão da Teoria da Relatividade teve como sua hipótese principal a covariância das

equa¸cões de Maxwell e da equa¸cão da for¸ca de Lorentz. Uma das principais conseqüências

dessa teoria foi a necessidade de se reformular a Mecânica Clássica, de modo que suas equa¸cões

permanecessem covariantes sob as transforma¸c˜oes de Lorentz entre referenciais inerciais.

A Relatividade Restrita nada nos fala sobre como as leis da F´ısica se transformam entre

referenciais não-inerciais e nem se a Teoria de Gravita¸cão de Newton está conceitualmente

correta.

Para tentar resolver esses problemas, Einstein propˆos, em 1911, o Princ´ıpio da

Equivalˆencia (PE), que foi o ponto inicial para o desenvolvimento de uma nova teoria de

gravita¸c˜ao. Em 1916, ele publicou a Relatividade Geral, uma teoria mais geral, que tem a

Teoria da Gravita¸c˜ao de Newton e a Relatividade Restrita como casos limites.

A forma forte do Princ´ıpio da Equivalˆencia pode ser enunciada como:

Em cada ponto do espa¸co-tempo em um campo gravitacional arbitrário, é poss´ıvel escolher um sistema de coordenadas inercial local, tal que, dentro de uma região suficientemente pequena e próxima deste ponto, todas as leis da F´ısica tomam a mesma forma que na Relatividade Especial.

Neste enunciado acima, a expressão “uma região suficientemente pequena e próxima do

ponto” se refere a uma regi˜ao em que o campo gravitacional seja praticamente uniforme.

A principal conseqüência desta forma forte do PE é que, dentro de uma região em que

exista gravidade, os sistemas de coordenadas inerciais s´o podem existir localmente. Outra

conseqüência é que o conceito de acelera¸cão passa a ser relativo, uma vez que as leis da F´ısica

(25)

Como foi dito anteriormente, a Relatividade Geral ´e uma generaliza¸c˜ao da Relatividade

Restrita e da Lei da Gravita¸cão de Newton. Essa última possui como uma das suas rela¸cões

fundamentais a equa¸c˜ao de Poisson

∇2φ= 4πGρm, (3.1)

ondeφ´e o potencial gravitacional,ρm´e a densidade de massa eG= 6,67×10−11m3kg−1s−2

´e a constante de gravita¸c˜ao universal.

Quando passamos para a Relatividade Geral, o tensor m´etricogαβ faz o papel do potencial

φ e o tensor momento-energia Tαβ passa a fazer o papel da densidade ρm. A componente

00 deste último tensor é proporcional a densidade de massa e a equa¸cão (3.1) pode ser

generalizada para

Rαβ−

1

2gαβR=kTαβ, (3.2)

ondeRαβ é o tensor de Ricci,Ré o escalar de Ricci,ké a constante de gravita¸cão de Einstein

e Tαβ ´e o tensor momento-energia com dois ´ındices covariantes.

A rela¸cão (3.2) fornece as equa¸cões de Einstein para a gravita¸cão.

O tensor e o escalar de Ricci são obtidos do tensor métrico através das rela¸cões

Γγ_αβ = Γγ_{β α} = 1 2g

δγ∂gαδ

∂xβ +

∂gδβ

∂xα −

∂gαβ

∂xδ

, (3.3)

Rαβ =Rβα =

∂2ln√₋g ∂xα_xβ −

∂Γγ αβ

∂xγ + Γ δ µαΓ

µ δ β−Γ

µ αβ

∂ln√₋g

∂xµ , (3.4)

R =Rαα =gαβRαβ, (3.5)

ondegé o determinante do tensor métricogαβ e Γγαβsão denominados s´ımbolos de Christoffel.

A rela¸c˜ao (3.2) tamb´em pode ser escrita em termos de tensores mistos como

Rαβ−

1 2δα

β_R₌_kT

αβ, (3.6)

ondeδαβ ´e o tensor misto delta de Kronecker.

Definindo o tensor de Einstein como

Gαβ =Rαβ−

1

2gαβR, (3.7)

podemos escrever (3.2) na forma

Gαβ =kTαβ. (3.8)

Esta equa¸c˜ao mostra como a mat´eria (representada pelo tensor momento-energia) afeta a

(26)

Se contra´ırmos os ´ındices α e β na rela¸c˜ao (3.2) obtemos

R=₋kT, (3.9)

ondeT =Tαα=gαβTαβ ´e o tra¸co do tensor momento-energia.

Utilizando-se (3.9) em (3.2), temos que

Rαβ =k

Tαβ−

gαβT

2

. (3.10)

Para o espa¸co vazio, o tensor momento-energia ´e nulo e as equa¸c˜oes de Einstein se reduzem

a

Rαβ = 0. (3.11)

As equa¸cões de Einstein no espa¸co vazio também são chamadas de equa¸cões de Einstein

para o vácuo. O fato do tensor de Ricci ser nulo não implica que o espa¸co tempo é plano.

Para que isso aconte¸ca é necessário que o tensor de Riemann se anule. Este tensor é definido

como

Rαβγδ=

∂Γα β γ

∂xδ −

∂Γα β γ

∂xγ + Γ µ

β γΓαδ µ−Γ µ

β δΓαγ µ. (3.12)

A constante de gravita¸c˜ao de Einstein k pode ser determinada se tomarmos o limite no

qual a equa¸c˜ao (3.8) se reduz a (3.1). No SI, esta constante tem o valor

k= 8πG

c4 . (3.13)

A derivada covariante de um tensor misto de segunda ordemE_βα ´e dada pela rela¸c˜ao

∇kEβα=

∂E_βα ∂xk −Γ

l

β kElα+ Γαk mEβm. (3.14)

Tomando-se a derivada covariante do primeiro membro da equa¸c˜ao (3.6), obtemos

∇β

Rβ_α₋1

2δ

β αR

= 0. (3.15)

Portanto, o tensor momento-energia satisfaz a igualdade

∇βTαβ = 0. (3.16)

Esta rela¸c˜ao expressa a conserva¸c˜ao de energia e do momento na Relatividade Geral.

Uma das propriedades importantes das equa¸cões de Einstein é que elas são não-lineares em

rela¸cão às componentes do tensor métrico. Conseqüentemente, o princ´ıpio da superposi¸cão

(27)

Na Relatividade Geral (RG), a distribui¸cão e o movimento da matéria são obtidos através

das equa¸cões de campo. Conseqüentemente, a distribui¸cão e o movimento da matéria não

podem ser determinados separadamente na RG.

Existe ainda outra versão para (3.2), proposta pelo próprio Einstein, na qual as equa¸cões

de campo tomam a forma

Rαβ−

1

2gαβR+ Λgαβ =

8πG

c4 Tαβ, (3.17)

onde Λ ´e a chamada “constante cosmol´ogica”.

O termo Λgαβ ´e chamado de termo cosmol´ogico e foi introduzido por Einstein para que

se pudesse obter solu¸cões estáticas para as equa¸cões do campo gravitacional. Sabe-se hoje

que a n´ıvel cosmológico esse tipo de solu¸cão não é válida, uma vez que o universo está em

expans˜ao.

Nas últimas décadas, a constante cosmológica ressurgiu em vários contextos da Cosmologia

Moderna. Observa¸c˜oes recentes envolvendo as supernovas do tipo 1a, indicando um universo

acelerado têm levantado a possibilidade de existência atual de uma constante cosmológica

positiva [14]. A constante cosmol´ogica tamb´em tem sido utilizada no contexto do problema

da idade do universo [15] e em contextos inflacion´arios [16].

3.2 O Princ´ıpio da Covariˆancia Geral e o Princ´ıpio do Acoplamento Gra-vitacional M´ınimo

Quando Einstein formulou a Relatividade Geral, ele elegeu dois princ´ıpios como sendo

fun-damentais para a sua teoria. Um deles é o Princ´ıpio da Equivalência e o outro é o Princ´ıpio

da Covariˆancia Geral. O primeiro foi utilizado para se obter as Leis de Einstein para a

Gravita¸c˜ao, enquanto que o segundo ´e utilizado para encontrar a forma tomada pelas leis da

F´ısica em qualquer referencial.

Sabe-se, da Relatividade Restrita, que n˜ao existe referencial inercial privilegiado, ou seja,

as leis da F´ısica s˜ao as mesmas para os referenciais desse tipo. Na Relatividade Geral, este

con-ceito é extendido para todos os referenciais e não apenas para os inerciais. Conseqüentemente,

as equa¸c˜oes que descrevem as leis da F´ısica devem ter a mesma forma para todos os sistemas

de coordenadas. Essa última afirma¸cão é o que nós conhecemos por Princ´ıpio da Covariância

(28)

(a) As equa¸cões na Relatividade Geral devem se reduzir às equa¸cões da Relatividade Restrita

quando a gravidade estiver ausente ;

(b) As equa¸c˜oes devem ser covariantes para qualquer transforma¸c˜ao geral de coordenadas.

Existe tamb´em outra forma de enunciar o princ´ıpio da covariˆancia geral:

As equa¸c˜oes da F´ısica devem ter uma forma tensorial.

Alguns f´ısicos acham esse enunciado muito vazio, uma vez que ´e poss´ıvel escrever equa¸c˜oes

na forma tensorial sem que estas representem, de fato, leis da F´ısica. Na realidade, o Princ´ıpio

da Covariˆancia Geral apenas nos diz como escrever a forma das equa¸c˜oes da F´ısica quando

a gravita¸cão está presente. Como foi dito anteriormente, este princ´ıpio será de grande valor

para se tentar obter as leis da natureza. No entanto, essas leis s´o estar˜ao corretas se tiverem

comprova¸c˜ao experimental.

Outro importante princ´ıpio ´e o do acoplamento gravitacional m´ınimo. Ele nos diz que,

para generalizarmos as equa¸cões da Relatividade Especial para a Relatividade Geral, não é

necessário adicionar termos a essas equa¸cões. Essa generaliza¸cão é feita substituindo-se o

tensor m´etrico de Minkowskiηαβ pelo tensor m´etrico generalizadogαβ e as derivadas comuns

pelas derivadas covariantes. Este princ´ıpio pode ser mais precisamente enunciado na forma:

Nenhum termo que contenha explicitamente o tensor de Riemman deve ser adicionado às equa¸cões da F´ısica quando elas são generalizadas da Relatividade Restrita para a Relatividade Geral.

Atualmente este princ´ıpio é pouco utilizado, uma vez que há ind´ıcios de que ele não é válido

para várias equa¸cões da F´ısica. Apesar de não ter sido formulado por Einstein, este princ´ıpio

foi utilizado implicitamente pelo mesmo no desenvolvimento da Teoria da Relatividade Geral.

3.3 Equa¸c˜oes de Maxwell na Relatividade Geral

Quando Minkowski introduziu o tensor intensidade de campo na eletrodinˆamica, ele pensava

que Fαβ _{deveria transformar-se como um tensor apenas sob as transforma¸c˜}_{oes de Lorentz.}

Entretanto, o Princ´ıpio da Covariˆancia Geral afirma que todas as leis da F´ısica devem ser

covariantes sob qualquer transforma¸c˜ao geral. Sendo assim, podemos concluir que Fαβ

transforma-se como um tensor sob qualquer transforma¸c˜ao de coordenadas.

Para a se obter a forma das equa¸c˜oes da F´ısica na Relatividade Geral ´e usual adotar-se

(29)

(a) Escrever as equa¸c˜oes na Relatividade Especial ;

(b) Verificar como cada grandeza f´ısica contida nestas equa¸c˜oes se transforma sob uma

trans-forma¸c˜ao geral de coordenadas ;

(c) Substituir o tensor m´etrico da Relatividade Restrita pelo da Relatividade Geral e as

derivadas comuns por derivadas covariantes.

Esses procedimentos constituem o Princ´ıpio do Acoplamento Gravitacional M´ınimo. As

equa¸cões resultantes possuirão covariância geral e serão verdadeiras na ausência de gravita¸cão.

Sendo assim, elas também serão válidas em quaisquer campos gravitacionais, desde que o

sistema em quest˜ao seja pequeno comparado com a escala dos campos.

Usando-se os procedimentos (a), (b) e (c), vemos que a defini¸c˜ao do tensor intensidade de

campo eletromagn´etico Fαβ na Relatividade Geral ´e a mesma da Relatividade Restrita, uma

vez que

Fαβ =∇βAα− ∇αAβ, (3.18)

onde_∇α e∇β representam as derivadas covariantes.

Repetindo-se o tratamento anterior para as equa¸cões de Maxwell não-homogêneas,

obte-mos a rela¸c˜ao

∇βFαβ =µ0Jα. (3.19)

As derivadas covariantes para os tensores de segunda ordem contravariante e covariante

s˜ao dadas, respectivamente, por

∇γFαβ =

∂Fαβ ∂xγ + Γ

α

δ γFδβ+ Γβν γFαν, (3.20)

∇γFαβ =

∂Fαβ

∂xγ −Γ δ

αγFδβ−Γν_{β γ}Fαν. (3.21)

Conseq¨uentemente, a rela¸c˜ao (3.19) pode ser escrita como

∂Fαβ

∂xβ + Γ α

δ βFδβ+ Γβν βFαν =µ0Jα. (3.22)

Utilizando a rela¸c˜ao (3.3) para os s´ımbolos de Christoffel, obtemos

Γβ_{ν β} = 1 2g

∂g ∂xν =

1

√ −g

∂√₋g

∂xν . (3.23)

Como Fαν é antissimétrico e Γβ_{ν α} é simétrico, o terceiro termo do primeiro membro de

(3.22) se anula. Usando-se este fato em combina¸c˜ao com (3.23), reduzimos (3.22) a

∂Fαβ

∂xβ +

1

√ −g

_∂√₋_g

∂xν

(30)

ou, de forma alternativa,

1

√ −g

₍_∂√

−gFαν₎

∂xν

=µ0Jα . (3.25)

Pode-se definir um novo tensor intensidade de campo eletromagn´etico fαβ _{e uma nova}

quadricorrente jβ atrav´es das rela¸c˜oes

fαβ = √₋g Fαβ, (3.26)

jα = √₋g µ0 Jα. (3.27)

Multiplicando (3.25) por √₋g e usando (3.26) e (3.27), podemos rescrever (3.25) como

∂fαβ

∂xβ =j

α_. _(3.28)

Derivando (3.28) em rela¸c˜ao a xβ_{, temos que}

∂2_fαβ

∂xα_∂xβ =

∂jα

∂xα. (3.29)

Comofαβ é antissimétrico, o primeiro membro da equa¸cão acima é igual a zero, portanto

∂jα

∂xα = 0. (3.30)

A rela¸c˜ao (3.30) expressa a equa¸c˜ao da continuidade na Relatividade Geral.

As equa¸cões de Maxwell homogêneas na Relatividade Restrita são dadas pela rela¸cão

(2.39). Para a Relatividade Geral, essas equa¸c˜oes s˜ao

∇αFβγ +∇βFγα+∇γFαβ = 0. (3.31)

Usando-se a rela¸c˜oes (3.21) e (3.3) e o fato do tensor intensidade de campo ser

antis-sim´etrico, reduzimos (3.31) a

∂Fβγ ∂xα +

∂Fγα ∂xβ +

∂Fαβ

∂xγ = 0, (3.32)

que ´e a mesma rela¸c˜ao da Relatividade Especial.

3.3.1 C´alculo Variacional para a Eletrodinˆamica de Maxwell na Relativida-de Geral

Uma outra forma de se obter as equa¸c˜oes de Maxwell na Relatividade Geral ´e utilizando a

lagrangeana LG para o campo eletromagnético, que é dada pela rela¸cão

LG=−

1 4µ0

√

(31)

No entanto, sabemos que

FαβFαβ =gαµgβνFαβFµν. (3.34)

As equa¸cões de Euler para a lagrangeana do campo eletromagnético são

∂ ∂xβ

"

∂LG

∂(∂βAα)

#

−∂L_∂AG

α

= 0. (3.35)

Usando-se a lagrangeana (3.33) na rela¸c˜ao acima e a defini¸c˜ao de Fαβ_{, dada por (2.29),}

obtemos

∂LG

∂Aα

= ₋√₋gJα e (3.36)

∂LG

∂(∂βAα)

= 1

µ0

√

−ggαµgβνFνµ =

1

µ0

√

−gFβα. (3.37)

Substituindo as rela¸c˜oes (3.36) e (3.37) nas equa¸c˜oes de Euler e utilizando um pouco de

c´alculo tensorial, achamos a equa¸c˜ao

₁

√ −g

₍_∂√

−gFαβ₎

∂xβ =µ0J

α_. _(3.38)

Pode-se ver que as rela¸cões (3.38) são iguais às rela¸cões (3.25), representando as equa¸cões

de Maxwell n˜ao-homogˆeneas na Relatividade Geral.

Outra rela¸cão que pode ser generalizada é a equa¸cão de movimento de uma part´ıcula

carregada com carga q num campo eletromagn´etico. Usando-se o Princ´ıpio da Covariˆancia

Geral, a rela¸c˜ao (2.49) fica, na presen¸ca da gravita¸c˜ao,

m

_dUα

dτ + Γ

α

β γUβUγ

=qFβαUβ. (3.39)

3.4 O tensor momento-energia para o campo eletromagn´etico na Relativi-dade Geral

As equa¸c˜oes de Einstein, dadas pela rela¸c˜ao (3.8), possuem um tensor de segunda ordemTµν,

chamado tensor momento-energia, que representa o momento e a energia de toda a mat´eria

e energia que gera o campo gravitacional.

Também é poss´ıvel definir um tensor momento-energiaTµν para o campo eletromagnético.

Esse tensor expressa as densidades de momento e energia do campo eletromagn´etico e, para

uma região do espa¸co sem fontes, é definido pela rela¸cão

Tµν =−4

∂_LG

∂F F

α µFαν +

_∂

LG

∂F∗F∗− LG

(32)

onde_LG= √L₋G_g. Utilizando-se a lagrangeana (3.33) na rela¸c˜ao anterior encontramos que

Tµν =

₁

µ0

FµαFαν +

₁

4

FαβFαβgµν

(3.41)

que ´e v´alida para a Relatividade Geral.

O tensor momento-energia contravariante do campo eletromagn´etico Tαβ ´e definido pela

rela¸c˜ao

Tαβ =

₁

µ0

FαδFδβ+

₁

4

FγδFγδgαβ

. (3.42)

Tomando-se a derivada covariante da rela¸c˜ao (3.42) em rela¸c˜ao a xβ _{e utilizando as}

equa¸c˜oes de Maxwell com Jα _{= 0, obtemos a rela¸c˜}_{ao (3.16), que expressa a conserva¸c˜}_ao

da energia e do momento na RG.

Combinando-se as rela¸c˜oes (3.8), (3.13) e (3.41), temos que

Gµν =

₈_πG

c4_µ 0

FµαFαν +

₁

4

FαβFαβgµν

. (3.43)

As equa¸cões de campo expressadas por (3.43) são conhecidas como equa¸cões de

Maxwell-Einstein no espa¸co-tempo sem fontes.

Para o espa¸co-tempo com fontes de campo, deve-se incluir todas as quantidades f´ısicas

significativas (matéria, pressão do fluido, campos eletromagnéticos, etc) no tensor

momento-energia. Sendo assim, garantimos que a divergˆencia desse tensor ser´a nula e,

(33)

CAP´

ITULO 4

Propostas Alternativas de Eletromagnetismo

4.1 Eletrodinˆamica N˜ao-Linear

O estudo da eletrodinâmica na Relatividade Geral está principalmente restrito à análise das

solu¸cões das equa¸cões de Einstein-Maxwell. A primeira solu¸cão obtida para essas equa¸cões

era baseada na validade do Princ´ıpio do Acoplamento M´ınimo descrito no cap´ıtulo anterior.

No dom´ınio da Relatividade Geral, a energia eletromagnética é responsável pela curvatura

do espa¸co-tempo. No contexto de campos gravitacionais fortes, ou pontos do espa¸co-tempo

de grande curvatura, o acoplamento entre a Eletrodinâmica e a Gravita¸cão não é bem

con-hecido. Nessas condi¸cões, algumas leis e princ´ıpios clássicos como o Princ´ıpio da Equivalência

podem não ser totalmente válidos, podendo surgir alguns desvios em regiões de grande

cur-vatura. Portanto, é razoável propor uma intera¸cão entre a Gravita¸cão e o Eletromagnetismo

mais espec´ıfica do que a intera¸c˜ao proposta pelo Princ´ıpio do Acoplamento M´ınimo. Essas

intera¸cões são denominadas acoplamentos não-m´ınimos.

A utiliza¸cão de acoplamentos não-m´ınimos entre a Gravita¸cão e o Eletromagnetismo tem

como uma de suas conseqüências o surgimento de uma Eletrodinâmica não-linear. Essa não

linearidade no campo eletromagnético é observada apenas nas equa¸cões de Einstein-Maxwell,

onde os campos eletromagn´etico e gravitacional se encontram acoplados. As equa¸c˜oes da

eletrodinâmica obtidas do cálculo variacional não evidenciam essa importante conseqüência.

Outras formas de se obter uma eletrodinâmica não-linear é introduzindo, de formaad hoc_,

termos aditivos na lagrangeana de Maxwell ou, ainda, através de corre¸cões quânticas.

Várias propostas para eletrodinâmicas não-maxwelianas têm sido apresentadas nas últimas

décadas. Uma das motiva¸cões para essas propostas é a possibilidade de gera¸cão de campos

eletromagnéticos de larga escala no universo em estágios primordiais da sua expansão.

(34)

com os termos que são adicionados à lagrangeana de Maxwell. Com rela¸cão à invariância de

Gauge (ver cap´ıtulo 2), podemos distinguir duas classes.

Primeira classe:

L1 = RAµA

µ

µ0

, (4.1)

L2 =

RµνAµAν

µ0

. (4.2)

Segunda classe:

L3 = RFµνF

µν

µ0

, (4.3)

L4=

RFµνF∗µν

µ0

, (4.4)

L5=

RµαFλµFλα

µ0

, (4.5)

L6=

RαβµνFαβFµν

µ0

, (4.6)

L7 =

RαβµνFαβF∗µν

µ0 . (4.7)

onde a constante µ0 aparece nas rela¸c˜oes (4.1)-(4.7) devido a utiliza¸c˜ao do SI.

As lagrangeanas da primeira classe s˜ao obtidas de todas as combina¸c˜oes poss´ıveis do

ten-sor de Ricci e/ou escalar de curvatura com o quadripotencial, donde resulta a n˜ao invariˆancia

de gauge. De forma an´aloga, as lagrangeanas da segunda classe resultam de todas as

com-bina¸c˜oes do tensor de Riemann e/ou suas contra¸c˜oes com o tensor intensidade de campo

eletromagn´etico e/ou o seu tensor dual, donde resulta a invariˆancia de gauge.

Existe ainda uma classe de lagrangeanas efetivas para uma teoria n˜ao-linear, tamb´em

invariante de gauge, mas que n˜ao possui termos que envolvem o tensor de Riemann e/ou

suas contra¸cões. Portanto, essa classe não envolve acoplamento entre a eletrodinâmica e

a gravita¸c˜ao como as duas classes mostradas anteriormente, mas ´e constru´ıda a partir dos

invariantes de Lorentz e de gauge. Nessa classe, a n˜ao-linearidade do campo eletromagn´etico

é observada nas equa¸cões da Eletrodinâmica.

Lagrangeanas efetivas para uma teoria n˜ao-linear:

L=L(F, F∗). (4.8)

onde os escalares F e F∗ _s˜_{ao definidos, respectivamente, atrav´es das rela¸c˜}_{oes (2.42) e}

(35)

4.2 Lagrangeanas de Primeira Classe

As constantes de acoplamento para as lagrangeanas de primeira classe s˜ao adimensionais, uma

vez que essas lagrangeanas j´a possuem a mesma dimens˜ao que a lagrangeana de Maxwell.

As rela¸c˜oes principais para esse tipo de acoplamento s˜ao

L=₋ 1 4µ0

√

−gFµνFµν+

1

µ0

√

−g (λRAµAµ+δRµνAµAν), (4.9)

∇µFµν−2λRAν−2δRµνAµ= 0, (4.10)

∂aFbc+∂bFca+∂cFab = 0. (4.11)

A rela¸cão (4.9) é obtida através da combina¸cão linear das lagrangeanas da primeira classe

com a lagrangeana de Maxwell, onde λe δ são constantes adimensionais. A rela¸cão (4.10) é

obtida da rela¸cão (4.9) através das equa¸cões de Euler-Lagrange, enquanto que a rela¸cão (4.11)

resulta das defini¸c˜oes (2.32) e (3.18) para o tensor intensidade de campo eletromagn´etico.

Novello [3] e Turner [4] analisaram as altera¸c˜oes que surgem quando s˜ao introduzidos os

acoplamentos da primeira classe nas equa¸c˜oes de Einstein-Maxwell.

Os principais resultados obtidos s˜ao os seguintes:

A massa do f´oton depende do escalar de curvaturamγ ∼R

1 2.

As solu¸c˜oes das equa¸c˜oes de Einstein-Maxwell produzem mudan¸cas efetivas na

Eletro-dinˆamica apenas nas regi˜oes de altos valores de curvatura.

Apenas o acoplamento dado pela rela¸c˜ao (4.1) admite uma solu¸c˜ao

de Friedmann-Robertson-Walker (FRW), na qual o fator de escala pode ser obtido

explicitamente em termos do tempo c´osmico [3], enquanto a rela¸c˜ao (4.2) produz uma

solu¸c˜ao anisotr´opica.

A lei da conserva¸cão da carga é modificada, permitindo duas possibilidades: a cria¸cão

de carga pelo campo gravitacional ou a conserva¸c˜ao da carga, desde que a derivada

covariante de RAµ _{seja nula .}

O escalar de curvatura n˜ao nulo pode induzir efeitos como, por exemplo, o decaimento

de f´otons em outras part´ıculas [3].

Utilizando o primeiro resultado, temos que a massa do f´oton deveria ser da ordem da

(36)

limite inferior para a massa do fóton que é 5_×10−63 kg [4]. A não conserva¸cão da carga

s´o aparece em escalas de horizonte maiores do que 1026 _m_{, entretanto este efeito n˜}_{ao tem}

conseq¨uˆencias observacionais conhecidas [4].

Outro aspecto observado ´e que, somente durante as fases de De Sitter e de reaquecimento

em um universo inflacion´ario, para a equa¸c˜ao de estado da poeira , os acoplamentos de

primeira classe podem produzir campos magn´eticos significantes [4].

4.3 Lagrangeanas de Segunda Classe

Como n˜ao possuem a mesma dimens˜ao que a lagrangeana de Maxwell, as lagrangenas de

segunda classe necessitam de constantes de acoplamento com a dimens˜ao de (comprimento)2.

Não são todas as densidades lagrangeanas de_L1 aL7 que satisfazem todas as conserva¸cões

de simetria conhecidas (carga, paridade, etc). _L4 e L7 n˜ao obedecem a conserva¸c˜ao de

paridade, pois dependem do tensor intensidade de campo dual.

As rela¸c˜oes principais para esse tipo de acoplamento s˜ao

L= ₋₄_µ1₀√₋gFµν_F

µν+_µ1₀√−g (bRFµνFµν+cRµνFµδFδν+

+dRµνλδFµνFλδ), (4.12)

∇µFµν− ∇µ[4bRFµν+ 2c(RλµFλν−RλνFλµ) + 4dRλδ µνFλδ] = 0, (4.13)

onde as rela¸cões (4.12) e (4.13) são obtidas de forma análoga as rela¸cões (4.9) e (4.10). As

constantes b, c e d s˜ao constantes de acoplamento. Uma vez que o tensor de Weyl conforme

se anula na geometria conforme de FRW, ent˜ao o termo_L3, L5 e L6 ´e reduzido a um par.

Em uma an´alise de acoplamento n˜ao-m´ınimo restrita ao uso da densidade lagrangeana

L3, Novello [5] obtém duas conclusões: tanto para o acoplamento m´ınimo como não-m´ınimo,

os f´otons seguem uma geod´esica tipo nula para a geometria de FRW; no acoplamento

não-m´ınimo, o número de fótons no universo não necessariamente será conservado. A quebra

da conserva¸cão de fótons é vinculada à quebra da invariância conforme do eletromagnetismo,

a qual ´e analisada por Novello [5] e Turner [4] num contexto de FRW com fase inflacion´aria.

Por outro lado, Turner [4] mostra que a quebra da invariˆancia conforme n˜ao possibilita a

gera¸cão de campos magnéticos de larga escala significantes e utiliza a combina¸cão de _L3,L5

e _L6 em sua análise. Nos primórdios do universo, em que a temperaturaT é maior do que

1021_K _{[4], os termos de segunda classe dominam o termo referente a lagrangeana de Maxwell,}

(37)

Em outro trabalho, Acioly [6] analisou a densidade lagrangena _L3 no caso est´atico

es-fericamente simétrico. A solu¸cão obtida das equa¸cões de Einstein-Maxwell apresenta um

parˆametro a com comportamento similar ao raio de Schwarzschild e se reduz a solu¸c˜ao

padrão de Reissner-Nordström (veja o cap´ıtulo 6 para uma discussão mas detalhada sobre

essa solu¸c˜ao) para a constante de acoplamento nula.

4.4 Lagrangeanas efetivas para uma teoria n˜ao-linear

As lagrangeanas efetivas são constru´ıdas seguindo-se quatro critérios principais: invariância

de gauge, invariância de lorentz, conserva¸cão de paridade e não-linearidade. Essa constru¸cão

fornece uma descri¸cão de como os efeitos do vácuo alteram os fenômenos eletromagnéticos,

além de introduzir modifica¸cões na descri¸cão maxwelliana de toda a eletrodinâmica.

Além dos quatro critérios do parágrafo anterior, consideraremos que qualquer contribui¸cão

para a lagrangeana envolvendo termos da forma ∂cFab deve ser desprezada. Portanto, a

expressão da densidade lagrangeana efetiva para a eletrodinâmica não-linear é

L=₋ 1 4µ0

F+aF2+bF∗2, (4.14)

onde foram considerados apenas os primeiros termos n˜ao-lineares. As constantes a e b s˜ao

determinadas pela teoria eletromagn´etica utilizada.

Heisenberg e Euler [7] obtiveram corre¸c˜oes quˆanticas de primeira ordem para a eletrodinˆ

a-mica a fim de permitir a cria¸c˜ao de pares el´etron-pos´ıtron virtuais. A densidade lagrangeana

obtida por eles tem a mesma forma da rela¸c˜ao (4.14), onde as constantes a e b s˜ao dependentes

das constantes fundamentais: ¯h ,c eme (massa do el´etron) .

Novello [1] analisou as conseqüências cosmológicas dessas corre¸cões quânticas até a primeira

ordem, que surgem no regime semicl´assico em um universo de FRW. O principal resultado

obtido ´e a retirada da singularidade primordial do modelo padr˜ao da cosmologia. Uma

dis-cussão mais detalhada dessa solu¸cão é apresentada no cap´ıtulo 5, bem como uma generaliza¸cão

para modelos com parˆametro cosmol´ogico Λ.

Dentro do contexto de uma teoria eletromagn´etica n˜ao-linear, Munhoz [8] analisa as

im-plica¸c˜oes da lagrangeana acima em problemas simples de eletrodinˆamica, como o capacitor

de placas paralelas, o elemento infinito de corrente e a birrefringˆencia eletromagn´etica. Os

resultados obtidos para esses problemas mostraram que a adi¸c˜ao de termos n˜ao-lineares de

(38)

Em outro artigo, Novello [9] analisa a propaga¸c˜ao da luz em uma

eletrodi-nâmica não-linear e mostra que, para regiões do vácuo em que o campo eletromagnético é

descont´ınuo, os fótons se propagam ao longo de geodésicas que não são mais nulas no

espa¸co-tempo de Minkowski, mas em outra geometria efetiva que depende da dinˆamica dos

campos eletromagnéticos. A origem da não-lineariedade na eletrodinâmica pode ser atribu´ıda

ao vácuo da eletrodinâmica quântica ou a resposta não linear de um meio dielétrico. O

resultado mais interessante obtido ´e a possibildade de gera¸c˜ao de dom´ınios compactos onde

os fótons são presos por um campo eletromagnético não linear. Isto sugere a possibilidade

de fazer-se uma analogia com o buraco negro gravitacional, na qual esses dom´ınios poderiam

ser denominados de buracos negros eletromagn´eticos.

Ayón-Beato e Garcia [10] obtiveram solu¸cões exatas para as equa¸cões de

Einstein--Maxwell para a massa puntual carregada com a mesma estrutura da solu¸c˜ao de

Reissner--Nordström, exceto pela retirada da singularidade f´ısica. Nesta solu¸cão, o módulo da carga

elétrica tem um valor máximo e o campo elétrico é sempre regular e se reduz ao campo

cl´assico para valores assint´oticos da cooordenada radial (r). A lagrangeana para o campo

eletromagn´etico utilizada por eles foi escolhida de forma a satisfazer duas condi¸c˜oes: a

cor-respondˆencia com a teoria de Maxwell, ou seja, a lagrangeana se reduz `a de Maxwell para

campos eletromagn´eticos fracos; e a condic˜ao de energia fraca, ou seja, a densidade de energia

deve ser sempre positiva.

4.5 Coment´arios Adicionais

As propostas discutidas nesse cap´ıtulo s˜ao apenas algumas das que foram discutidas e

anali-sadas nas ´ultimas d´ecadas.

Existem também outras propostas interessantes de eletrodinâmica não-linear como a

eletrodinˆamica de Born-Infeld que ´e discutida em Chernitskii [17] e Rasheed [18]. O

acopla-mento da Gravita¸cão e da Eletrodinâmica Clássica com campos escalares é outra proposta