Análise da magnetohidrodinâmica com transferência de calor em canais de placas paralelas via transformação integral

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA

MARIA DAS GRAÇAS OLIVEIRA RÊGO

A

EM CANAIS DE PLACAS PARALELAS VIA TRANSFORMAÇÃO INTEGRAL

MARIA DAS GRAÇAS OLIVEIRA RÊGO

A

EM CANAIS DE PLACAS PARALELAS VIA TRANSFORMAÇÃO INTEGRAL

Dissertação submetida à Universidade Federal do Rio Grande do Norte como parte dos requisitos para a obtenção do grau de Mestre em Engenharia Mecânica.

Orientador: Prof. Dr. João Alves de Lima

Área de Concentração: Mecânica Computacional

Natal - RN

Divisão de Serviços Técnicos

Catalogação da Publicação na Fonte. UFRN / Biblioteca Central Zila Mamede Rêgo, Maria das Graças Oliveira.

Análise da magnetohidrodinâmica com transferência de calor em canais de placas paralelas via transformação integral / Maria das Graças Oliveira Rêgo. – Natal, RN, 2010.

108 f.

Orientador: João Alves de Lima.

Dissertação (mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Tecnologia. Programa de Pós-Graduação em Engenharia Mecânica.

1. Magnetohidrodinâmica – Dissertação. 2. Escoamento laminar – Dissertação. 3. Calor – Convecção forçada – Dissertação. 4. Transformada integral – Dissertação. I. Lima, João Alves de. II. Universidade Federal do Rio Grande do Norte. III. Título.

Dedico este trabalho aos meus pais: Francisco Gomes de Oliveira e Ana Dantas de Oliveira (in memorian);

A Deus, por tudo que sou e tenho.

Aos Meus Pais, por todo amor dedicado na construção do meu ser. Ao meu esposo Sérgio, pelo incentivo, apoio e companheirismo.

Ao professor João Alves de Lima, meu orientador, por sua dedicação e seus ensinamentos. À UFRN, pela a oportunidade de realização desse mestrado.

Às minhas filhas, Camila e Lara por me compreender e apoiar.

Aos meus irmãos Clóvis, pela ajuda nas apresentações, Míriam, Pedro e Luis.

Os problemas significativos que enfrentamos não podem ser resolvidos no mesmo nível de pensamento em que estávamos quando os criamos.

RESUMO

O propósito do estudo desenvolvido nesse trabalho está relacionado com a dinâmica do escoamento incompressível, laminar, em regime permanente, com transferência de calor, de um fluido newtoniano condutor elétrico, no interior de um canal de placas planas paralelas, submetido a um campo magnético externo uniforme. Para a solução das equações de governo, modeladas através da formulação parabólica de camada limite em função corrente, foi empregado o método híbrido, numérico-analítico, conhecido como Técnica da Transformada Integral Generalizada (GITT). O escoamento analisado é sustentando por um gradiente de pressão e assume-se que o campo magnético externo, aplicado na direção normal ao escoamento, permanece uniforme, muito maior do que quaisquer outros campos gerados em outras direções, não sendo, dessa forma, influenciado por nenhum efeito magnético interno. Para avaliar a influência do campo magnético sobre o desenvolvimento térmico e hidrodinâmico desse problema de convecção forçada, e também para fins de validação da metodologia de solução adotada, foram empregados dois tipos de condições de contorno para o campo de velocidade na entrada no canal: perfil uniforme e perfil parabólico do escoamento sem campo magnético completamente desenvolvido. Para o problema térmico, por outro lado, empregou-se apenas o perfil uniforme de temperatura na entrada do canal e considerou-se que as placas se mantém à temperatura constante, iguais ou diferentes uma da outra. Resultados para os campos de velocidade, temperatura e potenciais correlatos são produzidos e comparados aos da literatura em função dos principais parâmetros de governo, a saber, número de Reynolds, número de Hartmann e parâmetro elétrico, para algumas situações típicas. Com o objetivo de ilustrar a consistência da técnica da transformada integral generalizada, análises de convergência são também efetuadas e apresentadas.

ABSTRACT

The main goal of the present work is related to the dynamics of the steady state, incompressible, laminar flow with heat transfer, of an electrically conducting and Newtonian fluid inside a flat parallel-plate channel under the action of an external and uniform magnetic field. For solution of the governing equations, written in the parabolic boundary layer and stream-function formulation, it was employed the hybrid, numerical-analytical, approach known as Generalized Integral Transform Technique (GITT). The flow is sustained by a pressure gradient and the magnetic field is applied in the direction normal to the flow and is assumed that normal magnetic field is kept uniform, remaining larger than any other fields generated in other directions. In order to evaluate the influence of the applied magnetic field on both entrance regions, thermal and hydrodynamic, for this forced convection problem, as well as for validating purposes of the adopted solution methodology, two kinds of channel entry conditions for the velocity field were used: an uniform and an non-MHD parabolic profile. On the other hand, for the thermal problem only an uniform temperature profile at the channel inlet was employed as boundary condition. Along the channel wall, plates are maintained at constant temperature, either equal to or different from each other. Results for the velocity and temperature fields as well as for the main related potentials are produced and compared, for validation purposes, to results reported on literature as function of the main dimensionless governing parameters as Reynolds and Hartman numbers, for typical situations. Finally, in order to illustrate the consistency of the integral transform method, convergence analyses are also effectuated and presented.

LISTADEFIGURAS

CAPÍTULO 2

Figura 2.1

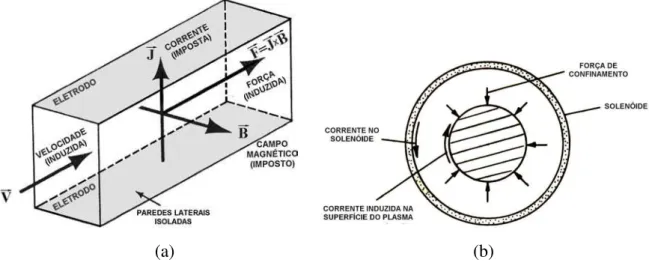
Esquema (a) de uma bomba eletromagnética (adaptado de Shercliff, 1965) e (b) do confinamento magnético de plasma (adaptado de Davidson, 2001).

25

Figura 2.2

Esquema (a) de agitação magnética de um lingote, (b) do amortecimento magnético de movimento durante fundição e (c) de uma válvula eletromagnética. Adaptado de Davidson (2001).

26

Figura 2.3 Instabilidade em uma célula de redução de alumínio. 27

Figura 2.4 Interação entre um campo magnético e um fio circular em

movimento. 29

Figura 2.5 Lei de Ohm em um condutor (a) estacionário e (b) em movimento. 33

Figura 2.6 Lei de Ampère aplicada a um fio. Adaptado de Davidson (2001). 34

Figura 2.7

Lei de Faraday (a) fem gerada pelo movimento de um condutor, (b) fem gerada por um campo magnético dependente do tempo. Adaptado de Davidson (2001).

35

CAPÍTULO 4

Figura 4.1

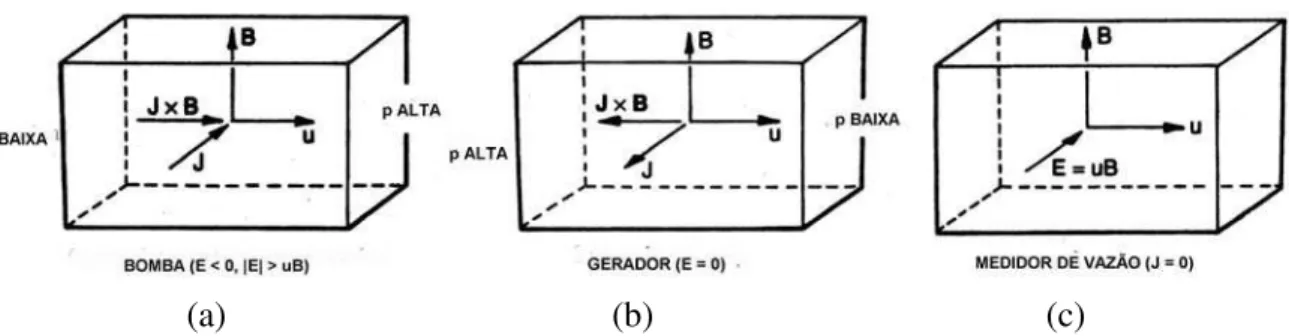
Esquema de possibilidades tecnológicas magnetohidrodinâmicas: (a) bomba eletromagnética, (b) gerador eletromagnético e (c) medidor de vazão eletromagnético. Adaptado de Davidson (2001).

53

Figura 4.2

Esquema da geometria e das características elétricas e magnéticas do canal. Adaptado de Setayesh e Sahai (1990) e Sutton e Sherman (2006).

55

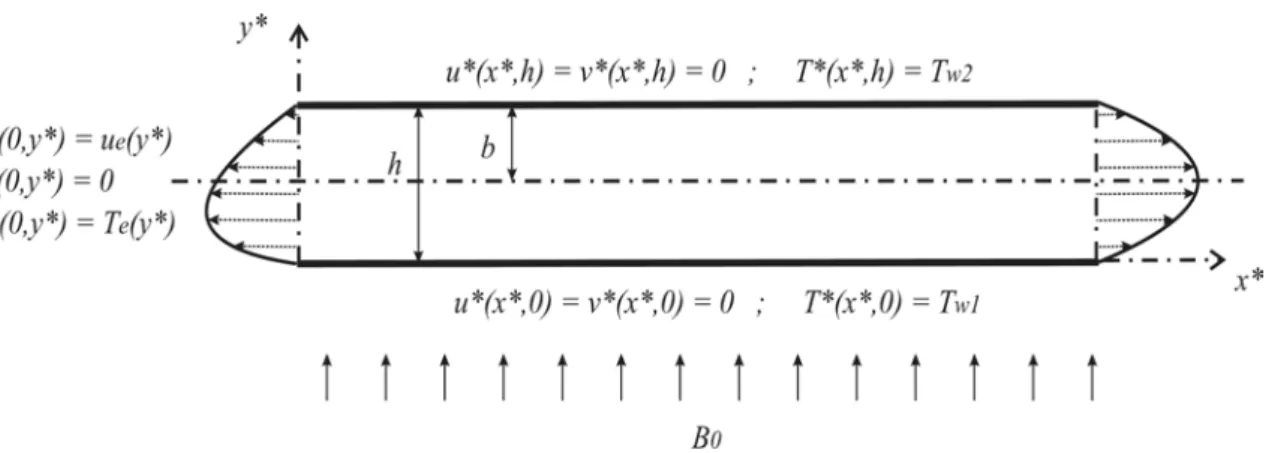
Figura 4.3 Representação esquemática do problema analisado (plano central

CAPÍTULO 6

Figura 6.1

Comparação com os resultados de Hwang et al. (1966) da componente axial de velocidade ao longo do canal, em diferentes posições transversais, para Ha = 8 e perfil de velocidade parabólico na entrada do canal.

87

Figura 6.2

Comparação com os resultados de Hwang et al. (1966) da componente axial de velocidade ao longo do canal, em diferentes posições transversais, para Ha = 20 e perfil de velocidade parabólico na entrada do canal.

87

Figura 6.3 Influência do campo magnético sobre o desenvolvimento do perfil da componente axial de velocidade e comparação com os resultados de Hwang et al. (1966).

88

Figura 6.4

Comparação com os resultados de Manohar (1966) da componente axial de velocidade ao longo do canal, em diferentes posições transversais, para Ha = 0 e perfil de velocidade uniforme na entrada do canal.

89

Figura 6.5

Comparação com os resultados de Shohet et al. (1962) e Manohar (1966) da componente axial de velocidade ao longo do canal, em diferentes posições transversais, para Ha = 8 e perfil de velocidade uniforme na entrada do canal.

90

Figura 6.6

Comparação com os resultados de Manohar (1966) da componente axial de velocidade ao longo do canal, em diferentes posições transversais, para Ha = 12 e perfil de velocidade uniforme na entrada do canal.

90

Figura 6.7

Comparação com os resultados de Manohar (1966) da componente axial de velocidade ao longo do canal, em diferentes posições transversais, para Ha = 20 e perfil de velocidade uniforme na entrada do canal.

91

Figura 6.8

Comparação com os resultados de Shohet et al. (1962) do campo de temperatura ao longo do canal, em diferentes posições transversais, para Ha = 8, Pr = 0,1, Ec = -1,0 e Ez = 0,0. Perfis de temperatura e velocidade uniformes na entrada.

92

Figura 6.9

Comportamento do campo de temperatura ao longo do canal, em diferentes posições transversais, para Ha = 8, Pr = 0,1, Ec = -1,0 e Ez = 0,0. Perfil de temperatura uniforme e de velocidade parabólico na entrada do canal.

Figura 6.10

Influência do tipo de perfil de velocidade na entrada do canal sobre o desenvolvimento da temperatura média de mistura, para Ha = 8, Pr = 1, Ec = 0 e Ez = 0. Perfil de temperatura uniforme na entrada do canal.

94

Figura 6.11

Influência do tipo de perfil de velocidade na entrada do canal sobre o desenvolvimento do número de Nusselt médio local, para Ha = 8, Pr = 1, Ec = 0 e Ez = 0. Perfil de temperatura uniforme na entrada do canal.

94

Figura 6.12

Comparação com os resultados de Setayesh e Sahai (1990) da temperatura média de mistura e do número de Nusselt médio local ao longo do canal, para Ha = 20, Pr = 0,75, Ec = 0,1 e Ez = -0,5. Perfis de temperatura e velocidade uniformes na entrada.

95

Figura 6.13

Comparação com os resultados de Hwang (1962) e Setayesh e Sahai (1990) do número de Nusselt médio local ao longo do canal, para Ha = 20, Pr = 1, Ec = (1,0 e 0,1) e Ez = (0,0 e -1.0). Perfis de

temperatura e velocidade uniformes na entrada.

95

Figura 6.14

Influência dos números de Hartmann e de Eckert sobre o desenvolvimento da temperatura média de mistura, para Pr = 0,75 e Ez = -0,5.

96

Figura 6.15

Influência dos números de Hartmann e de Eckert sobre o desenvolvimento do número de Nusselt médio local, para Pr = 0,75 e Ez = -0,5.

LISTADETABELAS

CAPÍTULO 6

Tabela 6.1 Análise de convergência dos principais campos, em diferentes _{posições axiais. (Ha = 8, Pr = 1,0, Ec = 0,0, Ez = 0,0 e perfil de} velocidade parabólico na entrada).

84

Tabela 6.2 Análise de convergência dos principais campos, em diferentes _{posições axiais. (Ha = 20, Pr = 0,75, E} c = 0,1, Ez = - 0,5 e perfil de velocidade uniforme na entrada).

LISTADESÍMBOLOS

A Área total das placas 0

B Vetor campo magnético externo ( )

i

C yɶ Autofunção relacionada ao campo de temperatura

p

c Calor específico à pressão constante dℓ Elemento diferencial de comprimento

dS Elemento diferencial de área/superfície E Vetor campo elétrico

c

E Número de Eckert

i

E Campo elétrico induzido 0

E Campo elétrico externo

r

E Campo eletrostático

z

E Parâmetro elétrico adimensional F Vetor força eletromagnética

( )

m

f x Coeficiente de atrito médio local

z

G Número de Graetz

Ha Número de Hartmann

ef

Ha Número de Hartmann efetivo

( ) m

h x Coeficiente médio local de transferência de calor por convecção ( )

tot

I x Corrente total por unidade de comprimento J Vetor densidade de corrente elétrica

k Condutividade térmica

e

k Condutividade térmica na entrada do canal ( )

m

k x Condutividade térmica média local ,1,2( )

m

k x Condutividade térmica média nas paredes 1 e 2 do canal

i

M Norma da autofunção associada ao campo de função corrente N Parâmetro de interação magnética

i

N Norma da autofunção associada ao campo de temperatura ( )

m

Nu x Número de Nusselt médio local

Nφ Número de termos empregado nas expansões do campo de função corrente Nθ Número de termos empregado nas expansões do campo de temperatura

P Campo de pressão

r

P Número de Prandtl

joule

q Taxa de geração de energia por efeito Joule

visc

q Taxa de geração de energia por efeitos de dissipação viscosa

( )

Q x Taxa de transferência de calor local

q Carga do elétron

Re Número de Reynolds

m

Re Número de Reynolds magnético

( )

T x y Campo escalar de temperatura do fluido ( )

b

T x Temperatura média de mistura local

e

T Temperatura na entrada do canal

1

w

T Temperatura na parede inferior do canal

2

w

T Temperatura na parede superior do canal

u Campo vetorial de velocidade

( )

u x y Componente longitudinal de velocidade do fluido

e

U Velocidade média do fluido na entrada do canal

( )

v x y Componente transversal de velocidade do fluido

( ) i

Y yɶ Autofunção relacionada ao campo de função corrente

LETRASGREGAS

α Expoente da expressão da viscosidade

β Expoente da expressão da condutividade elétrica

i

β Autovalores relacionados à autofunção do campo de temperatura γ Expoente da expressão da condutividade térmica

0

ε Permissividade do espaço livre

ew

θ Parâmetro relacionado à razão entre as temperaturas na entrada e na placa inferior do canal

( , )x y

θ Campo escalar filtrado de temperatura ( )

i x

θ Campo filtrado e transformado de temperatura µ Viscosidade dinâmica/absoluta do fluido

i

µ Autovalor relacionado ao campo de função corrente

m

µ Permeabilidade magnética

1,2

w

µ Viscosidade absoluta do fluido avaliada à temperatura das placas inferior e superior do canal

ρ Massa específica do fluido

e

ρ Densidade de carga elétrica σ Condutividade elétrica do fluido

1,2

w

σ Condutividade elétrica do fluido avaliada à temperatura das placas inferior e superior do canal

( )

φ Campo filtrado de função corrente ( )

i x

φ Campo filtrado e transformado de função corrente ( )

F y

ψ Filtro relacionado ao campo de função corrente ( , )x y

SUMÁRIO

1 INTRODUÇÃO ... 20

2 MAGNETOHIDRODINÂMICA:FUNDAMENTAÇÃO TEÓRICA ... 24

2.1 INTRODUÇÃO ... 24

2.2 CONCEITOS BÁSICOS ... 28

2.3 EQUAÇÕES DA ELETRODINÂMICA ... 31

2.3.1 CAMPO ELÉTRICO E FORÇA DE LORENTZ ... 31

2.3.2 LEI DE OHM E FORÇA DE LORENTZ VOLUMÉTRICA ... 32

2.3.3 LEI DE AMPÈRE ... 33

2.3.4 LEI DE FARADAY ... 34

2.3.5 CONSERVAÇÃO DE CARGA - DIVERGÊNCIA: ∇⋅ =J 0 e ∇⋅ =B 0 _{... 36}

2.3.6 EQUAÇÃO DE TRANSPORTE DO CAMPO MAGNÉTICO ... 40

2.4 EQUAÇÕES DE NAVIER-STOKES E A FORÇA DE LORENTZ ... 40

2.4.1 TENSÕES DE MAXWELL ... 42

3 REVISÃO BIBLIOGRÁFICA ... 44

3.1 MAGNETOHIDRODINÂNICA EM CANAIS ... 44

3.2 TÉCNICA DA TRASNFORMADA INTEGRAL ... 48

4 FORMULAÇÃO MATEMÁTICA ... 53

4.1 MODELAGEM MATEMÁTICA ... 53

4.2 ADIMENSIONALIZAÇÃO E GRUPOS ADIMENSIONAIS ... 58

5 METODOLOGIA DE SOLUÇÃO ... 67

5.1 FORMULAÇÃO EM FUNÇÃO CORRENTE ... 67

5.2 FILTRAGEM DOS CAMPOS DE FUNÇÃO CORRENTE E TEMPERATURA ... 68

5.2.1 EXPRESSÃO DO FILTRO PARA O CAMPO DE FUNÇÃO CORRENTE ... 70

5.2.2 EXPRESSÃO DO FILTRO PARA O CAMPO DE TEMPERATURA ... 71

5.3 PROBLEMAS DE AUTOVALOR AUXILIARES ... 72

5.3.1 PROBLEMA DE AUTOVALOR PARA O CAMPO DE FUNÇÃO CORRENTE ... 72

5.3.2 PROBLEMA DE AUTOVALOR PARA O CAMPO DE TEMPERATURA ... 74

5.4 TRANSFORMAÇÃO INTEGRAL DAS EQUAÇÕES ... 76

5.5 RECUPERAÇÃO DOS PRINCIPAIS CAMPOS ... 79

6 RESULTADOS E DISCUSSÃO ... 83

6.1 ANÁLISE DE CONVERGÊNCIA ... 83

6.2 RESULTADOS OBTIDOS E VALIDAÇÃO ... 86

7 CONCLUSÕES E SUGESTÕES ... 99

7.1 CONCLUSÕES ... 99

7.2 SUGESTÕES PARA TRABALHOS FUTUROS ... 100

REFERÊNCIAS BIBLIOGRÁFICAS ... 102

__________________________

CAPÍTULO I

1INTRODUÇÃO

O escoamento, laminar ou turbulento, e a transferência de calor envolvendo fluidos condutores elétricos (não magnéticos) submetidos a campos magnéticos externos (Magnetohidrodinâmica - MHD) tem se apresentado em importantes aplicações industriais atuais sob as mais variadas formas e situações, como por exemplo, no desenvolvimento de bombas e geradores magnetohidrodinâmicos, no resfriamento de reatores nucleares, e mais fortemente nas indústrias de alumínio (células de redução de alumínio) e siderúrgicas. Iniciando-se no começo do século vinte, estudos sobre a magnetohidrodinâmica aplicada à engenharia reapareceram nos anos sessenta, tendo ganhado, atualmente, forte atenção devido principalmente às necessidades energéticas e ambientais, tornando-se, consequentemente, o objeto de muitas investigações científicas (Shercliff, 1965; Davidson, 2001 e Sutton e Sherman, 2006).

Paralelamente, o desenvolvimento de métodos numéricos, empregados na solução das equações que governam o escoamento e a transferência de calor dos mais diversos campos das ciências, tem ganhado cada vez mais espaço na comunidade científica e tecnológica, principalmente no que diz respeito ao seu uso e aplicação. Atualmente, os métodos conhecidos como volumes finitos e elementos finitos formam a base das metodologias numéricas empregadas nos núcleos de cálculo dos “softwares” atuais encontrados nos campos de dinâmica dos fluidos computacional e de análise estrutural computacional (ANSYS, 2009).

Em função de tal panorama, o principal objetivo do presente trabalho consiste no desenvolvimento de soluções híbridas, através da aplicação da Técnica da Transformada Integral Generalizada (GITT), para o problema do desenvolvimento simultâneo do escoamento e da transferência de calor de fluidos newtonianos condutores elétricos submetidos a campos magnéticos constantes, em um canal de placas planas e paralelas. Tal geometria se apresenta como boa simplificação para muitos escoamentos encontrados na prática e facilita extremamente o procedimento de análise e validação da técnica.

O escoamento, modelado através das equações parabólicas e na formulação de função corrente, é mantido por um gradiente de pressão e o campo magnético é aplicado na direção normal ao escoamento. Assume-se que tal campo magnético não é afetado pelo escoamento, permanecendo muito maior do que qualquer campo gerado em outras direções coordenadas. Analisa-se, assim, a interação de uma via apenas entre o escoamento de um fluido condutor elétrico e um campo magnético, uma vez que o campo magnético afeta o campo de escoamento, mas o campo de escoamento não afeta o campo magnético imposto. Esta simplificação implica que não há necessidade da resolução das equações de Maxwell, uma vez que o campo magnético aplicado não é alterado pelo escoamento.

Para avaliar mais efetivamente a influência do campo magnético aplicado sobre as regiões de entrada hidrodinâmica e de entrada térmica, dois tipos de condições de entrada para o campo de velocidade na entrada do canal são empregadas: perfil uniforme e perfil parabólico do escoamento completamente desenvolvido sem aplicação de campo magnético. Para o campo de temperatura, considera-se um perfil de entrada uniforme. Resultados para os campos de velocidade, temperatura e outras variáveis correlatas são mostrados em função dos principais parâmetros governantes, como número de Reynolds, número de Hartmann e parâmetro elétrico, entre outros, para situações típicas encontradas na prática. Para fins de validação, os resultados obtidos com a presente metodologia são ainda confrontados com outros resultados numéricos e experimentais previamente reportados na literatura.

A seguir, no Capítulo 2, é realizada uma breve descrição, baseada em Shercliff (1965) e Davidson (2001), dos fundamentos do escoamento de fluidos condutores elétricos (não magnéticos) submetidos a campos magnéticos. Nesse capítulo, são mostradas as equações básicas da eletrodinâmica, os seus parâmetros característicos e a forma de interação entre os campos magnéticos e do escoamento.

No Capítulo 3, é realizada uma revisão bibliográfica acerca dos trabalhos numéricos e experimentais desenvolvidos anteriormente sobre o estudo da magnetohidrodinâmica com e sem transferência de calor em dutos. No final do capítulo, é mostrado ainda o estado da arte de aplicação da técnica da transformada integral generalizada a problemas de mecânica dos fluidos e transferência de calor.

No Capítulo 4, é desenvolvida a formulação matemática do problema, ilustrando-se a geometria estudada e as condições de contorno associadas ao fenômeno físico analisado. O problema é mostrado nas suas formas dimensional e adimensional, e os grupos adimensionais empregados são, nesse momento, definidos. As definições dos principais parâmetros correlatos aos campos de velocidade e magnético são também estabelecidas no final desse capítulo.

O Capítulo 5 descreve completamente a metodologia de solução empregada nas equações de governo do problema. O uso da formulação em função corrente, o emprego do processo de “filtragem” numérica dos campos de função corrente e temperatura, o estabelecimento dos problemas de autovalores associados, o desenvolvimento do processo analítico de transformação integral das equações de governo e a recuperação dos potenciais (campos) originais são detalhadamente descritos nesse capítulo.

No Capítulo 6 são mostrados, na forma gráfica e em tabelas, os resultados obtidos no presente trabalho com aplicação da técnica da transformada integral generalizada. Validação numérica, análises de convergências dos principais campos do escoamento e uma completa discussão de tais resultados são nesse momento efetuadas.

Finalmente, no Capítulo 7, são traçadas as conclusões obtidas com o desenvolvimento do presente trabalho e as principais sugestões de continuidade para trabalhos futuros são apresentadas.

______________________________

CAPÍTULO II

2MAGNETOHIDRODINÂMICA:FUNDAMENTAÇÃO TEÓRICA

2.1 INTRODUÇÃO

Campos magnéticos influenciam muitos escoamentos naturais e artificiais. Na indústria, eles são rotineiramente usados para aquecer, bombear, agitar e levitar metais líquidos. Por outro lado, tem-se conhecimento da existência do campo magnético terrestre, o qual é mantido pelo movimento do fluido no núcleo da terra, do campo magnético solar, o qual gera manchas e chamas solares e do campo magnético galáctico, o qual se atribui à formação de estrelas a partir de nuvens solares. O estudo desses escoamentos é denominado magnetohidrodinâmica (MHD). Formalmente, a magnetohidrodinâmica está voltada para a interação mútua entre o escoamento de fluidos e campos magnéticos. Os fluidos em questão devem ser eletricamente condutores e não-magnéticos, os quais se limitam a metais líquidos, gases quentes ionizados (plasmas) e eletrólitos fortes.

As leis do magnetismo e do escoamento de fluidos foram desenvolvidas por volta do século XIX, no entanto, a magnetohidrodinâmica tornou-se um assunto completamente desenvolvido apenas no final da década de 1930 e início da década de 1940. A razão era, provavelmente, que existia pouco incentivo para as possibilidades oferecidas pela magnetohidrodinâmica. Assim, enquanto poucos experimentos isolados eram realizados por físicos, como Faraday, o assunto permaneceu inexplorado até a virada daquele século. O panorama começou a mudar quando os astrofísicos perceberam o quão onipresentes são campos magnéticos e plasmas por todo o universo. Isto culminou em 1942 com a descoberta das ondas de Alfvén, um fenômeno peculiar à magnetohidrodinâmica e importante em astrofísica (uma linha de campo magnético pode transmitir ondas inerciais transversais). Ao mesmo tempo, geofísicos começaram a suspeitar que o campo magnético da terra era gerado pela ação de dínamo do metal líquido de seu núcleo, uma hipótese inicialmente fomentada por Larmor em 1919 no contexto do campo magnético do sol.

Apesar de alguns trabalhos pioneiros terem sido realizados pelo engenheiro Hartmann que, em 1918, inventou a bomba eletromagnética (ilustrada na Figura 2.1a) e também, em 1937, empreendeu uma sistemática investigação teórica e experimental do escoamento de mercúrio sob um campo magnético homogêneo (Hartmann é considerado o pai da magnetohidrodinâmica de metal líquido, sendo o termo “escoamento de Hartmann” usado para descrever escoamentos em dutos na presença de um campo magnético), o desenvolvimento da magnetohidrodinâmica na engenharia só aconteceu efetivamente a partir da década de 1960. Esse lento progresso deveu-se especialmente à baixa condutividade elétrica dos fluidos comumente empregados na engenharia, a saber, o mercúrio e alguns eletrólitos.

O ímpeto à mudança veio, principalmente, a partir de três inovações tecnológicas: a) reatores de alimentação/produção rápida, que usam sódio líquido como fluido

refrigerante e necessita ser bombeado (bomba eletromagnética – Figura 2.1a); b) fusão termonuclear controlada, que requer que um plasma quente seja mantido

distante das superfícies do reator por forças eletromagnéticas (Figura 2.1b), c) geração de potência magnetohidrodinâmica, na qual um gás ionizado é

propelido através de um campo magnético. Tal inovação mostrou-se, posteriormente, tecnicamente inviável.

(a) (b)

Enquanto a pesquisa por geração de potência declinava, a indústria metalúrgica demonstrava interesse por MHD. Duas décadas mais tarde, campos magnéticos eram rotineiramente empregados para aquecer, bombear, agitar (Figura 2.2a), amortecer o movimento (Figura 2.2b) e levitar (Figura 2.2c) metais líquidos em indústrias metalúrgicas de todo o mundo.

(a) (b)

(c)

Figura 2.2 – Esquema (a) de agitação magnética de um lingote, (b) do amortecimento magnético de movimento durante fundição e (c) de uma válvula eletromagnética.

Adaptado de Davidson (2001).

A magnetohidrodinâmica também é importante no processo de eletrólise, particularmente em células de eletrólise usadas para reduzir óxido de alumínio em alumínio. Essas células consistem de camadas largas, mas rasas, de eletrólito/criolita e alumínio líquido, com o eletrólito permanecendo no topo. Uma corrente elétrica extrema (aproximadamente 200 kA) passa verticalmente para baixo através das duas camadas, reduzindo continuamente o óxido de metal. Esse processo é energeticamente intensivo, principalmente por causa da elevada resistência elétrica do eletrólito. Sabe-se que campos magnéticos dispersos podem desestabilizar a interface entre o eletrólito e o alumínio, através de ondas de gravidade interfaciais, as quais absorvem energia do campo magnético convertendo-a em energia cinética (Figura 2.3). De maneira a evitar estas instabilidades, a camada de criolita deve ser mantida em uma espessura acima de algum valor crítico, às custas de uma severa penalidade energética.

Figura 2.3 – Instabilidade em uma célula de redução de alumínio. Adaptado de Davidson (2001).

Entre outras aplicações da magnetohidrodinâmica na engenharia e na metalurgia podem-se citar ainda a fundição eletromagnética de alumínio, a reformulação de super ligas baseadas em titânio e níquel, a remoção eletromagnética de inclusões não-metálicas de metal fundido, propelidores/lançadores eletromagnéticos e o chamado processo de fundição à frio por indução em cadinhos (vitrificação de lixo nuclear altamente ativo).

2.2 CONCEITOS BÁSICOS

A interação mútua de um campo magnético, B, e um campo de velocidade, V , surge parcialmente como resultado das leis de Faraday e Ampère, e parcialmente por causa da força de Lorentz experimentada por um corpo condutor de corrente elétrica. De maneira conveniente, embora artificial, divide-se essa interação em três ações:

i) O movimento relativo de um fluido condutor e um campo magnético gera uma força eletromotriz, fem (da ordem de u B× ), de acordo com a lei de Faraday da indução. Em geral, correntes elétricas são geradas/induzidas, a densidade de corrente, J , sendo da ordem de σ

( )

gerar/induzir um segundo campo magnético. Esse campo magnético se “soma” ao campo magnético original e a mudança é geralmente tal que o fluido parece “arrastar” as linhas de campo magnéticas.

iii) O campo magnético combinado interage com a densidade de corrente induzida, J , gerando/induzindo uma força por unidade de volume, a força de Lorentz, J×B. Essa força age sobre o condutor e, geralmente, é dirigida de maneira a inibir o movimento relativo entre o campo magnético e o fluido.

As duas últimas ações têm conseqüências similares. Em ambos os casos, o movimento relativo entre o fluido e o campo magnético tende a ser reduzido. Fluidos podem “arrastar” linhas de campo magnético (efeito ii) e campos magnéticos podem “segurar” fluidos condutores (efeito iii). É este “congelamento” parcial do meio e do campo magnético que é o ponto principal da magnetohidrodinâmica.

Figura 2.4 – Interação entre um campo magnético e um fio circular em movimento. Adaptado de Davidson (2001).

O campo magnético associado com a corrente induzida perturba o campo magnético original, e o resultado líquido é que as linhas de campo magnéticas parecem ser “arrastadas” pelo fio (efeito ii). A corrente induzida também faz surgir a força de Lorentz, J×B, a qual age no fio na direção oposta ao do movimento (efeito iii). Assim, é necessário fornecer uma força para movimentar o fio.

Para um melhor entendimento do efeito (ii), inicia-se pela percepção de que o campo magnético imposto deverá ser influenciado (a) pela velocidade típica do fluido, (b) pela condutividade elétrica do fluido e, de maneira não tão explícita, (c) por uma escala característica de comprimento, ℓ, do movimento. Se o fluido não é condutor ou a sua

velocidade é desprezível, não existirá campo magnético induzido significante. Por outro lado, se σ ou u são grandes, então o campo magnético induzido pode alterar o campo magnético imposto (ver Figura 2.4). Conforme citado, a fem gerada pelo movimento relativo entre o campo magnético imposto e o meio é da ordem de u B× , de maneira que, pela lei de Ohm, a densidade de corrente induzida é da ordem de σ

( )

Logo, é o produto σuℓ que determina a razão do campo magnético induzido para o

campo magnético aplicado. No limite em que σuℓ→ ∞ (típico dos condutores ideais), os

A astrofísica se situa mais próxima do primeiro caso, não apenas pela alta condutividade dos plasmas, mas devido à grande escala de comprimento envolvida. A MHD de metal líquido, por outro lado, se situa no segundo limite, de maneira que o campo de velocidade não perturba significativamente o campo magnético imposto. Apesar desse fato, o efeito (iii) ainda é forte em metais líquidos, de maneira que um campo magnético imposto altera substancialmente o campo de velocidade (interação de uma via).

Considerando-se a permeabilidade do espaço livre, µ_m, a condutividade elétrica, σ , a massa específica do meio, ρ, e uma escala de comprimento característica,

ℓ, pode-se construir os três seguintes parâmetros chaves da magnetohidrodinâmica.

Re_m=µ σ_m uℓ Número de Reynolds Magnético _(2.1)

a

m

B v

ρµ

= Velocidade de Alfvèn _(2.2)

1 2 B σ τ

ρ

−

 

= 

  Tempo de Amortecimento Magnético (2.3)

O número de Reynolds magnético é uma medida adimensional da condutividade elétrica, de maneira que é Re_m, e não apenas σ , o fator importante em MHD.

Quando Re_m é grande, as linhas de campo magnéticas agem como cordas elásticas “agarradas” ao meio, implicando em duas conseqüências. Primeiro, o fluxo magnético através de uma curva material fechada tende a ser conservado durante o movimento do fluido (as linhas de fluxo tendem a acompanhar a curva, Figura 2.4). Segundo, pequenos distúrbios no meio resultam em oscilações quasi-elásticas, o campo magnético fornecendo a força de restauração para as oscilações. Isso resulta nas ondas de Alfvèn, de freqüência

/

a

v

ω ≈ ℓ. Quando Re

m é pequeno, u tem pouca influência sobre B, pois o campo

2.3 EQUAÇÕES DA ELETRODINÂMICA

As leis básicas do eletromagnetismo são denominadas de leis de Lorentz, de Ohm, de Faraday e de Ampère, e serão discutidas em maiores detalhes nesta seção.

2.3.1 CAMPO ELÉTRICO E FORÇA DE LORENTZ

Uma partícula se movendo com velocidade u e transportando uma carga q está, em geral, submetida a três forças eletromagnéticas:

s i

f =qE +qE +qu B× _(2.4)

- O primeiro termo é a força eletrostática, ou força de Coulomb, a qual surge da repulsão ou atração mútua de cargas elétricas (E_s é o campo eletrostático),

- O segundo termo é a força que a carga experimenta na presença de um campo magnético dependente do tempo (E_i é o campo elétrico induzido pelo campo),

- O terceiro termo é a força de Lorentz, a qual surge com o movimento da carga em um campo magnético.

A lei de Coulomb afirma que E_s é irrotacional, e a lei de Gauss estabelece a sua divergência (Eq.2.8). Assim:

0

e s

E ρ

ε

∇⋅ = ; ∇×E_s =0 _(2.5.a-b)

onde ρ_e é a densidade de carga total (cargas livres e de ligação) e ε₀ é a permissividade do espaço livre. Em função da Eq. (2.5.b), pode-se introduzir o potencial eletrostático V , definido por E_s = −∇V , de maneira que da Eq. (2.5a) tem-se ∇ = −2V ρ ε_e/ ₀.

Por outro lado, o campo elétrico induzido tem divergência nula, enquanto o seu rotacional é finito e governado pela lei de Faraday (ver Eq. 2.7):

0

i

E

∇⋅ = ; E_i B

t

∂ ∇× = −

Assim, é conveniente definir o campo elétrico total como E=E_s+E_i, de tal maneira que se pode escrever de maneira generalizada:

0

e

E

Lei de Gauss ρ ε

∇ ⋅ =

;

B E

t Lei de Faraday

∂ ∇× = −

∂ (2.8, 2.9)

(

)

f =q E+ ×u B Força Eletrostática + Força de Lorentz _(2.10)

Se, diferentemente de u, E e B, for medido um campo elétrico em um sistema de coordenadas fixo na carga em movimento, define-se o campo elétrico relativo/efetivo:

r

f =qE ; E_r = + ×E u B _{(2.11, 2.12)}

2.3.2 LEI DE OHM E FORÇA DE LORENTZ VOLUMÉTRICA

Em MHD, o interesse é na força global agindo sobre o meio, não nas forças sobre partículas individuais. Assim, um somatório sobre um volume unitário do condutor produz:

e

q

Densidade de Carga ρ

=

∑

qu J

Densidade de Corrente

=

∑

(2.13,2. 14)

Logo, a versão volumétrica da Eq. (2.10), isto é, da força de Lorentz é:

e

F =ρ E+ ×J B Força p/ Unidade de Volume _(2.15)

Por outro lado, as velocidades comumente encontradas em aplicações de engenharia são muito menores do que a velocidade da luz e a densidade de carga é muito pequena, de maneira que o primeiro termo da Eq. (2.15) pode ser desprezado. Assim, na magnetohidrodinâmica de metais líquidos, a força de Lorentz é escrita na forma:

Sabe-se por outro lado que à densidade de corrente, J , em um condutor estacionário é proporcional à força gerada pelas cargas livres, qE, sendo descrita pela lei de Ohm convencional como J =σE (Figura 2.5a).

Figura 2.5 – Lei de Ohm em um condutor (a) estacionário e (b) em movimento. Adaptado de Davidson (2001).

Se, em adição, o condutor se move com velocidade u sob um campo magnético, as cargas livres experimentarão uma força adicional qu B× , e a lei de Ohm é agora escrita de maneira generalizada como (Figura 2.5b):

(

)

r

J =σE =σ E+ ×u B Lei de Ohm (MHD/Não-MHD) _(2.17)

Se o condutor é um meio fluido, o campo de velocidade u variará, em geral, com a posição. Esta característica torna a interação entre u e B mais sutil e mais difícil de quantificar.

2.3.3 LEI DE AMPÈRE

Simplificadamente, a lei de Ampère trata do campo magnético gerado por uma distribuição de corrente (Figura 2.6). Se C é uma curva fechada, composta de elementos de linha dℓ, e S é qualquer superfície limitada por essa curva, a lei de Ampère estabelece:

m

C S

B d⋅ =µ J dS⋅

Figura 2.6 – Lei de Ampère aplicada a um fio. Adaptado de Davidson (2001).

Essa lei pode ser entendida como a circulação do campo magnético em torno da curva C é igual ao fluxo (densidade) de corrente através da superfície (área, S) delimitada pela curva sobre a qual a circulação está sendo calculada. Na forma diferencial, aplicando o teorema de Gauss, a lei de Ampère é descrita como:

m

B µ J

∇× = Lei de Ampère _(2.19)

Posteriormente, Maxwell verificou que a lei necessitaria levar em conta a antes desconhecida corrente de deslocamento (a qual se fazia necessária para satisfazer o princípio de conservação da carga, ver Eq.2.23), de maneira que a lei passou a ser denominada lei de Ampère-Maxwell. Na forma diferencial ela é escrita como:

0

m

E

B J

t µ  ε ∂ 

∇× =  + 

∂

  Lei de Ampère-Maxwell (2.20)

Entretanto, a correção de Maxwell não é necessária em MHD de metal líquido, de maneira que é empregada na sua forma pré-Maxwelliana dada pela Eq. (2.19).

2.3.4 LEI DE FARADAY

Figura 2.7 – Lei de Faraday (a) fem gerada pelo movimento de um condutor, (b) fem gerada por um campo magnético dependente do tempo. Adaptado de Davidson (2001).

Em um ou outro caso, a lei de Faraday pode ser escrita como:

r

C S

d

fem E d B dS

dt

=

∫

∫

Onde C é uma curva fechada, composta de elementos de linha dℓ e S é qualquer superfície limitada por essa curva. Novamente, como na Eq. (2.12), E_r é o campo elétrico efetivo, medido em uma referência fixa na carga/elemento dℓ em movimento.

Similarmente à lei de Ampère, a lei de Faraday pode ser entendida como a circulação do campo elétrico em torno da curva C (fem gerada) é igual ao decréscimo da taxa de variação como tempo do fluxo (densidade) magnético através da superfície (área, S) delimitada pela curva sobre a qual a circulação está sendo calculada.

Na forma diferencial, aplicando o teorema de Gauss e supondo que a curva é rígida e está em repouso (e logo a carga de cada elemento dℓ), a lei de Faraday é descrita como:

B E

t

∂ ∇× = −

∂ Lei de Faraday(MHD/Não-MHD) (2.22)

2.3.5 CONSERVAÇÃO DE CARGA - DIVERGÊNCIA: ∇⋅ =J 0 e ∇⋅ =B 0

Conforme já citado, o requerimento de conservação da carga requer que a taxa na qual a carga decresce em um volume de controle deve ser igual ao fluxo de carga para fora através de sua superfície (densidade de corrente, Eq.2. 14):

e

J

t ρ

∂ ∇⋅ = −

∂ Eq. Conservação da Carga (2.23)

Tomando o divergente em ambos os lados da equação anterior, e usando a lei de Gauss, obtém-se:

( )

e e

e

u B t

ρ _{ρ σ}

τ

∂ + + ∇⋅ × =

∂ ; e 0

ε τ

σ

= _(2.24.a,b)

A quantidade τ_e é o tempo de relaxação da carga, e para um condutor típico é aproximadamente 10-18 s, um valor extremamente pequeno. Para apreciar a origem do seu nome, considere a situação onde u=0. Nesse caso a Eq. (2.24.a), e sua solução, são:

0

e e

e

t

ρ ρ

τ

∂ + =

∂ ; e( ) e(0) exp

e

t t

ρ ρ

τ

 

= − 

  (2.25a,b)

Qualquer densidade de carga líquida que, no tempo t = 0, estiver no interior de um condutor se moverá rapidamente para a superfície sob a ação de forças de repulsão eletrostáticas. Assim, ρ_e é sempre zero em condutores estacionários, exceto durante

algum minúsculo período, como, por exemplo, quando uma bateria é ligada.

Agora, considere a situação em que u≠0. Desde que se está interessado em eventos que ocorrem em uma escala de tempo muito maior do que τ_e, pode-se desprezar

e

t ρ

∂

∂ em comparação com ρ τe/ e, de maneira que a Eq. (2.24) é escrita como:

( )

e u B

Logo, quando existe movimento, pode-se sustentar uma densidade de carga finita no interior de um condutor. Entretanto, como se verá, ρ_e é muito pequena, incapaz de produzir qualquer força elétrica significante, ρ_eE, de maneira que se justifica a Eq. (2.16).

Em termos de escalas características a equação anterior pode ser aproximada porρ_e ∼ε₀uB/ℓ, enquanto da lei de Ohm por _E∼_J /σ , de maneira que

(

)(

)

e

u

E uB J τ J B

ρ ∼ ε ℓ σ ∼

ℓ . Por argumentos dimensionais,

18

/ 10

e

uτ _{ℓ ∼} − _{, assim, a}

força de Lorentz domina completamente a Eq. (2.15), a qual passa a ser escrita como:

F = ×J B Força de Lorentz volumétrica (MHD) (2.27)

Observa-se também que para u ≠0, uma hipótese básica foi desprezar e

t ρ

∂

∂ de

maneira que a equação da conservação da carga, Eq. (2.23), passa a ser escrita como:

0 J

∇⋅ = Eq. Conservação da Carga (MHD) _(2.28)

Com relação à lei de Ampère-Maxwell, explicitando a densidade de corrente J, aplicando o divergente sobre a equação obtida e fazendo uso da lei de Gauss, obtém-se:

( )

0 e

J E

t t

ρ

ε ∂ ∂

∇⋅ = − ∇⋅ = −

∂ ∂ (2.29)

Esta é exatamente a equação da conservação da carga, a qual demonstra que se a lei de Ampère for empregada sem a corrente de deslocamento (correção de Maxwell), a conservação da carga seria violada. Entretanto, como já citado, em condutores, o termo

e

t ρ

∂

∂ é desprezível, ou, por argumentos dimensionais, a corrente de deslocamento é muito

menor do que J. Assim a Eq. (2.19) é suficiente para análises de MHD.

m

B µ J

Em adição, essa equação é consistente com a Eq. (2.28), a equação da conservação da carga simplificada, uma vez que, tomando-se o divergente da Eq. (2.19), obtém-se a Eq. (2.31).

Finalmente, com relação à lei de Faraday, Eq. (2.23), tomando-se o divergente em ambos os lados, obtém-se:

(

)

t

∂ ∇⋅ ∇× = −∇⋅ =

∂ (2.31)

Tal resultado mostra que B t

∂

∂ é solenoidal. Na realidade, o próprio B é solenoidal:

0 B

∇⋅ = (MHD/Não-MHD) _(2.32)

Isto permite a introdução de um outro campo, A, denominado vetor potencial, o qual é definido tal que:

A B

∇× = ; ∇⋅ =A 0 (2.33, 2.34)

Essa definição assegura, automaticamente, que B é solenoidal, uma vez que

(

)

∇ ⋅ ∇× = . Agora a substituição de A na lei de Faraday, Eq. (2.23),

(

)

E A E

t t

∂ ∂

∇× = − ∇× = −∇×

∂ ∂

A

E V

t

∂

⇒ _{∇× = − −∇}

∂ (2.35)

onde V é uma função escalar arbitrária (potencial eletrostático), necessária no resultado, tendo em vista que E=E_s+E_i e as restrições impostas pelas Eqs. (2.6), ∇×E_s =0, e (7),

0

i

E

∇⋅ = .

s

E = −∇V E_i A

t

∂ = −

Para concluir a presente seção, é mostrado um resumo das equações que descrevem todos os fenômenos da eletrodinâmica: as Equações de Maxwell e as equações adicionais da força eletromagnética e da conservação da carga (materiais não magnéticos nem dielétricos).

0

e

E ρ

ε

∇⋅ = Lei de Gauss _(2.37)

B E

t

∂ ∇× = −

∂ Lei de Faraday diferencial (2.38)

(

)

f =q E+ ×u B Força eletromagnética _(2.39)

0

m

E

B J

t µ  ε ∂ 

∇× =  + 

∂

  Lei de Ampère-Maxwell (2.40)

e

J

t ρ

∂ ∇⋅ = −

∂ Conservação da carga (2.41)

0 B

∇⋅ = Natureza solenoidal de B (2.42)

Por outro lado, quando são consideradas as simplificações de MHD, as equações da eletrodinâmica se reduzem à forma pré-maxwelliana:

B E

t

∂ ∇× = −

∂ Lei de Faraday diferencial (2.43)

(

)

F = J×B Força eletromagnética _(2.44)

(

)

J =σ E+ ×u B Lei de Ohm _(2.45)

m

B µ J

∇× = Lei de Ampère _(2.46)

0 J

∇⋅ = Conservação da carga (2.47)

0 B

2.3.6 EQUAÇÃO DE TRANSPORTE DO CAMPO MAGNÉTICO

Conforme já comentado, em situações em que o número de Reynolds magnético é de moderado a elevado, o campo magnético é influenciado pelo campo de escoamento. Para se obter a equação de transporte (advecção/difusão) do campo magnético, algumas vezes denominada de equação da indução, para esta situação, basta combinar as leis de Ohm, Faraday e Ampère:

(

)

(

)

B

E J u B u B B

t σ µ σ

∂ = −∇× = −∇× − × = ∇× × −∇×

∂ (2.49)

Notando que 2

B B

∇×∇× = −∇ , uma vez que B é solenoidal, a equação da advecção/difusão do campo magnético é:

( )

m

B

u B B

t λ

∂ =∇× × + ∇

∂ (2.50)

onde λm

(

)

−

= é denominada de difusividade magnética. Observe-se o forte acoplamento entre o campo do escoamento e o campo magnético, caracterizando a interação de duas vias entre os dois campos. Condições de contorno e condições iniciais devem ser especificadas para o campo magnético, de maneira a se estabelecer a solução de cada problema (Shercliff, 1965).

Quando essa equação é escrita na forma adimensional, aparece um parâmetro (adimensional) o qual indica a intensidade relativa entre a advecção e a difusão do campo magnético. Por sua analogia com a equação de transporte de quantidade de movimento, tal parâmetro recebeu o nome de número de Reynolds magnético, já introduzido na Eq. (2.1):

Re_{m m}

m

u u µ σ

λ

= ℓ= ℓ Número de Reynolds Magnético _(2.51)

2.4 EQUAÇÕES DE NAVIER-STOKES E A FORÇA DE LORENTZ

Campos magnéticos, como qualquer outra força de campo/corpo, atuam em todo ponto do escoamento, de maneira que seu efeito é diretamente incluído através de um termo adicional de força por unidade de volume, a força de Lorentz por unidade de volume. Assim, levando em conta tal força de corpo, as equações de Navier-Stokes para um fluido incompressível com propriedades físicas constantes são escritas como:

2 1

Du F

p u

Dt = − ∇ + ∇ +ρ ν ρ ⇒

(

)

2

1 J B

Du

p u

Dt ρ ν ρ

×

= − ∇ + ∇ + (2.52)

Três grupos adimensionais aparecem quando a equação é escrita na forma adimensional. O primeiro é o número de Reynolds, Re u

ν

= ℓ, o qual, como na mecânica dos fluidos convencional, indica a razão das forças inerciais,

(

)

2 B N

u u

σ

ρ τ

= ℓ= ℓ _(2.53)

onde τ é o tempo de amortecimento magnético, Eq. (2.3). O parâmetro de interação magnética é importante em situações onde a densidade de corrente J se deve principalmente à u B× na lei de Ohm. Em tal situação, N representa a razão das forças de Lorentz,

(

)

(

)

(

)

(

)

Ha N B σ

ρν

 

= =  

 

2.4.1 TENSÕES DE MAXWELL

A força de Lorentz pode ser escrita em termos do campo magnético, B, apenas. Tendo em vista a identidade vetorial:

( )

2 B

B B B B

 

∇ = ⋅∇ + ×∇×

  (2.55)

e a lei de Ampère, ∇× =B µ_mJ , a força de Lorentz é então:

( )

2

m m

B B

J B B

µ µ

   

× = ⋅∇  − ∇ 

    (2.56)

O segundo termo do lado direito da equação age sobre o fluido da mesma maneira que a força de pressão −∇p. Tal termo é irrotacional, de maneira que não influencia o campo de escoamento. Em escoamentos internos, sua função é simplesmente aumentar a pressão do fluido. Por essa razão, 2_{/ 2}

(

)

m

B µ é comumente denominada de pressão magnética. Por outro lado, o primeiro termo do lado direito pode ser escrito em notação indicial como:

( )

j m

B B B

B

x

µ µ

 

  _∂

⋅∇  =  

∂

    (2.57)

Pode-se entender, assim, que o efeito dessa parte da força de corpo é equivalente a uma ação fictícia de tensões,

( )

Em suma, pode-se substituir a força de corpo de Lorentz, J×B, por um efeito equivalente de tensões superficiais imaginárias, denominadas tensões de Maxwell:

2 2

i j

ij ij

m m

B B B

τ δ

µ µ

______________________________

CAPÍTULO III

3REVISÃO BIBLIOGRÁFICA

3.1 MAGNETOHIDRODINÂMICA EM CANAIS

A pesquisa efetuada no presente trabalho é voltada à determinação dos campos de velocidade e de temperatura na região de entrada de um canal de placas planas e paralelas (desenvolvimento térmico e hidrodinâmico), considerando o escoamento laminar, não-isotérmico, de um fluido condutor elétrico sob a influência de um campo magnético. O fluido troca calor com as placas do canal, as quais estão a temperaturas diferentes do fluido. Conforme já citado, tal problema de convecção forçada de um fluido viscoso e eletricamente condutor (magnetoconvecção) tem sua aplicação voltada para a indústria do petróleo, em reatores nucleares e nos campos da engenharia metalúrgica, em particular na produção de alumínio por eletrólise em células de redução, e no desenvolvimento de geradores magnetohidrodinâmicos. Os interesses estão direcionados, principalmente, nos processos da conversão de energia associados ao aumento da eficiência térmica e energética.

Os estudos iniciais sobre essa geometria se mostraram focados apenas na dinâmica do escoamento (Chang e Lundgren,1959; Tao, 1960, Manohar, 1966, Hwang et al. 1966). Ao mesmo tempo, os efeitos térmicos começaram também a ser levados em conta principalmente no estudo do problema da entrada térmica (desenvolvimento térmico sob condições de escoamento completamente desenvolvido sob um campo magnético, o denominado escoamento de Hartmann). Nesses estudos, as propriedades termofísicas dos fluidos foram consideradas uniformes (Nigam e Singh, 1960; Alpher, 1961; Shohet et al., 1962; Eraslan e Eraslan, 1969).

Embora uma melhora substancial sobre o entendimento da física governante do escoamento magnetohidrodinâmico com transferência de calor em um canal tenha sido realizada através desses trabalhos, é bem sabido que o escoamento no interior de tais dispositivos dificilmente é completamente desenvolvido sobre toda a sua extensão, e que grandes fluxos de calor podem ocorrer nas suas regiões de entrada, independente da influência da variação das propriedades termofísicas com a temperatura.

Consequentemente, estudos sobre o desenvolvimento hidrodinâmico e sobre o desenvolvimento simultâneo de escoamentos MHD com transferência de calor tornou-se o objeto de muitas investigações científicas por muitos anos. Assim, a seguir são revisados, em função do discutido nos parágrafos anteriores, alguns dos trabalhos considerados os mais importantes para o desenvolvimento do presente trabalho.

Shercliff (1953, 1965) desenvolveu métodos aproximados para resolver o problema da entrada magnetohidrodinâmica em medidores de vazão de seção circular, mas não chegaram a determinar, explicitamente, perfis de velocidades.

Roidt e Cess (1962) aplicaram o método aproximado desenvolvido por Schilichting para resolver o problema do escoamento magnetohidrodinâmico na região de entrada de um duto plano. As equações governantes foram inicialmente linearizadas e as equações resultantes foram resolvidas analítica ou numericamente. O perfil de velocidade na entrada do duto foi considerado uniforme.

Manohar (1966) estudou o mesmo problema, aplicando um procedimento numérico semelhante ao de Hartree (1949), onde os termos das equações de governo envolvendo derivadas na direção x eram substituídos por diferenças finitas, enquanto as outras quantidades eram substituídas por suas médias. De acordo com o autor, o método empregado é mais acurado do que o anterior, uma vez que o mesmo corresponde apenas à primeira iteração do esquema desenvolvido por ele.

Maciulaitis e Loeffler (1964) empregaram o método integral de Karman-Pohlhausen para tratar o escoamento magnetohidrodinâmico na região de entrada de um canal, considerando um perfil de velocidade parabólico na entrada.

Posteriormente, Hwang et al. (1966), empregando um esquema de diferenças finitas semelhante ao desenvolvido por Hwang e Fan (1963), resolveram o mesmo problema de entrada magnetohidrodinâmica, considerando agora um perfil parabólico na entrada do canal. Por empregarem um método mais robusto, chegaram a resultados mais confiáveis do que os de Maciulaitis e Loeffler (1964).

Hwang (1972) analisou a região de entrada hidrodinâmica de um canal sob a presença de um campo magnético constante através de um procedimento de linearização das equações. Os seus resultados, considerando um perfil de velocidade parabólico na entrada do canal, foram comparados com os produzidos por Hwang et al. (1966).

Chen e Chen (1972) adaptaram o método desenvolvido por Sparrow et al. (1964) para o estudo de escoamentos em dutos, e analisaram a região de entrada do escoamento magnetohidrodinâmico induzido por uma distribuição de velocidade arbitrária na entrada do canal. Resolveram uma forma linearizada das equações de camada limite que descrevem o escoamento.

Dentre os trabalhos pesquisados, o único trabalho que relatava a solução do problema da entrada hidrodinâmica na presença de um campo magnético, considerando as equações de Navier-Stokes, foi o reportado por Brandt e Gillis (1966). Empregando a formulação de função corrente, empregaram um esquema de diferenças finitas para resolver as equações sem recorrer a nenhum recurso simplificador.

Até esse ponto, todos os trabalhos citados consideram as propriedades termofísicas e de transporte constantes. Por outro lado, como já comentado, em função das condições de operação de determinados dispositivos, a atenção foi voltada para o estudo do problema do escoamento sob condições de propriedades de transporte dependentes da temperatura.

Em um trabalho pioneiro, Rosa (1971) discutiu, experimental e teoricamente, o efeito de propriedades de transporte variáveis em escoamentos sob campos magnéticos.

Lohrasbi (1987) considerou a variação das propriedades de transporte com a temperatura em um escoamento bifásico uni-dimensional submetido a campos magnéticos.

Mittal et al. (1987) estudaram o desenvolvimento do escoamento e da transferência de calor de dois gases compressíveis com propriedades de transporte variáveis no interior de um canal. Assumindo que as placas estavam à mesma temperatura, resolveram numericamente as equações parabólicas, mas limitaram o domínio de cálculo na própria região de camada limite e não em todo domínio do canal.

Setayeshpour e Sahai (1985) também discutiram o efeito de propriedades de transporte dependentes da temperatura na região de entrada de um canal, considerando um tipo de condição de contorno generalizada, na qual o fluxo de calor é função linear da temperatura local.

Finalmente, baseados nos trabalhos anteriormente citados, Setayesh e Sahai (1990) realizaram um estudo, baseado na discretização em diferenças finitas das equações de camada limite que governam o problema do desenvolvimento simultâneo em um canal de placas paralelas, considerando propriedades de transporte dependentes da temperatura. Eles consideraram um escoamento uniforme na entrada do canal, assumindo que as placas se mantinham a temperatura constante.

3.2 TÉCNICA DA TRANSFORMADA INTEGRAL

Nos últimos anos, devido ao avanço tecnológico, têm surgido problemas cada vez mais complexos na área de engenharia, os quais necessitam de soluções mais acuradas e em tempos de processamento mais reduzidos, visando o maior aproveitamento dos recursos empregados. Esses problemas, que na sua maioria não apresentam soluções analíticas, podem ser tratados por técnicas de aproximação numéricas, graças ao desenvolvimento de computadores de alta velocidade de processamento e de grande capacidade de armazenamento de dados.

Os métodos híbridos consistem de uma combinação de técnicas analíticas associadas a aproximações numéricas e surgiram como alternativa aos métodos puramente numéricos para a solução de problemas complexos de engenharia, antes tratados apenas numericamente.

Com a restrição do método de separação de variáveis em resolver certas equações diferenciais parciais lineares, como as equações de condução de calor envolvendo não homogeneidade nas condições de contorno e/ou termos de geração na equação diferencial, procurou-se desenvolver métodos mais gerais para o tratamento destes problemas. A primeira tentativa nessa direção se concretizou com o estabelecimento da técnica da transformada integral clássica (Mikhailov e Özisik, 1984), conhecida como um método ideal para a solução analítica de certas classes de problemas difusivos lineares. Tendo como base o método de separação de variáveis, um par transformada/inversa necessário à solução de um dado problema é proposto considerando-se a representação de uma função arbitrária, definida no mesmo domínio, em termos de autofunções inerentes à parte homogênea do problema original.

A partir do trabalho de Özisik e Murray (1974) sobre a solução de problemas difusivos com coeficientes variáveis nas condições de contorno, e com o crescente desenvolvimento de técnicas matemáticas e computacionais que permitiram o cálculo, cada vez mais preciso, de sistemas de equações diferenciais não-lineares, o método foi vislumbrado como capaz de fornecer soluções analíticas aproximadas a uma faixa muito maior de problemas “a priori” não transformáveis, quer lineares ou não-lineares. O progressivo desenvolvimento a partir daquele trabalho levou ao estabelecimento de um método, denominado como Técnica da Transformada Integral Generalizada – GITT. A idéia principal na nova metodologia generalizada é relaxar-se a necessidade de se encontrar uma transformação integral exata que resulte em um sistema diferencial ordinário desacoplado.

Essa nova técnica proporciona soluções de natureza híbridas numérico-analíticas para problemas de convecção-difusão cuja transformação integral resulta em sistemas de equações diferenciais ordinárias acopladas, ou cujos problemas auxiliares são complexos do ponto de vista computacional. Além de ser um método computacional alternativo, a abordagem proporcionada pela GITT é particularmente adequada na obtenção de soluções para validação (benchmarking) de códigos numéricos, devido à sua característica de controle automático de erro (garantia de convergência das soluções para ordens crescentes de truncamento nas séries), mantendo ainda suas características originais de uma solução analítica pura (soluções com um número de algarismos significativos "exatos" (convergidos) para um determinado número de termos nas expansões).

Outro aspecto destacável do método é a extensão direta a situações multidimensionais com um aumento não muito grande no esforço computacional, comparativamente ao caso unidimensional. A característica híbrida é a responsável por esse comportamento, uma vez que a solução analítica é empregada em todas as variáveis independentes, com exceção de uma, fazendo com que a tarefa numérica seja sempre reduzida à integração de um sistema diferencial ordinário em apenas uma direção.