Estudo do efeito de escala na taxa crítica de libertação de energia do betão

ESTUDO DO EFEITO DE ESCALA NA TAXA CRÍTICA

DE LIBERTAÇÃO DE ENERGIA DO BETÃO

DISSERTAÇÃO DE MESTRADO EM

ENGENHARIA CIVIL

EDUARDO JORGE GONÇALVES LUCIANO

Vila Real, 2010

ESCOLA DE CIÊNCIAS E TECNOLOGIA

DEPARTAMENTO DE ENGENHARIAS

ESTUDO DO EFEITO DE ESCALA NA TAXA CRÍTICA

DE LIBERTAÇÃO DE ENERGIA DO BETÃO

Eduardo Jorge Gonçalves Luciano

Dissertação apresentada à Universidade de Trás-os-Montes e Alto Douro para obtenção do grau de Mestre em Engenharia Civil, realizada sob a orientação científica do Professor Doutor Nuno Miguel Magalhães Dourado, e da co-orientação do Sr. Engenheiro Ilídio Manuel Miranda Faria, do Departamento de Engenharias da Escola de Ciências e Tecnologia da Universidade de Trás-os-Montes e Alto Douro.

Aos meus pais irmã e namorada

i

Desejo aqui, expressar a minha gratidão para todos aqueles que tornaram possível a realização deste trabalho, nomeadamente ao meu orientador, Prof. Nuno Dourado, pelo seu apoio incondicional, disponibilidade e proximidade, por tudo ter feito no sentido de responder a todas as minhas dúvidas.

Gostaria igualmente de remeter um enorme agradecimento ao Eng.º Cristóvão Santos das oficinas de Engenharia Mecânica pelo seu apoio e ajuda na fase experimental , ao Sr. Armindo das oficinas do Departamento de Florestais na ajuda no corte das pranchas para fabricação dos moldes, a todas as pessoas que ajudaram no processo moroso de transporte dos provetes, ao Sr. Eng.º Vasco Fernandes da empresa Brivel por ter fornecido todos os serviços requeridos e necessários para a aquisição do betão de forma gratuita, ao meu amigo e colega Eng.º Luís Carmo pela total disponibilidade e espírito de ajuda sempre que precisei.

Agradeço ainda à instituição Universidade de Trás-os-Montes e Alto Douro , e à empresa Brivel e Sport Zone pelos meios que me proporcionaram para a realização deste trabalho, agradeço também pela ajuda financeira concebida pelo CITAB (Center for the Research and Technology of Agro-Environmental and Biological Sciences), destinada à preparação dos provetes.

Por último, mas não menos importante, agradeço aos meus pais, Eduardo A. R. Luciano e Maria C. C. Gonçalves, à minha irmã Cláudia Luciano e namorada Sara Martins, pelo apoio e tranquilidade emocional de sempre.

ii

Agradecimentos

i

Lista de figuras

v

Lista de tabelas

viii

Nomenclatura

ix

Acrónimos

xi

Resumo

xii

Abstract

xiii

Capítulo I

Considerações sobre o material: betão

1

1.1 Introdução ₂

1.2 Modos puros de propagação ₂

1.3 Material: Betão ₃

1.3.1 Betão 3

1.3.2 Composição 4

1.3.2 Principais caracteristicas mecânicas do betão 4

1.4 Modelos coesivos 5

Capítulo II

Curva-R: contabilização do peso próprio

15

2.1 Introdução 16

2.2 Descrição do ensaio SEN-TPB 16

2.3 Compensação do peso próprio 18

2.3.1 Carga equivalente ao peso próprio: abordagem estática 18 2.3.2 Carga equivalente ao peso próprio: abordagem cinemática 20

iii

2.3.3.1 Comprimento de fenda equivalente 28

2.3.3.2 Avaliação da curva de Resistência 30

2.4 Validação do método exacto de determinação da curva de Resistência 33

2.4.1 Simulação pelo método dos elementos finitos 34

2.4.1.1 Modelo numérico 34

2.4.1.2 Curvas força-deslocamento 35

2.4.1.3 Curvas de Resistência: validação 37

Capitulo III

Descrição do procedimento experimental

42

3.1 Introdução 43

3.2 Fabrico do betão 43

3.3 Fabrico dos provetes 46

3.4 Transporte e colocação dos provetes 48

3.5Preparação dos ensaios mecânicos 50

Capítulo IV

Resultados experimentais

52

4.1 Introdução 53

4.2 Curvas P-δ _{e curvas-R 53}

iv

v

Lista de figuras

Figura 1.1 Ilustração dos modos puros de fractura: (a) Modo I: abertura; (b) Modo II: corte no plano; (c) Modo III: corte fora do plano

3

Figura 1.2 Zona de Processo de Fractura na extremidade da fenda de um material quase-frágil e respectiva tensão normal ao longo do plano de fractura

8

Figura 1.3 Modelo de dano de Petersson 9

Figura 1.4 Propagation of the main crack with its Fracture Process Zone (FPZ): (a) FPZ development, (b) critical size of the FPZ (i.e., fully developed) and (c) FPZ under crack propagation. Parameters: a₀, initial crack length (actual traction-free crack length); ∆a=a−a0, equivalent crack length increment;

δ

a, infinitesimal crack propagation extension; l_FPZ, extent of the FPZ

10

Figura 1.5 Esquematização das fases de desenvolvimento da zona coesiva (ZC): (a) antes de atingida a dimensão crítica da ZC: lcoh < lcoh c; (b) uma vez atingida a dimensão crítica da ZC: lcoh = lcoh c; e (c) fase posteriores ao crescimento integral da ZC, com a propagação da fenda.

12

Figura 1.6 Curva de Resistência típica obtida para o sistema de propagação TL da madeira de pícea (Adaptado de Dourado N, 2008).

13

Figura 2.1 Ilustração do ensaio SEN-TPB. Os deslocamentos indicados são medidos a meia altura do provete (a) δ1: no ponto médio da barra suportada no plano dos apoios e (b) δ2: na vizinhança da extremidade inicial da fenda.

17

Figura 2.2 Ilustração da configuração geométrica do provete 18

Figura 2.3 Curva P-δ não compensada obtida no ensaio SEN-TPB 19

Figura 2.4 _{Representação simplificada do ensaio de flexão em três pontos,} evidenciando a sobreposição do efeito gerado pela (a) carga central P [N] e pela (b) densidade linear de carga distribuída q [N/m]. δPP representa o deslocamento induzido pela carga P, medido no eixo de P. δPq representa o deslocamento devido à carga distribuída q, medido no eixo de P

20

Figura 2.5 Representação esquemática da curva P-δ no regime linear elástico (a = a0)

vi

Figura 2.6 Compensação do peso próprio pelo método da carga equivalente 23

Figura 2.7 Viga simplesmente apoiada sujeita à sobreposição de (a) uma carga central P [N] e a (b) uma carga distribuída q [N/m]. Os parâmetros δiP and δiq, representam, respectivamente, o deslocamento devido a P e a q medido no eixo i

25

Figura 2.8 Sobreposição de curvas força-deslocamento obtidas no ensaio mecânico e através da análises pelo MEF no regime linear elástico (para a=a0)

27

Figura 2.9 Curva força-deslocamento modificada como resultado da compensação do peso próprio (linha a traço-ponto)

28

Figura 2.10 Energia de deformação associada à carga externa P para dois pontos consecutivos da curva força-deslocamento modificada

29

Figura 2.11 Representação esquemática dos campos de deslocamento vertical (valores absolutos) obtidos para o ensaio SEN-TPB, ao longo do eixo médio, para dois quaisquer pontos consecutivos da curva P-δ , com L =6D

32

Figura 2.12 Malha de elementos finitos do ensaio SEN-TPB 35

Figura 2.13 Curvas P-δ obtida por aplicação de modelos coesivos, para o intervalo de massas específicas de 1700 a 3200 kg/m3

36

Figura 2.14 Curvas de Resistência obtidas para as massas específicas de 1700 a 3200 kg/m3, usando o método exacto de compensação do peso próprio

37

Figura 2.15 Evolução da taxa de libertação de energia associada às cargas P e q, para ρ = 2700 kg/m3, de acordo com o método exacto de compensação do peso próprio

38

Figura 2.16 Rácio de flexibilidades definido pela Eq. (2.8) para D=100 (Figura 2.12)

39

Figura 2.17 Curva-R avaliada pelo método da carga equivalente ao peso próprio do provete: abordagem cinemática (Secção 2.3.2)

40

Figura 3.1 Curva de gradação de acordo com a Tabela 3.2 45

Figura 3.2 Compactação da mistura 46

Figura 3.3 Condições do processo de cura: (a) manta geotêxtil e (b) plástico impermeabilizante

46

Figura 3.4 Fabrico de fenda inicial: (a) Guilhotina e (b) posição na cofragem

vii

Figura 3.5 Introdução de filme de Teflon® 48

Figura 3.6 Transporte do provete: (a) rotação no solo e (b) posicionamento sobre perfil HEB

49

Figura 3.7 Colocação do provete (a) sobre calços e (b) nos suportes 49

Figura 3.8 Operação de remoção dos calços 49

Figura 3.9 Posição do perfil HEB100 com os apoios 50

Figura 3.10 Apoios do provete SEN-TPB 51

Figura 3.11 Medição dos deslocamentos (a) padrões de Speckle e (b) apoio da cantoneira

51

Figura 4.1 Curvas P-δ obtidas nos ensaios mecânicos da série H1 54

Figura 4.2 Curvas P-δ obtidas nos ensaios mecânicos da série H2 54

Figura 4.3 Curvas de Resistância obtidas nos ensaios mecânicos da série H1

55

Figura 4.4 Curvas de Resistância obtidas nos ensaios mecânicos da série H2

viii

Lista de tabelas

Tabela 1.1 Características do betão relativas à resistência 7

Tabela 2.1 Dimensões nominais dos provetes 17

Tabela 3.1 Distribuição granulométrica dos agregados utilizados na mistura 44 Tabela 3.2 Resultado da análise granulométrica e da curva de Gradação 45

Tabela 3.4 Proporções de cada material a utilizar na mistura 45

Tabela 4.1 Resumo dos resultados experimentais obtidos para a série H1 55

ix

Nomenclatura

a Comprimento de fenda equivalente

c

a

Comprimento crítico de fenda equiv.

num

a Comprimento de fenda numérico

au Comprimento de fenda equiv para Pu

a0 Comprimento de fenda inicial

b

Largura da secção transversal

D Dimensão característica

E Módulo de elasticidade (Young)

E′ Módulo de elasticidade efectivo

b

f

Resistência no início do f.-bridging

t

f

Resistência local à tracção

Pu Carga máxima

q _{Densidade de carga linear}

w

Abertura de fenda

b

w

Abertura de fenda devido f.-bridging

c

w

Abertura crítica de fenda

o

w

Abertura de fenda devido m-cracking

W(a) Energia de deformação elástica

*

W

Energia de deformação complement.

α

Compr. relativo de fenda equivalente

δ

Deslocamento (vertical)

δa Extensão infinitesimal de fenda δexp(a) Deslocamento obtido ensaio mecân.

E

δ

Energia deformação elástic. dissipada

PP

δ

Deslocamento vertical devido a P

( )

w

φ Função de amaciamento

g Aceleração da gravidade

Gf Energia de fractura (coesiva)

Gfb Energia de fractura devido f.-bridging

Gfµ Energia de fractura devido m.-fissur.

) (a

x )

(a

G_q Taxa de libert. energia devido a q

)

(

R

a

G Taxa de libertação de energia

Ic

G Taxa crítica de libertação de energia

Rc

G Taxa crítica de libertação de energia

lcoh Extenção da zona coesiva

L Distância entre apoios

m

Massa

P Carga externa

q

P Carga (estática) equivalente Pq

δ

Desl. devido a q no eixo de P

U

δ

Energia complementar

q

U

δ

Energia complementar devido a q

) , (x a_i

δ

Campo deslocamentos associado a

a

_i

W

δ

Trabalho realizado pela carga P

a

∆ Incremento de fenda equivalente

c

a

∆

Incremento critico de fenda equivalente

)

(

a

₀ PP

δ

∆

Variação de

δ

_PP quando

a

=

a

₀ ) ( ₀ exp a P

∆ Variação de carga quando

a

=

a

₀ λ(a) Função de flexibilidade numérica λcor(a) Função corrigida de flexib. numérica λexp(a) Flexibilidade experimental

λmod (a) Flexibilidade modificada

) ,

(xa_i

qP

λ Campo flexib. devido a

δ

_Pq qdo

a

=

a

_i

)

, (xa_i

qq

λ _{Campo flexib. devido a q (}

a

=

a

_i

)

PP

λ

Flexibilidade associada a

δ

PP Pq

λ

Flexibilidade associada a

δ

_Pq

ν

Coeficiente de Poisson

ψ

_{Factor de correcção multiplicativo}

xi

Acrónimos:

CoV

Coeficiente de variação

MEF

Método dos Elementos Finitos

FPZ

Zona de Processo de Fractura

GA

Algoritmo Genético

LEFM

Mecânica da Fractura Linear Elástica

xii

Nesta Tese efectuou-se um estudo de averiguação do efeito de escala sobre um parâmetro relevante da Mecânica da Fractura, designado por taxa crítica de libertação de energia GIc. Para esse efeito, escolheu-se a geometria Single-Edge-Notched beam loaded in Three-Point-Bending (i.e., o ensaio de flexão em três pontos, de uma viga pré-entalhada a meio vão), por forma a induzir a fractura em puro modo I. Escolheu-se o betão como material de teste, tendo-se ensaiado duas dimensões de provetes em regime de controlo de deslocamento. Como as dimensões dos provetes escolhidos são consideráveis, desenvolveram-se dois métodos alternativos destinados à determinação da propriedade de fractura, que tem em conta o efeito do peso próprio. De seguida, procedeu-se à validação dos métodos de avaliação da taxa crítica de libertação de energia, recorrendo a modelos coesivos. Tendo por base a informação experimental relativa às dimensões testadas, bem como um método fiável de determinação da propriedade de fractura, constatou-se o que parece ser um ténue efeito de escala sobre

xiii

A study was carried out to investigate the size effect on a relevant parameter of Fracture Mechanics, known as the critical energy release rate GIc. To this end, the Single-Edge-Notched beam loaded in Three-Point-Bending (SEN-TPB) was chosen in order to induce fracture under pure mode I. Concrete was chosen as the testing material, involving specimens geometrically similar of two sizes. As mass is not negligible, two alternative methods have been proposed evaluate the Resistance curve (R-curve), taking into account the specimen self weight. Then, based on the cohesive modeling (CZ) of the material damage, the numerical validation of the proposed methods has been performed, realizing that the proposed methods are able to retrieve an R-cure with a horizontal asymptote equal to the fracture energy used in the FEM computations. Based on experimental data (i.e., P-δ _{curves) of both specimen sizes, a method has been} chosen to determine fracture properties, thus permitting to observe what appears to be a slight size effect on GIc.

- 2 -

Capítulo I

Considerações sobre o material: betão

1.1 Introdução

Neste Capítulo apresenta-se uma Secção dedicada à classificação dos Modos puros de propagação, de acordo com a convenção adoptada pela Mecânica da Fractura. A seguir, apresenta-se uma Secção destinada à discussão sobre as características mais relevantes do material estudado nesta Tese – o betão -, com particular enfoque na composição e nas características mecânicas, que fazem dele um material de grande importância no contexto estrutural. Finalmente, apresenta-se uma Secção dedicada aos modelos coesivos, como forma de previsão do comportamento à fractura de um material como o betão (material quase-frágil).

1.2 Modos puros de propagação

Em Mecânica da Fractura identificam-se três modos puros de rotura (Figura 1.1a-c), consoante a natureza da solicitação a que uma estrutura pré-entalhada se encontrar sujeita. Com efeito, convencionou-se designar modo I ou modo de abertura, àquele modo que der origem a tensões normais de tracção, passíveis de conduzir à separação, de forma simétrica, das superfícies (adjacentes) de fractura, relativamente aos planos identificados na Figura 1.1.(a), por x1x2 e x1x3. O modo II, por seu turno, resulta da instalação de tensões de corte que induzem o deslocamento relativo das superfícies de fractura, ao longo do plano de fractura. O deslocamento relativo destas superfícies, como se pode observar na Figura 1.1(b), ocorre de forma simétrica em relação ao plano x1x2, e de forma antissimétrica relativamente ao plano x1x3. No que respeita ao modo III, também ocorre o deslizamento entre as superfícies de fractura, induzido por tensões de corte. No entanto, este faz-se de forma antissimétrica em relação aos planos x1x2 e x1x3 (Figura 1.1.c)

- 3 - X2 X1 X3 X1 X3 X2 X1 X3 X2 Modo I

Modo II _{Modo III}

Figura 1.1 – Ilustração dos modos puros de fractura: (a) Modo I: abertura; (b) Modo II: corte no plano; (c) Modo III: corte fora do plano. (Adaptado de Kanninen MF e Popelar CH, 1985).

1.3 Material: o betão

1.3.1 Betão

O betão é um material composto pela mistura de cimento, de agregados grossos e finos e de água, decorrente do endurecimento da pasta de cimento. Para além destes componentes básicos, pode também conter adjuvantes e adições. Caso a máxima dimensão do agregado seja igual ou inferior a 4 mm, o material resultante é denominado argamassa. Além destes requisitos de composição, para que o material possa ser considerado betão é necessário que seja convenientemente colocado e compactado. Para se classificar o material resultante como um betão, este, depois da compactação, deve apresentar uma estrutura fechada. Isto significa que quando a dimensão máxima dos agregados for maior ou igual a 16 mm, o teor em ar, em volume, não deve exceder 3 %, ao passo que se a dimensão máxima dos agregados for menor que 16 mm, o teor em ar, em volume, não deve exceder os 4 % (a medição do teor, em ar em volume, aqui descrita, diz apenas respeito ao ar aprisionado, em resultado da operação de compactação, que não foi expulso). Sempre que a mistura resultante obedecer às características que acabam de ser descritas, o betão pode ser utilizado no projecto e no fabrico de estruturas de betão simples, betão armado ou betão pré-esforçado.

- 4 -

O betão é normalmente utilizado para desempenhar funções estruturais. No entanto, para poder ser utilizado nessas funções, no processo de fabrico, este passa por dois estados diferentes, sendo então designado por betão fresco e por betão endurecido. Uma vez preparado (e.g., central de betonagem), este designa-se por betão fresco, exibindo um comportamento plástico, capaz de ser compactado e moldado por métodos normais. Uma vez iniciado o processo de endurecimento (poucas horas após o seu fabrico), este passa a ser designado por betão endurecido, adquirindo então uma resistência crescente, que se estima em 60 a 90% do valor final (i.e., resistência final), decorridos que estejam 28 dias de cura. Este comportamento, no entanto, considera-se dependente do tipo de cimento utilizado, bem como das condições de cura.

1.3.2 Composição

Nesta Secção, não se pretende determinar a composição do betão, mas apenas indicar alguns conceitos que influenciam o comportamento deste, antes e após o endurecimento.

Normalmente, o que se procura obter no fabrico do betão, é uma resistência e durabilidade elevadas. Desta forma, o estudo da composição do betão deve ser efectuado tendo por base o objectivo de, para cada situação em particular, o betão atingir a resistência, a durabilidade e a trabalhabilidade adequadas. Para além da composição granulométrica dos agregados, o comportamento do betão, depende principalmente de três factores. São eles o tipo e a dosagem do ligante; a dosagem de água; e a dosagem dos adjuvantes. Para que uma determinada composição de betão possa vir a desenvolver todas as suas potencialidades, a colocação, a compactação, a cura e a protecção da mistura, desempenham um papel fundamental.

1.3.3 Principais características mecânicas do betão

A característica mecânica mais importante do betão, é a resistência à compressão, dado que em contexto estrutural, a função principal do betão é essencialmente a de resistir aos esforços de compressão - enquanto que as armaduras (em estruturas de betão armado) têm a função de resistir aos esforços de tracção.

- 5 -

A norma NP EN 206-1 estabelece que a resistência à compressão deve ser determinada em provetes cúbicos com 150 mm de aresta, ou em provetes cilíndricos de 150/300 mm (i.e., ∅150 e altura 300 mm). A resistência cilíndrica (i.e., dos provetes cilíndricos) é da ordem dos 80% da resistência cúbica (provetes de configuração cúbica). Esta diferença explica-se pela existência de atrito entre as faces dos provetes e os pratos das máquinas de ensaios, que impedem a deformação transversal do betão, conduzindo a maiores valores da resistência.

A resistência à compressão do betão, é expressa em termos da resistência característica

fck, definida como o valor da resistência que apenas não é atingido em 5% de todos

os resultados possíveis, a partir de ensaios para o betão especificado. Uma vez que o endurecimento do betão se processa ao longo do tempo, a resistência à compressão, tal como as outras características deste material, evoluem também no tempo. Como para efeito de dimensionamento das estruturas, se considera a resistência do betão aos 28 dias, estabeleceu-se esta idade (i.e., tempo de cura) para caracterizar esta propriedade.

Em relação ao módulo de elasticidade deste material, ele depende não só da classe de resistência do betão, mas também das propriedades dos agregados utilizados e outros parâmetros associados à composição do betão e às condições de cura. Deste modo, quando for necessário efectuar cálculos mais rigorosos, recomenda-se a realização de ensaios mecânicos d o betão, fabricado com os agregados utilizados na obra.

Na Tabela 1.1 exibem-se os valores característicos da resistência de diferentes classes do betão, desde C12/15 até C90/105, assim como o respectivo módulo de elasticidade.

1.4 Modelos coesivos

A teoria da Mecânica da Fractura Linear Elástica (LEFM) assume a existência de uma fenda, para a qual o campo de tensões pode ser determinado. Apesar das soluções elásticas preverem que a tensão na extremidade da fenda tende para infinito, isso, no entanto, não corresponde à verdade, dado que o desenvolvimento de mecanismos de dano local no material impede que isto se verifique. Apesar de algumas leis constitutivas permitirem descrever com sucesso a rotura de materiais frágeis como o vidro e o ferro fundido, revelam-se no entanto inadequadas na previsão do

- 6 -

comportamento à fractura de materiais que se caracterizam pelo desenvolvimento de fenómenos de amaciamento, como é o caso do betão (Bažant ZP e Planas J 1998). Estes fenómenos dão origem à formação de uma região não linear, de dimensões não negligenciáveis, denominada por Zona de Processo de Fractura (FPZ), localizada na extremidade da fenda (Figura 1.2). Os fenómenos anteriormente referidos também têm como consequência, a impossibilidade prática de se realizar com exactidão, a identificação da extremidade da fenda.

No que se refere à forma como esta região (ou zona) é modelada numericamente, existem duas abordagens distintas. A primeira sustenta que (a) a totalidade da FPZ deve ser colapsada num segmento de recta, segundo a direcção do caminho da fenda, sendo caracterizada mediante uma lei de relaxação do tipo: tensão versus deslocamento relativo (i.e., f vs w); de acordo com a segunda, (b) as deformações elásticas que ocorrem na FPZ são distribuídas ao longo de uma banda de espessura constante (crack-band), disposta ao longo do caminho da fenda, de um, e de outro lado desta. No âmbito desta Tese, enveredar-se-á apenas pela primeira abordagem. De acordo com a literatura (Bažant ZP and Planas J 1998, Morel S et al. 2002 e 2005), os modelos desenvolvidos de acordo com esta abordagem, são conhecidos por modelos de fenda coesiva, modelos de fenda fictícia, modelos de Dugdale-Barenblatt, ou modelos de fenda em ponte de fibras (crack with bridging stresses). Por uma questão de uniformidade e simplificação, nesta Tese utilizar-se-á a designação de modelos coesivos.

Os modelos coesivos constituem a forma mais simples de descrever numericamente os processos de degradação que ocorrem no material, tendo em conta os aspectos básicos que estão na origem do comportamento não linear observado na região próxima da extremidade de uma fenda. O pressuposto fundamental dos modelos coesivos (por exemplo em Modo I) é o de que a FPZ pode ser substituída por um domínio capaz de transferir tensões normais f(x) segundo uma ou várias funções (monótonas decrescentes) da abertura de fenda, do tipo f = φ(w).

O aspecto mais importante dos modelos coesivos é a curva de amaciamento do material, que, de certa forma, substitui a curva de tensão-deformação, característica da abordagem normalmente feita nos modelos de plasticidade. Neste sentido, cada material (quase-frágil) é caracterizado por uma curva de amaciamento, que pode ser identificada

- 7 -

Classes de resistência do betão

fck (MPa) _{12 16 20 25 30 35 40 45 50 55 60 70 80 90} fck,cube (MPa) 15 20 25 30 37 45 50 55 60 67 75 85 95 105 fcm (MPa) 20 24 28 33 38 43 48 53 58 63 68 78 88 98 fctm (MPa) 1,6 1,9 2,2 2,6 2,9 3,2 3,5 3,8 4,1 4,2 4,4 4,6 4,8 5,0 f_{ctk, 0,05} (MPa) 1,1 1,3 1,5 1,8 2,0 2,2 2,5 2,7 2,9 3,0 3,1 3,2 3,4 3,5 f_ctk,0,95 (MPa) 2,0 2,5 2,9 3,3 3,8 4,2 4,6 4,9 5,3 5,5 5,7 6,0 6,3 6,6 E_cm (GPa ) 27 29 30 31 33 34 35 36 37 38 39 41 42 44

Tabela 1.1– Características do betão relativas à resistência mecânica

Legenda:

fck = valor característico da tensão de rotura à compressão em cilindros (de acordo com

a NP EN206-1);

fck, cube = valor característico da tensão de rotura à compressão em cubos (de acordo

com a NP EN206-1);

fcm= resistência média do betão aos 28 dias de idade; fctm = valor médio da resistência à tracção;

fctk 0,05 = valor característico inferior da tensão de rotura à tracção; fctk 0,95 = valor característico superior da tensão de rotura à tracção; Ecm= valor aproximado para o módulo de elasticidade.

- 8 - Linear-elastic Softening

σ

Nonlinear plastic hardening FPZ

Figura 1.2 Zona de Processo de Fractura na extremidade da fenda de um material quase-frágil e respectiva tensão normal ao longo do plano de fractura. Adaptado de Bažant ZP (1985).

com o recurso a métodos inversos, que combinam informação numérica com experimental (Dourado N et al., 2008).

Os primeiros estudos que se conhecem, de aplicação de modelos coesivos, são da autoria de Dugdale DS (1960) e Barenblatt GI (1962). Segundo estes autores, a extremidade da fenda (real) é modelada como uma zona plástica (fenda fictícia), com tensões normais que resistem à propagação da fenda real. Consequentemente, a dimensão desta zona plástica, é dada pela diferença entre a dimensão da fenda fictícia e a fenda real, sendo a tensão normal igual à resistência local à tracção do material. Na sequência destes estudos pioneiros, os modelos coesivos foram utilizados na descrição do comportamento de uma grande variedade de materiais, como metais, materiais cerâmicos, geo-materiais e polímeros. Na década de setenta do último século, Hillerborg et al. (1976) aplicaram um modelo semelhante ao de Dugdale e Barenblatt para simular os efeitos da FPZ no betão, tendo por base mecanismos de micro-fissuração e de crack-branching observados no processo de degradação do material. Em contraste com o modelo desenvolvido por Dugdale e Barenblatt, no modelo de

Comportamento linear-elástico

Amaciamento

Região não-linear ZPF

- 9 -

Hillerborg a tensão instalada ao longo da fenda fictícia não permanece constante, sendo definida (determinada) em função da abertura de fenda (w). Na sequência destes trabalhos, surgiu o modelo de dano bilinear (Figura 1.3) proposto por Petersson PE (1981), para o betão, que permite traduzir, do ponto de vista fenomenológico, o comportamento do material em processo de degradação (irreversível) observado nesse material. Este modelo de relaxação (Figura 1.3) é constituído por dois tramos lineares descendentes, que caracterizam o comportamento do material em regime de amaciamento (i.e., redução gradual das tensões na extremidade da fenda): ponto de coordenadas (wo, ft) e o ponto de inflexão (wb, fb); e deste, para o ponto (wc,0). No primeiro tramo, a energia dissipada é designada por Gfµ, enquanto que no segundo, recebe a designação de Gf b. A energia de fractura Gf resulta do somatório destas duas energias (i.e., Gf = Gfµ+Gfb).

Nos primeiros trabalhos de modelação do comportamento não linear à fractura do betão, Petersson PE (1981) concluiu que o ponto de inflexão da lei de dano do betão (i.e., o ponto de coordenadas (wb, fb)) é igual a 0,8/ft, ft/3 (Figura 1.3). Trabalhos subsequentes, designados por códigos modelo CEB-FIP (CEB 1991), e outros trabalhos fundamentais, da autoria de Wittmann et al. (1988) e Rokugo et al. (1989), confirmaram a posição do ponto de inflexão da lei de dano do betão. A diferença, no entanto, reside na posição do ponto de coordenadas (wc, 0), que culmina numa forma conhecida por cauda (tail) da lei de dano, que, de acordo com aqueles estudos, aponta para valores maiores do que os que

G (Componente: "micro-fissuração") Abertura de fenda T en sã o w_o b f w_b f t f fµ

G fb (Componente: "ponte de fibras")

w_c

w

- 10 -

foram determinados por Petersson. Esta, contudo, depende da dimensão do agregado utilizado na mistura.

Apesar do sucesso da lei de configuração bilinear proposta por Petersson, outros estudos posteriores, envolvendo funções exponenciais (Gopalaratnam e Shah, 1985; Cornelissen, Hordijk e Reinhardt 1986a, b; Planas e Elices 1986, 1990), leis de potência (Reinhardt 1984), e o modelo trilinear (Cho et al., 1984; Liaw et al., 1990) revelaram-se igualmente válidos para descrever o comportamento do dano no betão.

Num estudo recente, realizado por Dourado N et al. (2008), envolvendo a geometria SEN-TPB (Figura 1.4), identificou-se a combinação de parâmetros da lei de Petersson capaz de reproduzir o fenómeno de fractura de duas espécies de madeira comummente utilizadas em componentes estruturais.

Neste estudo, combinou-se informação experimental e um Algoritmo Genético (GA) (desenvolvido), tendo sido identificadas, para cada uma das espécies envolvidas no estudo, as extensões da zona coesiva (CZ), em processo de perturbação da FPZ com os

F

_b

a

0

= D/2

SEN-TPB

F

/2

_F

_/2

- 11 -

limites do provete de geometria SEN-TPB. Nesse estudo avaliou-se a extensão da zona coesiva lcoh (modelação da FPZ do material) a partir da simulação por EF do dano desenvolvido na extremidade de uma fenda, mediante a disposição de EF de interface (de Moura MFSF et al., 1997), com parâmetros coesivos característicos do material a simular, previamente dispostos ao longo do caminho da fenda. De acordo com este procedimento (e.g., em modo I), uma vez instalada na extremidade da fenda (i.e., localmente) uma tensão f igual à resistência local à tracção ft (Figura 1.3), considera-se que tem início o dano. Atendendo a que a evidência experimental, demonstra que num material quase-frágil (como o betão), uma vez observada uma fenda, a estrutura ainda é capaz de resistir ao carregamento que lhe é imposto, na modelação por EF, a tensão normal instalada f não é atirada bruscamente a zero (como se referiu atrás), seguindo, desse modo, uma lei (e.g., linear, bilinear, trilinear, exponencial, de potência), em função da abertura de fenda w. Sendo assim, considera-se que a propagação da fenda só tem lugar assim que a abertura de fenda w seja igual ou superior a wc (também designado por abertura crítica da fenda). Consequentemente, como o EF de interface tem espessura nula, a propagação da fenda (numérica) corresponde à separação de dois nós inicialmente coincidentes – que permaneceram nessa posição até que a tensão (transmitida) entre eles se anulou. Por esse motivo, considera-se que a extensão da zona coesiva lcoh é dada pela distância (medida ao longo do caminho da fenda), entre o primeiro par de nós (ainda) coincidentes (w < wc), e a posição do ponto de integração do EF de interface oposto, para o qual a tensão instalada f = ft. O comprimento de fenda numérico anum representa a distância, medida ao longo do caminho da fenda, entre o eixo de aplicação da carga F (ou extremidade livre, no caso do SEN-TPB) e a posição do primeiro par de nós do EF de interface (ainda) coincidentes (w < wc).

Constatou-se numericamente (Dourado N et al., 2008; de Moura MFSF et al. 2010; Morel S, 2010), que se a região onde ocorrer o dano (zona coesiva: CZ) não for afectada por tensões compressivas, esta atinge uma dimensão crítica (i.e., lcoh = lcohc) antes de ter início a propagação da fenda (i.e., a > a0), mantendo-se inalterada ao longo do processo de carregamento (ver Figura 1.5 a-c). Como consequência deste fenómeno, dá-se o crescimento da energia de fractura (GR), cuja consequência é a revelação da curva de Resistência do material (Figura 1.6). De facto, a propagação de uma fenda de comprimento a, de uma quantidade infinitesimal δa (na frente da qual existe a FPZ), está associada à dissipação de uma quantidade de energia (de deformação elástica) δW =

- 12 -

Gf (bδa); sendo Gf a energia requerida para produzir a separação do material (fenda), para uma determinada força P, e (bδa) a área da superfície fracturada (b: largura da secção transversal: Figura 1.4).

+

Fenda eq. LEFM Fenda coesiva Fenda eq. LEFM

coh Fenda coesiva 0 a₀ a t f num (c) a a (b) num w_c l 0 w_c coh c t f σ l_coh a_c c 0 a = a_c= a0 = a a_num coh l ₌l a (a) anum w a₀ coh _{coh c} coh l 0

Fenda eq. LEFM

σ a₀< a < ac a_{num= a0} f_t σ l Fenda coesiva l < > a a_c > a_num a₀ = l_coh l coh c c ∆a c

Figura 1.5 – Esquematização das fases de desenvolvimento da zona coesiva (ZC): (a) antes de atingida a dimensão crítica da ZC: lcoh < lcoh c; (b) uma vez atingida a dimensão crítica da ZC:

lcoh = lcoh c; e (c) fase posteriores ao crescimento integral da ZC, com a propagação da fenda.

- 13 -

Tal como esperado (Bažant, 1990), uma vez alcançado o comprimento de fenda característico ac (que corresponde a uma extensão do comprimento de fenda ∆ac = ac –

a0), a resistência à propagação da fenda torna-se independente do comprimento (equivalente) a desta (Figura 1.6). Neste regime, a resistência constante define um valor crítico da resistência ao crescimento da fenda, e representa-se por GRc=GR(a≥ac) = cte. De notar, que o início da curva de Resistência (curva-R) representada na Figura 1.6, tem lugar antes de alcançada a carga máxima Pu, estendendo-se para além desta. Com efeito, o comprimento de fenda equivalente au, correspondente a Pu, é inferior ao comprimento de fenda característico, ac, que define o início da propagação a resistência de fractura constante, GRc (Ferreira LET et al., 2002). Deste modo, à carga máxima Pu registada experimentalmente, corresponde uma taxa de libertação de energia de fractura, GR (au), inferior à taxa crítica de libertação de energia de fractura, GRc.

Figura 1.6 – Curva de Resistência típica obtida para o sistema de propagação TL da madeira de pícea (Adaptado de Dourado N, 2008).

0,000 0,005 0,010 0,015 0,020 0,025 50 55 60 65 70 75 80 85 GR (N /m m ) a (mm) G_Rc GR(au) au ac

- 14 -

Este comportamento, no entanto, é mais nítido porque a altura D do provete (ver Figura 1.4) se encontra próximo da dimensão crítica Dcrit, abaixo da qual as condições de comprimento de ligamento (i.e., D/2 – (a-a0)), não se encontram totalmente reunidas. Pormenores relacionados com este tema são fornecidos nas referências: de Moura MFSF et al. (2010) e Dourado N et al. (2010).

Este comportamento, no entanto, é mais nítido porque a altura D do provete (ver Figura 1.4) se encontra próximo da dimensão crítica Dcrit, abaixo da qual as condições de propagação em regime de auto-semelhança (regime estacionário), ao longo do comprimento de ligamento (i.e., D/2 – (a-a0)), não se encontram totalmente reunidas. Pormenores relacionados com este tema são fornecidos nas referências: de Moura MFSF et al. (2010) e Dourado N et al. (2010).

- 16 -

Capítulo II

Curva-R: contabilização do peso próprio

2.1 Introdução

Neste Capítulo apresentam-se dois métodos alternativos para avaliar a taxa crítica de libertação de energia de fractura em modo I, recorrendo ao ensaio Single-Edge-Notched

beam loaded in Three-Point-Bending (SEN-TPB). Assim, servido-se de um provete em

betão, e do ensaio SEN-TPB - a realizar com controlo de deslocamento -, apresenta-se a formulação dos dois métodos alternativos, destinados à determinação da curva de Resistência do material, levando em conta o efeito do peso próprio. A validação do método será realizada, numericamente, com base na aplicação de modelos coesivos.

2.2 Descrição do ensaio SEN-TPB

Com o propósito de induzir a fractura do betão em puro modo I, escolheu-se o ensaio SEN-TPB (Figura 2.1). Neste ensaio, submete-se uma viga pré-entalhada na secção central, a um ensaio de flexão em três pontos. Nele, mede-se a força P aplicada a meio-vão, e regista-se o deslocamento δ imposto à força. Para evitar erros de medição do deslocamento δ no decorrer do processo de carregamento - decorrentes da deformação do perfil, que permite a fixação dos apoios (i.e., acentamento vertical dos apoios) -, posiciona-se uma barra rígida (de massa desprezível) ao longo do comprimento do provete, suportada em dois pontos alinhados com os planos de apoio do provete (deslocamento δ1 na Figura 2.1), localizados a meia altura deste. Uma segunda medição do deslocamento (i.e., δ2) é realizada num ponto localizado na vizinhança da extremidade da fenda inicial (secção central do provete). Assim, a obtenção do deslocamento induzido pela força, resulta da diferença: δ = δ2 – δ1. Como se verá no Capítulo IV, este procedimento permite realizar a medição do deslocamento δ, sem contacto com o provete, pelo que se utilizou a técnica de correlação digital de imagem (CDI).

- 17 -

Na Tabela 2.1 apresentam-se as dimensões nominais dos provetes que se analisarão nesta Tese, de acordo com a notação da Figura 2.2. A medida da pré-fenda tem o comprimento a0 = D/2, sendo a largura do entalhe igual a 0,4 mm em todos os provetes. Atendendo a que os provetes envolvidos no estudo experimental (Capítulos III e IV), são homotéticos, pode escolher-se para dimensão característica, uma qualquer medida da estrutura (i.e., D ou b). Neste caso, escolheu-se a dimensão D. Assim, realizou-se um estudo de efeito de escala, que perfaz uma relação dimensional (size range) de 1:1,33 (i.e., 280/210), conforme se poderá comprovar na Tabela 2.1.

6D δ Célula de carga 6D δ Célula de carga 1 2

Figura 2.1 Ilustração do ensaio SEN-TPB. Os deslocamentos indicados são medidos a meia altura do provete (a) δ1: no ponto médio da barra

suportada no plano dos apoios e (b) δ2: na vizinhança da extremidade

inicial da fenda.

Tabela 2.1 Dimensões nominais dos provetes de acordo com a Fig. 2.2

Série D (mm) b (mm)

H1 280 80

- 18 -

D/2

b

D

8D

Figura 2.2 Ilustração da configuração geométrica do provete.

2.3 Compensação do peso próprio

Em ensaios de fractura envolvendo provetes de geometria SEN-TPB (Single-Edge-Nothed loaded in Three-Point-Bending), assim como em outras geometrias, o peso do provete contribui para a contabilização da carga total do sistema. Nos métodos de avaliação de propriedades de fractura, a contribuição do peso próprio do provete não é normalmente tida em conta (Bažant Z e Planas J, 1998), conduzindo assim a erros não negligenciáveis na avaliação dos parâmetros de fractura. Assim, nas Secções que se seguem, apresentam-se dois métodos alternativos destinados à avaliação de uma propriedade relevante da Mecânica da Fractura (i.e., a taxa crítica de libertação de energia, GIc).

2.3.1 Carga equivalente ao peso próprio: abordagem estática

Tal como se ilustra na Figura 2.3, para uma configuração geométrica simples do ensaio SEN-TPB, a célula de carga foi calibrada (ponto O ) quando o provete já se tinha deformado por acção do peso próprio (Bažant Z e Planas J, 1998). Isto significa, que por acção do peso próprio (célula de carga com P = 0), já existe um momento flector

qL2 /8 aplicado na secção transversal central (sendo q a carga distribuída correspondente

ao peso próprio da viga, e L o vão). Consequentemente, se se considerar um carregamento estático equivalente Pq (i.e., uma carga concentrada), actuando a meio vão, que produz o mesmo momento flector que aquele que é produzido pela carga

- 19 - O 0 (a ) O´ _δ q P Carga, P Deslocamento, mg/2 (a) δ_exp L 0 a mg/2 P

Figura 2.3 Curva P-δ não compensada obtida no ensaio SEN-TPB. Adaptado de Bažant Z and Planas P (1998).

distribuída q (correspondendo ao peso próprio da viga), resultará o momento flector: Mq =Pq L/∕4. Assim, estabelecendo a igualdade entre os dois momentos flectores anteriores, é possível obter a carga central Pq =qL/∕2 , com qL= mg (sendo m a massa da viga e g a aceleração da gravidade).

De um ponto de vista estritamente teórico, se esta carga estaticamente equivalente (i.e.,

Pq) pudesse actuar sozinha no sistema, ela produziria uma curva P-δ dada pela linha a traço interrompido (com origem no ponto O ’ de acordo com a Figura 2.3). No entanto, nos ensaios mecânicos a curva obtida é simplesmente aquela que se encontra representada a traço contínuo - o que obviamente resulta da sobreposição dos efeitos produzidos pela aplicação da carga P e do peso próprio do provete. Contudo, deve ter-se presente, que o valor da carga P registada no ensaio, é a que é medida pela célula de carga (Figura 2.1), enquanto que o deslocamento δ se deve à acção combinada de P com o peso próprio do provete.

Nas duas Secções que se seguem, propõem-se dois métodos de avaliação da curva de Resistência, tendo em linha de conta o efeito do peso próprio da estrutura, usando a geometria SEN-TPB. O primeiro é um método aproximado, seguindo uma abordagem

- 20 -

cinemática, enquanto que o segundo é um método exacto, que prevê a avaliação precisa da curva de Resistência do material, realizando a compensação do peso próprio.

2.3.2 Carga equivalente ao peso próprio: abordagem cinemática

Considere a representação do ensaio de flexão em três pontos ilustrada na Figura 2.4, na qual a viga se encontra sujeita à acção simultânea da carga externa P, actuada a meio vão L/2, e à carga linear distribuída q, correspondente ao peso próprio da viga.

De acordo com o princípio da sobreposição de efeitos, a deformada (da viga) resulta da acção conjunta dos dois efeitos (i.e., P e q), ilustrados, respectivamente, nas Figuras 2.4 (a) e (b). Consequentemente, o deslocamento do ponto C (i.e., um ponto localizado sobre o eixo neutro, à distância x = L/2), é dado por:

(2.1)

Figura 2.4 Representação simplificada do ensaio de flexão em três pontos, evidenciando a sobreposição do efeito gerado pela (a) carga central P [N] e pela (b) densidade linear de carga distribuída q [N/m]. δPP representa o deslocamento induzido pela carga P,

medido no eixo de P. δPq representa o deslocamento devido à carga distribuída q,

medido no eixo de P. O deslocamento total é dado por: .

PP Pq PPP Pqq δ =δ +δ =λ +λ x O x y L/2 (a) δ_PP P L/2 x O x y L/2 δ x (b) L/2 O x y Pq L/2 q q δ P L/2 Pq PP δ δ δ= +

- 21 -

onde λPP e λPq representam, respectivamente, a flexibilidade devida a P e a q (com λPP expresso em [m/N] e λPq em [m2/N), ambas medidas no eixo de P.

A flexibilidade inicial λexp(a0) é avaliada considerando os valores registados no ensaio mecânico (Figura 2.5), de acordo com

(2.2)

sendo δ exp(a0), de acordo com a Figura 2.5, dado por

(2.3)

Na Eq.(2.3), o termo δ PP (a0) é a única quantidade que varia. Na verdade, δ Pq (a0) é uma quantidade impossível de medir nos ensaios mecânicos, permanecendo constante (desde que a=a0). Como resultado disso,

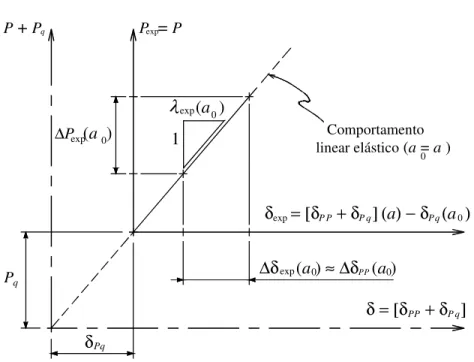
q P δPq δ = [δ + δ ]P q λ 1 P = P ∆Pexp (a )0 q P + P exp δ = [δ + δ ](a) − δ (a ) Comportamento linear elástico (a = a) ∆δ (a ) ≈ ∆δ (a )exp exp 0 P 0 P q (a ) exp ₀ q 0 0 P P P P P P

Figura 2.5 Representação esquemática da curva P-δ no regime linear elástico (a = a0). exp 0 exp 0 exp 0 ( ) ( ) ( ) a a P a δ λ =∆ ∆ exp( ) [a0 PP( )a0 Pq( )]a0 Pq( )a0 δ = δ +δ −δ

- 22 -

(2.4) Assim, reequacionando a expressão (4.2), pode estabelecer-se que (ver Figura 2.5)

(2.5)

O segundo termo da Eq. (2.1) pode ser reorganizado de modo a incorporar a carga central Pq, o que na prática produz o mesmo deslocamento que é induzido pelo peso da viga δ Pq no ponto C (i.e., equivalência cinemática) (ver Figura 2.4), de modo que

(2.6)

Então, eliminando δ entre as Eqs. (2.1) e (2.6), resulta

(2.7)

que é válido se a relação

(2.8) com o intervalo de validade [a0 , aexpl], a ser estimado numericamente (MEF).

Assim, usando a carga registada na curva P-δ obtida experimentalmente (Figura 2.6), e desde que a igualdade estabelecida através da Eq. (2.8) seja verificada, a Eq. (2.7) permite definir

(2.9)

com λPP exp(a0) definido através Eq. (2.5)

Assim, para um ponto M da curva P-δ (Figura 2.6), para o qual se pretende estimar o comprimento de fenda equivalente a, a compensação devida ao peso próprio é realizada, estabelecendo-se (2.10) exp( )a0 PP( )a0 δ =δ 0 exp 0 exp 0 exp 0 ( ) ( ) ( ) ( ) PP PP a a a P a

δ

λ

= ∆ =

λ

∆ ( ) PP P Pq δ =λ + ( ) ( ) Pq q PP a P q a

λ

λ

= ( ) ( ) constante Pq a PP a λ λ ≅ ∀ ∈a [ ,a a_{0 expl}] 0 exp 0 exp 0 ( ) ( ) ( ) Pq a q PP a Pq Pq a λ =λ =δ 0 exp 0 exp( ) ( ) PP a a

λ

=

λ

exp comp( ) q a P P

δ

λ

= +

- 23 - que, de acordo com as Eqs. (2.1) e (2.6), resulta

(2.11)

Os valores resultantes de

λ

exp comp(a0) serão posteriormente utilizados para executar cálculos sobre o comprimento de fenda equivalente a, bem como das quantidades resultantes da taxa de libertação de energia GR(a), por meio de uma aproximação equivalente à LEFM, proposta por Morel S. et al. (2005). Deve referir-se, que os dois termos

λ

PP(a) e

λ

Pq(a) nas Eqs. (2.6)-(2.8) e (2.11), representam os valores corrigidos da flexibilidade, dada pelas funções polinomiais que resultam, respectivamente, do melhor ajuste das simulações pelo método os elementos finitos (MEF), para a carga central P e para a carga distribuída q, que actuam no provete, para diferentes cumprimentos de fenda a,

(2.12) (2.13)

Figura 2.6 Compensação do peso próprio pelo método da carga equivalente.

expcomp ( )( ) ( ) PP Pq PP q ( ) PP q q a P P a a P P P P δ δ λ λ = + = + =λ + + * ( ) ( ) PP a PP a λ =ψλ * ( ) ( ) Pq a Pq a λ =ψλ δ _{= δ} Pq δ expcomp comp q P+ P λexp (a ) λ 1 exp 0 comp P Pexp = P

M

exp δ λ (a) = = δ 1 a PP(a) PP [ ](a)+δPq - δPq(a )0 PP+δPq (a ) λ0 = exp Pq δ PP_exp(a ) P0 q

- 24 -

O objectivo desta correcção, tal como foi proposto por Morel S. et. al. (2005), é o de ter

em conta a dispersão das propriedades elásticas do material. Com efeito, o parâmetro

ψ

nas Eqs. (2.12) e (2.13), representa o factor de correcção multiplicativa, estimado para cada provete, da forma

(2.14)

Pode demonstrar-se pelo método dos elementos finitos (MEF), que

λ

PP(a) do provete

SEN-TPB é fundamentalmente proporcional a 1/∕E_’ (com E_’= E, para o estado plano de

tensão, e E’=E/(1-

ν

2) para o estado plano de deformação (Bazant 2002, :69 EFM, Morel

et al. 2005). Assim, conforme detalhado por Morel S. et. al. (2005), o factor de correcção multiplicativo definido na Eq. (4.14) fica,

(2.15) A abordagem cinemática, detalhada nesta Secção, deve ser comparada com um método exacto de avaliação da curva de Resistência, que tenha em linha de conta o efeito do peso próprio. Esta ideia será concretizada na próxima Secção.

2.3.3 Método exacto de compensação do peso próprio

Analisando uma vez mais o ensaio SEN-TPB, representado na Figura 2.7, submetido à sobreposição de efeitos decorrente da aplicação da carga externa P a actuar a meio vão,

e o peso próprio da viga, representado pela carga distribuída q, o deslocamento

δ

, de um

dado ponto localizado na secção central do provete (i.e., no eixo da carga central), será o resultado da contribuição dos dois sistemas de carregamento: P e q. Dado que o resultado de

δ

(a) é condicionado pela medida do comprimento de fenda a na secção média (Figura 2.3), o deslocamento anterior será, doravante, designado por

δ

PP (a),

apesar de mais tarde vir a ser referido como

δ

Pq (a), o que levará, de forma semelhante,

por aplicação da Eq. (2.1), a

(2.16) exp 0 * 0 ( ) ( ) PP a a

λ

ψ

λ

= num exp E E

ψ

≅ ( ) ( ) ( ) P a PP a Pq a δ =δ +δ

- 25 - O y x (x, a) δqP x δ (a) (a) PP L/2 P L/2 O x x y L/2 (b) x x O (x, a) δqq y (x, a) q δ _{δ (a)} P L/2 q (a) δPq L/2 L/2 P q

Figura 2.7 Viga simplesmente apoiada sujeita à sobreposição de (a) uma carga central P [N] e a (b) uma carga distribuída q [N/m]. Os parâmetros δiP and δiq,

representam, respectivamente, o deslocamento devido a P e a q medido no eixo i.

com o segundo índice (de

δ

) a ser usado para designar o sistema de carga (P ou q),

enquanto o primeiro (i.e., P) é usado para se referir ao eixo utilizado para obter o

deslocamento

δ

. Em alternativa, pode também preferir-se uma notação baseada na

flexibilidade, em função do comprimento de fenda a,

(2.17) (com

λ

PP expresso em [m/N] e

λ

Pq em [m2/N], uma vez que P e q são expressos em [N]

e [N/m], respectivamente).

Por outro lado, é possível definir o campo de deslocamentos obtido ao longo do eixo do

provete (eixo médio denominado por x na Figura 2.7), em relação à abcissa x, e para um

dado comprimento de fenda a, da forma

(2.18) que, em termos da flexibilidade, é expressa por

( ) ( ) ( ) P a PP a P Pq a q δ =λ +λ ( , ) ( , ) ( , ) q x a qP x a qq x a δ =δ +δ

- 26 -

(2.19) As funções

λ

PP (a) e

λ

Pq (a) na Eq. (2.17), assim como

λ

qP (x,a) e

λ

qq (x,a) na Eq.(2.19)

representam, respectivamente, as flexibilidades corrigidas e o campo de flexibilidades corrigidas (Figura 2.7), estimadas através de

(2.20) (2.21) (2.22) (2.23) Nas Eqs.(2.20) e (2.21), as funções de flexibilidade

λ

*

PP (a) e

λ

*Pq (a) são obtidas a partir do melhor ajuste aos cálculos efectuados pelo MEF, em estado plano de deformação, realizados para diferentes valores de a0 no intervalo [D∕2 , D] (Figura 2.2). Quanto às Eqs.(2.22) e (2.23), os campos de flexibilidade

λ

*

qP (x,a) e

λ

*qq (x,a) são determinados através do melhor ajuste aos cálculos efectuados pelo MEF, no estado plano de deformação, realizados ao longo do eixo Ox da Figura 2.7 (i.e., ao longo da

linha central média), para cada comprimento de fenda a . Na verdade, os cálculos são

realizados nos pontos de integração situados ao longo da meia altura da malha de EF, usada para calcular os valores dos deslocamentos. Portanto,

λ

*

PP (a) e

λ

*qP (x,a) são expressos em [m/N], enquanto

λ

*_{Pq (}

a) e

λ

*_{qq (}

x,a) são definidos em [m2/N], uma vez que P e q são expressos em [N] e [N/m], respectivamente. No que se refere ao factor de correcção multiplicativo

ψ

, definido pela Eq. (2.14),

De uma forma semelhante à que foi vista na Secção 2.3.2,

λ

exp(a0) representa a flexibilidade inicial (para a = a0) obtida nos ensaios mecânicos (Figura 2.8),

(2.24) com δexp(a0) dado pela Eq.(2.3),

( , ) ( , ) ( , ) q x a qP x a P qq x a q δ =λ +λ * ( ) ( ) PP a PP a λ =ψλ * ( ) ( ) Pq a Pq a λ =ψλ * ( , ) ( , ) qP x a qP x a λ =ψλ * ( , ) ( , ) qq x a qq x a λ =ψλ exp 0 * 0 ( ) ( ) PP a a

λ

ψ

λ

= exp 0 exp 0 exp 0 ( ) ( ) ( ) a a P a δ λ = ∆ ∆

- 27 -

Portanto, se a estrutura (Figura 2.3) ainda não tiver sofrido dano (pelo menos) antes da carga central P ter sido aplicada, pode observar-se que

δ

PP (a0) na Eq.(2.3), é a única quantidade que realmente varia. Com efeito, o deslocamento

δ

Pq(a0), apesar de ser impossível de medir experimentalmente, é mantido constante, pelo que

(2.25) De facto, a quantidade

λ

exp (a0) na Eq.(2.14) deve ser reformulada, para se ajustar com a notação

δ

PP exp (a0) da Figura 2.8. Assim, a introdução desta modificação de uma só vez, resulta (2.26) λ ∆P (a )exp 0 P = Pexp (a 0) _{Comportamento} linear elástico (a = a ) PPexp (a ) * λ ∆δ (a ) ≈ ∆δ _exp (a ) P P 0 P exp P 0 0 1 1 0 δ δ exp= Ensaios mecânicos FEM

Figura 2.8 Sobreposição de curvas força-deslocamento obtidas no ensaio mecânico e através da análises pelo MEF no regime linear elástico (para

a=a0). exp( ) [a0 PP( )a0 Pq( )]a0 Pq( )a0 δ = δ +δ −δ exp( )a0 PP( )a0 δ =δ 0 exp 0 exp 0 exp 0 ( ) ( ) ( ) ( ) PP PP a a a P a

δ

λ

= ∆ =

λ

∆

- 28 - 2.3.3.1 Comprimento de fenda equivalente

No decorrer do ensaio de fractura ilustrado na Figura 2.3, a monitorização do deslocamento resulta da acção combinada (sobreposição) dos sistemas de carga actuantes no provete (i.e., P e q). Assim, tem-se

(2.27) A compensação do peso próprio, no entanto, implica a alteração dos deslocamentos registados, tal como se ilustra, esquematicamente, na Figura 2.9,

(2.28) com

δ

Pq (a0) representando o deslocamento que resulta do peso próprio da estrutura, que

ocorre antes de se efectuar o zero da célula de carga (ponto O Figura 2.3). O segundo

termo da Eq. (2.28) pode ser definido como se segue

(2.29)

Figura 2.9 Curva força-deslocamento modificada como resultado da compensação do peso próprio (linha a traço-ponto).

exp( ) [a PP( )a Pq( )]a Pq( )a0 δ = δ +δ −δ mod( )a exp( )a Pq( )a0 δ =δ +δ 0 0 ( ) ( ) Pq a Pq a q δ =λ δ_Pq(a ₀) mod δ_exp(a) δ (a) 1 P λ 1 exp(a )0 Pexp λ_mod(a) 1 M' M λ_exp(a) δ 1 (a ) λexp 0

- 29 -

que é estabelecido em função da flexibilidade corrigida

λ

Pq (a0), possível de ser obtida a partir da Eq.(2.21), para a=a0=D∕2 (Figura 2.2).

Ainda focado na operação de modificação do deslocamento registado, esquematicamente representada na Figura 2.9, pode reescrever-se a Eq.(2.28) com base na flexibilidade, para um determinado comprimento de fenda a ,

(2.30)

com a correspondente flexibilidade modificada

λ

mod (a), definida por

(2.31) com as duas funções

λ

PP(a) e

λ

Pq(a) a serem corrigidas por meio das Eqs.(2.20) e

(2.21), respectivamente (a≥a0). Assim, a combinação da Eq.(2.31) com as Eqs.(2.20) e

(2.21), resulta

(2.32)

Figura 2.10 Energia de deformação associada à carga externa P para dois pontos consecutivos da curva força-deslocamento modificada.

mod( )a PP( )a P Pq( )a q mod( )a P δ =λ +λ =λ mod( ) PP( ) Pq( ) q a a a P

λ

=

λ

+

λ

* * mod( ) PP( ) Pq( ) q a a a P

λ

=

ψ λ

_ +

λ

_   mod λ 1 λ_mod exp P P2 1 P (a ) δ_mod 2 (a ) δ 1 mod(a )2 1 1 (a ) δ_mod

- 30 -

Assim, em jeito de resumo, deve referir-se que o primeiro passo consiste em obter as

curvas P-

δ

modificadas (Eqs. 2.11, 2.21 e 2.28), fazendo uso das funções de calibração

da flexibilidade

λ

*

PP (a) e

λ

*Pq (a), previamente avaliadas no intervalo a ∈ [D/2, D].

Posteriormente, para um dado ponto M′ (Figura 2.9) de uma curva P-

δ

modificada (o

que corresponde a um comprimento de fenda desconhecido a), efectua-se o cálculo da flexibilidade correspondente

λ

mod (a); (i.e.,

δ

mod (a)∕P como primeiro membro da Eq. 2.32). Consequentemente, fazendo uso da carga P correspondente, juntamente com os

escalares

ψ

e q, estimados para cada provete, avaliar-se-á o segundo membro da

Eq.(2.32), com base numa primeira estimativa do valor da extensão do comprimento de fenda a = ai (tomada ao acaso). O comprimento de fenda equivalente a será então o valor usado como ai, que propiciar a igualdade entre os dois membros da Eq. (2.32). Neste trabalho, implementou-se o método da bissecção (Chapra SC e Canale RP 1985), como rotina de pesquisa, para localizar o comprimento de fenda equivalente a.

Na próxima Secção, apresentar-se o método usado para avaliação das curvas de

resistência, usando as curvas P-

δ

modificadas (assunto desta Secção), juntamente com

os valores correspondentes do comprimento de fenda equivalente a (para

δ

, P).

2.3.3.2 Avaliação da curva de Resistência

Considerem-se dois pontos consecutivos da curva P−

δ

modificada (Figura 2.9) de

coordenadas [

δ

mod (a1), P1] e [

δ

mod (a2), P2], a que correspondem, respectivamente, as flexibilidades representadas por

λ

mod (a1) e

λ

mod (a2); (ver Figura 2.10).

A energia de deformação elástica

δ

E associada à propagação infinitesimal de uma fenda

δ

a (com

δ

a=a2-a1), é dada por

(2.33) com

δ

W e

δ

U, representando, respectivamente, o trabalho realizado pela carga externa P

e a correspondente energia complementar. Como o peso próprio intervém nesta contabilidade, a Eq. (2.33) pode ser rescrita de uma forma mais pormenorizada, entrando em linha de conta com a contribuição da carga central P e a carga distribuída q

E W U

- 31 -

(2.34) O cálculo do trabalho realizado pela carga externa (Figura 2.10) na Eq. (2.34), faz-se da seguinte forma

(2.35) Por seu turno, o trabalho devido à carga distribuída

δ

Wq na Eq.(2.34), é calculado

através do integral

(2.36)

Ambos os campos de deslocamento

δ

q(x,a1) e

δ

q(x,a2) na Eq. (2.36) são estimados com

o recurso ao MEF, para pontos localizados ao longo do eixo médio ( y = D∕2) da malha,

seguindo o esboço esquematicamente representado na Figura 2.11. Assim, pode concluir-se que é legítimo que cada um dos campos de deslocamentos referidos inclua um termo associado à carga central P, e outro à carga distribuída q, de tal forma que

,(i = 1, 2) (2.37) ,(i = 1, 2) (2.38) sendo que ambas as quantidades

λ

qP(x,ai) e

λ

qq(x,ai) são definidas em função da flexibilidade normalizada (0 < x < L) calculadas para comprimentos de fenda a ≥ a0 , como se fez para as Eqs. (2.22) e (2.23), para um dado comprimento de fenda equivalente a.

O termo

δ

UP na Eq.(2.34) refere-se à energia complementar associada à carga aplicada

P (Figura 2.10), que é calculada através,

(2.39)

enquanto que a energia complementar associada à carga distribuída

δ

Uq,

correspondendo ao peso próprio do provete (último termo da Eq. 2.34), é avaliada da seguinte forma (2.40) ( P q) ( P q) E W W U U δ = δ +δ − δ +δ

[

]

1 2 mod( )2 mod( )1 2 P P P W a a

δ

= +

δ

−

δ

2 1 0 ( , ) ( , ) L q q q W q x a x a dx δ =

∫

_δ −δ _ ( , ) ( , ) ( , ) q x ai qP x ai qq x ai δ =δ +δ ( , ) ( , ) qP x a Pi i qq x a qi λ λ = + 2 mod 2 1 mod 1 1 _{( )} 1 _{( )} 2 2 P U P a P a

δ

=

δ

−

δ

2 1 ₀ 2 1 1 ( , ) ( , ) 2 L q q q q q U U U q x a x a dx

δ

= − =

∫

_

δ

−

δ

_