PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO
PUC-SP
Marília Valério Rocha
UMA PROPOSTA DE ENSINO PARA O ESTUDO DA
GEOMETRIA HIPERBÓLICA EM AMBIENTE DE
GEOMETRIA DINÂMICA
MESTRADO EM EDUCAÇÃO MATEMÁTICA
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO
PUC-SP
Marília Valério Rocha
UMA PROPOSTA DE ENSINO PARA O ESTUDO DA
GEOMETRIA HIPERBÓLICA EM AMBIENTE DE
GEOMETRIA DINÂMICA
MESTRADO EM EDUCAÇÃO MATEMÁTICA
Dissertação apresentada à Banca Examinadora da Pontifícia Universidade Católica de São Paulo, como exigência parcial para obtenção do título de
MESTRE EM EDUCAÇÃO MATEMÁTICA, sob a orientação do Prof. Dr. Saddo Ag Almouloud.
Banca Examinadora
________________________________________
________________________________________
Autorizo, exclusivamente para fins acadêmicos e científicos, a reprodução total ou parcial desta Dissertaçãopor processos de fotocopiadoras ou eletrônicos.
Há um tempo em que é preciso abandonar as roupas usadas que já têm a forma do nosso corpo…
Esquecer os nossos caminhos que nos levam sempre aos mesmos lugares.
É o tempo da travessia.
E se não ousarmos fazê-la, teremos ficado para sempre à margem de nós mesmos.
AGRADECIMENTOS
Agradeço a todos que de alguma maneira contribuíram para a realização deste trabalho, em especial:
A Deus, a meus pais e minha irmã pela presença constante;
Ao Prof. Ms. Sc. João Tomás do Amaral, por ter me apresentado à obra de Poincaré;
Ao Prof. Dr. Saddo Ag Almouloud, pela orientação e compreensão nos momentos difíceis;
Aos professores Dr. Claudemir Murari e Dra Celina Abar, pelas valiosas sugestões apresentadas na qualificação; Aos amigos de todos os momentos, Gina Miranda, Susan de Faria, Ederson Manduca, Orlando Gomes e Vicente Abdoral;
Ao prof. Ms. José Miguel Sousa, que permitiu minha participação no curso de História da Matemática com o Cinderella, em 2005;
Aos professores do Programa de Mestrado em Educação Matemática da PUC-SP, que contribuíram para minha formação, em particular, os professores Dr. Vicenzo Bongiovanni e Dra Ana Paula Jahn pelas discussões sobre geometria e Educação Matemática;
RESUMO
Esta dissertação teve como principal objetivo propor um ambiente computacional ao aprendizado da Geometria Hiperbólica na formação do professor de Matemática. Com base na Teoria das Situações Didáticas desenvolvida por Guy Brousseau (1986) e nos estudos sobre a compreensão das demonstrações, de Raymond Duval (1993), foi elaborada uma seqüência didática sobre o tema. A presente pesquisa orienta-se pela questão “Em que medida a geometria dinâmica pode interferir na construção dos conceitos da Geometria Hiperbólica, no estudo axiomático realizado pelo professor de Matemática e como esse novo conhecimento pode contribuir para sua formação?”. É fundamentada em alguns pressupostos da Engenharia Didática, descrita por Artigue (1988). Entende-se que a relevância desta pesquisa justifica-se nas orientações das Diretrizes Curriculares Nacionais para os cursos de Matemática, Bacharelado e Licenciatura (DCN) e na escassez de material didático para o estudo desse conteúdo. Visando a responder à questão de pesquisa e colher informações que possibilitem a melhoria desta proposta didática, aplicou-se um projeto-piloto com alunos do curso de Mestrado Profissional em Ensino de Matemática, ministrado pela Pontifícia Universidade Católica (PUC-SP). Os resultados apontaram que a utilização da geometria dinâmica na formação dos conceitos da Geometria Hiperbólica, em uma proposta axiomática inicial, é um recurso que contribui para a interiorização desses conceitos.
ABSTRACT
This dissertation had as its main objective to propose an environment computational to the learning of Hyperbolic Geometry in the training of teachers of mathematics. Based on the Theory of Didactical Situation developed by Guy Brousseau (1986) and studies with the Comprehension of Demonstrations from Raymond Duval (1993), a didactic sequence has been prepared on the subject. The present work is oriented by the question “to what extent the dinamic geometry could interfere in the build of hyperbolic geometry’s concepts, in the axiomatic study by the professor of mathematics and how this new knowledge could contribute to your formation?” This research is founded on some assumptions of Didactic Engieneering, described for Artigue (1988). The relevance of this research is justified by the Nacional Curriculum Guidelines for the courses off Bachelor’s Degree in Mathematics, and shortage of teaching-material for the study of this content. Aimed at responding the question of research and gather information that enable the improvement of this didactic proposal, a pilot project was implemented with students of the Professional Master’s Degree in Mathematics Education given by PUC-SP University. The results showed that the use of dinamic geometry in the formation of concepts of Hiperbolic Geometry, in the inicial axiomatic proposal, is a resource that contribute to understing these concepts.
SUMÁRIO
ESTUDOS PRELIMINARES... 17
1.1 Introdução ... 17
1.2 Estudos Preliminares ... 18
1.2.1 Internet e Educação ... 18
1.2.2 Diretrizes Curriculares Nacionais (DCN)... 25
1.2.3 Publicações (livros e artigos) sobre a Geometria Hiperbólica ... 26
1.2.4 Dissertações sobre a Geometria Hiperbólica... 34
1.2.5 Descrição de alguns Softwares que possibilitam o estudo da Geometria Hiperbólica... 42
1.2.6 Modelos da Geometria Hiperbólica... 47
ASPECTOS TEÓRICO-METODOLÓGICOS ... 56
2.1 Introdução ... 56
2.2 Questão de Pesquisa e Hipóteses levantadas ... 56
2.3 Metodologia de Pesquisa... 58
2.4 Procedimentos Metodológicos... 63
ELABORAÇÃO DA PÁGINA DA INTERNET ... 76
3.1 Introdução ... 76
3.2 Idealização da página da Internet... 76
SEQUÊNCIA DIDÁTICA... 83
4.1 Introdução ... 83
4.2 Delineamento da experimentação ... 83
4.2.1 Preparação do Ambiente... 83
4.2.2 Público-alvo... 83
4.2.3 Dinâmica dos Encontros ... 84
4.3 Análises da Seqüência Didática e Resultado da Experimentação... 84
4.3.1 Introdução: Explicando o software Cinderella e as atividades propostas... 84
4.3.2 Atividade 1: Axiomatização de Hilbert... 91
4.3.3 Atividade 2: Explorando o Disco de Poincaré ... 98
4.3.4 Atividade 3: Retas no Plano... 102
4.3.5 Atividade 4: Ângulo de Paralelismo ... 108
4.3.6 Atividade 5: Explorando as retas hiperbólicas ... 113
4.3.7 Atividade 6: Biângulo... 123
4.3.8 Atividade 7: Quadrilátero de Saccheri... 132
4.3.9 Atividade 8: Quadrilátero de Lambert ... 141
4.3.10 Atividade 9: Triângulos... 150
4.3.11 Atividade 10: Explorando as Circunferências ... 156
4.3.12 Atividade 11: Circunferência, Horocírculo e Hipercírculo ... 159
4.3.13 Atividade 12: Área ... 163
4.3.14 Questionário Inicial... 166
4.3.15 Primeira Série de Exercícios... 169
4.3.16 Segunda Série de exercícios ... 176
4.3.17 Atividade Final... 182
4.3.18 Questionário Final ... 194
4.3 Reflexão e alteração do material didático... 204
CONSIDERAÇÕES FINAIS... 207
REFERÊNCIAS ... 211
LISTA DE FIGURAS
Figura 1.1: construção geométrica com o software Cabri-Géomètry ... 43
Figura 1.2: construção geométrica com o software Cinderella... 44
Figura 1.3: construção geométrica com o software Sketchpad ... 45
Figura 1.4: construção geométrica com o software NonEuclid... 45
Figura 1.5: construções geométricas com os softwares Poincaré Disc e PoincaréDraw... 46
Figura 1.6: Modelo de Beltrami ... 49
Figura 1.7: Modelo de Klein ... 50
Figura 1.8: Modelo de Poincaré ... 51
Figura 1.9: Modelo do Semiplano de Poincaré ... 53
Figura 1.10: Distância hiperbólica entre dois pontos ... 54
Figura 1.11: Distância hiperbólica entre dois pontos, representada no eixo cartesiano ... 55
Figura 1.12: Distância hiperbólica entre dois pontos apresentada pelo software Cinderella ... 55
Figura 2.1: Estrutura Ternária de um passo da demonstração ... 66
Figura 3.1: Página - Tela Inicial... 77
Figura 4.1: Introdução (a) - Apresentação do Cinderella... 85
Figura 4.2: Introdução (b) - Apresentação da Seqüência ... 86
Figura 4.3: Introdução (c) - Exercício de construção geométrica com o uso do Cinderella ... 88
Figura 4.4: Introdução (d) - Exercício resolvido com a ferramenta “visualizar próximo passo”.. 89
Figura 4.5: Introdução (e) - Notações e Bibliografia ... 90
Figura 4.6: Atividade 1 (a) - Apresentação da Axiomatização de Hilbert ... 92
Figura 4.7: Atividade 1 (b) - Resumo da Geometria Absoluta e Propriedades... 95
Figura 4.8: Atividade 1 (c) - Exercício de Construção e demonstração... 96
Figura 4.9: Atividade 2 (a) - Exploração: retas, segmentos, ângulos ... 99
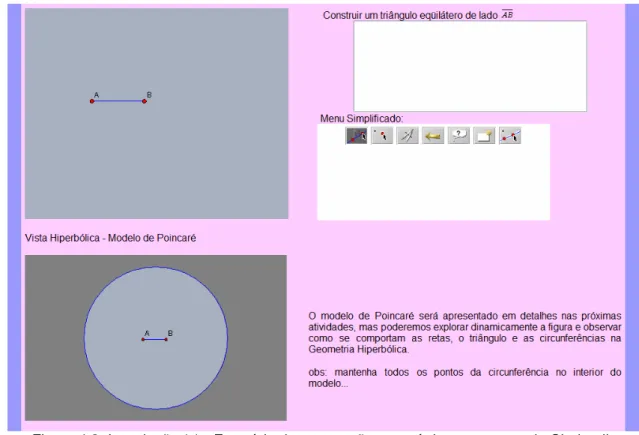
Figura 4.10: Atividade 2 (b) - Apresentação do modelo de Poincaré ... 101
Figura 4.11: Atividade 3 (a) - Definições e Teoremas da Geometria Hiperbólica ... 103
Figura 4.12: Atividade 3 (b) - Exploração dinâmica das retas hiperbólicas... 103
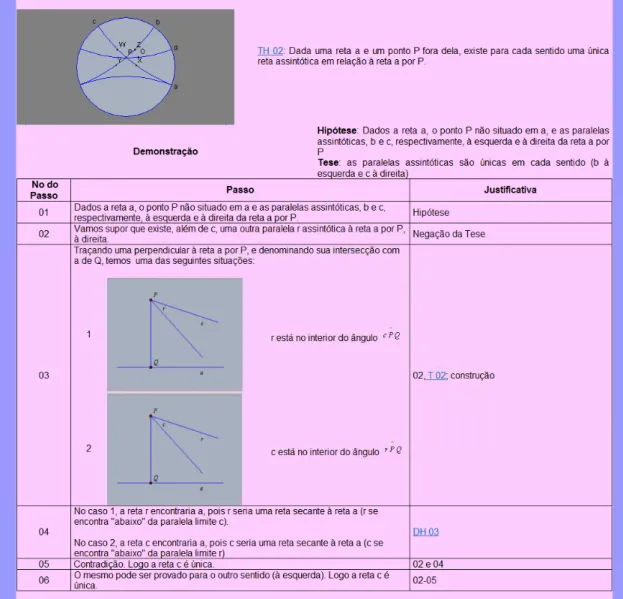
Figura 4.13: Atividade 3 (c) - Demonstração dos teoremas hiperbólicos 1 e 2 ... 105
Figura 4.14: Atividade 3 (d) - Reflexão sobre a transitividade das paralelas ... 106
Figura 4.15: representação de um passo da demonstração do TH 02 ... 107
Figura 4.16: Atividade 4 (a) - Exploração dinâmica do ângulo de paralelismo... 108
Figura 4.17: Atividade 4 (b) - Demonstração dos teoremas hiperbólicos 2 e 3... 110
Figura 4.18: Atividade 4 (c) - Exploração dinâmica: altura e o ângulo de paralelismo... 111
Figura 4.19: atividade 4: análise de situação... 112
Figura 4.20: Atividade 5 (a) - Investigações dinâmicas das retas hiperbólicas ... 115
Figura 4.21: Atividade 5 (b) - Exercício de demonstração do teorema 08... 116
Figura 4.22: representação das retas ... 117
Figura 4.23: representação do TH 10 ... 118
Figura 4.24: Atividade 6 (a) - Definição de biângulo e teorema do ângulo externo... 125
Figura 4.25: Atividade 6 (b) - Exercício de demonstração do teorema 12... 126
Figura 4.26: Atividade 6 (c) - Casos de Congruência dos Biângulos ... 128
Figura 4.27: representação do TH 12 ... 129
Figura 4.29: Atividade 7 (a) - Quadrilátero de Saccheri... 133
Figura 4.30: Atividade 7 (b) - Exercício de demonstração do teorema 16... 134
Figura 4.31: Atividade 7 (c) -Demonstração do teorema 17 ... 135
Figura 4.32: Atividade 7 (d) - Exploração dinâmica e questionamento sobre os quadriláteros 136 Figura 4.33: Atividade 8 (a) - Teorema sobre o Quadrilátero de Lambert... 141
Figura 4.34: Atividade 8 (b) - Teoremas sobre os Quadriláteros... 143
Figura 4.35: Atividade 8 (c) - Demonstração do teorema hiperbólico 22... 144
Figura 4.36: Atividade 8 (d) - Demonstração do teorema hiperbólico 23 ... 144
Figura 4.37: Atividade 8 (e) - Demonstração do teorema hiperbólico 8 ... 145
Figura 4.38: Atividade 9 (a) - Construção e investigação: soma dos ângulos de um triângulo 150 Figura 4.39: Atividade 9 (b) - Demonstração do teorema hiperbólico 24 ... 151
Figura 4.40: Atividade 9 (c) - Exercício de demonstração ... 151
Figura 4.42: Atividade 9 (e) - Pontos Ideais e Triângulos Ômega ... 153
Figura 4.43: Atividade 10 (a) - Construção e investigação dinâmica:círculos ... 157
Figura 4.44: Atividade 10 (b) - Demonstração do teorema hiperbólico 28 ... 158
Figura 4.45: Atividade 10 (c) - Investigação Dinâmica... 159
Figura 4.46: Atividade 11 (a) - Demonstração do Teorema 29... 161
Figura 4.47: Atividade 11 (b) - Apresentação dos lugares geométricos... 162
Figura 4.48: Atividade 11 (c) - Proposta de análise de situação ... 163
Figura 4.49: Atividade 12 (a) - Definição de deficiência... 163
Figura 4.50: Atividade 12 (b) - Apresentação do Teorema 30... 164
Figura 4.51: Atividade 12 (c) - Área ... 165
Figura 4.52: Atividade 12 (d) - Análise de Situação... 166
Figura 4.53: Questionário Inicial... 167
Figura 4.54: Início da primeira série de exercícios complementares... 169
Figura 4.55: 1ª série de exercícios complementares ... 171
Figura 4.56: representação do teorema do triângulo inscrito ... 172
Figura 4.57: representação de um passo da demonstração do teorema do triângulo inscrito. 173 Figura 4.58: 2º série de exercícios complementares ... 176
Figura 4.59: Atividade Final (a) - Questão 1 ... 183
Figura 4.60: Atividade Final (b) - Demonstração dos teoremas 16 e 17 ... 184
Figura 4.61: Atividade Final (c) - Questão 2 ... 185
Figura 4.62: Atividade Final (d) - Questão 3 ... 185
Figura 4.63: Atividade Final (e) - Questão 4 ... 186
Figura 4.64: Atividade Final (f) - Questão 5 ... 186
LISTA DE QUADROS
Quadro 1.1: Características do Modelo de Beltrami ... 49
Quadro 1.2: Características do Modelo de Klein ... 50
Quadro 1.3: Características do Modelo de Poincaré ... 51
Quadro 1.4: Características do Modelo do Semiplano de Poincaré ... 53
Quadro 2.1: Argumentação x Demonstração... 67
Quadro 2.2: Raciocínio Dedutivo x Argumentação x Raciocínio por Absurdo ... 71
Quadro 2.3: Tabela Verdade... 72
Quadro 2.4: Verificação do método de RAA ... 72
Quadro 2.5: Demonstração da Proposição XXVII - Elementos ... 73
Quadro 2.6: Esquema de RAA... 74
Quadro 4.1: protocolos da análise de situação – atividade 3 ... 107
Quadro 4.2: protocolos da análise de situação – atividade 4 ... 112
Quadro 4.3: protocolos da tese e hipótese do TH 10 ... 120
Quadro 4.4: protocolos da demonstração do TH10 ... 121
Quadro 4.5: protocolos da demonstração do TH12 ... 130
Quadro 4.6: protocolos da demonstração do TH 16 ... 138
Quadro 4.7: protocolos da demonstração do TH 23 ... 147
Quadro 4.8: protocolo da demonstração do TH 25... 154
Quadro 4.9: 1ª série de exercícios - protocolos da 1ª questão... 174
Quadro 4.10: 1ª série de exercícios - protocolos da 2ª questão... 174
Quadro 4.11: 1ª série de exercícios - protocolos da 3ª questão... 175
Quadro 4.12: 1ª série de exercícios - protocolos da 4ª questão... 175
Quadro 4.13: protocolos das respostas da 1ª questão do 2º fórum ... 177
Quadro 4.14: protocolos das respostas da 2ª questão do 2º fórum ... 180
Quadro 4.15: protocolos das respostas da 3ª questão do 2º fórum ... 181
Quadro 4.16: atividade final – protocolos das respostas da primeira questão ... 187
Quadro 4.17: atividade final – protocolos das respostas da segunda questão ... 187
Quadro 4.18: atividade final – protocolos das respostas da terceira questão ... 190
Quadro 4.19: atividade final – protocolos das respostas da quarta questão... 191
Quadro 4.20: atividade final – protocolos das respostas da quinta questão ... 193
Quadro 4.21: questionário final – protocolos das respostas da primeira questão... 195
Quadro 4.22: questionário final – protocolos das respostas da segunda questão ... 197
Quadro 4.23: questionário final – protocolos das respostas da terceira questão... 198
Quadro 4.24: questionário final – protocolos das respostas da quarta questão... 199
Quadro 4.25: questionário final – protocolos das respostas da quinta questão ... 200
Quadro 4.26: questionário final – protocolos das respostas da sexta questão ... 201
APRESENTAÇÃO
Só pela ciência e pela arte as civilizações têm valor. (Poincaré, 1995, p.172)
Como aluna de graduação em Matemática, estudei a Geometria Euclidiana e sempre me interessei pelo estudo de outras geometrias que, infelizmente, não faziam parte do currículo, fato freqüente na maioria dos cursos do País1.
Ao buscar conhecimento a respeito desse conteúdo, deparei-me com a dificuldade de encontrar material didático escrito em língua portuguesa.
No período da graduação, durante o estudo da Geometria Euclidiana, de maneira geral, os graduandos mostravam dificuldades para a compreensão das demonstrações formais e, mais tarde, verifiquei que tal dificuldade é comum à maioria dos alunos, sejam eles do Ensino Fundamental, Médio ou Universitário. Elas levam muitos professores à exposição de teoremas sem as devidas demonstrações, ainda no ensino fundamental, fato que priva o aluno de uma possibilidade de desenvolver seu raciocínio lógico-dedutivo e faz com que essas dificuldades acompanhem-no por toda sua vida acadêmica.
Com o advento do Movimento da Matemática Moderna que, durante o final da década de 1960 e início de 1970, esteve presente nas escolas e universidades, podemos observar que muitos dos professores que, atualmente, lecionam, não tiveram contato satisfatório com as demonstrações, fato que também os inibem de incorporá-las às suas aulas. Após esse movimento, muito pouco se privilegiou o estudo das demonstrações, em todos os níveis de ensino, inclusive, nos de formação de professores de Matemática.
No início do mestrado em Educação Matemática, travei contato com o grupo de pesquisa “Conceitos: Formação e Evolução”, coordenado por meu
orientador, o Prof. Dr. Saddo Ag Almouloud, que tem como uma de suas prioridades o estudo das demonstrações em Geometria e a contribuição do computador na criação de conceitos geométricos. Embora a importância da utilização de novas tecnologias na Educação seja amplamente discutida, no estudo de Geometria sua importância parece ainda mais evidente. Mas é fundamental não reduzir esse estudo à utilização das mesmas, que devem ser vistas como mais uma alternativa didática, facilitadoras no processo de ensino e aprendizagem.
Minhas expectativas aliadas aos trabalhos do grupo de pesquisa levaram-me a propor a criação de um material didático para o estudo de outras geometrias. Visando a atingir um número maior de professores e alunos de graduação, foi idealizada a elaboração de uma página na Internet, que pudesse contemplar uma seqüência didática na apresentação da Geometria Hiperbólica. A seqüência inspirou-se nos conceitos da Teoria das Situações Didáticas (TSD) de Guy Brousseau (1986) e, também, no trabalho sobre a compreensão das demonstrações, de Raymond Duval (1993).
Foi realizado um projeto-piloto com alunos do curso de Mestrado Profissional em Ensino de Matemática, ministrado pela PUC-SP, a fim de validar nossas intenções didáticas, apresentadas nos capítulos III e IV, bem como identificar pontos de melhoria do material.
O principal objetivo foi propor um ambiente ao aprendizado da Geometria Hiperbólica na formação do professor de Matemática. Procuramos investigar, também, se a apresentação das demonstrações feitas passo a passo, em três colunas, favorece a aprendizagem do raciocínio lógico. Verificamos em que medida uma seqüência de ensino provoca mudanças no conhecimento do professor em relação ao estudo da Geometria Hiperbólica e ainda propomos uma reflexão sobre sua prática no ensino de Geometria nos Ensinos Fundamental e Médio.
e contribuir com a prática pedagógica do professor e também para sua formação específica.
As Diretrizes Curriculares Nacionais para os cursos de Matemática, Bacharelado e Licenciatura (DCN) reforçam a importância do desenvolvimento do raciocínio lógico no graduando em Matemática e entendemos que propostas como esta poderão contribuir nesse sentido, conforme será exposto no capítulo I.
Acreditamos ainda que este estudo contribua para o questionamento atual sobre a introdução de outras geometrias no conteúdo do Ensino Médio, uma vez que estas são contempladas nos currículos de outros países. Segundo Centomo (2002), mesmo considerando a crise atual no ensino de Geometria, existem vários motivos para se introduzir o estudo desse tema no Ensino Médio:
• Considerando o plano lógico e demonstrativo: na geometria plana, freqüentemente os alunos confundem as definições com os teoremas, não conseguindo identificar qual deve provar logicamente ou ainda ao se depararem com teoremas considerados “óbvios” não conseguem perceber a necessidade de uma demonstração formal. Como a Geometria Hiperbólica é menos familiar e menos intuitiva, seu estudo favorece a potencialização do raciocínio lógico e do rigor das demonstrações.
• Considerando o estudo da Geometria Euclidiana: o estudo da Geometria Hiperbólica favorece o estudo da Geometria Euclidiana, uma vez que seu estudo é feito com modelos euclidianos, o que leva o aluno a aprofundar seus conhecimentos sobre esta geometria que, de outra forma, não seria necessário.
• Considerando o plano cultural: o estudo de outras geometrias amplia o conhecimento do aluno e possibilita a percepção de que a geometria não é uma teoria que nasceu e morreu na Grécia antiga, mas que passou e passa por um processo de desenvolvimento até os dias atuais. (CENTOMO, 2002, tradução nossa do original italiano).
da obra de Euclides e do próprio conceito de raciocínio lógico-dedutivo. Assim, esse amadurecimento impulsionou o surgimento de outras geometrias. Entendemos que a abordagem histórica proposta poderá contribuir no processo de ensino e aprendizagem da Geometria Hiperbólica, sendo ainda enriquecedora para o futuro professor de Matemática.
Em nosso entender, conhecer provas na perspectiva de conhecimento substantivo significa que o professor deve possuir um conjunto suficiente de conhecimentos, que lhe dê autonomia intelectual sobre esse tema. Essa autonomia significa, por exemplo, não apenas conhecer as demonstrações dos teoremas e fórmulas que irá desenvolver futuramente, mas também ter a capacidade de selecionar e organizar tais teoremas e respectivas aplicações. Saber diferenciar o que é importante daquilo que é secundário. Ele precisa, sobretudo, saber problematizar as demonstrações de modo a integrá-las ao assunto que está desenvolvendo. Para isso, ele precisa ser mediador entre os conhecimentos produzidos historicamente e aquele que será apropriado pelos alunos.(PIETROPAOLO, 2005, p.222)
A apresentação do presente trabalho foi elaborada em cinco capítulos, descritos na seqüência:
• Em Estudos Preliminares realizamos levantamentos referentes à literatura disponível, em língua portuguesa, sobre a Geometria Hiperbólica e os softwares disponíveis para o tratamento do tema proposto e ainda como potencializar o uso das novas tecnologias na Educação. Complementamos os estudos preliminares com um levantamento histórico do surgimento de outras geometrias, necessário para complementar a proposta. Optamos por apresentar o resultado final do último levantamento por meio do material produzido, exibido em nossa página (anexos I a XIII).
• No Capítulo III, expomos como a página foi idealizada e construída com a intenção de apresentar nossas atividades e munir o aprendiz das informações necessárias ao estudo proposto.
• No Capítulo IV, apresentamos os elementos da análise a priori feita nas atividades elaboradas, que foram estruturadas, pretendendo a criação de situações que proporcionem um aprendizado e possam nos oferecer subsídios para responder à questão de pesquisa. Apresentamos, também, a experimentação propriamente dita, a análise a posteriori e os resultados obtidos na pesquisa.
CAPÍTULO I
ESTUDOS PRELIMINARES
Cada ator, desviando e reinterpretando as possibilidades de uso de uma tecnologia intelectual, acaba por conferir-lhe um novo significado. (LÉVY, Pierre. 1993, p.146)
1.1 Introdução
A apresentação dos estudos preliminares foi segregada em dois blocos. No primeiro bloco, iniciamos com a apresentação do uso da Internet na educação e pesquisamos sobre a importância e os cuidados necessários para o emprego desse veículo no ensino. Pesquisamos nas Diretrizes Curriculares Nacionais para os cursos de Matemática, Bacharelado e Licenciatura (DCN) as orientações pertinentes ao estudo das geometrias e levantamos a literatura publicada a respeito da Geometria Hiperbólica. Na seqüência, listamos os softwares destinados ao estudo de geometria e finalizamos com a apresentação dos modelos da Geometria Hiperbólica. Tais levantamentos nos foram particularmente úteis para a elaboração da página da Internet, oferecendo subsídios para a escolha do software, a delineação da forma, a linguagem do texto e a definição do conteúdo matemático.
1.2 Estudos Preliminares
1.2.1 Internet2 e Educação
O uso da Internet é uma realidade que, em um mundo globalizado, possibilita acesso às informações nunca antes imaginado. Embora esse acesso seja imediato, nem sempre nos deparamos com materiais voltados ao ensino, que sejam apresentados em uma linguagem apropriada e que fundamentalmente sejam capazes de produzir um novo saber.
Se olharmos, ao mesmo tempo, a velocidade na qual os conhecimentos se desenvolvem, a extensão da capacidade cognitiva individual mediante as tecnologias, as novas possibilidades de aprendizagem cooperativa e de colaboração entre as pessoas, no nível intelectual, eu acredito que nos deparamos com uma paisagem completamente nova na relação com o saber e somos obrigados a constatar que muitas de nossas concepções pedagógicas a respeito do ensino e aprendizagem, muitas das nossas instituições de ensino e dos nossos métodos para reconhecer ou validar competências foram elaboradas em um período em que a relação com o conhecimento era muito diferente do atual. Então, há muito trabalho a fazer para que os nossos conceitos, as nossas instituições, os nossos modos de organização se adaptem a essa nova fase. (LÉVY, 1997, p.2, tradução nossa do original em italiano)
Como professores, temos, também, o desafio de contribuir para que os alunos sejam capazes de optarem por boas escolhas, distinguindo produções de qualidade e que desenvolvam as habilidades necessárias para o estudo individual.
Os professores do futuro serão manager do conhecimento e encorajadores, ao invés de pessoas que detêm e distribuem um saber. Deverão ensinar aos seus estudantes como procurá-lo, porque os alunos deverão continuar a fazê-lo por toda a sua vida social e profissional, e não terá sempre um professor que os colocará de frente a uma informação certa e pronta. (LÉVY, 1997, p.3)
O acesso às mídias pode ser aproveitado como mais uma possibilidade de contribuição à educação tradicional, ou ainda, como um veículo que viabiliza o ingresso de muitos estudantes a uma formação ou especialização.
Nesse cenário, entendemos que a concepção de materiais que possam ser disponibilizados na Internet permite sua utilização no ensino nas modalidades presencial, semipresencial, ou ainda, a distância. Nossa pretensão é criar um material que tenha tal funcionalidade, embora esta pesquisa seja voltada à modalidade presencial.
Na elaboração de materiais didáticos para utilização em ambientes virtuais, vários aspectos específicos desse ambiente devem ser observados. Os textos propostos via Internet podem e devem ser apresentados como hipertextos, possibilitando aos usuários transitarem por textos não-lineares, construindo assim sua própria leitura.
Lévy (1999, p.55) ressalta que “o hipertexto é constituído por nós (os elementos de informação, parágrafos, páginas, imagens, seqüências musicais, etc.) e por links entre esses nós, referências, notas, ponteiros, ‘botões’ indicando a passagem de um nó a outro”.
O autor acrescenta que podemos considerar a hipertextualização dos documentos como “uma tendência à indeterminação, à mistura das funções de leitura e de escrita”, pois, o autor, definindo os links, atua como um leitor que selecionou uma possível leitura e o leitor, ao definir sua navegação, cria uma leitura particular possível do texto. Temos, então, que “com o hipertexto toda leitura é uma escrita potencial” (LÉVY, 1999, p.57). Desse modo, percebemos que esse aspecto do hipertexto torna-o sempre inacabado e o indivíduo pode construir um mesmo conhecimento por caminhos diferentes, respeitando suas necessidades e carências próprias.
Peters (2003) reforça a possibilidade de um aprendizado não-linear:
exposição e explanação de saber são perfeitamente possíveis, se forem tecnicamente viáveis e talvez até mais apropriadas. (PETERS, 2003, p.237)
Kalinke (2003) ressalta também certos aspectos negativos do uso da Internet na Educação, levantados por alguns pesquisadores, mas, em seguida, reforça que estes pesquisadores também apontam alternativas, deixando um saldo positivo para seu emprego em atividades pedagógicas.
A quantidade de informações pode levar à perda de foco no assunto principal, além da facilidade de dispersão durante a navegação, a falta de fidedignidade de muitas informações, a lentidão de acesso em função da qualidade das linhas telefônicas, os efeitos colaterais das máquinas, tais como sonolência, resignação e sensação de impotência intelectual e a possibilidade de acesso a informações não educacionais, como pornografia, drogas e materiais explosivos, por exemplo. (KALINKE, 2003, p.53)
Para idealizar um hipertexto, seu autor deve estar atento aos aspectos levantados, no sentido de possibilitar ao leitor condições para uma navegação intuitiva e produtiva. Inserir sua produção em uma plataforma e-learning limita algumas das questões citadas, e as demais podem ser minimizadas por uma concepção eficiente da página.
Na introdução de um material didático em uma plataforma e-learning, vimos alguns pontos positivos e podemos citar outros, pois ela proporciona o acompanhamento do aprendiz, permite discussões em fóruns, possibilita ao mediador sanar eventuais dúvidas dos alunos, propicia um convívio enriquecedor entre o grupo e ainda permite a extração de dados para subsidiar a avaliação.
Alguns dispositivos de ensino em grupo são especialmente projetados para o compartilhamento de diversos recursos computacionais e o uso dos meios de comunicação próprios do hiperespaço3. Falamos, então, de aprendizagem cooperativa assistida
3 Lévy (1999) em suas pesquisas sobre tecnologias da inteligência define importantes
por computador (em inglês, computer supported cooperative learning, CSCL). Estes dispositivos permitem a discussão coletiva, a divisão de conhecimentos, as trocas de saberes entre indivíduos, o acesso a tutores on-line aptos a guiar as pessoas em sua aprendizagem e o acesso à base de dados, hiperdocumentos e simulações. Nos sistemas mais aperfeiçoados, os hipertextos encontram-se estruturados e enriquecidos em função das perguntas e navegações dos aprendizes.(LÉVY,1999, p.101)
Kalinke4 (2003) baseou-se nos conceitos das teorias Construtivista e Ergonômica5 para propor uma lista mínima de critérios para análise de sites educacionais, como abaixo é descrita e nos guiou na elaboração da página.
Aspectos como clareza, facilidade de acesso, disposição de links, distribuição e visualização do conteúdo, compatibilidade entre faixa etária e linguagem são considerados pela ergonomia. Entendemos que tais aspectos são fundamentais para que os benefícios desse veículo sejam usufruídos pelos usuários, contribuindo para o processo de aprendizagem.
A ergonomia trata do estudo de interfaces homem computador que permitam ao usuário utilizar o recurso de forma adequada e com o menor desgaste possível, tanto físico quanto intelectual. Ressalve-se que minimizar o desgaste intelectual significa direcionar a capacidade intelectual do usuário para atividades de cunho pedagógico. Dessa forma, a ergonomia preocupa-se com que ele não se desgaste com aspectos técnicos e de navegação, podendo direcionar seus esforços intelectuais para a aprendizagem. (KALINKE, 2003, p.22)
Os itens da lista mínima de critérios para análise de sites educacionais são:
1. Critérios relativos a aspectos construtivistas
(materiais e intelectuais), de práticas, de atitudes, de modos de pensamento e de valores que se desenvolvem juntamente com o crescimento do ciberespaço”.
4 A dissertação Uma proposta para análise e seleção de sites educacionais de matemática, à
luz das teorias Construtivista e Ergonômica, foi apresentada como requisito parcial à obtenção do grau de Mestre em Educação, Curso de Pós-Graduação em Educação, Setor de Educação, Universidade Federal do Paraná, orientada pelo professor Dr. Alexandre Luís Trovon de Carvalho e defendida em 2002. Esse trabalho originou o livro Internet e Educação.
• Ferramentas de Interação
Um ambiente propício ao aprendizado possibilita a interação do aluno com o conteúdo proposto, com outros alunos e ainda com o mediador.
O aluno participa ativamente de seu processo de aprendizado, ao encontrar um meio que favoreça as investigações e as trocas de experiências, podendo extrair dessas conjecturas um novo conhecimento.
Para os contatos entre alunos e entre alunos e mediador, é necessária a inclusão de ferramentas de comunicação síncronas (salas de Chat) e assíncronas6 (e-mail, fórum de discussões, mural). Estes contatos favorecem o diálogo entre o grupo para levantamento de hipóteses, sugestões e exposição de conjecturas. Permitem, também, ao mediador exercer suas funções em momentos-chave como na “observação” da evolução individual, como articulador de discussões, bem como no momento de reforçar as institucionalizações disponíveis no material didático.
• Tratamento do Erro
O site não deve se limitar a apresentar as respostas, ou ainda, classificar o desempenho alcançado pelo aluno. O erro, uma vez identificado, deve orientar a proposta de outras atividades sobre o mesmo tema, dando oportunidade do aluno adquirir o conhecimento em jogo.
• Ambiente Dinâmico
Um ambiente dinâmico pode ser entendido como um local que permita a manipulação de objetos, favorecendo a investigação por parte do aluno. O movimento, permitido nos softwares computacionais é, sem dúvida, um diferencial em relação às figuras estáticas (livro, quadro negro) que contribui para a análise de uma determinada situação, que pode levar a aquisição do saber em questão.
• Modelagens, Simulações e Inovações
O autor sugere o uso de ferramentas tecnológicas (softwares educacionais, ferramentas de autoria intuitivas) na elaboração da página, por possibilitem a experimentação, a modelagem e a simulação. Dessa forma o aluno sente-se motivado e desafiado, favorecendo o seu avanço na busca do conhecimento almejado.
A possibilidade de simulação permite que o aluno, mesmo antes de conhecer os conceitos matemáticos envolvidos, possa elaborar conjecturas e levantar hipóteses que, posteriormente, poderão ser devidamente validadas.
2. Critérios relativos a aspectos ergonômicos
• Legibilidade
A legibilidade está ligada aos aspectos de criação como clareza, simplicidade, linguagem adequada ao público-alvo, tamanho e estilo das letras, cores e disposição lógica do conteúdo e dos ícones empregados para os links. Estes aspectos, quando bem empregados, contribuem para o aprendizado, pois minimizam o cansaço frente ao computador, fazendo com que o aluno se atente mais facilmente ao conteúdo proposto.
• Documentação
Para que o site seja devidamente explorado, deve apresentar manuais para o professor, para o aluno, ajuda on-line e mapa do site, possibilitando ao leitor conhecer os objetivos, o público-alvo e os aspectos pedagógicos. Enfim, as instruções prévias para sua melhor utilização.
• Navegabilidade
permitindo que o aluno possa focar seu tempo e interesse no conteúdo proposto.
Outro aspecto fundamental que deve ser considerado na estruturação do material é a inclusão de situações que possibilitem o processo de avaliação, pois devemos analisar o aproveitamento efetivo em termos de aquisição do conhecimento conquistado pelo aluno, verificar se essa experiência contribuiu para sua formação e ainda analisar a qualidade do material proposto.
O processo de avaliação pode ser feito por meio de avaliações diagnósticas, formativas ou somativas. É vasta a discussão acadêmica sobre estas alternativas, mas vislumbramos uma tendência na caracterização de avaliações contínuas, nas quais as características de cada uma sejam mescladas com o objetivo de avaliar o crescimento individual de cada aluno, bem como do professor.
O professor se torna um aprendiz do processo, pois se aprofunda nas estratégias de pensamento do aluno, nas formas como ele age, pensa e realiza essas atividades educacionais, desta forma, o professor poderá intervir, colaborar e orientar esse estudante. (HOFFMANN7, 2001, apud LOPES, 2004, p.19)
As três modalidades de avaliação foram descritas por Lopes (2004), inspirado em Bloom et al8 (1985):
Avaliação Diagnóstica: tem como objetivo identificar alunos com padrão aceitável de conhecimentos, constatar as deficiências em termos de pré-requisitos e as particularidades dos alunos. Ao identificar os alunos com problemas de aprendizagens, o correto é propor atividades com vistas a superar tais deficiências e isso faz com que se individualize o processo. Em suma, é uma preparação inicial para a aprendizagem;
Avaliação Formativa: esta é contínua e ocorre durante o processo de instrução, incluindo todos os conteúdos importantes, fornecendo
feedback ao aluno no tocante ao que ele aprendeu e do que precisa
7 HOFFMANN, Jussara. Avaliação Mediadora: uma prática em construção da pré-escola à Universidade. 8ª ed. Porto Alegre: Mediação, 1996.
aprender, fornecendo feedback ao professor quanto à identificação das falhas dos alunos e quais os aspectos da instrução que devem ser modificados, buscando o atendimento às diferenças individuais dos alunos e, ainda, prescrevendo medidas alternativas para a recuperação de falhas de aprendizagem. Resumidamente, é uma verificação da existência de dificuldades por parte do aluno durante a aprendizagem;
Avaliação Somativa: ocorre ao final da instrução com a finalidade de verificar o que o aluno efetivamente aprendeu; inclui conteúdos mais relevantes e os objetivos mais amplos do período de instrução; visa à atribuição de notas; fornece feedback ao aluno; presta-se à comparação de resultados obtidos com diferentes alunos, métodos e materiais de ensino. Enfim, há um controle se os alunos atingiram os objetivos fixados previamente. (LOPES, 2004, p.21)
1.2.2 Diretrizes Curriculares Nacionais (DCN)
Como competências a serem desenvolvidas pelo graduando em Matemática nas Diretrizes Curriculares Nacionais para os cursos de Matemática, Bacharelado e Licenciatura (DCN), são citadas “o raciocínio lógico, a postura crítica e a capacidade de resolver problemas” (DCN, Brasil, 2001, p.1).
Entendemos que atividades que proponham trabalhos com as demonstrações podem contribuir para o desenvolvimento do raciocínio lógico-dedutivo do aluno, preparando-o melhor para entender e interagir criticamente com a sociedade em que vive.
Em linhas gerais, optamos pela inclusão, no link Tópicos Históricos, das influências que a Física Moderna sofreu, após a nova concepção do espaço, que surgiu com a apresentação das novas geometrias.
1.2.3 Publicações (livros e artigos) sobre a Geometria Hiperbólica
Como parte dos estudos preliminares, pesquisamos as publicações (livros ou artigos) em língua portuguesa que abordam a Geometria Hiperbólica, sob a ótica histórica, filosófica ou matemática. Preocupamo-nos, também, em verificar quais, eventualmente, se propunham a expor as demonstrações dos principais teoremas dessa Geometria, com os axiomas de Euclides ou de Hilbert, seu público-alvo e a preocupação didática da obra.
1. AVILA, G. Legendre e o postulado das paralelas. Revista do Professor de Matemática. n. 22. p.16-28. 1992
Geraldo Ávila nos lembra que o trabalho de um pesquisador pode conter também publicações com erros que, posteriormente, serão revistos por ele ou por outros investigadores. O artigo objetiva descrever as tentativas de Legendre em provar o V postulado e suas várias publicações feitas no sentido de corrigir as anteriores. Por fim, ele nos remete a algumas reflexões sobre o ensino de geometria.
Depois de uma introdução biográfica de Legendre, o autor introduz o postulado de Palyfair, como sendo equivalente ao V postulado de Euclides. Descreve a obra Elementos e apresenta, em linguagem atual, os cinco postulados e as proposições XVI, XVII e XXVII, devidamente demonstradas.
Em seguida, é provada a equivalência entre os postulados de Euclides e de Playfair e, então, o autor propõe o postulado de Legendre e sua demonstração. Finalmente, o erro do matemático é apresentado.
que ensina, inclusive sobre fundamentos e axiomática, justamente para que possa ter senso crítico que o auxilie a decidir sensatamente sobre o que deve ensinar e como”.
2. BARBOSA, João Lucas, M. Geometria Hiperbólica, Rio de Janeiro: IMPA, 1985. 167p.
Segundo a apresentação do livro, este destina-se a servir de texto a uma disciplina de Geometria não-euclidiana dirigida a alunos de cursos de licenciatura e bacharelado em Matemática. O autor propõe-se a apresentar uma continuação de seu livro Geometria Euclidiana Plana (Rio de Janeiro: SBM, 1985, Coleção Fundamentos da Matemática Elementar).
A obra apresenta um capítulo inicial sobre os fundamentos da Geometria Euclidiana e expõe a axiomática de Euclides. O capítulo seguinte destina-se a apresentação de algumas das proposições equivalentes ao quinto postulado. Na seqüência, é dado um enfoque histórico, no qual os trabalhos antecessores ao surgimento das outras geometrias são apresentados. As proposições de Ptolomeu, Proclus, Nasir-Edin, Wallis, Saccheri e Lambert são discutidas.
O próximo capítulo destina-se à apresentação de alguns teoremas de Legrendre, entre eles, sua tentativa de provar o quinto postulado. A descoberta da nova Geometria é apresentada no capítulo 5, em um contexto histórico, e é mostrada a influência dos trabalhos de Gauss, Bolyai e Lobachewsky. No capítulo 6, os principais teoremas da Geometria Hiperbólica são apresentados, com as devidas demonstrações. O capítulo 7 é dedicado à trigonometria hiperbólica e, finalmente, o último capítulo, trata da consistência dessa geometria, apresentando o modelo de Poincaré.
3. BARKER, S.F. Filosofia da Matemática. Rio de Janeiro: Zahar, 1969. 141p. (Curso Moderno de Filosofia).
e expõe a maneira moderna de encarar os sistemas dedutivos. Levanta alguns postulados substitutivos do V postulado, o trabalho de Saccheri, a importância de Gauss e o surgimento das geometrias não-euclidianas feita por Lobachewsky e Bolyai. Comenta sobre o sentido de consistência de um sistema. Apresenta o conceito de geometria interpretada e seu caráter empírico e a priori.
O livro apresenta uma visão geral da revolução que sofreu a Matemática, influenciada pelas concepções filosóficas.
4. BRITO, Arlete de Jesus e MORAES, Lafayette. A obra de Gerolamo Saccheri e a história da geometria não-euclidiana. Zetetiké, Campinas, CEMPEM, v. 6, n.10, jul-dez 1998.
O artigo tem uma preocupação histórica e destina-se à tradução de parte do livro9 de Gerolamo Saccheri e são tecidos comentários sobre o V postulado de Euclides. Brito e Moraes justificam esse trabalho, citando a importância histórica da obra, seu caráter inovador, pois, segundo os autores, “foi o primeiro geômetra ocidental a tentar uma demonstração por absurdo”. Acrescentam ainda a interferência da crença de Saccheri na veracidade da obra de Euclides, impedindo-o de admitir a existência de outras geometrias, que estavam se descortinando no decorrer de suas descobertas e, ainda, ressaltam a dificuldade de encontrar textos traduzidos para o português, referentes às outras geometrias10.
O prefácio da obra é apresentado, e Saccheri ressalta a importância dos Elementos, cita três de suas imperfeições, uma delas versa sobre o V postulado (livro I). O autor não questiona sua veracidade, mas refere que Euclides assumiu esse postulado como se fosse auto-evidente, e o fato de
9 Euclides ab omni naevo vindacutus: sive conatus geometricus quo stabiliuntur prima ipsa
universae Geometriae Principia (Milão, 1733)
somente o utilizar a partir do teorema 29 fez surgir nos matemáticos o desejo de torná-lo um teorema.
Quatro proposições da obra são traduzidas, bem como as demonstrações, que tratam de seu trabalho com os quadriláteros, na tentativa de dar uma nova redação ao V postulado e torná-lo, finalmente, aceito.
5. COSTA, Manuel Amoroso. As Ideias Fundamentaes da Mathematica. Rio de Janeiro: Pimenta de Mello, 1929. 246p.
O reconhecido matemático do início do séc. XX escreveu sobre as questões filosóficas da Matemática. Dedicou o capítulo XVII às geometrias não-euclidianas e não-archimedianas, mas não avaliamos seus comentários sobre esta última.
Um esboço histórico é apresentado, no qual se define o que se entende por geometrias não-euclidianas, as tentativas de demonstração do V postulado em que são lembrados os trabalhos de Ptolomeu, Proclo, os matemáticos árabes e Wallis. A obra de Saccheri evidencia que a questão foi tratada, utilizando a redução por absurdo. Ressalta o trabalho pioneiro de Gauss, embora não publicado e cita a descoberta de Lobachewsky e Bolyai.
Costa dedicou-se a apresentar a noção de paralelismo nas três geometrias: Euclidiana, Hiperbólica e a de Riemann. Em seguida, expõe as principais características das geometrias lobachewskiana e riemanniana e apresenta as relações entre as três geometrias.
Antes de explanar sobre as geometrias não-archimedianas, o autor afirma que
6. COSTA, Sueli I. Rodrigues & SANTOS, Sandra Augusta. Geometrias não-euclidianas. Ciência Hoje. v. 11, n. 65, p.14-23, Ag./90.
O artigo tem um enfoque histórico, comentando sobre a geometria na Grécia, o trabalho de Euclides, as controvérsias do V postulado, os trabalhos de Saccheri, Lambert, Bolyai, Lobachewsky e Riemann. Comenta ainda sobre os modelos desenvolvidos por Beltrami, Klein e Poincaré.
Apresenta um quadro sobre o trabalho de Hilbert, intitulado “Hilbert e a ratificação de Euclides”, em que apresenta a axiomática hilbertiana para as três geometrias: euclidiana, hiperbólica e elíptica e argumenta sobre suas consistências. Na seqüência, explora a construção dos modelos construídos em cartolina.
Finalmente, apresenta no quadro “Medindo Dessemelhanças” a possibilidade de se utilizar um modelo hiperbólico semelhante ao de Poincaré, para representar a curva de distribuição normal, considerando a noção de distância de Fisher.
7. COUTINHO, Lázaro. Convite às Geometrias não-Euclidianas. Rio de Janeiro: Interciência. 2001.
Conforme o autor, o livro destina-se a um leitor com formação pré-universitária ou interessado em geometria. Elaborado em uma linguagem acessível, no final de cada capítulo alguns exercícios são deixados ao leitor. Como introdução, temos a apresentação de um método axiomático, seguido dos axiomas e postulados de Euclides. Uma breve introdução histórica sobre o questionamento do V postulado é feita para introduzir a possibilidade dos dois tipos clássicos de geometrias não-euclidianas: a Hiperbólica e a Elíptica.
os modelos de Felix Klein e Poincaré. Os principais teoremas são apresentados e devidamente demonstrados nos capítulos III (Pontos e Triângulos Impróprios), IV (Quadriláteros e Triângulos), V (Ponto Ultra-Ideal e Conceito de Área) e VI (Curvas).
Os demais capítulos tratam da exposição da Geometria Elíptica, que não estaremos observando neste trabalho.
8. EVES, Howard. História da Geometria. Tradução de Hygino H. Domingues. 8 ed. São Paulo: Atual, 1992. 77 p. v.3. (Tópicos da História da Matemática para uso em sala de aula).
Em razão da preocupação de se inserir a história da Matemática no ensino dessa disciplina, esta série, elaborada em uma linguagem simples, tem a pretensão de contribuir com uma nova proposta, sendo apresentadas passagens importantes da história da Matemática elementar. Segundo o tradutor, a proposta tem a preocupação de criar um texto no qual os pré-requisitos do leitor não são considerados; contemplar temas de valor matemático significativo a todos os níveis escolares; fornecer material para uso imediato na sala de aula; e, finalmente, ser um texto motivador para que os professores e alunos possam buscar outros textos de caráter histórico. Toda a série consta de duas partes: uma visão geral, “com o objetivo de dar ao leitor um quadro tão amplo quanto possível do desenvolvimento histórico da área focalizada” e uma visão mais específica, que visa a “tornar facilmente acessíveis fatos pertinentes relativos a importantes teoremas, conceitos e avanços em Matemática”.
Após a apresentação do V postulado, são citados os principais matemáticos que tentaram prová-lo como teorema e é dada ênfase no trabalho de Saccheri. A seguir, são citados os descobridores da Geometria Hiperbólica e os trabalhos de Riemann.
O texto ressalta a importante contribuição do desenvolvimento de outras geometrias para a revisão dos fundamentos da Matemática.
9. KASNER, E. e NENNAN, J. Matemática e imaginação. Tradução de Jorge Fortes. Rio de Janeiro: Zaha, 1968. 347p.
É um livro destinado a leitores comuns e pode ser lido por alunos do ensino médio. No capítulo Geometrias Diversas – Plana e Fantasia, os autores apresentam em linguagem acessível a quarta dimensão no sentido matemático e físico, introduzindo o conceito de “agregado” e discutindo sobre nossas limitações sensoriais. Em seguida, expõe a idéia principal das geometrias não-euclidianas: o questionamento do quinto postulado e a possibilidade de substituí-lo. Em uma visão histórica, apresentam os trabalhos de Bolyai e Lobachewsky que consideraram a existência no plano de duas linhas paralelas, por um ponto, a uma terceira. Da mesma forma, apresentam o trabalho de Riemann que considerou que, por um ponto do plano, não se pode traçar nenhuma paralela a uma reta dada. Citam alguns teoremas euclidianos válidos, e outros não válidos nessas geometrias. Na seqüência, introduzem algumas superfícies (da pseudo-esfera e esférica) e apresentam de forma intuitiva o conceito de curvatura.
10. MARTINS, Roberto de Andrade. A influência das Geometrias Não-Euclidianas no pensamento físico do século XIX. Revista da Sociedade Brasileira de História da Ciência. Jan.-Jun., n.13, p. 67–79, 1995.
XX”. O artigo inicia pelo conceito de espaço-tempo e são apresentadas algumas referências históricas sobre a consideração do tempo como a quarta dimensão, a partir do séc. XVIII. Na seqüência, são apresentadas uma abordagem clássica e uma abordagem diferencial sobre as geometrias não-euclidianas. O texto é finalizado com a seguinte observação: “Foi apenas com o desenvolvimento da teoria da relatividade que surgiu, como uma proposta física propriamente dita, a utilização da geometria não-euclidiana na descrição dos fenômenos naturais”.
11. OLIVA, W.M. A independência do axioma das paralelas e as Geometrias não-euclidianas. Revista do Professor de Matemática, São Paulo, n.2, p.28 – 31, 1º sem.1983.
Conforme nota da revista, o trabalho foi o texto de uma conferência proferida em Presidente Prudente (SP), pelo então reitor da USP (Universidade de São Paulo), por ocasião da aula inaugural do curso de Matemática, em 1981.
O texto expõe brevemente a abrangência da Geometria: a necessidade prática dos povos antigos, a axiomatização grega, geometria analítica, geometria diferencial, geometria projetiva e a topologia diferencial.
Em seguida, apresenta o V postulado, cita o trabalho de Saccheri e as descobertas de Gauss da possibilidade de outras geometrias. Apresenta as primeiras publicações de Lobachewsky e Bolyai e ainda os trabalhos de Riemann. Finalmente, expõe o modelo do semiplano de Poincaré para a Geometria Hiperbólica.
É um texto breve que, provavelmente, tenha despertado interesse nos ouvintes por descortinar possibilidades que os alunos, recém-chegados à universidade, talvez não imaginassem.
12. SOUZA, J.C.M. O escândalo da geometria. RJ: Gráfica Ed. Aurora. 1948.
euclidiano, descrevendo os cinco postulados, seguidos das tentativas de demonstrações do V postulado. Na seqüência, descreve os trabalhos de Saccheri, Lambert e Gauss. Finalmente, apresenta em linhas gerais a obra de Lobachewsky e Bolyai. Os modelos de Beltrami e de Poincaré (no semiplano) são descritos seguidos de uma discussão sobre o espaço e a geometria e ainda sobre a indemonstrabilidade do V postulado. O trabalho de Riemann, o universo e a geometria, a curvatura das superfícies, os espaços homogêneos são outros argumentos tratados no texto.
O levantamento da literatura disponível reforça o número reduzido de publicações voltadas ao estudo axiomático dessa geometria. Em nossa pesquisa, tal levantamento contribuiu para listar as obras de Barbosa (1985) e Coutinho (2001), em complemento a outras obras não editadas em língua portuguesa, como referencial da proposta. O trabalho de Barker (1969) enriqueceu a apresentação histórico-filosófica do presente estudo.
1.2.4 Dissertações sobre a Geometria Hiperbólica
Uma análise similar à feita na literatura foi elaborada para as dissertações.
1. ARCARI, Inedio. Um texto de Geometria Hiperbólica. 2008. Dissertação (Mestrado em Matemática) – Universidade Estadual de Campinas, Campinas.
Cabri-Géomètre, GeoGebra e o NonEuclid. Ele utiliza este último em algumas das construções apresentadas.
2. BONETE, Izabel Passos. As geometrias não-euclidianas em cursos de licenciatura: algumas experiências. 2000. Dissertação (Mestrado em Educação) – Universidade Estadual de Campinas, Campinas.
A dissertação de Bonete é voltada a uma reflexão e discussão sobre o ensino das geometrias não-euclidianas nos cursos de licenciatura, fato que poderia melhor preparar os futuros professores não só para o ensino da Geometria Euclidiana como também para ampliar a possibilidade do estudo das outras geometrias nos Ensinos Fundamental e Médio.
Uma pesquisa bibliográfica e empírica foi elaborada com trabalho de campo. A geometria não-euclidiana foi apresentada por meio de três experiências em diferentes salas de aula, em duas turmas do primeiro ano do Curso de Ciências-Licenciatura Plena e uma turma do segundo ano do Curso de Ciências Ciências- Licenciatura-Curta. Optou-se pelo uso de material concreto nas atividades propostas, como esfera de isopor (plano esférico), chuveiro (plano hiperbólico), fitas adesivas para a representação de retas que se mostraram úteis nos processos de investigação.
O capítulo I apresenta um levantamento da situação do ensino de geometria no Brasil, o que levou a autora a optar pelo construtivismo em suas atividades. O capítulo II mostra o estudo bibliográfico a respeito das mudanças qualitativas ocorridas na geometria. O último capítulo relata o contexto filosófico que permitiu o surgimento de outras geometrias, bem como a experiência e os resultados da pesquisa.
Nas considerações finais a autora afirma que
Na seqüência, a autora complementa que o conhecimento de outras geometrias
Permitirá a melhoria da qualidade do ensino da Geometria Euclidiana e possibilitará também a inclusão dessas geometrias nesses níveis de ensino [fundamental e médio], uma vez que, com esse conhecimento não terão a Geometria Euclidiana como a única geometria possível e verdadeira, mas como, uma das possíveis e verdadeiras. (BONETE, 2000, p.229)
3. BRITO, Arlete de Jesus. Geometrias não-euclidianas: um estudo histórico-pedagógico. 1995. 187f. Dissertação (Mestrado em Educação) - Universidade Estadual de Campinas, Campinas.
Brito apresenta um estudo histórico-pedagógico voltado à reconstituição histórica do surgimento das geometrias não-euclidianas. Simulando o andamento de uma sala de aula, a professora e quatro alunos, de um suposto curso de licenciatura em Matemática, inicialmente, vão apresentando a Geometria Euclidiana, as tentativas de demonstração do V postulado e a influência de Kant para o surgimento das outras geometrias. Preocupam-se em apresentar os contextos filosóficos e culturais desde os gregos do séc. V a. C., até Kant no séc. XIX. A obra apresenta alguns dos principais teoremas da Geometria Hiperbólica com as devidas demonstrações, mas seu foco é a compreensão do contexto que possibilitou uma nova concepção da geometria.
Sua proposta, de um estudo histórico-pedagógico, pode ser explicada no texto de Miguel:
diversas atividades teóricas especificas e práticas produtivas setorizadas.(MIGUEL11, 1993, apud BRITO, 1995, p. 173)
4. CABARITI, Eliane. Geometria Hiperbólica: uma proposta didática em ambiente informatizado. 2004. 180f. Dissertação (Mestrado em Educação Matemática) – Pontifícia Universidade Católica, São Paulo.
Este trabalho visa a contribuir com o processo de ensino e aprendizagem da Geometria Hiperbólica, propondo seqüências didáticas, com o uso do software Cabri-géomètre, para um curso de formação de professores de Matemática.
Segundo a apresentação de Cabariti,
Nossas análises baseiam-se em dois aspectos: a dinâmica das trocas entre os domínios geométricos – Geometria Euclidiana e Hiperbólica – além de interações entre os campos espaço-gráfico e teórico, e o papel do Cabri como ferramenta de construção, exploração e verificação, especialmente relacionadas aos ”modos de arrastar”. (CABARITI, 2004, p. 16)
É feita uma breve introdução histórica da Geometria Euclidiana, das geometrias não-euclidianas e do modelo do disco de Poincaré, este último necessário para a utilização do menu hiperbólico do software.
Em seguida, a autora apoiada nas pesquisas em Educação Matemática, apresenta a distinção entre desenho e figura e versa sobre a importância que o desenho associado ao objeto geométrico exerce na formação da imagem mental. Os aspectos didáticos da utilização de ambientes de geometria dinâmica são abordados, bem como o papel dos diferentes modos de “arrastar” no processo de raciocínio do aluno.
A metodologia utilizada é qualitativa, e na elaboração das seqüências foi empregado um tipo de método clínico (model eliciting ou thought revealing).
A proposta previu uma apresentação histórica inicial aos professores que conteve: o livro I dos Elementos, os enunciados equivalentes ao V postulado, a Geometria Absoluta, a interpretação dos objetos hiperbólicos no disco de Poincaré.
Resumindo as demais atividades propostas temos: atividade de familiarização com o menu hiperbólico; investigações utilizando o software (soma das medidas dos ângulos internos de um triângulo, congruência dos ângulos da base de um triângulo isósceles, medida dos ângulos internos de um triângulo eqüilátero, teorema de Pitágoras, inscrição de triângulos na circunferência, propriedade das medianas de um triângulo); Quadrilátero de Saccheri; Quadrilátero de Lambert; construção dos objetos hiperbólicos (retas, ângulos) no modelo de disco de Poincaré.
Como resultados da pesquisa, a autora ressalta a importância de um ambiente dinâmico que favoreceu a compreensão dos conceitos e relações. Cita, também, a insegurança dos pesquisados na construção de objetos hiperbólicos, por não serem intuitivos e a dúvida sobre os teoremas que compõem a Geometria Absoluta.
5. LINS, Geraldo Henrique Botelho. Introdução à Geometria Hiperbólica: Semelhanças e Diferenças. 2002. 200 f. Dissertação (Mestrado em Matemática Aplicada) - Universidade Federal do Rio de Janeiro, Rio de Janeiro.
O capítulo I destina-se a uma apresentação histórica dos Elementos, como proposta de um método axiomático, seguido por mais de dois mil anos. Cita suas falhas e a proposta de Hilbert para saná-las.
No capítulo II, são apresentadas as noções comuns, postulados de Euclides, Axioma de Dedekind e as tentativas de prova direta do V postulado (Proclus, Clavius, Clairaut, Simson, Playfair). O estudo da Geometria Hiperbólica é feito a partir dos Fundamentos de Geometria de Hilbert, cujos postulados (incidência, ordem, congruência e continuidade) são apresentados.
O capítulo III é destinado à apresentação da Geometria Hiperbólica. Inicialmente, são mostrados os principais matemáticos envolvidos em sua descoberta (Gauss, Bolyai, Lobachewsky), e a caracterização do plano hiperbólico. Os principais teoremas dessa Geometria são apresentados e devidamente demonstrados neste e no capítulo seguinte.
Na seqüência, os capítulos são destinados às isometrias do plano hiperbólico, à sua métrica, à aritmética dos pontos ideais e, finalmente, à trigonometria hiperbólica.
No capítulo X, o autor propõe uma comparação entre as Geometrias Hiperbólica X Euclidiana, tendo como objetivo mostrar que muitos dos teoremas de Euclides são também válidos na Geometria Hiperbólica.
No último capítulo, destinado à Construções com Régua e Compasso, Lins preocupa-se em fornecer uma base teórica para as construções apresentadas, segundo o livro The Non-Euclidean Hiperbólica Plane, de Paul Kelly.
6. SOUZA, Márcia Cristina Garrido. O 5º Postulado de Euclides: a Fagulha que Desencadeou uma Revolução no Pensamento Geométrico. 1998. 225p. Dissertação (Mestrado em Matemática) - Universidade Federal do Rio de Janeiro, Rio de Janeiro.
Segundo a autora, o trabalho analisa o 5º Postulado de Euclides sob três pontos de vista: o matemático, o histórico e o qualitativo. O conhecimento dos professores sob o tema é analisado, bem como a influência dos livros didáticos no ensino de Geometria e, ainda, examina a importância das geometrias não-euclidianas para a atualidade.
Em uma pesquisa qualitativa, são entrevistados 35 alunos de graduação e 30 professores de Matemática para investigar questionamentos a respeito do conhecimento dos pesquisados sobre o tema, o ensino das demonstrações nos cursos de graduação, as concepções dos professores de geometria a respeito da problemática gerada pelo Axioma das Paralelas e ainda a abordagem do tema nos livros didáticos.
Hiperbólica e a Elíptica. A Geometria Diferencial é utilizada para demonstrar que tais geometrias são completas.
A partir dos dados levantados na pesquisa, o capítulo seguinte apresenta as concepções dos entrevistados a respeito do tema bem como a pertinência desse conteúdo em todos os níveis de ensino. Mostra ainda a descrição das atividades propostas e, finalmente, uma análise da Geometria em seis livros didáticos, de épocas diferentes (1933-1997), que foram influenciados pelas correntes pedagógicas em vigor na época. A conclusão final é listada no capítulo IV, após a apresentação do estudo de caso.
Como resultado da pesquisa, a autora afirma que
Os alunos de graduação em Matemática, geralmente, não conseguem ver relações entre as disciplinas que estudam e – no caso dos alunos de licenciatura - entre estas e o que irão lecionar. (SOUZA, 1998, p.172)
Pelos resultados das atividades que envolviam argumentação e demonstrações a pesquisadora concluiu que a origem do despreparo dos entrevistados deve-se
a uma atitude não questionadora, infelizmente comum aos nossos alunos. Esse é um fator que apóia-se tanto na postura passiva do graduando quanto na afirmação da autoridade do saber do professor de 3º grau. Por exemplo, se a demonstração – um dos “choques” universitários para alunos da área de exatas – surgisse naturalmente, desde cedo, como conseqüência de uma dúvida, de uma conjectura não confirmada, isto é, da real necessidade de fazê-la, as argumentações apareceriam e, provavelmente, demonstrar tornar-se-ia um hábito. (SOUZA, 1998, p.173)
7. TERDIMAN, Esther Wajskop. A Geometria Hiperbólica e sua consistência. 1989. 203 p. Dissertação (Mestrado em Matemática). Pontifícia Universidade Católica, São Paulo.
Posteriormente, apresenta os principais teoremas da Geometria Hiperbólica, devidamente demonstrados. Expõe o modelo de Beltrami-Klein e os dois modelos de Poincaré apresentando a consistência dessa Geometria.
Da leitura das dissertações, extraímos alguns aspectos relevantes que contribuíram diretamente na elaboração da presente pesquisa: Brito (1995), reforça a importância histórica do surgimento de outras geometrias na formação do futuro educador. Souza (1998) mostra como resultado de sua pesquisa a importância da apresentação das demonstrações nos primeiros níveis escolares diminuindo, assim, o “choque” sofrido no ingresso da universidade. Entendemos que os resultados de pesquisas didáticas voltadas a uma aprendizagem axiomática podem contribuir para que os educadores compreendam e minimizem esse “choque”.
Bonete (2000) relata que sua experiência emergiu nos professores uma mudança das concepções de espaço físico e verdade Matemática, o que ratificou nossa inserção nos Tópicos Históricos dos subtítulos: Geometria e Espaço Físico e a Influência do surgimento das geometrias não-euclidianas na Física Moderna.
Cabariti (2004) expõe em seus resultados a influência positiva de um ambiente dinâmico na apreensão dos conceitos apresentados. As dúvidas demonstradas pelos pesquisados sobre quais teoremas compõem a Geometria Absoluta, reforçam a importância de explicitá-los no início de nossas atividades. Em sua proposta para o estudo da Geometria Hiperbólica, Arcadi (2008) ressalta a contribuição do uso de softwares dinâmicos. Das publicações na área da educação, comentadas nestes parágrafos em ordem cronológica, podemos observar uma crescente importância dada ao fato de se incluir no programa dos educadores de Matemática uma visão não só histórica como geométrica das outras geometrias.