Operações Unitárias na Engenharia Química - ( Marco Antonio Farah)

(1)

A Destilação

Capítulo

₃

Ao final deste Capítulo o estudante será capaz de:

• calcular gráfica e analiticamente as vazões e composições de um processo de destilação integral de misturas binárias, conhecendo-se dados térmicos, de pressão e de equilíbrio;

• definir as condições operacionais necessárias para se obter a vaporização desejada de uma mistura de composição

conhecida;

• estabelecer as equações para a destilação integral de uma mistura multicomponente;

• calcular o estado térmico de misturas binárias e multicomponentes.

• estabelecer as equações do processo de retificação com vapor;

• calcular a quantidade de vapor necessária para produzir determinada retificação;

• entender os princípios da destilação diferencial;

• calcular as quantidades vaporizadas de uma carga e as concentrações dos constituintes das fases em função da temperatura no processo de destilação diferencia; descrever e entender o funcionamento de uma coluna de fracionamento e as influencias das variáveis operacionais;

• calcular número de estágios, localização da carga e condições operacionais - razão de refluxo, vazões e quantidade

de calor cedida e retirada de uma torre de fracionamento operando em misturas binárias e multicompo- nentes;

• utilizar os métodos de McCabe-Thiele e de Ponchon-Savarit para projeto e cálculo de condições de operação de colunas de fracionamento;

• identificar componentes chave de uma separação multicomponente;

• calcular o número de estágios (mínima e total) e a razão de refluxo (mínima e operacional) de destilação fracionada

multicomponente;

Pré-Requisitos Matemáticos:

• Nenhum.

Pré-Requisitos de Engenharia e Científicos:

• Balanço material e Energético;

• Equilíbrio de Fases e Termodinâmico;

• Cálculos de Equilíbrio de Fases.

3.1 Princípio da Destilação Integral

Uma substância pura entra em ebulição a uma temperatura constante, que é função da pressão do sistema no qual ela está contida. As misturas, ao contrário, para um par de valores de pressão e temperatura apresentarão vaporização em uma faixa de temperaturas, que vai do Ponto de Bolha ao Ponto de Orvalho.

(2)

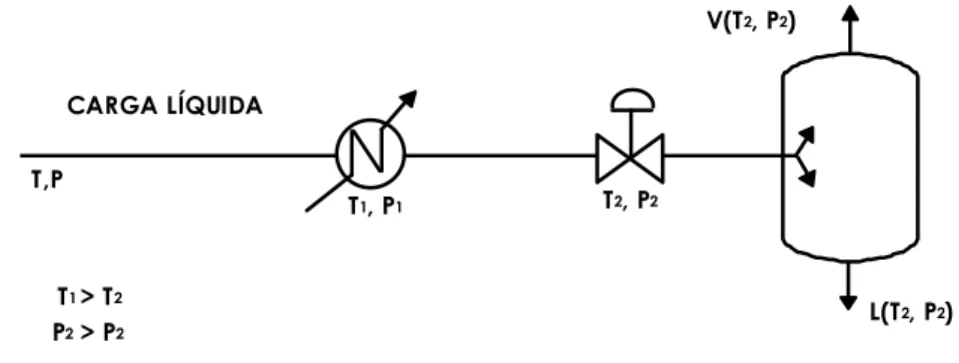
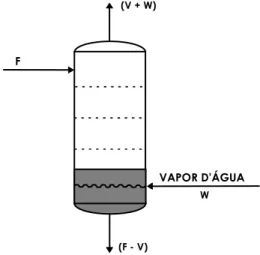
Operações Unitárias na Engenharia Química - ( 3-2 Figura 3.1 - Destilação integral

A separação obtida através deste método não é boa, uma vez que só se dispõe de um estágio de equilíbrio, o que não é suficiente para a adequada separação dos componentes da carga. Isto se deve a interação intermolecular dos componentes da mistura ou do arraste mecânico de uma fase pela outra. Assim, na faixa de temperaturas em que a mistura entra em vaporização estarão sempre presentes na fase vapor todos os constituintes da carga. Isto implica em que estarão presentes na fase L componentes leves que interagiram ou que foram arrastados pelos constituintes pesados da mistura, que pelas suas características de volatilidade já deveriam ter se vaporizado. Também na fase vapor estarão presentes, indevidamente, alguns componentes pesados arrastados pelos mais leves.

Caso houvessem outros estágios de equilíbrio, obter-se-ia melhor separação das fases, pois se possibilitaria uma separação gradual em cada estágio.

Se procedermos a separação por destilação integral de uma dada mistura binária em vários níveis de temperatura, mantendo-se a pressão constante, obteríamos uma curva do seguinte tipo:

% VAPORIZADA DE a

Ta, Tb - temperatura de ebulição dos componentes A e B puros à pressão do sistema.

Figura 3.2 - Curva de destilação integral de uma mistura binária

(3)

Operações Unitárias na Engenharia Química - ( 3-3

3.2 A Destilação Integral de Misturas Binárias

Na destilação integral o vapor e o líquido gerados no processo, estão em equilíbrio termodinâmico, de forma que as pressões e temperaturas das duas fases são iguais.

Esta igualdade de temperaturas e pressões das fases, é conseqüência da condição de equilíbrio termodinâmico: no equilíbrio o potencial termodinâmico dos constituintes de cada fase são iguais nas duas fases.

As condições em que ocorrem o equilíbrio são determinadas a partir das equações de balanço material e energético, relações de equilíbrio e estequiométricas aplicadas para este processo.

Para misturas binárias, estas equações são as seguintes:

− balanço material total :

F = L + V (3.1)

− balanço material parcial (a):

=

+

(3.2)

− relações estequiométricas:

xa + xb = 1,0 (3.3)

ya + yb = 1,0 (3.4)

− relações de equilíbrio:

ya = Ka xa (3.5)

yb = Kb xb (3.6)

3.3 Cálculos em Destilação Integral

As variáveis intensivas deste sistema são: P, T, ya, yb, xa, xb. Pela regra das fases, o número de variáveis intensivas independentes é:

− número de fases = 2

− componentes = 2

V = 2 + 2 - 2 = 2

Assim, fixando-se duas destas variáveis o sistema estará definido. Por exemplo, se fixarmos a pressão e a temperatura do processo, pode-se determinar as constantes de equilíbrio Ka e Kb, restando a determinar as composições xa, xb, ya, yb de cada constituinte em cada fase e as quantidades L e X destas.

(4)

a) Soluções ideais:

Ka = T P Pv_a Kb = T b P Pv xa = b a b Pv Pv Pv P − − (3.7)

ya = Pv_Paxa (3.8)

Dividindo a equação 3.7 por P:

xa =

(

)

(

PvaP

) (

Pv P

)

P Pv 1 b b − − _(3.9)

Calculado xa, tira-se ya pela equação 3.8

b) para um sistema real

xa = b a b K K K 1 − − _(3.10) ya = b a b a a K K K K K − − _(3.11)

As equações de balanço material permitem calcular V e L:

a a a a x y x z F V − − = (3.12)

a qual se torna, substituindo os valores de xa e ya, dados pelas equações 3.10 e 3.11:

1 K z K 1 z F V a b b a − − − = (3.13)

No caso de misturas reais, Ka e Kb são determinados sobre o Ábaco de De Priester e

levados nas equações 3.10, 3.11 e 3.13 que permitem o cálculo de xa, ya e da fração vaporizada       F V .

Para soluções ideais, os valores de Pva e Pvb podem ser calculados por equações ou por meio de gráficos.

3.3.1 Previsão do Estado de Equilíbrio

É possível prever o estado de equilíbrio de um sistema a partir da equação 2.13, levando-se em consideração que:

F

(5)

Operações Unitárias na Engenharia Química - ( 3-5 F

V

= 1

→

vapor saturado

0 < F V

< 1

→

duas fases

F V

= 0

→

líquido saturado

F

V _{< 0}

_→

_{líquido subresfriado}

Assim, teremos as seguintes situações

a) Ponto de bolha: F V

= 0

b a

k 1

z

− - K 1

z

a b

− = 0 ∴ Ka za + Kb zb = 1,0 (3.14)

b) Ponto de orvalho: F

V _{= 1,0}

1 =

b a

K 1

z

− - K 1

z

a b

− ∴ a a

K z

+

b b

K z

= 1,0 (3.15)

c) Líquido subresfriado: F V

< 0

∴ Ka za + Kb zb < 1,0 (3.16)

d) vapor superaquecido: F V

> 1,0

∴

a a

K z

+

b b

K z

< 1,0 _(3.17)

e) Duas fases:

a a

K z

+

b b

K z

> 1,0 (3.18)

(6)

3.4 Casos de Cálculo em Destilação Integral

3.4.1 Temperatura e Pressão Conhecidas

3.4.1.1 Cálculo Gráfico

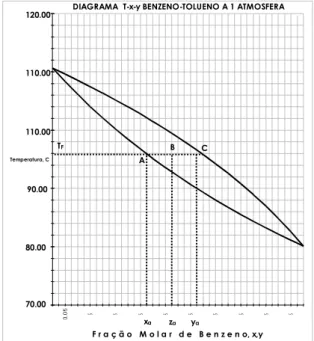
Tal como foi visto no equilíbrio de fases, dispondo-se do diagrama equilíbrio T-x-y, pode-se determinar sobre este diagrama - Figura 3.3 - o ponto B, que reprepode-senta a carga do sistema nas condições do "flash".

! " #

$% &'

("(# )*+)*,( , )*, ,- ) ./..

./..

0./..

1./..

2./..

" ! #

Figura 3.3 - Resolução gráfica de um "flash"

Considerando-se que as fases L e V estejam em equilíbrio e a mesma temperatura, pode-se marcar os pontos A e C, que estão sobre a reta horizontal (isoterma) que passa por B. Isto porque L e V saem em equilíbrio, estando assim na condição de líquido saturado (Curva de Pontos de Bolha) e vapor saturado (Curva de Pontos de Orvalho). Desta forma pode-se determinar as composições xa, xb e ya, yb, sobre este mesmo diagrama. Conhecidos xa e ya, calcula-se pela regra do braço de alavanca os valores de V e L:

f =

a a

x y

x z F V

− −

= _(3.20)

1 - f =

a a

x y

z y F L

− −

= _(3.21)

3.4.1.2 Cálculo Analítico

Para um sistema binário, conhecidas a temperatura e a pressão das fases em equilíbrio, pode-se calcular a constante de equilíbrio dos constituintes do sistema. Assim, podemos calcular as composições de cada fase bem como suas quantidades através das equações 3.10, 3.11 e 3.13:

xa =

b a

b

K K

K 1

−

(7)

Operações Unitárias na Engenharia Química - ( 3-7 ya =

b a

b a a

K K

K K K

−

− (3.11)

1 K

z K 1

z F V

a b b a

− − −

= (3.13)

3.4.2 Pressão e Quantidades das Fases Conhecidas

3.4.2.1 Cálculo Gráfico

Neste caso, F V

e F L

conhecidos, dispondo-se do diagrama y-x de equilíbrio do sistema

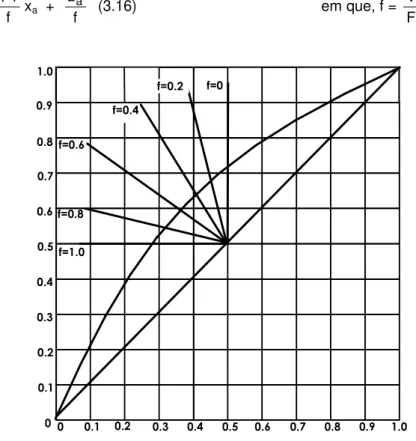
(Figura 3.4), pode-se rearranjar a equação 3.16 para:

f f 1

y_a=− − xa + f z_a

(3.16) em que, f =

F V

/.

./0

./1

./2

./3

./4

./5 ./6

./

. . ./ ./ ./5 ./6 ./4 ./3 ./2 ./1 ./0 /. 78.

78./ 78./6

78./3

78./1

78 /.

Figura 3.4 - Resolução gráfica de um "flash", dada porcentagem vaporizada (f)

A equação 3.16 representa uma reta de coeficiente angular -f

f

1− _{e que passa pelo ponto}

xa = ya = za. Se então, marcarmos sobre o diagrama y-x, este ponto xa = ya = za e por ele traçarmos

uma reta de coeficiente angular -f

f

1− _{, estaremos localizando esta reta sobre este diagrama.}

A interseção desta reta com a curva de equilíbrio representa a condição de equilíbrio do sistema, fornecendo os valores ya e xa das fases resultantes deste equilíbrio. Localizando então este ponto ya, xa sobre o diagrama T-x-y, teremos a temperatura necessária para se obter a vaporização

F V

(8)

3.4.2.2 Cálculo Analítico

Se a temperatura é desconhecida, também é desconhecida a constante de equilíbrio de cada componente. Caso não se disponha de relações matemáticas entre a temperatura, composição das fases e constantes de equilíbrio, o cálculo analítico será iterativo. O método de cálculo utilizado consiste em se arbitrar uma temperatura e verificar se para a temperatura arbitrada, as constantes de equilíbrio determinadas conduzem a relação V/F fixada para o problema. Caso isto não ocorra, prosseguir no processo de cálculo até que esta situação seja verificada. Aí então, calcular as composições de cada fase pelas equações 3.10 e 3.11. Caso sejam conhecidas a temperatura e a composição das fases, a resolução é análoga, deslocando-se a temperatura pela pressão e vice-versa.

3.4.3 Mistura de Produtos Líquido e Vapor Saturados

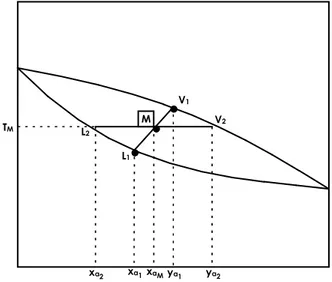
Tal como definido pelas equações do equilíbrio de fases em estágios ideais, a mistura destas duas fases estará situada sobre a reta que liga os pontos L1 e V1 (Figura 3.5), cuja composição xaM é dada por :

1 1 a a

a a

1 1

ML MV x x

x y V L

1 M

M 1 ₌

− −

= (3.22)

Determinado o ponto xam e como as duas fases L2 e V2 saem em equilíbrio, elas estão a mesma temperatura TM e saturadas.

Figura 3.5 - Mistura de cargas

Desta forma traça-se sobre o diagrama T-x-y, uma reta horizontal passando por M, que dará o valor de TM e as composições y_a2 e x_a2 das fases L2 e V2.

" #

"

••••

(9)

3.5 Destilação Integral Multicomponente

Quando se tem mais de dois componentes na mistura, as equações de balanço material, energético e de equilíbrio podem ser escritas para cada componente e a solução do problema pode se tornar complexa, pois não se pode utilizar o diagrama T-x -y neste caso. A separação de misturas multicomponentes de hidrocarbonetos é o caso industrial de maior importância. As constantes de equilíbrio, apesar de dependerem da composição, podem ser calculadas com boa aproximação pelo ábaco de De Priester, por serem os hidrocarbonetos substâncias quimicamente similares:

yi = Ki xi (3.23)

onde Ki é a constante de equilíbrio do constituinte i, que é função da temperatura e pressão, mas serão consideradas independentes da composição da mistura.

3.5.1 Caso em que a Temperatura e Pressão são Conhecidas

As equações de balanço material e energético, relações de equilíbrio e estequiométricas são as seguintes:

Fzi = Lxi + Vyi i = 1, n (3.24)

F = L + V (3.25)

FHF = LH_L + VH_v (3.26)

∑

=

n

1 i

i

z = 1,0 (3.27)

∑

=

n

1 i

i

x = 1,0 (3.28)

∑

=

n

1 i

i

y = 1,0 (3.29)

yi = Ki xi i = 1, n (3.30)

Ki = fi (T,P) i = 1,n (3.31)

F

H = f1 (T,P, zF) (3.32)

L

h = f2 (T,P, xi) (3.33)

v

H = f (T,P, yi) (3.34)

Existem portanto (3n + 7) equações independentes; (4n + 11) variáveis, de forma, que devem ser fixadas (n + 4) variáveis para se definir o sistema.

Freqüentemente a solução é simplificada, podendo se obter a seguinte solução:

yi =

(

)

1 F V 0 , 1 K

z K

i i i

+

− (3.35)

xi =

(

)

1 F V 0 , 1 K

z

i i

+

− (3.36)

(10)

Para se calcular a porcentagem vaporizada, pode-se aplicar uma das equações, 3.35 ou 3.36, para todos os componentes obtendo-se:

∑yi = ∑

(

)

1 F V 0 , 1 K z K i i i + − (3.37) ou:

∑xi =∑

(

)

1 F V 0 , 1 K z i i + − (3.38)

Ambas as equações são resolvíveis para V/F.

3.5.2 Determinação do Ponto de Bolha e Orvalho

Quando se deseja conhecer a Ponto de Bolha e o Ponto de Orvalho de uma mistura multicomponente, procede-se de modo similar ao de misturas binárias.

Assim, as equações 3.14 e 3.15 adaptadas para multicomponentes, se escrevem como:

Ponto de Bolha: ∑yi = ∑ ki xi (3.39)

Ponto de Orvalho: ∑xi = ∑ (yi / ki) (3.40)

As temperaturas de bolha e de orvalho são obtidas iterativamente, assumindo-se valores para as mesmas, determinando-se ki e verificando se as equações 3.39 e 3.40 são satisfeitas.

As composições de cada constituinte no ponto de bolha e de orvalho serão dadas respectivamente por:

Ponto de Bolha: yi = (ki xi )/ (∑ki xi ) (3.41)

Ponto de Orvalho: xi = (yi / ki )/ (∑ yi / ki ) (3.42)

3.5.3 Estudo do Caso em que se Fixa a Pressão e a Porcentagem Vaporizada

Para se obter a temperatura e a composição de uma mistura, cuja fração vaporizada seja dada por f =

F

V _{, usamos a expressão do flash para cada componente:}

yi =

f f 1 f

z_i ₋ − _x

i (3.43)

(yi / xi) = ki =       f 1       − +f 1 x z

i

i _(3.44)

Aplicando-se estas equações a todos os componentes, tem-se:

∑

= n 1 i i

x = 1,0 =

(

k 1

)

1,0 f z i i n 1

i − +

∑

=

(3.45)

(11)

3.6 Princípio da Retificação com Vapor

Determinadas misturas apresentam características desfavoráveis para serem vapori-zadas por aquecimento, pois se decomporiam nas temperaturas correspondentes ao seu ponto de ebulição.

Estas misturas podem ser separadas através do processo de retificação com vapor o qual permite obter a vaporização da mistura a um nível menor de temperatura (Figura 3.7). Como agente de retificação usa-se, em geral, vapor d'água, o qual também pode agir como fonte de aquecimento.

A vaporização da substância se dá pela redução da sua pressão na fase vapor obtida pela injeção de vapor de uma outra substância inerte na fase líquida, mantendo-se a pressão total do sistema.

Normalmente neste processo o vapor é injetado no produto líquido através de um tubo perfurado, ficando em contato direto com este líquido. O vapor utilizado para a retificação sendo inerte em relação ao líquido, nele não se solubiliza. Desta forma, o equilíbrio líquido-vapor da substância, mesmo que se

9 :

:

, ;<

(

Figura 3.7 - Retificação com vapor

mantenha a pressão total, será alterado, pois como se terá mais de um produto na fase vapor, o equilíbrio se passa a pressão parcial da substância e não mais a pressão total.

3.7 Equilíbrio de Fases na Retificação com Vapor

Cada um dos constituintes da fase vapor, contribuirá com sua pressão parcial para o

equilíbrio líquido-vapor, permanecendo a fase líquida com apenas um constituinte. A pressão total sendo mantida, a substância (a) entrará neste caso em ebulição, quando sua pressão de vapor na mistura for maior do que sua pressão parcial - pressão que o constituinte exerceria se tivesse

sozinho na mistura. Desta forma o líquido estará em equilíbrio com o seu vapor à sua pressão parcial. Como:

pa = PT . ya (3.46)

pa é menor do que PT uma vez que ya < 1,0. Como na fase líquida só existe o constituinte i (xa = 1), pois o vapor (g) usado é inerte no líquido:

pa = Pva . xa = Pv_a (3.47)

Então: Pv_a = PT . ya (3.48)

Supondo que a temperatura do líquido não se altere (Pva) é o mesmo, poderá então haver

a vaporização em um nível menor de temperatura, pois a pressão do equilíbrio(pa = PT ya) é menor do

que a pressão anterior (PT ), pois (ya) é menor que 1.

(12)

3.8 Cálculo do Consumo de Vapor de Retificação

Escrevendo-se as equações estequiométricas para a fase vapor deste processo:

g a

a a

n n

n y

+

=

g a

g g

n n

n y

+

= _(3.49)

g g

a a g a g a

PM / m

PM / m n

n y

y ₌ ₌

(3.50)

Pela lei de Dalton:

g a g a

p p y y

= _(3.51)

Então:

g g

a a g a

PM p

PM p m m

= _(3.52)

onde:

ma, mv − massa da substância e do vapor de retificação;

pa, pv − pressão parcial da substância e do vapor de retificação; PMa, PMv − peso molecular da substância e do vapor de retificação.

Esta equação é valida quando se utiliza vapor apenas para a redução da pressão parcial da substância a vaporizar, dispondo-se de outros meios para qualquer aquecimento que se fizer necessário. Nos casos em que isto não acontece, deve-se calcular a quantidade de vapor necessária para o aquecimento desejado. Isto deve levar em conta o calor sensível para se alcançar a temperatura de vaporização e o calor latente de vaporização. Esta quantidade será somada aquela necessária a retificação do líquido.

3.9 Princípio do Processo de Destilação Diferencial

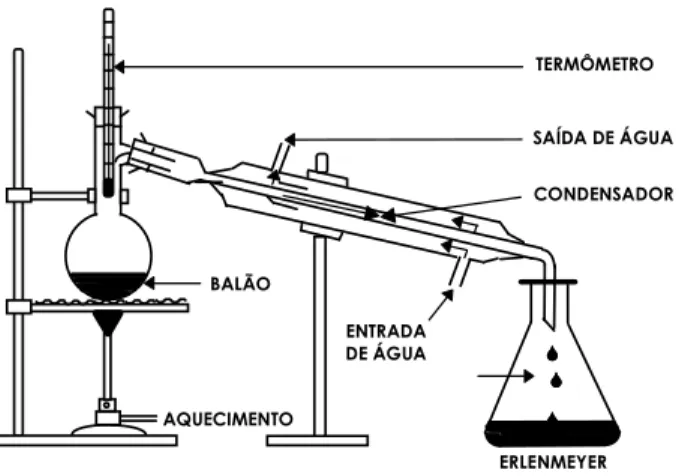
A destilação diferencial é um processo em batelada, no qual a substância colocada no equipamento é submetida a um aquecimento contínuo. Sucessivamente forma-se uma fase vapor, que é separada da fase líquido, a qual permanece com resíduo no equipamento. O vapor é retirado do vaso, condensado e coletado como líquido (Figura 3.8).

) = ) ,

- ) <

>,

) )* , )*

) <

,* )*- ,

) )* )?)

Figura 3.8 - Destilação ASTM D-86 - Exemplo de destilação diferencial

(13)

3.10 Cálculo do Equilíbrio de Fases da Destilação Diferencial

Se em uma mistura binária de (n) mols, (xa) representa a fração molar do componente (a)

na carga, tem-se:

na + nb = n na = xa . n nb = xb . n (3.53)

onde (na)é o número de mols de (a) na mistura.

Admitindo-se em um instante (dt), que se vaporize uma quantidade (dn) de líquido, a quantidade de (a) que passa para a fase vapor de composição (ya), contida no elemento (dn)

vaporizado é dada por:

dna = ya . dn (3.54)

como (na = xa . n), a quantidade de (a) que se vaporizou é:

dna = d(xa . n) = xa . dn + n . dxa (3.55)

Igualando as equações 3.54 e 3.55 tem-se:

xa . dn + n . dxa = ya . dn (3.56)

a a

a n

x y

dx n d

−

= _(3.57)

Integrando-se esta equação entre os limites (no) da carga inicial e (n1) do líquido residual,

os limites concentração do líquido seriam (xo ) - inicial - e (x1) -final:

∫

= = o ₋

1

o x

x 1 o n

n

x y

dx n

n n

d _(3.58)

Esta equação é conhecida como equação de Rayleigh, podendo ser integrada numericamente a partir dos dados da curva de equilíbrio(y = k . x ), a qual fornece (y) em função de

(x). Quando a volatilidade relativa é constante, pode-se obter uma equação mais simplificada para

representar o processo.

Considerando (na) e (nb) o número de mols de (a) e (b) que permanecem na fase líquida

em cada instante, as quantidades iniciais de (a) e (b) seriam (noa) e (nob).

Para uma fração elementar de líquido vaporizado, a quantidade de (a) neste vapor será

(dna) igual a (ya . dn) na fase vapor e (yb .dn) para o componente b.

Assim:

dna = ya . dn (3.59)

dnb = yb . dn (3.60)

Como: yb = 1-ya vem que: dnb = (1-ya) . dn (3.61)

ou ainda:

a a b

a

y 1

y dn

dn

−

= _(3.62)

Como:

₍

(

_{) (}

)

₎

_ab

a a

x 1 y 1

x y

α = −

(14)

Pode-se obter que:

a a ab b a x 1 x dn dn − α = (3.64)

Desde que: xa =

b a a n n n

+ tem-se que: 1 - xa = a b b n n n + (3.65)

Então, vem que:

b b ab a a n dn n dn α = (3.66)

Se αab constante e considerando-se a equação 5.14, tem-se:

∫

= α b b a a n no b b n no a a ab n dn n dn 1 _(3.67) ab 1 oa a ob b n n n n α         = ) 1 ( 1

1

0 0 −













−

=

ab oa a a a

x

L

αααα _(3.68)

A Equação 3.68 mostra que se αab é constante, a equação log

( )

ab ob b ₁ n n α

= log

oa a

n n

é

uma reta, cujo coeficiente angular é

( )

ab

1

α , que passa pelo ponto oa a

n n

1,0 e

ob b

n n

1,0.

A Figura 3.9 mostra a variação de relação dos números de mols

ob b n n _e oa a n n em um

processo de destilação diferencial de uma mistura de benzeno e tolueno, contendo 50% em mol de

benzeno a uma atmosfera .

.(

.(5 _.( _.(

,

(15)

Operações Unitárias na Engenharia Química - ( 3-15 Figura 3.9 - Variação dos mols dos constituintes na destilação diferencial

Para esta mesma mistura, a Figura 3.10 mostra a variação do número total de mols destilado versus a temperatura e a fração molar de benzeno na fase vapor e na fase líquido. Estes cálculos foram obtidos a partir dos dados do diagrama T-x-y, que permitem definir os limites de temperatura em que o processo vai se passar (92,2oC) para a primeira gota e (110,6oC), ponto de ebulição do tolueno, para a última gota. Com estes valores de temperatura determina-se o valor de αAB (0,41 e 0,42), o que permite traçar a reta da Figura 3.10, que é traçada a partir dos dados retirados da Figura 3.9 e do diagrama T-x-y, arbitrando-se valores de na e calculando-se nb.

. . . 5 . 6 . 4 . 3 . 2 . 1 . 0 . ..

.

0.

. . 6 . 3 . 1 .

, *- * A*), )- , B , ,* )* C>, ) )*+)*,

) )

FRAÇÃO VAPORIZADA

Figura 3.10 - Fração vaporizada versus temperatura e composição

3.11 Princípio de Destilação Fracionada

Como foi visto a destilação integral não permite alcançar um bom nível de separação dos componentes insuficiente para atender o

necessário teor de pureza em um produto acabado. Para se aumentar este teor, é necessário se dispor de equipamentos que permitam melhor separação dos constituintes. Preliminarmente, poderia se pensar em se

introduzir uma série de estágios

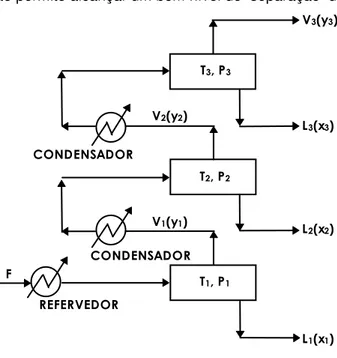
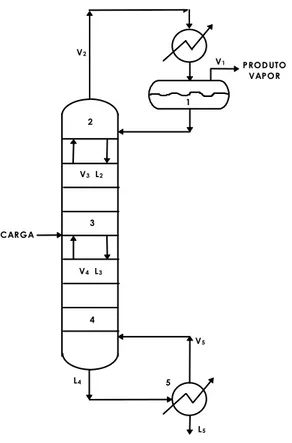
interconectados para se obter produtos de maior pureza, como no esquema apresentado na Figura 3.11.

Neste arranjo, o vapor V3 teria um maior grau de pureza no componente mais volátil, mas o esquema tem como desvan-tagens:

− excesso de produtos intermediários;

− número excessivo de equipamentos

(condensadores e tambores de “flash”);

− baixo rendimento de produto (V3);

− elevado custo operacional.

5 5

5#5

5"5

,* )*- ,

#

,* )*- ,

"

) ) ) ,

Figura 3.11 - Alternativas de Separação por Destilação Neste esquema deve ser registrada a função dos condensadores, os quais retirando calor do vapor que sobe, permitem a ocorrência de sucessivas condensações, enriquecendo o componente mais volátil no vapor ao gerar novas fases líquido e vapor.

(16)

Operações Unitárias na Engenharia Química - ( 3-16 +

,

; #; " <

" #

;

; "; ,

,

;5 #;5

5;

;5 ";5 5 "5

5

<

#

5 #5

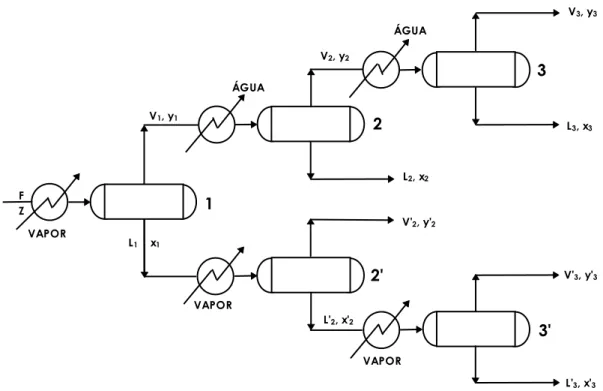
Figura 3.12 - Arranjos de múltiplos estágios

Deve-se observar que os refervedores introduzidos permitem vaporização do líquido que desce, formando novas fases

líquido e vapor, aumentando o teor de mais pesado na corrente líquida. Através destes esquemas alterna-tivos obtem-se maior pureza em ambos componentes, mas, em contrapartida, nos deparamos com muitas desvantagens - inúmeros produtos e equipamentos. Isto pode ser superado, eliminando-se os condensadores e refervedores parciais intermediários através de contato direto entre as fases líquido

e vapor em contracorrente,

eliminando-se as etapas

intermediárias (Figura 3.13).

Pode-se realizar todas

as etapas em apenas um

equipamento, Figura 3.14, que fosse dotado de dispositivos

internos que permitissem o

contacto e separação das fases em cada estágio.

, , ,

5

6 5

6

4

)- )* ,

) )* ,

(17)

Operações Unitárias na Engenharia Química - ( 3-17 Figura 3.13 - Esquema de destilação fracionada

, ,

,

6 4

4

4 5

5

6 5

6

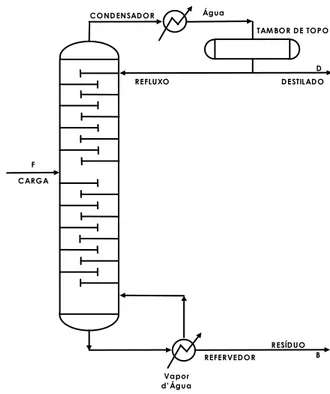
Figura 3.14 - Coluna de destilação fracionada

Com este esquema, aumenta-se o rendimento dos produtos, eliminando-se os condensadores e refervedores intermediários, mantendo-se apenas um no topo e outro no fundo. No topo da torre ocorre remoção de calor e ao se reintroduzir a corrente líquida - refluxo - resfria-se esta seção. Inversamente, no fundo da torre ocorre fornecimento de calor e o vapor retornando aquece esta região. Existe então um gradiente de temperatura ao longo da torre: menor no topo e maior no fundo, o que se traduz em temperaturas diferentes em cada estágio.

A função dos condensadores e refervedores intermediários é agora exercida pelas correntes de líquido que desce e de vapor que sobe, que retiram e cedem calor respectivamente, das fases em contato contra-corrente. Assim, o líquido do estágio n-1 resfria o vapor do estágio n+1 Figura 3.15, quando entram em contato no estágio n. Devido à diferença de temperaturas, pois o estágio n-1 está a uma temperatura menor que o estágio (n+1) - calor sensível - e ao fato de o líquido estar no ponto de bolha à Tn-1 e o vapor no ponto de orvalho à Tn+1 - calor de condensação -, o líquido atua como um condensador parcial para o vapor e o vapor atua como refervedor parcial para o líquido.

Em cada estágio, o vapor e o líquido que ali chegam não estão em equilíbrio entre si, porém as fases que deixam cada estágio o estão. O líquido que chega a cada estágio é mais rico no componente mais volátil que o vapor que ali também chega. Isto é o que produz a força motriz para o contínuo

enriquecimento dos vapores no componente

mais volátil, ao longo da torre. Na seção inferior

de estágios ocorre, ao contrário, o

empobrecimento do componente mais volátil

no líquido.

A seção superior, acima da

introdução de carga, é conhecida como de

enriquecimento. A inferior é a de

esgotamento sempre se referindo a

composição do componente mais leve.

A destilação fracionada é uma operação de separação em que se obtém produtos com maior pureza, através de contatos diretos e separações sucessivas das fases líquido descendente e vapor ascendente, ali ocorrendo sucessivas condensações (fase vapor) e vaporizações (fase líquido).

(

" (

(

# (

9

# 9

"

9

# 9 9

" 9 (

" ( #

)- < , (

)- < ,

)- < , 9

Figura 3.15 - Contato e separação de fases em contracorrente

(18)

separação das fases líquido e vapor. Estes dispositivos podem ser do tipo bandejas ou recheios, os quais foram descritos no Capítulo 2.

O condensador de topo ao retirar calor do vapor de topo - condensando-o - e o refervedor do fundo da coluna ao fornecer calor ao líquido de fundo - vaporizando-o -produzem um gradiente de temperatura ao longo da torre. Isto possibilita as sucessivas condensações do vapor ao subir e vaporizações do líquido ao descer.

No topo, parte do líquido formado pela condensação do vapor de topo retorna a torre o mesmo acontecendo com o vapor formado pela vaporização parcial do líquido de fundo. Isto faz com que haja sempre líquido na parte superior da coluna e vapor em sua parte inferior, o que de outra forma não ocorreria.

3.12 Esquema Básico de Colunas de Destilação Fracionada

O esquema básico de colunas de destilação fracionada (Figura 3.16) deve contar com os seguintes tipos de equipamentos, os quais tem como função:

− a coluna de fracionamento propriamente dita, composta pelo vaso e seus internos, onde

destacam-se os dispositivos de contato líquido-vapor, os vertedores de líquido, os distribuidores de carga e os coletores ou panelas de retirada de produtos líquidos;

− condensador, cuja função é liqüefazer total ou parcialmente o produto de topo, removendo calor

desta região da torre;

− tambor de topo, cuja função é permitir a separação do gás do produto de topo condensado e

acumular este último, separando a água que possa estar presente;

− refervedor, cuja função é vaporizar parte do produto de fundo, fornecendo calor a este região da

coluna;

− aquecedor ou vaporizador de carga, cuja função é ceder calor a carga, levando-a ao estado

térmico desejado;

− linhas e bomba de refluxo, cuja função é adepermitiroretornoderefluxoparaa torre.

O funcionamento de colunas de fracionamento será descrito a partir da introdução da carga, o que se dá em um ponto intermediário da coluna denominando-se esta região como zona de "flash". Pode ocorrer a introdução da carga em mais de um ponto, quando se tiver misturas de composição ou estado térmico diferentes.

A carga sendo composta por duas fases, a fase vapor se encaminha para o topo da coluna, enquanto que a fase líquida segue para o fundo. Estas fases trocam matéria e energia com as respectivas fases líquida e vapor que escoam em contracorrente, originadas pelo refluxo líquido de topo e pelo vapor de fundo.

Assim, o vapor que sai pelo topo da coluna é condensado, total ou parcialmente, pelo condensador de topo, se encaminhando para o tambor, onde o líquido e o vapor formados seguirão caminhos diferentes. O líquido é dividido em duas

)- , ) ) ) ,

% D <E'

,* )*- , <E'

, ) , ,

) F, )- ,

Figura 3.16 - Coluna de fracionamento

(19)

Operações Unitárias na Engenharia Química - ( 3-19 então no primeiro estágio da torre uma fase líquido, descendo para o estágio seguinte, o que não seria possível, se não houvesse o refluxo. Este primeiro estágio estará também a uma temperatura inferior a do segundo estágio. Este processo de transferência de massa e de energia se propaga nesta seção da coluna, provocando a ocorrência de duas fases - líquido (refluxo) e vapor (parte da carga) - a temperaturas sempre crescentes no sentido do fundo da torre.

A existência de vapor na seção de fundo se dá de forma similar, devido a trocas térmicas que também aí ocorrem, só que em sentido inverso, pois o líquido que desce pela coluna é

encaminhado a um refervedor, onde parte dele é vaporizado. O vapor formado retorna a torre e por possuir maior entalpia que o líquido de fundo, lhe fornecerá energia, acarretando a vaporização parcial deste líquido e sua condensação também parcial. Haverá, então, no último estágio da torre uma fase vapor, subindo para o estágio seguinte, o que não seria possível se não houvesse o refluxo. Este último estágio estará a uma temperatura superior a do penúltimo. Este processo também se propaga nesta seção da coluna, provocando a ocorrência de duas fases - vapor (refluxo) e líquido (parte da carga) - a temperatura sempre decrescentes no sentido do topo da torre.

A existência de um gradiente de temperatura ao longo da torre, maior temperatura no fundo e menor no topo, permite que se tenha vaporização e ou condensação seletiva em toda a coluna, ocasionando enriquecimento dos constituintes mais voláteis (leves) no topo e dos menos voláteis (pesados) no fundo. Ou seja, ocorre fracionamento da carga em constituintes, de acordo com seus pontos de ebulição. Assim, a parte superior à entrada de carga na coluna é denominada de seção de enriquecimento, enquanto que a inferior chama-se esgotamento.

3.13 Projeto e Operação de Colunas de Fracionamento

As colunas de fracionamento objetivam separar uma dada mistura (F) em produtos (D e

B), cujos teores de um dos componentes sejam preestabelecidos.

De forma geral, conhece-se a vazão, composição e estado térmico da carga e fixa-se determinadas variáveis operacionais que permitem o cálculo das variáveis de projeto.

As variáveis operacionais definidas a priori são, em geral, a razão de refluxode topo e o

seu estado térmico, o que permite calcular:

− a carga térmica do condensador de topo e do refervedor;

− as vazões internas de líquido e vapor na coluna.

Estas variáveis operacionais permitem a definição do número, tipo e tamanho de estágios de equilíbrio e do diâmetro da coluna.

De forma geral, o projeto destas colunas se inicia com o cálculo das condições operacionais necessárias para o dimensionamento do número de estágios de equilíbrio, vindo a seguir o cálculo deste número.

Para o cálculo das condições operacionais, parte-se das equações de balanço material e energético aplicada a torre com um todo. Para cada estágio de cada seção usa-se as relações de equilíbrio T-x-y e estequiométricas.

(20)

Antes de fazer uma abordagem mais rigorosa do problema, para maior facilidade de compreensão, será tratado o método simplificado de McCabe Thiele, que apresenta como principal vantagem a visualização mais fácil e imediata da influência das diversas variáveis, rapidez e razoável precisão obtida. Pode também ser aplicado a estimativas preliminares de projetos e avaliação operacional de colunas de fracionamento.

3.14 Método Gráfico de McCabe-Thiele

Este método, apesar de ter sido desenvolvido há bastante tempo (1925), é extremamente útil na ilustração dos conceitos e na estimativa preliminar do projeto de uma coluna. É um método simplificado que utiliza apenas o balanço material e necessita do diagrama de equilíbrio y-x. É extremamente didático, possibilitando entendimento conceitual das influencias do refluxo e estado térmico da carga sobre o número de estágios e da separação obtida.

A simplificação assumida pelo método ocorre nas vazões molares de cada fase, as quais são consideradas constantes em cada seção, como será mostrado em seguida. Esta simplificação elimina a necessidade de se fazer iterações para solucionar o problema.

A admissão feita pelo método gráfico de McCabe - Thiele, de que as vazões molares de

líquido e vapor (L e V) são constantes ao longo de cada seção, se baseia na hipótese de que para

cada mol de líquido vaporizado, ocorre a condensação de um mol do vapor que chega no mesmo

estágio.

Esta premissa depende dos seguintes fatores:

− calor de vaporização molar das misturas;

− calor de misturas nas fases vapor e líquido;

− variação do calor sensível em função do gradiente de temperatura ao longo da coluna;

− perdas de calor através das paredes da coluna. Fazendo as seguintes considerações:

− calor de misturas desprezíveis ou nulo, no caso de misturas de compostos quimicamente semelhantes;

− efeito do calor sensível pequeno, porque a diferença de temperaturas prato a prato é pequena, sendo que o líquido atua em sentido oposto ao do vapor;

− troca de calor com o exterior desprezível, quando as colunas são bem isoladas;

(21)

Operações Unitárias na Engenharia Química - ( 3-21 #

"

9

# 9

$

# 9

$ ₉

"$

*9

#*9