CAPÍTULO 8
8. Equações de Maxwell
Introdução
As Equações de Maxwell representam o fundamento teórico do Eletromagnetismo. Todo o nosso desenvolvimento terá como origem tais equações.
Inicialmente consideraremos o vácuo como meio, contudo abordaremos outros meios materiais posteriormente.
Daremos inicio ao estudo do Eletromagnetismo, lembrando que na verdade este curso teve seu inicio efetuado nos cursos de Eletricidade e Magnetismo I e II onde foram estudados os conceitos básicos da Eletrostática e da Magnetostática. Uma noção preliminar de análise vetorial no sistema de coordenadas cartesianas foi efetuada.
A carga elétrica foi o tema principal de todo nosso estudo preliminar. Vimos que existem dois tipos de carga elétrica, a saber, as positivas e as negativas. Sendo os portadores fundamentais dessas cargas as chamadas partículas elementares (há fortes indícios da existência de cargas fracionárias na natureza, tais
como 1/3 e –2/3 da carga do elétron. Contudo estas ainda não foram detectadas experimentalmente). Até o momento a menor carga conhecida na natureza é a carga do elétron, que é a mesma do pi-menos, do muon, etc, cujo módulo é o mesmo do próton, do pósitron etc. Portanto qualquer quantidade de carga, é apenas um múltiplo desta quantidade elementar. Quando falamos numa distribuição continua de cargas, estaremos na verdade nos referindo a uma aproximação.
8.1 Leis Básicas da Eletricidade e do Magnetismo
Faremos a seguir uma revisão qualitativa das leis básicas da eletricidade e do magnetismo vista nos capítulos precedentes. Esta revisão tem por objetivo convergir estas equações para um ponto comum, ou seja, mostrar como tais equações estão intimamente relacionadas e representam um mesmo tipo de fenômeno denominado Eletromagnetismo representado pelo conjunto conhecido como as Equações de Maxwell.
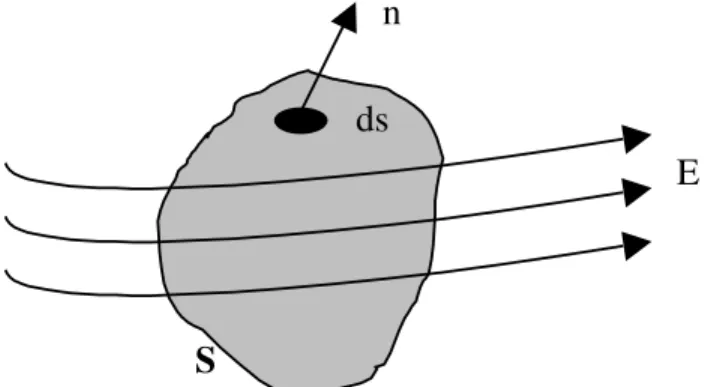
Iniciemos pois a dedução das Equações de Maxwell pela introdução da lei de Gauss, como segue
S
E
n
ˆ
ds
Q
/
0
(8.1)
A Eq. 8.1 nos diz que “Q ” é toda a carga existente no interior da superfície fechada S, onde 0 é a constante
de permissividade do meio. No sistema gaussiano 0
1
/
4
.
ds
n
S
E
Sendo Q a carga distribuída por todo o volume, podemos escrever,
V
dV
Q
(8.2)e portanto,
V
S
E
n
ds
dV
0
1
ˆ
(8.3)
usando o teorema do divergente (ver apêndice A), o primeiro membro da equação acima torna-se
V
S
E
n
ds
E
dV
ˆ
e a Eq. 8.3, fica
V
V
E
dV
dV
0
1
(8.4)
ou de outro modo colocando dV em evidência
0
0dV
E
V
(8.5)
como dV é arbitrário, temos finalmente que
0
/
E
(8.6)que representa a forma diferencial da lei de Gauss (estado estacionário).
Considerando agora a figura abaixo, chamando de C o circuito limitado por uma superfície S, temos que o
fluxo magnético será dado por
B
S
B n ds
(8.7)A força eletromotriz induzida ( ) ou f.e.m. induzida no circuito C será: ds
n
S
B C
dl
E dl
C (8.8)
onde aqui, o campo
E
representa o campo elétrico induzido no elementod
l
do circuito C devido a variaçãodo fluxo magnético através do circuito.
A lei de indução de Faraday nos diz que: a fem induzida somente aparecerá numa espira sem fonte, quando houver uma variação do fluxo magnético através desta espira.
Assim, podemos escrever sob forma de equação a lei de indução de Faraday
d
d t
B (8.9)
Substituindo (8.8) em (8.9), podemos escrever a lei de indução de Faraday, como segue:
E dl
d
d t
CB
(8.10)
Usando (8.7) em (8.10), temos que
E dl
B
t
n ds
C S
(8.11)fazendo uso do teorema de Stokes (ver apêndice A), o primeiro membro da equação acima torna-se
C
E
d
l
SE
n
ˆ
ds
e a Eq. (8.11), fica
E
n ds
B
t
n ds
S
S
(8.12)ou de outro modo
E
B
t
n ds
S
0
(8.13)sendo S uma superfície arbitrária, ds 0, logo
E
B
t
0
(8.14)V
S
B
n
ˆ
ds
B
dV
0
(8.15)
novamente se levarmos em conta que dV é arbitrário, teremos que
0
B
(8.16)O fato de ser o divergente do campo magnético nulo, isto revela a inexistência de monopólos magnéticos. Fecharemos esta seção com a introdução do Teorema de Ampère. Em 1820, o físico dinamarquês, Christian Oersted, observou que a corrente elétrica que percorria um fio produzia efeitos magnéticos no mesmo. Dizemos então que quando um condutor é percorrido por uma corrente elétrica (campo elétrico variável), surge um campo magnético
B
em torno do condutor dado pela seguinte relação:i
l
d
B
C 0
(8.17)
onde 0 é a constante permeabilidade do meio. No sistema gaussiano 0
4
/
c
2, e c é a velocidade da luzno vácuo. Temos também a corrente elétrica i, já apresentada no capítulo 4, e que pode ser vista como
S
J
n
ds
i
ˆ
(8.18)logoa a Eq. 8.17 pode agora ser escrita como
C
B
d
l
0 SJ
n
ˆ
ds
(8.19)
e novamente usando o Teorema de Stokes, podemos rescrever a equação acima como segue
S
S
B
n
ˆ
ds
0J
n
ˆ
ds
ou ainda
0
ˆ
0
J
n
ds
B
S
(8.19)
e do fato que ds é arbitrário, temos que ds 0, logo
0
0
J
B
(8.20)que representa a forma diferencial da Lei de Ampère (correntes estacionárias).
FORMA
INTEGRAL
FORMA DIFERENCIAL
REGIME
A Lei de Gauss nos diz
que “Q” é toda a carga
existente no interior da superfície fechada S.
S
E
n
ˆ
ds
Q
/
0
0
/
E
EstacionárioA Lei de Gauss para o magnetismo devido a não existência de monopólos magnéticos.
S
B
n
ˆ
ds
0
0
B
EstacionárioA Lei de Ampère é válida para correntes estacionárias. I é a
corrente limitada pela curva C.
I
l
d
B
C 0
J
B
0
EstacionárioA Lei de Faraday para indução
Eletromagnética
C
B
dt
d
l
d
E
t
B
E
Não-Estacionário
O conjunto das quatro equações apresentadas tanto na forma integral quanto na forma diferencial na tabela acima não descrevem a teoria electromagnética. A Lei de Ampère ou a terceira das equações está incompleta. Na próxima seção abordaremos a questão do princípio de conservação da carga, e entenderemos porque este conjunto de equações na forma como está apresentada não representam as Equações de Maxwell.
8.2 Equação da continuidade
Seja uma região do espaço com um volume V e superfície S onde haja uma distribuição de cargas, caracterizada por uma densidade volumétrica
(
r
,
t
).
Se as cargas estiverem em repouso, temos apenas que
(
r
),
revelando a não dependência temporal, logoV
dV
const
ou
V
n
ˆ
0
t
De modo geral, as cargas podem estar em movimento. Assim, a conservação da carga estabelece que a quantidade de cargas que entra (ou sai) através da superfície S, na unidade de tempo, é igual à quantidade de cargas que aumentou (ou diminuiu) no interior da região limitada por S.
Uma corrente I é produzida pelo movimento da carga e é determinada por
S
v
n
ds
Sj
n
ds
I
ˆ
ˆ
(8.21)onde é a densidade,
v
é a velocidade da carga e
j
v
a densidade de corrente elétrica, en
ˆ
o vetor unitário normal.A carga total no volume será
V
r
t
dV
Q
(
,
)
(8.22)como a corrente pode ser obtida como a variação da carga na unidade de tempo, temos que
dt
dQ
I
(8.23)onde o sinal negativo indica que a carga está decrescendo, ou seja, saindo da superfície S, neste caso temos de (8.21), (8.22) e (8.23)
V
r
t
dV
sj
n
ds
dt
d
ˆ
)
,
(
(8.24)usando o Teorema da divergência (ou T. de Gauss, apresentado no apêndice A) rescrevemos (8.24) como
V
r
t
dV
Vj
dV
dt
d
)
,
(
ou
V
V
dt
r
t
dV
d
dV
j
(
,
)
0
devemos substituir
d
dt
port
dentro da integral, visto que(
r
,
t
)
é uma função der
e t , de modo que0
)
(
V
j
t
dV
como dV é arbitrário,
0
t
j
A Eq. (8.25) é chamada Equação da continuidade, que expressa o princípio de conservação da carga elétrica.
Este tipo de equação expressa sempre a conservação de alguma coisa, não exclusivamente à carga elétrica. Na Hidrodinâmica, por exemplo, temos que a equação
0
)
(
t
v
onde é a densidade de massa e
v
a velocidade, expressa a conservação da massa. Retornando ao caso particular em que não há variação de no tempo, ou seja, se(
r
)
entãot
0
. Logo,0
j
(8.26)
Não havendo variação de no tempo pode-se dizer que não há fonte nem sorvedouro na região considerada. No entanto nesta região poderá haver um campo gerado por uma fonte externa a esta região, de modo que nesta região haverá campo porém não haverá fonte nem sorvedouro.
8.3 Equações de Maxwell (no vácuo)
Veremos a seguir, que a Eq. 8.20 conhecida como Lei de Ampère trata apenas de situações particulares ou isoladas por não está em acordo com a Equação da continuidade que expressa o Princípio de conservação da carga.
Aplicando o operador divergência à equação de Ampère, obtemos
)
(
)
(
B
0
j
como o divergente do rotacional de qualquer vetor é identicamente nulo, i. e,
0
0
)
(
B
e
0
temos finalmente que
0
j
(8.27)
Comparando a Eq. (8.27) com a equação da continuidade (8.25), observamos que a condição (8.27) só acontece no caso estático, ou seja, quando não é função explícita do tempo (
(
r
,
t
)
t
0
). Como se apresenta, a equação de Ampère trata apenas de correntes estacionárias e, portanto não é compatível com a conservação da carga.Em substituição à Eq. 8.20, usamos a equação abaixo com a introdução do segundo termo do lado direito e, mostraremos que a presença deste termo faz com que a equação fique em acordo com a equação da continuidade.
t
E
j
B
0 0
0 (8.28)
)
(
)
(
0 0 0E
t
j
B
(8.29)
o termo do lado esquerdo é nulo, como já vimos. Substituindo o segundo termo do lado direito dentro do parêntesis pela lei de Gauss, obtemos
0
)
/
(
00 0 0
t
j
de forma simplificada podemos escrever
0
0t
j
como 0é arbitrário, obtemos
0
t
j
(8.30) que é a Equação da continuidade vista anteriormente. Como podemos ver a Eq. (8.28) está em acordo com o Princípio de conservação da carga. O termo a mais, usado na equação de Ampère (conhecido como corrente de deslocamento) foi introduzido pelo Físico inglês J. C. Maxwell. Por esta razão a Eq. (8.28) é mais propriamente chamada de Lei de Ampère-Maxwell ou Lei de Ampère generalizada. Esta mudança aparentemente pouco significativa foi à responsável por uma das maiores revoluções da Física. Através dela Maxwell previu a existência de ondas eletromagnéticas.
O conjunto das quatro equações básicas da eletricidade e do magnetismo, com a nova forma da equação de Ampère-Maxwell passa a ser denominadas Equações de Maxwell ou Equações do Eletromagnetismo.
EQUAÇÕES DE MAXWELL
F. INTEGRAL F. DIFERENCIAL REGIME
S
E
n
ˆ
ds
Q
/
0
0
/
E
Estacionário0
ˆ
SB
n
ds
0
B
Estacionáriot
d
d
i
l
d
B
EC 0 0 0
t
E
j
B
0 0
0 Não-estacionário
E dl
d
d t
CB
t
B
E
Observação: É possível demonstrar o porquê do termo corrente de deslocamento. A forma integral da equação de Ampère-Maxwell nos dá:
t
d
d
i
l
d
B
EC 0 0 0
ou ainda
t
d
d
i
l
d
B
EC 0 0
onde “i” é a corrente de condução. Logo o termo
t
d
d
E0 tem dimensão de corrente e por isso foi
chamado por Maxwell de corrente de deslocamento.
Estas quatro equações são chamadas Equações de Maxwell. Estas equações como apresentadas pelo conjunto visto na tabela acima, sem o termo introduzido por Maxwell descrevia efeitos isolados, não constituindo equações que configurassem a teoria eletromagnética. As equações acima conduzem à equação das ondas
eletromagnéticas (na ausência do termo 0 0
E
t
isto não acontece). É importante neste pontofazermos algumas considerações. O campo eletromagnético é caracterizado por dois vetores
E
e
B
, representativos dos campos elétricos e magnéticos respectivamente. Nenhum é mais importante que o outro. Eletricidade e magnetismo não são assuntos isolados.E
e
B
, devem sempre ser vistos juntos, como formadores do campo eletromagnético.Na ausência de fontes, isto é, no vácuo, podemos finalmente escrever as Equações de Maxwell como
0
E
(8.31)
0
B
(8.32)
t
E
B
0
0 (8.33)
t
B
E
(8.34)
8.4 O campo eletromagnético
O campo eletromagnético produzido por distribuição de carga e seu movimento (distribuição de corrente) é descrito pelos vetores
E
(
r
,
t
)
e
B
(
r
,
t
).
Uma força de Lorentz é a forçaF
sofrida por uma carga “Q” que se move com uma velocidadev
(
r
,
t
)
no campo eletromagnético e é dada por)
(
E
v
B
q
F
(8.35)quando uma carga de prova é introduzida num campo elétrico efetivo com objetivo de medida, ela deve ser tão pequena que não interfira com os campos originais. Neste caso (8.35) pode ser expressa como
B
v
E
q
F
q
0
lim
Podemos ainda constatar a condição de linearidade das Equações de Maxwell introduzindo os vetores
D
que representa a densidade de fluxo elétrico ou deslocamento elétrico eH
a intensidade de campo magnético.Num dado meio
D
e
H
estão relacionados aE
e
B
por relações funcionais características do meio.Para um meio linear, homogêneo e isotrópico, as relações aproximadas são
E
D
(8.36)H
B
(8.37)onde e são constantes chamadas permissividade e permeabilidade do meio, respectivamente.
A densidade de corrente
J
e a intensidade de campo elétricoE
estão relacionadas porE
g
J
(8.38)onde g é condutividade do meio. As equações (8.36–38) são freqüentemente apresentadas como relações constitutivas.
Como conseqüência da linearidade, uma superposição de campos
n
i i n
i i
B
B
B
B
E
E
E
E
1 2
1
1 2
1
...
...
também satisfazem às Equações de Maxwell. Este é o chamado Princípio da Superposição.
Em termos de
D
e
H
as Equações de Maxwell podem ser escritas para um dado meio comoD
(8.39)
0
B
(8.40)
t
D
J
H
(8.41)
t
B
E
(8.42)
E
D
,H
1
B
e homogêneo, e não existem cargas livres ou correntes, tal que e não variam de ponto para ponto, então as Eqs. (8.39-42) reduzem-se a
0
E
0
B
t
E
B
(8.43)
t
B
E
8.5 Onda eletromagnética
Vivemos num universo permeado de vibrações de toda natureza. São estas vibrações que dão forma e caracterizam a estrutura da matéria que percebemos ou não através de nossos sentidos objetivos, a saber, visão, audição, tato, paladar e olfato, além de outros que talvez não possamos classificar como sentidos do ponto de vista tradicionalmente aceito.
Contudo, nosso cérebro é o grande gerenciador de todo este processo dinâmico que desencadeia através de nós. Do ponto de vista científico, estas distintas vibrações estão separadas por faixa de freqüência e agrupadas numa escala denominada, espectro eletromagnético. Este espectro compreende todas as freqüências de que temos conhecimento, indo desde radiações de alta às mais baixas freqüências. Muitas dessas radiações tem origem em pontos muito distantes de nós aqui na Terra (por exemplo, estrelas como o Sol, são
Esta é uma das mais importantes previsões das Equações de Maxwell, ou seja, a existência de ondas eletromagnéticas.
Seja o meio ou região em que estamos tomando os vetores
E
e
B
na ausência de fonte ( = 0 eJ
0
).Neste caso, as Equações de Maxwell como já vimos tornam-se
0
E
0
B
t
E
B
0 0
t
B
E
Aplicando o operador rotacional à terceira e quarta equações, teremos
0
2 2 0 0 2
t
B
B
(8.44)
0
2 2 0 0 2
t
E
E
(8.45)
As Eqs. 8.44 e 8.45, representam equações de onda. Estas equações mostram que os vetores
E
e
B
satisfazem a equação da onda, no caso chamada de onda eletromagnética.A velocidade de propagação dessa onda para os valores conhecidos de 0 e 0 é
c
s
m
/
10
9979250
,
2
1
80 0
Esta é a velocidade da luz, ou seja, uma perturbação no campo eletromagnético se propagando no vácuo com a velocidade da luz.
8.6 O Maravilhoso Mundo Eletromagnético de Maxwell
A final de contas o que é este maravilhoso mundo eletromagnético descoberto por Maxwell?
Uma resposta simples, objetiva e direta, que atenderia desde os mais exigentes aos mais acomodados seria simplesmente LUZ!
Isto mesmo, esta palavra de uma sílaba só resume o que chamamos de mundo eletromagnético. Do ponto de vista científico, dito em simples palavras, Luz é uma forma natural de transferir energia através do espaço. É notável, e é uma dádiva que recebemos todos os dias, embora não reflitamos sobre isso na maior parte do tempo. Em outras palavras, podemos temperar um pouco mais nosso vocabulário e falarmos de Luz em termos da interação dos campos elétricos e magnéticos, da mecânica quântica, e de tantas outras coisas, contudo devemos sempre lembrar que luz é energia.
Apesar de viajar muito rapidamente, sua velocidade não é infinita como pensou muitos cientistas. No vácuo, a velocidade da luz é de aproximadamente 300.000 quilômetros por segundo, dito em palavras, trezentos mil quilômetros por segundo, o que significa um valor exagerado dentro dos padrões de velocidade de objetos como nossos carros, aviões, foguetes, etc. Entretanto, quando queremos nos referir as incríveis distancias em astronomia, a natureza finita da velocidade da Luz torna-se bastante evidente. Por exemplo, o tempo gasto numa comunicação de ondas de rádio viajando à velocidade da luz para alcançar a lua e retornar à Terra é da ordem de dois e meio segundos.
Isto nos faz relembrar fatos interessantes, como o que ocorre quando olhamos para o céu à noite. Todas as vezes que vislumbramos um céu estrelado estamos olhando para o passado, ou seja, estamos vendo um quadro cuja imagem viajou alguns minutos ou milhares de anos antes de ser projetado em nossa retina e constituir uma imagem de fato. A próxima vez que você assistir a um lindo nascer ou por do sol, lembre-se que este ocorreu oito minutos antes, que é na verdade o tempo que a luz leva para viajar do sol até a Terra. Em geral artigos de jornais e revistas que tratam de algum tema envolvendo astronomia, irá sempre incluir a
necessária declaração, “ Um ano luz é a distancia que a luz percorre em um ano à velocidade de 300.000
quilômetros por segundo, que representa na verdade uma distância percorrida da ordem de 9,5 trilhões de
quilômetros no período de um ano.” Já imaginou o que é isto?
Bem, a esta altura já estamos em condições de sermos mais precisos em nossa análise e deveríamos focalizar nossa atenção adiante no fato de que o termo Luz é mais geralmente referido como uma radiação eletromagnética. Mas muito freqüentemente quando nós dizemos “Luz” é equivocado querer com isto significar “luz ótica ou luz visível”, que é rigorosamente a radiação visível para os nossos olhos. A luz visível
é uma pequenina porção de uma grande parte da Luz chamada de espectro eletromagnético. Por conveniência
nomes, tais como raios-gama, raios-X, ultravioleta, visível, infravermelho e rádio. Entretanto, é importante relembrar que todas estas partes são nada mais que Luz. Na verdade não há fraturas nem ríspidas fronteiras no espectro eletromagnético, mas somente uma faixa contínua de energia.
8.7 Onda ou Partícula
Nem onda nem partícula, porém ambas as características encontram-se mutuamente envolvidas na natureza da luz. Experimentos em física tem demonstrado nos últimos séculos que a luz tem uma natureza dual. Em
muitos exemplos é conveniente representar a luz como um fenômeno de “partícula”, pensando na luz como um pacote discreto de energia chamado fótons. Nesta linha de pensamento, nenhum dos fótons são igualmente
criados, pelo menos em termos da quantidade de energia que eles contém. Cada fóton de luz de raio-X por exemplo, contém muita energia em comparação com um fóton de luz visível ou um fóton de rádio. É esta
“energia contida por fóton” que caracteriza a distinção das diferentes faixas de Luz descritas acima. Mesmo
que não seja estritamente correto, é difícil não pensar em um feixe de luz como uma coleção de pequenas
“balas de luz” juntamente enfileiradas numa linha.
A outra forma de representar a luz é como um fenômeno ondulatório. Esta forma é mais complexa para a maioria das pessoas entender, mas talvez uma analogia com ondas de som seja bastante útil. Quando você toca uma nota alta e uma nota baixa em um piano, ambas produzem som, mas a principal diferença entre as duas notas é a freqüência da vibração das cordas produzindo as ondas de som. Quanto mais rápida a vibração
mais alto o tom da nota. Se agora nós trocamos nosso enfoque das próprias ondas de som, em vez da corda vibrante, nós acharíamos que as notas de tons mais altos têm comprimentos de onda menores, ou distancia
entre cada onda sucessiva. Igualmente para a luz visível, a luz azul e a luz vermelha são ambas somente luz, porém a luz azul tem uma freqüência de vibração mais alta (ou um comprimento de onda mais curto) do que a luz vermelha.
Figura 1: modelo ondulatório da luz Figura 2: espectro visível
A Fig. 2 mostra as cores familiares do arco-íris de luz visível correspondendo a diferentes comprimentos de onda da luz, aqui mostrado numa escala em nanometros. O comprimento de onda torna-se sucessivamente maior quando este move-se da esquerda para a direita. A luz visível estende-se em torno de 4000 a 7000 nanometros.
É o mesmo modo como nós movemos ao longo do espectro eletromagnético. Cada faixa de luz definida acima corresponde a uma faixa de freqüência (ou comprimento de onda)de vibração da luz. Estes comprimentos de onda são um dos primeiros indicadores que usamos para descrever a luz e espectros em gráficos. Exibindo um espectro como um gráfico em vez somente de uma barra de cores permite-nos medir a luz.
Por exemplo, o “arco-íris” de cores mostrado na figura acima é o que você vê quando você deixa uma luz
branca atravessar um prisma. O que pode não ser óbvio, entretanto, é que a “intensidade” ou brilho da luz também está mudando ao longo com as cores. Se nós convertermos o “arco-íris” num gráfico de intensidade de luz versus comprimento de onda, isto pareceria como:
Figura 3: O familiar arco-íris do espectro de luz visível pode ser convertido em um gráfico que mostra como a intensidade da luz muda ao longo do espectro.
Observe que o espectro é mais brilhante no meio (região amarelo-verde) e diminui nas duas extremidades (na
conseguir mais informações fora da luz desta forma, e porque eles podem ainda plotar e analisar a luz que não é diretamente visível aos nossos olhos.
Mencionamos agora que a energia de cada fóton de luz era também uma propriedade básica. Isto mostra que existe uma relação entre a energia de um fóton e o correspondente comprimento de onda daquele fóton:
E(fóton) = (constante) / (comprimento de onda).
Esta simples equação basicamente vincula a natureza ondulatória e de partícula da luz permitindo-nos converter de um lado para o outro do comprimento de onda para os fótons e dos fótons para seus correspondentes comprimentos de onda. Esta equação está também em acordo com o que nós dissemos anteriromente, por exemplo que um fóton de raio-X tem uma grande energia (e um pequeno comprimento de onda) comparado com um fóton de luz visível.
8.8 Interação entre Luz e Matéria: Absorção e Emissão de Luz
Não deveria ser nenhuma novidade para nós que átomos e moléculas possam absorver luz (ou energia). Caso não pudessem, voce poderia simplesmente ligar e desligar a luz dentro de um quarto, e então sentar-se enquanto os fótons continuassem saltando ao redor do mesmo! Fótons de luz mais energéticos, como raios-X, tendem a abrir caminho através da matéria antes de ser absorvido. Consequentemente, seu uso em imagens médicas (popularmente conhecido como imagens de raio-X) é largamente utilizado, visto poder este passar
através de tecidos “suaves,” mas serem mais prontamente absorvidos em seus ossos, que são mais densos.
Como e por que os fótons são absorvidos pela matéria?
Bem, já é hora de desenvolvermos um outro dispositivo conceitual a fim de ajudar-nos a compreender este processo. Em física, frequentemente achamos útil termos a pretensão de estarmos olhando para um único átomo. Átomos são feitos de prótons, neutrons e elétrons, e cada elemento químico tem um número específico desses componentes. É isto que os fazem diferentes! Prótons (e neutrons) são mais massivos do que os elétrons, e assim nós às vezes visualizamos um átomo como um sistema solar em miniatura, com as partículas
mais pesadas no centro (os núcleos) e os elétrons zumbindo ao redor em “órbitas” específicas como planetas. (Na realidade este quadro não é muito exato. Elétrons não são pensados serem pequenas bolas “em órbita” ao
redor de um sol “nuclear.” Entretanto, se você tem a idéia que os elétrons são encontrados somente em “distancias” específicas discretas dos núcleos, e que cada distancia permitida corresponde a um diferente “nível de energia” para o elétron, isso estaria mais próximo da realidade. )
Sem pesquisar muito distante da física atômica e da mecânica quântica, vamos admitir por enquanto a seguinte afirmação: os elétrons ligados a qualquer átomo em particular podem apenas ser encontrados em certos níveis específicos de energia com respeito ao núcleo do átomo. O átomo de hidrogênio contém
somente um próton e um elétron, e é o mais simples (e o mais comum) elemento no Universo, assim vamos usa-lo como exemplo. A figura mostra um átomo esquemático de hidrogênio onde em vez de desenhar as órbitas permitidas para o elétron nós desenhamos as linhas exibidas verticalmente para representar os níveis de energia permitido para o elétron.
Figura
Se não perturbado, nosso átomo de hidrogênio prenderá seu elétron tão firme quanto possa, e assim nós
encontraríamos o elétron no nível mais baixo de energia, que é chamado de “nível fundamental.” Entretanto,
Agora nosso átomo de hidrogênio está no que é chamado um “estado excitado,” tal como uma criança numa
dança de quadrilha na noite de São João. Porém todos nós sabemos que este não é o estado natural de uma criança, da mesma forma que não é também o estado natural de um átomo. Se outros fótons não são absorvidos pelo átomo, o elétron eventualmente retornará ao seu nível mais baixo de energia ou estado fundamental. Entretanto, o elétron tem que perder energia para fazer isto, e assim liberar um fóton de mesma energia daquele que foi absorvido (embora mais provavelmente em alguma outra direção da qual este foi absorvido). Este processo é chamado emissão porque um fóton de luz é emitido pelo átomo, outravez em um
comprimento de onda muito específico.
É lógico, que o átomo poderia ter absorvido um outro fóton com exatamente a energia certa para saltar para um outro nível energético, ou mesmo dois ou três mais. Igualmente, depois de cada uma destas possíveis excitações do átomo, o elétron poderia saltar de volta um ou mais passos, emitindo fótons como este foi. Se um fóton com energia suficientemente grande é absorvido, este pode mesmo fazer com que um elétron torne-se desligado de torne-seu núcleo, um processo que é chamado de ionização. Nosso átomo de hidrogênio tornou-se
incapacitado não podendo mais absorver ou emitir luz até que este administre a captura de outro elétron livre de volta ao seu nível ligado de energia.
Nós temos discutido uma transição específica ou “salto de energia” em um átomo, mas é lógico que em
qualquer sistema físico existem muitos átomos. Num gás de hidrogênio, todos os átomos separados poderiam estar absorvendo e emitir fótons correspondendo ao grupo inteiro de transições permitidas entre os vários níveis de energia, cada qual absorveria ou emitiria no comprimento de onda específico correspondendo a diferentes energias entre os níveis de energia. Este modelo de absorção (ou emissão) é único para o hidrogênio. Ele causa um padrão reconhecível de linhas de absorção (ou emissão) num espectro. Nenhum
outro elemento pode ter o mesmo padrão.
Deveríamos ainda tornar claro que desde que qualquer elemento químico tem seu próprio conjunto de níveis de energia permitido, cada elemento também tem seu próprio padrão distinto de linhas de absorção espectral
(e emissão). É nesta “impressão digital” espectral que os astrônomos usam para identificar a presença dos
vários elementos químicos em objetos astronômicos. Linhas espectrais de um espectro é o que nos permite, extrair tanta informação dos objetos observados.
Vamos retornar as equações de onda dadas nas Eqs. (53) e (54)
0
1
0
1
2 2 2 2 2 2 2 2t
E
c
E
t
B
c
B
ou 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 21
1
t
E
c
z
E
y
E
x
E
t
B
c
z
B
y
B
x
B
(8.46)onde c2 = 1/ 0 0 é a velocidade da luz no vácuo. As duas equações de onda expressam ondas propagando-se em todas as direções a partir de um ponto P.
As Eqs. (8.46) tem a mesma forma, portanto podemos encontrar facilmente que cada componente cartesiana de
E
(
r
,
t
)
e
B
(
r
,
t
)
satisfaz a equação de onda.Por comodidade escrevemos em termos de
U
(
r
,
t
).
em vez de
E
(
r
,
t
)
ou
B
(
r
,
t
)
, visto queU
(
r
,
t
)
também é função de duas variáveis. Não é do nosso interesse aqui resolver explicitamente a equação acima, contudo a equação encontra-se resolvido sucintamente no apêndice A.A solução geral para
E
(
r
,
t
)
é)
)(
(
)
,
(
1 ik r 2 ik r 1 ikct 2 ikcte
b
e
b
e
a
e
a
t
r
U
sendo o numero de onda k = /c, então, k c = , onde é a freqüência angular da onda
assim, desmembrando a equação acima temos que
) ( 2 2 ) ( 1 2 ) ( 2 1 ) ( 1 1
)
,
(
i kr t i kr t i kr t i kr te
b
a
e
b
a
e
b
a
e
b
a
t
r
U
(8.47)A Eq. (8.47) representa uma onda propagando-se em todas as direções. Considerando inicialmente um observador muito distante de P, neste caso as frentes de onda definidas por
E
e
B
representam ondas planas. Além disso focaremos atenção nas ondas de freqüência , visto que freqüência está associado a percepção de cores, tais ondas são chamadas de monocromáticas.Por hipótese supomos que a onda se propaga na direção x, ou seja uma onda unidimensional, de modo que a solução fundamental de (8.47) é
) ( ) (
)
,
(
i kx t i kx te
B
e
A
t
x
U
(8.48)A Eq. (8.48) representa uma onda viajando para a direita e para a esquerda com velocidade de propagação igual a c, que é chamada de velocidade de fase da onda.
Analogamente para o vetor campo elétrico
)
,
(
x
t
E
E
Contudo, verificamos pela lei de Gauss que na ausência de fonte
0
E
logo, visto que a propagação é na direção x
0
)
,
(
x
t
x
E
x
E
x
(8.49)
Esta equação mostra que
E
não está na direção de propagação da onda (onda transversal).Se a onda se propaga na direção x e E = EY, então como o vetor
E
é perpendicular a
B
(
E
B
)
, temos que B = BZ.2 2 2 2 2
1
t
E
c
x
E
y yRetornando a Eq. (8.48), e restringindo-nos ao fato de que a onda se propaga a partir de uma origem P para a direita, temos como solução
) (
)
,
(
i kx te
A
t
x
U
(8.50)ou
]
Re[
)
,
(
i(kx t)e
A
t
x
U
(8.51)onde
A
representa a amplitude (possivelmente complexa) do campo da onda. O campo físico representa a parte real deU
(
x
,
t
).
Lembrando que (fórmula de Euler)
)
sen(
)
cos(
) (t
kx
i
t
kx
e
i kx tpodemos assim escrever a equação da onda como
)
sen(
)
cos(
)
,
(
x
t
kx
t
i
kx
t
U
(8.52)se a amplitude é complexa e do fato que o campo físico representa a parte real de
U
(
x
,
t
),
podemos simplesmente escrever a equação de onda como)
sen(
)
,
(
x
t
0kx
t
U
(8.53)ou
]
)
cos[(
)
,
(
x
t
0kx
t
U
(8.54)onde agora
A
0 é real.Finalmente com a convenção de que a parte física para os campos elétrico e magnético
)
,
(
)
,
(
x
t
e
B
x
t
E
respectivamente são obtidas tomando as partes real das quantidades complexas, assumimos que os campos das ondas planas são da formaj
e
E
t
x
E
(
,
)
~
i(kx t)ˆ
e (8.55)
k
e
B
t
x
B
(
,
)
~
i(kx t)ˆ
ou
)
sen(
)
,
(
x
t
E
0kx
t
E
e (8.56)
)
sen(
)
,
(
x
t
B
0kx
t
18
Observe queE
e
B
estão em fase, ondeE
0e
B
0 são as amplitudes ou valores máximos dos campos eletromagnéticos.Evidentemente,
E
(
x
,
t
)
e
B
(
x
,
t
)
estão em fase e mutuamente perpendiculares, suas amplitudes reais estão relacionadas como veremos a seguir,da relação de Faraday
t
B
E
como
E
E
Ye
B
B
Z,
temos quet
B
x
E
Y Z(8.57)
derivando (70) temos que
)
cos(
)
,
(
0
kx
t
E
k
x
t
x
E
y
e (8.58)
)
cos(
)
,
(
0
kx
t
B
x
t
x
B
Z
substituindo (8.56) em (8.57) obtemos
)
cos(
)
cos(
00
kx
t
B
kx
t
E
k
ou simplesmente
0
0
B
E
k
e finalmente a relação entre os módulos das amplitudes reais é
0 0
0