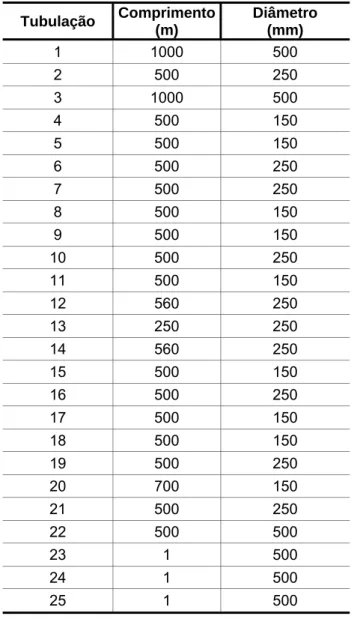
Calibração do coeficiente de decaimento do cloro (Kw) em redes de abastecimento de água utilizando o método iterativo do gradiente hidráulico alternativo (MIGHA)

Bento Pereira apresenta uma lista de autores e obras em língua portuguesa, de vários pendores: religioso, enciclopédico, dicionarístico, e literário.A escolha destas obras

O 6º ano do Mestrado Integrado em Medicina (MIM) é um estágio profissionalizante (EP) que inclui os estágios parcelares de Medicina Interna, Cirurgia Geral,

Por fim, na terceira parte, o artigo se propõe a apresentar uma perspectiva para o ensino de agroecologia, com aporte no marco teórico e epistemológico da abordagem

Diretamente relacionados ao estágio do curso de Nutrição da UFJF, temos as Normas para os Estágios Obrigatórios que disciplinam as atividades desta comissão no âmbito dos

- Identificar os fatores dificultadores da Certificação ISO 9001:2008 na Escola Estadual Eduardo Ribeiro, a partir da percepção de funcionários administrativos,

da equipe gestora com os PDT e os professores dos cursos técnicos. Planejamento da área Linguagens e Códigos. Planejamento da área Ciências Humanas. Planejamento da área

Vale ressaltar que, para direcionar os trabalhos da Coordenação Estadual do Projeto, é imprescindível que a mesma elabore seu Planejamento Estratégico, pois para Mintzberg (2006,

O fortalecimento da escola pública requer a criação de uma cultura de participação para todos os seus segmentos, e a melhoria das condições efetivas para