UNIVERSIDADE FEDERAL DE OURO PRETO Dˆ ENIS RICARDO XAVIER DE OLIVEIRA

(1)

Dˆ

ENIS RICARDO XAVIER DE OLIVEIRA

O Problema de Detec¸

c˜

ao de

Clusters

Espaciais Irregulares: Uma Nova

Abordagem Multiobjetivo

(2)

Dˆ

ENIS RICARDO XAVIER DE OLIVEIRA

O Problema de Detec¸

c˜

ao de

Clusters

Espaciais

Irregulares: Uma Nova Abordagem Multiobjetivo

Disserta¸cão apresentada ao Departa-mento de Computa¸cão da Universidade Federal de Ouro Preto para obten¸cão do t´ıtulo de Mestre em Ciência da Computa¸cão pelo Programa de Pós-gradua¸cão em Ciência da Computa¸cão.

´

Area de concentra¸cão: Ciência da Com-puta¸cão

Orientador: Prof. Dr. Gladston Juliano Prates Moreira

(3)

Catalogação: www.sisbin.ufop.br

Abordagem Multiobjetivo [manuscrito] / Dênis Ricardo Xavier de Oliveira. -2017.

75f.: il.: color; grafs; tabs; mapas.

Orientador: Prof. Dr. Gladston Juliano Prates Moreira.

Dissertação (Mestrado) - Universidade Federal de Ouro Preto. Instituto de Ciências Exatas e Biológicas. Departamento de Computação. Programa de Pós-Graduação em Ciência da Computação.

Área de Concentração: Ciência da Computação.

1. Problema de Detecção de Clusters Espaciais. 2. Particle Swarm

Optimization. 3. Otimização Multiobjetivo. 4. Funções de Penalização. I. Moreira, Gladston Juliano Prates. II. Universidade Federal de Ouro Preto. III. Titulo.

(4)

(5)

(6)

Ao Professor e Orientador Gladston Juliano Prates Moreira, pelo incentivo e orienta¸c˜ao.

`

A minha M˜ae Maria Aparecida e ao meu Pai Amantino (in memorian) e aos meus Irm˜aos Raquel e Raul.

`

A Tia Deolinda e Fam´ılia. `

A todos da Gerência de Tecnologia da Informa¸cão do Câmpus Rio Pomba (GTI) e ao Professor João Paulo, pelo incentivo e por terem possibilitado o meu afastamento para a realiza¸cão deste curso.

Ao Programa de Pós-Gradua¸cão em Ciência da Computa¸cão (PPGCC) da Univer-sidade Federal de Ouro Preto.

Aos Professores Gladston e Eduardo coordenadores do CSI-Lab (Laborat´orio de Computa¸c˜ao de Sistemas Inteligentes), pelos recursos e infraestrutura disponibilizados.

Aos Professores e Funcion´arios do PPGCC.

Aos amigos da Turma do Caf´e Leandro, Paulo, Lauro, Tales, Adriano, Matheus, Rodolfo A., Rodolfo M. e Raul. E as amigas La´ıs e Priscila.

`

A todos os colegas e amigos, que ajudaram e contribu´ıram ao longo deste per´ıodo. Ao Câmpus Rio Pomba do Instituto Federal de Educa¸cão, Ciência e Tecnologia do Sudeste de Minas Gerais (IF Sudeste MG), pelo programa de incentivo à qualifica¸cão dos Servidores Técnicos Administrativos.

`

A Universidade Federal de Ouro Preto, pelos recursos e infraestrutura disponibili-zados.

(7)

lutaste. ”

(8)

Métodos visando a deteçcão e inferência de clusters espaciais são de grande relevância. Isso se deve a aplicabilidade em problemas de notória importância como na saúde pública, mas também pelo interesse cient´ıfico no desenvolvimento eficaz destes métodos. As principais técnicas são baseadas na estat´ıstica espacial scan e muitas abordagens vinculam esta estat´ıstica a métodos estocásticos de otimiza¸cão. Recentemente, em conjunto com a estat´ıstica, fun¸cões de penaliza¸cão têm sido propostas, com a finalidade de controlar a irregularidade excessiva da forma dos clusters candidatos. Este estudo apresenta um novo método baseado na estat´ıstica scan em conjunto com uma nova fun¸cão de penaliza¸cão geográfica dos clusters candidatos que apresentam enormes lacunas em suas áreas, a fun¸cão de Dispersão. O objetivo principal é propor uma abordagem de otimiza¸cão multiobjetivo para o problema visando maximizar o valor da estat´ıstica e minimizar o valor da nova fun¸cão de penaliza¸cão, usando a técnica de computa¸cão evolucionária Particle Swarm Optimization, resultando ao final em um conjunto de solu¸cões não-dominadas representadas pela fronteira Pareto-ótimo. Resultados obtidos com a realiza¸cão de experimentos usando um conjunto de aplica¸cões do problema mostram que a abordagem multiobjetivo associada a fun¸cão de dispersão é um método satisfatório para o problema. Demonstrou-se que, em compara¸cão com a fun¸cão de penaliza¸cão por não-conectividade e compacidade geométrica, a abordagem associada a fun¸cão de dispersão é rápida e adequada para a deteçcão de

clusters espaciais irregulares.

(9)

Methods for the detection and inference of spatial clusters are of great relevance. It is due to its applicability in problems of notorious importance as in public health, but also for the scientific interest in the effective development of these methods. The main techniques are based on spatial scan statistics and many approaches link this statistic to stochastic optimization methods. Recently, in conjunction with this statistic, penalty functions have been proposed, for the purpose to control the excessive irregularity of the shape of candidate clusters. This study presents a new method based on scan statistics in conjunction with a new geographic penalization function of candidate clusters that present huge gaps in their areas, the Dispersion function. The main objective is to propose a multiobjective optimization approach to the problem aiming to maximize the value of the statistic and to minimize the value of the new penalty function using the evolutionary computation technique Particle Swarm Optimization, resulting in a set of non-dominated solutions represented by the Pareto-optimal front. Results obtained with experiments using a set of applications of the problem show that the multiobjective approach associated with the dispersion function is a satisfactory method for the problem. It has been shown that, comparing to the non-connectivity and geometric compactness penalty function, the approach associated with the dispersion function is faster and more appropriate for the detection of irregular shape spatial clusters.

(10)

Figura 1 – Uma poss´ıvel zona obtida para uma dada janela circular, Fonte: Moreira

(2011). . . 21

Figura 2 – Cluster encontrado pelo algoritmoSimulated Annealing sem penaliza¸c˜ao,

fonte: Can¸cado (2009) . . . 24

Figura 3 – Exemplo de dois subconjuntos de regi˜oes em destaque (cinza) que

assumem os formatos circular (a) e retangular (b). . . 28

Figura 4 – Exemplo de trˆes zonas (a), (b) e (c) em destaque e o subgrafo associado. 29

Figura 5 – Exemplo de um conjunto de centroides em um cluster e os considerados

para o cálculo da fun¸cão de penaliza¸cão por Dispersão. . . 31

Figura 6 – Clusters (a) e (b) dispostos em um espa¸co bidimensional (x, y) e

centroi-des associados e considerados para o cálculo da fun¸cão de penaliza¸cão.

. . . 32

Figura 7 – Exemplo de rela¸cão de dominância e um conjunto de solu¸cões

n˜ao-dominadas. . . 33

Figura 8 – Diagrama de blocos indicando o fluxo de execu¸c˜ao das principais etapas

do algoritmo PSO em seu modelo global. . . 36

Figura 9 – Fun¸c˜oes f1 e f2, e o conjunto O = {x1, x2, x3, x4} das solu¸c˜oes

n˜ao-dominadas e os espa¸cos R0 e R1. . . 39

Figura 10 – Mapa do Nordeste dos Estados Unidos: `A esquerda um mapa dividido

em um conjunto de regi˜oes; `A direita o grafo correspondente.. . . 42

Figura 11 – a) Exemplo de um conjunto de regi˜oes e uma zona em destaque (cinza);

b) Vetor de vari´aveis bin´arias associado a). . . 43

Figura 12 – C´alculo do valor da Crowding Distance Computation. . . 46

Figura 13 – Aplica¸cão do operador de muta¸cão em um indiv´ıduo (a): inclusão de

vértice no indiv´ıduo (b); e exclusão de vértice no indiv´ıduo(c). . . 50

Figura 14 – Clusters artificiais gerados no mapa do Nordeste dos EUA: A, B, C e D. 55

Figura 15 – Clusters artificiais gerados no mapa do Nordeste dos EUA: E e F. . . . 55

Figura 16 – Clusters artificiais gerados no mapa do Nordeste dos EUA: BOS, NYC

(11)

Gerais, Brasil, por regi˜ao em 2006: (a) mapa taxa de doen¸ca; (b) Mapa

da popula¸c˜ao em risco. . . 60

Figura 18 – Parte superior - (_•) solu¸cões não-dominadas, 999 conjuntos de solu¸cões

n˜ao-dominadas simuladas sobre a hip´otese nula e a isolinha de p-valor

= 0,05; Parte inferior - mapa em escala de cinza para as solu¸c˜oes

n˜ao-dominadas observadas, obtidas pelo algoritmo MOBPSO-DP. . . . 62

Figura 19 – Parte superior - (_•) solu¸cões não dominadas, 999 conjuntos de solu¸cões

n˜ao dominadas simuladas sob a hip´otese nula e a isolinha de p-valor

= 0,05; Parte inferior - mapa em escala de cinza para as solu¸c˜oes

n˜ao-dominadas observadas, obtidas pelo algoritmo MOBPSO-NC. . . . 63

n˜ao dominadas simuladas sob a hip´otese nula e a isolinha de p-valor=

0,05; Parte inferior - mapa em escala de cinza para as solu¸c˜oes

n˜ao-dominadas observadas, obtidas pelo algoritmo MOBPSO-CG. . . 64

Figura 21 – Cluster encontrado com maior valor obtido pela estat´ıstica de teste T

pelo algoritmo MOBPSO-DP. . . 65

Figura 22 – Cluster encontrado com maior valor obtido pela estat´ıstica de teste T

pelo algoritmo MOBPSO-NC e MOBPSO-CP. . . 66

Figura 23 – Cluster encontrado pelo m´etodo Scan El´ıptico com maior valor obtido

pela estat´ıstica de teste T, constitu´ıda por 86 regi˜oes. . . 67

n˜ao dominadas simuladas sobre a hip´otese nula e a isolinha de p-valor

= 0,05 ; Parte inferior - mapa em escala de cinza para as solu¸c˜oes

n˜ao-dominadas observadas, obtidas pelo m´etodo Scan El´ıptico. . . 68

Figura 25 – Fronteiras Pareto-´otimas obtidas pelos m´etodos MOBPSO-DP (C´ırculos)

(12)

Algoritmo 1 – - Pseudocódigo para a constru¸cão gulosa da popula¸cão de part´ıculas/indiv´ıduos. 45

Algoritmo 2 – - Pseudoc´odigo para a Crowding Distance Computation.. . . 47

Algoritmo 3 – - Pseudoc´odigo para o Operador de Muta¸c˜ao. . . 49

Algoritmo 4 – - Pseudocódigo do MOBPSO para o problema de deteçcão de clusters

(13)

Tabela 1 – Valores obtidos com o c´alculo do poder pelos algoritmos MOBPSO-DP,

MOBPSO-NC e MOBPSO-CP e pelo M´etodo Scan El´ıptico. . . 57

Tabela 2 – Valores obtidos com o c´alculo da Sensibilidade pelos algoritmos

MOBPSO-DP, MOBPSO-NC e MOBPSO-CP e pelo M´etodo Scan El´ıptico. . . . 58

Tabela 3 – Valores obtidos com o c´alculo do Valor Preditivo Positivo pelos

algorit-mos MOBPSO-DP, MOBPSO-NC e MOBPSO-CP e pelo M´etodo Scan

El´ıptico. . . 58

Tabela 4 – Tempo de execu¸cão nas simula¸cões na aplica¸cão. . . 69

(14)

AGs Algoritmos Gen´eticos.

BPSO Binary Particle Swarm Optimization.

MOPSO Multi-Objective Particle Swarm Optimization.

MOPSO-CD Multi-objective Particle Swarm Optimization with Crowding Distance.

NSGA-II Nondominated Sorting Genetic Algorithm II.

(15)

1 Introdu¸c˜

ao

. . . 16

1.1 Objetivos

. . . 18

1.1.1 Objetivo Geral

. . . 18

1.1.2 Objetivos Espec´ıficos

. . . 18

1.2 Estrutura do texto

. . . 19

2 Fundamenta¸c˜

ao Te´

orica

. . . 20

2.1 O Problema de Detec¸c˜

ao de

Clusters

Espaciais

. . . 20

2.1.1 Estat´ıstica Espacial

Scan

. . . 22

2.1.2 M´

etodos de detec¸

c˜

ao de

clusters

. . . 23

2.1.2.1 O M´etodo

Scan

El´ıptico

. . . 26

2.1.3 Fun¸c˜

oes de Penaliza¸

c˜

ao

. . . 26

2.1.3.1 Penaliza¸c˜ao por Compacidade Geom´etrica

. . . 27

2.1.3.2 Penaliza¸c˜ao por N˜ao-Conectividade

. . . 28

2.1.3.3 A Penaliza¸c˜ao por Dispers˜ao

. . . 30

2.2 Otimiza¸

c˜

ao Multiobjetivo

. . . 32

2.3 Particle Swarm Optimization

. . . 34

2.3.1 Binary Particle Swarm Optimization

. . . 37

2.4 C´

alculo de significˆ

ancia das solu¸c˜

oes

. . . 37

2.4.1 Fun¸c˜

oes de Aproveitamento

. . . 39

3 Algoritmo Proposto

. . . 41

3.1 Vis˜

ao Geral

. . . 41

3.2 Aspectos Estruturais

. . . 41

3.2.1 Vari´

aveis de decis˜

ao

. . . 43

3.3 Inicializa¸

c˜

ao

. . . 44

3.4 Defini¸

c˜

ao dos guias pBest e gBest

. . . 45

3.4.1 Crowding Distance Computation

. . . 46

3.5 Atualiza¸

c˜

oes da Velocidade e da Posi¸

c˜

ao

. . . 47

3.6 Operador de Muta¸

c˜

ao/Turbulˆ

encia

. . . 48

(16)

4.1 Configura¸

c˜

oes dos Algoritmos, do m´

etodo

Scan

El´ıptico

e do Ambiente de Execu¸

c˜

ao dos Experimentos

. . . 53

4.2 Avalia¸c˜

oes Num´

ericas

. . . 54

4.3 Ocorrˆ

encias de Casos Reais da Doen¸

ca de Chagas no

Estado de Minas Gerais

. . . 59

5 Conclus˜

oes

. . . 71

5.1 Trabalhos Publicados

. . . 72

Referˆ

encias

1

. . . 73

(17)

1 Introdu¸c˜

ao

O problema de deteçcão e inferência de clusters (ou pela tradu¸cão aglomerados) possui aplicabilidade em áreas de evidente importância como em problemas ligados à saúde pública (epidemiologia e vigilância sindrômica), criminologia, pesquisas de mercado, entre outros. As análises das deteçcões podem ser realizadas em intervalos, que caracterizam as três diferentes abordagens do problema, sendo elas no espa¸co (cluster espacial), no tempo (cluster temporal), ou em ambos (cluster espa¸co-temporal).

As análises têm como objetivo verificar se um número de ocorrências é discrepante em um subconjunto no espa¸co, no tempo ou em ambos em rela¸cão a toda área em estudo. Estudos sobre a incidência de doen¸cas são de grande interesse na comunidade cient´ıfica. Algoritmos para deteçcão e inferência de clusters são ferramentas úteis para o alerta precoce de surtos de doen¸cas infecciosas (KULLDORFF et al., 2007).

Um cluster pode ser visto como um subconjunto limitado definido no espa¸co, no tempo ou em ambos, em que o risco da ocorrência de um fenômeno de interesse (uma determinada doen¸ca, ocorrências criminais, entre outros) é discrepante, ou seja, muito alta ou muito baixa quando comparada com o risco do conjunto como um todo, e simultaneamente significativo do ponto de vista estat´ıstico.

A Estat´ısticaScan proposta porKulldorff(1997) é o método mais usual, atualmente, empregado nos procedimentos de deteçcão de clusters em suas abordagens. O método é baseado em um teste da razão de verossimilhan¸cas. O valor máximo obtido pela estat´ıstica caracterizará a ocorrência do cluster mais veross´ımil em um subconjunto limitado no espa¸co (ou tempo, ou em ambos) em estudo, ou seja, a solu¸cão para o problema. Neste sentido o problema é facilmente modelado como um problema de otimiza¸cão sendo a estat´ıstica Scan a principal fun¸cão objetivo a ser otimizada.

A aplica¸cão da estat´ısticascan, limitada à abordagem espacial do problema, inde-pende da forma das solu¸cões a serem pesquisadas, entretanto o delineamento dos clusters

(18)

trabalhos de (DUCZZMAL; ASSUNÇ ÃO, 2004; DUCZMAL et al., 2007; DUCZMAL; CANÇ ADO; TAKAHASHI, 2008).

A importância do desenvolvimento de métodos de deteçcão de clusters irregulares surge diante do fato do fenômeno de interesse muitas vezes estar atrelado a áreas que comumente assumem formas diversas das convencionais. Exemplo dessa situa¸cão podem ocorrer em um subconjunto de regiões ligadas, como por exemplo, a curso de rios, rodovias, costas litorâneas, entre outros. Diante disso, e dos problemas anteriormente relatados, trabalhos recentes propõem abordagens empregando técnicas de otimiza¸cão e fun¸cões de penaliza¸cão na tentativa da obten¸cão de solu¸cões satisfatórias para o problema.

Um ponto chave no desenvolvimento de métodos para a deteçcão declusters espaciais de forma irregular é que, diante dos vários graus de liberdade inerente às formas geométricas, algum mecanismo de corre¸cão deve ser empregado objetivando compensar o aumento da flexibilidade, evitando a ocorrência de falsos-positivos (DUCZMAL et al.,2007;DUCZMAL; KULLDORFF; HUANG, 2006). Este fato tem sido reconhecido desde o estudo inicial de clusters de forma el´ıptica (KULLDORFF et al.,2006). Neste sentido Yiannakoulias, Rosychuk e Hodgson (2007) propuseram uma fun¸cão de penaliza¸cão topológica sobre os

clusters candidatos. Estas corre¸cões também foram tratadas em abordagens multiobjetivo para o problema (DUCZMAL; CANÇ ADO; TAKAHASHI, 2008; CANÇ ADO et al.,2010;

DUARTE et al., 2010). No entanto, o custo computacional dos procedimentos ligados a tais funcionais tende a elevar, em geral, pois testes de conectividade das solu¸c˜oes precisam ser inclu´ıdos.

Particle Swarm Optimization (PSO) é uma técnica de computa¸cão evolutiva similar em alguns aspectos a Algoritmos Genéticos (AGs), sendo aplicada eficientemente em uma série de problemas de otimiza¸cão (KENNEDY; SPEARS, 1998). No problema de deteçcão de clusters abordagens baseadas em PSO foram pouco exploradas. Um estudo feito por Izakian e Pedrycz (2012) define uma estrutura geométrica para as janelas de busca aplicando posteriormente PSO como otimizador. Propostas multiobjetivo para o problema em estudo têm sido bem avaliadas como reportam o trabalho feito por Can¸cado et al. (2010) usando AGs. Em alguns problemas, como descrevemKennedy e Spears(1998), PSO tem como vantagens ser de fácil implementa¸cão, tem poucos parâmetros, requer menos recursos computacionais e pode convergir mais rapidamente. Em Eberhart e Yuhui

(19)

multiobjetivo baseadas em PSO n˜ao foram ainda exploradas, tonando-se assim, uma ´area promissora para estudos.

1.1 Objetivos

1.1.1 Objetivo Geral

Esta disserta¸cão tem como principal objetivo apresentar uma nova abordagem de otimiza¸cão para o problema de deteçcão e inferência de clusters espaciais irregulares e também propor uma fun¸cão de penaliza¸cão aplicada sobre a topologia das solu¸cões candidatas. A abordagem utiliza como base a técnica de computa¸cão evolucionáriaParticle Swarm Optimizationversão binária e multiobjetivo visando maximizar o valor da estat´ıstica Espacial Scan e minimizar o valor da nova fun¸cão de penaliza¸cão.

1.1.2 Objetivos Espec´ıficos

Os objetivos espec´ıficos definidos com a realiza¸cão desta disserta¸cão são os seguintes:

• Realizar uma revis˜ao bibliogr´afica sobre o problema em estudo;

• Propor uma fun¸c˜ao de penaliza¸c˜ao sobre a topologia dos clusters candidatas.

• Desenvolver e implementar uma abordagem de otimiza¸cão multiobjetivo para o problema com base na técnica de computa¸cão evolutivaParticle Swarm Optimization;

• Aplicar medidas de avalia¸cão do porder deteçcão e qualidade da abordagem proposta;

• Aplicar o algoritmo multiobjetivo em um conjunto de dados reais do problema;

• Comparar os resultados obtidos com a fun¸cão de penaliza¸cão proposta com demais fun¸cões descritas na literatura por meio do algoritmo multiobjetivo;

• Comparar os resultados obtidos pela abordagem com o m´etodo de defini¸c˜ao de janelas de busca de clusters, Scan El´ıptico; e

(20)

1.2 Estrutura do texto

(21)

2 Fundamenta¸c˜

ao Te´

orica

Este cap´ıtulo apresentada uma revisão sobre os fundamentos teóricos dos principais temas tratados e utilizados como base para o desenvolvimento deste trabalho de disserta¸cão. A Se¸cão 2.1descreve o problema de deteçcão e inferência de clusters em sua abordagem espacial, a se¸cão compreende a principal metodologia usada nos métodos deteçcão de

clusters (Subse¸cão 2.1.1), um resumo sobre métodos de deteçcão (Subse¸cão 2.1.2), o métodoScan El´ıptico (Subse¸cão 2.1.2.1) e as fun¸cões de penaliza¸cão adotadas em métodos de deteçcão declusters de forma irregular (Subse¸cão2.1.3). A Se¸cão2.2descreve uma s´ıntese dos conceitos de otimiza¸cão multiobjetivo. A Se¸cão 2.3 relata a técnica de computa¸cão evolucionária Particle Swarm Optimization e sua extensão para aplica¸cão em problemas de otimiza¸cão discretos (Subse¸cão 2.3.1). E, por último, a Se¸cão 2.4 descreve a abordagem adotada para o cálculo de significância estat´ıstica das solu¸cões obtidas pelo algoritmo proposto.

2.1 O Problema de Detec¸c˜

ao de

Clusters

Espaciais

Esta se¸cão tem como objetivo apresentar as defini¸cões que se limitam à versão espacial do problema de deteçcão e inferência de clusters. Em muitas aplica¸cões frequente-mente existe a necessidade da delimita¸cão de um subconjunto de regiões em detrimento de outras onde a ocorrência do número de casos para um fenômeno de interesse seja maior ou menor do que o esperado e que ao mesmo tempo seja estatisticamente significativo. Muitas dessas aplica¸cões estão ligadas à problemas relacionados a epidemiologia, vigilância sindrômica, criminologia, entre outros. Esta questão é o objetivo primordial da abordagem espacial do problema de deteçcão de clusters.

(22)

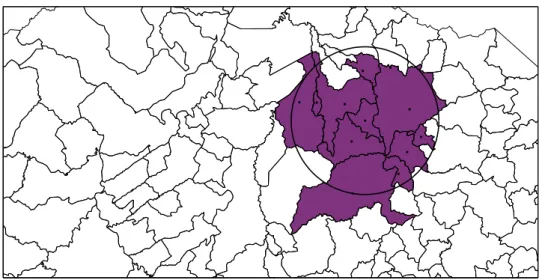
A Figura1 ilustra um exemplo de um subconjuntoz considerando as regiões cujos centroides são internos a uma determinada janela circular sobrepondo a área do mapa em estudo.

Figura 1 – Uma poss´ıvel zona obtida para uma dada janela circular, Fonte:Moreira(2011).

Nestes termos um cluster espacial é um subconjunto de zonas geograficamente limitadas em que o risco de ocorrência do fenômeno de interesse é alto ou baixo o suficiente para serem considerados significativos do ponto de vista estat´ıstico em rela¸cão à região de estudo como um todo.

Análises simplórias na tentativa de inferir quanto a significância de um cluster

poderiam levar em conta simplesmente a incidência de casos do fenômeno de interesse em cada zona, ou seja, o número de casos observados dividido pela popula¸cão, ou ainda o risco relativo que é o número observado de casos dividido pelo número esperado de casos (DUARTE, 2009). Apesar de parecer razoável, essa análise não resolve o problema de deteçcão de clusters, pois é poss´ıvel que clusters candidatos com popula¸cões muito discrepantes possam apresentar uma mesma propor¸cão de casos. Diante disso, estas solu¸cões candidatas seriam comparadas em situa¸cão de igualdade. Um aumento no risco relativo é tão mais significativo quanto maior é a popula¸cão de risco do cluster candidato. Isso significa que, embora uma região, ou uma zona possa apresentar um alto risco relativo, se sua popula¸cão é pequena, ela se torna pouca significativa.

Can¸cado(2009) exemplifica a ocorrência deste problema diante do seguinte cenário, considere duas cidades X e Y com popula¸cões de risco para um fenômeno de interesse

(23)

popula¸cão total de risco do mapa igual a n= 10.000.000 e o número total de casos reais igual a c= 100.000. Em um cenário sobre hipotese nula, ou seja, caso não haja cluster no mapa, a frequência de casos esperados deve ser de 1 caso para cada 100 habitantes para todas as regiões do mapa. Assim, o número de casos esperados nas cidades X e Y devem ser ωx = 1 eωy = 10.000, respectivamente. Sejam os casos reais nas cidades X e Y iguais a cx = 2 e cy = 20.000, respectivamente. Neste cenário, ambas as cidades apresentam risco relativo, ou seja, o número de casos reais dividido pelo número de casos esperados, iguais a cx/ωx =cy/ωy = 2. Nesta situa¸cão, através da análise pelo risco relativo as duas regiões são equivalentes. Todavia, para a cidade Y uma varia¸cão de 10.000 para 20.000 casos não deve ser considerada como uma simples flutua¸cão estat´ıstica, necessitando-se de estudos mais detalhados.

A estat´ısticaScan proposta por Kulldorff (1997) resolve o problema descrito acima, sendo adotada atualmente como a principal técnica nas abordagens de deteçcão e inferência de clusters em suas versões. A se¸cão 2.1.1 descreve os principais aspectos conceituais deste método.

2.1.1 Estat´ıstica Espacial

Scan

A estat´ıstica espacial scan proposta porKulldorff (1997), é atualmente o método mais usual empregado em abordagens de deteçcão e inferência declusters espacial, temporal e espa¸co-temporal. A estat´ıstica é baseada em um teste de razão de verossimilhan¸cas que busca um subconjunto de regiões ao longo de um mapa em estudo, o valor máximo para a estat´ıstica .

(24)

O logaritmo da raz˜ao de verossimilhan¸cas Λ(z) =log(L(Z)/L0) ´e, segundoKulldorff

(1997) definido pela equa¸c˜ao (1):

Λ(z) =   

 

czlog

cz

µz

+ (C₋cz) log

C₋cz

C₋µz

, se cz > µz

0, caso contr´ario

(1)

A fun¸cão Λ(z) é maximizada sobre o conjunto de todas as zonas Z do mapa, identificando a zona que constitui o cluster mais veross´ımil. Logo se tem a estat´ıstica de teste que é dada por T =maxz∈ZΛ(z).

2.1.2 M´

etodos de detec¸

c˜

ao de

clusters

Definida a estat´ıstica de teste, a busca por solu¸cões ótimas, ou seja, aquelas que obtém o valor máximo para a estat´ıstica, poderia ser feita dentro do conjuntoZ. Entretanto, o emprego de métodos baseados em busca completa (ou seja, for¸ca bruta) torna essa tarefa computacionalmente impraticável diante do grande número de zonas poss´ıveis de serem formadas em mapa com número de regiões na ordem de algumas centenas. Em um mapa com n regiões, deverão ser analisados aproximadamente 2n _{subconjuntos de zonas fact´ıveis} para o problema.

Para contornar esse problema, os métodos de deteçcão declusters espaciais normal-mente fazem uso de duas técnicas:

• A redu¸c˜ao do conjunto das solu¸c˜oes em Z para um subconjuntoZ′ _de _Z _{das zonas} promissoras ou que permita uma busca completa; e

• O emprego de métodos estocásticos de otimiza¸cão.

Todavia, em ambas as técnicas não existe a garantia do encontro da solu¸cão ótima global, mas comumente tendem a proporcionar solu¸cões de boa qualidade. Um outro problema relacionado aos métodos de deteçcão de clusters está ligado à forma das solu¸cões encontradas.

Muitos métodos da literatura não são adequados para controlar a forma dosclusters

(25)

2009). As solu¸cões que apresentam essa configura¸cão claramente descaracterizam o signifi-cado de limita¸cão geográfica do fenômeno em estudo. Esse cenário comumente ocorrerá diante da falta de uma estratégia de penaliza¸cão que deve ser incorporada aos métodos de deteçcão e inferência de clusters, visto que essas abordagens tendem a obter o máximo valor para a estat´ıstica de teste T.

Figura 2 – Cluster encontrado pelo algoritmo Simulated Annealing sem penaliza¸c˜ao, fonte:

Can¸cado (2009) .

Em outros métodos existe somente a garantia do encontro de solu¸cões com um formato espec´ıfico. Nesta linha há, por exemplo, o método Scan Circular proposto por

Kulldorff e Nagarwalla (1995) garante apenas a busca restrita de clusters de forma circular. Uma extens˜ao do formato circular visando uma maior cobertura das formas poss´ıveis

clusters candidatos ´e o Scan el´ıptico, proposto por Kulldorff et al.(2006).

No entanto, existem muitas situa¸cões em que ocluster verdadeiro apresenta uma forma que não se ajusta em nenhum dos formatos prescritos anteriormente. Em muitos casos, o fenômeno de interesse pode estar atrelado a zonas que apresentam formas diversas das convencionais. Exemplos desta situa¸cão poderia ser a ocorrência do fenômeno de interesse ao longo do percurso de rios, estradas, rodovias, costas litorâneas e entre outros, o que daria, nestas circunstâncias, uma forma mais alongada ao cluster verdadeiro.

(26)

adotada é o emprego de uma fun¸cão de penaliza¸cão para a forma ou topologia associada a estrutura do cluster candidato.

Can¸cado(2009) classifica os métodos de deteçcão declusters quanto à geometria das solu¸cões que podem ser encontradas, sendo os seguintes:

• Os clusters regulares, aqueles que possuem formato espec´ıfico, comumente o circular, o el´ıptico, e entre outros. Tais métodos são restritos em suas análises aos formatos predefinidos e fazem uso da técnica de redu¸cão do conjunto de solu¸cões candidatas; e

• Os clusters irregulares, os que apresentam formas diversas. Existem métodos desta classe que fazem tanto o uso da redu¸cão do conjunto de solu¸cões candidatas quanto o uso de métodos estocásticos de otimiza¸cão.

As técnicas de computa¸cão evolucionária são bem conhecidas pela sua habilidade de busca global, e tem sido amplamente aplicadas ao problema de deteçcão e inferência de clusters espaciais (WU; GRUBESIC, 2010), (DUCZMAL et al., 2007) e (DUCZMAL; CANÇ ADO; TAKAHASHI, 2008). Tais técnicas são baseadas em um esquema que não restringe diretamente o conjunto de solu¸cões, mas através de mecanismos espec´ıficos, pesquisam algumas das solu¸cões candidatas durante o procedimento, descartando as solu¸cões menos promissoras.

Algoritmos Genéticos (AGs) abordados em Duczmal et al. (2007) e Duczmal, Can¸cado e Takahashi (2008) especificamente implementados para o problema de deteçcão e inferência de clusters, possuem operadores desenvolvidos especialmente para este problema. Os operadores genéticos promovem a busca de solu¸cões que maximizam o valor da estat´ıstica de teste, todavia ocorrem em problemas semelhantes ao da abordagem implementada por meio da metaheur´ıstica Simulated Annealing.

Similar aos AGs, Particle swarm optimization ou pela tradu¸cão Otimiza¸cão por Enxame de Part´ıculas é uma técnica de computa¸cão evolutiva inicializada com uma popula¸cão de solu¸cões aleatórias e que a cada solu¸cão potencial também é atribu´ıda uma velocidade aleatória e essas solu¸cões potenciais, denominadas de part´ıculas, sobrevoam o espa¸co de busca (EBERHART; KENNEDY, 1995a). E igualmente a outras abordagens de algoritmos de computa¸cão evolutiva, PSO pode ser aplicada para resolver a maioria dos problemas de otimiza¸cão (EBERHART; YUHUI, 2001).

(27)

a técnica de otimiza¸cão PSO multiobjetivo, visando maximizar o valor da estat´ıstica de teste T e minimizar a fun¸cão de penaliza¸cão também proposta neste trabalho que será descrita na se¸cão 2.1.3.3 .

2.1.2.1 O M´etodo

Scan

El´ıptico

O método Scan El´ıptico proposto por Kulldorff et al. (2006) surgiu como uma extensão imediata ao Scan circular, definindo janelas em formas de elipses em suas análises de busca, não se restringindo com isso apenas à forma circular.

Uma elipse pode ser definida pelos seguintes parâmetros: as coordenadasx e y de seu centroide, o comprimento de seus eixos maior e menor e o ângulo entre seu eixo maior e o eixo das abscissas. O método utiliza as janelas de busca no mapa em estudo analisando as zonas, cujos centroides são cobertos pela janela, e avaliando-as através da estat´ıstica espacial. A zona referente ao maior valor de a Λ(z) determinará a ocorrência do cluster, ou seja, a solu¸cão.

O Scan El´ıptico além de reduzir o conjunto de solu¸cões candidatas através da utiliza¸cão de janelas de busca de forma el´ıptica, também compreende a aplica¸cão de varia¸cões sobre as janelas, ligadas ao tamanho, à orienta¸cão e à excentricidade, aumentando assim o range dos formatos dos potenciais clusters incidentes em um mapa sob estudo.

Todavia, como descrito na se¸cão anterior, mesmo com a defini¸cão prévia de diversos formatos para determina¸cão das janelas de busca a delimita¸cão do cluster real de formato qualquer é uma tarefa computacionalmente impraticável diante do tamanho do espa¸co de busca das solu¸cões e dos variados graus inerentes à liberdade da forma.

2.1.3 Fun¸c˜

oes de Penaliza¸

c˜

ao

As fun¸cões de penaliza¸cão constituem uma técnica normalmente incorporada aos métodos de deteçcão de clusters espaciais de forma irregular, são aplicadas sobre a forma geométrica e/ou topológica do subgrafo associado ao cluster candidato e são utilizadas tanto em abordagens de otimiza¸cão mono-objetivo quanto multiobjetivo.

(28)

para a estat´ıstica de testeT. Em abordagens multiobjetivo a fun¸c˜ao de penaliza¸c˜ao torna-se um dos objetivos a serem otimizados no problema juntamente com Λ(z).

As se¸cões seguintes trazem uma breve descri¸cão sobre as fun¸cões de penaliza¸cão por Compacidade Geométrica e Não-Conectividade. A última se¸cão descreve a fun¸cão proposta nesta disserta¸cão, denominada Dispersão.

2.1.3.1 Penaliza¸c˜ao por Compacidade Geom´etrica

A penaliza¸cão por Compacidade Geométrica proposta por Duczmal, Kulldorff e Huang (2006) tem como finalidade penalizar os clusters candidatos que possuem um formato muito irregular, privilegiando os clusters cujo formato se aproxima da forma circular. Por defini¸cão a Compacidade Geométrica K(z) de uma zona z é dada pela

Equa¸c˜ao 2:

K(z) = 4πA(z)

H(z)2 . (2)

em que A(z) ´e a ´area da zona z eH(z) o per´ımetro da zona z.

O valor da Compacidade Geométrica de uma zonaz não está ligada ao tamanho da zona mas sim a sua forma. O c´ırculo é o formato que possui o maior valor de compacidade, cujo valor é K(z) = 1. Quanto mais arredondado é o formato de uma zona mais próximo de 1 será seu valor. Por outro lado, quanto mais irregular for a forma, mais próximo de 0 será o valor da compacidade. O formato de um quadrado possui o valor de compacidade igual a K(z) = 0.785. Já o valor para um retângulo com a base sendo o dobro da altura temos K(z) = 0.698.

(29)

(a)

(b)

Figura 3 – Exemplo de dois subconjuntos de regi˜oes em destaque (cinza) que assumem os formatos circular (a) e retangular (b).

2.1.3.2 Penaliza¸c˜ao por N˜ao-Conectividade

A penaliza¸cão por Não-Conectividade foi proposta por Yiannakoulias, Rosychuk e Hodgson (2007) e é baseada na rela¸cão entre o número de arestasa(z) e o número de vértices v(z) do subgrafo associado à zona z candidata.

A penaliza¸cão por Não-Conectividade de uma zonaz é definida pela Equa¸cão 3:

Y(z) = a(z)

3(v(z)₋2). (3)

(30)

não estar ligada à forma geométrica do cluster candidato, mas sim ao grau de conexidade do subgrafo associado ao cluster candidato.

A fun¸cão de Não-Conectividade objetiva penalizar solu¸cões candidatas cujo subgrafo associado possui estrutura baseada em árvores e priorizando solu¸cões mais conexas (valores mais próximos de 1 para Y(z)). Para exemplificar sua aplica¸cão, a Figura 4 apresenta três zonas (a), (b) e (c) e os respectivos subgrafos associados. A penaliza¸cão por Não-Conectividade será na zona (a) considerando o número de vértices v(z) = 7 e o número de arestas a(z) = 6 o valor de aproximadamente Y(z) = 0,40, na zona (b) o número de vértices v(z) = 8 e o número de arestas a(z) = 7, assim Y(z) = 0,39 e na zona (c) o número de vértices v(z) = 9 e o número de arestas a(z) = 20 e Y(z) = 0,95.

(a)

(b)

(c)

Figura 4 – Exemplo de trˆes zonas (a), (b) e (c) em destaque e o subgrafo associado.

(31)

2.1.3.3 A Penaliza¸c˜ao por Dispers˜ao

Esta se¸cão propõe uma nova fun¸cão de penaliza¸cão sobre a topologia do cluster

potencial a ser minimizada. Denomina-se penaliza¸cão por dispersão por estar ligada com a distribui¸cão das regiões da zona candidata no mapa dispostas em um espa¸co bidimensional (x, y).

Considere um mapa em estudo dividido emm regiões, onde cada região é associada a um ponto de coordenadas (x, y) denominado centroide, e uma zona z, ou seja, qualquer subconjunto de regiões, com os centroides correspondentes (x1, y1), . . . ,(xnz, ynz), 1 ≤

nz ≤m. Seja x= max{xi} ex= min{xi} em que i∈ {1, . . . , nz} e defina d1 =x−x. Da mesma forma, defina-se d2 =y₋y.

A fun¸cão de penaliza¸cão por dispersão de uma zonaz é definido como:

D₍_z_{) =} 2(d1d2)

d1+d2. (4)

Ou seja, é a média harmônica do maior intervalo de coordenadas de centroides x e y da zona z, a ser minimizada e independente da forma do cluster.

Nota-se que uma zona z com valore alto para D₍_z_{) tendem ser um conjunto de} regiões com alto valor de verossimilhan¸ca que se espalham de forma aleatória por todo o mapa ou um conjunto de regiões desconexas distantes geograficamente, ou seja, uma solu¸cão indesejável na prática. Por outro lado uma zona com valor mais baixo de D₍_z₎ pode representar um clusters de forma arbitrária sendo um conjunto de regiões conexas ou desconexas, mas geograficamente próximas (tamanho moderado).

(32)

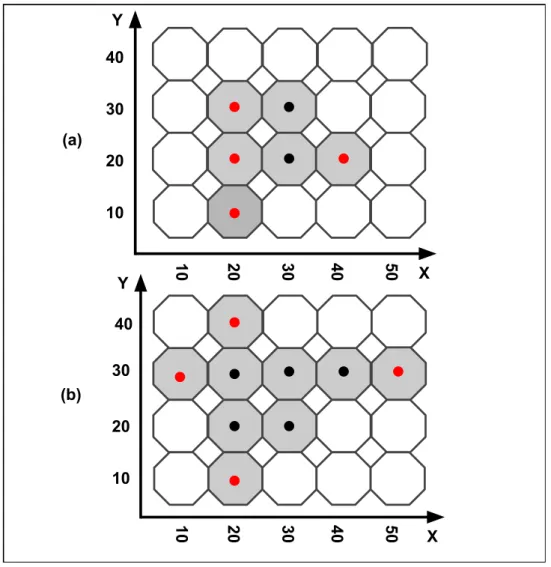
Figura 5 – Exemplo de um conjunto de centroides em um cluster e os considerados para o cálculo da fun¸cão de penaliza¸cão por Dispersão.

Para demonstrar o comportamento da aplica¸cão da fun¸cão de penaliza¸cão proposta, a Figura 6 exibe dois exemplos de clusters (a) e (b) dispostos em um espa¸co (x, y), cujas zonas estão em destaque, e seus respectivos centroides. Para o cálculo da Dispersão no

(33)

(a)

Y X

X 10

20 30 40

10 20 30 40

10 20 30 40 50

Y

(b)

Figura 6 – Clusters (a) e (b) dispostos em um espa¸co bidimensional (x, y) e centroides associados e considerados para o cálculo da fun¸cão de penaliza¸cão.

2.2 Otimiza¸

c˜

ao Multiobjetivo

(34)

min f(x) = (f1(x), f2(x), ..., fm(x))∈ Y ⊂ Rm

sujeito a:

Fx =

        

gi(x)≤0∀i= 1, ..., p

hj(x) = 0 ∀j = 1, ..., q

x_{∈ X}

Quando temos dois ou mais objetivos conflitantes, pode ser imposs´ıvel encontrar uma solu¸cão que satisfa¸ca todas elas. Uma forma de resolver este problema é encontrar um conjunto de solu¸cões, cada um dos quais representando um compromisso (trade-off )

entre os objetivos, diretamente relacionado ao conceito de dominˆancia, definido a seguir:

Defini¸cão 1 (Rela¸cão de Dominância). Seja f(x) = (f1(x), f2(x), ..., fm(x)) uma fun¸cão

definida em um espa¸co X. Um ponto x1 domina um ponto x0, denotado por, x1 _≺x0 e

x0, x1 _∈X se fi(x1)≤fi(x0), i= 1, ..., n e se existe pelo menos um ´ındice j ∈ {1, ..., m}

tal que fj(x1)< fj(x0).

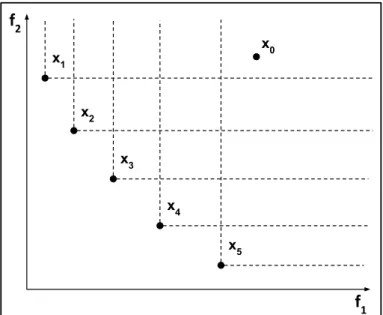
A Figura7ilustra o conceito da rela¸cão de dominância para duas fun¸cões objetivosf1

ef2 a serem minimizadas. No exemplo, o ponto x1 domina o pontox0, poisf1(x1)> f1(x0) e f2(x1) > f2(x0). O mesmo acontece quando x0 ´e comparado com os pontosx2, x3, x4

e x5. Porém entre os pontos x1, x2, x3, x4 e x5 não existe essa rela¸cão, esses pontos são não-dominados. f₂ f₁ x₀ x₅ x₄ x₃ x₂ x₁

(35)

A solu¸cão para os problemas de otimiza¸cão multiobjetivo consiste na determina¸cão de solu¸cões Pareto-ótimas.

Defini¸cão 2 (Solu¸cão Pareto-ótima). Diz-se que uma solu¸cão x1 _∈f é Pareto-ótima se não existe x2 _∈f tal que x2 domina x1.

O conjunto _YN D _⊂ _Rm _{denota o conjunto de todas as solu¸cões não-dominadas} (espa¸co dos objetivos) e _XE _{o conjunto de todas as solu¸cões Pareto-ótimas (ou eficientes)} (variáveis de decisão).

Tradicionalmente as meta-heur´ısticas são boas técnicas aplicadas na resolu¸cão de problemas de otimiza¸cão usadas para guiar outras heur´ısticas ou algoritmos em seus espa¸cos de busca aplicadas tanto em problemas de otimiza¸cão mono-objetivo quanto multiobjetivo na convergência de solu¸cões (DONOSO; FABREGAT,2016).

2.3 Particle Swarm Optimization

Particle Swarm Optimization (PSO) é uma técnica de computa¸cão evolucionária desenvolvida por Kennedy e Eberhart em 1995. O PSO consiste em um método de otimiza¸cão que visa simular um modelo social simplificado inspirado no comportamento da revoada de bando de pássaros e no movimento de cardume de peixes (EBERHART; KENNEDY, 1995a).

A inten¸cão inicial na concep¸cão da técnica era o de simular a coreografia da revoada de bandos de pássaros e, todavia, em algum ponto do desenvolvimento do método foi obser-vado potencial de aplicabilidade do modelo como uma técnica de otimiza¸cão (EBERHART; KENNEDY, 1995b). A abordagem PSO é inicializada de forma aleatória, no espa¸co de busca do problema, com uma popula¸cão de potenciais solu¸cões denominadas part´ıculas. A cada part´ıcula é atribu´ıda uma velocidade também inicializada de forma aleatória.

Eberhart e Kennedy (1995a) apresentam duas versões de Particle Swarm Opti-mization. A primeira é o modelo da proposta original denominado Global (gbest) que adota o conjunto de todas as part´ıculas da popula¸cão como vizinhan¸ca e a segunda é o modelo denominado Local (lbest) que adota subconjuntos de vizinhan¸cas de part´ıculas da popula¸cão total.

(36)

fun¸cão da posi¸cão da part´ıcula no espa¸co de busca, obtido por cada part´ıcula até o momento recebe a denomina¸cão de pbest. Outra posi¸cão armazenada pelo PSO é o melhor valor global obtido até o momento por qualquer part´ıcula da popula¸cão. Esse valor recebe a denomina¸cão de gbest.

O modelo global da Particle Swarm Optimization segue a execu¸c˜ao das seguintes etapas:

1. Inicializar uma popula¸cão P de part´ıculas com suas posi¸cões pi e velocidades vi definidas de forma aleatória nas dimensões d no espa¸co do problema.

2. Para cada part´ıcula pi, calcule sua fun¸cão de aptidão (f itness) nas dimensões d. 3. Compare a fun¸cão de aptidão da part´ıcula pi com seu valor pbesti. Se o valor da

fun¸cão de aptidão for melhor que pbesti, então defina o novo valor do pbesti para o valor atual obtido pela fun¸cão de aptidão, e a localiza¸cão do pbesti igual a atual localiza¸cão definida nas dimensões d do espa¸co.

4. Compare a fun¸cão de aptidão com o melhor global da popula¸cão (gbest) definido. Se o valor da fun¸cão de aptidão for melhor do que a determinada por gbest redefina o valor de gbest para o valor obtido pela fun¸cão de aptidão.

5. Atualize a velocidade e a posi¸c˜ao das part´ıculas de acordo com as equa¸c˜oes (5) e (6), respectivamente:

vid=w∗vid+c1∗rand()∗(pbestid−xid) +c2∗rand()∗(gbestd−xid). (5)

xid=xid + vid. (6)

6. Se um critério de parada não for atendido, geralmente associado a um bom valor para a fun¸cão de aptidão ou a um número máximo de itera¸cões, o processo deve ser repetido a partir da segunda etapa.

A velocidadevid das part´ıculas nas dimensões do problema são limitadas a uma velocidade máxima vmax definida pelo desenvolvedor:

if(vid> vmax){ vid=vmax }.

(37)

A velocidade máxima consiste em um parâmetro importante, a defini¸cão de um valor alto para vmax possibilita com que as part´ıculas explorem boas solu¸cões e por outro lado a defini¸cão de um valor baixo restringem o alcance de explora¸cão das part´ıculas, podendo delimitar a busca a ótimos locais no espa¸co do problema.

As constantes de acelera¸cãoc1 ec2 da equa¸cão 5 representam os coeficientes dos termos de acelera¸cão que direciona cada part´ıcula às posi¸cões pbest e gbest. O ajuste destas constantes altera a quantidade de tensão no sistema. Em Eberhart e Yuhui (2001), os autores definem para as constante c1 e c2 o valor 2.0 para a maioria das aplica¸cões desenvolvidas.

A figura8 apresenta uma diagrama indicando o fluxo de execu¸c˜ao das principais etapas definidas anteriormente do algoritmo PSO em seu modelo global.

Inicializar população e

velocidades.

Calcular

aptidão.

Definir os guias

pBest

e

gbest

.

Atualizar velocidade e

posição.

Critério

de

parada.

Fim.

Início.

Sim

Não

(38)

No modelo local deParticle Swarm Optimization, as part´ıculas têm a informa¸cão de seu pbeste a melhor solu¸cão obtida por seus vizinhos mais próximos recebe a denomina¸cão de lbest opondo-se nesta questão ao modelo global, o qual as part´ıculas compartilham a melhor solu¸cão obtida com toda a popula¸cão de part´ıculas.

2.3.1 Binary Particle Swarm Optimization

A técnicaParticle Swarm Optimization foi proposta para a resolu¸cão de problemas de otimiza¸cão que ocorrem em espa¸co de busca real. Todavia, muitos problemas de otimiza¸cão são caracterizados por ocorrerem em um espa¸co de busca discreto, ou binário, como por exemplo o problema de deteçcão de clusters espaciais. Diante disso, Kennedy e Eberhart (1997) desenvolveram a Binary Particle Swarm Optimization (BPSO) uma adapta¸cão do PSO voltada para a aplica¸cão em problemas cujo espa¸co de busca é discreto. Nesta versão a equa¸cão (5) de atualiza¸cão da velocidade ainda é utilizada, em que

xid, pbestid, gbestd, estão restritos a 0 ou 1. A velocidade nesta implementa¸cão aponta a probabilidade de o elemento da posi¸cão correspondente assumir o valor 1. Na atualiza¸cão da posi¸cão das part´ıculas uma fun¸cão sigmoide (7) é introduzida para converter vid para o intervalo (0, 1).

A equa¸cão (8) é utilizada para a atualiza¸cão da posi¸cão de cada part´ıcula da popula¸cão:

s(vid) =

1

1 +exp−vid (7)

vid=  



1, rand()< s(vid). 0, caso contrario.´

(8)

Em querand() é um gerador de números aleatórios uniformes no intervalo [0.0,1.0]. E vid a nova posi¸cão assumida pela part´ıcula no espa¸co.

2.4 C´

alculo de significˆ

ancia das solu¸c˜

oes

(39)

será a que, dentre todas as analisadas, apresentar a maior valor de Λ(z). Antes de podermos afirmar que essa solu¸cão é um cluster, devemos lembrar que um cluster deve apresentar um número anormal de casos, ou seja, devemos comparar o mapa estudado contra vários mapas aleatórios.

No caso mono-objetivo, se fosse conhecida a distribui¸cão de probabilidade da estat´ıstica de teste T sob a hipótese de não existência de cluster no mapa em estudo, poderia ser determinado um valor cr´ıtico, Tcritico, resolvendo P(T > Tcritico) = α, com

α sendo a probabilidade de que T supere o valor cr´ıtico Tcritico, chamado de n´ıvel de significância, tradicionalmente α = 0,05. Assim, um valor de T abaixo de Tcritico pode ocorrer por mero acaso 95% das vezes, mas um valor acima deTcritico só acontece por acaso com probabilidade menor que ou igual a 5% e, portanto, a solu¸cão pode ser considerada um cluster. Essa probabilidade de que o valor observado da estat´ıstica de teste ocorra por mero acaso sob hipótese nula é chamada de probabilidade de significância do teste (p-valor). Se o p-valor de um cluster é menor que o n´ıvel de significância α dizemos que a existência daquele cluster é significativa ao n´ıvel α. Como, em princ´ıpio, essa distribui¸cão de probabilidade é desconhecida, utiliza-se simula¸cões de Monte Carlo (DWASS, 1957) para obter uma distribui¸cão emp´ırica dos valores da estat´ıstica sob a hipótese nula. Essas simula¸cões são executadas várias vezes e os valores da estat´ıstica T obtidos são ordenados (o valor correspondente ao quantil de 95% é a estimativa do valor cr´ıtico a um n´ıvel de significância de 5%). Dado o valor da estat´ıstica de teste dos casos observados, Tobs, a estimativa de seu p-valor é nobs+1

n , em que nobs é número de vezes de T sob a hipótese nula que são maiores que o valor de Tobs, em quen é o número de simula¸cões sob hipótese nula.

Em abordagens de otimiza¸cão multiobjetivo, de maneira análoga o cálculo da significância estat´ıstica dos clusters obtidos do mapa de casos observados é feita através da compara¸cão com os clusters obtidos através de simula¸cões de casos de vários mapas sob a hipótese nula, geradas por meio de simula¸cões de Monte Carlo. Sob a hipótese nula, casos simulados são distribu´ıdos aleatoriamente ao longo do mapa em estudo conforme a distribui¸cão de Poisson, de forma que cada região receba, em média, um número de casos proporcional à sua popula¸cão. Com isso, a estat´ıstica de testeT é calculada para o conjunto Pareto e este procedimento é repetido n vezes (Em que né o número de simula¸cões).

(40)

encontrar uma curva cr´ıtica acima do qual consideramos que um cluster seja significativo. Essa curva cr´ıtica divide o plano em duas regi˜oes de maneira que um ponto do plano no espa¸co Λ(z)_×P(z) ser´a considerado um cluster significativo se estiver acima dessa curva.

Can¸cado (2009) apresenta três técnicas utilizadas na estima¸cão desta curva cr´ıtica, nos problemas de otimiza¸cão multiobjetivo. Nesta disserta¸cão adotou-se o conceito das fun¸cões de aproveitamento (FONSECA; FONSECA; PAQUETE,2005) descrita na Se¸cão

2.4.

2.4.1 Fun¸c˜

oes de Aproveitamento

Considere um problema de otimiza¸cão biobjetivo, com as fun¸cões f1 e f2, e O o conjunto das solu¸cões não-dominadas definidas no espa¸co de objetivos de uma única execu¸cão do algoritmo (Veja a Figura 9). O conjuntoO_{está associado a uma fronteira que} divide o espa¸co de objetivos em duas regiões R1 e R0. R1 é a região de pontos dominados por, ou iguais a, pelo menos, um ponto em O _e _R0 _{a região dos pontos que não são} dominados por nenhum ponto em O_{. Uma solu¸cão}_x _{que é dominada por pelo menos uma} solu¸cão de um determinado resultado O_{, é dita atingida por} O_{. Na Figura} ₉_{, qualquer} solu¸cão localizada na região R1 atingida por O_.

f₁ f₂

R

₁

R

₀

x₁

x₂

x₃

x₄

(41)

Consideren execu¸cões do algoritmo. Como cada execu¸cão produz resultados dife-rentes podemos obter múltiplas fronteiras. Com isso, pode-se dividir o espa¸co objetivo em

n+ 1 tipos de regiões de acordo com a frequência com que estas regiões são atingidas. Os limites dessas regiões são denominadas fronteiras de aproveitamento. Estas frequências são usadas para estimar a probabilidade de atingir um ponto no espa¸co de objetivos, quando um grande número de execu¸cões do algoritmo são realizados.

A fun¸cão de aproveitamento avaliada em algum pontoO no espa¸co objetivo pode ser estimada pelos conjuntos de resultados O₁_{,... ,}O_n _{obtido através de} _n _{execu¸cões} independentes do algoritmo, como:

An(O) = 1

n

n X

i=1

I(O_iDO) (9)

Em que o s´ımbolo ”D” significa que O_i _atingiu _O _e_I _{é a fun¸cão indicadora, assumindo o} valor 1 se O_iDO, e 0 caso contrário.

No problema em estudo estamos interessados em estimar o p-valor das solu¸cões não-dominadas de clusters candidatos representados por pontos (Λ(z), P(z)) no espa¸co objetivo, em que P(z) é uma fun¸cão de penaliza¸cão.

(42)

3 Algoritmo Proposto

Este cap´ıtulo tem como objetivo apresentar o algoritmo proposto nesta disserta¸cão para a aplica¸cão ao problema de deteçcão e inferência de clusters espaciais irregulares. Utilizou-se como base a técnica de computa¸cão evolucionária Particle Swarm Optimization

adotando uma abordagem de otimiza¸cão multiobjetivo visando maximizar a estat´ıstica de teste e minimizar a fun¸cão de penaliza¸cão por dispersão. As principais estruturas e etapas do algoritmo são apresentadas ao longo das se¸cões deste cap´ıtulo.

3.1 Vis˜

ao Geral

O algoritmo MOBPSO (Multi-Objective Binary Particle Swarm Optimization) para o problema de deteçcão e inferência de clusters espaciais irregulares é baseado na técnica de computa¸cão evolucionária Particle Swarm Optimization em sua versão binária (KENNEDY; EBERHART, 1997) e no algoritmo MOPSO-CD (Mult-Objective Particle Swarm Optimization with Crowding Distance) proposto por Raquel e Naval Jr. (2005) para aplica¸cão em problemas de otimiza¸cão multiobjetivo.

No tratamento do problema através de uma abordagem multiobjetivo o algoritmo MOBPSO encontrará as solu¸cões (clusters) através da maximiza¸cão da estat´ıstica Scan

e minimiza¸cão da fun¸cão de penaliza¸cão por dispersão (vide se¸cão 2.1.3). Ao longo das gera¸cões do algoritmo e do emprego do conceito de dominância das solu¸cões (vide se¸cão

2.2) obtém-se como resultado um subconjunto de solu¸cões não-dominadas, representadas pela fronteira Pareto- Ótimo. O par (Λ(z),D₍_z_{)) representa, respectivamente, os valores} da estat´ıstica Scan e o da fun¸cão de penaliza¸cão, computados para cada part´ıcula da popula¸cão.

3.2 Aspectos Estruturais

(43)

Defini¸cão 3 ( Grafo ). Um Grafo G é um par (V, E), em que V é um conjunto finito e

E é uma rela¸cão binária em V. O conjunto V é denominado conjunto de vértices de G, e

seus elementos são denominados vértices. O conjunto E é denominado conjunto de arestas

de G, e seus elementos s˜ao denominados arestas.

Para o problema em estudo adotou-se o modelo de grafo não orientado. Em um Grafo G(V, E) não dirigido, o conjunto E de arestas é constitu´ıda por pares de vértices não ordenados, ou seja, _{u, v_}, em que u, v _∈ V e u ₆= v e as arestas (u, v) e (v, u) são consideradas as mesmas.

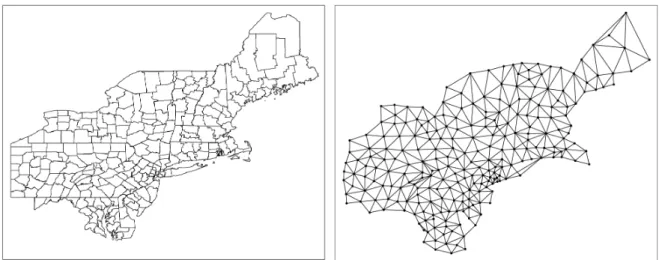
A Figura10 apresenta o mapa do nordeste dos Estados Unidos, dividido em um conjunto de regiões (à esquerda) e o grafo correspondente ao mapa (à direita). Nesta representa¸cão, as regiões do mapa são simbolizadas pelo conjunto de Vértices do Grafo. As rela¸cões de vizinhan¸ca entre as regiões, ou seja, quando uma região r1 faz fronteira com uma região r2 no mapa, são simbolizadas pelo conjunto de Arestas.

Figura 10 – Mapa do Nordeste dos Estados Unidos: À esquerda um mapa dividido em um conjunto de regiões; À direita o grafo correspondente.

Solu¸cões declusters adequadas para o problema são intrinsecamente caracterizadas pela conexidade das regiões que o constitui. A representa¸cão por meio de estruturas baseadas em grafos facilita a verifica¸cão desta condi¸cão diante do emprego do conceito de caminho.

Defini¸cão 4 ( Caminho ). Um caminho de um vértice u a um vértice u′ _{em um Grafo}

(V, E) é uma sequência (v0, v1, v2, ..., vn) de vértices tais que u= v0, u′ =vn e (vi−1, vi)

(44)

Neste sentido, um grafo não dirigido é conexo se todo vértice pode ser alcan¸cado, ou seja, existe um caminho, por todos os outros vértices. Assim, a conexidade de um

cluster candidato representado como um subgrafo do grafo que representa as regi˜oes de um mapa em estudo pode ser validada.

3.2.1 Vari´

aveis de decis˜

ao

As solu¸cões do problema em estudo podem ser representadas por meio de um vetor de variáveis binárias. Neste sentido, dado um mapa dividido emnregiõesR =_{r1, r2, r3, ..., rn} e uma zona z como qualquer subconjunto de regiões do mapa. Considere um vetor de variáveis binárias _{x1, x2, x3, ..., xn}, em que xi = 1 se a i-ésima região está presente na zona z ou xi = 0 caso contrário.

A Figura11simboliza a rela¸cão descrita anteriormente em que (a) representa um conjunto de 12 regiões e um subconjunto de regiões ou zona em destaque (cinza) e (b) o vetor de variáveis binárias correspondente.

(45)

3.3 Inicializa¸

c˜

ao

A fase de inicializa¸cão de um clássico algoritmo baseado na técnica PSO compreende a gera¸cão da popula¸cão de part´ıculas (ou indiv´ıduos). Nesta fase, para cada part´ıcula é atribu´ıda uma posi¸cão no espa¸co de busca do problema e uma velocidade, ambos de forma aleatória.

Todavia, na abordagem proposta, para o problema em estudo uma gera¸cão aleatória comumente originará solu¸cões inviáveis implicando na necessidade de um maior número de gera¸cões para a convergência de solu¸cões viáveis. Uma estratégia adotada para contornar essa situa¸cão é através de uma distribui¸cão uniforme e gulosa da popula¸cão de part´ıculas ao longo do mapa. Essa abordagem é utilizada no estudo de Can¸cado(2009) para o problema de deteçcão de clusters através do algoritmo genético NSGA-II na gera¸cão dos indiv´ıduos.

Nesta abordagem, como apresenta o Algoritmo 1, a popula¸cão é gerada a partir de cada vértice vi do grafoG, que representa a instância do mapa, gerando um subgrafo Gi. O processo de gera¸cão continua com a constru¸cão do conjunto de subgrafos Gis feita por meio de uma estratégia gulosa. Para cada vérticevi, são selecionados os vértices vizinhos e escolhido aquele cuja zona tem maior valor da razão verossimilhan¸cas Λ(z) definida em1.

(46)

Algoritmo 1 - Pseudocódigo para a constru¸cão gulosa da popula¸cão de part´ıculas/indiv´ıduos.

1: function gerarPopulac¸˜ao(graf o G(V, E), pmgig)

2: n← N´umero de v´ertices do grafo G ( V, E );

3: for (i←1; i≤n; i←i+ 1) do

4: populacao[i] ← vi ∈Graf o G(V, E) ;

5: u1 ←vi;

6: for ( j ←2; j ≤pmgig; j ←j+ 1) do

7: uj ←v´ertice vizinho de uj−1 de maior Λ(z),uj ∈ {/ populacao[i]} ;

8: populacao[i] ← populacao[i] ∪ uj ;

9: returnpopulacao;

Apesar de parecer uma estratégia razoável para o problema em estudo, normalmente o método guloso, assim como para muitos problemas em que ele é aplicado, não encontra a solu¸cão ótima global, uma vez que o método não leva em conta todo o espa¸co de busca em que a fun¸cão a ser otimizada está definida e restringe-se apenas a solu¸cões ótimas locais. Ocasionalmente, algumas das solu¸cões encontradas pelo método guloso podem coincidir com a solu¸cão ótima global, todavia não existe garantia de que isso aconte¸ca (CANÇ ADO,

2009).

3.4 Defini¸

c˜

ao dos guias pBest e gBest

O modelo global da técnica PSO, adotado no algoritmo proposto para o problema desta disserta¸cão, define duas principais métricas para a popula¸cão de part´ıculas que são definidas ao longo das gera¸cões, sendo eles os guias pBest egBest.

Na defini¸cão do guiapBestem uma abordagem de otimiza¸cão multiobjetivo aplica-se o conceito de dominância das solu¸cões (veja se¸cão2.2). Em resumo, para uma determinada part´ıcula i se seu valor corrente pBesti for dominado pelo atual valor obtido pi por essa part´ıcula então seu valor pBesti é atualizado para o novo valor obtido: pBesti =pi.

(47)

Crowding Distance (veja a se¸c˜ao3.4.1), definindo assim osgBesti para cada part´ıcula ida popula¸c˜ao.

3.4.1 Crowding Distance Computation

O mecanismo Crowding Distance Computation é originalmente incorporado ao algoritmo NSGA-II objetivando garantir uma melhor distribui¸cão das solu¸cões ao longo da fronteira de Pareto. O valor da Crowding Distance de uma determinada solu¸cão fornece uma estimativa da densidade das solu¸cões circundante a essa solu¸cão (DEB et al.,2002). A Figura 12apresenta o cálculo daCrowding Distance do pontoicomo sendo uma estimativa do tamanho do maior delimitador cuboide isem incluir qualquer outro ponto.

O cálculo daCrowding Distance é inicializada classificando o conjunto de solu¸cões em ordem ascendente dos valores das fun¸cões objetivo. O valor Crowding Distance de uma solu¸cão i particular é a distância média das suas duas solu¸cões vizinhas: (i₋1)&(i+ 1). As solu¸cões de limite que têm o maior e menor valor de fun¸cão objetivo são atribu´ıdas “valores infinitos” para a Crowding Distance de maneira que essas solu¸cões são sempre

selecionadas. Este processo ´e feito para cada fun¸c˜ao objetivo.

(48)

O valor final daCrowding Distance de uma determinada solu¸cãoi é calculada pela soma dos valores individuais deCrowding Distance para cada fun¸cão objetivo do problema. Um pseudocódigo para a Crowding Distance pode ser visto em 2, onde A simboliza o arquivo externo de solu¸cões não dominadas e nf o o número de fun¸cões objetivos.

Algoritmo 2 - Pseudoc´odigo para aCrowding Distance Computation. 1: function CrowdingDistanceComputation(A, nf o)

2: n←size(A);

3: for (i←1;i≤n;i←i+ 1) do 4: DIST AN CE(i)←0;

5: for (i←1;i≤nf o;i←i+ 1) do 6: Asort ←sort(A, i);

7: DIST AN CE(1)_{← ∞}; 8: DIST AN CE(n)← ∞;

9: for (j _←2;j _≤n₋1;j _←j + 1) do

10: DIST AN CE(j)←DIST AN CE(j) + (Asort(j+ 1)−Asort(j −1));

11: returnDISTANCE;

3.5 Atualiza¸

c˜

oes da Velocidade e da Posi¸

c˜

ao

A técnica PSO possui duas opera¸cões fundamentais, responsáveis por determinar um novo valor no espa¸co de busca do problema para as part´ıculas da popula¸cão que são executadas também ao longo das gera¸cões do algoritmo, sendo elas a atualiza¸cão da velocidade e da posi¸cão.

Na atualiza¸cão da velocidade foi incorporado à opera¸cão o fator de constri¸cão (K) como pode ser visualizado na equa¸cão (10). O trabalho desenvolvido por Clerc (1999) indica o uso do fator de constri¸cão como necessário, em alguns casos, para assegurar a convergência da técnica PSO.

vt+1

id =K[w t_vt

(49)

Na atualiza¸cão da posi¸cão das part´ıculas foi empregada a mesma equa¸cão, como pode ser revista em (11), adotada na extensão do PSO para a aplica¸cão em problemas que ocorrem em espa¸co de busca discreto, ou seja, binário.

xid=   

 

1, rand()< s(vid)

0 caso contr´ario.

(11)

Em que s(vid) = _1+exp1−vid, e rand() um número aleatório positivo de distribui¸cão uniforme

entre [0; 1.0]. E K ´e o fator de Constri¸c˜ao definido como: k = 2

|2−ϕ−√ϕ2₋₄_ϕ_| em que

ϕ =c1+c2, ϕ >4.

Os parˆametros a serem ajustados foram definidos da seguinte forma: os coeficientes

c1 ec2 com o valor 2.05;r1 e r2 como sendo um número aleatório positivo uniformemente distribu´ıdo no intervalo [0; 1.0]; e o coeficiente de inércia w pela fórmula w = wmax− ((i)/ni)_×(wmax−wmin), em que wmax = 0.3, wmin = 0.2, ni número de itera¸cões do sistema e i o valor da itera¸cão corrente. A velocidade das part´ıculas são limitadas por um fator vmax = 2.0.

3.6 Operador de Muta¸

c˜

ao/Turbulˆ

encia

O operador de muta¸cão ou turbulência, como recebe a denomina¸cão em PSO, implementado para o algoritmo MOBPSO segue uma abordagem semelhante aos operadores descritos nos trabalhos de Can¸cado (2009) para o problema de deteçcão de clusters

irregulares atrav´es do algoritmo NSGA-II e Coello, Pulido e Lechuga(2004) para aplica¸c˜ao em abordagens PSO multiobjetivo.

A inclusão de um operador de muta¸cão tem como finalidade proporcionar maior capacidade exploratória ao algoritmo. Ela constitui uma opera¸cão computacionalmente cara para o problema em questão, diante da necessidade de verifica¸cão de conexidade do subgrafo obtido quando o novo indiv´ıduo é gerado. Todavia sua aplica¸cão possui abrangência reduzida sobre a popula¸cão ao longo das gera¸cões do algoritmo.

(50)

acrescentar ou remover um vértice neste indiv´ıduo, respeitando a restri¸cão de que o subgrafo permane¸ca conexo. A escolha de acrescentar ou remover um vértice é aleatória, do mesmo modo que a escolha do vértice a ser acrescentado ou removido.

O Algoritmo3apresenta as principais etapas do operador de muta¸cão implementado. As variáveistxpetxptbsimbolizam a subpopula¸cão selecionada para a aplica¸cão da muta¸cão e a taxa de pertuba¸cão que será aplicada sobre os indiv´ıduos selecionados, respectivamente. A Figura13ilustra a aplica¸cão do operador de muta¸cão em um indiv´ıduo a um pertuba¸cão inicial. Em b) um vértice é inclu´ıdo ao indiv´ıduo e em c) um vértice é exclu´ıdo do indiv´ıduo.

Algoritmo 3 - Pseudoc´odigo para o Operador de Muta¸c˜ao. 1: function OperadorDeMutacao(txp, txptb)

2: n← tamanho de txp;

3: for (i←1;i≤n;i←i+ 1) do

4: pi ←indiv´ıduo i detxp;

5: for (j ←1;j ≤txptb;j ←j+ 1) do

6: v ← selecione aleatoriamente um v´ertice de pi;

7: r ← aleat´orio( 0 , 1 );

8: if (r= 1) then

9: vz ← selecione aleatoriamente um v´ertice vizinho dev;

10: M P _{← {}vz} ∪pi;

11: if (r= 0) then 12: M P ← pi\ {v};

13: if M P nao ´e um graf o conexothen 14: M P ←pi;

15: pi ←M P;

(51)

2

3 4 5 6

7 8 9 10

11 12

1

2

3 4 5 6

7 8 9 10

11 12

1 2

3 4 5 6

7 8 9 10

11 12

1 a)

c) b)

Figura 13 – Aplica¸cão do operador de muta¸cão em um indiv´ıduo (a): inclusão de vértice no indiv´ıduo (b); e exclusão de vértice no indiv´ıduo(c).

3.7 Pseudoc´

odigo do MOBPSO

O Algoritmo4 descreve a sequência de execu¸cão das principais etapas do algoritmo MOBPSO para o problema de deteçcão e inferência de clusters espaciais, que foram descritas previamente nas se¸cões deste cap´ıtulo.

A linha 2 é responsável pela chamada ao método gerador da popula¸cão inicialP das part´ıculas pela estratégia gulosa descrita na se¸cão 3.3. A linha 3 inicializa a velocidade V

(52)

ocorre a defini¸cão do guia gbest para as part´ıculas da popula¸cão P como relata a se¸cão

3.4. Nas linhas 11 a 13 ocorrem a aplica¸cão das opera¸cões de atualiza¸cão de velocidade e posi¸cão das part´ıculas em P, se¸cão3.5. E por último, na linha 14, ocorre a incidência do operador de muta¸cão em P como definido na se¸cão 3.6.

Algoritmo 4 - Pseudocódigo do MOBPSO para o problema de deteçcão de clusters

espaciais irregulares.

1: function MOBPSO(c1, c2, vmax, np, nd, ng, pmut, pmgig )

2: P ← Gerar a popula¸c˜ao de part´ıculas pelo m´etodo guloso;

3: V ← Inicializar a velocidade de cada part´ıcula deP de forma aleat´oria;

4: for (i←1;i≤ng;i←i+ 1) do

5: Calcular o valor para o componente de in´erciaw;

6: Avaliar as part´ıculas deP;

7: Selecionar o guia pBestde cada part´ıcula de P;

8: Armazenar as solu¸c˜oes n˜ao dominadas em um arquivo externo A;

9: Calcular a Crowding Distance das solu¸c˜oes de A e classific´a-las em ordem decrescente do valor;

10: Selecionar aleatoriamente de uma por¸c˜ao especifica de 10% do topo de A o guia gBest para cada part´ıcula de P;

11: Atualizar a velocidade v e a posi¸c˜aox de cada part´ıcula de P de acordo com as equa¸c˜oes:

12:

vt_id+1 =K[wtvtid+c1r1(pid−xtid) +c2r2(gid−xtid)]

13:

xid = (

1, rand()< s(vid) 0 caso contr´ario.

14: Aplicar o operador de Muta¸c˜ao em P;

(53)

Uma das etapas fundamentais na concep¸cão do algoritmo envolve a configura¸cão ou ajuste dos parâmetros responsáveis pelo correto funcionamento e que se adequam ao tipo de problema. Os principais parâmetros a serem definidos no algoritmo MOBPSO são:

• w, c1 e c2 : componentes de in´ercia, cognitivo e social, respectivamente;

• np: N´umero de part´ıculas da popula¸c˜ao;

• nd: N´umero de dimens˜oes do problema;

• ng: N´umero de gera¸c˜oes;

• pmut: Probabilidade de muta¸c˜ao; e

• vmax: Velocidade m´axima.