setembro de 2014
Juliana Maria Prado Braga
UMinho|20 14 Juliana Maria Pr ado Br aga
Universidade do Minho
Instituto de Educação
A resolução de problemas no
ensino-aprendizagem do tópico
circunferência: uma experiência com
alunos do 9.º ano de escolaridade
A resolução de problemas no ensino-aprendizagem do tópico circunferência: uma e
Relatório de Estágio
Mestrado em Ensino de Matemática no 3.º Ciclo
do Ensino Básico e no Ensino Secundário
Trabalho realizado sob a orientação da
Doutora Maria Helena Martinho
Universidade do Minho
Instituto de Educação
outubro de 2014
Juliana Maria Prado Braga
A resolução de problemas no
ensino-aprendizagem do tópico
circunferência: uma experiência com
alunos do 9.º ano de escolaridade
iii
AGRADECIMENTOS
Ao terminar um trabalho desta natureza e olhando o caminho percorrido, é inevitável o agradecimento sincero a quem caminhou a meu lado pela minha estrada:
Às minhas duas estrelinhas que marcaram este último ano com a sua ausência presencial e que lá do alto me iluminaram e acompanharam nesta caminhada.
À minha supervisora, Professora Doutora Maria Helena Martinho, que com a sua amizade, a sua prontidão, os comentários oportunos, as ideias partilhadas, o seu incentivo constante e a confiança depositada me guiou para o caminho do sucesso.
Ao meu orientador, Professor Mário Ferreira, pela amizade, a cumplicidade, a troca de experiências, a disponibilidade, as sugestões e comentários oportunos, o estímulo positivo e por acreditar em mim, mostrando verdadeiramente que a “essência da Matemática é a liberdade”.
Aos maravilhosos alunos que participaram com gosto e dedicação no estudo desenvolvido, sempre preocupados com o sucesso deste, mostrando-se desde logo motivados e recetivos à presença de mais uma professora na sua sala de aula.
À Escola que tornou possível a implementação deste estudo, disponibilizando todos os recursos necessários à sua concretização e aos Professores e Funcionários pelo acolhimento e as palavras de afeto.
Ao Paulo e à Paula, meus colegas de mestrado e amigos, pela amizade, incentivo, apoio e companheirismo.
À Sofia, minha amiga, por todas as palavras de apoio e incentivo, sempre presente com a sua fiel amizade.
À minha mana académica Sara, pelas horas de conversa, o apoio, o incentivo e o ombro amigo em todos os momentos e à sua irmã Joana pela ajuda na tradução do resumo.
Aos meus afilhados académicos Joana e João pelas palavras sempre encorajadoras, os momentos de risos, as conversas relaxadoras, pela amizade presente.
À minha irmã e ao meu cunhado por todo o incondicional apoio, confiança, que me ouvem, aconselham e estão sempre presentes e ao seu novo rebento, minha querida afilhada Benedita, que me alegrou com o seu nascimento neste ano muito intenso, mostrando-me sempre o seu brilhozinho nos olhos, transmitindo-me assim o seu apoio.
Aos meus pais e à minha avó, pelos valores que me transmitem, pela educação que me proporcionam, pelo apoio incondicional que sempre me dão na concretização dos meus ideais, pela energia e confiança que me transmitiram ao longo desta caminhada, por todos os momentos de partilha, de escuta e de compreensão.
Ao Nuno, meu namorado, pelo seu amor, amizade, carinho e ternura, tranquilizador nos momentos emocionais mais fortes, sempre acreditando e confiando no sucesso do meu trabalho e aos seus pais pelo apoio e amizade demonstrados.
iv
A realização deste mestrado foi apoiada financeiramente por fundos nacionais através da FCT – Fundação para a Ciência e Tecnologia no âmbito do Projeto LiDEs – a literacia das disciplinas escolares: Características e desafios para mais engagement e aprendizagem (FCOMP-01-0124-FEDER-041405 (Refª. FCT, EXPL/MHC-CED/0645/2013)).
v
A RESOLUÇÃO DE PROBLEMAS NO ENSINO-APRENDIZAGEM DO TÓPICO CIRCUNFERÊNCIA: UMA EXPERIÊNCIA COM ALUNOS DO 9.º ANO DE ESCOLARIDADE
Juliana Maria Prado Braga
Mestrado em Ensino de Matemática no 3.º Ciclo do Ensino Básico e no Ensino Secundário Universidade do Minho, 2014
RESUMO
O presente estudo resulta de uma intervenção pedagógica implementada junto de alunos de uma turma do 9.º ano de escolaridade no ano letivo 2013/2014, centrando-se na resolução de problemas no processo ensino-aprendizagem do tópico circunferência. Tendo como principal intuito compreender o papel da resolução de problemas na atividade matemática dos alunos, formularam-se três objetivos orientadores no delineamento da estrutura desta investigação, a saber: i) averiguar as perceções dos alunos acerca do contributo da resolução de problemas; ii) identificar os erros dos alunos na resolução de problemas; iii) compreender o desempenho dos alunos na aprendizagem do tópico “a circunferência” através da resolução de problemas.
O estudo seguiu uma abordagem metodológica de natureza qualitativa, correspondendo a sua problemática a um estudo de caso, com recolha de dados através de observação com recurso a gravações áudio, questionário e produções dos alunos. De referir que ao longo do estudo optou-se pelo trabalho em grupo, sendo os grupos selecionados aleatoriamente no início de cada aula.
Em termos de resultados, evidencia-se o reconhecimento por parte dos alunos da relevância da resolução de problemas para a aprendizagem da Geometria e, ainda, a opinião favorável da utilização da resolução de problemas em grupo. Como aspectos mais críticos das dificuldades dos alunos na resolução de problemas salientam-se a interpretação/compreensão do problema, o delineamento de uma estratégia de resolução e a avaliação, ou seja, dificuldades que se prendem com as fases do modelo de Polya. Numa ótica geométrica destacam-se dificuldades nas construções geométricas, na aplicação de conhecimentos/conceitos geométricos e, ainda, dificuldades que se prendem com a visualização, nomeadamente, interpretação de imagens. Sobressai ainda deste estudo, que as atividades implementadas mostraram influenciar positivamente o desempenho dos alunos relativamente à resolução de problemas geométricos.
vii
SOLVING TEACHING-LEARNING ISSUES OF THE SUBJECT-MATTER CIRCUMFERENCE: AN EXPERIMENT WITH 9TH YEAR GRADE STUDENTS
Juliana Maria Prado Braga
Master’s in Mathematics Teaching in the 3rd Cycle of Basic Education and Secondary Education University of Minho, 2014
ABSTRACT
This report is the result of a learning intervention implemented in a 9th year grade class students, during the year 2013/2014; it focuses in solving issues during the teaching/learning process of the subject-matter circumference.
Being the main goal of this study to understand the role of problem solving whilst the students’ mathematics activities, three principal guiding goals were created when structuring this investigation: i) to understand the students perceptions on the importance of problem solving; ii) to identify the mistakes of the students when resolving problems; iii) to evaluate the students’ performance when learning the subject-matter circumference.
A qualitative methodology research was followed in this investigation, correspondent to a case study, with data collection through observation, and with the use of audio recording, a survey and student’s work.
It is important to mention also that during this investigation, priority was given to group work; the groups were randomly formed in the starting of each class.
When it comes to results, it became clear that students recognize the importance of problem solving whilst learning Geometry, and also, the positive feedback from problem solving inside a group. On the other hand, the most critical aspects where seen in students at the moment of interpretation/comprehension of the problem, as well as the defining of a strategy to resolve a problem and its evaluation. So, students struggle throughout the phases of the Polva model.
In regards to geometry, there were detected several difficulties in constructing, in the use of geometry knowledge and in visualization (e.g. image interpretation).
It is crucial to conclude that, as a result of this investigation, the previously implemented activities proved to have a positive effect in the students’ performance when solving geometry problems.
ix ÍNDICE DECLARAÇÃO ... ii AGRADECIMENTOS ... iii RESUMO ... v ABSTRACT ... vii ÍNDICE ... ix ÍNDICE DE TABELAS ... xi
ÍNDICE DE FIGURAS ...xii
ÍNDICE DE QUADROS ... xiv
CAPÍTULO I ...1
INTRODUÇÃO ...1
1.1. Tema, finalidades e objetivos ... 1
1.2. Pertinência ... 2
1.3. Estrutura do relatório ... 2
CAPÍTULO II ...5
ENQUADRAMENTO TEÓRICO ...5
2.1. Resolução de Problemas ... 5
2.1.1. Conceito de Problema e de Resolução de Problemas ... 5
2.1.2. Modelos de Resolução de Problemas ... 9
2.1.3. Tipos de Problemas ... 12
2.1.4. Resolução de Problemas no processo ensino-aprendizagem ... 16
2.1.5. Dificuldades dos alunos na Resolução de Problemas ... 19
2.2. Ensino-aprendizagem de Geometria ... 20
2.2.1. Geometria nos documentos curriculares... 21
2.2.2. Dificuldades na aprendizagem da Geometria... 23
CAPÍTULO III ...25
INTERVENÇÃO: CONTEXTO E ESTRATÉGIAS DE AVALIAÇÃO ...25
3.1. Contexto de intervenção ... 25
3.1.1. A escola ... 25
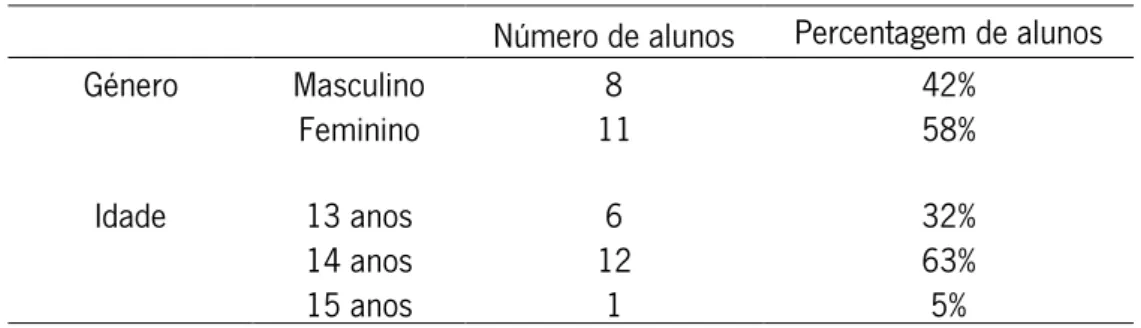
3.1.2. A turma ... 26
3.2. Intervenção... 28
x
3.3.1. Opções metodológicas ... 33
3.3.3. Análise dos dados ... 36
CAPÍTULO IV ...39
APRESENTAÇÃO DOS RESULTADOS ...39
4.1. Tarefas propostas ao longo da intervenção ... 39
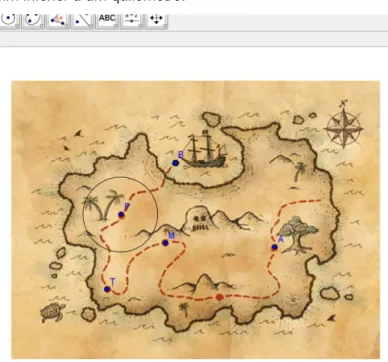
4.1.1. Tarefa 1 – O tesouro perdido ... 39
4.1.2. Tarefa 2 – O centro da mó do moinho ... 46
4.1.3. Tarefa 3 – O lago de água quente ... 51
4.1.4. Tarefa 4 – Vamos desvendar as propriedades ... 55
4.1.5. Síntese ... 60
4.2. Perceções dos alunos acerca do contributo da resolução de problemas para a aprendizagem da Geometria ... 60
CAPÍTULO V ...75
CONCLUSÕES ...75
5.1. Conclusões do estudo ... 75
5.1.1. Objetivo 1 – Averiguar as perceções dos alunos acerca do contributo da resolução de problemas para a aprendizagem da Geometria ... 75
5.1.2. Objetivo 2 – Identificar os erros e dificuldades dos alunos na resolução de problemas de Geometria ... 76
5.1.3. Objetivo 3 – Compreender o desempenho dos alunos na aprendizagem do tópico “a circunferência” através da resolução de problemas ... 77
5.2. Implicações para o ensino e aprendizagem ... 78
5.3. Limitações do estudo e recomendações para futuras investigações ... 79
REFERÊNCIAS BIBLIOGRÁFICAS ...81 ANEXOS ...85 ANEXO 1 ...87 ANEXO 2 ...89 ANEXO 3 ...91 ANEXO 4 ...99
xi
ÍNDICE DE TABELAS
Tabela 1 – Distribuição dos alunos por género e idade ... 26
Tabela 2 – Interesse dos alunos a nível de disciplinas ... 27
Tabela 3 – Preferência dos alunos em trabalhar na escola... 27
Tabela 4 – Hábitos de utilização do computador ... 28
xii
ÍNDICE DE FIGURAS
Figura 1 – Ilustração dos três critérios que um problema deve satisfazer, segundo Krulik e Rudnick (1993,
p.6)... 7
Figura 2 – Ciclo de resolução de problemas, segundo Sternberg (2008, p. 430). ... 9
Figura 3 – Competência matemática que os alunos devem desenvolver no domínio da geometria, segundo Ministério da Educação (2001, p. 62). ... 22
Figura 4 – Enunciado da tarefa O tesouro perdido. ... 40
Figura 5 – Resolução apresentada pelo grupo GIV à primeira pista do código. ... 41
Figura 6 – Resolução apresentada pelo grupo GV às três primeiras pistas do código. ... 42
Figura 7 – Construção incorreta do grupo GII ao resolver a quarta pista do código. ... 44
Figura 8 – Construção correta do grupo GI ao resolver a quarta pista do código. ... 44
Figura 9 – Resolução do grupo GIII à tarefa. ... 45
Figura 10 – Enunciado da tarefa O centro da mó do moinho. ... 46
Figura 11 – Resolução do problema apresentada pelo grupo GI. ... 47
Figura 12 – Resolução do problema apresentada pelo grupo GII ... 49
Figura 13 – Resolução apresentada pelo grupo GIII ao problema. ... 50
Figura 14 – Resposta apresentada pelo grupo GIII. ... 51
Figura 15 – Enunciado da tarefa O lago de água quente. ... 52
Figura 16 – Resolução apresentada pelo grupo GII ao problema. ... 53
Figura 17 – Resolução do problema apresentada pelo grupo GIII. ... 54
Figura 18 – Pistas deixadas pelos grupos na resolução do problema. ... 55
Figura 19 – Enunciado da tarefa Vamos desvendar as propriedades. ... 56
Figura 20 – Resolução apresentada pelo grupo GII ao problema. ... 57
Figura 21 – Resolução do problema apresentada pelo grupo GIII. ... 58
Figura 22 – Pistas deixadas pelos grupos na resolução do problema. ... 59
Figura 23 – Percentagem de alunos segundo as opções de resposta no que concerne às aulas se tornarem mais motivadoras com o recurso à resolução de problema... 62
Figura 24 – Percentagem de alunos segundo as opções de resposta relativamente a existirem diferenças entre um exercício e um problema. ... 63
Figura 25 – Percentagem de alunos segundo as opções de resposta relativamente ao tempo dispensado para a realização dos problemas. ... 65
Figura 26 – Percentagem de alunos segundo as opções de resposta relativamente à importância de resolver problemas em grupo. ... 67
xiii Figura 27 – Percentagem de alunos segundo as opções de resposta relativamente à importância da apresentação dos resultados à turma. ... 68 Figura 28 – Percentagem de alunos segundo as opções de resposta relativamente à utilização do Geogebra ter estimulado a aprendizagem. ... 70 Figura 29 – Número de alunos segundo as opções de resposta relativamente ao local onde utilizam a plataforma moodle. ... 71 Figura 30 – Número de alunos segundo as opções de resposta relativamente à não utilização da plataforma na maioria das vezes. ... 72 Figura 31 – Percentagem de alunos segundo as opções de resposta relativamente à importância do recurso à plataforma moodle como complemento à aprendizagem presencial. ... 72
xiv
ÍNDICE DE QUADROS
Quadro 1 – Fases de construção do conhecimentos matemático, segundo Brousseau (1998, in Corts&Callejo de la Vega, 2006, p. 139) ... 19 Quadro 2 – Percentagem de alunos segundo as opções de resposta relativamente à utilização da resolução de problema na lecionação do tópico “circunferência” ... 61 Quadro 3 – Percentagem de alunos segundo as opções de resposta relativamente às principais dificuldades sentidas na resolução de problemas ... 62 Quadro 4 – Percentagem de alunos segundo as opções de resposta relativamente à realização dos problemas em grupo ... 65 Quadro 5 – Percentagem de alunos segundo as opções de resposta relativamente à fase de apresentação/discussão após a realização dos problemas em grupo ... 68 Quadro 6 – Percentagem de alunos segundo as opções de resposta relativamente do recurso ao Geogebra ... 69 Quadro 7 – Percentagem de alunos segundo as opções de resposta relativamente ao recurso à plataforma moodle ... 71
1
CAPÍTULO I INTRODUÇÃO
Neste capítulo, dividido em três secções, apresenta-se de modo sucinto o tema, as finalidades e os objetivos a que este estudo se propôs. Além disso, é referida a pertinência do estudo e faz-se uma breve descrição da estrutura do relatório.
1.1. Tema, finalidades e objetivos
O tema a que este estudo diz respeito é a resolução de problemas no ensino-aprendizagem do tópico circunferência: uma experiência com alunos do 9.º ano de escolaridade. Desde aluna que a resolução de problemas me desperta a atenção, uma vez que através desta estratégia de ensino e aprendizagem era convidada a encontrar estratégias, a raciocinar de maneira diferente, a tomar o gosto pelo trabalho mental, bem como a desenvolver a entreajuda com os meus colegas ao trabalharmos em grupo, existindo assim uma partilha de conhecimentos. Ou seja, a resolução de problemas fomenta o gosto pela matemática, desenvolvendo um espírito crítico e uma aprendizagem significativa nos alunos (Polya, 1985; Carrillo, 2000; Vieira, Cebolo & Araújo, 2006), sendo “fundamental para a construção, consolidação e mobilização de conhecimentos matemáticos dos diversos temas, em conexão com o raciocínio e a comunicação” (Ministério da Educação, 2007, p. 62).
É através da resolução de problemas que pretendo partir para o ensino-aprendizagem do tópico “a circunferência”. Este tópico pertence ao tema Geometria, e aparece contemplado no Programa do Ensino Básico (2007) com o intuito dos alunos relacionarem e estudarem as propriedades da circunferência com os diversificados elementos geométricos.
Neste contexto, acho pertinente o ensino do tópico referido através da resolução de problemas por forma a os problemas serem um veículo para a aprendizagem e para o aprofundar de conhecimentos, tal como sustenta o Programa de Matemática do Ensino Básico (2007), “a resolução de problemas não só é um importante objetivo de aprendizagem em si mesmo, como constitui uma atividade fundamental para a aprendizagem dos diversos conceitos, representações e procedimentos matemáticos” (p. 8).
Desta forma, ambiciono com este plano de intervenção que os alunos contactem com o tópico a circunferência através da resolução de problemas, averiguando que influência esta estratégia exerce no ensino e aprendizagem deste tópico da Geometria.
2
Assim sendo, estabeleço os seguintes objetivos de investigação:
- Averiguar as perceções dos alunos acerca do contributo da resolução de problemas; - Identificar os erros dos alunos na resolução de problemas;
- Compreender o desempenho dos alunos na aprendizagem do tópico “a circunferência” através da resolução de problemas.
1.2. Pertinência
A Matemática é mais do que cálculos. É resolver os mais variados problemas, quer matemáticos quer exteriores à matemática. E um dos grandes temas matemáticos onde a resolução de problemas ganha ênfase é na Geometria. Esta perspetiva encontra-se no Programa de Matemática do Ensino Básico (Ministério da Educação, 2007) acerca do processo de ensino-aprendizagem da Geometria e da resolução de problemas, ou seja, separadas ou coligadas, a Geometria e a resolução de problemas destacam-se consideravelmente.
Contudo, para que exista um processo correto quer na resolução de problemas quer na aprendizagem da Geometria, é fundamental perceber as dificuldades dos alunos e agir perante estas para que o seu desempenho ao longo dos tempos se torne positivo e possam ver a Matemática como uma área maravilhosa e enriquecedora.
Assim, pretendo na minha intervenção proporcionar aos alunos experiências diversificadas que lhes permitam tomar consciência da veracidade da importância da resolução de problemas e da Geometria. Estando o contexto de intervenção em consonância com as minhas pretensões, pois os alunos da turma são trabalhadores, empenhados e participativos, salientando-se ainda a discussão de ideias entre eles, facto este que pode favorecer o trabalho dos alunos aquando a resolução de problemas, é pertinente a realização deste estudo.
1.3. Estrutura do relatório
O presente Relatório de Estágio está organizado em cinco capítulos, apresentando-se nesta secção uma breve descrição de cada um. No Capítulo I – Introdução –, para além de se descrever o que consta em cada capítulo, apresentam-se o tema, as finalidades, os objetivos e a pertinência do estudo.
No Capítulo II – Enquadramento Teórico – justifica-se a relevância do estudo à luz da literatura, fundamentando-se desta forma as temáticas consideradas fundamentais e que recaem sobre a resolução de problemas e a Geometria.
3
No terceiro capítulo – Intervenção: Contexto e Estratégias de Avaliação – dá-se a conhecer o contexto de intervenção caracterizando-se a escola e a turma onde decorreu este estudo. Apresenta-se, ainda, a forma como recorreu a intervenção e fundamenta-se à luz da literatura a metodologia utilizada, referenciando-se as estratégias de avaliação da ação.
O Capítulo IV – Apresentação dos Resultados – descrevem-se, analisam-se e avaliam-se as resoluções a cinco problemas realizados durante as aulas, com vista a dar resposta aos objetivos que suportaram a investigação. Para tal, recorreu-se às produções dos alunos e aos diálogos transcritos que ocorreram durante as atividades realizadas. Ainda neste capítulo apresenta-se a apreciação geral da turma em relação ao estudo desenvolvido, analisando-se para tal as respostas ao questionário.
Por último, no Capítulo V – Conclusões –, apresentam-se e discutem-se as principais conclusões do estudo, dando-se resposta aos objetivos que nortearam este estudo. São feitas ainda referências às limitações do estudo e apresentadas algumas recomendações para trabalhos futuros.
5
CAPÍTULO II
ENQUADRAMENTO TEÓRICO
Neste capítulo, que se encontra dividido em três secções, pretende-se fazer uma análise da literatura, num domínio de resolução de problemas e de Geometria, abordando-se temáticas consideradas fundamentais como alicerces neste estudo.
2.1. Resolução de Problemas
Esta secção, dividida em cinco subsecções, aborda o conceito de problema e de resolução de problemas como também as heurísticas de resolução de problemas. Referem-se ainda os tipos de problemas considerados por alguns autores e a importância que a resolução de problemas tem no processo ensino-aprendizagem. São ainda mencionadas dificuldades que os alunos sentem na atividade de resolver problemas.
2.1.1. Conceito de Problema e de Resolução de Problemas
O ensino da Matemática viu a essência do seu desenvolvimento na década de 90 com o importante papel que a resolução de problemas assumiu a todos os níveis. Esta importância da resolução de problemas no currículo da matemática é referida num artigo publicado nos finais da década de 80 na Revista Educação e Matemática, o qual refere que “um programa de Matemática para os anos 90 deve ser claro a respeito do lugar que ocupam e do papel que desempenham aspetos decisivos como a resolução de problemas” (APM, 1989, p. 13). É, assim, que ao longo dos anos a resolução de problemas tem marcado a sua notória presença, quer como parte integral da atividade matemática quer como objetivo de aprendizagem da matemática. Prova disso é o que refere o Programa de Matemática do Ensino Básico de 2007 (Ministério da Educação, 2007) ao pronunciar que “a resolução de problemas não só é um importante objetivo de aprendizagem em si mesmo, como constitui uma atividade fundamental para a aprendizagem dos diversos conceitos, representações e procedimentos matemáticos” (p. 8), tendo já sido mencionado também por NCTM (1994) que “quando a resolução de problemas faz parte integral do currículo, as crianças desenvolvem uma perspetiva sobre o que significa aprender Matemática e resolver problemas em matemática” (p. 32).
É com esta saliência que os conceitos de problemas e de resolução de problemas mereceram atenção por parte de vários autores. Contudo, antes de abordar os conceitos de
6
problema e de resolução de problemas convém apresentar as diferenças existentes entre o conceito de exercício e de problema, visto serem dois conceitos que geram ainda algumas controvérsias.
Vale e Pimentel (2004) referem que esta distinção é importante no processo de ensino-aprendizagem, aludindo a que “uma determinada situação pode ser um problema para um dado indivíduo, num dado momento, e para o mesmo indivíduo, num outro momento, ser apenas um exercício” (p. 12). Corts e Callejo de la Vega (2004) apontam possíveis diferenças entre exercício e problema, sendo estas as seguintes.
1. Ao ler-se um exercício, vê-se imediatamente em que consiste a questão e qual o meio de a resolver.
1. Face a um problema, não sabemos, à primeira vista, como enfrentá-lo e resolvê-lo; às vezes, nem se consegue ver claramente em que consiste o problema.
2. O objetivo pretendido pelo professor, ao propor um exercício, é que o aluno aplique de forma mecânica conhecimentos e algoritmos já adquiridos e fáceis de identificar. 2. O objetivo pretendido pelo professor, ao propor um problema, é que o aluno
pesquise, investigue, recorra à intuição, aprofunde o seu conjunto de conhecimentos e experiências anteriores e elabore uma estratégia de resolução.
3. Em geral, a resolução de um exercício exige pouco tempo, podendo este ser previsto antecipadamente.
3. Em geral, a resolução de um problema exige um determinado tempo impossível de prever antecipadamente.
4. A resolução de um exercício não costuma implicar a afetividade.
4. A resolução de um problema implica um forte investimento de energias e de afetividade. No decorrer da resolução é costume experimentar sentimentos de ansiedade, de confiança, de frustração, de entusiasmo, de alegria, etc.
5. Em geral, os exercícios são questões fechadas.
5. Os problemas estão sempre abertos a possíveis variações e generalizações e a novos problemas.
6. Os manuais estão cheios de exercícios.
6. Costuma haver poucos problemas nos manuais. (Corts & Callejo de la Vega, 2004, p. 55)
Após esta breve explicitação acerca das diferenças entre exercício e problema dá-se seguimento às definições de problema e de resolução de problemas à luz da literatura.
Para Díaz e Poblete (2001) um problema implica uma situação que supõe uma solução a ser alcançada, contudo com obstáculos para a sua conquista, sendo necessária uma estratégia visto não existir um algoritmo pronto para resolvê-lo.
Krulik e Rudnick (1993) referem que um problema é uma situação, quantitativa ou de outro tipo, enfrentada por um individuo ou grupo de indivíduos em que nenhum caminho para a resposta é conhecido, salientando que a chave da definição de problema está no caminho
7
desconhecido para encontrar a resposta. Estes autores referem ainda que um problema deve satisfazer três critérios: aceitação, bloqueio e exploração, pois a existência de um problema implica que o indivíduo é confrontado com algo que não reconhece e que não pode simplesmente aplicar um modelo. A figura seguinte (Figura 1) retrata explicitamente a ideia que os autores referem relativamente a estes três critérios.
Figura 1 – Ilustração dos três critérios que um problema deve satisfazer, segundo Krulik e Rudnick (1993, p.6).
Kantowski (1977) refere que um indivíduo está perante um problema quando não pode responder a uma dada questão ou situação usando imediatamente o conhecimento que lhe é inato, ou seja, é necessário descobrir o caminho que lhe permita chegar à resposta, pelo que Lopes et al. (1992) mencionam que “um problema deve despertar a curiosidade do indivíduo, provocar-lhe uma certa tensão durante a procura de um plano de resolução e, finalmente, fazê-lo sentir a alegria inerente à descoberta da solução” (p. 8).
Segundo Polya (1985) estar perante um problema significa encontrar um processo por forma a alcançar um objetivo que não era imediatamente alcançável, ultrapassar uma dificuldade, pois onde não há dificuldade, não há problema.
Palhares (1997), ao construir a definição de problema, concluiu que este
é constituído por um conjunto de informações sobre uma situação inicial e sobre a situação final que é requerida, ou sobre a transformação que é requerida; existe um obstáculo que impede uma classe de indivíduos de obter a transformação requerida sem recorrer a algum tipo de raciocínio para que obtenha a solução pelos seus próprios meios (…); finalmente não pode existir indicação precisa de qual o procedimento a utilizar (p. 167).
No mesmo sentido, Mayer (2003) refere que o aluno está perante um problema quando tem um objetivo mas não tem um procedimento imediato para alcançá-lo. Menciona ainda que um problema é composto por três elementos: uma determinada situação, um objetivo a atingir e um obstáculo que impede o aluno de passar diretamente da situação para o objetivo. Também
8
nesta linha de pensamento, Ponte (1992) salienta que “um problema consiste numa tarefa para a qual o aluno não dispõe de um método imediato de resolução, mas em cuja solução se empenha ativamente” (p. 95).
É esta tarefa que abre o caminho à resolução de problemas, uma vez que a “resolução de problemas implica o envolvimento numa tarefa, cujo método de resolução não é conhecido antecipadamente” (NCTM, 2007, p. 57), tendo o aluno de encontrar uma estratégia de resolução que irá “gerar o gosto pelo trabalho mental e deixar, por toda a vida, a sua marca na mente e no caráter” (Polya, 1985, p.v). Nesta linha de pensamento, Kantowski (1977) refere que a resolução de problemas deve ter em conta dois aspetos, sendo eles o processo ou o conjunto de comportamentos que direcionam para a descoberta de uma solução e o produto, ou seja, a própria solução. Estes dois aspetos são, para o autor, componentes essenciais para a experiência de resolução de problemas.
Palhares (1997) menciona que a resolução de problemas ocorre quando se está perante um problema e ao resolvê-lo aplicam-se “procedimentos que não estão a priori estabelecidos ou não são a priori conhecidos” (p. 167). Para Díaz e Poblete (2001) a resolução de problemas, ou o encontrar de uma solução, é avançar até que se tenha encontrado uma resposta correta à pergunta feita.
Mayer (2003)refere que a resolução de problemas ocorre quando o resolvedor determina como resolver o problema, como atingir a meta. Assim, alude o autor, a definição de resolução de problemas inclui três elementos: cognitivo – ocorre internamente no sistema cognitivo, processo – envolve cálculo mental, sendo necessária a aplicação de uma representação mental e orientado – com base num objetivo e nos resultados da atividade.
Krulik e Rudnick (1993) apontam a resolução de problemas como um processo, afirmando que é o meio pelo qual um indivíduo usa conhecimentos adquiridos, habilidades e compreensão, sendo que o processo começa com o confronto inicial e conclui-se quando uma resposta for obtida e analisada em relação às condições iniciais. O aluno deve sintetizar o que aprendeu e aplicar essa aprendizagem à nova situação.
Charles, Lester e O’Daffer (1994) defendem que a resolução de problemas é uma atividade extremamente complexa, uma vez que envolve a recolha de dados, o uso de uma grande variedade de procedimentos, a capacidade de avaliar o próprio modo de pensar bem como outros recursos, o que vai ao encontro da ideia de Abrantes (1989), pois para este autor “a resolução de problemas consiste numa larga variedade de processos, atividades e
9
experiências” (p. 9). Também nesta linha de pensamento se encontram Vale e Pimentel (2004) ao defenderem que a resolução de problemas constitui uma atividade em que o aluno identifica e descobre formas para resolver um problema com o qual é confrontado, ou seja, “é uma atividade complexa, de um aprendiz motivado, que põe em jogo várias capacidades cognitivas de ordem superior” (p. 11).
É com estas diversas linhas de pensamento que se pode concluir que um problema é uma situação à qual não se possui um conhecimento inato para lhe dar resposta, pelo que a sua resolução constitui uma atividade que fará com que através do delinear de uma estratégia de resolução se encontre a solução.
2.1.2. Modelos de Resolução de Problemas
A importância de aprender a resolver problemas é unânime entre diversos autores, pelo que são propostos modelos que suportam métodos/processos para encontrar a solução de um determinado problema.
Numa perspetiva mais abrangente, Sternberg (2008) dá-nos a conhecer um modelo de resolução de problemas denominado ciclo de resolução de problemas e que compreende sete etapas, a saber: identificação do problema, definição do problema, formulação de uma estratégia de resolução do problema, organização da informação do problema, alocação de recursos, monitorização e avaliação (Figura 2).
10
A identificação do problema é a etapa considerada como a mais difícil, não podendo deixar de se reconhecer que existe um objetivo a cumprir. Após a identificação da existência de um problema tem de se definir e representar bem o problema para perceber como resolvê-lo, surgindo desta forma a etapa definição do problema. A etapa formulação de uma estratégia de resolução do problema ocorre após a definição de forma eficaz do problema. Na etapa formulação de uma estratégia, o autor refere que a estratégia a formular pode envolver análise – quebrar a vertente complexa do problema em elementos gerenciáveis – como pode envolver um processo complementar de síntese – reunir vários elementos para organizá-los em algo útil. A etapa organização da informação do problema é considerada pelo autor como fundamental para uma boa resolução do problema, pois por vezes não se sabe como resolver um problema, não porque este seja de impossível resolução mas porque não se compreende a informação disponível ou se desconhece como a utilizar. Na etapa alocação de recursos faz-se a seleção dos recursos necessários à resolução do problema, tendo como exemplos destes recursos o tempo, os equipamentos, o espaço, etc. A monitorização é a etapa definida pelo autor como o acompanhamento do processo de resolução do problema e que permite analisar se a resolução se está a aproximar da resposta correta. Por último, na etapa da avaliação, avalia-se a solução encontrada, ajudando esta avaliação a analisar se a solução está incompleta ou errada. O autor refere que esta avaliação pode ser imediata ou pode ocorrer mais tarde.
Ao sugerir este ciclo de resolução de problemas, o autor relembra a importância da existência de flexibilidade na sequência das várias etapas, pois poderá ser necessária a ambiguidade de se proceder da melhor forma, alterando a ordem das etapas ou até mesmo ignorar ou adicionar da forma que melhor parecer.
Já numa perspetiva matemática, Krulik e Rudnick (1993) enunciam cinco fases do processo de resolução de problemas, a saber: ler e pensar, explorar e planear, selecionar uma estratégia, encontrar uma resposta e refletir e ampliar. Na primeira fase, ler e pensar, à medida que o aluno lê o problema deve fazer conexões bem como recordar situações semelhantes. Os autores referem que nesta fase o pensamento crítico é realçado. Na fase explorar e planear, o aluno analisa e sintetiza as informações contidas no problema que foram reveladas durante a fase anterior, ocorrendo ideias e planos. Os autores aludem a que conscientemente as possíveis soluções estão previstas e mentalmente examinadas, daí o nome explorar e planear. Como resultado das anteriores fases, na fase selecionar uma estratégia, o aluno deve optar pelo caminho que parecer ser o mais adequado. Após estar o problema compreendido e escolhida
11
uma estratégia, o aluno deve estimar, entrando na fase encontrar uma resposta, realizando a matemática necessária para obter uma resposta mais precisa. A última fase, refletir e ampliar, serve para o aluno verificar se a pergunta já foi respondida e se a matemática está correta. É nesta fase que o aluno tem a oportunidade de refletir sobre o processo que foi utilizado e discutir as várias soluções com a turma e de ampliar o problema resolvido a uma generalização ou a um conceito matemático. Os autores referem que esta fase exige que o aluno pense criativamente.
As fases anteriormente descritas apontam para um modelo de cunho forte e que continua a ser uma referência para a área de investigação de resolução de problemas, o modelo de Polya. Este modelo contempla quatro fases fundamentais: compreensão do problema, estabelecimento de um plano, execução do plano e retrospecto, tendo cada uma delas a sua importância, pois
acontecerá o pior se o estudante atirar-se a fazer cálculos e a traçar figuras sem ter compreendido o problema. É geralmente inútil executar detalhes sem perceber a conexão principal ou sem ter feito uma espécie de plano. Muitos enganos podem ser evitados se, na execução do seu plano, o estudante verificar cada passo. Muitos dos melhores efeitos podem ficar perdidos se ele deixar de reexaminar e de reconsiderar a solução completa (Polya, 1985, p. 4).
Na fase compreensão do problema o aluno deve certificar-se que compreendeu o problema e identificou os elementos principais deste: a incógnita, os dados e as condições que lhe são impostas. Estabelecimento de um plano é a fase em que o aluno deve formular um plano que lhe permita encontrar uma solução, referindo o autor que “o caminho que vai desde a compreensão do problema até o estabelecimento de um plano, pode ser longo e tortuoso” (p. 5). Na fase seguinte, execução do plano, o aluno implementa o plano formulado, aludindo o autor que “paciência é o de que mais se precisa” (p. 8), pois deve o aluno ser paciente examinando todos os passos que percorre por forma a tudo ficar claro e nenhum erro ficar oculto. Na última fase, retrospecto, o aluno deve examinar o resultado final e o processo que o levou até este, podendo assim consolidar conhecimentos e aprimorar a capacidade de resolver problemas. O autor refere que se os alunos não passarem por esta fase “perdem uma fase importante e instrutiva do trabalho da resolução” (p. 10).
Como já foi referido, este modelo é uma referência e inspiração para muitos autores. Fernandes, Vale, Fonseca e Pimentel (1995, in Vale & Pimentel, 2004) fazem uma adaptação ao modelo de Polya, pois a segunda e terceira fase aparecem juntas, uma vez que para alunos do ensino básico estas duas fases são difíceis de distinguir. Assim, os estádios propostos por estes
12
autores passam por ler e compreender o problema, fazer e executar o plano e verificar a resposta.
2.1.3. Tipos de Problemas
Ao longo dos anos, são vários os autores que dão o seu contributo acerca dos tipos de problemas, os quais se procura de seguida apresentar.
Burkhardt (1983), tendo em conta que os problemas se devem abordar consoante o interesse dos alunos, menciona quatro tipo de problemas, a saber: problemas de ação – action problems –, problemas credíveis – believable problems –, problemas curiosos – curiousproblems –, problemas duvidosos – dubious problems – e problemas educacionais – educational problems. Relativamente aos problemas de ação, estes estão relacionados com a vida do dia-a-dia e os problemas credíveis são problemas que podem ser considerados de problemas de ação mas para o futuro. Já os problemas curiosos são problemas que fascinam o aluno intelectualmente, esteticamente ou de outra forma. Os problemas duvidosos são o tipo de problemas em que o aluno apenas pratica matemática, ou seja, que requerem somente o uso de técnicas. Por fim, os problemas educacionais são problemas que se enquadram nos duvidosos, contudo abrilhantam perceções matemáticas, possuindo assim uma relevância educativa.
Frederiksen (1984), baseando-se nas sugestões de outros autores, distingue os problemas em três tipos categorizando-os pela sua estrutura como problemas bem-estruturados – well-structured problems–, problemas estruturados mas que requerem um pensamento mais produtivo – structured problems requiring productive thinking – e problemas mal-estruturados – ill-structured problems. Os problemas bem-estruturados são problemas com enunciado bem formulado e no qual o resolvedor dispõe de um algoritmo adequado que lhe garante a veracidade da solução. Os problemas estruturados são problemas semelhantes ao do primeiro tipo, uma vez que são problemas de enunciado bem estruturado, contudo para que seja descoberta a solução correta, o resolvedor tem de gerar por ele próprio o processo de resolução não tendo em sua posse um algoritmo. Os problemas mal-estruturados são os problemas em que o enunciado carece de formulação e para o qual não existe um processo que percorra todas as possibilidades em descobrir a solução correta.
Polya (1985) considera importante que se conheçam vários tipos de problemas, pelo que enuncia cinco tipos baseando-se na sua resolução. O primeiro tipo de problemas, os problemas auxiliares, são problemas que resolvemos como meio de resolver o problema original,
13
ou seja, perante a resolução de um problema, o aluno sente a necessidade de resolver outro problema para que consiga resolver o problema inicialmente proposto. Os problemas rotineiros, outro tipo de problemas que o autor refere, são problemas em que o aluno segue passo a passo um exemplo já muito “desgastado”, ou seja, neste tipo de problemas o aluno apenas precisa de algum cuidado e paciência para seguir uma fórmula já estabelecida, sem que tenha a oportunidade de fazer as suas conjeturas. O terceiro tipo de problemas, os problemas de determinação, têm como objetivo encontrar a incógnita do problema, referindo o autor que os problemas deste tipo “podem ser teóricos ou práticos, abstratos ou corretos, problemas sérios ou simples enigmas” (p. 124). Um quarto tipo de problemas, os problemas de demonstração, engloba os problemas onde o objetivo é mostrar conclusivamente que uma certa afirmação é verdadeira ou então é falsa, sendo que para resolver um problema deste tipo é “preciso conhecer, com grande exatidão, as suas partes principais, a hipótese e a conclusão” (p. 126). O autor, após abordar estes dois últimos tipos de problemas refere que “os “problemas de determinação” são mais importantes na Matemática elementar; os “problemas de demonstração” o são na Matemática superior” (p. 126). Por fim, o quinto tipo de problemas, os problemas práticos, são aqueles que requerem procedimentos mais complexos e menos nítidos e, ainda, conhecimentos previamente adquiridos.
Abrantes (1989) enuncia sete tipos de problemas segundo critérios concretos, sendo eles problemas de palavras, problemas para equacionar, problemas para demonstrar, problemas para descobrir, problemas da vida real, situações problemáticas e situações. O primeiro tipo de problemas, problemas de palavras, enunciado pelo autor diz respeito aos problemas em que os alunos são convidados a trabalhar com operações matemáticas, atribuindo-lhes um significado. Contudo, o autor refere que este tipo de problemas pode facilmente tornar-se em exercícios disfarçados devido à excessiva repetição de um mesmo procedimento, acabando o contexto do enunciado por não ser relevante. Os problemas para equacionar assemelham-se em certa medida aos problemas do primeiro tipo, visto terem, geralmente, como objetivo determinar o valor de uma incógnita traduzindo-se o enunciado numa equação, podendo assim tornar-se em meras repetições onde o contexto do enunciado acaba por perder relevância. Os problemas para demonstrar são problemas em que é necessário não só descobrir o caminho para demonstrar um pressuposto mas também produzir uma apresentação formal dessa demonstração, o que constitui uma atividade matemática rica para a aprendizagem. Os problemas para descobrir, quarto tipo de problemas que o autor enuncia, têm como objetivo estimular a curiosidade e o
14
interesse pela matemática, sendo a sua resolução conseguida através da descoberta do caminho correto, através de um pensamento brilhante. Os problemas da vida real são problemas que requerem que o aluno recorra a diversos conhecimentos. Apesar da denominação atribuída, não significa que este tipo de problemas aborde obrigatoriamente situações do dia-a-dia, mas antes situações que visam o desenvolvimento de aptidões no aluno. O autor refere ainda que neste tipo de problemas não existe uma única solução mas sim várias soluções que se aproximam. O sexto tipo de problemas é designado pelo autor de situações problemáticas. Este tipo de problemas requer que o aluno faça conjeturas, coloque questões a si próprio e recorra à formulação de outros problemas. Também neste tipo de problemas não existe uma única solução e o enunciado é considerado vago. Como último tipo de problemas o autor enuncia as situações, encontrando-se os alunos perante uma atividade em que não existe a formulação de um problema, ou seja, o aluno tem de explorar o contexto, recolhendo dados e informação.
Díaz e Poblete (2001) também deram o seu contributo categorizando os problemas segundo a sua natureza em rotineiros e não rotineiros e segundo o seu contexto classificam os problemas rotineiros de problemas de contexto real, problemas de contexto realista, problemas de contexto fantasista e problemas de contexto puramente matemático. Devido à sua natureza os problemas rotineiros assemelham-se aos desenvolvidos durante as aulas em que o aluno efetua uma série de procedimentos que envolvem a compreensão de conceitos e algoritmos por forma a encontrar soluções válidas. São problemas não rotineiros, no sentido em que o aluno não domina um procedimento anteriormente estabelecido para encontrar a solução. Relativamente aos problemas rotineiros e tendo agora em conta o seu contexto, os problemas de contexto real são aqueles que ocorrem na realidade e que o aluno se compromete a agir. Os problemas de contexto realista dizem respeito aos problemas que são suscetíveis de ocorrer, podendo ainda tratar-se de simulações da realidade ou parte de uma realidade. Os problemas de contexto fantasista são aqueles que partem da imaginação sem estarem ligados com a realidade. E, por último, os problemas de contexto puramente matemático são aqueles que fazem unicamente referência a objetos matemáticos (por exemplo, relações e operações aritméticas, figuras geométricas, etc.).
Charles, Lester e O’Daffer (1994) acreditam que existem problemas que devem ser utilizados na sala de aula, distinguindo-os em quatro tipos: problemas de uma etapa; problemas de múltiplas etapas; problemas de processo e problemas de aplicação. Os problemas de uma etapa e os problemas de múltiplas etapas são problemas em que os alunos são estimulados a
15
interpretar o enunciado passando o que lhes é fornecido em linguagem natural para linguagem matemática. É nesta passagem que se encontra a diferença entre os problemas de uma etapa e os problemas de múltiplas etapas, pois para encontrar a solução de um problema de uma etapa os alunos terão como estratégia de resolução a utilização de apenas uma operação matemática, ou seja, adição, subtração, multiplicação ou divisão, enquanto nos problemas de múltiplas etapas a estratégia consiste em utilizar mais do que uma operação elementar. Os problemas de processo são problemas em que não está evidenciada no enunciado a solução, ou seja, não se resolve este tipo de problemas utilizando operações matemáticas ou fazendo a aplicação direta de um algoritmo mas sim recorrendo a esquemas, a um problema mais simples, à descoberta de um padrão, etc. Por último, os problemas de aplicação requerem que o aluno utilize dados que não se encontram no enunciado do problema, ou seja, o aluno precisa de tomar uma decisão exigindo este tipo de problemas mais tempo visto não ser dada toda a informação necessária para construir uma estratégia por forma a encontrar uma solução.
Palhares (1997), ao classificar os problemas segundo o procedimento, considera que esta classificação “está dependente, tal como a noção de problema, da classe de indivíduos que são destinatários” (p. 168), anunciando sete tipos de problemas, a saber: problemas de processo, problemas de conteúdo, problemas de capacidades, problemas tipo puzzle, problemas de aplicação, problemas abertos e problemas de aparato experimental. Os problemas de processo são aqueles que requerem a utilização de estratégias de resolução, enquanto os problemas de conteúdo carecem do uso de conhecimentos matemáticos adquiridos recentemente como também do uso de conhecimentos que de certa forma ainda estão em fase de interiorização. Ou seja, dependendo dos alunos a que o problema se destina este pode ser ou de processo ou de conteúdo, uma vez que se for um problema em que os alunos não têm o conhecimento matemático presente terão de identificar uma estratégia e testá-la estando perante um problema de processo, se pelo contrário, os alunos tiverem presente o conhecimento matemático necessário para a sua resolução, bastar-lhes-á aplicá-lo pelo que se encontram perante um problema de conteúdo. Os problemas de capacidades, e como o próprio nome sugere, são problemas que intimam ao uso de capacidades matemáticas como o cálculo mental e a estimativa. Os problemas tipo puzzle são problemas que visam o alargamento do espaço de resolução, tendo de se ir mais além. Os problemas de aplicação estão ligados à recolha e tratamento de dados, pelo que para a sua resolução é necessária mais informação para além daquela presente no enunciado, o que vai ao encontro do que foi enunciado por Charles, Lester
16
e O’Daffer. No que diz respeito aos problemas abertos, estes requerem que os alunos façam uma escolha entre possíveis procedimentos, pelo que o autor considera mais sensato caraterizar este tipo de problemas como uma subcategoria de outros. E, por último, os problemas de aparato experimental em que é necessário o uso de esquemas investigativos, ou seja, processos que implicam a exploração de possibilidades que se visam ser imensas.
Mayer (2003) considera útil distinguir alguns tipos de problemas, ou seja, problemas rotineiros versus problemas não rotineiros, problemas bem definidos versus problemas mal definidos e problemas que requerem computação versus problemas que requerem compreensão. Os problemas rotineiros são aqueles em que o aluno conhece um procedimento imediato para encontrar a solução, sendo que o autor ainda refere que este tipo de problema não é problema em tudo visto não existir nenhum obstáculo. Em contraste a estes problemas o autor refere os problemas não rotineiros em que o aluno não conhece um procedimento que possa aplicar imediatamente. Os problemas bem definidos são problemas onde está claramente especificado o objetivo e o conjunto de operações a utilizar, enquanto nos problemas mal definidos nada está especificado. Por último, os problemas que requerem computação e como o próprio nome diz são problemas em que é necessário o recurso à computação, enquanto os problemas que requerem compreensão são aqueles em que é necessária compreensão para além da computação. O autor refere ainda que no caso dos problemas que requerem computação os alunos devem realizar procedimentos básicos, mas nos problemas que requerem compreensão já devem construir uma representação mental da situação do problema. 2.1.4. Resolução de Problemas no processo ensino-aprendizagem
A nossa sociedade é caraterizada por rápidas alterações, onde surgem determinadas situações complexas que precisam ser interpretadas e resolvidas. Assim, é necessária a presença de indivíduos com capacidades de adaptação, capazes de resolverem habilmente problemas resultantes de situações, ou seja, indivíduos com pensamento crítico, criativo e eficaz. A aula de Matemática pode ser o local privilegiado para preparar os alunos (indivíduos) que a nossa sociedade exige, dando-se ênfase a um ensino que desenvolva nos alunos a capacidade de resolver problemas.
Desde sempre que a resolução de problemas ocupa um lugar central no ensino da Matemática, tornando notória e cada vez maior a sua importância ao longo do tempo. Já na história antiga grega, chinesa e egípcia se encontram registos de problemas matemáticos,
17
embora com uma visão limitada da resolução de problemas (Estrada, Sá, Queiró, Silva & Costa, 2000). Nos tempos presentes, a visão da resolução de problemas começa a ser mais abrangente, não sendo entendida como um tópico distinto, mas sim como “parte integrante de toda a aprendizagem matemática” em que os alunos adquirem “modos de pensar, hábitos de persistência e curiosidade, e confiança perante situações desconhecias” (NCTM, 2007, p. 57).
A APM valoriza o envolvimento dos alunos em atividades matemáticas ricas e significativas, pelo que realizou um estudo entre os anos de 1996 e 1998, intitulado Matemática 2001 – Diagnóstico e Recomendações para o Ensino e Aprendizagem da Matemática (APM, 1998), que visava conhecer a realidade vivida nas escolas e partindo desse diagnóstico elaborar um conjunto de recomendações. Nesse diagnóstico, surgem recomendações ligadas à prática pedagógica que se prendem com a necessidade de: i) implementar tarefas que valorizem o desenvolvimento do pensamento matemático dos alunos, incluindo situações de trabalho que incentivem diversificadas formas de interação na sala de aula; ii) expor contextos diversificados, ligados não só a situações da realidade mas também à história matemática, recorrendo a materiais didáticos que envolvam fortemente os alunos no processo de aprendizagem; iii) não encarar o manual escolar como uso exclusivo, mas sim encará-lo como um elemento que pode “promover a capacidade de autoaprendizagem e o espírito crítico dos alunos” (p. 41); e iv) diversificar as formas de avaliação dos trabalhos dos alunos. É, ainda, de destacar o estudo do GAVE (2006) que ao fazer uma reflexão acerca dos resultados do exame do 9.º ano de 2005, indica que “os melhoramentos a introduzir nas práticas de sala de aula incidiram, com maior frequência, na resolução de problemas” (p. 62).
A nível internacional têm sido realizados estudos semelhantes ao estudo realizado pela APM e pelo GAVE. Estes estudos debruçam-se sobre a forma como as escolas preparam os seus alunos para enfrentarem os desafios do dia-a-dia. É de destacar o estudo PISA 2003 do GAVE (2004) que teve como pretensão não só avaliar o desempenho dos alunos a nível da literacia em vários domínios como também recolher dados relacionados com a capacidade de resolução de problemas. Salienta-se aqui os fracos resultados obtidos pelos alunos portugueses no que se refere não a cálculos rotineiros mas à sua capacidade de interpretar e resolver situações problemáticas. Um estudo mais recente é o PISA 2012 do ProjAVI (2013) que lança o seu relatório sobre a capacidade de resolver problemas não rotineiros. Neste relatório é visível o melhoramento relativamente a esta capacidade, sendo que Portugal se encontra dentro da média da OCDE, ou seja, é notório o desenvolvimento referente à capacidade de resolver
18
problemas e que muito era valorizada no Programa de Matemática do Ensino Básico de 2007. Contudo, este desenvolvimento pode novamente voltar a cair água abaixo, pois o atual Programa de Matemática do Ensino Básico (Ministério da Educação, 2013) inferioriza o papel da resolução de problemas no processo de ensino-aprendizagem da matemática, uma vez que preconiza a simples aplicação de procedimentos já previamente estudados, empobrecendo assim a capacidade de resolução de problemas.
Deve a resolução de problemas continuar a ocupar um lugar de destaque nas atividades matemáticas desenvolvidas na sala de aula, pois “aquilo que se faz na sala de aula influenciará extremamente as convicções dos alunos” (Frank, 1992, p. 23). Por isso, é preciso ter em atenção o modo como a importância da resolução de problemas pode afectar o processo de ensino-aprendizagem. Vale e Pimentel (2004) referem que a resolução de problemas pode ser encarada segundo três perspetivas
por um lado, como um processo, quando pretendemos dotar os alunos com estratégias de resolução tornando-os solucionadores cada vez mais aptos de problemas; é também uma finalidade, quando tentamos atender aos aspectos matemáticos como explorar, questionar, investigar, descobrir e usar raciocínios plausíveis; e, por fim, é um método de ensino, que surge para introduzir conceitos envolvendo exploração e descoberta, de acordo com as finalidades do ensino da matemática e de factos, conceitos e procedimentos matemáticos (p. 11).
Siemon e Booker (1990) destacam a relevância de ensinar para, sobre e através da resolução de problemas no processo de ensino-aprendizagem da matemática. O ensino para a resolução de problemas faz com que o aluno tenha acesso à aquisição de conhecimentos, competências e estratégias. No ensino sobre a resolução de problemas o aluno deve reconhecer e aceitar o processo de resolução de problemas. Já o ensino através da resolução de problemas faz com que o aluno tenha a confiança necessária para refletir criticamente, monitorizar e dirigir acerca do processo de resolução de problemas, aprendendo assim de forma mais significativa.
É, portanto, evidente a importância do contributo do papel do professor para que os alunos ganhem consciência das suas ações num processo de resolução de problemas. Contudo, não existe uma habilidade de atuação que ajude o professor a desenvolver nos alunos a capacidade de resolver problemas, pelo que quantos mais professores houver a levarem em prática a resolução de problemas, maior é a oportunidade do intercâmbio de ideias.
Subjacente à ideia de os alunos ganharem consciência das suas ações, está a concepção construtivista da aprendizagem, em que o aluno não é um mero espectador que
19
recebe o conhecimento de forma passiva, mas antes ele próprio o construtor dos novos conhecimentos “em interação com situações problemáticas e com outros sujeitos que obrigam o aluno a ir modificando a sua estrutura cognitiva mediante uma série de ações” (Corts&Callejo de la Vega, 2006, p. 138). Neste seguimento, Brousseau (1998, in Corts&Callejo de la Vega, 2006) sugere como implementar esta forma de construção do conhecimento, presente no Quadro 1.
Quadro 1 – Fases de construção do conhecimentos matemático, segundo Brousseau (1998, in Corts&Callejo de la Vega, 2006, p. 139)
Fases Intervenção do Professor Trabalho dos alunos
Fase de ação O professor propõe o problema Os alunos trabalham individualmente ou em grupo
Fase de
formulação O professor anima, estimula, desbloqueia…, mas deve evitar intervir acerca do conteúdo Os alunos explicitam oralmente ou por escrito como resolveram o problema e a solução encontrada
Fase de validação O professor modera as intervenções dos alunos mas deve evitar intervir acerca do conteúdo
Os alunos devem apresentar argumentos em apoio da validade da sua solução, procurando convencer os seus colegas Fase de
institucionalização O professor deve identificar o novo saber e saber-fazer e especificar as convenções. Trata-se de tornar homogéneos os conhecimentos da turma e de especificar quais dos saberes construídos se devem reter e de que forma Os alunos reestruturam os seus conhecimentos Fase de exercitação seguida de uma avaliação
O professor ajuda os alunos a familiarizarem-se com os novos conhecimentos, a pô-los a funcionar em diferentes situações, a fim de tomarem consciência do seu campo de aplicação
Os alunos resolvem novos problemas e aplicam os novos conhecimentos
2.1.5. Dificuldades dos alunos na Resolução de Problemas
Aquando a resolução de problemas poderão aparecer obstáculos à sua realização, que se tornarão em dificuldades para os alunos e que implicará a perda de entusiasmo da descoberta impedindo o avanço na resolução de um dado problema podendo ainda ser cruciais no aparecimento de erros.
Do estudo do GAVE (2006) ressaltam dificuldades que se prendem com a compreensão do enunciado, a resolução de problemas que envolvam mais do que uma solução, o delinear de
20
estratégias de resolução de problemas mais complexos e a explicação dos raciocínios aplicados, dificuldades estas referenciadas também nos estudos efetuados por Fonseca (1997), Vale (1997), Esteves (2010), Teixeira (2011), Gonçalves e Viseu (2013).
Vale e Pimentel (2004) referem que certas dificuldades dos alunos ressaltam das suas concepções como, por exemplo, a de que um problema tem sempre uma solução e que esta é única. Mencionam, ainda, que uma das dificuldades principais na resolução de problemas é a compreensão, “fase de extrema importância no ensino da resolução de problemas” (p. 16).
Sternberg (2008) anuncia três dificuldades que podem surgir na resolução de um dado problema. São estas: configuração mental (mental sets), rigidez mental (entrenchment) e fixação (fixation), existindo uma grande ligação entre elas, pois a primeira (configuração mental) pode-se desdobrar nas duas últimas (rigidez mental e fixação) como se pode ver a seguir. A configuração mental prende-se como envolvimento num modelo existente para a representação de um contexto do problema ou num procedimento de resolução de problemas. A rigidez mental, que o autor refere poder ser um termo para configuração mental, tem a ver com o solucionador se fixar numa estratégia que normalmente funciona bem na resolução de outros problemas e que não resulta para o problema que tem perante ele. Por fim, a fixação, que o autor também refere como um termo que pode ser dado à configuração mental, envolve por parte do solucionador a fixação num determinado objecto. O autor refere que neste caso o que acontece especificamente é a fixação funcional, ou seja, a incapacidade por parte do solucionador de se aperceber de que algo conhecido para uma utilização particular pode também ser utilizado na realização de outras funções.
Pode-se verificar que as principais dificuldades apontadas nos diferentes estudos estão bastante ligadas às fases do modelo de resolução de problemas apresentado por Polya referido em 2.1.2..
2.2. Ensino-aprendizagem de Geometria
Nesta secção, que se encontra dividida em duas subsecções, começa-se por fazer uma breve análise da presença da Geometria nos documentos curriculares, pois como refere Abrantes (2005) “a riqueza e variedade da Geometria constituem, de facto, argumentos muito fortes para a sua valorização no currículo e nas aulas de Matemática” (pp. 121-122) terminando por mencionar as dificuldades que podem surgir na aprendizagem deste tema.
21
2.2.1. Geometria nos documentos curriculares
A Geometria tem ganho ao longo dos tempos um papel relevante nos documentos curriculares. Esse papel foi assumido após o movimento da Matemática Moderna (Veloso, 2000), momento em que a Geometria começou a ser uma prioridade nos currículos de matemática. É de salientar que anteriormente a este movimento o ensino da Geometria estava restringido à Geometria Euclidiana que “consistia numa tentativa de levar os alunos (dos 12 aos 14 anos) a adquirir hábitos de raciocínio rigoroso e sistemático” (Veloso, 2000, p. 19), ignorando-se a geometria não euclidiana, outro tema da geometria escolar.
O movimento da Matemática Moderna ergue-se na década de 60 conduzindo a alterações significativas no que se refere ao ensino e aprendizagem da geometria. Esta reforma chega a Portugal pelas mãos de José Sebastião e Silva, contudo com a generalização desta reforma aos ciclos de ensino e com a sua morte prematura, o ensino da Matemática entra em declínio, nomeadamente a Geometria, que se afasta lentamente dos currículos.
Entretanto, por forma a travar este afastamento da Geometria e a preconizá-la como tema fundamental dos currículos da matemática escolar, o seu papel começa a ser repensado no final dos anos 80, tendo a APM (2009) produzido a Renovação do Currículo de Matemática com princípios e orientações curriculares onde a geometria é merecedora de uma revalorização no que se refere ao ensino e aprendizagem deste tema.
É assim que ao longo dos anos esta revalorização da geometria tem sido fortalecida, surgindo documentos essenciais como o Currículo Nacional do Ensino Básico – Competências Essenciais (Ministério da Educação, 2001), o Princípios e Normas para a Matemática Escolar (NCTM, 2007) e o Programa de Matemática do Ensino Básico (Ministério da Educação, 2007).
O documento Currículo Nacional do Ensino Básico – Competências Essenciais publicado em 2001 pelo Ministério da Educação define as várias competências matemáticas a serem desenvolvidas ao longo de todos os ciclos do ensino básico. No que concerne ao domínio da geometria, este documento defende que os estudantes devem desenvolver os seguintes aspetos (Figura 3):
22
Figura 3 – Competência matemática que os alunos devem desenvolver no domínio da geometria, segundo Ministério da Educação (2001, p. 62).
Recentemente este documento foi revogado, sendo que se pode ler no Despacho n.º 17169/2011 que “não reúne condições de ser orientador da política educativa preconizada para o Ensino Básico, pelo que se dá por finda a sua aplicação”, lendo-se ainda que “o desenvolvimento do ensino em cada disciplina curricular será referenciado pelos objetivos curriculares e conteúdos de cada programa oficial e pelas metas de aprendizagem de cada disciplina”. Após ler esta observação é caso para expressar o descontentamento pessoal em anunciarem que as metas de aprendizagem reúnem condições para serem um documento orientador da política educativa.
Os Princípios e Normas para a Matemática Escolar traduzido pela APM é um documento de referência a nível internacional e que serve de orientação e recurso desde o pré-escolar ao 12.º ano. Referentemente ao domínio da geometria, este documento preconiza que os alunos devem ser capazes de
Analisar as características e propriedades de formas geométricas bi e tridimensionais e desenvolver argumentos matemáticos acerca de relações geométricas;
Especificar posições e descrever relações espaciais recorrendo à geometria de coordenadas e a outros sistemas de representação;
23 Aplicar transformações geométricas e usar a simetria para analisar situações
matemáticas;
Usar a visualização, o raciocínio espacial e a modelação geométrica para resolver problemas. (NCTM, 2007, p. 44)
Relativamente ao Programa de Matemática do Ensino Básico, opta-se por fazer referência ao programa homologado em 2007, visto que este relatório refere-se ao 9.º ano de escolaridade e para este está ainda em vigor o anunciado programa. Neste documento curricular que está dividido por ciclos de escolaridade, na aprendizagem relativamente ao tema geometria os alunos devem
Desenvolver a visualização e o raciocínio geométrico e ser capazes de os usar;
Compreender e ser capazes de utilizar propriedades e relações relativas a figuras geométricas no plano e no espaço;
Compreender e ser capazes de usar as relações de congruência e semelhança de triângulos;
Desenvolver a compreensão das isometrias e semelhanças;
Compreender a noção de demonstração e ser capazes de fazer raciocínios dedutivos;
Ser capazes de resolver problemas, comunicar e raciocinar matematicamente em contextos geométricos e trigonométricos. (Ministério da Educação, 2007, p. 51)
Contudo, não se pode deixar de referir que o Programa de Matemática homologado em 2013 poderá ter um efeito negativo na aprendizagem da matemática e, em particular, da geometria, pois trata-se de “um programa alicerçado na preocupação do axiomatizar” (Albuquerque, Barroso, Gouveia, Nápoles, Sequeira e Torres, 2013), de um programa que dá ênfase à memorização. Esperamos não voltar a um declínio do ensino-aprendizagem da geometria.
2.2.2. Dificuldades na aprendizagem da Geometria
Sendo indubitável a importância da Geometria, é necessário ter em conta as dificuldades que surgem na aprendizagem da mesma, por forma a colmatar possíveis desinteresses por este tema da matemática e a ter em conta diferentes estratégias de ensino-aprendizagem.
Do estudo do GAVE (2006) ressaltam dificuldades na aprendizagem da geometria, como por exemplo: aplicação de conhecimentos de Geometria a situações concretas, visualização espacial, construções geométricas e sentido de abstração. Estas dificuldades estão patentes nos vários relatórios dos exames nacionais (GAVE, 2010, GAVE, 2011, GAVE, 2012, GAVE, 2013,