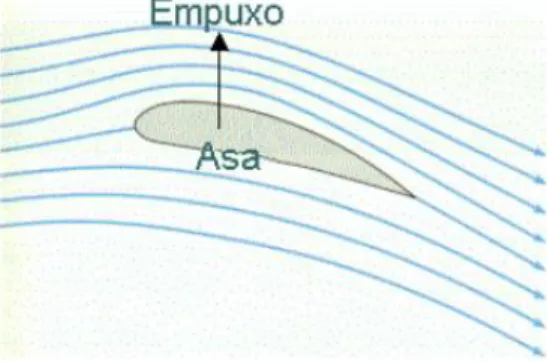
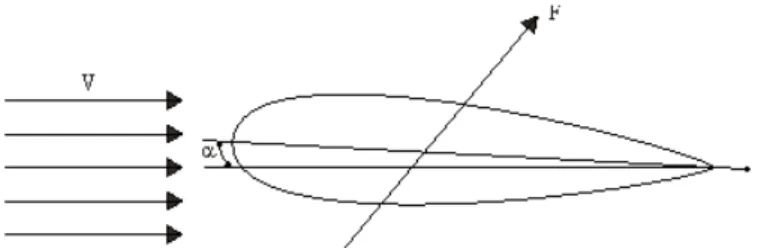
O USO DO AÇO INOX NAS ESTRUTURAS DA FUSELAGEM DE AERONAVES
Texto
Imagem


Outline
Documentos relacionados
Nessa situação temos claramente a relação de tecnovívio apresentado por Dubatti (2012) operando, visto que nessa experiência ambos os atores tra- çam um diálogo que não se dá
No caso dos dispositivos para testes de rastreio do sangue (à excepção dos testes de HBsAg e anti-HBc), todas as amostras verdadeiras positivas devem ser identificadas como
Nesse contexto, a análise numérica via MEF de vibrações sísmicas induzidas por detonações se mostra como uma metodologia que pode contribuir significativamente
Como já destacado anteriormente, o campus Viamão (campus da última fase de expansão da instituição), possui o mesmo número de grupos de pesquisa que alguns dos campi
É primeiramente no plano clínico que a noção de inconscien- te começa a se impor, antes que as dificuldades conceituais envolvi- das na sua formulação comecem a ser
No entan- to, na análise comparativa das respostas obtidas para cada questão do protocolo QVV entre os sujeitos do GP e do GNP que perceberam a mu- dança vocal, foi encontrada
A prova do ENADE/2011, aplicada aos estudantes da Área de Tecnologia em Redes de Computadores, com duração total de 4 horas, apresentou questões discursivas e de múltipla
Este estudo apresenta como tema central a análise sobre os processos de inclusão social de jovens e adultos com deficiência, alunos da APAE , assim, percorrendo