Governo Federal Presidente da República

André Gustavo Campos Pereira

Joaquim Elias de Freitas

Roosewelt Fonseca Soares

Cálculo I

D I S C I P L I N A

Mais aplicações – Gráficos de funções

Autores

aula

Divisão de Serviços Técnicos

Catalogação da publicação na Fonte. UFRN/Biblioteca Central “Zila Mamede”

Governo Federal

Presidente da República Luiz Inácio Lula da Silva Ministro da Educação Fernando Haddad

Secretário de Educação a Distância – SEED Carlos Eduardo Bielschowsky

Universidade Federal do Rio Grande do Norte

Reitor

José Ivonildo do Rêgo

Vice-Reitora

Ângela Maria Paiva Cruz

Secretária de Educação a Distância Vera Lúcia do Amaral

Secretaria de Educação a Distância- SEDIS

Coordenadora da Produção dos Materiais Marta Maria Castanho Almeida Pernambuco

Coordenador de Edição Ary Sergio Braga Olinisky

Projeto Gráfico Ivana Lima

Revisores de Estrutura e Linguagem Eugenio Tavares Borges

Jânio Gustavo Barbosa Thalyta Mabel Nobre Barbosa

Revisora das Normas da ABNT Verônica Pinheiro da Silva

Revisoras de Língua Portuguesa Janaina Tomaz Capistrano Sandra Cristinne Xavier da Câmara

Revisores Técnicos Leonardo Chagas da Silva Thaísa Maria Simplício Lemos

Revisora Tipográfica Nouraide Queiroz

Ilustradora Carolina Costa

Editoração de Imagens Adauto Harley Carolina Costa

Diagramadores Bruno de Souza Melo Dimetrius de Carvalho Ferreira Ivana Lima Johann Jean Evangelista de Melo

Adaptação para Módulo Matemático André Quintiliano Bezerra da Silva Kalinne Rayana Cavalcanti Pereira Thaísa Maria Simplício Lemos

Colaboradora Viviane Simioli Medeiros Campos

Apresentação

T

emos tantas aplicações para derivadas que apenas uma aula para tratar desse tópico seria até um pecado. Nesta aula, usaremos as derivadas para ajudar-nos a esboçar gráficos de funções, pois, muitas vezes, precisaremos apenas de um esboço do gráfico de uma função para obter informações iniciais sobre: em que intervalos a função decresce ou cresce, de que forma tal crescimento/decrescimento acontece (concavidade); em que pontos ocorrem seus máximos ou mínimos etc.

Objetivo

Crescimento e

concavidade de funções

Você estudou na disciplina Pré-Cálculo vários tipos de funções e até esboçou os gráficos de muitas delas, lembra?

Por exemplo, na aula 9 (Funções II) você estudou zeros, sinal, crescimento e decrescimento e, logo em seguida, construiu alguns gráficos e utilizou técnicas para construção de um gráfico a partir de outro (cisalhamento horizontal e translação); e, a partir da aula 11 (Funções afins), todas as aulas apresentavam gráficos.

Nesta aula, então, refaremos alguns daqueles exemplos para recordar, pois recordar é viver!

Dada uma função f ฀฀ ฀R, sabemos (de acordo com a aula 8 da disciplina Pré-Cálculo – Funções I) que seu gráfico é o subconjunto Graf฀f) =฀฀x฀ y)_฀R฀ :x_฀Iey =f฀x) _. Ou seja, se o domínio I tiver uma infinidade de pontos, teremos também uma infinidade

de pontos que comporá o gráfico da função. Se quisermos realmente traçar esse gráfico, deveremos plotar no plano todos os seus pontos, que é uma tarefa impossível. Entretanto, se quisermos apenas estudar as propriedades das funções como comportamento (crescimento/ decrescimento, pontos extremos etc.) a precisão absoluta do local dos pontos do gráfico não será mensurada, mas os intervalos de crescimento, bem como o modo pelo qual a função cresce (concavidade) e onde se localizam exatamente os pontos extremos são informações que serão checadas com rigor, a partir das perguntas seguintes:

1.

quais são os intervalos onde a função cresce e os intervalos onde ela decresce?

2.

e se ela cresce, como é esse crescimento? Segundo uma reta ou segundo uma curva que não é uma reta?

Neste momento pedimos que você relembre os conceitos de função crescente e decrescente estudadas na aula 9 da disciplina Pré-Cálculo.

Para respondermos à primeira pergunta, utilizaremos o teorema seguinte.

Teorema 1

Teste da primeira derivada – Seja f uma função contínua no intervalo fechado

฀a฀ b] e derivável no intervalo aberto ฀a฀ b):

a)

se f฀฀x)฀0 para todo x em ฀a฀ b), então f é crescente em ฀a฀ b];

b)

se f฀฀x)฀0 para todo x em ฀a฀ b), então f é decrescente em ฀a฀ b];

c)

se ฀฀฀x) = 0 _{para todo} x em ฀a฀ b), então f é constante em ฀a฀ b].

Demonstração - Dados x฀฀ x2, com ฀฀ e ฀฀ em ฀a฀ b], então, pelo teorema do

valor médio, existe c entre ฀฀ e ฀฀,conseqüentemente, c em ฀a฀ b), de modo que

f฀x2) =f฀x฀) +f฀฀฀)฀x2฀x฀)ouf฀x2)฀f฀x฀) =f฀฀฀)฀x2฀x฀)_,

então:

a)

se f฀฀c)฀0 para todo c em ฀a฀ b), então f฀x2)฀f฀x฀) =f฀฀c)฀x2฀x฀)฀0 e

f฀x฀)฀ f฀x2), portanto, fé crescente em ฀a฀ b];

b)

se f฀฀c)฀0 _{para todo} c em ฀a฀ b), então f฀x2)฀f฀x฀) =f฀฀c)฀x2฀x฀)฀0 e f฀x฀)฀ f฀x2), portanto, f é decrescente em ฀a฀ b];

c)

se f฀฀฀) = 0 para todo c em ฀a฀ b), então f฀x2)฀f฀x฀) =f฀฀฀)฀x2฀x฀) = 0 e ฀฀x฀) =฀฀x2), portanto, f é constante em ฀a฀ b].

Exemplo 1

Verifique os intervalos de crescimento das seguintes funções (exemplos presentes na aula 9 de Pré-Cálculo):

a)

฀฀x) = 3x฀1.

b)

฀฀x) =x฀_.

Atividade 1

Solução

a)

Calculando a derivada da função f, teremos ฀฀฀x) = 3. Para quais valores de x temos

f฀฀x)฀0 ?

Ora, ฀฀_{฀x) = 3 para qualquer valor da variável x, logo f}฀_{฀x) = 3฀0 para todo valor} de x. Pelo Teorema 1, se f฀฀x)฀0 para todo x em ฀a฀ b), então f é crescente em ฀a฀ b], portanto, temos que ฀฀x) = 3x฀1 é crescente em todos os pontos de seu domínio.

b)

Calculando a derivada da função f, teremos ฀฀฀x) = 2x. Para quais valores de x temos

f฀฀x) = 2x ฀0_?

Resolvendo essa inequação, conforme aprendemos na aula 7 de Pré-Cálculo (Inequações algébricas e intervalos), temos 2x ฀฀฀x ฀฀.

Logo, para os valores positivos de x, temos que a função ฀฀x) =x฀ é crescente.

c)

Calculando a derivada da função f, teremos ฀฀฀x) = 3x฀. Para quais valores de x temos

f฀฀x) = 3x฀฀0?

Resolvendo essa inequação, temos 3x฀฀฀_฀x฀฀฀_฀x_= ฀_.

Logo, a função ฀฀x) =x฀ _{é crescente nos intervalos ฀฀∞฀0) e} ฀0฀_฀)_.

Verifique os intervalos de decrescimento das mesmas funções apresentadas no exemplo 1.

Volte à aula 9 de Pré-Cálculo e visualize os gráficos das funções dos itens b) e c) nas páginas 7 e 8, respectivamente, para constatar graficamente o que você já havia detectado analiticamente.

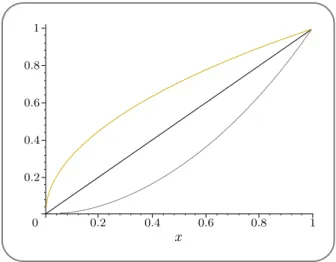
Figura 1 - Três possibilidades de uma função, saindo de ฀0฀0), atingir ฀1฀1). Para entender o que essas funções têm de diferente, precisamos saber o que significa concavidade.

Já vimos na aula 4 (A derivada) que se f é derivável no intervalo I a reta tangente ao

gráfico no ponto ฀p฀ f฀p)) é dada por y=฀฀p) +฀฀฀p)฀x฀p).

Denotemos essa reta por ฀฀x) =f฀p) +f฀฀p)฀x_฀p).

Definição 1

Dizemos que f tem concavidade para cima no intervalo aberto I se f฀x)฀ T฀x) quaisquer que sejam x e p em I, com x฀฀฀.

Tal situação pode ser interpretada geometricamente como: a reta tangente ao gráfico em qualquer ponto sempre se encontra abaixo do gráfico da função em todos os pontos diferentes do ponto de tangência.

Na figura 2, traçamos o gráfico da função f : [_฀฀฀฀]_→R definida por ฀฀x) =x฀ e três retas tangentes a esse gráfico para ilustrar o que foi dito.

Atividade 2

Utilizando o gráfico da função f : [฀฀฀฀]→R _{definida por} ฀฀x) =x฀_{, com} uma régua, trace retas tangentes em diversos pontos e observe que a reta traçada se encontra sempre abaixo do gráfico da função.

Da mesma forma, chegamos à seguinte definição.

Definição 2

Dizemos que f tem concavidade para baixo no intervalo aberto I se

f฀x)฀ T฀x) , quaisquer que sejam x e p em I, com x_฀฀฀.

Essa situação pode ser interpretada geometricamente como: a reta tangente ao gráfico em qualquer ponto sempre se encontra acima do gráfico da função em todos os pontos diferentes do ponto de tangência.

Na figura 3, traçamos o gráfico da função f : [_฀฀฀฀]_→R definida por ฀฀x) =_฀x฀ e três retas tangentes a esse gráfico para ilustrar o que foi dito.

Atividade 3

Utilizando o gráfico da função f : [_฀฀฀฀]_→R definida por ฀฀x) =฀x฀, com uma régua, trace retas tangentes em diversos pontos e observe que a reta traçada se encontra sempre abaixo do gráfico da função.

Você deve estar se perguntando: “eu terei que traçar as retas tangentes em todos os pontos do gráfico para saber a concavidade, mas como o gráfico possui infinitos pontos terei que traçar infinitas tangentes, ou seja, não acabarei nunca de fazer isso?”.

Você está certo, o procedimento seria esse, se não tivéssemos as derivadas para nos ajudar!

Uma conseqüência imediata do Teorema 2, apresentado mais adiante, é que o gráfico de uma função f derivável em um intervalo aberto I é:

a)

côncavo para cima, se ฀฀ é crescente em I;

b)

côncavo para baixo, se ฀฀ é decrescente em I.

Por côncavo para cima, entenderemos: tem concavidade para cima; e por côncavo para baixo: tem concavidade para baixo.

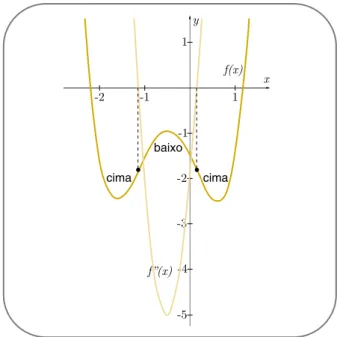
Na Figura 4, mostraremos os gráficos da função e de sua derivada, e perceberemos que quando a derivada é decrescente a função terá concavidade para baixo neste mesmo intervalo e quando a derivada é crescente a concavidade é para cima neste mesmo intervalo. Vejamos.

Veja que quando particionamos o domínio em sub-intervalos de crescimento e decrescimento da derivada, nestes mesmos intervalos vemos que o gráfico da função apresentará concavidades definidas.

Como já havíamos mencionado anteriormente, o teorema a seguir será nosso ponto de apoio no estudo de concavidades.

Teorema 2

Teste da Concavidade – Seja f uma função definida no intervalo aberto I que

possui derivadas de ordens 1 e 2 no intervalo I:

a)

se f฀฀฀x)฀0 _{para todo} x em I, então o gráfico de fé côncavo para cima;

b)

se f฀฀฀x)฀0 para todo x em I, então o gráfico de f é côncavo para baixo.

Demonstração - A demonstração deste teorema é uma conseqüência do teorema anterior, pois se f฀฀฀x)฀0 para todo x em I, então ฀฀ é crescente em I, portanto, a inclinação

da tangente ao gráfico de f cresce com x, logo, o gráfico de f é côncavo para cima. Se f฀฀฀x)฀0 para todo x em I, então ฀฀ é decrescente em I, portanto, o gráfico de f é

côncavo para baixo.

A seguir, na Figura 5, destacamos nos gráficos que quando a derivada segunda é positiva a função tem curvatura para cima e quando é negativa a curvatura é para baixo.

Figura 5 - Gráficos das funções f฀x) =x4+ 2x3฀x฀฀2x฀1฀5 e ฀฀฀_{฀x) = 12x}฀_{+ 12x฀2. Destacam- se}

Veja que quando particionamos o domínio em sub-intervalos em que a derivada segunda é positiva ou negativa, nestes mesmos intervalos vemos que o gráfico da função apresentará concavidades definidas.

Note que até o momento, em todas as situações estudadas, estávamos preocupados com os pontos onde a concavidade era para cima ou para baixo. E o que acontece com o ponto no qual a concavidade muda, quer dizer, se antes de um dado ponto a concavidade era de um tipo e depois desse ponto ela mudou para o outro tipo, teremos algum interesse nesse ponto? Claro que sim, podemos dizer que este é o ponto de guinada, ou seja, é o ponto em que houve uma “ruptura” no processo. Veja a situação a seguir.

Imagine que seu negócio estava com o gráfico do lucro com concavidade para baixo e a partir de um certo ponto a concavidade muda para cima, será que saber onde essa mudança ocorreu é importante? Pois é, esse ponto é tão importante que até temos um nome só para ele, conforme apresentamos na definição a seguir.

Definição 3

Uma função f definida em um intervalo I tem um ponto de inflexão em ฀฀ se o

gráfico da f muda de concavidade em ฀฀.

Se em um ponto ฀฀ do domínio de f, ฀฀฀ é contínua, positiva de um lado de

฀฀ e negativa do outro temos um ponto de inflexão em ฀฀, pois existe uma

mudança de concavidade, conseqüentemente, ฀฀฀_฀x

฀) = 0. Observe que onde

฀฀฀ é positiva ฀฀ é crescente e onde ฀฀฀ é negativa ฀฀ é decrescente, portanto, nos pontos de inflexão ฀฀ _{tem um extremo local.}

Considere uma função f definida em um intervalo I que possui derivada de

segunda ordem em I, os pontos de inflexão de f são soluções da equação

฀฀฀฀x฀) = 0 _{, podendo haver casos em que} ฀฀฀฀x฀) = 0 e ฀฀ é um ponto de

máximo ou mínimo local.

E para responder à última pergunta proposta no início da aula, como estaremos trabalhando com funções deriváveis, os pontos críticos serão aqueles da solução da equação ฀฀฀x) = 0, como vimos na aula 6 (Aplicações da derivada).

Agora, com as respostas prontas

Esboço do gráfico de funções

usando propriedades das derivadas

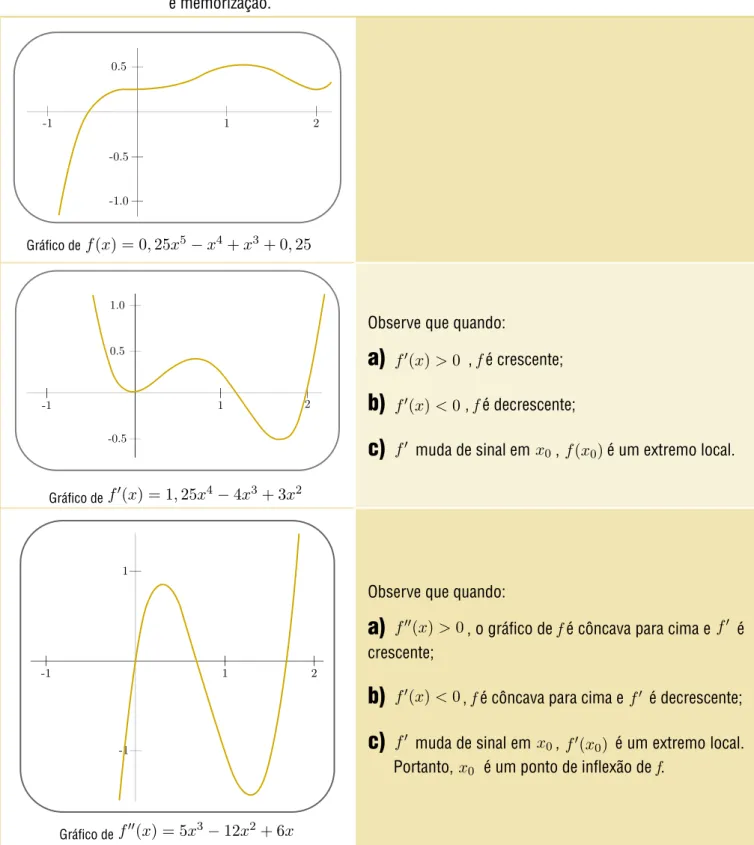
A visualização dos conceitos apresentados é muito importante para a sua compreensão e memorização.

Gráfico de f฀x) = 0฀25x5_฀x4_+x฀_{+ 0฀25}

Gráfico de f฀฀x) = 1฀25x4฀4x3_{+ 3x}฀

Observe que quando:

a)

f฀฀x)฀0 , fé crescente;

b)

f฀฀x)฀0, f é decrescente;

c)

฀฀ muda de sinal em ฀฀, ฀฀x฀) é um extremo local.

Gráfico de ฀฀฀฀x) = 5x3฀12x฀+ 6x

Observe que quando:

a)

f฀฀฀x)฀0, o gráfico de fé côncava para cima e ฀฀ é

crescente;

b)

f฀฀x)฀0, fé côncava para cima e ฀฀ é decrescente;

c)

฀฀ muda de sinal em ฀฀, ฀฀฀x฀) é um extremo local.

Portanto, ฀฀ é um ponto de inflexão de f.

Após os três exemplos que apresentaremos a seguir, proporemos algumas atividades mais simples.

Exemplo 2

Esboçar o gráfico da função f฀x) = x

4

4 ฀0฀4x3฀2฀7x฀+ 10, inicialmente determinando os pontos críticos, estudando o crescimento e decrescimento da função.

Solução

Calculemos a primeira derivada

f฀x) = 4x 4฀฀

4 ฀0฀4·3x3฀฀฀2฀7·2x2฀฀+ 0 =x3฀1฀2x2฀5฀4x f฀฀x) =x3฀1฀2x฀฀5฀4x

Encontremos os pontos críticos, inicialmente determinando as raízes da equação f฀฀x) = 0

f฀฀x) =x3฀1฀2x฀_{฀5฀4x= 0}

x฀x฀_{฀1฀2x฀5฀4) = 0}

Tem-se uma raiz ฀฀= ฀ e, resolvendo a equação do segundo grau, encontramos mais

duas raízes x฀ =฀฀฀8ex3 = 3, totalizando três pontos críticos, os índices de x foram escolhidos de modo que x฀฀ x2฀ x3. No gráfico de f, temos os pontos críticos:

P฀฀x฀฀ f฀x฀)),P2฀x2฀ f฀x2))eP3฀x3฀ f฀x3)).

Substituindo ฀฀, ฀฀ e ฀฀ nos pontos anteriores e seus respectivos ฀฀x) listados

a seguir

f฀฀1,8) = 6฀2,f฀0) = 10ef฀3) =฀4,8.

Substituindo esses valores, obtemos os pontos críticos:

P฀฀฀1฀8 ; 6฀2),P2฀0 ; 10)eP3฀3 ;฀4฀8).

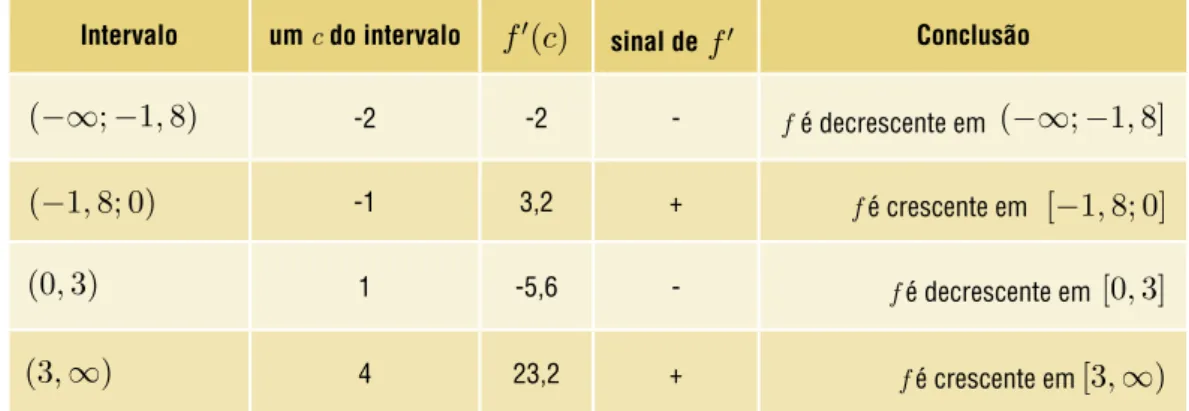
Temos agora três pontos importantes para esboçar o gráfico. As três raízes ฀฀, ฀฀ e

฀฀ determinam quatro intervalos abertos, onde a derivada ฀฀฀x) tem o mesmo sinal; para conhecermos esse sinal, basta saber o sinal de f฀฀฀)_{, sendo} c um número qualquer no

Intervalo um c do intervalo f฀฀฀) _{sinal de ฀}฀ Conclusão

฀฀∞;฀1฀8) -2 -2 - _{f é decrescente em} ฀_฀∞;_฀1฀8]

฀฀1฀8; 0) -1 3,2 + _{f é crescente em [฀1฀8; ฀]}

฀0฀3) 1 -5,6 - f é decrescente em [฀฀3]

฀3฀฀) 4 23,2 + _{f é crescente em [3฀฀฀}

Quadro 1 - Encontrando as respostas às perguntas 1, 2 e 3 para a função f฀x) =x₄4฀0฀4x3_฀2฀7x฀_{+ 10}

Neste ponto de nosso estudo, conhecemos os pontos críticos, suas tangentes horizontais e comportamento da função, crescente ou decrescente nos intervalos delimitados por tais pontos.

A partir do quadro anterior e confirmação do gráfico ao lado, analisando os crescimentos e decrescimentos da função, podemos ver que P฀฀฀1฀8 ; 6฀2) é um mínimo local, P฀฀0฀10)

é um máximo local e P฀฀3 ;฀4฀8) é um mínimo local e absoluto.

Figura 7 - Gráfico da função _{f฀x) =} x4

4 ฀0฀4x3฀2฀7x฀+ 10

Exemplo 3

Esboçar o gráfico da função f฀x) = x 5

Solução

Calculemos a primeira derivada

f฀x) = 5x5฀฀

5 ฀0฀3·4x4฀฀฀1฀8·3x3฀฀+ 0 =x4฀1฀2x3฀5฀4x2

f฀฀x) =x4_฀1฀2x3_฀5฀4x฀

Encontremos os pontos críticos, inicialmente determinando as raízes da equação ฀฀฀x) = 0.

f฀฀x) =x4_฀1฀2x3_฀5฀4x฀ _{= 0}

x฀฀x฀฀1฀2x฀5฀4x) = 0

Tem-se uma raiz dupla ฀฀= ฀, a raiz dupla será muito importante no estudo

das concavidades e, resolvendo a equação do segundo grau, encontramos mais duas raízes x฀ =฀฀฀8ex3 = 3, totalizando três pontos críticos. No gráfico de f, temos os

pontos críticos:

P฀฀x฀฀ f฀x฀)),P2฀x2฀ f฀x2))eP3฀x3฀ f฀x3)).

Substituindo ฀฀, ฀฀ e ฀฀ nos pontos anteriores e seus respectivos ฀฀x) listados a seguir

f฀_฀1฀8) = 13฀6,f฀0) = 10ef฀3) =_฀14฀3,

obteremos os pontos críticos:

P฀฀฀1฀8; 13฀6),P2฀0฀10)eP3฀3;฀14฀3).

Da mesma forma que no exemplo anterior, temos três pontos importantes para esboçar o gráfico. As três raízes ฀฀, ฀฀ e ฀฀ determinam quatro intervalos abertos, onde a derivada ฀฀฀x) tem o mesmo sinal; para conhecermos esse sinal, basta saber o sinal de f฀_{฀฀), sendo}

Intervalo um c do intervalo f฀฀฀) _{Sinal de ฀}฀ Conclusão

฀฀∞;฀1฀8) -2 4 + _{f é crescente em ฀฀∞;฀1฀8]}

฀1฀8; 0) -1 -3,2 - _{f é decrescente em} [฀1฀8; ฀]

฀0฀3) 1 -5,6 - f é decrescente em _[฀฀3]

฀3฀฀) 4 92,8 + _{f é crescente em} [3฀฀฀

Quadro 2 - Encontrando as respostas às perguntas 1, 2 e 3 para a função f฀x) =x 5

5 ฀0฀3x4฀1฀8x฀+ 10

Procuremos agora os possíveis pontos de inflexão de fque são soluções da equação

฀฀฀฀x) = 0, lembrando que pode haver casos em que ฀฀฀฀x฀) = 0 e ฀฀ é um ponto de

máximo ou mínimo local.

Neste caso, já vimos que

f฀฀x) =x4_฀1฀2x3_฀5฀4x฀

e

f฀฀฀x) = 4x3_฀3·1฀2x฀_฀2·5฀4x

f฀฀฀x) = 4x3฀3฀6x฀_฀10฀8x

Vamos agora resolver a equação ฀฀฀฀x) = 0_{, isto é,}

4x3_฀3฀6x฀_฀10฀8x= 0,

4x฀x฀฀0฀9x฀2฀7) = 0.

Encontramos três raízes nessa equação, inicialmente ฀฀= ฀ e, resolvendo a equação

do 2º grau x฀_{฀฀฀9x฀2฀7 = ฀, encontramos mais duas raízes x}

฀ =฀฀฀25ex6= 2฀฀5. No gráfico de f (Figura 5), vemos os possíveis pontos de inflexão:

P฀฀x฀฀ f฀x฀)),P5฀x5฀ f฀x5))eP6฀x6฀ f฀x6))

Substituindo x₄, x₅ e x₆ nos pontos anteriores e seus respectivos ฀฀x) listados

a seguir

f฀฀1฀25) = 12฀4,f฀0) = 10ef฀2฀15) =_฀5.

Atividade 4

A partir do Quadro 2 e confirmação do gráfico ao lado, analisando os crescimentos e decrescimentos da função, podemos ver que P฀฀฀1฀8; 13฀6) é um máximo local e P฀฀3;฀14฀3) é um mínimo local.

Analisando a variação das curvaturas nos possíveis

pontos de inflexão P฀฀฀1฀25 ; 12฀4),P5฀0฀10) eP6฀2฀15 ;฀5)

P฀฀฀1฀25 ; 12฀4) P5฀0฀10)eP6฀2฀15 ;฀5)., vemos que os três são pontos

de inflexão.

Um mesmo ponto não pode ser ponto de inflexão e extremo local simultaneamente, como P฀฀0฀10) é um ponto de inflexão e P฀฀0฀10) =P5฀0฀10)฀ como vemos no gráfico, P฀฀0฀10) foi um

candidato a extremo local que não teve sucesso.

Figura 8 - Gráfico da função _{f฀x) =} x5

5 ฀0฀3x4฀1฀8x฀+ 10

a) Esboce o gráfico da função

฀฀x) =x฀_฀12x_฀4, inicialmente determinando os pontos críticos, estudando o crescimento e decrescimento da função.

Propriedades das derivadas

de ordem superior

A seguir, apresentaremos alguns teoremas que nos servirão de suporte quando o que estudamos anteriormente não puder ser usado.

Teorema 3

Teste da segunda derivada – Sejam f uma função com derivadas contínuas

até a ordem dois em um intervalo aberto ฀a฀ b) e ฀฀ um ponto em ฀a฀ b).

Se ฀฀฀x฀) = 0 e ฀฀฀฀x฀)฀= 0, então ฀฀x฀) é um extremo local em ฀฀ e, além disso:

a)

se ฀฀฀x฀) = 0 e f฀฀฀x)฀0, então, ฀฀x฀) é um mínimo local em ฀฀;

b)

se ฀฀฀x฀) = 0 e f฀฀฀x)฀0, então, ฀฀x฀) é um máximo local em ฀฀.

Demonstração - Usemos a propriedade 2 do Teorema de Taylor com ฀= ฀ e x no

lugar de b:

f(x) =฀1(x฀) +

f฀฀(c)(x_฀x฀)2

2฀ , c entre ฀฀ e x, ฀฀ e x em ฀a฀ b). Como ฀฀x) =฀฀x฀) +฀฀฀x฀)฀x฀x฀), tem-se

f฀x) =f฀x฀) +f฀฀x฀)฀x฀x฀) +f฀฀฀฀)฀x฀x฀) 2

2 ,

com ฀฀฀x฀) = 0.

Assim,

f฀x) =f฀x฀) +

f฀฀฀฀)฀x_฀x฀)2

2 ,

f฀x)฀f฀x฀) +f฀฀฀฀)฀x฀x฀) 2

2 . (1)

Observemos que devido à continuidade de ฀฀฀ _{em ฀}

฀ e ฀฀฀฀x฀)฀= 0 podemos admitir

Seguimos com os dois casos separadamente:

a)

se ฀฀฀x฀) = 0 e f฀฀฀x)฀0, pela observação anterior, f฀฀฀c)฀0 e, portanto, para x

em ฀a฀ b), tem-se

f฀x)_฀f฀x฀) = f฀฀฀c)฀x฀x฀)

2

2 ฀0,com ฀฀฀฀฀. Portanto,

f฀x)฀ f฀x฀).

Resumindo, para

฀_฀฀฀฀

e

x

em

฀a฀ b)

, tem-se

f฀x)฀ f฀x฀)

, isto é,

฀฀x฀)

é um

mínimo local em

฀฀

_.

b)

se ฀฀_{฀x฀) = 0 e f}฀฀_฀x

฀)฀0 , pela observação anterior, f฀฀฀c)฀0 e, portanto, para x em ฀a฀ b), tem-se

f฀x)_฀f฀x฀) +

f฀฀฀c)฀x฀x฀)2

2 ฀0, com ฀฀฀฀฀. Portanto,

f฀x)฀ f฀x฀).

Resumindo, para ฀_฀฀฀฀ e x em ฀a฀ b), tem-se f฀x)฀ f฀x฀), isto é, ฀฀x฀) é um máximo

local em ฀฀.

Exemplo 4

Usando o teste da segunda derivada, determine os extremos locais da função ฀฀x) =x฀_฀12x_฀4.

Solução

Inicialmente, calculemos a primeira derivada

f฀x) =x3฀12x฀4, f฀฀x) = 3x฀฀12฀

Em seguida, vamos encontrar os pontos críticos resolvendo a equação ฀฀_{฀x) = 0:} ฀฀฀x) = 0,

3x฀_{฀12 = 0,}

x฀ ₌ 12 3 ,

x=_±2.

Temos então dois pontos críticos; calculemos seus respectivos valores na segunda derivada:

f฀฀฀x) = 6฀x,

f฀฀฀2) = 6฀2 = 12,

f฀฀฀฀2) = 6฀฀฀2) =฀12฀

Atividade 5

Usando o teste da segunda derivada, determine os extremos locais da função ฀฀x) =x฀x฀1)฀.

O teste da segunda derivada será generalizado a seguir para o caso em que a derivada de ordem ฀฀ é diferente de zero e todas as derivadas de ordem menor que ฀฀ são nulas.

Teorema 4

Teste da derivada de ordem par – Sejam f uma função com derivadas contínuas

até a ordem ฀฀ em um intervalo aberto ฀a฀ b) e ฀฀ um ponto em ฀a฀ b).

Se ฀฀x0) =฀฀x0) =฀ ฀ ฀=฀฀2฀฀1)฀x0) = 0 e ฀2฀฀x฀)฀= 0, então ฀฀x฀) é

um extremo local em ฀฀ e, além disso:

a)

se f฀2฀)_฀x

0)฀0, então, ฀฀x฀) é um mínimo local em ฀฀;

b)

se f฀2฀)_฀x

0)฀0, então, ฀฀x฀) é um máximo local em ฀฀.

Demonstração - Usemos a propriedade 2 do Teorema de Taylor com x no lugar de b, do

seguinte modo:

f(x) =฀2฀฀1(x0) +

f฀2฀)(c)(x฀x0)฀2฀)

(2k)฀ , c entre

฀฀ e x, ฀฀ e x em ฀a฀ b).

Como ฀2฀฀1(x0) =f(x0) +f(x0)(x฀x0)· · ·+

f฀2฀฀1)_(x

0)(x฀x0)

(2k฀1)฀ , tem-se

f(x) =f(x0) +f(x0)(x฀x0)· · ·+

f฀2฀฀1)_(x

0)(x฀x0)

(2k฀1)฀ +

f฀2฀)_(฀)(x฀x 0)฀2฀)

(2k)฀

,

mas ฀฀x0) =฀฀x0) =฀ ฀ ฀=฀฀2฀฀1)฀x0) = 0.

Assim,

f(x) =f(x0) +

f฀2฀)(฀)(x_฀x0)฀2)

(2k)฀ ,

f(x)_฀f(x0) =

f฀2฀)_(฀)(x฀x 0)฀2) (2k)฀

Observemos que devido à continuidade de ฀2฀฀x฀) em ฀฀ com ฀2฀฀x฀)฀= 0 podemos admitir a e b próximos de ฀฀ , de modo que ฀฀2฀)_{฀x) tem o mesmo sinal em} ฀_{a฀ b}). Seguimos com os dois casos separadamente:

a)

se f฀2฀)฀x0)฀0, pela observação anterior, f฀2฀)฀c)฀0 e, portanto, para x em

฀a฀ b). , tem-se

f(x)฀f(x0) = f

฀2฀)_(c)(x฀x 0)2฀

(2k)฀ ฀0, com ฀฀฀฀฀.

Portanto,

f฀x)฀ f฀x฀).

Resumindo, para ฀_฀฀฀฀ e x em ฀a฀ b)., tem-se f฀x)฀ f฀x฀), isto é, ฀฀x฀) é um mínimo

local em ฀฀ .

b)

se f฀2฀)฀x0)฀0 e, pela observação anterior, f฀2฀)฀c)฀0 e, portanto, para x em ฀a฀ b).

tem-se

f฀x)_฀f฀x0) =

f฀2฀)฀c)฀x฀x0)2฀

2 ฀0, com ฀฀฀฀฀. Portanto,

f฀x)฀ f฀x฀).

Resumindo, para ฀_฀฀฀฀ e x em ฀a฀ b)., tem-se f฀x)฀ f฀x฀), isto é, ฀฀x฀) é um

máximo local em ฀฀ .

Teorema 5

Teste da derivada de ordem ímpar – Sejam f uma função com derivadas

contínuas até a ordem 2฀฀ 1 em um intervalo aberto ฀a฀ b). e ฀฀ um ponto

em ฀a฀ b).. Se ฀฀฀฀x฀) =฀฀฀฀฀x฀) =฀ ฀ ฀=฀฀2฀)฀x฀) = 0 e ฀฀2฀+1)฀x฀)฀= 0, então, f tem um ponto de inflexão em ฀฀.

Demonstração - Como a derivada de ordem ฀2฀+ 1) _de f é a derivada de ordem ฀2฀) de

฀฀, pelo teorema, temos um máximo ou mínimo local para ฀฀ em ฀฀, portanto, ฀฀ muda de

Atividade 6

1

2

Exemplo 5

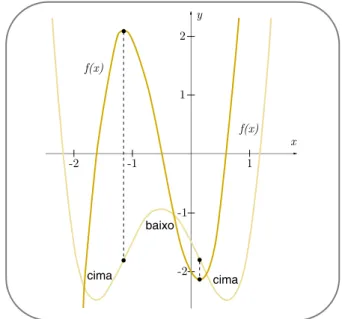
Dada a função f฀x) = 0฀25x5฀x4+x฀+ 0฀25, cujo gráfico apresentamos na Figura 1, mostremos que x = 0 é um ponto crítico e usemos os testes de derivadas de ordens

superior para concluir se esse ponto crítico é um extremo local ou ponto de inflexão.

Solução

Temos que

f฀x) = 0,25x5฀x4+x3+ 0,25,

f฀฀x) = 1,25x4฀4x3+ 3x฀, f฀฀0) = 0, f฀฀฀x) = 5x3฀12x฀+ 6x, f฀฀฀0) = 0, f฀฀฀฀x) = 15x฀฀24x+ 6, f฀฀฀฀0) = 6฀

Aplicando o teste da derivada de ordem ímpar, como a primeira diferente de zero é ímpar, com ฀= ฀ , pois f é uma função com derivadas contínuas até a ordem 3 ฀3 = 2฀1 + 1)

em um intervalo aberto ฀฀1฀1) _{e 0 é um ponto em ฀฀1}฀1) com ฀฀฀0) =฀฀฀฀0) = 0 e ฀฀฀฀฀0) = 6_฀= 0, temos, portanto, um ponto de inflexão em 0.

Aplique o teste da segunda derivada para concluir se 0 é um extremo local da função _{f฀x) =} x4

4 ฀0฀4x3฀2฀7x฀+ 10. Verifique o resultado no gráfico da Figura 7.

Esboce o gráfico das funções a seguir, utilizando a derivada primeira e os pontos críticos.

a)

฀฀x) =x฀฀6x.

b)

฀฀x) =x฀_฀6x+ 9.

3

4

Resumo

1

2

Esboce o gráfico das funções seguintes, utilizando derivada, os pontos críticos e os possíveis pontos de inflexão (sendo ฀฀฀_{฀x) = 0)).} Determine os pontos de máximo, mínimo e inflexão.

a)

฀฀x) = ฀x฀1)฀+ 1.

b)

฀฀x) =x4฀2x฀+ 1.

Dada a função ฀฀x) =x4฀2x5+x฀, verifique se ฀= ฀ é um ponto de máximo mínimo ou ponto de inflexão.

Nesta aula, estudamos como utilizar os conceitos de derivadas (também de ordem superior) para esboçar o gráfico de funções. Para fazer isso, precisamos identificar os máximos e mínimos, as regiões onde as funções crescem ou decrescem e a relação entre crescimento e concavidade.

Auto-avaliação

Imagine-se um grande empresário e alguém chegando com o gráfico do lucro de sua empresa até o momento atual. Supondo que esse gráfico seja uma função derivável, que pontos você procuraria destacar no tempo para tentar repeti-lo? (crescimento, decrescimento, máximo, mínimo, ...)?

Referências

ANTON, Howard. Cálculo: um novo horizonte. 6. ed. Porto Alegre: Bookman, 2000. v 1.

SIMMONS, George F. Cálculo: com geometria analítica. São Paulo: McGraw-Hill, 1987. v 1.

THOMAS, George B. Cálculo. São Paulo: Addison Wesley, 2002.