Modelo de regressão log-Weibull modificado e a nova distribuição Weibull modificada...

(1)

Escola Superior de Agricultura “Luiz de Queiroz”

Modelo de regress˜ao log-Weibull modificado e a nova distribui¸c˜ao Weibull modificada generalizada

Jalmar Manuel Farf´an Carrasco

Disserta¸cão apresentada para obten¸cão do t´ıtulo de Mestre em Agronomia. Área de concentra¸cão: Es-tat´ıstica e Experimenta¸cão Agronômica

(2)

Licenciado em Matem´atica

Orientador:

Prof. Dr. Edwin Moises Marcos Ortega

Disserta¸cão apresentada para obten¸cão do t´ıtulo de Mestre em Agronomia. Área de concentra¸cão: Es-tat´ıstica e Experimenta¸cão Agronômica

(3)

Dados Internacionais de Catalogação na Publicação (CIP) DIVISÃO DE BIBLIOTECA E DOCUMENTAÇÃO - ESALQ/USP

Farfán Carrasco, Jalmar Manuel

Modelo de regressão log-Weibull modificado e a nova distribuição Weibull modificada generalizada / Jalmar Manuel Farfán Carrasco. - - Piracicaba, 2007.

128 p.

Dissertação (Mestrado) - - Escola Superior de Agricultura Luiz de Queiroz, 2007. Bibliografia.

1. Análise de sobrevivência 2. Dados censurados 3. Simulação (estatística) I. Título

CDD 519.53

(4)

Dedicat´oria

A Deus ea Virgem Inmaculada Concep¸c˜ao por aben¸coar meu caminho

A Mar´ıa e Manuel por todo o amor, o carinho, a paciˆencia e o apoio incondicional dedicados a min

A Carmen, Jeny, Nancy, Jackeline e Cristel por uma eterna amizade

A Tula por seu eterno amor e compren¸c˜ao

´

(5)

AGRADECIMENTOS

Ao professor Dr. Edwin Moises Marcos Ortega, pela compreens˜ao, e

princi-palmente pela orienta¸c˜ao na elabora¸c˜ao deste trabalho.

Ao conselho do programa de Pós-Gradua¸cão em Estat´ıstica e Experimenta¸cão

Agronˆomica, os professores Dra. Clarice Garcia Borges Dem´etrio e Dra. Roseli Aparecida

Leandro, pelas valiosas sugest˜oes e confian¸ca.

Aos professores do Departamento de Ciˆencias Exatas da ESALQ/USP, Dr.

Carlos Tadeu dos Santos Dias, Dr. C´esar Gon¸calves de Lima, Dr. Gerson Barreto, Dr.

Silvio Sandoval Zocchi e Dra. Sˆonia Maria Stefano Piedade, pela amizade e forma¸c˜ao.

Aos funcion´arios do Departamento de Ciˆencias Exatas da ESALQ/USP, as

secretárias Solange de Assis Paes Sabadin e Luciane Brajão e aos técnicos em informática

Jorge Alexandre Wiendl e Eduardo, pelos aux´ılios permanentes.

Aos colegas de estudo do mestrado e do doutorado, pela amizade,

companhei-rismo e paciˆencia.

Um agradecimento especial aos colegas, Eduardo e Elton, pelo incentivo,

mo-tiva¸c˜ao, companheirismo, paciˆencia e principalmente a grande amizade dedicada.

Um agradecimento a Jackeline, Liliam, Alexsandro, Elenilson, Casio, Celso,

Wirifram, Bruno, Lucielio, Vanderley, D´arcio, Marina, Julieth, Andreza, Michele, Deise pelo

incentivo, motiva¸c˜ao, companheirismo, paciˆencia e principalmente a grande amizade durante

o tempo que fiquei morando na Vila estudiantil da P´os Gradua¸c˜ao.

A todas as pessoas que contribu´ıram direta ou indiretamente para a realiza¸c˜ao

(6)

SUM ´ARIO

RESUMO . . . 8

ABSTRACT . . . 9

LISTA DE FIGURAS . . . 10

LISTA DE TABELAS . . . 13

1 INTRODU ¸C ˜AO . . . 14

1.1 Proposta de trabalho . . . 16

1.2 Suporte computacional . . . 17

2 REVIS ˜AO . . . 18

2.1 An´alise de sobrevivˆencia . . . 18

2.2 Distribui¸c˜ao Weibull modificada . . . 22

2.2.1 Formula¸c˜ao da distribui¸c˜ao Weibull modificada . . . 23

2.2.2 Estudo da fun¸c˜ao de risco da distribui¸c˜ao Weibull modificada . . . 23

2.2.3 Rela¸c˜ao com outras distribui¸c˜oes . . . 24

2.2.4 Inferˆencia na distribui¸c˜ao Weibull modificada incorporando censura . . . 26

2.3 Modelos de regress˜ao . . . 27

2.3.1 Modelos de loca¸c˜ao-escala . . . 27

2.4 Estrat´egias de inferˆencia . . . 28

2.4.1 Estima¸c˜ao por m´axima verossimilhan¸ca . . . 28

2.4.2 M´etodo de Jackknife . . . 29

2.5 An´alise de sensibilidade . . . 31

2.5.1 Influˆencia Global . . . 32

2.5.2 Influˆencia Local . . . 32

2.5.2.1 Influˆencia Local de Cook (1986) . . . 34

2.5.2.1.1 Perturba¸c˜ao de casos . . . 37

2.5.2.1.2 Perturba¸c˜ao na vari´avel resposta . . . 37

2.5.2.1.3 Perturba¸cão na variável explanatória . . . 37

2.5.2.2 Influˆencia local conformal . . . 37

2.6 An´alise de res´ıduo . . . 39

(7)

2.6.2 Res´ıduo deviance . . . 40

2.7 Nova distribui¸c˜ao Weibull modificada . . . 40

3 MATERIAL E M´ETODOS . . . 41

3.1 Material . . . 41

3.1.1 Dados de peixes da esp´ecie Golden shiner . . . 41

3.1.2 Dados de soro-revers˜ao . . . 42

3.1.3 Dados de pacientes com cˆancer . . . 43

3.2 M´etodos . . . 43

3.2.1 Modelo de regress˜ao log-Weibull modificado . . . 43

3.2.1.1 Descri¸c˜ao do MRLWM . . . 44

3.2.1.2 Procedimentos inferˆenciais do MRLWM . . . 45

3.2.1.3 An´alise de sensibilidade para o MRLWM-influˆencia global . . . 46

3.2.1.4 An´alise de sensibilidade para o MRLWM-influˆencia local . . . 47

3.2.1.4.1 Pondera¸c˜ao de Casos . . . 47

3.2.1.4.2 Perturbando a vari´avel resposta . . . 48

3.2.1.4.3 Perturbando a vari´avel explanatoria . . . 49

3.2.1.5 An´alise de res´ıduos para o MRLWM . . . 51

3.2.1.5.1 Res´ıduo martingale . . . 51

3.2.1.5.2 Res´ıduo deviance modificado . . . 51

3.2.1.5.3 Estudo de simula¸c˜ao . . . 52

3.2.1.5.4 Envelope simula¸c˜ao . . . 53

3.2.2 Distribui¸c˜ao Weibull modificada generalizada . . . 59

3.2.2.1 Formula¸c˜ao da DWMG . . . 60

3.2.2.2 Estudo da fun¸c˜ao risco da DWMG . . . 60

3.2.2.3 Rela¸c˜ao com outras distribui¸c˜oes do DWMG . . . 62

3.2.2.4 Inferˆencia da DWMG . . . 62

3.2.2.5 Testes de hip´oteses . . . 63

3.2.2.6 Avalia¸c˜ao Num´erica dos EMV . . . 64

3.2.2.7 Inferˆencia da DWMG incorporando censura . . . 64

(8)

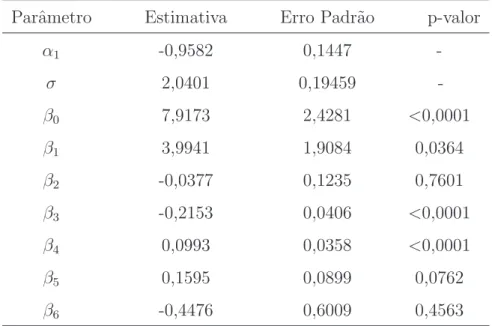
4.1 Aplica¸c˜ao I . . . 67

4.1.1 Fun¸c˜ao de risco emp´ırico . . . 67

4.1.2 Estima¸c˜ao de parˆametros . . . 67

4.1.2.1 Estimadores por m´axima verossimilhan¸ca . . . 67

4.1.2.2 Estimadores Jackknife . . . 67

4.1.3 An´alise de sensibilidade . . . 69

4.1.3.1 Influˆencia global . . . 69

4.1.3.2 Influˆencia local proposta por Cook (1986) . . . 71

4.1.3.2.1 Pondera¸c˜ao de Casos . . . 71

4.1.3.2.2 Perturba¸c˜ao na Vari´avel Resposta . . . 71

4.1.3.2.3 Perturbando uma Covari´avel . . . 72

4.1.3.3 Influˆencia local conformal . . . 75

4.1.3.3.1 Pondera¸c˜ao de casos . . . 75

4.1.3.3.2 Perturbando a vari´avel resposta . . . 76

4.1.3.3.3 Perturbando uma covari´avel . . . 80

4.1.4 An´alise de res´ıduos . . . 83

4.1.4.1 Exclus˜ao de Casos . . . 83

4.1.4.2 Envelope Simulado . . . 87

4.2 Aplica¸c˜ao II . . . 89

4.2.1 Qualidade de ajuste . . . 90

4.3 Aplica¸c˜ao III . . . 90

4.3.1 Qualidade de ajuste . . . 92

5 CONSIDERA ¸C ˜OES FINAIS . . . 93

5.1 Trabalhos futuros . . . 93

REFERˆENCIAS . . . 95

APˆENDICES . . . 101

(9)

RESUMO

Neste trabalho propomos um modelo de regress˜ao utilizando a distribui¸c˜ao

Weibull modificado, esta distribui¸c˜ao pode ser usada para modelar dados de sobrevivˆencia

quando a de fun¸c˜ao de risco tem forma de U ou banheira. Assumindo dados censurados,

é considerado os estimadores de máxima verossimilhan¸ca e Jackknife para os parâmetros

do modelo proposto. Foram derivadas as matrizes apropriadas para avaliar influiˆencia local

sobre os parâmetros estimados considerando diferentes peturba¸cões e também é

apresen-tada alguma medidas de influˆencia global. Para diferentes parˆametros fixados, tamanhos de

amostra e porcentagem de censuras, varia simula¸c˜oes foram feitas para avaliar a distribui¸c˜ao

emp´ırica do res´ıduo deviance modificado e comparado coma distribui¸c˜ao normal padr˜ao.

Esses estudos sugerem que a distribui¸c˜ao emp´ırica do res´ıduo devianve modificado para o

modelo de regress˜ao log-Weibull modificado com dados censurados aproxima-se de uma

dis-tribui¸c˜ao normal padr˜ao. Finalmente analisamos um conjunto de dados utilizando o modelo

de regressão log-Weibull modificado. Uma nova distribui¸cão de quatro parâmetros é definida

para modelar dados de tempo de vida. Algumas propriedades da distribui¸c˜ao ´e discutida,

assim como ilustramos com exemplos a aplica¸c˜ao dessa nova distribui¸c˜ao.

(10)

ABSTRACT

Log-modified Weibull regression models and a new generalized modified Weibull distribution

In this paperwork are proposed a regression model considering the modified

Weibull distribution. This distribution can be used to model bathtub-shaped failure rate

functions. Assuming censored data, we consider a classic and Jackknife estimator for the

parameters of the model. We derive the appropriate matrices for assessing local influence

on the parameter estimates under different perturbation schemes and we also present some

ways to perform global influence. Besides, for different parameter settings, sample sizes and

censoring percentages, various simulations are performed and the empirical distribution of the

deviance modified residual is displayed and compared with the standard normal distribution.

These studies suggest that the residual analysis usually performed in normal linear regression

models can be straightforwardly extend for a martingale-type residual in log-modified Weibull

regression models with censored data. Finally, we analyze a real data set under log-modified

Weibull regression models. A diagnostic analysis and a model checking based on the deviance

modified residual are performed to select an appropriate model. A new four-parameter

distribution is introduced. Various properties the new distribution are discussed. Illustrative

examples based on real data are also given.

(11)

LISTA DE FIGURAS

Figura 1 - Gr´aficos ilustrativo de alguns TTT plots . . . 21

Figura 2 - Fun¸c˜ao de densidade da distribui¸c˜ao Weibull modificada . . . 24

Figura 3 - Fun¸c˜ao de risco da distribui¸c˜ao Weibull modificada para λ= 0.1 . . . 25

Figura 4 - Gráfico da fun¸cão densidade para um modelo de regressão log-Weibull

mo-dificado . . . 45

Figura 5 - Gr´aficos normais de probabilidade para os res´ıduos deviance

modifi-cados com fun¸c˜ao de taxa de falha em forma de banheira para um

MWM(2;0,8;0,1) com tamanhos de amostra de 30 e 50 . . . 54

Figura 6 - Gr´aficos normais de probabilidade para os res´ıduos deviance

modifi-cados com fun¸c˜ao de taxa de falha em forma de banheira para um

MWM(2;0,8;0,1) com tamanhos de amostra de 100 e 200 . . . 55

Figura 7 - Gr´aficos normais de probabilidade para os res´ıduos deviance modificados

com fun¸c˜ao de taxa de falha crescente para um MWM(1;1,4;0,1) com

tamanhos de amostra de 30 e 50 . . . 56

Figura 8 - Gr´aficos normais de probabilidade para os res´ıduos deviance modificados

com fun¸c˜ao de taxa de falha crescente para um MWM(1;1,4;0,1) com

tamanhos de amostra de 100 e 200 . . . 57

Figura 9 - Fun¸c˜ao de densidade da distribui¸c˜ao Weibull modificada generalizada . . . 61

Figura 10 - Fun¸c˜ao risco da distribui¸c˜ao Weibull modificada generalizada com λ= 0.1 61

Figura 11 - TTT-plot para tempo de sobrevivência dos dados da espécie Golden shiner 68 Figura 12 - Distância de Cook Generalizada . . . 70

Figura 13 - Distˆancia da Verossimilhan¸ca . . . 70

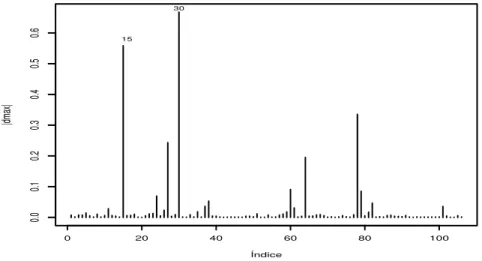
Figura 14 - Gráfico de_|dmax| para θ versus o ´ındice das observa¸cões sob o esquema de perturba¸cão pondera¸cão de casos . . . 71

Figura 15 - Influência local total Ci versus o ´ındice das observa¸cões sob o esquema de perturba¸cão pondera¸cão de casos . . . 72

(12)

Figura 17 - Influência local total Ci versus o ´ındice das observa¸cões sob o esquema de perturba¸cão da variável resposta . . . 73

Figura 18 - Gráfico de_|dmax| para θ versus o ´ındice das observa¸cões sob o esquema de perturba¸cão da variável x2 . . . 74

Figura 19 - Influência local total Ci versus o ´ındice das observa¸cões sob o esquema de perturba¸cão da variável x2 . . . 74

Figura 20 - Gráfico de_|dmax| para θ versus o ´ındice das observa¸cões sob o esquema de perturba¸cão da variável x5 . . . 75

Figura 21 - Influência local total Ci versus o ´ındice das observa¸cões sob o esquema de perturba¸cão da variável x5 . . . 76

Figura 22 - Autovalores normalizados em m´odulo, com valores de q considerando a

pondera¸c˜ao de casos . . . 77

Figura 23 - Influˆencia devida a contribui¸c˜oes de todos os autovetores para o esquema

de pondera¸c˜ao de casos . . . 77

Figura 24 - Contribu¸c˜ao agregada dos autovetores correspondentes aos dois maiores

autovalores (q=7), provenientes da perturba¸c˜ao de casos. . . 78

Figura 25 - Autovalores normalizados em m´odulo, com valores de q considerando a

perturba¸c˜ao da vari´avel resposta . . . 78

de perturba¸c˜ao da vari´avel resposta . . . 79

Figura 27 - Contribu¸c˜ao agregada dos autovetores correspondentes aos trˆes maiores

autovalores (q=5), provenientes da perturba¸c˜ao da vari´avel resposta. . . . 79

Figura 28 - Autovalores normalizados em m´odulo, com valores de q, para a covari´avel x2 80

Figura 29 - Influˆencia devido a contribui¸c˜oes de todos os autovetores para o esquema

de perturba¸c˜ao da covari´avel x2 . . . 81

Figura 30 - Contribu¸c˜ao agregada dos autovetores correspondentes aos trˆes maiores

autovalores (q=1), provenientes da perturba¸c˜ao da covari´avel x2. . . 81

Figura 31 - Autovalores normalizados em m´odulo, com valores de q . . . 82

(13)

Figura 33 - Contribui¸c˜ao agregada dos autovetores correspondentes aos trˆes maiores

autovalores (q=4), provenientes da perturba¸c˜ao da covari´avel x5. . . 83

Figura 34 - Res´ıduo martingale . . . 84

Figura 35 - Res´ıduo deviance modificado . . . 84

Figura 36 - Gr´afico normal de probabilidade para o res´ıduo deviance modificado com

envelopes para o modelo (41) proposto . . . 88

Figura 37 - Gr´afico normal de probabilidade para o res´ıduo deviance modificado com

envelopes para o modelo (42) proposto . . . 88

Figura 38 - TTT plot para tempo de sobrevivência até o soro-reversão de 148 crian¸cas

expostas ao HIV por via vertical, nascidas no Hospital da Facultade de

Medicina de Ribeir˜ao Preto . . . 89

Figura 39 - Fun¸cão de sobrevivência da distribui¸cão Weibull modificada generalizada

conjuntamente com a curva de Kaplan-Meier . . . 90

Figura 40 - TTT plot para o conjunto de dados de sobrevivˆencia de pacientes com

cˆancer, submetidos `a radioterapia . . . 91

Figura 41 - Fun¸cão de sobrevivência da distribui¸cão Weibull modificada generalizada

(14)

LISTA DE TABELAS

Tabela 1 - Algumas fun¸cões de distribui¸cão geradas a partir da distribui¸cão Weibull

modificada generalizada . . . 62

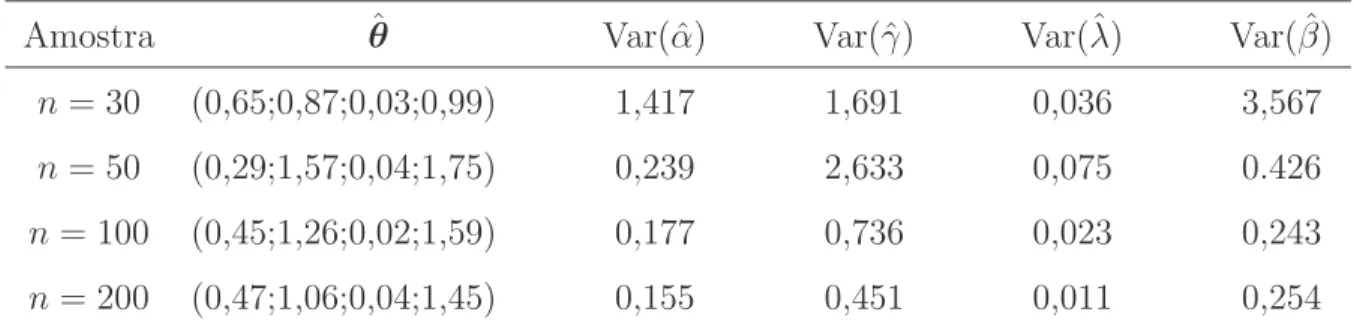
Tabela 2 - Variâncias dos estimadores de máxima verossimilhan¸ca dos parâmetros com

α= 0,5, γ = 1,0, λ= 0,1 e β= 0,5 . . . 65

Tabela 3 - Variâncias dos estimadores de máxima verossimilhan¸ca dos parâmetros com

α= 0,5, γ = 0,8, λ= 0,1 e β= 0,8 . . . 65

Tabela 4 - Estimativas de máxima verossimilhan¸ca para os dados da espécie Golden shiner . . . 68 Tabela 5 - Estimativas Jackknife para os dados da espécie Golden shiner . . . 69 Tabela 6 - Mudan¸ca relativa (em porcentagem), estimativa de máxima

verossimi-lhan¸ca e os correspondentes p-valores em parenteses excluindo as

obser-va¸c˜oes ♯5,♯30 e ♯101 . . . 85

Tabela 7 - Estimativas de m´axima verossimilhan¸ca para o conjunto de dados da esp´ecie

Golden shiner para o modelo (41) proposto . . . 86 Tabela 8 - Estimativas de m´axima verossimilhan¸ca para o conjunto de dados da esp´ecie

Golden shiner para o modelo (42) proposto . . . 87 Tabela 9 - Estimativas de m´axima verossimilhan¸ca para o conjunto de dados de

soro-revers˜ao . . . 90

Tabela 10 -Estimativas de m´axima verossimilhan¸ca para o conjunto de dados de

(15)

1 INTRODU ¸C ˜AO

A análise de sobrevivência é uma das áreas da estat´ıstica que mais cresceu nas

´

ultimas duas décadas. A razão desse crescimento é o desenvolvimento e aprimoramento de

t´ecnicas estat´ısticas combinadas com computadores cada vez mais velozes. Uma evidˆencia

quantitativa desse sucesso é o número de aplica¸cões de análise de sobrevivência em ciências

biom´edicas.

Em análise de sobrevivência, a variável resposta é, geralmente, o tempo até a

ocorrˆencia de um evento de interesse. Esse tempo ´e denominado tempo de falha, podendo

ser o tempo at´e a morte do paciente, bem como at´e a cura ou recidiva de uma doen¸ca.

A principal caracter´ıstica de dados de sobrevivˆencia ´e a presen¸ca de censura,

que é a observa¸cão parcial da resposta. Isso se refere à situa¸cões em que, por alguma razão,

o acompanhamento do paciente foi interrompido, o estudo terminou para a an´alise dos dados

ou, o paciente morreu de causa diferente da estudada.

Sem a presen¸ca de censura, as técnicas estat´ısticas clássicas, como análise de

regress˜ao e o planejamento de experimentos, poderiam ser utilizadas na an´alise desse tipo

de dados, provavelmente usando uma transforma¸c˜ao para a vari´avel em estudo.

Em análise de sobrevivência, distribui¸cões usuais de tempo de sobrevida, como

a distribui¸c˜ao exponencial, Weibull, log-gamma generalizada, F-generalizada, acomodam

al-gumas formas de risco, como a forma constante (distribui¸c˜ao exponencial) e a forma crescente

e decrescente (distribui¸cão Weibull). Entretanto, é comum encontrar na prática, dados de

sobrevivˆencia com fun¸c˜ao de risco de diferentes formas, como por exemplo, em forma de

U ou banheira e unimodal. Os modelos conhecidos para essas situa¸c˜oes, em geral, detˆem

uma estrutura inicial baseada no modelo Weibull, que tradicionalmente pode modelar formas

constantes, crescentes e decrescentes.

Lai, Xie e Murthy (2003) apresentam a distribui¸c˜ao Weibull modificada, cuja

fun¸c˜ao de risco apresenta forma de U ou banheira. Nesse contexto surge a id´eia de abordar

um modelo param´etrico utilizando a distribui¸c˜ao Weibull modificada.

Na prática há situa¸cões em que existem uma ou mais covariáveis associadas

com o tempo de vida. Por exemplo, na ind´ustria o tempo de vida de um determinado

(16)

nas ´areas m´edicas o tempo de vida de um paciente pode estar relacionado, com o tipo de

tumor, tamanho do mesmo, quantidade de hemoglobina na sangue, ra¸ca ou idade do mesmo.

Uma maneira de estudar os efeitos dessas covariáveis no tempo de vida t é através de um modelo de regressão. Nesse sentido será proposto um modelo de regressão

log-Weibull modificado na presen¸ca de dados censurados.

A técnica de análise de sensibilidade é uma etapa importante no ajuste do

modelo de regressão, verificando poss´ıveis afastamentos das suposi¸cões do modelo. Métodos

como influência global, influência total e influência local são apresentadas.

A teoria de influˆencia local, tem como objetivo verificar atrav´es de algumas

medidas de influˆencia, o quanto as estimativas obtidas a partir do modelo proposto s˜ao

resistentes a pequenas perturba¸cões nas observa¸cões. Se essas perturba¸cões causarem efeitos

desproporcionais em determinados resultados, significa que h´a ind´ıcios de que o modelo est´a

mal ajustado. A identifica¸cão das observa¸cões responsáveis por essa discrepância pode ajudar

na escolha de um modelo mais adequado.

Por outro lado, sabe-se que quando se procura ajustar um modelo a um

con-junto de dados, a valida¸cão desse ajuste deve passar também pela análise de res´ıduos em

que se procura detectar pontos mal ajustados (aberrantes), bem como verificar se h´a ind´ıcios

de afastamentos sérios das suposi¸cões feitas para o erro do modelo. Com esse objetivo, é

proposto o estudo dos res´ıduos martingale e deviance utilizados em modelos de an´alise de

sobrevivˆencia.

A distribui¸c˜ao Weibull ´e muito utilizada em estudos relacionados ao tempo de

falha devido à grande aplicabilidade tanto na área de confiabilidade, bem como na análise

de sobrevivˆencia. Neste sentido introduzimos uma nova distribui¸c˜ao denominada Weibull

modificada generalizada. Essa nova distribui¸c˜ao devido `as sua flexibilidade em acomodar

muitas formas de riscos ´e uma distribui¸c˜ao importante pois pode ser utilizada nos mais

variados problemas de modelagem de dados de sobrevivˆencia ou confiabilidade.

A vantagem dessa nova distribui¸cão em rela¸cão as demais distribui¸cões, é

aco-modar não apenas fun¸cõeso de risco crescentes, decrescentes ou constantes, mas também a

fun¸cões de risco não monótonas, como por exemplo, forma de banheira e unimodal. Outra

(17)

Weibull, exponencial exponenciada (Gupta 2001), Weibull exponenciada (Mulholkar 1996),

Weibull modificada (2003) dentre outras.

1.1 Proposta de trabalho

Inicialmente o presente trabalho tem como objetivo o estudo da distribui¸c˜ao

Weibull modificado, proposto por Lai, Min Xie e Murthy (2003) com a presen¸ca de

ob-serva¸cões censuradas. Será estudada a formula¸cão da distribui¸cão Weibull modificado, as

respectivas propriedades que caracterizam a sua fun¸c˜ao de risco e a rela¸c˜ao que tem com

outras distribui¸cões. Finalmente duas metodologias de estima¸cão de parâmetros como a de

m´axima verossimilhan¸ca e Jackknife ser˜ao utilizadas.

O modelo de regress˜ao log-Weibull modificado ser´a proposto na forma de

loca¸cão-escala, a fim de verificar a robustez do modelo será feito uma análise de

sensibi-lidade baseado nas técnicas de influência global e local. No caso da influência local será

considerando três esquemas de perturba¸cão: pondera¸cão de casos, perturba¸cão da variável

resposta e a perturba¸c˜ao das covari´aveis.

Poon & Poon (1999) prop˜oem uma nova medida de influˆencia local denominada

influência local conformal. Essa nova metodologia será aplicada como parte da análise de sensibilidade para os três tipos de perturba¸cão anteriormente mencionados.

Com o objetivo de verificar a adequa¸c˜ao do modelo aos dados e poss´ıveis

ind´ı-cios de afastamentos s´erios das suposi¸c˜oes feitas para o erro do modelo proposto utilizamos

a análise de res´ıduos. O res´ıduos deviance será modificado para o modelo de regressão

log-Weibull modificado e mediante as t´ecnicas de simula¸c˜ao de Monte Carlo sera determinada

a distribui¸c˜ao emp´ırica do res´ıduo proposto, considerando diferentes tamanhos de amostra e

propor¸c˜oes de censura.

Mediante estudo básico da fun¸cão acumulada da distribui¸cão Weibull

modifi-cada ´e proposta uma nova distribui¸c˜ao que chamaremos de Weibull modifimodifi-cada generalizada,

essa nova distribui¸cão além de modelar dados onde a fun¸cão de risco tem formas crescentes,

decrescente e banheira ou de U, modela fun¸c˜oes de riscos com forma unimodal, e ´e um

modelo que caracteriza a modelos mais simples como a Weibull, valor extremo, Weibull

(18)

Finalmente, é aplicado um conjuntos de dados reais das áreas biológica e

biom´edicas, para avaliar os modelos propostos.

1.2 Suporte computacional

A linguagem de programa¸c˜ao Ox V.4.0., criada por Jurgen Doornik, constitui

a plataforma computacional utilizada no desenvolvimento da disserta¸c˜ao. Esta linguagem

permite a implementa¸c˜ao de t´ecnicas estat´ısticas com facilidade e atende a requisitos como

precisão e eficiência, o que tem contribu´ıdo para sua ampla utiliza¸cão no campo da

com-puta¸cão numérica. Detalhes sobre esta linguagem de programa¸cão podem ser encontrados

(19)

2 REVIS ˜AO

2.1 An´alise de sobrevivˆencia

O termo análise de sobrevivência e/ou confiabilidade refere-se à cole¸cão de

procedimentos estat´ısticos para a análise de dados relacionados ao tempo até a ocorrência

de um determinado evento de interesse. Geralmente, a an´alise de sobrevivˆencia relaciona-se

a dados biomédicos, biológicos, agronômicos, enquanto a confiabilidade refere-se à pesquisa

industrial, etc.

S˜ao comumente encontrados conjuntos de dados de tempo de falha em diversas

áreas de pesquisa. Por falha, entenda-se a ocorrência de um evento pré-especificado e, por

tempo de falha, o per´ıodo de tempo decorrido para o evento ocorrer.

Uma caracter´ıstica importante dos dados de tempo de falha ´e a possibilidade

de serem censurados. Isso refere-se `as circunstˆancias em que alguns indiv´ıduos encontram-se

livres do evento por terem, por exemplo, sido retirados mais cedo do estudo ou pelo t´ermino

do experimento. Dentre os tipos de censura destacam-se: censura `a direita, `a esquerda e

intervalar. As censuras `a direita podem ainda ser caracterizadas como: Censura do tipo I,

Censura do tipo II e a Censura Aleat´oria.

A censura do tipo I é aquela em que o estudo será terminado após um per´ıodo

pré-estabelecido de tempo. Censura do tipo II é aquela em que o estudo será terminado

após ter ocorrido o evento de interesse em um número pré-estabelecido de indiv´ıduos. O

mecanismo de censura do tipo aleatório, é o que mais ocorre na prática. Isto acontece

quando um indiv´ıduo em estudo ´e retirado no decorrer do estudo sem ter ocorrido a falha,

ou tamb´em por exemplo, se o indiv´ıduo morrer por uma raz˜ao diferente da estudada.

Uma representa¸cão simples do mecanismo de censura aleatória é feita usando

suas variáveis aleatórias. Seja T uma variável aleatória representando o tempo de falha de

um indiv´ıduo e C, uma outra vari´avel aleat´oria independente de T, representando o tempo

de censura associado a esse indiv´ıduo. Observa-se, portanto,

ti = min(T, C) e δi =

  

1 se T _≤C

0 se T > C.

(20)

indiv´ıduos. Observa-se que se todoCi =C, uma constante fixa sob o controle do pesquisador, tem-se a censura do tipo I, ou seja, a censura do tipo I ´e um caso particular da censura

aleat´oria.

A censura `a esquerda ocorre quando o tempo registrado ´e maior do que o

tempo de falha, isto ´e, o evento de interesse j´a aconteceu quando o indiv´ıduo foi observado.

A censura intervalar ´e um tipo mais geral de censura que acontece, por exemplo,

em estudos em que os pacientes são acompanhados em visitas periódicas e é conhecido

somente que o evento de interesse ocorreu em um certo intervalo de tempo. Pelo fato de que

o tempo de falha T n˜ao ser conhecido exatamente, mas sim, pertencer a um intervalo, isto

é, T _∈(L, U], tais dados são denominados de sobrevivência intervalar ou, mais usualmente,

de dados de censura intervalar. Lindsey et.al. (1998) observam que tempos exatos de falha,

bem como censura à direita e à esquerda, são casos especiais de dados de sobrevivência

intervalar com L =U para tempos exatos de falha, U =_∞ para censuras `a direita e L= 0

para censuras `a esquerda.

Em an´alise de sobrevivˆencia tem-se interesse de estimar a probabilidade de um

indiv´ıduo sobreviver até o tempo t, a qual é chamada de fun¸cão de sobrevivência, e a razão

instantˆanea de falha ou morte no tempo t de um indiv´ıduo, dado que ele sobreviveu at´e o

tempo t, a qual ´e chamada de fun¸c˜ao de risco.

Os dados de sobrevivˆencia para o indiv´ıduo i(i = 1,2, . . . , n) sob estudo s˜ao

representados, em geral, pelo par (ti, δi) sendo ti o tempo de falha ou de censura e δi a vari´avel indicadora de falha ou censura, isto ´e,

δi =

        

1 se for um tempo de falha

0 se for um tempo censurado

Na presen¸ca de covariáveis medidas no i-ésimo indiv´ıduo, tais como, xi = (sexoi,idadei,tratamentoi), dentre outras, os dados ficam representados por (ti, δi,xi). No caso particular de dados de sobrevivência intervalar tem-se, ainda, a representa¸cão

(li, ui, δi,xi) em que li e ui s˜ao, respectivamente, os limites inferior e superior do intervalo observado para o i-´esimo indiv´ıduo.

(21)

levam em considera¸c˜ao covari´aveis relacionadas com o tempo de vida. Para considerar essas

covariáveis devem-se utilizar modelos paramétricos, para os quais se supõe uma distribui¸cão

de probabilidade conhecida para o tempo de vida, ou modelos semi-param´etricos, tais como,

o de riscos proporcionais de Cox, para o qual não é suposta nenhuma distribui¸cão para o

tempo de vida.

Portanto, em análise de sobrevivência alguns conceitos são de suma

importân-cia como por exemplo a fun¸cão de sobrevivênimportân-cia e a fun¸cão de taxa de falha ou de risco, em

que

S(t) =P[T _≥t] = 1₋F(t) =

Z ∞

t

f(t)dt, (1)

é a probabilidade de um indiv´ıduo sobreviver até o tempot, em queT é uma variável aleatória

cont´ınua não negativa e f(t) é a sua fun¸cão de densidade de probabilidade.

A fun¸c˜ao de taxa de falha ou de risco ´e a probabilidade da falha ocorrer em

um intervalo de tempo [t1, t2) pode ser expressa em termos da fun¸c˜ao de sobrevivˆencia como:

S(t1)−S(t2). (2)

A taxa de falha no intervalo [t1, t2) ´e definida como a probabilidade de que a falha ocorra

nesse intervalo, dado que n˜ao ocorreu antes de t1, dividida pelo comprimento do intervalo.

Assim, a taxa de falha no intervalo [t1, t2) ´e expressa por:

S(t1)−S(t2)

(t2−t1)S(t1)

. (3)

De forma geral, redefinindo o intervalo como [t, t+ ∆t), a expres˜ao (3) assume a seguinte

forma:

h(t) = S(t)−S(t+ ∆t) ∆tS(t) .

Assumindo ∆t bem pequeno, h(t) representa a taxa de falha instantˆanea no tempo t

condi-cional à sobrevivência até o tempo t. Observe que as taxas de falha são números positivos,

mas sem limite superior. A fun¸cão de taxa de falha h(t) é bastante útil para descrever a

distribui¸c˜ao do tempo de vida de indiv´ıduos em estudo. Ela descreve a forma com que a

(22)

21

i/n

T

-p

lo

t

A

B C

D E

Figura 1 – Gr´aficos ilustrativo de alguns TTT plots

como:

h(t) = lim

∆t→0

P[t_≤T < t+ ∆t_|T > t]

∆t =

f(t)

S(t). (4)

Em muitas aplica¸c˜oes existem informa¸c˜oes qualitativas e, muitas vezes,

estru-turais a respeito do fenômeno em questão, que pode ser utilizada na determina¸cão emp´ırica

da forma da fun¸cão de risco. Informa¸cões estruturais estão diretamente vinculadas ao

co-nhecimento do pesquisador sobre o fenˆomeno, enquanto que informa¸c˜oes qualitativas podem

ser extra´ıdas por médio de uma análise gráfica. Neste contexto, um gráfico conhecido como

gr´afico TTT-plot ´e de grande utilidade.

Este gr´afico foi inicialmente proposto por Aarset (1987). O gr´afico TTT-Plot

´e obtido a partir de:

G³r n

´

=

Pr

i=1T_Pi:n+ (n−r)Tr:n

n i=1Ti:n

versus A = r

n (5)

em que r = 1,2, . . . , n e Ti:n, i = 1,2, . . . , n, s˜ao estat´ısticas de ordem da amostra. (Mud-holkar et.al.,1996).

A Figura 1 ilustra as v´arias formas que podem ser observadas para uma fun¸c˜ao

de risco. Se uma reta diagonal é observada (A), uma fun¸cão de risco constante é indicada.

Se a curva é convexa (B) ou côncava (C), a fun¸cão de risco e monotonicamente decrescente

ou crescente. Se a curva é convexa e então côncava (D) , a fun¸cão de risco tem forma de

(23)

ajuste de uma fun¸c˜ao de risco multinomial. Essas curvas provavelmente podem ser ajustadas

através da distribui¸cão de múltiplos riscos (LOUZADA-NETO, 2000).

Caso se tenha informa¸c˜oes sobre covari´aveis para cada indiv´ıduo e uma

quan-tidade significativa de indiv´ıduos em cada n´ıvel ou combina¸c˜ao destas covari´aveis, a curva

TTT-plot pode ser constru´ıda considerando cada n´ıvel de covari´avel ou combina¸c˜ao das

mesmas, separadamente.

2.2 Distribui¸c˜ao Weibull modificada

Utilizando a fun¸c˜ao de risco pode-se caracterizar classes especiais de

dis-tribui¸cão de tempo de sobrevivência, de acordo com o seu comportamento em fun¸cão do

tempo. A fun¸cão de risco pode ser constante, crescente, decrescente ou não monótona.

Dis-tribui¸c˜oes usuais de tempo de sobrevivˆencia, como exponencial, Weibull, log-normal, gama,

entre outras, acomodam algumas formas de risco, como a forma constante, crescente,

decres-cente, unimodal, etc.

Entretanto é comum encontrar, na prática, dados de sobrevivência com fun¸cão

de risco com diferentes formas, como por exemplo, fun¸c˜ao de risco em forma de U ou banheira.

Esses modelos conhecidos, em geral, det´em uma estrutura inicial baseada na distribui¸c˜ao

Weibull. Dentre as distribui¸cões que apresentam essas caracter´ısticas são a distribui¸cão

Weibull generalizada proposto por Mudholkar et. al. (1996); a distribui¸c˜ao Weibull expo-nenciada descrita por Mudholkar e Srivastava (1993), dentre outras. Nessa mesma linha

aparecem os modelos de riscos mútliplos cuja vantagem é a sua flexibilidade em rela¸cão ao

modelo de risco usual, pois, acomoda n˜ao apenas fun¸c˜ao de risco crescente, decrescente ou

constante, como também a fun¸cão de risco não-monotona, como por exemplo, forma de U

e curvas multimodais. Outra distribui¸c˜ao pouco conhecida ´e a Weibull modificada proposto

por Lai, Min Xie e Murthy (2003), onde uma das caracter´ısticas ´e que apresenta fun¸c˜ao de

risco de diferentes formas entre elas forma de U; Perdona (2006) ilustra a estima¸c˜ao dos

parâmetros e teste de hipóteses para a distribui¸cão Weibull modificada com a presen¸ca de

dados censurados.

Nesta parte do trabalho, ser˜ao discutidas as propriedades do modelo Weibull

(24)

censuradas. Na se¸c˜ao 2.2.1 apresentamos a formula¸c˜ao do modelo e algumas propriedades

importantes; na se¸cão 2.2.2 são descritas algumas caracter´ısticas da fun¸cão de risco; na se¸cão

2.2.3 abrange uma descri¸cão da rela¸cão existente entre a distribui¸cão Weibull modificada

com outras distribui¸c˜oes, e finalmente, discutimos a parte inferencial da distribui¸c˜ao Weibull

modificada com a presen¸ca de dados censurados.

2.2.1 Formula¸c˜ao da distribui¸c˜ao Weibull modificada

Seja T uma variável aleatória cont´ınua não negativa com distribui¸cão Weibull

modificada (WM) proposta por Lai, Min Xie e Murthy (2003), cuja fun¸c˜ao de densidade ´e

dada por:

f(t) =α³γ+λt´tγ−1_exp(_λt_{) exp}n

−αtγexp(λt)o. (6)

A fun¸cão de distribui¸cão acumulada, de sobrevivência e de risco são dadas, respectivamente,

por:

F(t) = P[T _≤t] =

Z t

0

f(q, α, γ, λ)dq

= 1₋expn₋αtγexp(λt)o, (7)

S(t) = expn₋αtγexp(λt)o, (8)

h(t) = α³γ+λt´tγ−1_exp(_λt₎_, ₍₉₎

em que o parâmetro α > 0 controla a escala da distribui¸cão e o parâmetro γ _≥ 0 controla

a forma, e λ _≥ 0. O fator exp(λt) pode ser visto como um fator acelerador na sobrevida;

isto significa que, `a medida que o tempo aumenta o parˆametroλ funciona como um fator de

fragilidade na sobrevivˆencia do indiv´ıduo.

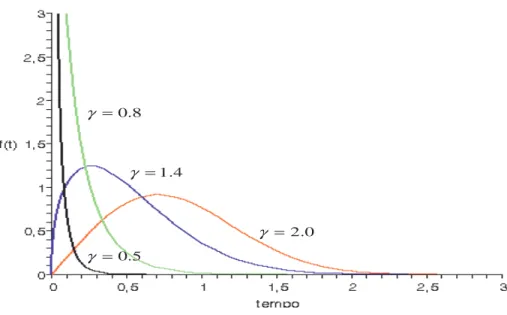
A Figura 2 apresenta o gráfico da fun¸cão de densidade da distribui¸cão WM, para diferentes valores do parâmetro de forma γ.

2.2.2 Estudo da fun¸c˜ao de risco da distribui¸c˜ao Weibull modificada

Uma caracter´ıstica dessa distribui¸cão é que a fun¸cão de risco dada pela equa¸cão

(25)

0 . 2

=

γ

4 . 1

=

γ

8 . 0

=

γ

5 . 0

=

γ

Figura 2 – Fun¸c˜ao de densidade da distribui¸c˜ao Weibull modificada

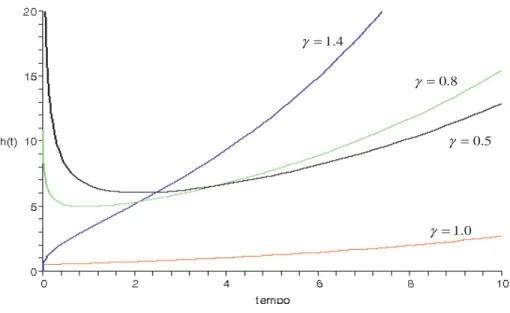
forma de h(t) depende somente do parˆametroγ em tγ−1_{. Portanto quando} _γ _≥ _{1, a fun¸c˜ao}

de risco apresenta forma crescentes, e quando 0 < γ < 1, a fun¸c˜ao de risco inicialmente

decresce e depois cresce em t, implicando risco em forma de U. A Figura 3, apresenta as

caracter´ısticas da fun¸c˜ao risco anteriormente mencionadas.

2.2.3 Rela¸c˜ao com outras distribui¸c˜oes

A distribui¸c˜ao Weibull modificada apresenta algumas distribui¸c˜oes como casos

particulares que s˜ao mencionadas a seguir

1. para λ = 0 na equa¸c˜ao (6) a distribui¸c˜ao Weibull modificada se reduz a uma

dis-tribui¸cão Weibull simples, com fun¸cão de sobrevivência da forma:

S(t) = exp(₋αtγ).

2. paraγ = 0 na equa¸cão (6) a distribui¸cão Weibull modificada se reduz a uma distribui¸cão

Valor extremo tipo I, com fun¸c˜ao de sobrevivˆencia da forma:

(26)

5 . 0

=

γ

8 . 0

=

γ

4 . 1

=

γ

0 . 1

=

γ

Figura 3 – Fun¸c˜ao de risco da distribui¸c˜ao Weibull modificada paraλ= 0.1

3. a fun¸c˜ao de risco acumulada de um modelo Beta Integral (Lai, Min Xie e Murthy,

2003) ´e dada pela seguinte express˜ao:

H(t) = atb(1₋dt)c,

em que 0 < t < 1/d, a > 0, b > 0, d > 0, c > 0. Por outro lado sabe-se que para

n_{→ ∞}, d= 1/n, ec=₋λn, tem-se que,

³

1₋ t n

´−λn

→exp(λt),

Assim sendo, pode-se observar claramente que a fun¸c˜ao de risco acumulada de um

modelo Beta integral nessas condi¸c˜oes assume a forma

H(t) = atbexp(ct).

a qual corresponde a uma fun¸c˜ao de risco acumulada da distribui¸c˜ao Weibull

modifi-cado.

Essas caracter´ısticas possibilitam uma flexibilidade maior na utiliza¸c˜ao dessa

(27)

2.2.4 Inferência na distribui¸cão Weibull modificada incorporando censura Seja a situa¸cão em que se tem dispon´ıvel uma amostra aleatória

T1, T2, . . . , Tn de tempos de sobrevivência. Supondo que os dados consistem de n pares (t1, δ1),(t2, δ2), . . . ,(tn, δn), observados em que ti é o tempo de falha ou censura,δi é o indi-cador de falha ou censura cuja distribui¸cão envolve um vetor de parâmetros θ. Nesse caso,

a fun¸cão de verossimilhan¸ca considerando censura não informativa é dada por:

L(θ) = n

Y

i=1 h

f(ti)iδihS(ti)i1

−δi

= n

Y

i=1

h(ti)δi_S₍_t_i)_, ₍₁₀₎

em quef(t),S(t) e h(t) são as fun¸cões de densidade, de sobrevivência e de risco da variável

aleat´oria T respectivamente.

No caso da distribui¸cão Weibull modificada o vetor de parâmetros é θ =

(α, γ, λ)T _{e substituindo as fun¸cões de densidade e de sobrevivência dada nas expressões} (6) e (8) respectivamente, o logaritmo da fun¸cão de verossimilhan¸ca nesse caso é dado por

l(θ) = rlog(α) +X iǫF

½

log(γ+λti) + (γ−1) log(ti) +λti

¾

−αX

i∈F

tγ_i exp(λti)₋αX i∈C

tγ_i exp(λti),

em queré o número total de falhas,F, representa o conjunto das observa¸cões que falharam

e C, representa o conjunto das observa¸cões censuradas. As fun¸cões escore, para α, γ, λ são

dadas respectivamente, por:

Uα(θ) = r α −

n

X

i=1

tγ_i exp(λti),

Uγ(θ) = −

X

iǫF 1 γ+λti

+X

iǫF

log(ti)−α n

X

i=1

tγ_i exp(λti) log(ti),

Uλ(θ) = X iǫF

ti γ+λti

+X

iǫF

ti−α n

X

i=1

tγ_i+1exp(λti).

Os estimadores de máxima verossimilhan¸ca são solu¸cões simultâneas das

equa¸cões Uα(θ) = 0, Uγ(θ) = 0 e Uλ(θ) = 0. Porém, para obter o estimador de máxima verossimilhan¸ca para os parâmetros γ e λ, é necessário a utiliza¸cão de métodos iterativos.

Esses podem ser obtidas numericamente, maximizando o logaritmo da fun¸c˜ao de

(28)

um algoritmo quase-Newton (BFGS, etc) apresentada no anexoA.3, além disso no apêndice A.4, apresenta-se a matriz das segundas derivadas parciais para uma distribui¸cãoWM, mais detalhes sobre o estudo inferencial da distribui¸cão WM, pode ser visto em Perdona (2006).

2.3 Modelos de regress˜ao

Na prática, existem situa¸cões em que uma ou mais covariáveis estão associadas

ao tempo de vida. Por exemplo, na ind´ustria o tempo de vida de um determinado

equipa-mento pode ser influenciado pelo n´ıvel de voltagem a que o equipaequipa-mento ´e submetido; nas

´areas m´edicas o tempo de vida de um paciente pode estar relacionado, com o tipo de tumor,

tamanho do mesmo, quantidade de hemoglobina no sangue, ra¸ca, idade do paciente.

Considere T uma variável aleatória representando tempo até a falha de uma

indiv´ıduo e seja x = (x1, x2, . . . , xp)T um vetor formado por observa¸cões de p regressores também chamadas de variáveis explanatórias ou covariáveis que podem ser quantitativas ou

qualitativas. Uma maneira de determinar o relacionamento entre T e x é através de um modelo de regressão. Existem duas classes importantes do modelos de regressão em análise

de sobrevivˆencia: Os modelos de riscos proporcionais para T e modelo de loca¸c˜ao e escala

para o logaritmo deT. Abordaremos aqui apenas a segunda classe. Uma descri¸c˜ao detalhada

sobre modelos de riscos proporcinais pode ser obtida em Kalbfleisch e Prentice (1980), Lee

(1980), Collett (2003), entre outros.

2.3.1 Modelos de loca¸c˜ao-escala

A classe de modelos de loca¸c˜ao e escala se caracteriza pelo fato de Y = log(T)

ter uma distribui¸cão com parâmetros de loca¸cão µ(x) dependendo das variáveis regressoras,

e um parˆametro de escala σ constante. Podemos ent˜ao escrever

Y=µ(x) +σZ

em queσ >0. A fun¸cão de sobrevivência deY dadoxé da formaS(y−µ(x)

σ ) em queS(.) é a fun¸cão de sobrevivência deZ. Uma conhecida caracter´ıstica deste modelo é que as variáveis

regressoras atuam multiplicativamente sobre T. Podemos assumir v´arias formas para µ(x)

(29)

mais natural ´e assumirµ(x) = xT_β_{, em que} _β_{= (}_β

1, β2, . . . , βp)T ´e um vetor de parˆametros

desconhecidos (tratamos aqui apenas desta forma para µ(x)). Com esta suposi¸c˜ao temos

que

Y=xTβ+σZ (11)

que ´e um modelo log linear para T com res´ıduoZ.

2.4 Estrat´egias de inferˆencia

Assumindo um modelo param´etrico como adequado para a an´alise dos dados,

desejamos elaborar inferˆencias com base neste modelo. Em geral esta an´alise torna-se mais

complicada quando precisamos incorporar dados censurados, mesmo quando o mecanismo

de censura é simples. Abordamos aqui os métodos de máxima verossimilhan¸ca e Jackknife

para estima¸cão e testes nos modelos paramétricos de regressão.

2.4.1 Estima¸c˜ao por m´axima verossimilhan¸ca

Sejam (y1,xi1, δ1),(y2,xi2, δ2), . . . ,(yn,xin, δn), n observa¸c˜oes independentes em queyi = log(ti), representa o logaritmo do tempo de falha ou censura, xi = (xi1, . . . , xip)T

o vetor de covariáveis e δi é o indicador de censura, para todo i= 1,2, . . . , n. Assim sendo, o logaritmo da fun¸cão de verossimilhan¸ca considerando uma amostra completa, é dado por:

l(θ) = X i∈F

loghf(yi)i+X i∈C

loghS(yi)i (12)

em que f(y) e S(y) são as fun¸cões de densidade e sobrevivência da variável aleatória Y e o

vetor de parˆametros desconhecidos nesse caso ´e dado por θ = (β1, β2, . . . , βp)T. Para obter

os estimadores de máxima verossimilhan¸ca será preciso derivar l(θ) em rela¸cão ao vetor de

parˆametros desconhecidos θ.

As propriedades assintóticas dos estimadores de máxima verossimilhan¸ca são

necessárias para construir intervalos de confian¸ca e testar hipóteses sobre os parâmetros do

modelo, utilizando do fato que ˆθ tem distribui¸c˜ao normal assint´otica multivariada sob certas

(30)

que I(θ) =₋EhL¨(θ)i, tal que, ¨L(θ) = n∂

2_l₍_θ₎

∂θ∂θT o

, isto ´e,

ˆ

θ_∼Np

³

θ,I−1(θ)´.

Visto que o cálculo de I(θ) (matriz de informa¸cão de Fischer) é dificil devido

`a presen¸ca de censura, pode-se utilizar alternativamente a matriz₋L¨(θ) avaliada em θ = ˆθ,

denominada matriz de informa¸c˜ao observada, que ´e uma estimativa consistente de I(θ).

Assim, o intervalo de confian¸ca assint´otico para βj em que j = 1, . . . , p, con-siderando (1₋α)100% de confian¸ca, ser´a dado por

ˆ

βj ±zα/2 q

d

V ar( ˆβj). (13)

Para a constru¸cão de um teste de hipótese para os parâmetros também será

utilizada a diagonal principal da matriz ₋L¨−1₍_θ_{) como uma estimativa para a variˆancia dos}

estimadores, logo, a estat´ıstica para testar as hip´oteses

        

H0 : βj =βj0

Ha: βj 6=βj0

ser´a dada por: z = qβˆj −βj0 d

V ar( ˆβj)

∼N(0,1).

2.4.2 M´etodo de Jackknife

O m´etodo de Jackknife foi introduzido em 1949 por M. H. Quenouille, para

reduzir o viés de um estimador de correla¸cão, como base na divisão da amostra original

em duas semi-amostras. Anos depois, este estudo foi completado com a generaliza¸c˜ao do

m´etodo (Quenouille, 1956). Assim, a amostra original de tamanho n passa a ser dividida

em m sub-amostras de tamanho v, de modo que se tem n = mv. O m´etodo Jackknife

produz melhores estimativas amostrais de alguns parˆametros de posi¸c˜ao, como por exemplo,

a média e a curtose, também fornecem freqüentemente variância e intervalos de confian¸ca

(31)

SejaT1, T2, . . . , Tn uma amostra aleatória de tamanhon, a sua média amostral é dada por

¯ T =

n

X

i=1

Ti

n (14)

que ´e usada para estimar a m´edia populacional.

Para o método Jackknife calcula-se a média amostral sem al-ésima observa¸cão,

ou seja,

¯ T−l =

Pn

i=1Ti−Tl

n₋1 . (15)

Então da equa¸cão (15) obtém-se que

Tj =nT¯−(n−1) ¯T−j. (16)

Em uma situa¸cão geral, suponha que um parâmetro θé estimado por alguma

fun¸c˜ao dosnvalores amostrais. Denote esse estimador por ˆE(T1, T2, . . . , Tn). Para simplificar

a nota¸c˜ao foi omitido (T1, T2, . . . , Tn). Remova Tl e obtenha o estimador parcial ˆE−l. Pela

analogia com a equa¸c˜ao (16) existe um conjunto de pseudo-valores que podem ser calculados:

ˆ E∗

i =nEˆ−(n−1) ˆE−i , i= 1, . . . , n. (17)

Esses pseudos-valores preservam a mesma lei dos valores Ti em estimar a média. A média amostral dos pseudo-valores é dada por

ˆ E∗

=

Pn

i=1Eˆ ∗

i

n . (18)

que ´e o estimador Jackknife de θ. Considerando os pseudos-valores como uma amostra

aleatória de estimativas independentes, então, sugere-se que a variância desse estimador

Jackknife pode ser estimada por s2_/n_{, em que}_s2 _{´e a variˆancia amostral dos pseudo-valores.}

Assim, pode-se sugerir que um intervalo de confian¸ca 100(1 ₋ α)% para θ ´e dado por ˆ

E∗

±tα/2,n−1s/√n, em que tα/2,n−1 ´e o valor que ´e excedido com probabilidade α/2 para

a distribui¸c˜ao t com (n₋1) graus de liberdade.

Uma vantagem de substituir um estimador pela sua vers˜ao Jackknife ´e que

(32)

2.5 An´alise de sensibilidade

An´alise de sensibilidade ´e uma etapa importante no ajuste do modelo de

re-gressão, pois nos auxilia na verifica¸cão de poss´ıveis afastamentos das suposi¸cões feitas para

o modelo, especialmente para a parte aleat´oria e a parte sistem´atica do modelo, bem como

a existência de observa¸cões extremas com alguma interferência desproporcionadas nos

resul-tados do ajuste.

Tal etapa, conhecida como análise de diagnóstico, iniciou-se com a análise de

res´ıduos para detectar a presen¸ca de pontos extremos e avaliar a adequa¸c˜ao da distribui¸c˜ao

proposta para a variável resposta. Uma referência importante nesse tópico é o artigo de Cox

e Snell (1968) que apresenta uma forma bastante geral de definir res´ıduos usada at´e os dias

atuais.

A dele¸c˜ao de pontos talvez seja a t´ecnica mais conhecida para avaliar o impacto

da retirada de uma observa¸cão particular nas estimativas da regressão. A distância de

Cook (1977), originalmente desenvolvida para modelos normais lineares, foi rapidamente

assimilada e estendida para diversas classes de modelos. Por exemplo, Moolgavkar, Lustbader

e Venzon (1984) estendem a metodologia para regressão não linear com aplica¸cão em estudos

emparelhados.

Contudo, uma das propostas mais inovadoras na ´area de diagn´ostico em

re-gressão foi apresentada por Cook (1986) que propõe avaliar a influência conjunta das

obser-va¸cões sob pequenas mudan¸cas (perturba¸cões) no modelo, ao invés da avalia¸cão pela retirada

individual ou conjunta de pontos. Essa metodologia, denominada influˆencia local, teve uma

grande receptividade entre os usuários e pesquisadores de regressão, havendo inúmeras

pu-blica¸c˜oes no assunto em que se aplica a metodologia em classes particulares de modelos ou

em que se propõe extensões da técnica.

Nesta se¸cão apresenta-se um breve histórico acerca de medidas de diagnóstico

como: Influˆencia global apresentada na se¸c˜ao 2.5.1 considerando duas medidas como:

distˆan-cia de Cook generalizado e o afastamento da verossimilhan¸ca. Na se¸c˜ao 2.5.2 estudada-se a

metodologia de influência total e influência local, para a deteçcão de observa¸cões com maior

afastamento do conjunto delas, considerando três estudos de perturba¸cão. Nas se¸cões 2.5.2.1

(33)

e a proposta de Poon & Poon (1999) respectivamente.

2.5.1 Influˆencia Global

A primeira ferramenta para avaliar a an´alise de sensibilidade s˜ao as medidas

de influência global partindo do caso-dele¸cão, que é um enfoque para estudar o efeito de

retirar o i-´esimo indiv´ıduo de um conjunto de dados.

Para uma variável aleatória cont´ınua T com distribui¸cãoWM o logaritmo da fun¸cão de verossimilhan¸ca com parâmetro θ é denotado por l(θ). Seja ˆθ(i) o estimador de

m´axima verossimilhan¸ca deθ usandol(i)(θ), ondeirepresenta aoi-´esimo indiv´ıduo deletado.

A influência do i-ésimo indiv´ıduo no estimador de máxima verossimilhan¸ca de ˆθ, é avaliada pela diferen¸ca entre ˆθ₍_i₎ e ˆθ.

Se a dele¸cão de um indiv´ıduo provoca varia¸cões nas estimativas, mais aten¸cão

deve ser dada para este indiv´ıduo. Se ˆθ₍_i₎ está distante de ˆθ, então o i-ésimo indiv´ıduo é considerado como uma observa¸cão influente.

Uma primeira medida de influˆencia global ´e definida como a norma padronizada

de ˆθ(i)−θˆ, e é conhecida também como a distância de Cook generalizada.

CDi(θ) = (ˆθ(i)−θˆ)T[−L(¨ θ)](ˆθ(i)−θˆ). (19)

Outra alternativa ´e usar os valores de θ1 e θ2 em que θT = (θT1,θT2)T que

revelam o impacto do i-´esimo caso na estimativa de θ₁ e θ₂, respectivamente.

Apresentamos outra medida popular para verificar a existˆencia de pontos

in-fluentes ao modelo, esta é conhecida como a distância da verossimilhan¸ca e é dada por:

LDi(θ) = 2

n

l(ˆθ)₋l(ˆθ₍_i₎)o. (20)

2.5.2 Influˆencia Local

Numa análise estat´ıstica é importante levar em considera¸cão a estabilidade dos

resultados obtidos e das inferências de um modelo geral, com rela¸cão a poss´ıveis perturba¸cões

nos dados ou no modelo estat´ıstico.

Os elementos do conjunto de dados que efetivamente controlam aspectos da

(34)

altera¸c˜oes relevantes no resultado na an´alise quando a mesma for exclu´ıda ou submetida a

uma pequena perturba¸c˜ao.

Uma maneira eficaz para detectar observa¸cões influentes é a análise de

diag-nóstico. A dele¸cão de pontos é talvez a técnica mais conhecida para avaliar o impacto da

retirada de uma observa¸c˜ao, ou de um conjunto de observa¸c˜oes, nas estimativas dos

parâme-tros da regressão. Tal técnica foi introduzida por Cook (1977) em modelos normais lineares

e depois foi adaptada para diversas classes de modelos. Uma desvantagem que pode ocorrer

com a dele¸c˜ao individual de pontos ´e que essa metodologia pode deixar de detectar pontos

conjuntamente influentes. Entretanto, Cook(1986) propõe o método de influência local que é

uma importante ferramenta na análise da influência conjunta das observa¸cões nos resultados

de um ajuste de regress˜ao.

O m´etodo de influˆencia local proposto por Cook (1986) tem como objetivo

principal avaliar mudan¸cas nos resultados da análise quando pequenas perturba¸cões são

incorporadas ao modelo e/os dados. Se essas perturba¸c˜oes causam efeitos desproporcionados,

podem ser ind´ıcios de que o modelo est´a mal ajustado ou que possam existir afastamentos

s´erios das suposi¸c˜oes feitas para o mesmo.

Vários autores têm aplicado a metodologia de influência em modelos de

re-gress˜ao mais gerais do que modelo de rere-gress˜ao linear. Bolfarine e Vilca-Labra (2005)

apli-cam a técnica de influência local a um modelo estrutural com distribui¸cãot-student; Ortega,

Bolfarine e Paula (2003) consideram o problema de an´alise de influˆencia local em modelos

de regress˜ao log-gama generalizados com observa¸c˜oes censuradas; Zhu e Lee (2003)

apli-cam esquemas de perturba¸c˜ao a modelos lineares mistos generalizados; Galea, Leiva e Paula

(2004), derivaram as curvaturas de influência local sobre vários esquemas de perturba¸cão em

modelos de regress˜ao log-Birnbaum Saunders; Zhu e Zhang (2004) apresentam um estudo

baseado na influˆencia local de Cook (1986) que possibilitaria o teste de discrepˆancia entre o

modelo proposto e o verdadeiro modelo que teria gerado os dados, e ainda propˆos uma forma

de identifica¸cão dos pontos onde esta discrepância é mais evidente.

Por outro lado, Labra et.al. (2005) fez um estudo de influˆencia local em um

modelo t-student com o intercepto nulo; Rasekh (2006) fez um estudo de influˆencia local

(35)

afirmam que as medidas seriam invariantes e prop˜oe uma nova medida de curvatura que

seria invariante em rela¸c˜ao a transforma¸c˜oes uniformes de escala.

De souza, Ortega e Cancho (2006) aplicou um estudo de influˆencia local para

o modelo de regress˜ao log´ıstica; Rizzato e Ortega (2007) considerou o problema de an´alise

de influência local em modelos de regressão log-gamma generalizado com fra¸cão de cura;

Fachini, Ortega e Louzada-Neto (2007) aplicarão a técnica de influência local sobre vários

esquemas de perturba¸c˜ao em modelos de riscos m´ultiplos.

Seguidamente ´e apresentada as propostas de Cook (1986) como a de Poon &

Poon (1999) respectivamente.

2.5.2.1 Influˆencia Local de Cook (1986)

Nesta parte do trabalho ´e revisada a metodologia utilizada no estudo de

influˆen-cia local proposta por Cook (1986). Seja l(θ) a fun¸c˜ao de verossimilhan¸ca correspondente

ao modelo postulado, onde θ ´e um vetor p_×1 de parˆametros desconhecidos.

Considere agora uma perturba¸c˜ao neste modelo realizada atrav´es de um vetor

ω =ω_q×1, restrito a algum subconjunto aberto Ω∈Rq. Seja l(θ|ω) o logaritmo da fun¸c˜ao

de verossimilhan¸ca do modelo perturbado. Assumiremos que existe ω0 ∈ Ωtal que l(θ) =

l(θ_|ω₀), em quel(θ_|ω) é duas vezes continuamente diferenciável em (θT,ωT). Iremos denotar por ˆθe ˆθω os estimadores de máxima verossimilhan¸ca deθeml(θ) el(θ_|ω) respectivamente.

Uma medida sugerida por Cook (1986) ´e definida como:

LD(ω) = 2hl(ˆθ)₋l(ˆθω)i. (21)

essa medida ´e denominada afastamento pela verossimilhan¸ca, de modo que a distˆancia entre ˆ

θ e ˆθω passa a depender da concavidade do logaritmo da fun¸c˜ao de verossimilhan¸ca, ou seja,

se l(θ) é suficientemente achatada, ˆθ e ˆθω podem ser julgados que estão próximos entre si,

enquanto que sel(θ) for suficientemente concentrada em torno de ˆθ estas estimativas podem

estar distantes entre si. A proposta ´e estudar o comportamento local da fun¸c˜ao LD(ω)

em torno de ω0 e selecionar uma dire¸c˜ao unit´aria d que determina o plano normal de Ω

e cont´em o eixo LD(ω). O procedimento consiste em avaliar como a superf´ıcie geom´etrica

α(ω) = (ω, LD(ω))T _{desvia-se de seu plano tangente em} _ω

(36)

lentamente deω0, ou seja, quando pequenas perturba¸c˜oes s˜ao introduzidas ao modelo. Para

cada dire¸cão d, a interseçcão deste plano com a superf´ıcie pode ser analisada pelo gráfico de

LD(ω0+ad) versus a∈R.

Como LD(ω) é uma fun¸cão não negativa com m´ınimo global emω0,LD(ω0+

ad) tem um m´ınimo local ema= 0. Cada linha ajustada pode ser caracterizada considerando

a curvatura normalC_d ema = 0, que pode ser interpretada como o c´ırculo de melhor ajuste

em ω0.

Quanto maior os valores de C_d, maior ´e a sensibilidade e a perturba¸c˜ao

intro-duzida na dire¸cãod. A sugestão de Cook (1986) é considerar a dire¸cãodmax, correspondente a maior curvatura Cmax que contém a informa¸cão de diagnóstico mais importante, ou seja, para detectar observa¸cões que mais influenciam em LD(ω), basta fazer o gráfico de dmax pelo ´ındice de observa¸cões e verificar quais pontos se destacam dos demais.

Cook (1986) mostra que a curvatura normal na dire¸c˜ao d em que estamos

interessados fica resumida ao m´odulo da segunda derivada de LD(ω₀+ad) com respeito a

a, que avaliada em a= 0 mostrando que

C_d = 2_|dTF¨d_|, (22)

com,

¨

F = ∆T(₋L¨)−1_∆_, _{∆ =} ∂2l(θ|ω)

∂θT∂ω ,

em que ∆ ´e uma matriz p_×n, que depende do esquema de perturba¸c˜ao usado. Com todas

as quantidades sendo avaliadas em θ = ˆθ, ω = ω0 e −L¨(θ) e a matriz de informa¸c˜ao

observada do modelo postulado. Então C_dmax = λ1 > λ2 > . . . > λn são os autovalores da matriz ¨F e dmax = e1 >e2 > . . . > en são os autovetores correspondentes. O interesse particular está na dire¸cão que produz a maior influência local, essa dire¸cãod_maxé o autovetor normalizado correspondente ao maior autovalor C_d_max da matriz ¨F. Com esse autovetor

dmax, identificamos as observa¸cões mais influentes para o esquema de perturba¸cão em análise. Por outro lado, Lesaffre e Verbeke (1998) sugerem olhar também a dire¸cão do

(37)

dada por:

Ci = 2|∆Ti (−L¨)

−1_∆i

|. (23)

em que ∆i denota a i-ésima linha da matriz ∆. Por tanto sugere-se estudar o gráfico deCi contra a ordem das observa¸cões. É sugerido que as observa¸cões tais que Ci > 2 ¯C tenham aten¸cão especial.

Neste contexto, se o interesse ´e avaliar a influˆencia parcial em um subconjunto

deθ=(θT₁,θT₂)T_,_θ

1 por exemplo, temos que a curvatura normal na dire¸c˜ao do vetord´e dada

por:

C_d(θ₁) = 2¯¯_¯dT∆Tn_{[ ¨}_L₍_θ_)]−1₋_D 1

o

∆d ¯ ¯

¯,

com

D1 = 

 0 0

0 ( ¨L22)−1 

, L¨22=

∂2_l₍_θ_|_ω₎

∂θT₂∂θ2 ¯ ¯ ¯

¯_θ=_θˆ.

O gr´afico do autovetor associado ao maior autovalor da matriz₋∆T_{_{[ ¨}_L₍_θ_)]−1₋

D1}∆ versus os ´ındices de observa¸c˜oes pode revelar quais destas est˜ao influenciando θ1.

Analogamente, se o interesse está em θ₂, então a curvatura normal na dire¸cão do vetor dé

dada por:

C_d(θ₂) = 2¯¯_¯dT∆Tn[ ¨L(θ)]−1

−D₂o∆d ¯ ¯

¯,

com

D2 = 

 0 0

0 ( ¨L11)−1 

, L¨11=

∂2_l₍_θ_|_ω₎

∂θT₁∂θ1 ¯ ¯ ¯

¯_θ=_θˆ.

A influˆencia local das observa¸c˜oes em ˆθ2 pode ser avaliada considerando o

gr´afico d_max para a matriz ₋∆T_{_{[ ¨}_L₍_θ_)]−1₋_D

2}∆ versus o ´ındice das observa¸c˜oes.

Assim, ´e derivada as curvaturas normais de um o modelo de regress˜ao

con-siderando três esquemas de perturba¸cão, dadas por: pondera¸cão de casos, perturba¸cão na

(38)

2.5.2.1.1 Perturba¸c˜ao de casos

O primeiro esquema de perturba¸cão é o esquema de pondera¸cão de casos. Como

define Cook (1986), o vetor de perturba¸cão ω₀ = (ω1, ω2, . . . , ωn)T, de dimensão (n×1) é introduzido em cada elemento da fun¸cão de verossimilhan¸ca é dado por:

l(θ_|ω) =X i∈F

ωilog

n

f(θ)o+X i∈C

ωilog

n

S(θ)o

Nesse caso, o vetor correspondente a não perturba¸cão é o vetor ω0 =

(1,1, . . . ,1)T_.

2.5.2.1.2 Perturba¸c˜ao na vari´avel resposta

Seja ω = (ω1, ω2, . . . , ωn)T os pesos que perturbam as vari´aveis resposta da

forma, y∗ ₌ _y

i +Syωi, com Sy sendo um fator de escala dada pela estima¸cão do desvio padrão da variável Y e ωi pertencente a R. Neste caso, o vetor de não perturba¸cão é dado por ω₀ = (0,0, . . . ,0)T_.

2.5.2.1.3 Perturba¸cão na variável explanatória

Considera-se uma nova perturba¸c˜ao aditiva em uma particular vari´avel

con-t´ınua, então, xitω =xit+Sxωi, onde Sx é um fator escala da estima¸cão do desvio padrão da variável xi ewi ǫ R. Neste caso o vetor de não perturba¸cão é ω0 = (0,0, . . . ,0)T.

2.5.2.2 Influˆencia local conformal

Nesta parte do trabalho iremos apresentar a metodologia utilizada no estudo de

influˆencia local proposta por Poon & Poon (1999), eles apresentam uma medida denominada

curvatura normalcomformalem um pontoω₀na superficie geom´etricaα(ω) = (ω, LD(ω))T_, numa dire¸c˜ao d representada por:

B_d=₋ d

T_F_¨_d

q

tr( ¨F2₎_|_ω=ω

0

=₋ d

T_∆T_{( ¨}_L₎−1_∆_d q

tr(∆T_{( ¨}_L₎−1_∆)2_|

θ=θˆ,ω=ω0

. (24)

As medidas C_d eB_d das express˜oes (22) e (24) diferem apenas por um fator

(39)

um autovetor correspondente ao maior autovalor para a curvatura normal ir´a produzir

tam-b´em a maior curvatura normal conformal. No entanto, B_d possui algumas propriedades interessantes, como o fato de que 0_{≤ |}B_d_{| ≤} 1, o que facilita sua interpreta¸c˜ao, para

qual-quer dire¸cão d. Essa propriedade descreve realmente que a expressão (24) é uma medida

normalizada, al´em disso, podemos calcular o autovetor e∗

i com seu respectivo autovalor λ∗i para i= 1, . . . , n da matriz

¨ F∗

= ∆

T_{( ¨}_L₎−1_∆ q

tr(∆T_{( ¨}_L₎−1_∆)2

,

a qual pode ser utilizada para identificar poss´ıveis pontos influentes.

Poon & Poon (1999) apresentam ent˜ao uma forma de decidir se um autovetor

´e influente o n˜ao, utilizando o valor √1

n com a seguinte defini¸cão. Defini¸cão 2.1: Um autovetor é q influente se _|Bei| ≥ √q

n.

Ou seja, escolhendo valores de q, decidimos se uma dire¸cão é influente ou não

de acordo com a magnitude de seu autovalor normalizado

Na pr´atica, normalizamos os autovalores fazendo ˆλ∗

i =

λ∗

i

pPn

k=1λ∗k2

, ordenando

em m´odulos os autovalores normalizados da forma

|λˆ∗

max|=|ˆλ ∗

1| ≥. . .≥ |λˆ ∗

k| ≥ q √

n >|ˆλ

∗

k+1|. . .|λˆ ∗

n| ≥0,

os autores mostram a contribui¸c˜ao no j-´esimo vetor de base a todos os autovetores q

-influentes ´e obtida por

m(q)j =

v u u

tXk

i=1

|λˆ∗

i|e∗ij2. (25)

Para a interpreta¸cão dessa contribui¸cão, pode-se construir um gráfico dos

valo-res obtidosm(q)j pelos indicesj = 1,2, . . . , ne verificar se existem pontos que se distanciam

dos demais.

Poon & Poon (1999) sugerem uma quantidade que ser´a utilizada para decidir

se una dire¸cão exerce grande influência ou não, dada por

b= tr( ¨F

∗₎

n

q

(40)

Por outro lado, para decidir si um determinado ponto ´e influente ou n˜ao

con-siderando a contribui¸cão agregada dosk maiores autovalores maiores em módulo do que _√q n, será utilizada a contribui¸cão m(q)j dada pela equa¸cão (25), e para decidir se um caso é ou

n˜ao influente, utiliza-se o valor b dados na equa¸c˜ao (26). No entanto, Poon & Poon (1999)

prop˜oe ¯m(q)j√2 como um ponto de corte para a contribui¸c˜ao agregada dosk autovalores e

2b como um ponto de corte da contribui¸c˜ao agregada de todos os autovalores, onde a ¯m(q)j,

tem a forma seguinte

¯ m(q) =

v u u

t1

n k

X

i=1

|λˆ∗

i|.

2.6 An´alise de res´ıduo

Quando se procura ajustar um modelo a um conjunto de dados, a valida¸c˜ao

desse ajuste passa pela an´alise de uma estat´ıstica especial, que tem a finalidade de medir

a qualidade do modelo ajustado. Uma vez que os res´ıduos s˜ao usados para identificar

dis-crepˆancias entre um modelo ajustado e o conjunto de dados, ´e conveniente buscar uma

defini¸cão para o res´ıduo que leve em considera¸cão a contribui¸cão de cada observa¸cão sobre

essa medida de qualidade de ajuste. Varios res´ıduos s˜ao discutidos em Cox e Snell (1968),

McCullagh e Nelder (1989), Collett (2003), Ortega, Paula e Bolfarine (2003), entre outros.

De uma maneira geral, podemos definir o res´ıduo referente a i-ésima observa¸cão através de

uma fun¸cão ri = r(yi,θˆ) que objetiva identificar discrepâncias entre o modelo e os dados. Nas se¸cões seguintes, os res´ıduos de martingale e deviance são descritos.

2.6.1 Res´ıduo martingale

Os res´ıduos martingale são assimétricos e assumem valores máximo em +1 e

valor m´ınimo em _−∞. Na área de análise de sobrevivência, o res´ıduo martingale pode ser

expresso como

rMi =δi+ log[S(yi)], (27)