1
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO Escola de Minas da Universidade Federal de Ouro Preto
Departamento de Engenharia de Minas
Programa de Pós-Graduação em Engenharia Mineral – PPGEM
DIMENSIONAMENTO ÓTIMO DE CÂMARAS E PILARES EM
CAMADAS INCLINADAS
Mestrando: Alcides Eloy Cano Nunez
Orientador: Prof. Dr. Ivo Eyer Cabral
2
DIMENSIONAMENTO ÓTIMO DE CÂMARAS E PILARES EM
CAMADAS INCLINADAS
Mestrando: Alcides Eloy Cano Nunez
Orientador: Prof. Dr. Ivo Eyer Cabral
Co-orientador: Prof. Dr. Rodrigo Pelucci
Dissertação apresentada ao Programa de Pós-Graduação do Departamento de Engenharia de Minas da Escola de Minas da Universidade Federal de Ouro Preto, como parte integrante dos requisitos para obtenção do título de Mestre em Engenharia Mineral.
Área de concentração: Lavra de Minas.
Ouro Preto – MG Dezembro, 2016
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO Escola de Minas da Universidade Federal de Ouro Preto
Departamento de Engenharia de Minas
4
5
Nenhum homem realmente produtivo pensa como se estivesse escrevendo uma dissertação - “Albert Einstein”.
6
DEDICATÓRIA
Dedico o presente trabalho de dissertação à minha mãe, que com seus conselhos, apoio e exemplo de vida me soube guiar para aprender a lutar.
A meus irmãos, pelo apoio e paciência.
A meus professores da UFOP, deles aprendi e recebi seus conhecimentos.
7
AGRADECIMENTOS
A Deus, meu eterno mestre
À Universidade Federal de Ouro Preto e seus profissionais, pela formação acadêmica que me faz credor.
Ao Prof. Rodrigo Peluci de Figueiredo, pelo encaminhamento e direcionamento da presente dissertação; assim como, também, pelo apoio, compreensão, ensino e
conselhos.
Aos professores Ivo Eyer Cabral e Adilson Curi pela ajuda e amizade.
A meu grande amigo Carlos Arroyo, por sua amizade incondicional.
A Bruno e Vladimir; meus bons colegas e amigos. Com eles aprendi e compartilhei ensinamentos.
8
RESUMO
Um dos problemas mais importantes na mineração por “câmaras e pilares” em camadas
inclinadas, é tornar máxima a sua recuperação, isto é, obter o maior aproveitamento da jazida. A recuperação é uma função não-linear das dimensões dos pilares e dos vãos das câmaras. Por outro lado, tanto os pilares quanto os vãos têm suas dimensões restringidas por questões geomecânicas, pois devem satisfazer a certos limites de resistência. A maximização da recuperação sujeita às restrições de resistência, caracteriza um problema de programação matemática não-linear. Neste trabalho, propõe-se tratar o dimensionamento das câmaras e pilares em camadas inclinadas via técnicas de programação não-linear, tendo como objetivo maximizar a recuperação.
Por outro lado, os pilares em camadas inclinadas estão sujeitos a momentos, forças normais e forças cisalhantes antisimétricas. Para contemplar tais carregamentos, será utilizada a mecânica dos meios contínuos generalizados de Cosserat. Objetiva-se também avaliar a estabilidade de pilares com planos de descontinuidade por essa mesma formulação da mecânica do contínuo.
9
ABSTRACT
One of the most important problems in mining by "room and pillars" in inclined seams, is to maximize the recovery, that is, gets the most use of the deposit. Recovery is a nonlinear function of the pillar dimensions and spans of the rooms. On the other hand, the dimensions of pillars and spans of rooms are constrained by geomechanical issues: the limits of strength must be satisfied. Recovery maximization, subject to the constraints of strength, is a problem of nonlinear mathematical programming. This work proposes to address the room and pillars design in inclined beds by means of nonlinear optimization techniques, aiming at to maximize the recovery. On the other hand, the pillars on inclined seams are subject to moments, normal and anti-symmetric shear forces. To address such loads will be used the Cosserat generalized continuum mechanics. We also intend to evaluate the stability of pillars with discontinuities according to this same formulation of continuum mechanics.
10
SUMARIO
1 CAPÍTULO I 19
1.1 INTRODUÇÃO. 19
1.2 JUSTIFICATIVA. 20
1.3 PERGUNTAS DA PESQUISA. 21
1.4 OBJETIVO DO ESTUDO. 21
1.5 METODOLOGIA DO ESTUDO. 22
2 CAPÍTULO II 23
2.1 REVISÃO BIBLIOGRÁFICA 23
2.2 CONSIDERAÇÕES PARA O DIMENSIONAMENTO DE UM PILAR. 24
2.2.1 ESTADO DE TENSÕES IN SITU. 24
2.2.2 ÁREA TRIBUTÁRIA. 25
2.2.2.1 CONSIDERAÇÕES SOBRE O MÉTODO DA ÁREA TRIBUTÁRIA. 25
2.2.3 EFEITO DA FORMA DO PILAR. 28
2.2.4 ANÁLISE BIDIMENSIONAL DO ESTADO DE TENSÕES E TENSÕES-MOMENTO PARA MEIOS CONTÍNUOS GENERALIZADOS DE COSSERAT. 31 2.2.5 CÍRCULO DE MOHR CLÁSSICO PARA UM ESTADO DE TENSÕES 2D. 33 2.2.5.1 APRESENTAÇÃO NÃO-CLÁSSICA DO ESTADO DE TENSÕES DUM PILAR NO ESPAÇO DE MOHR
34 2.2.6 OUTRAS PARTICULARIDADES EM UMA AVALIAÇÃO DE PILARES. 38 2.2.6.1 PILARES ALINHADOS COM A FORÇA RESULTANTE. 38 2.2.6.2 PILARES NORMAIS À CAMADA E COM PLANOS DE FRAQUEZA. 42 2.2.7 RESTRIÇÕES NO DIMENSIONAMENTO DE CÂMARAS E PILARES 44
2.2.7.1 FLEXÃO PURA EM VIGAS E LAJES. 44
2.2.7.2 TENSÕES DEVIDO AO PESO PRÓPRIO DA LAJE. 45
2.2.8 CAPACIDADE DE CARGA DAS FUNDAÇÕES DOS PILARES 46
3 CAPÍTULO III 48
3.1 DIMENSIONAMENTO ÓTIMO DE PILARES DE SEÇÃO QUADRADA. 48 3.1.1 ÁREA TRIBUTÁRIA PARA UM PILAR EM CAMADA INCLINADA. 49
3.1.1.1 ESFORÇOS E TENSÕES IN SITU. 49
3.1.1.2 TENSÕES QUE ATUAM NO PILAR. 49
3.1.1.3 TENSÕES SOLICITADAS AO PILAR. 51
3.1.2 EFEITO DA FORMA NO DESENHO DO PILAR. 52
3.1.2.1 FATOR SE SEGURANÇA – ESFORÇO APLICADO E ESFORÇO
ADMISSÍVEL. 53
3.1.2.1.1 RELAÇÃO ENTRE O ESFORÇO DE RESISTÊNCIA DO PILAR E O ESFORÇO APLICADO
54
3.1.2.1.2 TENSÃO CISALHANTE NO PILAR. 54
3.1.3 ANÁLISES DE MOMENTOS. 55
3.1.3.1 TENSÃO MOMENTO ASSOCIADO À GRADIENTE DE TENSÕES. 55 3.1.3.1.1 CALCULO DO MOMENTO TENSOR GERADO PELA GRADIENTE DO
ESFORÇO VERTICAL. 57
3.1.3.1.2 CALCULO DO MOMENTO TENSOR GERADO PELA GRADIENTE DO
ESFORÇO HORIZONTAL. 58
3.1.3.2 CALCULO DA TENSÃO CISALHANTE ANTISSIMÉTRICA
RESPONSÁVEL POR GERAR TENSÃO MOMENTO. 58
3.1.3.3 TENSÃO MOMENTO ATUANTE NO TOPO DO PILAR. 60
11
3.1.3.4.1 MOMENTO NO CONTATO TETO E TOPO DO PILAR. 62 3.1.3.4.2 MOMENTO RESULTANTE NA METADE DA ALTURA DO PILAR. 62 3.1.4 TENSÕES INDUZIDAS DEVIDO AO MOMENTO RESULTANTE NA METADE
DO PILAR. 63
3.1.4.1 ESFORÇOS DE COMPRESSÃO MÁXIMO E MÍNIMO NA SEÇÃO DE SUPORTE DO PILAR.
64 3.1.5 RESTRIÇÕES NO DIMENSIONAMENTO DE CÂMARAS E PILARES. 65 3.1.5.1 RESTRIÇÃO POR FLEXÃO DE UMA LAJE SIMPLES. 65 3.1.5.1.1 TENSÕES DE TRAÇÃO E COMPRESSÃO DEVIDO AO MOMENTO
GERADO PELO PESO DA LAJE. 66
3.1.5.1.2 TENSÕES DE TRAÇÃO E COMPRESSÃO DEVIDO A PESO DE UMA
LAJE. 67
3.1.5.1.3 TENSÕES DE TRAÇÃO E COMPRESSÃO DEVIDO AO PESO DE UM CONJUNTO DE LAJES.
68
3.2 PILARES DE SEÇÃO RETANGULAR. 71
3.2.1 RELAÇÃO ENTRE FATOR DE SEGURANÇA, ESFORÇO DE RESISTÊNCIA E
TENSÃO NORMAL SOLICITADA AO PILAR. 73
3.3 PILARES NÃO PERPENDICULARES À CAMADA MINERAL. 73
3.3.1 MOMENTO ANTISSIMÉTRICO NUM PILAR INCLINADO COM RELAÇÃO À
CAMADA. 74
4 CAPÍTULO 4 75
4.1 AVALIAÇÃO VIA ALGORITMOS DE PROGRAMAÇÃO. 75
4.2 DADOS GERAIS DA ZONA DE ESTUDO. 75
4.2.1 DADOS GERAIS. 75
4.2.2 TEORIAS A SEREM ANALISADAS. 76
4.2.2.1 TEORIA DOS MEIOS CONTÍNUOS COMPARADA COM A MECÂNICA
CLÁSSICA. 77
4.2.3 PROCESSO DE OTIMIZAÇÃO. 78
4.2.3.1 ANÁLISE MECÂNICA DE COSSERAT E MECÂNICA CLÁSSICA. 78
4.2.3.2 RESPOSTAS DE OTIMIZAÇÃO E ALGORITMOS. 79
5 CAPÍTULO 5 80
12
LISTA DE FIGURAS.
FIGURA 1. TENSÕES PRINCIPAIS IN SITU (AUTOR). ... 24 FIGURA 2. ARRANJO SISTEMÁTICO DE CÂMARAS E PILARES DE SEÇÃO
QUADRADA: (A) ADAPTADA DE HOEK & BROWN (1980); (B) CASO DE UMA ÁREA DE LAVRA LIMITADA. ... 27 FIGURA 3. PILAR NUMA CAMADA INCLINADA SUJEITO A TENSÕES CISALHANTES
ANTISSIMÉTRICAS E TENSÕES-MOMENTO. ... 28 FIGURA 4. CURVAS TENSÃO X DEFORMAÇÃO: ANALOGIA ENTRE OS
COMPORTAMENTOS DE CORPO DE PROVA EM COMPRESSÃO UNIAXIAL E PILARES DE MINA (ADAPTADA DE HUDSON & HARRISON, 1997). ... 30 FIGURA 5. ANÁLISE DE UM PONTO SUBMETIDO A TENSÕES MOMENTO, NORMAIS E CISALHANTES (MODIFICADA DE FIGUEIREDO, 1999, 2011). ... 32 FIGURA 6. EFEITO DAS TENSÕES DE CISALHAMENTO NÃO SIMÉTRICAS DE
COSSERAT: ΤS PRODUZ DISTORÇÕES ANGULARES E ΤA PRODUZ ROTAÇÃO
(ADAPTADA DE MINDLIN, 1963)... 33 FIGURA 7. CÍRCULO DE MOHR CLÁSSICO (FIGUEIREDO, 2014). ... 34 FIGURA 8. PILAR NUMA CAMADA INCLINADA SUBMETIDA A TENSÕES DE
COMPRESSÃO E DE CISALHAMENTO NÃO CONJUGADAS. ... 36 FIGURA 9. APRESENTAÇÃO DO CÍRCULO DE MOHR NÃO-CLÁSSICO PARA
PILARES EM CAMADAS INCLINADAS (MODIFICADO DE PARISEAU, 2007). .... 37 FIGURA 10. PILAR INCLINADO EM RELAÇÃO AO EIXO PERPENDICULAR À
CAMADA. ... 39 FIGURA 11. FORÇA RESULTANTE FR E SUAS COMPONENTES ORTOGONAIS FH E
FV (AUTOR). ... 40 FIGURA 12. FORÇA RESULTANTE FR E SUAS COMPONENTES ORTOGONAIS
SEGUNDO H’-V’ (AUTOR). ... 41 FIGURA 13. TENSÕES NO PLANO H’-V’ PARA UM PILAR ALINHADO COM A FORÇA RESULTANTE (AUTOR E FIGUEIREDO). ... 42 FIGURA 14. PILAR COM PLANO DE FRAQUEZA (AUTOR). ... 42 FIGURA 15. ESTADO DE ANÁLISES DE FLEXÃO PURA (AUTOR). ... 44 FIGURA 16. ESFORÇOS DEVIDO AO SEU PRÓPRIO PESO (ADAPTADA DE COATES).
... 45 FIGURA 17. MECANISMO DE COLAPSO DA FUNDAÇÃO DE UM PILAR (BRADY &
BROWN, 2004). ... 46 FIGURA 18. TENSÕES IN SITU EM EIXOS HV E TENSÕES IN SITU EM UM PLANO
H’V’ (AUTOR). ... 49 FIGURA 19. SITUAÇÃO DO PILAR SUBMETIDO A ESFORÇOS NUM PLANO HV E
H’V’ (AUTOR E FIGUEIREDO). ... 50 FIGURA 20. CARREGAMENTO SOLICITADO AO PILAR (AUTOR). ... 51 FIGURA 21. PILAR SUBMETIDO A UMA TENSÃO MÉDIA E UMA GRADIENTE DE
ESFORÇOS (AUTOR). ... 56 FIGURA 22. TENSÃO MOMENTO DEVIDO À TENSÃO GRADIENTE VERTICAL “MVZ”
13
FIGURA 24. ESFORÇOS DE MOMENTO EM RELAÇÃO AO CENTRO O’ (AUTOR). ... 61
FIGURA 25. ESTADO DOS MOMENTOS QUE AGEM NO PILAR (AUTOR). ... 63
FIGURA 26. CAMADAS INCLINADAS SUJEITAS À DEFORMAÇÃO POR FLEXÃO PURA (AUTOR). ... 66
FIGURA 27. ZONA DA LAJE SUJEITA A ESFORÇOS DE COMPRESSÃO – TRAÇÃO. .. 67
FIGURA 28. GRUPO DE LAJES SEPARADAS DE UM CONJUNTO DE LAJES. ... 69
FIGURA 29. SEÇÃO DE PLANTA NUM PLANO XY’- CÂMARAS E PILARES. ... 71
FIGURA 30. PERFIL BB’ E SEÇÃO DE UM PILAR RETANGULAR NO PLANO XY’. .... 72
FIGURA 31. ESTADO DE TENSÕES CISALHANTES E MOMENTOS NUM PILAR COM INCLINAÇÃO À CAMADA. ... 74
FIGURA 32. APRESENTAÇÃO 3D DE CÂMARAS E PILARES EM CAMADAS INCLINADAS. ... 76
FIGURA 33. DISPOSIÇÃO DE PILARES COM RELAÇÃO À CAMADA A SEREM ANALISADOS. ... 77
FIGURA 34. CÍRCULO DE MOHR NÃO CONVENCIONAL. ... 88
FIGURA 35. TENSÃO CISALHANTE, SIMÉTRICA E ANTISSIMÉTRICA, QUE ATUAM EM UM PILAR. ... 89
FIGURA 36. MOMENTO E ESFORÇOS CISALHANTES QUE ATUAM GERANDO MOMENTO NUM PILAR. ... 90
FIGURA 37. APRESENTAÇÃO EM 3D DE UM SISTEMA DE CÂMARAS E PILARES (AUTOR). ... 91
FIGURA 38. VIGA EM BALANÇO (ADAPTADA DE BEER ET AL.,2007). ... 91
FIGURA 39. FLEXÃO E RAIO DE CURVATURA DE UMA VIGA. ... 92
FIGURA 40. FLEXÃO E ÂNGULO DE CURVATURA DE UMA VIGA. ... 92
FIGURA 41. ESTADO DE TENSÕES EM UMA VIGA SUBMETIDA À TRAÇÃO E COMPRESSÃO INDUZIDA PELA FLEXÃO. ... 93
FIGURA 42. LAJES FLEXIONADAS PELA AÇÃO DO SEU PRÓPRIO PESO (AUTOR). . 97
FIGURA 43. SISTEMA DE UM DIFERENCIAL DE LAJE (AUTOR). ... 97
FIGURA 44: SITUAÇÃO DE UMA LAJE COMO APOIOS SIMPLES (AUTOR). ... 102
FIGURA 45 PILARES DE LARGURA INFINITA. ... 106
FIGURA 46. ESQUEMA DE UM PILAR RETANGULAR E A CARGA DISTRIBUÍDA... 110
FIGURA 47. VISTA EM PLANO DAS DISTRIBUIÇÕES DE CARGA EM UM PILAR COM SEÇÃO RETANGULAR... 110
14
LISTA DE QUADROS.
QUADRO 1. FÓRMULAS PARA O DIMENSIONAMENTO DE CÂMARAS E PILARES PELO MÉTODO DA ÁREA TRIBUTÁRIA. ... 26 QUADRO 2. FÓRMULAS PARA SE DETERMINAR A RESISTÊNCIA DO PILAR,
CONFORME O EFEITO DE FORMA. ... 31 QUADRO 3. FÓRMULAS PARA SE DETERMINAR AS TENSÕES E
TENSÕES-MOMENTO NUM DADO PLANO (ADAPTADA DE FIGUEIREDO, 2011) -
15
LISTA DE TABELAS.
TABELA 1. LITOLOGIA E PROPRIEDADES DO MATERIAL ROCHOSO. ... 75 TABELA 2. INFORMAÇÃO GERAL PARA OS PILARES E AS CAMADAS. ... 77 TABELA 3. RESUMO DE DADOS OTIMIZADOS VIA ALGORITMOS COM
16
LISTA DE ANEXOS
ANEXO A: DEDUÇÃO DAS FÓRMULAS APRESENTADAS NO QUADRO N° 3 ... 85
ANEXO B: ANÁLISE DE TENSÕES E MOMENTOS EM UM PILAR ... 89
ANEXO C: ANÁLISE DE ESTABILIDADE DAS LAJES. ... 91
ANEXO D: ALGORITMO PARA AVALIAR UM SISTEMA DE LAJES INSTÁVEIS. ... 103
ANEXO E: DEDUÇÃO DA EQUAÇÃO DE RESISTÊNCIA DE UM PILAR COM SEÇÃO RETANGULAR, APARTIR DA EQUAÇÃO DE BENIAWSKI. ... 106
ANEXO F: DEDUÇÃO DA EQUAÇÃO DE RESISTÊNCIA DE UM PILAR COM SEÇÃO RETANGULAR, APARTIR DA EQUAÇÃO DE SALOMON E MUNRO. ... 113
17
LISTA DE SIMBOLOS.
σV = Esforço vertical.
σ1 = Esforço principal maior.
σH = Esforço horizontal.
σ3 = Esforço principal menor.
K = Constante de proporção entre os esforços horizontal e vertical. Z = Profundidade.
WP = Comprimento do pilar.
WO = Comprimento dos vãos ou distancia entre as laterais de um pilar a outro numa câmara. LO = Largura do vão.
LP = Largura do pilar. HP = Altura do pilar.
σV’ = Esforço que atua no sentido do eixo V’.
σH’ = Esforço que atua no sentido do eixo H’.
τH’V’ = Esforço cisalhante no pano H’V’.
τV’H’ = Esforço cisalhante no pano V’H’.
M = Momento.
τa = Esforço antissimétrico.
τs = Esforço simétrico.
γ = Peso específico.
At = Área total correspondente à zona de influência definida pela região de suporte do pilar. AP = Área do pilar.
σadm = Esforço admissível ou esforço de resistência máxima.
σaplic = Esforço a que é submetido o pilar. Fs = Fator de segurança.
R = Fator de recuperação de minério num método de lavra de câmaras e pilares.
σr = Esforço de resistência admissível para o pilar em função da forma. = Esforço de resistência à compressão de um bloco de dimensões unitárias.
σxx = Esforços atuantes no plano X; e variantes para eixos relativos.
σyy = Esforços atuantes no plano Y; e variantes para eixos relativos.
τxy = Esforço cisalhante no pano X; e variantes para eixos relativos.
τyx = Esforço cisalhante no pano Y; e variantes para eixos relativos.
σx’ = Esforços atuantes no plano X’; e variantes para eixos relativos.
σy’ = Esforços atuantes no plano Y’; e variantes para eixos relativos.
τx’y’ = Esforço cisalhante no pano X’ com sentido a Y’; e variantes para eixos relativos.
τy’x’ = Esforço cisalhante no pano Y’ com sentido a X’; e variantes para eixos relativos.
σp = Esforço normal atuante na seção de contato do pilar com rocha sobrejacente.
τp = Esforço cisalhante na seção de contato do pilar com rocha sobrejacente.
A = Denominação do comprimento nas análises de esforços, e ponto em algumas imagens. MX’Z = Momento no eixo X’.
MXZ = Momento no eixo X. MYZ = Momento no eixo Y. MVZ = Momento no eixo X. MHZ = Momento no eixo Y. C = Coesão.
Φ = Ângulo de atrito.
αj = Ângulo que forma o plano a camada inclinada com a descontinuidade do pilar. E = Módulo de Young.
ICG = Momento de inércia com relação ao centro da seção.
∆z = Diferença de altura entre dois pontos.
∆σV = Acréscimo de esforço vertical.
∆σH = Acréscimo de esforço horizontal.
MO = Momento em relação ao centro de um determinado elemento.
1
C
18 MP = Momento que atua no topo do pilar.
σt = Esforço de resistência à tração.
σc = Esforço de resistência à compressão. RB/A = Reação do corpo A em B.
19
1 CAPÍTULO I
1.1 INTRODUÇÃO.
O esgotamento dos recursos naturais nas últimas décadas vem sendo um problema para as sociedades no mundo inteiro; a demanda de minério é cada vez maior e está ligada ao aumento do consumo. Em decorrência, as empresas dedicadas á indústria mineral precisam fornecer volumes crescentes destes recursos.
Percebe-se que, nos últimos anos, as jazidas a céu aberto disponíveis, cada vez mais, foram diminuindo em volume e quantidade. No passado elas forneceram, com relativa facilidade e rapidez, os recursos minerais necessários, além de um maior retorno econômico às empresas. Devido à escassez de minério próximo à superfície, os estudos de pesquisa mineral direcionaram-se para a mineração subterrânea, a qual foi se tornando de maior relevância. Os estudos de geotecnia, no entanto, não acompanharam totalmente as necessidades dos projetos de mineração subterrânea. Ainda assim, isto não foi um entrave à implantação de vários projetos de mineração subterrânea até a atualidade, não obstante, muitas vezes com baixas recuperações.
Os tipos de corpos de minério, suas formas e distribuição na natureza dependem de fatores como: solução mineralizante, a disponibilidade da rocha para receber soluções magmáticas, descontinuidades que facilitem a intrusão etc. Cada rocha é particular e diferente, mesmo em se tratando de um mesmo litotipo; suas características são determinadas pela textura, mineralogia, arranjo dos minerais constituintes; características essas que irão depender muito do posicionamento espacial da rocha. Este estudo abordará corpos de minério horizontais ou sub-horizontais, cujo método de lavra é por Câmaras e Pilares.
20
possível, estabelecendo-se funções de recuperação do jazimento, cujas variáveis são geométricas: dimensões de pilares e câmaras. Tais variáveis, por sua vez, são sujeitas a restrições geomecânicas (limites de resistência das rochas), as quais devem ser respeitadas para garantir a estabilidade do arranjo de lavra. A combinação dessas funções de recuperação e das restrições goemecânicas apropriadas pode ser codificada em algoritmos de programação matemática1 não linear, cujo objetivo é achar as respostas ótimas (no caso, o máximo da recuperação).
Atualmente, na mineração subterrânea aplicam-se principalmente técnicas de avaliação e estimativas determinísticas; conseqüentemente, as análises computacionais utilizadas costumam se basear em premissas (dados e teorias) tidas como conservadoras. Em decorrência, os resultados são muitas vezes ruins, levando a problemas geomecânicos e/ou a ganhos baixos. Estudos estocásticos podem melhorar a situação no que diz respeito aos dados determinísticos conservadores. Porém, com relação às teorias conservadoras há que se refiná-las, tornando-as mais realistas, para que se possa obter uma solução otimizada.
1.2 JUSTIFICATIVA.
É relevante para a indústria dimensionar pilares com seção mínima, maximizando, assim, a recuperação dos jazimentos. Particularmente, para pilares em camadas inclinadas, pretende-se demonstrar nesta dissertação que, devido aos esforços cisalhantes anti-simétricos e aos momentos neles atuantes, a aplicação da teoria dos meios contínuos generalizados de Cosserat (Cosserat & Cosserat, 1896, 1909 - apud Figueiredo, 1999), cuja formulação teórica incorpora tais grandezas estáticas, aplica-se com propriedade ao seu dimensionamento ótimo. Para tanto, serão criados modelos de programação matemática não-linear, em que o objetivo de maximizar a recuperação ficará expresso por uma função dependente das variáveis geométricas do arranjo de
1 Far-se-á uso, nesta dissertação, do software MathCad na busca de soluções via programação
21
lavra, sujeito a restrições de resistência de pilares e vãos das câmaras, que dependem das tensões cisalhantes anti-simétricas e dos momentos incidentes nos pilares.
1.3 PERGUNTAS DA PESQUISA.
Algumas perguntas específicas são focadas nesta pesquisa, a saber:
- É determinante uma análise que considere corretamente todos os esforços atuantes em pilares de camadas inclinadas (cisalhamento anti-simétrico e momentos)?
- Existe diferença para a recuperação final entre orientar os pilares perpendicularmente à camada ou alinhá-los com a direção dos esforços in situ?
- Quais são as particularidades do dimensionamento de pilares em camadas inclinadas?
1.4 OBJETIVO DO ESTUDO.
O objetivo principal desta dissertação é dimensionar de maneira ótima pilares e vãos em camadas inclinadas, maximizando a recuperação resultante, ao mesmo tempo em que são respeitadas as restrições geotécnicas impostas pela resistência dos pilares e dos estratos sobrejacentes. Para tanto, será considerada a mecânica do contínuo generalizada de Cosserat (Cosserat & Cosserat, 1896, 1909 - apud Figueiredo, 1999), com a existência de carregamentos por cisalhamento anti-simétrico e momentos.
22
1.5 METODOLOGIA DO ESTUDO.
23
2 CAPÍTULO II
2.1 REVISÃO BIBLIOGRÁFICA
O dimensionamento de pilares e vãos numa lavra pelo método de câmara e pilares é um problema que concerne à mecânica das rochas aplicada. Existem alguns métodos consagrados, com embasamento racional e/ou empírico, que foram formulados originalmente para camadas sub-horizontais. A aplicação desses métodos ao projeto de pilares em camadas inclinadas fornece, entretanto, soluções inadequadas, já que a hipótese adotada para as cargas atuantes não tem abrangência suficiente para o problema de um pilar numa camada inclinada, na medida em que contemplam apenas a força axial (ou normal ao plano da camada). Nesse sentido, acredita-se que sejam requeridas teorias mais apropriadas, nas quais fiquem definidos não só a força axial, mas todos os esforços, tensões cisalhantes e momentos atuantes.
24
dos meios contínuos generalizados de Cosserat ao caso de camadas inclinadas, que é o tema central desta dissertação.
2.2 CONSIDERAÇÕES PARA O DIMENSIONAMENTO DE UM PILAR.
2.2.1 ESTADO DE TENSÕES IN SITU.
As tensões in situ são a causa primária das tensões atuantes em um pilar. A escavação do arranjo de lavra irá apenas concentrar tais tensões. Para estimá-las, faremos uso da hipótese básica de estimação, qual seja (Brady & Brown, 2004): a tensão vertical, σV, e a tensão horizontal, σH, são componentes principais; essa hipótese é válida para topografia plana e/ou profundidades elevadas. Abaixo se definem o valor dessas componentes principais (ver Fig. 1):
z
V
(1)
V H Kz K
(2)
onde é o peso específico médio das rochas sobrejacentes ao ponto considerado (Fig. 1); z a sua profundidade (Fig. 1) e K o valor da razão H/V (se K > 1, H é a tensão principal maior (1) e V é a tensão principal menor (3); se K < 1, V é a tensão principal maior (1) e H é a tensão principal menor (3))
Figura 1. Tensões principais in situ (Autor). Superfície
z
z
K z
V
H
25
z
1 1000
1 7 25 . 0
O valor de K deve ser estimado ou medido. Por exemplo, de acordo com a teoria de Sheorey (1994), pode-se estimá-lo como segue:
(3)
onde,
E é o Módulo de Young médio das rochas sobrejacentes em GPa e z é a profundidade dada em metros.
2.2.2 ÁREA TRIBUTÁRIA.
A teoria da área tributária (Brady & Brown, 2004; Pariseau, 2007 etc.) é um método simples, que permite determinar as tensões médias atuantes nos pilares com base em simples considerações de equilíbrio de forças na direção vertical (Brady & Brown, 2004). Para tanto, iguala-se o peso da coluna de rocha sobrejacente à reação vertical exercida sobre a área de influência (ou "tributária") do pilar (que abrange o próprio pilar e suas cercanias indo até a metade dos vãos adjacentes). A tensão média assim determinada é comparada com a resistência do pilar majorada por um fator de segurança, devendo ser inferior ou igual a essa última. Nos itens seguintes, será apresentado tal método e as respectivas fórmulas de cálculo que permitem dimensionar os pilares, sendo ainda tecidas algumas considerações sobre o comportamento dos mesmos e sobre o fator de segurança a ser adotado.
2.2.2.1CONSIDERAÇÕES SOBRE O MÉTODO DA ÁREA TRIBUTÁRIA.
26
TENSÕES ATUANTES RECUPERAÇÃO FATOR DE SEGURANÇA
p v At Ap v Z
R At At
Ap
R 1 WpL p Wo
R
Fs p
p : Tensão média no pilar v : Tensão vertical in situ At : Área total (área de influência) Ap : Área do pilar
R : Recuperação R : Resistência do Pilar
Wp : Largura do pilar L p : Comprimento do pilar Wo : Largura do vão L o : Comprimento do vão : Peso específico
Z : Profundidade da escavação
Wp Lo Lp
carregados (também em decorrência da hipótese de extensão infinita da área de lavra). Além disso, costuma-se assumir um valor de peso específico médio para as rochas sobrejacentes e uma profundidade uniforme para a camada lavrada.
O método da área tributária fornece uma tensão média no pilar (P) que é função da tensão vertical in situ (V, Eq. (1)) e da razão (At/Ap) da área de influência (ou tributária, At) pela área da seção resistente do pilar (Ap), a qual vem a ser a área de contato com o teto, a saber: P V
At/Ap
. A expressão resultante considera que opeso do prisma de rocha sobrejacente à área tributária (=V
At ) é equilibrado pela reação vertical gerada na seção resistente do pilar (=P
Ap ). Naturalmente, a resistência do pilar deverá ser igual ou maior que P (para efeito de projeto, considera-se, ainda, uma majoração da mesma pelos fatores de segurança). Para um maior entendimento da questão apresentamos a Fig. 2.No Quadro 1 apresentam-se as fórmulas de cálculo próprias do método da área tributária.
Quadro 1. Fórmulas para o dimensionamento de câmaras e pilares pelo método da área tributária.
27 p
t lavrada A A
A
t p t t lavrada
A A A A
A
t p t
lavrada
A A R
A
A
1
Wp
Lp
Wo
Lo
Area Lavrada
Area total
Lo/2
Wo
/2
Area do Pilar
Limite de lavra Limite
Wo Wp Wp
( Wo W )p Área do pilar
Área de influência (tributária)
Wo+
Wp
Wp
Wo+Wp
Wp
Figura 2. Arranjo sistemático de câmaras e pilares de seção quadrada: (a) adaptada de Hoek & Brown (1980); (b) caso de uma área de lavra limitada.
Da Fig. 2 pode-se concluir o seguinte:
(a)
28
) )(
( 1
P C P O
P P
L W W W
L W R
p t
P P O
A A R W
W W
1 1
2
Z
Wo/2
Wp
Wo/2
Wo/2: Metade do vão Wp : Comprimento do pilar Hp : Altura do pilar
Hp
Superfície
W
Pilar
Ponto A
Z : Altura da superfície até o ponto A
(4)
onde,
R = recuperação do minério. Quando WP = LP e WO = LO:
(5)
e
Daí vem que: p V/(1R) (Brady & Brown, 2004; Pariseau, 2007).
No que foi apresentado acima, considerou-se o caso básico da teoria da área tributária, para camada sub-horizontal, em que apenas atua uma tensão normal à seção resistente do pilar. Na Fig. 3 pode-se visualizar o caso de uma camada inclinada, em que atuam no pilar também uma tensão cisalhante anti-simétrica (a
H'V'V'H'
/2, com H'V' 0) e um momento (M) por unidade de área (tensão-momento), Cosserat & Cosserat (1896 - apud Figueiredo, 1999). O efeito do carregamento por essas novas tensões constitui ponto central do tema desta tese e será abordado mais adiante.Figura 3. Pilar numa camada inclinada sujeito a tensões cisalhantes antissimétricas e tensões-momento.
2 2
) (
1
P O
P W W
W R
Ponto A
M
Região de compressão
Região de tração
a
p V'
p
Momento gerado por; -Esforços anti-simétricos -Diferenças de altura H'V'
M :
Pilar
29
P P C
R
H W
22 . 0 78 . 0
1
2.2.3 EFEITO DA FORMA DO PILAR.
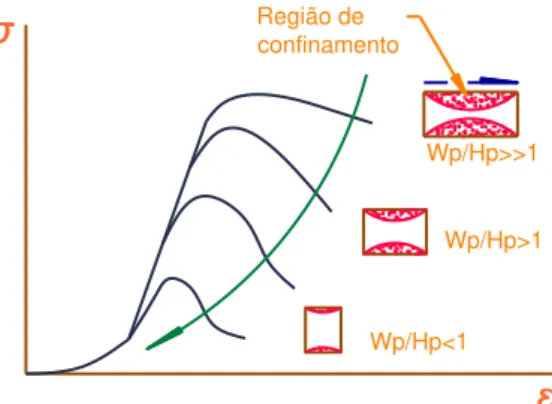
Para entender o efeito da forma (esbelteza) do pilar sobre a sua resistência é interessante fazer uma analogia com um corpo de prova de laboratório. Um pilar de mina carregado pelo peso da rocha sobrejacente, embora de seção resistente quadrada, é submetido a condições semelhantes àquelas verificadas no carregamento axial aplicado por uma prensa ao corpo de prova. E se sabe experimentalmente, que a resistência à compressão uniaxial de um corpo de prova depende da sua razão altura/diâmetro ou esbelteza (Obert & Duvall, 1967).
Nos contatos pilar-teto e pilar-base existem zonas nas quais ocorre uma restrição à livre deformação transversal, devido à resistência ao cisalhamento ali disponível; exatamente como ocorre entre topo e base do corpo de prova e os pratos da prensa. O resultado dessa restrição é o aparecimento de tensões confinantes nas proximidades dos contatos pilar-teto e pilar-base, que serão tão mais abrangentes quanto maior for a razão largura/altura do pilar (= WP/HP) ou, o que dá no mesmo, quanto menos esbelto for o
pilar (Fig. 4). Em decorrência da influência desse confinamento gerado pela resistência ao cisalhamento, quanto menor for a esbeltez WP/HP, maior será a resistência do pilar
(Fig. 4).
A Eq. (6), abaixo, estabelecida empiricamente por Obert & Duvall (1967), permite relacionar a resistência de um corpo de prova à sua esbeltez e, em função da analogia suprareferida, pode ser também aplicada a pilares. A equação de Obert & Duvall que governa o efeito da forma é:
(6)
onde,
WP é a largura do pilar;
30
1
C
é a resistência à compressão uniaxial para uma razão WP/HP = 1 (ou seja, para um
cubo do maciço rochoso que constitui o pilar) e
é a resistência de um pilar com esbeltez igual a WP/HP.
É oportuno observar que a Eq. (6) tem um embasamento racional, como mostrou Pariseau (2007), pags. 281 a 284. Esse autor admitiu que a resistência ao cisalhamento no teto e base do pilar seja governada pelo critério de Mohr-Coulomb. Assumindo, por outro lado, que a ruptura se dê por um mecanismo de clivagem axial e igualando a tensão necessária para produzi-la à tensão gerada pela resistência ao cisalhamento no teto e base, chega-se exatamente a uma expressão com o formato da Eq. (6) de Obert & Duvall.
A Fig. 4, a seguir, apresenta como o aspecto das curvas tensão x deformação e a resistência variam com a esbeltez do pilar, analogamente ao que ocorre com corpos de prova em ensaios de compressão uniaxial. Deduz-se que há uma ruptura frágil com baixa resistência quando Wp/Hp é menor que 1. Se a relação Wp/Hp for maior que 1, a
resistência aumenta e a ruptura tende a ser dúctil, refletindo uma maior influência do confinamento nas extremidades.
Wp/Hp
Região de confinamento
Wp/Hp<1 Wp/Hp>1 Wp/Hp>>1
Figura 4. Curvas tensão x deformação: analogia entre os comportamentos de corpo de prova em compressão uniaxial e pilares de mina (adaptada de Hudson & Harrison, 1997).
Existem ainda outros tipos de fórmulas para contemplar o efeito da forma do pilar sobre a sua resistência (ver, p. ex., Figueiredo & Curi, 2004; Brady & Brown, 2004 etc.). A seguir, um quadro resumo traz exemplos de fórmulas dos dois tipos principais.
R
31
AUTOR EQUAÇÃO
Obert & Duvall 1967
r 0.778 0.222 Wp Hp c
1
TIPO DE PESQUISA
Laboratório c
1
: Resistência à compressão quando Wp:Hp é 1
Salomon & Munro 1967
r : Resistência máxima do pilar
c Wp Hp
0.46 0.66 r
r : Resistência máxima do pilar
In situ
Quadro 2. Fórmulas para se determinar a resistência do pilar, conforme o efeito de forma.
2.2.4 ANÁLISE BIDIMENSIONAL DO ESTADO DE TENSÕES E TENSÕES-MOMENTO PARA MEIOS CONTÍNUOS GENERALIZADOS DE COSSERAT.
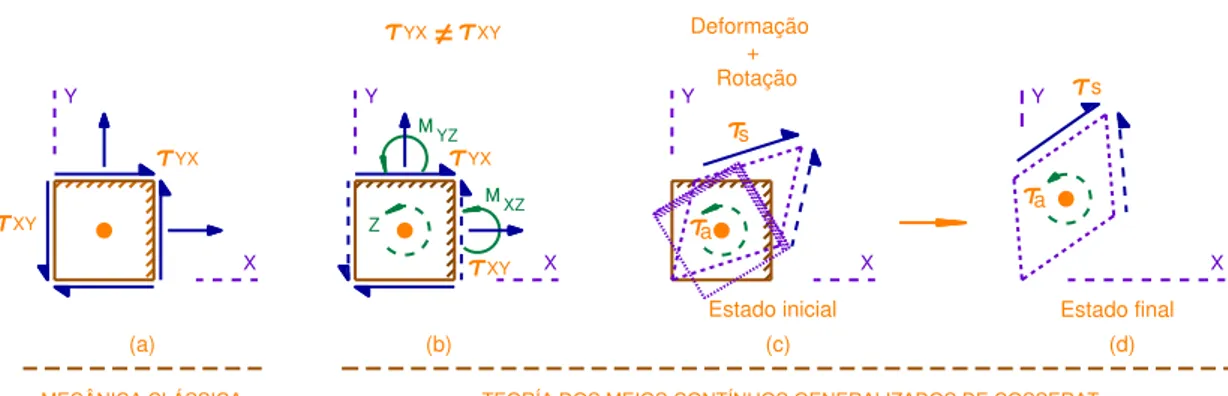
Na mecânica clássica, em qualquer plano, atuam tensões normais e cisalhantes (Fig. 5(a)), as quais podem ser determinadas a partir de um tensor de tensões simétrico (Jaeger & Cook, 1979). Porém, se as tensões cisalhantes não forem conjugadas, isto é, se não forem iguais em planos perpendiculares entre si (Fig. 5(b)), além do tensor de tensões simétrico, existirá uma parcela antissimétrica (associada justamente à diferença entre as tensões cisalhantes) que gera momentos desequilibrados. Tal desequilíbrio é contrabalançado pelo aparecimento de novas grandezas denominadas tensões-momento (momentos por área), Fig. 5(b). Isso é justamente o que sucede na mecânica dos meios contínuos generalizados de Cosserat (Cosserat & Cosserat, 1896 apud Figueiredo, 1999).
32
Y
X yx
xy yx xy y
x
(a)
Z Y
X yx
xy
yx xy
y
x
(b)
MYZ
MXZ
X
yy
xx x'y'
x'y' xy
yx Y
X' Y'
Myz Mxz
Mx'z
Acos
Asen
A
Ponto O
O'
OO' : Asen cos
X
yy xx
x'y'
yx Y
X'
Myz
Mx'z A
Ponto O
O'
Aco
s 2
Asen 2 Mxz
OO' : Asen cos Y'
(c) (d)
horário são positivas (Figueiredo, 2011). A análise bidimensional do estado de tensões permite determinar as tensões num plano qualquer, cujo eixo normal (x') faça um ângulo
α medido em sentido anti-horário a partir do eixo x positivo. Para tanto, basta aplicar ao ponto as condições de equilíbrio de forças e de momentos (Figueiredo, 1999, 2011). Para ilustrar o efeito das tensões de cisalhamento não conjugadas na deformação do ponto citamos a Fig, 6, que mostra a parcela simétrica das tensões cisalhantes (S (xy yx)/2) produzindo as distorções angulares clássicas, enquanto a parcela
antissimétrica (a (xyyx)/2) gera uma rotação. O efeito final é dado pela
superposição de ambas as parcelas.
33
TIPO EQUAÇÕES
Tensões 2D
Tensões Momento 2D
x' x cos2 y sen2 xy yx sen cos y' x sen2 y cos2 xy yx sen cos x'y' xycos2 yxsen2 x y sen cos
M x'z M xzcos M yzsen A y sen 2 2
x cos2
2 asen cos
Teoría
dos meios cont
ínuos
generalizad
os
d
e Cos
ser
at
O Quadro 3 apresenta um resumo das equações que podem ser deduzidas por equilíbrio de forças e momentos a partir da Fig. 5(a)-(b). Tais equações são explicadas no ANEXO A.
XY
YX
Y
X
Y
X
s Deformação
+ Rotação
Estado inicial Estado final
Z
Y
X Y
X
MECÂNICA CLÁSSICA TEORÍA DOS MEIOS CONTÍNUOS GENERALIZADOS DE COSSERAT YX
(a) (b) (c) (d)
YX XY
a s
a
XY MYZ
M XZ
Figura 6. Efeito das tensões de cisalhamento não simétricas de Cosserat: τS produz distorções
angulares e τa produz rotação (adaptada de Mindlin, 1963).
Quadro 3. Fórmulas para se determinar as tensões e tensões-momento num dado plano (adaptada de Figueiredo, 2011) - Equações de Transformação. Obs.: ver Fig. 5 para significado dos símbolos.
2.2.5 CÍRCULO DE MOHR CLÁSSICO PARA UM ESTADO DE TENSÕES 2D.
34 t
n nt 3
n 1
1
vem a ser um círculo cujo centro fica sobre o eixo das abscissas (). As tensões em planos perpendiculares entre si ficam representadas pelas coordenadas de pontos
diametralmente opostos do círculo, que têm ordenadas (τ) de mesmo valor. A Fig. 7 ilustra tal círculo, conhecido por Círculo de Mohr (Jaeger & Cook, 1979; Goodman, 1989; Brady & Brown, 2004 etc.), considerando a convenção de sinais da mecânica das rochas (compressão positiva).
Figura 7. Círculo de Mohr clássico (Figueiredo, 2014).
2.2.5.1 APRESENTAÇÃO NÃO-CLÁSSICA DO ESTADO DE TENSÕES DUM PILAR NO ESPAÇO DE MOHR
Das equações apresentadas no Quadro 3 para um meio com tensões de cisalhamento não conjugadas pode-se deduzir a equação de um círculo no espaço de Mohr, análoga àquela apresentada no item precedente. Para um plano genérico, como X' da Fig. 3(c), em que, por conveniência, optou-se por denominar as tensões atuantes de α e τα,
tem-se:
2 2
2 2
2 2
2
2
Y X XY YX Y X YX XY
cos2
2 2
3 1 3
1
n
sen2
2
1 3
nt
2 3 1 2 2 3
1 )
2 ( )
2
(
C 1 ( )
n ( )n,
N nt
nt
0 ( )
3, 3
( )t, nt T
+
1 3
2
1 3
2 AH
H
35 2
a P
2 P S 2 2 2 2 2 0 2 0 2 0 2 0
P P P P
2 2 2 2 2 2 2
2
P P P P
Pode-se igualmente aplicar a equação acima para um sistema de eixos ortogonais H’V’
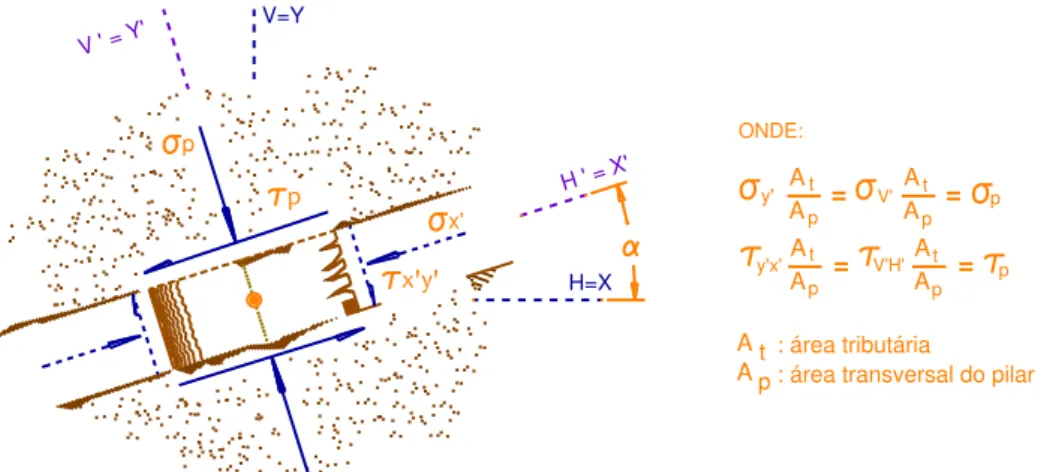
associado ao pilar duma camada inclinada, como aquele apresentado nas figuras 3 e 8. Nesse caso, os valores de σY’ e τY’X’ corresponderiam, respectivamente, a V' e τV'H'. Essas são as componentes que "carregam" o topo do pilar e, por isso, aqui vamos denominá-las de “σP” e “τP” uma vez afetadas pela razão “AT/AP” (ver Fig. 8). Já os
valores de σX’e τX’Y’ correspondem, respectivamente, a H'e τH'V'.O plano H' da face do pilar, por ser uma superfície livre onde não existe sólido, tem tensões nulas. Assim sendo, pode-se finalmente reescrever a equação precedente como:
ou
(7)
A Eq. (7) representa uma circunferência no espaço de Mohr, com centro de coordenadas (σP/2; -τP/2) - ver Fig. 9 -, fora, portanto, do eixo dos , como no caso do círculo clássico da Fig. 7. Tal círculo ilustra o estado de tensões dum pilar numa camada inclinada como o da Fig. 8. Tendo em vista as definições para as parcelas simétrica (τS) e antissimétrica (τa) das tensões cisalhantes (dadas no subitem 2.2.4), tem-se que:
;parcela que provoca distorções angulares.
; parcela que provoca rotações.
O raio do círculo, por sua vez, vale: . 2
2
2
2
36
Figura 8. Pilar numa camada inclinada submetida a tensões de compressão e de cisalhamento não conjugadas.
Segundo a convenção de sinais da mecânica de rochas, o momento produzido por τa é positivo quando produz uma rotação no sentido horário. Observamos na Fig. 8 que o valor da tensão de cisalhamento antissimétrica gerada pelo carregamento do pilar é negativo, indicando que o pilar gira em sentido anti-horário. Pariseau (1982) (apud Pariseau, 2007) mostrou que, pela teoria da área tributária (item 2.2.2), duma maneira análoga ao que acontece com P (Fig. 8), o valor de τP equivaleria a τV’H’(AT/AP).
Pelo acima exposto, fica perceptível que o estado de tensões em pilares de camadas inclinadas pode ser descrito pela mecânica generalizada de Cosserat (item 2.2.4), uma vez que neles atuam tensões de cisalhamento não conjugadas.
Na seqüência apresenta-se o respectivo círculo de Mohr não-clássico (dado pela Eq. (7)), válido para o pilar da Fig. 8, no qual atua a tensão de cisalhamento antissimétrica
(τa) devida a uma τP não conjugada.
p
x'
p
x'y' V ' = Y'
H ' = X'
H=X V=Y
V'H' y'x'
y' V' p
p
At : área tributária
Ap : área transversal do pilar Ap
At
Ap At
Ap At
37
( y' y'x')
(
x' x'y')
p
p Ccos
C
R' R'sen
AH
H R'=Rc=raio do círculo grande
Figura 9. Apresentação do Círculo de Mohr não-clássico para pilares em camadas inclinadas (modificado de Pariseau, 2007).
38 ' ' ' ' ' ' arctan arctan arctan V H V y x y p p
Fig. 9 está ilustrado um círculo de ruptura, em linha tracejada, para o qual houve tanto um aumento do diâmetro quanto da ordenada do centro.
Pariseau (2007) realizou a análise dessa possível condição de ruptura, que o levou a formular uma equação para o Fator de Segurança do pilar, senão vejamos (Fig. 9):
- , raio do círculo pequeno, em linha cheia, que representa o estado de tensão atuante no pilar;
- , raio do círculo grande, em linha tracejada, que representa o círculo na condição de ruptura, ou seja, aquele cujo estado de tensão equivale à resistência;
- o Fs (Fator de Segurança) é então dado pela razão resistência/(tensão atuante), ou seja,
. (8)
Na Eq. (8) corresponde ao ângulo de inclinação da linha onde se situam os centros dos círculos não-clássicos ilustrados na Fig. 9 e é dado por:
2.2.6 OUTRAS PARTICULARIDADES EM UMA AVALIAÇÃO DE PILARES.
2.2.6.1 PILARES ALINHADOS COM A FORÇA RESULTANTE.
Num pilar inclinado submetido a tensões σVe σH atua uma força resultante cuja direção não é, em geral, perpendicular ao eixo H’, ou seja, ao topo do pilar. Considerando-se a Fig. 10, no ponto A, atuam as forças concorrentes FV e FH que estão associadas às tensões σVe σH, respectivamente. A direção da força resultante “FR” faz um ângulo “β” com o eixo normal à camada (topo do pilar). Troumbatchev & Mel'nikov (1964),
2 2
2 2
pequeno p p
círculo
Raio
1 senccos
Raiocírculogrande
39
mostraram por meio de modelos fotoelásticos, que, em se alinhando a direção das paredes do pilar com a direção de FR, são reduzidas as concentrações de tensões e as mesmas se tornam mais uniformes. Dessa forma, consegue-se aproveitar ao máximo a capacidade resistente da seção pilar. Para que o pilar fique alinhado com o modulo dessa força resultante, suas paredes devem ser inclinadas de “β” no sentido horário, tomando-se como referência o eixo V’ (ver Fig. 10).
FR FH
FV
Pilar alinhado com a força resultante
M
D' A'
B'
D
E
B
C
Pilar normal à camada Wp
Wo (Wo+Wp)cos
(W
o+W
p)
se
n
A V
H
H V
m n
MB : Hp MA' : Hp cos
A : Ponto meio de A'B'
MD : Wp
H' V'
MD' : Wp cos
FR : Força resultante
Figura 10. Pilar inclinado em relação ao eixo perpendicular à camada.
Uma análise da geometria contemplada na Fig. 10 permite deduzir que a orientação
ótima é dada pela Eq. (9) abaixo:
tan
cos sen cos
sen
tan
P O V
P O V
P O V
P O H
V H
W W
W W W
W W W F
F
tan1tan
40 A V H' FV FH V'
F coV s F seV n
H
F coH s F seH n
FR
Plano da ca mada
2 2 2 2 2
2
2 cos cos
sen W W sen W W W W F F
FR V H V O P V O P O P
sen sen cos cos
onde é o mergulho; K é a razão (tensão horizontal)/(tensão vertical) in situ definida no item 2.2.1; WOWPsen e WOWPcos são as projeções vertical e horizontal, respectivamente, da área tributária do pilar.
Quando a diferença “-β” for positiva, o valor do ângulo “β” deverá ser medida segundo o sentido horário a partir do eixo V’; o contrário sucede se “-β” for negativa.
Figura 11. Força resultante FR e suas componentes ortogonais FH e FV (Autor).
Das figs. 10 e 11 têm-se ainda que (Oyangüren et al., 1984):
(9)
onde:
tan tan
cos sen cos sen
cos tan cos
cos sen
sen
cos2 tan cos2
O P
R W W
F
cos cos tan 1 cos tan 1cos2 2 2 O P
41
H=x
m
Plano da cama da
Ponto A
R R
R
F
F sen
F cos
A'
B'
Pilar inclinado em um ângulo
V' = y'
H' = x'
no sentido horário do eixo V' =y' A''
Por conseguinte a força resultante pode ser escrita como (Troumbatchev & Mel'nikov, 1964):
Daí, considerando-se a área do pilar e as componentes de FR segundo as direções normal e paralela ao topo (Fig. 12), pode-se obter, respectivamente, as tensões médias, normal (P) e cisalhante (τP), que ficam dadas por (note-se que se está considerando pilares 2D, ou seja, bastante alongados perpendicularmente ao plano de análise):
(11)
(12)
Figura 12. Força resultante FR e suas componentes ortogonais segundo H’-V’ (Autor).
É interessante observar que, diferentemente do que sucedia com os pilares perpendiculares à camada, discutidos no item 2.2.5 (ver figs. 8 e 9), em pilares alinhados com a força resultante, as tensões no plano H'V' não são nulas (Fig. 13). Isso, naturalmente, vai se refletir no círculo de Mohr não-clássico correspondente ao estado de tensões no pilar (como aquele da Fig. 9), alterando seu raio e a posição do centro. Conseqüentemente, o seu fator de segurança tenderá a ser mais favorável que aquele dado pela Eq. (10).
sen sen P O R
W W F
sen
sen sen
P P O P
W W W
cos
sen sen
P P O P
42
m n
j
ângulo de atrito: j
Pilar
m n
X' Y'
Teto
Chão p
p
Pilar submetido às tensões médias devidas ao carregamento da rocha sobrejacente
Tensões no plano de fraqueza ("m")
A'
A'' H'V' V'
A' - A'' H'
H H' Pilar inclinado
Mergulho da camada
H'V' Cisalhante no plano H'V' - (diferente de zero) Seção
K'
K
Figura 13. Tensões no plano H’-V’ para um pilar alinhado com a força resultante (Autor e
Figueiredo).
2.2.6.2 PILARES NORMAIS À CAMADA E COM PLANOS DE FRAQUEZA.
Numa situação real, podem existir planos de fraqueza (descontinuidades) atravessando o pilar. Em tais condições, deve-se considerar a possibilidade de deslizamento sobre tais planos para avaliar, de maneira mais realista, a respectiva resistência. Independentemente do sentido de mergulho do plano de fraqueza, seja no mesmo sentido do mergulho da camada ou inverso, há uma faixa de valores de mergulho em que poderá ocorrer deslizamento sobre o plano. Nas nossas análises vamos considerar o critério de resistência de Mohr-Coulomb para o plano. Seja
cja coesão do plano e j seu ângulo de atrito.
43
Segundo as equações de transformação para um meio de Cosserat (Quadro 3), as tensões no plano de fraqueza são:
(13)
(14)
onde αj é a inclinação do plano em relação ao mergulho α da camada (ver Fig. 14). Substituindo as componentes acima na expressão do critério de Mohr-Coulomb, a resistência ao escorregamento no plano “m” pode ser escrita em função das componentes σp e τp, senão vejamos:
(15)
Se o valor de τnm for maior ou igual a τresistência o pilar rompe por escorregamento no plano e vice-versa. Isso permite encontrar a faixa de ângulos do plano que instabilizam o pilar, senão vejamos:
j j j P j j P j j j j j j j P j j P j j j P j P j j P j P c c cos sen 2 ) 2 ( sen cos sen 2 ) 2 cos( 2 1 cos cos cos cos 2 ) 2 ( sen cos cos 2 ) 2 cos( 2 1 tan 2 ) 2 ( sen cos 2 ) 2 ( sen
cos2 2
Rearranjando a expressão vem que:
j j j P j P j j P j j
P c
sen(2 ) cos(2 ) sen cos 2 cos (16)
Conhecidos os valores de τp, σp,cj, αj e j, existe uma faixa de valores de “2αjj”, que
é solução da desigualdade; essa faixa corresponde àqueles ângulos do plano em que ocorrerá escorregamentos; quando houver igualdade ter-se-á um escorregamento iminente (equilíbrio-limite). É oportuno observar que a Eq. (16) generaliza os conceitos apresentados por Pariseau (2007) - pag. 311 (Eq. (6.45)) - que não considerou o efeito de τP no estado de tensões que induz escorregamento sobre os planos.
2 ) 2 ( sen
cos2 P j
j P n ) 2 ) 2 ( sen cos
( P 2 j P j
nm j j P j P j a
resistênci c
tan 2 ) 2 ( sen
cos2
44
A B
P d
d
P2
1
Y
X
x dx
y
dy
ds
R
2.2.7 RESTRIÇÕES NO DIMENSIONAMENTO DE CÂMARAS E PILARES
No dimensionamento ótimo de câmaras e pilares via técnicas de programação matemática, como proposto por Figueiredo & Curi (2003, 2204), faz-se necessário estabelecer o limite máximo dos vãos, bem como, a capacidade de carga das fundações dos pilares. Essas duas questões limitam a recuperação do jazimento e, portanto, devem ser consideradas como restrições na formulação do problema de programação matemática em causa. A colocação dessas questões limitantes na forma de restrições matemáticas (desigualdades) pode ser feita recorrendo-se a diferentes formulações analíticas/empíricas para a mecânica dos processos envolvidos. Na seqüência serão abordadas brevemente as formulações adotadas nesta dissertação.
2.2.7.1 FLEXÃO PURA EM VIGAS E LAJES.
Para limitar os vãos máximos estáveis das câmaras pode-se considerar que os estratos sobrejacentes à camada lavrada se comportem como lajes ou vigas elásticas sujeitas à ação do peso próprio (p.ex., ver Obert & Duval, 1967; Jaeger & Cook, 1979; Pariseau, 2007 etc.). Para explicar a flexão que acontece em uma laje, vamos supor um comportamento de uma viga. Existem equações que governam o estado de equilíbrio de vigas submetidas a cargas por flexão pura e devido a seu próprio peso. Em uma mina, existem situações semelhantes, em que, podem ser assumidas as lajes como um arranjo de vigas; ver a figura15.
45
CG M
R
1
M dx
y
d
22
dy
dl
P
y
dy Wo Corpo rochoso de
largura unitária
t
Espessura
Wo-y
(17)
onde:
R : raio de curvatura; M : momento máximo; E : módulo de Young;
ICG: momento de inércia com relação ao centro de gravidade da seção.
Assim também a relação de raio de curvatura é equivalente a uma função de momento que é fornecida pela seguinte equação.
(18) As equações 17 e 18 são explicadas no ANEXO B.
2.2.7.2 TENSÕES DEVIDO AO PESO PRÓPRIO DA LAJE.
Uma coluna de rocha com seção transversal quadrada está submetida a esforços de compressão axial devido ao seu próprio peso e, tem uma variação na sua dimensão inicial (WO) (Coates, 1973). Considerando uma altura dy de magnitudes infinitesimais, a
qual possui uma deformação diferencial dl. Então, a deformação unitária correspondente é dl/dy. Na figura 16, pode-se perceber que o valor P é o esforço associado a essa deformação, cujo valor fica definido por γ(WO-y).
46
W y dy
dl
o
W ydy
dl o
0
0
W
o ydy W
dl
2
2 Wo
l
Pilar
Zona de possível
plastificação Wp
Pela lei de Hooke:
. (19)
onde:
l: deformação total no corpo rochoso de altura WO e comprimento t.
2.2.8 CAPACIDADE DE CARGA DAS FUNDAÇÕES DOS PILARES
A capacidade de carga das fundações dos pilares (ou seja, a resistência do piso), principalmente daqueles pouco esbeltos e, portanto, de alta resistência é um fator importante na sua estabilidade (Figueiredo & Curi, 2004). Independentemente da resistência do pilar, a pressão transmitida à sua fundação deverá ser menor que a respectiva capacidade de carga, evitando, assim, o seu colapso por "puncionamento" do piso (Fig. 17).
Figura 17. Mecanismo de colapso da fundação de um pilar (Brady & Brown, 2004).
47
1 cot
2 4 tan tan
1 2 4 tan 2
3 2
1 tan 2 tan 2
W e S cS e
Qb P q
Num dimensionamento ótimo, deverá, portanto, ser sempre respeitada a restrição de que a tensão média atuante no pilar seja menor que a capacidade de carga (Figueiredo & Curi, 2004). Para cálculo da capacidade de carga da fundação, Brady & Brown (2004) recomendam utilizar a expressão clássica aplicável a fundações rasas proposta por Terzaghi, qual seja:
(20)
onde,
Qb é a capacidade de carga da fundação em unidades de força/área; é o ângulo de atrito da rocha da fundação;
c é a coesão da rocha da fundação;
γé o peso específico da rocha da fundação; WP é a largura do pilar;
Sγ = 1.0 0.4(WP/LP) e Sq = 1.0 + sen(WP/LP), com LP sendo o comprimento do pilar;
48
3 CAPÍTULO III
3.1 DIMENSIONAMENTO ÓTIMO DE PILARES DE SEÇÃO QUADRADA.
No dimensionamento ótimo de pilares deve-se determinar a seção resistente que permite maximizar a função recuperação para o jazigo (Eq. 5). A resistência do pilar (Eq. 6) depende da relação de sua esbelteza enquanto a tensão resultante aplicada ao pilar depende de várias tensões associadas que atuam conjuntamente, as quais são expressadas por equações em função de variáveis e parâmetros geomecânicos. Neste estudo foram desenvolvidos algoritmos que permitem avaliar as equações matemáticas que representam o estado das tensões que atuam no pilar, lajes e fundações, sendo que; o objetivo é maximizar a recuperação do jazigo, como já supracitado. Para um dimensionamento ótimo é necessário aplicar teorias apropriadas, no qual estejam consideradas todas variáveis que definem o modelo que melhor se ajuste ao problema real; um pilar disposto de maneira perpendicular à camada inclinada tem a particularidade de estar submetido a tensões normais, cisalhantes e tensões momento (Figueiredo, 2011), sendo que, o aparecimento das tensões momento são resposta à tensão anti-simétrica (τa) que produz rotação no pilar e sua parcela tensão simétrica (τS) responsável pela deformação conforme definido no item 2.2.4; esta nova condição de desequilíbrio não poderia ser resolvida pela mecânica clássica, entanto, a tensão-momento (tensão-momento de reação do pilar para equilibrar o sistema) está bem definida na mecânica de Cosserat e, por tanto, sua aplicação se adapta ao tipo de estudo proposto nesta dissertação. A seguir, apresentam-se as análises a serem desenvolvidos no pilar.
- Área tributária (fig. 2); - Efeito da forma (fig. 4);
- Análise das tensões e tensões-momento (fig. 5(c) e 5(d)); - Análises de tensões efetivas (fig. 3 e 8);
- Análise da resistência das fundações;
49
W
S
Camada de minério
Futuro pilar
S'
TENSÕES A SEREM ENCONTRADAS
H'
V' A
Superfície
H V'
V'H' H'
S'
TENSÕES IN SITU
H'
V' A
Superfície
H H
V W
S
Camada de minério Futuro pilar
(b) (a)
3.1.1 ÁREA TRIBUTÁRIA PARA UM PILAR EM CAMADA INCLINADA.
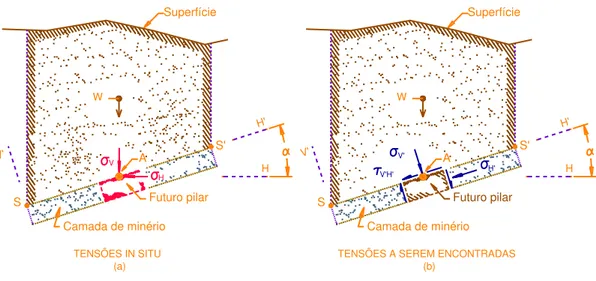
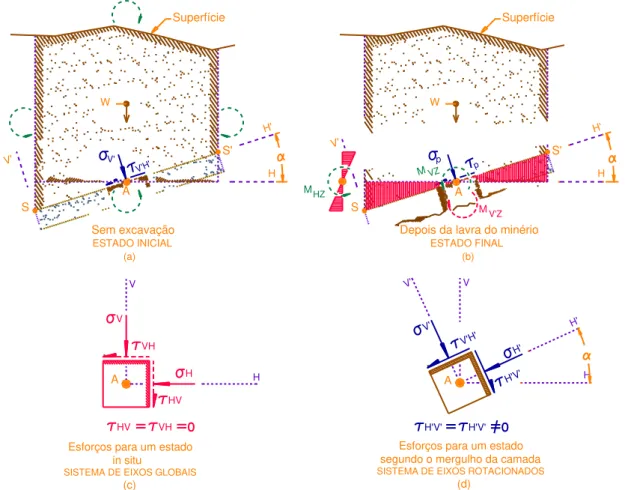
3.1.1.1 ESFORÇOS E TENSÕES IN SITU.
Conforme já supracitado no item 2.2.1, as tensões in situ “σV” (x) e “σH” (y) (considerando os eixos H e V como eixos globais X e Y respectivamente) atuam em planos perpendiculares conforme a Fig. 1 e Fig. 18 (a); por outro lado, a fim de simplificar o problema pressupõe-se que σV e σH são tensões principais, então, utilizando-se as equações de transformação (quadro 3) se obtém as tensões “σV’” e “σH’”
(Fig 18 (b)), cujos valores são funções do peso específico médio da rocha sobrejacente
m e da profundidade
Z . Na camada inclinada haverá futuramente um pilar disposto de maneira perpendicular em relação a mesma, necessitando, por isso, determinar os valores das tensões que atuarão no topo deste pilar.Figura 18. Tensões in situ em eixos HV e tensões in situ em um plano H’V’ (Autor).
3.1.1.2 TENSÕES QUE ATUAM NO PILAR.
50
2
2 1 2
2
'
'H H V sen sen
V
cos2 cos2 2
2 2
' V H V H sen
V
(a) (b)
p
V'H' p
W
S
S'
Depois da lavra do minério
H' V'
A
Superfície
H
ESTADO FINAL MV'Z
MVZ
MHZ
ESTADO INICIAL
H
Superfície
A
V'
H'
S'
S
W
V'
Sem excavação
conforme a Fig. 19 (a), a tensão normal (σV’) e a tensão cisalhante (τV’H’) atuam no topo
do “pre-pilar” (ponto A), estas tensões são apenas magnitudes que são estimadas com as equações de transformação apresentadas no quadro 3; após escavação (Fig. 19 (b)) , o pilar ficara carregado num fator “At/Ap” conforme discutido no item 2.2.2.1 . As figuras 19 (c) e 19 (d) detalham o estado de tensões in situ e tensões que agem na interface entre a rocha sobrejacente e o topo do futuro pilar respectivamente.
Figura 19. Situação do pilar submetido a esforços num plano HV e H’V’(Autor e Figueiredo).
Conhecidos σV e σH e considerando-os como tensões principais, pode se encontrar os valores de σV’ e σH’ da seguinte maneira:
(21)
(22)
V
H
A
VH
HV
V
H
HV VH
Esforços para um estado in situ
Esfo segu
SISTEMA DE EIXOS GLOBAIS
(c)
SIS
V'
H'
A
V'H'
H'V'
V'
H'
V
H
H'V' H'V'
Esforços para um estado segundo o mergulho da camada