219 REnCiMa, v. 11, n.1, p. 219-236, 2020 doi.org/10.26843/rencima eISSN: 2179-426X
PADRÕES E O TRABALHO COM SEQUÊNCIAS RECURSIVAS: UMA
ABORDAGEM NO DESENVOLVIMENTO DO PENSAMENTO ALGÉBRICO
PATTERNS AND WORK WITH RECURSIVE SEQUENCES: AN APPROACH TO THE DEVELOPMENT OF ALGERIAN THOUGHT
Ronaldo Theodorovski
Universidade Estadual do Centro-Oeste – Campus Irati, theodorovski@unicentro.br http://orcid.org/0000-0001-5522-2100
Fabiane Oliveira
Universidade Estadual de Ponta Grossa, faboliveira@uepg.br http://orcid.org/0000-0002-9187-3629
Resumo
Este trabalho tem por objetivo apresentar propostas pedagógicas para o ensino da álgebra tendo em vista promover o desenvolvimento do pensamento algébrico dos alunos. Para tanto foi realizado um levantamento bibliográfico buscando trabalhos que demonstram que tal objetivo pode ser alcançado por meio de um ensino que prioriza o reconhecimento e a generalização de padrões matemáticos. Para contemplar o Ensino Médio, deram-se destaques às sequências definidas recursivamente, que se revelam como um bom ponto de partida para a generalização de padrões. Além disso, com o estudo de recorrências matemática, é possível propor uma abordagem alternativa para o ensino de progressões. Buscando trabalhar com regularidades numéricas para descrever e generalizar relações, sugere-se a utilização das questões da Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP), por meio da resolução de problemas, como proposta metodológica no ensino da álgebra.
Palavras-chave: pensamento algébrico, padrões, sequências recursivas, OBMEP. Abstract
This paper aims to present educational proposals for the teaching of algebra in order to promote the development of students' algebraic thinking. To do so a bibliographical survey searching for papers that demonstrate that such goal can be achieved through an education that prioritizes the recognition and the generalization of mathematical patterns was conducted. To address high school, we highlighted the sequences defined recursively, which appear as a good starting point for the generalization of patterns. moreover, with the study of recurrences mathematics, it is possible to propose an
220 REnCiMa, v. 11, n.1, p. 219-236, 2020 alternative approach to teaching progressions. Seeking to work with numerical regularities to describe and generalize relations, we suggest the use of the questions of the Brazilian Olympiad of Mathematics of Public Schools (OBMEP), by solving problems, as a methodological proposal in the teaching of algebra.
Keywords: algebraic thinking, patterns, recursive sequences, OBMEP.
Introdução
Em diversas situações a matemática pode ser vista como uma ciência constituída por padrões (DEVLIN, 2002). Desde a antiguidade, matemáticos buscam regularidades em sequências, expressas por números ou figuras. Por exemplo, na natureza existem fenômenos que fluem com certa regularidade tal que, se for identificada, será possível fazer previsões e formular conjecturas. O reconhecimento de padrões em diversas situações reais, muitas vezes, leva a novas e importantes ideias.
Uma alternativa viável para diversificação das estratégias docentes é a utilização do estudo de padrões nas aulas de matemática, principalmente no ensino da álgebra. Pesquisadores da Educação Matemática como Vale e Pimentel (2005), são favoráveis ao seu uso na sala de aula, porque além de ser uma estratégia que se torna o ensino mais interessante, a busca por regularidades, induz ao aluno a realizar descobertas, investigações matemáticas realizando generalizações com números.
Entretanto, ao trabalhar com atividades envolvendo padrões matemáticos e generalizações, acredita-se que por meio dessa abordagem despertará a curiosidade e o interesse dos alunos por essa disciplina, pois tem como critério central a contextualização entre os diferentes tópicos da matemática. A construção dessas generalizações e de suas respectivas representações permite a aproximação do conhecimento matemático, possibilitando que os estudantes possam atribuir sentido e compreensão da álgebra e ao uso da linguagem algébrica.
Nessa perspectiva será desenvolvida uma abordagem metodológica de caráter qualitativo a fim de apresentar uma proposta de estudo sobre recorrências lineares como alternativas no processo de ensino e aprendizagem da álgebra. Na formulação da problemática de pesquisa a seguinte questão foi levantada: O conteúdo de recorrências lineares permitirá ao professor propor atividades exploratório-investigativas a fim de levar os alunos a mobilizar os aspectos do pensamento algébrico?
É por essa razão que neste artigo tem como objetivo apresentar métodos de resolução de recorrências lineares para a construção de uma fórmula para o termo geral de sequências recursivas e modelar problemas usando recorrências lineares, haja visto que as relações de recorrência matemática, normalmente não são abordadas nos currículos da Educação Básica. Ainda, destaca-se como finalidade deste trabalho, abordar o cálculo do termo geral de uma progressão aritmética e geométrica por meio da utilização de recorrências lineares de primeira ordem. Sendo assim, com essa proposta
221 REnCiMa, v. 11, n.1, p. 219-236, 2020 de conteúdo, está se ampliando o horizonte dos alunos na forma de observar e generalizar padrões.
Portanto, como instrumento de análise, serão apresentados problemas matemáticos que requerem o uso de padrões numéricos na sua resolução. No entanto, optou-se em selecionar três questões das provas anteriores da Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP), porque permitem a exploração de padrões em sequências numéricas que levem os alunos a fazer generalizações e compreender, por um processo de resolução de sequências recursivas, a natureza das representações algébricas.
Referencial teórico
A seguir será apresentado a revisão bibliográfica e o referencial teórico utilizado na estruturação do presente trabalho, no tocante ao papel do ensino da álgebra, à importância do estudo de padrões numéricos ou geométricos. Também será apresentado um estudo de recorrências lineares de primeira ordem e os métodos de resolução das relações de recorrência, para uma possível abordagem desse conteúdo no Ensino Médio. Pensamento algébrico: algumas considerações
Nos últimos anos, as pesquisas na área da Educação Matemática sobre o ensino e a aprendizagem de álgebra consideram o que chama-se de pensamento algébrico. Ponte, Branco e Matos (2009, p.10) defendem que o grande objetivo do estudo da álgebra tanto no Ensino Fundamental quanto no Médio é “desenvolver o pensamento algébrico nos alunos”. O objetivo desse trabalho não é um aprofundamento das caracterizações de pensamento algébrico referenciados na literatura acadêmica, contudo, dar um panorama com algumas considerações e perspectivas desse pensamento.
Os estudos demonstram a manifestação do pensamento algébrico por alunos da Educação Básica, dentre eles como as publicações dos autores Fiorentini, Miorim e Miguel (1993), Lins e Gimenez (1997), Portanova (2005) e Walle (2009) que abordam diferentes concepções de álgebra, a partir de visões pautadas em fundamentos teóricos distintos.
Recentemente, pesquisas também evidenciaram o interesse no ensino da álgebra. De acordo com Coelho e Aguiar (2018), descrevem que ao se enfatizar o pensamento algébrico ao invés de apenas se restringir a questões técnicas e operacionais, o ensino de álgebra auxilia no desenvolvimento do pensamento lógico-abstrato do aluno, sendo essencial para o desenvolvimento de um cidadão capaz de viver na sociedade atual.
Ribeiro (2016) busca investigar os conhecimentos algébricos desenvolvidos por professores, ao ensinar álgebra na Educação Básica e como a abordagem baseada em perfis conceituais pode contribuir para constituir e/ou ampliar conhecimentos algébricos de professores e futuros professores. Ao final, o autor conclui que a maior parte das concepções de álgebra (ou de educação algébrica) encontradas na literatura aparece nas
222 REnCiMa, v. 11, n.1, p. 219-236, 2020 falas dos professores investigados, convergindo em alguns momentos, divergindo em outros, quando são comparados as compreensões que têm os professores do Ensino Superior e os da Educação Básica. Com esse estudo, o autor aponta a necessidade para uma reorganização curricular dos cursos de Licenciatura, no que se refere ao ensino de álgebra para os futuros professores de matemática.
No cenário brasileiro, conforme apontado por Ferreira (2017), os principais documentos de orientações curriculares referentes ao ensino e aprendizagem, apontam para um trabalho com o Pensamento Algébrico, notadamente os Parâmetros Curriculares Nacionais (PCNs) e o documento mais recente, a Base Nacional Comum Curricular (BNCC), que apresenta a álgebra como uma das unidades temáticas a ser tratada desde os anos iniciais do Ensino Fundamental.
Outro documento importante, as Diretrizes Curriculares do Estado do Paraná (DCEs) para a disciplina de matemática, destacam a importância de se trabalhar com atividades que envolvem a observação de regularidades e a generalização de padrões no ensino da álgebra. Para as DCEs a ação do professor é articular o processo pedagógico que dê condições ao estudante constatar regularidades e realizar generalizações. Além disso, a aprendizagem da matemática consiste em criar estratégias que possibilitam ao aluno atribuir sentido e construir significado às ideias matemáticas de modo que, tornar-se capaz de estabelecer relações, justificar, analisar, discutir e criar (PARANÁ, 2008, p. 45).
Dentro desta perspectiva do pensamento algébrico, analisa-se as orientações metodológicas propostas na BNCC, para uma reflexão que contribua com a construção de ambientes de aprendizagem com novas formas de pensar e aprender.
A unidade temática Álgebra, por sua vez, tem como finalidade o desenvolvimento de um tipo especial de pensamento – pensamento algébrico – que é essencial para utilizar modelos matemáticos na compreensão, representação e análise de relações quantitativas de grandezas e, também, de situações e estruturas matemáticas, fazendo uso de letras e outros símbolos. Para esse desenvolvimento, é necessário que os alunos identifiquem regularidades e padrões de sequências numéricas e não numéricas, estabeleçam leis matemáticas que expressem a relação de interdependência entre grandezas em diferentes contextos, bem como criar, interpretar e transitar entre as diversas representações gráficas e simbólicas, para resolver problemas por meio de equações e inequações, com compreensão dos procedimentos utilizados. (BRASIL, 2018, p. 270).
No que tange ao pensamento algébrico, as orientações curriculares nacionais para o Ensino Médio, por exemplo, sugerem algumas alternativas:
[...] colocar os alunos em um processo de aprendizagem que valorize o raciocínio matemático – nos aspectos de formular questões, perguntar-se sobre a existência de solução, estabelecer hipóteses e tirar conclusões, apresentar exemplos e contraexemplos, generalizar situações, abstrair regularidades, criar modelos, argumentar com fundamentação lógico-dedutiva. (BRASIL, 2006, p. 70).
223 REnCiMa, v. 11, n.1, p. 219-236, 2020 Dessa forma, os principais documentos norteadores do processo de ensino e aprendizagem recomendam o estudo das sequências numéricas para desenvolver o pensamento algébrico, pois proporcionam oportunidades de analisar, identificar regularidades, sendo possível, em alguns casos, generalizá-las e expressá-las por meio de sentenças algébricas.
Em relação à concepção de pensamento algébrico considera-se uma definição apresentada por Portanova (2005): “o pensamento algébrico é desenvolvido a partir de estudos básicos empreendidos na área da aritmética, uma vez que o aluno já perceba a existência de diferentes conjuntos numéricos e das operações possíveis de se realizar entre os seus elementos” (p. 24). Ainda de acordo com autora concorda-se com a mesma ao enfatizar que o desenvolvimento do pensamento algébrico torna-se essencial na educação matemática do aluno, pois nesse contexto, o aluno consegue realizar abstrações e generalizações em nível mais profundo do que o pensamento aritmético.
Percebe-se, portanto, que o pensamento algébrico se desenvolve por meio da compreensão das relações, investigação de regularidades ou padrões em sequências, inicialmente no campo da aritmética.
Conforme Booth (1995, p. 24), na aritmética, a ênfase está nas respostas numéricas particulares, enquanto que na álgebra, buscam-se os procedimentos e relações para expressá-las genericamente. Tais conceitos se relacionam ao que coloca Kaput (1999) citado por Walle (2009, p. 288), onde descreve o pensamento algébrico sobre as cinco diferentes formas de raciocínio algébrico: (i) Generalização da aritmética e de padrões em toda a matemática; (ii) Uso significativo do simbolismo; (iii) Estudo da estrutura no sistema de numeração; (iv) Estudo de padrões e funções; e (v) Processos de modelagem matemática, que integra as quatro anteriores.
De acordo Walle (2009, p. 287), “o pensamento algébrico ou raciocínio algébrico envolve formar generalizações a partir de experiências com números e operações, formalizar essas ideias com uso de um sistema de símbolos significativo, explorando conceitos de padrão e de função”.
O autor Walle (2009) defende o estudo de padrões no ensino da álgebra, “aprender a procurar por padrões e como descrever, traduzir e ampliá-los é parte do fazer matemática e do pensar algebricamente” (p. 296). Nesse contexto, Vale e Pimentel (2005, p. 16) ressaltam que o uso de padrões é um importante componente da atividade matemática, isto é, permite conjecturar e generalizar.
Entre outras vantagens sobre as tarefas que envolvem a procura de padrões, é o fato que elas permitem: (i) evidenciar como os diferentes conhecimentos matemáticos se relacionam entre si e com outras áreas do currículo; (ii) promover o desenvolvimento do raciocínio matemático dos alunos tornando-os bons solucionadores de problemas e pensadores abstratos; e (iii) melhorar a compreensão do sentido do número, da álgebra e de conceitos geométricos (VALE E PIMENTEL, 2005).
224 REnCiMa, v. 11, n.1, p. 219-236, 2020 Nessa perspectiva, o trabalho com a álgebra, no início da escolaridade, contribui para que os estudantes desenvolvam um tipo de raciocínio específico, Ferreira (2017, p. 20-21) denomina como pensamento algébrico que pode ser entendido como “uma forma de estruturação do pensamento – passível de ser desenvolvida desde a Educação Infantil, percorrendo toda a escolaridade – que pressupõe a generalização, transpondo situações particulares a ideias gerais”.
De acordo com a organização dos conteúdos apresentados na BNCC (BRASIL, 2018), são nos anos finais do Ensino Fundamental que os conteúdos algébricos começam a ser ensinados, tais como as expressões algébricas, equações do primeiro e segundo grau, polinômios, funções, sistemas de equações e inequações. Apesar de que nos anos iniciais (1º ao 5º ano) já se possa incluir alguns tópicos da álgebra, como as ideias de sequências numéricas segundo uma determinada regra de formação e que podem ser generalizadas. Embora que nesta etapa da Educação Básica, deve-se compreender que a existência do eixo da Álgebra deve propiciar o desenvolvimento do pensamento algébrico, e não o formalismo algébrico desenvolvido nos anos Finais do Ensino Fundamental e ampliados no Ensino Médio.
Sequências numéricas e as relações de recorrência
De acordo com Walle (2009, p.297) os padrões numéricos encontrados em sequências numéricas baseados em uma regra particular proporcionam desafios apropriados no desenvolvimento do pensamento algébrico em todos os níveis da Educação Básica.
Conforme Hefez (2011), uma sequência é uma função cujo domínio é conjunto dos números naturais, denotado por ℕ = {1,2,3, ...}, em um conjunto .A
:
( )
a A
n a n
Para cada 𝑛∈ℕ, o valor a(n) é usualmente representado por a Escreve-se n.
1 2 3 4
( ,a a a a, , ,...,an,...), ou (an) para indicar a sequência a.
Em alguns casos, o domínio de uma sequência é o conjunto de inteiros não negativos {0,1,2,3,...}, em vez de ℕ. Ou seja, a sequência inicia em n0. Quando o domínio da função é {1, 2,3,4,..., },m para algum 𝑚∈ℕ, sobre um conjuntoA, a sequência é dita finita e denotada por: a a a a1, 2, 3, 4,...,a m.
De acordo com Lima et al. (2006), muitas sequências são definidas recursivamente, ou seja, existem sequências numéricas onde se conhece o primeiro termo e uma lei que permite relacionar o termo a com alguns de seus termos anteriores: n
. ,...,
, 2 1
1 a a
225 REnCiMa, v. 11, n.1, p. 219-236, 2020 Quando isso ocorre, diz-se que os termos podem ser obtidos recursivamente ou através de uma equação de recorrência. Conforme apresenta-se nos exemplos a seguir. Exemplo 2.1:
(a) Sequência dos números naturais ímpares (1, 3, 5, 7, 9, ...), sequência numérica que pode ser escrita recursivamente como an an12, com n1 e valor inicial a1 1;
(b) progressão aritmética (PA): an1anr, n1, onde o número r é a razão da progressão;
(c) progressão geométrica (PG): an1 qan, n1, onde o número q é a razão da progressão;
(d) A sequência de Fibonacci, é uma sucessão de números inteiros, começando normalmente por 0 e 1, na qual apresenta um padrão matemático, onde cada termo corresponde à soma dos dois termos anteriores (0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...). Em notação matemática, a sequência é definida recursivamente pela fórmula:
,
1
2 n n
n F F
F com as condições iniciais F10 e F2 1.
Uma recorrência é dita de primeira ordem quando um termo a depende somente n do termo an1, os itens (a), (b) e (c) do exemplo acima são exemplos de recorrências de primeira ordem.
Determinar uma fórmula fechada seria encontrar uma solução para calcular a n apenas em função de n e das condições iniciais. Com tal solução é possível encontrar o valor de qualquer termo sem necessidade de determinar os termos que o antecedem.
Segundo Lima et al. (2006), será necessário verificar as soluções para os termos iniciais e perceber um padrão, encontrar a relação de recorrência correspondente e verificar a validade de tal relação por meio do Princípio da Indução (Para mais detalhes sobre o Princípio da Indução Matemática consultar Hefez, 2011).
Exemplo 2.2: Uma progressão aritmética é uma recorrência linear de primeira ordem r a an1 n . Sendo assim: 2 1 3 2 4 3 1 n n a a r a a r a a r a a r
Somando os membros das igualdades ordenadamente, obtém-se:
2 3 4 n 1 n 1 2 3 n 2 n 1
226 REnCiMa, v. 11, n.1, p. 219-236, 2020 Subtraindo em ambos os membros a2a3an1 e escrevendo a soma das n1 parcelas de r da Eq. 2.1, obtém-se o termo geral de uma progressão aritmética em função da razão e do primeiro termo:
Outra fórmula bastante conhecida em progressão aritmética é a soma dos n primeiros termos da progressão. Para chegar à fórmula será utilizado o mesmo raciocínio que se afirma ter sido deduzido por Carl Friedrich Gauss (1777-1855). Conta-se que certa vez, o seu professor para manter a classe ocupada e em silêncio, pediu que seus alunos calculassem a soma dos inteiros de 1 a 100 (1 + 2 + 3 + ...+ 98 + 99 + 100). Gauss, que estava na época com aproximadamente sete anos, apresentou o resultado correto em poucos minutos, anunciando que a soma era 5050 (MORGADO; WAGNER, ZANI, 2001, p. 04).
Para chegar à resposta, ele notou que somando os termos equidistantes o valor é constante, ou seja, a soma do primeiro número com o último (1+100) é igual ao resultado do segundo com o penúltimo (2+99), assim como a do terceiro com o antepenúltimo (3+98), e assim sucessivamente.
1 + 100 = 2 + 99 = 3 + 98 = ... = 50 + 51 = 101
Com isso, ele concluiu que a soma de todos os inteiros de 1 a 100, que será denotado por S,é igual a 50 vezes a soma 1+100.
5050 101 50 ) 100 1 ( 50 S
É possível perceber que a soma sugerida 1 + 2 + 3 + 4 + ... + 97 + 98 + 99 + 100, trata-se de uma PA de razão 1. Utilizando o mesmo raciocínio aritmético apresentado por Gauss é possível generalizar a fórmula da soma para qualquer progressão aritmética, dada por:
O raciocínio algébrico, consiste em somar o primeiro termo a com o último 1 a em n, seguida, multiplicar pela quantidade de termos e dividir o resultado encontrado por 2.
De maneira semelhante, como para a determinação da expressão que exprime uma PA, as recorrências podem ser utilizadas para a determinação da expressão que exprime os termos de uma progressão geométrica (PG).
Exemplo 2.3: Uma progressão geométrica é uma sequência numérica na qual o quociente entre dois termos consecutivos quaisquer é sempre igual a uma constante real q, a qual se chama de razão da progressão, isto é, 1 q.
a a
n
n Portanto, trata-se de uma recorrência
1 ( 1) n a a n r (2.2) 2 ) ( 1 n n a a n S (2.3)
227 REnCiMa, v. 11, n.1, p. 219-236, 2020 linear de primeira ordem, definida pela igualdade an1anq. No entanto, é possível determinar uma fórmula fechada para a De fato, n.
2 1 3 2 4 3 1 n n a a q a a q a a q a aq
Multiplicando membro a membro as igualdades acima, obtém-se:
Dividindo ambos os membros da Eq. 2.4 por a a a a2 3 4 5 an1 de termos não nulos e escrevendo o produto dos n1 fatores iguais a q na forma de potência, obtém-se o termo geral de uma PG, dada por:
Em uma progressão geométrica (a ,a ,a ,...,a1 2 3 n1,an), indicando por S a soma dos n n primeiros termos, ou seja:
Multiplicando a Eq. 2.6 pela razão q, com q0, obtém-se:
Da definição de progressão geométrica, an an1q, a Eq. 2.7 pode ser reescrita:
Subtraindo os termos da Eq. 2.6 dos termos da Eq. 2.8, resulta-se:
Anulando os termos inversos aditivos da Eq. 2.9, tem-se:
Como 1
1
n
n a q
a , ao ser substituído na Eq. 2.10 encontra-se Sn
q1 a1(qn 1). Isolando Sn, obtém-se a seguinte fórmula:2 3 4 n1 n 1 2 3 n 2 n1 a a a a a a qa qa q a qa q (2.4) 1 1 n n a q a (2.5) n n n n a a a a a a S 1 2 3 2 1 (2.6) q a q a q a q a q a q a qSn 1 2 3 n2 n1 n (2.7) q a a a a a a a qSn 2 3 4 n2 n1 n n (2.8) n n n n n n S a a a a a a a a a q a qS 2 1 3 2 4 3 1 (2.9) 1 ) 1 (q a q a Sn n (2.10) 1 1 1 q q a S n n , para q1 (2.11)
228 REnCiMa, v. 11, n.1, p. 219-236, 2020 Dessa maneira, a soma dos n primeiros termos de uma PG pode ser calculada conhecendo-se a razão e o primeiro termo.
Conforme BNCC (BRASIL, 2018) espera-se que o aluno do Ensino Médio generalize cálculos para a determinação de termos de uma sequência numérica. Sendo assim, a partir da definição de progressão aritmética e progressão geométrica, o trabalho com recorrências possibilita aos estudantes a generalização e a obtenção de uma fórmula para o termo geral.
Solução de uma recorrência do tipo xn+1 = xn + f(n)
De Lima et al. (2006), as recorrências lineares de primeira ordem da forma
1 ( ),
n n
x x f n com f uma função de n,são facilmente resolvidas. De fato,
2 1 3 2 4 3 1 (1) (2) (3) ( 1) n n x x f x x f x x f x x f n
Somando membro a membro as equações acima, obtém-se:
Subtraindo x2 x3x4...xn1 em ambos os membros da Eq. 2.12, obtém-se:
Dessa forma, a Eq. 2.13 refere-se à solução da recorrência xn1 xn f n( ). Questões envolvendo recorrências: uma recomendação ao Ensino Médio
Nesta seção apresentar-se-ão propostas de atividades possíveis de serem aplicadas no contexto escolar do Ensino Médio. As regularidades e os padrões em sequências numéricas são bastante explorados, bem como as relações de recorrências. Sendo necessário utilizar os métodos de resolução vistos na seção anterior para encontrar o termo geral da sequência recursiva apresentada.
As atividades propostas são baseadas em algumas questões da Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP), seja nas provas de edições anteriores. Como os problemas propostos na OBMEP englobam uma grande variedade de conhecimentos matemáticos, optou-se por examinar somente alguns que tinham em sua essência algo relacionado com recorrências matemáticas, tal abordagem que normalmente não é contemplado neste nível de Ensino.
) 1 ( ... ) 3 ( ) 2 ( ) 1 ( ... 1 1 2 3 1 4 3 2 x x x x x f x f x f x f n x n n n (2.12)
1 1 1 1 (1) (2) (3) ... ( 1) () n i n x f f f f n x f i x (2.13)229 REnCiMa, v. 11, n.1, p. 219-236, 2020 No entanto, apresentaram-se soluções alternativas para os problemas, o que pode fazer com que os sujeitos envolvidos tenham novas perspectivas quando buscarem soluções de atividades que envolvem generalizações de padrões matemáticos.
Considerações a respeito da OBMEP
Muitas questões propostas pela Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP), partem da exploração de padrões numéricos em sequências, culminando com a generalização dos padrões observados, elementos essenciais para a manifestação do pensamento algébrico.
A OBMEP é uma avaliação externa que abrange as escolas do país e ofertada a todos os alunos de uma rede de ensino que tem como seu foco a aprendizagem em matemática. E tem conseguido isso por apresentarem situações contextualizadas que requerem raciocínio lógico, estratégias de resolução, autonomia e criatividade. Contrapondo o modelo tradicional de ensino que a tempo domina as salas de aula que é o de retransmitir problemas e soluções padronizadas apresentados em livros didáticos.
Considerada a maior competição científica nacional, a olimpíada é uma realização do Instituto de Matemática Pura e Aplicada (IMPA), tem como objetivo estimular o estudo da Matemática e revelar talentos na área. A OBMEP que apenas contemplava alunos das escolas públicas desde sua primeira edição em 2005, no ano de 2017 as escolas privadas de todo o país foram convidadas para a realização das provas. Participam da OBMEP estudantes do 6º ano ao 9º ano do Ensino Fundamental e alunos do Ensino Médio, separados em três níveis diferentes, de acordo com a sua escolaridade. Os alunos do 6º e 7º anos fazem a prova do nível 1; já os do 8º e 9º anos fazem a prova do nível 2; e os do 1º, 2º e 3º anos do Ensino Médio fazem a prova do nível 3. A partir deste ano, agora a OBMEP também acontece no Nível A, voltado para o Ensino Fundamental anos iniciais.
As provas são constituídas de duas fases. Na primeira fase é aplicada prova objetiva (múltipla escolha) a todos os inscritos da escola. A escola seleciona aproximadamente 5% dos alunos em cada nível que se destacaram na primeira fase para participar da segunda fase. Nesta os selecionados são submetidos a uma prova discursiva de acordo com o seu nível 1, 2 ou 3.
No endereço eletrônico da OBMEP (http://www.obmep.org.br/provas.htm) encontram-se as provas realizadas nos anos de 2005 a 2019 com as respectivas soluções, bem como o regulamento e informações gerais.Além disso, é disponibilizada a versão eletrônica do Banco de Questões, materiais que auxiliam os estudantes na preparação para as edições da OBMEP, que consiste em atividades elaboradas com base na metodologia da Resolução de Problemas e quando utilizadas poderão tornar as aulas de matemática mais desafiadoras para os alunos.
A seguir será apresentado algumas questões que podem ser resolvidas via recorrências, ou seja, soluções alternativas das soluções apresentadas no endereço eletrônico da OBMEP.
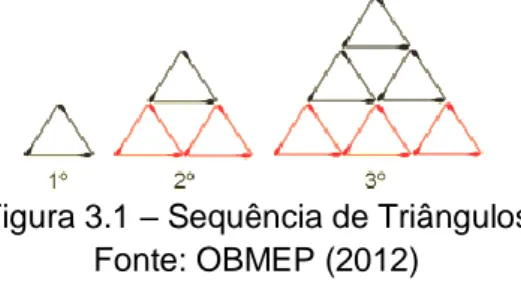
230 REnCiMa, v. 11, n.1, p. 219-236, 2020 Questão 3.1 (Questão 02 - OBMEP 2012 - 1ª Fase - Nível 1) Renata montou uma sequência de triângulos com palitos de fósforo, seguindo o padrão indicado na Fig. 3.1. Quantos palitos ela vai usar para construir o quinto triângulo da sequência?
Figura 3.1 – Sequência de Triângulos Fonte: OBMEP (2012)
SOLUÇÃO: Observe que no 2º desenho, a figura anterior foi esboçada e dois triângulos foram acrescentados, isto é, 3239 palitos. De forma semelhante, no 3º desenho, tem-se a figura anterior mais três triângulos, isto é, 93318palitos. Como as próximas figuras seguem o mesmo padrão, a quantidade de palitos a necessários para formar a n figura que está na posição n é composta pela quantidade de palitos da figura anterior
1
n
a , acrescentados de n triângulos.
O padrão é descrito por meio da recorrência: an an1 + 3 n, n1 e a1 3. Escrevendo os termos da relação de recorrência, observa-se:
2 1 3 2 4 3 1 3 2 3 3 3 4 3 n n a a a a a a a a n
Somando ordenadamente os termos de cada igualdade, resulta-se:
Subtraindo a2a3a4...an1 em ambos os membros da Eq. 3.1, obtém-se:
Como a1 3, fatora-se a Eq. 3.2, conforme indicado abaixo:
Usando a Eq. 2.3, que determina a soma dos n primeiros termos de uma progressão aritmética, resulta-se:
Substituindo n5 na Eq. 3.4, verifica-se que 45. 2 ) 1 5 ( 5 3 5 a Portanto, Renata utilizará 45 palitos. n a a a a a a a a a2 3 4 ... n1 n 132 233 334... n13 (3.1) n a an 1323334...3 (3.2) ) ... 3 2 1 ( 3 n an (3.3) 2 ) 1 ( 3 n n an (3.4)
231 REnCiMa, v. 11, n.1, p. 219-236, 2020 Com a resolução dessa primeira questão (Questão 3.1) apresenta-se a generalização do problema, ou seja, um modelo matemático com a finalidade de calcular a quantidade de palitos para uma figura em qualquer posição. Pois, seria demais trabalhoso realizar a construção de desenhos em posições mais distantes, como por exemplo, saber a quantidade de palitos na figura de número 50. Em situações como essas, é possível obter fórmulas e ir além das operações no campo da aritmética, fazendo o uso da linguagem algébrica cada vez mais formal, evidenciando assim o desenvolvimento do pensamento algébrico dos alunos.
A próxima questão também envolve o reconhecimento de padrões. A sequência numérica formada por pontos é conhecida como números figurados, neste caso os pentagonais. Na resolução do problema espera-se que os alunos façam análises, testem conjecturas e elaborem estratégias para encontrar a lei de formação dos números figurados.
Questão 3.2 (Questão 14 - OBMEP 2015 - 1ª Fase - Nível 3) Abaixo temos três figuras pentagonais: a primeira com 5 pontos, a segunda com 12 pontos e a terceira com 22 pontos. Continuando esse processo de construção, a vigésima figura pentagonal terá 651 pontos. Quantos pontos terá a vigésima primeira figura?
Figura 3.2 – Questão 3.2 (Números Pentagonais) Fonte: OBMEP (2015)
SOLUÇÃO: Se mantiver o padrão geométrico e representar o quarto número pentagonal ele terá 35 pontos, conforme visto na Fig. 3.3:
Figura 3.3 – Solução da Questão 3.2 (Números Pentagonais) Fonte: Autores (2019)
Assim, a primeira figura dos números pentagonais possui 5 pontos, em notação matemática,P1 5. Segue que, P2 12, P3 22 e P4 35. Podemos encontrar uma fórmula
geral P para que dado qualquer n, n , tenhamos o quantidade de pontos na figura de ordem n.
232 REnCiMa, v. 11, n.1, p. 219-236, 2020 Para isto, deve-se ficar atento no seguinte padrão que compõe essa sequência:
35 2 2 12 5 7 10 13
Observa-se que os termos adicionados, isto é, a sequência (7, 10, 13, ..., a ) forma n uma PA de razão 3, cujo termo geral é an 7(n1)3(conforme visto na Eq. 2.2) que pode ser reescrito na forma simplificada an 3n4.
Podemos dizer que esse problema trata-se de uma relação de recorrência de primeira ordem. Pois,
1 1 5 (3 4) 1 n n n a P P = P + n , n
Escrevendo os termos da relação de recorrência, verifica-se:
1 3 1 2 3 1 2 ] 4 ) 1 ( 3 [ 10 7 n n n P n P P P P P
Somando ordenadamente os termos de cada igualdade, obtém-se:
Subtraindo P2 P3P4 ...Pn1 em ambos os membros da Eq. 3.5, chega-se a equaçãoPn P171013...3n1, como P1 5, que pode ser representado de forma estratégica por P114, pois assim tem-se a soma dos termos de uma PA
) 1 3 ..., , 13 , 10 , 7 , 4
( n com n termos e razão 3. Assim:
Usando a Eq. 2.3, para calcular S, tem-se:
Substituindo a Eq. 3.7 na Eq. 3.6, encontra-se , 2 5 3 1 2 n n
Pn que pode ser reescrita conforme indicado a seguir:
Agora, se tem uma fórmula geral que calcula o número de pontos em qualquer posição. Pode-se conferir que na posição 20 (n20)existem 651 pontos como foi dado no
) 1 3 ( ... 13 10 7 1 3 2 1 1 4 3 2P P ...P P P P P ...P n P n n n (3.5) S n n P 1471013...(3 1) (3.6) 2 5 3 2 ] 1 3 4 [ n n2 n n S (3.7) 2 2 5 3 2 n n Pn (3.8)
233 REnCiMa, v. 11, n.1, p. 219-236, 2020 enunciado do problema. Para isso, basta fazer a substituição de n20 na fórmula do termo geral que corresponde a Eq. 3.8:
651 2 1302 2 2 20 5 20 3 2 20 P
Como o problema propõe que se encontre a quantidade de pontos na vigésima primeira figura, de maneira análoga, substituindo n21 na fórmula do termo geral da Eq. 3.8: 715 2 1430 2 2 21 5 21 3 2 21 P
Logo, a vigésima primeira figura, será composta por 715 pontos.
A solução proposta para o próximo problema, novamente difere da solução apresentada no material da OBMEP, pois sugerimos a resolução por meio do uso de sequências recursivas (ou equações de recorrência) com a exploração de padrões matemáticos, uso de progressões geométricas para a generalização do problema.
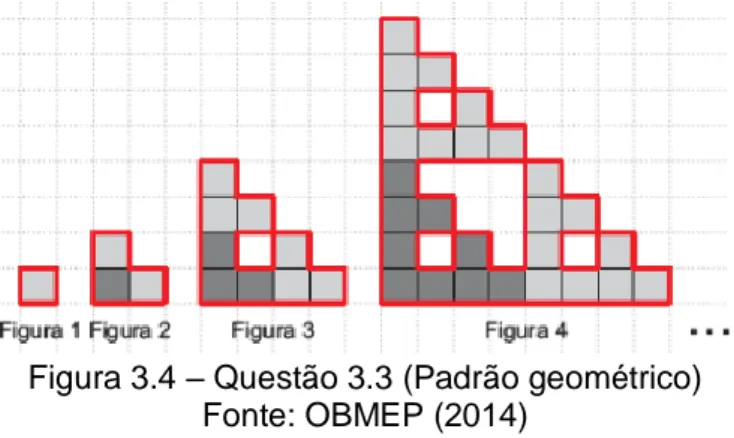
Questão 3.3 (Questão 8 - OBMEP 2014 - 1ª Fase - Nível 3) – Começando com um quadrado de 1 cm de lado, forma-se uma sequência de figuras, como na ilustração da Fig. 3.4. Cada figura, a partir da segunda, é formada unindo-se três cópias da anterior. Os contornos destacados em vermelho das quatro primeiras figuras medem, respectivamente, 4 cm, 8 cm, 20 cm e 56 cm. Quanto mede o contorno da Figura 6?
Figura 3.4 – Questão 3.3 (Padrão geométrico) Fonte: OBMEP (2014)
SOLUÇÃO: Quando a figura possui apenas um quadrado seu contorno mede 4 cm, em notação, C1 4. O contorno de vermelho da segunda figura C2 8, da terceira figura
3 20
C e C4 56. Pretende-se encontrar uma fórmula geral Cn, para que dado qualquer ,
n tenha a medida do contorno de vermelho na figura de ordem n.
Pode-se perceber que cada figura é formada por cópias da figura anterior. O contorno de vermelho da figura 2 possui a medida da figura 1 aumentada 4 cm, ou seja,
2 1 4.
C C Com o mesmo raciocínio para a figura 3, temos C3 C212. A figura 4,
4 3 36.
234 REnCiMa, v. 11, n.1, p. 219-236, 2020 Observe que os valores adicionados são termos de uma PG (4, 12, 36, ...) de razão 3.
q Portanto, pode-se escrever:
2 1 3 2 2 4 3 2 1 4 4.3 4.3 4.3n n n C C C C C C C C
Adicionando membro a membro todas as igualdades segue que:
Subtraindo C2C3C4...Cn1 em ambos os membros da Eq. 3.9, obtém-se:
Usando a Eq. 2.11 para calcular S, que corresponde à soma de uma PG com (n1) termos e razão q3.
Substituindo a Eq. 3.11 na Eq. 3.10, encontra-se 12.3 12, n n C C mas como , 4 1
C tem-se então Cn 42.3n12,que pode ser reescrita conforme a seguir:
Para concluir, basta substituir n6 na Eq. 3.12, ou seja, C6 2(3611)488. Logo, a medida do contorno da sexta figura mede 488 cm.
Conclusão
A exploração de padrões matemáticos no ensino da álgebra é considerada por diversos autores a base para o desenvolvimento do pensamento algébrico.
Sendo assim, o presente trabalho teve como objetivo apresentar propostas pedagógicas que proporcionem aos alunos a oportunidade de observar e generalizar padrões, tratando-se de sequências numéricas associada a regularidades, tornando-os capazes de identificar e encontrar uma fórmula para o termo geral em sequências numéricas.
Os estudos de recorrências matemáticas são uma ótima oportunidade para que os estudantes desenvolvam seu raciocínio, percebendo padrões, por meios de atividades investigativas e com isso aprendam a organizar ideias, fazendo o uso da linguagem
2 1 2 3 2 1 1 4 3 2 4 4 3 4 3 4 3 n n n n C C C C ... C C ... C C C (3.9) , 3 4 ... 3 4 3 4 4 2 2 1 S n n C C (3.10) 2 3 2 ) 1 3 ( 2 1 3 1 3 4 1 1 1 n n n S (3.11) ) 1 3 ( 2 1 n n C (3.12)
235 REnCiMa, v. 11, n.1, p. 219-236, 2020 matemática. Assim, através da generalização e abstração é possível ampliar os conceitos de número, dos sistemas de numeração, das operações, permitindo o equacionamento das situações-problema e o uso de linguagem algébrica cada vez mais formal.
As provas da OBMEP possuem um grande valor educacional como material a ser usado tendo em vista que suas questões permitem trabalhar mais de um conceito matemático e, além disso, buscam desenvolver o raciocínio. Cabe ao professor estimular seus alunos na construção do conhecimento, priorizando que eles estabeleçam generalizações de números ou eventos quaisquer, deixando de lado a aplicação sistemática de fórmulas prontas.
A abordagem do conteúdo de sequências definidas recursivamente, isto é, por recorrência, como uma proposta para o Ensino Médio, certamente é uma possibilidade de ampliar o conhecimento dos alunos e de mostrar a aplicação dos conteúdos matemáticos presentes no currículo da Educação Básica. Sendo as funções de domínio natural e no estudo de progressões aritméticas e geométricas. Além disso, as atividades propostas estão de acordo com as orientações curriculares, porque proporcionam aos educandos formas de como generalizar situações, abstrair regularidades, criar modelos e argumentar com fundamentação lógico-dedutiva, que visam o desenvolvimento do pensamento algébrico.
Referências
BOOTH, L. R. Dificuldades das crianças que se iniciam em álgebra. In: COXFORD, A. F.; SHULTE, A. P. (Org.). As ideias da álgebra. Tradução de Hygino H. Domingues. São Paulo: Atual, 1995. p.23-27.
BRASIL. Ministério da Educação e Cultura. Base Nacional Comum Curricular: Matemática. Brasília, DF, 2018.
_______. Ministério da Educação e Cultura. Orientações Curriculares Nacionais (Ensino Médio): Ciências da Natureza, Matemática e suas Tecnologias. 2006.
_______. Ministério da Educação e Cultura. Parâmetros Curriculares Nacionais (Ensino Fundamental): Matemática. 1998.
COELHO, F. U; AGUIAR, M. A história da álgebra e o pensamento algébrico: correlações com o ensino. Estudos Avançados (USP. Impresso). v. 32, n. 34, p. 171-187, 2018.
236 REnCiMa, v. 11, n.1, p. 219-236, 2020 FERREIRA, M. C. N. Álgebra nos anos iniciais do Ensino Fundamental: uma análise dos documentos curriculares nacionais. REnCiMa, v. 8, n. 5, p. 16-34, 2017.
FIORENTINI, D.; MIORIM, M. A.; MIGUEL, A. Contribuições para um repensar... a educação algébrica elementar. Pro-Posições, Campinas, v.4, n.1, p.78-90, mar.1993. HEFEZ, A. Elementos de aritmética. 2 ed. Rio de Janeiro: SBM, 2011.
LIMA, E. L. et al. A Matemática do Ensino Médio. v. 2. 6. ed. Rio de Janeiro: SBM, 2006. LINS, R.C.; GIMENEZ, J. Perspectivas em aritmética e álgebra para o século XXI. 6.ed. Campinas: Papirus, 1997.
MORGADO, A. C.; WAGNER, E.; ZANI, S. Progressões e matemática financeira. 5. ed. Rio de Janeiro: SBM, 2001.
PARANÁ. Secretaria de Estado de Educação. Departamento de Educação Básica. Diretrizes Curriculares da Educação Básica: Matemática. Curitiba: SEED, 2008.
PORTANOVA, R. (Org.). Um currículo de matemática em movimento. 1.ed. Porto Alegre: EDIPUCRS, 2005.
PONTE, J.; BRANCO, N.; MATOS, A. Álgebra no Ensino Básico. Ministério da Educação, Portugal. Direção Geral de Integração e de Desenvolvimento Curricular (DGIDC). Portugal, 2009.
RIBEIRO, A. J. Álgebra e seu Ensino: dando eco às múltiplas “vozes” da Educação Básica. REnCiMa, v. 7, n. 14, p. 1-14, 2016.
VALE, I.; PIMENTEL, T. Padrões: um tema transversal no currículo. Revista Educação e Matemática, Portugal, n. 85, p. 14-20, nov./dez., 2005.
WALLE, J. A. V. de. Matemática no Ensino Fundamental: formação de professores e aplicação em sala de aula. Tradução: Paulo Henrique Colonese. 6. ed. Porto Alegre: Artmed, 2009.