Controladores robustos DLQI e DAlocação de polos otimizados via LMI aplicados a um consor boost alto ganho com célula de comutação três estados

(1)

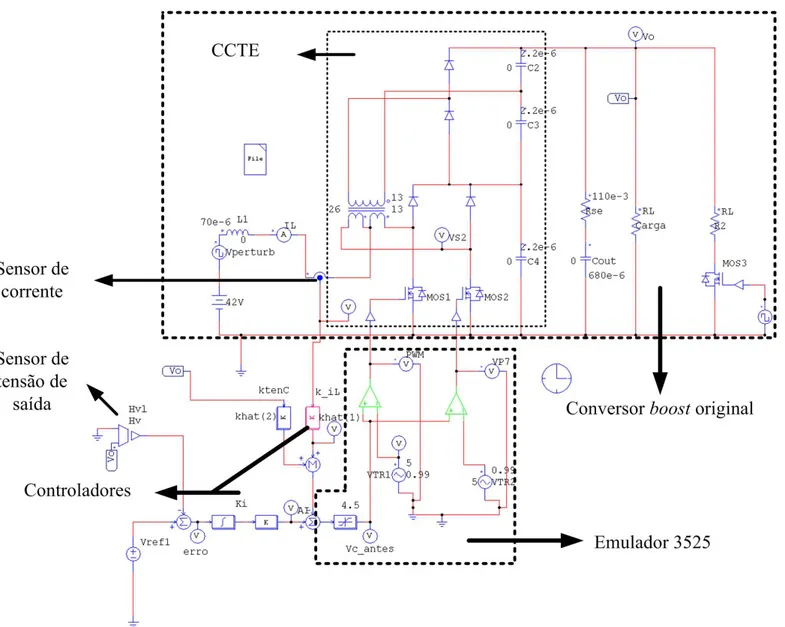
Universidade Federal do Cear´

a

Centro de Tecnologia

Programa de P´

os Gradua¸c˜

ao em Engenharia El´

etrica

Controladores Robustos

D

_{-LQI e}

D

_-Aloca¸c˜

_{ao de}

polos Otimizados via LMI Aplicados a um

Conversor Boost Alto Ganho com C´

elula de

Comuta¸c˜

ao Trˆ

es Estados

Marcus Vinicius Silv´

erio Costa

(2)

i

Marcus Vinicius Silv´

erio Costa

Controladores Robustos

D

_{-LQI e}

D

_-Aloca¸c˜

_{ao de}

polos Otimizados via LMI Aplicados a um

Conversor Boost Alto Ganho com C´

elula de

Comuta¸c˜

ao Trˆ

es Estados

Dissertação submetida à Universidade Fede-ral do Ceará como parte dos requisitos para a obtenção do grau de mestre em Engenharia Elétrica.

Orientador:

Prof. Jos´e Carlos Teles Campos, Dr

Fortaleza

(3)

Dados Internacionais de Catalogação na Publicação Universidade Federal do Ceará

Biblioteca de Ciências e Tecnologia

VM315c Costa, Marcus Vinicius Silvério.

Controladores robustos D-LQI e D-Alocação de polos otimizados via LMI aplicados a um conversor boost alto ganho com célula de comutação três estados / Marcus Vinicius Silvério Costa – 2012.

120 f. : il., color., enc. ; 30 cm.

Dissertação (mestrado) – Universidade Federal do Ceará, Centro de Tecnologia, Departamento de Engenharia Elétrica, Programa de Pós-Graduação em Engenharia Elétrica, Fortaleza, 2012.

Área de Concentração: Engenharia Elétrica (Engenharias IV). Orientação: Prof. Dr. José Carlos Teles Campos.

1.Controle robusto. 2. Realimentação de estados. I. Título.

(4)

(5)

iv

Dedicat´

oria

Este trabalho ´e dedicado `a Deus, ao meu

(6)

v

Agradecimentos

Primeiramente a Deus, que me deu forc¸as para conclus˜ao deste trabalho.

Ao meu pai Emilson Santos Costa (in memorian) que se sacrificou, acreditando na minha

capacidade em superar desafios, à minha mãe Maria Joita Silvério Costa, que testemunhou

minhas longas horas para conclus˜ao desta obra.

Ao orientador professor Dr. Jos´e Carlos Teles Campos , que me orientou e acompanhou na

conclus˜ao deste trabalho.

Ao Francisco Everton Uchˆoa Reis, que contribuiu significativamente pelo desenvolvimento

desta obra.

Ao meu colega de pesquisa, Vandilberto Pereira Pinto, pelo suporte na pesquisa e na teoria

sobre controle. Agradeço também ao Kelson Leite pelas ajudas nas referências bibliográficas

sobre LMIs.

Aos meus colegas de laborat´orio J. Gleidson e J. Oliveira pela ajuda e suporte.

Ao CNPQ pelo suporte financeiro por meio da bolsa de estudo e ao PPGEE pelo suporte

acadˆemico.

Aos meus Pastores que me apoiaram, durante o per´ıodo de mestrado, para buscar a Paz de

Esp´ırito em Deus.

A todas as pessoas que por motivo de esquecimento n˜ao foram citadas anteriormente, vou

(7)

vi

“Bem-aventurado o homem que acha sabedoria, e o homem que adquire conhecimento; porque

´e melhor a sua mercadoria do que artigos de prata, e maior o seu lucro que o ouro mais fino.

Mais preciosa ´e do que os rubis, e tudo o que mais possas desejar n˜ao se pode comparar a ela. ”

(8)

vii

Resumo

Este trabalho visa a aplicação dos controles robustos D_{-LQI e}D_{-Alocação de polos}

oti-mizados via LMIs em um conversorboost de alto ganho de tensão com célula de comutação de três estados. Este conversor consiste numa topologia moderna derivada do conversorboost clássico. Oboost é considerado um elevador de tensão, o qual converte uma entrada na faixa de 42−54V à 400V. O conversorboostproposto é reduzido ao modelo de um conversor equi-valente e é modelado no espaço de estados médio, em que é observado que a matriz D6=0, sendo então uma modelagem que apresenta uma peculiaridade de acordo com a literatura, pois a solução de controle é mais complexa. As estratégias de controle aplicadas usam de procedi-mentos matemáticos denominados de Desigualdades Matriciais Lineares (LMIs-Linear Matrix Inequalities), que podem ser resolvidos por otimização convexa ou programação semidefinida positiva (SDP procedures). As ferramentas matemáticas utilizadas para resolução das LMIs neste trabalho são o Yalmip e SeDuMi , que são inseridas no MATLAB . Além disso são anali-sadas as incertezas presentes no processo, bem como a robustez do modelo em malha fechada. São obtidos os resultados de simulação via MATLAB -PSIM e são feitas as análises referentes a estes resultados, além da análise dos resultados experimentais e a conclusão do estudo, além das propostas de trabalhos futuros. O Apêndice mostra os procedimentos de instalação dos resolvedores além do uso correto com base nas equações descritas na teoria sobre LMIs.

N´umero de p´aginas:120

Palavras-chave:D_-LQI,D_{-Alocac¸˜ao de polos, Controle Robusto, Conversor}_boost_{de Alto}

(9)

viii

Abstract

This work involves the application of robust controls D_{-LQI and} D_{-pole placement via}

LMIs in a high-gainboostwith three states switching cell. This converter consists of a modern topology derived the classic boost converter . This boost converter is considered a step-up converter, which a range of 42−54V voltage input to 400V voltage output. The proposedboost converter is reduced to equivalent model and is modeled at space state avarage, in which is observed that the matrix D6=0, being then a modeling that presents a peculiarity according to literature, thus the control solution is more complex. The control strategies applied use mathematical procedures called Linear Matrix Inequalities (LMIs), which can be solved by convex optimization or positive semidefinite procedures (SDP). The mathematical tools used to solve the LMIs this work are Yalmip and SeDuMi , which are inserted in MATLAB . Further analyzes the uncertainties present in the process, as well as the robustness of closed loop model. The simulation results are obtained via MATLAB and PSIM and analyzes made regarding these results, besides the analysis of experimental results and conclusion of study, in addition to proposals for future work. The Appendix shows the installation procedures and use correct solvers based on the equations described in LMI theory.

Number of pages:120

(10)

ix

Sum´

ario

Lista de Figuras xii

Lista de Tabelas xvi

Lista de S´ımbolos xvii

Lista de Acrˆonimos e Abreviaturas xxi

1 Introdu¸c˜ao 1

1.1 Estado da arte sobre os temas . . . 1

1.1.1 Estado da arte sobre o conversorboost . . . 1

1.1.2 Estado da arte sobre as Desigualdades Matriciais Lineares e a teoria do controle . . . 3

1.2 Revis˜ao bibliogr´afica . . . 5

1.3 Objetivos e contribuic¸˜oes deste trabalho . . . 6

1.3.1 Objetivos deste trabalho . . . 6

1.3.2 Contribuic¸˜oes deste trabalho . . . 7

1.3.3 Publicac¸˜oes em congressos . . . 7

1.4 Resumo dos cap´ıtulos . . . 7

1.5 Considerac¸˜oes finais . . . 8

2 Teoria das Desigualdades Matriciais Lineares no Controle por Aloca¸cão de Polos e LQR 9 2.1 Introdução às desigualdades matriciais lineares - LMIs . . . 9

2.2 Conceitos b´asicos de LMIs . . . 12

2.3 Estabilidade de Lyapunov via LMIs . . . 13

2.4 Politopos . . . 14

2.5 Complemento de Schur . . . 15

2.6 Estabilizac¸˜ao . . . 17

2.7 Controle LQR via otimizac¸˜ao LMI . . . 17

2.8 Restric¸˜ao LMI porD_{-estabilidade . . . .} ₁₉

(11)

Sum´ario x

2.9.1 Controle LQR com restric¸˜ao LMI viaD_{-estabilidade -}D_-LQR _{. . . .} ₂₂

2.10 An´alise das incertezas polit´opicas . . . 23

3 Teoria e Modelagem do Conversor boost 28 3.1 Topologia cl´assica dos conversores CC-CC . . . 28

3.2 Conceito do conversor original . . . 32

3.2.1 Reduc¸˜ao do Conversorboostoriginal ao modelo equivalente . . . 33

3.3 Modelagem equivalente do conversorboostno espac¸o de estados . . . 34

3.3.1 Modelo linearizado de conversores CC no espac¸o de estados . . . 34

3.3.2 Modelo no espac¸o de estados doboostequivalente . . . 36

3.4 An´alise das incertezas no conversor . . . 39

4 Estratégias de Controle Aplicado ao Conversor Boost 42 4.1 Servomecanismo com ação integral . . . 42

4.2 Projeto do controlador robusto otimizado por LMI via alocação de polos -D -Alocação de polos . . . 45

4.3 Projeto do controlador robusto otimizado via LQI comD_{-estabilidade -}D_-LQI ₄₆ 4.4 Considerac¸˜oes finais . . . 47

5 Análise e Resultados de Simula¸cão do Conversor 48 5.1 Modelo numérico em malha aberta do conversorboostequivalente . . . 48

5.2 Simulac¸˜ao no PSIM . . . 49

5.3 Resposta do sistema em malha fechada do controle robusto . . . 52

5.3.1 Resultados numéricos em malha fechada do controle por D_{-Alocação} de polos . . . 52

5.3.2 Resultados num´ericos em malha fechada do controle porD_{-LQI . . . .} ₅₂

5.3.3 An´alise das curvas no regime transit´orio e permanente . . . 53

5.3.4 An´alise das curvas em regime permanente . . . 55

5.3.5 An´alise de robustez das curvas na frequˆencia . . . 60

6 Análise e Resultados Experimentais do Conversor 65 6.1 Ambiente real de implementação . . . 65

6.2 Resultados experimentais do controleD_{-Alocac¸˜ao de polos robusto . . . .} ₆₇

(12)

Sum´ario xi

6.2.2 Resultados experimentais paraVg=54V . . . 70

6.3 Resultados experimentais do controleD_{-LQI robusto . . . .} ₇₀

6.4 Complicac¸˜oes durante o experimento . . . 84

7 Conclus˜oes Finais e Propostas de Trabalhos Futuros 85 7.1 Conclus˜oes . . . 85

7.2 Propostas de trabalhos futuros . . . 86

Referências Bibliográficas 87 Apêndice A -- Introdu¸cão aos pacotes computacionais SeDuMi e Yalmip no MA-TLAB 92 A.1 Procedimento de Instalação dos Pacotes SeDuMi e Yalmip . . . 92

(13)

xii

Lista de Figuras

2.1 Soluc¸˜ao de politopos via LMIs. . . 11

2.2 Exemplo de um politopo de 5 v´ertices (PALHARES; GONC¸ ALVES, 2008). . . 15

2.3 Restric¸˜oes LMI. . . 21

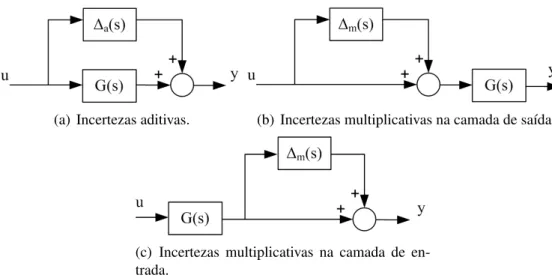
2.4 Representac¸˜ao em diagramas de blocos dos tipos de incertezas aplicado na planta (SHAHIAN; HASSUL, 1993). . . 24

2.5 (a) Func¸˜ao sensibilidadeS(s).(b) Sensibilidade complementarT(s). . . 25

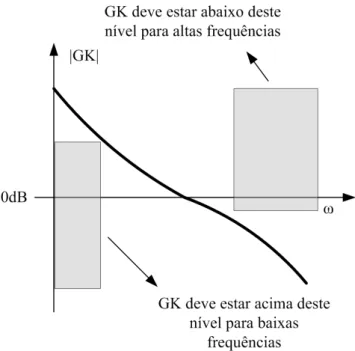
2.6 Curva desejável da função de transferência de malha aberta do de um sistema de realimentação. . . 26

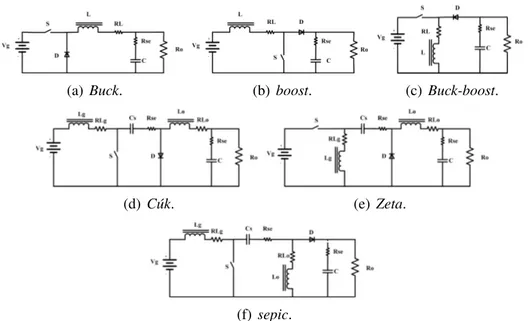
3.1 Topologias cl´assicas de conversores CC-CC. . . 29

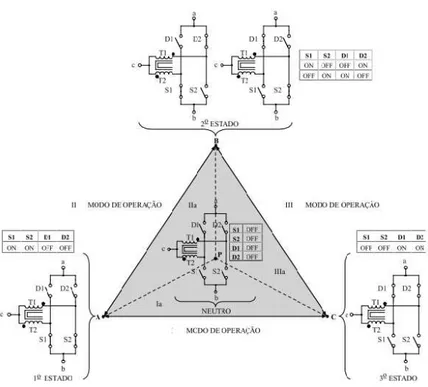
3.2 Conversorboostproposto por Bascop´e e Barbi (2000). . . 30

3.3 Princ´ıpio de chaveamento da célula de comutação em 3 estados proposto por Bascopé e Barbi (2000) e aplicado por Santero (2006) . . . 31

3.4 Conversor proposto por Torrico-Bascopeet al.(2006b, 2006c), Bascop´e e Barbi (2000) doboostalto ganho . . . 31

3.5 Topologia do conversorboostde alto ganho de tensão com célula de comutação de três estados conforme Orellana-Lafuenteet al.(2010), Reiset al.(2011). . . 32

3.6 Circuito do conversorboostcl´assico equivalente. . . 34

3.7 Definic¸˜ao dos intervalos de chaveamento do conversor (MIDDLEBROOK; CUK, 1976) . . . 35

3.8 Conversorboostnos est´agios de chaveamento. . . 37

3.9 Regi˜ao de incertezas polit´opicasPot×Vg. . . 41

4.1 Servomecanismo de ac¸˜ao integral. . . 42

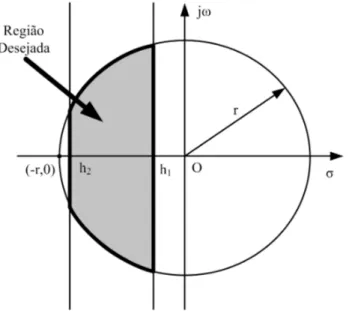
4.2 Regi˜ao desej´avel para o projeto de controle. . . 45

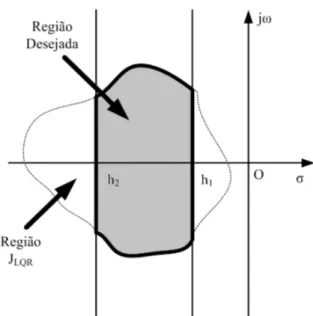
4.3 Regi˜ao desejada aplicada ao LQR comD_{-estabilidade. . . .} ₄₇

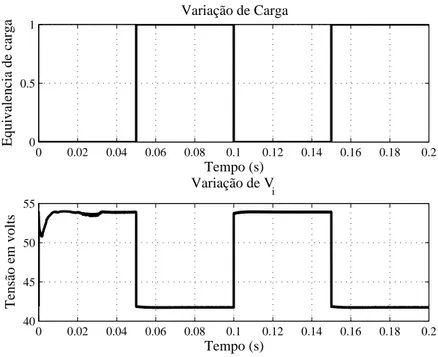
5.1 Variação da carga e da tensão de entrada no conversor. . . 50

5.2 Modelo do conversor original em malha fechada no PSIM. . . 51

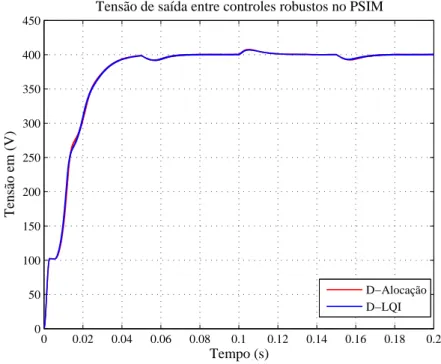
5.3 TensãoVo dos controlesD-alocação de polos eD-LQI para o conversorboost original. . . 53

(14)

Lista de Figuras xiii

5.5 Tensão de referência PWM tanto pelo controle porD_{-alocação de polos como} D_{-LQI para o conversor}_boost_original. _{. . . .} ₅₄

5.6 Tensão e corrente de sa´ıda para o controlador robustoD_{-Alocação de polos para}

Vg=42V. . . 55 5.7 Tensão de sa´ıda e corrente no indutor para o controlador robustoD_{-Alocação}

de polos paraVg=42V. . . 56 5.8 Tens˜ao de sa´ıda e corrente de sa´ıda no conversor para o controlador robusto

D_{-Alocac¸˜ao de polos}_V_g₌₅₄_V_{. . . .} ₅₆

5.9 Tens˜ao de sa´ıda e corrente no indutor no conversor para o controlador robusto

D_{-Alocac¸˜ao de polos}_V_g₌₅₄_V_{. . . .} ₅₇

5.10 Tens˜ao de sa´ıda e corrente de sa´ıda no conversor para o controlador robusto via

D_-LQI_V_g₌₄₂_V_. _{. . . .} ₅₈

viaD_-LQI_V_g₌₄₂_V_. _{. . . .} ₅₈

5.12 Tens˜ao de sa´ıda e corrente de sa´ıda no conversor para o controlador robusto via

D_-LQI_V_g₌₅₄_V_. _{. . . .} ₅₉

viaD_-LQI_V_g₌₅₄_V_. _{. . . .} ₅₉

5.14 Comparac¸˜ao de incertezas na escolha da mais representativa. . . 62

5.15 Análise da curvaG(jω)K(jω). . . 62 5.16 Curvas deS(jω)eT(jω)do modelo compensado porD_{-Alocação de polos e}

D_{-LQI. . . .} ₆₃

5.17 Análise de estabilidade robusta dos controladores D_{-Alocação de polos e} D

-LQI em relação à incerteza∆_m₃. . . 64 6.1 Diagrama geral do circuito com a configuração de controle. . . 66

6.2 Conversorboostoriginal. . . 67

6.3 Tens˜ao e corrente de sa´ıda, sinal de controle aplicada ao conversor em regime

permanente. CanalVo 100V/div, canalIo 200mA/dive canalVPW M 20V/div.

Eixo do tempo (horizontal) 10µs/div. . . 68

6.4 Tens˜ao e corrente de sa´ıda durante a mudanc¸a do degrau de carga. CanalVo

100V/div, canalIo 200mA/div. Eixo do tempo (horizontal) 1ms/div para

Fi-gura 6.4(a) e 20ms/divpara Figura 6.4(b). . . 69

6.5 Tens˜ao e corrente de sa´ıda no momento do degrau de carga . CanalVo 2V/div,

(15)

Lista de Figuras xiv

6.6 Tens˜ao e corrente de sa´ıda e sinal de PWM aplicado ao conversor paraVg=54V em regime permanente. CanalVo 100V/div, canal Io 200mA/div. Eixo do

tempo (horizontal) 10µs/div. . . 72

6.7 Tensão e corrente de sa´ıda durante a mudança do degrau de carga paraVg=54V. CanalVo100V/div, canalIo200mA/div. Eixo do tempo (horizontal) 20ms/div. 73 6.8 Tensão e corrente de sa´ıda no momento do degrau de carga. CanalVo 2V/div, canalIo200mA/div. Eixo do tempo (horizontal) 20ms/div. . . 74

6.9 Tens˜ao de sa´ıda, tens˜ao de entrada e corrente no indutor no momento do degrau de carga. CanalVo 100V/div, canalVg 20V/dive o canal IL 5A/div. Eixo do tempo (horizontal) 20ms/div. . . 75

6.10 Tens˜ao e corrente de sa´ıda e sinal de PWM para o controle D_{-LQI, sendo} Vg=42V.CanalVo100V/div, canalIo200mA/div. Eixo do tempo (horizontal) 10µs/div. . . 77

6.11 Tensão e corrente de sa´ıda para o controleD_{-LQI com variação de carga, sendo} Vg =42V. Canal Vo 100V/div, Io 200mA/div. Eixo do tempo (horizontal) 5ms/divpara Figura 6.11(a) e 20ms/divpara Figura 6.11(b). . . 78

6.12 Tens˜ao e corrente de sa´ıda, sendoVg=42V. CanalVo 2V/div, Io 200mA/div. Eixo do tempo (horizontal) 20ms/div. . . 79

6.13 Tens˜ao de sa´ıda, tens˜ao de entrada e corrente no indutor, sendoVg=42V. Canal Vo100V/div, canalVg20V/dive canalIL 5A/div. Eixo do tempo (horizontal) 20ms/div. . . 80

6.14 Tens˜ao de sa´ıda, corrente no indutor para o controle D_{-LQI, sendo}_V_g₌₅₄_V_. CanalVo 100V/div, canal IL 5A/div. Eixo do tempo (horizontal) 200ms/div para Figura 6.14(a) e 50ms/divpara Figura 6.14(b) . . . 81

6.15 Tensão de sa´ıda, corrente no indutor com variação de carga, sendoVg=54V. CanalVo2V/div, canalIL 5A/div. Eixo do tempo (horizontal) 20ms/div. . . . 82

6.16 Tens˜ao de sa´ıda, corrente no indutor, sendoVg=54V.CanalVo100V/div, canal Vg20V/dive canalIL5A/div. Eixo do tempo (horizontal) 20ms/div. . . 83

6.17 Tens˜ao de sa´ıda, corrente no indutor para o controleD_{-LQI em regime} perma-nente, sendoVg=54V.Canal Vo 100V/div, canal IL 5A/div. Eixo do tempo (horizontal) 20µs/div. . . 84

A.1 Descompactando pastas SeDuMi e Yalmip . . . 92

A.2 Pasta dotoolboxdo MATLAB . . . 93

A.3 Instalac¸˜ao dos pacotes SeDuMi e Yalmip no MATLAB . . . 93

(16)

Lista de Figuras xv

A.5 Instalando o pacote Yalmip no MATLAB . . . 94

A.6 Confirmando os pacotes SeDuMi e Yalmip no MATLAB . . . 95

A.7 Testando o pacote Yalmip nopromptdo MATLAB . . . 95

(17)

xvi

Lista de Tabelas

3.1 Parˆametros do conversor original adaptado de Orellana-Lafuenteet al. (2010),

Reiset al.(2011). . . 33

3.2 Parˆametros do conversor equivalente (ORELLANA-LAFUENTEet al., 2010;

REISet al., 2011). . . 34

3.3 Incertezas de Projeto do conversor conforme e Tabela 3.1 condic¸˜oes f´ısicas de

aplicac¸˜ao. . . 40

5.1 Frequˆencias de canto resultantes de cada controle. . . 60

5.2 Autovalores do modelo de malha aberta e fechada do conversor boost equivalente. 61

(18)

xvii

Lista de S´ımbolos

Vo- Tensão de sa´ıda do conversor em função do tempo,Vo=Vo(t);

Vg- Tensão de entrada do conversor em função do tempo,Vg=Vg(t)

Dd - Ciclo de trabalho do conversor;

Voeq- Tensão de sa´ıda equivalente do conversor em função do tempo,Voeq =Voeq(t);

Vgeq- Tensão de entrada equivalente do conversor em função do tempo,Vgeq=Vgeq(t);

Ddeq- Ciclo de trabalho do conversor equivalente;

rv - Relação de tensão entre conversor original e o conversor equivalente;

x - Vetor de estados do sistema no espaço de estados dimensão xm×1(t) ou dimensão compat´ıvel,x=x(t);

u- Vetor de controle do sistema no espac¸o de estados dimens˜aou1×1(t),u=u(t);

A- Matriz de estado de dimens˜aoAm×mou dimens˜ao compat´ıvel;

B- Matriz de controle de dimens˜aoBm×1ou dimens˜ao compat´ıvel;

C- Matriz de estado de sa´ıda de dimens˜aoC1×mou dimens˜ao compat´ıvel;

D- Matriz de controle de sa´ıda de dimens˜aoD1×1;

∆A- Matriz de estado de incertezas de dimens˜aoAp×pou dimens˜ao compat´ıvel;

∆B- Matriz de controle de incertezas de dimens˜aoBp×1ou dimens˜ao compat´ıvel;

∆C- Matriz de estado de incertezas de sa´ıda de dimens˜aoC1×pou dimens˜ao compat´ıvel;

∆D- Matriz de controle de sa´ıda de incertezas de dimens˜ao;D1×1;

V(x)- Func¸˜ao de Lyapunov;

J - Função custo ou ´ındice de desempenho quadrático em função do tempo,J=J(t);

P- Vari´avel semi definida positiva de dimens˜ao de ordemmou compat´ıvel com a matriz

(19)

Lista de S´ımbolos xviii

Y - Vari´avel auxiliar de dimens˜ao compat´ıvel com a transposta deB,dim(Y) =dim(B′);

Q- Matriz de ponderação arbitrária compat´ıvel com a dimensão deA;

R- Matriz de ponderação arbitrária de ordem compat´ıvel ao número de entradas de

con-troleu;

K - Ganho de realimentac¸˜ao de estados compat´ıvel com a transposta de B, dim(K) =

dim(B′);

Z - Matriz auxiliar de minimização compat´ıvel de ordem compat´ıvel ao número de

entra-das de controleu;

z- Vari´avel complexa no plano da transformada de Laplace;

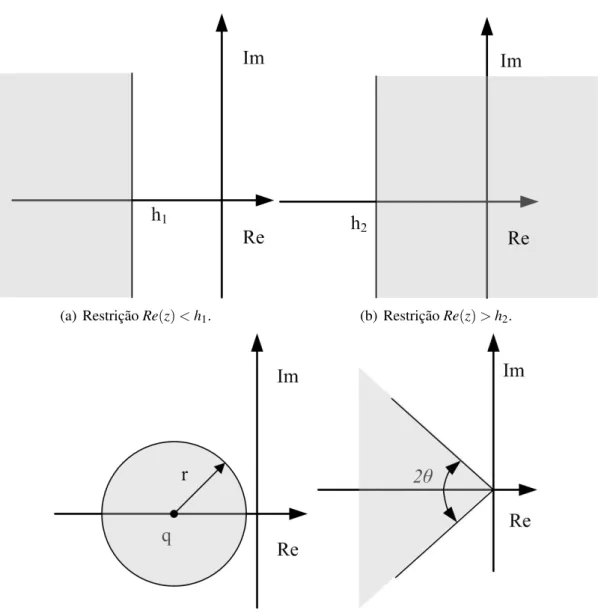
h1- Limite m´ınimo de restric¸˜ao;

h2- Limite máximo de restrição;

rr - Raio do disco centrado em(−q,0);

θ - Ângulo de restrição do setor cônico da origem;

D _{- S´ımbolo de regi˜oes LMIs;}

Co- Capacitor de sa´ıda no lado da carga;

Coeq - Capacitor equivalente de sa´ıda no lado da carga;

Rse - Resistˆencia intr´ınseca em serie com o capacitor;

Rseeq - Resistˆencia equivalente intr´ınseca em serie com o capacitor equivalente;

L- Indutˆancia de projeto no conversor original;

Leq- Indutˆancia equivalente de projeto no conversor equivalente;

Ro- Resistˆencia de carga do conversor original;

Roeq - Resistˆencia equivalente de carga do conversor equivalente;

fs- Frequˆencia de chaveamento do conversor;

fseq- Frequˆencia de chaveamento equivalente do conversor;

(20)

Lista de S´ımbolos xix

Td - Intervalo de chaveamento;

¯

B- Matriz de controle auxiliar de dimens˜ao ¯Bm×1ou dimens˜ao compat´ıvel;

¯

D- Matriz de controle de sa´ıda auxiliar de dimens˜ao ¯Dm×1ou dimens˜ao compat´ıvel;

X - Vari´avel de estado em regime permanente;

Vo- Vari´avel de sa´ıda em regime permanente;

χ - Variável de estado com pertubação do ciclo de trabalho;

vo- Variável de sa´ıda com perturbação do ciclo de trabalho;

A1,A2- Matrizes de estado do conversor no intervalo de chaveamentoS1eS2;

B1,B2 - Matrizes de entrada de controle do conversor no intervalo de chaveamentoS1 e

S2;

C1,C2- Matrizes de estado de sa´ıda do conversor no intervalo de chaveamentoS1eS2;

D1,D2- Matrizes de entrada de controle do conversor no intervalo de chaveamentoS1 e

S2;

r(t)- Entrada de referˆencia;

S(s)- Função sensibilidade ou função S(s);

T(s)- Função co-sensibilidade ou função T(s);

ξ - Erro de regime integrado;

ˆ

A,Bˆ,Cˆ,Dˆ - Matrizes expandidas de dimens˜oes compat´ıveis com as matrizesA,B,C,D;

VT - Tens˜ao de 5 volts;

u- entrada de controle no conversor, sendou=d;

x - variável de estado, considerando o modelo espaço de estado médio x=χ+X, na teoria do controle aplicado ao conversor,x=χ;

G(s)- Função de transferência sem incertezas;

˜

G(s)- Função de transferência com incertezas;

m f a - Sub´ındice do modelo espac¸o de estados m´edio em malha fechada do controle por

(21)

Lista de S´ımbolos xx

m f lqi - Sub´ındice do modelo espac¸o de estados m´edio em malha fechada do controle por

(22)

xxi

Lista de Acrˆ

onimos e Abreviaturas

LMI -Linear matrix Inequalities- Desiguladades Matriciais Lineares;

CC - Corrente Cont´ınua;

CA - Corrente Alternada;

LQR -Linear Quadratic Regulator- Regulador Linear Quadr´atico;

LQI - Linear Quadratic Regulator with Integral Action - Regulador Linear Quadr´atico

com Ac¸˜ao Integral;

LQG -Linear Quadratic Gaussian- Regulador Linear Quadr´atico Gaussiano;

PDC -Parallel Distribuition Compesation- Compensac¸˜ao Paralela Distribu´ıda;

PWM -Pulse Width Modulation- Modulac¸˜ao por Largura de Pulso;

SVD -Singular Value Decomposition- Decomposic¸˜ao de Valores Singulares;

FTMF - Função de Transferência em Malha Fechada;

MCC - Modo de Conduc¸˜ao Cont´ınua;

GPEC - Grupo de Pesquisa em Energia e Controle;

(23)

1

1 Introdu¸c˜

ao

Este cap´ıtulo aborda sobre o estado da arte dos conversoresbooste sobre os trabalhos

en-volvendo LMIs. Além disso, é feita uma revisão bibliográfica sobre os principais trabalhos que

motivaram esta dissertação. São mostrados os objetivos bem como as contribuições propostas,

além do breve resumo dos cap´ıtulos desta dissertação.

1.1 Estado da arte sobre os temas

1.1.1 Estado da arte sobre o conversor

boost

O trabalho de Middlebrook e Cuk (1976), embora não seja recente, é uma referência

rele-vante na modelagem de conversores CC-CC, pois aborda al´em do modelo linearizado no espac¸o

de estados aplicado aos conversoresbuckeboost, apresenta tamb´em a modelagem no espac¸o de

estados em pequenos sinais destes conversores. Esse trabalho ´e base para o modelo no espac¸o

de estados adotado para o projeto de controle do conversorboostdesta dissertac¸˜ao.

O trabalho de Leung et al. (1991, 1993) elabora o projeto de controle ´otimo discreto em

conversores CC-CC, levando em consideração o uso de observadores e análise dos zeros e

polos e an´alise no dom´ınio da frequˆencia para o projeto usando o controle LQR.

Mohan (1995) apresenta o n´ıvel de conte´udo semelhante ao apresentado por Erickson

(2001). Contudo, seu livro visa o aspecto computacional e aplicado `a modelagem de

con-versores. Além disso, essa referência apresenta a teoria aplicada, levando em consideração os

tipos de modelagens matem´aticas que podem ser utilizadas nos conversores, entre estas

mode-lagens está o modo de condução cont´ınuo. O livro de Mohan (2003) aborda a teoria clássica

dos conversores semelhante ao conceito empregado por Erickson (2001).

Gezginet al.(1997) elaboram uma metodologia sistem´atica para o projeto de controle ´otimo

LQR considerando os parâmetros de projeto variantes e a minimização da potência consumida

pelo conversor. Seu trabalho faz uso de um algoritmo que busca as matrizes de ponderac¸˜ao Q e

R que satisfaz o ´ındice de desempenho e as faixas de tolerˆancias dos parˆametros do dispositivo.

O estudo sobre o conversor boost faz uso pela literatura cl´assica de Rashid (2001). A

(24)

1.1 Estado da arte sobre os temas 2

(1995, 2003), Sira-Ram´ırez e Silva-Ortigoza (2006).

Erickson (2001) aborda os fundamentos sobre conversores de potˆencia. Seu livro abrange

os principais tipos de conversores tanto CC-CC como CC-CA ou CA-CC est´aticos. Al´em disso,

é mostrado o conteúdo de modelagem e controle clássico aplicado em conversores em geral.

Casale et al.(2002) elaboram uma metodologia para obtenção dos parâmetros do

contro-lador considerando uma regi˜ao de tolerˆancia factivel com os dispositivos f´ısicos existentes,

como resistores e capacitores para o controlador anal´ogico. Cita-se tamb´em que Garceraet al.

(2002) fazem a an´alise de projeto de controle do conversor CC-CC considerando as incertezas

param´etrica do processo, visando o projeto de um controlador robusto.

Todorovicet al.(2004) fazem uma an´alise dos parˆametros de entrada e de sa´ıda do

conver-sor para o projeto do controlador. Seu trabalho considera uma faixa de variação das tensões de

entrada e de sa´ıda, pois seu conversor é projetado para satisfazer as condições de operação de

um painel fotovoltaico.

O livro de Sira-Ram´ırez e Silva-Ortigoza (2006) aborda o conceito de conversores pela

modelagem n˜ao linear e pela modelagem linearizada do conversor. Al´em disso, sua teoria

considera que os parˆametros dos conversores s˜ao variantes. Bryant e Kazimierczuk (2007)

fazem uma análise de projeto dos conversores usando o modo de condução cont´ınua - MCC.

Este conceito é abordado também na literatura da eletrônica de potência de Erickson (2001),

Mohan (1995, 2003).

Os trabalhos feitos por Bascop´e e Barbi (2000), Torrico-Bascope et al. (2006a, 2006b,

2006c) fazem an´alise do principio de funcionamento do conversorboostde alto ganho de tens˜ao

com célula de comutação de três estados . De Torrico-Bascopeet al.(2006a), foi publicado o

trabalho de Araujoet al.(2010), que trata-se da generalizac¸˜ao do conceitos do conversorboost

de alto ganho com comutac¸˜ao em 3 estados. Este trabalho aborda os conceitos fundamentais

para o projeto f´ısico do conversor de acordo com as especificac¸˜oes exigidas. Arango et al.

(2005) fazem a aplicac¸˜ao do controle LQR em um conversorboostdo tipointerleaved, sendo

então uma estratégia de controle ótimo em variações doschoppersclássicos.

Orellana-Lafuenteet al.(2010), Reiset al.(2011), Reis (2012) aplicam os conceitos de

con-versores de alto ganho de tens˜ao de Torrico-Bascopeet al.(2006a, 2006b), utilizando os

mes-mos parˆametros de projeto, contudo com estrat´egias de controle diferentes. Orellana-Lafuente

et al.(2010) usam dos m´etodos cl´assicos de projeto de conversoresboost, enquanto Reiset al.

(2011), Reis (2012) faz uso do controle LQR com ação integral via resolução da equação de

Riccati para obter os parˆametros do controlador. O trabalho deste ´e inspirado em Gezginet al.

(25)

1.1.2 Estado da arte sobre as Desigualdades Matriciais Lineares e a teoria

do controle

Os livros de Ogata (1986), Dorf e Bishop (1998), Chen (1999), Ogata (2003), apesar de

fazerem parte da literatura cl´assica da teoria do controle, abordam teorias fundamentais para

os projetos dos controladores. Entre estas teorias est˜ao as topologias de controle por

servo-mecanismo ou modelo interno de controle, que são topologias que visam anular a ação de

um determinado sinal persistente. Al´em disso, Maciejowski (1989), Shahian e Hassul (1993)

também são considerados livros que abordam a teoria clássica do controle. Contudo, sua teoria

aborda os conceitos de controle robusto e an´alise das incertezas do processo, assim como Dorf

e Bishop (1998), Skogestad e Postlethwaite (2005).

O artigo de Bernussou et al. (1989) mostra os procedimentos de programac¸˜ao para

pro-blemas envolvendo estabilidade quadr´atica. Trata-se de um trabalho relevante, pois relaciona

os teoremas de Lyapunov e programação linear para resolução de problemas de estabilidade.

A metodologia de programação empregada neste artigo é base para diversos problemas de

otimização por LMIs. Além disso, Peres (2011) possui um conjunto de materiais didáticos

sobre LMIs baseadas nas principais referˆencias bibliogr´aficas relacionadas ao assunto.

Ghaouiet al.(1992) mostram uma metodologia para solução do regulador linear quadrático

- LQR - utilizando desigualdade de Lyapunov via LMIs. Este trabalho apresenta um algoritmo

de resolução desta metodologia por meio de programação linear.

Os trabalhos de Boydet al.(1994), Gahinetet al.(1995) s˜ao o marco inicial para o

conhe-cimento sobre as LMIs. O material de Boydet al. (1994) aborda os conceitos fundamentais

de LMIs e seu uso em situações que mostra a necessidade de restrição matemática. Já

Gahi-netet al.(1995) mostram os conceitos de LMIs aplicado à programação semi definida. Além

disso, aborda os teoremas de estabilidade Lyapunov, complemento de Schur e a teoria daD

-estabilidade atrav´es doLMI Control Toobox, que ´e uma ferramenta computacional do MATLAB

capaz de resolver problemas via LMIs.

Chilali e Gahinet (1996) apresentam uma nova metodologia de resoluc¸˜ao de problemas

com controleH∞utilizando restrições por alocação de polos otimizados via LMIs. A inovação

deste trabalho está no emprego de uma metodologia versátil de otimização, pois um conjunto

de restrições f´ısicas de projeto no âmbito da estabilidade pode ser modelado matematicamente

via restric¸˜oes LMIs.

Deve-se citar ainda que Feronet al.(1996), Wang e Burnham (2002) fazem uma an´alise de

estabilidade via LMIs de sistemas modelados por sistemas lineares com parˆametros variantes

-LPVs. Este tipo de an´alise ´e relevante pois permite que sistemas f´ısicos sejam modelados

(26)

tais variac¸˜oes.

Os trabalhos de Trofino (2000), Trofino et al. (2003) constituem uma referˆencia did´atica

sobre LMIs. Suas referências são compilações resumidas de controle otimizado via

desigual-dades matriciais lineares. Em sua teoria são abordados controles por alocação de polos, LQR,

H2-H∞, estabilidade e controle via LMIs em sistemas LPV e filtro de Kalman via LMIs. Al´em

disso, seus trabalhos fazem menc¸˜ao ao trabalho de Dullerud e Paganini (2000), que aborda a

resolução de sistemas LMIs por otimização convexa.

O trabalho de Souza (2002) trata de uma aplicac¸˜ao sobre LMIs voltada para os aspectos

computacionais. Seu trabalho propõe melhorias de otimização LMIs em sistemas modelados

no tempo cont´ınuo e discreto, principalmente em sistemas mal condicionados.

Zanchin (2003) faz aplicação do conceito de LMIs em geração distribu´ıda. Seu trabalho

usa o controleH∞via LMI por sistemas descritores em geradores s´ıncronos ligados a rede.

Johnson e Erkus (2005) aplicam os conceitos de LMIs em um sistema de amortecimento

massa-mola.

O livro de Skogestad e Postlethwaite (2005) tamb´em faz breve estudo sobre LMIs, com

ênfase na aplicação em controleH∞. A ferramenta de otimização abordada nessa bibliografia é

oLMI Control Toolboxde Gahinet et al.(1995). Cita-se ainda que sua bibliografia aborda os

conceitos fundamentais de incertezas estruturadas e n˜ao estruturadas.

Além disso, o trabalho de Faria (2005) trata o controle por realimentação de estados por

alocação de polos via LMIs, em que Faria () também possui um tutorial voltado para o público

leigo no assunto sobre LMIs. Trata-se de um tutorial didático que é bastante amigável para o

aprendizado sobre controle e estabilidade via otimizac¸˜ao por LMIs, pois aborda a teoria

jun-tamente com a aplicação computacional. Este tutorial também faz uso do MATLAB e das

ferramentas de otimização SeDuMi e Yalmip , além de ensinar a correta instalação destes

oti-mizadores. Cita-se ainda que o mesmo autor possui uma tese utilizando controle por alocac¸˜ao

de polos via LMIs por realimentac¸˜ao derivativa (FARIA, 2009).

O trabalho de Ko et al.(2006) constitui-se numa aplicac¸˜ao do controle LQR via LMIs de

Ghaouiet al.(1992). Esse trabalho aplica os conceitos de controle ´otimo via LMIs num sistema

de aerogeradores de máquinas ass´ıncronas de dupla excitação. Além disso, Olallaet al.(2009)

aplicam os conceitos de LQR via LMIs em conversores est´aticos CC-CC, sendo uma referˆencia

importante para esta dissertac¸˜ao. Este trabalho inspirou Montagner e Dupont (2010) fazer a

mesma aplicação sendo usado uma busca de parâmetros Q e R por Algoritmos Genéticos para

otimizar a resposta no tempo.

Os trabalhos de Filho (2007), Assunção et al. (2007) trata de aplicações voltadas para o

(27)

1.2 Revis˜ao bibliogr´afica 5

trabalhos que propõem o conceito de controle por alocação de polos e modificação de zeros via

LMIs.

A dissertac¸˜ao de Gabe (2008) faz uso do controle H∞ em inversores com filtro LCL. Este

trabalho aplica o controle robusto via LMI em conversores de potˆencia semelhante ao trabalho

de Olallaet al.(2009).

O livro de Palhares e Gonc¸alves (2008), possui uma abordagem did´atica e bastante aplicada,

sendo útil para aplicações na área de controle e automação. Tal literatura contém teorias LMI

de Boydet al.(1994), Gahinetet al.(1995), Chilali e Gahinet (1996).

O minicurso de Oliveira e Peres (2010) é um pequeno tutorial voltado para ensino e aplicação

das LMIs no controle e na estabilidade de sistemas lineares. Ele consiste em aplicac¸˜oes

vol-tadas para o p´ublico leigo no assunto sobre LMIs. Este minicurso faz uso do MATLAB e das

ferramentas de otimizac¸˜ao SeDuMi e Yalmip .

1.2 Revis˜

ao bibliogr´

afica

Middlebrook e Cuk (1976) oferecem uma modelagem alternativa no modelo de espac¸o de

estados médio no MCC. Observa-se ainda que as matrizes modeladas no formato ˙x=Ax+Bu, y=Cx+Du assumirão condições incomuns, pois existe D6=0 para o modelo do conversor boost. Esta modelagem não foi abordada nem por Reiset al.(2011), nem pelos autores Olalla

et al. (2009), Montagner e Dupont (2010), estes por sua vez apresentaram uma modelagem

simplificada e ideal dos conversores. O modelo Middlebrook e Cuk (1976), no entanto, oferece

uma modelagem mais completa, considerando as perdas em todos os componentes do conversor.

A condição D6=0 torna a solução de uma estratégia de controle mais complexa. Para

contornar este problema, muitos autores utilizam modelos linearizados em queD=0. Contudo, considerando as condições que geraramD6=0, deve-se projetar uma estratégia de controle que

resolva este problema.

Os trabalhos de Boydet al.(1994), Gahinetet al.(1995), Chilali e Gahinet (1996), Palhares

e Gonc¸alves (2008) mostram teorias que podem ser facilmente aplicadas no controle de

con-versores CC-CC utilizando restrições LMIs. Além disso, deve-se considerar que para garantir

os conceitos de estabilidade robusta dentro das especificações desejadas, os critérios de

robus-tez devem ser satisfeitos de acordo com Maciejowski (1989), Shahian e Hassul (1993), Dorf e

Bishop (1998), Chen (1999), Skogestad e Postlethwaite (2005).

Os trabalhos de Olallaet al.(2009), Montagner e Dupont (2010) mostraram que ´e poss´ıvel

aplicar os conceitos de LMIs como estrat´egias de controle para seus respectivos conversores

CC-CC. Deve-se considerar que, para projeto de conversores, existem limitac¸˜oes de projeto e

(28)

1.3 Objetivos e contribuic¸˜oes deste trabalho 6

para o projeto de seus controladores. Contudo, tais autores n˜ao consideraram os efeitos das

incertezas em seus trabalhos. Apenas usaram o conceito de politopos, não sendo condições

necess´arias e suficientes que atestam que seus sistemas s˜ao robustos.

Cita-se ainda que, apesar da soluc¸˜ao LQR destes autores se mostrarem eficazes em seus

trabalhos, n˜ao foram feitas an´alises mais profundas a respeito dos autovalores encontrados e seu

comportamento na frequência. Isto porque, frequências de canto em malha fechada próximo à

frequˆencia de chaveamento PWM podem comprometer o desempenho do conversor. Portanto,

apesar de seus trabalhos oferecerem propostas alternativas às estratégias de controle clássico, é

poss´ıvel desenvolver técnicas mais bem elaboradas que considerem as limitações de projeto e

garantam a robustez do processo.

Reiset al.(2011), Reis (2012) apresentaram uma modelagem alternativa ao modelo cl´assico

aplicado em conversores CC-CC, semelhante `as modelagens de Olallaet al.(2009), Montagner

e Dupont (2010), porém considerando perdas no capacitor e levando-se em consideração que

o conversor proposto ´e bem mais complexo, porque trata-se de um conversorboost com alto

ganho de tensão e com célula de comutação em 3 estados. Portanto exige mais cuidado do

ponto de vista de modelagem e implementac¸˜ao. Seu trabalho faz uso do controle LQR com

ação integral via equação de Riccati. Deste modo, a estratégia de controle é o controle ótimo

LQI. O controle ótimo considera a minimização do ´ındice de desempenho como parâmetro

sistem´atico para a garantia de uma resposta eficiente para o processo(CHEN, 1999; OGATA,

2003). No entanto, seus parâmetros de carga e tensão de entrada são variáveis e em seu trabalho

considera-se o ponto de operação em plena carga. Esta condição de operação é considerada

comum na modelagem de conversores CC-CC (MOHAN, 1995; ERICKSON, 2001; MOHAN,

2003; ARANGOet al., 2005; ORELLANA-LAFUENTEet al., 2010).

1.3 Objetivos e contribui¸c˜

oes deste trabalho

1.3.1 Objetivos deste trabalho

• Aplicar os conceitos de otimizac¸˜ao via LMI com D_{-estabilidade no conversor} _boost _de

alto ganho de tensão com célula de comutação de três estados utilizando as estratégias

de controle D_{-LQI e} D_{-Alocação robusta de acordo com Palhares e Gonçalves (2008),}

Boyd et al.(1994), Gahinetet al. (1995), Chilali e Gahinet (1996) utilizando o modelo

no espac¸o de estados m´edio(MIDDLEBROOK; CUK, 1976);

• Analisar as incertezas do processo bem como as restrições na frequência e estabelecer as

estratégias de controle de acordo com tais restrições, isso com base nos parâmetros de

(29)

1.4 Resumo dos cap´ıtulos 7

• Fazer a análise teórico experimental das estratégias de controle aplicadas, levando-se em

consideração a viabilidade do conceito fundamentado na teoria em uma situação real.

1.3.2 Contribuic¸˜oes deste trabalho

Mostrar que os controles robustosD_{-Alocação de polos e}D_{-LQI otimizados via LMIs são}

estratégias de controle válidas e eficazes no controle do conversorboostde alto ganho de tensão

com célula de comutação de três estados , considerando-se as incertezas nos parâmetros da

tensão de entrada e variação da potencia da carga e a modelagem no espaço de estados médio

comD6=0. Isto é comprovado via simulação e experimentalmente e está fundamentado nos

trabalhos citados nesta dissertac¸˜ao, comprovando-se como um controle estavelmente robusto

conforme exigido na literatura.

1.3.3 Publicac¸˜oes em congressos

Vide Costaet al.(2012).

1.4 Resumo dos cap´ıtulos

Além da introdução, os resumo dos cap´ıtulos são:

• Capitulo 2: mostra a teoria de LMI. ´E abordada tamb´em os teoremas de estabilidade de

Lyapunov e o conceito de complemento de Schur, além dos conceitos de estabilização e

malha fechada e incerteza politópica. Mostra-se ainda a teoria de minimização LQR

oti-mizado via LMIs e os conceitos deD_{-estabilidade e sua aplicação no LQR e na alocação}

de polos, desenvolvendo oD_{-LQR e a}D_{-Alocac¸˜ao de polos.}

• Cap´ıtulo 3: neste cap´ıtulo s˜ao abordados os conceitos de conversores cl´assicos e do

con-versor original, é mostrado ainda os parâmetros do concon-versor original e a sua redução do

modelo equivalente. Além disso aborda a modelagem no espaço de estados e as análises

de incertezas do processo.

• Cap´ıtulo 4: Estuda as estrat´egias de controle aplicado ao conversor, mostra a topologia

do servomecanismo com ação integral e a aplicação das estratégias de controleD_{-LQI e}

aD_{-Alocação de pólos robusto, além dos procedimentos de otimização.}

• Cap´ıtulo 5: apresentam os resultados numéricos das matrizes no espaço de estados médio

bem como os resultados numéricos dos ganhos de realimentação de estados. Além disso,

mostra os resultados das funções de transferência das incertezas, além da análise dos

(30)

1.5 Considerac¸˜oes finais 8

• Cap´ıtulo 6: faz-se a an´alise dos resultados experimentais das estrat´egias de controle

apli-cadas ao conversor conforme as especificac¸˜oes de projeto.

• Cap´ıtulo 7: trata-se as conclus˜oes sobre o estudo do conversor como tamb´em analisa os

efeitos das estrat´egias de controle adotadas sobre a planta com os crit´erios de robustez.

Al´em disso, s˜ao mostradas propostas para trabalhos futuros.

• Apêndice A: é um pequeno tutorial que ensina o uso dos pacotes Yalmip e SeDuMi e são

também mostrados os procedimentos de instalação, bem como o uso dos tais pacotes com

exemplos aplicados no MATLAB .

1.5 Considera¸c˜

oes finais

Neste cap´ıtulo ´e mostrado sobre o estado da arte sobre os temas al´em dos trabalho que

motivaram a produção desta dissertação. Com base nos cumprimentos dos objetivos desta

dissertação, os cap´ıtulos seguintes mostrarão as bases teóricas necessárias além da formulação

das estratégias de controle, além dos resultados de simulação e resultados experimentais. Todos

estes tópicos foram brevemente resumidos na Seção 1.4 com o objetivo de orientar o leitor a

(31)

9

2 Teoria das Desigualdades Matriciais Lineares

no Controle por Aloca¸c˜

ao de Polos e LQR

Este cap´ıtulo visa mostrar os conceitos iniciais e básicos necessários para formulação das

LMIs. S˜ao abordados os conceitos de Teorema de Lyapunov no modelo no espac¸o de estados

e a obtenção do ganho de realimentação por meio do tal teorema e a definição de politopos.

Cita-se também o conceito do LQR otimizado via LMIs, além da definição de regiões LMI via

D_{-estabilidade, que pode ser utilizada tanto na alocação de polos como no LQR. Além disso,}

são mostrados os conceitos de incertezas e sua finalidade em relação ao conceito de politopos e

a extração do modelo das incertezas através da planta com variações politópicas.

2.1 Introdu¸c˜

ao `

as desigualdades matriciais lineares - LMIs

As desigualdades matriciais lineares (LMIs) e t´ecnicas LMI surgiram como poderosas

ferra-mentas de projeto em áreas que vão desde a engenharia de controle para o sistema à identificação

e concepção estrutural (GAHINETet al., 1995). Três fatores fazem com que técnicas LMI

se-jam atraentes:

• Uma variedade de especificações de projeto e restrições podem ser expressas como LMIs.

• Uma vez formulado em termos de LMIs, um problema pode ser resolvido exatamente

pela eficiência dos algoritmos de otimização convexa (os “resolvedores LMI”).

• Enquanto a maioria dos problemas com múltiplas restrições ou objetivos carecem de

análise de soluções em termos de equações matriciais, estes muitas vezes permanecem

trat´aveis nos quadros LMIs. Isso faz com que o projeto baseado em LMIs seja uma

alter-nativa valiosa para cl´assicos m´etodos “anal´ıticos”.

A hist´oria das LMIs comec¸a em aproximadamente 1890, quando Lyapunov publicou sua

obra, uma introdução, do que hoje é conhecida por teoria de Lyapunov. Ele mostrou que uma

equac¸˜ao diferencial do tipo

dx(t)

(32)

2.1 Introdução às desigualdades matriciais lineares - LMIs 10

é estável se e somente se existir uma matriz P semi definida positiva (isto é, P>0) de modo

que

A′P+PA<0.

A condição que Lyapunov desenvolveu é denominada de estabilidade de Lyapunov em P, que

é uma forma especial de LMI. Além disso Lyapunov mostrou que dado um ponto de operação

Q=Q′>0, na equaçãoA′P+PA=−Qexiste um P>0 em que a equação diferencial citada é estável. Logo, a LMI usada pela primeira vez para analisar a estabilidade de um sistema

dinˆamico foi a desigualdade de Lyapunov, que pode ser resolvido analiticamente (BOYDet al.,

1994). Portanto, um resumo dos principais acontecimentos na hist´oria de LMIs na teoria de

controle desde a resolução da primeira LMI segue-se então:

• 1890: Surge a primeira LMI. Uma solução anal´ıtica por LMI através da equação de

Lya-punov.

• Década de 1940: Aplicação de métodos de Lyapunov para engenharia de problemas de

controle real. Pequenas LMIs resolvidas “`a m˜ao”.

• In´ıcio da década de 1960: Lema Positivo-Real dá técnicas gráficas para resolver uma

outra fam´ılia de LMIs.

• Final da década de 1960: A observação de que a mesma fam´ılia de LMIs pode ser

resol-vida através da resolução de uma Equação Algébrica de Riccati (Algebric Riccati

Equa-tion- ARE).

• In´ıcio da d´ecada de 1980: Reconhecimento de que muitas LMIs podem ser resolvidas por

computador através de programação convexa.

• Final da d´ecada de 1980: Desenvolvimento de algoritmos dos pontos interiores para

resoluc¸˜ao de LMIs.

Atualmente, tˆem-se desenvolvido maneiras de resolver uma forma geral de LMIs (BOYD

et al., 1994). Um exemplo de LMI clássico é a resolução da equação de Riccati (OGATA, 2003;

DORF; BISHOP, 1998), que é utilizada para busca do ganho ótimo LQR, é dada por

A′P+PA+Q−PBR−1B′P<0. (2.1)

Em 1971, J. C. Willems,de (2.1) propˆos a seguinte LMI para (2.1):

"

A′P+PA+Q PB

B′P R

#

(33)

2.1 Introdução às desigualdades matriciais lineares - LMIs 11

A expressão (2.2) foi obtida pela autodecomposição da matriz Hamiltoniana (BOYD et al.,

1994), que é a composição original da equação de Riccati.

Seja a seguinte equac¸˜ao diferencial do tipo

dx(t)

dt =Aix(t), (2.3)

em que o sub´ındiceiindica vários pontos de operação de A ou politopos. Do ponto de vista

f´ısico, isto ´e uma incerteza do tipo param´etrica. Portanto, o teorema de Lyapunov pode ser

generalizado de modo a encontrarP>0 est´avel, sendo que

A′₁P+PA1<0, A′₂P+PA2<0,

.. .

A′_iP+PAi<0, ..

.

A′_nP+PAn<0,

(2.4)

em que existemn incertezas, cada incerteza pode ser considerada um ponto de operac¸˜ao,

matematicamente, um politopo. Dado um conjuntonde politopos, existirá uma solução fact´ıvel

se e somente se o conjunto politopo for convexo. Na Figura 2.1(a), ´e ilustrada uma regi˜ao a

soluçãoP>0 encontra-se fora da região politópica válida, portanto esta solução é infact´ıvel. Já

na Figura 2.1(b), é mostrada que a soluçãoP>0 encontra-se dentro da ragião politópica válida,

sendo então uma solução fact´ıvel.

(a) Solução não fact´ıvel. (b) Solução fact´ıvel.

Figura 2.1: Soluc¸˜ao de politopos via LMIs.

No entanto, o conceito de factibilidade ´e bem mais abrangente. O sistema ´e considerado

fact´ıvel, se somente se forem satisfeitas todas as condições de restrições impostas(BOYDet al.,

1994; GAHINETet al., 1995). A ilustração da Figura 2.1 apenas mostra uma pequena aplicação

(34)

2.2 Conceitos b´asicos de LMIs 12

2.2 Conceitos b´

asicos de LMIs

Definição 2.1 Uma desigualdade matricial linear (Linear Matrix Inequalities - LMI) é descrita

pela seguinte express˜ao (BOYD et al., 1994):

F(x) =x1F1+x2F2+x3F3+. . .+xmFm≥ −F0 (2.5)

ou

F(x) =F0+

m

∑

k=1

xiFi,≥0 (2.6)

sendo x∈Rm_{e F}₍_x₎ _{é uma função afim, em que F}_i_∈Rn×m_,_i₌₀_{, ...,}_{m são matrizes simétricas} semi-definidas positivas. Umas das suas caracter´ısticas é apresentar o formato simétrico

em suas matrizes. A restrição em (2.6) consiste numa restrição convexa, isto é, o conjunto

x|F(x)≥0´e convexo.

´

E importante enfatizar que uma LMI pode ser representada de v´arias formas e dificilmente

aparece num problema na forma gen´erica afim (2.6). Por exemplo, dada uma matrizA e uma

matrizQ≥0, a função matricial F(P) =A′P+PA+Q, que aparece em vários problemas de estabilidade, é afim na variávelPe, portanto a desigualdadeF(P)≤0 é uma LMI que pode ser facilmente reescrita na forma (2.6), em quexé o vetor contendo os elementos da matrizPa ser

obtida. A vantagem da representação em (2.6) é que toda LMI pode ser reescrita nessa forma

e, portanto, todos os algoritmos de resolução de LMIs são desenvolvidos nessa representação.

Existem diversos pacotes de resoluc¸˜ao LMI que podem ser usados para resolver problemas

relacionados `as desigualdades matriciais lineares. Segundo Palhares e Gonc¸alves (2008), os

resolvedores mais conhecidos para problemas que usam de LMI s˜ao:

• LMILAB: instalado no Matlab, ´e uma referˆencia muito conhecida no estudo de LMIs.

Seu método de resolução foi desenvolvido por Nesterov e Nemirovski em 1994, também

disponibilizado em 1994. O manual de resoluc¸˜ao do LMILAB foi escrito por Gahinetet

al.(1995) e ´e uma base bibliogr´afica muito citada em trabalhos com LMIs;

• LMITOOL: disponibilizado no software livre do Scilab, é um pacote matemático amigável,

baseado no método de resolução por programação semi definida desenvolvido por

Van-denberghe e Boyd 1996;

• SeDuMi: é um pacote de otimização de matrizes semi definidas desenvolvido por Jos

Sturm. Além disso, oSeDuMi é de uso bastante amigável e versátil em diversas

interfa-ces para resolução matemáticas de problemas com LMIs, como o YALMIP e o próprio

(35)

2.3 Estabilidade de Lyapunov via LMIs 13

• LMISol: é um pacote de otimização desenvolvidos pelos brasileiros Oliveira, Farias e

Geromel em 1997;

• SDPT3: é um pacote desenvolvido para problemas de programação cônica por K.C. Toh,

R. H. Tütüncü e M. J. Todd.

2.3 Estabilidade de Lyapunov via LMIs

A Estabilidade de Lyapunov na teoria do controle ´e formulada inicialmente no conceito

da equação homogênea simples linearizada em um ponto de operação qualquer e uma função

de Lyapunov t´ıpica. Esta função é derivada em um ponto de qualquer ou nulo. A busca da

solução desta função é obtida via otimização LMI. As definições utilizadas seguem as

mode-lagens cl´assicas da teoria do controle (OGATA, 1986; CHEN, 1999; MACIEJOWSKI, 1989;

SKOGESTAD; POSTLETHWAITE, 2005) e da teoria do controle otimizado via LMIs (BOYD

et al., 1994; GAHINETet al., 1995).

Definic¸˜ao 2.2 Considere o seguinte sistema linear invariante no tempo (LTI) modelado no

espac¸o de estados do tipo

˙

x(t) =Ax(t). (2.7)

Definição 2.3 Seja o modelo definido em (2.7) submetido a uma função de Lyapunov do tipo (OGATA, 1986; CHEN, 1999):

V(x) =x′Px>0, (2.8)

conhecida como função de quadrática positiva. Em que P>0 é hermitiana, real e simétrica.

Para encontrar seu ponto de equil´ıbrio,(2.8) ´e derivada de modo que

˙

V(x) =x′ A′P+PAx. (2.9)

Proposição 2.0.1 Para garantir o critério da estabilidade assintótica para sistemas LTI, é

ne-cess´ario que(2.9)seja negativa, portanto

˙

V(x) =x′ A′P+PAx<0⇒A′P+PA<0. (2.10)

Generalizando (2.10) segundo Ogata (1986), Chen (1999), Palhares e Gonc¸alves (2008), vem

˙

V(x) =x′ A′P+PAx<−x′(N)x⇒A′P+PA<−N. (2.11)

Para que (2.11) seja satisfeita para todoAi,i=1,2, ...,mcom base em (2.5), (2.11) torna-se

(36)

2.4 Politopos 14

que ´e o crit´erio da estabilidade de Lyapunov descrito para desigualdades.

Teorema 2.1 (Estabilidade de Lyapunov) (OLIVEIRA; PERES, 2010; BOYD et al., 1994;

GAHINET et al., 1995) Dado o sistema do tipox˙=Ax, existe uma solução P>0 simétrica de modo que A′P+PA+N<0,∀x6=0, sendo N>0simétrica, uma matriz arbitrária forçada ao ponto de operação.

Corol´ario 2.1.1 Do Teorema 2.1, dado o sistema do tipox˙= ∑n

i=1

Aix,n∈N, existe uma soluc¸˜ao

P>0sim´etrica de modo que A′_iP+PAi+N <0,∀x6=0, sendo N >0 sim´etrica, uma matriz

arbitr´aria.

Portanto, o processo de otimização via restrição por LMI é dado por:

       min P=P′tr{P}

su jeito a: P>0

(A′P+PA)<−Q

(2.13) ou        min P=P′tr{P}

su jeito a: P>0

(A′_iP+PAi)<−Q,i=1,2, ...,m,m ∈N

, (2.14)

em que (2.14) ´e aplicado quando existe um conjunto de matrizes conhecido como politopos.

Este tipo de conhecimento ´e bastante ´util para se determinar a estabilidade de modelos que

cont´em uma faixa de incertezas, definida como incertezas polit´opicas.

2.4 Politopos

Definição 2.4 (GAHINET et al., 1995; PALHARES; GONÇ ALVES, 2008) Um politopo consiste

num conjunto poliedral limitado e ´e uma casca convexa de um conjunto finito de v´ertices , sendo

que todo elemento no politopo pode ser gerado pela combinação convexa dos seus vértices.

Considere um politopo descrito por 5 v´ertices na Figura 2.2, mostrado por Palhares e

Gonc¸alves (2008), em queP₌_co_{_v₁_,_v₂_{, ...,}_v₅_}₍_co_{- casca convexa). Qualquer ponto} _p_∈P

pode ser descrito na forma convexa dos v´erticesp= ∑5

i=1

αivi,αi≥0,

5

∑

i=1

αi=1. A propriedade de convexabilidade ´e suficiente para que possa formular a estabilidade de um sistema incerto

(37)

2.5 Complemento de Schur 15

Teorema 2.2 (GAHINET et al., 1995; PALHARES; GONC¸ ALVES, 2008) Dado um sistema

incerto com k v´ertices:

∆[x(t)] =Ax(t),A∈P₌∆ (

A|A= k

∑

i=1

αiAi, ,αi≥0, k

∑

i=1

αi=1 )

. (2.15)

O sistema incerto descrito por(2.15)pode ser dito quadraticamente est´avel se, para sistemas

de tempo cont´ınuo, existe uma matriz P=P′>0, tal que A′P+PA<0,∀A∈P _{ou A}′

iP+PAi< 0,∀i=1,2, ...,k,que é a demonstração do processo de otimização descrito em(2.14).

Figura 2.2: Exemplo de um politopo de 5 v´ertices (PALHARES; GONC¸ ALVES, 2008).

Na teoria do controle, sistemas n˜ao lineares podem ser linearizados em v´arios pontos de

operação. Cada ponto de operação pode ser considerado um politopo, que é uma condição de

estabilidade a ser satisfeita. Tais aplicac¸˜oes podem ser vistas em Bernussouet al.(1989), Koet

al.(2006), Rossiet al.(2007), Olallaet al.(2009), Oliveira e Peres (2010), Montagner e Dupont

(2010).

2.5 Complemento de Schur

OComplemento de Schur ´e um artif´ıcio matem´atico frequentemente usado para converter

uma desigualdade convexa em uma LMI ou vice-versa (PALHARES; GONC¸ ALVES, 2008;

BOYDet al., 1994; GAHINETet al., 1995; PERES, 2011; OLIVEIRA; PERES, 2010). Al´em

disso, ocomplemento de Schur é ideal para casos em que estão presentes expressões matriciais

n˜ao lineares, convertendo-as em LMIs.

Lema 2.1 (Complemento de Schur) (BOYD et al., 1994) Seja a seguinte matriz de blocos

M=

"

A B

C D

#

(38)

2.5 Complemento de Schur 16

sendo D uma matriz quadrada n˜ao singular (ou seja, D−16=0). O complemento de Schur de D

em M, denotado por (M/D), ´e definido por:

M=

"

A B

C D

#

=A−BD−1C⇒(M/D) =A−BD−1C. (2.17)

Teorema 2.3 De(2.17), podem ser formuladas as seguintes express˜oes:

(M\A) =D−CA−1B, (2.18)

(M\B) =C−DB−1A, (2.19)

(M\C) =B−AC−1D. (2.20)

Teorema 2.4 (PALHARES; GONC¸ ALVES, 2008) Do Lema 2.1. Para matrizes sim´etricas do

tipo:

M=M′= "

M1 M2

M₂′ M3

#

, (2.21)

o complemento de Schur ´e aplicado na seguinte forma:

(M\M1) =M3−M2M1−1M2′, (2.22)

(M\M3) =M1−M2M₃−1M2′. (2.23)

As seguintes propriedades aplicadas ao conceito de complemento de Schur em (2.21) de

acordo com Palhares e Gonc¸alves (2008), Oliveira e Peres (2010), Peres (2011) s˜ao:

i. M=M′>0se, somente se M1>0e(M/M1)>0(ou M3>0e(M/M3)>0);

ii. Se M1>0, ent˜ao M=M′≥0, se, somente se(M/M1)≥0(idem para M3e(M/M3)).

Lema 2.2 Outra forma equivalente, usando as propriedades da transformação de congruência conforme Oliveira e Peres (2010) é

M=

"

M1 M2

M₂′ M3

# ⇔

"

M1−M2M3M2′ 0

0 M3

#

. (2.24)

Isto para o caso da matriz arbitr´aria T definida por

T =

"

I 0

−M₂′M1 I

#

, (2.25)

(39)

2.6 Estabilizac¸˜ao 17

2.6 Estabiliza¸c˜

ao

Definição 2.5 Dado o sistema no espaço de estados do tipo:

˙

x=Ax+Bu (2.26)

e o modelo de realimentac¸˜ao de estados dado por

u=−Kx, (2.27)

substituindo(2.27)em(2.26), tem-se

˙x= (A−BK)x⇒ ˙x=A˜x. (2.28)

Corolário 2.4.1 (Estabilidade de Lyapunov Alternativa) Do Teorema 2.1, fazendoP¯=P−1 e multiplicando P−1 à esquerda e à direita a expressão(2.10), sendo P=P′>0, tem-se

A′P¯−_PA¯ _<₀_, _(2.29)

logo

AP−PA′<0. (2.30)

Substituindo-se (2.28) em (2.30) tem-se

(A−BK)P+P(A−BK)′<0. (2.31)

FazendoY =KP em (2.31), proposto por Palhares e Gonc¸alves (2008), Gahinetet al.(1995), Boyd et al. (1994), Rossi et al. (2007), Oliveira e Peres (2010), Skogestad e Postlethwaite

(2005), segue-se ent˜ao que

(AP−BY) + (AP−BY)′<0 (2.32)

ou

AP+PA′−BY−Y′B′<0. (2.33)

em queK=Y P−1,Y ∈Rm×n_e_P₌_P′_>_0.

2.7 Controle LQR via otimiza¸c˜

ao LMI

Definic¸˜ao 2.6 (Linear Quadratic Regulator- LQR) (OGATA, 2003; DORF; BISHOP, 1998)

(40)

2.7 Controle LQR via otimizac¸˜ao LMI 18

de estados baseado na minimização do ´ındice de desempenho quadrático

J= ∞

Z

0

x′Qx+u′Rudt. (2.34)

sendo Q e R são as matrizes de ponderação tal que Q=Q′≥0e R=R′>0.

O ´ındice de minimização (2.34) utiliza-se da definição de equação de estados em (2.26). Ghaoui

et al.(1992) estabeleceu a proposic¸˜ao 2.4.1.

Proposição 2.4.1 (GHAOUI et al., 1992) O processo de otimização

             min

P,Z tr(QP) +tr(Z)

su jeito a

AP+PA′−BY−Y′B′+I<0

"

Z R1/2Y

Y′R1/2 P

#

>0,P>0

(2.35)

corresponde ao problema de solução LQR, se a matriz de ponderação R é simétrica definida

positiva, o par(A,B)é controlável e o par(Q,A) é observável.

Com base em Ghaouiet al.(1992), Olallaet al.(2009) segue o Teorema 2.5:

Teorema 2.5 (GHAOUI et al., 1992) A função custo em (2.34) é minimizada via LMI, se

min

P,Z tr(QP) +tr(Z) é m´ınimo, de modo que Z é obtida através da desigualdade

"

Z R1/2Y

Y′R1/2 P

#

>0,P>0. (2.36)

Prova 2.5.1 Usando-se os conceitos de minimizac¸˜ao do ´ındice de desempenho LQR de(2.34)

e o conceito de realimentac¸˜ao de estados em(2.27), substituindo em(2.34), tem-se

J= ∞

Z

0

x′Qx+xK′RKxdt = ∞

Z

0

x′ Q+K′RKxdt, (2.37)

aplicando o trac¸o da matriz em ambos os lados, e utilizando-se a propriedade da

comutativi-dade do trac¸o da matriz, de acordo com Ghaoui et al. (1992), Olalla et al. (2009), Ko et al.

(2006), segue-se que

tr(J) =tr



 Q+K′RK

∞

Z

0 xx′dt



, (2.38)

fazendo P= ∞

R

0

xx′dt e substituindo-o em(2.38), tem-se