BELÉM 2014 UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE GEOCIÊNCIAS PROGRAMA DE PÓS-GRADUAÇÃO EM GEOLOGIA E GEOQUÍMICA DISSERTAÇÃO DE MESTRADO Nº 437

Assegurada a reposição da normalidade das condições de vida da população da área afetada pelo acidente grave ou catástrofe, deverá ser declarada a desativação

Cargas pontuais (F ou M): Matematicamente, a aplicação pontual de cargas não existe (é preciso uma área para aplicar, ainda que pequena) e sua ocorrência provocará uma

Também são observadas dobras en echelon desenhada pela camada de minério (Bióxido) métricos e eixos com ângulos baixos entre 4° a 10° para SE. c) As vergências das

Não obstante a reconhecida necessidade desses serviços, tem-se observado graves falhas na gestão dos contratos de fornecimento de mão de obra terceirizada, bem

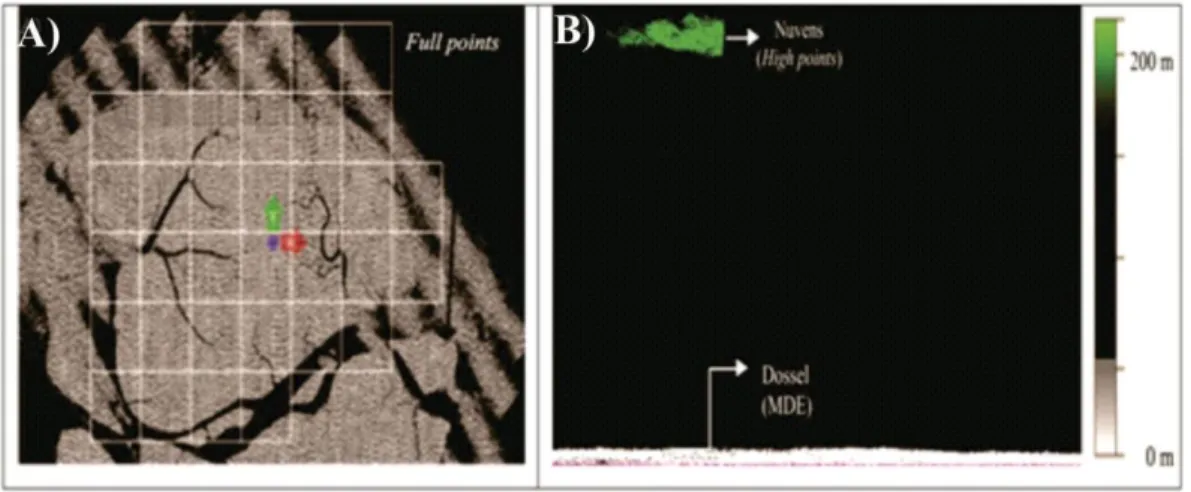
Este trabalho apresenta dados que contribuem para uma melhor avaliação da extensão dos efeitos do UMG no leste da Floresta Tropical Amazônica (elevação de ~ 100 m) tendo como base

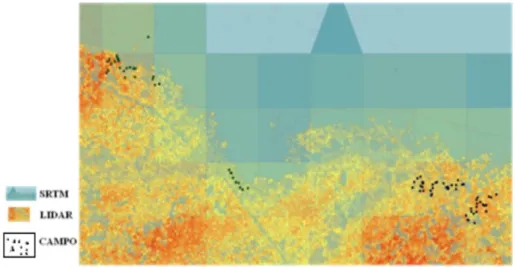
• Avaliação da qualidade altimétrica do SRTM a partir do cálculo do PEC altimétrico, usando como base as Referências de Nível (RN 1 ) presentes na carta Salinópolis e as RN

As principais formas de fósforo: biodisponível (P-Bio), ligado aos oxi-hidróxidos de ferro (P-Fe), ligado à apatita biogênica, autigênica e aos carbonatos

Color–period diagram without reddening correction, demon- strating the variability period as a function of the color index (J − H) for the final sample described in Sect.. Circle