Um problema de sequenciamento em máquinas paralelas não-relacionadas com tempos de preparação dependentes de máquina e da sequência:: modelos e algoritmos exato.

UM PROLEMA DE SEQÜENCIAMENTO EM MÁQUINAS

PARALELAS NO-RELACIONADAS COM TEMPOS DE

PREPARAÇO DEPENDENTES DE MÁQUINA E DA

SEQÜÊNCIA: MODELOS E ALGORITMO EXATO

Instituto de Ciênias Exatas

Programa de Pós-Graduação em Ciênia da Computação

UM PROLEMA DE SEQÜENCIAMENTO EM MÁQUINAS

PARALELAS NO-RELACIONADAS COM TEMPOS DE

PREPARAÇO DEPENDENTES DE MÁQUINA E DA

SEQÜÊNCIA: MODELOS E ALGORITMO EXATO

Dissertação apresentada ao Curso de

Pós-GraduaçãoemCiêniadaComputaçãoda

Uni-versidadeFederalde MinasGeraisomo

requi-sitoparialpara aobtençãodograu deMestre

emCiênia da Computação.

PEDROLEITE ROCHA

Um problema de seqüeniamento em máquinas paralelas não-relaionadas, tempos de

pre-paração dependentes de máquina e da seqüênia, datas de entrega e tarefas ponderadas é

onsiderado neste trabalho. Dois modelos de programação inteira e mista baseados em

es-tratégias lássias da literatura são avaliados. Um algoritmo Branh-and-bound (B&B) é

desenvolvidoe a solução enontrada pela metaheurístiaGRASP é utilizada omolimite

su-perior. Tambémpropomosumonjunto deinstâniasparaestetipodeproblema. Resultados

omputaionais são realizados em vários tipos de testes, onde o algoritmo tem umbom

de-sempenho em instânias de até 30 tarefas. Finalmente, onlusões e direções para futuros

A sheduling problem with unrelated parallel mahines, sequene and mahine dependent

setup times, due dates and weighted jobs is onsidered in this work. Two mixed integer

programing (MIP) models based on lassi strategies from the literature are evaluated. A

Branh-and-Bound algorithm (B&B) is developed and a solution provided by the

metaheu-risti GRASP is used as an upper bound. We also propose a set of instanes for this type

of problem. Computational experiments are arried out in several types of tests, where the

algorithm performs well on instanes withup to 30 jobs. Finally,onlusions and diretions

order in a nite, but very large, disrete universe that is intriately intertwined.

And a seond, but not less important hallenge is how to mould what you have

ahievedin solvingtherstproblem,intoateahable disipline: it does notsue

tohoneyourownintellet(thatwilljoinyouinyourgrave),youmustteahothers

how tohonetheirs. The more youonentrate on thesetwo hallenges,the learer

you will see that they are only two sides of the same oin: teahing yourself is

disovering what isteahable.

Agradeço atodosqueontribuíram paraqueeupudessehegaratéaqui. Agradeço

prinipal-menteameus pais,a quem dedioesta dissertação.

À toda minha família, prinipalmente meus avós Antnio, Cota, Di e Dora, meu tio e

padrinhoJoão, meustiosAfrânioeRiardo eminhastias Elisa,Frane,MaríliaeMariaInês,

todosquesempremederamforça. Tambémaminha madrinhaSabrinaea tia Bel,quenão

são dafamília, masé omosefossem.

Ao meu orientador, Robson, ao meu o-orientador, Martín, que é argentino mas é gente

boa,e aosmembrosda bana quevieram prestigiareste trabalho.

Aosgrandes amigos desdea infânia atéhoje: Luizinho,Riardo e Thiago.

Atodososamigos doLaPO, em espeialaDoinho, Dri,Fred,Gurvan,Lu eOlga.

Aos que tiveram que me agüentar morando debaixo do mesmo teto desde a graduação:

Alla, minha irmã Diana,Lama, Manoel, Mauríio, Menotti eRafael.

Aosamigos parasempre: George, Ismaele Zeniel.

AoOverow: Gudee Torres, easOvergirls: Alê, Camila e Lud.

Aosgrandes amigos doGAAL: Ana,Carlos,Cazita, Delboni,Gaspar, Lidia e Luis.

Aosamigos do peito: Bebex, Clara, Fujii,Gripp, Igorele,Juliano, Lilianee Leonardo.

Atodososamigosdo mestradoe doutorado: AraellyePedrão,Bárbara, Bigonhinha, os

earenses César, Ju eOsama, Diego, Fabíola eNaka,Mauríio eIngrid, Raquele Ruiter.

Aoshefesque tivenasempresas onde trabalheiduranteo perurso: Alberto, Ana,Leo e

Zé Carlos.

E a todas as outras pessoas que zeram parte da minha vida de alguma forma ou se

1 Introdução 1

1.1 Sistemade Produção . . . 1

1.2 Problemasde Seqüeniamento . . . 1

1.3 NotaçãoparaProblemas de Seqüeniamento . . . 2

1.4 ProblemaAbordado . . . 6

1.5 Organização . . . 8

2 Formulações Matemátias 9 2.1 ModeloBaseado noTrabalho de Manne . . . 9

2.2 Modelo BaseadonoTrabalho de Wagner . . . 11

3 Algoritmo Branh-and-Bound 15 3.1 Iniializaçãoom GRASP . . . 16

3.2 OProedimento de Branhing . . . 18

3.3 OProedimento de Bounding . . . 20

3.4 Branh-and-Bound Diotmio . . . 24

4 Testes e Resultados 27 4.1 Instânias . . . 28

4.2 Avaliando GRASPomo limitesuperior . . . 29

4.3 Comparandoosmodelos . . . 31

4.4 DiferentesCenários de Máquinas . . . 32

4.5 Variando a Datade Entrega . . . 33

4.6 Variando o Tempo de Proessamento . . . 34

4.7 Variando o Tempo de Preparação . . . 34

4.8 Branh-and-bound Diotmio. . . 36

4.9 Instâniasde Grande Porte . . . 38

5 Conlusões 41

A Instânia Exemplo 43

3.1 Seqüêniadepassosdaonstruçãoomasposiçõesanalisadasparaadatarefaem

destaque . . . 17

3.2 Seqüêniade passosda busaloalom astroasanalisadas emdestaque . . . . 18

3.3 Seqüêniade passosde PRom asposiçõesanalisadas emdestaque . . . 19

3.4 Primeira fasede branhing . . . 19

3.5 Segunda fasede branhing . . . 20

4.1 Número de nósexpandidosvariando onúmero deiteraçõesdoGRASP . . . 30

4.2 Modelosvs. B&B. . . 31

4.3 Número de nósexpandidosvariando oenário de máquinas omo B&B . . . 32

4.4 Soluções enontradas peloGRASP . . . 34

4.5 Número de nósexpandidosvariando adatade entrega omoB&B . . . 35

4.6 Número de nósexpandidosvariando ostemposde proessamento omo B&B . . 36

4.7 Número de nósexpandidosvariando ostemposde preparação om oB&B . . . . 37

4.1 Valorespadrãoparaasinstânias . . . 28

4.2 NúmerodenósexpandidosedesviopadrãovariandonúmerodeiteraçõesdoGRASP 30

4.3 Tempode CPU gastoe variação dosdois modelos e doB&B. . . 31

4.4 Número de nósexpandidos e desvio padrão variando o enário de máquinas om

o B&B. . . 33

4.5 Número de nósexpandidose desviopadrão variando a datadeentrega omo B&B 35

4.6 Número denósexpandidos edesvio padrãovariando ostemposde proessamento

omo B&B . . . 36

4.7 Númerodenósexpandidosedesviopadrãovariandoostemposdepreparaçãoom

o B&B. . . 37

4.8 Número de nósexpandidose desviopadrão variando o fatordiotmiodo B&B 38

3.1 UmBranh-and-Boundgenério . . . 15

3.2 Bloo prinipaldo B&Be algoritmo de iniialização(GRASP) . . . 16

3.3 Pseudo-ódigo paraoPath-relinking implementado . . . 18

3.4 Primeira fasede branhing . . . 20

3.5 Segunda fasede branhing . . . 21

3.6 B&BDiotmio . . . 24

Introdução

1.1 Sistema de Produção

Oplanejamentodaproduçãoévistoomooplanejamentodaaquisiçãodereursosematérias

primas, assimomooplanejamentodasatividadesdeprodução,neessáriasparatransformar

matériaprima emprodutosaabados,atendendoademandadosonsumidoresdaformamais

eientee eonmia possível[Pohete Wosley (2006 )℄.

No ontexto industrial, problemas de seqüeniamento estão relaionados à área de

Ma-nufaturing Resoure Planning (MRP).A programação éfeita de aordoom ohorizontede

planejamento. Deisõesde longoprazotêmaraterístias estratégias,eportanto são

toma-das pela alta administração. O médio prazo é onheido omo nível tátio. Este trabalho

foano urtoprazo,onheido omoníveloperaional, onde oobjetivoé ordenaraseqüênia

de produção om o objetivo de minimizar osustos de fabriação. Neste nível, ademanda e

datas de entrega já estãodenidas.

Neste tipo de problema, oobjetivo prinipal é denir aseqüênia de proessamento para

atender as demandas e datas de entrega. Além disso, os algoritmos desenvolvidos também

prouram minimizar otempo deprodução e o atrasode ada produto.

1.2 Problemas de Seqüeniamento

Oproblemadeseqüeniamentoestáassoiadoàaloaçãodereursosaumonjuntodetarefas

num dado tempo. Esalonar signia designar reursos para a exeução dastarefas até que

todas tenham sido exeutadas sob as restrições impostas om o objetivo de minimizar o

omprimento do seqüeniamento, dado pelo tempo de proessamento das tarefas, ou um

outro ritério estabeleido no ontexto do problema [Bªa»ewizetal. (1996 )℄. Apliações

desse problema podem ser enontradas em diversas situações do mundo real, por exemplo,

no planejamento da produção,no gereniamento de projetose no seqüeniamento de tarefas

pelaunidade entral deproessamento doomputador.

EsseproblematemsidoestudadodesdeoiníiodoséuloXX,omosprimeirostrabalhos

de50,surgiramasprimeiraspubliaçõesomostrabalhosde Johnson(1954 ),Jakson(1955 ,

1956)e Smith (1956 ). Iniialmente, a maioria dostrabalhos relaionava-se oma análise de

problemas om uma únia máquina ou sistemas om máquinas paralelas. Nesses sistemas,

onsidera-se um onjunto de máquinas idêntias em paralelo, sendo que as tarefas podem

ser proessadas em qualquer uma das máquinas. Com o passar do tempo, situações mais

omplexasdeseqüeniamentodemáquinasforaminvestigadas,omoautilizaçãodemáquinas

omveloidades de proessamento diferentes e a utilizaçãode mais de uma máquina paraa

exeuçãodamesma tarefa.

1.3 Notação para Problemas de Seqüeniamento

Na maioria dosproblemas de seqüeniamento, o número de tarefas e onúmero de máquinas

é assumido nito. O número de tarefas é denotado por

n

, e o número de máquinas por

m

.

Normalmente, o sub-esrito

j

se refere a uma tarefa, e o sub-esrito

i

a uma máquina. Se

uma tarefa requer um número de passos ou operações de proessamento, então o par

(

i, j

)

serefere ao passo ouoperação de proessamento da tarefa

j

na máquina

i

. Essa notação foi

retiradado trabalho dePinedo (1995 ). Osdados seguintes sãorelaionadosà tarefa

j

.

•

Tempo de proessamento (

p

ij

). O

p

ij

representa o tempo de proessamento da

tarefa

j

na máquina

i

. O sub-esrito

i

pode ser omitido seo tempo de proessamento

de

j

não dependerda máquina, ouse

j

for proessadoapenasemumamáquina.

•

Tempo de disponibilidade (

r

j

). Éotempo noqualatarefa

j

hega aosistema,isto

é, omenor tempo paraqueo proessamento datarefa

j

possa omeçar.

•

Data de entrega (

d

j

). Adata de entrega

d

j

representa adata de entrega prometida

da tarefa

j

. Atrasos na data de entrega podem ser permitidos, mas uma penalidade

deveserinserida. Quandoadatadeentregativerqueserabsolutamenteobedeida,ela

é hamadade deadline.

•

Prioridade ou peso (

w

j

). A prioridade ou peso

w

j

da tarefa

j

basiamente denota

a importânia da tarefa

j

relativa às outras tarefas no sistema. Por exemplo, essa

prioridade pode representar ousto dearmazenagem datarefa.

Um problema de seqüeniamento é desrito por um trio

α

|

β

|

γ

. O ampo

α

desreve

o ambiente de máquinas, e ontém uma únia entrada. O ampo

β

fornee detalhes das

araterístias de proessamento e restrições e pode ser vazio, onter uma únia entrada

ou onter entradas múltiplas. O ampo

γ

ontém o objetivo que deve ser minimizado e

normalmente ontém umaúnia entrada.

Osseguintes sãoexemplosde possíveisambientes demáquinas:

•

Uma máquina (

1

). O aso de uma únia máquina é o mais simples de todos os

•

Máquinas idêntias (Pm). Existem

m

máquinas idêntias em paralelo. A tarefa

j

requerumaúniaoperaçãoepodeserproessadaporqualquer umadas

m

máquinasou

porqualquerumapertenenteaumsubonjunto. Seatarefa

j

nãopodeserproessado

em qualquer máquina, mas em um subonjunto, digamos o subonjunto

M

j

, então a

entrada

M

j

aparee no ampo

β

.

•

Máquinas paralelas om veloidades diferentes (Qm). Existem

m

máquinas em

paraleloomveloidades diferentes. Asmáquinasrealizam otrabalho damesmaforma,

diferindoapenasnaveloidade,queédenotadapor

v

i

paraamáquina

i

. Otempo

p

ij

da

tarefa

j

namáquina

i

éiguala

p

j

v

i

,assumindoqueelapossaserproessadapelamáquina

i

. Esseambientedemáquinastambéméonheidoomomáquinasuniformes. Setodas

as máquinas têm a mesma veloidade,isto é,

v

i

= 1

∀

i

, então

p

ij

=

p

j

e o ambiente se

torna idêntio aoanterior.

•

Máquinas não-relaionadas (Rm). Esseambiente éumageneralizaçãodoanterior.

Existem

m

máquinasdiferentesemparalelo. Amáquina

i

podeproessaratarefa

j

om

umaveloidade

v

ij

. Otempo

p

ij

quea tarefa

j

gasta namáquina

i

é iguala

p

j

v

ij

. Se as

veloidades das máquinas são independentes da tarefa, isto é,

v

ij

=

v

i

∀{

i, j

}

, então o

ambiente setornaidêntioao anterior.

•

Flowshop(Fm). Existem

m

máquinasemsérie. Cadatarefatemqueserproessada

por ada uma das

m

máquinas. Todas astarefas têm o mesmo roteiro, isto é, devem

ser proessados primeiro pela máquina

1

, depois pela máquina

2

, e assim por diante.

Após o término em uma máquina um tarefa entra na la para a próxima máquina.

Normalmente,todasaslasoperamomrstinrstout (FIFO),istoé,umatarefanão

pode passar outrana la. Se FIFOé adotado, o owshop é referidoomo ow shop

om permutação, e oampo

β

deve inluira entradaprmu,queé apresentadaabaixo.

•

Flow shop exível (FFs). Umow shopexível éumageneralização dosambientes

owshopemáquinas paralelas. Emvez de

m

máquinasemsérie,existem

s

estágios em

série om umnúmero de máquinas em paralelo em ada estágio. Cada tarefa deve ser

proessada primeiro no estágio

1

, depois no estágio

2

, e assim por diante. Umestágio

funiona omo umbano de máquinas paralelas: emada estágio, uma tarefa

j

requer

apenasumamáquinae,normalmente,qualquermáquinapodeproessarqualquertarefa.

Aslas entreosvários estágiostambém operam, emgeral,oma estratégiaFIFO.

•

Open shop (Om). Existem

m

máquinas. Cada tarefa tem que ser proessada em

ada uma das

m

máquinas. No entanto, alguns dos temposde proessamento podem

serzero. Não hárestriçõesquantoao roteirodeadatarefapeloambientedemáquinas.

Épossíveldeterminarumroteiroparaadatarefa,etarefasdiferentespodemterroteiros

diferentes.

máquina no máximo umavez e job shops onde uma tarefa pode visitar uma máquina

maisde umavez. Noúltimo, o ampo

β

ontém aentrada rer para reirulação, que

é apresentada abaixo.

As restrições espeiadas no ampo

β

podem inluir múltiplas entradas. São algumas

dasentradas possíveis:

•

Data de disponibilidade (

r

j

). Se estesímboloestiverpresentenoampo

β

,atarefa

j

não pode iniiar seu proessamento antes da data de disponibilidade

r

j

. Se

r

j

não

apareeem

β

,oproessamentodatarefa

j

podeomeçaraqualquerhora. Emontraste

om datas de disponibilidade, datas de entrega não são espeiadas neste ampo. O

tipode função objetivo dáindiação suiente seexistemdatas deentrega ounão.

•

Tempos de preparação dependentes da seqüênia (

s

jk

). Representa o tempo

de preparação dependente da seqüênia entre astarefas

j

e

k

;

s

0k

denota o tempo de

preparação paraatarefa

k

seatarefa

k

éa primeiranaseqüênia e

s

j0

denotaotempo

de limpeza após a tarefa

j

se for a última na seqüênia. Se o tempo de preparação

entre as tarefas

j

e

k

depende da máquina, o sub-esrito

i

é inluído, isto é,

s

ijk

.

Se

s

jk

não aparee no ampo

β

, todos os tempos de preparação são assumidos zero

ou independentes da seqüênia, podendo ser simplesmente adiionados aos tempos de

proessamento.

•

Preempções (prmp). Preempções sugerem que não é neessário manter um tarefa

em umamáquina atéo término. É possívelinterromper o proessamento de umtarefa

a qualquer hora, e oloar um tarefa diferente na máquina. A quantidade de tempo

de proessamento que uma tarefa interrompida já reebeu não é perdida. Quando

uma tarefa interrompida volta à máquina (ou a outra máquina no aso de máquinas

paralelas), elasópreisadamáquinaparaotempodeproessamentorestante. Quando

preempçõessãopermitidas, prmp é inluídoao ampo

β

.

•

Restrições de preedênia (pre). Restrições de preedênia podem apareer em

ambientes de uma únia máquina ou de máquinas paralelas, determinando que uma

ou maistarefastenham quetersido ompletadas antesqueoutra tarefasejapermitida

omeçar. Existem várias formasespeiais de restriçõesde preedênia. Se ada tarefa

tem nomáximo umasuessora,asrestriçõessãoreferidas omoumaárvoreinterna. Se

ada tarefa tem no máximo uma predeessora, as restrições são referidas omo árvore

externa. Seadatarefatemnomáximoumapredeessoraeumasuessora,asrestrições

são referidasomo orrentes.

•

Quebras (brkdwn). Quebras de máquinas sugerem que máquinas não estão sempre

disponíveis. Os períodosemque umamáquina nãoestá disponível sãoassumidosxos

(por exemplo,devidoaturnosoumanutenções). Sehámáquinasidêntiasemparalelo,

•

Restrições de elegibilidade (

M

j

). Uma restrição que pode apareer no ampo

β

quando o ambiente de máquinas ontiver

m

máquinas em paralelo (Pm). Quando

M

j

estápresente,nemtodasas

m

máquinassãoapazesdeproessaratarefa

j

. Oonjunto

M

j

denota o onjunto demáquinas apazes de proessar atarefa

j

. Se oampo

β

não

ontém

M

j

,a tarefa

j

podeser proessadopor qualquer umadas

m

máquinas.

•

Permutação (prmu). Umarestrição quepode serapliadanoambientedeowshop,

é que as las na entrada de ada máquina operam de aordo om a polítia FIFO.

Isso quer dizer que a ordem (ou permutação) em que as tarefaspassam pela primeira

máquina émantidaatravésdo sistema.

•

Bloqueio (blok). Bloqueioéumfenmenoqueoorreemowshop. Seumowshop

temumbuerlimitadoentreduasmáquinassuessivas,podeserque,quandoumbuer

ar heio, a máquinaanterior nãopossa liberar atarefa terminada. Esse fenmeno se

hamabloqueio: atarefaterminadatemquepermaneernamáquinaanteriorevitando,

ou bloqueando,a máquinade proessaroutros tarefas.

•

Sem espera (nwt). A restrição sem-espera é outro fenmeno que pode oorrer em

ow shop. Tarefas não podem esperar entre duas máquinas suessivas. Isso quer dizer

queo tempo deiníiodeumatarefapodeseratrasado paragarantirquea tarefapossa

atravessaroowshopsemterqueesperarpornenhumamáquina. Umexemplodeuma

operação é uma linha de fabriação, onde uma determinada peça de metal não pode

esperarpelapróximaetapaporque elaesfriaria.

•

Reirulação (rer). Reirulação pode oorrer em job shop, quando uma tarefa

pode visitarumamáquina maisde umavez.

Outrasentradas doampo

β

sãoauto-expliativas. Por exemplo,

p

j

=

p

india quetodos

os tempos de proessamento são iguais, e

d

j

=

d

india que todas as datas de entrega são

iguais. Como ditoantes, datasde entrega, aoontráriodasdatasdedisponibilidade,não são

normalmente expliitadasno ampo

β

; o tipo da função objetivo nosdá indiação suiente

se ostarefastêm datade entrega ou não.

O objetivo a ser minimizado é sempre uma função dos tempos de término das tarefas,

que, é laro, dependem do seqüeniamento, ou também pode ser uma função das datas de

entrega. Otempode términodaoperaçãoda tarefa

j

na máquina

i

édado por

c

ij

. Otempo

em que a tarefa

j

sai do sistema (o tempo de término na última máquina onde ele requer

proessamento)é denotado por

c

j

. O lateness de umtarefa

j

édenido omo

L

j

=

c

j

−

d

j

que é um valor positivo quando a tarefa

j

é terminada atrasada e negativo quando é

ompletada adiantada. Oatraso, outardiness,datarefa

j

é denidaomo

Adiferençaentreoatrasoelatenesséqueovalordoatrasonunaénegativo. Apenalidade

unitáriada tarefa

j

é denidaomo

U

j

=

(

1

se

c

j

> d

j

0

..

A seguir,temosalguns exemplosde possíveis funções objetivoa seremminimizadas.

•

Makespan (

c

max

). O makespan, denido omo

max(

c

1

, . . . , c

n

)

é equivalente ao

tér-mino da últimatarefa asair dosistema. Ummakespan mínimogeralmenteindia uma

alta utilizaçãodasmáquinas.

•

Lateness máximo (

l

max

). Omáximo lateness,

l

max

,édenido omomax

(

l

1

, . . . , l

n

)

.

Mede a piorviolação dasdatas deentrega.

•

Tempo de término total ponderado (

P

_w

j

·

c

j

). A soma dostempos ponderados

de término das

n

tarefas, utilizando a prioridade

w

j

omo fator de ponderação, dá

uma indiação do usto total do seqüeniamento. A soma dos tempos de término é

freqüentemente referida na literatura omo tempo de uxo (ow time). O tempo de

término total ponderado éhamado detempo deuxo ponderado.

•

Tempo de término total ponderado desontado (

P

(1

−

e

−

rc

j

₎

). Essa é uma

função deustomaisgeralqueaanterior,ondeosustossãodesontadosaumataxade

r

,

0

< r <

1

,porunidadedetempo. Issoé,seatarefa

j

nãoterminaatéotempo

t

,um

ustoadiional

w

j

re

−

rt

_dt

éadiionadoduranteoperíodo

[

t, d

+

dt

]

. Seatarefa

j

termina

no tempo

t

, o usto total do período

[0

, t

]

é

w

j

(1

−

e

−

rt

₎

. O valor de

r

geralmente é

pertode

0

,omo

0

,

1

(ou

10%

).

•

Atraso total ponderado (

P

w

j

T

j

). Também é umafunção de usto mais geral que

o tempo de términototal ponderado.

•

Número ponderado de tarefas atrasadas (

P

_w

j

U

j

). O número ponderado de

tarefas atrasadas, não somente é uma métria de interesse aadêmio, mas também é

um objetivofreqüente na vida real.

1.4 Problema Abordado

Oproblemaonsiderado neste trabalho é umproblema de seqüeniamento em máquinas

pa-ralelasnão-relaionadas omtemposde preparação dependentes demáquina e da seqüênia,

datasde entrega e tarefasponderadas. Este tipo de problemaonsiste emprogramar várias

tarefas para serem proessadas por várias máquinas. Cada tarefa deve ser seqüeniada em

umamáquinaespeía,e aordem em queada máquina iráproessar suastarefasdeve ser

da máquina antes que ela possa proessar a próxima tarefa. Este tempo existe para que a

máquina possaserpreparada paraapróximatarefa(e.g. limpaou re-ongurada)e também

é diferente para ada par de tarefas e ada máquina. Cada tarefa tem também uma data

de entrega e umaprioridade. Emboraa data de entrega possa ser exedida, isso ausa uma

penalidade na função objetivo dependente da prioridade da tarefa. Seguindo a notação de

Pinedo (1995) itada na Seção 1.3, este problema pode ser formalmente denido omo um

Rm

|

s

ijm

|

c

max

+

P

T

i

·

w

i

,onde osigniado de ada membro é:

•

Rm

: problemade seqüeniamento om

m

máquinas paralelas não-relaionadas,

•

s

ijm

: temposde preparação dependentes demáquina eda seqüênia,

•

c

max

+

P

T

i

·

w

i

oobjetivo éminimizar o makespan aresidodo atraso ponderado.

Optamos por uma abordagem exata para o problema, utilizando modelos baseados em

estratégias lássias da literatura, e desenvolvendo umalgoritmo espeío paraele baseado

em Branh-and-Bound (B&B) e GRASP (Greedy RandomizedAdaptive Searh Proedure).

Algoritmos baseados em B&B e na metaheurístia GRASP não são inomuns ao se lidar

omproblemasde seqüeniamento,assimomoemoutrosproblemassimilares[Roundyetal.

(1999 )℄. Rabadietal. (2004) propõe um B&B para um problema de seqüeniamento om

datas deentregaiguaise umamáquinaomtemposde preparação dependentes daseqüênia

(TPDS).UmaadaptaçãodeGRASP[Resendee Feo(1995)℄éusadaparaenontrarumlimite

superiorparaoproblemaexploradonestadissertação. Tambémpodemseritadosostrabalhos

deFeoetal.(1991 );Dahs etal.(1996 ),ondeapliaçõesdeGRASPparaseqüeniamento em

umamáquinasãomostradas,eResende etal.(2002 ),quemostramumaapliaçãointeressante

da metaheurístia paraproblemasde job-shop.

O estudo de problemas de seqüeniamento om TPDS tem atraído muita atenção nos

últimos anos [Kim e Bobrowski (1994 )℄. Eles também são alguns dos problemas de

seqüen-iamento mais omplexos. Considerando apenas uma máquina e um estágio, o problema é

equivalente ao do aixeiro viajante [Bªa»ewizetal. (1996 )℄. Gareye Johnson (1979 )

mos-traram que minimizar o makespan em duas máquinas idêntias é um problema NP-difíil.

Certamente, umproblemaommáquinas não-relaionadase datasdeentregatambémé

NP-difíil.

Há muitos trabalhosonsiderando máquinas paralelas,mas pouos onsideram máquinas

paralelas e TPDS. Luhetal. (1998 ) apliam uma solução baseada em relaxação

lagrange-ana, programação dinâmia e heurístias para um ow-shop om TPDS. LiueLiao (2000 )

onsideram vários estágios, exibilidade e TPDS. Eles também utilizam relaxação

lagrange-ana em um modelo que onsidera restrições de uxo e máquinas idêntias em ada estágio.

Aero eDelgado (2000 ) utilizamumaheurístia baseadaembusa tabu emumproblemade

ow-shopommáquinas não-relaionadas emada estágio, massem onsiderarTPDS.Meyr

(2000 ) utiliza busa loal ombinada om re-otimização dual para resolver um problema de

traba-Hans-Joahim eJohn (1996 ) exploram umproblema de job-shop sem TPDS utilizando

pro-gramaçãoporrestrições. Koulamase Kyparisis(2004 )onsideraumproblemademinimização

demakespanemmáquinas paralelas uniformes omtemposde disponibilidade.

Na mesma linha, foram publiados vários trabalhos apliando GRASP e B&B ao

pro-blemaaquiestudado [Gómez Ravetti e Mateus(2003 );GómezRavetti etal.(2004a ,b ,2006 );

Rohaetal.(2004 , 2006 )℄. Noentanto,nãofoipossívelenontrartrabalhosdeoutrosautores

onsiderandoumproblema omtantasaraterístias quanto oaqui estudado.

1.5 Organização

Estetrabalho estáorganizado na seguinte seqüênia. No Capítulo 2 é detalhado oproblema

abordadoesãodisutidasasformulaçõesmatemátias utilizadas. OCapítulo3apresenta um

algoritmoBranh-and-Bound, eomoelefoiadaptadopara oproblemaabordado. Ageração

Formulações Matemátias

Dois modelos são apresentados nesta seção para produzir soluções ótimas. O primeiro é

baseado no modelo de Manne (1960) para Job Shop, e já foi previamente proposto por

Gómez Ravetti (2003 ). O segundo é baseado no modelo de Wagner (1959 ), também para

Job Shop. Ambostêm osseguintes dados:

•

N

éo onjunto detarefasque devemser proessadas;

•

M

é o onjunto demáquinas;

•

i

representa umatarefaespeía;

•

m

representa uma máquinaespeía;

•

d

i

é adata deentrega datarefa

i

;

•

w

i

éa prioridadeda tarefa

i

;

•

p

im

é otempo deproessamento da tarefa

i

na máquina

m

;

•

s

ii

′

_m

é otempode preparação da máquina

m

ao passar datarefa

i

paraa tarefa

i

′

;

•

G

éumvalorinteiro muitograndeque atuaomopenalidade.

2.1 Modelo Baseado no Trabalho de Manne

O primeiro modelo de programação inteira mista é baseado no modelo de Manne para Job

Shop. Eletrabalha disretizando a ordemdastarefasnasmáquinas eonta om asseguintes

variáveisde deisão:

•

t

i

: tempode iníiodo proessamento datarefa

i

;

•

α

im

:

(

1

se atarefa

i

éproessadapelamáquina

m,

•

β

ii

′

_m

:

(

1

seastarefas

i

e

i

′

sãoproessadasna máquina

m

e

i

éproessada antes de

i

′

_,

0

asoontrário;

•

ρ

i

: atraso datarefa

i

;

•

Z

: makespan (tempo parao términode todasastarefas).

A formulação matemátiado modeloé dada edesrita a seguir:

min

Z

+

X

i

∈

N

(

ρ

i

·

w

i

)

!

(2.1)

X

m

∈

M

α

im

= 1

,

∀

i

(2.2)

Z

≥

t

i

+

p

im

−

(1

−

α

im

)

·

G,

∀

i,

∀

m

(2.3)

ρ

i

≥

t

i

+

p

im

−

d

i

−

(1

−

α

im

)

·

G,

∀

i,

∀

m

(2.4)

t

i

′

≥

t

_i

+

p

_im

+

s

_ii

′

_m

−

(1

−

α

_im

)

·

G

−

(1

−

α

_i

′

_m

)

·

G

−

(1

−

β

_ii

′

_m

)

·

G,

∀

i,

∀

i

′

> i,

∀

m

(2.5)

t

i

≥

t

i

′

+

p

_i

′

_m

+

s

_i

′

_im

−

(1

−

α

_im

)

·

G

−

(1

−

α

_i

′

_m

)

·

G

−

β

_ii

′

_m

·

G,

∀

i,

∀

i

′

> i,

∀

m

(2.6)

α

im

∈ {

0

,

1

}

,

∀

i,

∀

m

β

ii

′

_m

∈ {

0

,

1

}

,

∀

i,

∀

i

′

> i,

∀

m

(2.1) A função objetivo é minimizar o makespan somado ao atraso ponderado. Apesar de

onsiderar dois objetivos (makespan e atraso), ela é onsiderada mono objetivo, pois

apenas soma os valores dos dois objetivos. No aso deste trabalho, preferiu-se essa

abordagem porque elagarante sempreaexistêniade umasoluçãoviável, emontraste

om umaabordagemem queasdatas deentrega nãopoderiamservioladas.

(2.2) Impõeque ada tarefadeve ser proessada por exatamente umamáquina.

(2.3) Calula o makespan. Ele deve ser maior ou igual ao tempo de iníio de ada tarefa

i

adiionado ao tempo deproessamento de

i

namáquina

m

onde

i

é proessada.

(2.4) O iníiodo proessamento da tarefa

i

adiionado ao tempo de proessamento na

má-quina

m

onde

i

éproessadadevesermenor ouigualàsuadatade entrega

d

i

aresida

de umpossívelatraso

ρ

i

.

(2.5) Impõequeoproessamento datarefa

i

′

poderáomeçarsomenteapósoproessamento

datarefa

i

eotempodepreparaçãode

i

para

i

′

,seambasforemproessadasnamáquina

m

(

α

im

=

α

i

′

m

= 1

) e

i

′

forproessadaapós

i

na máquina

m

(

β

ii

′

m

= 1

).

(2.6) Impõe o reíproo, que o proessamento da tarefa

i

poderá omeçar somente após

o proessamento da tarefa

i

′

e o tempo de preparação de

i

′

para

i

, se ambas forem

proessadasna máquina

m

(

α

im

=

α

i

′

m

= 1

) e

i

′

nãofor proessadaapós

i

na máquina

Omodeloaindaseriaválido seasrestrições(2.5 )e (2.6 )fossemsubstituídaspelas

Restri-ções(2.5)

∀

i

6

=

i

′

eadiionando

β

ii

′

m

= 1

−

β

i

′

im

,masessanovaformulaçãoexigiriaduasvezes

o número devariáveis

β

. Com aformulação atual,

β

ii

′

m

existeapenasse

i < i

′

,diminuindoo

número devariáveis

β

pelametade emantendoo número derestrições.

2.2 Modelo Baseado no Trabalho de Wagner

Enquanto o primeiro modelo utiliza

α

para disretizar a aloaçãode tarefasem máquinas,o

segundo modelo adiiona maisinformação a essasvariáveis, utilizando-as para disretizar as

posiçõesnaseqüênia de proessamento. Eletem asseguintesvariáveis de deisão:

•

t

(l)

m

: tempo deiníio doproessamento da

l

a

tarefa na máquina

m

;

•

α

(l)

_im

:

(

1

se atarefa

i

for proessadapelamáquina

m

na

l

a

posição,

0

aso ontrário;

•

δ

m

(l)

: tempo depreparação neessárioentre as

l

a

e

(

l

+ 1)

a

posiçõesna máquina

m

;

•

ρ

i

: atrasoda tarefa

i

;

•

Z

: makespan.

Aformulação matemátiaé dada edesrita abaixo:

min

Z

+

X

i

∈

N

(

ρ

i

·

w

i

)

!

(2.7)

X

m

∈

M

|

N

|

X

l=1

α

(l)

_im

= 1

,

∀

i

(2.8)

X

i

∈

N

α

(l)

_im

≤

1

,

∀

m, l

= 1

, . . . ,

|

N

|

(2.9)

X

i

∈

N

α

(l)

_im

≤

X

i

∈

N

α

(l

_im

−

1)

,

∀

m, l

= 2

, . . . ,

|

N

|

(2.10)

Z

≥

t

(l)

_m

+

X

i

∈

N

α

(l)

_im

·

p

im

,

∀

m, l

= 1

, . . . ,

|

N

|

(2.11)

ρ

i

≥

t

(l)

m

+

p

im

−

d

i

−

1

−

α

(l)

_im

·

G,

∀

m,

∀

i, l

= 1

, . . . ,

|

N

|

(2.12)

t

(1)

_m

= 0

,

∀

m

(2.13)

δ

(l

_m

−

1)

≥

s

ii

′

_m

−

2

−

α

(l

_im

−

1)

−

α

(l)

_i

′

_m

·

G,

∀

m,

∀

i,

∀

i

′

6

=

i, l

= 2

, . . . ,

|

N

|

(2.14)

t

(l)

_m

≥

t

_m

(l

−

1)

+

δ

_m

(l

−

1)

+

X

i

∈

N

α

(l

_im

−

1)

·

p

im

,

∀

m, l

= 2

, . . . ,

|

N

|

(2.15)

(2.7) A função objetivo é similar à do primeiro modelo: minimizar o makespan somado ao

atraso ponderado.

(2.8) Cada tarefaé proessadaemexatamente umamáquinaem umaposição.

(2.9) Há nomáximo uma tarefaemada posição deada máquina.

(2.10) Devehaverumatarefanaposição

l

−

1

sehouveroutranaposição

l

namesmamáquina

para

l

≥

2

.

(2.11) Omakespanémaiorouigualaotempodeiníiodoproessamentodastarefasemada

posição emada máquina somadoao tempode proessamento datarefa namáquina.

(2.12) Otempodeiníiodoproessamentodatarefana

l

a

posiçãonamáquina

m

adiionado

aotempodeproessamentodatarefadevesermenorouigualàdatadeentregadatarefa

adiionada de umpossívelatraso

ρ

i

.

(2.13) Otempodoiníiodoproessamentodetodasastarefasdasprimeirasposiçõeséigual

a zero.

(2.14) O tempo de preparação entre as

(

l

−

1)

a

e

l

a

posições na máquina

m

é maior ou

igual ao tempo de preparação neessárioda tarefa

i

para

i

′

namáquina

m

se

i

e

i

′

são

proessadas por

m

nas

(

l

−

1)

a

e

l

a

posições respetivamente.

(2.15) Otempo de iníiodo proessamento para a tarefa na

l

a

posição é maior ou igual ao

tempo de iníio do proessamento da tarefa da posição anterior somado ao tempo de

preparação neessárioentreas

(

l

−

1)

a

e

l

a

posiçõesdamáquina

m

aluladoem(2.14 ),

e o tempo de proessamento da tarefana

(

l

−

1)

a

posição.

Ao utilizar um valor inteiro

G

muito grande para transformar o modelo em um modelo

linear,asrestriçõesontendoaonstante

G

dãolimitesinferioresfraosdurantearesoluçãose

assoiadasavariáveisinteirasoubinárias,assimomononossomodelo. Issoaonteeporque,

durantearesolução, osolverrelaxaasvariáveisbinárias,permitindoqueelasassumamvalores

nãointeiros. Noprimeiro modelo, nasRestrições(2.3-2.6 ),se

0

< α

im

<

1

,o valorresultante

no lado direito será fortemente negativo, não inueniando o limite inferior da variável do

ladoesquerdo. Assim, olimiteinferior dafunção objetivo tambémserá frao.

No segundo modelo, apenas as Restrições (2.12) e (2.14 ) utilizam

G

, fazendo om que

apenas

δ

(l)

m

e

ρ

i

tenham limitesinferiores fraos. Grande parte do valorda função objetivo é

dadopelomakespan,queéemgrandepartedadopelotempodeproessamentodeadatarefa.

Como a parte do modelo quealula esses dados

P

α

(l

_im

−

1)

·

p

im

não possuia onstante

G

assoiada avariáveis binárias ouinteiras, o limiteinferior nãoé prejudiado.

Valeapena destaarquenestetrabalho onsideramosqueada máquinatemumnúmero

de posições igual ao número de tarefas. Embora o aso em que a solução ótima ontenha

Apesardeo segundomodelo terumnúmero devariáveisbemmaior queoprimeiro, eleé

umaformulaçãomaisforteomumlimiteinferiormaisjustodurantearesolução. Éesperado

que ele sejamais rápido pararesolverproblemas omnúmerosde tarefas maiores, quandoo

tempo deiníio deproessamento (

t

i

ou

t

(l)

Algoritmo Branh-and-Bound

Um Branh-and-Bound (B&B) é uma estratégia espeía de enumeração da árvore de

so-luções. Em um B&B, há três proedimentos prinipais: iniialização, branhing e bounding.

Durante a iniialização, uma rápida heurístia é utilizada para enontrar uma boa solução

iniial que servirádelimitesuperior (

LS

)no iníio doalgoritmo.

Branhing divideo problema emsub-problemas menores. Cadasub-problema representa

uma solução parial e é representado por um nó na árvore de soluções. Uma estratégia

de busa deve estar assoiada ao proedimento de branhing para deidir qual nó deve ser

expandido aseguir. Olimite superior ajuda apodar nósda árvore debusa quetiverem um

limiteinferior(

LI

)maiorqueolimitesuperiorenontradoatéomomento (numproblemade

Algoritmo 3.1: UmBranh-and-Boundgenério

Proedimento:BranhAndBound()

Sol

←

SoluçãoIniial(); 1

LS

←

ValorDaSolução(

Sol

); 2

LI

←

LimiteInferior(); 3

Branh(

primeiroN o

); 4

retorna

Sol

; 5

Proedimento:Branh(

no

) seSoluçãoCompleta(

no

) então 6

Sol

←

no

; 7

LS

←

ValorDaSolução(

Sol

); 8

se

LS

=

LI

então 9 TerminaProedimento(); 10 m se 11 retorna; 12 m se 13

para todo

n

∈

FilhosDe(

no

)faça 14

seBound(

n

)

< LS

então 15

Branh(

n

); 16

m se 17

minimização).

O proedimento de bounding alula o limite inferior de ada nó para deidir quais nós

devem ser podados e quais devem ser expandidos. A estrutura básia de um

Branh-and-Bound genério é mostrada no Algoritmo 3.1 . Nas seções seguintes, os três proedimentos

sãopersonalizados paraesteproblema de seqüeniamento e desritosemmaiores detalhes.

3.1 Iniialização om GRASP

Durante a iniialização, uma solução iniial ompleta é enontrada para servir de limite

superior. Qualquer nó na árvore de enumeração om um limite inferior maior que o

li-mite superior pode ser podado. Neste trabalho, um algoritmo baseado na metaheurístia

GRASP [Resendee Feo (1995 )℄ é utilizado para enontrar essa primeira solução. GRASP

é uma metaheurístia de multi-iníio para problemas ombinatórios [ResendeeFeo (1995 );

Dahs etal. (1996 )℄, e é omposta por duas fases: a onstrução de uma solução aleatória

viável e uma busa loal. Essas duas fases são repetidas em ada iteração. Uma desrição

estádisponível noalgoritmo3.2 .

Iniialmente,éonstruídoumvetoromastarefasordenadas pelaregradamenordatade

entrega (earliest due date - EDD). Durante a fasede onstrução, o algoritmo re-ordena esse

vetordeforma aleatória,seguindo umafunção deprobabilidade espeía. Neste trabalho,a

funçãoutilizadaé

f

(

x

)

∼

1

x

,onde

f

(

x

)

representa aprobabilidade dea

x

a

tarefaseresolhida

omopróxima. Aada passodare-ordenação, umanova tarefaéesolhida dalistadetarefas

queainda não fazem parteda nova ordenação. Aprobabilidade de umatarefa espeía ser

esolhidaé proporionala

1

x

,onde

x

é aposição atualda tarefa nalista.

Após a re-ordenação, ada tarefa é aloada a uma máquina apaz de proessá-la. Para

Algoritmo 3.2: Bloo prinipaldo B&Be algoritmo de iniialização(GRASP)

Proedimento:BranhAndBound()

Sol

←

GRASP(

iteracoes

); 1

Branh1(

1

); 2

retorna

Sol

; 3

Proedimento:GRASP(

iteracoes

)

tars

←

Ordena(

N

); 4

para

i

←

1

até

iteracoes

faça 5

tarsAleatorias

←

ReOrdena(

tars

); 6

solucaoLocal

←

ConstróiSolução(

tarsAleatorias

); 7

BusaLoal(

solucaoLocal

); 8

PathRelinking(

solucaoLocal

); 9

seValorDaSolução(

Sol

)

>

ValorDaSolução(

solucaoLocal

) então 10

Sol

←

solucaoLocal

; 11

m se 12

m para 13

isso, umafunção gulosa aloaada uma naordem resultanteà máquinaapazde terminá-la

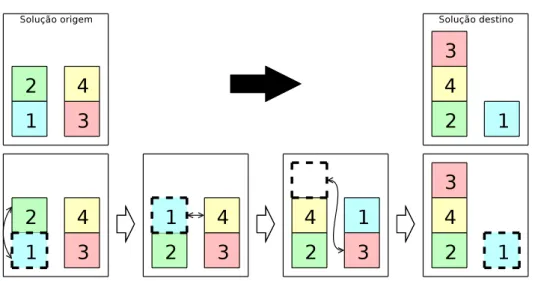
primeiro. Umexemplo éexibido na Figura3.1.

Abusaloaltroatodososparesdetarefasaloadosamáquinasdiferentes. Seumatroa

melhora o valor da solução, a nova solução é armazenada e a antiga é abandonada. Nada é

feito aso ontrário. Umexemplo é mostrado na Figura 3.2. Foram feitostestes om várias

estratégiasdebusas,tantobusasmaisrestritasomomaisvariadas. Emboraessaestratégia

seja omputaionalmente pesada, ela foi a que enontrou melhores soluções em uma mesma

quantidade detempo.

Path-relinking éumaténiautilizadaomoestratégiadebusaemváriasheurístias[Glover

(1996 , 2000 ); Glovere Laguna (1997 )℄, inluindo emonjunto om GRASP [Laguna eMartí

(1999 )℄. Glovere Kohenberger (2003 ) apresentamduasestratégias prinipais:

•

PR omoumaferramenta paramelhorara solução enontrada peloGRASP.

•

PR omoumaestratégia paraintensiar abusaloal.

Oalgoritmoesolheduassoluçõeseanalisaoaminhodesoluçõesentreelas. Esseaminho

é feito através de movimentos de tarefas. Para ada movimento, a solução enontrada é

analisada.

Nestetrabalho, PRfuniona omoumaestratégiaparaintensiar abusa loal. Mesmo

assim, há várias formas de se implementar a ténia. GlovereKohenberger (2003 ) itam

algumas:

•

Uso periódiode PR.

•

Uso dePR emduasdireçõespossíveis,isto é,da solução 1à solução 2 ede 2a 1.

•

Uso dePR emapenas umadireção.

•

Uso dePR trunado. Istoé,fazera análisede apenaspartedo aminho.

Oalgoritmo de PRdeste trabalho funiona daseguinteforma:

1. O onjunto das ino melhores soluções é mantido (as ino melhores soluções, neste

trabalho).

Figura 3.2: Seqüênia depassosda busaloal omastroasanalisadas em destaque

2. Cada vez que PR é usado, uma solução é esolhida aleatoriamente deste onjunto e

todas as soluções no aminho entre a solução enontrada pela busa loal e a solução

seleionada doonjunto sãoanalisadas.

3. Se umasolução melhor forenontrada, ela éadiionada ao onjunto.

As transformações feitas por PR são detalhadas no Algoritmo 3.3 e um exemplo om 2

máquinase 4 tarefasé mostrado naFigura 3.3.

3.2 O Proedimento de Branhing

Oproedimento debranhing onstróia árvoredeenumeração. Eleé divididoemduasfases.

Naprimeira,astarefassãoaloadasàsmáquinas,masaseqüêniadeproduçãonãoédenida.

Aseqüênia de produção emada máquinaserá deididaapenasna segundafase.

A primeira fasede branhing omeçaordenando astarefasutilizando a regra deEDD. A

funçãoPróximaMáquina(

tar

)retornaasmáquinas seguindoa ordememqueadamáquinaé

apazde proessara tarefa

tar

. Cada vez que uma tarefa é aloada, um novo nó na árvore

Algoritmo 3.3: Pseudo-ódigo paraoPath-relinking implementado

Proedimento:PathRelinking(

solOrig

)

solDest

←

SoluçãoAleatória(

poolDeM elhoresSolucoes

); 1

para

m

←

1

até

numeroDeM aquinas

faça 2

para ada posição

l

oupada na máquina

m

de

solDest

faça 3

se

(

solOrig.posicao

[

m

][

l

]

6

=

solDest.posicao

[

m

][

l

])

então 4

seexiste uma tarefa em

solOrig.posicao

[

m

][

l

]

então 5

Troa astarefas

solOrig.posicao

[

m

][

l

]

om

solDest.posicao

[

m

][

l

]

em 6

solOrig

;

senão 7

Retira atarefa

solDest.posicao

[

m

][

l

]

daposição emqueela estiverem 8

solOrig

e oloa naposição

l

damáquina

m

em

solOrig

;

m se 9

m se 10

Figura3.3: Seqüêniade passosdePR omasposiçõesanalisadas emdestaque

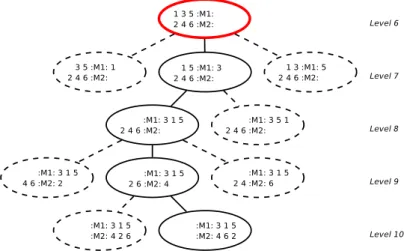
de enumeração é riado. Aprimeira faseé desrita no Algoritmo3.4 , e umexemplo de uma

árvorede enumeraçãoparialpara

2

máquinas e

6

tarefasé dadona Figura3.4 .

A segunda fase deide a seqüênia de produção em ada máquina. A ordem é deidida

para uma máquina de ada vez. Em ada máquina, a primeira tarefa a ser proessada é

esolhida, depois a segunda, até que não haja mais tarefas aloadas àquela máquina. A

função PróximaTarefaNaMáquina(

m

) retorna ada tarefa na máquina

m

seguindo a regra

da EDD. Cada vez que umatarefa éseqüeniada emumaposição de produção espeía na

máquina, um novo nó na árvore de enumeração é riado. Esta fase é desrita no Algoritmo

3.5, e a Figura3.5 mostra o exemplo da árvore de enumeração parial ontinuando o nó em

destaque naFigura 3.4 .

Paraevitar aenumeraçãoompleta daárvorede enumeração, umproedimento de

boun-ding éutilizadoparaenontrarumlimiteinferiorparaadanó. Paraumertonó

i

,seolimite

inferior Bound(

i

) for piorque olimitesuperior, onó é podado. Oproedimento de bounding

Figura3.5: Segunda fasede branhing

limitessuperior e inferior.

3.3 O Proedimento de Bounding

Oproedimento de bounding é provavelmente o maisimportante emum branh-and-bound.

Umlimiteinferiorpreisopermiteao algoritmopodarumgrandenúmerodenós, eliminando

muitoproessamento desneessário. Seja:

LI

k

: Olimite inferior do makespan.

LI

t

: Olimiteinferiordo atraso ponderado.

LI

kf

: Olimite inferiordo makespan onsiderandoostemposde todasastarefas.

LI

_m

ka1

: Olimiteinferiordomakespan onsiderandoumamáquinaespeíaduranteaprimeira

fase debranhing.

Algoritmo 3.4: Primeira fasede branhing

Proedimento:Branh1(

i

)

seTodasAsTarefasEstãoAloadas() então 1

Branh2(

1

,

1

); 2

retorna; 3

m se 4

tar

←

N

[

i

]

; 5

para ada

m

←

PróximaMáquina(

tar

) faça 6

AloaTarefa(

tar, m

); 7

seBound(

solucaoAtual

)

<

ValorDaSolução(

Sol

) então 8

Branh1(

i

+ 1

); 9

m se 10

N

u

: Oonjunto de tarefasnão-aloadas.

N

_m

a

: Oonjunto de tarefasaloadasà máquina

m

.

S

a

_m

: Oonjunto depares de tarefas

{

ii

′

_}

pertenentes ao onjunto detarefas

N

a

m

.

u

: Omenortempode preparaçãoonsiderando todososparesdetarefasemtodasas

máqui-nas.

Oproedimentodeboundingdestetrabalhoébaseadonaestratégiadereduçãodedomínio,

retirada daárea deProgramação por Restrições[Lustig ePuget (2001 )℄.

Neste trabalho, o proedimento de bounding alula separadamente os valores de

LI

k

e

LI

t

emada nó. Paraalular

LI

k

na primeira fase debranhing, o proedimento onsidera

duasformas, utilizando apenasomaiorvalor dentre elas,omo mostraaEquação (3.2).

LI

k

é formalmente denido nasEquações (3.2-3.3 ). Na Equação (3.4),

LI

kf

é dado pela

soma dosmenorestemposde proessamento de todasastarefasnão-aloadase ostemposde

proessamento dastarefasaloadas ao menortempode preparação multipliado por

n

,onde

n

é o número de tempos de preparação neessários para todas as máquinas (neste aso, o

número de tarefassubtraído do número de máquinas).

LI

ka1

m

é dado pela soma dostempos

de proessamento de adatarefa aloada àmáquina

m

aos

n

menorestemposdepreparação,

onde

n

éomenornúmerodetemposdepreparaçãoneessárioàmáquina

m

(ouseja,onúmero

de tarefasaloadas a

m

menos um).

LI

=

LI

k

+

LI

t

(3.1)

LI

k

= max

max

m

∈

M

LI

_m

ka

, LI

kf

(3.2)

Algoritmo 3.5: Segunda fasede branhing

Proedimento:Branh2(

i, m

) seSoluçãoEstáCompleta()então 1

Sol

←

solucaoAtual

; 2

retorna; 3

m se 4

seOrdemEstáDeididaNaMáquina(

m

) então 5

Branh2(

1

, m

+ 1

); 6

retorna; 7

m se 8

para

tar

←

PróximaTarefaNaMáquina(

m

)faça 9

AloaTarefaÀPosição(

tar, m, i

); 10

seBound(

solucaoAtual

)

<

ValorDaSolução(

Sol

) então 11

Branh2(

i

+ 1

, m

); 12

LI

_m

ka1

=

X

i

∈

N

a

m

(

p

im

) +

X

{

ii

′

_}∈

_S

a

m

(

s

ii

′

_m

)

(3.3)

LI

kf

=

X

i

∈

N

u

min

m

∈

M

(

p

im

) +

X

m

∈

M

X

i

∈

N

a

m

p

im

+

n

·

u

(3.4)

|

M

|

Durante a segunda fase de branhing não existem tarefas não-aloadas. Portanto, as

Equações(3.5 -3.6 )sãoutilizadas paraalular

LI

k

. Seja:

LI

_m

ka2

: Olimiteinferiordomakespan onsiderandoumamáquinaespeíaduranteasegunda

fase debranhing.

N

as

m

: Oonjunto de tarefasnamáquina

m

seqüeniadasemumaposição espeía.

S

as

m

: Oonjunto de temposde preparação usados pelas tarefasem

N

as

m

.

N

_m

au

: Oonjunto detarefasna máquina

m

queainda nãoforam seqüeniadas.

S

_m

au

: O onjunto dos

n

menores tempos de preparação entre as tarefas em

N

au

m

e a tarefa

na última posição seqüeniada de

m

, onde

n

é o número de tempos de preparação

neessários para astarefasem

N

au

m

.

LI

_m

ka2

é dadopelasoma domakespanparial(onsiderandoapenasasposiçõesjá

seqüen-iadas) aos tempos de proessamento das tarefas não-seqüeniadas e osmenores tempos de

preparaçãoentreelas. Issoéaluladosomandoostemposdeprodução dastarefasaloadasà

máquina

m

,aostemposde preparação utilizadospelas tarefasjáseqüeniadase aosmenores

tempos de preparação das tarefas não aloadas. Isto é feito para ada máquina, e o maior

valor enontradofornee

LI

k

.

LI

k

= max

m

∈

M

LI

_m

ka2

(3.5)

LI

_m

ka2

=

X

i

∈

N

a

m

(

p

im

) +

X

{

ii

′

_}∈

_S

as

m

(

s

ii

′

_m

) +

X

{

ii

′

_m

_}∈

_S

au

m

(

s

ii

′

_m

)

(3.6)

Olimiteinferiorparaoatraso ponderado (

LI

t

)é aluladode formasimilara

LI

k

. Eleé

dadode aordoom asEquações(3.7-3.12 ). Seja:

LI

tu

: Olimiteinferior do atrasoponderadoonsiderando apenasastarefasnão-aloadas.

LI

_m

ta

: O limite inferior do atraso ponderado onsiderando apenas as tarefasaloadas à

má-quina

m

.

t

i

: Otempo de iníiodo proessamento da tarefa

i

noseqüeniamento atual.

t

′

_i

: Omenor tempo de iníioparaatarefa

i

omo se

i

fossea próximaseqüeniada.

LI

ta

m

édadoonsiderandoqueastarefassãoproessadasseguindoumaordemnão-deresente

de datade entrega, utilizando o tempo de proessamento omo ritério de desempate, e um

tempo de preparação xoentre ada tarefa. Estetempo de preparação é igual ao menor

en-ontradoentreastarefasnão-seqüeniadasdamáquina

m

,eéutilizadoparaalularotempo

de iníio

t

′′

i

deaordo omessa seqüênia. Seja:

LI

t

=

LI

tu

+

X

m

∈

M

LI

_m

ta

(3.7)

LI

tu

=

X

i

∈

N

u

w

i

·

max

min

m

∈

M

(

p

im

)

−

d

i

,

0

(3.8)

LI

_m

ta

=

LI

_m

ta1

+ max

LI

_m

ta2

, LI

_m

ta3

,

(3.9)

onde

LI

ta1

m

representa a penalidade de atraso para as tarefas seqüeniadas e

t

i

é o tempo

de iníio do proessamento da tarefa

i

. Olimite inferior para as tarefasnão-seqüeniadas é

alulado de duas formas diferentes (

LI

ta2

m

e

LI

ta3

m

), e apenas o maior valor é onsiderado.

LI

_m

ta2

onsideraquetodasastarefaspodemserproessadasna próximaposiçãodisponível,e

t

′

_i

é o menor tempo de iníio paraa tarefa

i

.

LI

ta3

m

onsidera queas tarefassãoproessadas

seguindoumaordemnão-deresentededatadeentrega,utilizandootempodeproessamento

omoritério dedesempate, eumtempodepreparação xoentreada tarefa. Estetempode

preparação éigual aomenorenontradoentreastarefasnão-seqüeniadas damáquina

m

,eé

utilizado paraalular otempo deiníio

t

′′

i

de aordoomessa seqüênia.

LI

_m

ta1

=

X

i

∈

N

as

m

[

w

i

·

max (

t

i

+

p

im

−

d

i

,

0)]

(3.10)

LI

_m

ta2

=

X

i

∈

N

au

m

w

i

·

max

t

′

i

+

p

im

−

d

i

,

0

(3.11)

LI

_m

ta3

=

min

i

∈

N

au

m

(

w

i

)

·

X

i

∈

N

a

m

max

t

′′

_i

+

p

im

−

d

i

,

0

(3.12)

É importante destaar algumas diferenças entre estasvariáveis duranteas primeira e

se-gundafasesdebranhing. Naprimeirafase,

t

′

i

ésemprezero,omonãohátarefasseqüeniadas

em qualquerposição. Nasegunda fase,

N

u

ésemprevazio, poisada tarefa jáestáaloadaa

alguma máquina. Portanto,

LI

tu

é sempre zero. No entanto, na primeira fase

LI

tu

é maior

que zero apenas quando o menor tempo de proessamento de alguma tarefa for maior que

a suadata de entrega. Pequenas variações no limite inferior de uma solução parial podem

signiar grandes quantidadesde nóspodados. Portanto,essa equação é mantida.

Comosepodepereber, nestetrabalhotodososlimitesinferiorespodemseraluladosde

Algoritmo 3.6: B&BDiotmio

Proedimento:BranhAndBound()

Sol

←

SoluçãoIniial(); 1

LI

←

Bound(

primeiroN o

); 2

LS

←

LI

+ (

ValorDaSolução(

Sol

)

−

LI

)

·

d

; 3

enquantoExisteSoluçãoInteiraEntreLIeLS()faça 4

Branh(

primeiroN o

); 5

LI

←

LS

; 6

LS

←

LI

+ (

ValorDaSolução(

Sol

)

−

LI

)

·

d

; 7

m enquanto 8

retorna

Sol

; 9

Proedimento:Branh(

no

) seSoluçãoCompleta(

no

) então 10

Sol

←

no

; 11

LS

←

LI

+ (

ValorDaSolução(

Sol

)

−

LI

)

·

d

; 12

retorna; 13

m se 14

para todo

n

∈

FilhosDe(

no

)faça 15

seBound(

n

)

< LS

então 16

Branh(

n

); 17

m se 18

m para todo 19

3.4 Branh-and-Bound Diotmio

Além do B&Bnormal, foi riada umavariação diotmia. Num algoritmo diotmio

lás-sio, ao enontrar uma solução melhor que o limite superior atual, o novo limite superior é

dadopor

LS

=

LI

+

ValorDaMelhorSolução()

2

,

em vez de ser dado diretamente pelo valor da nova solução. Ao terminar a busa, o limite

inferioréatualizado omovalordolimitesuperior,olimitesuperioréatualizadoomovalor

dafórmulaaimaparaonovolimiteinferior,eabusaéreiniiadapartindodaúltimasolução

enontrada. Isso érepetido atéque nãoexistammais soluções inteirasentre

LI

e

LS

.

No diotmio desenvolvido, esse oneito foi estendido. Em vez de o limite superior

sempre ser a média do limite inferior e do valor da melhor solução atual, é utilizado um

parâmetro

d

entre 0 e 1 para identiar à qual distânia o novo

LS

está de

LI

. O limite

superioré então dado por

LS

=

LI

+ (

ValorDaMelhorSolução()

−

LI

)

·

d.

Limitar abusaaumlimite superiormenorquea melhorsolução enontrada podetrazer

entre

LI

e

LS

. Se

d

= 0

,

5

, a versão desenvolvida se torna idêntia à lássia, e se

d

= 1

,o

B&Bdeixadeserdiotmio. UmB&Bdiotmiogenérioestádesritoemmaioresdetalhes

Testes e Resultados

Resultados são apresentados omparando as soluções enontradas pelo B&B desenvolvido

om assoluções enontradas por ambosos modelos quando resolvidos pelo CPLEX 9.0 1

na

seção 4.3. Testes om o B&B resolvendo instânias das várias lasses desritas na seção 4.1

são mostrados nas seções seguintes. As lasses de instânias utilizadas neste trabalho estão

denidas na seção4.1 .

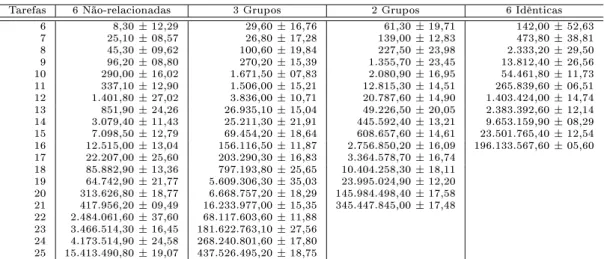
Para apresentação dos resultados dos testes, é utilizada uma média trunada onheida

omointer-quartis[WikimediaFoundation(2005 )℄,quedesarta50%dosvaloresenontrados.

Como há 20 instâniasde ada tamanhoemada lasse, os5 menorese os5maiores valores

enontrados sãodesartados de adaamostra. A médiatrunada nãoé tãosensívelavalores

muito fora da média omo é a média aritmétia, mas utiliza mais informação da amostra.

Além disso,o desviopadrãoéapresentadoemformadeporentagem, aluladopelafórmula

σ

=





100

x

·

v

u

u

t

1

N

·

N

X

i=1

(

x

i

−

x

)

2





%

,

onde

x

i

representa o valor medido para a instânia

i

, e

x

representa a média aritmétia de

todosos

x

i

.

Durante os testes, busa-se variar o número de tarefas de apenas uma tarefa de uma

instânia para outra. No entanto, um problema om

n

tarefas não é sempre mais fáil de

resolverqueumom

n

+ 1

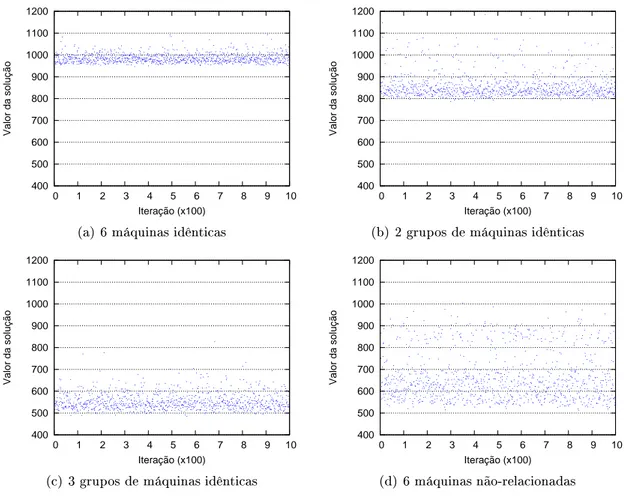
tarefas. Dependendodonúmero demáquinasede omoastarefas

estão nelas distribuídas, o último pode ser bem mais fáil de resolver que o primeiro. Nos

gráos apresentados, pode-se veriaralgumas perturbações dessetipo.

O número de iterações do GRASP foi xado em 1.000 para alular o limite superior,

a não ser quando for espeiado o ontrário, e todos os gráos são mostrados em forma

logarítmia. Para ostestes do B&B, o tempo máximo de resolução foi xo em 7200s (duas

horas). Os resultados são apresentados até o número de tarefas em que o B&B onseguiu

resolver, deforma quepelomenos 15 instâniasdeada onjunto de 20 nãoultrapassaram o

1

CPLEXSoftware: UmotimizadorparaproblemaslinearesdesenvolvidopelaILOG.Maisinformaçõesno