REDUÇÃO DA INFLUÊNCIA DA MASSA ESPECÍFICA NA DETERMINAÇÃO
DO TEOR DE UMIDADE DE SEMENTES DE TRIGO1
PEDRO AMORIM BERBERT2 e BRIAN CHRISTOPHER STENNING3
RESUMO - A medição da capacitância e da condutância de um capacitor contendo amostras de trigo permite a determinação de duas de suas propriedades dielétricas: a permissividade relativa (ε') e o fator de perda dielétrica (ε"). A utilização dessas propriedades, medidas simultaneamente em duas freqüên-cias de oscilação do campo elétrico, permite reduzir ou eliminar o efeito da massa específica aparente na determinação do teor de umidade do trigo. Tal procedimento torna possível o monitoramento con-tínuo e em tempo real, sem a necessidade de retirar amostras, do teor de umidade de uma coluna de grãos em movimento, situação em que ocorrem as maiores variações na massa específica do produto. O objetivo deste trabalho consistiu na obtenção de equações que permitam reduzir ou eliminar o efeito da massa específica na determinação em linha do teor de umidade do trigo. Foram utilizadas amostras das variedades Hussar, Mercia e Hereward com teor de umidade entre 11% e 22% b.u. e massa espe-cífica no intervalo 666 kg m-3≤ρ≤ 873 kg m-3. A equação que apresentou melhor desempenho permite calcular o teor de umidade do trigo com erros-padrão de calibração e de predição de 0,4 e 0,5 ponto percentual, respectivamente.
Termos para indexação: capacitância, propriedades dielétricas, instrumentação.
DENSITY-INDEPENDENT MOISTURE CONTENT MEASUREMENT OF WHEAT SEED ABSTRACT - Measurement of the capacitance and conductance of a capacitor filled with samples of wheat allows the determination of two dielectric properties of the material: the relative permissivity (ε'), and the dielectric loss factor (ε"). The use of these two properties, measured simultaneously at two different frequencies of the electric field, permits bulk density-independent measurement of moisture content of wheat. This procedure makes it possible to monitor moisture content continuously, and on-line, of a moving column of grain, a situation where the greatest variations in bulk density are to be expected. The objective of the present research was the derivation of density-independent equations for the determination of moisture content of wheat. Samples of varieties Hussar, Mercia and Hereward at moisture contents ranging from 11% to 22% w.b., and bulk densities ranging from 666 to 873 kg m-3 have been used. The best-performance equation was capable of estimating moisture con-tent of wheat with standard errors of calibration and prediction of 0.4 and 0.5 percentage point mois-ture, respectively.
Index terms: capacitance, dielectric properties, instrumentation.
INTRODUÇÃO
A determinação indireta do teor de umidade de grãos e sementes de cereais e oleaginosas por meio de medidores elétricos ou eletrônicos é um método amplamente utilizado nas unidades de pré-processamento de produtos agrícolas. No entanto, a utilização desses medidores restringe-se ao empre-go de amostras estáticas de massa previamente de-1Aceito para publicação em 15 de outubro de 1998.
Extraído da Tese de Doutorado do primeiro autor, apresentada à Cranfield University, UK. Trabalho financiado pela CAPES. 2Eng. Agrícola, Ph.D., Dep. de Engenharia Agrícola, Universi-dade Federal de Viçosa (UFV), CEP 36571-000 Viçosa, MG. E-mail: pberbert@mail.ufv.br
terminada. O teor de umidade é um dos fatores pre-ponderantes na preservação da qualidade dos grãos durante o armazenamento e para a obtenção de um produto de melhor qualidade depois do pro-cessamento. Para que isso seja possível, no caso es-pecífico do trigo, é necessário que haja informações contínuas e em tempo real a respeito do teor de umidade do produto durante a secagem e imediata-mente antes do processo de moagem. O teor de umidade (U) em decimal base úmida, é definido como:
U = Ma/(Ma + Mms) (1)
em que Ma e Mms representam as massas de água e
matéria seca contidas na amostra, respectivamente. Como o cálculo do teor de umidade está sempre as-sociado a um determinado volume (v) do produto, a Equação (1) pode ser reescrita da seguinte forma (Kraszewski, 1988):
U = {(Ma/v)/[(Ma + Mms)/v]} = (ξ/ρ) (2)
em que ξ representa a concentração volumétrica de água no material ( 3
O H m
kg 2 − ), e ρ é a massa
específi-ca aparente do produto úmido (kg m-3).
De acordo com Kraszewski (1988), as alterações que ocorrem em sinais elétricos que interajam com amostras úmidas de grãos são proporcionais à con-centração volumétrica de água, ξ, sendo praticamen-te independenpraticamen-tes da massa de matéria seca do pro-duto. Desta forma, após a medição indireta de ξ ob-serva-se, na Equação (2), que a determinação do teor de umidade, U, requer o conhecimento prévio da massa específica, ρ, do produto. A medição do va-lor de ρ pode ser feita separadamente por meio da técnica de atenuação de raios-γ, porém, a utilização desse tipo de sensor em unidades de pré-pro-cessamento de grãos é atualmente inviável devido aos altos custos envolvidos. Desta forma, a solução usualmente empregada consiste na utilização de amostras com massa constante tanto na calibração dos medidores elétricos quanto em sua posterior uti-lização em unidades comerciais e de pesquisa. De acordo com a Equação (2), na determinação do teor de umidade de grãos, as alterações no valor da mas-sa específica provocam efeitos similares aos
provo-cados por alterações na concentração volumétrica de água. Um maior ou menor grau de compactação dos grãos no compartimento eletricamente ativo terá uma grande influência no resultado final indicado pelo medidor. Portanto, o controle da massa especí-fica do produto é uma exigência comum a todos os métodos indiretos de determinação do teor de umi-dade de grãos.
No entanto, para aplicações industriais de con-trole em que se deseja medir o teor de umidade de uma coluna de grãos em movimento de forma con-tínua e em tempo real, sem a necessidade de retirar amostras, o método acima descrito não pode ser apli-cado. Vários métodos têm sido propostos para re-duzir ou eliminar o efeito da massa específica na determinação em linha do teor de umidade de pro-dutos agrícolas. As soluções encontradas baseiam-se, geralmente, na obtenção de equações empíricas envolvendo propriedades dielétricas do produto, uma vez que seria praticamente impossível controlar a massa específica de grãos em movimento.
Dzhemella & Pustynnikov (1965) desenvolveram um protótipo de medidor do teor de umidade de grãos que se baseava na medição simultânea, em duas fre-qüências, da capacitância de um capacitor de cilin-dros coaxiais tendo o produto como material dielétrico. O efeito da massa específica do produto sobre a leitura fornecida pelo equipamento foi eli-minado por meio da solução de um conjunto de equa-ções lineares do tipo Cf1 = aCf2 + b, para cada teor
de umidade, em que Cf1 e Cf2 representavam as
capacitâncias medidas em duas freqüências diferen-tes (f1 e f2). Os pontos em que estas retas intercep-tavam o eixo das ordenadas, ou seja, os pontos re-presentados por b = Cf1 - aCf2, dependiam apenas
do teor de umidade, sendo independentes da massa específica das amostras.
desvio-pa-drão das diferenças entre os teores de umidade cal-culados por meio da equação e os obtidos com o método-padrão de estufa foi de 0,6 ponto percentual, e o erro máximo foi de 1,0 ponto percentual.
O objetivo deste trabalho foi confirmar experi-mentalmente o método proposto por McFarlane (1987) e estudar outros métodos que permitam eli-minar ou reduzir o efeito da massa específica na determinação em linha do teor de umidade de grãos.
MATERIAL E MÉTODOS
O trabalho foi realizado no Laboratório de Pré-Processamento de Grãos do Departamento de Tecnologia Pós-Colheita do Silsoe College, Universidade de Cranfield, Condado de Bedford, Reino Unido. Todas as medições de propriedades dielétricas foram feitas utili-zando-se sementes certificadas de trigo (Triticum aestivum
L.) variedades Hussar, Hereward e Mercia. As sementes da variedade Hussar foram fornecidas pela ICI Seeds UK Ltd, logo após a colheita em setembro de 1992, com teor de umidade inicial de 14% b.u. As sementes das varieda-des Hereward e Mercia foram colhidas em 1993 e fornecidas pela Plant Breeding International (PBI Cambridge), também com teor de umidade inicial de 14% b.u.
Para manutenção das características originais, os lotes de sementes foram armazenados inicialmente em sacos de politeno numa câmara climática sob temperatura de 5°C e umidade relativa de 50%. Posteriormente, os lotes foram subdivididos em amostras de 0,8 kg e o teor de umidade de cada amostra foi alterado artificialmente. Para obter as amostras, de cada variedade, com teores de umi-dade entre 15% e 22% b.u., com incrementos de um pon-to percentual de umidade, adicionavam-se quantidades pré-determinadas de água destilada às amostras iniciais. Para a obtenção de amostras com teores de umidade de 11%, 12% e 13% b.u., as amostras com teor de umidade inicial de 14% b.u. foram secadas, por diferentes perío-dos de tempo e à temperatura de 30°C, em um protótipo de secador de leito fixo. Depois dos tratamentos de reumedecimento e secagem, as amostras foram colocadas em recipientes de vidro herméticos e armazenadas a 5°C por, no mínimo, 15 dias. Durante o período de armazenamento as amostras eram revolvidas três vezes ao dia para permitir uma maior homogeneidade na distri-buição de umidade entre os grãos. Todas as medições elé-tricas foram feitas num ambiente com temperatura e umi-dade relativa variando de 21°C a 24°C e 50% a 65%, res-pectivamente. O teor de umidade dos grãos foi
determi-nado de acordo com as Regras Britânicas de Testes para Cereais e Leguminosas (British Standards Institution, 1987).
A medição dos parâmetros elétricos das amostras foi feita mediante utilização de um medidor LCR, modelo 4285A, fabricado pela Hewlett-Packard. Este equipamento é capaz de medir 12 parâmetros de impedância, |Z|ejθ, em freqüências de teste de 75 kHz a 30 MHz. As proprieda-des dielétricas foram determinadas em incrementos de 100 kHz no intervalo entre 500 kHz e 1 MHz e em incre-mentos de 1 MHz no intervalo entre 1 MHz e 5 MHz, utilizando-se uma voltagem efetiva de 1,0 Vef. Utilizou-se a configuração com quatro pares de terminais para conectar o capacitor ao medidor HP 4285A. Esse tipo de conexão minimiza os problemas relacionados com a indutância mútua, as resistências de contato e os ruídos elétricos.
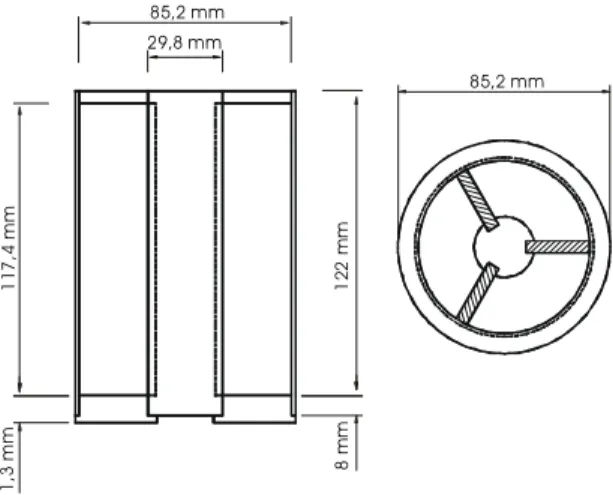
O dispositivo utilizado para conter as amostras duran-te as medições das propriedades dielétricas do trigo foi um capacitor de cilindros concêntricos (Fig. 1). Para cons-trução do eletrodo externo do capacitor utilizou-se tubu-lação de latão com diâmetro interno de 85,2 mm e o ele-trodo interno foi construído usando-se um tarugo de latão com diâmetro de 29,8 mm. Para manter os dois cilindros em posição concêntrica, utilizou-se uma base anular de 11,3 mm de espessura construída de politetrafluoroetileno (PTFE), um termoplástico conhecido comercialmente comoteflon. Além de ser um excelente isolante elétrico em uma ampla faixa de freqüências, o teflon também é inerte a todos os reagentes químicos em condições nor-mais de temperatura. Tal fato permite a calibração do capacitor utilizando-se líquidos-padrão cujas
proprieda-FIG. 1. Capacitor utilizado na determinação das pro-priedades dielétricas do trigo.
85,2 mm 29,8 mm
1
1
7
,4
m
m
1
2
2
m
m
85,2 mm
8
m
m
1
1
,3
m
des dielétricas sejam conhecidas. Devido ao fato de ser constituído por moléculas simétricas e não-polares, o teflon possui uma permissividade relativa muito reduzida, ε'PTFE = 2, e praticamente constante em um amplo espec-tro de freqüências (Kinney, 1961; Mathes, 1988).
O capacitor foi projetado considerando-se que, no fu-turo, seria também utilizado para medições em linha do teor de umidade de uma coluna de grãos em movimento. Nesse caso, para fixar os eletrodos e manter sua concentricidade, três peças retangulares de teflon foram firmemente ajustadas em cavidades abertas no eletrodo interno. Cada uma das peças foi fixada ao eletrodo exter-no por meio de dois parafusos de teflon. Para facilitar o preenchimento do capacitor com as amostras de trigo, fi-xou-se um anel de proteção sobre o eletrodo externo e um cone sobre o eletrodo interno, ambos construídos com teflon. O volume livre do capacitor era de 5,5 x 10-4 m3, sendo capaz de conter aproximadamente 0,45 kg de trigo com teor de umidade de 13% b.u.
Os valores dos dois parâmetros que compõem a permissividade complexa relativa do trigo, ε* = ε' - jε", foram obtidos indiretamente utilizando-se os valores me-didos de capacitância e condutância do capacitor, com e sem a amostra entre os eletrodos, de acordo com o méto-do proposto por Lawrence & Nelson (1993). Todas as medições elétricas feitas neste trabalho utilizaram o cir-cuito paralelo equivalente do medidor. Este circir-cuito inter-preta o capacitor como parte integrante de uma combina-ção capacitor-resistor em paralelo. O valor da permissividade relativa do trigo, ε', foi calculado por meio da equação apresentada a seguir, desenvolvida por Berbert (1995), em que Cm representa o valor medido da capacitância do capacitor preenchido com a amostra (pF) e Cf representa a capacitância relacionada à deformação das linhas de campo nas bordas do capacitor e a capacitância devido a campos elétricos de circuitos próxi-mos (pF):
ε' = (Cm - Cf - 2,1837)/5,7896. (3) O fator de perda dielétrica do trigo, ε", foi calculado por meio da seguinte equação:
ε" = (Gm - Ga)/ωC0 (4)
em que:
Gm = condutância do capacitor preenchido com a amos-tra, S;
Ga = condutância do capacitor vazio, S;
ω = 2πf, freqüência angular do campo elétrico, em que f = freqüência, Hz;
C0 = capacitância do capacitor vazio, F.
RESULTADOS E DISCUSSÃO
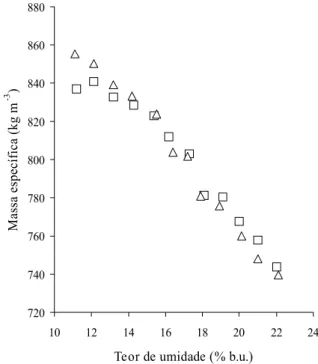
Mostra-se, na Fig. 2, a variação da massa especí-fica aparente do trigo, variedades Mercia e Hereward, em função do teor de umidade das amos-tras. Cada valor de massa específica representa a média obtida em dez repetições utilizando-se uma balança de peso hectolítrico. Verifica-se que, nas condições do presente trabalho, a massa específica decresce com o aumento do teor de umidade.
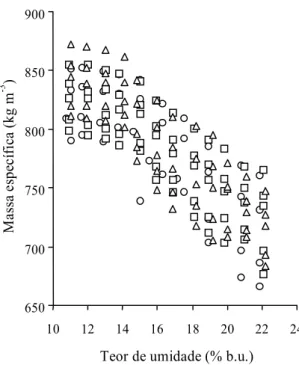
Os intervalos de variação da massa específica do trigo, referentes às três variedades e a cada valor de teor de umidade, podem ser observados na Fig. 3. A massa das amostras variou entre 0,37 e 0,48 kg, e os valores de massa específica variaram no intervalo entre 666 a 873 kg m-3. Nas amostras com teor de
umidade de 22% b.u., a diferença entre os maiores e menores valores de massa específica, nas três varie-dades, foi de, aproximadamente, 14%. DeVoe et al. (1985) afirmam que podem ocorrer variações de até 8% na massa específica do produto que escoa em um secador de fluxo contínuo. Portanto, acredita-se
FIG. 2. Variação da massa específica aparente do tri-go em função do teor de umidade, para as variedades Mercia (¨¨¨¨¨) e Hereward (∆∆∆∆∆), a 24°C.
720 740 760 780 800 820 840 860 880
10 12 14 16 18 20 22 24
Teor de umidade (% b.u.)
M
as
sa
e
sp
ec
íf
ic
a
(k
g
m
que os intervalos de variação de massa específica obtidos neste trabalho representam, com boa mar-gem de segurança, as situações encontradas na prá-tica de secagem de grãos.
Determinação do teor de umidade utilizando-se a permissividade relativa medida simultaneamente em duas freqüências
Utilizando-se o método proposto por McFarlane (1987) e fazendo-se regressões múltiplas com os valores de permissividade relativa, ε', teor de umi-dade, U, e massa específica aparente, ρ, obtiveram-se equações do tipo U = F(ε', ρ) e ρ = F(ε', U) para oito freqüências selecionadas no intervalo entre 500 kHz e 5 MHz (Tabela 1). Tais equações foram obtidas utilizando-se valores de teor de umidade no intervalo de 13,0 a 22,1% b.u. As análises de re-gressão também revelaram que, para o intervalo de freqüências estudado, a permissividade relativa é função linear do teor de umidade e da massa especí-fica do trigo. Observou-se também a ocorrência de
relações lineares entre as raízes quadrada e cúbica da permissividade relativa e os valores de teor de umidade e massa específica. Porém, os coeficientes de correlação obtidos para os modelos quadrático e cúbico foram praticamente os mesmos obtidos com o valor inalterado de ε'. Por exemplo, na freqüência de 5 MHz, obtiveram-se as equações apresentadas a seguir, todas com r2 = 0,96. Os resultados revelam
que apenas 4% da variação de ε' não podem ser ex-plicados pelas variações no teor de umidade e massa específica das amostras.
ε' = 0,236 U + 0,0102 ρ - 6,785; (5) (ε')1/2 = 0,0517 U + 0,00223 ρ - 0,351; (6)
(ε')1/3 = 0,0262 U + 0,00113 ρ + 0,399. (7)
Os resultados mostrados na Tabela 1 também re-velam que os maiores coeficientes de correlação para
TABELA 1. Equações que relacionam a per-missividade elétrica relativa (εεεεε), o teor de umidade, 13,0% ≤≤≤≤≤ U ≤≤≤≤≤ 22,1%, e a massa específica aparente, ρρρρρ (kg m-3), de amos-tras de trigo, variedades Mercia e Hereward, para diversos valores de fre-qüência e temperaturas de 21°C a 24°C.
Freqüência (MHz)
Equações r2
0,5 U = 1,981e' - 0,0301r + 28,328 0,98
r = 55,995e' - 29,626U + 939,700 0,92
0,6 U = 2,128e' - 0,0311r + 28,460 0,98
r = 59,125e' - 28,995U + 916,977 0,93
0,7 U = 2,256e' - 0,0319r + 28,560 0,98
r = 61,748e' - 28,466U + 898,115 0,93
0,8 U = 2,368e' - 0,0327r + 28,705 0,98
r = 63,900e' - 27,981U + 882,018 0,94
0,9 U = 2,460e' - 0,0334r + 28,868 0,98
r = 65,352e' - 27,506U + 869,441 0,94
1,0 U = 2,551e' - 0,0340r + 28,904 0,98
r = 67,285e' - 27,232U + 857,149 0,94
2,0 U = 3,214e' - 0,0384r + 29,520 0,98
r = 77,846e' - 24,711U + 777,160 0,96
5,0 U = 4,057e' - 0,0436r + 30,121 0,99
r = 88,914e' - 22,154U + 698,440 0,97
FIG. 3. Intervalos de variação da massa específica aparente em função do teor de umidade, para temperaturas entre 21°C e 24°C, para as va-riedades Mercia (¨¨¨¨¨), Hereward (∆∆∆∆∆) e Hussar
(¡¡¡¡¡). 650 700 750 800 850 900
10 12 14 16 18 20 22 24
Teor de umidade (% b.u.)
M
as
sa
e
sp
ec
íf
ic
a
(k
g
m
as funções do tipo ρ = F(ε', U) foram obtidos para os maiores valores de freqüência. Além disso, con-siderando-se que para dada alteração no valor do teor de umidade, as correspondentes alterações no valor de ε' são maiores no intervalo de baixas freqüências, foram escolhidas as funções ρ = F(ε', U) a 5 MHz e U = F(ε', ρ) a 0,5 MHz, para integrar o modelo da medição simultânea de ε' em duas freqüências. Incorporando-se, então, a função ρ = F(ε'5 MHz, U) na função U = F(ε'0,5 MHz, ρ),
obte-ve-se a seguinte equação de calibração para o cálcu-lo do teor de umidade do trigo que é, teoricamente, independente da massa específica da amostra:
U = 5,949 ε'0,5 MHz - 8,036 ε'5 MHz + 21,937. (8)
Para testar a exatidão da Equação (8) no cálculo do teor de umidade do trigo, utilizaram-se valores de permissividade relativa obtidos com amostras das variedades Mercia e Hereward, e os resultados fo-ram comparados com os valores de teor de umidade determinados pelo método-padrão de estufa. Ape-sar dos valores elevados dos coeficientes de corre-lação das funções originais, observou-se que a com-binação dessas funções não resulta em um modelo confiável para o cálculo do teor de umidade que seja independente da massa específica da amostra. O desvio-padrão das diferenças entre os valores medi-dos e estimamedi-dos do teor de umidade foi de 0,7 ponto percentual, e a diferença máxima chegou a 1,6 pon-tos percentuais. Esses resultados indicam que a com-binação de duas equações não é um procedimento adequado para obtenção de um modelo que permita a determinação do teor de umidade do trigo com o grau de exatidão exigido em práticas pós-colheita. Apesar disso, para efeitos comparativos, utilizou-se a Equação (8) para calcular o teor de umidade de amostras da variedade Hussar. O desvio-padrão das diferenças entre os valores medidos e estimados do teor de umidade foi de 1,2 ponto percentual, e a di-ferença máxima foi de 2,7 pontos percentuais.
A inclusão de valores de permissividade relativa obtidos para amostras da variedade Hussar com va-lores de massa específica muito diferentes dos utili-zados na derivação da equação de calibração iria comprometer ainda mais os resultados apresentados anteriormente. Por essa razão, esses valores não
fo-ram utilizados na análise de verificação da equação. Por exemplo, os valores de massa específica para as variedades de calibração, Mercia e Hereward, com teor de umidade de 21% b.u., variaram no intervalo 702 kg m-3≤ρ≤ 770 kg m-3, ao passo que o
interva-lo de variação da massa específica para amostras da variedade de verificação Hussar, para o mesmo teor de umidade, foi de 674 kg m-3≤ ρ≤ 769 kg m-3.
Desta forma, para a variedade Hussar, apenas as amostras com massa específica superior a 702 kg m-3 tiveram o teor de umidade estimado pela
equação de calibração.
Devido ao fato de, estatisticamente, o método semi-empírico utilizado para solução de expressões analíticas por separação de variáveis não ser rigoro-so, optou-se por relacionar o teor de umidade das amostras diretamente, por meio de regressão linear, aos valores de permissividade relativa medidos nas duas freqüências utilizadas anteriormente, obtendo-se a obtendo-seguinte equação, com coeficiente de correla-ção igual a 0,94:
U = 5,655 ε'0,5 MHz - 7,231 ε'5 MHz + 19,607. (9)
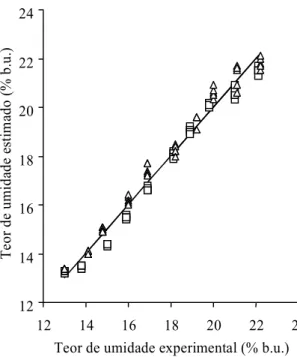
Utilizou-se, então, a Equação (9) para estimar o teor de umidade de amostras de trigo das variedades Mercia e Hereward, e os resultados são mostrados na Fig. 4, onde se vê o gráfico de correspondência entre valores experimentais e estimados de teor de umidade. Nesta figura, a linha contínua representa a correspondência ideal entre esses dois valores. O erro-padrão de calibração (EPC) foi de 0,7 ponto percentual. O erro ou desvio-padrão de calibração é uma indicação do grau de distanciamento dos valo-res de teor de umidade determinados pelo método-padrão de estufa em relação aos valores estimados pela equação de calibração, e é calculado da seguin-te maneira:
(
n p 1)
e
EPC n
1 i
2
i − −
=
∑
=
(10)
em que ei representa a diferença entre os teores de
calibração (Jarret & Kraft, 1989; Lawrence & Nel-son, 1993).
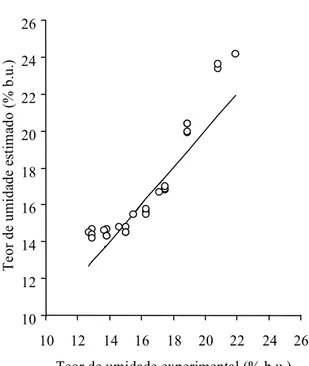
A seguir, utilizou-se a equação de calibração (9) para calcular o teor de umidade de amostras de trigo da variedade Hussar, e os resultados são apresenta-dos na Fig. 5, onde se vê o gráfico de correspondên-cia entre valores experimentais e estimados de teor de umidade. O erro-padrão de predição (EPP) e o erro máximo foram de 1,1 e 2,8 pontos percentuais, respectivamente. O erro-padrão de predição repre-senta o desvio-padrão das diferenças entre os valo-res de teor de umidade determinados em estufa e os estimados pela equação de calibração, utilizando-se os dados da variedade de verificação (Hussar), e é calculado utilizando-se a seguinte equação, em que
erepresenta o valor médio dessas diferenças:
( )
e e(
n 1)
EPP n
1 i
2
i −
−
=
∑
=
. (11)
Observa-se que não houve uma melhora sensível nos resultados quando o desempenho da Equação (9) é comparado ao da Equação (8). A avaliação preliminar do desempenho de equações obtidas de maneira semelhante, utilizando-se porém um maior intervalo de teor de umidade, 11% ≤ U ≤ 22%, re-sultou em valores ainda menos convincentes dos erros-padrão de calibração e predição. A utilização da massa específica como variável dependente re-sultou na equação apresentada a seguir, com coefi-ciente de correlação igual a 0,99. Esse resultado mos-tra que a massa específica tem influência
significa-FIG. 4. Gráfico de correspondência entre os valores de teores de umidade determinados pelo mé-todo-padrão de estufa e aqueles estimados pela Equação (9), para amostras de trigo das variedades Mercia (¨¨¨¨¨) e Hereward (∆∆∆∆∆).
FIG. 5. Gráfico de correspondência entre os valores de teores de umidade determinados pelo mé-todo-padrão de estufa e aqueles estimados pela Equação (9), para amostras de trigo da variedade de verificação Hussar.
12 14 16 18 20 22 24
12 14 16 18 20 22 24 Teor de umidade experimental (% b.u.)
T
eo
r
de
u
m
id
ad
e
es
ti
m
ad
o
(%
b
.u
.)
10 12 14 16 18 20 22 24 26
10 12 14 16 18 20 22 24 26 Teor de umidade experimental (% b.u.)
T
eo
r
de
u
m
id
ad
e
es
ti
m
ad
o
(%
b
.u
tiva quando se tenta estimar o teor de umidade de amostras do trigo por meio da medição simultânea da permissividade relativa em duas freqüências:
U = 0,291 ε'0,5 MHz + 3,469 ε'5 MHz - 0,0416 ρ +
29,798. (12)
Determinação do teor de umidade utilizando-se a permissividade relativa e o fator de perda dielétrica medidos simultaneamente em duas freqüências
Stetson & Nelson (1972) sugeriram que, devido à variação irregular do fator de perda dielétrica com a freqüência de oscilação do campo no intervalo de 0,25 a 20 kHz, o valor de ε" não deveria ser utiliza-do no desenvolvimento de equações para estimar o teor de umidade de grãos e sementes. Nelson (1977) afirmou que a predominância de medidores elétri-cos de teor de umidade que utilizam a permissividade relativa como parâmetro dielétrico deve-se ao fato de o valor de ε', em comparação com ε", exibir me-nor variabilidade para diferentes lotes de uma mes-ma variedade ou mesmo para lotes de diferentes va-riedades. No entanto, Lawrence & Nelson (1993) revelaram que, devido à linearidade entre ln(ε") e a massa de água no trigo a 1,0 MHz, a utilização do logaritmo neperiano do fator de perda dielétrica como covariável contribuiria para melhorar o de-sempenho das equações para o cálculo do teor de umidade. Os resultados obtidos no presente traba-lho para as variedades Mercia e Hereward revela-ram que, de fato, o valor de ln(ε") é um bom indica-dor da quantidade de água presente no trigo em fre-qüências de 0,5, 1,0 e 5,0 MHz. Mostra-se, na Fig. 6, a variação de ln(ε") em função da massa de água presente nas amostras destas duas variedades de trigo a 5,0 MHz. As retas de mínimos quadrados que se ajustam ao conjunto de valores tiveram co-eficientes de correlação de 0,94 e 0,96, para freqüên-cias de 0,5 e 5,0 MHz respectivamente. Concluiu-se então que o valor de ln(ε") também seria um bom indicador do teor de umidade do trigo. Assim, obte-ve-se a seguinte equação para o cálculo do seu teor de umidade no intervalo 13,0% ≤ U ≤ 22,1%, utili-zando-se duas propriedades dielétricas, ε' e ε", de
amostras das variedades Mercia e Hereward, para duas freqüências de oscilação do campo elétrico, 0,5 e 5,0 MHz:
U = 0,663 ε'0,5 MHz + 1,715 ln(ε")0,5 MHz
-2,820 ε'5 MHz + 4,769 ln(ε")5 MHz + 30,437. (13)
A Equação (13) tem um coeficiente de correla-ção igual a 0,98, e os erros-padrão de calibracorrela-ção e predição foram de 0,4 e 0,5 ponto percentual, res-pectivamente. Esses resultados demonstram que o desempenho da equação de calibração torna-se re-almente superior quando foram incluídos os valores de ln(ε") na análise de regressão. O desempenho da Equação (13) no cálculo do teor de umidade de amostras das variedades de calibração, Mercia e Hereward, e da variedade de calibração Hussar, é mostrado graficamente nas Figs. 7 e 8, respectiva-mente.
-1,6 -1,4 -1,2 -1,0 -0,8 -0,6 -0,4 -0,2 0,0 0,2 0,4
55 65 75 85 95
Massa de água (g)
ln
(
e")
CONCLUSÕES
1. O método proposto por McFarlane não permi-te a obpermi-tenção de um modelo para o cálculo do permi-teor de umidade do trigo que seja independente da mas-sa específica aparente dos grãos.
2. A inclusão do valor de ln(ε") como covariável contribui para melhorar o desempenho do modelo. 3. Os erros-padrão de calibração e predição da equação resultante são de 0,4 e 0,5 ponto percentual, respectivamente.
REFERÊNCIAS
BERBERT, P.A. On-line density-independent moisture content measurement of hard winter wheat using the capacitance method. Silsoe: Cranfield University, 1995. 227p. Tese de Doutorado. BRITISH STANDARDS INSTITUTION. British
standard methods of test for cereals and pulses. Part 3. Determination of moisture content of cereals and cereal products (routine method). Londres, 1987. 3p. (BS 4317).
DeVOE, D.R.; BRUSEWITZ, G.H.; STONE, M.L.
Quantitative importance of bulk density when using dielectric measurements to predict percent moisture of hard red winter wheat. St Joseph, MI: American Society of Agricultural Engineers, 1985. 9p. (ASAE Paper 85-3027).
DZHEMELLA, V.V.; PUSTYNNIKOV, V.G. Two-parameter instrument for automatic measurement of moisture content in corn.
Instrument Construction, v.7, p.32-34, 1965. JARRET, J.; KRAFT, A. Statistical analysis for decision
making. Boston: Allyn and Bacon, 1989. 712p. KINNEY, G.F. Engineering properties and applications
of plastics. New York: John Wiley & Sons, 1961. 278p.
KRASZEWSKI, A. Microwave monitoring of moisture content in grain - further considerations. Journal of Microwave Power and Electromagnetic Energy, v.23, n.4, p.236-246, 1988.
LAWRENCE, K.C.; NELSON, S.O. Radio-frequency density-independent moisture determination in wheat. Transactions of the ASAE, v.36, n.2, p.477-483, 1993.
FIG. 7. Gráfico de correspondência entre os valores de teores de umidade determinados pelo mé-todo-padrão de estufa e os estimados pela Equação (13), para amostras de trigo das va-riedades Mercia (¨¨¨¨¨) e Hereward (∆∆∆∆∆).
FIG. 8. Gráfico de correspondência entre os valores de teores de umidade determinados pelo mé-todo-padrão de estufa e os estimados pela Equação (13), para amostras de trigo da va-riedade de verificação Hussar.
12 14 16 18 20 22 24
12 14 16 18 20 22 24 Teor de umidade experimental (% b.u.)
T
eo
r
de
u
m
id
ad
e
es
ti
m
ad
o
(%
b
.u
.)
10 12 14 16 18 20 22 24
10 12 14 16 18 20 22 24 26 Teor de umidade experimental (% b.u.)
T
eo
r
de
u
m
id
ad
e
es
ti
m
ad
o
(%
b
.u
MATHES, K.N. Electrical properties. In: KROSCHWITZ, J.I. (Ed.). Electrical and electronic properties of polymers: a state-of-the-art compendium. New York: John Wiley & Sons, 1988. p.101-181. McFARLANE, N.J.B. Two-frequency capacitance
measurement of the moisture content of grain. Silsoe: AFRC Institute of Engineering Research, 1987. 12p.
NELSON, S.O. Use of electrical properties for grain-moisture measurement. Journal of Microwave Power, v.12, n.1, p.67-72, 1977.
![FIG. 6. Variação da massa de água presente em amos- amos-tras de trigo em função do logaritmo neperiano do fator de perda dielétrica [ln(εεεεε")], a 5 MHz, para as variedades Mercia (¨¨¨ ¨) e¨ Hereward ( ∆∆∆∆∆ ).](https://thumb-eu.123doks.com/thumbv2/123dok_br/15843147.139523/8.892.458.761.594.954/variação-presente-logaritmo-neperiano-dielétrica-εεεεε-variedades-hereward.webp)