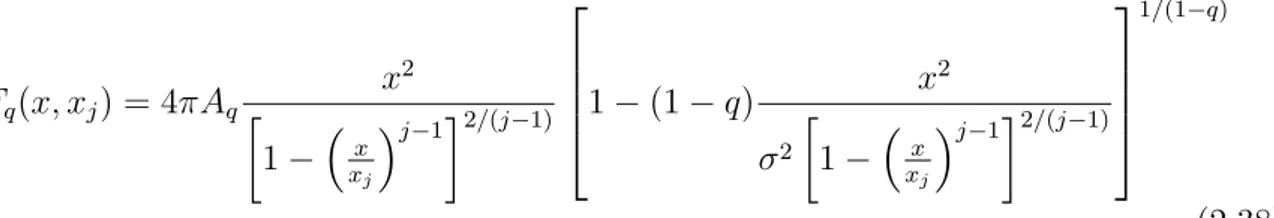Efeitos do freio magnético sobre a distribuição da rotação estelar

(1)

centro de ciˆ

encias exatas e da terra

departamento de f´ısica te´

orica e experimental

programa de p´

os-graduac

¸˜

ao em f´ısica

Efeitos do freio magn´

etico sobre a distribui¸c˜

ao da

rota¸c˜

ao estelar

Rodrigo da Silva Sobrinho

(2)

Efeitos do freio magn´

etico sobre a

distribuic

¸˜

ao da rotac

¸˜

ao estelar

Disserta¸cão de mestrado apresentada ao Programa de Pós-Gradua¸cão em F´ısica do Departamento de F´ısica Teórica e Experimental da Universidade Federal do Rio Grande do Norte como requisito parcial para a obten¸cão do grau de mes-tre em F´ısica.

Orientador: Prof. Dr. Daniel Brito de Freitas.

(3)

(4)

• A Deus pela minha vida e por tê-la transformado de forma tão profunda por in-termédio de Cristo;

• Ao meu orientador, Prof. Dr. Daniel Brito de Freitas, pelo apoio e pelas pala-vras de incentivo, por ter acreditado em mim quando até eu não acreditava e pela disponibilidade de seu tempo ao me orientar tão bem;

• A todos os meus colegas do DFTE/UFRN, em especial aos amigos de sala, pelas d´uvidas tiradas, pelo aux´ılio nas dificuldades acadˆemicas e pela companhia;

• Aos meus irmãos em Cristo da Igreja Batista Independente do Brasil Novo, pelo apoio espiritual e f´ısico. Obrigado pelas ora¸cões em meu favor, muito das minhas vitórias são também de vocês. Obrigado Pastor Davi Jr. pelo carinho e cuidado que tem por mim;

• A todos os professores do PPGF-UFRN, em particular ao Prof. Dr. Daniel Brito de Freitas, Prof. Dr. Francisco George Brady, Prof. Dr. Dory H´elio Aires de L. Anselmo, Prof. Dr. Luciano Rodrigues e Prof. Dr. Gandhi Mohan pelos conheci-mentos transmitidos;

• A minha linda amiga, namorada, noiva e esposa Lene Giovanni Calixto da Silva,` pelo amor que tem por mim e por estar sempre ao meu lado quando preciso;

• Aos meus familiares e amigos por todos os momentos juntos;

• A Antonio de Carvalho Filho, colega e amigo de gradua¸c˜ao que se foi t˜ao jovem. E Zanoni Tadeu, professor e educador, que nos deixou saudades;

• Aos funcion´arios do PPGF-UFRN;

(5)

´

E a volta central na mola que contrabalan¸ca o giro da via l´actea ´

E a fraqueza na for¸ca da gravidade ´

E o fim da gravidez de um nascimento estelar ´

E a sutil caduquice na explosão de uma supernova A f´ısica é o metal na fivela do cinturão de Orion

A f´ısica ´e os feriados em um ano luz ´

E o retorcer dos elos de uma corrente alternada ´

E a areia branca do ch˜ao de um buraco negro ´

E o ringir nas engrenagens de uma nebulosa ´

E a frieza no molhar por ondas de mat´eria ´

E a poeira de part´ıculas de luz que cega o olhar

A f´ısica ´e o orvalho nas relvas de um campo magn´etico

A f´ısica ´e o nada no tudo, ´e o tudo no nada ´

E o pouco no muito, ´e o muito no pouco ´

E a parte que sobra do que n˜ao existiu ´

E a existˆencia do que n˜ao sobrou ´

E o que n˜ao se tem, e mesmo assim, ´

E colocado onde n˜ao se cabe A f´ısica ´e o sorriso de Deus.

(6)

O pioneiro trabalho proposto por Skumanich (1972) mostrou que a velocidade de rota¸cão projetada média< v sini >para estrelas do tipo solar obedece uma lei de decres-cimento no tempo, dada port−1/2_{, onde} _t_{é a idade da estrela. Essa rela¸cão é consistente}

com as teorias de perda de momentum angular através do vento estelar ionizado, que por sua vez está acoplado à estrela pelo seu campo magnético. Vários autores (e.g.: Silva

et al. 2013 e de Freitas et al. 2014) analisaram as poss´ıveis correla¸cões entre o decai-mento rotacional e o perfil da distribui¸cão de velocidade. Esses autores chegaram a uma simples rela¸cão heur´ıstica, mas não constru´ıram uma passagem direta entre o expoente do decaimento rotacional (j) e o expoente da distribui¸cão da velocidade rotacional (q). Todo esse cenário teórico foi proposto usando uma eficiente e robusta mecânica estat´ıstica bem conhecida como mecânica estat´ıstica não-extensiva. A presente disserta¸cão propõe efetivamente fechar essa questão, elaborando um caminho teórico para modificar as dis-tribui¸cões q-Maxwellianas em q-Maxwellianas com v´ınculos f´ısicos extra´ıdos da teoria do freio magnético. Para testar nossas distribui¸cões, usamos um pacote de dados do catálogo de Geneva-Copenhagem Survey com aproximadamente 6000 estrelas F e G limitadas em idade. Como resultado, obtivemos que os expoentes da lei de decaimento e da distribui¸cão seguem uma rela¸cão similar àquela proposta por Silvaet al. (2013).

(7)

The pioneering work proposed by Skumanich (1972) has shown that the projected mean rotational velocity < v sini > for solar type stars follows a rotation law decreases with the time given by t−1/2_{, where} _t _{is the stellar age. This relationship is consistent}

with the theories of the angular momentum loss through the ionized stellar wind, which in turn is coupled to the star through its magnetic field. Several authors (e.g.: Silva et al. 2013 and de Freitas et al. 2014) have analyzed the possible matches between the rotational decay and the profile of the velocity distribution. These authors came to a simple heuristic relationship, but did not build a direct path between the exponent of the rotational decay (j) and the exponent of the distribution of the rotational velocity (q). The whole theoretical scenario has been proposed using an efficient and strong statistical mechanics well known as non-extensive statistical mechanics. The present dissertation proposes effectively to close this issue by elaborating a theoretical way to modify the

q-Maxwellians’ distributions into q-Maxwellians with physics links extracted from the theory of magnetic braking. In order to test our distributions we have used the Geneva-Capenhagen Survey data with approximately 6000 F and G field stars limited by age. As a result, we obtained that the exponents of the decay law and distribution follow a similar relationship to that proposed by Silva et al. (2013).

.

(8)

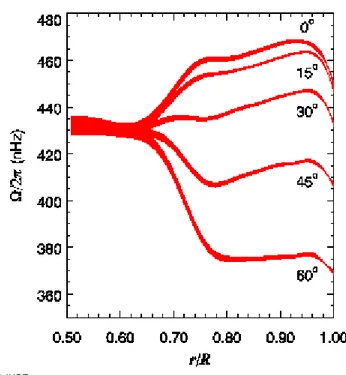
1.1 Frequˆencia angular Ω/2π em fun¸c˜ao do raio para cinco diferentes latitu-des: 0◦

(equador), 15◦ , 30◦

, 45◦ e 60◦

. A envoltória convectiva segue a rota¸cão diferencial, entretanto a envoltória radiativa segue aproximada-mente a rota¸cão de um corpo r´ıgido. Cortesia do National Solar Observa-tory. Ω/2π é medido em nHz (nanohertz). http://soi.stanford.edu . . . 3 1.2 Esquema de determina¸cão da velocidade rotacional de uma estrela pelo

método das linhas espectrais. http://hsc.csu.edu.au/physics/options/astrophysics 4 1.3 Velocidade de rota¸cão projetada (v sini), onde ié o ângulo entre o eixo de

rota¸cão e a linha de visada. . . 5 1.4 Estrutura solar. Figura retirada de: http://astro.if.ufrgs.br/esol/esol.htm . 7 1.5 As zonas radiativa e convectiva em fun¸cão da massa. http://www.sun.org . 8 1.6 Diagrama-HR; Foto do Observatório Nacional: http://www.on.br/ead2013/ 9

1.7 No painel (a) representando as flutua¸cões da velocidade do vento solar no per´ıodo do ano de 2003 a 1 UA (Unidade Astronômica) pelo telescópio espacial ACE (Advanced Composition Explorer). No painel (b) estão re-presentados as flutua¸cões da intensidade do campo magnético também me-didas sob as mesmas condi¸cões que a velocidade do vento. Burlaga e Vinãs (2004) . . . 11 1.8 Linhas do campo magnético ao redor da estrela Tau-Scorpii. Em azul,

as linhas do campo aberto que fazem o fluxo de part´ıculas provenientes do vento estelar escaparem para fora da estrela. Em branco, as linhas de campo fechadas. Figura retirada de Donati et al. (2006). . . 12

2.1 Fun¸cão distribui¸cão q-Maxwelliana para diferentes valores de q. . . 23 2.2 Comparativo entre a fun¸cão Maxwelliana e aq-Maxwelliana para diferentes

(9)

2.3 Comparativo entre as fun¸cões distribui¸cões Maxwelliana padrão,q-Maxwelliana e a q-Maxwelliana com v´ınculo para a lei de Skumanich (j = 3). Escala arbitrária. Usando q = 1.5. Fator de freioxj = 20. . . 28

2.4 q-Maxwelliana com v´ınculo (para a lei de Skumanich) para diferentes va-lores de q. x3 = 20 . . . 28

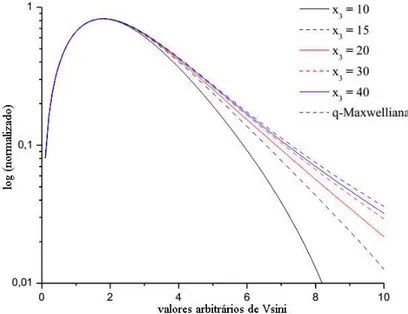
2.5 q-Maxwelliana com v´ınculo (para a lei de Skumanich) para diferentes va-lores de x3. q= 1.4. . . 29

2.6 q-Maxwelliana com v´ınculo para a lei de decaimento proposta por Soder-blom et al. (1991). Variando o fator de freio e mantendo q fixo em 1.9. . . 31 2.7 q-Maxwelliana com v´ınculo para a lei de decaimento proposta por

Soder-blom et al. (1991). Variando o ´ındice entr´opico q por um fator de 0.5. Fator de freio fixo em 20. . . 32 2.8 q-Maxwelliana com v´ınculo para a lei de decaimento proposta por Pace e

Pasquini (2004). Variando o fator de freio. O ´ındice entr´opico q fixo em 1.9. 32 2.9 q-Maxwelliana com v´ınculo para a lei de decaimento proposta por Pace e

Pasquini (2004). Variando o ´ındice entr´opico q por um fator 0.5. Fator de freio fixo em 20. . . 33 2.10 q-Maxwelliana com v´ınculo para a lei de decaimento proposta por Reiners

e Mohanty (2012). Variando o fator de freio. O ´ındice entr´opico q fixo em 1.9. . . 33 2.11 q-Maxwelliana com v´ınculo para a lei de decaimento proposta por Reiners

e Mohanty (2012). Fator de freio fixo em 20. O ´ındice entrópico qvariando por um fator 0.5. . . 34 3.1 Distribui¸cão de v sini das estrelas F e G da amostra. As linhas sólidas

referem-se aos dados de v sini, enquanto as linhas tracejadas referem-se aos dados de v sini multiplicados pelo fator estat´ıstico de corre¸cão 4/π. Figura retirada de de Freitas e De Medeiros (2013). . . 37 3.2 Histograma da velocidade de rota¸cão projetada das estrelas F single. . . 38 3.3 Histograma da velocidade de rota¸cão projetada das estrelas G single. . . . 38 3.4 Rela¸cão rota¸cão-idade das estrelas F e G da amostra. São mostradas as

m´edias dev sinino intervalo de idade correspondendo a 0,5 Gyr. As linhas cont´ınuas representam o fit usando a lei de Skumanich e as linhas tracejadas representam o fit utilizando as equa¸c˜oes v(t) =v0exp[−λ1(t−t0)] ev(t) =

vsat[1 + (q−1)λq(t−tsat)]1/(1−q) respectivamente. de Freitas e De Medeiros

(10)

3.8 Histograma da massa em fun¸c˜ao da massa solar das estrelas G single. . . . 42

3.9 Histograma da metalicidade em fun¸c˜ao da metalicidade solar das estrelas F single. . . 43

3.10 Histograma da metalicidade em fun¸c˜ao da metalicidade solar das estrelas G single . . . 43

4.1 Distribui¸c˜ao de v sini das estrelas early F. . . 46

4.2 Distribui¸c˜ao de v sini das estrelas F tardias. . . 47

4.3 Distribui¸c˜ao de v sini das estrelas early G. . . 48

4.4 Distribui¸c˜ao de v sini das estrelas G tardias. . . 49

4.5 Distribui¸c˜ao de v sini de todas as estrelas F da amostra. . . 50

(11)

2.1 Algumas leis de decaimento presentes na literatura escritas em fun¸c˜ao do expoente j. . . 30

4.1 Valores do expoente j obtidos por de Freitas e De Medeiros (2013). . . 45 4.2 Melhores valores dos parâmetros j, xj e q do ajuste não-linear via método

LM das distribui¸cões teóricas e emp´ıricas para o intervalo do tipo espectral F0-F5. . . 47 4.3 Melhores valores dos parâmetros j, xj e q do ajuste não-linear via método

LM das distribui¸cões teóricas e emp´ıricas para o intervalo do tipo espectral F6-F9. . . 47 4.4 Melhores valores dos parâmetros j, xj e q do ajuste não-linear via método

LM das distribui¸cões teóricas e emp´ıricas para o intervalo do tipo espectral G0-G5. . . 48 4.5 Melhores valores dos parâmetros j, xj e q do ajuste não-linear via método

LM das distribui¸cões teóricas e emp´ıricas para o intervalo do tipo espectral G6-G9. . . 49 4.6 Melhores valores dos parâmetros j, xj e q do ajuste não-linear via método

LM das distribui¸cões teóricas e emp´ıricas para o intervalo do tipo espectral F0-F9 . . . 49 4.7 Melhores valores dos parâmetros j, xj e q do ajuste não-linear via método

(12)

Agradecimentos i

Resumo iii

Abstract iv

Lista de Figuras vii

Lista de Tabelas viii

Sum´ario x

1 Introdu¸c˜ao 1

1.1 Rota¸c˜ao Estelar . . . 1

1.1.1 Um breve resgate histórico da Rota¸cão Estelar até os trabalhos de Otto Struve em 1945 . . . 2

1.1.2 A Rota¸c˜ao Estelar depois dos trabalhos de Otto Struve . . . 4

1.1.3 A rela¸c˜ao rota¸c˜ao-atividade-idade . . . 6

1.2 Decaimento rotacional como uma consequência da a¸cão do freio magnético 11 1.3 Mecânica Estat´ıstica: Ser ou não ser (não)-extensiva . . . 14

1.3.1 Mecˆanica estat´ıstica de Boltzmann-Gibbs . . . 14

1.3.2 Mecˆanica estat´ıstica n˜ao-extensiva de C. Tsallis . . . 16

1.4 Plano de trabalho . . . 18

2 Distribui¸cão q-Maxwelliana com v´ınculos 19 2.1 Fun¸cão distribui¸cão q-Maxwelliana . . . 19

2.2 Um novo elemento no contexto: O fator de freio generalizado . . . 24

2.3 A fun¸c˜ao de distribui¸c˜ao q-Maxwelliana Skumanichiana . . . 27

(13)

3 Dados observacionais 36

3.1 Levantamento Geneva-Copenhagen . . . 36

3.2 Parˆametros estelares importantes . . . 36

3.2.1 Velocidade de rota¸c˜ao projetada v sini . . . 36

3.2.2 Idade . . . 39

3.2.3 Massa e Metalicidade . . . 40

3.2.4 Defini¸c˜ao da amostra . . . 43

4 Resultados e Discussões 45 4.1 Distribui¸cões teóricas versus distribui¸cões emp´ıricas . . . 45

4.1.1 Correla¸c˜oes entre os expoentes q ej . . . 51

5 Conclus˜oes e perspectivas 53 5.1 Conclus˜oes . . . 53

5.2 Perspectivas . . . 54

(14)

Cap´ıtulo

1

Introdu¸c˜

ao

1.1 Rota¸c˜

ao Estelar

Sem dúvida, um dos fenômenos mais intrigantes da matéria é o fato dela poder gi-rar. Esse comportamento denominado de rota¸cão está fortemente presente em nossa vida cotidiana, seja pelo simples fato de uma crian¸ca girar um pião ou pela forma como marca-mos o tempo. Podemarca-mos verificar rota¸cão em quase todas as coisas que nos rodeiam: das menores part´ıculas subatômicas como o elétron, passando pelos gigantescos aglomerados de galaxias até o próprio Universo. Sua popularidade no Universo nos mostra o quanto é importante o conhecimento sobre esse fenômeno. Infelizmente, não teremos na presente disserta¸cão como abordar essa temática em sua completude, mas apenas mergulhar em águas rasas no oceano da Rota¸cão das Estrelas.

No caso espec´ıfico da Rota¸cão Estelar, vivenciamos ultimamente a comemora¸cão dos 400 anos da Rota¸cão Estelar. Essa importante data remete às observa¸cões feitas pelo pensador italiano Galileo Galilei em 1613, registradas no seu livro “l’Istoria e dimostra-zioni intorno alle macchie solari e loro accidenti”, onde ele descreve as manchas no Sol e a interpreta¸cão dos seus movimentos devido à rota¸cão solar. Tal marco histórico foi celebrado na cidade de Natal no workshop intitulado “400 Years of Stellar Rotation”. Na ocasião se fizeram presentes os maiores nomes da rota¸cão em todo o mundo. Oworkshop

focou nas mais recentes descobertas das miss˜oes espaciaisCoRot1 _e_Kepler2_{, com vi´es na}

rota¸c˜ao.

Nesse contexto nosso trabalho ir´a focar no estudo do comportamento da rota¸c˜ao

este-1_{O projeto}_CoRoT _{foi desenvolvido pela}_{Agˆencia Espacial Francesa (CNES)}_{, em conjunto com v´}_arios

laborat´orios franceses e parceiros internacionais, incluindo o Brasil.

2_{A sonda}_Kepler_{consiste em um observat´orio espacial projetado pela}_NASA_{com o objetivo de procurar}

(15)

lar projetadav sini, ondeié o ângulo de inclina¸cão em rela¸cão à linha de visada. Devemos destacar que a rota¸cão estelar é um assunto bastante vasto na Astrof´ısica, existem vários estudos sobre rota¸cão de estrelas tanto no campo das estrelas single3 _{como também das}

binárias. Esse assunto é tão vasto que também pode ser estudado segregando as estrelas por massa (ou tipo espectral), por magnitude, presen¸ca ou não de planeta(s) e/ou fase evolutiva, ou ainda para os casos mais at´ıpicos, investigar o comportamento da rota¸cão de galáxias e outros objetos astrof´ısicos exóticos, como quasares e buracos negros.

1.1.1 Um breve resgate hist´

orico da Rota¸c˜

ao Estelar at´

e os

tra-balhos de Otto Struve em 1945

Os estudos sobre rota¸cão estelar tiveram in´ıcio em meados do século XVII com a ob-serva¸cão do movimento de manchas escuras (manchas solares) na superf´ıcie do Sol. As medidas do movimento dessas manchas foram originalmente feitas pelo alemão Johannes Fabricius (1587-1616), o italiano Galileo Galilei (1564-1642), o inglês Thomas Harriot (1560-1621), e o alemão Christopher Scheiner (1573-1650). Através dessas observa¸cões, eles chegaram a um per´ıodo de rota¸cão do Sol de 27 dias. Scheiner considerava que os padrões escuros na superf´ıcie do Sol eram planetas, (Hipótese Planetária). Mas, em 1613 Galileo refutou a Hipótese Planetária de Scheiner ao publicar suas ideias e observa¸cões no artigo intituladoIstoria e Dimostrazioni intorno alle Macchie Solari e loro Accidenti. Galileo observou que as manchas sofriam alargamento e aceleravam à medida que se des-locava da borda em dire¸cão ao centro solar.

Com rela¸cão à rota¸cão em outras estrelas, o pioneirismo fica por conta dos trabalhos do astrônomo francês Ismaël Boulliand (1605-1694). Em 1667 Boulliand atribuiu a varia-bilidade das curvas de luz de algumas estrelas, como Mira Ceti, ao efeito de rota¸cão, onde a estrela ao girar exibia hemisférios: hora com manchas, hora sem manchas.

Depois de um longo per´ıodo de inatividade, em 1850 a questão da rota¸cão estelar sofre avan¸cos significativos. O britânico Richard Carrington (1826-1875) e Gustav Spörer (1822-1895), de forma independente, entre os anos de 1853-1861, mostraram que a en-voltória externa vis´ıvel do Sol não girava como um corpo r´ıgido, mas que o per´ıodo de rota¸cão variava com a latitude. Essa espetacular constata¸cão é o que se conhece hoje como rota¸cão diferencial. A Fig 1.1 nos mostra que próximo do equador solar (0◦

), a rota¸cão é maior que próximo aos polos (60◦

).

3_{O termo em inglˆes} _single _{no contexto da Astrof´ısica ´e de dif´ıcil tradu¸c˜}_{ao. Por esse motivo iremos}

(16)

Figura 1.1: Frequˆencia angular Ω/2π em fun¸c˜ao do raio para cinco diferentes latitu-des: 0◦

(equador), 15◦ , 30◦

, 45◦ e 60◦

. A envoltória convectiva segue a rota¸cão dife-rencial, entretanto a envoltória radiativa segue aproximadamente a rota¸cão de um corpo r´ıgido. Cortesia do National Solar Observatory. Ω/2π é medido em nHz (nanohertz). http://soi.stanford.edu

Com o avan¸co da tecnologia, em especial o advento da espectroscopia, a f´ısica este-lar entrou em uma nova era. O astrônomo alemão Hermann Vogel (1834-1898) mostrou em 1871, que a taxa de rota¸cão do Sol poderia ser determinada por desvio Doppler das linhas espectrais. Nils Dúner e Jakob Halm, depois de inúmeras observa¸cões feitas entre 1887-1906, demostraram que a taxa de rota¸cão determinada espectroscopicamente e as realizadas pelas observa¸cões das manchas solares eram compat´ıveis. Em 1877, William de Wiveleslie Abney (1877) foi o primeiro a expor a ideia de determinar a taxa de rota¸cão estelar através das larguras das linhas espectrais. Outro método de determina¸cão da taxa de rota¸cão estelar, o método gráfico, foi desenvolvido por Shajn e Struve (1929). Esse método sistemático consiste em determinar o valor da velocidade de rota¸cão projetada

v sini. Na Fig 1.2 podemos mostrar de forma esquemática como o método para determi-nar a velocidade de rota¸cão estelar, por meio do espectro, funciona.

(17)

razão para suspeitar que os eixos de rota¸cão não sejam essencialmente distribu´ıdos aleato-riamente. Mais tarde, como veremos, outros autores baseados nesse princ´ıpio constru´ıram as bases estat´ısticas para investigar o perfil da distribui¸cão das velocidades rotacionais. Sem dúvidas, esse trabalho é um divisor de águas para a descri¸cão estat´ıstica da rota¸cão estelar.

Figura 1.2: Esquema de determina¸c˜ao da velocidade rotacional de uma estrela pelo m´etodo das linhas espectrais. http://hsc.csu.edu.au/physics/options/astrophysics

1.1.2 A Rota¸c˜

ao Estelar depois dos trabalhos de Otto Struve

Como já frisamos no in´ıcio do Cap´ıtulo, a rota¸cão é um dos parâmetros mais impor-tantes no estudo da evolu¸cão estelar. Ela é importante para descrever uma variedade de questões em Astrof´ısica Estelar e nos fornece importantes informa¸cões sobre intera¸cões de maré gravitacional em binárias, magnetismo estelar, assim como a transferência de momentum angular ou desacelera¸cão devido a planetas ou efeito magnético. A rota¸cão influencia e acompanha toda a vida da estrela, do nascimento ( onde há a distribui¸cão do momento angular ainda na fase de proto-estrela), até a morte, onde a massa desempenha um papel importante.

(18)

entanto, seria necessário um avan¸co muito grande na tecnologia dos telescópios ópticos para se obter uma amostra estatisticamente satisfatória utilizando-se o segundo método.

Figura 1.3: Velocidade de rota¸cão projetada (v sini), onde i é o ângulo entre o eixo de rota¸cão e a linha de visada.

O método que utiliza as linhas espectrais tem se mostrado bem útil na determina¸cão de velocidades projetadas de estrelas do tipo espectral O, B, A e F. Entretanto, as medidas dev sinisó podem ser utilizadas de uma forma estat´ıstica, já que o ângulo de inclina¸cão

i é, em geral, desconhecido. Uma contribui¸cão importante nesse sentido foi feita por Struve (1945), que propôs que esses ângulos estariam distribu´ıdos de forma aleatória. Tal afirma¸cão consiste em uma das mais importantes no estudo da rota¸cão estelar. Usando esse argumento, pode-se então relacionar a média da velocidade projetada < v sini >

para um grupo de estrelas com a média da velocidade equatorial< v >, tendo em conta que o valor médio de < sini > é igual a π/4 (ver Chandrasekhar e Münch, 1950; Gray, 1992; e, mais recentemente, Silva, Soares e de Freitas, 2014).

Como vimos, as observa¸cões nos fornecem somente as velocidades rotacionais proje-tadas, mas estamos interessados nas velocidades equatoriais das estrelas. Nessa mesma linha, Chandrasekhar e Münch (1950) sugeriram duas equa¸cões integrais para descrever a distribui¸cão de velocidades rotacionais verdadeirasf(x) e projetadasφ(y), ondey =x sini

(19)

f(x) = ₋2 πx 2 ∞ Z x

φ(y)dy

y2₍_y2₋_x2₎1/2 (1.1)

φ(y) =y

∞

Z

y

f(x)dx

x(x2₋_y2₎1/2 (1.2)

Outra questão intrigante e que possui inúmeras controvérsias na Astrof´ısica Estelar está relacionada com a natureza estat´ıstica que controla a velocidade de rota¸cão, de ma-neira que podemos nos perguntar sobre algumas questões como: qual é a distribui¸cão que controla as velocidades rotacionais? Como foi distribu´ıdo o momento angular da nuvem que formou as estrelas? Será que esta distribui¸cão é oriunda de uma lei f´ısico-estat´ıstica?

´

E preciso assim fazer uma outra pergunta: Existiria uma mecânica estat´ıstica que melhor descreve a distribui¸cão da rota¸cão estelar? Uma poss´ıvel solu¸cão dada a esta per-gunta foi proposta por Soares et al. (2006) quando sugeriu uma fun¸cão de distribui¸cão para velocidade de rota¸cão estelar baseada na entropia generalizada de Constantino Tsal-lis (1988). Essa entropia, dita não-extensiva, surgiu como uma poss´ıvel generaliza¸cão da entropia de Boltzmann-Gibbs. Soares et al. (2006) levaram em conta os argumentos propostos por Silva et al. (1998) para uma generaliza¸cão da fun¸cão de distribui¸cão de velocidades de Maxwell-Boltzmann.

A entropia proposta por Boltzmann-Gibbs é muito bem utilizada para explicar o com-portamento de divessos sistemas f´ısicos, porém ela falha em um número considerável de outros sistemas, também conhecidos como sistemas complexos. Nesse sentido, surgiram várias entropias que buscavam investigar os casos em que a teoria de Boltzmann-Gibbs não era satisfatória. Dentre elas podemos citar, além da não-extensiva de Tsallis (1988), a de Druyvenstein (1930, 1934), Renyi (1970), Sharma-Mittal (1975), Abe (1997), Papa (1998), Borges e Roditi (1998), Landsberg e Vedral (1998), Anteneodo e Plastino (1999), Frank e Daffertshofer (1999) e Kaniadakis (2001).

1.1.3 A rela¸c˜

ao rota¸c˜

ao-atividade-idade

(20)

A cromosfera solar é uma região da atmosfera solar situada um pouco acima da fotos-fera e que possui uma baix´ıssima densidade. Já a fotosfotos-fera solar é uma região de cerca de 330 km de espessura e temperatura de aproximadamente 5785 K, sendo a camada vis´ıvel do Sol. A envoltória convectiva representa 15% do raio solar, é uma região de temperatura relativamente baixa (2 milhões ◦

C), onde o plasma por conveçcão transporta energia no interior solar. A Fig 1.4 mostra de forma esquemática, a estrutura solar.

Figura 1.4: Estrutura solar. Figura retirada de: http://astro.if.ufrgs.br/esol/esol.htm

A rota¸cão afeta não apenas a atmosfera, mas de forma substancial o interior estelar. Fenômenos turbulentos na envoltória convectiva provocam uma circula¸cão meridional cau-sando o efeito conhecido como rota¸cão diferencial. Deste modo, a envoltória convectiva segue uma rota¸cão diferencial, enquanto que a envoltória radiativa parece seguir uma rota¸cão de corpo r´ıgido, (ver Faulkner et al., 1968; Kosovichev et al., 1997), como ilus-trado para o Sol na Fig 1.1.

(21)

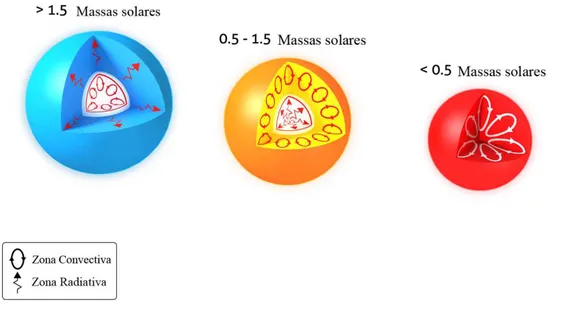
Algo que também influencia bastante a rota¸cão estelar e outros mecanismos estelares principalmente o d´ınamo, é a localiza¸cão das envoltórias convectiva e radiativa e suas es-pessuras. A Fig 1.5 mostra que existe uma inversão na localiza¸cão dessas zonas, e a massa da estrela é que define essa inversão e também a espessura das envoltórias (de Freitas, 2006).

A diferen¸ca na forma como gira a zona radiativa (quase como corpo r´ıgido) e a zona convectiva (diferencial ), faz existir uma região de transi¸cão de rota¸cão. Essa região onde existe essa brusca transi¸cão na velocidade de rota¸cão entre um interior que gira como um corpo r´ıgido e a envoltória convectiva, onde o plasma gira mais rápido no equador, é determinada por uma fina camada imediatamente abaixo da envoltória convectiva deno-minada detachocline4 _{(ver Silva (2006)). Na Fig 1.4 essa zona de transi¸cão é representada}

como a linha preta entre a zona convectiva e a zona radiativa.

Figura 1.5: As zonas radiativa e convectiva em fun¸c˜ao da massa. http://www.sun.org

A rota¸cão também causa um efeito levitacional onde as estrelas apresentam luminosi-dade intr´ınseca e temperatura efetiva menores. A luminosiluminosi-dade também é um importante parâmetro em astrof´ısica. Tal fato gera fortes consequências na determina¸cão da posi¸cão das estrelas no Diagrama HR5 _{(de Freitas, 2006).}

4_O_tachocline_{´e uma camada de transi¸c˜}_{ao entre dois regimes de rota¸c˜}_{ao distintos: O envelope}

convec-tivo que gira de forma diferencial e o interior radiaconvec-tivo que rotaciona como um corpo r´ıgido.

5_{HR significa} _{Hertzsprung-Russel} _{em homenagem ao astrˆonomo dinamarquˆes Ejnar Hertzsprung e o}

(22)

O diagrama HR é um gráfico que relaciona a luminosidade de algumas estrelas com as temperaturas que elas apresentam, esse diagrama pode relacionar outros pares de parâmetros. Ele é o mapa que orienta todo astrof´ısico. A figura 1.6 mostra um exemplo de diagrama HR.

Figura 1.6: Diagrama-HR; Foto do Observat´orio Nacional: http://www.on.br/ead2013/

Outro trabalho de destaque é o de Schatzman (1962), que fez um importante estudo so-bre o papel da rota¸cão na atividade magnética estelar. Como mencionamos anteriormente, a rota¸cão estelar tem um papel importante no comportamento da atividade magnética da estrela. Schatzman mostrou que a atividade magnética em uma estrela com rota¸cão para cada região do diagrama-HR depende da profundidade da envoltória convectiva.

No contexto da estat´ıstica, destaca-se os trabalhos de Su-Shu Huang (1965, 1967) que utilizando as fun¸cões de distribui¸cão de Chandrasekhar e Münch (1950), analisou o com-portamento da rota¸cão para estrelas da sequência principal com foco nas consequências pertencentes à perda de momento angular devido a presen¸ca de planetas6_.

6

(23)

Esses importantes estudos (Su-Shu Huang, 1965, 1967) e outros trabalhos decorrentes, proporcionaram uma descri¸cão estat´ıstica das distribui¸cões devsini para diferentes tipos espectrais, mostrando que o mecanismo de desacelera¸cão, que é fun¸cão da idade da estrela, tem um comportamento que muda de perfil com o tipo espectral. O autor considerou que a taxa de perda de momento angular poderia ser descrita como uma lei de potência:

dx dt =−

X

ajxj (1.3)

onde xrepresenta qualquer grandeza f´ısica que n˜ao se conserva (de Freitas, 2006).

Outro trabalho muito importante no âmbito astrof´ısico foi o de Skumanich (1972). Ele mostrou em seu trabalho, que medidas de rota¸cão e atividade para as Hyades e Pleia-des, efetuadas anos antes por Kraft (1967), eram consistentes com a rela¸cão vrot ∝t−1/2.

Esta rela¸cão é bem comportada para teorias simples de perda de momento angular em que o vento ionizado é acoplado à estrela pelo campo magnético. Alguns autores como Soderblom (1983), Barryet al.. (1987) e Soderblom et al. (1991) chegaram a resultados parecidos para estrelas do tipo solar, entretanto com leis de potência apresentando expo-entes diferexpo-entes. Em seus trabalhos, eles encontraram expoexpo-entes que iam de -1/2 (rela¸cão de Skumanich) a -4/3. Mais recentemente, Pace e Pasquini (2004) argumentaram que essas leis de potência não representam o perfil da curva que relaciona atividade com idade de estrelas anãs com tipo espectral F em aglomerados abertos.

Podemos destacar também o trabalho de de Freitas e De Medeiros (2013) que propõe uma nova abordagem, baseada na Mecânica Estat´ıstica não-extensiva de Tsallis (Tsallis, 1988), para o estudo da rela¸cão rota¸cão-idade estelar. Nesse sentido os autores generali-zam a lei de decaimento usando a estat´ıstica não-extensiva. Com isso, em seu modelo, os mesmos levam em conta fatores que são de suma importância quando falamos de rota¸cão estelar (e.q.: geometria do campo magnético, taxa de perda de massa e temperatura co-ronal) e que não são poss´ıveis de serem tratados no âmbito da estat´ıstica de BG.

´

(24)

1.2 Decaimento rotacional como uma consequˆ

encia

da a¸c˜

ao do freio magn´

etico

Os dados observacionais mostram que as estrelas diminuem sua rota¸cão ao longo do tempo. Um dos mecanismos propostos para explicar esse efeito é a perda de momento angular por vento estelar magnético (Nariai, 1969).

As estrelas possuem em geral um campo magnético remanescente da nuvem que a criou ou que foi desenvolvido posteriormente por algum efeito processual de d´ınamo. Com exce¸cão do nosso Sol, a configura¸cão do campo magnético não é bem conhecida, fato esse devido principalmente à distância e às limita¸cões instrumentais.

A Fig 1.7, retirada de Burlaga e Vinãs (2004), é um bom exemplo da correla¸cão entre o campo magnético e o vento estelar. Ela faz referência ao comportamento do vento solar na fase de decl´ınio do ciclo de atividade solar 23. É poss´ıvel ver que os picos de maior intensidade do campo magnético coincidem com os picos de maior velocidade dos ventos.

Figura 1.7: No painel (a) representando as flutua¸cões da velocidade do vento solar no per´ıodo do ano de 2003 a 1 UA (Unidade Astronômica) pelo telescópio espacial ACE (Advanced Composition Explorer). No painel (b) estão representados as flutua¸cões da intensidade do campo magnético também medidas sob as mesmas condi¸cões que a veloci-dade do vento. Burlaga e Vinãs (2004)

(25)

com a rota¸c˜ao tem um papel importante na perda de quantidade de momento angular (de Freitas, 2009).

Figura 1.8: Linhas do campo magn´etico ao redor da estrela Tau-Scorpii. Em azul, as linhas do campo aberto que fazem o fluxo de part´ıculas provenientes do vento estelar escaparem para fora da estrela. Em branco, as linhas de campo fechadas. Figura retirada de Donatiet al. (2006).

A perda de massa é um processo comum durante a evolu¸cão da estrela. Esse processo pode ocorrer de uma forma súbita e catastrófica - na explosão de uma supernova, por exemplo - como também pode ocorrer de uma forma mais lenta e cont´ınua através dos ventos estelares (de Freitas, 2009). Pode ocorrer ainda transferência de massa de uma estrela para outra em um sistema binário de contato.

As primeiras evidências da perda de massa nas estrelas remontam ao século XVI, com as observa¸cões de uma supernova pelo famoso astrônomo Tycho Brahe7 _{em 1572 e a}

pos-terior com as primeiras observa¸cões da estrela variável P Cygni. Mas somente a partir de 1920 e 1930 as observa¸cões come¸caram a ser feitas de forma sistemática.

Essas primeiras observa¸cões eram feitas de forma que imagens obtidas em épocas di-ferentes mostravam cascas concêntricas em expansão à medida do tempo, configurando

7_{Tycho Brahe apenas observou a supernova. Ele n˜}_{ao creditou o fenˆ}_{omeno `}_{a perda de massa estelar}

(26)

assim uma eje¸cão. O que ocorre é que alguns mecanismos fornecem energia à matéria oriunda da superf´ıcie estelar, essa matéria então é acelerada até superar a velocidade de escape da estrela, configurando assim uma perda de massa para o espa¸co (ver Maciel, 2005).

O fenômeno dos ventos estelares pode ocorrer tanto em estrelas anãs, como no Sol por exemplo, como também em estrelas gigantes vermelhas e supergigantes quentes. A perda de massa por vento estelar varia muito com a massa da estrela. No Sol essa perda é muito pequena, algo em torno de ˙M _≤ 10−₁₄

M⊙/ano, onde ˙M8 é taxa de perda de massa. Já em estrelas mais massivas (M > 20M⊙) essa taxa é bem significativa, che-gando a 10−5_M

⊙/ano, ainda na sequência principal. Além do tipo espectral, o estágio evolutivo da estrela também influencia na perda de massa. Em estrelas menos massivas (M < 10M⊙) quando em seus estágios finais de sua evolu¸cão, podem apresentar uma taxa de perda de massa de 10−6_M

⊙/ano ou at´e maiores.

Um dos mecanismos respons´aveis pela perda de massa ´e o chamado ventos coronais

(Maciel, 2005). Esse mecanismo ocorre em estrelas relativamente frias da sequência prin-cipal, com tipo espectral F5 ou acima, e pode também ocorrer em algumas gigantes, pois essas estrelas apresentam cromosferas e coroas semelhantes ao Sol. Os ventos coronais são produzidos pela pressão do gás nesta região onde a temperatura chega próximo de 106K, no caso do Sol.

Os ventos estelares também podem ser gerados por ondas sonoras(Maciel, 2005). Es-sas ondas são geradas por movimentos convectivos na região subfotosférica, que criam ondas acústicas que se propagam ao longo da atmosfera.

Outro mecanismo é o causado pelapoeira circunstelar (Maciel, 2005). Esse fenômeno ocorre em estrelas gigantes frias que podem condensar diversas espécies de grão em suas fotosferas e envelopes. Desse modo, a a¸cão da pressão da radia¸cão estelar pode produzir elevadas taxas de perda de massa, que ocorre pela transferência da quantidade de movi-mento do campo de radia¸cão para os grãos, e dos grãos para o gás circunvizinho.

Em s´ıntese, a perda de massa afeta significativamente a evolu¸c˜ao das estrelas9_,

princi-palmente em estrelas mais massivas, pois como vimos, essas apresentam uma maior taxa de perda de massa. Outro parâmetro importante que é afetado por essa perda é a lumi-nosidade e, consequentemente, as escalas de tempo evolutivo, pois sabemos que a massa é

8_dM/dt_{descreve quanto material ´e perdido pela estrela por unidade de tempo.}

9_{Para estrelas de pequena massa e na sequˆencia principal a perda de massa n˜}_{ao influencia de forma}

(27)

o principal parˆametro que influencia a evolu¸c˜ao estelar (ver Lamers et al. (1999); Castor

et al. (1975); Nariai (1969); Maciel (2005))

Que argumentos poderiam sustentar a tese de que os ventos magnéticos seriam res-ponsáveis por tal fenômeno de desacelera¸cão rotacional? Segundo Nariai (1969), embora o vento das estrelas da sequência principal não influencie fortemente a evolu¸cão estelar, devido às altas velocidades de eje¸cão de massa, da ordem de centenas de km/s, depen-dendo da classe espectral, ele provoca torques externos que podem ser responsáveis pelo decaimento rotacional. Segundo Castor et al. (1975), podemos atribuir a taxa de perda de massa e a velocidade terminal que corresponde a velocidade do vento atingida assinto-ticamente a grandes distâncias da estrela, como os mecanismos que controlam os ventos estelares.

Nesse sentido destacamos o trabalho de de Freitas e De Medeiros (2013) que anali-saram a evolu¸cão rotacional de estrelas F e G limitadas em idade e massa e dentro da vizinhan¸ca solar. Eles atribu´ıram o ´ındice entrópicoq, extra´ıdo do formalismo de Tsallis, como sendo o parâmetro que descreve o n´ıvel do freio magnético e também associaram este parâmetro com o expoente da teoria do d´ınamo (a) e a topologia do campo magnético (N) através da rela¸cão q = 1 + 4aN/3.

Para construir o cenário ideal para descrever, investigar e correlacionar todos esses fenômenos é necessário um background teórico da mecânica estat´ıstica que possa nos dar um caminho lógico entre a a¸cão do freio magnético e o perfil da distribui¸cão da velocidade rotacional. Deste modo, como o expoente do decaimento rotacional afeta a distribui¸cão? Ou seja, seria o perfil da distribui¸cão um reflexo da a¸cão do freio magnético? Ele pode ser quantificado estudando apenas a distribui¸cão da velocidade sem ser necessário fazer uso da idade das estrelas? Na próxima se¸cão iremos destacar dois poss´ıveis grandes cenários da mecânica estat´ıstica, um no âmbito extensivo e outro no âmbito não-extensivo, que podem preencher essa lacuna.

1.3 Mecˆ

anica Estat´ıstica: Ser ou n˜

ao ser (n˜

ao)-extensiva

1.3.1 Mecˆ

anica estat´ıstica de Boltzmann-Gibbs

(28)

termo-dinâmico do sistema é o estado macroscópico10 _{no qual a entropia é máxima} _(Boltzmann,

1872).

Desse modo, a Termodinâmica descreve os efeitos macroscópicos do sistema formado por inúmeros entes microscópicos que estão sujeitos às leis fundamentais da Mecânica Clássica (leis de Newton) ou da Mecânica Quântica. Como esse número de entes mi-croscópicos é muito grande, utiliza-se como ponte entre os micro e os macro estados uma teoria probabil´ıstica: Mecânica Estat´ıstica. Sendo assim, tem-se que a mecânica estat´ıstica é uma teoria probabil´ıstica que estabelece uma conexão entre os dois n´ıveis de descri¸cão: o macroscópico (Termodinâmica) e o microscópio (Mecânica).

O conjunto de microestados compat´ıveis com os valores das variáveis macroscópicas do sistema, como energia interna U, o volume V e o número de part´ıculas N constituem o macroestado ou estado macroscópio do sistema. Isso é considerável, pois possibilita o estudo do comportamento mais geral do sistema, que em geral é mais importante, em vez do tratamento de maneira individual de cada part´ıcula do sistema. O que torna oportuna a teoria probabil´ıstica, pois o número de part´ıculas é muito grande.

Um dos pilares do trabalho de Boltzmann-Gibbs ´e a aditividade da entropia, ou seja, o fato queSAB =SA+SB. Dessa forma ´e que Boltzmann e posteriormente Gibbs, partindo

dos conceitos de Clausius, formularam o que chamamos hoje de Mecˆanica Estat´ısica de Boltzmann-Gibbs ou do equil´ıbrio.

A Mecânica Estat´ıstica de Boltzmann-Gibbs foi formulada a mais de um século, e desde então tem tido um sucesso notável para uma enorme variedade de sistemas. A entropia foi termodinamicamente formulada por Clausius no século XIX. Posteriormente, Boltzmann e Gibbs desenvolveram a teoria da Mecânica Estat´ıstica, com a entropia ocupando um papel central. Eles associaram a ideia termodinâmica de entropia com uma abordagem probabil´ıstica do sistema onde se tem microestadosi com probabilidade pi . Com efeito,

a entropia, na forma de Shannon, ´e

SBG =−k W

X

i=1

pilnpi (1.4)

onde k é uma constante positiva (que, sem perda de generalidade, consideramos igual à unidade), W é a quantidade de microestados.

10_{Quando se fala em estado microsc´}_{opico (microestado) de um sistema de} _N _{part´ıculas, fala-se dos}

(29)

Quando se tem equiprobabilidade dos microestados,pi = _W1 , (hip´otese de

equiproba-bilidade) a entropiaSBG pode ser expressa como

SBG =klnW (1.5)

onde k é uma constante positiva e W é o número de microestados compat´ıveis com o estado microscópico do sistema isolado. Esta equa¸cão, conhecida como o princ´ıpio de Boltzmann, é uma das expressões fundamentais da Mecânica Estat´ıstica (ver Salinas, 2013).

Apesar da estat´ıstica de Boltzmann-Gibbs representar bem muitos sistemas na na-tureza, existem outros tipos de sistemas (muitas vezes considerados dentro da classe de sistemas complexos) que apresentam desvios em rela¸cão às predi¸cões desse formalismo. Exemplos t´ıpicos são sistemas com intera¸cões de longo alcance (por exemplo, gravitaci-onais), sistemas não-lineares no limiar do caos, turbulência, sistemas granulares, entre outros. Nesse sentido, se faz necessário uma maneira alternativa de descrever a estat´ıstica do sistema.

No geral, o maior problema em usar tal Mecânica Estat´ıstica para descrever o com-portamento da distribui¸cão da rota¸cão está na homogeneidade do espa¸co de fase. Em outras palavras, existe um equil´ıbrio entre a cria¸cão e a destrui¸cão de rota¸cão elevadas e, por consequência, não há produ¸cão de cauda de altas energia tão comum no cenário da rota¸cão estelar (e.g.: Soares et al. 2006, de Freitas 2006 e Silvaet al. 2013). A dinâmica do espa¸co de fase no contexto da rota¸cão estelar é essencialmente heterogênea, ou seja, a estrutura hierárquica desse espa¸co de fase obedece a um modelo de estat´ıstica mais com-plexo e que consegue descrever esses estados quase ou meta-estáveis. Dentre as inúmeras Mecânicas Estat´ısticas que descrevem sistemas fora do equil´ıbrio, está a Mecânica Es-tat´ısitica Não-Extensiva de C. Tsallis proposta em 1988.

1.3.2 Mecˆ

anica estat´ıstica n˜

ao-extensiva de C. Tsallis

(30)

que apresentem geometria fractal, ou que sejam sens´ıveis às condi¸cões inicias, ou ainda que possuam memória de longa dura¸cão. Desse modo foi que em 1988, o f´ısico greco-brasileiro Constantino Tsallis propôs um novo formalismo que seria uma generaliza¸cão da entropia de BG.

Inspirado por sistemas multifractais, Tsallis (1988) apresentou uma generaliza¸c˜ao para a entropia de BG. Para isso ele violou um dos princ´ıpios da mecˆanica estat´ıstica de BG: a aditividade da entropia.

Sq(A+B) = Sq(A) +Sq(B) + (1−q)Sq(A)Sq(B) (1.6)

Assim a entropia generalizada por Tsallis fica da forma

Sq =k

1₋PW_i₌₁pq_i

q₋1 (1.7)

onde q11 _{é denominado ´ındice entrópico e mede o grau de não-extensividade do}

sis-tema. O Sq ´e, dessa forma, a entropia generalizada, que difere da de BG por n˜ao ser

aditiva.

Refor¸ca-se que a Eq. (1.7) é uma generaliza¸cão da entropia SGB e não uma

substi-tui¸c˜ao. Para q= 1 a entropia SGB ´e recuperada.

A equa¸cão acima generaliza a entropia de BG e podemos recuperá-la fazendo o limite em queq tende à unidade. O ´ındice entrópicoqmede o quanto não-extensivo é o sistema. Quanto mais diferente de 1, mais complexo é o sistema. O parâmetro mais importante na Mecânica Estat´ıstica não-extensiva é o ´ındice q. Moyano (2006) argumenta que sua implica¸cão f´ısica vem do próprio sistema em estudo, ou da classe de universalidade do sistema. Depois de inúmeras aplica¸cões em diversos sistemas que englobam diversas áreas do conhecimento, é acreditado que o valor deqpara um sistema espec´ıfico pode ser deter-minadoa priori. Tal argumento tem como pano de fundo a própria origem dinâmica da Mecânica Estat´ıstica. Então podemos pensar que se existem inúmeros sistemas (simples) que obedecem à Mecânica Estat´ıstica de BG, também devem existir inúmeros sistemas (complexos) que não obedecem tal mecânica.

Desse modo, conclu´ımos que o formalismo não-extensivo é o que se ajusta ao propósito deste trabalho, pois é o que melhor descreve sistemas de intera¸cão de longo alcance (gra-vitacional, por exemplo), memória de longa dura¸cão (que tem a ver com auto grau de correla¸cão) e fractalidade espacial. Em s´ıntese, temos uma teoria estat´ıstica muito

ro-11

(31)

busta e amplamente testada em diferentes sistemas f´ısicos e não-f´ısicos. Caberão aos cap´ıtulos que seguem unir de forma lógica todos os pressupostos que emergem da teoria da rota¸cão estelar e da mecânica estat´ıstica não-extensiva, assim como, verificar as im-plica¸cões f´ısicas que surgem quando correlacionarmos essas diferentes vertentes por seus espec´ıficos parâmetros.

1.4 Plano de trabalho

Nosso trabalho consiste em propor uma nova distribui¸cão q-Maxwelliana da veloci-dade rotacional projetada com v´ınculos f´ısicos oriundos da dinâmica da rota¸cão estelar. Para isso, teremos como pressuposto elaborar uma abordagem teórica que possibilite uma correla¸cão entre o expoente do decaimento rotacional (j) e o expoente da distribui¸cão (q). No geral, tal v´ınculo f´ısico é advindo da teoria de perda da taxa de momentum angular pelo vento estelar magnético ou, em outras palavras, da teoria do freio magnético.

No Cap´ıtulo 2 é exposto o trabalho feito pelos autores Soareset al. (2006) que propu-seram uma nova fun¸cão distribui¸cão de velocidade baseada na estat´ıstica não-extensiva. Esta fun¸cão, proposta por estes autores, consiste em uma generaliza¸cão da fun¸cão Maxwel-liana proposta por Deutsch (1970). Ainda no Cap´ıtulo 2, relacionamos as fun¸cões q -Maxwellianas generalizadas, obtidas por Soareset al. (2006), com um parâmetro de freio proposto por de Freitas (2006). Esse autor, partindo dos trabalhos de Huang (1965 e 1967) elaborou uma generaliza¸cão para a lei de Skumanich. Por fim, nós iremos genera-lizar a fun¸cão q-Maxwelliana utilizando v´ınculo advindo do parâmetro proposto por de Freitas (2006) denominado defator de freio.

No Cap´ıtulo 3, focamos nossa aten¸cão na descri¸cão detalhada da amostra de estrelas utilizadas em nosso trabalho. Tal amostra foi retirada da versão atualizada do catálogo

Geneva-Copenhagen Survey por Holmberg et al. (2007, 2009) com foco nos parâmetros estelares mais relevantes para o nosso trabalho, como: massa, metalicidade, idade e velo-cidade de rota¸cão projetada (v sini). A sele¸cão foi definida apenas por estrelas do tipo F e G com idades bem definidas.

No Cap´ıtulo 4, mostramos os resultados e discussões obtidos dos ajustes das nossas distribui¸cões e as distribui¸cões emp´ıricas. Além disso, mostraremos que existe uma de-pendência entre os expoentesj e q acima mencionados.

(32)

Cap´ıtulo

2

Distribui¸c˜

ao

q

-Maxwelliana com v´ınculos

Nesse Cap´ıtulo teremos como objetivo modificar as q-Maxwellianas propostas inici-almente por Silva, Plastino e Lima (1998) e contextualizada para a rota¸cão estelar por Soares et al. (2006). No geral, enquanto as Maxwellianas generalizadas propostas por Silva, Plastino e Lima (1998) tem como arcabou¸co teórico a teoria cinética dos gases, a versão contextualizada de Soares et al. (2006) apresenta também como base central a questão da aleatoriedade dos eixos de rota¸cão. No entanto, essa versão não traz à tona outros elementos extra´ıdos do contexto da rota¸cão estelar, tais como o decaimento ro-tacional pelo freio magnético, os efeitos da topologia do campo e/ou da lei do d´ınamo. Nossa proposta está inteiramente baseada nos efeitos desses parâmetros sobre o compor-tamento da distribui¸cão emp´ırica da velocidade de rota¸cão. Enfim, nossa hipótese inicial está associada à ideia de que o expoente do decaimento rotacional controla a dinâmica do espa¸co de fase das velocidades rotacionais, ou seja, tal expoentej controla o perfil da distribui¸cão que por sua vez depende do ´ındice entrópico q, como veremos mais tarde.

2.1 Fun¸c˜

ao distribui¸c˜

ao

q

-Maxwelliana

No contexto da não-extensividade, as distribui¸cões gaussianas das velocidades que le-varam Maxwell a usar uma exponencial é um caso particular de uma fam´ılia de leis de potência. Essas são as q-exponenciais, exp_q(f)_≡[1 + (1₋q)f]1₋1q, ondef é uma fun¸cão de variáveis aleatórias1_{, que inclui a exponencial padrão para o caso onde}_q_{= 1. Esse}

for-1_{Uma vari´}_{avel aleat´}_oria_discreta _{pode assumir valores em um conjunto finito. A fun¸c˜}_{ao associada a}

essa variável é afun¸cão de probabilidade, que obedece a duas regras:

p(x)≥0 (2.1)

X

p(x) = 1 (2.2)

(33)

malismo, diferentemente das fun¸cões padrão de BG, proporciona uma notável ponte com a Mecânica Estat´ıstica não-extensiva, onde asq-exponencias desempenham um papel fun-damental (assim como a exponencial faz dentro da estat´ıstica de Boltzmann-Gibbs). Se-gundo Limaet al. (2000), esta observa¸cão permitiu aq-generaliza¸cão do teorema clássico da equiparti¸cão da energia produzindo também uma distribui¸cão tipo lei de potência em que o parâmetro variável é a energia cinética. Por outro lado, Latora et al. (2002) tem usado a velocidade de rota¸cão como um parâmetro variável em seus trabalhos sobre dinâmica de um sistema Hamiltoniano com N spins clássicos planares. Ao passo que Campaet al. (2001) tem usado os mesmos princ´ıpios no estudo de rotatores interagindo através de um potencial de alcance infinito.

Deutsch (1970) considerou a fun¸cão de distribui¸cão para a magnitude de um vetor que tem orienta¸cão aleatória. Por isto, é necessário encontrar a fun¸cão de distribui¸cão de um escalar positivo ω (velocidade angular da estrela), que é a magnitude de um vetor~ω. As-sumimos que a distribui¸cão de~ω é isotrópica. Assumimos também que se for decomposta em eixos cartesianos, a distribui¸cão de qualquer componente é independente dos outros.

Deutsch (1970) definiu Ω como uma quantidade adimensionaljω, ondejé um parâmetro com dimensão deω−₁

, assim

~

Ω = Ωxˆi+ Ωyˆj + Ωzkˆ (2.6)

A probabilidade de que Ωxse encontre no intervalo [Ωx,Ωx+dΩx], Ωyem [Ωy,Ωy+dΩy]

e Ωz em [Ωz,Ωz +dΩz] ´e ent˜ao

F(Ω)d3Ω =f(Ωx)f(Ωy)f(Ωz)dΩxdΩydΩz (2.7)

com Ω = pΩ2

x+ Ω2y + Ω2z. ´E simples (ver Deutsch, 1970) mostrar que F(Ω) ´e a

distri-bui¸c˜ao Maxwelliana padr˜ao

F(Ω) = 4

πΩ

2_exp₍

−Ω2) (2.8)

Assim, serão relevantes as probabilidades em que a variável assuma valores em determinados intervalos. Esses são calculados por meio dafun¸cão densidade de probabilidade, que obedece as três regras:

f(x)≥0 (2.3)

+∞

Z

−∞

f(x)dx= 1 (2.4)

b

Z

a

(34)

Dessa forma, podemos analisar o problema no âmbito não-extensivo proposto por Tsal-lis (1988), modificando a hipótese básica de independência estat´ıstica entre a distribui¸cão associada com as componentes de Ω. Como foi salientado por Silva, Plastino e Lima~ (1998), a independência entre as três componentes da velocidade não se mantém em sis-temas de intera¸cão de longo alcance, onde o caráter não-extensivo é observado. Levando em conta tais argumentos, Silva, Plastino e Lima (1998) propôs a seguinte generaliza¸cão para Eq. (2.7):

F(Ω)d3Ω = exp_q(lnqf(Ωx) + lnqf(Ωy) + lnqf(Ωz))dΩxdΩydΩz (2.9)

onde aq-exponencial exp_q(f) e q-logaritmo lnq(f) s˜ao fun¸c˜oes definidas como

exp_q(f) = [1 + (1₋q)f]1/(1−q) _(2.10)

lnq(f) =

f1−q₋₁

1₋q (2.11)

nota-se que no limite q = 1, exp_q(f) e lnq(f) reproduzem as fun¸c˜oes exponenciais e

lo-gar´ıtmicas habituais recuperando a forma padr˜ao da Eq. (2.7).

A diferencia¸cão parcial da q-log em rela¸cão a Ωi é (ver Deutch., 1970)

∂lnqF

∂Ωi

= ∂

∂Ωi

(lnqfx+ lnqfy + lnqfz) (2.12)

desde que exp_q(lnq(f)) = lnq(expq(f)) =f, onde i=x, y, z. Equivalentemente,

Ωi

χ F′

(χ)

Fq₍_χ₎ =

∂ ∂Ωi

(lnqfi) (2.13)

onde χ=pΩ2

x+ Ω2y+ Ω2z eF

′

(χ) ´e a derivada total de F(χ).

Definindo Φ(χ)_≡(1/χ)F′

(χ)/Fq₍_χ_{), podemos rescrever a Eq. (2.13) como}

Φ(χ) = 1 Ωx

∂ ∂Ωx

(lnqfx) =

1 Ωy

∂ ∂Ωy

(lnqfy) =

1 Ωz

∂ ∂Ωz

(lnqfz) (2.14)

Esta equa¸cão pode ser satisfeita apenas se todos os termos forem iguais a uma cons-tante que não contém os componentes Ω. Assim, podemos fazer Φ(χ) =₋γ, que é,

1 Ωi

∂ ∂Ωi

(35)

Assim, as solu¸c˜oes da Eq. (2.15) para f(Ωi) ser˜ao dados por

lnqfi =−

γΩ2

i

2 + lnqA, (2.16) OndeA ´e uma constante de integra¸c˜ao. Tomando a q-exponencial obtemos

f(Ωi) =

1 + (1₋q)

lnqA−

γΩ2

i

2

1/(1−q)

(2.17)

Definindo uma nova constante como 2

σ2 ≡

γ

1 + (1₋q) lnqA

= γ

A1−q (2.18)

onde o parˆametro σ ´e a largura da q-Maxwelliana, e substituindo na Eq. (2.17) resulta em

f(Ωi) =Aq

1₋(1₋q)Ω

2

i

σ2

1/(1−q)

. (2.19)

Aqui introduzimos o sub-´ındice q para explicitar a q-dependˆencia de A2_{. Eq. (2.19)}

recupera os termos da exponencial padr˜ao da fun¸c˜ao Gaussiana para q= 1.

Ent˜ao a probabilidade de Ω esta no intervalo [Ω,Ω +dΩ] pode ser determinada como se segue:

F(Ω) =

Z

f(Ω)d3Ω

Colocando d3_{Ω = Ω}2_sinθdθdϕd_{Ω, para um dado Ω obtemos}

Fq(Ω) =

Z Z AqΩ2

1₋(1₋q)Ω

2

σ2

1/(1−q)

sinθdθdϕ,

e após a integra¸cão nós temos que

Fq(Ω) = 4πAqΩ2

1₋(1₋q)Ω

2

σ2

1/(1−_q₎

. (2.20)

Uma vez que a distribui¸cão padrão da velocidade verdadeira x para uma amostra de estrela é F(x) _∝ x2_e−_x2

, como mostrado por Deutsch (1970), o padrão da distribui¸cão de velocidade de rota¸cão projetadaxsini, para eixos orientados aleatoriamente, deve ser dado por φ(y)_∝ ye−y2

(ver Kraft., 1970), com y _≡xsini. Agora, a q-distribui¸c˜ao φq(y)

deve reproduzir o padr˜ao, da mesma forma que Fq(x) recupera F(x) para o caso limite

(36)

q= 1.

Desta forma, propomos a seguinte fun¸cão distribui¸cão para as velocidades de rota¸cão estelar observadas:

φq(y) = Bqy

1₋(1₋q)y

2

σ2

1/(1−q)

(2.21)

onde Bq ´e uma constante que depende deq e deve ser determinada analiticamente da

normaliza¸c˜ao deφq(y).

´

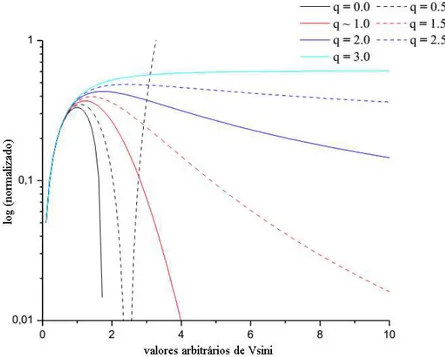
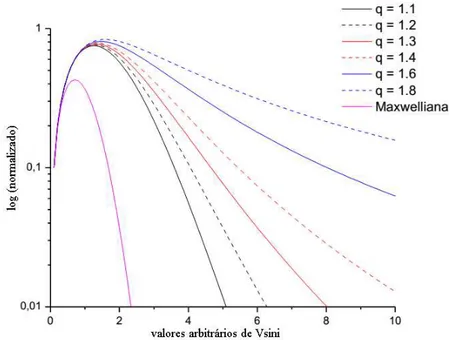
E visto na Fig 2.1 o comportamento da fun¸cão q-Maxwelliana para diferentes valores deq. Nota-se a influência do ´ındice entrópicoqna cauda da distribui¸cão. Nota-se também que existe uma descontinuidade na fun¸cão para q = 0.5. Esse comportamento já havia sido observado por Tsallis (1988), onde o autor propõe umacut-off na fun¸cão para alguns valores de q menores que a unidade onde a fun¸cão q-generalizada apresentaria um com-portamento at´ıpico. Já na Fig 2.2 pode-se ver a compara¸cão entre a fun¸cão Maxwelliana padrão e a fun¸cãoq-generalizada q-Maxwelliana.

Figura 2.1: Fun¸c˜ao distribui¸c˜ao q-Maxwelliana para diferentes valores deq.

´

(37)

Ressaltamos que as variáveisypresentes naq-Maxwelliana são aleatórias (estocásticas). No contexto do nosso trabalho, essas variáveis obedecem uma lei determin´ıstica que está associada aos efeitos do freio magnético durante a evolu¸cão estelar na sequência principal. Nesse sentido, se faz necessário incluir esses efeitos que dependem do tempo. Na se¸cão posterior iremos extrair o parâmetro que engloba tais efeitos.

Figura 2.2: Comparativo entre a fun¸c˜ao Maxwelliana e a q-Maxwelliana para diferentes valores deq.

2.2 Um novo elemento no contexto: O fator de freio

generalizado

O v´ınculo f´ısico extra´ıdo do cenário da rota¸cão estelar está relacionado com o decres-cimento (ou perda) da rota¸cão com a idade. Tal comportamento depende da massa da estrela e existem várias leis de freio na literatura, dentre elas podemos destacar a lei de Skumanich (1972), Barryet al. (1987), Soderblom et al. (1991), Pace e Pasquini (2004), e a forma generalizada obtida do contexto não-extensivo proposta por de Freitas e De Medeiros (2013).

(38)

derivada de uma série de potência de uma grandeza que decai com o tempo; 2) encontrou uma distribui¸cão de frequência da velocidade rotacional projetada, utilizando as distri-bui¸cões q-Maxwelliana propostas por Soares et al. (2006), para a lei de Skumanich; 3) obteve distribui¸cões teóricas de rota¸cão que foram comparadas aos dados observacionais.

Nosso trabalho consiste em um generaliza¸c˜ao desse fator de freio. Enquanto de Freitas (2006) utilizou o fator de freio apenas para a lei de Skumanich, iremos generaliz´a-lo para qualquer lei de decaimento.

Segundo Huang (1967) e, mais recentemente, de Freitas (2006), a taxa de diminui¸c˜ao do momento angular de uma dada estrela pode ser descrita por uma lei de potˆencia do tipo:

dx

dt =−a0−a1x−a2x

2

−a3x3−...

| {z }

n vezes

. (2.22)

O parâmetro adimensional x é uma rela¸cão entre v sini e seu valor mais provável

Vm =< vrot >. De forma geral, se j > 1 a distribui¸c˜ao de y desaparece em y = 0. Por

outro lado, se 0_≤j _≤1 a distribui¸cão assume um valor finito em y= 0, devido à rota¸cão de algumas estrelas serem muito baixas. Isto equivale a dizer que, para um caso j > 1, as distribui¸cões teóricas tem um máximo em y com uma certa distância ∆y da origem que depende do fator de freio. Os dados observacionais revelam que as distribui¸cões de rota¸cão para estrelas simples, no sentido das F até K, tendem a deslocar tal pico para baixas velocidades; da mesma forma, a cauda da distribui¸cão também se desloca neste sentido, como mostra Huang (1967).

Desse modo, a Eq. (2.22) denota, para uma determinada dimensão de x, a não con-serva¸cão da grandeza f´ısica considerada, seja ela por exemplo, o momento angular, a massa, a velocidade rotacional ou fluxo cromosférico. Os três primeiros termos da série foram estudados por Huang (1965 e 1967) supondo uma rota¸cão de corpo r´ıgido para a estrela, que os eixos de rota¸cão são aleatórios e que as velocidades rotacionais sejam baixas para que o efeito da cauda da distribui¸cão presente para grandes velocidades não afete a estrutura da fun¸cão. Nesse sentido, cada caso proposto por Huang tem por objetivo definir a forma como o fator de freio se comporta na distribui¸cão da velocidade rotacional projetaday, considerando que

y=xsini, (2.23)

ondei denota o ângulo de inclina¸cão com rela¸cão à linha de visada. Com isso, de Freitas (2006) partindo da Eq. (2.22) e escolhendo um certo termo da sériexj com

dxj

dt =−ajx

j

(39)

obteve uma express˜ao geral para determinar o fator de freio xj, dada por:

xj = [(j−1)ajt]

1 1

−j, j 6= 1. (2.25)

O passo seguinte foi, partindo das Eqs. (2.22) e (2.24), encontrar uma express˜ao para

xcomo uma fun¸c˜ao da condi¸c˜ao inicial xa e do fator de freioxj:

dx dt =

dx dxj

dxj

dt , (2.26)

e com isso, para cada valor de j = 0,1 e 2, obt´em-se os casos descritos por Huang. Substituindo as Eqs. (2.22) e (2.24) chega-se a:

x

Z

xa

dx xj =

xj

Z dxj

xj_j . (2.27)

Deste modo, a Eq. (2.27) denota, para cada valor de j, uma determinada equa¸cão para o parâmetro inicial xa como uma fun¸cão do fator de desacelera¸cão e do parâmetro

x. De posse dexa e da fun¸cão de distribui¸cão q-maxwelliana, o autor obteve uma fun¸cão

distribui¸c˜ao da velocidade rotacional projetada, que de maneira geral ´e expressa como

φ(y, xj) = y

∞

Z

y

f(x, xj)dx

x(x2₋_y2₎1/2

Nesse contexto, de Freitas (2006), em sua disserta¸c˜ao de mestrado, define o fator de freio para a lei de Skumanich, dada por:

dx3

dt =−a3x

3

3, (2.28)

e que foi extra´ıda da série proposta por Huang (1965 e 1967). O autor procurou, com base nos casos desenvolvidos por Huang (1967), obter uma equa¸cão parax3 como uma fun¸cão

do tempo. Para isso, usando a Eq. (2.28), ele obteve uma equa¸c˜ao de decaimento em t

que pode ser comparada a lei de Skumanich, a menos de uma constante. Deste modo, temos que:

x3 =

1

√

2a3

t−0.5_. _(2.29)

Recorrendo a Eq. (2.27), de Freitas (2006) obteve uma equa¸cão para x em fun¸cão do fator de desacelera¸cão x3 dada por:

1

x2 =

(40)

Desta equa¸c˜ao pode-se encontrar _dxdx₃, que juntamente com a Eq. (2.28) satisfaz a Eq. (2.26). O autor partiu da Eq. (2.30) e expressou xa como uma fun¸c˜ao de x e x3

para tornar a distribui¸cão q-maxwelliana, expressa pela Eq. (2.8), uma fun¸cão do tempo através da inclusão do parâmetrox3. Assim, temos que

xa =

x3x

(x2 3−x2)

1/2. (2.31)

2.3 A fun¸c˜

ao de distribui¸c˜

ao

q

-Maxwelliana

Skuma-nichiana

A Eq. (2.31) é o fator de freio obtido por de Freitas (2006). Já a Eq. (2.20) representa aq-Maxwelliana para as velocidades verdadeiras. De acordo com o contexto do presente trabalho, essa distribui¸cão é válida apenas para t = 0. Para introduzir a dependência temporal é necessário substituirxa na equa¸cão abaixo

Fq(xa) = 4πAqx2a

1₋(1₋q)x

2

a

σ2

1/(1−q)

(2.32)

Assim, escolhendo o caso particular j = 3, i.e., a lei de Skumanich, n´os obtemos uma nova q-distribui¸c˜ao que depende do fator de freio x3, dada por

Fq(x, x3) = 4πAq

x2 3x2

x2 3−x2

1₋(1₋q) x

2 3x2

σ2₍_x2 3−x2)

1/(1−q)

. (2.33)

Vale ressaltar quexa representa a variável aleatória da nossa nova fun¸cão distribui¸cão.

Ela é fun¸cão da velocidade verdadeirax e do fator de freio x3. O xa, portanto, irá fazer

o papel do Ω da equa¸cão q-Maxwelliana proposta por Soares et al. (2006). Com base na Eq. (2.33), que representa a velocidade real, levando em conta a considera¸cão feita por Deutsch (1970) e o algebrismo seguido para obter a equa¸cão acima, nós propomos a seguinte distribui¸cão para a velocidade projetada:

Φq(y, x3) = Bq

x3y

(x2 3−y2)

1/2

1₋(1₋q) x

2 3y2

σ2₍_x2 3−y2)

1/(1−_q₎

(2.34)

(41)

Figura 2.3: Comparativo entre as fun¸cões distribui¸cões Maxwelliana padrão, q -Maxwelliana e a q-Maxwelliana com v´ınculo para a lei de Skumanich (j = 3). Escala arbitrária. Usandoq = 1.5. Fator de freio xj = 20.

Figura 2.4: q-Maxwelliana com v´ınculo (para a lei de Skumanich) para diferentes valores deq. x3 = 20

(42)

Figura 2.5: q-Maxwelliana com v´ınculo (para a lei de Skumanich) para diferentes valores dex3. q= 1.4.

verificamos que ao fazer x3 → ∞ recuperamos a q-Maxwelliana. Percebe-se que o fator

de freio também exerce influência na cauda da distribui¸cão. Já a Maxwelliana padrão é recuperada no limiteq_→1.

2.4 A fun¸c˜

ao de distribui¸c˜

ao

q

-Maxwelliana com v´ınculo:

o caso geral

Na se¸cão anterior obtivemos uma fun¸cão de distribui¸cão para o caso da lei de Sku-manich. Para generalizar, o procedimento é bem simples: generalizamos o fator de freio para o caso geralxj. Assim, partindo da Eq. (2.24), encontramos uma expressão paraxj

em fun¸c˜ao do tempo

xj = [(j−1)ajt]1/1−j, (2.35)

assumindo que a velocidade inicial ´e nula. Para o caso de uma velocidade inicial qualquer

x0, a express˜ao muda para

xj =x0[1+(j −1)xj

−₁

0 ajt]1/1−j. (2.36)

A expressão acima é semelhante à exponencial generalizada denotada por exp_q(₋x).

(43)

encontra-mos que a vari´avelxa pode ser expressa de uma forma geral por:

xa(xj) =

x

1₋_xx j

j−11/j−1 (2.37)

Com a equa¸c˜ao acima vemos claramente que no limite xj → ∞ temos que a vari´avel

para condi¸cão t= 0, isto é, xa, é a própria variável aleatória x.

De posse da Eq. (2.37) podemos substitu´ı-la na Eq. (2.32) e obtermos uma fun¸c˜ao

q-Maxwelliana com v´ınculo para rota¸c˜ao verdadeira em um caso mais geral, que fica:

Fq(x, xj) = 4πAq

x2

1₋x xj

j−12/(j−1)



   

1₋(1₋q) x

2

σ2

1₋x xj

j−12/(j−1)



   

1/(1−q)

(2.38) De forma semelhante a nossa fun¸cão de distribui¸cão para as rota¸cões projetas genera-lizadas para qualquer lei de decaimento é dada por:

Φq(y, xj) = Bq

y

1₋_xy j

j−11/(j−1)



   

1₋(1₋q) y

2

σ2

1₋_xy j

j−12/(j−1)



   

1/(1−_q₎

(2.39)

Com isso obtemos uma fun¸cão de distribui¸cão no contexto não-extensivo, que leva em conta o v´ınculo f´ısico responsável pela perda de momento angular, o que torna essas fun¸cões estatisticamente mais robustas e fisicamente mais adequadas.

Tabela 2.1: Algumas leis de decaimento presentes na literatura escritas em fun¸c˜ao do expoente j.

Soderblom et al. (1991) t−2/3 _j _{= 5}_/₂

Pace e Pasquini (2004) t−5/2 _j _{= 7}_/₅

Reiners e Mohanty (2012) t−₁_/₄

j = 5

Na tabela 2.1 mostramos algumas leis de decaimentos presentes na literatura. Desse modo, podemos verificar o comportamento da fun¸c˜ao q-Maxwelliana com v´ınculo (Eq. (2.39)) generalizado para essas leis.

(44)

entrópico q em 1.9 e variamos o valor do fator de freio para essa lei de decaimento (j = 5/2). Nela é poss´ıvel verificar o papel do fator de freio sobre a cauda da distri-bui¸cão. Já na Fig 2.7 fixamos o valor do fator de freio em 20 e variamos o valor doq por um fator 0.5, verifica-se que a fun¸cão tem um comportamento esperado para valores deq

menores que a unidade (Tsallis, 1988). Verifica-se também que a fun¸cão q-Maxwelliana com v´ınculo generalizada tende a Maxwelliana padrão para q _∼1. Esse comportamento também é verificado para as leis de freio propostas por Pace e Pasquini (2004) e Reiners e Mohanty (2012) (Ver as Fig 2.9 e Fig 2.11).

Figura 2.6: q-Maxwelliana com v´ınculo para a lei de decaimento proposta por Soderblom et al. (1991). Variando o fator de freio e mantendoq fixo em 1.9.

Na Fig 2.8 é apresentado o comportamento da fun¸cãoq-Maxwelliana com v´ınculo para a lei de freio proposta por Pace e Pasquini (2004). Nesse caso também fixamos o ´ındice entrópicoq em 1.9 e variamos o valor do fator de freio. Mais uma vez é visto o papel do fator de freio sobre a cauda da distribui¸cão. Nela podemos notar que ao mudar o valor do fator de freio em 10 unidades, há uma mudan¸ca considerável na cauda. Esse compor-tamento já não é verificado para o caso da lei de freio proposta por Reiners e Mohanty (2012), nesse caso a mudan¸ca no valor do fator de freio não exerce um papel tão forte sobre a cauda quanto no caso de Pace e Pasquini (2004), isso é visto na Fig 2.10.

(45)

com-Figura 2.7: q-Maxwelliana com v´ınculo para a lei de decaimento proposta por Soderblom et al. (1991). Variando o ´ındice entr´opicoq por um fator de 0.5. Fator de freio fixo em 20.

(46)

Figura 2.9: q-Maxwelliana com v´ınculo para a lei de decaimento proposta por Pace e Pasquini (2004). Variando o ´ındice entr´opico q por um fator 0.5. Fator de freio fixo em 20.