Universidade do Minho
Instituto de Educação
Paula Francisca Pereira Rodrigues
outubro de 2015
O desenvolvimento do pensamento
algébrico de alunos do 1.º e 2.º ciclo
do ensino básico
Paula F rancisca P er eir a Rodrigues O desenvolvimento do pensamento algébrico de alunos do 1
.º e 2.º ciclo do ensino básico
UMinho|20
Paula Francisca Pereira Rodrigues
O desenvolvimento do pensamento
algébrico de alunos do 1.º e 2.º ciclo
do ensino básico
Trabalho efetuado sob a orientação do
Doutor Floriano Augusto Veiga Viseu
Relatório de Estágio
Mestrado em Ensino do 1.º e 2.º Ciclo do Ensino Básico
Universidade do Minho
AGRADECIMENTOS
Nunca poderia deixar de referir o nome das pessoas sem qual seria absolutamente impossível elaborar este trabalho e que tanto me ajudaram ao longo do meu percurso académico e pessoal. Desta forma simples, expresso os meus agradecimentos:
Ao Doutor Floriano Viseu, pelo apoio e disponibilidade incondicional. Pelas críticas, conselhos, e sobretudo, pelo incentivo a continuar e fazer sempre melhor.
Às professoras Tita Pinto e Sandra Rodrigues, que nunca vou conseguir esquecer. Obrigada por serem duas excelentes profissionais e sobretudo pessoas especiais. Obrigada por todos os conselhos, ensinamentos e carinho.
Aos alunos dos dois ciclos de ensino que me permitiram não só implementar o meu projeto como foram as principais inspirações. Obrigada pela partilha de experiências, pela alegria e pelas aprendizagens que também me deram.
Tanto à direção das escolas, como a todos os funcionários e outros professores com que me cruzei e que sempre me auxiliaram da melhor maneira que conseguiram.
À Marta, minha colega de estágio, por toda a paciência, companheirismo e apoio em momentos difíceis. Foi uma longa e extenuante experiência mas conseguimos Martinha!
Às manas da UM, por toda a partilha do cansaço e frustração. Pelo incentivo e motivação que sempre demos umas às outras, sendo ‘sempre raios de sol em dias de nuvens’.
Ao Pedro, pelo apoio e carinho nesta fase final, e compreensão pelas minhas ausências e à Marta pela amizade sempre constante, sei que posso sempre contar contigo.
À Catarina. Não há palavras para descrever o quanto significas e quanto te agradeço pelo teu apoio em mais uma fase da minha vida. Obrigada por todos os milhares de pequenos gestos. Aos meus heróis e pessoas mais importantes do mundo, os meus pais, a minha irmã e o meu cunhado. Obrigada pela paciência e por todo o amor e serenidade que sempre me deram e por me ensinarem o valor do trabalho, do esforço e da humildade. Obrigada por me fazerem feliz!
O DESENVOLVIMENTO DO PENSAMENTO ALGÉBRICO DE ALUNOS DO 1.º E 2.º CICLO DO ENSINO BÁSICO
Paula Francisca Pereira Rodrigues
Mestrado em Ensino do 1.º e 2.º Ciclo do Ensino Básico
Universidade do Minho, 2015
RESUMO
Nos anos iniciais da escolaridade, os alunos começam a apreender noções matemáticas através das atividades que realizam com os números. A noção do número surge conciliada a factos estáveis e concretos, relacionados com conjuntos e objetos. À medida que progridem nos seus estudos, os alunos desenvolvem conceitos abstratos, tomados como objetos independentes do pensamento, tais como, por exemplo, as propriedades de conceitos matemáticos e a noção de variabilidade. Na transição entre o pensamento concreto e o pensamento algébrico muito contribui a aprendizagem de noções algébricas. Este estudo, ao debruçar-se sobre o ensino de tópicos Sequências e Regularidades, no 1.º ciclo, e Números Racionais, no 2.º ciclo, procura averiguar o contributo da aprendizagem destes tópicos na promoção do pensamento algébrico de alunos destes ciclos de escolaridade. Para concretizar este objetivo estabeleceram-se as seguintes questões de investigação: (1) Que aspetos do pensamento algébrico estão contemplados nos raciocínios de alunos do 1.º e 2.º ciclo do ensino básico? (2) Que dificuldades apresentam os alunos na aprendizagem de tópicos que visam a promoção do pensamento algébrico? (3) Que perceções têm os alunos sobre as estratégias de ensino-aprendizagem de tópicos que visam a promoção do pensamento algébrico? Para dar respostas a estas questões de investigação foram desenvolvidas duas experiências de ensino, uma no 1.º ciclo do ensino básico, numa turma do 2.º ano de escolaridade, e outra no 2.º ciclo, numa turma do 6.º ano de escolaridade. As duas experiências focaram a realização de tarefas e a discussão sobre a sua atividade, exploradas em grupos (no 1.º ciclo) e em pares (no 2.º ciclo), promotoras de tópicos específicos. Com o intuito de responder às questões de investigação delineadas, recorreu-se aos seguintes métodos de recolha de dados: gravação vídeo de aulas; produções dos alunos; questionários; grelha de observação; diário de bordo reflexivo.
Da análise dos dados recolhidos, foi possível extrair algumas conclusões do estudo. Relativamente a aspetos do pensamento algébrico, nos dois ciclos de ensino, os alunos estabeleceram relações e generalizações. Os alunos de ambos os ciclos desenvolveram a sua capacidade de comunicação matemática e de representação das suas formas de pensar, na identificação de sequências, análise de regularidades, em estabelecer relações e expressar generalizações, nalguns casos utilizando símbolos algébricos. No 1.º ciclo emergiram diferenças na exploração de sequências repetitivas e crescentes, sendo as últimas mais fáceis de explorar. No 2.º ciclo evidencia-se que os alunos foram capazes de generalizar utilizando símbolos algébricos. As dificuldades mais evidenciadas, por ambos os ciclos, foram a comunicação matemática e a determinação de termos distantes. No 1.º ciclo emergiram também as dificuldades dos alunos em descrever sequências e no 2.º ciclo a utilização de retas numéricas e manipulação de letras. Como vantagens da experiência de ensino, os alunos salientaram o trabalho de grupo/pares e a existência de momentos de discussão sobre a resolução das tarefas propostas. Já a exploração de perguntas de natureza aberta e o seu tempo elevado de exploração foram referidas como desvantagens.
THE DEVELOPMENT OF THE ALGEBRAIC THINKING IN STUDENTS IN THE 1ST AND 2ND CYCLE OF BASIC EDUCATION
Paula Francisca Pereira Rodrigues
Master’s in Teaching in the 1st and 2nd Cycle of Basic Education University of Minho, 2015
ABSTRACT
In the initial years of schooling, students begin to learn mathematical notions through activities where they use numbers. The notion of number appears connected to stable and concrete facts, related to sets and objects. As they progress in school, students develop abstract concepts – taken independent objects of thinking – such as the properties of mathematical concepts and the notion of variability. In the transition between the concrete thinking and the algebraic thinking, the learning of algebraic notions is essential. This study, by addressing to the topics Sequences and Regularities, in the 1st cycle, and Rational Numbers, in the 2nd cycle, tries to determine the contribution to the learning of these topics, in the development of the algebraic thinking in students from these cycles of basic education. To accomplish this goal, the following research questions were posed: (1) What aspects of the algebraic thinking are part of the reasoning of students from the 1st and 2nd cycle of basic education? (2) What type of difficulties do the students present regarding the development of the algebraic thinking? (3) What are the students’ perceptions considering the teaching-learning strategies for the development of the algebraic thinking? To answer these research questions two teaching experiences were developed: one in the 1st cycle of basic education in a 2nd grade class, and other in the 2nd cycle in a 6th grade class. The two experiences focused on the accomplishment of tasks and the discussion of the activities, explored in groups (1st cycle) and in pairs (2nd cycle), promoting specific topics. In order to answer the research question the following methods of data gathering were used: video recordings of classes; students’ works; questionnaires; observation grids; reflective logbook. From the gathered data’s analysis, it was possible to reach a few conclusions. Regarding the aspects of the algebraic thinking in the two cycles, the students stablished relations and generalizations. Students from both cycles developed their ability to communicate mathematically and to represent their ways of thinking in the identification of sequences, in the analysis of regularities, in stablishing relations and expressing generalizations, using in some cases algebraic symbols. In the 1st cycle, appeared differences in the exploration of repetitive and growing sequences, being the latter easier to explore. In the 2nd cycle, it is clear that the students were able to generalize using algebraic symbols. The more evident difficulties for both cycles were the mathematical communication and the determination of distant terms. In the 1st cycle, the students had difficulties describing sequences and in the 2nd cycle, the use of the number lines and the manipulation of letters. As advantages from the teaching experience, the students highlighted the group/pair work and the existing of moments to discuss the resolution of the proposed tasks. The exploring of open questions and the time consumed in said exploration were referred to as disadvantages.
ÍNDICE
AGRADECIMENTOS ... iii
RESUMO ... v
ABSTRACT... vii
ÍNDICE DE TABELAS... xi
ÍNDICE DE FIGURAS ... xii
INTRODUÇÃO ... 1
1.1. Pertinência do estudo ... 1
1.2. Objetivo e Questões de Investigação ... 3
1.3. Organização do relatório ... 4
ENQUADRAMENTO CONTEXTUAL E TEÓRICO ... 5
2.1. Enquadramento contextual ... 5
2.1.1. O Agrupamento de escolas ... 5
2.1.2. A escola e a turma do 1.º ciclo do ensino básico ... 7
2.1.3. A escola e a turma do 2.º ciclo do ensino básico ... 9
2.2. Enquadramento teórico ... 11
2.2.1. Sequências e regularidades no currículo do 1.º e 2.º ciclo do ensino básico ... 12
2.2.2. Números racionais no currículo do 1.º e 2.º ciclo do ensino básico ... 13
2.2.3. O pensamento algébrico ... 14
2.2.4. A early algebra ... 20
2.2.5. O pensamento algébrico no currículo do 1.º e 2.º ciclo do ensino básico ... 23
2.2.6. O lugar da generalização no pensamento algébrico ... 24
2.2.7. A importância das representações no pensamento algébrico ... 27
2.2.8. A exploração de padrões, relações e sequências ... 30
2.2.9. Análise de alguns estudos empíricos sobre o pensamento algébrico ... 31
2.3. Estratégias de intervenção ... 33
2.3.1. Metodologias de ensino e de aprendizagem ... 34
2.3.2. Estratégias de avaliação da ação ... 37
INTERVENÇÃO PEDAGÓGICA ... 41
3.1. Intervenção pedagógica no 1.º ciclo ... 42
3.1.1. Sequências e regularidades – Sequências repetitivas e crescentes ... 42
3.2. Intervenção pedagógica no 2.º ciclo ... 70
3.2.1. Números racionais ... 70
3.2.2. Dificuldades sentidas pelos alunos ... 90
3.3. Avaliação da intervenção ... 91
3.3.1. Avaliação das estratégias utilizadas na intervenção pedagógica no 1.° Ciclo ... 91
3.3.2. Avaliação das estratégias utilizadas na intervenção pedagógica no 2.° Ciclo ... 94
CONCLUSÕES, IMPLICAÇÕES, LIMITAÇÕES E RECOMENDAÇÕES ... 101
4.1. Conclusões ... 101
4.1.1. Que aspetos do pensamento algébrico estão contemplados nos raciocínios de alunos do 1.º e 2.º ciclo do ensino básico? ... 101
4.1.2. Que dificuldades apresentam os alunos na aprendizagem de tópicos que visam a promoção do pensamento algébrico? ... 105
4.1.3. Que perceções têm os alunos sobre as estratégias de ensino-aprendizagem de tópicos que visam a promoção do pensamento algébrico? ... 107
4.2. Implicações para o ensino e a aprendizagem ... 108
4.3. Limitações e recomendações ... 108 REFERÊNCIAS BIBLIOGRÁFICAS ... 111 ANEXO 1 ... 117 ANEXO 2 ... 118 ANEXO 3 ... 120 ANEXO 4 ... 122 ANEXO 5 ... 125 ANEXO 6 ... 126 ANEXO 7 ... 127 ANEXO 8 ... 128 ANEXO 9 ... 130 ANEXO 10 ... 131 ANEXO 11 ... 132 ANEXO 12 ... 133 ANEXO 13 ... 135 ANEXO 14 ... 137
ÍNDICE DE TABELAS
Tabela 1. Desempenhos dos alunos ao longo do ano letivo... 8
Tabela 2. Médias das avaliações finais dos alunos ao longo do ano ... 9
Tabela 3. Desempenhos dos alunos ao longo do ano letivo... 10
Tabela 4. Médias das avaliações finais dos alunos ao longo do ano ... 11
Tabela 5. Temas curriculares que integram o tema Sequências e Regularidades... 12
Tabela 6. Categorização de várias estratégias de generalização utilizadas pelos alunos (Barbosa, Vale & Palhares, 2009, p. 139) ... 27
Tabela 7. Tópicos abordados nas intervenções pedagógica no 1.º e no 2.º ciclo ... 41
Tabela 8: Diferentes raciocínios numéricos apresentados pelos grupos para descobrir o número da cadeiras quando duas mesas estão unidas……….65
Tabela 9: Diferentes raciocínios numéricos apresentados pelos grupos, quando pretenderam descobrir quantas cadeiras havia em quatro mesas unidas ... 65
Tabela 10. Aspetos que os alunos mais e menos gostaram de fazer ao longo das aulas ... 91
Tabela 11. Aspetos referidos na justificação da escolha da estratégia mais utilizada ... 93
Tabela 12. Percentagens das dificuldades sentidas pelos alunos do 1.º ciclo ... 93
Tabela 13. Opinião dos alunos quanto ao método de trabalho em pares ... 95
Tabela 14. Opinião dos alunos quanto à dinâmica de sala de aula... 95
Tabela 15. Opinião dos alunos quanto à adequação das tarefas ... 96
Tabela 16. Opinião dos alunos quanto a aspetos do pensamento algébrico... 97
Tabela 17. Aspetos referidos pelos alunos como vantagens sobre o decurso das aulas ... 98
Tabela 18. Aspetos referidos pelos alunos como desvantagens sobre o decurso das aulas ... 98
ÍNDICE DE FIGURAS
Figura 1. Componentes que integram a construção de uma generalização pelo aluno ... 25
Figura 2. Alunos a disporem as cartolinas representando a sequência ... 43
Figura 3. Prolongamento da sequência pelo Grupo B até ao 12.º elemento... 43
Figura 4. Diferentes figuras padrão identificadas pelos alunos ... 44
Figura 5. Evolução das respostas dos alunos à mesma questão antes e depois da colocação dos números associados às ordens das figuras ... 45
Figura 6. Previsão da figura que estava associada ao 20.º elemento e justificação dos Grupos B e C………46
Figura 7. Estratégia de contagem pelos alunos que desenharam 20 elementos para descobrir qual seria o 20.º termo da sequência ... 46
Figura 8. Apresentação de exemplos de números que estariam associados a quadrados e círculos pelo grupo C ... 46
Figura 9. Previsão do número de elementos de cada figura pelos Grupos C e D ... 48
Figura 10. Prolongamento da sequência até 12.º elemento pelo Grupo B ... 50
Figura 11. Justificação de qual a peça que estava em maior quantidade num prolongamento da sequência pelos Grupos B e C ... 50
Figura 12. Justificação icónica de qual seria a 20.º peça da pulseira pelo Grupo D ... 51
Figura 13. Identificação do padrão, através de um desenho e da linguagem natural ... 53
Figura 14. Descrição da sequência pelo Grupo C ... 53
Figura 15. Desenho elaborado pelos alunos do Grupo A para descobrir o 15.º elemento ... 54
Figura 16. Tabelas construídas pelos Grupos A e C que consideraram colares de 15 missangas ... 54
Figura 17. Tabela apresentada pelo Grupo B considerando quantas missangas de cada cor haveria em 4 colares ... 55
Figura 18. Tabela apresentada pelo Grupo D, considerando quantas missangas seriam necessárias para três colares ... 55
Figura 19. Preenchimento da tabela proposta indicando quantos colares seriam feitos ao longo dos dias se todos os dias se fizessem quatro colares, pelos Grupos C e A ... 56
Figura 20. Alunos a representarem a sequência com rolhas de plástico ... 58
Figura 21. Caracterização da sequência pelos Grupos B, C e D ... 58
Figura 23. Representação em tabela de termos da sequência fornecida pelos Grupos A e D…..59 Figura 24. Descoberta do número de rolhas da 10.ª figura através da construção de uma tabela pelo Grupo A ... 60 Figura 25. Desenho das figuras desde a primeira até à décima pelo Grupo B ... 60 Figura 26. Justificações do Grupo D sobre a possibilidade da existência de uma figura com número ímpar de rolhas ... 61 Figura 27. Justificações dos Grupos C, D e E sobre como poderiam descobrir o número da figura com um número qualquer de rolhas ... 62 Figura 28. Determinação do número de pessoas que se podem sentar se forem unidas duas mesas (Grupo A, Grupo B, Grupo C)……….64 Figura 29. Descoberta do número de pessoas que se podem sentar se forem unidas duas mesas (Grupo D) ... 64 Figura 30. Descoberta do número de pessoas que se podem sentar se forem unidas duas mesas (Grupo E)………...65 Figura 31. Esquema elaborado por um aluno do Grupo B no quadro para representar como descobriria o número de cadeiras para um determinado número de mesas ... 67 Figura 32. Esquema elaborado por um aluno do Grupo B no quadro para representar como descobriria o número de mesas para um determinado número de cadeiras ... 68 Figura 33. Descoberta da regularidade de crescimento da temperatura (PE) ... 72 Figura 34. Representação na reta numérica das coordenadas das temperaturas. A reta representada em cima pelo Par A e as representadas em baixo pelo Par C ... 73 Figura 35. Previsão da temperaturas às seis horas (uma hora antes da primeira temperatura conhecida) pelo Par E ... 74 Figura 36. Descoberta da temperatura às 6 horas pelo Par B ... 74 Figura 37. Previsão da temperatura que estaria às 20 horas na casa apresentada pelo Par H . 75 Figura 38. Respostas corretas às questões 4.1 à 4.4 ... 76 Figura 39. Tradução da viagem que representava uma subida do piso 0 ao piso 6, através de um desenho, pelo Par A... 76 Figura 40. Tradução da viagem que representava uma subida do piso 0 ao piso 6, através de uma expressão numérica, pelo Par B ... 77 Figura 41. Tradução da viagem que representava uma descida do piso 6 Para o piso simétrico pelos Pares A e B ... 77
Figura 42. Tradução da viagem que representava uma subida do piso −𝟔 ao piso −𝟏 pelos
Pares B, C e H ... 77
Figura 43. Tradução da viagem que representava uma subida desde o piso 6 até aos 5 pisos consecutivos acima, pelo Par A ... 78
Figura 44. Tradução da viagem que representava uma descida do piso -1 ao piso -7, pelos Pares B e C ... 78
Figura 45. Determinação do valor de S pelo Par B... 79
Figura 46. Determinação do valor de S pelo Par E ... 79
Figura 47. Tradução da situação A numa expressão numérica pelo Par A ... 81
Figura 48. Tradução da soma de dois números racionais positivos pelo Par B ... 81
Figura 49. Tradução da situação que representava a soma de dois números racionais negativos numa expressão numérica pelo Par C ... 81
Figura 50. Tradução da situação que representava a soma de dois números racionais positivos, numa uma expressão algébrica pelo Par B ... 82
Figura 51. Tradução da situação que representava a soma de dois números racionais simétricos, numa expressão numérica, pelo Par B ... 82
Figura 52. Tradução da situação que representava a soma de dois números racionais simétricos, numa expressão numérica, pelo Par C ... 83
Figura 53. Frequência das respostas corretas nas diferentes situações apresentadas ... 83
Figura 54. Tradução da situação que representava a adição, onde o valor absoluto do número racional positivo era maior que o do número racional negativo, por uma expressão numérica, pelo Par A ... 84
Figura 55. Justificação da resposta à situação que representava a adição onde o valor absoluto do número racional positivo é maior do que o do número racional negativo, pelos Pares G e E.84 Figura 56. Tradução da situação que representava uma adição onde o valor absoluto do número racional positivo era maior que o do número racional negativo) numa expressão algébrica pelos Pares G e F ... 84
Figura 57. Comentário sobre o resultado de uma adição de dois números racionais com sinais contrários (PE) ... 85
Figura 58. Determinação do número de apertos de mão entre três pessoas pelos Pares A e E . 85 Figura 59. Representações utilizadas pelos Pares A e E para descobrir quantos apertos de mão ocorreriam entre cinco pessoas ... 86
Figura 60. Representação utilizada pelo Par B do número de apertos de mão ocorreria para um número n de pessoas ... 86 Figura 61. Justificação, pelos Pares A e E, do valor lógico da expressão 𝒂 + 𝒃 = 𝒃 ... 87
Figura 62. Justificação do Par B da impossibilidade da soma de um número qualquer com 0 ser um número diferente desse número ... 87 Figura 63. Justificações apresentadas pelos Pares D e E sobre a impossibilidade da adição de dois números racionais negativos resultar num número racional positivo ... 88 Figura 64. Justificação do Par A da sobre a situação E ... 88 Figura 65. Justificação das situações que representavam adições de números racionais com sinais contrários pelos Pares A e E ... 89 Figura 66. Justificação do valor que poderia tomar 0 pelo par B ... 89 Figura 67. Frequência de respostas sobre os momentos que os alunos consideraram mais importantes no decorrer das aulas ... 92 Figura 68. Distribuição das estratégias utilizadas pelos alunos... 92
CAPÍTULO 1 INTRODUÇÃO
No presente capítulo, atendendo ao tema que orienta o Projeto de Intervenção Pedagógica Supervisionada, apresenta-se a pertinência do estudo e o objetivo e as questões de investigação que fundamentam a realização do projeto. Por fim, é elaborada uma explicação sobre a organização deste relatório.
As intervenções pedagógicas implementadas neste projeto foram realizadas em duas escolas do mesmo Agrupamento de escolas. Numa das instituições, realizaram-se intervenções pedagógicas numa turma do 2.º ano de escolaridade do ensino básico com vinte alunos. Na outra instituição, concretizaram-se intervenções pedagógicas numa turma do 6.º ano de escolaridade do ensino básico com dezoito alunos.
1.1. Pertinência do estudo
O interesse por este tema e motivação para elaborar este projeto surgiu da observação contextual e consequente identificação de algumas dificuldades dos alunos do 1.º e 2.º ciclo de ensino. No período de observação emergiram características que evidenciaram que alguns destes alunos revelam boa capacidade de cálculo porém manifestam pouca desenvoltura na elaboração de diferentes formas de expressar o seu pensamento, o que se traduz na dificuldade de justificar as respostas que elaboram.
Da mesma forma, identificaram-se dificuldades em pensar de maneira mais abstrata, verificando que os alunos focavam muito os seus raciocínios em casos particulares e dando muita ênfase à manipulação de números e operações aritméticas. Estes problemas podem ser complicados numa fase mais avançada da escolaridade dos alunos, uma vez que, ao longo do seu percurso, se torna cada vez mais importante que consigam comunicar e representar raciocínios e respostas e pensar de forma mais abstrata chegando a níveis onde os números já não são os focos dos seus raciocínios.
A fim de tentar colmatar estas dificuldades e proporcionar experiências ricas e significativas aos alunos, considerou-se importante promover uma temática em que estes tivessem oportunidade de desenvolver a capacidade de comunicar os seus raciocínios como de
promover um ‘olhar’ mais geral e algébrico em detrimento de uma forte ênfase na aritmética. Deste modo, tentou-se promover o pensamento algébrico no ensino de tópicos específicos de cada um dos ciclos de ensino.
Não existe uma conceção precisa do que seja o pensamento algébrico. Apesar disso, emergem, na teoria, algumas características que se podem atribuir quando se fala da capacidade de pensar algebricamente. Alguns autores, como Kaput (1999), salientam que a generalização é o centro deste raciocínio, outros apontam para a importância também do uso de símbolos - a simbolização (Arcavi, 1994; Kieran, 1992). Para além destas, emergem outras capacidades de foco, quando se procura ser capaz de pensar de modo algébrico, como, entre outras, a capacidade de “compreender padrões, relações e funções, representar e analisar situações matemáticas, usar modelos matemáticos, e analisar a variação” (NCTM, 2007, p. 104).
De modo a que estas capacidades sejam potenciadas nos alunos é necessário mudar o que se considera ser o objeto de estudo central da Álgebra (as equações) e, para além disso, promover o ensino de conteúdos deste tema mais cedo do que tem sido habitual (Borralho & Barbosa, s.d.). Nos últimos anos, segundo Canavarro (2007), tem-se assistido a um movimento que defende “a integração do pensamento algébrico na matemática escolar desde o seu início” (p. 91). Esta introdução precoce do pensamento algébrico permite aos alunos uma melhor preparação para a aprendizagem de conteúdos algébricos nos anos posteriores (Cardoso, 2010) e proporciona oportunidades de desenvolver um modo de pensamento mais geral e abstrato (Ponte, 2006).
Deste modo, e atendendo às potencialidades referidas da promoção desde anos muito precoces, é necessário ter em conta alguns aspetos num ensino que pretende promover o pensamento algébrico. Um dos aspetos centrais é a criação de um ambiente de sala de aula que valorize os raciocínios dos alunos, fomente a discussão e promova as generalizações e a comunicação de respostas (Blanton & Kaput, 2005).
No sentido de valorizar os raciocínios dos alunos é necessário dar-lhes voz. Uma forma de concretizar esta pretensão passa por fazer com que, ao longo das aulas, os alunos construam os seus próprios caminhos seja para representar o que pensam, para justificar o que respondem ou para partilhar os seus resultados. A mobilização dos conhecimentos prévios e intuitivos dos alunos ao longo das aulas decorre, também, dessa preocupação.
No sentido de promover uma discussão rica é essencial que as tarefas exploradas na sala de aula providenciem contributos para esse momento, de modo que os alunos possam beneficiar tanto em partilhar as suas respostas como em ouvir e analisar as respostas de outros. As tarefas devem promover o pensamento algébrico, na medida em que possibilitem esta partilha e ainda a oportunidade de conjeturar, generalizar e justificar raciocínios e relações (Blanton & Kaput, 2005). Para além disso, devem ser apoiadas por contextos significativos e baseados em “situações reais” (Ponte, 2006, p 16).
Estes dois aspetos juntamente com o desenvolvimento, por parte do professor, de olhos e ouvidos para a Álgebra a fim de identificar e explorar oportunidades onde os alunos possam estabelecer e expressar generalizações, constituem as três dimensões consideradas necessárias, por Blanton e Kaput (2005), para a algebrização do ensino básico.
Uma análise ao Programa referente ao Ensino Básico (Ministério da Educação, 2007) referente à disciplina de Matemática revela uma preocupação de promover o pensamento algébrico desde o 1.º ciclo. Neste programa, a Álgebra não é introduzida como um tema matemático até ao 2.º ciclo. No entanto, no 1.º ciclo tem já lugar uma iniciação ao pensamento algébrico, como por exemplo através do trabalho com sequências e regularidades, possibilitando, segundo o Ministério da educação (2007), um maior sucesso na aprendizagem posterior da Álgebra.
1.2. Objetivo e Questões de Investigação
De acordo com as considerações anteriormente referidas, que orientaram a intervenção pedagógica, este estudo, ao debruçar-se sobre o ensino de tópicos Sequências e Regularidades, no 1.º ciclo, e Números Racionais, no 2.º ciclo, procura averiguar o contributo da aprendizagem destes tópicos na promoção do pensamento algébrico de alunos destes ciclos de escolaridade. Com a finalidade de concretizar este objetivo, pretende-se responder às seguintes questões de investigação:
Q1. Que aspetos do pensamento algébrico estão contemplados nos raciocínios de alunos do 1.º e 2.º ciclo do ensino básico?
Q2. Que dificuldades apresentam os alunos na aprendizagem de tópicos que visam a promoção do pensamento algébrico?
Q3. Que perceções têm os alunos sobre as estratégias de ensino-aprendizagem de tópicos que visam a promoção do pensamento algébrico?
1.3. Organização do relatório
Este relatório de estágio apresenta a conceção, desenvolvimento e avaliação do Projeto de Intervenção Pedagógica Supervisionada e está organizado em quatro capítulos. O primeiro e presente capítulo diz respeito à Introdução, onde é apresentada uma contextualização da problemática em questão, a motivação e pertinência do tema, o objetivo e as questões de investigação que foram a base do projeto e, por fim, a organização do documento.
O segundo capítulo enquadra contextual e teoricamente a temática do relatório, apresentando uma caracterização dos contextos das intervenções pedagógicas e uma fundamentação teórica acerca da discussão sobre o conceito e importância do pensamento algébrico e a sua integração no currículo português. Ainda, é delineada a metodologia de ensino-aprendizagem que orientou a prática pedagógica.
A análise da intervenção pedagógica e avaliação dessa intervenção é apresentada no terceiro capítulo, destacando-se cada uma das intervenções nos dois ciclos de ensino e as perceções dos alunos sobre as mesmas.
Por fim, o quarto capítulo apresenta as conclusões extraídas através da análise dos dados recolhidos durante a intervenção pedagógica, as implicações para o ensino e aprendizagem e as limitações e recomendações para futuros estudos.
CAPÍTULO 2
ENQUADRAMENTO CONTEXTUAL E TEÓRICO
Neste capítulo, apresenta-se a contextualização dos ambientes escolares e educativos onde decorreram as intervenções pedagógicas que serviram de base à composição deste relatório. Ainda se explicita o contexto teórico que fundamenta o tema do projeto e as estratégias de intervenção pedagógica utilizadas ao longo do mesmo.
2.1. Enquadramento contextual
Este subcapítulo destina-se à caraterização do Agrupamento que envolve as duas instituições, onde decorreu a prática pedagógica no 1.º ciclo e no 2.º ciclo do ensino básico, particularizando as duas escolas e as turmas onde se desenvolveu o projeto de intervenção pedagógica supervisionada.
2.1.1. O Agrupamento de escolas
A prática pedagógica no 1.º e 2.º ciclo do ensino básico, que deu origem a este relatório, realizou-se em duas escolas do mesmo Agrupamento, que inclui ofertas educativas desde a educação pré-escolar até ao ensino secundário. Trata-se de um Agrupamento de escolas que se situa na periferia da cidade de Guimarães, pertence ao distrito de Braga, e integra seis estabelecimentos de educação e ensino: uma escola básica do 1.º Ciclo, um centro escolar, três escolas básicas do 1.º Ciclo com educação pré-escolar e a escola básica e secundária, que é a escola-sede do Agrupamento. Esta diversidade de escolas que abrangem o Agrupamento conduz a uma elevada diversidade socioeconómica e ambiental dos alunos.
O Agrupamento capta uma população estudantil diversificada oriunda de várias zonas e, sobretudo, pertencentes a estratos sociais distintos. A maioria dos alunos reside nas freguesias onde estão sediadas as diferentes escolas que integram o Agrupamento, possuindo, no entanto, alunos de outras freguesias dos concelhos de Guimarães. A proveniência socioeconómica dos alunos do Agrupamento é heterogénea, tendo-se agudizado as situações de carência vividas por algumas famílias nos dois últimos anos, tal como é evidenciado no Projeto Educativo. As habilitações dos encarregados de educação são distribuídas ao longo dos anos de escolaridade não havendo uma predominância forte de qualquer habilitação. O acompanhamento das famílias
e integração das mesmas é um aspeto relevante e sempre fator de preocupação. O trabalho das Associações de Pais, fundadas em todos os estabelecimentos de ensino que integram o Agrupamento, tem-se revelado uma mais-valia e contam já com uma existência e experiência de anos.
A educação e o ensino são assegurados por 127 docentes, dos quais 90% pertencem ao quadro de professores do Agrupamento. O pessoal não docente, maioritariamente com contrato de trabalho em funções públicas por tempo indeterminado, integra 48 profissionais. O Agrupamento dispõe de vários serviços de apoio aos alunos (como serviços de psicologia e orientação, apoios especializados para crianças e jovens com necessidades educativas especiais e apoios pedagógicos para colmatar as dificuldades de aprendizagem), bem como promove projetos relevantes no âmbito do desporto, do ambiente, da saúde, da literatura, da cultura e do desenvolvimento pessoal e social dos alunos.
O projeto educativo do Agrupamento de escolas é um documento transversal a todas as instituições, uma vez que se torna projeto curricular educativo das mesmas, não havendo um documento particular de cada uma. Este projeto integra três temas fundamentais relacionados com a saúde, educação sexual, segurança e educação para a cidadania, o que traduz a preocupação com a forma como as crianças e os alunos se preocupam com o Mundo e se responsabilizam pela sua sustentação e como promovem o desenvolvimento da cultura, desporto e educação cívica.
O Agrupamento revela ainda uma preocupação pelo enriquecimento das suas condições e ofertas através de uma cuidada autoavaliação. Com o intuito de melhorar a prática educativa e os procedimentos desta avaliação, a Inspeção Geral da Educação avalia externamente os agrupamentos no sentido de indicar os pontos fortes e áreas de melhoria, contribuindo assim para uma avaliação que permita às instituições estabelecer estratégias de atuação, que permitam uma melhoria dos pontos menos favoráveis e/ou dos constrangimentos detetados. No último relatório de avaliação externa das escolas (AAE), este Agrupamento revelou: (i) um desempenho “Bom” no domínio dos “Resultados” (académicos, sociais e de reconhecimento da comunidade), tendo o Agrupamento produzido melhorias da aprendizagem dos alunos e dos percursos escolares nos níveis esperados; (ii) um nível de classificação “Bom” ao nível da prestação do serviço educativo (planeamento e articulação, práticas de ensino, monitorização e avaliação do ensino e das aprendizagens), apresentando uma maioria de pontos fortes nos campos em análise, em resultado de práticas organizacionais eficazes; e (iii) um nível de
classificação de “Muito Bom” em relação ao domínio da “Liderança e Gestão” (que inclui, para além de avaliações à liderança e gestão, também a autoavaliação das melhorias realizadas). Em consequência deste relatório, o Agrupamento formou uma comissão para o efeito, mostrando, mais uma vez, a sua preocupação na melhoria das suas instituições.
2.1.2. A escola e a turma do 1.º ciclo do ensino básico
A escola onde foi realizada a prática de ensino supervisionada (PES) no 1.º Ciclo fica sediada numa freguesia dos arredores de Guimarães, sendo envolvida por um ambiente tranquilo com algumas zonas verdes, e foi construída em 1991, tendo sofrido ao longo do tempo obras de recuperação e de ampliação. Em termos estruturais, a escola possui sete salas de aula, um polivalente, cozinha, cantina, sala de professores e uma biblioteca, com variados recursos tecnológicos e materiais escolares.
A escola inclui ofertas educativas constituídas pela educação pré-escolar e ensino do 1.º ciclo do ensino básico, com duas turmas do 1.º e 2.º ano e uma turma do 3.º e outra do 4.º ano de escolaridade do ensino básico. Existem, assim, seis docentes que lecionam estes anos de escolaridade e duas que se dedicam a apoios educativos. A escola contém um ATL (Atividades de Tempos Livres) que juntamente com a cantina é gerida pela associação de pais.
A escola e o Agrupamento têm uma estreita ligação uma vez que os projetos do Agrupamento são promovidos pela escola e todos os acontecimentos da escola são pautados por uma conexão com o Agrupamento. Assim, e como referido, a escola não tem um projeto curricular educativo particular mas sim integra o projeto curricular educativo de Agrupamento.
Caracterização da turma do 1.º ciclo. A turma do 1.º ciclo onde decorreu a PES era do 2.º ano de escolaridade, composta por vinte alunos (catorze do sexo feminino e os restantes do sexo masculino), dos quais a maior parte tinha sete anos de idade. Nenhum dos alunos era aluno com NEE (necessidades educativas especiais). Um dos alunos não tinha como língua materna o Português, embora não tivesse dificuldades em ler e escrever nesta língua. Uma das alunas integrou a turma apenas no 2.º período, o que não a impediu de ter uma boa integração no grupo turma com o passar do tempo.
O horário dos alunos apresentava-se muito diversificado ao longo da semana, alternando os tempos de atividade letiva com espaços para a oficina de artes (duas vezes por semana), inglês (uma vez por semana) e atividades físicas e desportivas (três vezes por semana).
Nos três períodos do ano letivo em análise, os alunos tiveram uma assiduidade regular, um bom comportamento e um bom aproveitamento. A participação da turma era caraterizada no Projeto Curricular de Turma (PCT) como Boa. Apesar disso, revelava-se que existiam alunas com características tímidas que não participavam com tanta frequência nas atividades das aulas. Existiam ainda alunos que apesar de serem bastante participativos se distraíam facilmente. Da análise do PCT emergiu ainda a preocupação de concretizar os objetivos específicos de cada ano escolar para cada disciplina, desenvolver capacidades transversais (como a resolução de problemas, a comunicação e o raciocínio) e de seguir os temas do projeto educativo do Agrupamento dedicados à promoção da saúde, desporto e educação para a cidadania.
Uma das preocupações também realçadas era que o acompanhamento dos alunos fosse sustentado por um acompanhamento dos encarregados de educação. O acompanhamento destes, ao longo destes períodos letivos, foi muito satisfatório, visto que todos eles estiveram presentes em todas as reuniões realizadas sobre a avaliação dos seus educandos. Para além destas reuniões, as famílias encontraram-se presentes em variadas ocasiões, proporcionadas pela escola, sobretudo nos dias comemorativos (como o dia do pai, da mãe, dos avós ou do livro), nas festas (como a festa de natal, reis e festa final de ano) e nas semanas/meses temáticos (como a semana dos afetos e o mês Rosa).
Relativamente ao desempenho dos alunos, estes apresentavam percursos escolares constantes e semelhantes sem apresentar nenhuma retenção em anos anteriores. Na análise da caracterização dos alunos da turma, enquadrada no PCT, constata-se que a maioria dos alunos revela boas capacidades matemáticas e linguísticas e têm um bom cálculo mental. Relativamente ao desempenho de avaliação dos alunos, podemos verificar na Tabela 1 que se tratou de uma turma com desempenho sempre positivo ao longo do ano letivo.
Tabela 1. Desempenhos dos alunos ao longo do ano letivo.
Insuficiente Suficiente Bom Muito Bom
1.º Período – 15% 55% 30%
2.º Período – 15% 65% 20%
3.º Período – 5% 50% 45%
O nível dos desempenhos dos alunos situa-se, com maior percentagem, no nível Bom. Alguns alunos têm um nível de desempenho Suficiente, o que se traduz por uma percentagem abaixo dos 20%, ao longo dos três períodos letivos. Enquanto outros alunos têm um nível Muito
Bom, numa percentagem não inferior aos 20%. Nenhum aluno atingiu níveis de desempenhos Insuficientes.
Como a média das avaliações finais, em percentagem ao longo dos períodos (Tabela 2), se traduz por um valor superior aos 80%, os alunos desta turma tiveram um nível Bom de desempenho.
Tabela 2. Médias das avaliações finais dos alunos ao longo do ano. Avaliação final do 1.º Período (𝑿̅) Avaliação final do 2.º Período (𝑿̅) Avaliação final do 3.º Período (𝑿̅) Avaliação final 82,9% 80,1 % 84,9%
O segundo período ficou pautado por uma ligeira descida da média das avaliações dos alunos. Porém, esse valor aumentou no 3.º período, onde se obteve a maior percentagem de média das avaliações finais dos alunos.
A maioria dos alunos revelou gostar da área disciplinar de Matemática, apesar de não ser a favorita, sendo que três dos vinte alunos referiram não gostar desta disciplina porque não conseguem obter bons resultados. Relativamente ao modo como veem esta área disciplinar, metade dos alunos referiu que gosta de efetuar cálculos. Esta prevalência indicia dever-se às boas capacidade que a turma apresenta em cálculo.
Alguns alunos revelaram ainda gostar de se envolver na obtenção de uma resposta enquanto outros admitiram preferir esperar por uma resposta dos colegas. Quase a totalidade dos alunos pensa ser importante partilhar resultados e da mesma forma gosta de trabalhar em grupo.
A maioria dos alunos manifestou gostar de resolver situações problemáticas, atribuindo às dificuldades que sentem em Matemática a atividade de justificar uma resposta, o que pode considerar-se normal para estes anos de escolaridade onde a capacidade de argumentação não está ainda muito desenvolvida.
2.1.3. A escola e a turma do 2.º ciclo do ensino básico
A escola onde decorreu a PES no 2.º Ciclo do ensino básico é a escola-sede do Agrupamento, sendo constituída por um bloco e por um pavilhão gimnodesportivo. A escola possui vinte e sete salas de aula, com características não específicas, dez salas de aula destinadas a disciplinas específicas — tais como laboratórios de Química, Física e Biologia, salas
de Informática, Desenho e Educação Tecnológica — e inclui ainda uma biblioteca inserida na rede de bibliotecas escolares (RBE), com recursos áudio, vídeo, informáticos e ligação à Internet, o centro de aprendizagem, com recursos informáticos e uma grande variedade de manuais, um anfiteatro e o serviço de psicologia e orientação e assistência social. O espaço envolvente é pautado por uma diversidade ambiental com espaços verdes e amplos.
Caracterização da turma do 2.º ciclo. A turma do 2.º Ciclo onde decorreu a PES é do 6.º ano de escolaridade e era composta por dezoito alunos (onze do sexo masculino e os restantes do sexo feminino), com idades entre os doze e os treze anos. No decorrer do 3.º período integrou a turma um aluno com dezasseis anos, transferido de uma escola de outra cidade. A maioria dos alunos não apresenta casos de retenção em nenhum ano. Um aluno integra o grupo de alunos apoiados pelos serviços de educação especial, tendo paralisia cerebral. Este aluno não passa grande parte do tempo com a turma e não estava presente por ter apoio educativo especial nos momentos de intervenção pedagógica do projeto. Sete alunos beneficiaram, durante o ano escolar, de apoio à disciplina de Matemática e dois alunos eram apoiados por assistentes sociais devido a dificuldades específicas de aprendizagem. A afluência dos pais desta turma às reuniões de pais era muito elevada, tendo 100% de assistência em reuniões nos dois primeiros períodos letivos e 96% no terceiro período. A presença das famílias e dos alunos nas comemorações e festas da comunidade escolar era elevada.
O nível geral de desempenho dos alunos é diversificado, havendo oito alunos com nível final de desempenho negativo à disciplina de Matemática, seis deles com PAPI (planos de acompanhamento pedagógico individual). Dois alunos da turma constaram nos quadros de excelência da escola.
Relativamente a estes desempenhos, os alunos apresentaram diferenças significativas ao longo dos períodos do ano letivo (Tabela 3).
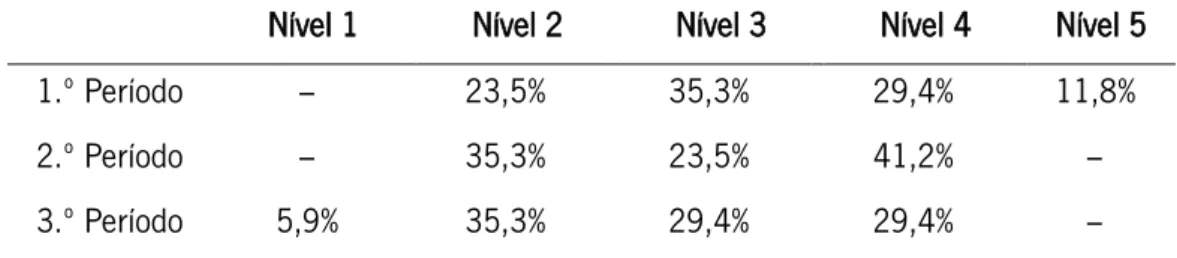
Tabela 3. Desempenhos dos alunos ao longo do ano letivo.
Nível 1 Nível 2 Nível 3 Nível 4 Nível 5
1.º Período – 23,5% 35,3% 29,4% 11,8%
2.º Período – 35,3% 23,5% 41,2% –
No primeiro período verificou-se uma aproximação entre o número de alunos com nível 2, 3 e 4, tendo havido uma pequena percentagem no nível de desempenho 5. No segundo período, a maior percentagem atribuiu-se aos alunos de nível 4, sendo a diferença entre este nível e o nível 2 muito pequena. No terceiro período, a percentagem de alunos no nível 4 baixou significativamente aparecendo mesmo uma pequena percentagem de alunos com nível de desempenho 1. Estas variações não se manifestaram de forma significativa nas médias da turma ao longo do ano letivo, que se manteve aproximadamente por volta dos 60% (Tabela 4).
Tabela 4. Médias das avaliações finais dos alunos ao longo do ano. 1.º Período (𝑿̅) 2.º Período (𝑿̅) 3.º Período (𝑿̅) Avaliação final 64,6% 61,4% 56,3%
A média desta turma nunca desceu os 60%, percentagem que representa o nível 3, o que realça os desempenhos médios desta turma. Constata-se efetivamente que o terceiro período foi o pior ao longo do ano letivo, o que pode dever-se à realização do exame nacional do 6.º ano.
A maioria dos alunos desta turma (62,5 %) revela gostar da disciplina de Matemática, embora admitam as suas dificuldades, tendo quase metade dito que era a disciplina em que sentiam as maiores dificuldades. Grande parte dos alunos (59%) prefere trabalhar em grupo e mais de 88% consideram importante partilhar e discutir os resultados.
2.2. Enquadramento teórico
Neste subcapítulo apresenta-se um enquadramento teórico que fundamenta a PES subdivididos em nove partes, relevantes para o tema em questão: (i) Sequências e Regularidades no currículo do 1.º e 2.º ciclo do ensino básico; (ii) Números racionais no currículo do 1.º e 2.º ciclo do ensino básico; (iii) O pensamento algébrico; (iv) A early algebra; (v) O pensamento algébrico no currículo do ensino básico; (vi) O lugar da generalização no pensamento algébrico; (vii) A importância das representações no pensamento algébrico; (viii) A exploração de Padrões, Relações e Sequências; (ix) Análise de alguns estudos empíricos sobre o pensamento algébrico.
2.2.1. Sequências e regularidades no currículo do 1.º e 2.º ciclo do ensino básico
A exploração do tema Sequências e Regularidades é considerada importante pelos programas de Matemática, desde os anos iniciais de escolaridade, através da observação de padrões, sequências de números, regularidades de fenómenos ou de rotinas. O trabalho com regularidades que se podem generalizar pode, segundo o Ministério da Educação (2007), desenvolver a capacidade de abstração e contribuir “para o desenvolvimento do pensamento algébrico” (p. 14), estabelecendo uma ponte entre os todos os ciclos de ensino.
O tema Sequências e Regularidades é transversal a todos os anos de escolaridade do ensino básico e abrange vários tópicos matemáticos, que integram outros temas matemáticos de formas diferentes nos anos de escolaridade (Tabela 5).
Tabela 5. Temas curriculares que integram o tema Sequências e Regularidades. Programa de Matemática do Ensino Básico (2007) e Metas curriculares de Matemática do ensino básico (2013)
1.º Ciclo 1.º e 2.º anos Números e Operações 3.º e 4.º anos Números e Operações
2.º Ciclo 5.º e 6.º anos Álgebra
Até ao 4.º ano de escolaridade, fim do 1.º ciclo do ensino básico, o tópico Sequências e Regularidades encontra-se inserido no tema Números e Operações, enquanto no 2.º ciclo já se encontra inserido no tema Álgebra. Em ambos os documentos analisados acontece esta diversificação, uma vez que a Álgebra nem sequer é considerada como um dos grandes temas a desenvolver até ao 2.º ciclo. Considerada diluída nos outros temas fundamentais (Números e Operações, Geometria e Medida e Organização e Tratamento de Dados), a Álgebra nos primeiros dois ciclos iniciais surge como forma de pensamento matemático, que possibilita promover bases para o desenvolvimento de aprendizagens significativas posteriores.
Relativamente ao 1.º ciclo, uma análise àsmetas curriculares de Matemática do ensino básico (Ministério da Educação, 2013) mostra que é importante que os alunos se envolvam em situações problemáticas em que o objetivo é “a determinação de termos de uma sequência dada a lei de formação” (p. 11) e de forma inversa “a determinação de uma lei de formação compatível com uma sequência parcialmente conhecida” (idem, p. 11). Os alunos devem ter oportunidades de aplicar uma lei de formação a uma dada sequência e, da mesma forma, tendo os termos de uma sequência, descobrir a lei de formação pela qual esta se constitui.
Ainda relativamente ao 1.º ciclo, uma análise ao Programa do Ensino Básico (Ministério da Educação, 2007) revela uma preocupação com a exploração de sequências de números e de regularidades em sequências e não só. O ensino das Sequências e Regularidades apresenta-se assim como a investigação “de regularidades em sequências e em tabelas de números” e a elaboração de “sequências de números segundo uma dada lei de formação” (p. 17).
Ambos os documentos focam a necessidade de os alunos elaborarem sequências, embora o atual documento das Metas Curriculares (Ministério da Educação, 2013) foque também a elaboração de leis de formação. Segundo o National Council of Teacher of Mathematics (NCTM), os alunos devem ser incentivados a reconhecer, descrever e ampliar padrões desde muito cedo para além de terem oportunidades de observar, “agrupar, classificar e ordenar objetos” (2007, p. 104), pondo em evidência as propriedades dessa classificação.
Relativamente ao 2.º ciclo do ensino básico, o tópico Sequências e Regularidades já se encontra inserido na Álgebra. O tópico apresenta-se, então, como um momento de os alunos continuarem a aprendizagem de anos anteriores, determinando um termo numa dada sequência segundo a sua lei de formação ou expressão geradora, e usando esta para determinar qualquer termo, qualquer que seja a ordem considerada. Na elaboração de uma lei de formação, os alunos são já capazes, segundo o Ministério da Educação (2007), de a encontrar através do estabelecimento de relações e da representação das mesmas. Os alunos devem ser ainda capazes de “identificar e dar exemplos de sequências e regularidades” (p. 41). Os documentos analisados focam a necessidade de estabelecer e formalizar relações através de representações simbólicas e linguagem natural.
2.2.2. Números racionais no currículo do 1.º e 2.º ciclo do ensino básico
A aprendizagem dos números racionais inicia-se nos dois primeiros anos de escolaridade como um conhecimento posterior à abordagem dos números naturais e às suas operações aritméticas. Nestes anos iniciais, começa a aprendizagem dos números racionais não negativos. Dentro dos números racionais, a abordagem e o modo de trabalhar as frações é substancialmente diferente no Programa do Ensino Básico (2007) e nas Metas Curriculares (2013). No Programa do Ensino Básico (2007), a abordagem a estes números é feita de forma intuitiva através de situações de “partilha equitativa e de divisão da unidade em partes iguais” (p. 17), a modelos e à representação em forma de fração nos casos mais simples. Este documento confere, ainda, importância em compreender os operadores. Os alunos aprofundam
a aprendizagem dos números racionais não negativos explorando problemas que permitam trabalhar outros significados das frações. Até ao fim do 1.º ciclo do ensino básico, os alunos trabalham com números racionais positivos sob a forma fracionária, decimal e percentual e atribuindo os significados de parte-todo, quociente e operador às frações.
No 2.º ciclo do ensino básico, os alunos operam aritmeticamente os números sobre a forma de fração. São ainda introduzidos conceitos de fração equivalente e irredutível e são abordados os numerais mistos. Neste ciclo, são apresentados mais dois significados de fração, completando os cinco significados que são atribuídos aos números fracionários: parte-todo, operador, quociente, razão e medida. O significado de parte-todo deve-se à identificação do número de partes que tomam o todo; Operador é a transformação do cardinal de um conjunto de dados; Quociente é atribuído à compreensão da divisão de dois números racionais; Razão à comparação entre duas quantidades da mesma natureza ou de naturezas distintas; e por fim, o significado de medida abarca a comparação entre duas grandezas, uma das grandezas sendo tomada como unidade (Ponte & Quaresma, 2011).
Os números racionais negativos não são abordados até ao 2.º ciclo do ensino básico neste programa e este facto constitui uma grande diferença em relação ao atual documento em vigor que orienta o ensino da Matemática. Nas Metas Curriculares (Ministério da Educação, 2013), os números racionais negativos são lecionados no 6.º ano de escolaridade, o que no programa anterior só acontecia no 3.º ciclo.
As Metas Curriculares (Ministério da Educação, 2013) trazem ainda uma grande diferença em relação ao tema dos números racionais, sugerindo desde o seu início uma introdução às frações com uma abordagem geométrica através da “decomposição de retas em segmentos de igual comprimento” (p. 6).
A aprendizagem dos números racionais é extremamente importante, o que é corroborado pelo NCTM (2007), que defende que o investimento nos números racionais entre o 3.º e o 5.º ano é significativo sendo importante desenvolver “a sua compreensão, representações e cálculo” (p. 172). O cálculo com destreza com números racionais será desenvolvido nos anos posteriores.
2.2.3. O pensamento algébrico
A Álgebra “sempre foi considerada uma das áreas essenciais da Matemática” (Boavida & Guimarães, 2007), área que tem merecido cada vez mais a atenção da investigação. O ensino
desta temática está fortemente relacionado com a manipulação de símbolos e a resolução de equações, porém vai muito para além disso (Vale, Palhares, Cabrita & Borralho, 2007). Na evolução deste campo, ao longo dos anos “foram surgindo várias perspetivas e formas de a concetualizar” (Boavida & Guimarães, 2007). Muitas das discussões realizadas ao longo do tempo tentam delimitar e caraterizar o campo da Álgebra. Dessas discussões surgiu “o interesse pela caracterização do pensamento algébrico” (Ponte, Branco & Matos, 2009, p. 9). Aliás, as investigações realizadas sobre a Álgebra e, particularmente, sobre o pensamento algébrico, nos anos iniciais, têm vindo a ser cada vez mais crescentes (Canavarro, 2007). Autores como Blanton e Kaput (2003, 2005), Carraher e Schliemann (2007), Kaput (1999, 2008), Kieran (1992, 2004) e Radford (2006, 2010a, 2010b) têm contribuído para algumas das mais importantes discussões e publicações sobre o tema. Discute-se, de seguida, algumas perspetivas sobre o que se entende por pensamento algébrico e por Álgebra.
A propósito da definição de pensamento algébrico, Kieran (1992), uma das principais autoras sobre este tema, distingue duas perspetivas da Álgebra: a processual e a estrutural. Na Álgebra processual, o destaque é a substituição de variáveis por números. Apenas num momento posterior a esta substituição acontece a realização de operações aritméticas. Na Álgebra estrutural, o foco é dado ao conjunto de operações realizadas com expressões algébricas em detrimento do uso de números. A Álgebra processual trabalha assim com a concretização numérica em expressões algébricas, enquanto a Álgebra estrutural trabalha com expressões algébricas.
Definindo o pensamento algébrico, Kieran (1992) destaca o uso de símbolos quando afirma que o pensamento algébrico “desenvolve formas de pensamento através de atividades nas quais o simbolismo algébrico pode ser usado como uma ferramenta” (p. 149). Apesar desta definição, Kieran (2004) faz questão de ressalvar que estas atividades podem também ser abordas sem o uso destes símbolos, usando outras capacidade como a análise de relações entre quantidades, evidência de estruturas e estudo das variações, permitindo generalizar, resolver problemas, modelar, justificar, provar e prever.
O uso de símbolos é também destacado por outros autores, como Radford (2006, 2010a, 2010b), como um importante aspeto quando falamos em pensar algebricamente. Este autor adotou uma caracterização de pensamento algébrico com base em três elementos: o caráter indeterminado, próprio dos objetos algébricos básicos (como incógnitas, variáveis e
parâmetros), a forma se como lida com esses objetos e o modo simbólico como os mesmos são designados.
Apesar do destaque que ambos os autores conferem ao uso de símbolos algébricos, ambos acautelam que a utilização de letras não é a única ferramenta de raciocínio algébrico. Radford (2010a) considera mesmo que no pensamento algébrico existem muitas outras ferramentas (que não são algebricamente simbólicas) que são utilizadas para expressar ideias algébricas. Carraher e Schliemann (2007) corroboram com esta perspetiva, especialmente quando se consideram alunos mais jovens, já que "os estudantes mais precoces fazem por vezes generalizações algébricas sem usar notação algébrica" (p. 681). Os alunos que não possuem capacidades algébricas conseguem assim expressar generalizações e identificar relações – aspetos que se incluem no pensamento algébrico – e então ‘fazer Álgebra’ sem necessitar manipular símbolos formais como letras, através de outras formas de comunicação matemática, como a linguagem ou a elaboração de tabelas, por exemplo.
Carraher e Schliemann (2007), em consonância com os autores anteriores, também atribuem importância ao simbolismo, uma vez que consideram que pensamento algébrico se pode definir como o conjunto dos “processos psicológicos envolvidos na resolução de problemas em que os matemáticos conseguem facilmente expressar usando notação algébrica" (p. 670). Acrescentando a esta definição, Carraher e Schliemann (2007) também consideram essencial atribuir importância no pensamento algébrico às capacidades aritméticas. Esta relação com a aritmética é valorizada por outros autores. O estudo da aritmética generalizada é uma das vertentes mais comuns de pensamento algébrico no ensino elementar, conjuntamente, com o pensamento funcional (Blanton & Kaput, 2005; Canavarro, 2007; Carraher & Schliemann, 2007).
A aritmética generalizada baseia-se no que Carraher e Schliemann (2007) definiram como caráter potencialmente algébrico da aritmética e é caraterizada pelo “uso da aritmética com um domínio para expressar e formalizar generalizações” (Blanton & Kaput, 2005, p. 413). Existem alguns aspetos que podem descrever esta vertente como “a exploração de relações e de propriedades das operações de números inteiros; exploração da igualdade como expressão de uma relação de quantidade; tratamento algébrico dos números; resolução de expressões com incógnitas (números desconhecidos em falta)” (Blanton & Kaput, 2005, pp. 419-422).
A outra vertente diz respeito à “generalização de padrões numéricos para descrever relações funcionais” – pensamento funcional. Este aspeto permite “a descrição de regularidades
através de símbolos, comparar diferentes expressões relativas à mesma regularidade ou determinar valores particulares de uma função” (Canavarro, 2007, p. 90). Esta vertente inclui as capacidades de “simbolização de quantidades e operações com expressões simbólicas; representação gráfica de dados; descoberta de relações funcionais; previsão de resultados desconhecidos através de dados conhecidos; e identificação e descrição de padrões numéricos e geométricos” (Blanton & Kaput, 2005, pp. 423-427).
Blanton e Kaput (2005) referem para além destas mais duas vertentes para caraterizar o pensamento algébrico: “a modelação como um domínio para expressar e formalizar generalizações e a generalização sobre os sistemas matemáticos abstratos através da computação e relações” (p. 413). A modelação é uma forma de pensamento algébrico que envolve “a generalização de regularidades através da análise de situações e fenómenos” (Blanton & Kaput, 2005, p. 413). A última vertente, menos comum nos currículos dos ensinos elementares, é descrita como uma matemática mais abstrata e diz respeito à generalização de objetos e sistemas abstratos.
Do estudo das várias vertentes, uma das grandes capacidades que emergem da promoção do pensamento algébrico é a capacidade de generalizar. A generalização é o “coração do pensamento algébrico” (Carraher, Schliemann & Brizuela, 2007, p. 12). Pensar algebricamente pode mesmo ser visto como um “processo em que os alunos generalizam ideias matemáticas a partir de um conjunto de casos particulares, estabelecem essa generalização através do discurso da argumentação e a expressam, gradualmente, de formas cada vez mais formais e adequadas à sua idade” (Blanton & Kaput, 2005, p. 413). Kaput (2008), numa das suas últimas publicações, refere que a generalização e a sua expressão gradual são, juntamente com o raciocínio sintaticamente orientado sobre as generalizações, os dois aspetos essenciais do pensamento algébrico. Estes dois aspetos materializam-se em três vertentes para a Álgebra, segundo Kaput (2008). Este autor começou por definir cinco vertentes da Álgebra em 1999, quatro em conjunto com Blanton em 2005 e por fim numa das últimas publicações, em 2008, definiu então nas vertentes seguintes:
a) O estudo das estruturas e sistemas abstraídos a partir do resultado de operações e estabelecimento de relações, incluindo os que surgem na Aritmética (Álgebra como Aritmética generalizada) ou no raciocínio quantitativo;
b) O estudo das funções, relações e (co) variação.
c) A aplicação de um conjunto de linguagens de modelação, tanto no domínio da Matemática, como no seu exterior. (Kaput, 2008, p. 11)
Apresentadas algumas perspetivas da Álgebra e do pensamento algébrico, entende-se que não há uma definição concisa e convergente que defina ambos. Embora se possam considerar alguns aspetos que foram enunciados. Esta não existência de uma definição concisa que permita definir o que significa pensar algebricamente (Lins & Gimenez, 1997), pode dever-se, como Radford (2006) afirma, à variedade de objetos algébricos, tais como “equações, funções ou padrões”, e processos próprios como a “inversão, simplificação” (p. 89).
Quando falamos sobre a Álgebra e o pensamento algébrico nos primeiros anos existem algumas premissas a considerar. Embora a Álgebra ainda não seja valorizada por todos, vários são os autores que referem que o ensino de conteúdos algébricos serve de base ao desenvolvimento de competências futuras na Matemática, desde anos muito iniciais (Canavarro, 2007). Mesmo antes de entrarem no ensino básico, as crianças reconhecem e expressam as mudanças que ocorrem à sua volta, estabelecem relações de quantidade, preveem qual será o termo seguinte numa sequência de dados ou identificam um padrão. Tudo isto contribui para que progressivamente mergulhem num pensamento de natureza cada vez mais algébrico (NCTM, 2007). Esta precoce ligação dos alunos a modos de pensamento algébricos não significa que não seja necessário promover capacidades neste campo. De acordo com o NCTM (2007), os professores podem preparar os seus alunos para terem sucesso na Álgebra se desde o início os ensinarem a pensar algebricamente, isto é, se promoverem o seu pensamento algébrico.
Radford (2010b) aponta que “o pensamento algébrico não surge por acaso, nem surge como uma consequência necessária da maturação cognitiva. Para fazer surgir o pensamento algébrico algumas condições pedagógicas têm de ser criadas” (p. 4). O trabalho com o desenvolvimento da Álgebra não parte de nada que os alunos tenham de começar do zero, é preciso sim ‘algebrizar’ (Blanton & Kaput, 2003) as tarefas que se usam na sala de aula, a maneira como se ‘olha’ o pensamento dos alunos e de como os professores agem na sala de aula. Estes autores indicam três dimensões baseadas na atividade do professor que devem ocorrer quando se algebrizam as atividades das aulas de Matemática: a criação de oportunidades onde se possa desenvolver o pensamento algébrico; a capacidade de identificar quando existem possibilidades de fazer e expressar generalizações; e a criação de um ambiente de sala de aula que promova essa capacidade. A algebrização é assim conseguida “encontrando e apoiando o pensamento algébrico dos alunos e criando uma cultura de sala de aula e práticas de ensino que promovam o pensamento algébrico” (Blanton & Kaput, 2003, p. 70).
Redesenhando tarefas preexistentes numa perspetiva que valorize a atividade do aluno, em que ele tenha oportunidades de reconhecer o que é geral numa dada situação, estabelecendo relações e expressando de forma mais ou menos informal essas generalizações é conseguir algebrizar as tarefas que são usadas na atividade matemática. Porém, esta algebrização das tarefas não alcança, por si só, a promoção do pensamento algébrico, se os alunos não forem envolvidos e estimulados a pensar, expressar e comunicar algebricamente. Precisa-se, por isso, não só de dar oportunidades aos alunos para trabalharem com tarefas que promovam este raciocínio como explorar e valorizar o que eles fazem com essas tarefas.
A voz dos alunos assume um papel fundamental nestas práticas de sala de aula e, em consequência, o professor tem de surgir como um percutor de oportunidades e tem de desenvolver “ouvidos e olhos para a Álgebra” (Blanton & Kaput, 2003, p. 73), a fim de identificar quando as oportunidades de generalizar e expressar possam ocorrer. O simples questionamento de perguntas — tais como, como é que estão a pensar sobre isto? Alguém resolveu de forma diferente? Como sabemos que isso é verdade? O que utilizaram para expressar essa ideia? Isso é verdade para todos os casos? Como convenceriam os outros dessa ideia? Porquê é que pensaste assim? — Permitem não só perceber o que os alunos estão a ponderar sobre a tarefa em questão como desenvolver neles capacidades de argumentação que possibilitam expressar e defender provando aquilo que pensam. É passível perceber que, para que este questionamento aconteça e para que possam ocorrer oportunidades de valorizar a atividade do aluno, é necessário criar um ambiente de sala de aula que promova discussões entre os alunos e entre os alunos e o professor e considere o que os alunos dizem e fazem.
A criação de um ambiente de sala de aula capaz de promover o pensamento algébrico implica práticas que permitam aos alunos ter oportunidade de conjeturar, generalizar, argumentar e representar os seus raciocínios.
Uma premissa tem de ser apoiada pela outra. Se por um lado, se torna fulcral trabalhar e transformar os tarefas já existentes de maneira a transformá-las com potencial algébrico – seja pela transformação de uma resposta unicamente numérica em uma resposta menos limitada, variando os parâmetros de um problema, fazendo extensões das perguntas já existentes, solicitando a justificação de respostas, por exemplo – também por si só isso não desenvolve o pensamento algébrico nos alunos (Blanton & Kaput, 2003). É importante, por isso, reforçar os papéis que o professor tem numa sala de aula que promove o pensamento algébrico dos alunos. Como Abrantes, Serrazina e Oliveira (1999) referem, o professor tem a responsabilidade de não