Aula 11 – Conseq¨
uˆ
encias da semelhan¸
ca de
triˆ
angulos
Objetivos
• Apresentar o Teorema de Pit´agoras
• Apresentar o teorema da bissetriz interna.
O Teorema de Pit´
agoras
Com os casos de semelhan¸ca de triˆangulos j´a estabelecidos, podemos agora provar o famoso teorema de Pit´agoras:
Teorema de Pit´agoras
Em todo triˆangulo retˆangulo, o quadrado da medida da hipotenusa ´e igual `a soma dos quadrados das medidas dos catetos.
Vocˆe sabia que...
Segundo uma lenda, como prova de sua gratid˜ao pela descoberto do teorema que leva o seu nome, Pit´agoras sacrificou 100 bois aos deuses. Na verdade, o Teorema de Pit´agoras j´a era conhecido pelos babilˆonios atrav´es da observa¸c˜ao e da experimenta¸c˜ao, mas a primeira prova formal ´e atribu´ıda aos pitag´oricos. N˜ao se sabe, contudo, se o teorema foi provado por Pit´agoras pessoalmente.
Prova:
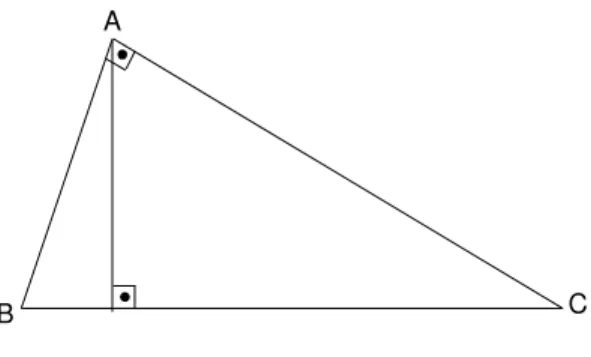
SejaABC um triˆangulo retˆangulo com ˆangulo reto no v´ertice A. Que-remos provar que [m(BC)]2 = [m(AB)]2+ [m(AC)]2.
Para isso, considere a altura AD do triˆangulo ABC a partir do v´ertice A (figura 208).
A
B C
Os triˆangulos ABC e ABD s˜ao triˆangulos retˆangulos e possuem o ˆangulo ˆB em comum. Segue da proposi¸c˜ao 23 que ABC ∼ DBA (n˜ao se esque¸ca de que quando escrevemos ABC ∼ DBA queremos dizer que ABC e DBA s˜ao semelhantes segundo a correspondˆencia A ↔ D, B ↔ B e C ↔A). Logo,
m(AB)
m(BC) =
m(BD)
m(AB) .
Da mesma forma, conclui-se que os triˆangulos ABC e DAC s˜ao seme-lhantes e que
m(AC)
m(BC) =
m(DC)
m(AC) .
Segue das igualdades acima que [m(AB)]2 =m(BC).m(BD) e [m(AC)]2 =
m(BC)m(DC). Somando membro a membro essas igualdades, obtemos
[m(AB)]2+ [m(AC)]2 = m(BC).m(BD) +m(BC).m(DC) = m(BC).[m(BD) +m(DC)]
= m(BC).m(BC) = m(BC)2
Q.E.D.
A rec´ıproca do Teorema de Pit´agoras ´e tamb´em verdadeira, ou seja, se um triˆangulo ABC tem lados de medidas a, b e c com a2 = b2 +c2, ent˜ao ABC ´e um triˆangulo retˆangulo (veja exerc´ıcio 2 desta aula).
A prova dada aqui para o Teorema de Pit´agoras n˜ao ´e a mesma dada por Euclides. A prova de Euclides faz uso da teoria de ´area de figuras planas.
O Teorema de Pit´agoras ´e t˜ao famoso que inspirou um quadro humor´ıstico do comediante Agildo Ribeiro nos anos 80.
Existe outra rela¸c˜ao v´alida para triˆangulos retˆangulos que ´e bastante usada. Ela est´a destacada na proposi¸c˜ao que se segue.
Proposi¸c˜ao 26
Em todo triˆangulo retˆangulo, a medida da altura relativa `a hipotenusa ´e igual `a m´edia geom´etrica das medidas dos segmentos que ela determina sobre a hipotenusa.
Vocˆe sabia que...
A m´edia geom´etrica entre dois n´umerosmen´e definida como a raiz quadrada do produto desses n´umeros.
Prova:
Para isso, novamente utilizaremos semelhan¸ca de triˆangulos. Como ˆB + BADb = 90o
(poisBDAb ´e reto) e ˆB+ ˆC = 90o
(poisBACb ´e reto) segue que BADb = ˆC. Da mesma forma, comoDACb + ˆC= 90o
e ˆB+ ˆC = 90o
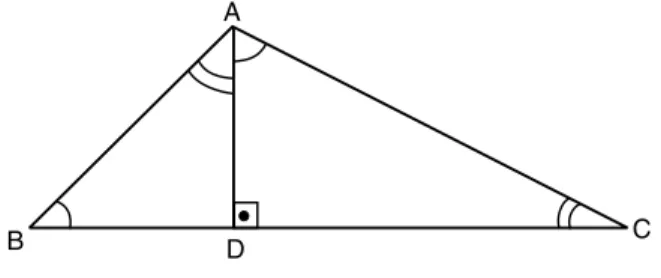
, obtemos DACb = ˆB (veja figura 209).
A
B D C
Fig. 209: ABD∼CAD.
A proposi¸c˜ao 23 nos garante que ABD∼CAD.
Logo,
m(AD) m(DC) =
m(BD) m(AD) .
Da´ı conclui-se que [m(AD)]2 =m(BD).m(DC).
Q.E.D.
Usando o Teorema de Pit´agoras, podemos mostrar agora a existˆencia de segmentos incomensur´aveis. Considere um quadrado ABCD e trace a diagonal DB (figura 210).
A B
C D
Fig. 210: Existˆencia de segmento incomensur´avel.
A escola pitag´orica tinha como lema que tudo poderia ser explicado pelos n´umeros inteiros. Em particular, a raz˜ao entre dois segmentos quaisquer seria sempre igual a um n´umero racional (raz˜ao entre dois n´umeros inteiros), ou seja, quaisquer dois segmentos seriam comensur´aveis. A descoberta da inscomensurabilidade entre o lado e a diagonal de um quadrado colocou em cheque o lema da Escola. Segundo uma lenda, Hiparcus (400 a.C.) foi expulso da Escola e depois afogado no mar como puni¸c˜ao por ter se tornada p´ublica a descoberta de grandezas incomensur´aveis.
O triˆanguloBCD´e retˆangulo com ˆangulo reto no v´erticeC. Usando-se o segmentoCB como unidade de medida, obt´em-se doTeorema de Pit´agoras
que [m(DB)]2 = [m(DC)]2 + [m(CB)]2 = 1 + 1 = 2, ou seja, m(DB) =
√
O teorema da bissetriz interna
Apresentamos, agora, um resultado que se mostra ´util em muitas si-tua¸c˜oes:
Teorema (da bissetriz interna)
Uma bissetriz interna de um triˆangulo divide o lado oposto em segmentos proporcionais aos lados adjacentes.
Prova:
Seja ABC um triˆangulo qualquer e considere a bissetriz interna AD (figura 211). Queremos provar que m(BD)
m(AB) =
m(DC)
m(AC).
A
C D
B
Fig. 211: Teorema da bissetriz interna.
Se AB ≡ AC, tem-se por L.A.L. que ABD ≡ ACD. Como
con-seq¨uˆencia,BD ≡DC e, ent˜ao, m(BD) m(AB) =
m(DC)
m(AC). Suponha agora que AB e AC n˜ao sejam congruentes. Por exemplo, suponha que AB < AC. Nesse caso, ACB < Ab BC. Existe ent˜ao uma semi-retab BE−−→ tal que ABEb ≡ACB.b SejaF o ponto em que essa semi-reta intersecta AD (figura 212).
A
B D C
E
F
Pela proposi¸c˜ao 24, os triˆangulos ABF e ACD s˜ao semelhantes, pois ABFb ≡ACDb eBAFb ≡CADb . Em conseq¨uˆencia,AF Bb ≡ADCb e m(BF)
m(DC) = m(AB)
m(AC).
Como AF Bb ≡ ADCb , segue que BF Db ≡ BDFb e, assim, BF ≡ BD. Substituindo na equa¸c˜ao, obtemos finalmente que m(BD)
m(DC) =
m(AB)
m(AC), ou,
equivalentemente, que m(BD) m(AB) =
m(DC)
m(AC).
Q.E.D.
Resumo
Nesta aula vocˆe aprendeu...
• Que em qualquer triˆangulo retˆangulo o quadrado da medida da
hipote-nusa ´e igual `a soma dos quadrados das medidas dos catetos (Teorema de Pit´agoras).
• Que a medida da altura relativa `a hipotenusa ´e a m´edia geom´etrica das
medidas dos segmentos que ela determina sobre a hipotenusa.
• Que uma bissetriz interna de um triˆangulo divide o lado oposto em
segmentos proporcionais aos lados adjacentes (Teorema da Bissetriz Interna)
Exerc´ıcios
1. Determine o raio do c´ırculo inscrito e o raio do c´ırculo circunscrito em um triˆangulo equil´atero de 10 cm de lado.
2. (Rec´ıproca do Teorema de Pit´agoras.) Prove que se em um triˆangulo ABC tem-se [m(BC)]2 = [m(AB)]2+ [m(AC)]2, ent˜aoABC
3. SejaABCum triˆangulo retˆangulo de hipotenusaBCe sejaADa altura relativa `a hipotenusa. Para facilitar, fa¸camosc=m(AB),b =m(AC), a = m(BC), h = m(AD), m = m(BD) e n = m(DC) (veja a figura 213).
C D
A
B
c b
a n m
h
Fig. 213: Exerc´ıcio 3.
Prove que b2 = a.n , c2 = a.m e a.h = b.c. Essas equa¸c˜oes,
junta-mente com o Teorema de Pit´agoras e a proposi¸c˜ao 26, constituem o que chamamos derela¸c˜oes m´etricas em um triˆangulo retˆangulo.
4. Determine x no triˆangulo retˆangulo da figura 214.
x
2x
3 2 7
Fig. 214: Exerc´ıcio 4.
5. Determinexna figura 215, sabendo queAB´e tangente aos dois c´ırculos.
O O'
A
B x
3 C 3 D 2
6. Determine x na figura 216.
B D C
A
10 6
x
Fig. 216: Exerc´ıcio 6.
7. Na figura 217, AD ´e mediana, AE ´e altura e BACb ´e reto. Determine o per´ımetro de ABC.
A
B 3
5
E D C
Fig. 217: Exerc´ıcio 7.
8. Determine a medida do segmento AD da figura 218, sabendo que AD ´e bissetriz e BACb ´e reto.
A
C D
4
B 3
Fig. 218: Exerc´ıcio 8.
9. Um observador vˆe um edif´ıcio, constru´ıdo em um terreno plano, sob um ˆangulo de 60o
. Se ele se afastar do edif´ıcio mais 30m, passar´a a vˆe-lo sob um ˆangulo de 45o
. Determine a altura do edif´ıcio.
10. Na figura 219, ABCD ´e um quadrado de 4cm de lado, m(AE) = 1
3m(AD) e m(CF) = 1
4m(BC). Determine m(GH).
A G
E
B
F
C D
H
Fig. 219: Exerc´ıcio 10.
11. Na figura 220, AS ´e bissetriz de BACb e AP ´e bissetriz de CAD. De-b terminem(SP).
A
B C
D
S P
20 40
30
Fig. 220: Exerc´ıcio 11.
12. Determine x na figura 221.
A
B C
D
F E
3
6
7
x
G
13. (U. MACK- 1975) Um ponto P dista 5cm do centro de um c´ırculo de 13cm de raio. Pelo ponto P tra¸ca-se a corda AB de 25cm. Os comprimentos dos segmentos que P determina sobre a corda AB s˜ao iguais a:
(a) 11cm e 14cm (b) 7cm e 18cm (c) 16cm e 9cm
(d) 5cm e 20cm (e) 8cm e 17cm
14. (UFMG-1982) Num c´ırculo, a corda CD ´e perpendicular ao diˆametro AB no ponto E. Se m(AE).m(EB) = 3, a medida de CD ´e:
(a) √3 (b) 2√3 (c) 3√3 (d) 3 (e) 6
15. (VUNESP-1991) Na figura 222, o triˆangulo ABD ´e reto em B eAC ´e bissetriz de BADb .
A
B
C
D
Fig. 222: Exerc´ıcio 15.
Se m(AB) = 2m(BC), fazendo m(BC) = b e m(CD) = d, podemos concluir que:
(a) d=b (b) d=
5 2
b (c) d=
5 3
b
(d) d =
6 5
b (e) d=
5 4
16. (UFGO-1980) O per´ımetro de um triˆangulo is´osceles de 3cmde altura ´e 18cm. Os lados desse triˆangulo, em cm, s˜ao:
(a) 7,7,4 (b) 5,5,8 (c) 6,6,6 (d) 4,4,10 (e) 3,3,12
17. (CESGRANRIO-1991) Uma folha quadrada de papelABCD´e dobrada de modo que o v´erticeCcoincida com o ponto m´edio deAB(veja figura 223).
A
M
º
B P D
C D
A B
M C
Fig. 223: Exerc´ıcio 17.
Se o lado deABCD ´e 1, o comprimento deBP ´e igual a:
(a) 0,300 (b) 0,325 (c) 0,375
(d) 0,450 (e) 0,500
18. (FATEC-1978) Na figura 224, as circunferˆenciasC1 eC2 tangenciam-se
no pontoP e a reta t tangenciaC1 eC2 nos pontosA e B,
respectiva-mente.
P
A B
C
1
2
C
t
Fig. 224: Exerc´ıcio 18.
Se o raio deC1 ´e 8 cm e o raio de C2 ´e 2 cm, ent˜ao:
(a) m(AB) = 8cm (b) m(AB) = 13 cm (c) m(AB) = 10 cm
19. (COVEST - 1990) Na figura 225, temos duas circunferˆencias concˆentricas, com raios medindo 4cm e 5cm, respectivamente. Por um ponto P da circunferˆencia menor, tra¸ca-se a reta tangente `a mesma, a qual deter-mina pontos A e B na circunferˆencia maior.
P B
A
Fig. 225: Exerc´ıcio 19.
O comprimento do segmento AB´e:
(a) 3√2cm (b) 6cm (c) 3√3cm (d) 6,1cm (e) 5,8cm
20. (CESGRANRIO, COMCITEC-1973) Na figura 226, as circunferˆencias de centros P e S s˜ao ambas tangentes `a reta u no mesmo ponto Q, e a reta que passa por P eR tangencia a circunferˆencia menor no ponto T.
P
T
S
Q R
u
Fig. 226: Exerc´ıcio 20.
Sendo os raios das circunferˆencias 8me 3m, respectivamente, a medida do segmento QR ´e igual a:
(a) 4 m (b) 6 m (c) 8 m
21. (EPUSP-1966) Os lados de um triˆangulo est˜ao na raz˜ao 6 : 8 : 9. Ent˜ao:
(a) O triˆangulo ´e obtusˆangulo
(b) O triˆangulo ´e acutˆangulo
(c) Os ˆangulos est˜ao na raz˜ao 6 : 8 : 9
(d) O ˆangulo oposto ao lado maior ´e o dobro do ˆangulo oposto ao lado menor
(e) Nenhuma das respostas anteriores
22. (UFF, 1993) No triˆangulo is´osceles P QRda figura 227, RH ´e a altura relativa ao lado P Q,m(P Q) = m(RQ) = 10cm em(P R) = 6cm.
P H
Q
R T
Fig. 227: Exerc´ıcio 22.
Se M ´e o ponto m´edio de P R, ent˜ao o semic´ırculo de centro M e tangente a RH tem raio igual a: