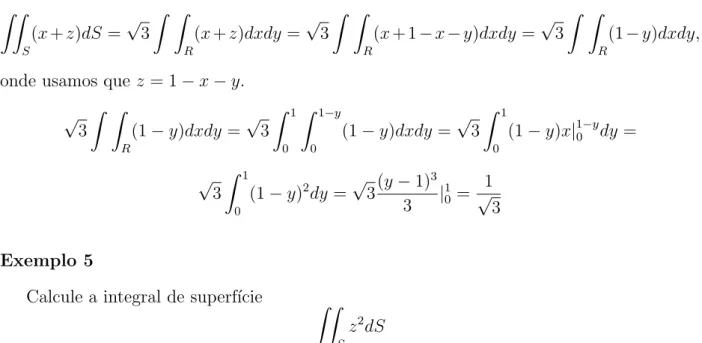Notas para o Curso de C´

(1)

Notas para o Curso de C´

alculo Vetorial

Dayse Haime Pastore

(2)

(3)

Sum´

ario

1 Fun¸c˜oes Vetoriais 5

1.1 Introdu¸c˜ao . . . 5

1.2 Gradiente, Divergente e Rotacional . . . 7

1.3 Exerc´ıcios . . . 10

2 Integrais de Superf´ıcies e Divergˆencia 13 2.1 O vetor normal unit´ario . . . 13

2.2 Defini¸c˜ao de Superf´ıcie Integr´aveis . . . 16

2.3 Calculando integrais de Superf´ıcies . . . 18

2.4 A Divergˆencia . . . 25

2.5 A divergˆencia em coordenadas cil´ındricas e esf´ericas . . . 26

2.6 O Teorema da Divergˆencia . . . 27

3 Integral de Linha e o Rotacional 35 3.1 Trabalho e Integral de Linha . . . 35

3.2 Integral de Linha Envolvendo Campo Vetorial . . . 37

3.3 O Rotacional . . . 41

3.4 O Rotacional em Coordenadas Cil´ındricas e Esf´ericas . . . 45

3.5 O Teorema de Stokes . . . 48

(4)

(5)

Cap´ıtulo 1

Fun¸c˜

oes Vetoriais

1.1 Introdu¸c˜

ao

Um exemplo muito importante de campo vetorial s˜ao os campos el´etricos estudados em eletricidade.

Vamos come¸car revendo o que é uma fun¸cão. Uma fun¸cão de uma variável, geralmente escrita como y = f(x), é uma regra que associa dois números x e y, onde x pertence a um dom´ınio ey a um contra-dom´ınio. Exemplo, se y=f(x) =x2₋_{2, então calculamos} _y _como sendo a raiz quadrada de xsubtraida de 2. Assim, se x= 3,

y = 32₋2 = 7.

Fun¸cões de mais de uma variável podem ser vistas como regras para associar conjuntos de números. Exemplo, uma fun¸cão de três variáveis, w = f(x, y, z) associa um valor a w

referente a x, y e z. Um exemplo no plano cartesiano é a fun¸cão, T(x, y, z) que mede a temperatura de uma sala no ponto (x, y, z). Um outro exemplo de fun¸cão vetorial é a que associa a um ponto (x, y, z) do espa¸co a velocidade do flu´ıdo.

Defini¸cão 1 Em três dimensões, um fun¸cão é dita escalar, ou um campo escalar, se associa um ponto (x, y, z) a um escalar T = f(x, y, z). E é dita vetorial, ou um campo vetorial, se associa ao ponto (x, y, z) um vetor w=f(x, y, z).

Assim a fun¸cão que mede a temperatura é uma fun¸cão escalar, e a fun¸cão que mede a velocidade de um flu´ıdo é uma fun¸cão vetorial.

Em geral, uma fun¸cão vetorialF(x, y, z) especifica amagnitudee adire¸cão de cada ponto em uma região do espa¸co.

A figura 1.1 mostra uma fun¸cão vetorial como uma cole¸cão de setas, uma para cada ponto (x, y, z). A dire¸cão de cada seta em qualquer ponto é a dire¸cão especifica dada pela fun¸cão vetorial, o seu comprimento é proporcional a magnitude da fun¸cão. Uma fun¸cão vetorial pode ser representada através de suas componentes, como na figura 1.2. Seja i, j e k os vetores unitários ao longo dos eixos x, y ez, respectivamente, temos

F(x, y, z) = iFx(x, y, z) +jFy(x, y, z) +kFz(x, y, z).

(6)

Figura 1.1: exemplo

Figura 1.2: exemplo

As três quantidades Fx,Fy eFz, todas fun¸cões escalares de x,yez, são as três componentes

cartesianas1 _{da fun¸c˜ao vetorial} _F₍_{x, y, z}_).

Um exemplo de fun¸cão vetorial (em duas dimensões para simplificar) é

F(x, y) = ix+jy,

ilustrada na figura 1.3. Neste exemplo, a posi¸cão dos vetores são representados pelas setas, vemos que elas estão na posi¸cão radial (isto é, na dire¸cão de uma linha passando pela origem) e tem como comprimento sua distância da origem. Um segundo exemplo,

G(x, y) = p−iy+jx

x2₊_y2

1

(7)

1.2. GRADIENTE, DIVERGENTE E ROTACIONAL 7

Figura 1.3: exemplo

é mostrado na figura 1.4. Verificamos que para essa fun¸cão vetorial todas as setas estão na

Figura 1.4: exemplo

dire¸cão tangente (isto é, cada uma é tangente a um c´ırculo centrado na origem) e todos tem o mesmo comprimento.

1.2 Gradiente, Divergente e Rotacional

Seja F um campo escalar no espa¸co, se suas derivadas parciais existem ent˜ao elas formam as componentes do vetor gradF, o gradiente da fun¸c˜ao escalar F. Assim,

gradF =_∇F =i∂F

∂x +j ∂F

∂y +k ∂F

(8)

Exemplo 1

F(x, y, z) = x2y₋z2

gradF =_∇F =i∂F

∂x +j ∂F

∂y +k ∂F

∂z =i2x y+jx

2

−k2z.

A componente do gradiente em uma dada dire¸c˜ao representa a taxa de varia¸c˜ao de F

nessa dire¸c˜ao.

Propriedades do Gradiente

1. grad (F +G) = gradF + gradG

2. grad (F G) =F gradG+GgradF

3. cgradF =cgradF

Vamos provar a propriedade 2, as demais s˜ao deixadas como exerc´ıcio. Prova:

grad (F G) = i∂F G

∂x +j ∂F G

∂y +k

∂F G ∂z

= i(∂F

∂x G+F ∂G

∂x) +j( ∂F

∂y G+F ∂G

∂y) +k( ∂F

∂z G+F ∂G

∂z)

= (i∂F

∂x +j ∂F

∂y +k ∂F

∂z)G+F (i ∂G

∂x +j ∂G

∂y +k ∂G

∂z )

= GgradF +F gradG

Dado um campo vetorialV no espa¸co. Temos trˆes fun¸c˜oes escalaresVx, Vy e Vz. Se essas

três fun¸cões possu´ırem derivadas parciais primeira, a partir delas, constrói-se o escalar divV, a divergência de V, ou o divergente deV

divv =_{∇ ·}V = ∂Vx

∂x + ∂Vy ∂y + ∂Vz ∂z . Exemplo 2

V =ix2₋_j_{x y}₊_k_{x y z}

divV =_{∇ ·}V = ∂V

∂x + ∂V

∂y + ∂V

∂z = 2x−x+x y=x+x y.

Na dinâmica dos flu´ıdos, a divergência surge como uma medida da taxa de diminui¸cão da densidade num ponto. Mais precisamente, seja U = U(x, y, z) o vetor velocidade do movimento de um flu´ıdo e indiquemos por ρ = ρ(x, y, z, t) a densidade. Então V = ρ U é um vetor cuja a divergência satisfaz à equa¸cão

divV =₋∂ρ

∂t,

(9)

1.2. GRADIENTE, DIVERGENTE E ROTACIONAL 9

Propriedades da Divergˆ

encia

1. div (U+V) = divU+ divV

2. div (F V) =F divV + gradF _·V

onde F ´e um campo escalar e V ´e um campo vetorial. Vamos deixar a prova destas propriedade como exerc´ıcio.

O rotacional de um campo vetorial com derivadas parciais primeiras e dado pelo campo vetorial abaixo:

rotV =i

∂Vz ∂y − ∂Vy ∂z +j ∂Vx ∂z − ∂Vz ∂x +k ∂Vy ∂x − ∂Vx ∂y ou ainda,

rotV =_{∇ ×}V =

i j k

∂/∂x ∂/∂y ∂/∂z

Vx Vy Vz

O rotacional é importante na análise de campos de velocidades na mecânica dos flu´ıdos e na análise de campos de for¸cas eletromagnéticos. Podemos interpretar o rotacional como uma medida de movimento angular de um flu´ıdo, e a condi¸cão rotV = 0 para o campo de velocidades V caracteriza os chamados fluxos irrotacionais.

Propriedades do Rotacional

1. rot (U +V) = rotU+ rotV

2. rot (F V) = FrotV + gradF _×V

onde F ´e um campo escalar e V ´e um campo vetorial. Vamos deixar a prova destas propriedade como exerc´ıcio.

Combina¸c˜

oes de Opera¸c˜

oes

Quando se examinam as combina¸c˜oes poss´ıveis entre rot, div e grad chega-se a uma longa lista de identidades. Algumas da quais vamos considerar.

Rotacional de um gradiente

rot gradF = 0

∇ ×(_∇F) = 0 Divergˆencia de um rotacional

div rotV = 0

∇ ·(_{∇ ×}V) = 0 Divergˆencia de um gradiente

div gradF = ∂ 2_F

∂x2 +

∂2_F

∂y2 +

∂2_F

(10)

Uma fun¸cão F (que tem derivadas parciais segunda cont´ınuas) tal que div gradF = 0 é chamada harmônica. A equa¸cão

∂2_F

∂x2 +

∂2_F

∂y2 +

∂2_F

∂z2 = 0,

satisfeita por F, ´e chamada equa¸c˜ao de Laplace. Rotacional de um rotacional

rot rotU = grad divU ₋(i_∇2Ux+j∇2Uy+k∇2Uz)

Se definirmos o Laplaciano de um vetor U como sendo o vetor,

∇2U =i_∇2Ux+j∇2Uy+k∇2Uz

ent˜ao

rot rotU = grad divU _{− ∇}2U

e dessa forma,

grad divU = rot rotU +_∇2_U

1.3 Exerc´ıcios

1. Esbou¸car os seguintes campos vetoriais:

a) iy+jx; b) (i+j)/sqrt2;

c) ix₋jy; d) iy;

e) jx;

f) i(x2₋_y2₎2₊_j2_xy_; g) i(x₋y) +j(x+y); h) ₋iy+jx+k.

2. Esbou¸car as curvas ou superf´ıcie de n´ıvel:

a) f =xy;

b) f =x2₊_y2₋_z2_.

3. Determinar gradfpara os campos escalares do exerc´ıcio anterior e tra¸car alguns vetores correspondentes.

(11)

1.3. EXERC´ICIOS 11

5. Dado o campo vetorial v = 2xi +yj ₋ 3zk,verificar que divv = 0. Achar todos os vetores u tais que rotu = v.[Sugestão: Observar inicialmente que, em virtude de div(f u) = fdivu+ gradf _·u, todas as solu¸cões da equa¸cão rotu = v são dadas por

(12)

(13)

Cap´ıtulo 2

Integrais de Superf´ıcies e Divergˆ

encia

2.1 O vetor normal unit´

ario

A palavra normal nesse contexto deve ser linda como, perpendicular. Assim, um vetor n

normal ao planoxy ´e um vetor paralelo ao planoz (figura 2.1). Enquanto um vetor normal

Figura 2.1: exemplo

à esfera está na dire¸cão radial (figura 2.2). A defini¸cão precisa de um vetor normal a uma

Figura 2.2: exemplo

superf´ıcie, como mostra a figura 2.3. Considere uma superf´ıcie arbitrária S construa dois vetores não colineares u e v tangentes a S passando por um ponto p. Um vetor n que é perpendicular ao mesmo tempo aos vetores u e v por defini¸cão é normal à superf´ıcie S

no ponto p. Agora, sabemos que o vetor que resulta do produto vetorial entre u e v ´e perpendicular a ambos. Assim podemos escrever n=u_×v. Para tornar esse vetorunit´ario

(14)

Figura 2.3: exemplo

(isto ´e, ter comprimento igual a 1) ´e muito simples: basta dividi-lo por seu comprimento. Dessa forma,

n= u×v

|u_×v_|

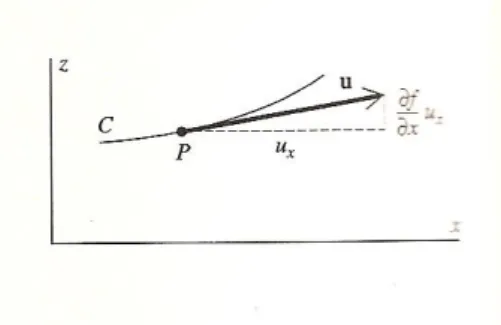
é umvetor normal unitárioà superf´ıcieS no pontoP. Vamos encontrar uma expressão para n. Considere a superf´ıcieSdada pela equa¸cãoz =f(x, y), figura 2.4. Assim, como sugerimos antes, vamos come¸car encontrando dois vetoresv eu. Para isso construa um plano paralelo

Figura 2.4: exemplo

ao plano-xy passando por P em S, como na figura 2.4. Este plano intersecta a superf´ıcie S

em uma curva C. Constru´ımos o vetor u tangente aC em P que tenha a componente x de comprimento arbitrário. A componente z deu é (∂f /∂x)ux; nesta expressão usamos o fato

da inclina¸cão de user a mesma, por constru¸cão da superf´ıcie S na dire¸cão x, ver figura 2.5. Assim

(15)

2.1. O VETOR NORMAL UNIT ´ARIO 15

u=iux+k

∂f ∂x

ux =

i+k

∂f ∂x

ux

Para encontrar o vetorv, passaremos um outro plano no pontoP emS, por´em neste caso o plano ser´a paralelo ao plano-yz (figura 2.6) Este intersecta S em uma curva C′_{, e o vetor}

Figura 2.6: exemplo

v ser´a constru´ıdo tangente a curva C′ _em _P _{com componente} _y _{de comprimento arbitr´ario}

vy. Temos

v=juy +k

∂f ∂y

uy =

j+k

∂f ∂y

uy.

Vamos calcular agora o produto vetorial entre u e v. O resultado,

u_×v=

−i

∂f ∂x

−j

∂f ∂y

+k

uxvy

´e um vetor que ´e normal a superf´ıcieS no pontoP, se dividirmos ele por sua norma teremos:

n= u×v

|u_×v_| =

−i ∂f_∂x

−j∂f_∂y+k

r

1 + ∂f_∂x2

+∂f_∂y2

. (2.1)

Este ´e o vetor normal unit´ario a uma superf´ıcie z =f(x, y) no ponto (x, y, z) da superf´ıcie. Note que esse vetor independe do valor das quantidadesux e vy.

Exemplo 3

Um primeiro exemplo trivial é: Qual o vetor normal unitário ao plano-xy? Claro que a resposta é k. Vejamos como variamos usando a equa¸cão 2.1. A equa¸cão do plano-xyé:

z =f(x, y) = 0,

Obviamente,

∂f /∂x= 0 e ∂f /∂y = 0.

Substitu´ındo na equa¸c˜ao 2.1 temos n=k/√1 =k.

Um segundo exemplo, considere a esfera de raio 1 centrada na origem, figura 2.2, A semi-esfera superior ´e dada por

(16)

Assim,

∂f ∂x =−

x

z e

∂f ∂y =−

y z

Usando a equa¸c˜ao 2.1

n= i

x z +j

y z +k

q

x2

z2 +

y2

z2 + 1

= pix+jy+kz

x2₊_y2₊_z2 =ix+jy+kz,

Como estamos usando a esfera unitária temos quex2₊_y2₊_z2 _{= 1. Assim, como já tinhamos} afirmado,né um vetor na dire¸cão radial com norma 1. Observe quen_·n=x2₊_y2₊_z2 _{= 1.} Agora que temos os vetores normais a nossa disposi¸cão podemos passar para a próxima questão, superf´ıcies integrais.

2.2 Defini¸c˜

ao de Superf´ıcie Integr´

aveis

Sejaz =f(x, y) a equa¸cão de uma superf´ıcie. Cosidere uma parcela limitada dessa superf´ıcie. que chamaremos deS (ver figura 2.7) Nosso primeiro passo na formula¸cão da defini¸cão dessa

Figura 2.7: exemplo

integral de superf´ıcie é aproximar S por um poliedro que consisti de N faces planas cada uma tangente a S em um ponto. A figura 2.8 mostra essa aproxima¸cão polinomial para um octante da esfera. Concentre sua aten¸cão em uma de suas faces planas, digamos a l

-Figura 2.8: exemplo

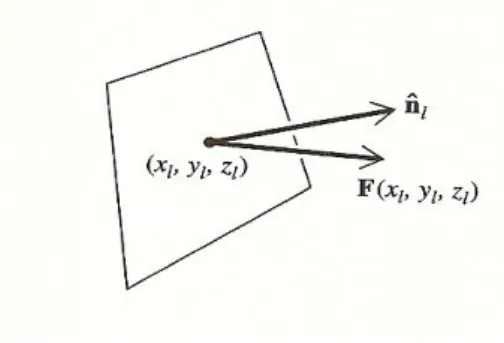
´esima face (figura 2.9). Denote a ´area dessa face por ∆Sl e seja (xl, yl, zl) as coordenadas do

(17)

2.2. DEFINIÇ ÃO DE SUPERFÍCIE INTEGR ÁVEIS 17

Figura 2.9: exemplo

produto com nl, o vetor normal unitário para al-ésima face. O resultado,F(xl, yl, zl)·nl, é

multiplicado pela ´area ∆Sl da face, temos

F(xl, yl, zl)·nl∆Sl

Repita esse processo para todas as N faces da aproxima¸c˜ao polinomial. Ent˜ao fa¸ca a soma de todas asN faces.

N

X

l=1

F(xl, yl, zl)·nl∆Sl.

A superf´ıcie integral

Z Z

S

F_·ndS ´e definida como o limite desta soma no n´umero de faces,

N, quando o n´umero de faces se aproxima de infinito a ´area de cada uma dessas faces se aproxima de zero. Assim,

Z Z

S

F_·ndS = lim

N→∞

cada ∆Sl_→0

N

X

l=1

F(xl, yl, zl)·nl∆Sl.

Muitas vezes encontramos integrais de superf´ıcies que s˜ao um pouco mais simples. Essas integrais s˜ao da forma

Z Z

S

G(x, y, z)dS,

onde o integrando G(x, y, z) ´e uma fun¸c˜ao escalar.

Agora aproximamosSnovamente por um poliedro, formamos os produtosG(xl, yl, zl)∆Sl,

somamos todas as faces, e ent˜ao passamos o limite:

Z Z

S

G(x, y, z)dS= lim

N→∞

cada ∆Sl_→0

N

X

l=1

G(xl, yl, zl)·∆Sl.

Um exemplo de integral de superf´ıcie simples ´e

Z Z

S

dS.

(18)

2.3 Calculando integrais de Superf´ıcies

Agora que já definimos a integral de uma superf´ıcie, vamos desenvolver métodos para calcula-las Por simplicidade come¸caremos calculando integrais de superf´ıcie onde o integrando é uma fun¸cão escalar. Para calcular a integral

Z Z

S

G(x, y, z)dS

considere a parte S da superf´ıcie z = f(x, y) (figura 2.10) Nossa estrat´egia ser´a relacionar

Figura 2.10: exemplo

∆Slcom a ´area ∆Rlda sua proje¸c˜ao no plano-xy, como mostra a figura 2.11 Relacionar ∆Sla

∆Rl não é dif´ıcil, se lembramos que (como na área de superf´ıcies planas) pode-se aproximar

com qualquer grau de exatidão desejado por um grupo de retângulos, como mostrado na figura 2.12. Por essa razão só iremos encontrar a rela¸cão entre a área de um retângulo e sua proje¸cão no plano-xy. Assim, considere um retângulo orientado de forma que dois dos seus lados seja paralelos ao plano-xy(figura 2.13). Se chamarmos o comprimento desses lado dea, claramente o comprimento das suas proje¸cões no plano-xyéa. Porém o outro par de lados, de comprimento b, tem proje¸cões de comprimentob′_{, e em geral}_b _e_b′ _{não são iguais. Assim}

para relacionarmos a área do triângulo ab coma área de sua proje¸cão ab′_{, basta expressar} _b

em termos de b′_{. Isto é fácil de fazer, se considerarmos o ângulo}_θ _{mostrado na figura 2.13,}

temos que b= _cosb′_θ, e assim

(19)

2.3. CALCULANDO INTEGRAIS DE SUPERF´ICIES 19

Se n denota o vetor normal unitário para o retângulo, então temos que cosθ = n_·k, onde ké sempre o vetor normal unitário que representa a dire¸cão positiva z. Dessa forma,

ab= ab

′

n_·k.

Assim cada áreaδSl pode ser aproximada por esses retângulos, isto é,

δSl =

δRl

nl·k ,

onde o vetornl é o normal unitário a l-ésima face da superf´ıcie.

Assim a defini¸c˜ao de integral de superf´ıcie fica

Z Z

S

G(x, y, z)dS = lim

N→∞

cada ∆Rl→0

N

X

l=1

G(xl, yl, zl)

∆Rl

n_·k,

onde substitu´ımos o ‘cada ∆Sl’ por ‘cada ∆Rl’ muito mais apropriado e conveniente.

Escre-veremos a integral da superf´ıcieS como uma integral sobre R. De fato,

lim

N→∞

cada ∆Rl_→0

N

X

l=1

G(xl, yl, zl)

∆Rl

n_·k =

Z Z

R

G(x, y, z)

n(x, y, z)_·kdxdy,

(20)

variável z em fun¸cão de x e y. Por esse motivo teremos que olhar para a representa¸cão da superf´ıcie z =f(x, y). E assim, tiramos a dependência de z da integral anterior,

Z Z

R

G[x, y, f(x, y)]

n[x, y, f(x, y)]_·kdxdy,

Nessa expressão a única dificuldade que nos resta é calcular n(x, y, f(x, y))_·k , para isso basta lembramos da expressão 2.1 para o vetor normal unitário de uma superf´ıcie. Dessa forma, encontramos,

n(x, y, f(x, y))_·k= r 1

1 + ∂f_∂x2

+∂f_∂y2

que nos leva a express˜ao:

Z Z

S

G(x, y, z)dS =

Z Z

R

G[x, y, f(x, y)]_·

s

1 +

∂f ∂x

2

+

∂f ∂y

2

dxdy.

Note que essa última integral está definida em uma região do plano-xy, e só contém expressões facilmente calculáveis.

Exemplo 4

Calcule a integral de superf´ıcie

Z Z

S

(x+z)dS

onde S ´e a parte do plano x+y+z = 1 que pertence ao primeiro octante, ver figura 2.14

A proje¸cão de S no plano-xy é o triângulo R mostrada na figura. A equa¸cão de S pode ser escrita como:

z =f(x, y) = 1₋x₋y

o que nos d´a,

∂f ∂x =

∂f

∂y =−1 e

s

1 +

∂f ∂x

2

+

∂f ∂y

2

(21)

Assim,

Z Z

S

(x+z)dS =√3

Z Z

R

(x+z)dxdy=√3

Z Z

R

(x+ 1₋x₋y)dxdy =√3

Z Z

R

(1₋y)dxdy,

onde usamos que z = 1₋x₋y.

√

3

Z Z

R

(1₋y)dxdy =√3

Z 1

0

Z 1−y

0

(1₋y)dxdy=√3

Z 1

0

(1₋y)x_|1−y

0 dy=

√

3

Z 1

0

(1₋y)2dy=√3(y−1) 3 3 | 1 0 = 1 √ 3 Exemplo 5

Calcule a integral de superf´ıcie

Z Z

S

z2dS

onde S ´e a parte da esfera de raio 1 que pertence ao primeiro octante, ver figura 2.15 A

proje¸cão deS no plano-xyé o quarto de circuloRmostrada na figura. A equa¸cão de S pode ser escrita como x2₊_y2₊_z2 _{= 1 ou}

z =f(x, y) =p1₋x2₋_y2_.

Assim temos que:

∂f ∂x =−

x

z e

∂f ∂z =−

y z, assim, s 1 + ∂f ∂x 2 + ∂f ∂y 2 = s 1 + x2 z2 2 + y2 z2 2 = 1 z p

x2₊_y2₊_z2 ₌ 1

z,

onde usamos que, em v´arios passos, x2₊_y2 ₊_z2 _{= 1. Assim,}

Z Z

S

z2dS =

Z Z

R

z21

zdxdy =

Z Z R zdxdy = Z Z R p

(22)

Para resolver essa equa¸c˜ao usaremos coordenadas polares x=rcosθ ey =rsenθ,

Z Z

R

p

1₋x2₋_y2_dxdy ₌

Z π2

0

Z 1

0

r√1₋r2_drdθ₌

Z π2

0 − 1 3(1−r

2₎3 2|1

0dθ =

Z π2

0 1 3dθ =

π

6.

Até o momento, tratamos de superf´ıcieSdescritas pela formaz =f(x, y). Nessa situa¸cão é conveniente resolver a integral sobre o plano-xy. Agora se a superf´ıcie é convenientemente escrita na formay=g(x, z) como mostra a figura 2.16. Analogamente ao feito anteriormente

chegamos a integral de superf´ıcie:

Z Z

S

G(x, y, z)dS =

Z Z

R

G[x, g(x, y), z]_·

s

1 +

∂g ∂x

2

+

∂g ∂z

2

dxdz.

onde R ´e uma regi˜ao do plano-xz.

Similarmente, se temos uma superf´ıcie descrita na forma x=h(y, z) como na figura 2.17 usamos

Z Z

S

G(x, y, z)dS =

Z Z

R

G[h(y, z), y, z]_·

s

1 +

∂h ∂y

2

+

∂h ∂z

2

dydz,

onde agora R ´e uma regi˜ao do plano-yz.

(23)

Vamos voltar ao nosso problema inicial, que era calcular o valor da integral de superf´ıcie sobre um campo vetorial,

Z Z

S

F_·ndS,

onde trocamos o campo escalar G(x, y, z) porF_·n . Pelo que j´a feito at´e agora,

Z Z

S

F_·ndS =

Z Z

R

F_·n

s

1 +

∂f ∂x

2

+

∂f ∂z

2

dxdy.

Novamente usando a express˜ao 2.1 para o vetor normal unit´ario n e que F = (Fx, Fy, Fz),

temos que

F_·n= −Fx[x, y, f(x, y)]

∂f

∂x−Fy[x, y, f(x, y)] ∂f

∂y +Fz[x, y, f(x, y)]

q

1 + ∂f_∂x2

+ ∂f_∂z2

Z Z

S

F_·ndS =

Z Z

R

−Fx[x, y, f(x, y)]

∂f

∂x −Fy[x, y, f(x, y)] ∂f

∂y +Fz[x, y, f(x, y)]

dxdy.

Onde lembramos que podemos fazer formulas an´alogas para superf´ıcies dadas pory=g(x, z) e x=h(y, z).

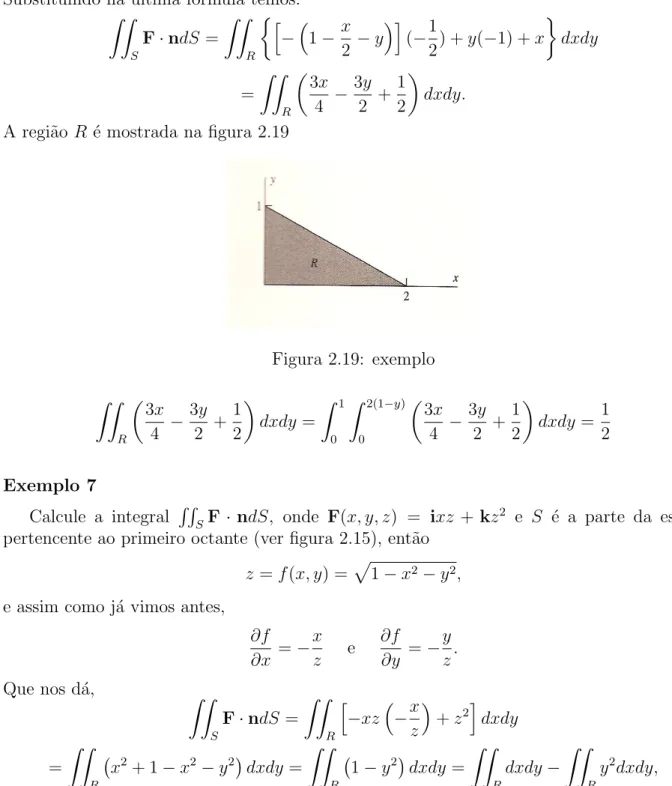
Exemplo 6

Calcule a integral RR

SF·ndS, ondeF(x, y, z) =iz−jy+kx e S ´e a parte do plano,

x+ 2y+ 2z = 2

limitado pelas coordenadas planas, isto ´e, o triˆangulo inclinado que mostra a figura 2.18. Assim temos,

z =f(x, y) = 1₋x 2 −y,

∂f ∂x =−

1 2 e

∂f

∂y =−1.

Que nos d´a,

Fx =z= 1−

x

(24)

Substituindo na ultima formula temos:

Z Z

S

F_·ndS =

Z Z

R

h

−1₋x 2 −y

i

(₋1

2) +y(−1) +x

dxdy = Z Z R 3x 4 − 3y 2 + 1 2 dxdy.

A regi˜ao R ´e mostrada na figura 2.19

Z Z R 3x 4 − 3y 2 + 1 2 dxdy= Z 1 0

Z 2(1−y)

0 3x 4 − 3y 2 + 1 2

dxdy= 1 2

Exemplo 7

Calcule a integral RR

SF· ndS, onde F(x, y, z) = ixz +kz

2 _e _S _{´e a parte da esfera} pertencente ao primeiro octante (ver figura 2.15), ent˜ao

z =f(x, y) =p1₋x2₋_y2_, e assim como j´a vimos antes,

∂f ∂x =−

x

z e

∂f ∂y =−

y z.

Que nos d´a,

Z Z

S

F_·ndS =

Z Z

R

h

−xz₋x z

+z2idxdy

=

Z Z

R

x2+ 1₋x2₋y2

dxdy=

Z Z

R

1₋y2

dxdy = Z Z R dxdy₋ Z Z R

y2dxdy,

onde a região R é mostrada na figura 2.15. Note que a primeira integral representa a área de um quarto do c´ırculo de raio 1, que é igual a π₄. Vamos aplicar coordenadas polares para resolver a outra integral,

Z Z

R

y2dxdy=

Z π₂

0

Z 1

0

r2sen2θrdrdθ =

Z π₂

0

sen2θdθ

Z 1

0

r3dr= π 16

Assim,

Z Z

S

F_·ndS = π 4 −

π

16 = 3π

(25)

2.4. A DIVERG ˆENCIA 25

2.4 A Divergˆ

encia

Considere a integral de superf´ıcie sobre o campo vetorial qualquerF:

Z Z

S

F_·ndS.

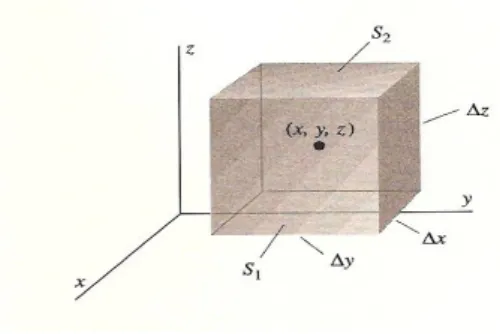
Vamos tentar encontrar uma rela¸c˜ao entre a integral de um campo e a divergˆencia desse campo. Assim, considere um cubo com lados ∆x, ∆y e ∆z paralelos aos eixos coordenados, figura 2.20. Suponha que o ponto central do cubo tenha coordenadas (x, y, z). Calculemos

a integral de superf´ıcie de F sobre a superf´ıcie do cubo. Essa integral pode ser dividida em 6 termos, onde cada uma ser´a uma face do cubo. Vamos come¸car considerando a face S1, indicada na figura 2.20, assim

Z Z

S1

F_·ndS.

O vetor normal unit´ario dessa face ´e claramente o vetor i. Temos assim que F_·i =Fx, e a

integral correspondente,

Z Z

S1

Fx(x, y, z)dS.

Suponha que esse cubo é tal pequeno quando necessário (eventualmente, faremos sua área tender a zero). Consequentemente, calculamos está integral aproximando o valor deFx pelo

seu valor no centro da face S1 e multiplicaremos pela ´area dessa face1. As coordenadas do centro de S1 s˜ao (x+ ∆x/2, y, z). Assim,

Z Z

S1

Fx(x, y, z)dS ≈Fx

x+∆x 2 , y, z

∆y∆z.

O mesmo procedimento pode ser aplicado a faceS2, porém o vetor normal unitário para essa face é₋i e o ponto central da face será (x₋∆x/2, y, z), assim,

Z Z

S2

F_·ndS =₋

Z Z

S2

Fx(x, y, z)dS ≈ −Fx

x₋ ∆x

2 , y, z

∆y∆z.

1

Existe um teorema do valor médio, que diz que a integral deFxsobreS1é igual a área deS1multiplicada

pela fun¸c˜ao calculada em algum ponto de S1. Desde que S1 seja suficientemente pequena o ponto onde

dever´ıamos calcularFx e o ponto central do cubo estarão suficientemente próximos, além disso, faremos a

´

(26)

Somando a contribui¸c˜ao dessas duas faces, temos que

Z Z

S1+S2

F_·ndS _≈

Fx

x+ ∆x 2 , y, z

−Fx

x₋ ∆x

2 , y, z

∆y∆z

= Fx x+ ∆x

2 , y, z

−Fx x− ∆₂x, y, z

∆x ∆x∆y∆z.

Considerando que ∆V = ∆x∆y∆z, o volume do cubo, temos que

1 ∆V

Z Z

S1+S2

F_·ndS _≈ Fx x+

∆x

2 , y, z

−Fx x− ∆₂x, y, z

∆x

Agora fa¸ca esse limite quando o valor de ∆V se aproxima de zero. Claramente quando o volume de ∆V tende a zero2_{, a mesma coisa acontece para cada lado do cubo. Assim do} lado direito da equa¸c˜ao temos que lim∆x→0 no lugar de lim∆V→0, e finalmente

lim ∆V→0

1 ∆V

Z Z

S1+S2

F_·ndS = lim ∆x→0

Fx x+∆₂x, y, z

−Fx x− ∆₂x, y, z

∆x =

∂Fx

∂x

em (x, y, z). Essa última igualdade segue da defini¸cão de derivadas parciais. Não deve ser nenhuma surpresa que os outros dois pares de faces do cubo contribuem com ∂Fy/∂y e

∂Fz/∂z. Assim,

lim ∆V→0

1 ∆V

Z Z

S

F_·ndS = ∂Fx

∂x + ∂Fy

∂y + ∂Fz

∂z .

O limite do lado esquerdo da última equa¸cão é a divergência de F. Assim demostramos, o que já hav´ıamos definido,

divF= ∂Fx

∂x + ∂Fy

∂y + ∂Fz

∂z .

2.5 A divergˆ

encia em coordenadas cil´ındricas e esf´

ericas

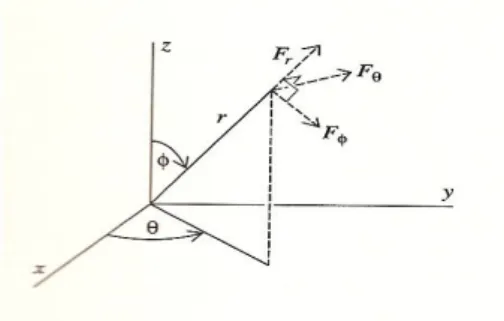
Agora ao invés de usarmos as coordenadas cartesianas para o calculo do da divergência usaremos outro sistema de coordenadas. Come¸caremos usando o sistema de coordenadas cil´ındricas. Neste sistema o campo vetorial Ftem três componentes que chamaremos deFr,

Fθ eFz, ver figura 2.21 Para obtermos a divergˆencia deFem coordenadas cil´ındricas, vamos

considerar ‘cubo cil´ındrico’ como mostra a figura 2.22 com volume ∆V =r∆r∆θ∆z e centro no ponto (r, θ, z)3_{. O fluxo de} _F_{na face 1 ´e}

Z Z

S1

F_·ndS =

Z Z

S1

FrdS ≈Fr

r+ ∆r

2 , θ, z r+ ∆r

2

∆θ∆z,

j´a na face 2,

Z Z

S2

F_·ndS =₋

Z Z

S2

FrdS ≈ −Fr

r₋ ∆r

2 , θ, z r− ∆r

2

∆θ∆z,

2

Note que a proposta ´e calcularmos esse mesmo limite em todas as faces do cubo.

3

Note que em coordenadas cartesianas 2.20 cada face do cubo tem ´e dada por uma equa¸c˜ao da forma,

(27)

2.6. O TEOREMA DA DIVERG ˆENCIA 27

Como fizemos no cubo, vamos somar as duas faces e dividir o resultado pelo seu volume,

Z Z

S1+S2

F_·ndS _≈ 1 r∆r

r+ ∆r 2

Fr

r+ ∆r 2 , θ, z

−

r₋∆r

2

Fr

r₋ ∆r

2 , θ, z

,

quando mandamos o limite de ∆r (consequentemente o de ∆V) para zero, temos

1

r ∂

∂r(rFr).

Fazendo o mesmo procedimentos para as outras 4 faces temos que a divergˆencia em coorde-nadas cil´ındricas ´e:

divF= 1

r ∂

∂r(rFr) +

1

r ∂Fθ

∂θ + ∂Fz

∂z . (2.2)

Em coordenadas esf´ericas as componentes deFs˜aoFr,FθeFφ(ver figura 2.23), procedendo

como no caso anterior temos que a divergência em coordenadas esférica é dada pela expressão,

divF= 1

r2

∂ ∂r(r

2_F

r) +

1

rsenφ ∂

∂φ(senφFφ) +

1

rsenφ ∂Fθ

∂θ . (2.3)

2.6 O Teorema da Divergˆ

encia

(28)

N˜ao daremos uma prova formal e rigorosa desse teorema, tal prova pode ser encontrada em um livro de calculo mais avan¸cado.

Considere um superf´ıcie fechada. Subdivida o volume V delimitado por S em N sub-volumes, isso ´e mostrado na figura 2.24(desenhamos um cubo por conveniˆencia). Come¸caremos

a prova afirmando que o fluxo de um campo vetorialF(x, y, z) sobre a superf´ıcieS ´e igual a soma dos fluxos de todas as superf´ıcies de cada sub-volume:

Z Z

S

F_·ndS =

N

X

l=1

Z Z

Sl

F_·ndS. (2.4)

Agora Sl´e a superf´ıcie fechada que tem sub-volume ∆Vl. Para estabelecermos a equa¸c˜ao

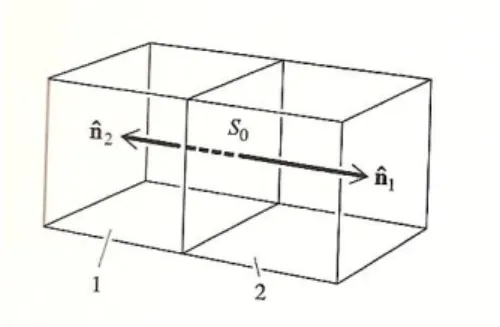
2.4, considere 2 sub-volumes adjacentes (ver figura 2.25). Seja S0 a face em comum a essas duas superf´ıcies. Claramente o fluxo nos dois sub-volumes tˆem suas contribui¸c˜oes na face

S0, ou seja, temos

Z Z

S0

F_·n1dS e Z Z

S0

F_·n2dS,

onde n1 é o vetor normal unitário a face S0, na conven¸cão usual, nos pontos do sub-volume

1. Já n2 é o vetor normal unitário as pontos do sub-volume 2. Claramente,n1=-n2.

Dessa forma, todos as faces comuns a dois sub-volumes iram se cancelar na soma da equa¸c˜ao 2.4, pois

Z Z

S0

F_·n1dS+ Z Z

S0

F_·n2dS = Z Z

S0

F_·n1dS− Z Z

S0

(29)

2.6. O TEOREMA DA DIVERG ˆENCIA 29

Como vimos todos esses termos são cancelados na equa¸cão 2.4, ou seja eles não contribuem na soma. De fato, isso acontece para qualquer dois sub-volume adjacentes. Mais toda superf´ıcie dos sub-volumes, salvo as que pertencem a superf´ıcie original, são adjacentes a alguma outra superf´ıcie de um outro sub-volume. Assim os únicos termos que não se cancelam na equa¸cão 2.4 são os que pertencem a superf´ıcie S. O que valida a equa¸cão 2.4.

Agora re-escreva a equa¸c˜ao 2.4 na seguinte forma curiosa:

Z Z

S

F_·ndS =

N

X

l=1

1 ∆Vl

Z Z

Sl

F_·ndS

∆Vl. (2.5)

Claramente, isto não altera nada desde que nós apenas multiplicamos o termo dividido da soma por ∆Vl, o sub-volume fechado pela superf´ıcie Sl. Nós agora podemos particionar o

volume original V em um número grande de sub-volumes cada vez menores. Em outras palavras, nós passamos o limite na soma da Equa¸cão 2.5 com o número de sub-divisões tendendo a infinito e cada ∆Vl tendendo para zero. Nós reconhecemos que o limite da

quantidade nos cubos da Equa¸cão 2.5 é, por defini¸cão (_{∇ ·}F)l, que é, a divergência de F

calculada em um ponto de ∆Vl que ´e pequeno. Assim, para cada ∆Vl realmente pequeno,

temos da Equa¸c˜ao 2.5 que

Z Z

S

F_·ndS =

N

X

l=1

(_{∇ ·}F) ∆Vl. (2.6)

No limite, essa soma, por defini¸c˜ao ´e a integral tripla de _{∇ ·}F sobre o volume fechado por

S:

lim

N→∞

cada ∆Vl→0

N

X

l=1

(_{∇ ·}F) ∆Vl ≡

Z Z Z

V ∇ ·

FdV.

Juntando a última equa¸cão com a equa¸cão 2.4, encontramos o resultado desejado:

Z Z

S

F_·ndS =

Z Z Z

V ∇ ·

FdV. (2.7)

(30)

a maior razão da prova dada não ser considerada rigorosa é que a integral tripla é definida como o limite de uma soma da forma:

N

X

l=1

g(xl, yl, zl)∆Vl,

onde a fun¸cão g é bem definida. Na equa¸cão 2.5, entretanto, o quantidade que multiplica o elemento de volume ∆Vl em cada termo da soma não é uma fun¸cão bem definida neste

sentido. Isto ´e, como ∆Vl tende a zero a quantidade nos cubos muda; pode ser identificada

como a divergência de F somente no limite. Felizmente, um estudo rigoroso mostra que a Equa¸cão 2.7 é valida se F (que é, Fx, Fy e Fz) é continua e diferenciável, e suas primeiras

derivadas s˜ao continuas emV e em S.

Vamos agora ilustrar o teorema da divergência. Para isso vamos resolver um exemplo simples. Seja F(x, y, z) = ix+jy+kz e escolha para S a superf´ıcie da figura 2.26, que é a semi-esfera de raio 1 e a região R do plano xy é limitada pelo circulo unitário. Neste hemisfério temos que n=ix+jy+kz, assimF_·n=x2₊_y2₊_z2 _{= 1. Neste hemisfério,}

Z Z

F_·ndS =

Z Z

dS = 2π,

onde a última igualdade segue do fato que a integral é meramente a área do hemisfério unitário. Na região R temos que n=₋k com issoF_·n=₋z,

Z Z

F_·ndS =₋

Z Z

z dx dy= 0,

pois z = 0 em toda região R. Dessa forma, não existe contribui¸cão da região circular R na integral de superf´ıcie e

Z Z

S

F_·ndS = 2π.

Por outro lado, trivialmente calculamos o _{∇ ·}F= 3. Segue que

Z Z Z

V ∇ ·

FdV = 3

Z Z Z

V

dV = 32π 3 = 2π

(31)

2.7 Exerc´ıcios

1. Encontre o vetor normal unit´ario nos seguintes casos:

a) z= 2₋x₋y; b) z= (x2₊_y2₎1/2_;

c) z= (1₋x2₎1/2_; d) z=x2₊_y2_;

e) z= (1₋x2_/a2₋_y2_/a2₎1/2_.

2. a) Mostre que o vetor normal unit´ario para o plano

ax+by+cz=d

´e dado por

n=_± ia+jb+kc (a2₊_b2₊_c2₎1/2

b) Explique geometricamente por que o vetor normal n˜ao depende da constante d.

3. Calcule a integral de superf´ıcie RR

SG(x, y, z)dS

a) G(x, y, z) = z, onde S ´e a parte do plano x+y+z = 1 no primeiro octante;

b) G(x, y, z) = 1

1 + 4(x2₊_y2₎, onde S ´e a parte do paraboloide z = x

2 ₊_y2 _entre

z= 0 e z = 1;

c) G(x, y, z) = (1₋x2₋y2)3/2, onde S ´e o hemisf´erio z = (1₋x2₋_y2₎1/2_.

4. Calcule a integral de superf´ıcie

Z Z

S

F_·ndS

a) F(x, y, z) =ix₋kz, ondeSé a parte do planox+y+ 2z = 2 no primeiro octante; b) F(x, y, z) =ix+jy+kz, onde S é o hemisfério z = (1₋x2₋_y2₎1/2_;

c) F(x, y, z) =jy+k, ondeS ´e a parte do paraboloidez = 1₋x2₋_y2 _{no plano-}_xy_.

5. `As vezes as integrais de superf´ıcie podem ser calculadas sem usar os procedimentos

esbo¸cados no texto. Calcule

Z Z

S

F_·ndS para cada item abaixo. Pense um pouco e evite muito trabalho!

(32)

Figura 2.27: exerc´ıcio

b) F= (ix+jy) ln(x2₊_y2_{), onde} _S _{´e o cilindro (incluindo o fundo e o topo) de raio}

R e alturah, como mostra a figura 2.28;

c) F = (ix+jy+kz)e−x2+y2+z2_{, onde} _S _{´e a esfera de raio} _R _{centrada na origem,}

como mostra a figura 2.29;

d) F=iE(x), onde E(x) é um fun¸cão escalar qualquer que só depende dex. E S é o cubo de ladob, como mostra a figura 2.30.

(33)

vetores unit´arios em coordenadas cil´ındricas. Mostre que

i = ercosθ−eθsenθ,

j = ersenθ−eθcosθ,

k = ez.

b) Escreva a fun¸cão (₋ixy+jx2)/(x2+y2), onde (x, y) ₆= (0,0), em coordenadas cil´ındricas e calcule sua divergência utilizando a equa¸cão 2.2.

7. a) Sejam i, j e k os vetores unit´arios em coordenadas cartesianas e er, eθ, e eφ os

vetores unit´arios em coordenadas esf´ericas. Mostre que

i = ersenφcosθ+eφcosφcosθ−eθsenθ,

j = ersenφsenθ+eφcosφsenθ+eθcosθ,

k = ercosθ−eφsenφ.

[Sugestão: É mais fácil expressar er, eθ, e eφ em termos de i, j e k e a seguir

resolve algebricamente para i, j e k. Para fazer isto, use primeiramente que er = r/r = (ix +jy + kz)/r. Depois, resolva geometricamente, mostre que

eθ =−isenθ+jcosθ. Finalmente, calcule eφ =eθ×er ]

b) Escreva a fun¸cão ix+jy+kz, em coordenadas esféricas e calcule sua divergência utilizando a equa¸cão 2.3.

8. Verifique o teorema da divergˆencia

Z Z

S

F_·ndS =

Z Z Z

V ∇ ·

FdV

para os seguintes casos:

a) F=ix+jy+kz, ondeS s˜ao os quadrados de lado b, mostrados a figura 2.30; b) F= err+ezz), r = ix+jy e S ´e um quarto do cilindro (de raio R e altura h),

como mostra a figura 2.31;

c) F=err2, r=ix+jy+kz, ondeS ´e a esfera de raioR centrada na origem, como

(34)

9. a) Use o teorema da divergˆencia para mostrar que

1 3

Z Z

S

n_·rdS =V,

onde S é fechada que limita uma região de volume V, n é um vetor unitário normal a superf´ıcie S, er=ix+jy+kz.

b) Use a express˜ao dada no item a) para encontrar o volume de: i) um paralelep´ıpedo de lados a, b ec.

ii) um cone circular com altura h e base de raio R. [Sugest˜ao: O calculo ´e simples com o cone orientado como mostra a figura 2.32].

(35)

Cap´ıtulo 3

Integral de Linha e o Rotacional

3.1 Trabalho e Integral de Linha

A propriedade dos campos eletrostáticos que nós come¸caremos agora a discutir está intima-mente ligada com a pergunta do trabalho e da energia. Você se lembra da defini¸cão elementar de trabalho, for¸ca vezes distância. Assim, em uma dimensão, se a for¸caF(x) atua de x=a

para x=b, o trabalho ´e dado, por defini¸c˜ao,

Z b

a

F(x)dx.

Para podermos falar de uma situa¸c˜ao mais geral, devemos introduzir o conceito de integral de linha.

Figura 3.1: exemplo

Suponha que tenhamos uma curva em três dimensões (figura 3.1) e suponha que essa curva seja direcionada. Isso significa que colocamos uma seta sobre a curva e definimos esse sentido como o positivo. Seja s um comprimento de arco ao longo da curva medido de algum ponto arbitrário nela com s = s1 em um ponto P1 e s = s2 em P2. Suponha que tenhamos uma fun¸cão f(x, y, z) definida sobre essa curva, C. Subdivida a curva C entreP1 e P2 em N peda¸cos arbitrários. A figura 3.1 mostra um exemplo com 4 subdivisões. Em seguida, junte os pontos sucessivos da subdivisão por segmentos de reta, diga que l-ésimo, tem comprimento ∆Sl. Agora, calcule o valor de f(x, y, z) em (xl, yl, zl), qualquer ponto na

(36)

l-´esima subdivis˜ao da curva, e fa¸ca o produtof(x, y, z) ∆Sl. Feito isso para cada um dos N

segmentos de C, fa¸ca a soma

N

X

l=1

f(x, y, z) ∆Sl.

Por defini¸cão, a integral de linha de f(x, y, z) ao longo da curva C é o limite dessa soma quando o numero de subdivisõesN se aproxima do infinito fazendo o o comprimento de cada arco se aproximar a zero:

Z

C

f(x, y, z)ds= lim

N→∞

cada ∆Sl_→0

N

X

l=1

f(x, y, z) ∆Sl.

Para calcular a linha integral, precisamos saber o caminho de C. Geralmente a maneira mais conveniente de especificar este caminho ´e usar s para parametriza-lo via comprimento de arco. Assim, escrevemos x = x(s), y = y(s) e z = z(s). Neste caso, a integral de linha se reduz a:

Z

C

f(x, y, z)ds =

Z s2

s1

f(x(s), y(s), z(s))ds.

Vamos ver um exemplo, por simplicidade trabalharemos em duas dimens˜oes, calcule

Z

C

(x+y)ds,

onde C ´e a linha reta que sai da origem at´e a coordenada (1,1), ver figura 3.2. Se (x, y)

Figura 3.2: exemplo

são a coordenada de qualquer pontoP em C e se s é a medida do seu comprimento de arco desde a origem, então x=s/√2 e y=s/√2. Dessa forma, x+y= 2s/√2 = √2s. Assim,

Z

C

(x+y)ds =√2

Z √2

0

s ds=√2.

Vamos integrar agora a mesma fun¸c˜ao x+y de (0,0) para (1,1) considerando as subdi-vis˜oes mostradas na figura 3.3. Temos que separar a integral em duas partes, ao longo de

C1, e ao longo de C2. Em C1 temos x=s ey= 0. Assim, x+y =s, e

Z

C1

(x+y)ds =

Z 1

0

(37)

3.2. INTEGRAL DE LINHA ENVOLVENDO CAMPO VETORIAL 37

Figura 3.3: exemplo

Ao longo de C2,x= 1 e y =s, note que o comprimento de arco desse segmento ´e medido a partir do ponto (1,0). Segue que,

Z

C2

(x+y)ds=

Z 1

0

(1 +s)ds= 3 2.

Somando os dois resultados temos que,

Z

C

(x+y)ds=

Z

C1

(x+y)ds+

Z

C2

(x+y)ds= 1 2+

3 2 = 2.

A li¸cão a ser aprendida é esta: o valor de uma integral pode (geralmente) depender do caminho de integra¸cão.

3.2 Integral de Linha Envolvendo Campo Vetorial

Embora a discussão precedente nos diga o que é uma integral de linha, o tipo de integral de linha que nós devemos tratar aqui tem uma caracter´ıstica que ainda não foi mencionada. Nós introduzimos as integrais de linha através do conceito de trabalho. Trabalho, no sentido mais elementar, é o deslocamento da for¸ca no tempo. Essa elabora¸cão torna-se mais clara quando reconhecemos que for¸ca e deslocamento são vetores.

Assim, considere uma parti¸cão da curva C em três dimensões (figura 3.4). Vamos supor

(38)

que sob a a¸cão de uma for¸ca um objeto se move neste caminho des1 para s2. Em qualquer ponto P da curva designaremos f(x, y, z) como a a¸cão dessa for¸ca. A componente de f que exerce o trabalho é, por defini¸cão, simplesmente a que atua ao longo da curva, isto é, a componente tangencial. Sejat o vetor unitário que é tangente a curva no ponto P 1_{. Então} o trabalho realizado pela for¸ca em mover o objeto de s1 para s2 ao longo da curva C é

T =

Z

C

f(x, y, z)_·tds,

onde se compreende, naturalmente, que a integra¸cão come¸ca ems=s1 e termina ems =s2. A nova caracter´ıstica desta integral é que o integrando é o produto escalar de duas fun¸cões vetoriais. Para avaliarmos essa integral devemos saber encontrar t, e é esse o problema que tentaremos resolver agora.

Considere um curva arbitr´aria C (ver figura 3.5) parametrizada pelo comprimento de arco. Em algum ponto s na curva temos que x =x(s), y = y(s) e z =z(s). Em um outro

Figura 3.5: exemplo

pontos+ ∆s temosx+ ∆x=x(s+ ∆s),y+ ∆y=y(s+ ∆s) ez+ ∆z =z(s+ ∆s). Assim, o segmento de reta que une os dois pontos na curva direcionada do primeiro ao segundo ´e o vetor ∆r=i∆x+j∆y+k∆z, onde

∆x = x(s+ ∆s)₋x(s),

∆y = y(s+ ∆s)₋y(s),

∆z = z(s+ ∆s)₋z(s).

Se dividirmos esse vetor por ∆s, temos

∆r ∆s =i

∆x

∆s +j

∆y

∆s +k

∆z

∆s

Tomando o limite quando ∆s se aproxima de zero, temos

idx

ds +j dy ds +k

dz ds

1_t

(39)

3.2. INTEGRAL DE LINHA ENVOLVENDO CAMPO VETORIAL 39

afirmamos que esse limite é o campo t. Para come¸car, é claro que quando ∆s _→0, o vetor ∆rtangência a curva s. Além disso, no limite ∆s _→0, vemos que_|∆r_→∆s_|. Portanto, no limite a norma deste vetor é 1. Segue que

t=idx

ds +j dy ds +k

dz ds

Se retornarmos agora a express˜ao do trabalho T e usarmos a formula de t, encontramos

T =

Z

C

f(x, y, z)_·tds =

Z

C

f(x, y, z)_·

idx

ds +j dy ds +k

dz ds ds = Z C

(fxdx+fydy+fzdz).

Esta é uma expressão formal; frequentemente, para realizar a integra¸cão, é útil restaurar o

ds como ilustra o exemplo a seguir. Considere

f(x, y, z) = iy₋jx

e a curva mostrada na figura 3.6. Para calcular R

C(f ·t)ds neste caso, divida a curvaC em

trˆes partes, C1,C2 eC3 como mostramos. Considerando fz = 0, temos

Figura 3.6: exemplo

Z

C

f _·tds =

Z

C

fxdx+fydy =

Z

C

y dx₋x dy

Agora, em C1, y = 0 e dy = 0, assim C1 não contribui na integral. Similarmente, em C3 temos x = 0 e dx = 0, o que dá resultado igual a zero. Assim, a única contribui¸cão para a integral sobre C e a parte emC2. Restaurando o ds, temos

Z

C

ydx ds −x

dy ds

ds.

Mas (1₋x)/s= cos 450 _{= 1}_/√_{2 e (1}₋_x₎_/s_{= sen 45}0 _{= 1}_/√_{2 (figura 3.7). Assim,}

x= 1₋ √s

2 ⇒

dx ds =−

1

√

2

y= _√s 2 ⇒ dy ds = 1 √ 2         

(40)

Figura 3.7: exemplo

Dessa forma, a integral ´e

Z √

2

0

s

√

2

−√1

2

−

1₋ _√s 2

1

√

2

ds=₋_√1 2

Z √

2

0

ds =₋1.

Um segundo exemplo de integral de linha envolvendo fun¸c˜oes vetoriais, seja

f(x, y, z) =ix2₋jxy,

e tome C o quarto de circulo de raio R orientado como mostra a figura 3.8. Ent˜ao temos

Figura 3.8: exemplo

Z

C

f _·tds=

Z

C

x2dx₋xy dy.

Considerando x=Rcosθ,y =Rsenθ, encontramos esta integral como

Z π/2

0

[R2cos2θ(₋Rsenθ)₋R2senθcosθ(Rcosθ)]dθ=₋2R3

Z π/2

0

(41)

3.3. O ROTACIONAL 41

3.3 O Rotacional

Se nós é dado uma fun¸cão vetorial F(x, y, z) e perguntado, “ Poderia ser esse um campo eletrostático?”, podemos, a principio, responder. Se

I

F_·tds₆= 0

sobre uma curva entãoF não pode ser um campo eletrostático. Se

I

F_·tds= 0

sobre qualquer curva fechada, então F pode (mas não tem que ser) ser um campo ele-trostático. Claramente, este critério não é fácil de aplicar, pois devemos saber que a cir-cula¸cão de Fé zero sobre todos os caminhos poss´ıveis.

Vamos tentar encontrar um critério mais útil. Considere a circula¸cão de F em um retângulo pequeno paralelo ao planoxy, com lados ∆x e ∆ye com o ponto central (x, y, z), ver figura 3.9 Como é mostrado na figura 3.9, faremos a integra¸cão no sentido anti-horário de que olha de cima do plano xy. Vamos quebrar essa integral de linha em quatro par-tes: CB (parte inferior), CR (lado direito), CL (lado direito) e CT (parte superior). Essa

Figura 3.9: exemplo

retângulo é pequeno (eventualmente no limite faremos ele tender a zero), nós aproximare-mos a integral sobre cada segmento por F_·t avaliado no centro do segmento, multiplicado pelo comprimento do segmento2_.

Consideraremos CB primeiro, temos que

Z

CB

F_·tds =

Z

CB

Fxdx∼=Fx

x, y₋ ∆y

2 , z

∆x. (3.1)

EmCT encontramos,

Z

CT

F_·tds =

Z

CT

Fxdx∼=−Fx

x, y+∆y 2 , z

∆x. (3.2)

2

(42)

O sinal negativo aqui se refere ao fato que

Z

CT

Fxdx=

Z

CT

Fx

dx ds ds

e dx/ds=₋1 emCT. Somando as equa¸c˜oes 3.1 e 3.2 temos,

Z

CT+CB

F_·tds ∼= −

Fx

x, y+∆y 2 , z

∆x₋Fx

x, y₋ ∆y

2 , z

∆x ∼ = − Fx

x, y+ ∆y 2 , z

−Fx

x, y₋∆y

2 , z

∆y ∆x∆y.

Claramente ∆x∆yé a área de ∆S do retângulo. Assim,

1 ∆S

Z

CT+CB

F_·tds∼=₋

Fx

x, y+∆y 2 , z

−Fx

x, y₋ ∆y

2 , z

∆y . (3.3)

Exatamente a mesma an´alise se aplica ao lado esquerdo e direito do retˆangulo (CLeCR)

resultando em

1 ∆S

Z

CL+CR

F_·tds ∼=

Fy

x+ ∆x 2 , y, z

−Fy

x₋ ∆x

2 , y, z

∆x . (3.4)

Fazendo a soma da equa¸c˜oes 3.3 e 3.4 e tomando o limite quando ∆S se fecha sobre o ponto (x, y.z) (neste caso, ∆x e ∆y_→0 ao mesmo tempo), encontramos

lim ∆S→0 sobre (x,y,z)

1 ∆S

Z

F_·tds= ∂Fy

∂x − ∂Fx

∂y ,

onde estamos considerando a circula¸cão em torno do retângulo pequeno. Você pode querer se perguntar sobre a generalidade e a unicidade deste resultado pois ele é obtido usando uma curva especial para a integra¸cão: primeiro, um retângulo, e segundo, ele é paralelo ao plano

xy. Se a curva não for um retângulo, mas uma curva plana da forma arbitrária, não afetaria nosso resultado (exerc´ıcios 1 e 12). Mas nosso resultado definitivamente depende em especial da orienta¸cão da curva na integra¸cão. A escolha da orienta¸cão A escolha da orienta¸cão feita acima sugere claramente duas outras, que são mostradas na figura 3.10 junto com o resultado do cálculo, para cada uma de

lim ∆S→0

sobre (x,y,z) 1 ∆S

Z

F_·tds.

(43)

3.3. O ROTACIONAL 43

sempre a esquerda, como mostra a figura 3.11. Então escolha o vetor normal de modo que ele aponte para “acima” no sentido mostrado na figura 3.11. Esta conven¸cão é chamada da regra da mão direita, para que se a mão direita é orientada de modo que os dedos ondulem no sentido em que a curva é seguida, o polegar, estendido, aponte no sentido do vetor normal (figura 3.11). Usando a regra da mão direita, temos o seguinte:

calculando lim ∆S→0

I

F_·t ds ∆S

para uma curva `a qual o normal ´ei, temos ∂Fz

∂y − ∂Fy

∂z ,

para uma curva `a qual o normal ´ej, temos ∂Fx

∂z − ∂Fz

∂x ,

para uma curva `a qual o normal ´ek, temos ∂Fy

∂x − ∂Fx

∂y ,



        

        

(3.5)

Dizemos que essas trˆes quantidades s˜ao as coordenadas cartesianas do vetor. Daremos o nome a este vetor de o “rotacional de F”, que escreveremos como rotF. Assim, temos que

rotF=,i

∂Fz

∂y − ∂Fy

∂z

+j

∂Fx

∂z − ∂Fz

∂x

+k

∂Fy

∂x − ∂Fx

∂y

(44)

Esta expressão é frequentemente é dada como a defini¸cão do rotacional, mas nós preferi-mos considerá-la meramente como o forma do rotacional em coordenadas cartesianas. Nós definiremos o rotacional como o limite da circula¸cão quando a área tende a zero. Mas

preci-samente, seja

Z

Cn

F_·tds a circula¸c˜ao de F sobre uma curva com normal n como mostra a

figura 3.12. Ent˜ao por defini¸c˜ao

n_·rotF= lim ∆S→0 sobre (x,y,z)

1 ∆S

I

F_·tds.

Tomandon sucessivamente igual ai, jek, temos de volta o resultado dado na Equa¸cão 3.6. Esse limite, em geral, tem valores diferentes para pontos (x, y, z) diferentes, o rotacional de Fé a fun¸cão vetorial da posi¸cão 3_{. Embora em nosso trabalho supomos sempre que a área} delimitada pela curva de integra¸cão é plana, isto, necessariamente não precisa acontecer. Desde que o rotacional seja definido em termos de um limite no qual a superf´ıcie fechada se aproxime de zero para qualquer ponto, no estagio final desse processo de limite a superf´ıcie fechada é infinitessimalmente próxima do plano, e todas as considera¸cões feitas se aplicam.

A expressão 3.6 dada para o rotF em coordenadas cartesianas é quase imposs´ıvel de ser lembrada, por sorte existe uma forma mais fácil de memoriza-la. Se expandirmos o determinante de

i j k

∂/∂x ∂/∂y ∂/∂z

Fx Fy Fy

e se certos “produtos” s˜ao interpretados como derivadas parciais (por exemplo, (∂/∂x)Fy =

∂Fy/∂x), o resultado é idêntico ao dado na expressão 3.64. Assim, a angústia de recordar a

fórmula de rotFem coordenadas cartesianas pode ser substitu´ıda pela dor de recordar como expandir o determinante três por três. A vontade do cliente.

3

A palavrarota¸cão(abreviada “rot”) já foi usada para o que nós chamamos agora de rotacional. Embora esse terno tenha deixado de ser usado a muito tempo: Se rotF_{= 0, a fun¸c˜}_aoF_{é dita irrotacional.}

4

(45)

3.4. O ROTACIONAL EM COORDENADAS CIL´INDRICAS E ESF ´ERICAS 45

Um exemplo de calculo do rotacional, considere a fun¸c˜ao vetorial

F(x, y, z) = ixz+jyz₋ky2.

Temos,

rotF=

i j k

∂/∂x ∂/∂y ∂/∂z

xy yz ₋y2

=i(₋2y₋y) +j(x₋0) +k(0₋0) =₋3iy+jx.

Você pode ter observado que o operador rotacional pode ser escrito em termos da nota¸cão com delta que introduzimos anteriormente. Você mesmo pode verificar que

rotF=_{∇ ×}F,

que ´e lida “delta versos F”. A partir de agora usaremos_{∇ ×}F para indicar o rotacional.

3.4 O Rotacional em Coordenadas Cil´ındricas e Esf´

ericas

Para obtermos a forma do_{∇ ×}Fem outro sistema de coordenadas procederemos da mesma maneira que fizemos para coordenadas cil´ındricas, meramente usaremos a curva para inte-gra¸cão apropriada. Como um exemplo, usaremos o caminho mostrado na figura 3.14 isso nos dará a componentez do_{∇ ×}Fem coordenadas cil´ındricas5_{. Note que o tra¸co da curva está} em concordância com a regra da mão direita dada na outra se¸cão. Vendo a curva de acima (como nós fazemos na figura 3.14), a integral de linha deF(r, θ, z)_·t ao longo do segmento

do caminho marcado 1 ´e

Z

C1

F_·tds _≃Fr

r, θ₋ ∆θ

2 , z

∆r,

5

Analogamente a forma cartesiana de ∇ ×F_{, cada curva de integra¸c˜}_{ao (ver figuras 3.9 e 3.10) tem a}

(46)

enquanto oo longo do segmento 3 temos

Z

C3

F_·tds _{≃ −}Fr

r, θ+ ∆θ 2 , z

∆r.

A ´area limitada pela curva ´er∆r∆θ, e

1 ∆S

Z

C1+C3

F_·tds_{≃ −} ∆r r∆r∆θ

Fr

r, θ+ ∆θ 2 , z

−Fr

r, θ₋ ∆θ

2 , z

.

No limite quando ∆r e ∆θ tendem a zero, isto ´e

−1_r_∂θFr

avaliado no ponto (r, θ, z).

Ao longo do segmento 2 encontramos

Z

C2

F_·tds _≃Fθ

r+∆r

2 , θ, z r+ ∆r

2

∆θ,

e ao longo do segmento 4

Z

C4

F_·tds_{≃ −}Fθ

r₋ ∆r

2 , θ, z r− ∆r 2 ∆θ. Assim, 1 ∆S Z

C2+C4

F_·tds_{≃ −} ∆θ r∆r∆θ

r+ ∆r 2

Fθ

r+∆r 2 , θ, z

−

r₋ ∆r

2

Fθ

r₋∆r

2 , θ, z

.

No limite temos (1/r)(∂/∂r)(rFθ) avaliado em (r, θ, z). Dessa forma,

(_{∇ ×}F)z ≡ lim

∆S→0

I

C

F_·tds= 1

r ∂

∂r(rFθ)−

1

r ∂Fr

∂θ .

Para encontrar as componentes r e θ de _{∇ ×}F os caminhos s˜ao mostrados na figura 3.14, respectivamente. Deixaremos como exerc´ıcio a obten¸c˜ao dessas duas componentes.

Para completar as trˆes componentes do _{∇ ×}Fem coordenadas cil´ındricas s˜ao dadas por:

(_{∇ ×}F)r =

1 r ∂Fz ∂θ − ∂Fθ ∂z ,

(_{∇ ×}F)θ =

∂Fr

∂z − ∂Fr

∂r ,

(_{∇ ×}F)z =

1

r ∂

∂r(rFθ)−

1

r ∂Fr

∂θ .

Vamos calcular um exemplo de rotacional em coordenadas cil´ındricas, considere a fun¸c˜ao

(47)

3.4. O ROTACIONAL EM COORDENADAS CIL´INDRICAS E ESF ´ERICAS 47

ent˜ao

(_{∇ ×}F)r =

1

r ∂ ∂θ(r

3₎

−_∂z∂ (rz2cosθ) =₋2rzcosθ,

(_{∇ ×}F)θ =

∂ ∂z(r

2_z₎

− _∂r∂ (r3) =₋2r2,

(_{∇ ×}F)z =

1

r ∂ ∂r(r

2_z2_cos_θ₎₋1

r ∂ ∂θ(r

2_z_{) = 2}_z2_cos_θ,

portanto

∇ ×F=₋2errzcosθ−2eθr2+ 2ezz2cosθ.

As três componentes do rotFem coordenadas esféricas são as seguintes:

(_{∇ ×}F)r =

1

rsenφ ∂

∂φ(senφFθ)−

1

rsenφ ∂Fφ

∂θ ,

(_{∇ ×}F)φ =

1

rsenφ ∂Fr

∂θ −

1

r ∂

∂r(rFθ),

(_{∇ ×}F)θ =

1

r ∂

∂r(rFφ)−

1

r ∂Fr

∂φ.

Vamos calcular um exemplo de rotacional em coordenadas esf´ericas, considere a fun¸c˜ao

F(r, θ, φ) = er

rθ +

eφ

r +

eθ

rcosφ

ent˜ao

(_{∇ ×}F)r =

1

rsenφ ∂ ∂φ

senφ 1 rcosφ

− _r_sen1 _φ ·0 = sec 2_φ

r2_sen_φ,

(_{∇ ×}F)φ =

1

rsenφ ∂ ∂θ 1 rθ

−1_r_∂r∂ (cosφ) =₋ 1

r2_θ2_sen_φ,

(_{∇ ×}F)θ =

1

r ∂ ∂r(1)−

1 r ∂ ∂φ 1 rθ

(48)

Assim

∇ ×F= sec 2_φ

r2_sen_φer− 1

r2_θ2_sen_φeφ.

3.5 O Teorema de Stokes

Nos concentraremos a partir de agora em um famoso teorema. Este teorema, que tem o nome do matemático Stokes, relaciona uma integral de linha em torno de um caminho fechado a uma integral da superf´ıcie sobre o que é chamado uma “superf´ıcie cobrindo” o caminho, assim a primeira coisa a fazermos é definir este termo. Suponha que tenhamos uma curva fechada C, como mostra a figura 3.15, e imagine que ela é feita de fio. Agora suponha que

n´os anexamos uma membrana el´astica ao fio como indicado na figura 3.16. Essa membrana

é uma “superf´ıcie cobertura” da curva C. Qualquer outra superf´ıcie que possa ser formada esticando a membrana é uma “superf´ıcie cobrindo”; um exemplo é mostrado na figura 3.17. A figura 3.18 mostra quatro diferentes superf´ıcies cobertura de um caminho plano: (a) a

(49)

3.5. O TEOREMA DE STOKES 49

Após essas notas prévias, você não será surpreendido ao nós ver come¸car o teorema de Stokes considerando uma curva fechada C e uma superf´ıcie cobertura S (ver figura 3.19) Como temos feito anteriormente, aproxime essa superf´ıcie cobertura por poliedros de N

faces, onde cada um ´e tangente a S em apenas um ponto (ver figura 3.20). Note que com

isso automaticamente criamos uma poligonal (marcada com P na figura 3.20) que é uma aproxima¸cão para a curva C. Seja F(x, y, z) uma fun¸cão vetorial bem comportada definida em toda a região do espa¸co ocupada pela curva C e pela superf´ıcie coberturaS. Considere a circula¸cão de F em torno deCl, o bordo da l-ésima face do poliedro:

I

Cl

F_·tds.

Se nós fazemos isto para cada um das faces do poliedro e então adicionamos juntas todas as circula¸cões, afirmamos que esta soma será igual à circula¸cão de Fem torno da poligonal P:

N

X

l=1

I

Cl

F_·tds=

I

P

(50)

Isto n˜ao ´e dif´ıcil de ser provado. Considere duas faces adjacentes como mostra a figura 3.21.

A circula¸c˜ao em torno da face do lado esquerdo inclui o segmento AB, que ´e

Z B

A

F_·tds.

Mas o segmento ABé comum a ambas as faces, e contribui também para circula¸cão da face do lado direito que é

Z A

B

F_·tds =₋

Z B

A

F_·tds.

Note que o segmento AB tem uma dire¸cão na face a esquerda, e a dire¸cão contrária na face a direita. Dessa forma, quando olharmos a contribui¸cão do segmento AB na circula¸cão de F observamos que

Z B

A

F_·tds+

Z A

B

F_·tds= 0.

Dessa forma, se torna claro que qualquer segmento comum a duas faces adjacentes não con-tribui na soma da equa¸cão 3.7 porque tais segmentos sempre vem em pares que se cancelam. Mas todos os segmentos são comuns a pares de faces adjacentes exceto aqueles, somados juntos, que constituem a poligonalP. Isso estabelece a equa¸cão 3.7.

Agora vamos fazer uma an´alise muito similar a feita no caso do teorema da divergˆencia. Escreva

I

P

F_·tds =

n

X

l=1

I

Cl

F_·tds=

N

X

l=1

1 ∆Sl

I

Cl

F_·tds

∆Sl, (3.8)

onde ∆Sl é a área da l-ésima face. O valor entre parêntese, é aproximadamente, igual a

nl·(∇ ×F)l onde nl é o vetor normal unitário positivo em cada l-ésima face e (∇ ×F)l é

o rotacional da fun¸cão vetorial F avaliada no ponto da l-ésima face que é tangente a S. Dizemos “aproximadamente” porque é na realidade o limite quando ∆Sl tende para zero

na expressão entre parêntese na equa¸cão 3.8, que é identificada com nl·(∇ ×F)l. Ignorando

essa falta de rigor, escrevemos

lim

N→∞

cada ∆Sl_→0

N

X

l=1

1 ∆Sl

I

Cl

F_·tds