1 UNIVERSIDADE DE LISBOA
FACULDADE DE CIÊNCIAS
DEPARTAMENTO DE ESTATÍSTICA E INVESTIGAÇÃO OPERACIONAL
ANÁLISE ESTATÍSTICA MULTIVARIADA APLICADA A
DADOS HIDROGEOLÓGICOS
Vânia Sofia Pires Simões Gomes
Dissertação
Mestrado em Estatística
2013
2 UNIVERSIDADE DE LISBOA
FACULDADE DE CIÊNCIAS
DEPARTAMENTO DE ESTATÍSTICA E INVESTIGAÇÃO OPERACIONAL
ANÁLISE ESTATÍSTICA MULTIVARIADA APLICADA A
DADOS HIDROGEOLÓGICOS
Vânia Sofia Pires Simões Gomes
Dissertação orientada pela Prof.ª Doutora Fernanda Diamantino e
coorientada pela Prof.ª Doutora Catarina Silva
Mestrado em Estatística
2013
i
Índice
Índice de Figuras ... iii
Índice de Tabelas ... v Índice de Anexos ... vi Resumo ... vii Abstract ... ix Capítulo 1: Introdução ... 1 1.1. Objetivos do estudo ... 1 1.2. Enquadramento geológico ... 6 Capítulo 2: Metodologia ... 9
2.1. Conceitos de álgebra matricial ... 9
2.1.1. Conceito de matriz ... 9
2.1.2. Tipos de matrizes ... 9
2.1.3. Igualdade de matrizes ... 10
2.1.4. Operações com matrizes... 11
2.1.5. Traço de uma matriz ... 11
2.1.6. Vetores linearmente dependentes e independentes ... 11
2.1.7. Característica de uma matriz ... 12
2.1.8. Determinante ... 12
2.1.9. Matriz adjunta e matriz inversa ... 13
2.1.10. Matriz ortogonal ... 13
2.1.11. Valores próprios e vetores próprios ... 13
2.1.12. Decomposição espetral ... 14
2.2. Características amostrais ... 15
2.2.1. Características amostrais univariadas ... 15
2.2.2. Características amostrais bivariadas ... 16
2.3. Técnicas de Análise Multivariada ... 18
2.3.1. Análise em Componentes Principais ... 19
2.3.1.1. Introdução ... 19
2.3.1.2. O modelo matemático ... 20
ii
2.3.2. Análise Fatorial ... 23
2.3.2.1. Introdução ... 23
2.3.2.2. O modelo matemático ... 23
2.3.2.3. Número de fatores a reter ... 24
2.3.2.4. Rotação dos fatores ... 25
2.3.2.5. Método de extração dos fatores ... 26
2.3.2.6. Validação do modelo de análise fatorial... 27
2.3.2.7. Análise em Componentes Principais versus Análise Fatorial ... 28
2.3.3. Análise de Clusters ... 29
2.3.3.1. Introdução... 29
2.3.3.2. Medidas de proximidade ... 30
2.3.3.3. Métodos de agregação ... 32
2.3.3.4. Critérios de agregação ... 33
Capítulo 3: Análise de dados hidrogeológicos ... 35
3.1. Análise Exploratória dos Dados ... 39
3.1.1. Características amostrais ... 39
3.1.2. Correlação linear de Pearson ... 45
3.1.3. Representações gráficas ... 47
3.2. Análise Multivariada ... 63
3.2.1. Análise em Componentes Principais ... 63
3.2.2. Análise Fatorial ... 71 3.2.3. Análise de Clusters ... 78 Capítulo 4: Conclusões ... 89 Considerações Finais ... 95 Bibliografia ... 97 Anexos ... 101
iii
Índice de Figuras
Figura 1: Localização geográfica das amostras de água e respetivas formações
geológicas ... 4
Figura 2: Localização geográfica das amostras de água ... 36 Figura 3: Localização geográfica das amostras de água e respetivas formações
geológicas ... 37
Figura 4: Diagramas em caixa de bigodes paralelos de cada variável comparando
cada formação geológica ... 48
Figura 5: Diagramas em caixa de bigodes paralelos de cada formação geológica,
para cada ião... 51
Figura 6: Diagramas de dispersão das observações reorganizadas versus cada uma
das variáveis em estudo ... 54
Figura 7: Matriz de diagramas de dispersão para cada formação geológica com as
variáveis condutividade elétrica, cálcio, sódio e cloreto ... 58
Figura 8: Matriz de diagramas de dispersão para cada formação geológica com as
variáveis bicarbonato, cálcio e magnésio ... 60
Figura 9: Matriz de diagramas de dispersão para cada formação geológica com as
variáveis bicarbonato, cálcio e sulfato ... 61
Figura 10: Diagrama de dispersão para cada formação geológica com as variáveis
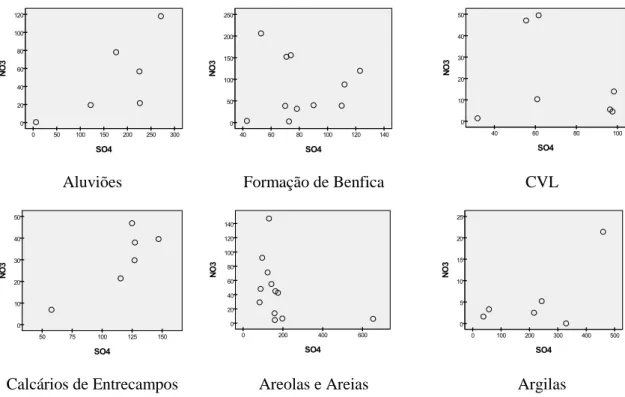
nitrato e sulfato ... 62
Figura 11: Scree plot (número de componentes principais versus valores próprios) ... 65 Figura 12: Representação gráfica dos loadings das duas primeiras componentes
principais... 67
Figura 13: Representação gráfica dos scores (observações) das duas primeiras
componentes principais ... 68
Figura 14: Representação gráfica dos scores (formações geológicas) das duas
primeiras componentes principais ... 69
Figura 15: Representação gráfica (biplot) dos loadings e dos scores (observações)
das duas primeiras componentes principais ... 70
Figura 16: Representação gráfica (biplot) dos loadings e dos scores (formações
geológicas) das duas primeiras componentes principais ... 70
iv
Figura 18: Dendograma (variáveis estandardizadas) para a amostra global
utilizando o método de Ward ... 79
Figura 19: Localização geográfica das amostras de água que constituem os clusters
(cluster1, cluster2 e cluster3) obtidos quando se utiliza o método de Ward com as variáveis estandardizadas ... 79
Figura 20: Dendograma (variáveis estandardizadas) para a amostra global
utilizando o método de Complete Linkage ... 80
Figura 21: Localização geográfica das amostras de água que constituem os clusters
(cluster1, cluster2 e cluster3) obtidos quando se utiliza o método de Complete Linkage com as variáveis estandardizadas ... 81
Figura 22: Dendograma (com os scores das 5 primeiras componentes principais)
para a amostra global usando o método de Ward ... 83
Figura 23: Localização geográfica das amostras de água que constituem os clusters
(cluster1, cluster2 e cluster3) obtidos quando se utiliza o método de Ward com as 5 primeiras componentes principais ... 84
Figura 24: Dendograma (com os scores das 5 primeiras componentes principais)
para a amostra global usando o método de Complete Linkage ... 85
Figura 25: Localização geográfica das amostras de água que constituem os clusters
(cluster1, cluster2 e cluster3) obtidos quando se utiliza o método de Complete Linkage com os scores das 5 primeiras componentes principais... 86
Figura 26: Dendogramas (observações) para cada formação geológica utilizando o
v
Índice de Tabelas
Tabela 1: Escala de avaliação da análise fatorial... 27
Tabela 2: Proveniência das amostras ... 38
Tabela 3: Características amostrais das variáveis (amostra global) ... 39
Tabela 4: Características amostrais (média e desvio padrão) das variáveis em cada grupo de formações geológica ... 44
Tabela 5: Valores próprios da matriz de correlações amostral ... 63
Tabela 6: Proporção de variância explicada por cada componente e proporção de variância acumulada explicada até à componente j. ... 64
Tabela 7: Matriz dos loadings das componentes principais ... 66
Tabela 8: Valores próprios da matriz de correlações amostral ... 71
Tabela 9: Proporção de variância explicada por cada fator e proporção de variância acumulada pelo fator j ... 72
Tabela 10: Comunalidades iniciais e extraídas através do método das componentes principais... 73
Tabela 11: Matriz dos loadings (sem rotação dos fatores) ... 73
Tabela 12: Matriz da transformação ortogonal obtida pelo método de rotação varimax ... 74
Tabela 13: Matriz dos loadings (após rotação varimax) ... 74
Tabela 14: Designação dos fatores ... 75
Tabela 15: KMO e teste de esfericidade de Bartlett ... 76
Tabela 16: Medida de adequação amostral para cada variável (MSA) ... 77
Tabela 17: Caracterização dos grupos de formações geológicas... 89
Tabela 18: Tabela resumo dos outliers por cada grupo de formação geológica e por cada variável ... 90
vi
Índice de Anexos
Anexo 1: Matriz dos dados ... 104
Anexo 2: Caracterização dos grupos de formações geológicas ... 105
Anexo 3: Tabelas com os valores extremos (os 5 maiores e os 5 menores valores) para cada variável... 107
Anexo 4: Matriz de correlações de Peason - amostra gobal... 108
Anexo 5: Matriz de correlações de Pearson - Aluviões ... 109
Anexo 6: Matriz de correlações de Pearson - Formação de Benfica... 110
Anexo 7: Matriz de correlações de Pearson - Complexo Vulcânico de Lisboa ... 111
Anexo 8: Matriz de correlações de Pearson - Calcários de Entrecampos ... 112
Anexo 9: Matriz de correlações de Pearson - Areolas da Estefânia e Areias do Vale de Chelas ... 113
Anexo 10: Matriz de correlações de Pearson - Argilas do Forno do Tijolo e Argilas e Calcários dos Prazeres ... 114
vii
Resumo
Para o presente estudo utilizaram-se análises químicas de 48 amostras de água subterrânea da cidade de Lisboa das quais se selecionaram 13 variáveis referentes a espécies dissolvidas (aniões e catiões) e parâmetros físico-químicos.
Este estudo teve como objetivo avaliar a existência de relação entre a composição química da água subterrânea e as formações geológicas por onde esta circulou, ou seja, pretendeu-se identificar as espécies dissolvidas que caracterizavam cada formação geológica, bem como, identificar o que distinguia cada uma das formações geológicas.
Deste modo, numa fase inicial procedeu-se a uma análise exploratória com o intuito de caracterizar a amostra global e as amostras parciais (correspondentes a cada formação geológica) e, numa fase final procedeu-se a uma análise multivariada, onde se utilizaram técnicas de redução de dimensionalidade (análise em componentes principais e análise fatorial) e técnicas de agrupamento de dados (análise de clusters).
Concluiu-se que as amostras provenientes da Formação de Benfica e do Complexo Vulcânico de Lisboa tinham composição química idêntica. Relativamente às restantes formações geológicas, não existia uma homogeneidade entre amostras provenientes da mesma formação, nem entre amostras provenientes de formações distintas, pelo que, a caracterização das formações geológicas tornou-se muito complexa.
Como os valores das correlações de Pearson, entre as variáveis, eram baixos, a aplicação das técnicas de redução de dimensionalidade não surtiu o efeito desejado.
Palavras – chave: Água subterrânea, análise exploratória, análise em componentes
ix
Abstract
For the present study we used chemical analyzes of 48 groundwater samples of Lisbon in which was selected 13 variables related to dissolved species (anions and cations) and physico-chemical parameters.
This study aims to evaluate whether there is a relationship between the chemical composition of the groundwater and the geological formations where it circulated, this is, it was intended to identify the dissolved species that characterize each geological formation, as well as to identify what distinguishes each geological formations.
Thus, initially we proceeded with an exploratory analysis in order to characterize the sample and partial samples (corresponding to each geological formation), and in a final stage, we applied a multivariate analysis, where techniques were used to reduce the dimensionality (principal component analysis and factor analysis) and techniques to data clustering (cluster analysis).
It was concluded that the samples from the Formação de Benfica and Complexo Vulcânico de Lisboa had identical chemical composition. For the other geological formations, there was no homogeneity among samples from the same formation, or between samples from different formations. Therefore, the characterization of the geologic formations has become very complex.
Since the values of the Pearson correlations among the variables were low, the application of reduce the dimensionality techniques do not have the desired effect.
Keywords:
Groundwater, exploratory analysis, principal component analysis, factor analysis, cluster analysis1
Capítulo 1: Introdução
Este trabalho surge com o intuito de dar resposta a algumas questões relativas à caracterização de águas subterrâneas da cidade de Lisboa, tendo como ponto de partida um conjunto de 48 análises de águas subterrâneas recolhidas não especificamente para este trabalho. Este conjunto resultou de recolhas para a concretização de unidades curriculares do 1º ciclo de estudos em Geologia da FCUL (Caria et al, 2009, Manca et
al, 2008 e Sanches et a,l 2006) e 2º ciclo de estudos em Geologia Aplicada e do
Ambiente da FCUL (Oliveira, 2010) e em Engenharia do Ambiente do IST (Lopes, 2007). A localização geográfica de, cada amostra de água encontra-se na figura 1, onde se pode observar a que formação geológica corresponde.
1.1. Objetivos do estudo
Para a realização deste trabalho foram definidos alguns objetivos, nomeadamente:
Calcular, analisar e interpretar as características amostrais;
Aferir sobre a qualidade das águas subterrâneas para consumo humano;
Analisar e interpretar as representações gráficas (análise exploratória);
Identificar as espécies dissolvidas que caracterizam cada formação geológica;
Relacionar a composição química da água subterrânea com a formação geológica aflorante no local de recolha;
Descrever a variabilidade dos dados com um menor número de variáveis não correlacionadas;
Explicar através de um menor número de fatores (não observados) as correlações entre as variáveis;
Utilizar uma análise de clusters para reagrupar as amostras de água subterrânea de acordo com a sua composição química;
Identificar características distintivas de cada uma das formações geológicas;
3
Destaca-se como objetivo principal a caracterização de cada grupo de formações
geológicas, através da análise das concentrações das espécies químicas dissolvidas nas
águas subterrâneas, bem como de alguns parâmetros físico-químicos.
O trabalho será dividido em duas partes. A primeira parte será constituída pelos capítulos 1 e 2 e corresponderá ao desenvolvimento teórico. A segunda parte será constituída pelos capítulos 3 e 4 e corresponderá ao desenvolvimento prático.
No capítulo 1 será feito o enquadramento geológico, no qual se fará uma breve introdução às características das formações geológicas.
No capítulo 2 será abordada a metodologia a desenvolver. Na primeira secção irão definir-se alguns conceitos de álgebra matricial. Na segunda secção, com o intuito de se efetuar uma análise exploratória dos dados, irão definir-se algumas características amostrais. Na terceira e última secção será feita uma breve abordagem das técnicas de análise multivariada a serem utilizadas, nomeadamente a análise em componentes principais, a análise fatorial e a análise de clusters.
No capítulo 3 serão apresentados os resultados obtidos. No capítulo 4 serão apresentadas as conclusões.
4
6
1.2. Enquadramento geológico
A composição química da água subterrânea da área de Lisboa está intimamente relacionada com as características do meio geológico, das condições climáticas e também das atividades humanas que decorrem na cidade.
O Concelho de Lisboa situa-se na Orla mesocenozóica, a qual é constituída por espessas séries de sedimentos, onde predominam os sedimentos carbonatados, os arenitos e os argilitos (Almeida et al., 2000).
Na área do concelho de Lisboa os terrenos mais antigos, cujos principais afloramentos se encontram nas zonas de Monsanto, Ajuda e Vale de Alcântara, são predominantemente constituídos por calcários, calcários margosos e margas. A geologia de Lisboa, de elevada complexidade, pode ser descrita de um modo simplificado em três setores: Setor SW, Monsanto-Ajuda-Alcântara; Setor NW, Formação de Benfica e Miocénico; Setor E, Série Miocénica.
Setor SW: Monsanto-Ajuda-Alcântara
As formações calcárias do Cenomaniano, que se apresentam dobradas e fraturadas (Cabral, 2006), estão sobrepostas por formações basálticas do Complexo Vulcânico de Lisboa (β1
). Neste setor, as formações cretácicas estendem-se desde a zona central e mais elevada da Serra de Monsanto, seguindo pelo Vale de Alcântara até praticamente ao Rio Tejo, prolongando-se para SW ao longo da encosta do Bairro da Ajuda, aflorando no seio do Complexo Vulcânico de Lisboa (Pais et al., 2006).
Esta zona compreende formações do Cretácico superior, como a Formação de Caneças (C2cn), constituída por calcários margosos e dolomíticos, datados do Albiano superior a
Cenomaniano médio. Sobre a formação anterior, assenta a Formação de Bica (C2Bi), do
Cenomaniano superior, representada por calcários compactos e apinhoados, com nódulos de sílex e com rudistas. No topo do Cretácico superior aflora o Complexo Vulcânico de Lisboa, constituído por rochas eruptivas básicas (Basaltos), sob a forma de escoadas lávicas alternando com piroclastos e aglomerados vulcânicos, com idade provável do Cenomaniano (Pais et al., 2006).
7
Setor NW: Formação de Benfica e Miocénico
É constituído por formações cenozóicas correspondentes à Formação de Benfica (Φ Bf)
e ao Miocénico. Este setor está na continuidade da estrutura de Monsanto e apresenta uma sucessão de ondulações suaves.
Sobre o Complexo Vulcânico de Lisboa, assenta, em discordância, a Formação de Benfica (Φ Bf), constituída por depósitos continentais, onde se intercalam níveis mais
argilosos, detríticos e carbonatados.
Setor Este: Série Miocénica
Compreende intercalações de formações detríticas e carbonatadas da Série Miocénica. Apresenta-se, de um modo geral, em monoclinal, inclinando suavemente para E-SE. O Neogénico abrange unidades miocénicas como as Camadas de Prazeres (Mpr), do
Aquitaniano a Burdigaliano inferior, constituídas por argilitos, argilitos siltosos e margosos, margas e calcários.
Sobrepostas a estas, estão as Areolas de Av. da Estefânia (MEs), datada do Burdigaliano
e constituída por areias finas, siltosas, micáceas (areolas) argilas silto arenosas e arenitos mais ou menos consolidados. De seguida, depositaram-se os Calcários de Entrecampos (MEC), formação representada por biocalcarenitos com fração detrítica
abundante, por vezes argilosa, ricos de moldes e/ou fragmentos de moluscos e calcários margosos, cinzento-esverdeado.
A formação anterior passa superiormente a areias muito finas argilosas, piritosas, e a siltitos argilosos de cor cinzenta, com moluscos, peixes e abundantes microfósseis, correspondente à unidade de Argilas de Forno do Tijolo (MFT).
A formação Areias do Vale de Chelas (Mvb) é constituída por areias feldspáticas,
fluviais, incoerentes ou fracamente cimentadas, às vezes grosseiras e compactas; em posição superior ocorrem areias dunares.
As aluviões (a) do Concelho de Lisboa incluem os depósitos diretamente associados ao leito principal do Rio Tejo e a todas as ribeiras e linhas de água que a este afluem, na sua margem direita. As espessuras das aluviões do Tejo são muito variáveis de local para local. Estas são predominantemente lodosas, com abundante matéria orgânica, ou arenosas. As aluviões das ribeiras afluentes do Tejo têm composição em muitos casos dependentes das litologias erodidas, contendo frequentemente, matéria orgânica (Almeida, 1991).
9
Capítulo 2: Metodologia
Neste capítulo procede-se ao desenvolvimento teórico das metodologias aplicadas no estudo a realizar.
2.1. Conceitos de álgebra matricial
Nesta secção relembram-se alguns conceitos cruciais de álgebra matricial que se utilizam no desenvolvimento das técnicas de análise multivariada. Naturalmente começa-se com o conceito de matriz (Monteiro, 2001, Searle, 1982 e Timm, 2002).
2.1.1. Conceito de matriz
Designa-se por matriz de ordem n m, a tabela A =
, com n linhas e m colunas.
Pode denotar-se a matriz A por [ ] com i = 1,…, n e j = 1,…, m.
As entradas aij são os elementos de A, em que i indica a linha e j indica a coluna.
Quando uma matriz tem ordem n 1 ou ordem 1 n designa-se por vetor, ou seja, tem n linhas e uma coluna ou tem 1 linha e n colunas, respetivamente. No primeiro caso designa-se por vetor coluna e representa-se do seguinte modo: x = . No segundo caso designamos por vetor linha e representa-se do seguinte modo: xT = .
Uma matriz de ordem 1 1 designa-se por escalar.
2.1.2. Tipos de matrizes
No que se segue definem-se alguns tipos de matizes, nomeadamente matriz quadrada, diagonal, identidade, transposta e simétrica.
10
Uma matriz quadrada é a matriz em que o número de linhas é igual ao número de colunas e diz-se que tem ordem n n, ou simplesmente ordem n.
Caso contrário, se o número de linhas for diferente do número de colunas, diz-se que a matriz é retangular de ordem n m.
Uma matriz quadrada de ordem n, em que
com i, j = 1, …, n, designa-se
por uma matriz diagonal, ou seja, a uma matriz da forma:
Em particular, se d11 = 1,…, dnn = 1, tem-se a matriz Identidade, que se denota por In, e
representa-se da forma:
.
Para qualquer matriz A quadrada de ordem n, verifica-se a seguinte propriedade: AI = IA = A.
Seja A uma matriz de ordem n m. Designa-se por matriz transposta de A, e representa-se por AT, à matriz que se obtém trocando as linhas com as colunas, ou seja, as linhas de A são as colunas de AT e as colunas de A são as linhas de AT.
Assim sendo, tem-se que:
se A = de ordem n m, então AT =
de ordem m n.
Seja A uma matriz quadrada de ordem n. Diz-se que A é simétrica se e só se A = AT.
2.1.3. Igualdade de matrizes
Duas matrizes são iguais se os elementos de uma coincidirem com os elementos da outra, tendo ambas, naturalmente, a mesma ordem.
11
Sejam A e B duas matrizes com a mesma ordem (n m), tais que A = e B = .
Diz-se que as matrizes A e B são iguais se e só se = , para todo i = 1,…, n e j = 1,…, m.
2.1.4. Operações com matrizes
Por vezes torna-se necessário efetuar algumas operações entre matrizes, como é o caso da adição, da subtração ou do produto de duas ou mais matrizes, bem como a multiplicação de um escalar por uma matriz.
Sejam A e B duas matrizes com a mesma ordem (n m), tais que A = e B = .
A sua soma (diferença), A + B (A – B) é igual a C, onde C = = (C = = ), com i = 1, …, n e j = 1, …, m.
Seja A uma matriz de ordem n m, tal que A = e um escalar. A multiplicação
da matriz A por um escalar representa-se por A ou A e é igual a , com
i = 1, …, n e j = 1, …, m.
Sejam A e B duas matrizes de ordem n m e m p, respetivamente. O produto de A por B origina C de ordem n p, tal que AB = C = , onde = .
2.1.5. Traço de uma matriz
Seja A uma matriz quadrada de ordem n n, tal que os elementos da diagonal são da forma aii, com i = 1,…, n. Então o traço de A é igual à soma dos elementos da diagonal,
ou seja, tr(A) = .
2.1.6. Vetores linearmente dependentes e independentes
Os vetores dizem-se linearmente dependentes se for possível escrever o vetor nulo como combinação linear de sem que os escalares sejam todos
12
nulos. Se o vetor nulo só se puder escrever como combinação linear de sendo os escalares todos nulos, então os vetores são linearmente independentes.
2.1.7. Característica de uma matriz
Designa-se por característica de uma matriz A de ordem n n o número de linhas (ou colunas) linearmente independentes. Representa-se a característica de A por r(A).
2.1.8. Determinante
O determinante de uma matriz quadrada de ordem n é dado por
onde K é o número de inversões1 da
permutação ( e p indica que a soma ocorre sobre todas as permutações de (1, 2, …, n), ou seja, existem n! permutações. O determinante de uma matriz A pode denotar-se por detA ou |A|.
Designa-se por menor complemento de um elemento de um determinante, ao determinante que se obtém, suprimindo a linha e a coluna a que pertence esse elemento (linha i e coluna j). Representa-se por .
O complemento algébrico de um elemento é igual ao menor complemento ou ao seu simétrico e representa-se por
.
Pode-se calcular o determinante de outra forma.
Teorema de Laplace: Seja A uma matriz quadrada de ordem n, o seu determinante é
igual à soma dos produtos dos elementos de uma linha (ou coluna) pelos respetivos complementos algébricos. Assim sendo,
, onde é o complemento algébrico de .
1Dada uma permutação dos inteiros 1, 2, …, n, existe uma inversão quando um inteiro precede outro
13
2.1.9. Matriz adjunta e matriz inversa
À matriz que se obtém calculando os respetivos complementos algébricos para cada entrada e fazendo a sua transposta, designa-se por matriz adjunta. Representa-se por adj A.
Uma matriz A quadrada de ordem n é invertível se existir uma matriz B quadrada de ordem n tal que AB = BA = In. Designamos B por matriz inversa de A e representa-se
por A-1.
Notas:
1) Uma matriz é invertível se e só se o seu determinante for diferente de zero. 2) A matriz inversa é única.
3) Pode ser obtida por: A-1 = .
2.1.10. Matriz ortogonal
Uma matriz A quadrada de ordem n, invertível, diz-se ortogonal se a inversa e a transposta coincidirem, ou seja, A-1 = AT.
2.1.11. Valores próprios e vetores próprios
Seja A uma matriz quadrada (n n), um escalar e x um vetor não nulo tal que Ax = x. Diz-se que é o valor próprio de A e x é um vetor próprio associado.
Considere-se a equação |A I| = 0, cujas soluções são os valores próprios da matriz A. O polinómio |A I| designa-se por polinómio característico.
Observações:
Uma vez que a matriz A tem ordem n, então o polinómio característico tem n raízes e deste modo têm-se n valores próprios, sejam , . Após a determinar os valores próprios determinam-se os vetores próprios, , , …,
14
, associados a cada valor próprio. Para esse efeito usa-se a igualdade (A I)x=0.
O vetor próprio obtido associado a cada valor próprio não é único, deste modo se
x for vetor próprio então cx (c é um escalar não nulo) também é vetor próprio.
Notas:
1) A soma dos valores próprios é igual ao traço de A, ou seja, tr(A) = .
2) O produto dos valores próprios é igual ao determinante de A, ou seja, det(A) = .
2.1.12. Decomposição espetral
Teorema da decomposição espetral: (Decomposição em valores próprios e vetores
próprios)
Seja A uma matriz simétrica e considere-se ainda os valores próprios de A e os vetores próprios normalizados. Temos que AQ = Q com QTQ = I, onde é a matriz diagonal dos valores próprios, =
e Q a matriz ortogonal dos vetores próprios. Se QT = Q-1, então A = Q QT.
15
2.2. Características amostrais
Nesta secção definem-se algumas características amostrais a utilizar na análise exploratória dos dados.
2.2.1. Características amostrais univariadas
Para se caracterizar um conjunto de dados, começa-se por calcular algumas características amostrais, de localização e de dispersão. No que se segue, definem-se algumas dessas características amostrais. Mais precisamente, a média, o desvio padrão, os extremos, a mediana e os quartis (Murteira, 2007).
Dado um conjunto de observações (x1, …, xn), diz-se que é a média amostral e que = é a variância amostral. O desvio padrão
amostral é dado pela raiz quadrada positiva da variância, ou seja, .
A média amostral é uma medida de localização, a variância e o desvio padrão amostrais são medidas de dispersão. Estas permitem medir a variabilidade dos em torno da média amostral.
Um conjunto de observações (x1, x2, …, xn) pode ser ordenado ordenado de modo
ascendente, tal que x1:n x2:n … xn:n, sendo x1:n o mínimo e xn:n o máximo.
Tendo um conjunto ordenado de observações, pode-se calcular a mediana do seguinte modo
16
Define-se quantil de ordem p por:
onde [np] designa a parte inteira de np.
Observações:
1) O quantil de ordem 0,5 designa-se por mediana.
2) Os quantis de ordem 0,25 e 0,75 designam-se por primeiro quartil e terceiro
quartil respetivamente.
3) Os quantis de ordem 0,1; … ; 0,9 designam-se por decis. 4) Os quantis de ordem 0,01; …; 0,99 designam-se por percentis.
Uma representação gráfica usual para representar os extremos, os quartis e a mediana é o diagrama em caixa de bigodes.
2.2.2. Características amostrais bivariadas
Na secção anterior definiram-se algumas características amostrais (no caso univariado). Nesta secção definem-se as características amostrais para o caso bivariado, ou seja, características que permitem comparar as variáveis duas a duas, de forma a avaliar o grau de associação entre as duas variáveis. Neste caso, calculam-se as covariâncias e correlações amostrais.
Considere-se um par de observações (xi, yi), com i, j = 1, …, n. Pode-se proceder à sua
representação gráfica num referencial cartesiano. Esse gráfico designa-se por diagrama
de dispersão.
Esta representação gráfica permite avaliar o grau de associação entre duas variáveis.
Para quantificar essa associação podem usar-se duas medidas: a covariância amostral e / ou coeficiente de correlação linear.
A covariância amostral é dada por cov(x,y) = . Também pode ser denotada por .
17
A covariância é uma estatística bivariada utilizada para quantificar a associação linear entre duas variáveis. Porém, é influenciada pelas unidades de medida. Neste caso, teria de se proceder à estandardização do conjunto de dados, ou por outro lado, calcular-se o coeficiente de correlação amostral.
O coeficiente de correlação ou coeficiente de correlação de Pearson é dado por r = , ou seja,
.
O coeficiente de correlação varia entre -1 e 1 e é usado para variáveis quantitativas.
Se as variáveis não forem quantitativas, usa-se o coeficiente de correlação de
Spearman.
Para calcular o coeficiente de correlação de Spearman procede-se de igual modo, mas substituem-se as observações (qualitativas) pelas respetivas ordens.
18
2.3. Técnicas de Análise Multivariada
Nesta secção procede-se ao desenvolvimento teórico das técnicas de análise multivariada a utilizar neste estudo, nomeadamente, a análise em componentes principais (ACP), a análise fatorial (AF) e a análise de clusters (AC).
Com estas técnicas pretende-se resumir a informação contida nos dados, de forma a tornar mais fácil a sua interpretação.
As duas primeiras técnicas (ACP e AF) relacionam-se diretamente com as variáveis, designam-se por análise modo-R, ao passo que a última técnica (AC) relaciona-se com os indivíduos, designa-se por análise modo-Q.
Mais claramente, a análise-modo R permite identificar as variáveis que mais contribuem para a explicação da variabilidade dos dados, com a menor perda de informação. A análise modo-Q é usada para agrupamento de indivíduos em classes/grupos homogéneos, através de características comuns entre os indivíduos.
19
2.3.1. Análise em Componentes Principais
2.3.1.1. Introdução
A análise em componentes principais é uma técnica de análise multivariada introduzida pelo estatístico Karl Pearson em 1901 e mais tarde desenvolvida por Hotelling em 1933 (Mardia et al, 1979).
A análise em componentes principais é um método de análise multivariada que consiste em transformar um conjunto de variáveis originais correlacionadas num conjunto de novas variáveis não correlacionadas: as componentes principais. As variáveis originais e as componentes principais têm a mesma dimensão.
O principal objetivo da ACP é a redução da dimensionalidade, ou seja, a diminuição do número de componentes, de forma a explicar a variabilidade dos dados. Esta redução consegue-se uma vez que as variáveis originais estão correlacionadas, sendo algumas delas redundantes, ao passo que as componentes principais são não correlacionadas, podendo explicar a informação dada pelas variáveis originais com um menor número de componentes. Caso as variáveis originais estejam fracamente correlacionadas, as componentes principais vão coincidir com as variáveis originais.
Estas novas variáveis (as componentes principais) são uma combinação linear das variáveis originais, com uma ordem decrescente de importância. A primeira componente principal é a mais importante, uma vez que descreve a maior parte da variabilidade dos dados.
Pretende-se que este número de componentes principais seja o menor possível, ou seja, parte-se de p variáveis originais para k componentes principais, com k muito inferior a p, de modo que a perda de informação seja a menor possível.
Assim sendo, se as variáveis originais estiverem muito correlacionadas, o número de componentes principais que expliquem a variabilidade é reduzido. Caso as variáveis originais estejam pouco correlacionadas essa redução é pouco significativa.
20
2.3.1.2. O modelo matemático
Considere-se o modelo matemático para as componentes principais Yj = a1jX1 + a2jX2 + … + apjXp
ou, Y = AX, em que X1, …, Xp são as variáveis originais, Y1, …, Yp são as
componentes principais não correlacionadas e de variância decrescente e aij é o peso da
j-ésima variável com a i-ésima componente principal, representados na matriz A de ordem p (Chatfield, 1980).
Para a determinação das componentes principais tem de se utilizar a matriz de covariâncias amostral ou a matriz de correlações amostral. Quando as escalas de medida das variáveis são diferentes usa-se a matriz de correlações amostral. Desta forma torna-se possível a comparação.
De salientar que, pelo facto de não existir invariância de escala na ACP, as componentes obtidas são diferentes quando se usa a matriz de covariâncias e quando se usa a matriz de correlações. As componentes principais obtidas também são diferentes quando a unidade de medida das variáveis originais é alterada (Gnanadesikan,1997).
Para determinar as componentes principais, começa-se por calcular os valores próprios da matriz de correlações amostral, seguidamente determinam-se os vetores próprios associados a cada valor próprio.
Desta forma, cada componente principal é um vetor próprio associado a cada um dos valores próprios. Mais precisamente, a primeira componente principal corresponde ao vetor próprio associado ao maior valor próprio. A segunda componente principal corresponde ao vetor próprio associado ao segundo maior valor próprio e, assim por diante, de modo que as componentes principais sejam ortogonais entre si.
Designam-se os valores próprios da matriz de correlações amostral por , e tem-se que 0. Estes valores próprios representam a variância das componentes principais, ou seja, var(Yj) = . A ordenação das componentes principais
é feita através da ordenação dos valores próprios, de modo que à i-ésima componente principal corresponda o i-ésimo maior valor próprio.
21
No modelo matemático para as componentes principais
com j = 1, …, p, os aij são estimados de modo que a primeira componente contenha a
maior variância (maior valor próprio) e assim por diante. Esses pesos são dados pelos vetores próprios associados a cada valor próprio. Tem-se que,
= 1 com i = 1, …, p e,
ai1aj1 + … + aipajp = 0 para todo o i diferente de j.
Os pesos das componentes principais (aij) representam a importância relativa das
variáveis originais em cada componente principal.
Os yj observados designam-se por scores das componentes principais.
A correlação entre as variáveis originais e as componentes principais designa-se por
loading. Estes fornecem a indicação de como as variáveis originais são importantes para
a formação das componentes principais. Assim sendo, loadings próximos de um indicam que essa variável é importante na formação da componente principal, enquanto
loadings próximos de zero indicam que a variável não é importante na formação da
componente principal. Os loadings são significantes se forem maiores que 0,3 em valor absoluto. O loading da j-ésima variável com a i-ésima componente principal é dado por
, em que aij é o peso da j-ésima variável com a i-ésima componente
principal, é o valor próprio da i-ésima componente principal e sj é o desvio padrão da
j-ésima variável.
A comunalidade da j-ésima variável é dada por , que se refere à proporção de variância das variáveis que são explicadas pelas componentes principais.
Neste processo, a variância é preservada, uma vez que a soma das variâncias das variáveis originais é igual à soma das variâncias das componentes principais.
22
2.3.1.3. Número de componentes a reter
Ao usar esta técnica de análise multivariada tem de se decidir o número de componentes a reter, ou seja, quantas componentes são necessárias para explicar a variabilidade dos dados. Desta forma, existem algumas regras para decidir o número de componentes principais a reter, de modo que estas expliquem a variabilidade dos dados e que a perda de informação seja a menor possível.
Um primeiro critério é reter o número de componentes principais que expliquem pelo menos 80% da variabilidade total. Sendo a variância da j-ésima componente principal e a variância total, tem-se que
é a proporção explicada pela j-ésima componente principal e
é a proporção explicada pelas k primeiras
componentes principais. Este valor deve ser superior a 80%.
O segundo critério (critério de Kaiser, proposto em 1960) consiste em excluir as componentes principais cujos valores próprios sejam inferiores à sua média aritmética (quando usada a matriz de correlações, a média dos valores próprios é um).
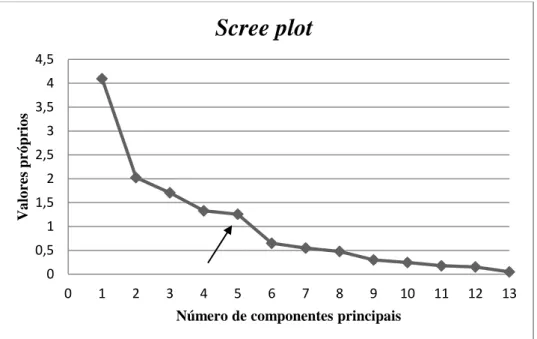
O terceiro critério consiste em utilizar uma representação gráfica do número de componentes principais versus os valores próprios. Este gráfico designa-se por scree
plot, proposto por Cattell em 1966. O gráfico tem a forma de um “cotovelo”. Deve-se
reter o número de componentes principais até o gráfico se tornar praticamente paralelo ao eixo Ox, uma vez que esses valores próprios são muito reduzidos e praticamente iguais, pouco ou nada contribuem para a explicação da variabilidade dos dados (Rencher, 1995).
23
2.3.2. Análise Fatorial
2.3.2.1. Introdução
A Análise Fatorial começou a ser desenvolvida pelo psicólogo Charles Spearman em 1904, para testar os fatores de inteligência e habilidade nos jovens, quando realizados testes a diferentes áreas do conhecimento (ciências e humanidades). Mais tarde foi também desenvolvida por Thurstone em 1931 (Harman, 1976).
A Análise Fatorial é uma técnica de análise multivariada que consiste em escrever p variáveis y1, y2, … , yp como combinação linear de novas variáveis f1, f2, … , fm, com m
menor que p. Estas novas variáveis designam-se por fatores latentes, sendo não observadas. As variáveis y1, y2, … , yp são moderadamente correlacionadas (Rencher,
1995).
O objetivo da análise fatorial é reduzir o número de fatores latentes, de forma a explicar a maior correlação existente no conjunto de dados. Pretende-se exprimir o que de comum existe nas variáveis iniciais, de modo a perder-se a menor informação possível.
2.3.2.2. O modelo matemático
Considere-se o modelo matemático para a análise fatorial:
Ou, alternativamente, usando notação matricial, Y = , onde
y = [y1, y2, … , yp]T é o vetor das variáveis, f = [f1, f2, … , fm]T é o vetor dos fatores
comuns , T é o vetor dos fatores específicos e
é a matriz dos pesos fatoriais, que não é única.
Assim sendo, cada variável é decomposta em duas: a parte comum e a parte específica. Os coeficientes são designados por loadings ou pesos, que permitem mostrar de que
24
as variáveis e os fatores, ou seja, cov(yi, fj) = com i = 1, … , p e j = 1, … , m desde
que cov(y, f) = .
Tem-se que E(fj) = 0, var(fj) = 1, cov(fi, fj) = 0, i j.
O é a parte residual de Yi, tendo-se E( ) = 0, var( = , que é a variância
específica, cov( ) = 0, i j e cov( fj) = 0 para todo i e j.
Tem-se ainda que var(Yi) = + + … + + = , em que é a
comunalidade, que se refere à variância comum e é a variância específica ou única, que se refere à variância residual (Rencher, 1995).
Se a matriz de correlações tiver valores elevados significa que as variáveis têm bastante em comum, formando grupos homogéneos. Se os valores das correlações forem reduzidos, significa que as variáveis têm pouco ou nada em comum, formando grupos heterogéneos.
2.3.2.3. Número de fatores a reter
Na análise em componentes principais tinha de se selecionar um número de componentes mais reduzido, ou seja, era necessário analisar o número de componentes a reter de modo que estas explicassem a variabilidade dos dados, mas também que o seu número fosse bastante reduzido. Teria de se encontrar uma relação parcimoniosa, no sentido de não se usar um número excessivo de componentes, mas também de não se perder informação preciosa. Na análise fatorial pretende-se fazer algo semelhante, decidir o número de fatores a reter de modo a explicar pelo menos 80% da variabilidade total. Escolher um número de fatores igual ao número de valores próprios maiores que a média dos valores próprios. Se for utilizada a matriz de correlações (R), a média é 1, se for utilizada a matriz de covariâncias (S), a média é , em que é o valor próprio da matriz S. À semelhança da análise em componentes principais, pode-se usar o teste do scree plot dos valores próprios de S ou R versus o número de fatores. O gráfico obtido apresenta inicialmente uma acentuada inclinação e no final uma reduzida inclinação, pelo que os valores próprios serão praticamente iguais e reduzidos. Deve-se então reter o número de fatores (m) a partir dos quais o gráfico fica uma reta paralela ao eixo das abcissas, tendo este gráfico a forma de um “cotovelo” (Rencher, 1995).
25
2.3.2.4. Rotação dos fatores
Para uma melhor interpretação dos fatores obtidos inicialmente, recorre-se à rotação dos eixos. Existem várias técnicas de rotação.
Este método de rotação consiste na transformação da solução inicial através da multiplicação de uma matriz de rotação ortogonal pela matriz dos loadings, de modo que a solução seja interpretada de uma forma mais eficiente. Com esta rotação pretende-se aumentar os valores absolutos dos grandes loadings e reduzir os valores absolutos dos pequenos loadings, distinguindo assim loadings significantes de loadings insignificantes.
As rotações podem ser ortogonais ou oblíquas. As mais utlizadas são as ortogonais, destacando-se, a rotação varimax, a rotação quartimax e a rotação equimax.
Com o método varimax pretende-se maximizar a variância dos loadings de cada coluna da matriz , de forma a existirem alguns loadings significativos e todos os
outros próximos de zero. Pretende-se maximizar V, com a restrição das comunalidades permanecerem inalteradas.
Para um dado fator j, tem-se
, onde é a variância da comunalidade das variáveis no fator j, é o quadrado do loading da i-ésima variável no j-ésimo fator,
é a média do quadrado dos loadings para o fator j, p é o número de
variáveis e k é o número de fatores.
A variância total V de todos os fatores é dada por:
Este método, desenvolvido por Kaiser em 1958, tornou-se muito popular.
Com o método quartimax pretende-se simplificar as linhas da matriz de loadings, ou seja, tornar os loadings de cada variável elevados para um pequeno número de fatores e próximos de zero para os restantes. Pretende-se maximizar Q, com a restrição das comunalidades não se alterarem.
26
Para uma dada variável i, tem-se
, onde é a variância da comunalidade na variável i e
é a média do quadrado dos loadings na variável i. A variância total Q de todas as variáveis é dada por:
Com o método equamax pretende-se fazer uma mistura dos dois anteriores métodos (Afifi, 1996, Harman, 1976, Rencher, 1995, Sharma, 1996 e Timm, 2002).
2.3.2.5. Método de extração dos fatores
Os métodos de extração dos fatores disponíveis no SPSS são: método das componentes principais (principal components), método da máxima verosimilhança (maximum
likelihood), método dos mínimos quadrados (unweighted least squares and generalized least squares), principal axis factoring, alpha factoring e image factoring.
Com estes métodos procede-se à extração dos fatores e consequentemente à estimação dos loadings e das comunalidades.
27
2.3.2.6. Validação do modelo de análise fatorial
Para avaliar a qualidade da análise efetuada realizam-se alguns testes. A análise fatorial é usada para descrever as correlações entre as variáveis. Deste modo, torna-se necessário que a matriz de correlações seja significativamente diferente da matriz identidade, efetuando-se o teste de esfericidade de Bartlett. Este teste usa-se para testar H0: R = I versus H1: R I, em que R é a matriz de correlações amostral e I a
matriz identidade.
A estatística de teste é – (n – 1 – ) com distribuição qui-quadrado com p (p - 1) graus de liberdade (Rencher, 1995).
Para avaliar se a análise fatorial é adequada aos dados usa-se a “medida de adequação de amostragem de Kaiser-Meyer-Olkin (KMO)” ou measure of sampling adequacy (MSA), proposta por Kaiser em 1970. Define-se por:
KMO / MSA =
,
onde R = e Q = = DR-1D, com D = .
O KMO toma valores entre 0 e 1. Recomendam-se valores superiores a 0.8. Na tabela 1 encontra-se a escala de avaliação da análise fatorial efetuada (Maroco, 2007, Reis, 2001 e Timm, 2002). KMO / MSA AF 0.9 – 1 Muito boa 0.8 – 0.9 Boa 0.7 – 0.8 Média 0.6 – 0.7 Medíocre 0.5 -0.6 Má < 0.5 Inaceitável
28
2.3.2.7. Análise em Componentes Principais versus Análise Fatorial
Na análise fatorial escrevem-se as variáveis como combinação linear dos fatores, enquanto na análise em componentes principais escrevem-se as componentes principais como combinação linear das variáveis, são procedimentos inversos. A análise em componentes principais permite explicar a maior parte da variabilidade total das variáveis, enquanto na análise fatorial pretende-se explicar as correlações entre as variáveis. No caso da ACP as componentes principais obtidas são únicas, no caso da AF os fatores dependem da rotação efetuada. No caso da ACP a solução obtida pode ser diferente se usada uma escala de medição diferente, enquanto na AF, há invariância de escala, ou seja, as soluções são invariantes com a mudança da escala de medição. Quando se aumenta o número de componentes retidas, as primeiras componentes principais mantêm-se inalteradas, enquanto na análise fatorial, os fatores podem tornar-se bastante diferentes quando o número de fatores retidos é modificado. (Everitt, 2011 e Maroco, 2007).
29
2.3.3. Análise de Clusters
2.3.3.1. Introdução
A análise de clusters é uma técnica de análise multivariada que tem como principal objetivo o agrupamento de elementos. Este agrupamento é efetuado de forma que elementos pertencentes ao mesmo grupo tenham características semelhantes e elementos de diferentes grupos tenham características dissemelhantes. Genericamente, parte-se de um conjunto com n observações e pretende-se formar k grupos com um menor número de observações.
Para a construção desses grupos usam-se métodos hierárquicos ou métodos não hierárquicos. Entre os métodos hierárquicos, estes podem ser aglomerativos ou divisivos.
Considere-se um conjunto de n observações e p variáveis dispostos na seguinte matriz de ordem n p,
.
O elemento representa o valor do objeto (indivíduo) i na variável j.
Seguidamente constrói-se a matriz D de ordem n, dada por
, em que dkl representa a distância entre os objetos k e l, com k, l = 1, …, n. Esta matriz
designa-se por matriz de proximidade.
Deste modo, o passo que se segue é escolher a medida de proximidade entre os indivíduos (Everitt et al, 2001, Maroco, 2007 e Reis, 1997).
30
2.3.3.2. Medidas de proximidade
Para a construção da matriz de proximidade D, definida anteriormente, é necessário selecionar uma medida de proximidade, podendo ser uma medida de distância, de dissemelhança ou de semelhança.
Segundo Everitt (2001), dois indivíduos estão próximos se a dissemelhança ou a distância entre eles é pequena ou, se a semelhança entre eles é grande.
Uma medida de semelhança caracteriza-se pelas seguintes propriedades: 1) 0 1
2) = 1 3) =
onde denota a medida de semelhança entre os indivíduos i e j.
Nos dados categóricos é habitual usar-se uma medida de semelhança.
Uma medida de dissemelhança caracteriza-se pelas seguintes propriedades: 1) 0
2) = 0 3) =
onde denota a medida de dissemelhança entre os indivíduos i e j.
Uma medida de distância caracteriza-se pelas seguintes propriedades: 1) 0
2) = 0 3) =
4) (desigualdade triangular)
31
Apresentam-se em seguida algumas medidas de distância (Everitt et al, 2001 Maroco, 2007, Reis, 1997 e Timm, 2002).
1) Distância Euclidiana
=
2) Quadrado da Distância Euclidiana
3) Distância de Manhattan ou distância absoluta ou City-Block Metric
4) Distância de Minkowski
é uma generalização da distância Euclidiana e coincidem quando r = 2.
5) Distância de Mahalanobis
onde S denota a matriz de covariâncias amostral.
A medida de distância mais usada é a euclidiana.
Em seguida, definem-se algumas medidas de dissemelhança.
1) Correlação de Pearson:
32 onde e . 2) Separação Angular com . 2.3.3.3. Métodos de agregação
Um dos objetivos da análise de clusters é reduzir a distância dentro dos grupos e aumentar a distância entre os grupos.
Após selecionada a medida de proximidade e construída a respetiva matriz de proximidade, pretende-se saber quantos clusters se obtém. Assim sendo, para a determinação desses k grupos usam-se métodos hierárquicos ou métodos não hierárquicos. Quanto aos métodos hierárquicos, estes podem ser aglomerativos ou divisivos. Um processo diz-se aglomerativo se no final do processo se obtém um único cluster com todos os elementos e diz-se divisivo se no fim do processo existirem n clusters com um único elemento cada.
Em qualquer dos métodos tem-se como objetivo a escolha da solução ótima, ou seja, número ótimo de clusters. Essa decisão fica a cargo do investigador.
As etapas resultantes deste processo hierárquico (aglomerativo ou divisivo) podem ser representadas através de um gráfico – o dendograma (Everitt, 2001).
33
2.3.3.4. Critérios de agregação
Após definidas as medidas de proximidade entre dois elementos, é necessário definir medidas de proximidade entre os clusters, ou seja, definir critérios de agregação entre os grupos (Everitt et al, 2001 Maroco, 2007, Reis, 1997 e Timm, 2002).
1) Complete Linkage ou método do vizinho mais afastado
A distância entre dois grupos é medida como sendo a distância máxima entre um par de objetos, entre todos os clusters. Utilizando este critério os clusters obtidos são mais compactos.
2) Single Linkage ou método do vizinho mais próximo
A distância entre dois grupos é medida como sendo a distância mínima entre um par de objetos, entre todos os clusters. Utilizando este critério os clusters obtidos são desequilibrados e desalinhados, em particular quando o número de dados é elevado.
3) Average Linkage
A distância entre dois grupos é medida como sendo a média da distância entre todos os pares de objetos dos dois grupos. Utilizando este critério os clusters obtidos têm pequenas variâncias.
Este é um critério intermédio entre o Complete Linkage e o Single Linkage, sendo relativamente robusto.
4) Critério do Centróide
A distância entre dois grupos é medida como sendo a distância entre os seus centróides. Cada centróide corresponde à média ponderada dos elementos dos dois grupos.
34
5) Critério de Ward
Neste método não são calculadas distâncias, formam-se os clusters de modo a minimizar a soma dos quadrados dos erros.
No que se segue, apresentam-se as etapas do método hierárquico aglomerativo.
Agrupamento hierárquico (método aglomerativo):
Dada a matriz de proximidades D = [dij] de ordem n n, seguem-se os passos seguintes
(Timm, 2002):
1. Começa-se com n clusters, cada um deles com um elemento.
2. Usando a matriz D, escolhemos os elementos mais semelhantes, digamos i e j.
3. Juntam-se esses dois elementos, i e j, formando um novo cluster (ij).
Recalculam-se as distâncias entre o novo cluster (ij) e os elementos já existentes, usando o critério de agregação selecionado. Obtém-se uma nova matriz de proximidade de ordem (n – 1) (n – 1).
4. Repetem-se os passos 2 e 3, (n – 1) vezes.
35
Capítulo 3: Análise de dados hidrogeológicos
O estudo baseia-se num conjunto de 48 amostras de água subterrânea recolhidas em furos, minas, nascentes e poços da cidade de Lisboa, conforme se pode visualizar na figura 2. Utilizam-se as análises químicas dessas 48 amostras de água e selecionam-se 13 variáveis referentes a parâmetros físico-químicos e espécies dissolvidas (aniões e catiões). Mais precisamente:
Os parâmetros físico-químicos: o pH, a condutividade elétrica (C.E.) e o potencial redox (Eh);
As espécies dissolvidas: o bicarbonato ( ), o cálcio (Ca2+), o sódio (Na+), o potássio (K+), o magnésio (Mg2+), o fluoreto ( ), o cloreto ( ), o brometo ( ), o nitrato ( ) e o sulfato ( ).
As amostras de águas subterrâneas agora utilizadas não foram recolhidas especificamente para este trabalho, resultaram de recolhas para a concretização de unidades curriculares do 1º ciclo de estudos em Geologia da FCUL (Caria et al, 2009, Manca et al, 2008 e Sanches et al, 2006)e 2º ciclo de estudos em Geologia Aplicada e do Ambiente da FCUL (Oliveira, 2010) e em Engenharia do Ambiente do IST (Lopes, 2007).
36
Figura 2: Localização geográfica das amostras de água
Como já foi referido anteriormente, a geologia de Lisboa é de grande complexidade, pelo que, para facilitar a análise estatística das amostras de água, as formações geológicas foram agrupadas, tendo em conta as suas semelhanças litológicas, da seguinte forma: Aluviões (1); Formação de Benfica (2); Complexo Vulcânico de Lisboa (CVL) (3); Calcários de Entrecampos (4); Areolas da Estefânia e Areias do Vale de Chelas (5) e Argilas do Forno do Tijolo e Argilas e Calcários dos Prazeres (6).
Na figura 3 encontram-se as localizações das amostras recolhidas e a respetiva formação geológica aflorante.
37
38
A partir da figura 3 pode construir-se a tabela 2 em que se indica a proveniência de cada amostra.
Grupos de formações geológicas Amostras recolhidas
(1) Aluviões Lis10/ Lis11/ Lis12/ Lis13/ Lis16 / Lis37
(2) Formação de Benfica Lis23/ Lis24/ Lis25/ Lis26/ Lis28/ Lis31/ Lis33/ Lis34/ Lis35/ Lis36/ Lis46
(3) CVL Lis27/ Lis29/ Lis30/ Lis32/ Lis44/ Lis47/ Lis48
(4) Calcários de Entrecampos Lis1/ Lis2/ Lis5/ Lis14/ Lis17/ Lis19
(5) Areolas da Estefânia e Areias do Vale de Chelas
Lis3/ Lis4/ Lis6/ Lis15/ Lis18/ Lis20/ Lis21/ Lis38/ Lis39/ Lis40/ Lis41/ Lis45
(6) Argilas do Forno do Tijolo e
Argilas e Calcários dos Prazeres
Lis7/ Lis8/ Lis9/ Lis22/ Lis42/ Lis43
39
3.1. Análise Exploratória dos Dados
3.1.1. Características amostrais
Na tabela 3 encontram-se algumas características amostrais obtidas para as 48 amostras de água provenientes de 6 grupos de formações geológicas distintas:
Variáveis Média Desvio
Padrão Mediana 1º Quartil 3º Quartil Mínimo Máximo
pH 7,53 0,80 7,460 6,985 8,030 6,13 10,45 C.E. 1161,96 364,27 1174,500 953,500 1411,500 395,00 2220,00 Eh 30,43 151,13 34,250 -102,100 187,000 -258,10 248,00 359,3 111,55 374,000 291,120 426,500 43,00 575,00 Ca2+ 123,17 49,39 114,500 82,000 152,500 40,00 245,60 Na+ 99,31 52,83 89,450 67,650 132,000 9,70 275,40 K+ 16,40 23,21 8,550 3,035 17,200 0,00 109,00 Mg2+ 32,39 20,45 28,650 17,650 42,300 0,00 91,40 0,26 0,22 0,185 0,132 0,335 0,00 1,01 93,48 43,72 88,100 58,950 118,900 18,50 195,00 0,44 0,83 0,180 0,000 0,385 0,00 3,40 43,35 48,13 30,800 5,785 52,250 0,00 206,00 138,20 111,88 113,700 71,800 160,750 6,10 653,00
Tabela 3: Características amostrais das variáveis (amostra global)
Da análise da tabela 3, podem-se observar algumas características amostrais para as 13 variáveis em estudo. O pH das amostras recolhidas varia entre 6.13 e 10.45, as amostras de água Lis4, Lis13, Lis5, Lis6 e Lis9 têm valores de pH 6.13, 6.20, 6.25, 6.26 e 10.45, respetivamente, que estão fora dos valores paramétricos, de acordo com o Decreto – Lei 306-2007 da qualidade da água para consumo humano (o pH deve estar compreendido entre 6.5 e 9, inclusive). A condutividade elétrica varia entre 395 e 2220 S/cm e a sua mediana (1174.5 S/cm) é superior à média (1161.96 S/cm). O Eh varia entre -258.1 e 248 mV e tem mediana (34.25 mV) superior à média (30.43 mV). Como existem valores Eh positivos e negativos a variabilidade em torno da média é muito grande, sendo o desvio padrão elevado (151.13 mV) e a média relativamente baixa (30.43 mV). As concentrações do ião bicarbonato variam entre 43 e 575 mg/L, apresentando uma mediana (374 mg/L) superior à média (359.3 mg/L). As concentrações do ião cálcio variam entre 40 e 245,6 mg/L, existindo um grande número de amostras de água com concentrações deste ião superiores ao valor paramétrico (100 mg/L), mais precisamente 29 amostras de água. As concentrações do ião sódio variam entre 9.7 e 275.4 mg/L e
40
apresentam uma grande variabilidade em torno da média, sendo o desvio padrão 52.83 mg/L. As amostras Lis21 e Lis31 apresentam concentrações, deste ião, de 275.4 e 217 mg/L, respetivamente, acima do valor paramétrico (200 mg/L). As concentrações do ião potássio variam entre 0 e 109 mg/L. O desvio padrão é elevado (23.21 mg/L), em comparação com a média (16.4 mg/L). Das 48 amostras, 19 apresentam concentrações do ião potássio acima do valor paramétrico (12 mg/L) e 20 amostras têm concentrações inferiores a 6 mg/L. Deste modo, a variabilidade em torno da média é muito grande. As concentrações do ião magnésio variam entre 0 e 91.4 mg/L. Nas amostras Lis22, Lis16, Lis20, Lis48, Lis47, Lis43 e Lis30 as concentrações deste ião são 91.4, 73.5, 69.5, 65.1, 65, 60.3 e 57.5 mg/L, respetivamente. Todas essas concentrações são superiores ao valor paramétrico (50 mg/L). As concentrações do ião fluoreto variam entre 0 e 1.01 mg/L. A variabilidade em torno da média é muito elevada, sendo a média de 0.26 mg/L e o desvio padrão de 0.22 mg/L. As concentrações do ião cloreto variam entre 18.5 e 195 mg/L. As concentrações do ião brometo variam entre 0 e 3.4 mg/L. Das 48 amostras, 40 apresentam concentrações deste ião inferior a 0.5 mg/L e em 17 dessas 40 amostras não se deteta a presença deste ião (0 mg/L). Desta forma, a variabilidade em torno da média é muito grande, sendo o desvio padrão de 0.83 mg/L e a média de 0.44mg/L. As concentrações do ião nitrato variam entre 0 e 206 mg/L. Das 48 amostras, 12 apresentam uma concentração superior ao valor paramétrico (50 mg/L). A variabilidade em relação à média é elevada, sendo a média e o desvio padrão 43.35 e 48.13 mg/L, respetivamente. As concentrações do ião sulfato variam entre 6.1 e 653 mg/L. Nas amostras Lis21, Lis9, Lis42 e Lis37 as concentrações deste ião são 653, 459.2, 329 e 271 mg/L, respetivamente, todas superiores ao valor paramétrico (250 mg/L). O desvio padrão muito grande (111.88 mg/L) é indicador de uma grande variabilidade em torno da média.
Sobre a qualidade da água para consumo humano pode-se aferir que, das 48 amostras de água, apenas 8 (Lis7, Lis12, Lis27, Lis29, Lis30, Lis33, Lis36 e Lis44) são consideradas apropriadas para o consumo humano, embora fosse necessário averiguar se, do ponto de vista bacteriológico, estariam de acordo com as recomendações da legislação que regula a qualidade das águas para o consumo humano.
Tal como sugere a tabela 2, a amostra global das 48 amostras de água pode ser subdividida em 6 amostrais parciais, correspondendo a cada grupo de formações