Mergulho de produtos de esferas e suas somas conexas em codimensão 1

Mergulho de produtos de esferas e suas somas conexas em

codimensão 1

SERVIÇO DE PÓS-GRADUAÇÃO DO ICMC-USP Data de Depósito: 17 de janeiro de 2007

Assinatura:

Mergulho de produtos de esferas e suas somas conexas em codimensão 1

Marcio Colombo Fenille

Orientador: Prof. Dr. Oziride Manzoli Neto

Dissertação apresentada ao Instituto de Ciências Matemáti-cas e de Computação - ICMC/USP, como parte dos requisi-tos para obtenção do título de Mestre em Matemática.

USP - São Carlos Fevereiro/2007

Agradecimentos

Resumo

Estudamos inicialmente resultados de classificação de difeomorfismos de produtos de esferas de mesma dimensão. Tratado isto, estudamos os mergulhos suaves de produtos de esferasS1_×Sq_×Sr_{, com 1≤q ≤r,}

na esfera Sq+r+2, e buscamos a total caracterização do fecho das duas componentes conexas do complementar de tais mergulhos. Tratamos com enfoque especial os mergulhos do toroT3(=S1×S1×S1)na esfera

Abstract

We study first results of the classification of difeomorphisms of the carte-sian product of spheres of the same dimension. In the sequence we study smooth embeddings of the cartesian product of spheres S1_×Sq_×Sr_,

Sumário

Introdução 17

1 Preliminares 19

1.1 Homologia e cohomologia . . . 19

1.2 Homotopia e grupo fundamental . . . 25

1.3 Homologia e cohomologia em variedades . . . 29

1.4 Nós e enlaçamentos . . . 31

1.5 Mergulho de produtos de esferas . . . 34

1.6 Topologia Linear por Partes (PL) . . . 37

2 Difeomorfismo de produtos de esferas 39 2.1 Algumas manipulações algébricas . . . 39

2.2 Classificação das matrizes que representam automorfismos . . . 44

3 Mergulho de produtos de três esferas em codimensão 1 53 3.1 Sobre as considerações e as espectativas . . . 53

3.2 Sobre a existência de mergulhos exóticos . . . 54

A construção c. . . 54

3.3 Sobre a existência de mergulhos não-exóticos . . . 58

3.4 Sobre as homologias das componentes do complementar de um mergulho . . . 70

3.5 O que completa o capítulo . . . 77

4 Mergulhos do toro T3 _{na esfera S}4 ₇₉ 4.1 Os Gêmeos de Montesinos . . . 80

4.2 Um problema envolvendo mergulhos de3-variedades em S4 . . . 83

4.3 O que responde o problema anterior . . . 83

4.4 O análogo da seção anterior para outras dimensões . . . 89

5.2 Esquema para a prova do teorema principal . . . 92

Primeira parte . . . 92

Segunda parte . . . 100

Terceira parte . . . 104

5.3 A prova do teorema principal . . . 106

Referências Bibliográficas 107

Lista de Símbolos 111

Lista de Figuras

3.1 Esquema gráfico da construção c . . . 55

4.1 Vizinhança regular da 2-esferaS . . . 81

4.2 Vizinhança regular da 2-esferaR . . . 81

4.3 Decomposição por alças dos Gêmeos de Montesinos . . . 82

Introdução

Este texto trata especialmente dos mergulhos de produtos de esferas e suas somas conexas em codimensão 1. As esferas estão entre os objetos de estudo mais antigos da matemática e desde o surgimento da Topologia o interesse pela pesquisa sobre esferas de dimensões mais altas tem se fortalecido. Quando trabalhamos com mergulhosf :Sp×Sq×Sr →Sp+q+r+1, ao contrário do que nos possa inicialmente parecer, os problemas de classificação do fecho das componentes conexas deSp+q+r+1−f(Sp ×Sq×Sr) tornam-se mais simples quando a dimensão de todas as esferas envolvidas no produto é maior ou igual a dois. Neste sentido, decidimos em nosso trabalho tratar especialmente os casos em que1 =p≤q≤r.

Antes porém de partimos ao estudo específico a que se propunha este trabalho, dedicamos um capítulo às definições e resultados básicos necessários para o progresso e entendimento do texto. É bastante provável que o leitor já esteja bastante familiarizado com grande parte do conteúdo que compõe este capítulo; no entanto, cremos que seja de demais valia esta breve apresentação, mesmo para fixarmos notações e terminologias. Vale ressaltar que não nos preocupamos em apresentar as demonstrações de tais resultados; antes disso, nossa preocu-pação consistiu em inserir com maior amplitude os tópicos básicos do desenvolvimento deste trabalho, para que o leitor sinta-se mais confortável com a leitura do restante do texto, sem necessidade freqüente de consulta a outros materiais.

O texto se divide efetivamente em cinco capítulos, sendo o primeiro como já mencionado no parágrafo anterior. Ao segundo capítulo ainda não compete os resultados mais importantes e aos quais se dedicou maior ímpeto ao estudo. Não obstante, é nele apresentado resultados conclusivos de classificação de difeomorfismos de produtos de esferas. O desenvolvimento desta parte do trabalho requer várias ferramentas algébricas, mas todas bastante simples. Alguns tópicos de Topologia Algébrica também aparecem, mas nenhum que não tenha sido apresentado do capítulo preliminar.

propriamente dita, e outros que descrevem maneiras de, sob certas condições, se construir infinitos mergulhos mutuamente distinto de modo que o fecho de nenhuma das componentes de seu complementar seja homotopicamente equivalente a um produto de esferas com um disco. Os resultados deste capítulo classificam totalmente os mergulhos estudados.

No quarto capítulo estudamos mais pormenorizadamente os mergulhos do toroT3na esfera

S4_{. O resultado principal do capítulo é Teorema 4.3.1, no qual se demonstra a existência de}

duas 3-variedades que sempre podem ser mergulhadas em S4 de modo que o fecho de cada componente de S4−f(T3), com f mergulho, seja difeomorfo ao fecho do complementar de um destes mergulhos. Sem dúvida, este é um resultado bastante atraente.

O último capítulo é destinado ao estudo dos mergulhos de somas conexas de toros em codi-mensão um. Nele apresentados uma série de resultados bastante expressivos que convergem a demonstração do Teorema 5.1.2, o principal do capítulo, que dá uma caracterização, a menos de pseudo-isotopias, dos referidos mergulhos.

Capítulo

1

Preliminares

1.1

Homologia e cohomologia

Complexo de cadeias e cocadeias - Teoremas dos Coeficientes Universais

Um complexo de cadeias C = (Cq, ∂q) é definido por um par de seqüências de grupos

abelianosCq,q ∈Z, e uma seqüência de homomorfismos∂q:Cq→Cq−1tal que∂q−1◦∂q = 0,

para todo q ∈ Z. É definido também _{Cq = 0}se _{q < 0}. Diremos que _{C = (Cq, ∂q)} é livre se

cada Cq é um grupo abeliano livre. Os elementos de Cq são denominados q-cadeias e os

homomorfismos ∂p operadores bordo. A um complexo de cadeias C = (Cq, ∂q) se associa

de modo natural certos subgrupos dos grupos de cadeias Cq. O grupo Zq(C) = Ker(∂q) é

chamado grupo dosq-ciclos, e o grupoBq(C) = Im(∂q+1)é chamado grupo dos q-bordos. São

ambos subgrupos normais deCq e, sendo ∂q◦∂q+1 = 0, temosBq(C)⊂Zq(C).

Definição 1.1.1. O grupo quociente Hq(C) = Zq(C)/Bq(C) é chamado grupo de homologia q-dimensional do complexo C.

SejamC= (Cq, ∂q) um complexo de cadeias e Gum grupo abeliano. Considere o produto

tensorial C ⊗G. Por definição, C ⊗G é o complexo de cadeias (Cq ⊗G, ∂q ⊗1G), onde 1G:G→G é o homomorfismo identidade.

Definição 1.1.2. O grupo de homologia q−dimensionalHq(C ⊗G) =Zq(C ⊗G)/Bq(C ⊗G)é

chamado grupo de homologia q-dimensional de C com coeficientes em G e será denotado por

Hq(C;G).

A relação entre Hq(C;G) eHq(C) é dada pelo seguinte resultado encontrado em [33, p. 243].

Teorema 1.1.3. (Teorema dos Coeficientes Universais para Homologia)Sejam C

um complexo de cadeias livre e G um grupo abeliano. Então

Hq(C;G)≈(Hq(C)⊗G)⊕Tor(Hq−1(C), G)

Agora, seCé um complexo de cadeias eGum grupo abeliano, formamos o grupo abeliano

Cq = Hom(Cq, G), cujos elementos são todos os homomorfismos h :Cq → G, os quais serão

chamados q-cocadeias de C. O cobordo de h é uma (q + 1)-cocadeia, denotada por δq_{h, e}

definida por δqh = (−1)q+1_h◦∂

q+1 : Cq+1 → G. Em outras palavras, temos dito que o

operador bordo ∂q+1 :Cq+1 →Cq induz homomorfismo ∂q+1∗ : Hom(Cq, G)→ Hom(Cq+1, G)

e δq = (−1)q+1_∂∗

q+1. Observe que δq ◦δq+1 = 0. Segue que (Cq, δq) é um complexo de

cocadeias com coeficientes em G. Denotaremos Hom(C, G) = (Hom(Cq, G), δq).

Definição 1.1.4. A homologia do complexo Hom(C, G) é a cohomologia deC com coeficientes em G, a qual será denotada por Hq(C;G), com Hq(C;G) = Ker(δq)/Im(δq−1). Além disso, um elemento de Ker(δq) é chamado de q-cociclo, e um elemento de Im(δq−1) é chamado de

q-cobordo.

Para o Teorema a seguir, ver [33, p. 222].

Teorema 1.1.5. (Teorema dos Coeficientes Universais para Cohomologia)Sejam

C um complexo de cadeias livre eG um grupo abeliano. Então

Hq(C;G)≈Hom(Hq(C), G)⊕Ext(Hq−1(C), G)

Faremos agora algumas definições que, por ora, parecerão totalmente abstratas, mas que utilizaremos na próxima seção para construirmos objetos e resultados que serão muito utiliza-dos neste trabalho.

Comecemos considerando um complexo de cadeia C = (Cq, ∂q). Por um sub-complexo de

cadeiasDdeCentendemos uma seqüência de subgrupos normaisDq⊂Cqe de homomorfismos ∂′

q : Dq → Dq−1 tais que ∂q′ = ∂q|Dq. Na verdade, uma seqüência de subgrupos Dq ⊂ Cq

definem um sub-complexo se, e somente se, a seqüência for estável em relação aos operadores bordo, isto é, se ∂qDq ⊂Dq−1. Dado, então, um sub-complexo Dde C, define-se ocomplexo

quociente E = C/D como o complexo de cadeias E = (Eq,∂¯q), onde Eq = Cq/Dq e ¯

∂q :Eq→Eq−1 é definido por passagem ao quociente de ∂q (visto que∂qDq⊂Dq−1). Como

anteriormente pode-se definir, então, os grupos de homologia do complexo quociente E por

Hq(E) = Ker( ¯∂q)/Im( ¯∂q+1), para cada inteiro q. Tudo isto pode ser feito para complexos de

cocadeias de maneira semelhante as já adotadas nesta seção.

Chama-se complexo aumentado de um complexo C = (Cq, ∂q) ao complexo de cadeias

e

C = (Ceq,∂eq), para o qual se define Ceq = Cq se q ≥ 0, Ce−1 = Z, e ∂eq = ∂q se q ≥ 1,

e

∂0 = εn : C0 → Z um homomorfismo conhecido por Índice de Kronecker. (Detalhes da

1.1 Homologia e cohomologia 21

seq >1 e∂e−q= 0 seq ≥1. Os grupos de homologia do complexo Cesão denominadosgrupos

de homologia reduzidos do complexo C e denotados por Heq(C). Uma construção semelhante

pode ser realizada a partir desta para complexos de cocadeias de modo que possamos definir osgrupos de cohomologia reduzidos do complexo C, que denotaremos por Heq_(C).

Homologia e cohomologia singular

Em [11] encontramos resultados de homologia e cohomologia singular para um espaço topológico X, descritos nos seguintes termos: Considere os vetores e0 = (0,0, . . .), e1 = (1,0, . . .), e2 = (0,1,0, . . .), . . . ∈ R∞. Identificamos Rn com o subespaço dos vetores nos

quais são nulas todas as componentes depois da n-ésima. Para qualquerq ≥ 0, definimos o

q-simplexo padrão∆q como sendo o simplexo geométricoq-dimensional gerado pore0, . . . , eq.

Sendo P0, . . . , Pq pontos em algum espaço afim E, (P0. . . Pq) denotará a restrição a ∆q da

única aplicação afimRq _→Eaplicando_e0em_P0, ...,_eq em_Pq. Assim,_{(e0. . . eq)}é a aplicação

identidade de∆q, denotada por δq.

Dado um espaço X, um q-simplexo singularem X é uma aplicação ∆q →X. Definimos Cq(X)como o grupo livre gerado por todos osq-simplexos singulares. Os elementos deCq(X)

são combinações lineares

X

σ νασ

onde σ corresponde aos q-simplexos singulares e os coeficientes να estão no anel do inteiros Z_{. Estas somas são chamadas q-cadeias singulares.}

Para q > 0, defina Fi

q : ∆q−1 → ∆q, para 0 ≤ i ≤ q, como sendo a aplicação afim (e0. . .eˆi. . . eq), ondeeˆisignifica omitirei. Para umq-simplexo singular arbitrárioσno espaço X, defina a i-ésima face σ(i) de σ como sendo o(q−1)-simplexo singular σ◦F_qi. Assim, F_qi

é ai-ésima face de δq, e seσ = (P0. . . Pq),X afim, entãoσ(i) = (P0. . .Pˆi. . . Pq). Além disso, F_qi aplica ∆q−1 afim e homeomorficamente sobre a face de ∆q oposta ao vértice ei. Agora,

definimos obordo de um q-simplexo singular como a(q−1)-cadeia singular

∂(σ) = q

X

i=0

(−1)iσ(i)

e, por esta definição, mostra-se que ∂◦∂ = 0. Uma q-cadeia singular c tal que ∂(c) = 0 é chamada ciclo; sec =∂(c′_{) para alguma (q+ 1)-cadeia c}′_{, então dizemos que c é umbordo.}

Duasq-cadeiasc1 e c2 que se diferem por um bordo são ditashomólogas e denota-se c1 ∼c2.

Como ∂◦∂ = 0, os bordos formam um subgrupo Bq do grupo Zq dos ciclos. Chamaremos

o grupo quociente Zq/Bq de q-ésimo grupo de homologia singular de X, e vamos denotá-lo Hq(X).

Se Y é um subespaço de X, podemos repetir todo o processo anterior para constru-irmos o complexo de cadeias com grupos livres Cq(Y), que serão subgrupos de Cq(X) para

cada inteiro q, e operadores bordo ∂′

q que para cada inteiro q será a restrição ∂q|Y do

C(Y) = (Cq(Y), ∂q′) do complexo C(X). Denotamos o q-ésimo grupo de homologia do

com-plexo quocienteC(X)/C(Y)porHq(X, Y) e o tratamos porq-ésimo grupo de homologia

rela-tiva do par (X, Y).

Definimos o grupoCq_{(X) de todas as q-cocadeias singulares sobre X como sendo o grupo} Hom(Cq(X),Z). Assim, uma cocadeia singular de dimensão q é um homomorfismo linear c : Cq(X) → Z. Se denotamos o valor desse homomorfismo sobre uma cadeia z por [z, c],

vê-se facilmente que [,]é bilinear. ComoCq é um funtor de espaços topológicos em grupos e Hom(,Z₎é um contrafuntor na categoria dos grupos, o funtor composto_Cqé um contrafuntor

de espaços topológicos em grupos. Além disso tudo, pode-se provar que, para cada inteiro

q, existe um único homomorfismo δq :Cq(X) → Cq+1(X), o operador cobordo, satisfazendo [∂z, c] = [z, δc] para toda (q+ 1)-cadeia z e q-cocadeia c. Ainda mais, δ◦δ = 0. Construí-mos assim um complexo e cocadeias C∗_{(X) = (C}q_{(X), δ}q_{) e definimos o q-ésimo grupo de}

cohomologia singular de X porHq_{(X) =H}

q(C∗(X)) = Ker(δq)/Im(δq−1).

SeY é um subespaço deX podemos construir em semelhança ao realizado para os grupos de homologia, os grupos de cohomologia relativa Hq(X, Y).

Propriedades dos grupos de homologia

Assuma que grupos abelianos Hn(X, A) estejam sempre definidos para n = 0,1,2, . . .,

quando X é um espaço topológico e A é um subespaço deX. Estes grupos têm as seguintes propriedades fundamentais, que podem ser melhor observadas em [30, p. 99 - 100].

(1) Se f : (X, A)→(Y, B)é uma aplicação de pares, então existe um homomorfismo natural induzindo f∗ :H∗(X, A) →H∗(Y, B). Naturalidadequer dizer que:

(a) Se1 : (X, A) →(X, A) é a identidade, então 1∗:H∗(X, A)→H∗(X, A) é isomorfismo.

(b) Se f : (X, A) → (Y, B) e g : (Y, B) → (Z, C) são aplicações de pares, então tem-se (f◦g)∗ =f∗◦g∗.

(2) Existe um homomorfismo bordo natural ∂ :Hn(X, A) →Hn−1(A)≡Hn−1(A,∅). Aqui a

naturalidade indica que sef : (X, A)→(Y, B)é uma aplicação entre pares, então é comutativo o diagrama abaixo:

Hn(X, A)

f∗

∂ _//

Hn−1(A)

(f|A)∗

Hn(Y, B) ∂ //Hn−1(B)

(3) (Exatidão) É exata a seqüência· · · →Hn(A)→Hn(X)→Hn(X, A)−→∂ Hn−1(A)→ · · ·,

onde os homomorfismo não indicados são induzidos por inclusões.

(4) (Homotopia) Sef, g : (X, A)→(Y, B)são homotópicas, então f∗ =g∗.

(5) (Excisão) Suponha que seja U ⊂A um aberto tal que seu fecho está contido no interior de A. Então o homomorfismo H∗(X−U, A−U) → H∗(X, A) induzido pela inclusão é um

1.1 Homologia e cohomologia 23

(6) (Dimensão)

Hn(pt.)≈

(

Z _{se n= 0}

0 se n6= 0

Definição 1.1.6. Seja(X, Y, Z) uma tríada de espaços topológicos com Y e Z subespaços de

X. Considere as aplicações de paresk1: (Z, Y∩Z)→(Y∪Z, Y)ek2 : (Y, Y∩Z)→(Y∪Z, Z).

Dizemos que a tríada (X, Y, Z) é exata se as induzidas das inclusões em homologia k1∗ e k2∗

são isomorfismos.

Teorema 1.1.7. (Seqüência de Mayer-Vietoris) Seja (X, Y, Z) uma tríada exata de espaços topológicos com X = Y ∪Z. Então existe uma seqüência exata, chamada seqüência de Mayer-Vietoris da tríada (X, Y, Z),

· · · →Hn(Y ∩Z) η∗

−→Hn(Y)⊕Hn(Z) ξ∗

−→Hn(X) ∂ ∗

−→Hn−1(Y ∩Z)→ · · ·

onde η∗(x) = i1∗(x) ⊕ −i2∗(x) e ξ∗(y ⊕z) = j1∗(y) + j2∗(z), com i1 : Y ∩ Z → Y, i2 :Y ∩Z →Z, j1 :Y →X e j2:Z →X inclusões.

Teorema 1.1.8. SeSndenota a esferan-dimensional e1Sn :Sn→Sné a identidade, temos:

(1) Hq(Sn) = 0, q6= 0, n;

Hn(Sn)≈Z≈H0(Sn), n >0; H0(S0)≈Z⊕Z.

(2) 1Sn :Sn→Sn é um gerador de H_n(Sn) (sob interpretação geométrica).

Para o afirmação (2) do último teorema veja a interpretação geométrica da Homologia descrita em [30, p. 98].

O seguinte resultado pode ser consultado em [33, p. 230].

Teorema 1.1.9. (Fórmula de Künneth) Se X e Y são espaços topológicos, existe um isomorfismo natural

Hn(X×Y)≈

M

p+q=n

(Hp(X)⊗Hq(Y)) ⊕

M

r+s=n−1

Tor(Hr(X), Hs(Y))

O produto de Kronecker

Dados dois complexos de cadeias C = (Cq, ∂q) e C′ = (Cq′, ∂q′), chama-se aplicação de

cadeias Λ :C → C′ a uma família de homomorfismos Λ ={Λq :Cq →Cq′}, tal que∂q′ ◦Λq = Λq−1◦∂q para todo inteiro q.

Proposição 1.1.10. Dado um complexo de cadeias C, existe um homomorfismo, chamado produto Kronecker,

Hn(C)⊗Hn(C)→Z,

onde a imagem de x⊗y se escreve ⋖_{x, y}⋗. Além disso, se _{f : C → D} é uma aplicação de

Note que se são dados um espaço topológicoXe um subespaçoY deste, podemos construir os complexos de cadeias C(X) eC(Y) deX e de Y, respectivamente, e a família de inclusão

iq :Cq(Y) → Cq(X) constituirá uma aplicação entre as cadeias C(Y) e C(X). Deste modo,

segundo a proposição anterior, teremos definido um homomorfismo, o produto de Kronecker,

Hn(Y)⊗Hn(X)→Z

tal que ⋖_i∗_{(y), x}⋗₌⋖_{y, i∗(x)}⋗, sempre que _y∈Hn_(Y) e_x∈Hn(X).

O resultado apresentado nesta seção pode ser encontrados em [24, p. 164], onde o leitor interessado poderá encontrar, além de sua demonstração, outras propriedades importantes neste mesmo contexto.

Produto cup e cap

Seja C = (Cq, ∂q) um complexo de cadeias e C⊕ =L_q≥0Cq. Seja C⊕ = L_q≥0Cq, onde C∗ = (Cq, δq) é o complexo de cocadeias dual de C, obviamente com Cq = Hom(Cq,Z) e δq _{: C}q _{→ C}q−1 _{definido por δ}q_{h = (−1)}q+1_{h ◦∂}∗

q+1 ∈ Cq+1 se h ∈ Cq. Nestes termos, Hn(C) =Hn(C∗).

Se C e C′ _{são complexos de cadeias, definimos C ⊗ C}′ _por(C⊗C′₎

n =L_i+j=nCi⊗Cj′ e ∂⊗∂′(c⊗c′) =∂c⊗c′+ (−1)k_c⊗∂′_c′_{, sec∈C}

k. Defina a aplicação chamada operador slant

/: (C⊗C′)n⊗C′k →Cn−k

pela fórmulaa/b=P_i+j=nb(a_j′)ai, onde a=L_i+j=n(ai⊗a′_j) eb(a′_j) = 0sempre quej 6=k.

Para ver que esta operação está, de fato, bem definida com imagem em Cn−k, note

ini-cialmente que sendo b ∈ C′k = Hom(C_k′,Z_{), temos que b é um homomorfismo b : C}′ k → Z.

Além disso, definimos b(a′_j) = 0 sej 6=k. Mas quando j =k, com k fixado, nas somas que definem o operador slantteremosi=n−k. Logo, ficamos com

a/b= X i+j=n

b(a′_j)ai =b(a′k)an−k∈Cn−k.

Sem muito esforço e como em [5] mostra-se que o operador slant é uma aplicação de cadeias; logo induz uma aplicação H∗((C ⊗ C′)⊗C′∗) →H∗(C). Compondo esta última com

a aplicação natural

H∗(C ⊗ C′)⊗H∗(C′)→H∗((C ⊗ C′),

chegamos ao operador slant

/:Hn(C ⊗ C′)⊗Hk(C′)→Hn−k(C).

Agora, seja C um complexo de cadeias aumentado com uma aplicação diagonal, digamos △ : C → C ⊗ C tal que (ε⊗1)△(c) = (1⊗ε)△(c) = c, onde ε : C → Z _{é o aumento, e}

1.2 Homotopia e grupo fundamental 25

porC∗⊗ C∗ →(C ⊗ C)∗ △

∗

−→ C∗, onde C∗⊗ C∗ →(C ⊗ C)∗ é a inclusão óbvia. Isto é chamado

produto cup, e em nível de cohomologia induz

Hn(C)⊗Hk(C)→Hn+k(C),

também chamado produtocup, x⊗y7→x`_y. Usando_△, podemos definir o produto cap

a_:Cn⊗Ck_→Cn−k

pela fórmulaaa_{b= (△a)/b. Como} a_{é a composição das aplicação de cadeias △e/, segue} queaé uma aplicação de cadeias e induz

a_{:Hn(C ⊗H}k_{(C))→Hn−q(C).}

Mais geralmente, suponha que A, B e C sejam complexos de cadeias aumentados e seja △ : A → B ⊗ C uma aplicação de cadeias. Então, similarmente ao anterior, obtemos uma aplicação em cohomologia

`_:Hp_(B)⊗Hq_(C)→Hp+q_(A)

e um produtocap

a_:Hn(A)⊗Hk_{(C)→Hn−k(B)}

Diversos resultados envolvendo os produtoscupecapserão utilizados nos capítulos seguintes deste trabalho; no entanto, não os poremos aqui devido a exaustão e delonga que isso causaria. Antes disso, aqui deixamos [5] e [11] como as duas principais referências ao leitor interessado.

1.2

Homotopia e grupo fundamental

O leitor deve estar bastante habituado com os conceitos envolvendo grupos de homotopia. Nesta convicção, expomos aqui somente algumas identificações destes grupos que faremos, em momentos oportunos, durante boa parte deste texto. Façamo-las:

Seja X um espaço topológico e x0 um ponto base fixado em X. Se identificamos o bordo

do disco Dn a um ponto, o espaço quociente obtido desta identificação é a n-esferaSn com um ponto distinguido s0. Assim, πn(X, x0) pode ser interpretado como o grupo das classes

de homotopia das aplicações de (Sn_{, s}

0) em (X, x0). Outra interpretação interessante, que

na realidade é a mesma vista de outra forma, é a identificação que se faz deπn(X, x0)com o

grupo das classes de homotopia das aplicações de (Dn_{, S}n−1_{) → (X, x}

0). Agora, se A é um

subespaço fechado e conexo por caminhos deX, os elementos do grupo de homotopia relativa

πn(X, A, x0)estão em correspondência com as classes de homotopia das aplicações contínuas κ: (Dn_{, S}n−1_{, s}

0)→ (X, A, x0), onde κ(Dn) ⊂X, κ(Sn−1) ⊂A e κ(s0) = x0. Note que um

Os Teoremas de Van Kampen

Sejam(X, x0)e (Y, y0)espaços topológicos com pontos base, e f : (X, x0)→(Y, y0) uma

aplicação contínua. Vamos denotar porf♯ohomomorfismo induzido pela aplicaçãof no grupo

de homotopia, ou seja, f♯ :πn(X, x0)→πn(Y, y0) definida pela equaçãof♯([h]) = [h◦f].

No transcorrer deste trabalho disporemos principalmente dos resultados relacionados ao grupo fundamental dos espaços que estaremos tratando, não sendo tão importante o estudo dos grupos de homotopia de dimensões mais altas. Nestas situações, um resultado que será sempre de grande valia é o chamado Teorema de Van Kampen que apresentamos agora em duas versões, podendo a primeira ser encontrada em [8, p. 63] e a última em [28, p. 371].

Sejam X, X0, X1 e X2 espaços topólógicos com X = X1 ∪X2 e X0 = X1 ∩X2 6= ∅, X1 e X2 abertos, X0, X1 e X2 conexos por caminhos e x0 ∈ X0 um ponto fixado. Denote G =π1(X, x0) e Gi = π1(Xi, x0), i = 0,1,2. Os homomorfismos induzidos pelas aplicações

inclusões formam um diagrama comutativo

G0 w0 θ2 ! ! B B B B B B B B θ1 } } |||| |||| G1 w1 ! ! C C C C C C C

C G2

w2 } } {{{{ {{{{ G

Teorema 1.2.1. (Teorema de Van Kampen)Os grupos wi(Gi),i= 1,2, imagens por wi

dos grupos Gi, geram o grupo G. Além disso, se H é um grupo arbitrário e ψi : Gi → H, i= 0,1,2, são homomorfismos que satisfazem ψ0 =ψ1◦θ1=ψ2◦θ2, então existe um único

homomorfismo Φ :G→H tal que ψi = Φ◦wi, i= 0,1,2.

Teorema 1.2.2. (Teorema de Van Kampen)Suponha que os grupos fundamentais de X0, X1 e X2 tenham as seguintes apresentações:

π1(X1, x0) =|x1, x2, . . .:r1, r2, . . .|,

π1(X2, x0) =|y1, y2, . . .:s1, s2, . . .|,

π1(X0, x0) =|z1, z2, . . .:t1, t2, . . .|.

Então o grupo fundamental de X é dado por

π1(X, x0) =|x1, x2, . . . , y1, y2, . . .:r1, r2, . . . , s1, s2, . . . , θ1(z1) =θ2(z1), θ1(z2) =θ2(z2), . . .|.

Observe que se π1(X0) é trivial, entãoπ1(X) é o produto livre deπ1(X1) e π1(X2).

1.2 Homotopia e grupo fundamental 27

Os Teoremas de Hurewicz

Outros resultados muito importantes são aqueles que relacionam os grupos de homotopia com os grupos de homologia. Estes resultados, que aqui apresentamos sumarizados, podem ser encontrados em [33], Seções 4 e 5 do Capítulo 7, e levam o mérito à Hurewicz.

Teorema 1.2.3. (Teorema do Homomorfismo de Hurewicz) Considere dois espaços topológicos com ponto base (X, x0) e (Y, y0), um subespaço A de X contendo x0 e uma

apli-caçãof : (X, A, x0)→(Y, A, y0). Sen≥2, ou sen= 1eA={x0}, existe um homomorfismo ϕque faz comutar o diagrama

πn(X, A, x0)

ϕ

f♯

/

/πn(Y, A, y0)

ϕ

Hn(X, A) f∗

/

/Hn(Y, A)

Teorema 1.2.4. SeXé um espaço conexo por caminhos, então o homomorfismo de Hurewicz

ϕ:π1(X) →H1(X) é sobrejetor e seu núcleo é o subgrupo comutador de π1(X).

Teorema 1.2.5. (Teorema de Hurewicz)SejaXum espaço simplesmente conexo. Então, são equivalentes as seguintes afirmações:

πj(X) = 1 para todo j= 1, . . . , n−1, Hj(X) = 0 para todo j= 1, . . . , n−1.

Além disso, no caso de uma das condições acima for satisfeita, tem-seHn(X)≈πn(X).

O Teorema de Whitehead

Definição 1.2.6. Sejam X e Y espaços topológicos e f :X → Y uma aplicação contínua. Dizemos que f é uma equivalência de homotopia fraca se f induz uma correspondência bi-unívoca entre as componentes conexas por caminhos de X e de Y e se para todo n ≥ 1 e

x∈X, f♯:πn(X, x)→πn(Y, f(x))é um isomorfismo.

Observe que se f :X→Y é uma equivalência de homotopia, então f é uma equivalência de homotopia fraca. Além disso, seXeY forem variedades infinitamente diferenciáveis, então ambas têm estrutura de complexos CW e os conceitos de equivalência de homotopia e equiva-lência de homotopia fraca coincidem, pelo Corolário 24 da página 405 de [33]. Para maiores detalhes consulte esta referência. Considerando este fato juntamente com o Teorema 7.15 de [35, p. 182], decorre o seguinte resultado, freqüentemente chamado Teorema de Whitehead.

Teorema 1.2.7. (Teorema de Whitehead) SejamX e Y complexos CW finitos simples-mente conexos e f : X → Y uma aplicação contínua tal que f∗ : Hn(X) → Hn(Y) é um

O produto Wedge

Dados espaços X e Y com pontos escolhidosx0 ∈X e y0 ∈Y, o produto wedge X∨Y

é o espaço quociente obtido da união disjunta X ⊔Y identificando-se os pontos x0 e y0 a

um único ponto. Mais geralmente, podemos formar o produto wedge ∨αXα de uma coleção

arbitrária de espaços Xα identificando no espaço ⊔αXα pontos escolhidos xα ∈ Xα. No

caso dos espaços Xα serem complexos celulares e os pontos xα serem 0-células, o produto ∨αXα é um complexo celular, já que é obtido do complexo celular ⊔αXα colapsando-se um

subcomplexo a um ponto. Para qualquer complexo celular X, o quociente Xn/Xn−1, onde

Xj denota o j-ésimo esqueleto de X, é um produto wedge de n−esferas, ∨αSαn, com uma

esfera para cada n−célula de X.

O produto de Whitehead

Considere o produtowedgeSp_∨Sq_=Sp_×{q

0}∪{p0}×Sq ⊂Sp×Sq, ondep0 ∈Sp,q0 ∈Sq, p, q≥2. Os elementos deπp+q(Sp×Sq, Sp∨Sq, ⋆) estão em correspondência com as classes

de homotopia das aplicações contínuas κ: (Dp_×Dq_{, ∂(D}p_×Dq_{), w)→(S}p_×Sq_{, S}p_∨Sq_{, ⋆),}

com w ∈ Sp−1_×Sq−1 _{= ∂D}p_×∂Dq _{⊂ ∂(D}p_×Dq_{) e ⋆ = (p}

0, q0). Assim, cada elemento γ ∈πp+q(Sp×Sq, Sp∨Sq, ⋆) é representado por uma aplicação contínua

κ: (Dp×Dq, ∂(Dp×Dq), w)→(Sp×Sq, Sp∨Sq, ⋆).

Observe que Hp+q(Sp ×Sq, Sp ∨Sq, ⋆) ≈ Z. Segue-se do Teorema de Hurewicz relativo,

enunciado em [33, p. 397], que

πp+q(Sp×Sq, Sp∨Sq, ⋆)≈Hp+q(Sp×Sq, Sp∨Sq, ⋆)≈Z

poisSp×Sq eSp∨Sq são simplesmente conexos. Defina o homomorfismo bordo

d:πp+q(Sp×Sq, Sp∨Sq, ⋆)→πp+q−1(Sp∨Sq, ⋆)

como sendo d(γ) =σ, onde σ é a classe de homotopia representada pela aplicação restrição

h|∂(Dp_×Dq₎: (∂(Dp×Dq), w)→(Sp∨Sq, ⋆).

Definição 1.2.8. Considere as classes de homotopia α ∈ πp(X, x0) e β ∈ πq(X, xo)

repre-sentadas pelas aplicações κ1 : (Sp, p0)→(X, x0) e κ2 : (Sq, q0)→(X, x0), respectivamente, e

a aplicação κ1∨κ2 : (Sp∨Sq, ⋆)→(X, x0) com κ1∨κ2(p0, q0) =x0,κ1∨κ2(x, q0) =κ1(x) e κ1∨κ2(p0, y) =κ2(y). Seja γ um gerador deπp+q(Sp×Sq, Sp∨Sq, ⋆)≈Z escolhido através

da fixação de uma orientação adequada de Sp×Sq. Para a composta abaixo

πp+q(Sp×Sq, Sp∨Sq, ⋆)−→d πp+q−1(Sp∨Sq, ⋆)κ−→1∨κ2 πp+q−1(X, x0)

defina

[[α, β]] = ((κ1∨κ2)♯◦d)(γ) = (κ1∨κ2)♯(σ)∈πp+q−1(X, x0).

1.3 Homologia e cohomologia em variedades 29

Observe que[[α, β]] apenas depende das classes de homotopiaα eβ e não dos particulares representantesκ1 e κ2.

Uma propriedade do produto de Whitehead que será utilizada no próximo capítulo deste texto é a “bilinearidade”, isto é, para quaisquera, b∈Z _tem-se

[[aα, bβ]] =ab[[α, β]].

Esta propriedade e outras mais sobre o produto de Whitehead podem ser encontradas em [35], esta especificamente no Capítulo 7, p. 478.

O seguinte resultado pode ser encontrado em [7].

Proposição 1.2.9. A aplicação contínua κ1∨κ2 :Sp∨Sq →X se estende a uma aplicação

contínua K_:Sp_×Sq_→X se, e somente se,_{[[α, β]] = 0} em_{πp+q−1(X, x0)}.

H-espaços

Definição 1.2.10. Seja (X, x0) um espaço topológico com ponto base x0 ∈X. Dizemos que X é um H-espaço se existe uma aplicação contínua f :X×X →X, comf(x0, x0) =x0 e tal

que as aplicação f1 :X →X, f1(x) = f(x, x0), e f2 :X → X, f2(x) = f(x0, x), são ambas

homotópicas a aplicação identidade 1X :X→X. O ponto x0 ∈X é o elemento neutro de X

a menos de homotopia.

Foi demonstrado em [1] que Sp tem estrutura de H-espaço se, e somente se, p= 1,3 ou 7. Nestes casos, a aplicaçãof :Sp_×Sp _→Sp _{é a multiplicação dos complexos, dos quatérnios e}

dos octônios unitários, respectivamente.

Proposição 1.2.11. Se p é um inteiro positivo ímpar, p 6= 1,3 e 7, e neste caso Sp não é um H-espaço, então o produto de Whitehead [[β, β]] é um elemento de ordem 2 de π2p−1(Sp),

ondeβ é um gerador de πp(Sp)≈Z.

1.3

Homologia e cohomologia em variedades

Dualidades

Os próximos resultados podem ser encontrados em [27, p. 419] e [13, p. 254], respectiva-mente, e serão de grande utilidade para os propósitos deste trabalho.

Teorema 1.3.1. (Dualidade de Poincaré-Lefschetz) Seja M uma n-variedade com-pacta com bordo ∂M. Se (M, ∂M) é orientável, então

Hp(M, ∂M)≈Hn−p(M) e Hp(M)≈Hn−p(M, ∂M).

Teorema 1.3.2. (Dualidade de Alexander) Seja X 6= ∅ um subconjunto próprio da esferaSn_{. Suponha que X seja um retrato de alguma vizinhança. Então}

e

O Teorema do h-cobordismo

Para os enunciados desta subseção veja [25].

Definição 1.3.3. Uma terna (W, V0, V1) é uma tríada de variedades se W é uma variedade

compacta e seu bordo é a reunião disjunta das variedades sem bordo V0 e V1.

Definição 1.3.4. Seja W uma variedade diferenciável compacta com duas componentes de bordo V0 e V1, tais que V0 e V1 são ambas retratos por deformação de W. Então W é dito

um h-cobordismo entre V0 e V1.

Definição 1.3.5. Uma tríada de variedades (W, V0, V1) é chamada cobordismo produto se for

difeomorfa à terna (V0×[0,1], V0× {0}, V0× {1}).

O Teorema a seguir é um resultado sensacional e será muito útil para o nosso trabalho.

Teorema 1.3.6. (Teorema do h-Cobordismo) Considere uma tríada(W, V0, V1) com as

seguintes propriedades:

1. W, V0 e V1 são simplesmente conexas,

2. H∗(W, V0) = 0,

3. dimW ≥6.

Então (W, V0, V1) é um cobordismo produto.

Teorema 1.3.7. (Conjectura de Poincaré Generalizada). Se M é uma n-variedade fechada, conexa e simplesmente conexa, e n≥4, então M é homeomorfa a esfera Sn.

Grau de uma aplicação diferenciável

SejamM eN variedades diferenciáveis orientadas de dimensãon, ambas sem bordo, com

M compacta eN conexa. Seja f :M →N uma aplicação diferenciável de classeC∞_ex∈M

um ponto regular de f. Observe que, nestas condições, a derivada de f no pontox, denotada por Df(x), é um isomorfismo entre os espaço tangente a M em x e o espaço tangente a N

em f(x). Dizemos que f preserva a orientação em x se Df(x) aplica uma base de TxM da

orientação de M numa base deTf(x)N da orientação de N. Se isto não ocorre dizemos que f

inverte a orientação em x.

Seja x ∈ M um ponto regular. Dizemos que o grau de f no ponto x é igual a 1 se f

preserva a orientação em x. Denotaremos deg_xf = 1. Sef inverte a orientação emx, então o grau de f no ponto x é dito ser igual a −1, e denotamos deg_xf = −1. Para cada valor regulary ∈N definimos também o grau de f sobrey como sendo

deg(f, y) = X x∈f−1_(y)

deg_xf.

Se f−1_{(y) for vazio, então diremos que deg(f, y) = 0. Observe que f}−1_{(y) tem um número}

1.4 Nós e enlaçamentos 31

O grau de uma aplicação contínuaf :M →N, denotado pordegf, é definido como sendo o grau de uma aplicação h, deg(h, z), onde h : M → N é um aplicação C∞ _{homotópica a} f e z ∈ N é um valor regular para h. Por resultados de Hirsch [14], uma tal aplicação h

existe edegf independe da escolha dehez. SeN é compacta, entãof∗[M] = (degf)[N]em Hn(N;Z), com [M]e [N]classes fundamentais de M e N respectivamente.

1.4

Nós e enlaçamentos

Todos as definições e resultados apresentados nesta seção podem ser encontrados em [28].

Considerações gerais

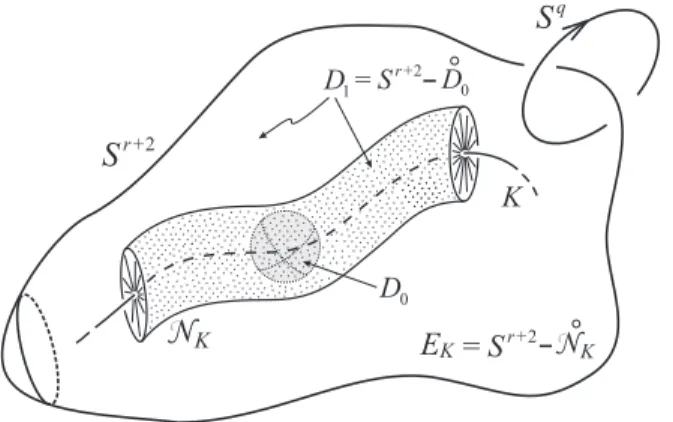
Definição 1.4.1. Um subconjunto K de um espaço X é um nó p-dimensional em X se K

é homeomorfo a uma esfera Sp_{. Mais geralmente, K é um enlaçamento se é homeomorfo a}

uma união disjunta Sp1_{⊔ · · · ⊔S}pr de uma ou mais esferas. Dois nós ou enlaçamentos _K e

K′ são equivalentes se existe um homeomorfismo h:X→X tal que h(K) =K′.

Alguns autores consideram nós como mergulhos de K : Sp → Sn preferivelmente à sub-conjuntos como na definição anterior. Quando o espaço X da definição anterior for a esfera

Sn_{, será, em geral, mais conveniente usarmos esta definição. Não obstante, usaremos o mesmo}

símboloK para denotar tanto a aplicaçãoK quanto sua imagem K(Sp) emSn.

Definição 1.4.2. SejaV uma subvariedade da variedadeM. Uma isotopia deV emM é uma família de mergulhos ft, t∈[0,1], de V em M, tal que f0 é a aplicação inclusão e a função F definida por F(t, x) =ft(x) é simultaneamente contínua em t e em x. As aplicações f0 e f1 são chamadas mergulhos isotópicos. QuandoV =M e cada ft é um difeomorfismo comf0

igual a aplicação identidade em M, então F é chamada difeotopia ou isotopia ambiente.

Definição 1.4.3. Dois nósK e K′ _{num espaçoX são ditos isotópicos se existe uma isotopia}

ambiente {ht} deX tal que h1(K) =K′.

Obviamente, se dois nós são isotópicos, então eles são equivalentes.

Será comum falarmos nesta seção do tipo de um nó; pois bem, diremos que dois nós têm o mesmo tipo se eles são equivalentes, e que são de tipos distintos se não são equivalentes.

Teorema 1.4.4. (Teorema da Separação e Brouwer)SeK é um nó(n−1)-dimensional emRn (ou _Sn), então Rn_−K (ou_Sn_−K) tem exatamente duas componentes conexas e_K

é o bordo de cada uma delas.

Definição 1.4.5. SejaX uma variedade de dimensão ne M uma variedade de dimensãom,

n < m, ambas sem bordo. Por uma vizinhança tubular deX emM entendemos um mergulho

N :X×Dn−m→M tal que N(x,0) =x para todo x∈X.

de um nóK de dimensão 1 em R3 é um toro sólido _S1_×D2 cujocerne é_K. Entendemos por

cerne de um toro S1×D2 o subconjuntoS1× {0}deste.

Notação: Em casos em que a variedade X da definição anterior for um nó K, denotaremos sua vizinhança tubular porNK.

Definição 1.4.6. Seja M uma variedade n-dimensional e f :Dk→ M um mergulho. Dize-mos que f é liso se f estende a um mergulho f :U → M, ondeU é uma vizinhança de Dk

emRn_(Dk_⊂Rn _{da maneira trivial). Também dizemos, neste caso, que o subconjuntof(D}k₎

de M é um disco liso.

Teorema 1.4.7. Um nó k-dimensional K emSn_{, k < n, é equivalente ao nó trivialS}k _⊂Sn

se, e somente se, K é o bordo de um (k+ 1)−disco liso em Sn.

Definição 1.4.8. Seja K um nó k-dimensional numa n-variedade M. Diremos que K é localmente liso em x∈K se existe uma vizinhança fechada V dex em M tal que (V, K∩V)

é homeomorfo, como um par, ao par de discos usuais (Dn_{, D}k_{). Se tal propriedade é válida}

para todo ponto deK diremos que K é liso. Ainda mais, diremos que um nóK emM é suave se é diferenciável.

O Grupo de um nó

Se K é um nó (ou um enlaçamento) (n−2)-dimensional em Rn, o grupo fundamental π1(Rn−K) do seu complementar será chamado, simplesmente, o grupo de K. Note que o

grupo é o mesmo, a menos de isomorfismo, se consideramos o nó em Sn ao invés de em Rn.

Deveras, temos o seguinte:

Proposição 1.4.9. SeB é qualquer subconjunto limitado do Rntal queRn_−B é conexo por

caminhos e n≥3, então a inclusão induz um isomorfismoi♯:π1(Rn−B)→π1(Sn−B).

A inclusão natural Sn−2 ⊂ Rn−1 _⊂ Rn _⊂ Rn_{∪ {∞} ∼= S}n é o nó trivial (ou

não-enodamento) de codimensão 2.

Proposição 1.4.10. O nó trivial tem grupo π1(Sn−Sn−2)≈Z.

Observação 1.4.11. O grupoπ1(R3−K)de um nó suave é isomorfo aos gruposπ1(R3−NK)

e π1(R3− ◦

NK). De fato, o complementar R3−K e o exterior R3− ◦

NK tem o mesmo tipo de

homotopia por uma retração de deformação óbvia.

Nós toroidais

Uma aplicação f :S1 _{→ T}2_{, onde T}2 _{é o toro S}1_×S1_{, pode ser considerada, uma vez}

queS1 _{é orientada, como um laço representando um elemento [f]deπ}

1(T2)≈Z⊕Z. Pontos

bases são imateriais neste caso, já queπ1(T2)é abeliano. Então[f]pode ser escrito em termos

1.4 Nós e enlaçamentos 33

Observação 1.4.12. Diferentemente do comum, estamos denotando classes em π1(T2) com

os símbolos≺ ·,· ≻não apenas para que não haja confusão com demais notações semelhantes e que já são utilizadas neste trabalho para outros fins, mas porque, uma vez de posse do próximo resultado que apresentamos, passaremos a tratar os mergulhos deS1 _{em T}2 _{especificando sua}

classe em π1(T2). Desta forma, a notação ≺ ·,· ≻ servirá, sobretudo, para representar nós

específicos emT2_.

Teorema 1.4.13. Uma classe≺a, b≻emπ1(T2) é representada por um mergulho S1 →T2

se, e somente se, a=b= 0 ou mdc(a, b) = 1.

Escolhidos inteiros p e q primos entre si, o nó toroidal Tp,q de tipo ≺ p, q ≻ é o nó que

“enrola” em torno do toro sólidopvezes na direção longitudinal eqvezes na direção meridional. O grupo de um tal nó Tp,q pode ser determinado sem muito trabalho encontrando-se sua

apresentação que, nestes termos, é dada por

Gp,q=|x, y:xp =yq|.

Pode-se classificar os tipos de nós toroidais observando-se que: T±1,q eTp,±1são de tipo trivial;

e o tipo deTp,q é imutável por mudança de sinal de pou de q, ou por permutação depe q.

Teorema 1.4.14. Se 1< p < q, então o grupo Gp,q determina o par p, q.

Corolário 1.4.15. Existem infinitos tipos de nós toroidais.

Dado um grupo G vamos denotar por Z(G) o seu centro, ou seja, o subgrupo Z(G) = {g∈G:gx=xg, ∀ x∈G}. Além disso, dado um elemento qualquer g ∈G vamos escrever hgi para expressar o subgrupo de G gerado por g, ou seja,hgi={gn:n∈Z_}.

Se C é o subgrupo cíclico (infinito) deG=Gp,q gerado pelo elemento xp(=yq), pode-se

demonstrar facilmente que C é subgrupo de Z(G), que C é normal em G e que G/C é o produto livre dos grupos cíclicosZ_p eZ_q. Escrevemos _G/C≈Z_p∗Z_q. Além disso, é apenas

um simples exercício de Álgebra provar que o centro de um produto livre de quaisquer dois grupos não triviais consiste apenas do elemento identidade. Sendo assim, Z(Z_{p ∗}Z_{q) = 1.}

Concluímos daí que o grupo C é exatamente o centro deG. Este resultado será utilizado no terceiro capítulo deste texto e, por isso, o apresentamos sumariamente no seguinte:

Lema 1.4.16. Z(Gp,q)≈ hxpi=hyqi e Gp,q/Z(Gp,q)≈Zp∗Zq.

Nós girados

EmR4, considere os subconjuntosR3_{+={(x1, x2, x3,0) :x3 ≥0}}, obviamente com bordo,

e R2 _{={(x1, x2,0,0)}. Podemos rotacionar um ponto x = (x1, x2, x3,0) de} R3

+ em torno de R2 _{de acordo com a fórmula}

Defina o giroX de qualquer conjunto X⊂R3

+ como sendo o subconjunto do R4 X ={xθ :x∈X, 0≤θ≤2π}.

Para obter um nó em R4_{, escolha um arco A em} R3

+ com pontos finais em R2. Então A

é uma 2-esfera em R4, que diremos ser um nó girado. A próxima proposição mostra que o

grupo de A é isomorfo aπ1(R+3 −A) que é por sua vez isomorfo ao grupo do nó A∪Lem R3_{, onde L⊂}R2 _{é o segmento ligando os pontos finais de A.}

Proposição 1.4.17. O nó girado A emR4 _{tem o mesmo grupo do nó A∪L em} R3_.

Agora, se Aé pontualmente linear e intercepta R2 _{transversalmente, é fácil ver que A é}

localmente liso.

Proposição 1.4.18. Existem infinitos nós localmente lisos não-equivalentes de S2 em R4.

Proposição 1.4.19. Se X é um subconjunto aberto e conexo por caminhos de R3

+, tal que X∩R2 _{6=∅, então a inclusão i:X →X induz um isomorfismo i♯ :π1(X)→π1(X ).}

Será interessante em nosso trabalho considerarmos X ⊂ R4 _⊂ R4_{∪ {∞} ∼= S}4_{. Note}

que isto pode ser feito com total naturalidade e que, em face da Proposição 1.4.9, temos provado que o grupo de um nó girado visto como subconjunto de R4 ou de _S4 é o mesmo,

ou seja, π1(S4−A )≈π1(R4−A ) e este último, pela Proposição 1.4.17, é homeomorfo a π1(R3−A∪L)que é por sua vez homeomorfo a π1(S3−A∪L).

Para pormos fim a esta seção observe que o processo de giro de um nó pode ser iterado de modo a se obter, a partir de um nó 1-dimensional em R3

+, um nó (n−2)-dimensional em Sn, qualquer que seja o inteiro n ≥ 4 previamente fixado. Construções neste sentido serão realizadas no Capítulo 3 e constituirão uma ferramenta essencial para demonstrarmos alguns dos mais importantes resultados daquele capítulo.

1.5

Mergulho de produtos de esferas

Dedicamos esta última seção deste capítulo para inserirmos algumas terminologias e resultados envolvendo a existência de mergulhos de produtos de três esferas em codimensão 1, bem como algumas de suas propriedades invariantes.

Em todo o texto, diremos que um mergulho é suave se é um difeomorfismo.

Sobre a existência de mergulhos de Sp×Sq×Sr em Sp+q+r+1

Nesta seção e em diversas ocasiões neste trabalho, vamos identificar a esferasSp+q+1com

Sp×Dq+1 ∪ Dp+1×Sq, através dos seguintes difeomorfismos:

Sp+q+1 ∼= ∂Dp+q+2

∼

= ∂(Dp+1_×Dq+1₎ ∼

= ∂Dp+1×Dq+1 ∪ Dp+1×∂Dq+1

∼

1.5 Mergulho de produtos de esferas 35

Considere as inclusões

i:Sp×Sq →Sp×Dq+1 e j:Sp×Dq+1 →Sp×Dq+1 ∪ Dp+1×Sq∼=Sp+q+1

onde identificamos Sp×Sq com∂(Sp×Dq+1). Tomando-se a composição abaixo

f :Sp×Sq−→i Sp×Dq+1 −→j Sp+q+1

conclui-se sobre a existência de um mergulho diferenciável de Sp×Sq emSp+q+1.

Foi demonstrado em [19, 21, 34] que, se p, q≥2, então mergulhos deSp×Sq emSp+q+1

são únicos a menos de difeomorfismo. Abordamos neste trabalho exatamente os casos que não cumprem estes quesitos sobrep e q, a saber, os casos 1 =p≤q.

Definição 1.5.1. Um mergulhog:Sm→Sn, com m < n, é dito trivial seg(Sm) é isotópico à imagem do mergulho dado pela composta de inclusões

Sm ∼=Sm× {0}֒→Sm×Dn−m ֒→Sm×Dn−m ∪ Dm+1×Sn−m−1∼=Sn

Neste caso, dizemos que Sm _{está mergulhada trivialmente em S}n_.

Definição 1.5.2. Um mergulho g:Sm×Sn→ Sp+q+r+1, com m, n =p, q ou r, é trivial se

g(Sm×Sn) é isotópico ao bordo de uma vizinhança tubular da esfera Sm (ou da esfera Sn) mergulhada trivialmente emSp+q+r+1_{. Um tal mergulho pode ser construído com a composta}

de inclusões

Sm×Sn֒→Sm×Dn+1 ֒→Sm×Dn+1∪Dm+1×Sn∼=Sm+n+1 ⊂Sp+q+r+1

onde a última inclusão é um mergulho trivial. Neste caso, dizemos que Sm×Sn está mergu-lhada trivialmente em Sp+q+r+1_.

Definição 1.5.3.Considere um mergulho diferenciável f :Sp_×Sq_×Sr_→Sp+q+r+1_{. Dizemos}

quef é trivial sef(Sp×Sq×Sr)é isotópico ao bordo de uma vizinhança tubular deSm×Sn, com m, n = p, q ou r, mergulhada trivialmente em Sp+q+r+1_{. Diremos, neste caso, que} Sp×Sq×Sr está mergulhada trivialmente em Sp+q+r+1.

Proposição 1.5.4. Existem mergulhos de Sp×Sq×Sr emSp+q+r+1.

Prova: Pela Definição 1.5.2, escolhendo-se m e napropriadamente, encontramos mergulhos triviais Sp _×Sq _{→ S}p+q+r+1_{, S}p _×Sr _{→ S}p+q+r+1 _{e S}q _×Sr _{→ S}p+q+r+1_.

Tomando-se os bordos de vizinhanças regulares desTomando-ses mergulhos Tomando-se obtém três mergulhos triviais de

Sp×Sq×Sr emSp+q+r+1.

Sobre a unicidade de mergulhos triviais

Que mergulhos triviais Sm _{→ S}n_{, com m < n, são únicos a menos de isotopia (ou de}

difeomorfismo) seque imediatamente da Definição 1.5.1. Mas quanto aos mergulhos que se referem as outras definições, ou seja, mergulhos Sm×Sn→Sp+q+r+1, comm, n=p, q ou r, e Sp_×Sq_×Sr_→Sp+q+r+1_{, estes podem não ser únicos.}

Pode-se mostrar, por exemplo, que para mergulhos f : Sm×Sn → Sp+q+r+1, temos no máximo dois mergulhos triviais a menos de difeomorfismo. Isto se deve ao fato de que para um tal mergulho podemos fazer duas escolhas, do Tipo 1 ou do Tipo 2, sendo a de Tipo 1 quando f(Sm_×Sn_{) borda S}m_×Dn+1 _{em S}p+q+r+1_{, e a de Tipo 2 quando f(S}m _×Sn₎

borda Dm+1 ×Sn em Sp+q+r+1. Em [21] foi mostrado que, para r = 0 e p, q ≥ 2, todo mergulho Sp ×Sq → Sp+q+1 é trivial. Também naquele trabalho, foi mostrado que, para

r = 1, considerando um mergulho f :Sp_×Sq _{→ S}p+q+2_{, pode ocorrer que f seja do Tipo}

1 e não seja do Tipo 2, e que a coincidência entre os dois tipos somente ocorre sob algumas condições adicionais, as quais não mencionamos aqui, mas podem também ser encontradas em [21, Teorema 1.9 e Observação 6.3].

No caso de mergulhosf :Sp_×Sq_×Sr_→Sp+q+r+1_{, temos seis mergulhos triviais a menos}

de difeomorfismo. Isto se deve ao fato de, neste caso, termos três escolhas para a imagem de

f, a saber, aos de: Tipo 1: quando f(Sp×Sq×Sr) borda Sp×Sq ×Dr+1 em Sp+q+r+1; Tipo 2: quando f(Sp _×Sq _×Sr_{) borda S}p _×Dq+1 _×Sr _{em S}p+q+r+1_{; e Tipo 3: quando} f(Sp×Sq×Sr) borda Dp+1×Sq×Sr em Sp+q+r+1; e para cada destes temos ainda duas escolhas para o mergulho trivial Sm_×Sn_→Sp+q+r+1_{, como já temos visto.}

O fato é que não sabemos se a unicidade é ou não válida para mergulhos triviais de produtos de duas ou de três esferas, com Sm_×Sn_→Sp+q+r+1 _{e S}p_×Sq_×Sr _→Sp+q+r+1_,

e um problema natural é analisar as relações entre os seis tipos de mergulhos triviais. Neste trabalho, como já ressaltamos, vamos estudar os mergulhos Sp_×Sq_×Sr _→Sp+q+r+1 _{no caso}

em que p= 1.

Sobre o número de componentes de Sp+q+r+1_−f(Sp_×Sq_×Sr₎

Vamos mostrar, neste penúltimo tópico preliminar, que apesar de todas as particulari-dades que possa ter um mergulho suave Sp_×Sq_×Sr _{→ S}p+q+r+1_{, com 1≤ p≤q ≤r, ele}

sempre desconecta a esfera Sp+q+r+1 em duas componentes.

Proposição 1.5.5. Sejaf :Sp_×Sq_×Sr_→Sp+q+r+1 _{um mergulho suave. EntãoS}p+q+r+1₋ f(Sp×Sq×Sr) possui duas componentes conexas.

Prova: Vamos calcular o grupo de homologia H0(Sp+q+r+1−f(Sp×Sq×Sr)). Por

simpli-cidade, denote X=Sp×Sq×Sr eY =Sp+q+r+1. Sabemos que

e

1.6 Topologia Linear por Partes (PL) 37

Além disso, pela Dualidade de Alexander, tem-se

e

Hn(f(X))≈Hep+q+r−n(Y −f(X))

E em particular Hep+q+r(f(X)) ≈ H˜0(Y −f(X)). Donde He0(Y −f(X)) ≈ Z. Portanto, H0(Y −f(X)) ≈ Z⊕Z e Y −f(X) possui duas componentes conexas. Isto completa a

prova.

1.6

Topologia Linear por Partes (PL)

Muitas definições e resultados de Topologia Linear por Partes (PL) serão utilizados princi-palmente no último capítulo deste trabalho. Não poremos aqui tal conteúdo, mas gostaríamos de deixar registrado que as notações, terminologias e resultados básicos que utilizaremos são os mesmos apresentados por C. P. Rourke e B. J Sanderson em [30].

Concluímos aqui nossa breve exposição e argumentação sobre os resultados básicos que serão utilizados no limiar do restante de todo este trabalho.

Capítulo

2

Difeomorfismo de produtos de

esferas

O objetivo deste capítulo é caracterizar todos os automorfismos deHp(M;Z)≈Znque são

realizados como isomorfismos induzidos por difeomorfismos de M, onde M = n

Y

Sp, p ≥1,

n≥ 2. Isto foi desenvolvido por L. A. Lucas em [20]. Antes, porém, de nos embrenharmos nesta empresa, dedicaremos a primeira seção deste capítulo às construções algébricas que nos serão úteis na empreita da classificação das matrizes que representam automorfismos deM. Desde já fixamosGL(n;Z₎ para denotar o grupo das matrizes de ordem_ncujo determinante

é±1, com as operações usuais de matrizes.

2.1

Algumas manipulações algébricas

Definição 2.1.1. Seja Sn o grupo das permutações de ordem n, ou seja, Sn é o grupo das

bijeções σ : {1,2, . . . , n} → {1,2, . . . , n}. Para cada σ ∈ Sn, defina a matriz Aσ = (aij) ∈ GL(n;Z_{) fazendo}

aij =

(

1 se i=σ(j) 0 c.c.

Vamos construir um argumento para identificarmos o grupo das permutaçõesSn com um

subgrupo deGL(n;Z₎. Nossa construção se inicia com o seguinte lema:

Lema 2.1.2. A aplicação γ :Sn→GL(n;Z) dada porγ(σ) =Aσ é um monomorfismo.

Prova: Provemos inicialmente queγ é um homomorfismo. Para tanto, considere permutações arbitrárias σ e µem Sn, com respectivas matrizes Aσ = (aij) e Aµ = (bjk) dadas em acordo

com a definição anterior, ou seja,

aij =

(

1 se i=σ(j)

0 c.c. e bjk=

(

1 se j =µ(k) 0 c.c.

Denotando AσAµ =C = (cik) podemos escrever cik = Pnj=1aijbjk. Agora, pelas definições

de Aσ e Bµ, temos

cik = n

X

j=1

aijbjk=aiµ(k)bµ(k)k=aiµ(k).

Logo

cik = 1⇐⇒aiµ(k)= 1⇐⇒i=σ(µ(k))

cik = 0⇐⇒aiµ(k)= 0⇐⇒i6=σ(µ(k)).

Mas isto implica em C =Aσ◦µ=γ(σ◦µ). Temos, então,

γ(σ)·γ(µ) =AσAµ=Aσ◦µ=γ(σ◦µ).

E portanto γ é um homomorfismo.

Provemos agora a injetividade de γ. Sejam γ(σ) = Aσ = (aij) e γ(µ) = Aµ = (bij), com σ distinta de µ. Sendo assim, existe um inteiro l, 1 ≤ l ≤ n, tal que σ(l) 6= µ(l). Escreva

k = σ(l). Então temos akl = 1, mas bkl = 0. Logo, akl 6= bkl e, deste modo, Aσ 6= Aµ.

Portanto γ(σ)6=γ(µ)e γ é injetivo.

Tendo provado este lema, obtemos um isomorfismoγ :Sn→γ(Sn), o qual nos permitirá,

a partir de agora, identificarmos o grupo das permutações Sn com o subgrupo γ(Sn) de GL(n;Z_{). Que γ(Sn) é de fato um subgrupo de GL(n;}Z_{) segue diretamente do fato de ser} Sn um grupo eγ um homomorfismo.

Seja η :GL(n;Z_{) → GL(n;}Z₂₎, onde Z₂ é o grupo cíclico de ordem 2, o homomorfismo

canônico definido por η(A) = ¯A, para toda matriz A em GL(n;Z_{), isto é, dada A = (aij)}

em GL(n;Z₎, fazemos _{η(A) = (¯aij)}, onde _a¯ij indica a classe de _aij em Z₂. Note que, para

quaisquer A, B∈GL(n;Z_{), tem-se:}

η(AB) =AB= ¯AB¯ =η(A)η(B)

Sendo assim, η um homomorfismo e η(Sn) é um subgrupo deGL(n;Z2).

Agora vamos definir, através do homomorfismo η, um subconjunto de GL(n;Z₎ que

2.1 Algumas manipulações algébricas 41

Definição 2.1.3. Defina G′ _=η−1_(η(S n)).

Note que uma matrizAdeGL(n;Z₎está em_G′ se, e somente se, cada uma de suas linhas

e colunas contém exatamente um inteiro ímpar.

Lema 2.1.4. G′ _{munido da multiplicação usual de matrizes é um subgrupo de GL(n;Z).}

Prova: Denote porIn a matriz identidade de ordemn, a qual é o elemento neutro do grupo GL(n;Z₎ e, conseqüentemente, do grupo_Sn. Claramente _{In ∈G}′, pois _{η(In) = ¯In=In}.

SejamA, B∈G′; entãoη(A)eη(B)estão emη(Sn), e temos: η(AB) =η(A)η(B)∈η(Sn),

pois, como vimos,η(Sn) é um grupo. LogoAB ∈G′.

SejaA∈G′; entãoη(A)∈η(Sn). Sendoη(Sn)um grupo, [η(A)]−1 ∈η(Sn). Agora, como η é homomorfismo segue[η(A)]−1 _=η(A−1_{). PortantoA}−1 _∈G′_.

Isto prova que G′ é um subgrupo de GL(n;Z₎.

Lema 2.1.5. η é um epimorfismo.

Prova: Já vimos que η é homomorfismo. Basta-nos então provar que η é sobrejetor. Para isto, seja A uma matriz arbitrária emGL(n;Z₂₎. Então _A tem apenas entradas ¯₀e ¯₁, e seu

determinante é não nulo. Tome a matrizB tal que suas entradas correspondam às de A com 1 no lugar de¯_{1 e 0 no lugar de}¯_{0. Claramente B ∈GL(n;}Z₎ e _{η(B) =A}.

Notação: Se H é um subgrupo de um grupoG, denotaremos por [G:H] o índice deH em

G, o qual, pelo teorema de Lagrange, é igual a |G|

|H|, onde|G|denota a ordem do grupo Ge |H|a ordem do grupoH. Resumindo, [G:H]|H|=|G|.

Lema 2.1.6. |GL(n;Z_{2)|= 2}(n2−n)/2₍₂1₋₁₎₍₂2 _{−1)· · ·(2}n₋₁₎

Prova: Para se construir uma matriz A em GL(n;Z₂₎, observe inicialmente que seu

deter-minante deve ser não-nulo, ou seja, A é não singular. Escreva A como matriz linha de seus vetores coluna, A = [C1 C2 · · · Cn]. Sendo A não singular, {C1, C2, . . . , Cn} deve ser um

conjunto linearmente independente sobre Z_{2. Com isso, vemos que existem 2}n_{−1 escolhas}

possíveis para C1, já que este não pode ser o vetor nulo. Uma vez escolhidos os vetores C1, . . . , Ck, o vetor Ck+1 pode ser escolhido como qualquer vetor que não pertença ao espaço

gerado pelos vetores linearmente independentes C1, . . . , Ck. Como este espaço contém2k

ve-tores e existem2n_{vetores no total,C}

k+1pode ser escolhido de2n−2kmodos distintos. Segue

que a matrizA pode ser construída de(2n−1)(2n−2)· · ·(2n−2n−1) maneiras. Portanto, a ordem do grupoGL(n;Z2) é:

|GL(n;Z_{2)| = (2}n₋₁₎₍₂n_{−2)· · ·(2}n₋₂n−1₎ = (2n−1)2(2n−1−1)· · ·2n−1(21−1) = 21+···+n−1₍₂1₋₁₎₍₂2_{−1)· · ·(2}n₋₁₎

Lema 2.1.7. [GL(n;Z_{) :G}′_{] = [GL(n;}Z_{2) :η(Sn)]}

Prova: Sejam= [GL(n;Z_{2) :η(Sn)]}. Considere as classes laterais à direita de_{S =η(Sn)}em GL(n;Z₂₎ dadas por _{Sk1,Sk2, . . . ,Skm}, onde _{k1, k2, . . . , km ∈GL(n;}Z₂₎ são representantes

de classes. Como η é um epimorfismo, existem elementos g1, g2, . . . , gm ∈GL(n;Z) tais que η(gj) =kj, para todo j= 1, . . . , m.

Afirmamos que G′g1, G′g2, . . . , G′gm são classes laterais à direita de G′ em GL(n;Z),

todas distintas. De fato: se G′gi =G′gj entãogjgi−1 ∈G′. E segueη(gjg−1i ) =η(gj)η(g−1i ) = η(gj)η(gi)−1 = kjk_i−1 ∈ S. Logo, Ski = Skj e, portanto, i = j. Isto prova que as classes G′g1, G′g2, . . . , G′gm são todas distintas.

Para completar a prova do lema resta-nos provar que G′_g

1, G′g2, . . . , G′gm são as únicas

classes à direita de G′ em GL(n;Z_{). Para tanto, seja g ∈ GL(n;}Z_{) fixado arbitrariamente;}

vamos mostrar que g ∈G′gj para algum j, 1 ≤j ≤m. Ora, temos η(g) ∈GL(n;Z2), então

temos também η(g)∈ Skj para algum inteiro j,1 ≤j≤m, ou seja, existe algumσ ∈ S tal

queη(g) =σkj. Tomex=gg−1j . Temos, então,η(x) =η(g)η(gj)−1 =σkjk−1j =σ ∈ S. Logo x∈η−1_(η(S

n)) =G′, ou seja,ggj−1 ∈G′, donde g∈G′gj.

Provado tudo isto, segue que{G′g1, G′g2, . . . , G′gm} consiste de todas as classes à direita

de G′ _{em GL(n:Z)e, portanto,}

[GL(n;Z_{) :G}′_{] = [GL(n;}Z_{2) :η(Sn)].}

Proposição 2.1.8. [GL(n;Z_{) :G}′_{] =} 2

(n2_−n)/2

(21₋₁₎₍₂2_{−1)· · ·(2}n₋₁₎ n!

Prova: Sabemos que |Sn| = n!. Assim, como η é homomorfismo, também |η(Sn)| = n!.

Agora, utilizando os dois lemas precedentes e o Teorema de Lagrange, temos:

[GL(n;Z_{) :G}′_{] = [GL(n;}Z_{2) :η(Sn)] =} |GL(n;Z2)| |η(Sn)|

= 2

(n2_−n)/2

(21−1)(22−1)· · ·(2n−1)

n!

Notação: Daqui por diante, dada uma matriz X de ordem n1 e outra Y de ordem n2,

denotaremos por X⊕Y a matriz de ordem n=n1+n2 definida como

X⊕Y =

"

X 0

0 Y

#

Notação: Denotaremos porR, em todo este capítulo, a matriz diagonal de ordem ndefinida como

R= [−1]⊕In−1 =

"

−1 0

0 In−1

#

Note que sendoRdefinida desta forma, temosR2 =In, de modo que o conjuntoR′ ={In, R},

munido da multiplicação usual de matrizes, é um grupo, o qual é subgrupo tanto deG′ _quanto

2.1 Algumas manipulações algébricas 43

Definição 2.1.9. Seja G′′ _{o subgrupo de GL(n;Z) gerado pelos subgrupos S}

n e R′.

Denota-mos, como comumente, G′′=hSn∪R′i.

Escrevamos o conjunto Sn∪R′ explicitanto os seus elementos com a seguinte notação: Sn∪R′ ={R, In, Aσ2, Aσ3, . . . , Aσn!}.

Como é sabido, o subgrupo gerado por um subconjunto não vazio é o conjunto de todas as suas palavras. Sendo assim,

hSn∪R′i=

Br1

1 B2r2· · ·Bmrm:Bs∈ Sn∪R′, rs=±1, 1≤s≤m, m∈Z .

Denote SnR ={AR:A∈ Sn}. Vamos provar quehSnRi=hSn∪R′i=G′′. Com efeito,

é evidente queSnR⊂ hSn∪R′i. LogohSnRi é subgrupo de hSn∪R′i. Por outro lado, para

todoA∈ Sn∪R′ podemos escrever

A=AIn=A(R2) = (AR)(InR)∈ hSnRi.

Desse modo, temos provado que Sn∪R′ ⊂ hSnRi e, assim, hSn∪R′i é subgrupo de hSnRi.

E portanto,hSnRi=hSn∪R′i=G′′.

Note que uma matrizAdeGL(n;Z_{)pertence ao subgrupoG}′′ _{se, e somente se, cada uma}

de suas linhas e colunas contém exatamente um inteiro não nulo, sendo estes iguais a ±1. Esta importante observação será lembrada oportunamente.

Proposição 2.1.10. O grupo G′′ é finito de ordem 2nn!. Ainda mais, G′′ é isomorfo ao produto direto de (Z₂₎n com _Sn.

Prova: Inicialmente, considere o grupoZ_{2em sua forma multiplicativa, isto é,}Z_{2= ({−1,1},·).}

Faça a identificação de (Z₂₎n com um subgrupo de _GL(n;Z₂₎ através do homomorfismo ν: (Z₂₎n_→GL(n;Z_{2) dado por}

(z1, . . . , zn) 7−→ν

      

z1 0 · · · 0 0 z2 · · · 0

... ... ... ... 0 0 · · · zn

      

Considere a seqüência

1 // (Z₂₎n ν // _G′′ ω _//S

n // 1

ondeω é o homomorfismo dado pela congruência módulo 2, ou seja,ω(A) = ¯A, onde −1≡1 mod 2. Deste modo, é fácil ver que a seqüência acima é uma seqüência exata curta, já que

ω(A) =In se, e somente se, A = (aij) é uma matriz diagonal tal que aii =±1 para todo i,

comi= 1, . . . , n. E sendo assim, temosA=ν(a11, . . . , ann), com(a11, . . . , ann)∈(Z2)n.

Considere a inclusão G′′ _{←− S}j

n. Ficamos então com a seqüência

1 // (Z₂₎n ν // _G′′ ω //_Sn j

o

o // 1