Otimização do parâmetro de forma para utilização no método numérico sem malhas

UNIVERSIDADE FEDERAL DO CEARÁ

CENTRO DE TECNOLOGIA

DEPARTAMENTO DE ENGENHARIA HIDRÁULICA E AMBIENTAL

PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA CIVIL – RECURSOS

HÍDRICOS

HÉRCULES LIMA DE MEDEIROS

OTIMIZAÇÃO DO PARÂMETRO DE FORMA PARA UTILIZAÇÃO NO MÉTODO

NUMÉRICO SEM MALHAS

HÉRCULES LIMA DE MEDEIROS

OTIMIZAÇÃO DO PARÂMETRO DE FORMA PARA UTILIZAÇÃO NO MÉTODO

NUMÉRICO SEM MALHAS

Dissertação apresentada ao Programa de

Pós-Graduação

em

Engenharia

Civil

da

Universidade Federal do Ceará, como requisito

parcial à obtenção do título de Mestre em

Engenharia Civil. Área de concentração:

Recursos Hídricos.

Orientador: Prof. Dr. Marco Aurélio Holanda

de Castro.

Dados Internacionais de Catalogação na Publicação Universidade Federal do Ceará

Biblioteca de Pós-Graduação em Engenharia - BPGE

M439o Medeiros, Hércules Lima de.

Otimização do parâmetro de forma para utilização no método numérico sem malhas / Hércules Lima de Medeiros. – 2014.

100 f. : il. color., enc. ; 30 cm.

Dissertação (mestrado) – Universidade Federal do Ceará, Centro de Tecnologia, Departamento de Engenharia Hidráulica e Ambiental, Programa de Pós-Graduação em Engenharia Civil, Fortaleza, 2014.

Área de Concentração: Recursos Hídricos.

Orientação: Prof. Dr. Marco Aurélio Holanda de Castro.

1. Recursos Hídricos. 2. Equações diferenciais. I. Título.

A Deus.

AGRADECIMENTO

Ao Prof. Dr. Marco Aurélio Holanda de Castro, pela excelente orientação,

paciência, amizade, e incentivo que tornaram esse estudo ainda mais proveitoso.

Aos professores participantes da banca examinadora Prof. Dr. José Maria Brabo

Alves e Prof. Dr. Rubens Sonsol Gondim pelo tempo, pelas valiosas colaborações e

sugestões.

Aos colegas Nelci Rones e João Marcelo pela inestimável ajuda, a qual agradeço

profundamente.

Aos colegas da turma de mestrado, em especial ao amigo Francisco Reis,

companheiro de batalha, Bárbara Alves pelos conselhos e paciência, e ao Marcos Vinícius e

Mazé que sempre lembraram desse querido amigo.

Agradecimento especial também ao amigo Francisco Marcelino, que esteve

presente em um momento fundamental, ao qual serei sempre grato.

RESUMO

O presente trabalho teve como meta desenvolver uma rotina computacional para obter

a solução numérica de equações diferenciais parciais através do Método sem malhas. Esse

método vem sendo aplicado na engenharia, visto que nos casos práticos muitas vezes

encontram-se descontinuidades ou condições de contorno que impossibilitam a solução

analítica, e muitas vezes dificultam bastante as soluções numéricas de equações diferenciais

parciais. No método utilizado, calcula-se as equações a partir do método numérico de Kansa,

onde toma-se uma Função de Base Radial (RBF) que vai calcular a matriz a partir da qual

chegaremos à solução analítica. A RBF utilizada foi a multiquadrática. Essa função irá

depender de um parâmetro de forma “c”. Esse parâmetro não tem um valor

definido, e o

objetivo da rotina é encontrar um valor para esse parâmetro, de forma que a solução analítica

se aproxime o máximo possível da solução numérica. Para se calcular esse valor do “c”, a

rotina irá calcular os valores do resíduo para o domínio, e os valores do resíduo para o

contorno, para cada valor de “c” em um intervalo determinado. Após calculados esses valores,

o programa compara os mesmos e fornece o ponto em que eles se aproximam mais. Nesse

ponto é encontrado o parâmetro de forma “c” otim

izado, e consequentemente a solução

numérica da equação proposta.

ABSTRACT

The present work was aimed at developing a computational routine for the numerical

solution of partial differential equations by the method without mesh. This method has been

applied in engineering, since in practical cases often are discontinuities or boundary

conditions precluding analytical solution, and quite often hinder the numerical solutions of

partial differential equations. In the method, we calculate the equations from the numerical

method of Kansas, where he takes a Radial Basis Function (RBF) that will calculate the

matrix from which we arrive at the analytical solution. The RBF used was multiquadrática.

This function will depend on a shape parameter "c". This parameter has a defined value, and

the goal of the routine is to find a value for this parameter, so that the analytical solution

closely match the numerical solution. To calculate this value of "c", the routine will calculate

the values of the residue to the domain, and the values of the residue to the outline, for each

value of "c" in a certain range. After these calculated values, the program compares them and

supplies the point where they come closest. This point is found the optimized shape parameter

"c", and consequently the numerical solution of the proposed equation.

LISTA DE ILUSTRAÇÕES

Figura 1

–

Corte da parede de uma barragem de terra... 4

Figura 2 – Sistema feito por Darcy... 6

Figura 3 – Fluxo através da parede de uma barragem... 8

Figura 4 – Sistema de coordenadas cartesianas... 9

Figura 5 – Domínio da função... 19

Figura 6. Comparação entre a Solução Analítica e a Solução Numérica... 36

Figura 7 – Corte da parede de uma barragem... 40

Figura 8 – Valores dos coeficientes da EDP... 43

Figura 9 – Número de pontos, e dimensões do domínio... 44

Figura 10 – Condições de contorno... 44

Figura 11 – Escolha do parâmetro de forma C... 45

Figura 12 – Refinamento do parâmetro de forma... 45

Figura 13 – Discretização com 9 pontos... 47

Figura 14 – Discretização do domínio com 16 pontos... 47

Figura 15 – Discretização do domínio com 25 pontos... 48

Figura 16

–

Carga hidráulica

u(m)

com

C

estimado (

C=

8,66) e 9 pontos no domínio... 50

Figura 17

–

Carga hidráulica

u(m)

com

C

estimado (

C=

5,77) e 16 pontos no domínio.... 51

Figura 18

–

Carga hidráulica

u(m)

com

C

estimado (

C=

4,33) e 25 pontos no domínio... 52

Figura 19

–

Carga hidráulica

u(m)

com

C

otimizado (

C=

449,2) e 9 pontos no domínio... 53

Figura 20

–

Resíduos com

C

otimizado: 9 pontos com refinamento 10

_{... 54}

Figura 21

–

Carga hidráulica

u(m)

com

C

otimizado (

C=436,7

) e 16 pontos no domínio. 55

Figura 22

–

Resíduos com

C

otimizado: 16 pontos com refinamento 10

_{... 56}

Figura 23

–

Carga hidráulica

u(m)

com

C

otimizado (

C=79,2

) e 25 pontos no domínio... 57

Figura 24

–

Resíduos com

C

otimizado: 16 pontos com refinamento 10

_{... 58}

Figura 25

–

Carga hidráulica

u(m)

com

C

otimizado (

C=0,01

) e 9 pontos no domínio... 59

Figura 26

–

Resíduos com

C

otimizado: 9 pontos com refinamento 10

_{... 60}

Figura 27

–

Carga hidráulica

u(m)

com

C

otimizado (

C=17,46

) e 16 pontos no domínio..61

Figura 29

–

Carga hidráulica

u(m)

com

C

otimizado (

C=80,23

) e 25 pontos no domínio. 63

Figura 30

–

Resíduos com

C

otimizado: 25 pontos com refinamento 10

_{... 64}

Figura 31

–

Carga hidráulica

u(m)

com

C

otimizado (

C=0,001

) e 9 pontos no domínio... 65

Figura 32

–

Resíduos com

C

otimizado: 9 pontos com refinamento 10

_{... 66}

LISTA DE TABELAS

Tabela 1

–

Valores de k para diferentes tipos de solo... 7

Tabela 2 – Valores de k de solos típicos... 8

Tabela 3 – Funções de Base Radial mais utilizadas... 27

Tabela 4 – Coordenadas dos nós escolhidos na discretização do domínio... 30

Tabela 5 – Matriz das distâncias entre os pontos definidos – Matriz R... 31

Tabela 6 _– Valores da Função _� para um _{= ,} ... 32

Tabela 7

–

Valores de L[ϕ] para c=0,5...

... 33

Tabela 8 – Matriz de colocação A... 34

Tabela 9 – Valores de y... 34

Tabela 10 – Matriz inversa de A... 35

Tabela 11- Valores de _�... 35

Tabela 12 _– Comparação entre a solução Analítica e a Solução numérica... 36

LISTA DE ABREVIATURAS E SIGLAS

EDO

–

Equação diferencial ordinária

EDP

–

Equação diferencial parcial

ICOLD - International Commission on Large Dams

–

Comissão Internacional de grandes

barragens

MDF

–

Método das Diferenças Finitas

MEC

–

Método dos Elementos de Contorno (MEC).

MEF

–

Métodos dos Elementos Finitos

MVF

–

Método dos Volumes Finitos

RBF

–

Radial basis function

–

Funções de base radial

SRC – somatório do resíduo do contorno

LISTA DE SÍMBOLOS

A– matriz de colocação

AS– área de contribuição média de um ponto discretizado

B– operador linear do contorno

C– parâmetro de forma

DS– espaçamento nodal médio

f(x)– valor da função no domínio

g(x)–valor da função do contorno

�– gradiente hidráulico

k– coeficiente de permeabilidade

L– operador linear do domínio

� _�– número de pontos em um domínio linear.

���– número de pontos em um domínio bidimensional.

���– número de pontos em um domínio em 3 dimensões.

q– vazão

R– resíduo

r– módulo da distância entre os nós interpolados

u– fluxo hidráulico

VS –volume de contribuição médio de um ponto discretizado

�– velocidade da percolação

α e β – constantes da solução de uma equação diferencial � - contorno

Δu – variação de potencial hidráulico

�– coeficiente de porosidade

j –coeficiente que indica o peso de cada RBF π – pi

 -função de base radial Ω - domínio

SUMÁRIO

1.

Introdução

... 1

1.2

Barragens

... 3

1.2.1 Percolação

... 4

1.2.2 Lei de Darcy

...5

1.2.3 Coeficiente

k... 7

1.2.4 Redes de fluxo

... 8

1.2.4.1 Modelagem matemática da rede de fluxo... 9

1.3

Equações diferenciais

...12

1.3.1 Ordem da equação diferencial

... 13

1.3.2 Linearidade de uma equação diferencial

... 13

1.3.3 Equações diferenciais homogêneas

... 13

1.3.4 Soluções de uma equação diferencial, e condições de Contorno

... 14

1.3.5 A equação diferencial parcial de segunda ordem

... 16

1.3.6 Solução analítica da equação de Laplace

... 17

1.3.7 Resolução da Equação de Laplace em um Retângulo

... 19

2.

MÉTODO SEM MALHA

... 23

2.1

Metodologia teórica

... 24

2.2

Funções de Base Radial

... 25

2.2.1 Parâmetro de forma

C... 25

2.2.2 Principais Funções de Base Radial

... 27

2.3

Método Kansa

... 28

2.4

Aplicação em uma equação diferencial ordinária

... 29

2.5

Conceito de Resíduo

... 37

2.7

Caracterização do problema

... 40

2.8

Processamento da Rotina

... 43

2.9

Resultados

... 46

2.10 Análise de resultados

... 69

3.

Conclusões

... 71

1

O desenvolvimento do estudo da engenharia, assim como todas as ciências ligadas à

tecnologia, sempre está ligada à questão da matemática, que serve de auxílio como uma ferramenta

desde previsões futuras, até os dimensionamentos.

Em engenharia a questão do cálculo exato na maioria das vezes não é imprescindível, e muitas

vezes nem é possível, mas mesmo assim sempre é necessário adotar aproximações que tornem

possível resolver esses problemas, e que também tenham uma solução que possa ser encontrada.

Baseado nisso se desenvolveram os Métodos Numéricos, que são formas de se calcular com

uma aproximação satisfatória os resultados necessários para a aplicação prática de engenharia e outras

ciências (Cigonsky, 1998).

Com o desenvolvimento da informática, e com o poder de processamento cada vez maior,

várias técnicas são desenvolvidas constantemente com o objetivo de buscar sempre resultados mais

próximos das soluções analíticas na resolução das equações diferenciais. Uma grande quantidade de

métodos numéricos foram desenvolvidos, onde inicialmente se trabalhou com métodos que formavam

uma malha com os pontos discretizados no domínio determinado para a situação procurada.

Posteriormente se desenvolveram métodos diferentes, que usavam pontos discretos mas sem ligação

entre si. Esses métodos foram chamados de Meshless, ou simplesmente métodos sem malha (Viana e

Mesquita, 1998).

A concepção de um método livre de malhas vem de antes de 1977, com o desenvolvimento de

um método Lagrangeano baseado em estimativas Kernel (estimador probabilístico não-paramétrico)

para a modelagem de problemas astrofísicos. Esse método ficou conhecido como Hidrodinâmica de

partículas suavizadas Smoothed Particle Hydrodynamics (Monaghan, 1982). Esse método se baseava

2

diferenciais parciais (EDP’s) que governavam o problema, em estimativas de Kernel integradas (Liu,

1995). Ao passar do tempo esse método sofreu modificações com o objetivo de melhorar sua precisão.

O primeiro método sem malhas com base na teoria de Galerkin, Element-Free Galerkin –

EFG (Belytscko, 1994), surgiu 10 anos depois da primeira publicação sobre SPH. O Método dos

elementos difusos (Diffuse Element Method – DEM) foi introduzido por Nayroles e Touzot (Nayroles

1992).

O objetivo desse trabalho é desenvolver uma rotina computacional para resolver equações

diferenciais parciais utilizando o método numérico sem malhas, e de maneira mais específica, fazer a

otimização do parâmetro de forma C para que se obtenha uma solução numérica mais próxima da

solução analítica.

O modelo utilizado como aplicação, é o modelo simplificado da uma parede de uma barragem,

onde será determinado o fluxo hidráulico através das fundações da mesma. Esse fluxo tem seu

comportamento definido pela Equação de Laplace, que é a equação diferencial que irá servir de caso

3

As barragens podem ser definidas como obstáculos artificias criados com o objetivo de reter

água em um determinado local para fins como armazenamento, controle de cheias, e geração de

energia elétrica (ICOLD, 1994).

As barragens são construídas pelo homem desde a antiguidade, onde tem-se registro de

barragens construídas a 5 mil anos como a barragem de Saad el Kafara no Egito. No Iêmen, em 750

a.C. começou a ser construída a Barragem de Marib, cuja construção demorou 100 anos, e dura até os

dias atuais. As dimensões iniciais indicavam a altura da parede de 4 metros. Em 1986 essa barragem

foi elevada a uma altura de 38 metros, o que criou um reservatório de quase 400 milhões de metros

cúbicos de água (ICOLD, 2003).

Nas primeiras barragens o principal objetivo era o armazenamento de água para evitar

escassez nos períodos secos. Com o desenvolvimento de novas técnicas veio a irrigação, controle de

cheias, e manter a vazão dos rios no período de estiagem. No final do século XIX, as barragens já

começaram a ter também objetivos adicionais que eram a energia hidrelétrica, e a navegação.

A classificação das barragens é feita pelo tipo de material que é utilizado em sua construção, e

se dividem em:

 Barragens rígidas: construídas com concreto, pedra, e alvenaria: podem ser barragens

de gravidade, arco e contraforte.

 Barragens de aterro: construídas com terra e rocha, se classifiacam em barragens de

terra, de enrocamento, e barragens de terra e enrocamento.

Cerca de 75% de todas as barragens do mundo são de aterro, motivo pelo qual concentraremos

4

Fonte: elaborado pelo autor

1.2.1 Percolação

A maioria dos solos apresenta boa parte do seu volume de vazios, ou até mesmo totalmente,

preenchido com água. Água essa que quando submetida a um potencial hidráulico permeia através

desses vazios. A percolação pode ser definida como esse movimento da água através do solo,

descrevendo linhas de fluxo hídrico através dele. Esse fluxo ocorre devido ao diferencial hidráulico

(energia potencial), podendo-se até dizer que essa energia corresponde à energia total, já que a parcela

de energia cinética pode ser desprezada em virtude da baixa velocidade da água através dos solos

compactados (Sousa, 2000).

As barragens de terra não impedem totalmente a passagem de água por seu aterro ou

fundações. Certa quantidade de água vai atravessar essa barragem através da percolação pelo aterro ou

pelas fundações. Pode se achar que esse volume de água percolada não influencie no cálculo do

projeto, pois é comumente pequeno se comparado aos volumes de manutenção da construção, ou

5

que essa percolação pode chegar a valores restritivos, mesmo em grandes barragens, já que

aproximadamente 66% das causas de ruptura em barragens de aterro estão associadas a essa erosão

que acontece no corpo da barragem e é provocada pela ação da água que percola no interior da

fundação (Sandroni, 2012).

O ponto que deve ser discutido é quando essa percolação põe em risco a integridade da

construção (Cruz, 1996), e como ele pode afetar a barragem. Esse risco se dá através do carreamento

do material que é causado pelo fluxo hídrico e que acontece das seguintes formas (Sandroni, 2012):

 Entre dois pontos no interior das fundações, causando colmatação, ou

seja, o entupimento dos elementos drenantes essenciais fundamentais à estabilidade da

obra.

 Da barragem para dentro das fundações, ou das fundações para fora da

barragem. Esse fluxo que em excesso irá criar canais nas fundações, ou na própria

parede, causa o entubamento.

1.2.2 Lei de Darcy

O francês Henry Philibert Gaspert Darcy descreveu em seus experimentos uma equação para

determinar o fluxo de água dentro de um meio poroso. Essa equação ficou conhecida como Lei de

Darcy, e é dada por (Sousa, 2000):

= ∙ (1.1)

Onde:

6

proporcionalidade, e é chamada de coeficiente de permeabilidade do solo. Fisicamente esta lei coloca

que a velocidade de percolação é proporcional à força da gravidade, e ao mesmo tempo inversamente

proporcional às forças de atrito que se geram do contato com o material percolado.

Na verdade a água só percorre uma parte do solo através desses pequenos canais encontrados

formados pelos vazios, pois a trajetória real é bastante variada, e nesse caminho passa por grandes

variações de velocidade devido ao alargamento ou estrangulamento desses canais. Para termos de

estudo se estipula uma trajetória linear à qual chamamos linha de fluxo.

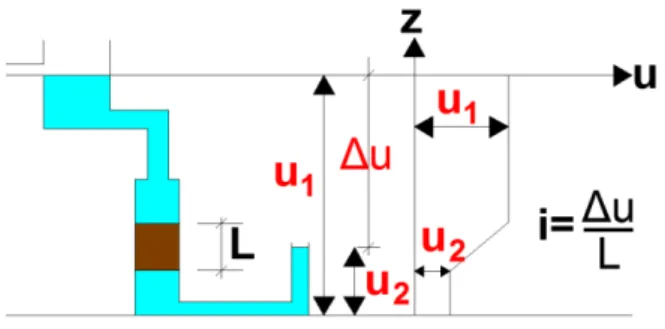
Em seu experimento, Darcy montou um sistema semelhante ao mostrado na Figura 2, para

equacionar essas propriedades na amostra de um corpo poroso (L):

Figura 2 – Sistema feito por Darcy

Fonte: elaborado pelo autor

A partir desse estudo Darcy relacionou o gradiente hidráulico (taxa de perda de energia

potencial) com a velocidade desse fluxo a partir de informações baseadas no seguinte: Os níveis u1 e

u2 permanecem constantes, e o escoamento acontece no sentido indicado. Ao se medir a vazão para

vários comprimentos de L, e a variação de potencial Δu, constatou-se que a vazão “q” é proporcional

ao gradiente hidráulico, i _ou ∆

� , o que nos leva à expressão:

7

a velocidade de percolação do fluxo de água através desse corpo:

= − ∆_� = ∙ (1.4)

Essa velocidade recebe a denominação de velocidade de descarga (v), apresentado, portanto,

um valor diferente da real. Da Mecânica dos Solos, em um determinado plano consideramos que a

razão entre a área da seção de vazios, e a área da seção transversal total é dada pelo coeficiente de

porosidade (

_�

percolação real:

�� =_� (1.5)

E para a velocidade de percolação (vp), temos:

�= �∙ (1.6)

Sempre que existir o gradiente hidráulico haverá a percolação, mas é importante observar que

a Lei de Darcy é valida para um escoamento “laminar”, ou seja, aquele em que as trajetórias de fluxo

não se cruzam, o que pode-se dizer que é valido para a maioria dos solos naturais.

1.2.3 Coeficiente k

O valor do coeficiente de permeabilidade normalmente é muito baixo, motivo pelo qual é

representado em forma de um produto com potência de base 10. Na Figura 1.2 temos uma escala para

exemplificar alguns tipos de solo e seus respectivos coeficientes k:

Tabela 1 – Valores de k para diferentes tipos de solo.

8

K

Material Características de _escoamento

cm/seg m/dia

10-2 _{1 a 100 864 a 86400 Pedregulho limpo}

Aquíferos bons 10-3 _{0,001 a 1 0,86 a 864 Areias limpas, misturas de areia limpa}

10-7 ₁₀-7 _{a 10}-3 _{8,64 x 10}-5 _{a 0,86 Areias muito finas; siltes, argilas estratificadas Aquíferos pobres}

10-9 ₁₀-7 _{a 10}-3 _{8,64 x 10}-7 _{a 10}-5 _{Argilas não alteradas Impermeáveis}

Fonte: elaborado pelo autor

Observa-se que os solos finos mesmo apresentando indíces de vazios normalmente maiores

que os de solos mais grosseiros, possuem um coeficiente de permeabilidade menor.

1.2.4 Redes de Fluxo

No estudo da percolação, utiliza-se do conceito de linhas de fluxo e linhas de equipotenciais

para se fazer a modelagem, e melhor compreender o comportamento da água no interior dos solos. As

linhas de fluxo funcionam como canais que irão dar vazão à água, enquanto que as linhas de

equipotenciais representam a carga hidráulica, ou energia potencial dessa água durante o percurso

(Souza, 2005). Abaixo temos uma representação das linhas de fluxo e linhas de equipotencial:

Figura 3 – Fluxo através da parede de uma barragem.

Fonte: Sousa, 2000, p. 148

De acordo com o gráfico podemos observar:

9

 As linhas de equipotencial (claras) indicam os caminhos que apresentam o

mesmo potencial.

1.2.4.1 Modelagem matemática da rede de fluxo

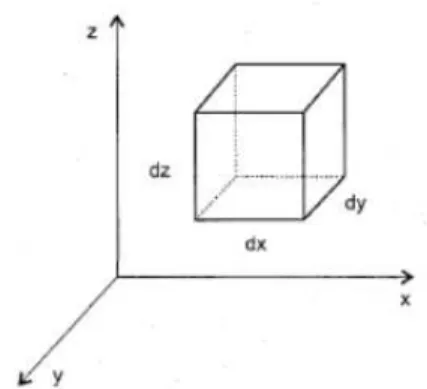
O estudo da percolação bi ou tridimensional se baseia na equação diferencial de fluxo à qual

deduzimos a seguir. Considerando um sistema cartesiano, decompomos um elemento diferencial em

três eixos ortogonais, submetido a um fluxo tridimensional, onde o coeficiente de permeabilidade é

diferente nas direções x, y e z. Para efeitos de dedução, assumimos que o escoamento é laminar

(validade da Lei de Darcy), um meio poroso homogêneo e não saturado, onde o solo e a água são

incompressíveis.

Figura 4 – Sistema de coordenadas cartesianas.

Fonte: Sousa, 2000, p. 152

De acordo com a Lei de Darcy (Sousa, 2000), O gradiente do fluxo ao longo de x é dado por:

=�_{� .}

E considerando que esse gradiente também irá variar na direção x, temos:

� � =

� � ∙ (

� � ) =

�

10

�

� + ( ) ∙ �

� .

E segundo a Lei de Darcy, a vazão de entrada é:

= �_{� −}�_{� ∙} ∙ ∙ .

O que nos dá na saída:

�= �_{� +}�_{� ∙} ∙ ∙ .

Fazendo a diferença entre as vazões de entrada e a saída temos:

�− = �_� ∙ ∙ ∙ .

Da mesma forma a diferença de vazão nos outros eixos é:

�− = �_� ∙ ∙ ∙ .

�− = �_� ∙ ∙ ∙ .

Como o volume do elemento permanece o mesmo durante o fluxo, os volumes de entrada e de

saída de água são iguais, o que significa que a soma da diferença entre as vazões de entrada e saída é

zero. Daí temos:

� � +

� � +

�

� ∙ ∙ ∙ = .

Normalmente considera-se o fluxo apenas em um plano infinitesimal e perpendicular ao eixo

11

superior às dimensões transversais. A partir daí temos:

� � +

�

� = .

Essa é a equação para o fluxo em duas dimensões. Considerando que o escoamento ocorre em

um meio isotrópico, temos que ₌ , a então equação passa a:

� � +

�

� = .

Aqui o fluxo vai ser definido por uma equação onde uma variação no gradiente de x vai ser

contrabalançada pela variação no gradiente de y. Essa função pode ser simplificada para:

= .

Onde representa o operador laplaciano:

= �

� +

�

� +

�

� .

O tipo de equação ₌ , onde u é uma função qualquer, é chamada de Equação de

Laplace, e a função u é chamada de harmônica. A Equação de Laplace tem como solução geral dois

conjuntos de funções onde os gráficos destas são perpendiculares no ponto em que se interceptam

12

Uma equação diferencial é uma equação onde a solução consiste em uma função que satisfaz

às suas derivadas. Segundo (Bronson, 1977), uma equação diferencial é uma equação que envolve

uma função incógnita e suas derivadas. As equações diferencias são divididas em:

 Equações diferenciais ordinárias

 Equações diferenciais parciais

Uma equação é dita ordinária (E.D.O.) se a função incógnita depende de apenas uma variável

independente (Bronson, 1977). Uma equação diferencial ordinária na variável dependente y e na

variável independente x, é uma equação que pode ser escrita da forma:

( , , ′_, ′′_{, … , ) = .}

Onde F é uma função das variáveis indicadas e pelo menos uma derivada (ordinária) aparece

nessa expressão (León e Castro, 2010).

Se a função incógnita depende de mais de uma variável independente, temos uma equação

diferencial parcial (Bronson, 1977). Uma equação diferencial parcial (EDP) na variável dependente u e

nas variáveis independentes x e y, é uma equação que pode ser posta na forma:

= ( , , , , , , , ) = .

Ou ainda:

= �_{� +} �_{� +} �_{� +} �_{� +} + + + − � .

Onde F é uma função das variáveis indicadas e pelo menos uma derivada aparece nessa

expressão. Note que ₌�

� , = �

13

A ordem de uma equação diferencial é ordem da maior derivada na equação (Zill, 2001). A

ordem de uma equação diferencial é o expoente da derivada mais alta. Por exemplo,

� � + (

�

� ) = sin .

É uma equação diferencial de segunda ordem, pois a maior derivada de maior ordem apresenta

valor 2.

No caso de equações diferenciais de primeira ordem adota-se ocasionalmente a notação:

+ + , = .

1.3.2 Linearidade de uma equação diferencial

Dizemos que uma equação diferencial de ordem n (1.20) é linear se F for linear em y,y’,...,y(n-1)

(Zill 2001).Isso significa que uma EDO ou EDP de n-ésima ordem é linear quando (1.20) for:

+ −

−

− + + + = .

As equações lineares apresentam duas propriedades:

 A variável dependente assim como suas derivadas, serão do primeiro grau

 Os coeficientes dependem no máximo da variável independente x.

1.3.3 Equações diferenciais homogêneas

A função definida por _{= ,} será uma função homogênea de grau m se tivermos

14

de mesmo grau como mostrado abaixo:

= �_{� +} �_{� +} �_{� +} �_{� +} + + + = � .

Se _{+ =} for uma equação diferencial homogênea, então ela poderá ser escrita da

forma:

= .

Onde a mudança de variáveis irá separar as variáveis.

1.3.4 Soluções de uma equação diferencial, e condições de Contorno.

Uma solução de uma equação diferencial na função incógnita y e na variável independente x,

no intervalo _�, é uma função y(x) que se verifica identicamente a equação para todo x em _� (Bronson,

1977). O que se nota sobre as equações diferencias é que algumas admitem infinitas soluções,

enquanto outras não admitem nenhuma solução analítica.

A solução de uma equação diferencial pode ser dada de duas formas:

 Solução particular: é qualquer caso particular da equação.

 Solução geral: é o conjunto de todas as soluções.

A solução particular de uma equação diferencial é a solução que se obtém a partir da solução

geral, satisfazendo as condições iniciais ou as de contorno. Normalmente as condições iniciais são

dadas para o instante inicial, enquanto as de contorno aparecem quando em equações de ordem

superior os valores da função e de suas derivadas são dadas em pontos distintos (Borges, 2006). Uma

15

( , + , + , + , , , , ) = .

sobre um conjunto _{⊂ ℝ} se:

1. _≡ é duas vezes continuamente diferenciável sobre o conjunto _⊂

ℝ .

2. satisfaz à Equação Diferencial Parcial dada.

A solução geral é a família de curvas que satisfazem à equação e às suas constantes arbitrárias,

ou seja, a solução geral u=f(x,y) de uma equação diferencial sobre um conjunto _{⊂ ℝ} é a solução

que engloba todas as possíveis soluções sobre M, enquanto uma solução particular é uma função

específica que satisfaz à equação para uma condição particular (Santos 2011).

Então para se obter a solução particular do conjunto universo da solução geral, são necessárias

condições que determinem como essa equação se comporta no seu domínio, e no contorno onde se

procura essa solução. Um problema de valor inicial consiste em uma equação diferencial, juntamente

com condições subsidiárias relativas à função incógnita e suas derivadas – tudo dado para um mesmo

valor da variável independente. As condições subsidiárias são condições iniciais se as condições

subsidiárias se referem a mais de um valor de variável independente, o problema é um problema de

valor de contorno e as condições se dizem condições de contorno (Bronson, 1977).

Dessa forma, a solução encontrada, ou solução particular, é aquela em que a função y(x)

satisfaz tanto a equação diferencial, como também as condições de valor inicial, e condições de

contorno.

Condições de contorno aparecem de maneira natural na descrição dos fenômenos físicos

estacionários (independentes do tempo) (León e Castro, 2010). Encontraremos muitas vezes as

condições do tipo:

16

� é a derivada de u na direção

normal a _�Ω. No caso em que ₌ , a condição (1.29) é conhecida como Condição de Dirichlet, e no

caso em que ₌ , temos uma condição de Neumann (León e Castro, 2010).

1.3.5 A equação diferencial parcial de segunda ordem

A forma geral de uma equação diferencial parcial de segunda ordem em duas variáveis

independentes x e y é:

( , + , + , = , , , , ) . Ou ainda: � � + � � + � � + � � + + + + + = .

Essa equação pode ser classificada em:

 Hiperbólica em _, , se _{, − , , >}

 Parabólica em _, , se _{, − , , =}

 Elíptica em _, , _{, − , , <}

Onde _{, − , ,} recebe a denominação de discriminante.

Como alguns exemplos de aplicação física dessas equações temos:

 A Equação da Onda: essa equação é linear, não homogênea, e se _{, = −} , _{, =}

, = , temos que _{� , = >} . Logo será do tipo hiperbólica no domínio de f.

� � −

�

� = , .

 A Equação do Calor: é linear, não homogênea, e como _{, = − , , =} , e _{, =}

17

� − �

� = , .

 A Equação de Laplace, que é a nossa equação de interesse, apresenta as seguintes

características: é linear, não homogênea _{, = − , , =} , e _{, =} , temos que

� , = − < . Logo será tipo elíptica no domínio de f.

� � −

�

� = , .

1.3.6 Solução analítica da equação de Laplace

O nosso caso apresenta interesse pela equação de Laplace no caso bidimensional, portanto,

vamos considerar a equação de Laplace _{� =} no sistema de coordenadas cartesianas:

� � +

�

� = .

Essa equação é de segunda ordem (apresenta derivadas de segunda ordem), e primeiro grau

(apresenta apenas a primeira potência). Como dito anteriormente, para se resolver equações

diferenciais parciais, é necessário de conhecer as condições de contorno do problema.

Para resolver a equação, aplicamos inicialmente o Método da Separação de Variáveis, onde

consideramos que u pode assumir a forma de produto de duas funções X e Y.

= .

onde:

 X é função de x apenas,

 Y é função de y apenas.

Substituindo (1.36) em (1.35), nós temos:

� � +

�

18

� � +

�

� = .

Como a soma dos 3 termos é uma constante, e as variáveis são independentes, cada um dos

termos deve ter um valor constante. Dessa forma podemos escrever:

�

� = .

ou também:

�

� = .

Fazendo da mesma forma tomando o segundo termo:

�

� = − .

Agora o próximo passo é achar a solução para cada uma das variáveis separadamente (daí a

separação de variáveis). Então a solução para a equação (1.39) passa a ser:

= + − _.

onde C1e C2 são constantes definidas a partir das condições de contorno. Da mesma forma temos:

= + − _.

Qualquer termo de (1.43) assim como a soma dos mesmos, será uma solução de (1.41). Sendo assim, a

solução geral da equação passa a ser:

= + − _{( +} − _{) .}

19

, = [ ℎ + ℎ ][ + ] .

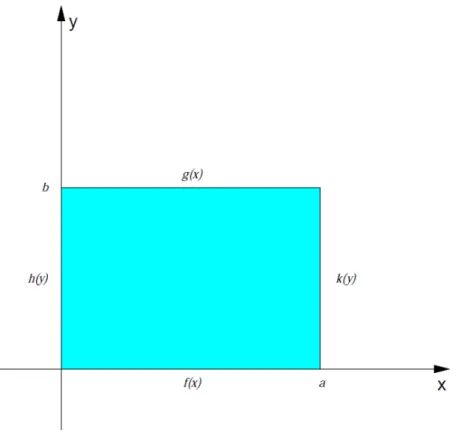
1.3.7 Resolução da Equação de Laplace em um Retângulo

No caso desse estudo, foi considerado um retângulo como o mostrado abaixo (Santos, 2007), onde

temos a equação e as condições de contorno a seguir:

{ �

� + �

� = , = , , = , < < . , = ℎ , , = , < <

Esse problema apresenta condições de Dirichlet. A solução será a soma das soluções dos

problemas com apenas uma das funções f(x), g(x), h(y), e k(y) não nulas (Santos, 2007).

Figura 5 _– Domínio da função

20

função de x por uma função de t :

, = .

Derivando, temos a equação a seguir:

�

� = −

�

� .

Essa igualdade só é possível se os termos forem iguais a uma constante:

�

� = −

�

� = � .

Daí, temos as seguintes EDO’s:

{ �

� − � = , = . �

� + � = , = , = .

A equação (1.51) com as condições de fronteira apresentadas só tem solução se _{� =} � , para ₌

, , , … e nesse caso a solução seria a seguinte:

= � , = , , , … .

A equação (1.50), considerando a condição de contorno ₌ tem a seguinte solução:

= � − − � − = ℎ � − .

O problema então apresenta solução na seguinte forma:

21

, = ∑ ,

∞

=

= � ℎ � − .

também são soluções para a equação.

Vale ressaltar que para termos a condição inicial _{, = ℎ ,} temos que ter:

= , = ∑ ,

∞

=

= ∑ � ℎ �

∞

=

.

Esta é a série de Fourier de senos de . Dessa forma os coeficientes são dados por (Boyce

[6]):

ℎ � = ∫ � , = , , … .

Tomando como um exemplo a Equação de Laplace no seguinte retângulo:

{ �

� + �

� = , = , , = , < < .

, = , , = , < <

com

= { _{− , ≤ ≤ .}, ≤ ≤

A solução então é:

, = ∑ � ℎ �

∞

=

.

22

= ∫ � .

=

�

� , = , , … .

=

�

� ℎ �, = , , … .

Dessa maneira a solução torna-se:

, _{= � ∑}

�

� ℎ �

∞

=

� �

23

Como visto, a resolução de equações diferenciais parciais pelo método analítico é sempre

muito trabalhosa, e na maioria dos casos práticos de aplicações em modelos físicos, as condições de

contorno tornam essa resolução impossível. Diante disso foram desenvolvidos métodos numéricos que

calculam a solução aproximada dessas equações de forma a se obter valores que satisfaçam as

necessidades de aplicação.

Entre os métodos numéricos mais conhecidos pode-se destacar o Método dos Elementos

Finitos (MEF), Método das Diferenças Finitas (MDF), Método dos Volumes Finitos (MVF), e Método

dos Elementos de Contorno (MEC). Esses métodos necessitam de uma malha para melhorar sua

precisão, e apresentar uma solução mais próxima do real. Quando se fala nos 3 primeiros métodos

(MEF,MDF, e MVF) se construir uma malha de 3 dimensões não é tarefa fácil, e no MEC, mesmo

sendo feita uma modelagem geométrica apenas na superfície de contorno, a malha também é um

problema complicado (Cheng et al, 2003).

A natureza em sua forma real apresenta domínios bastante irregulares, e uma opção viável

para resolver esse problema seria a discretização do domínio do sistema físico sem a construção dessas

malhas.

Tem se pesquisado métodos que dispensem a necessidade de ligação desses nós quando se vai

discretizar o domínio. Esse método tem sido chamado “meshless”. Esse método apresenta vantagens

como simplificação nos dados de entrada, e facilidade na redistribuição dos pontos discretos, mas o

que mais motiva esse método é a diminuição de custos no processo de modelagem, principalmente em

processos industriais onde a geração e modificação de malhas exige bastante em determinadas

situações. Esses custos se referem ao tempo gasto nas modelagens (Cheng et al, 2003). Outra

característica importante é que conforme cresce a dimensão espacial do domínio, também cresce a

ordem de convergência, o que significa um menor número de pontos para conseguir a mesma precisão

24

Smooth Particle Hydrodynamics (SPH), Método dos Pontos Finitos, e Radial Basis Functions (RBF).

Dentre os métodos citados, iremos utilizar nesse trabalho o método RBF.

2.1 Metodologia teórica

No método meshless, os nós do domínios são discretizados sem a necessidade de ligação entre

si, de forma a resolver a equação diferencial. Essa EDP atende ao domínio definido, tendo seu

comportamento completo dado pelas condições de contorno corretas.

A equação diferencial pode ser dada da seguinte maneira:

[ ] ⃗ = ⃗ .

Onde:

 L é um operador linear, que depende do problema.

 u é a função que se quer determinar.

 x é o vetor variável independente.

Essa variável independente é dividida em dois conjuntos: elementos do domínio da equação, e

elementos do contorno. Esses elementos do contorno deverão satisfazer às Condições de contorno, que

são expressas da seguinte forma:

[ ] ⃗ = ⃗ .

Em que B é um operador linear que vai depender do problema.

As condições de contorno, como dito anteriormente, podem ser: condições de Dirichlet, ou

25

domínio, isto é, um fluxo.

Para se resolver essa EDP a partir de um conjunto discretizado é preciso um interpolador

espacial, que no nosso caso será feito com o uso de Funções de Base Radial.

2.2 Funções de Base Radial

As Funções de Base Radial em duas dimensões apresentam a forma (Monaghan, 1992):

= = , .

Onde ri corresponde ao módulo da distância entre o nó _, e o ponto interpolado (x,y).

Essa distância num espaço Euclidiano é dada por:

= √[ − + − ] .

As RBF apresentam como característica a simetria radial, dessa forma, dependendo apenas da

distância _{= ‖ − ‖} entre o centro da função e o ponto genérico x, podendo ser escrito também na

forma _{� .}

2.2.1 Parâmetro de forma C

Além de depender de r, a RBF também depende de um parâmetro expresso por c _– fator de

forma, ou parâmetro de forma. Esse fator é utilizado para aumentar a suavidade da resposta, trazendo

26

método trabalha com o conceito de espaçamento nodal médio, e calcula os valores para uma, duas e

três dimensões. Para 1D temos a seguinte equação:

= �

( _�− ) .

Onde DSé o espaçamento nodal médio, ou a distância entre os nós dentro do domínio. O DS

seria o domínio de suporte, ou o intervalo de contribuição que um determinado ponto tem dentro do

domínio, o que no caso de uma discretização homogênea, dá o mesmo valor de contribuição para

todos os pontos dentro domínio. _� é o número de pontos dentro desse domínio. Para o caso 2D,

temos o valor calculado através de:

= √ �

√ ��−

.

Nesse caso fazemos analogia ao caso 1D. Aqui temos que AS é o valor da área de contribuição

de determinado ponto para demonstrar o comportamento da função dentro desse intervalo. No caso da

discretização homogênea, esse valor seria equivalente para todos os pontos dentro do domínio da

função. _�� seria a quantidade de pontos dentro desse domínio. Da mesma forma, para os casos em

3D, um método simples de definir esse coeficiente é:

= √�� √ ��−

.

Já aqui o _�� seria o volume de apoio, ou volume de contribuição de cada ponto, e o _��, a

27

Dentre as Funções de Base Radial mais utilizadas podemos destacar, (Buhmann, 2003):

Tabela 3. Funções de Base Radial mais utilizadas.

Spline de Placas infinitas _{| | | |}, com n par

Multiquadrática _{√ +}

Multiquadrática inversa

√ +

Gaussiana − �

Spline Harmônica , = , , , …

ln , = , , , … Quadrática inversa

+ Fonte: elaborado pelo autor

Outros trabalhos interessantes a respeito de diferentes funções podem ser vistos em Schaback

e Wendland (2002), e Wendland (1995). O método meshless vai trabalhar os pontos discretizados no

domínio da equação, e esses pontos serão interpolados por uma combinação linear de funções de base

radial centradas nos pontos xj da seguinte forma:

⃗, = ∑ � � ,

=

.

Onde:

 u é a função a ser determinada na equação diferencial;

 x é a variável independente, representado por um vetor;

 n é o número de pontos discretizados do domínio;

  é a função de base radial;

 j são os coeficientes a serem determinados, e que indicam os pesos de cada RBF.

Os coeficientes jserão determinados através da utilização da equação diferencial resolvida e

28

O Método de Kansa tem como fundamento a substituição da função de aproximação (2,7) na

equação diferencial (2.1) e nas condições de contorno (2.2), e dessa maneira gerar um sistema linear

que terá como resultado j (Kansa, 1990).Substituindo (2.7) em (2.1) e (2.7) temos:

⋮ã [∑ � � ,

�

=

] = ⃗ .

⋮� [∑ � � ,

�

=

] = ⃗ .

L é um operador linear, portanto, satisfaz às seguintes propriedades:

I. _{[ + ] = [ ] + [ ]}

II. _{[ ] =} [ ]

Aplicando em (2.8) e (2.9):

∑ � [� , ]

�

=

= ⃗ .

∑ � [� , ]

�

=

= ⃗ .

Dessa forma agora pode-se montar o sistema matricial do tipo _{� =} , onde a matriz A

(matriz de colocação) é formada por dois blocos (Kansa e Hon, 2000) :

= [ [�]_{[�]] .}

O vetor y é será composto pelos valores das funções _⃗ e _⃗ nos pontos discretizados,

29

Dessa maneira teremos então o seguinte sistema matricial:

� = [ [�]_{[�]] [� ] = = [} ⃗_{⃗ ] .}

A solução do sistema fornecerá os valores de _� que serão substituídos na função de

aproximação.

2.4 Aplicação em uma equação diferencial ordinária

Inicialmente iremos resolver uma EDO para uma melhor compreensão. Considere a EDO

linear de segunda ordem com condições de Dirichlet abaixo:

− = .

= , = .

Onde o domínio da função u é definida para o domínio _{= { �⁄ < < }}.

A solução analítica dessa equação é dada pela seguinte função:

� = _{− −} − _{− −} − − .

No nosso estudo nos concentraremos na RBF Multiquadrática. Inicialmente estimaremos o

valor de c em 0,5 , e discretizaremos o espaço em 11 pontos. Abaixo temos a tabela com os pontos

30

Pontos

x

x

1 0,1 0,1

2 0,2 0,2

3 0,3 0,3

4 0,4 0,4

5 0,5 0,5

6 0,6 0,6

7 0,7 0,7

8 0,8 0,8

9 0,9 0,9

10 1 1

11 0 0

Fonte: elaborado pelo autor

Uma observação importante é que na discretização acima, os pontos 10 e 11 correspondem aos

extremos do domínio.

Para dar continuação ao cálculo para a equação, determina-se a matriz de distâncias definida

como Matriz R. Nela são dispostos os valores dos módulos das distâncias entre os pontos. Essa

distância vai calculada através da expressão abaixo (Kansa, 2000):

� = √( − ) = | − | .

Onde:

, = √ − .

, = √ − .

, = √ − .

, = √ − .

� = [ , ⋱ ,

, ,

31

mostra a distância entre os pontos discretizados em relação a um determinado ponto de referência.

Tabela 5 – Matriz das distâncias entre os pontos definidos – Matriz R.

Matriz R

1 2 3 4 5 6 7 8 9 10 11

1 0 0.1 0.2 0.3 0.4 9 0.6 0.7 0.8 0.9 0.1

2 0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.2

3 0.2 0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.3

4 0.3 0.2 0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.4

5 0.4 0.3 0.2 0.1 0 0.1 0.2 0.3 0.4 0.5 0.5

6 0.5 0.4 0.3 0.2 0.1 0 0.1 0.2 0.3 0.4 0.6

7 0.6 0.5 0.4 0.3 0.2 0.1 0 0.1 0.2 0.3 0.7

8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0.1 0.2 0.8

9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0.1 0.9

10 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 1

11 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0

Fonte: elaborado pelo autor

O próximo passo é o cálculo da Matriz _�. Para isso determinamos qual a Função de Base

Radial a ser utilizada. No nosso caso iremos utilizar a RBF multiquadrática, onde para o caso

unidimensional é calculada por (Kansa, 2000):

� , = √ + .

Então a partir dos elementos nós montamos a Matriz _�:

� , , = √ , + .

� , , = √ , + .

� , , = √ , + .

32

� , � ,

] .

A partir da RBF escolhida, adotamos aleatoriamente um _{= ,} , e determinamos a Matriz _�

como mostrado na Tabela 6:

Tabela 6 – Valores da Função _� para um _{= ,} .

Matriz Φ

1 2 3 4 5 6 7 8 9 10 11

1 0.5000 0.5099 0.5385 0.5831 0.6403 9.0139 0.7810 0.8602 0.9434 1.0296 0.5099 2 0.5099 0.5000 0.5099 0.5385 0.5831 0.6403 0.7071 0.7810 0.8602 0.9434 0.5385 3 0.5385 0.5099 0.5000 0.5099 0.5385 0.5831 0.6403 0.7071 0.7810 0.8602 0.5831 4 0.5831 0.5385 0.5099 0.5000 0.5099 0.5385 0.5831 0.6403 0.7071 0.7810 0.6403 5 0.6403 0.5831 0.5385 0.5099 0.5000 0.5099 0.5385 0.5831 0.6403 0.7071 0.7071 6 0.7071 0.6403 0.5831 0.5385 0.5099 0.5000 0.5099 0.5385 0.5831 0.6403 0.7810 7 0.7810 0.7071 0.6403 0.5831 0.5385 0.5099 0.5000 0.5099 0.5385 0.5831 0.8602 8 0.8602 0.7810 0.7071 0.6403 0.5831 0.5385 0.5099 0.5000 0.5099 0.5385 0.9434 9 0.9434 0.8602 0.7810 0.7071 0.6403 0.5831 0.5385 0.5099 0.5000 0.5099 1.0296 10 1.0296 0.9434 0.8602 0.7810 0.7071 0.6403 0.5831 0.5385 0.5099 0.5000 1.1180 11 0.5099 0.5385 0.5831 0.6403 0.7071 0.7810 0.8602 0.9434 1.0296 1.1180 0.5000 Fonte: elaborado pelo autor

Agora calculamos a Matriz _[�]. Para determinar o valor dos coeficientes dessa matriz,

calculamos a função que irá definí-los a partir da expressão (Kansa, 2000):

[�] =_{� � , .}�

Considerando que usamos a RBF multiquadrática, substituímos _{� ,} pela mesma:

[�] = [√ + ] .

[�] = [ + − ] .

[�] =

33

Tabela 7:

Tabela 7 _– Valores de _[�] para _{= ,} .

Matriz L[Φ]

1 2 3 4 5 6 7 8 9 10 11

1 2.0000 1.8857 1.6008 1.2610 0.9523 0.0003 0.5247 0.3927 0.2978 0.2291 1.8857 2 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.7071 0.5247 0.3927 0.2978 1.6008 3 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.7071 0.5247 0.3927 1.2610 4 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.7071 0.5247 0.9523 5 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.7071 0.7071 6 0.7071 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.5247 7 0.5247 0.7071 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.3927 8 0.3927 0.5247 0.7071 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 0.2978 9 0.2978 0.3927 0.5247 0.7071 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 0.2291 10 0.2291 0.2978 0.3927 0.5247 0.7071 0.9523 1.2610 1.6008 1.8857 2.0000 0.1789 11 1.8857 1.6008 1.2610 0.9523 0.7071 0.5247 0.3927 0.2978 0.2291 0.1789 2.0000 Fonte: elaborado pelo autor

Procedemos então à montagem da nossa Matriz A, ou Matriz de Colocação. A montagem

dessa Matriz será feita a partir das Matrizes _[�] e _[�]. Considerando que nossas condições de

fronteira são condições de Dirichlet, podemos dizer que:

[�] = � .

Dessa forma, montamos a Matriz A da seguinte maneira (Hon e Kansa, 1999):

= [ [�]_{[�]] = [} [�]_{� ] .}

34

Matriz A

1 2 3 4 5 6 7 8 9 10 11

1 2.0000 1.8857 1.6008 1.2610 0.9523 0.0003 0.5247 0.3927 0.2978 0.2291 1.8857 2 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.7071 0.5247 0.3927 0.2978 1.6008 3 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.7071 0.5247 0.3927 1.2610 4 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.7071 0.5247 0.9523 5 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.7071 0.7071 6 0.7071 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.9523 0.5247 7 0.5247 0.7071 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 1.2610 0.3927 8 0.3927 0.5247 0.7071 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 1.6008 0.2978 9 0.2978 0.3927 0.5247 0.7071 0.9523 1.2610 1.6008 1.8857 2.0000 1.8857 0.2291 10 1.0296 0.9434 0.8602 0.7810 0.7071 0.6403 0.5831 0.5385 0.5099 0.5000 1.1180 11 0.5099 0.5385 0.5831 0.6403 0.7071 0.7810 0.8602 0.9434 1.0296 1.1180 0.5000 Fonte: elaborado pelo autor

Em seguida calculamos o vetor y a partir das funções e , que irá apresentar os

valores mostrados na Tabela 8:

Tabela 9 – Valores de y

y 0,4 0,8 1,2 1,6 2 2,4 2,8 3,2 3,6 0 0

Fonte: elaborado pelo autor

35

Matriz A-1

1 2 3 4 5 6 7 8 9 10 11

1 1.20 146.1 -495.8 954.09 -1325.7 1417.7 -1168.88 685.63 -233.59 -47.01 69.81 2 -2.20 -195.2 734.5 -1518.21 2212.2 -2430.85 2035.30 -1202.91 410.92 62.85 -116.09 3 2.67 150.15 -628.7 1426. -2232.9797 2568.85 -2210.70 1326.04 -456.40 -58.02 125.56 4 -2.51 -75.34 346.9 -869.5 1495.3321 -1845.45 1663.45 -1024.93 358.18 40.99 -98.18 5 2.00 21.82 -113.05 311.94 -596.7697 809.88 -784.76 506.33 -182.03 -20.13 50.87 6 -1.40 4.59 -9.0419 13.44 -16.4669 16.45 -13.09 7.52 -2.51 0.10 0.52 7 0.84 -13.97 50.11 -124.79 252.2611 -392.12 451.72 -338.49 136.53 15.64 -43.15 8 -0.41 14.14 -48.89 116.33 -235.1137 378.07 -471.63 388.49 -172.97 -22.88 63.23 9 0.13 -9.18 29.57 -64.55 124.4576 -196.62 255.40 -226.07 112.39 18.44 -51.10 10 -0.01 2.99 -9.05 18.04 -32.3915 48.22 -62.59 57.14 -31.39 -6.85 19.01 11 -0.30 -45.86 142.86 -262.27 353.8976 -372.82 304.82 -178.22 60.77 17.35 -19.97

Fonte: elaborado pelo autor

A partir das Matrizes A-1 _{e y, calcula-se a Matriz � a partir do produto:}

� = − _.

Tabela 11- Valores de _�

λ -2.1E+07 69280773 -1.3E+08 1.51E+08 -9.1E+07 -0.00057 47021770 -3.8E+07 14167441 -2148149 2737204

36

= ∑ � � ,

�

=

.

Substituindo na expressão acima encontraremos os valores da solução numérica nos pontos

discretizados inicialmente. Na Tabela 11 temos uma comparação numérica desses dois resultados,

mostrando o erro da solução numérica em relação à analítica.

Tabela 12 _– Comparação entre a solução Analítica e a Solução numérica.

X u(x) exata u(x) aproximada Erro

0,1 -0,044487524 -0,0655 0,0210

0,2 -0,086747137 -0,1235 0,0367

0,3 -0,124461515 -0,1775 0,0530

0,4 -0,155130917 -0,2195 0,0643

0,5 -0,175972863 -0,2455 0,0695

0,6 -0,183810463 -0,2515 0,0676

0,7 -0,174944915 -0,2334 0,0585

0,8 -0,145007062 -0,1874 0,0424

0,9 -0,088782044 -0,1093 0,0206

1 0 0,0047 -0,0047

0 0 0,0046 -0,0046

Fonte: elaborado pelo autor

Para uma melhor visualização, fez-se um gráfico comparativo mostrando as duas soluções:

Figura 6. Comparação entre a Solução Analítica e a Solução Numérica.

Fonte: elaborado pelo autor

0,0046 -0,0655 -0,1235 -0,1775 -0,2195 -0,2455-0,2515-0,2334 -0,1874 -0,1093 0,0047 -0,3 -0,25 -0,2 -0,15 -0,1 -0,05 0 0,05

1 2 3 4 5 6 7 8 9 10 11

u

(x)

Pontos

Comparação Gráfica

37

Observa-se que há uma diferença considerável entre as soluções, dessa forma não sendo

possível considerar essa solução numérica como uma aproximação. Essa diferença se deve à escolha

do parâmetro de forma, que nesse caso foi escolhido aleatoriamente para demonstrar esse erro.

E como saberemos se o parâmetro de forma escolhido foi o correto?

Observa-se que tomamos o módulo da diferença entre as soluções como medida de

aproximação para saber se a solução numérica será satisfatória ou não. A partir dessa diferença

começamos a trabalhar com o conceito de Resíduo.

O Resíduo no domínio é o resultado do produto da Matriz _[�] pelo vetor _�, menos o vetor y.

Nesse caso temos os valores de y dados pela função de domínio f(x). Então para o domínio o resíduo é

definido por (Belinha, 2010):

{� } = [� , ]{�} − { } .

O Resíduo no contorno é o resultado do produto da Matriz _[�] pelo vetor _�, menos o vetor y.

Analogamente ao resíduo do domínio, aqui o vetor y tem seus valores dados pela função g(x), o que

resulta na seguinte equação para o resíduo do contorno:

{� } = [� , ]{�} − { } .

Para atender simultaneamente às condições do domínio e contorno, pode-se definir o resíduo

por:

{� } = [� , ]{�} − { } .

Para se obter um resultado próximo do real, os resíduos do domínio e do contorno deverão ter

seu valor o mais próximo possível, e então nesse ponto calcula-se o C otimizado para ser aplicado na

38

do domínio e do contorno. Vale ressaltar que esse valor é dado em módulo, e se refere aos resíduos

normalizados tanto do domínio quando do contorno.

2.6 Rotina para se otimizar o parâmetro de forma C

Nos cálculos foi utilizado o software Scilab, pelo fato de o mesmo se livre, e ser assim de mais

fácil acesso a quem queira consultar o material. A rotina segue no Anexo I, e está dividida em cada um

dos passos descritos acima. Para uma compreensão sucinta, segue abaixo a forma que baseou o

código:

Os passos 10 e 11 se referem à otimização do parâmetro de forma para através do cálculo dos

resíduos. Esse cálculo é feito de maneira repetida para todos os ponto de um intervalo pré-definido de