UERJ – INSTITUTO DE QUÍMICA C0NTROLE DE PROCESSOS

UERJ – INSTITUTO DE QUÍMICA

C0NTROLE DE PROCESSOS

Prof.: Nilo Indio do Brasil

CONTROLE DE PROCESSOS INDUSTRIAIS

1. Introdução

O Controle de Processos está relacionado a manutenção em algum valor operacional desejado das seguintes variáveis de processo : temperatura, pressão, vazão, composição e outras semelhantes.

Os processos são dinâmicos por natureza, ou seja mudanças estão sempre ocorrendo e, se ações não são tomadas de imediato, as importantes variáveis de processo - aquelas relacionadas com a segurança, qualidade dos produtos e as vazões de produção - não atingirão as condições de projeto.

Nesta introdução serão apresentados dois sistemas de controle, através dos quais conheceremos os seus componentes e definiremos alguns termos usados na área de controle de processos. Finalmente, serão discutidos os assuntos necessários ao estudo do controle de processos.

Um Sistema de Controle de Processos

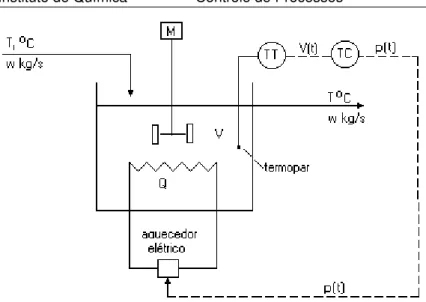
Considere o vaso de aquecimento continuamente agitado acima. A corrente líquida entra no vaso com uma vazão mássica w kg/s e uma temperatura Ti. O líquido no interior do vaso é bem agitado e é aquecido por um aquecedor elétrico que fornece ao líquido q watts.

Para simplificar, vamos considerar que:

• as vazões de entrada e de saída do líquido no vaso são sempre idênticas;

Com estas duas condições, o volume de líquido no interior do vaso permanece constante.

O objetivo de controle para o vaso é manter a temperatura de saída T em um valor de referência constante TR. Este valor de referência é conhecido na terminologia de controle como “set-point”, valor de ajuste ou valor desejado.

Pergunta 1: Qual a taxa de calor que deve ser fornecida ao líquido no vaso para aquecê-lo da temperatura de entrada Ti até a temperatura de saída TR?

Isto é determinado por um balanço de energia para o líquido no vaso. Vamos fazer as seguintes considerações:

• líquido no vaso é perfeitamente misturado;

• as perdas de calor para o exterior são desprezíveis.

Nestas condições não há gradiente de temperatura no líquido, no interior do vaso, e, conseqüentemente, a temperatura de saída é igual à temperatura do líquido no vaso.

O balanço de energia no regime permanente indica que a taxa de calor recebida pelo líquido é igual à variação de taxa de entalpia entre a saída e a entrada de líquido no vaso.

(

i

)

pT T

c w

q = − (1)

i

T T w

q, , , representam os valores de projeto destas variáveis( regime permanente ). cp = capacidade térmica específica do líquido (constante na faixa de temperatura

considerada)

Nas condições de projeto: T = TR Logo: q=wc_p

(

T_R −Ti

)

(2)

Esta equação 2 é a equação de projeto para o aquecedor. Se as considerações feitas estiverem corretas e, se a vazão e a temperatura da corrente líquida na entrada do vaso são iguais aos valores de projeto, então a taxa de calor q dada pela equação 2 manterá a temperatura de saída no valor desejado TR.

O que acontecerá se as condições mudarem?

Pergunta 2: Suponha que a temperatura de entrada Ti varia com o tempo. Como poderemos garantir que a temperatura de saída T permanecerá ou ficará próxima do valor desejado TR?

Vamos supor que a temperatura Ti aumenta de valor em relação a Ti. Se a taxa de calor q é mantida constante no valor nominal q, podemos afirmar que a temperatura de saída aumentará, ou seja, T > TR e vice-versa.

Para lidar com esta situação, podemos vislumbrar um número variado de estratégias possíveis para controlar a temperatura de saída T.

Um modo de controlar T apesar das perturbações ocorridas em Ti é ajustar q baseado na medição de T. Se T aumenta deve-se reduzir q e vice-versa.

Este método tenderá a conduzir T para o valor desejado TR e poderá ser implementada de duas formas:

a) um operador poderia ficar observando a temperatura medida T, compará-la com o valor desejado TR e alterando o valor de q. Isto seria um “Controle manual”.

b) provavelmente, será mais vantajoso e econômico fazer este controle de uma forma automática, por meio de um dispositivo eletrônico ao invés de usar uma pessoa, ou seja, é melhor utilizar um “Controle automático”.

Método 2 : Medir Ti e ajustar q

Se Ti > Ti , reduzir q ( q < q ) para manter a temperatura de saída. T. Se Ti < Ti , pode-se aumentar q (q > q )

Método 3 : Medir T e ajustar w

Ao invés de ajustar q, pode-se manipular a vazão w. Assim, se T ficar maior que TR pode-se aumentar w, o que para a mesma taxa de calor q fará reduzir T.

Método 4 : Medir Ti e ajustar w

Se Ti > Ti , para a mesma taxa de calor q, aumentando-se w reduzirá T.

Método 5 : Medir ambos Ti e T e ajustar q É uma combinação dos métodos 1 e 3.

Método 6 : Medir ambos Ti e T e ajustar w É uma combinação dos métodos 2 e 4.

Método 7 : Usar um vaso de grande capacidade.

Se o vaso tiver um grande volume, flutuações em Ti serão amortecidas devido a grande capacidade térmica do conteúdo do vaso. Entretanto, esta é uma solução cara, pois implica em aumento do custo de investimento, pelo uso de um tanque de grande volume. Note que esta solução é análoga ao uso de um banho de água (banho-maria) em laboratórios, onde a grande capacidade térmica do banho serve como “sumidouro de calor”, atuando como um ambiente isotérmico para aparelhagens de pesquisa de pequena escala.

Classificação das Estratégias de Controle

Os métodos 1 e 3 são exemplos de estratégias de controle feedback. No controle feedback , a variável de processo a ser controlada é medida, o seu valor é comparado com o valor desejado e uma outra variável de processo é manipulada. No método 1 , a variável manipulada é q e no método 3 é a vazão w. Note que a variável perturbadora Ti não é medida.

se T tende a aumentar, a taxa de calor q deve ser diminuída (feedback negativo) ao invés de ser aumentada (feedback positivo).

Os métodos 2 e 4 são exemplos de estratégias de controle feedforward. Nestes casos, a variável perturbadora Ti é medida, comparada com o valor nominal e uma outra variável de processo é manipulada q (método 2) e w (método 4). Note que no controle feedforward a variável controlada T não é medida.

Os métodos 5 e 6 são estratégias de controle feedback-feedforward, pois são combinações das duas estratégias básicas de controle.

O método 7, na realidade, não é uma estratégia de controle, pois consiste em mudança no projeto do equipamento.

No exemplo analisado, foi considerado apenas uma variável de perturbação, a temperatura de entrada Ti. No entanto, devem ser consideradas a possibilidade de perturbações em outras variáveis de processo, tais como a vazão w (se ela não for variável manipulada, como nos métodos 3 e 4) e a temperatura ambiente, que afetaria as perdas de calor do vaso (se este não for isolado térmicamente). Lembre que, as perdas de calor foram consideradas desprezíveis. Alterações no interior do equipamento de processo também podem ser fontes de perturbação; por exemplo, as características do aquecedor podem mudar com o tempo, devido à formação de depósitos pelo líquido, que aumentam a resistência à troca térmica. É importante analisar o efeito destas perturbações nas estratégias de controle feedforward e feedback.

Vamos considerar primeiro a estratégia de controle feedforward do método 2, onde as perturbações em Ti são medidas e usadas para ajustar a variável manipulada q. Do ponto de vista teórico, este esquema de controle é capaz de manter a variável controlada T exatamente no valor de set point TR apesar das perturbações em Ti. Idealmente, se medidas precisas de Ti são disponíveis e se os ajustes em q forem feitas de uma maneira apropriada, então a ação corretiva sobre o aquecedor cancelaria os efeitos das perturbações em Ti, antes que a temperatura de saída T seja afetada. Assim, em princípio, o controle feedforward é capaz de obter um controle perfeito, no sentido que a variável controlada seria mantida no set point, sem alterações do seu valor.

Vamos analisar como a estratégia de controle feedback do método 1 desempenhará na presença de perturbações em Ti e w. Com esta estratégia, nenhuma ação corretiva ocorrerá até que a perturbação tenha alterado o processo, ou seja, até que T fique diferente de TR. Assim, pela sua natureza, o controle feedback não é capaz de obter um controle perfeito, uma vez que a variável controlada deve desviar do valor desejado (set point) antes da ação corretiva ser tomada. Entretanto, uma vantagem extremamente importante do controle feedback é que a ação corretiva é tomada, sem se importar com a fonte da perturbação. Assim, no método 1, a ação corretiva será tomada (por ajuste de q) após uma perturbação em w, Ti ou na resistência à troca térmica, o que causa T desviar do set point TR. A habilidade de lidar com variáveis não medidas e de origens desconhecidas é a maior razão para o controle feedback ser largamente usado em controle automático de processos.

No exemplo acima, foram apresentadas algumas estratégias de controle, nas quais alguns termos usuais em controle de processos apareceram.

Variável controlada - é a variável que deve ser mantida ou controlada em algum valor desejado. No exemplo anterior, a temperatura do fluido na saída do vaso, T(t), é a variável controlada.

Valor de referência ("set point") - também conhecido como valor de controle, valor de ajuste ou valor desejado. É o valor desejável da variável controlada

Variável manipulada - é a variável usada para manter a variável controlada no seu valor de referência. É a variável onde o controlador vai atuar para fazer as correções, a fim de manter a variável controlada no valor de referência.

Variável perturbadora - também conhecida como variável de carga. É qualquer variável que pode fazer com que a variável controlada se desvie do valor de referência. Em muitos processos é grande o número das variáveis perturbadoras. São as demais variáveis do processo, que podem variar com o tempo, que não sejam a variável controlada e a variável manipulada. O que é importante entender é que nas indústrias, o controle de processo é necessário, justamente por causa destas variáveis perturbadoras. Se não houvessem perturbações, as condições operacionais de projeto prevaleceriam e, portanto não haveria necessidade de continuamente "policiar" o processo.

"O objetivo do sistema de controle automático de processos é usar a variável manipulada para manter a variável controlada no seu valor de referência, apesar das perturbações".

Tabela: Estratégias de Controle de Temperatura para o Vaso Aquecedor do Exemplo

Método Variável medida Variável manipulada Categoria

1 T q FB

2 Ti q FF

4 Ti w FF

5 T e Ti q FB/FF

6 T e Ti w FB/FF

7 mudança de projeto

FB = controle feedback FF = controle feedforward

Controle de Processos e o Diagrama de Blocos

Na seção anterior, discutimos várias estratégias de controle usando argumentos intuitivos sem fazer uma análise quantitativa e sem analisarmos a forma de implementar as estratégias de controle.

Vamos considerar novamente o vaso aquecedor agitado, usando o método 1, ou seja, medir a temperatura de saída T e ajustar a taxa de calor fornecida pelo aquecedor elétrico q, para controlar a temperatura de saída no valor desejado TR. O tipo mais simples de estratégia de controle feedback é dado pela lei de controle proporcional:

q(t) = q + Kc [ TR - T(t) ] (3)

Kc é chamado de ganho do controlador. Se Kc > 0, então esta lei de controle implementa o controle feedback negativo, uma vez que a taxa de calor varia na direção oposta à variação da temperatura de saída. O controlador é dito proporcional porque a variação da taxa de calor [ q(t) - q ] é proporcional ao desvio do set point, [TR - T(t)]. Um grande desvio do set point gera uma grande ação corretiva.

O diagrama esquemático para o vaso aquecedor e o sistema de controle feedback é mostrado na figura 2. O diagrama que mostra o processo e o sistema de controle aplicado é conhecido como P&ID (Diagrama de Processo e Instrumentação).

Figura 2 –P&ID de um controle feedback de temperatura para o vaso agitado.

A operação do sistema de controle de temperatura pode ser assim resumida:

1. A temperatura de saída do vaso, T(t) [oC] é medida por um sensor de temperatura, geralmente um termopar, que gera um correspondente sinal de tensão elétrica da ordem de milivolts. Este sinal que varia com o tempo deve ser ampliado para um sinal de tensão (corrente contínua), V (t), compatível com o sinal de entrada do controlador. Este sinal é enviado pelo transmissor ao controlador.

2. O controlador efetua 3 cálculos distintos. Primeiramente, ele converte o set point TR [o_{C] , fornecido pelo operador, em um sinal interno de tensão,}

VR. O bloco denominado conversor do set point indica esta operação. A seguir, ele calcula um sinal de erro e(t), subtraindo do set point (convertido) VR [volts], o sinal oriundo do transmissor V(t) [volts]. Assim, e(t) = VR - V(t). No diagrama de blocos, o comparador representa esta operação de subtração. Finalmente, a taxa de calor, q(t) [W], é calculada pela lei de controle do controlador, equação 3. A envoltória ao redor dos dois blocos e o comparador foi incluída para enfatizar que estes cálculos são efetuados no controlador.

3. O sinal de saída do controlador p(t) [volts] é enviado ao aquecedor elétrico para gerar a taxa de calor q(t) [W]. É assumido que o aquecedor possui um retificador de silício (SCR) que converte o sinal de corrente contínua em corrente alternada, que é compatível com o elemento de aquecimento.

Figura 3 – Diagrama de blocos do sistema de controle de temperatura do vaso agitado.

Cada bloco no diagrama de blocos representa um elemento dinâmico ou estático cujo comportamento pode ser descrito por uma equação diferencial ou algébrica. Uma das tarefas do engenheiro de controle de processos é desenvolver descrições matemáticas adequadas para cada bloco. O desenvolvimento e análise dos modelos matemáticos dinâmicos serão considerados ao longo deste curso. No final do curso, diagramas de bloco deste tipo serão analisados e as respostas dinâmicas do sistema controlado serão estudadas.

O trabalho de um engenheiro de controle é projetar um esquema de controle que mantenha a variável controlada no seu valor de referência. Uma vez isto feito, ele deve fazer a sintonia do controlador para que ele minimize o procedimento de tentativa e erro necessário ao controle. Para isto, o engenheiro deve conhecer as características ou "personalidade" do processo a ser controlado. Uma vez conhecida a "personalidade" do processo, o engenheiro pode projetar o sistema de controle com a melhor "personalidade" que mais se adapte ao processo. O que é entendido por "personalidade" será melhor explicado adiante. Entretanto, pode-se fazer a seguinte comparação : suponha que se deseja persuadir alguém de se comportar de um certo modo, ou seja, deseja-se controlar o comportamento de alguém. A atitude mais inteligente a tomar é conhecer a personalidade daquela pessoa e se adaptar aquela personalidade para conseguir persuadi-la ou controlá-la. Isto é o que se entende por sintonizar o controlador. Isto é, o controlador é sintonizado ou adaptado ao processo. Uma boa parte dos controladores convencionais tem até três parâmetros usados para sintonizá-lo.

Sinais de Transmissão

Atualmente, existem em uso três tipos principais de sinais:

elétrico ou eletrônico - varia normalmente entre 4 e 20 mA. Menos usuais, sinais de10 a 50 mA, 1 a 5 V ou 0 a 10 V também podem ser usados. A representação usual no fluxograma P&ID é :

digital ou discreto (sinais zero e um) - o uso de sistemas de controle de processo baseado em computadores de grande porte, minicomputadores ou microprocessadores tem tornado comum este tipo de sinal.

Frequentemente, é necessário mudar de um tipo de sinal em outro. Isto é feito pelo transdutor. Por exemplo, pode ser necessário mudar de um sinal elétrico, em mA, para um sinal pneumático em psig. Isto é feito por um transdutor (I/P) de sinal de corrente (I) para um sinal pneumático (P). É claro que existem muitos outros tipos de transdutores como : pneumático/corrente (P/I), tensão/pneumático (V/P), etc.

No início desta introdução, o objetivo do controle automático de processos foi definido como manter a variável controlada no ponto de controle, apesar das perturbações. É fundamental, no momento enumerar as razões porque isto é importante. As razões são baseadas na experiência industrial e, se não são as únicas, são pelo menos as mais importantes.

1. Evitar danos físicos às pessoas e aos equipamentos. A segurança deve estar sempre na mente de todos; é, sem dúvida a consideração mais importante.

2. Manter continuamente a qualidade do produto (composição, pureza, cor,etc.) a um mínimo custo.

3. Manter a produção da planta industrial a um custo mínimo.

Simplificando, pode-se dizer que as razões do controle automático de processos é fornecer um ambiente seguro de trabalho e ao mesmo tempo manter tanto a qualidade desejada do produto como a sua vazão de produção e reduzir a necessidade da intervenção humana no processo.

O que é necessário para projetar e conhecer bem um controle automático de processos?

Para o estudo do controle de processos, é também imprescindível compreender como os processos se comportam dinamicamente. Consequentemente, é necessário desenvolver sistemas de equações que descrevam diferentes processos. Isto é chamado de "modelagem". Para isto, o conhecimento dos princípios básicos mencionados acima, além da matemática, através das equações diferenciais, é extremamente essencial.. Em controle de processos, a aplicação da transformada de Laplace é feita maciçamente, pois simplifica demais a solução das equações diferenciais e a análise dinâmica dos processos e dos seus sistemas de controle. Uma outra ferramenta importante é a simulação por computador, pois muitas das equações desenvolvidas para descrever os processos são não lineares por natureza e, o método mais correto para resolvê-las usa "métodos numéricos", o que significa solução por computador. A solução por computador de modelos de processos é chamado de "simulação".

Controle Analógico ou Digital

2. Sistemas Dinâmicos de Primeira Ordem

Nesta parte pretendemos alcançar dois objetivos: o primeiro é aprender a desenvolver modelos simples de processos, o que é necessário quando desejamos analisar sistemas de controle de processos. O segundo objetivo, sub-produto do primeiro, é aprender o significado físico de alguns parâmetros de processo que descrevem a "personalidade" dos processos. Como vimos anteriormente, uma vez conhecida a "personalidade" do processo, então, o sistema de controle pode ser projetado. Também serão conhecidos novos termos e manipulações matemáticas importantes no estudo do controle automático de processos.

Modelagem Matemática de Sistemas de Primeira Ordem

A modelagem de processos, usualmente, inicia com um balanço material ou energético no regime transiente. Este balanço genericamente pode ser escrito:

Taxa demassa / energia que entra no processo

Taxa de massa / energia que sai do processo

Taxa de massa / energia acumulada no processo

⎛ ⎝

⎜ ⎞

⎠ ⎟ −⎛

⎝

⎜ ⎞

⎠ ⎟ =⎛

⎝

⎜ ⎞

⎠ ⎟

Ao escrever estas equações e outras auxiliares devemos fazer uso de quase toda a área da engenharia de processos, como a termodinâmica, transferência de calor, mecânica dos fluidos, transferência de massa, cinética química, etc.

Caso 1 : Nível de Tanque

Consideremos o sistema abaixo, que consiste de um tanque (ou vaso) de seção transversal uniforme, A, onde um fluido de massa específica constante e com vazão variável q_i(t) m3/s entra continuamente no tanque e sai, também, continuamente com

vazão variável qo(t) m3/s.

Vamos considerar que a vazão de saída, qo(t), esteja relacionada ao nível do tanque pela relação linear :

R t h t

Obs.: Esta equação linear só é válida se tivermos regime laminar. Quando o regime é turbulento, qo(t) é proporcional a raiz quadrada do nível e a relação não é mais linear.

Neste caso para aplicarmos a transformada de Laplace devemos linearizá-la, o que veremos adiante.

Balanço de Massa no Regime Transiente:

[

]

[

]

) 2 2 ( ) ( ) ( d ) ( d d ) (t d ) ( ) ( ) ( d ) ( d d ) ( d ) ( ) ( − = + = − = = = − t q R t h t t h A t h A t q t q dt t dh A t t Ah t t V t q t q i o i o i ρ ρ ρ ρ ρ

Balanço de Massa no Regime Permanente:

) 3 2 (

0 ∴ + = ∴ + = −

= = − − i i o o i q R h dt h d A q q dt h d A dt h d A q q

Subtraindo (2-3) de (2-2) vem :

1

d d

i i(t) q

q h ) t ( h R h ) t ( h t

A _⎥= −

⎦ ⎤ ⎢ ⎣ ⎡ − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡

− − − (2-4)

Vamos definir as variáveis desvio. Variável desvio é a diferença entre o valor atual de uma variável e o seu valor no regime permanente. A variável desvio, representa de quanto a variável principal está afastada do seu valor no regime permanente. No caso :

e H(t) h(t) h q ) t ( q ) t (

Q_i = _i − _i = − (2-5)

Vamos usar sempre as letras maiúsculas para designar as variáveis desvio. Então:

) ( ) t ( RQ ) t ( H t ) t ( H AR ) t ( Q R ) t ( H t ) t ( H A i i 6 2 d d d d − = + = +

O termo ARtem unidade de tempo, e é conhecido como a constante de tempo

(τ) deste processo. O termo R que multiplica a variável desvio Q_i(t) é conhecido como o

ganho (K) deste processo.

A equação diferencial fica então assim :

) ( ) ( d ) ( d t KQ t H t t H i = +

Nesta equação τ = AR e K = R

Esta é uma equação diferencial linear de 1a _{ordem, que fornece a relação entre a} vazão de entrada e a altura no tanque em qualquer instante. É importante notar que a variável dependente é H(t). É a variável de saída ou variável de resposta. Quando o sistema de controle for aplicado esta será a variável controlada.

A vazão de entrada, Q_i(t), será a variável de entrada ou a variável perturbadora.

Uma determinada variação será imposta a esta variável, para estudarmos como o nível do tanque responderá.

A constante de tempo e o ganho são os dois parâmetros relacionados à personalidade do processo (ou sistema) de 1a ordem. Conseqüentemente, eles dependem das propriedades físicas e dos parâmetros operacionais do processo. No exemplo considerado, o ganho só depende da resistência ao escoamento através da válvula de saída, e a constante de tempo depende desta mesma resistência e da área transversal do vaso. Se qualquer um destes parâmetros variarem, a "personalidade" do processo também variará, e esta variação será refletida no ganho e na constante de tempo do processo.

A definição e o uso da variável desvio na análise e no projeto de sistemas de controle é muito importante. Essas variáveis são quase que exclusivamente usadas no estudo da teoria de controle. Assim, o significado e a importância dessas variáveis desvio devem ser bem entendidos. A vantagem do seu uso é que os seus valores indicam o grau de desvio de alguma variável operacional em relação ao seu valor no regime permanente. Na prática, este valor da variável no regime permanente deve ser o valor desejado da variável. Uma outra vantagem no uso da variável desvio é que o seu valor inicial é zero, o que simplifica a solução da equação diferencial, como veremos adiante.

Caso 2 : Processo de Mistura em Vaso Bem Agitado

Considere o processo de mistura mostrado abaixo, onde uma corrente de solução contendo um sal dissolvido, escoa com vazão volumétrica constante q m3_/s

através de um vaso bem agitado e de volume de líquido constante igual a V m3. A

concentração do sal na corrente de entrada, c_Ai(t), (kg de sal / m3 _{de solução), varia}

com o tempo. A concentração de sal na saída c_A(t) é igual a concentração de sal no

interior do vaso, uma vez que o vaso é bem agitado.

massa específica da solução seja constante em toda a faixa de concentração de sal em consideração.

Balanço de Massa de sal no Regime Transiente:

[

]

t t c V t

t Vc t

qc t

qc_{Ai A} A A

d ) ( d d

) ( d ) ( )

( − = = (2-8)

Balanço de Massa de sal no Regime Permanente:

0 A

Ai− = =

dt c d V c q c

q A (2-9)

Subtraindo (2-9) de (2-8), vem :

[

Ai( ) Ai

]

[

A( ) A

]

_dd

[

cA(t) cA

]

t V c t c q c t c

q − − − = − (2-10)

Definindo as variáveis desvio: C_A(t)=

[

c_A(t)−c_A

]

e C_Ai(t)=

[

c_A(t)−c_Ai

]

, vem :

) t ( C ) t ( C dt

) t ( dC q V dt

) t ( dC q V ) t ( C ) t (

C_Ai − _A = A ∴ A + _A = _Ai (2-11)

O termo V/q que multiplica a derivada tem unidade de tempo e é conhecido

como a constante de tempo deste processo.

) ( )

( d

) ( d

Ai A

A _{C t C t}

t t

C _{+ =}

τ (2-12)

Nesta equação τ = V/q e K = 1

Esta é uma equação diferencial linear de 1a _{ordem, que fornece a relação entre a} concentração do sal na saída do vaso em qualquer instante e a concentração do sal na entrada do vaso. Nesta equação, a variável de resposta é a concentração de sal na saída, C_A(t), e a variável de entrada é a concentração de sal na entrada, C_Ai(t)..

Para simplificar, vamos considerar que a vazão de escoamento seja constante (q) e que a reação química seja de 1a _{ordem, na qual: r (t) kc (t)V}

A

A = .

r_{A =} taxa de reação, kmol/s

k = constante de velocidade, 1/s ou s-1

Balanço de Quantidade de Matéria do Componente A no Regime Transiente:

[

]

t ) t ( c V t

) t ( Vc V

) t ( kc ) t ( qc ) t ( qc

d d d

d _{A A}

A A

Ai − − = = (2-13)

Balanço de Quantidade de Matéria do Componente A no Regime Permanente:

0 A

A

Ai− − = =

dt c d V c V k c q c

q A (2-14)

Subtraindo (2-14) de (2-13) vem:

[

Ai( ) Ai

] [

A( ) A

]

[

A( ) A

]

[

cA(t) cA

]

dt d V c t c kV c

t c q c t c

q − − − − − = − (2-15)

Definindo as variáveis desvio:

[

A A

]

Ai

[

A Ai

]

A(t) c (t) c e C (t) c (t) c

C = − = − , vem

) ( )

( ) (

Ai A

A _{C t}

kV q

q t

C dt

t dC kV q

V

+ = +

+ (2-16)

O termo V/(q+kV) que multiplica a derivada tem unidade de tempo, e é

conhecido como a constante de tempo deste processo. O termo que multiplica a concentração do componente A na saída é conhecido como o ganho deste processo.

) ( )

( ) (

Ai A

A _{C t KC t}

dt t

dC _{+ =}

τ (2-17)

Nesta equação τ= V/(q + kV) e K = q /(q + kV)

As 3 equações diferenciais ordinárias e lineares, (2-7), (2-12) e (2-17) são semelhantes e podem ser representadas genericamente por:

) ( )

( ) (

t X K t Y dt

t dY

= +

τ (2-18)

dt t dC V t C kV q t

Vamos resolver esta equação, aplicando Transformada de Laplace.

)

s

(

G

s

K

)

s

(

X

)

s

(

Y

₌

+

=

∴

1

τ

(2-19)

Nesta equação, o termo G(s) é conhecido como a Função de Transferência

entre X e Y. Chamamos de função de transferência de 1a _{ordem, porque ela foi} desenvolvida a partir de uma equação diferencial de 1a _{ordem. Processos descritos por} esta função de transferência são chamados de processos ou sistemas de 1a _ordem.

O nome função de transferência vem do fato que a solução da equação transfere a variação da variável de entrada ou perturbadora, X(t) para a variável de saída ou de resposta, Y(t).

A relação funcional expressa pela função de transferência é freqüentemente expressa por uma representação em diagrama de bloco, como mostrado abaixo. A seta entrando no bloco é a variável de entrada e a seta saindo do bloco é a variável de resposta ou de saída. Dentro do bloco é colocada a função de transferência. Se diz que a função de transferência G(s) no bloco "opera" a variável de entrada ou função de entrada X(s), para produzir a função de saída Y(s). Esta notação em diagrama de blocos será vista em mais detalhes adiante, quando analisarmos um sistema de controle completo.

Respostas Transientes dos Sistemas de Primeira Ordem

1. Excitação pela Função Degrau ("Step Function")

Vamos considerar que a variável de entrada, X(t), sofra um aumento de M

unidades, ie, sofre uma variação degrau de M unidades em relação ao seu valor do regime permanente. Ou seja:

{

}

{

}

) s ( KX ) s ( Y s X

Y sY

X X

L e ) s ( Y ) t ( Y L

pois sY

dt t dY L

= +

τ ⇒ =

+ τ

∴

= =

= − = − = =

− =

⎭ ⎬ ⎫ ⎩

⎨ ⎧

) 1 ( (s) K (s) (s)

(s) (t)

0 y y y y(0) Y(0)

sY(s) Y(0)

(s) )

A transformada de Laplace da função degrau, X(t) = Mu(t) é :

{

} {

}

{ }

s M s M t u L M t Mu L t X

L ( ) = ( ) = ( ) = × 1 =

Da equação (2-19), vem:

⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ − =

⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ − =

+ = +

=

τ τ

τ τ

τ 1

1 1 1

1 1

) ( 1 )

(

s s M K s

s M K s M s

K s

X s

K s

Y (2-20)

A Transformada de Laplace Inversa desta equação nos fornece:

0 ,

1 )

( 1

)

( _ ⎟ ≥

⎠ ⎞ ⎜

⎝ ⎛ − +

= ⎟

⎠ ⎞ ⎜

⎝ ⎛ −

=KM e− ou y t y KM e− t

t

Y tτ tτ (2-21)

Depois de decorrido um tempo muito grande, o valor de Y(t) será igual a KM.

Basta fazer t tender para infinito na equação acima, que encontramos esse valor. O mesmo resultado seria obtido, se aplicássemos o teorema do valor final na equação (2-20).

Quando Y(t) alcança o valor final KM, dizemos que após aplicar a excitação

degrau na variável de entrada, a resposta completa da variável de saída foi alcançada.

Significado da Constante de Tempo τ

A solução da equação fornece o significado físico de τ, que é chamado de

constante de tempo do processo. Fazendo t = τ na solução da equação,

(

)

(

1

)

0,632 (2 23) 1

) (

) 22 2 ( 632

, 0 1

1 )

(

_ 1 _

_

1

− +

= − +

= ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ ₋ +

=

− =

− = ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

− =

− −

− −

M K y

e M K y e

M K y y

M K e

M K e

M K Y

t t

τ τ

τ τ

Quando o tempo decorrido é de uma constante de tempo, 63,2% da variação total da resposta completa do sistema de 1a _{ordem é alcançada. Isto é mostrado no gráfico ao} lado. Como se observa, a constante de tempo está relacionada à velocidade de resposta do processo. Quanto mais lento for o processo, para alcançar a resposta completa a uma variação degrau na variável de entrada, maior será o valor da constante de tempo e vice-versa.

Pode-se calcular também que quando o tempo decorrido após a perturbação na variável de entrada é de 2 τ , 3 τ, 4τ e 5τ, a variação da resposta final corresponde a 86,5%, 95%, 98% e 99%, respectivamente. Donde também se conclui que pode-se considerar que a resposta final ( ou resposta completa ) é alcançada após decorrido um tempo igual a 5 constantes de tempo.

Outra forma de se calcular a constante de tempo ( método 2)

Pode-se mostrar também que, na origem, a inclinação da curva de resposta para uma perturbação na variável de entrada igual ao degrau é exatamente igual a constante de tempo. Para provar isto, vamos fazer uma normalização da variável de resposta Y(t).

Obs: Normalizar significa permitir que a variável tenha o valor máximo igual a 1. Como o valor máximo da variável Y(t) é dado pelo seu valor final, KM, a normalização de Y(t)

será dada por:

τ = ⎥⎦ ⎤ ⎢⎣

⎡ ∴ τ = ⎥⎦ ⎤ ⎢⎣

⎡ ∴ −

=

= τ

− τ

− ₁

d d

d d 1

0 t t

t

t KM ) t ( Y e

t KM ) t ( Y

e KM

Outra forma de calcular a constante de tempo (Método 3)

Vamos aplicar logaritmo na equação de resposta normalizada incompleta. Se a resposta normalizada é completa, quando alcança o valor 1, a resposta normalizada

incompleta é dada por: 1−Y t

KM ( )

Logo:

) 25 2 ( )

( 1

) ( 1 1

) (

− −

= ⎥⎦ ⎤ ⎢⎣ ⎡ = ⎥⎦ ⎤ ⎢⎣

⎡ − ∴

= −

∴ −

=

−

− −

τ τ

τ τ

t e

Ln KM

t Y Ln

e KM

t Y e

KM t Y

t

t t

É importante salientar que a constante de tempo é dependente de diferentes propriedades físicas e parâmetros operacionais do processo. Para o caso 1, a constante de tempo depende da seção transversal do tanque A e da resistência R ao escoamento através da válvula; no caso 2, depende da vazão volumétrica q e do volume V do vaso e, no caso 3, além de q e V, a constante de tempo depende também da constante de velocidade k da reação Se qualquer uma destas características mudarem, a constante de tempo também mudará. Uma outra forma de dizer isto é que, se qualquer uma das condições de processo acima mudar, a "personalidade" do processo também mudará e, será refletida na velocidade de resposta do processo, ou seja, na constante de tempo.

Significado do Ganho do Processo

K

O ganho K é simplesmente o fator de conversão que relaciona a variável de

entrada X(t) com a variável de saída Y(t), quando o processo alcançar o novo regime

permanente. Quando aplicamos o teorema do valor final para determinar o valor de Y(t)

no novo regime permanente, se a variável de entrada X(t) sofre uma variação do tipo

degrau, obtivemos que Y(∞) = KM, ie, o ganho vezes a variação da variável de entrada

ou perturbadora.

O ganho nos informa quanto a variável de resposta Y(t) variará por variação unitária na variável de entrada, ou seja, o ganho define a sensitividade do processo. Matematicamente, o ganho é definido como:

entrada saída E

S K ganho

Δ Δ = Δ Δ =

= (2-26)

O ganho é outro parâmetro que está relacionado à "personalidade" do processo a ser controlado. Consequentemente, ele depende das propriedades físicas e dos parâmetros operacionais do processo. No caso 1, o ganho é igual à resistência (R) ao escoamento através da válvula; no caso 2, o ganho é unitário e, no caso 3, o ganho depende da vazão volumétrica q, do volume V do vaso e da constante de velocidade k

da reação. Se qualquer um destes parâmetros variarem a "personalidade" do processo também variará, e será refletida no ganho.

Os processos de 1a _{ordem podem ter mais de uma constante de tempo e mais} de um ganho, dependendo do número de variáveis de entrada ou perturbações existentes no processo. Adiante, veremos situações deste tipo.

Outros Sistemas de Primeira Ordem

Caso 4 : Processo Térmico : vaso adiabático

Consideremos o vaso adiabático bem agitado mostrado na figura abaixo.

O nosso interesse é conhecer como a temperatura de saída, T(t), responde a

variações na temperatura de entrada, T_i(t).

Neste exemplo, serão consideradas constantes: as vazões de entrada e de saída, as massas específicas e as capacidades térmicas específicas dos líquidos. Todas estas propriedades são conhecidas. O líquido no interior do tanque é bem misturado e o tanque é bem isolado, ou seja, trata-se de um processo adiabático.

( )

( ) {

}

t

t

u

V

t

h

q

t

h

q

_{i i}

d

d

ρ

(

)

ρ

ρ

−

=

(2-27)

ou em termos de temperatura :

t

t

T

c

V

t

T

c

q

t

T

c

q

_{i i p} v

d

d

pi

)

(

)

(

)

(

ρ

ρ

ρ

−

=

(2-28)

na qual:

ρ_i , ρ = massas específicas do líquido na entrada e na saída, kg/m3

cpi, cp = capacidades térmicas específicas do líquido a pressão constante , J/(kg.oC) cV = capacidade térmica específica do líquido a volume constante, J/(kg.oC)

V = volume do líquido no tanque, m3

h_i, h = entalpias específicas do líquido na entrada e na saída, J/kg

u = energia interna específica do líquido no tanque, J/kg

Desde que a massa específica e a capacidade térmica específica possam ser consideradas constantes na faixa de temperaturas de operação, a última equação pode ser escrita :

t ) t ( T c V ) t ( T c q ) t ( T c q

d d v p

i

p ρ ρ

ρ − = (2-29)

Esta é uma equação diferencial ordinária linear de 1a _{ordem que fornece a} relação entre a temperatura de entrada e a temperatura de saída da corrente de processo. É importante notar que esta equação só tem uma variável dependente, T(t). A temperatura de entrada, Ti(t), é a variável de entrada (ou variável perturbadora) e, se ela sofrer uma determinada variação, pode-se estudar como a temperatura de saída responderá.

Balanço de energia no regime permanente:

(2-30)

Subtraindo estas 2 últimas equações, encontramos:

{

}

t T t T c V T t T c q T t T c

q _i

d ) ( d )

( )

( _ _p _ _v

i

p _⎟⎟= −

⎠ ⎞ ⎜⎜

⎝ ⎛

− −

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

− ρ ρ

ρ (2-31)

0 _

p i

_

p − = =

dt T d c V T c q T c

As variáveis desvio são:

_ _

i i

i

T ) t ( T ) t (

T ) t ( T ) t (

− =

− =

θ θ

A solução desta equação fornece θ(t), o desvio da temperatura de saída em relação ao seu valor no regime permanente, quando ocorre um desvio na temperatura de entrada, θ_i(t).

A equação acima pode ser arranjada da forma abaixo:

t t c V t c q t c

q _i

d ) ( d )

( )

( _{p v}

pθ ρ θ ρ θ

ρ − = (2-32))

ou

( )

_{( )}

_{( )}

t t

t t c

q c V

i p

v θ _{θ θ}

ρ

ρ _{+ =}

d d

(2-33)

ou

) ( ) ( ) (

t t

dt t d

i θ θ θ

τ + = (2-34)

na qual :

p v

c q

c V

=

p v

c q

c V =

ρ ρ

τ (2-35)

Para líquidos, cp≈cV. Então, neste caso:

q V c q

c V

p v ₌ =

Transformada de Laplace

A transformada de Laplace desempenha um papel importante na solução de sistemas de equações diferenciais lineares, reduzindo o grau de complexidade do problema ao transformá-lo na solução de sistemas de equações algébricas lineares. Isto explica que, historicamente, esta ferramenta tenha sido tão importante no desenvolvimento da teoria de controle. A transformada de Laplace também permite o desenvolvimento de modelos entrada-saída que são úteis em controle de processos e uma análise de como os processos químicos reagem a várias influências externas.

Definição: £ [f(t)] = f(s) =

∫

∞

o

dt e ) (t -st

f

A transformação leva uma função da variável independente t (tempo no caso) à

outra função da variável independente s (variável de Laplace), que é uma variável complexa.

s = σ + ω i ; ω = freqüência angular

É importante notar que as funções f(t) e f(s) são diferentes, o que neste caso está implícito na

presença da variável independente s no lugar de t. Diferentes autores usam diferente

nomenclatura para a função transformada: F(s), fˆ (s) etc. A transformação leva o problema do

"domínio do tempo" ao "domínio da transformada de Laplace" ou simplesmente "domínio s" (um outro "mundo", “saturno” provavelmente).

Exemplos

1) f(t) = u(t) = 1 para t > 0 e u(t) = 0 para t ≤ 0 degrau unitário

f(s) =

∫

∞ −

o st

e

dt =

s e

s

st 1

1

0

= ⎥⎦ ⎤ ⎢⎣

⎡− − ∞

2) f(t) = t u(t) rampa

f(s) =

∫

₀∞te−stdt

integrando por partes: u = t du = dt ; dv = e

-st _{dt v = -} 1

s

e-st f(s) =

_∫

∞ ₌

_{[ ]}

∞₋

_∫

∞

0 0 udv uv 0 vdu

= − ∞₊

_∫

∞ − ₌

⎥⎦ ⎤ ⎢⎣

⎡−

0 2

0

1

s dt s e e

s

t _st st

3) f(t) = e-at _{u(t) exponencial} f(s) =

_∫

∞ − −

_∫

∞ − +

+ = =

0 ) ( 0

1

a s dt e

dt e

e at st a s t

Observa-se claramente em todos estes exemplos que f(t) e f(s) são funções diferentes. Através de procedimentos semelhantes são construídas tabelas f(t) vs f(s). Para controle de processos, basta a consideração de um número reduzido de pares de transformadas.

f(t) f(s) f(t) f(s)

δ(t) 1 e-at _{f(t) f(s+a)}

u(t) _{1 / s f(t-to) e-tos f(s)} t

2

1

s

cos ωt

2 2 _s

s + ω

e-at

a s+

1 _{sen ωt}

2 2_+s

ω ω 1

Propriedades de Maior Interesse

1) Linearidade: £ [c1 f1(t) + c2 f2(t)] = c1 f1(s) + c2 f2(s)

2)Teorema do deslocamento: £[ f(t-to) ] = e-tos f(s)

3)Transformada da derivada: £

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ n n dt ) t ( f d

= sn _{f(s) - s}n-1 _{fo - s}n-2 _f

o

' _{- ... - s}

f_on−2 - f_on−1

fo, f_o' ... f_on−1 representam a função f(t) e suas primeiras n -1 derivadas avaliadas em t=0.

£ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ dt ) t ( f

d _{= s f(s) - f(0) £}

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ 2 2 dt ) t ( f

d _{= s}2 _{f(s) - s f(0) - f´(0) etc}

Esta propriedade permite reduzir um sistema de equações diferenciais ordinárias no domínio t a

um sistema de equações algébricas no domínio s.

5) Teorema do valor final limf

( )

t limsf

( )

s

s t→∞ = →0

( )

_{( ) ( )}

( )

_[

_{( ) ( )}

_]

( )

_{( )}

_{[ ]}

_{( )}

_[

_{( ) ( )}

_]

( ) ( )

[

0

]

lim

[

( ) ( )

0

]

lim

( )

lim

( )

. . .

lim : vem (2), e (1) Igualando (2) 0 lim lim d lim d d d 0 lim d d d lim (1) 0 d d d 0 0 0 0 0 0 0 0 0 d q c s f s t f f s f s f t f f t f t f t f t t t f f s f s t e t t f f s f s t e t t f s t s t t t t t s st s st → ∞ → → ∞ → ∞ → ∞ → ∞ ∞ → ∞ → − ∞ → − ∞ = ∴ − = − − = = = − = − = ∫ ∫ ∫ ∫

6) Teorema do valor inicial: f

( )

limf

( )

t lim sf

( )

s

s t→ = →∞

= 0 0

( )

_{( ) ( )}

( )

_[

_{( ) ( )}

_]

( )

_[

_{( ) ( )}

_]

_{( ) ( )}

( )

s f

( )

t cqd f s f s f s f s f s t t t f f s f s t e t t f f s f s t e t t f t s s s s st s st . . lim lim 0 lim 0 lim 0 d 0 d d 0 lim d d d lim 0 d d d 0 0 0 0 → ∞ → ∞ → ∞ → ∞ ∞ → − ∞ ∞ → − ∞ = ∴ − = − = = − = − = ∫ ∫ ∫

7) Transformada de uma Integral:

{

}

( )

s s f t t f t = ∫0 ( )d £

Fazendo integração por partes, pode-se demonstrar a validade da expressão acima.

Solução de Equações Diferenciais

equação algébrica resultante e acha-se a transformada inversa da variável dependente transformada. Vamos ver a aplicação através de um exemplo.

Seja a equação diferencial:

2 2 _{( )}

dt t Y d + 5 dt t

dY() _{+ 6 Y(t) = 2 Y(0) = 0}

0 ) ( = t dt t y d

= 0 ( ) 0

0 2 2 = = t dt t Y d

Usando a transformada de Laplace, com as propriedades citadas

[

sY s Y t

]

Y s s

dt t y d t Y s s Y s t t t / 2 ) ( 6 ) ( ) ( 5 ) ( ) ( ) ( ₀ 0 0

2 _{+ − + =}

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − ₌ = =

Substituindo na equação acima, obtemos a seguinte equação algébrica: (s2 _{+ 5 s + 6) Y(s) = 2 / s Y(s) =}

s s s ⎟ ⎠ ⎞ ⎜ ⎝

⎛ _{+ 5 +6}

2 2

O passo seguinte é a obtenção da transformada inversa

Y(t) = £-1 _{[ Y(s) ] = £}-1

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝

⎛_{s +5s + 6 s}

2 2

Para achar a transformada inversa deve-se encontrar uma expressão similar nas tabelas de Transformada, no entanto, nem sempre a expressão final se encontra diretamente na tabela.

Inversão das Funções Transformadas

O método mais popular para resolver o problema de inverter uma função transformada, de uma forma simples, é o da EXPANSÃO EM FRAÇÕES PARCIAIS (desenvolvido por Heaviside). A idéia se baseia no fato de que, para os casos considerados, as funções cujas transformadas inversas se desejam calcular têm a forma de um quociente de polinômios.

f(s) = b s b s b s b

s a s a s a

N s D s m m m m o n n n o + + + + + + + + = − − − − 1 1 1 1 1 1 L L ( ) ( )

Se as raízes de D(s) = 0 forem p1, p2, ..., pn o polinômio denominador pode ser escrito na forma fatorada:

D(s) = sn _{+ an-1 s}n-1 _{+ ... + a1 s + ao = (s - p1) (s - p2) ... (s - pn)}

Assim f(s) =

₍

_{) (}

_{) (}

₎

n p s p s p s s N − −

− _{1 2}L

) (

Esta equação pode ser escrita na forma de uma expansão em frações parciais que, no caso de raízes distintas, é

f(s) = C

s p C s p C s p n n 1 1 2 2

Os coeficientes Ci devem ser determinados de tal forma que as duas equações sejam iguais. Usando a propriedade de linearidade da transformada, a determinação da transformada inversa se reduz à soma das transformadas inversas de funções simples.

f(t) = £-1 _{[f(s)] = C1 £} -1 1

1

s p−

⎛ ⎝

⎜ ⎞

⎠

⎟ + C2 £ -1 1

2

s p−

⎛ ⎝

⎜ ⎞

⎠

⎟ + ... + Cn £ -1 1

s p− _n

⎛ ⎝

⎜ ⎞

⎠ ⎟

No caso: £-1 1

s−p_i

⎛ ⎝

⎜ ⎞

⎠

⎟ = epit

Determinação dos Coeficientes Ci

As raízes de um polinômio com coeficientes reais podem ser distintas, reais ou complexas, ou repetidas. Os três casos possíveis são introduzidos através de exemplos:

1) Raízes reais e distintas: f(s) = s s

s s s

2 3 2 6 2 2 − − − − +

p1 = 1 p2 = -1 p3 = 2

f(s) =

(

s s

)

(

s s

)

(

s

)

C s C s C s 2

1 2 3

6

1 1 2 1 1 2

− −

− + − = − + + + −

Para determinar C1

(s-1) f(s) = (s-1)

₍

s

₎

₍

s

₎

₍

₎

(

)

₍

₎

(

)

(

)

s s s s

C s s C s s C s 2

1 2 3

6

1 1 2 1 1 1 1 1 2

− −

− + − = − − + − + + − −

Fazendo s=1 → C1 =

₍

_{) (}

₎

2 1 1 1 6 1 1 − + − − = 3

Isto é, na determinação de C1 foi feito:

C1 =( 1) ( ) lim( 1) ( ) Genericamente: lim

(

)

( ) 1 1 s f p s C s f s s f s _i p s i s s i − ≡ − ≡ − → → =

Para C2 e C3 o procedimento é o mesmo

C2 = lim

s→−1 (s+1) f(s) = slim→−1

(

)

(

)

s s s s 2 ₆ 1 2 2 3 − − − − = −

C3 = lim

s→2 (s-2) f(s) = slim→2

(

)

(

)

s s s s 2 ₆ 1 1 4 3 − − − + = −

Assim : f(s) =

2 3 4 1 3 2 1 3 − − + −

− s s

s → f(t) = 3

2 3

4 3

2

et− e−t− e t

2) Raízes complexas: f(s) =

₍

₎

2 2

2 2_{+ +}

+

s s

s

p1 = -1 + i

f(s) =

₍

₎

i s

C

+ − − 1

1 ₊

(

i

)

s C

− − − 1

2

Neste caso, as raízes são distintas e é usada a mesma metodologia do caso anterior para o cálculo dos Ci. Isto é:

Ci = lim

s p→ _i (s-pi) f(s)

Assim :

C1 = lim

( )

s→ − +1 i

[

(

)

]

[

(

)

]

[

(

)

]

₂

1

1

1

2

1

i

i

s

i

s

s

i

s

=

−

+

−

−

−

+

−

−

+

+

−

−

C2 = lim

( )

s→ − −1 i

[

(

)

]

*

C i ) s ( f i

s ₁

2 1 1− =− − = −

−

Na expansão em frações parciais, os coeficientes associados a pares de raízes complexas conjugadas são complexos conjugados (basta calcular um para conhecer o outro).

Assim f(s) = ⎛_⎝⎜ − +1 ⎞_⎠⎟

2

i 1

1 s− − +( i) +

− − ⎛

⎝⎜ ⎞⎠⎟

1 2

i 1

1 s− − −( i)

f(t) = − +1 − + +− − − −

2

1 2

1 1

i _e( i)t i_e( i)t

Vamos aproveitar este momento para relembrar alguns conceitos de variáveis complexas que, no caso, serão úteis para colocar a equação anterior em uma forma mais concisa. O número complexo c = a + i b, representa um ponto no plano complexo.

Além das coordenadas a e b, ρ e α podem ser usadas para localizar o mesmo ponto; isto conduz à representação polar do número complexo.

c = a + i b = ρ eiα ₍₁₎ na qual ρ = (a2 _{+ b}2₎½ _{e α = arctg}

a b

Assim, no exemplo considerado: C1 = ρ ei α C2 = C*₁ = ρ e-i α

ρ = 1

4 1 4

1

2

1 2 + ⎛

⎝⎜ ⎞⎠⎟ =

( )

4 3 1 2

12 1

arctg π

α = − =

−

= arctg

Então

f(t) = 1

2 e

i3

4π _e(-1+i) t ₊ 1

2 e

i

− 3

4π _e(-1-i) t = 1

2 e

-t ( ) ( )

⎥⎦ ⎤ ⎢⎣

⎡ + π₊ − +₄3π

4 3 _it t

i

e e

(2)

Para continuar com a simplificação desta equação vamos lembrar novos conceitos. Pela figura anterior, vem:

a = ρ cos α e b = ρ sen α

Então: c = a + i b = ρ (cos α + i sen α)

Im

Re

a

b ρ