1. Conceitos básicos e relações fundamentais

(1)

4

Iniciaremos com a revisão de cálculo numérico, com exemplos ilustrativos dos métodos numéricos. Recomenda-se para maiores informações a consulta à literatura de referência [1]–[3].

1.1 Multiplicação de matrizes e vetores

A multiplicação matricial pode ser efetuada desde que o número de colunas da primeira matriz seja igual ao número de linhas da segunda, ou seja, ( _{1 = 2}). A matriz resultante terá o número de linhas da primeira matriz e o número de colunas da segunda, ou seja:

(E 1.1) _, ∙ _, = _,

Cada elemento da matriz resultante é o somatório:

(E 1.2) _, ₌ _, _∙ _,

Para ilustração, seguem códigos em VBA.

'Subrotina multiplicação matriz A(NL1,NC1)*B(NC1,NC2) 'Subrotina multiplicação matriz A(NL1,NC1) por vetor B(NC1)

Sub MatrizMult(NL1, NC1, NC2, A, B, C)

Dim i, j, k As Integer Dim soma As Double For i = 1 To NL1 For j = 1 To NC2 soma = 0 For k = 1 To NC1

soma = soma + A(i, k) * B(k, j) Next

C(i, j) = soma Next

Next End Sub

Sub MatrizVetMult(NL1, NC1, A, B, C)

Dim i, j, k As Integer Dim soma As Double For i = 1 To NL1 soma = 0 For k = 1 To NC1

soma = soma + A(i, k) * B(k) Next

C(i) = soma

Next End Sub

1.2 A série de Taylor

Qualquer função contínua suave ℱ pode ser descrita por uma polinomial com infinitos termos. A série de Taylor nada mais é do que uma aproximação polinomial da função, construída tomando-se como base um ponto .

1.2.1 Para funções de uma variável

A série de Taylor pode ser escrita para funções univariável na forma:

(E 1.3) ℱ = ℱ + 1

! ∙! ℱ! ∙ " − $

(2)

5 Abrindo a série de Taylor:

(E 1.4)

ℱ = ℱ& ' +(ℱ_{( )}

*+ " − $ +

1

2( ℱ( ,_*+ " − $ +

1 3!(

._ℱ

( .,

*+ " − $ .

+_4!1(₍0ℱ₀,

*+ " − $ 0

…

Utilizando a outra notação de derivada, a série pode ser representada como: (E 1.5) ℱ = ℱ + ℱ2∙ " − $ +ℱ

22

2 " − $ +ℱ

222

3! ∙ " − $.+ℱ

2222

4! " − $0 + ⋯

Exemplo 1.1-) Represente a expansão em série de Taylor truncada no termo quadrático da função ℱ = .− cos em torno do ponto = 2.

Solução:

Precisamos calcular a função, sua derivada primeira e segunda em = 2. Assim:

ℱ = 2._{− cos 2 = 8,416}

ℱ2 _{= 3 ∙} _{+ sen} _{= 3 ∙ 2 + sen 2 = 12,909}

ℱ22 _{= 6 ∙ + cos} _{= 6 ∙ 2 + cos 2 = 11,583}

Agora podemos construir a série de Taylor até o termo quadrático na forma:

ℱ ≅ ℱ + ℱ2_{∙ " −} _{$ +}ℱ22

2 " − $

ℱ ≅ 8,416 + 12,909 ∙ − 2 +11,583₂ − 2

1.2.2 Para uma função com N variáveis*

Quando a dimensão das variáveis independentes é N, ou seja,

@ = A , , … , BC, os termos dos somatórios devem incluir todas as derivadas na

forma:

(E 1.6) _ℱ _{= ℱ} _{+ D + D + D}_._{+ ⋯}

Onde D respresenta os termos associados à derivada de ordem , dados por:

*_{São recomendados fortemente a visualização dos sites}

(3)

6 (E 1.7)

D = _{1! ∙}1 _{! ∙ E −}!ℱ F

B

D = _{2! ∙}1 _!! _{! ∙ E −}!ℱ F ∙ E − F

B B

D. = _{3! ∙}1 _!! _!! _!!ℱ

G∙ E − F ∙ E − F ∙ E G− G F

B

G B B

Em uma forma compacta, a série de Taylor fica:

(E 1.8) _ℱ _{= ℱ} ₊ _H1

! I E − F ∙!!

B

J K %

Por exemplo, para = 3, fazendo ∆ = − tem-se que:

(E 1.9) _D_.₌ 1

! I E − F ∙!!

B

J .

= _{3! M∆ ∙}1 _{! + ∆ ∙}! _{! + ∆}! .∙_!!

.N .

A conta não será aberta por simplicidade.

1.2.3 Expansão até o termo quadrático em notação matricial

É muito comum para aplicações sobretudo em otimização, que a função seja expandida em série de Taylor até o termo quadrático. Neste caso, a notação matricial torna-se adequada, pois simplifica a representação do sistema (em negrito são vetores ou matrizes).

(E 1.10) _{ℱ @ ≈ ℱ&@}P_{' + ∇R}S_{∙ "@ − @}P _{$ +}1

2 "@ − @P $S∇ R"@ − @ P$

Em que ∇R e ∇ R representam respectivamente, o vetor de derivadas primeiras (Jacobiana) e matriz de derivadas segunda (Hessiana). Para ilustrar, considere que o número de variáveis seja N=3, abrindo a representação de matrizes e vetores:

(E 1.11)

ℱ @ ≈ℱ&@P_{' + T}(ℱ

( ((ℱ ((ℱ.U V

− −

.− .

W

+1_{2 V} − −

.− .

W

S

X YY Z YY [ ( ℱ

( ( (( ℱ ( (( ℱ.

( ℱ

( ( (( ℱ ( (( ℱ.

( ℱ ( ( .

( ℱ

( . \

YY ] YY ^

V − −

.− .

(4)

7

1.3 Derivadas numéricas

É frequente a necessidade do uso de derivadas numéricas em torno de um ponto

@ , obtidas geralmente pela expansão e truncamento da série de Taylor. Veremos inicialmente para funções de uma variável.

1.3.1 Derivada primeira e segunda para função de uma variável

Tomamos a série de Taylor como base, ou seja, vamos considerar a Equação (E 1.5). Para cálculo de derivadas, efetuamos pequenas perturbações na variável , para frente = + ∆ , para e/ou trás = − ∆ e truncamos a função.

(E 1.12)

“Perturbação para frente”

ℱ& + ∆ ' = ℱ + ℱ2_{∙ ∆ +}ℱ22

2 ∙ ∆ +ℱ

222

3! ∙ ∆ .+ℱ

2222

4! ∙ ∆ 0+ ⋯

(E 1.13)

“Perturbação para trás”

ℱ& − ∆ ' = ℱ − ℱ2_{∙ ∆ +}ℱ22

2 ∙ ∆ −ℱ

222

3! ∙ ∆ .+ℱ

2222

4! ∙ ∆ 0+ ⋯

Se quisermos calcular a derivada primeira utilizando apenas das Equações, (E 1.12) ou (E 1.13), truncamos a derivada no termo linear. Se consideramos que ∆ ≪ 1, os termos de ordem superior devem tender a zero; logo, dos termos desprezados, o que seria de maior valor seria o termo quadrático, ou seja, o erro numérico cometido seria da ordem de _∆ .

A derivada numérica com perturbação para frente fica então:

(E 1.14)

“Derivada para frente a partir de (E 1.12), erro da ordem ∆ ”

ℱ `∆* = ℱ + ℱ2∙ ∆ + a ∆bcdce

fghijgklmn

ℱ2 _≅ ℱ `∆* − ℱ

∆

Analogamente, para trás, teríamos que:

(E 1.15)

“Derivada para trás a partir de (E 1.13),erro da ordem ∆ ”

ℱ o∆* ≅ ℱ − ℱ2∙ ∆ + a ∆bcdce

fghijgklmn

ℱ2 _≅ ℱ − ℱ o∆*

(5)

8 Poderíamos alternativamente utilizar as Equações (E 1.12) ou (E 1.13) simultaneamente, diminuindo uma da outra, obtendo a derivada central. Com isto, o termo da derivada segunda também se anula, e o erro será da ordem de ∆ ., ou seja:

(E 1.16)

“Derivada centrais, fazendo(E 1.12)- (E 1.13),erro da ordem ∆ .”

ℱ `∆* − ℱ o∆* ≅ 2 ∙ ℱ2∙ ∆ + a ∆ .

ℱ2 _≅ℱ `∆* − ℱ o∆*

2 ∙ ∆

O cálculo da derivada central é mais preciso que a derivada para frente ou para trás; porém, para aplicações na engenharia química, com frequência, tal forma de cálculo exige um maior número de avaliações da função, pois a função no ponto central geralmente é feita previamente ao cálculo da derivada.

Para o cálculo da derivada segunda, temos que utilizar simultaneamente as Equações (E 1.12) ou (E 1.13), somando as duas equações. O termo da derivada terceira se anula nesta soma, e o erro fica da ordem de _∆ 0. Assim:

(E 1.17)

“Derivada segunda, somando as Equações (E 1.12) ou (E 1.13)”

ℱ `∆* + ℱ o∆* = 2 ∙ ℱ + ℱ22∙ ∆ + a ∆bcdce0

fghijgkljgGnh

ℱ22 _≅ℱ `∆* − 2 ∙ ℱ + ℱ o∆*

∆

Exemplo 1.2-) Calcule a derivada numérica primeira e segunda no ponto = 2 da função ℱ = .− cos .

Solução: Em torno do ponto 2, precisamos calcular a função no ponto e calcular a

função perturbando x para frente e para trás. Vamos escolher uma perturbação de

∆ = 0,001, logo, como no termo da derivada segunda ∆ = 1 × 10oq, carregaremos

até à oitava casa. Temos que:

“Para frente”

ℱ + ∆ rs ℱ `∆* = 2 + 0,001 .− cos 2 + 0,001 = 8,4296193

“Ponto central”

ℱ rs ℱ = 2._{− cos 2 = 8,4161684}

“Para trás”

ℱ − ∆ rs ℱ o∆* = 2 − 0,001 .− cos 2 − 0,001 = 8,40324333

(6)

9

ℱ2 _≅ ℱ `∆* − ℱ o∆*

2 ∙ ∆ =8,4296193 − 8,403243332 ∙ 0,001 = 12,9093

A derivada segunda fica:

ℱ22 _≅ ℱ `∆* − 2 ∙ ℱ + ℱ o∆*

∆ = 8,4296193 − 2 ∙ 8,4161684 + 8,403243330,001

ℱ22 _{≅ 11,5838}

Os valores exados das derivadas analíticas são:

ℱ2_{= 3 ∙} _{+ sen} _ℱ2 _{= 3 ∙ 2 + sen 2 = 12,9093}

ℱ22 _{= 6 ∙ + cos} _ℱ2 _{= 6 ∙ 2 + cos 2 = 11,5838}

1.3.2 Derivada primeira (Jacobina) e segunda (Hessiana) para função de N

variáveis

1.3.2.1 A Jacobinana ∇R numérica

A matriz Jacobiana nada mais é do que a matriz de derivadas primeiras de funções. Como neste caso consideramos apenas uma função, trata-se de um vetor. A Jacobiana de uma função fica:

(E 1.18) ∇R =

X YY Z YY [₍(ℱ

(ℱ (…

(ℱ

( B\

YY ] YY ^

Cada elemento da Jacobiana pode ser computado numericamente da mesma forma que se computa as derivadas de uma função de uma única variável. Vamos designar ℱ a função calculada no ponto @ P e por ℱ_∆*_t a função calculada perturbando-se apenas a variável , ou seja:

(E 1.19) ℱ ≅ ℱ&@

P _{' ℱ}_∆*

u ≅ ℱ + ∆ , , ., …

ℱ∆*v ≅ ℱ , + ∆ , ., …

Assim, a derivada primeira pode em relção à uma variável por diferenças centrais e progressivas fica:

(E 1.20)

(ℱ ( ≅

ℱ∆*t − ℱo∆*t 2 ∙ ∆ bccccccdcccccce

gwxjl h

_{( ≅}(ℱ ℱ∆*t − ℱ ∆ bcccccdccccce

(7)

10 Exemplo 1.3-) Calcule a Jacobiana numérica, no ponto A ; C = A2; 3C da função

ℱ @ = . _{− cos ∙} _{. Utilize como perturbação numérica} _{A∆ ; ∆ C =}

A1 × 10o._{; 1 × 10}o _C_.

Solução: Primeiramente, vamos calcular a função no ponto central:

ℱ = ._{− cos} _∙ _{= 2}._{− cos 2 ∙ 3 = 7,03983}

Vamos perturbar em relação à :

ℱ∆*u = 2 + 0,001 .− cos" 2 + 0,001 ∙ 3$ = 7,05100

Vamos perturbar em relação à :

ℱ∆*v = 2.− cos"2 ∙ 3 + 0,001 $ = 7,03927

Calculando a derivada considerando perturbações para frente:

(ℱ ( ≅

ℱ∆*u − ℱ

∆ = 7,051003 − 7,03980,001 = 11,17208

(ℱ ( ≅

ℱ∆*v − ℱ

∆ =7,03927 − 7,03980,001 = −0,55691

A comparação com a derivada analítica fornece:

(ℱ

( = 3 ∙ + ∙ }~• ∙ = 3 ∙ 2 + 3 ∙ }~• 2 ∙ 3 = 11,6175

(ℱ

( = ∙ }~• ∙ = 2 ∙ }~• 2 ∙ 3 = 0,55883

1.3.2.2 A Hessiana ∇ R numérica de uma função

A matriz Hessiana de uma função é a matriz de derivadas segundas de uma função. Esta matriz, quadrada e simétrica, pode ser escrita como:

(E 1.21) ∇²R =

X YY Z YY [ ( ℱ

( ( (( ℱ … ( (( ℱB

( ℱ

( (_… _(…( ℱ … ( (_…( ℱB

( ℱ

( ( B

( ℱ

( ( B …

( ℱ

( B² \

YY ] YY ^

Vamos ilustrar o cálculo da Hessiana para um problema de duas variáveis, N=2. Neste caso, para calcular as derivadas•vℱ

•*uv, •v_ℱ •*u•*v,

•v_ℱ

•*vv precisamos de 3 equações. Para

(8)

11 (E 1.22)

+ ∆ − ∆ + ∆

− ∆ ‚ => „

ℱ∆*u,∆*v ℱ∆*u, ℱ∆*u,o∆*v

ℱ ,∆*v ℱ , ℱ ,o∆*v

ℱo∆*u,∆*v ℱo∆*u, ℱo∆*u,o∆*v …

Os termos da matriz de derivadas segunda ficam [4]:

(E 1.23)

“Termos da diagonal (ilustrado para x1)”

( ℱ

( =

ℱ∆*u, − 2 ∙ ℱ + ℱo∆*u, ∆

“Termos fora da diagonal”

( ℱ

( ( =14 M

ℱ∆*u,∆*v − ℱo∆*u, − ℱ ,o∆*v + ℱo∆*u,o∆*v

∆ ∙ ∆ N

Exemplo 1.4-) Calcule a matriz Hessiana numérica, no ponto A ; C = A2; 3C da função ℱ @ = . − cos ∙ . Utilize como perturbação numérica A∆ ; ∆ C =

A1 × 10o._{; 1 × 10}o _C_.

Solução: Para facilitar, vamos resolver em Excel. Criamos uma função em VBA,

digitando Alt+F11 para abir o VBA, abrindo um novo módulo e escrevendo a função:

Function f(x1, x2)

f = x1 ^ 3 - Cos(x1 * x2)

End Function

Agora, podemos acessar a função diretamente no Excel. Vamos então calcular as

funções na mesma forma que apresentado na Equação (E 1.11), para os valores de x1 e

x2 e suas respectivas perturbações.

(9)

12 Para comparação, podemos obter as derivadas analíticas na forma:

(ℱ

( = 3 ∙ + ∙ sen ∙

(ℱ

( = ∙ sen ∙

( ℱ

( = 6 ∙ + ∙ cos ∙

( ℱ

( ( = ∙ ∙ cos ∙ + sen ∙

( ℱ

( = ∙ cos ∙

A comparação das derivadas segunda numérica e analítica está apresentada a seguir,

indicando que a aproximação numérica é adequada.

Hessiana numérica Hessiana analítica

20.6415 5.4813 20.6415 5.4816

5.4813 3.8406 5.4816 3.8407

1.3.3 Códigos para cálculo da matriz Hessiana

Em VBA, segue o código que efetua o cálculo da matriz Hessiana.

‘Subrotina que calcula a matriz Hessiana de uma função F(x), sendo x(N) um vetor de dimensão N

Function F(x)

F = x(1) ^ 3 - cos(x(1) * x(2))

End Function

Sub Hessiana(N, x, H)

Dim i, j As Integer

Dim Ff0, F0, Ft0, Fff, Fft, Ftf, Ftt, dx() As Double

' Calcula as perturbações numéricas

ReDim dx(N)

For i = 1 To N

dx(i) = x(i) * 0.0001 + 0.0001

F0 = F(x)

For i = 1 To N ' perturba para frente

x(i) = x(i) + dx(i) Ff0 = F(x) ' perturba para trás

x(i) = x(i) - 2 * dx(i) Ft0 = F(x) ' Calcula a diagonal

H(i, i) = (Ff0 - 2 * F0 + Ft0) / dx(i) ^ 2 ' Volta o x(i) para o valor inicial

x(i) = x(i) + dx(i)

' Calcula os termos fora da diagonal

For j = i + 1 To N

' perturba ambas para frente

x(i) = x(i) + dx(i) x(j) = x(j) + dx(j) Fff = F(x)

' x(i) na frente, x(j) para trás

x(j) = x(j) - 2 * dx(j) Fft = F(x)

' x(i) para trás, x(j) para trás

x(i) = x(i) - 2 * dx(i) Ftt = F(x)

' x(i) para trás, x(j) para frente

x(j) = x(j) + 2 * dx(j) Ftf = F(x)

' Retorna os x's aos valores iniciais

x(i) = x(i) + dx(i) x(j) = x(j) - dx(j)

' Calcula o termo i,j da hessiana

H(i, j) = (Fff + Ftt - Fft - Ftf) / (4 * dx(i) * dx(j)) H(j, i) = H(i, j)

(10)

13

1.4 A inversa de uma matriz e a solução de sistemas lineares

Um sistema linear pode ser escrito da seguinte forma, onde o vetor @ contém as incógnitas do problema.

(E 1.24)

† ∙ @ = ‡

V

ˆ , ˆ , … ˆ ,B*

ˆ_…, ˆ , … ˆ ,B*

ˆB*,

… ˆB*,

…

… ˆB*,B*…

W ∙ „ … B*

… = „ … B*

…

A matriz _† deve ser quadrada, não podendo ter determinante nulo (o determinante nulo é indicativo de que a matriz possui linhas linearmente dependentes). Lembrem-se que:

A matriz identidade é o “1” da matemática vetorial, logo, † ∙ ‰ = †

Essencialmente, é necessário obter o vetor @ isolado do lado esquerdo da equação. Para tanto, multiplica-se pela esquerda por †oŠ ambos os lados da equação. O termo †oŠ† = ‰, onde ‰ é a matriz identidade, o “1” da matemática matricial, não precisando ser representado em uma multiplicação.

(E 1.25) †

oŠ_† bde

‰ mgwx mlmg∙ @ = † oŠ_{∙ ‡}

@ = †oŠ_{∙ ‡}

A questão consiste então em como obter a inversa de uma matriz. Aqui, será empregado o método de pivotação de Gauss. Para tanto, vamos nos lembrar que cada linha da matriz † equivale aos coeficientes de uma equação, e cada elemento ‡ ao lado direito da equação. Podemos efetuar operações como multiplicar uma linha toda por uma constante e somar com outra linha, sem que se altere a solução problema linear.

Vamos então escrever matrizes na seguinte forma:

(E 1.26)

† ∙ @ = ‰ ∙ ‡

V

ˆ , ˆ , … ˆ ,B*

ˆ_…, ˆ , … ˆ ,B*

ˆB*,

… ˆB*,

…

… ˆB*,B*…

W ∙ „ … B*

… = „_…1 0 … 00 1 … 0

0 …0 …… 1… „ …B*

(11)

14 Vamos então efetuar uma série de operações lineares com as equações, ou seja, a matriz †, de forma que esta seja gradualmente modificada até se obter a matriz identidade. Se guardarmos as operações efetuadas para a matriz identidade do lado direito da equação, obteremos a matriz inversa.

A ideia básica consiste então em gradualmente eliminar os elementos das colunas da matriz †, exceto os elementos das diagonais, mediante operações lineares com as equações do sistema. Por exemplo, para eliminar o elemento da segunda linha e primeira coluna, vamos substituir a segunda linha por uma operação linear entre a linha 1 e a linha 2, na forma:

(E 1.27) ‹Œ′ = ‹Œ −ˆ_ˆ ,

, ‹Š

O número pelo qual dividimos, neste caso o ˆ _, é chamado o pivot. Por questões de precisão numérica, o pivot da matriz deve ser o elemento de maior valor absoluto submatriz a partir do termo da diagonal restante. Para tanto, pode ser necessário trocar a linha e a coluna para que se obtenha o maior pivot possível (o exemplo numérico ilustrará melhor).

Após a operação (E 1.27), a nova linha _‹Œ′ conterá o termo da segunda linha e primeira coluna nula. Repetiremos o procedimento para as demais linhas, ou seja, para qualquer linha Ž tem-se que:

(E 1.28) ‹•′ = ‹• −_ˆˆ,

, ‹Š

Após efetuarmos todas estas operações, a nova matriz †′ conterá a primeira coluna nula, conforme segue.

(E 1.29)

X Y Z Y

[ˆ , ˆ , … ˆ ,B*

0 ˆ , − ˆ , ˆ_ˆ ,

, … ˆ ,B*− ˆ ,B*

ˆ ,

… 0

…

ˆB*, − ˆ , ˆ_ˆB*,

, … …

…

ˆB*,B*− ˆ ,B*ˆ_ˆ , , \Y

] Y ^

• •

Agora, toma-se como base para a segunda linha o elemento 2x2 da matriz nova matriz †′ como pivot, e repete-se o procedimento para eliminar os elementos da segunda coluna. Um exemplo numérico a seguir ilustra o passo a passo.

(12)

15

‘ −2 1,2 −41 3,4 −5

−1,5 3 6 ’ ∙ ‘ .

’ = ‘1,43,2

−12’

Solução:

Como multiplicar pela matriz I nada modifica, podemos escrever:

‘ −2 1,2 −41 3,4 −5

−1,5 3 6 ’ ∙ ‘ .

’ = ‘1 0 00 1 0

0 0 1’ ‘

1,4 3,2

−12’

Zerando a primeira coluna

Para solução, começamos tentando eliminar a primeira coluna. Por questões de

precisão numérica, observe que devemos escolher o maior pivot possível, em valor

absoluto. Da matriz de coeficientes, tal pivot é o número 6, associado ao elemento 3x3

da matriz de coeficientes. Vamos então re-escrever o sistema linear trocando a linha 3

com a linha 1 e a coluna 3 com a coluna 1:

“Trocamos a C3 com a C1, e os x’s correspondentes”

‘−4 1,2 −2−5 3,4 1

6 3 −1,5’ ∙ ‘

.

’ = ‘1 0 00 1 0

0 0 1’ ‘

1,4 3,2

−12’

“Trocamos a L3 com a L1, e os I’s correspondentes”

‘−5 3,46 3 −1,51

−4 1,2 −2 ’ ∙ ‘

.

’ = ‘0 0 10 1 0

1 0 0’ ‘

−12 3,2 1,4’

Observem que as equações permanecem as mesmas, ou seja, não modificamos o

sistema de equações. Agora, tendo como pivot o número 6, iniciamos o processo. Para

zerar o termo da segunda linha e primeira coluna, vamos fazer:

‹Œ2 _{= ‹Œ −} −5

6 ‹Š

Observe que isto significa:

V

6 3 −1,5

−5 + 65_{6 3,4 + 3}5_{6 1 − 1,5}5₆

−4 1,2 2

W ∙ ‘ .’ = V

0 0 1

0 1 0 +5₆

1 0 1

W ∙ ‘−123,2 1,4’

Resolvendo em números fica:

‘ 60 5,9 −0,253 −1,5

−4 1,2 −2 ’ ∙ ‘

.

’ = ‘0 00 1 0,8331

1 0 0 ’ ∙ ‘

−12 3,2 1,4’

Vamos fazer agora para a terceira linha, objetivando eliminar o termo 3x1 da matriz.

(13)

16 Logo:

V

6 3 −1,5

0 5,9 −0,25

−4 + 64_{6 1,2 + 3}4_{6 −2 − 1,5}4₆W ∙ ‘ .

’ = V

0 0 1

0 1 0,833

1 0 +4₆ W ∙ ‘

−12 3,2 1,4’

Que numericamente fica:

‘6 30 2,9 −4,75−1,5

0 3,2 −3 ’ ∙ ‘

.

’ = ‘0 00 1 0,8331

1 0 0,667’ ∙ ‘

−12 3,2 1,4’

Por fim, vamos dividir a primeira linha pelo primeiro elemento para surgir ali o termo

da identidade:

‹Š′ = ‹Š₆

Obtendo:

‘1 0,5 −0,250 5,9 −0,25

0 3,2 −3 ’ ∙ ‘

.

’ = ‘0 0 0,1670 1 0,833

1 0 0,667’ ∙ ‘

−12 3,2 1,4’

Zerando a segunda coluna

O pivot deve ser agora o elemento da segunda linha e segunda coluna. Agora, dentro

da submatriz formada pelos termos a partir da segunda linha e segunda coluna,

precisamos escolher um pivot.

”•~ Ž} ˆr} ~} r ℎ~• sˆ —Ž˜r™ !~}™ }s ˆ ™•Žš T5,9 −0,25_3,2 _{−3 U}

O maior valor absoluto é 5,9. Este elemento precisa ficar na posição 2x2 da matriz,

mas como já se encontra na posição, não precisamos trocar as colunas ou linhas.

Precisamos agora eliminar a segunda coluna toda, exceto o termo 2x2. Vamos iniciar

com a primeira linha, fazendo:

‹Š′′ = ‹Š′ − ‹Œ′0,5_5,9

Com isto temos que:

V1 0,5 − 5,9 ∙ 0,5

5,9 −0,25 + 0,250,55,9

0 5,9 −0,25

0 −3,2 −3

W ∙ ‘ .’ = V0 0 − 1 ∙ 0,5

5,9 1 − 0,833 ∙0,55,9

0 1 0,833

1 0 0,667

W ∙ ‘−123,2 1,4’

(14)

17

‘1 0 −0,22810 5,9 −0,25

0 3,2 −3 ’ ∙ ‘

.

’ = ‘0 −0,0847 0,09600 1 0,833

1 0 0,667’ ∙ ‘

−12 3,2 1,4’

Vamos então para a terceira linha, desejando eliminar o termo da terceira linha e

segunda coluna. Assim:

‹“′′ = ‹“′ −3,2_{5,9 ‹Œ′}

Ou seja, os termos podem ser calculados como:

V

1 0 −0,2281

0 −5,9 −0,25

0 3,2 − 5,9 ∙3,2_{5,9 −3 + 0,25}3,2_5,9W ∙ ‘

.

’ = V

0 −0,0847 0,0960

0 1 0,833

1 0 − 13,2_{5,9 0,667 − 0,833}3,2_5,9W ∙ ‘ −12

3,2 1,4’

‘1 0 −0,22810 5,9 −0,25

0 0 −2,864’ ∙ ‘

.

’ = ‘0 −0,0847 0,9600 1 0,833

1 −0,5423 0,2147’ ∙ ‘

−12 3,2 1,4’

Agora, dividimos a segunda linha por 5,9, pois desejamos obter a matriz identidade:

‹Œ′′ = ‹Œ′_5,9

Obtendo:

‘1 0 −0,22810 1 −0,0423

0 0 −2,864’ ∙ ‘

.

’ = ‘0 −0,0526 0,17540 0,1695 0,1412

1 −0,6315 0,7719’ ∙ ‘

−12 3,2 1,4’

Zerando a terceira coluna

Observe que agora, só sobrou o número 2,864 como pivot. Precisamos zerar os termos

da última coluna. Começamos com a primeira linha, fazendo:

‹Š′′′ = ‹Š′′ −−0,228_{−2,864 ‹“′′}

V1 0 −0,228 + 2,864 0,228 2,864

0 1 −0,0423

0 0 2,864

W ∙ ‘ .’ = V0 − 1 0,228

2,864 −0,0526 + 0,63150,2282,864 0,1754 − 0,77190,2282,864

0 0,1695 0,1412

1 −0,6315 0,7719

W ∙ ‘−123,2 1,4’

‘1 00 1 −0,04230

0 0 −2,864’ ∙ ‘

.

’ = ‘−0,0799 −0,0414 0,07880 −0,2105 0,1412

1 −0,6315 0,7719’ ∙ ‘

−12 3,2 1,4’

(15)

18

‹Œ222_{= ‹Œ}22₋−0,0423

−2,864 ‹“′′

Logo:

V

1 0 0

0 1 −0,0423 + 2,8640,0423_2,864

0 0 −2,864

W ∙ ‘ .’ = V

−0,0799 −0,0414 0,0788

0 − 10,0423_{2,864 −0,2105 + 0,6315}0,0423_{2,864 0,1412 − 0,7719}0,0423_2,864

1 −0,6315 0,7719

W ∙ ‘−123,2 1,4’

Por fim, para transformar na identidade, basta dividir a linha 3 por 2,864:

‹“222 ₌ ‹“′′

2,864

Obtemos por fim a resposta do problema:

‘1 0 00 1 0

0 0 1’ ∙ ‘

.

’ = ‘−0,0799 −0,0414 0,0788−0,0148 0,1775 0,1381

−0,3491 0,1839 −0,0745’ ∙ ‘

−12 3,2 1,4’

Agora, apenas para reobter na ordem x1, x2, x3, mantendo a matriz identidade, vamos

trocar a ordem das colunas e depois das linhas, ou seja:

“Trocamos a C1 com a C3, e os x’s correspondentes”

‘0 0 10 1 0

1 0 0’ ∙ ‘ .

’ = ‘−0,0799 −0,0414 0,0788−0,0148 0,1775 0,1381

−0,3491 0,1839 −0,0745’ ∙ ‘

−12 3,2 1,4’

“Trocamos a L1 com a L2, e M-1’s correspondentes”

‘1 0 00 1 0

0 0 1’ ∙ ‘ .’ = ‘

−0,3491 0,1839 −0,0745

−0,0148 0,1775 0,1381

−0,0799 −0,0414 0,0788 ’ ∙ ‘

−12 3,2 1,4’

A matriz inversa foi, portanto, obtida, como:

†oŠ_{= ‘}−0,3491 0,1839 −0,0745_{−0,0148 0,1775} _0,1381

−0,0799 −0,0414 0,0788 ’

Os valores de , e _. ficam, portanto:

‘ .

’ = ‘−0,3491 0,1839 −0,0745−0,0148 0,1775 0,1381

−0,0799 −0,0414 0,0788 ’ ∙ ‘

−12 3,2

1,4’ = ‘

4,6903 0,9388

0,9364’

1.4.1 Código para inversão de matrizes em VBA

A seguir está apresentado um código que usa o método de pivotação total de Gauss para obtenção da matriz inversa, escrevendo os resultados passo a passo.

Sub Inversa(N, M, M_inv, infoM)

Dim i, j, k, N_lin, N_col, lin_p, col_p, lin_esc As Integer Dim pivot, temp As Double

Dim Seq() As Integer

' troca as linhas com o pivot

If (k <> lin_p) Then

(16)

19

' Captura a dimensão da matriz

N_col = N N_lin = N

' Indicador de procedimento de inversão bem sucedido (0- bem ‘sucedido, 1- mal sucedido

infoM = 0

' Dimensiona o vetor que contém a sequencia dos x's

ReDim Seq(N_col)

Sheets("Resultado_Inversa").Activate

' Limpa o conteúdo que conterá o resultado

Range(Cells(N_lin + 2, 1), Cells(N_lin + 20000, N_col + 200)).ClearContents

' Inicia a escrita da inversa e a sequencia

For i = 1 To N_lin For j = 1 To N_col Cells(2 + i, j) = M(i, j) M_inv(i, j) = 0 Next

M_inv(i, i) = 1 Seq(i) = i

lin_esc = N_lin + 4

' Zera sequencialmente as linhas

For k = 1 To N_col pivot = 0 ' Captura o pivot

For i = k To N_lin For j = 1 To N_col

If (Abs(M(i, j)) > Abs(pivot)) Then

pivot = M(i, j) lin_p = i col_p = j End If

If (Abs(pivot) < 1E-18) Then

MsgBox ("Matriz não inversível") infoM = -1

GoTo 100 End If

Call TrocaLinha(N_col, k, lin_p, M, M_inv) Call Escreve(lin_esc, N_lin, M, Seq, M_inv) End If

' troca as colunas com o pivot

If (k <> col_p) Then

Cells(lin_esc, 1) = "Troca coluna " + Str(k) + " com coluna " + Str(col_p)

Call TrocaColuna(N_lin, k, col_p, M, Seq) Call Escreve(lin_esc, N_lin, M, Seq, M_inv) End If

' zera as colunas 'i' de todas as linhas

For i = 1 To N_lin If (i <> k) Then

temp = (M(i, k) / pivot) For j = 1 To N_col

M(i, j) = M(i, j) - M(k, j) * temp

M_inv(i, j) = M_inv(i, j) - M_inv(k, j) * temp Next

End If

For j = 1 To N_col M(k, j) = M(k, j) / pivot M_inv(k, j) = M_inv(k, j) / pivot Next

' Escreve os resultados

Cells(lin_esc, 1) = "Ajeitou a coluna " + Str(k) Call Escreve(lin_esc, N_lin, M, Seq, M_inv)

posições originais

For k = 1 To N_lin For j = 1 To N_col If (Seq(j) = k) Then

Call TrocaColuna(N_lin, k, j, M, Seq) Call TrocaLinha(N_col, k, j, M, M_inv) End If

Next Next

Cells(lin_esc, 1) = "Matriz inversa" Call Escreve(lin_esc, N_lin, M, Seq, M_inv)

100 'fim do programa

End Sub

‘Subrotinas que efetuam a troca de linhas e colunas ''''''''''''''''''''''' Subrotina que efetua a troca de linhas

Sub TrocaLinha(N_col, k, lin_p, M, M_inv)

Dim j As Integer Dim temp As Double For j = 1 To N_col temp = M(lin_p, j) M(lin_p, j) = M(k, j) M(k, j) = temp temp = M_inv(lin_p, j) M_inv(lin_p, j) = M_inv(k, j) M_inv(k, j) = temp

Next End Sub

'''''''''''''''' Subrotina que efetua a troca de colunas

Sub TrocaColuna(N_lin, k, col_p, M, Seq)

Dim i As Integer Dim temp As Double For i = 1 To N_lin temp = M(i, col_p) M(i, col_p) = M(i, k) M(i, k) = temp

End Sub

‘Subrotina de escrita dos passos e das matrizes ''''''''''''''''''''''''''''''''''''' Subrotina de escrita

Sub Escreve(lin_esc, N_lin, M, Seq, M_inv)

Dim i, j As Integer

' Captura a matriz

For i = 1 To N_lin

Cells(lin_esc + i, N_lin + 2) = "x" + Str(Seq(i)) For j = 1 To N_lin

Cells(lin_esc + i, j) = M(i, j)

Cells(lin_esc + i, j + N_lin + 3) = M_inv(i, j) Next

(17)

20

1.5 Solução de sistemas de equações não lineares

Seja um sistema não-linear com N equações e N incógnitas na forma:

(E 1.30) R @ = V

ℱ , , … , B

⋯

ℱB , , … , B

W = 0

Veremos alguns dos métodos para solução do sistema de equações.

1.5.1 Método de Newton-Raphson

O método clássico para solução de sistemas de equações não lineares é o método de Newton-Raphson. Vamos começar com uma função de duas variáveis, ou seja, R @ .

(E 1.31) _{R @ = Tℱ} ,

ℱ , U = 0

A idéia consiste em propor uma aproximação linear para cada função ℱ , ℱ a partir da série de Taylor em relação às variáveis _,, , a partir de um ponto › , œ. Propondo aproximação para _ℱ , obtendo-se _ℱ_,•ž, tem-se que:

(E 1.32) ℱ _,•ž = ℱ &@ ' + E − F(ℱ

( )_@+ + E − F

(ℱ

( )_@+

E para ℱ , obtendo-se ℱ _,•ž, tem-se que: (E 1.33) ℱ _,•ž = ℱ &@ ' + E − F(ℱ

( )_@+ + E − F

(ℱ

( )_@+

Observe que as duas equações acima podem ser escritas matricialmente como:

(E 1.34) T_ℱℱ,•ž

,•žU = X Y Z Y

[ℱ &@ ' + E − F(ℱ_{( )}

@+ + E − F

(ℱ

( )_@+

ℱ &@ ' + E − F(ℱ_{( )}

@+ + E − F

(ℱ ( )_@+ \Y

] Y ^

Tℱ_ℱ ,•ž

,•žU = Tℱℱ U)_@+ + X Z

[(ℱ₍ (ℱ₍

(ℱ

( (ℱ( \]

^ ••

@+

Ÿ − −

Onde a matriz Jacobiana é a matriz das derivadas primeiras, ou seja:

(E 1.35) ∇R =

X Z

[(ℱ₍ (ℱ₍

(ℱ

( (ℱ( \]

^

(18)

21 (E 1.36) R _¡ @ = R&@ P' + ∇R|_@P ∙ @ − @∗

A idéia do método consiste então em propor que a aproximação seja nula, e obter o vetor dos valores de @ que satisfaz tal condição.

(E 1.37) P = R|@P + ∇R|@P ∙ "@ − @

P _$

∇R ∙ @ − @∗ _{= R|}

@P

Para eliminar a matriz Jacobiana e isolar @, precisamos primeiro multiplicar ambos os lados da equação por "∇R|_@P $o pela esquerda. Com isto, "∇R|_@P $o ∇R|_@P = ¤, onde ¤ é a matriz identidade, o “1” da matemática vetorial, e

pode ser otimido. Ou seja:

(E 1.38)

"∇R|_@P $o ∙ ∇R|_@P bcccccdccccce

¥

∙ "@ − @P _{$ = −"∇R|}

@P $o ∙ @P

@ = @P _{− ∇R} o _{∙ R|}

@P

Esta equação fornece a forma de cálculo dos valores das variáveis que tornam a aproximação linear das funções nulas. O procedimento a partir de um novo ponto deve ser repetido até que ambas as funções em valor absoluto fiquem abaixo de uma dada tolerância numérica.

Note que reabrindo as matrizes, temos que:

(E 1.39) _{¦ §} ` _{= ¦ § − M ∇R} o _{∙ Tℱℱ UN}

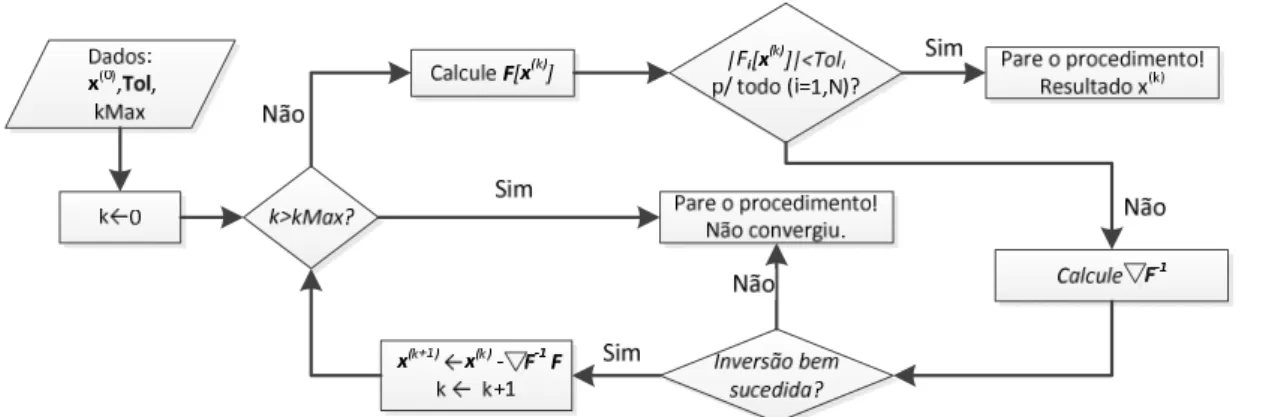
Notem que é necessário aplicar o procedimento de inversão de matrizes descrito na seção anterior para obter a inversa da Jacobiana. A regra recursiva deve ser feita até que as funções sejam suficientemente próximas de zero. O algoritmo para o procedimento está ilustrado na Figura 1.1.

(19)

22 Vejamos um exemplo numérico.

Exemplo 1.6-) Seja o seguinte sistema:

Tℱ_ℱ ,_, U = T + 2 ∙ ∙ − 3_{− exp ∙} _{U = ¦00§}

Pelo método de Newton-Raphson, obtenha e , a partir de A , C = A1,2C. Admita tolerância de 1 ∙ 10o..

Solução:

Para solução pelo método, vamos considerar o uso de derivada analítica para

elaboração da Jacobiana. Temos que:

(ℱ

( = 1 + 2 ∙ (ℱ( = +2 ∙ (ℱ

( = 1 − ∙ exp ∙ (ℱ( = − ∙ exp ∙

Logo, a Jacobiana fica:

∇R = T_{1 − ∙ exp ∙}1 + 2 ∙ _{− ∙ exp ∙}2 ∙ U

Partindo do ponto ª , « = A1,2C, pode-se calcular a função neste ponto. Assim:

Ÿℱ

ℱ = T1 + 2 ∙ 1 ∙ 2 − 31 − exp 1 ∙ 2 U = ¦−6,389§2

Como os dois valores da função são, em valor absoluto maiores do que 1 ∙ 10o., o

procedimento deve continuar. A matriz Jacobiana fica:

∇R = T_{1 − 2 ∙ exp 1 ∙ 2 −1 ∙ exp 1 ∙ 2 U = T}1 + 2 ∙ 2 2 ∙ 1 _{−13,778 −7,389U}5 2

Deve-se efetuar a inversão da matriz por um procedimento numérico. Em Excel,

pode-se utilizar a função Matriz.Inverso(). A inversão da matriz leva à:

"∇R $oŠ= ¦ 0,787_{−1,467 −0,533§}0,213

O valor de x da nova interação fica:

¦ § = ¦ § − ∇R o _{∙ Tℱℱ U}

(20)

23 O procedimento deve ser repetido até que ambos os valores ℱ e ℱ , em valor absoluto,

sejam menores do que a tolerência. A tabela a seguir ilustra a continuidade do

procedimento.

IT _R Convergiu? _¬R _¬RoŠ _¬RoŠ_{∙ R}

0 1,000 2,000 Não 5,000 2,000 0,787 0,213 0,213

2,000 -6,389 -13,778 -7,389 -1,467 -0,533 0,467

1 0,787 0,199 Não 4,065 1,574 0,625 0,375 -0,832

1,533 -2,553 -4,119 -2,629 -0,980 -0,967 2,275

2 1,619 -3,783 Não -0,484 3,237 0,131 0,869 0,651

-0,742 1,318 1,223 -0,487 0,328 0,130 -1,071

3 0,968 -1,394 Não 1,659 1,936 0,408 0,592 -0,810

0,329 -0,408 0,547 -1,331 0,167 -0,508 -0,026

4 1,778 0,043 Não 1,712 3,555 0,485 0,515 -0,033

0,356 -0,105 0,330 -3,346 0,048 -0,248 0,028

5 1,811 -0,002 Não 1,656 3,622 0,475 0,525 -0,001

0,328 0,000 0,406 -3,279 0,059 -0,240 0,000

6 1,812 0,000 Sim

0,328 0,000

Como resultado final, os valores de A , C = A1,812; 0,328C.

Vejamos sua implementação em linhas de programação.

1.5.1.1 Código de Newton-Raphson em VBA

A função em VBA fará uso da função Inversa(N,M,Minv), descrita na seção 1.4.1 e subrotina para o cálculo de multiplicação de matriz com vetor MatrizVetMult(N, N, JacInv, F, Passo) descrita na seção 1.1, além do cálculo da matriz Jacobiana. A seguir está apresentado o código.

' Subrotina que calcula a raiz de um sistema de Funções F(x) onde F e x possuem dimensão N e Tol representa a tolerância '''''''''''''''''

Sub Funcao(N, x, F) F(1) = x(1) - x(2) * x(1) + 3 F(2) = x(1) - Exp(x(2)) + 2

End Sub

' NewtonRaphson

Sub NewtonRaphson(N, x, F, Tol)

Dim i, j, IT, ITmax, infoM As Integer Dim Jac(), JacInv(), Passo(), dx As Double Dim conv As String

' Se houver erro numérico, vai para 12

On Error GoTo 12

For i = 1 To N x(i) = x(i) - Passo(i) Next

' Acrescenta uma iteração

IT = IT + 1

Loop

Sheets("Resultados_NR").Activate

If (infoM = 1) Then

Cells(1, 1) = "Sistema singular"

ElseIf (IT > ITmax) Then

Cells(1, 1) = "N° máximo de iterações sem convergência" MsgBox ("Não Convergiu")

(21)

24

' Redimensiona

ReDim Jac(N, N)

ReDim JacInv(N, N)

ReDim Passo(N)

ITmax = 1000 ' Número máximo de iterações

Tol = 0.001 ' Tolerância

dx = 0.001 ' Passo p/ cálculo da derivada

IT = 0

Do While (IT < ITmax) ' Chama a função objetivo

Call Funcao(N, x, F) ' Verifica a convergência

conv = "Sim" For i = 1 To N

If (Abs(F(i)) > Tol) Then

conv = "Não" Exit For

End If

Exit Do End If

' Calcula a Jacobiana e sua inversa

Call Jacobiana(N, x, dx, F, Jac) Call Inversa(N, Jac, JacInv, infoM)

' Se não conseguiu inverter, acusa sistema singular

If (infoM < 0) Then

MsgBox ("Matriz singular") Exit Do

End If

' Calcula novo valor de x

Call MatrizVetMult(N, N, JacInv, F, Passo)

12 Cells(1, 1) = "Erro no procedimento numérico"

Else

Cells(1, 1) = "Convergência atingida" For i = 1 To N

Cells(2, i) = "x" + Str(i) Cells(3, i) = x(i)

Cells(2, N + i) = "F" + Str(i) Cells(3, N + i) = F(i) Next

End If

100 ' Fim

End Sub

'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''' ' Calcula a Jacobiana (diferenças para frente)

Sub Jacobiana(N, x, dx, F, Jac)

Dim i, j, k As Integer Dim Ftemp() As Double ReDim Ftemp(N)

For i = 1 To N x(i) = x(i) + dx

Call Funcao(N, x, Ftemp) For j = 1 To N

Jac(j, i) = (Ftemp(j) - F(j)) / dx Next

x(i) = x(i) - dx

Next End Sub

1.6 Funções, relações e distribuições especiais

1.6.1 A fórmula de Euller

A fórmula de Euler relaciona a exponencial de um número imaginário com cosseno de um número real e o seno associado à uma parte imaginária.

(E 1.40) T ~ ∙*= cos + i ∙ sen

~o ∙* _{= cos} _{− i ∙ sen}

De onde vem? Para chegar a tal demonstração, pode-se propor as funções expandidas como séries de Taylor em torno do ponto = 0. Aplicando a série de Taylor, apresentada na Equação (E 1.5), para uma função ℱ em torno de = 0:

(E 1.5) _ℱ _{= ℱ + ℱ}2_{∙ +} ∙ ℱ22

2 +

._{∙ ℱ}222

3! +

0_{∙ ℱ}2222

4! +

® _{∙ ℱ} z

5! …

Para a função cosseno:

(E 1.5)

r} = r} 0 − }~• 0 ∙ − ∙ r} 0₂ + .∙ }~• 0_3! + 0∙ r} 0_4! − ®∙ }~• 0_5! …

(22)

25 Para a função seno:

(E 1.5)

}~• = }~• 0 + r} 0 ∙ − ∙ }~• 0₂ − .∙ r} 0_3! + 0∙ }~• 0_4! + ®∙ r} 0_5! …

}~• = − _{3! +}. _{5! −}® _{7! +}° _{9! …}±

Para a função ~o ∙*, notando que ~o ∙ = 1:

(E 1.5)

~o ∙* ₌_~o ∙ _{− Ž ∙}_~o ∙ _{∙ +} 2∙ Ž2∙~o ∙

2 −

3_{∙ Ž}3_∙_~o ∙

3! +

4_{∙ Ž}4_∙_~o ∙

4!

−

5_{∙ Ž}5_∙_~o ∙

5! +

6_{∙ Ž}6_∙_~o ∙

6! −

7_{∙ Ž}7_∙_~o ∙

7! …

~o ∙* ₌₁_{− Ž ∙ +} 2∙ Ž2

2 −

3_{∙ Ž}3

3! +

4_{∙ Ž}4

4! −

5_{∙ Ž}5

5! +

6_{∙ Ž}6

6! −

7_{∙ Ž}7

7! …

Lembrando que Ž² = −1, então os termos que contém Ž elevados à potências pares ficam Ž² = −1; Ž0 = −1 −1 = 1; Žq = −1 −1 −1 = −1, etc. Da forma análoga, os termos contendo números Ž elevados à potências ímpares conterão o número Ž, e ficam: Ž = Ž; Ž. = Ž Ž = −Ž; Ž® = Ž.Ž = Ž, etc. Com isto, a exponencial

~o ∙*_fica:

(E 1.5) _~o ∙*

= 1 − Ž ∙ − 2 + Ž ∙ 3! +.

0 4! − Ž ∙

® 5! −

q 6! + Ž ∙

° 7! +

¯ 8! …

Agrupando os termos que contém Ž:

(E 1.5) ~o ∙* = 1 − 2 +

0 4! −

q 6! +

¯ 8! bccccccdcccccce

nh *

+ Ž ∙ ²− + _{3! −}. _{5! +}® _{7! −}° _9!³± bccccccccdcccccccce

ohgw *

…

Como indicado na Equação acima, os grupos pares compõem a função r} e os grupos ímpares compõem a função −}~• . Assim:

(E 1.41) _~o ∙* _{= cos} _{− Ž ∙ sen}

1.6.2 A distribuição delta de Dirac

A distribuição delta de Dirac, ´ é definida como:

(E 1.42)

´ − = T0 }~ ≠_{∞ }~ ≠}

· ´ −`% ∙ !

o% = 1

(23)

26

(E 1.43) _{· ´ −}`% _{∙ ℱ} _{∙ !}

o% = ℱ

Não é tratada propriamente como função, mas como uma densidade de distribuição de probabilidade, totalmente concentrada em um único ponto.

De onde vem? Em uma maneira pouco formal de entender, vamos imaginar uma distribuição de probabilidade uniforme ¸ , para ∈ , . Como a probabilidade é uniforme, seu valor é constante para todo , ou seja, ¸ = ™~. Uma vez que a densidade de probabilidade integrada no intervalo deve ser igual à unidade, então:

(E 1.44) _{· ¸}º _{∙ !}

l = 1 → ™~ ∙ − = 1 → ¸ =

1 −

Podemos então imaginar que o intervalo diminua gradativamente, de forma que

→ . Nesta condição, o limite quando → levará à um ponto singular, um único ponto , no qual _¸ _{→ ∞}. Neste caso, _¸ será a função delta de Dirac, ou seja,

¸ = ´ − . Ainda assim, a integral será a unidade, poise:

(E 1.45) _lim

º→l· ¸ ∙ ! º

l = limº→l

1

− · ! º

l = limº→l

− − = 1

A propriedade (E 1.43) também pode ser demonstrada. Para tanto, vamos considerar a função ℱ integrável, cuja integral resulta em uma função ¾ , ou seja:

(E 1.46) _¾ _{= · ℱ} _{∙ ! ~ ℱ} ₌ !¾

!

Retornando à idéia da densidade de probabilidade ¸ =_ºol, a integral de

¸ ∙ ℱ fica:

(E 1.47) _lim

º→l· ¸ ∙ ℱ ∙ ! º

l = limº→l

1

− · ℱ ∙ !

º

l = limº→l

¾ − ¾

−

É possível observar que o último limite é exatamente uma das definições da derivada de ¾ em = . Mas a derivada de ¾ é a função ℱ . Assim:

(E 1.48) _lim

º→l· ¸ ∙ ℱ ∙ ! º