Avaliação de insurance linked bonds com taxas de juro estocásticas

UNIVERSIDADE DE LISBOA

FACULDADE DE CIÊNCIAS

DEPARTAMENTO DE MATEMÁTICA

ISCTE – BUSINESS SCHOOL

INSTITUTO UNIVERSITÁRIO DE

LISBOA

AVALIAÇÃO DE INSURANCE LINKED BONDS COM TAXAS

DE JURO ESTOCÁTICAS

Ana Cristina Alves Ventura

MESTRADO EM MATEMÁTICA FINANCEIRA 2009

UNIVERSIDADE DE LISBOA

FACULDADE DE CIÊNCIAS

DEPARTAMENTO DE MATEMÁTICA

ISCTE – BUSINESS SCHOOL

INSTITUTO UNIVERSITÁRIO DE

LISBOA

AVALIAÇÃO DE INSURANCE LINKED BONDS COM TAXAS

DE JURO ESTOCÁTICAS

Ana Cristina Alves Ventura

Dissertação orientada pelo Professor Doutor João Pedro Vidal Nunes MESTRADO EM MATEMÁTICA FINANCEIRA

Resumo

Com a presente dissertação pretende-se obter uma fórmula fechada para a avaliação de Insurance Linked Bonds. Esta avaliação foi efectuada primeiramente utilizando taxas de juro determinísticas, e seguidamente num ambiente onde imperam taxas de juro estocásticas, para as quais se aplicou o modelo de Vasicek. A abordagem utilizada consiste essencialmente na obtenção da first

passage time do índice pelo trigger. No caso determinístico, optou-se

por uma abordagem com recurso a mudanças de medida de probabilidade e ao Lema de Itô. Para o caso estocástico, foi utilizada uma equação integral de Volterra de segundo grau, sendo que se tornou necessário deduzir a distribuição condicional da taxa de juro, a distribuição condicional do índice e a distribuição incondicional do índice. Estas distribuições são posteriormente utilizadas para se obter implicitamente a first passage time density.

Palavras-Chave: Insurance Linked Bond, First Passage Time, Taxas de Juro Estocásticas, Modelo de Vasicek, Distribuições Condicionais

Abstract

The major question in the present thesis is to obtain a closed-form solution for the pricing of Insurance Linked Bonds and to make a contribute to the current literature on this kind of products. The current valuation was made firstly using constant interest rates and secondly with stochastic interest rates, through the Vasicek Model. The main purpose of this thesis is to compute the first passage time of the index through the trigger. In the determinist case, a change of measure was applied and Itô’s lemma was also used. Regarding the stochastic case, a Volterra integral equation of the second kink was applied, and it was necessary to deduce the interest rate conditional distribution, the index conditional distribution and the index unconditional distribution. These distributions are crucial to implicitly calculate the first passage time.

Key-Words: Insurance Linked Bond, First Passage Time, Stochastic Interest Rates, Vasicek Model, Conditional and Unconditional Distributions

Conteúdo

1 Introdução 2

2 Preliminares 4

2.1 Alguns Resultados Importantes . . . 4

2.2 First Passage Time . . . 6

2.3 Outros Resultados . . . 9

3 Mecanismos de transferência de riscos para os mercados …nanceiros 10 3.1 Securitização . . . 10

3.2 Securitização de Riscos de Seguros . . . 11

3.2.1 CAT Bonds . . . 12

3.2.2 Outros tipos de Insurance Linked Securities . . . 17

4 Avaliação de Insurance Linked Bonds 21 4.1 Pressupostos e Especi…cação do Modelo . . . 21

4.2 Modelo com taxas de juro determinísticas . . . 22

4.3 Modelo com Taxas de Juro Estocásticas . . . 25

4.3.1 Cálculo da distribuição condicional da taxa de juro . . . 26

4.3.2 Cálculo da distribuição incondicional do índice. . . 33

4.3.3 Cálculo da distribuição condicional do índice. . . 33

4.4 Conclusão . . . 34

5 Conclusão 35

1

Introdução

A presente dissertação tem o intuito de fornecer uma fórmula fechada para o cálculo do preço de uma Insurance Linked Bond. Uma Insurance Linked Bond é um instrumento …nanceiro (também denominado Insurance Linked Security - ILS) que não está ligado a um activo subjacente real, mas o seu payo¤ depende da veri…cação de determinados eventos, para os quais podem ser estabelecidos limites (denominados triggers). Estes eventos são normalmente mensurados através de índices.

Este tipo de produtos são actualmente bastante importantes, pois têm efeitos directos e observáveis como a grande capacidade para absorver perdas elevadas resultantes de acontec-imentos catastró…cos ou outros. Além disso, o facto de se pensar que as correlações entre os produtos …nanceiros normais e os ILS são relativamente baixas signi…ca que estes últimos poderão ser uma boa aposta em termos de efeitos de diversi…cação duma carteira. Se asso-ciarmos a este último facto, o facto da remuneração destes produtos ser mais elevada que a de um produto …nanceiro normal, então os ILS tem capacidade de atrair mais investidores e mais exigentes. Saliente-se também que durante a crise, estes produtos não tiveram grandes oscilações de cotação. No entanto, as desvantagens também são evidentes. O facto de estes produtos serem de uma natureza bastante complexa e das transacções não terem um padrão comum pode levar a que surjam oportunidades onde existe informação assimétrica. Outra grande di…culdade que estes produtos podem trazer prende-se com a sua adequada avali-ação, visto que os riscos inerentes são por vezes difíceis de mensurar, como por exemplo as catástrofes naturais, facto que pode ser uma agravante para o crescimento do mercado.

A literatura existente sobre avaliação de ISL é reduzida. Por um lado, no âmbito das ciências actuariais o facto de serem riscos com baixas probabilidades e altas severidades, faz com que a Lei dos Grandes Números não seja adequada e, por outro lado, a aplicação de uma abordagem neutra face ao risco tipicamente …nanceira (arbitrage-free framework ) está ainda pouco desenvolvida.

No entanto foram encontrados alguns exemplos: [7] que obtiveram fórmulas para os pro-dutos transaccionados no CBoT (catastrophe insurance futures e call spreads); [14] seguem uma estratégia semelhante modelizando também um índice das opções da Property Claim Services (PCS); [18] que fazem uma avaliação mas focando-se no risco de default através de um Processo de Wiener; [1] que modela as perdas catastró…cas através de um processo de Markov; e [5] que deduziu uma fórmula simples para cálculo do preço de cat bonds não catastró…cas e que surge como ponto de partida para esta dissertação.

Existem também alguns trabalhos efectuadas numa lógica de mercados incompletos dos quais se destaca [10].

No que respeita a restante bibliogra…a consultada referente a ILS, está essencialmente divida em duas categorias: o mercado e a história; e a estrutura e funcionamento das CAT bonds.

[11], [8] e [2] fazem uma breve exposição sobre a evolução histórica de instrumentos de securitização, bem como uma análise sobre o estado actual do mercado deste tipo de instru-mentos, com maior incidência em CAT bonds. No que respeita à estrutura e o funcionamento de CAT bonds, [6] e [24] explicitam com bastante rigor o seu funcionamento e estrutura.

No âmbito deste trabalho pretende-se aplicar a uma insurance linked bond não catastró…ca uma abordagem risk free para a determinação do seu preço, consistindo essencialmente no cálculo das funções de densidade da …rst passage time.

A tese está organizada da seguinte forma. No presente capítulo é efectuada uma breve introdução do trabalho desenvolvido, bem como uma revisão da literartura.

No capítulo 2 apresentam-se alguns resultados preliminares de grande importância no âmbito da presente dissertação.

No capítulo 3 efectua-se uma abordagem teórica sobre os mecanismos de transferência de risco para os mercados …nanceiros. Primeiramente, expõem-se de forma breve os mecan-ismos de transferência de riscos do sector …nanceiro para os mercados de capitais, mais concretamente no sector bancário que foi pioneiro nestas matérias. Seguidamente, explicita-se a estrutura existente para a transferência de riscos especí…cos de explicita-seguros, que é bastante semelhante à da securitização no sector bancário, caracterizando-se pela existência de um Special Purpose Vehicle (SPV) que formaliza um contrato com a empresa de seguros, no qual se de…ne que tipo de cobertura vai ser securitizada e qual o valor dos prémios a receber. Posteriormente, o SPV emite e transacciona títulos nos mercados …nanceiros, não havendo relação directa entre a empresa de seguros e os investidores …nais. Dentro das securitiza-ções efectuadas no âmbito dos riscos de seguros, é feita uma análise detalhada do tipo de mecanismos já utilizados , sendo que os mais conhecidos e utilizados são as CAT bonds.

No capítulo 4 apresenta-se primeiramente uma descrição do produto que vai ser avaliado. Seguidamente faz uma dedução da fórmula fechada para o preço da bond com taxas de juro determinísticas, calculando-se para tal a …rst passage time do índice pela barreira. No ponto seguinte deste capítulo deduz-se a fórmula para o cálculo da …rst passage time num ambiente de taxas de juro estocásticas. Para tal recorre-se à equação integral de Volterra de segundo grau, explicitada em [20].

2

Preliminares

Na presente secção apresentam-se alguns resultados considerados pertinentes no âmbito da presente dissertação.

Neste trabalho assume-se, como é usual na literatura, que o mercado é completo e livre de arbitragem e ainda que a negociação se faz continuamente e sem custos. Então existe uma única medida de martingala equivalente Q, tal que o processo dos preços descontados é uma martingala no espaço de probabilidade ( ; F; Q) onde F representa a …ltração (Ft)_t>0.

2.1

Alguns Resultados Importantes

De…nição 1 (Processo de Itô) Um processo estocástico X (t) é um processo de Itô desde que possa ser representado como

dX (t) = (t; X (t)) dt + (t; X (t)) dW (t) (1) ou seja X (t) = X (0) + Z t 0 [s; X (s)] ds + Z t 0 [s; X (s)] dW (s) (2) onde fW (t)gt 0 é um Brownian Motion com …ltration fF (t)gt 0, X (0) é F (0)-mensurável

e os processos estocásticos (t; X (t)) e (t; X (t)) são _{F (t)-adapted.}

Lema 2 (Lema de Itô) Seja X um processo de Itô tal como descrito na de…nição anterior, ou seja,

dX (t) = (t; X (t)) dt + (t; X (t)) dW (t) (3) e f : <+ < ! < uma função C1;2. Então, para todo o T 0,

f (T; X (T )) = f (0; X (0)) + Z T 0 @f (t; X (t)) @t dt + Z T 0 @f (t; X (t)) @x dX (t) +1 2 Z T 0 @2_{f (t; X (t))} @x2 dhX; Xi (t) (4) ou em notação diferencial, df (T; X (T )) = @f (t; X (t)) @t dt + @f (t; X (t)) @x dX (t) + 1 2 @2_{f (t; X (t))} @x2 dhX; Xi (t) (5)

Em alternativa, combinando a primeira e a terceira equação, df (T; X (T )) = @f (t; X (t)) @t + (t; X (t)) @f (t; X (t)) @x + 1 2 2_{(t; X (t))}@2f (t; X (t)) @x2 dt + (t; X (t))@f (t; X (t)) @x dW (t) (6) Demonstração. Ver [4].

Teorema 3 (Teorema de Girsanov) _{Seja fW (t)g0 t T} um Standard Brownian Motion de…nido no espaço de probabilidades ( ; F; P ) e fF (t)g0 t T a …ltration gerada por este

Brownian Motion. Se f (t)g0 t T for um adapted process que satisfaça a seguinte condição

(Novikov’s Condition) EP exp 1 2 Z T 0 2 (s) ds <₁ (7) então existe uma outra medida de probabilidade Q tal que:

1) Q é equivalente a P .

2) A Radon-Nikodym derivative de Q em relação a P (no momento T ) é dada por: dQ dP F (t) := exp Z T 0 (s) dW (s) 1 2 Z T 0 2 (s) ds (8) 3) fW (t) = W (t) +R₀t (s) ds é também um Standard Brownian Motion, mas de…nido na medida Q.

Ou seja, em notação diferencial

dfW (t) = dW (t) + (t) dt (9) Demonstração. Ver [4].

2.2

First Passage Time

De modo a ser possível o cálculo da …rst passage time considere-se as seguintes proposições. Proposição 4 Se WtQ é um Q-measured standard Brownian Motion tal que W

Q t0 = 0, então: Q Pr W_tQ x_{^ sup} t0 u t W_uQ y _Ft0 = x p t t0 x 2y p t t0 (10) e Q Pr W_tQ _{2 dx ^ sup} t0 u t W_uQ y _Ft0 = x; 0; p t t0 x; 2y; p t t0 dx (11) para y 0 e x y, e onde (x; ; ) = _p 1 2 2 exp " 1 2 (x )2 2 # (12) representa a função densidade de probabilidade de uma distribuição Normal univariada X, com média _{2 < e desvio padrão} > 0.

Demonstração. Temos que:

Q Pr W_tQ x_{^ sup} t0 u t W_uQ y _Ft0 = Q Pr W_tQ x _Ft0 Q Pr W_tQ x; sup t0 u t W_uQ > y _Ft0 = _p x t t0 Q Pr W_tQ x; sup t0 u t W_uQ > y _Ft0 (13)

Utilizando o Re‡exion Principle1 (ver [16]), vem: = _p x t t0 Q Pr W_tQ 2y x; sup t0 u t W_uQ > y _Ft0 (14)

1_{Re‡exion Priciple: For every sample path that hits level y before time t but …nishes below level x at time}

t, there is another equally probable path that hits y before time t and then travels upwards at least (y x) units to …nish above the level (2x y).

Mas, 2y x = y + (y x) > y, porque y x e portante a parte do supremo na equação anterior é redundante e …ca:

= _p x t t0 Q PrhW_tQ 2y x _Ft0 i = _p x t t0 x 2y p t t0 (15) Se derivarmos este resultado obtém-se (11).

Proposição 5 Se

dXt= dt + dWtQ (16)

onde _{2 < e Wt}Qt _{é um Q-measured standard Brownian Motion tal que Wt}Q₀ = 0, então:

Q Pr Xt x^ sup t0 u t (Xu) y Ft0 = x _p(t t0) t t0 exp 2 y 2 x 2y (t t0) p t t0 (17) Demonstração. Temos dXt= dt + dWtQ:

Fazendo uma mudança de medida (Q ! Q ), vem: dXt = dWtQ

dt + dW_tQ = dW_tQ

dW_tQ = dt + dW_tQ (18) Vem então que:

Q Pr Xt x^ sup t0 u t (Xu) y Ft0 = Q Pr W_tQ x_{^ sup} t0 u t W_uQ y _Ft0 = EQh_{11f W}Q t x^sup_{t0 u t}( W Q u ) yg Ft0 i (19) A Radon-Nikodym derivative é dada por:

EQ[ Xtj Ft0] = E

Q

Xt

dQ

Pelo Teorema de Girsanov, vem:

dW_tQ = dW_tQ dt (21) e as medidas são equivalentes, logo:

dQ dQ Ft0 = exp 2 4 t Z t0 dW_s 1 2 t Z t0 2 ds 3 5 = exp W_t W_t0 1 2 2 (t t0) = exp W_t 1 2 2 (t t0) (22)

Voltando à equação (19), vem: EQh_{11f W}Q t x^supt0 u t( W Q u ) yg Ft0 i = (23) = EQ exp W_t 1 2 2 (t t0) 11f _WQ t x^sup_{t0 u t}( W Q u ) yg Ft0 = EQ exp ₂ W_t 1 2 2 (t t0) 11f _WQ t x^sup_{t0 u t}( W Q u ) yg Ft0 = EQ exp ₂ W_t 1 2 2 (t t0) 11f _WQ t xg11fsup_{t0 u t}( W Q u ) yg Ft0 (24)

Fazendo uma mudança de variável z = Wt, …ca:

= EQ exp ₂z 1 2

2

(t t0) 11_{fz xg}11f_sup

t0 u t(z) yg Ft0 (25)

Utilizando a proposição anterior vem: = x Z 1 exp ₂z 1 2 2 (t t0) z; 0; p t t0 z; 2y; p t t0 dz (26)

com: (x; ; ) = _p 1 2 2 exp " 1 2 (x )2 2 # (27) Vem então: = x Z 1 exp 1 2 2z (t t0) + 2(t t0) 2 2_{(t t} 0) ! ( 1 p 2 2_{(t t} 0) exp 1 2 z2 2_{(t t} 0) 1 p 2 2_{(t t} 0) exp " 1 2 (z 2y)2 2_{(t t} 0) #) dz = x Z 1 ( 1 p 2 2_{(t t} 0) exp 1 2 z2 2z (t t0) + 2(t t0)2 2_{(t t} 0) ! 1 p 2 2_{(t t} 0) exp " 1 2 (z 2y)2 2z (t t0) + 2(t t0)2 2_{(t t} 0) #) dz (28) = x Z 1 ( 1 p 2 2_{(t t} 0) exp 1 2 (z (t t0)) 2 2_{(t t} 0) ! 1 p 2 2_{(t t} 0) exp " 1 2 (z ( (t t0) + 2y))2 2_{(t t} 0) + 2y₂ #) dz = x Z 1 z; (t t0) ; p t t0 exp 2y₂ z; (t t0) + 2y; p t t0 dz = x _p(t t0) t t0 exp 2 y 2 x 2y (t t0) p t t0

2.3

Outros Resultados

Lema 6 Para a; b; c; _{2 < e 2 <}+_, Z < z; ; 2 a bz c dz = a b p c2_{+ b}2 2 (29) Demonstração. Ver [20].

3

Mecanismos de transferência de riscos para os

mer-cados …nanceiros

3.1

Securitização

A securitização é uma técnica …nanceira que permite transformar riscos/activos (à partida não transaccionáveis) em activos transaccionáveis (securities), permitindo a sua posterior transferência para os mercados de capitais, onde são vendidos aos investidores.

As primeiras operações de securitização foram realizadas por instituições bancárias. Desde o início da sua existência que os bancos concedem empréstimos, principalmente com o intu-ito de promover a aquisição de bens. Por volta dos anos 70, ocorreu nos Estados Unidos da América (E.U.A.) um excesso de procura de capitais para aquisição de habitação própria, tendo os bancos enfrentado alguns problemas de falta de liquidez. Esta di…culdade levou a que se desenvolvessem formas alternativas de obtenção de capital, mais concretamente transferindo fundos dos mercados de capitais para os bancos e posteriormente para as pes-soas que requeriam empréstimos([15]). A resposta foi o desenvolvimento de uma técnica que consistia na transformação dos empréstimos (capitais e juros) em securities transaccionáveis nos mercados …nanceiros, ou seja, a securitização.

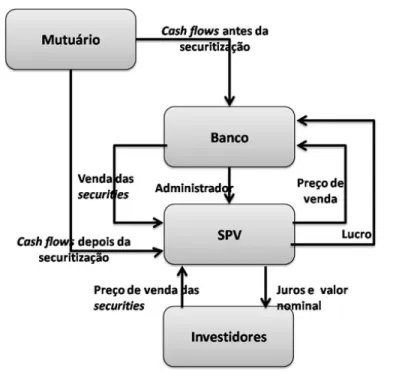
Para melhor entender o funcionamento deste tipo de mecanismos, considere-se um exem-plo simples. Admita-se que um banco tem uma carteira constituída por créditos concedidos a particulares para aquisição de habitação. Com o objectivo de obter capital adicional, para poder conceder mais empréstimos, o banco pode vender a carteira a um Special Purpose Ve-hicle (SPV). Esta entidade serve como intermediária entre o banco e os mercados …nanceiros e a sua principal função é a emissão e transacção das securities (asset-backed securities). Os SPVs são também denominados de bankruptcy remote entities, pois têm que garantir aos investidores o recebimento dos cash-‡ows associados às securities no caso de falência do banco. Tendo em conta esse objectivo, o SPV realiza aplicações consideradas seguras em Obrigações do Tesouro e/ou obrigações com rating elevado. Os SPVs estão normalmente

Figura 1: Estrutura Básica da Securitização no Sector Bancário

estabelecidos em o¤shores, pois nesse caso pagam menos impostos o que provoca também menos custos tanto para os bancos como para os investidores. O esquema apresentado na …gura 1 reproduz a estrutura básica da securitização utilizada na actividade bancária.

No sector bancário existem hoje em dia uma grande variedade de securitizações, mas essencialmente dividem-se em dois tipos, Asset-backed securities (ABS) associadas a crédi-tos (habitação, cartões de crédito, automóveis, etc.) e Collaterized debt obligation (CDO) associadas a obrigações e/ou outro tipo de dívidas de empresas.

Relativamente ao sector bancário as securitizações são realizadas desde 1970, mas no sector segurador só a partir de 1990 se começaram a realizar este tipo de operações.

3.2

Securitização de Riscos de Seguros

As empresas de seguros e resseguros têm como principal objectivo assumir riscos de várias naturezas, em troca do recebimento de prémios. Para que a cobertura dos riscos seja e…caz, as empresas têm que diversi…car ao máximo os riscos assumidos. Na maioria dos riscos, isso é possível devido ao grande número de apólices e graças à Lei dos Grandes Números. No

entanto, existem riscos com baixa probabilidade e elevada severidade (riscos catastró…cos: furacões, terramotos, tempestades, etc.) que por natureza são difíceis de diversi…car.

Um dos mecanismos existentes na actividade seguradora para lidar e…cazmente com riscos catastró…cos é o resseguro. Pode de…nir-se o resseguro como a cedência de uma parte dos riscos assumidos pela empresa de seguros (ou cedente) perante os segurados, a uma segunda empresa de seguros, sem nenhuma relação directa com o segurado (a empresa de resseguros ou cessionário). Através do resseguro as empresas de seguros directo cedem, parcialmente, riscos assumidos que excedem a sua capacidade ou que, por outros motivos, não queiram reter de forma integral ([23]).

Tradicionalmente, as empresas de seguros cobrem os seus riscos catastró…cos através do resseguro. No entanto, nos últimos 20 anos, foram colocadas em causa as capacidades do mercado ressegurador, devido às elevadas perdas originadas por algumas catástrofes natu-rais, nomeadamente o furacão Andrew em 1992 nos E.U.A., que originou perdas elevadís-simas, levando mesmo algumas empresas de seguros à insolvência. A partir dessa altura, a capacidade das empresas de resseguros para assumir riscos catastró…cos tornou-se mais limitada e também bastante mais cara. Numa tentativa de obter capital adicional para aux-iliar a cobertura destes riscos foi necessário procurar formas alternativas de transferir risco, mais concretamente, através dos mercados …nanceiros, por via de operações de securitização ([15]) ([11]). Esta securitização funciona de forma semelhante à realizada pelas instituições bancárias, mas as securities associadas, que captam os riscos de seguros e os transferem posteriormente para os mercados …nanceiros, são denominadas Insurance Linked Securities (ILS).

Os mercados …nanceiros podem ser uma boa alternativa ao resseguro tradicional, na medida em que uma variação de 10.000.000 milhões de dólares é facilmente absorvida por estes mercados, o mesmo não sucedendo no mercado segurador e ressegurador. Esta grande capacidade de absorção de perdas advém da sua dimensão e do elevado número de partici-pantes, em comparação com o mercado segurador e ressegurador. Mais ainda, estima-se que não existe correlação entre os riscos catastró…cos e a performance dos mercados …nanceiros, o que faz com que este tipo de produtos seja bastante e…caz na diversi…cação de uma carteira e atractivos para os investidores ([15]) ([11]).

3.2.1 CAT Bonds

Como já se referiu, após o furacão Andrew em 1992, o mercado de resseguro tornou-se mais caro e limitado e, de forma a contornar este facto surgiram, entre outros, as Catastrophic Bonds (CAT Bonds), também denominadas Act-of-God Bonds.

Figura 2: Estrutura de uma CAT bond

As CAT bonds são event-linked bonds, na medida em que o seu payo¤ depende da ocor-rência de um evento determinado. As mais conhecidas e transaccionadas são as CAT bonds associadas a eventos catastró…cos puros –furacões, terramotos, etc.

A sua estrutura geral de funcionamento está ilustrada na …gura 2.

Na estrutura apresentada, o SPV tem praticamente as mesmas funções que no caso da securitização realizada pelas instituições bancárias. As suas principais competências são a oferta de cobertura às empresas de seguros e a emissão de securities, sendo que devem também proteger os investidores de uma possível insolvência da empresa de seguros ou resseguros que cedeu os riscos.

A operação tem início com a criação do SPV que, após ter formalizado um contrato com a empresa de seguros no qual de…ne que tipo de riscos a securitizar e o tipo de cobertura de que é assegurada, emite e transacciona as securities nos mercados …nanceiros (2). Com os fundos obtidos nesta operação o SPV faz investimentos considerados seguros, nomeadamente em Obrigações do Tesouro e/ou Obrigações com rating elevado (3). Simultaneamente, a empresa de seguros faz o pagamento dos prémios ao SPV, em troca da cobertura (1). Os prémios e o retorno dos investimentos seguros são os fundos necessários para o pagamento dos cupões/juros aos investidores. Na maioria dos casos, é ainda efectuado um contrato swap

de modo a que o retorno dos investimentos seguros estejam indexados a uma taxa de juro de referência, geralmente à LIBOR (4). Os investidores vão ser compensados com LIBOR adicionada de um spread proveniente do prémio pago pela empresa de seguros, pelo facto de assumirem uma parte do risco da empresa de seguros. No caso de o evento associado à CAT bond ocorrer, o SPV disponibiliza o capital acordado no início do contrato, para fazer face aos sinistros, do qual poderão fazer parte os juros, ou o capital ou ambos. O capital a disponibilizar em caso de sinistro pode também estar dividido por tranches, ou seja, cada classe de investidores perde uma percentagem diferente do seu capital inicial

Como já foi referido, as CAT bonds foram desenvolvidas nos anos 90 para facilitar a transferência directa de riscos catastró…cos das empresas de seguros e resseguros para os mercados …nanceiros/investidores. O seu principal objectivo é proteger as empresas de se-guros das grandes perdas causadas por eventos catastró…cos, actuando como uma alternativa ou uma protecção adicional ao resseguro tradicional.

A primeira emissão bem sucedida de CAT bonds foi efectuada pela Hannover Re em 1994, e visou apenas a transferência de alguns riscos de resseguro para o mercado …nanceiro, mas constituiu a base da securitização na indústria seguradora([27]). Desde 1994, o mercado de CAT bonds tem sofrido uma grande evolução. Numa fase inicial, foram testados vários tipos de operações, com diferentes maturidades e tipos de risco, mas hoje em dia existe um mercado mais estandardizado, contribuindo para um maior grau de transparência para todos os intervenientes (investidores, empresas de seguros, agências de rating e supervisores).

Relativamente à maturidade destas obrigações, aquando da sua criação ela variava entre um e dez anos, mas com a evolução do mercado atingiu-se um certo equilíbrio, subsistindo hoje em dia apenas maturidades entre os dois e os quatro anos, prazo considerado mais vantajoso quer para as empresas de seguros quer para os investidores ([11]).

No que respeita ao número de riscos cobertos, as empresas de seguros preferem emitir obrigações associadas a um conjunto de riscos, pois tem obviamente menos custos. Por outro lado, os investidores preferem geralmente obrigações associadas a um único risco, pois acarretam menos incerteza. Apesar disso existem hoje em dia os dois tipos de obrigações ([11]).

No que se refere os ratings destas obrigações, eles são por norma inferiores a BBB (In-vestment Grade), mas este rating não re‡ecte apenas probabilidade de incumprimento da contraparte, estando também incorporada a probabilidade de, ocorrendo o evento, haver uma perda do principal da obrigação ([11]).

Estas obrigações apresentam yields elevadas (quando comparadas com corporate bonds com o mesmo rating) que compensam os investidores pela sua reduzida liquidez e pelo simples facto de não serem securities “normais”.

Até à data, a única CAT bond que originou perdas foi emitida pela Zurich Financial’s Kamp Re, e foi activada devido à ocorrência do furacão Katrina em 2005, o que resultou numa perda total do principal da CAT bond.

As CAT bonds, assim como outros insurance-linked securities, não estão ligadas a um activo subjacente, mas o seu payo¤ depende da veri…cação de determinado evento para o qual são estabelecidos limites (denominados triggers).

Existem quatro tipos de triggers: Indemnity triggers, Pure Parametric triggers, Index triggers e Hybrid triggers ([11]).

1. Indemnity triggers

Nas CAT bonds com Indemnity triggers associados, os payo¤s são determinados com base nas perdas reais da empresa de seguros ou resseguros. Este tipo de trigger foi o primeiro a surgir no mercado, sendo esta a abordagem que mais se aproxima do resseguro tradicional já que oferece garantias à empresa de seguros que minimiza o seu basis risk2_{. Outro risco a ter em consideração, em obrigações com este tipo de trigger,}

é o risco moral (moral hazard), que decorre do facto de haver um menor incentivo a uma adequada gestão de sinistros por parte da empresa de seguros. Por outro lado, o facto de os payo¤s serem determinados pelas perdas reais da empresa leva a que os investidores antes de investir queiram conhecer o negócio da empresa de seguros, exigindo que esta forneça informação detalhada acerca da carteira em causa, o que pode não ser favorável em termos de competitividade no mercado.

2. Pure Parametric triggers

Neste caso, o payo¤ é determinado por medidas físicas do evento ocorrido, como por exemplo a velocidade de um furacão atingir determinado valor ou a magnitude de um tremor de terra atingir determinada grandeza.

Um trigger deste tipo pode ter um basis risk elevado, devido ao facto dos payo¤s não dependerem das perdas reais da empresa de seguros. A carteira da empresa pode não replicar necessariamente a exposição do mercado ao risco, pelo que o grau em que é afectada pode ser maior ou menor do que a média do mercado. Por outro lado apresentam um risco moral bastante mais baixo que qualquer outro tipo de trigger. 3. Index triggers

Neste tipo de triggers, os payo¤s são calculados com base em índices, que não estão ligados directamente às perdas da empresa de seguros. Existem 3 tipos de índices: industry loss indices, modeled loss indices e parametric indices.

2_{Basis risk mede a variação entre as perdas que a empresa de seguros estimou que seriam cobertas pelo}

Em obrigações associadas a industry loss indices, o payo¤ é accionado quando as perdas, estimadas através de um índice associadas a um evento, atingem determi-nado valor. Estas estimativas são geralmente calculadas pelo Property Claim Services3

(PCS).

O segundo tipo de índice é calculado usando modelos (construídos por empresas com competências para tal, como por exemplo a Applied Insurance Research Worldwide, a EQECAT ou a Risk Management Solutions), nos quais são inseridos os parâmetros físicos do evento catastró…co ocorrido e que devolvem uma estimativa das perdas para a empresa de seguros. Se essas perdas atingirem um determinado valor, a obrigação é accionada.

Por último o parametric index, onde o payo¤ é determinado por medidas físicas do evento ocorrido introduzidas posteriormente num modelo, como por exemplo a veloci-dade e localização de um furacão ou a magnitude e localização de um tremor de terra. Neste caso o modelo não devolve as perdas estimadas para a empresa de seguros, mas uma medida relacionada com evento. A título de exemplo, considere-se que durante o período de um ano foi observada a velocidade dos furacões em determinada localização geográ…ca e assuma-se que o modelo devolvia a média das velocidades. Se esta média atingisse determinado valor, a obrigação era activada. Na prática os modelos utilizam fórmulas bastante mais complexas. Os parametric index triggers são os que têm menor risco moral porque se baseiam em medidas físicas do evento, mas podem ter um basis risk muito elevado.

Os index triggers são os preferidos dos investidores porque minimizam o risco moral, isto é, maximizam a transparência da transacção, não havendo hipótese de uma má política de gestão dos sinistros afectar o desempenho dos índices e consequentemente das securities. Outra grande vantagem deste tipo de transacções é que após a ocorrên-cia da catástrofe consegue-se rapidamente calcular o valor que a empresa de seguros vai receber, ao contrário dos indemnity triggers que implicam a avaliação de todas as perdas da empresa, processo que pode levar meses ou mesmo anos. Para as empresas de seguros, o facto de as transacções se basearem em índices também traz algumas van-tagens, pois não têm que disponibilizar informação relativa à sua carteira. A utilização dos index triggers tem também algumas desvantagens pois leva a que as empresas de seguros estejam expostas a um nível mais alto de basis risk, comparativamente aos indemnity triggers, já que as suas perdas podem não re‡ectir as perdas calculadas pelo índice.

Os modeled-loss index triggers são, à partida, os que apresentam menor basis risk mas, por outro lado, estão sujeitos ao risco de que o modelo esteja mal construído e não efectue uma correcta avaliação das perdas.

4. Hybrid triggers

No que respeita às obrigações com hybrid triggers, estas utilizam mais do que um trigger numa única transacção. A título de exemplo, pode ter-se uma CAT bond que cobre o risco de furacão nos E.U.A. e o risco de um terramoto no Japão, utilizando para o primeiro risco um industry loss index da PCS e, para o segundo, um índice paramétrico baseado na magnitude do terramoto.

3.2.2 Outros tipos de Insurance Linked Securities

O mercado de ILS traduz-se quase na totalidade por CAT bonds, geralmente associadas a riscos catastró…cos com probabilidades baixas de ocorrência. No entanto, nos últimos anos procedeu-se também à transferência de alguns riscos com características diferentes: severidades mais baixas e frequências de ocorrência mais elevadas.

No ramo Vida, existem também alguns tipos de CAT bonds, que funcionam de um modo semelhante às obrigações já referidas, e que estão associadas a eventos de mortalidade (ex-treme mortality bond ) ou de longevidade (longevity bond ). A estrutura da transacção é precisamente a mesma e estão também associadas a triggers.

Seguidamente descrevem-se sucintamente alguns dos ILS recentemente utilizados nos mercados.

CAT Futures e CAT Options Os primeiros ILS surgiram através da Chicago Board of Trade (CBoT), que em 1992 emitiu Catastrophe futures e Catastrophe options. Estes produ-tos baseavam-se em índices que re‡ectiam as perdas acumuladas causadas por determinada catástrofe. O índice era calculado pelo Insurance Service O¢ ce (ISO) e consistia num rácio entre as perdas da empresa e os prémios adquiridos (It = reported incurred losses=earned

premims). O índice baseava-se em dados de apenas 22 empresas de seguros e em riscos especí…cos (vento, granizo, sismos, motins e inundações).

Estes dois produtos foram no entanto retirados do mercado em 1995 devido ao reduzido número de transacção existentes ([19]).

As opções e os futuros considerados seguem a estrutura de outros produtos semelhantes transaccionados nos mercados …nanceiros.

Com o objectivo de atrair mais investidores, a CBoT emitiu então um novo produto, denominado CAT Options Spreads, que limitavam de certa maneira as perdas, através da

imposição de alguns limites. Tratavam-se de contratos muito semelhantes ao resseguro excess of loss, mas com nível de cobertura de…nido.

Em termos de estrutura, estes produtos revelaram-se demasiado simples, na medida em que os índices eram publicados trimestralmente e, como se baseavam nas perdas das empre-sas, dependiam da rapidez no reporte e resolução dos sinistros, o que podia provocar, por um lado, risco moral e, por outro, uma prestação pouco realista do índice.

Estes produtos não se revelaram muito atractivos quer para as empresas de seguros quer para os investidores, devido ao facto de ser um mercado muito recente e de pequena dimensão, o que trazia muita incerteza para ambos os intervenientes.

Em 1997, a Bermuda Commodities Exchange tentou também desenvolver o mercado das opções catastró…cas mas, tal como sucedeu no caso da CBoT, os contratos foram retirados ao …m de 2 anos devido ao reduzido número de transacções efectuadas ([11]).

Tornando-se claro o insucesso dos CAT futures e das CAT options, a CBoT substitui-os por outro tipo de produtos, as PCS options.

PCS Options As PCS options foram transaccionadas pela primeira vez na CBoT em Setembro de 1995. Estas opções baseavam-se em catastrophe loss indices calculados diari-amente pelo PCS. O índice re‡ectia as perdas catastró…cas da indústria seguradora num determinado período e existiam diversos índices que representavam diferentes catástrofes em áreas geográ…cas diversas.

Estes contratos diferiam das CAT options iniciais em 2 aspectos essenciais: primeiro, não se baseavam em dados do ISO para algumas empresas de seguros e relativas a certos riscos, mas em estimativas do PCS de todas as perdas catastró…cas na indústria seguradora, que são consideradas bastante …áveis ([12]); segundo, o seu valor não é calculado com base num rácio de perdas, mas num valor real em dinheiro. Cada ponto no índice do PCS representa 100 milhões de dólares em perdas catastró…cas e na opção o valor equivalente é de 200 dólares por cada ponto. Por exemplo, se as perdas estimadas forem de 1195 milhões de dólares, o índice seria de 12 pontos. A opção estava indexada ao índice e cada ponto do índice correspondia a 200 dólares em cash.

Ramo Automóvel4 _{([24]) A empresa de seguros AXA transferiu em 2005 parte do risco}

da sua carteira de seguro automóvel francesa (cerca de 15% do mercado), que cobria aproxi-madamente 3 milhões de veículos e 1.000.000 milhões de euros em prémios, para os mercados …nanceiros. A cobertura é accionada se a sinistralidade desta carteira exceder um trigger

de…nido à partida pela AXA e revisto pela Standard & Poor’s (S&P) e pela Fitch Ratings, em cada ano. Este excesso na sinistralidade é deduzido no principal das obrigações que foram adquiridas pelos investidores, até um valor máximo de 200 milhões de euros.

Em 2007 a AXA fez uma nova transferência de riscos da sua carteira automóvel para os mercados …nanceiros, desta vez cobrindo 6 milhões de veículos, 2.600.000 milhões de euros em prémios e a sinistralidade de 4 países (Bélgica 18%, Alemanha 30%, Itália 21% e Espanha 31%).

Credit Reinsurance ([24]) Em Janeiro de 2006 a Swiss Re realizou a primeira operação de securitização baseada no credit reinsurance. Esta operação, no valor de 252 milhões de euros, oferecia protecção à SwissRe contra perdas inesperadas na sua carteira de resseguro. A emissão consistiu em 3 tranches com um cupão de Euribor mais 3,93% por ano, pago trimestralmente e com maturidade de 3 anos. O trigger associado é um indemnity trigger calculado com base nas perdas da carteira de resseguro nos anos de 2006, 2007 e 2008. Extreme mortality bonds As mortality bonds são, como se disse, muito semelhantes às CAT bonds que cobrem eventos catastró…cos Não Vida, com a particularidade que o seu trigger é um evento de mortalidade que pode resultar de uma série de factores, tais como uma epidemia, ataques terroristas, acidentes nucleares, etc. O mortality trigger pode basear-se na experiência de mortalidade da empresa de basear-seguros ou resbasear-seguros, ou pode basear-ser calculado com base num índice de mortalidade.

A primeira emissão deste tipo de obrigações foi efectuada pela Swiss Re em Dezembro de 2003, com maturidade em 1 de Janeiro de 2007, 400 milhões de dólares de capital em risco e cobrindo riscos de mortalidade resultantes de catástrofes naturais ou catástrofes causadas pelo Homem, nos E.U.A. ou na Europa. O risco de mortalidade era de…nido através de um índice qt (t representa o ano) calculado com base numa média ponderada das taxas anuais

de mortalidade nos E.U.A., Reino Unido, França, Itália e Suíça. Se o índice qt (t = 2004,

t = 2005 ou t = 2006) excedesse 30% do valor da mortalidade do índice observado em 2002 (q0), os investidores teriam uma redução do pagamento no principal. Se excedesse em 50%,

todo o principal era perdido. A equação seguinte descreve o funcionamento desta obrigação, em percentagem de capital perdido:

P erdast = 8 < : 0 se qt 1; 3q0 1-1;5q0 qt 0;2q0 se 1; 3q0 < qt 1; 5q0 1 se qt> 1; 5q0 (30) Na maturidade da obrigação, em Janeiro de 2007, não tinham ocorrido eventos de mor-talidade para activar o trigger desta obrigação.

Esta operação de securitização da Swiss Re foi bem recebida pelos investidores porque se baseou directamente no risco de mortalidade e não no desempenho de determinada empresa. Além disso, é uma transacção muito simples e transparente para os investidores, o que leva a que estes estejam menos sujeitos ao risco moral. Por outro lado, pode-se considerar um investimento diversi…cado.

Como se referiu, a utilização de índices também tem as suas desvantagens, neste caso para a empresa de seguros, que está sujeita ao basis risk, pois a mortalidade da sua carteira pode diferir da observada através do índice. A Swiss Re realizou novas emissões deste tipo de obrigações nos anos seguintes ([9]).

Longevity bonds O risco de longevidade constitui também uma preocupação para as empresas de seguros, tendo em conta que a esperança média de vida é cada vez mais alta e que a população em geral tem cada vez mais preocupações com a reforma, adquirindo pensões. Para uma empresa de seguros, o incremento da longevidade vai aumentar o valor das responsabilidades a pagar relativos a anuidades.

Para se proteger, a empresa de seguros ou resseguros pode securitizar os riscos, utilizando uma estrutura semelhante à utilizada nas CAT bonds mas, neste caso, a empresa vai querer adquirir as obrigações, de modo a cobrir o seu risco de longevidade. Uma longevity bond é uma security cujos payo¤s dependem do valor do índice de sobrevivência em cada momento de pagamento. Este índice é dado pela proporção de pessoas ainda vivas, relativamente à população inicial.

A primeira emissão de longevity bonds foi levada a cabo pelo European Investment Bank (EIB) em cooperação com o Banco BNP Paribas e a empresa de resseguro PartnerRe, em Novembro de 2004, caracterizada por um capital em risco de 775 milhões de euros e maturi-dade de 25 anos. Os cash ‡ows da obrigação seriam calculados com base na longevimaturi-dade actual da população Inglesa masculina com 65 anos, publicada pelo O¢ ce for National Sta-tistics . Estas obrigações foram criadas para um público-alvo especí…co (fundos de pensões e empresas de seguros que emitem rendas vitalícias), mas não foram muito bem recebidas. Reclamava-se o preço e o basis risk elevados das mesmas, tendo sido retiradas do mercado em 2005 ([9]).

4

Avaliação de

Insurance Linked Bonds

4.1

Pressupostos e Especi…cação do Modelo

O modelo desenvolvido nesta secção pretende ser um instrumento de securitização de riscos de seguros semelhante ao descrito anteriormente (CAT bonds), mas associado apenas a riscos não catastró…cos.

Como já se disse, as CAT bonds e outros insurance-linked securities, não estão ligadas a um activo subjacente mas o seu payo¤ depende da veri…cação de determinado evento para o qual são estabelecidos limites (denominados triggers).

O evento associado ao insurance-linked security vai ser mensurado através de um índice (como numa Cat bond associada a um index trigger ). O facto de não considerarmos riscos catastró…cos, signi…ca que a nossa incerteza provém de um Processo de Wiener e não de um Processo de Poisson, ou seja o nosso índice vai seguir um Geometric Brownian Motion.

Consideremos uma obrigação associada a um índice:

dIt= Itdt + IItdWt (31)

onde é a variação esperada no índice, I é o desvio padrão e Wt é um standard brownian

motion.

Considere-se uma obrigação de cupão zero com maturidade T e face value F , associada ao índice anteriormente de…nido.

Seja K o trigger da obrigação e TI;K o …rst passage time de It por K, ou seja:

TI;K =finf (t 0; 0 < t < T ; It = K)g (32)

Considere-se o período de exposição ao risco T0, tal que T0 T. Os payo¤s da obrigação na maturidade T são:

Se o trigger não for activado, os detentores da obrigação recebem:

F 11fTI;K>T0g (33)

Se trigger for tocado durante o período de exposição os detentores da obrigação re-cebem:

(1 _{a) F 11fT}

I;K T0g (34)

onde a representa a percentagem do principal da obrigação que os investidores perdem por a obrigação ter sido activada.

4.2

Modelo com taxas de juro determinísticas

Nesta secção vai-se proceder à determinação de uma fórmula fechada para o preço da obri-gação utilizando taxas de juro constantes.

Tendo em consideração o pressuposto assumido no Capítulo 2, pode dizer-se que o preço da obrigação no momento 0 é o valor descontado dos cash-‡ows futuros na medida de prob-abilidade neutra face ao risco, Q:

P0 = EQ h e rT _{F 11fT} I;K>T0g+ (1 a) F 11fTI;K T0g i = e rTEQh_{F 11fT}

I;K>T0g+ F 11fTI;K T0g aF 11fTI;K T0g

i = e rTEQhF _{aF 11fT} I;K T0g i = e rTEQhF 1 _a11fT I;K T0g i = e rTF EQh1 _a11fT I;K T0g i = e rTF e rTF aEQh_11fT I;K T0g i = e rTF e rTF aQ [TI;K T0] = e rTF (1 aQ [TI;K T0]) (35)

Para obter uma fórmula fechada para a equação anterior é necessário calcular Q [TI;K T0],

com TI;K =finf (t 0; 0 < t < T ; It= K)g ; que é equivalente a calcular a função densidade

de probabilidade de TI;K na medida Q, sendo que TI;K é a …rst passage time, ou seja, a

primeira vez (deste o momento zero) que o processo It atinge a barreira K, sendo para tal

necessários alguns cálculos preliminares descritos seguidamente.

Como já se disse, o processo seguido pelo índice, na medida física P , é: dIt It = dt + IdWt (36) Tem-se que It e rt = EQ IT

e rT jFt é um Q-martingale e portanto _eItrt não tem drift na medida

Q:

Aplicando o Lema de Itô na equação (36), com f (t; x) = xe rt_{, vem:}

d It e rt = re rt_I tdt + e rtdIt = re rtItdt + e rt( Itdt + IItdWt) = e rtIt[( r) dt + IdWt] (37)

Considere-se um novo Brownian Motion WtQ tal que

dW_tQ = dWt+ tdt (38)

Combinando as equações (37) e (38), vem: d It e rt It ert = ( r) dt + I h dW_tQ tdt i = ( r I t) dt + IdWtQ (39)

Para que W_tQ _{seja Brownian Motion na medida de martingala Q, o drift da equação anterior} tem que ser nulo, isto é:

r I t= 0, t=

r

I

(40) Pelo Teorema de Girsanov, vem que W_tQ = Wt+ t é um Q-Brownian motion.

Combinando as equações (37), (38), e (40), vem: dIt It = dt + I h dW_tQ tdt i = dt + IdW Q t r I Idt = rdt + IdWtQ (41)

A solução da equação anterior, aplicando o Lema de Itô com f (x) = ln It

I0 , vem: d ln It I0 = 0 dt + @ ln It I0 @It dIt+ 1 2 @2_ln It I0 @I2 t d_{hI; Iit} = dIt It +1 2 1 I2 t 2 II 2 tdt = rdt + IdWtQ 2 I 2 dt = r 2 I 2 dt + IdW Q t (42) ou seja, d ln It I0 = r 2 I 2 dt + IdW Q t

Estão criadas as condições para o cálculo de Q [TI;K T0], como se apresenta seguida-mente: Q [TI;K T0] = 1 Q [TI;K > T0] = 1 Q IT0 < K^ sup 0<u<T0 (Iu) < K jF0 = 1 Q ln IT0 I0 < ln K I0 ^ sup0<u<T0 ln Iu I0 < ln K I0 jF 0

Utilizando agora a proposição 5, vem: = 1 8 < : 0 @ln K I0 r 2 I 2 T0 I p T0 1 A exp 0 @2 r 2 I 2 ln K I0 2 I 1 A 0 @ln K I0 2 ln K I0 r 2 I 2 T0 I p T0 1 A 9 = ; = 0 @ ln K I0 + r 2 I 2 T0 I p T0 1 A + exp 0 @2r ln K I0 2 I 2 2 Iln KI0 2 2 I 1 A 0 @ ln K I0 r 2 I 2 T0 I p T0 1 A = 0 @ln I0 K + r 2 I 2 T0 I p T0 1 A + exp 2r₂ I ln K I0 I0 K 0 @ ln I0 K r 2 I 2 T0 I p T0 1 A = (d1) + exp ln K I0 2r 2 I ! I0 K (d2) = (d1) + K I0 2r 2 I 1 (d2) (43)

com: d1 = ln I0 K + r 2 I 2 T0 I p T0 (44) d2 = ln I0 K r 2 I 2 T0 I p T0 (45)

Portanto, o preço da insurance linked bond vem dado por: P0 = e rTF 1 a ( (d1) + K I0 2r 2 I 1 (d2) )! (46)

4.3

Modelo com Taxas de Juro Estocásticas

Nesta secção vai-se proceder a determinação de uma fórmula fechada para o preço da obri-gação utilizando taxas de juro estocásticas.

O índice, de…nido anteriormente, na medida Q vem dado por:

dIt = rtItdt + IItdWtQ (47)

sendo:

drt= ( rt) dt + rdWtQ (48)

de acordo com o Modelo de Vasicek5. Tem-se também que:

dDW_IQ; W_rQE

t= dt (49)

Seja QT

a forward martingale measure equivalente a Q e associada ao numerário P (0; T ). Seguindo o mesmo raciocínio que na secção anterior, vem:

P0 = P (0; T ) F 1 aQT[TI;K T0] = P (0; T ) F 1 aQT[TI;K T0] = P (0; T ) F 1 a T0 R 0 QT ( TI;K 2 dvj F0) ! (50) 5_{Ver Anexo A.}

onde QT ( TI;K 2 dvj F0)é a …rst passage time density que se pretende calcular à semelhança

da secção precedente.

Considere-se a seguinte proposição, adaptada da Proposição 1 de [20] que apresenta uma equação integral de Volterra de segundo grau para a …rst passage time density.

Proposição 7 Considerando o modelo de…nido pelas equações (47), (48) e (49), a …rst passage time density do índice pelo trigger K é a solução implícita de

QT (Iu Kj Ft0) = u R t0 R < QT[Iu Kj Iv = K; rv] QT [rv 2 drj Iv = K; rt0] Q T _(T I;K 2 dvj Ft0) (51) com u 2 [t0; T ]. Demonstração. Ver em [20] Para se obter QT_(T

I;K 2 dvj Ft0) é necessário calcular os outros termos da equação

an-terior, o que é efectuada nas secções seguintes.

4.3.1 Cálculo da distribuição condicional da taxa de juro Pretende-se calcular QT _[r

v 2 drj Iv = K; rt0].

Fazendo a mudança de variáveis, xv = ln (Iv), vem:

QT [rv 2 drj Iv = K; rt0] = Q

T

[rv 2 drj xv = ln (K) ; rt0] (52)

Aplicando o Lema de Itô com f (t; x) = e t_{x à equação (48), vem:}

e uru = e t0rt0 + u R t0 rle ldl + u R t0 e ldrl+ 1 2 u R t0 0d_{hr; rit} = e t0_r t0 + u R t0 rle ldl + u R t0 e lh( rl) dl + rdW Q l i = e t0_r t0 + u R t0 rle ldl + u R t0 e ldl u R t0 rle ldl + u R t0 e l rdW_lQ = e t0_r t0 + u R t0 e ldl + u R t0 e l rdWlQ (53)

Isolando o termo ru do lado esquerdo da equação, vem: ru = e (u t0)rt0 + u R t0 e (u l)dl + u R t0 e (u l) rdWlQ = e (u t0)_r t0 + 1 e (u t0) ₊ u R t0 e (u l) rdW Q l = e (u t0)_r t0 + B (t0; u) + r u R t0 e (u l)dW_lQ (54) sendo B (t0; u) = 1 e (u t0) (55) A última parcela é um Integral de Itô poratnto segue uma distribuição Normal, ou seja:

r u R t0 e (u l)dW_lQ N1 0; r u R t0 e 2 (u l)dl ! r u R t0 e (u l)dW_lQ N1 0; r 2 1 e 2 (u t0) ₍₅₆₎

Logo conclui-se que: rujFt0 Q N1 e (u t0)_r t0 + B (t0; u) ; r 2 1 e 2 (u t0) ₍₅₇₎

Aplicando agora o Lema de Itô à equação (47) com f (x) = ln (x) e utilizando a mesma mudança de variável, …ca:

xu = ln (Iu) = xt0 + u R t0 0dl + u R t0 1 Il dIl+ 1 2 u R t0 1 I2 l d_{hI; Iil} = xt0 + u R t0 1 Il h rlIldl + IIldWlQ i ₁ 2 u R t0 1 I2 l 2 IIl2dl = xt0 + u R t0 rl 2 I 2 dl + u R t0 IdWlQ (58) Temos que dDW_IQ; WQ r E t = dt (49).

Estes Brownian Motions podem ser decompostos em 1 vector com duas dimensões ZQ_{(t) =}h_ZQ

I (t) ; ZrQ(t)

i

de Brownian Motions independentes, tais que: dW_IQ(t) dWQ_(t) = 1 0 p 1 2 dZ Q_{(t) (59)}

Assumindo que existe a medida QT e seguindo [21], mostra-se que: dZQT(t) = dZQ(t) + rB (t; T )

p

1 2 0_{dt (60)}

é também um Standard Brownian Motion em R2_{, para t T.}

Temos então que dDW_IQ; WQ r E t = dt e também que dDZ_IQ; ZQ r E t= 0. Tem-se: ru = e (u t0)rt0 + B (t0; u) + r u R t0 e (u l)dW_lQ (61) dW_rQ(t) = p1 2 _dZQ r (t) (62) dZQ(t) = dZQT(t) rB (t; T ) p 1 2 0_{dt (63)} Logo vem: ru = e (u t0)rt0 + B (t0; u) + r u R t0 e (u l) p1 2 _dZQ_(l) = e (u t0)_r t0 + B (t0; u) + r u R t0 e (u l) p1 2 n_dZQT _(l) rB (l; u) p 1 2 0_dlo = e (u t0)_r t0 + B (t0; u) + r u R t0 e (u l) p1 2 _dZQT _(l) 2 r u R t0 B (l; u) 2+ 1 2 e (u l)dl = e (u t0)_r t0 + u R t0 e (u l)dl + r u R t0 e (u l) p1 2 _dZQT _(l) 2 r u R t0 B (l; u) e (u l)dl = e (u t0)_r t0 + u R t0 e (u l) 2_rB (l; u) dl + r u R t0 e (u l) p1 2 _dZQT _{(l) (64)} Seja r(t0; u) = u R t e (u l) 2_rB (l; u) dl (65)

e r(rt; t0; u) = e (u t0)rt0 + r(t0; u) (66) Então vem: ru = r(rt; t0; u) + r u R t0 e (u l) p1 2 _dZQT _{(l) (67)}

A última parcela, utilizando o Corolário 4.5.6 de [3], segue uma distribuição Normal, ou seja:

u R t0 e (u l) p1 2 _dZQT_{(l) N}1 _0; u R t0 2 re 2 (u l) p 1 2 p₁ 2 0_dl ! u R t0 e (u l) p1 2 _dZQT_{(l) N}1 _0; u R t0 2 re 2 (u l)_dl ! u R t0 e (u l) p1 2 _dZQT_{(l) N}1 _0; 2 r(t0; u) (68) com: 2 r(t0; u) = 2 r 2 1 e 2 (u t0) ₍₆₉₎

Logo, conclui-se que:

QT [rv 2 drj Ft0] = r; r(rt; t0; u) ; 2 r(t0; u) dr (70) Temos: xu = xt0 + u R t0 rl 2 I 2 dl + u R t0 IdW_IQ(l) = xt0 + u R t0 rldl u R t0 2 I 2 dl + u R t0 IdW_IQ(l) = xt0 u R t0 2 I 2 dl + u R t0 " e (l t0)_r t0 + B (t0; l) + r l R t0 e (l v)dW_rQ(v) # dl + u R t0 IdW_IQ(l) = xt0 2 I 2 (u t0) + u R t0 e (l t0)_r t0dl + u R t0 B (t0; l) dl + r u R t0 ( l R t0 e (l v)dW_rQ(v) ) dl + u R t0 IdWIQ(l) (71) e também: dW_rQ(t) = p1 2 _dZQ r (t) (72)

e dW_IQ(t) = dZ_IQ(t) (73) e dZQ(t) = dZQT(t) rB (t; T ) p 1 2 0_{dt (74)} Logo, vem: xu = xt0 2 I 2 (u t0) + u R t0 e (l t0)_r t0dl + u R t0 B (t0; l) dl + r u R t0 ( l R t0 e (l v) p1 2 _dZQ_(v) ) dl + u R t0 I 1 0 dZQ(l) = xt0 2 I 2 (u t0) + rt0B (t0; u) + (u t0) B (t0; u) + r u R t0 ( l R t0 e (l v) p1 2 h_dZQT_(v) rB (v; u) p 1 2 0_dvi ) dl + u R t0 I 1 0 n dZQT(l) rB (l; u) p 1 2 0_dlo = xt0 + (u t0) 2 I 2 + B (t0; u) rt0 + r u R t0 ( l R t0 e (l v) p1 2 _dZQT _(v) l R t0 e (l v) rB (v; u) dv ) dl + u R t0 I 1 0 dZQ T (l) I r u R t0 B (l; u) dl = xt0 + (u t0) 2 I 2 + B (t0; u) rt0 + r u R t0 ( l R t0 e (l v) p1 2 _dZQT _(v) ) dl 2_r u R t0 l R t0 e (l v)B (v; u) dvdl + u R t0 I 1 0 dZQ T (l) I r u R t0 B (l; u) dl = xt0 2 I 2 (u t0) + B (t0; u) rt0 + u R t0 B (t0; l) dl 2r u R t0 l R t0 e (l v)B (v; u) dvdl I r u R t0 B (l; u) dl + r u R t0 ( l R t0 e (l v) p1 2 _dZQT_(v) ) dl + I u R t 1 0 dZQT(l)

= xt0 2 I 2 (u t0) + B (t0; u) rt0 I r u R t0 B (l; u) dl + u R t0 " B (t0; l) 2r l R t0 e (l v)B (v; u) dv # dl + r u R t0 ( l R t0 e (l v) p1 2 _dZQT _(v) ) dl + I u R t0 1 0 dZQT (l) = xt0 2 I 2 (u t0) + B (t0; u) rt0 I r u R t0 B (l; u) dl + u R t0 " l R t0 e (l v) dv l R t0 e (l v) 2_rB (v; u) dv # dl + r u R t0 ( l R t0 e (l v) p1 2 _dZQT _(v) ) dl + I u R t0 1 0 dZQT (l) = xt0 2 I 2 (u t0) + B (t0; u) rt0 I r u R t0 B (l; u) dl + u R t0 ( l R t0 e (l v) 2_rB (v; u) dv ) dl + r u R t0 ( l R t0 e (l v) p1 2 _dZQT _(v) ) dl + I u R t0 1 0 dZQT (l) = xt0 2 I 2 (u t0) + B (t0; u) rt0 I r u R t0 B (l; u) dl + u R t0 r(t0; u) dl + r u R t0 ( l R t0 e (l v) p1 2 _dZQT _(v) ) dl + I u R t0 1 0 dZQT (l) Seja: x(t0; u) = 2 I 2 (u t0) I r u R t0 B (l; u) dl + u R t0 r(t0; u) dl (75) e x(xt; rt; t; u) = xt+ B (t; u) rt+ x(t; u) (76)

Então vem que:

xu = x(xt; rt; t; u)+ r u R t ( l R t e (l v) p1 2 _dZQT _(v) ) dl+ I u R t 1 0 dZQT (l) (77)

Aplicando o Teorema de Fubini na segunda parcela da equação anterior, vem: xu = x(xt; rt; t; u) + u R t0 u R v re (l v) p 1 2 _{dl dZ}QT_{(v) +} I u R t0 1 0 dZQT (l) = _x(xt; rt; t; u) + u R t0 2 6 6 4 u R v r e (l v)dl + I u R v re (l v) p 1 2_dl 3 7 7 5 0 dZQT (l) = _x(xt; rt; t; u) + u R t0 I+ r B (v; u) r p 1 2_{B (v; u)} 0 dZQT (l) (78)

A última parcela, utilizando o Corolário 4.5.6 de [3], segue uma distribuição Normal, ou seja:

u R t0 I+ r B (v; u) r p 1 2_{B (v; u)} 0 dZQT(l) N1 0; u R t0 I+ r B (v; u) r p 1 2_{B (v; u)} I+ r B (v; u) r p 1 2_{B (v; u)} 0 dv ! u R t0 I+ r B (v; u) r p 1 2_{B (v; u)} 0 dZQT(l) N1 0; u R t0 2 I+ 2 I rB (v; u) + 2rB 2_{(v; u) dv} ! (79) Seja: 2 x(t0; u) = u R t0 2 I+ 2 I rB (v; u) + 2rB 2_{(v; u) dv (80)}

Então vem que:

QT [xu 2 dxj Ft0] = x; x(xt0; rt0; t0; u) ;

2

x(t0; u) dx (81)

Vamos provar que (xu; ru)segue uma distribuição Normal Bivariada.

Temos que: axu + bru = a x(xt; rt; t; u) + a u R t0 I+ r B (v; u) r p 1 2_{B (v; u)} 0 dZQT (l) +b _r(rt; t0; u) + b r u R t0 e (u l) p1 2 _dZQT _(l) = a _x(xt; rt; t; u) + b r(rt; t0; u) + u R t0 a ( I+ r B (v; u)) + b re (u l) a r p 1 2_{B (v; u) + b}p₁ 2 re (u l) 0 dZQT(l) (82) A última parcela, utilizando o Corolário 4.5.6 de [3], segue uma distribuição Normal, ou seja:

y; a _x(xt0; rt0; t0; u) + b r(rt; t0; u) ; a2 2x(t0; u) + b2 2r(t0; u) + 2ab x;r(t0; u) dy (83) com: x;r(t0; u) = I r+ 2 r B (t0; u) 2 r(t0; u) (84) rjx(xt0; rt0; t0; u) = a x(xt0; rt0; t0; u) + b r(rt; t0; u) (85) 2 rjx(t0; u) = a2 2x(t0; u) + b2 2r(t0; u) + 2ab x;r(t0; u) (86) Logo (xu; ru) N2(Ver [20]).

Portanto, seguindo novamente [20] e utilizando por exemplo equação 35.4 de [17] podemos concluir que xujru segue uma distribuição Normal, ou seja:

QT [rv 2 drj xv = ln (K) ; rt0] = r; _rjx(xt0; rt0; t0; u) ;

2

rjx(t0; u) dr (87)

4.3.2 Cálculo da distribuição incondicional do índice. Pretende-se calcular QT _[I u Kj Ft0]. Temos: QT[Iu Kj Ft0] = Q T _[x u ln (K)j Ft0] (88)

Através de (81) podemos concluir que: QT [Iu Kj Ft0] = Q T _[x u ln (K)j Ft0] = ln (K) x(xt0; rt0; t0; u) 2 x(t0; u) (89) 4.3.3 Cálculo da distribuição condicional do índice.

Pretende-se calcular QT _[I

u Kj Iv = K; rv].

Temos que

Usando (81) com t0 = v, vem: QT [Iu Kj Iv = K; rv] = QT [xu ln (K)j xv = ln (K) ; rv] = ln (K) x(xv; rv; v; u) 2 x(v; u) (91)

4.4

Conclusão

O grande objectivo deste trabalho era obter a solução implícita da Proposição 7, ou seja de: QT [Iu Kj Ft0] = u R t0 R < QT [Iu Kj Iv = K; rv] QT [rv 2 drj Iv = K; rt0] Q T _(T I;K 2 dvj Ft0) Temos: QT [Iu Kj Ft0] = ln (K) _x(xt0; rt0; t0; u) 2 x(t0; u) (92) QT [Iu Kj Iv = K; rv] = ln (K) _x(xv; rv; v; u) 2 x(v; u) (93) QT[rv 2 drj Iv = K; rt0] = r; _rjx(xt0; rt0; t0; u) ; 2 rjx(t0; u) dr (94)

Trocando (93) com (94), vem:

QT [Iu Kj Ft0] = = u R t0 R < QT[Iu Kj Iv = K; rv] QT [rv 2 drj Iv = K; rt0] Q T _(T I;K 2 dvj Ft0) (95) = u R t0 R < QT[rv 2 drj Iv = K; rt0] Q T _[I u Kj Iv = K; rv] QT (TI;K 2 dvj Ft0) (96) = u R t0 R < r; _rjx(xt0; rt0; t0; u) ; 2 rjx(t0; u) dr ln (K) _x(xv; rv; v; u) 2 x(v; u) QT (TI;K 2 dvj Ft0) (97)

Utilizando o Lema B1 (Lema 6 na presente tese) de [20], vem: QT [Iu Kj Ft0] = u R t0 0 @ x(v; u) + B (v; u) rjx(xt0; rt0; t0; u) q 2 x(v; u) + B2(v; u) 2_rjx(t0; v) 1 A QT _(T I;K 2 dvj Ft0) (98)

Logo, QT (TI;K 2 dvj Ft0)é a solução implícita de: ln (K) _x(xt0; rt0; t0; u) 2 x(t0; u) = u R t0 0 @ x(v; u) + B (v; u) rjx(xt0; rt0; t0; u) q 2 x(v; u) + B2(v; u) 2_rjx(t0; v) 1 A QT _(T I;K 2 dvj Ft0) (99)

5

Conclusão

Nesta tese apresenta-se uma fórmula fechada para a avaliação de Insurance Linked Bonds, utilizando um modelo com taxas de juros determinísticas e outro com taxas de juro estocás-ticas. Em qualquer dos casos, a presente análise assentou essencialmente na determinação da …rst passage time.

No caso determinístico, procedeu-se ao seu cálculo através da técnica de mudança de medida de probabilidade, bem como do Lema de Itô. Este processo mostrou-se bastante acessível devido à sua semelhança com temas abordados na literatura, tais como opções de barreira.

No que se refere, ao caso estocástico foi necessário recorrer a uma equação integral de Volterra de segundo grau e mostrou-se um processo moroso. Para o cálculo da …rst passage time teve que se obter, primeiramente, a distribuição condicional da taxa de juro, a dis-tribuição condicional do índice e a disdis-tribuição incondicional do índice. Estas distribuições foram posteriormente utilizadas para se obter implicitamente a …rst passage time density.

A aplicação prática do modelo apresentado mostrou-se de difícil execução devido ao facto de no mercado existirem poucos produtos deste género e quando existem são emissões privadas, para os quais não existem cotações/preços/informação de divulgação ao público em geral.

Em termos de investigações futuras, seria importante incorporar no índice a componente associada às perdas inerentes a catástrofes naturais, o que signi…cava incluir outra fonte de risco no índice, um processo de Poisson.

A

Apêndice - Modelo de Vasicek

O modelo de Vasicek é um modelo single factor (ou modelo de short rate), isto é, a variável de estado é a taxa de juro spot instantânea.

Vasicek assumiu que a taxa de juro instantânea (rt) segue um processo de

Ornstein-Uhlenbeck:

drt= ( rt) dt + dWtP (A-1)

onde é a média de longo prazo da taxa de juro instantânea, é a velocidade de reversão para a média e é a volatilidade instantânea de rt.

A solução de (A-1) é dada por:

rt= e (t t0)rt0 + 1 e (t t0) ₊ t Z t0 e (t s)dW_sP (A-2) e portanto, rtj Ft0 P N1 e (t t0)_r t0 + 1 e (t t0) _; 2 r(t0; t) (A-3) com 2 r(t0; t) = 2 2 1 e 2 (t t0) _(A-4)

Usando (A-1) e aplicando o Lema de Itô a yt= exp ( t) rt, então vem:

dyt = e trtdt + e t ( rt) dt + dWtP (A-5)

= e tdt + e tdW_tP

Integrando ambos os lados da equação anterior entre t0 e t, vem:

yt = yt0 + Z t t0 e sds + Z t t0 e sdW_sP (A-6) = yt0 + e t e t0 ₊ Z t t0 e sdW_sP combinando as equações, vem:

e trt = e t0rt0 + e t _e t0 ₊ Z t t0 e sdW_sP = e (t t0)_r t0 + 1 e (t t0) ₊ t Z t e (t s)dW_sP (A-7)

Como um Integral de Itô, com um integral determinístico segue uma distribuição Normal com média zero e variância igual à sua variação quadrática, então:

t Z t0 e (t s)dW_sP _Ft0 P N1 0 @0; t Z t0 e 2 (t s)ds 1 A (A-8)

Neste modelo assume-se que o market price of risk é constante, isto é:

dW_tQ = dt + dW_tP (A-9) Logo, na medida neutra face ao risco (Q), vem:

drt = ( rt) dt + dW Q

t (A-10)

com:

=

Note-se que, um modelo single-factor diz-se a¢ ne term structure (ATS) model se uma obrigação de cupão zero pode ser escrita do seguinte modo:

P (t; T ) = exp [A (t; T ) B (t; T ) rt] (A-11)

onde A (t; T ) e B (t; T ) são funções determinísticas. O modelo de Vasicek é ATS (ver [4]), ou seja:

P (t; T ) = exp [A ( ) B ( ) rt] (A-12) onde B ( ) = 1 e (A-13) e A ( ) = [B ( ) ] 2 r 2 2 2 r 4 (A-14) com = T t (A-15)

Referências

[1] Aase, K. (2001): A Markov Model for the Pricing of Catastrophe Insurance Futures and Spreads. Journal of Risk and Insurance. Vol. 68, pp. 25-50.

[2] AON (2008): Insurance-Linked Securities 2008: Innovation and Investor Demand Set the Stage for Continued Growth.

[3] Arnold, L. (1992): Stochastic di¤erential equations: theory and applications. Krieger Publishing Company, Malabar.

[4] Bjork, T. (1998): Arbitrage Theory in Continuous Time. Oxford University Press. [5] Bryis, E., M. Bellalah, H. Minh Mai and F. de Varenne (1998): Options, Futures and

Exotic Derivatives - Theory, Application and Practice. Willey Frontiers in Finance [6] Canabarro, E., M. Finkemeier, R. Andreson and F. Bendimerad (1998): Analyzing

Insurance-Linked Securities. Quantitative Fixed Income Research

[7] Cummins, J. D. and H. Geman (1995): Pricing Catastrophe Insurance Futures and Call Spreads: An Arbitrage Approach. Journal of Fixed Income, Vol. 1, pp. 46-57.

[8] Guy Carpenter (2008): The Catastrophe Bond Market at Year-end 2007: The Market Goes Mainstream.

[9] Cox, S. and Y. Lin (2008): Securitization of catastrophe mortality risks. Insurance: Mathematics and Economics, Vol. 42, pp. 628-637.

[10] Cox, S. H., and H. Pedersen (2000): Catastrophe Risk Bonds. North American Actuarial Journal. Vol.4, pp. 56-82.

[11] Cummnins, J. D. (2008): Cat Bonds and other risk-linked securities: state of the market and developments. Risk Management and Insurance Review, Vol. 11, 1, pp. 23-47 [12] D’Arcy, S., V. G. France and R. Gorvett (1999): Pricing catastrophe risk: could cat

futures have coped with Andrew?. Casualty Actuarial Society

[13] Froot, K. (2001): The market for catastrophe risk: a clinical examination. Journal of Financial Economics, Vol. 60, pp. 529-571

[14] Geman, H. and M. Yor (1997): Stochastic Time Changes in Catastrophe Option Pricing. Insurance: Mathematics and Economics. Vol. 21, pp. 185— 193.

[15] Gorvett, R.. (1999): Insurance Securitization: the development of a new asset class. Casualty Actuarial Society.

[16] Harrison, J. M. (1985): Brownian Motions and Sctochastic Flow Systems. Wiley, New York

[17] Johnson ,N., S. Kotz and N. Balakrishnan (1972): Distributions in Statistics: Continu-ous Multivariate Distributions. Wiley, New York.

[18] Lee, J. P., and M. T. Yu (2002): Pricing Default-Risky CAT Bonds with Moral Hazard and Basis Risk. Journal of Risk and Insurance. Vol. 69, pp. 25-44.

[19] Murmann, Alexander (2001): Pricing catastrophe insurance derivatives. Financial Mar-kets Group-London School of Economics.

[20] Nunes, J. (2007): Analytical valuation of american options under stochastic interest rates. CEMAF/ISCTE

[21] Nunes, J. (2004): Multi-factor valuation of ‡oating range notes. Mathematical Finance, Vol. 14, pp. 79-97.

[22] Pérez-Fructuoso, M.: Modelling Index Triggers for Cat Bonds: A Continuous Approach. Casualty Actuarial Society, Volume 2, Issue 2

[23] Swiss Re (1999): Introdução ao Resseguro 1999.

[24] Swiss Re (2006): Securitization: New Opportunities for Insurers and Investors. Sigma No. 7/2006

[25] Vasicek, O. (1977): An equilibrium characterization of the term structure. Journal of Financial Economics, Vol. 5, pp. 177-188.

[26] Vaurigard, V.. (2004): A canonical …rst passage time model to pricing nature-linked bonds. Economics Bulletin, Vol. 7, No. 2 pp. 1-7

[27] Zeller, W. (2008): Securitization and Insurance - Characteristics of Hannover Re’s Ap-proach. The Geneva Papers, Vol. 22, pp. 7-11.